Modeling Natural Forest Fire Regimes Based on Drought Characteristics at Various Spatial and Temporal Scales in P. R. China
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Source and Pre-Processing
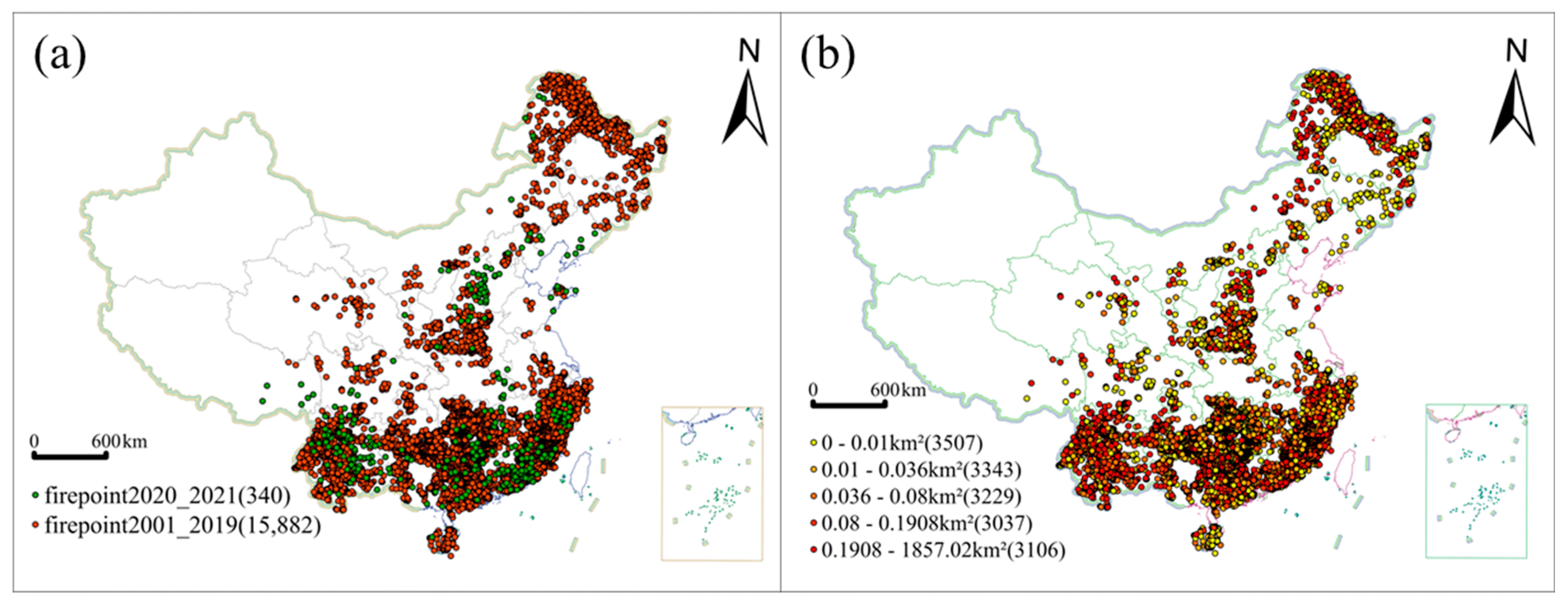
2.2.1. Forest Fire Regimes
2.2.2. Natural and Anthropogenic Factors
2.2.3. The Standard Precipitation Evapotranspiration Index (SPEI)
- The probability distribution of is set as follows:
2.2.4. Drought Characterization
2.2.5. Data Standardization
2.3. Data Analysis Methods
2.3.1. Diagnosis of Multicollinearity Among Explanatory Variables
2.3.2. Selection of Drought Characteristics Used for Model Building
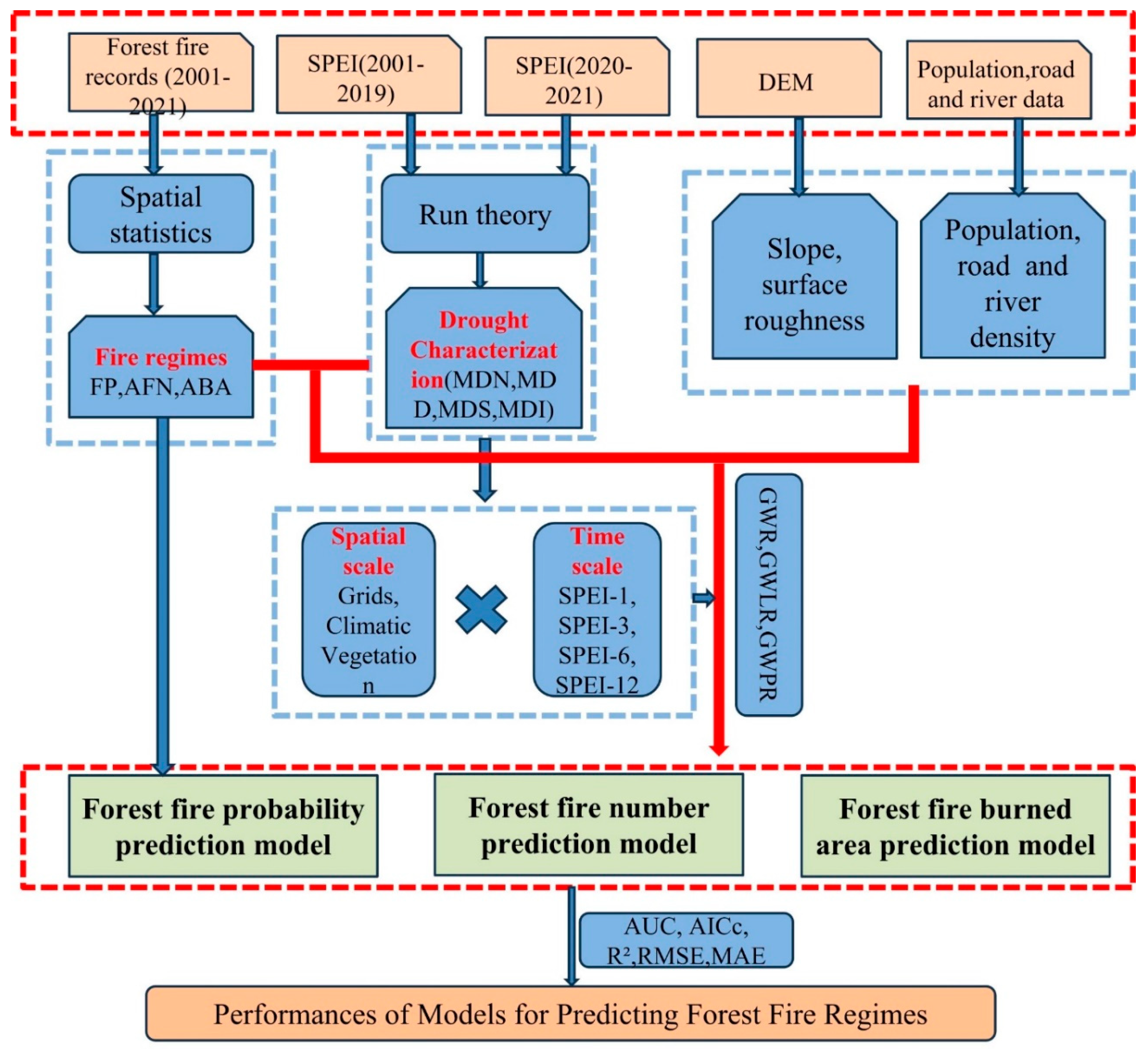
2.3.3. The Study Flowchart
2.3.4. Construction of Models for Forest Fire Regimes Based on Drought Characteristics
2.3.5. Model Prediction Accuracy Assessment
3. Results
3.1. Multicollinearity Among Explanatory Variables
3.2. Correlation Analysis Results
3.3. Goodness of Fit for Forest Fire Prediction Models
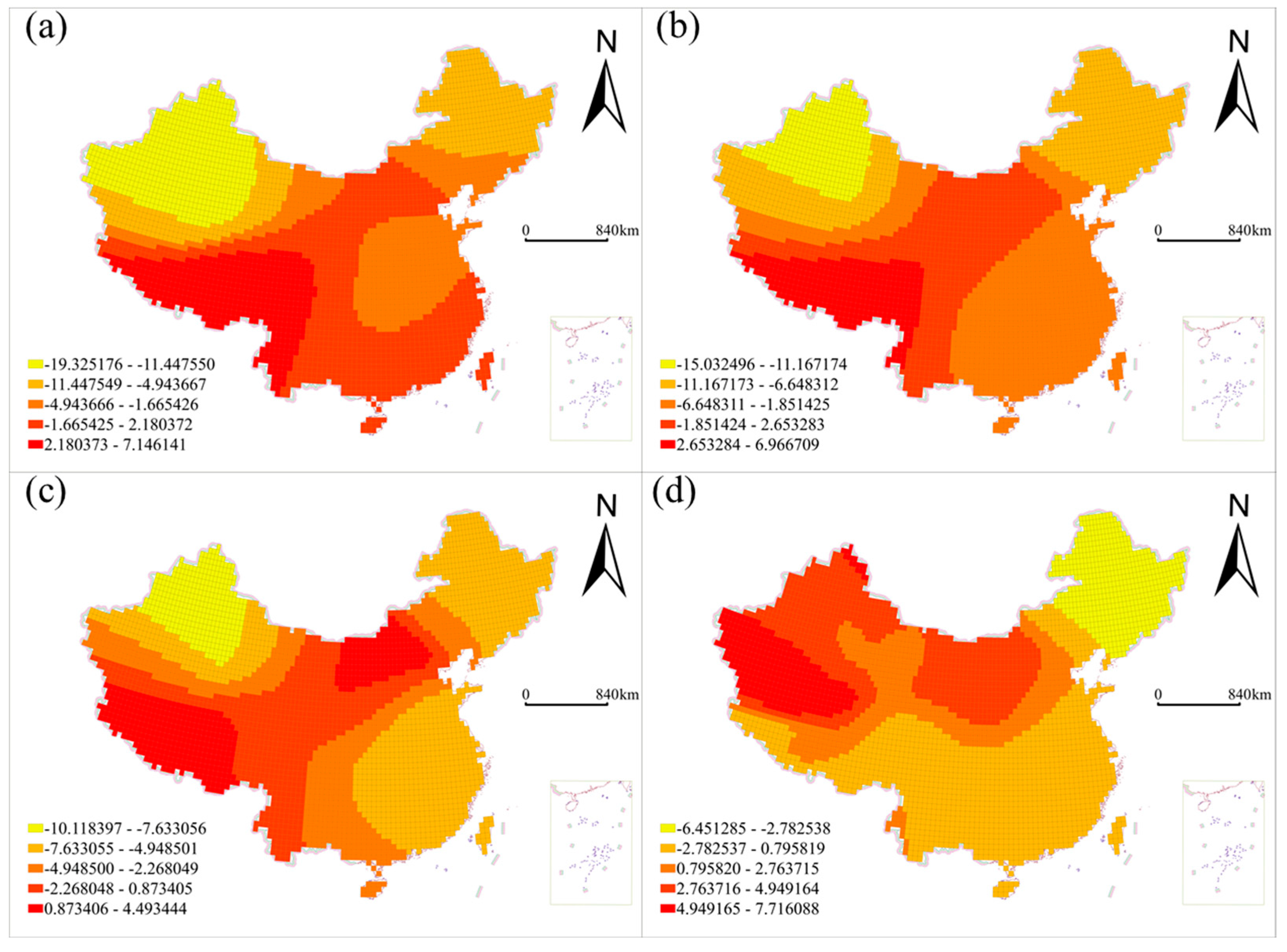
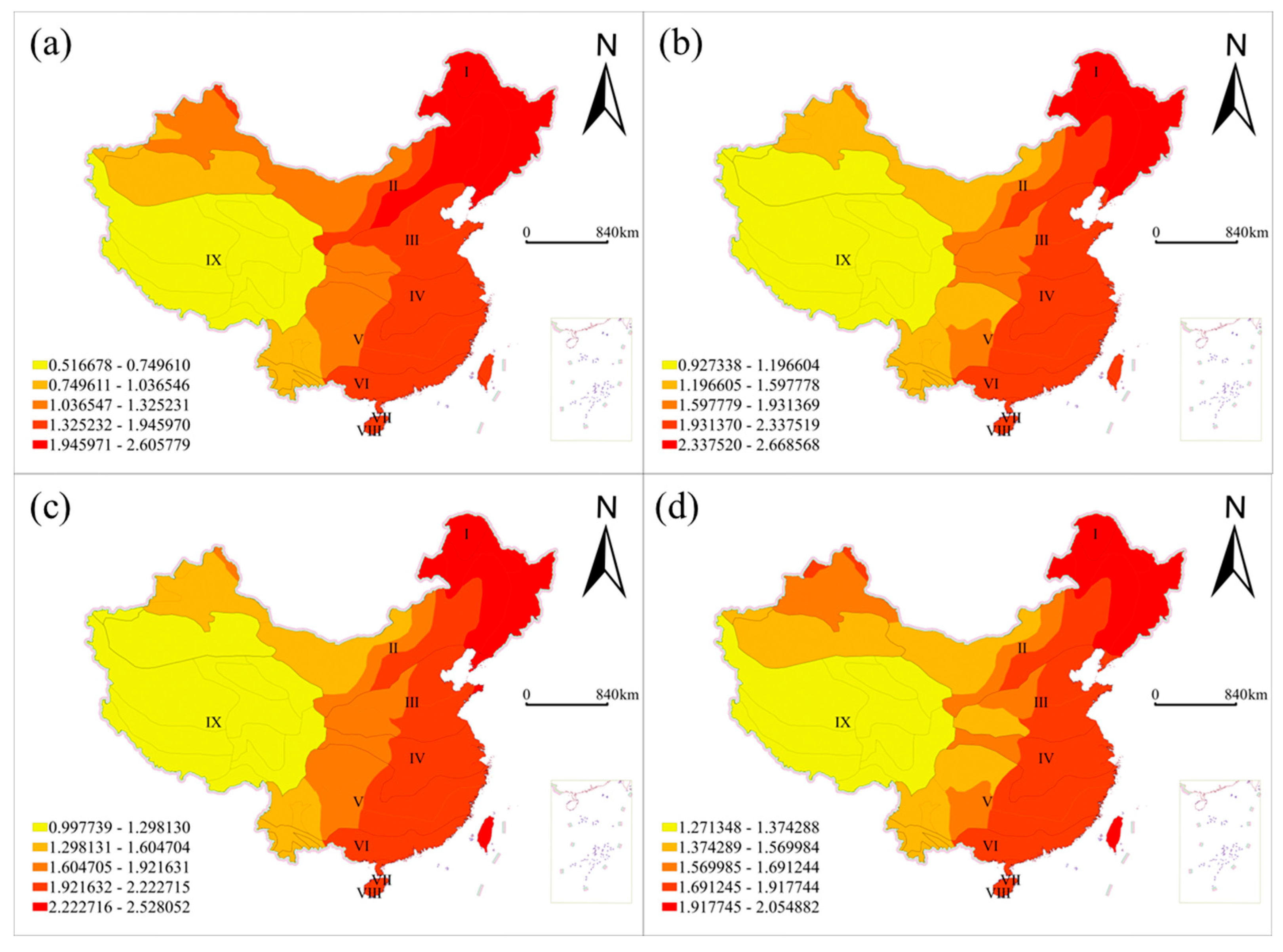
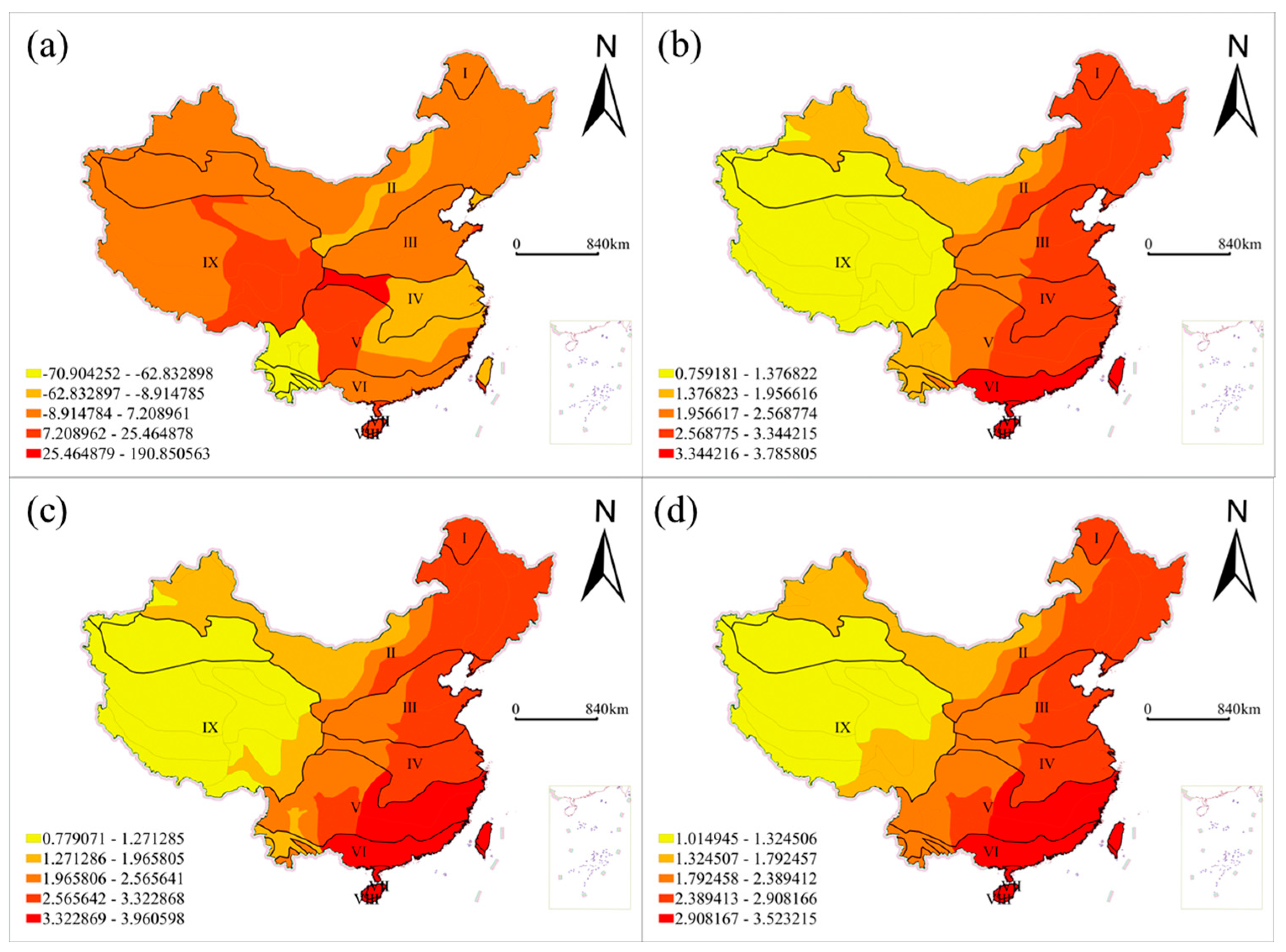
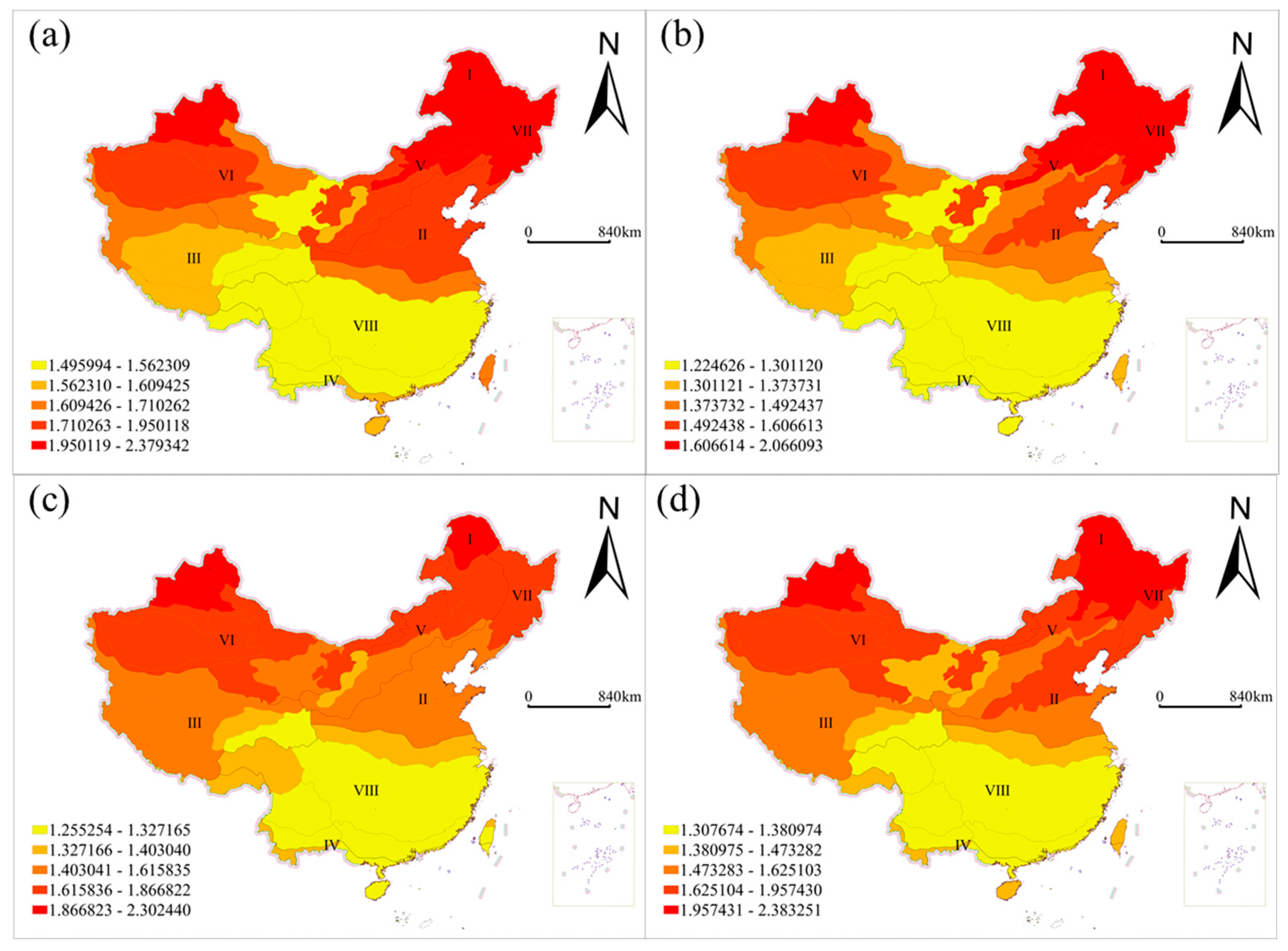
3.4. Spatial Non-Stationarity of the Effects of Drought Characteristics on Forest Fire Regimes
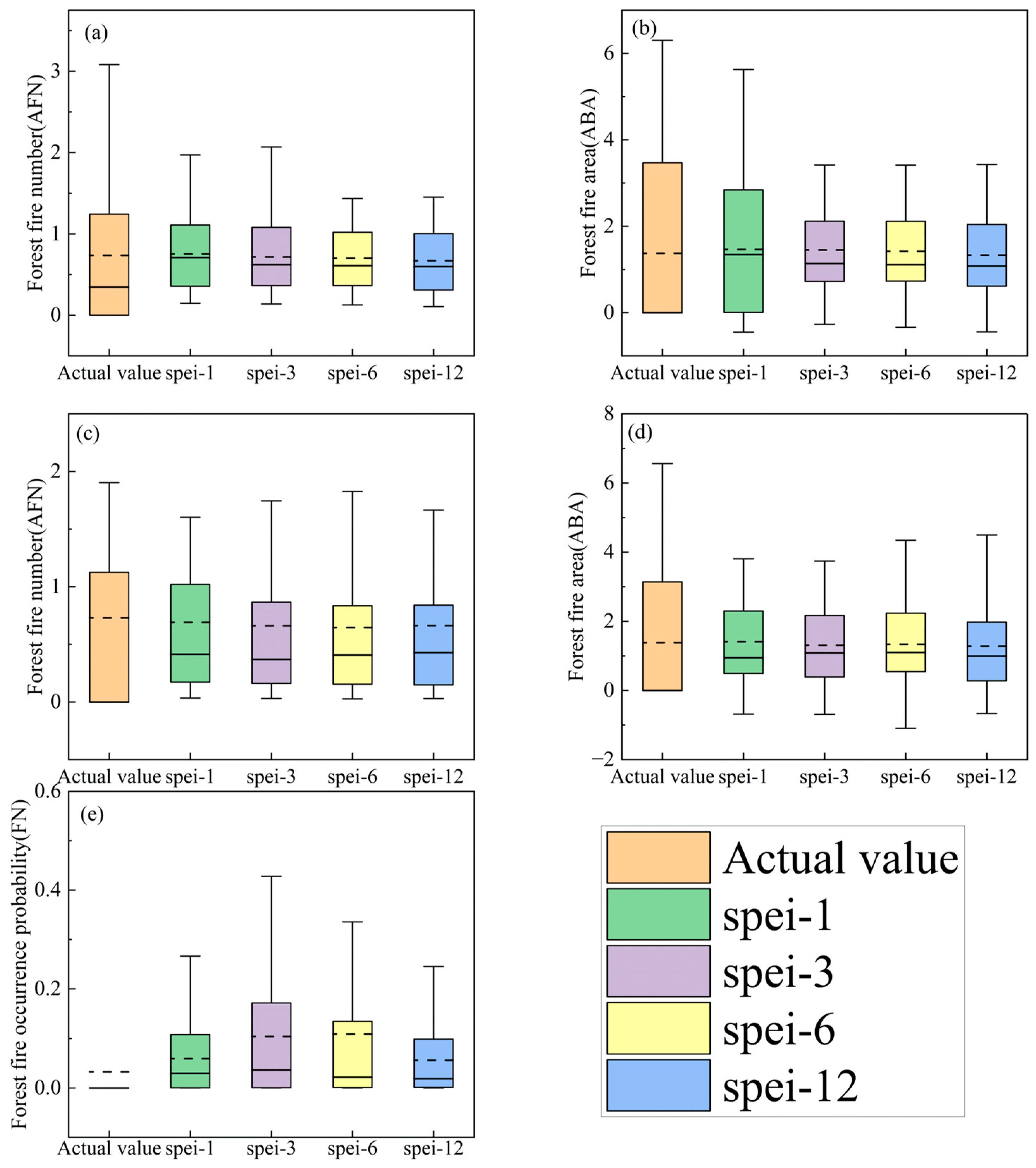
3.5. Main Influencing Factors and Accuracy of Forecasts
4. Discussion
4.1. Correlation Between Forest Fire Regimes and Drought Characteristics
4.2. Performances of Models for Predicting Forest Fire Regimes
4.2.1. Model Performance
4.2.2. Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Morgan, P.; Hardy, C.C.; Swetnam, T.W.; Rollins, M.G.; Long, D.G. Mapping fire regimes across time and space: Understanding coarse and fine-scale fire patterns. Int. J. Wildland Fire 2001, 10, 329–342. [Google Scholar] [CrossRef]
- Burnside, W. Altered fire regimes. Nat. Sustain. 2018, 1, 730. [Google Scholar] [CrossRef]
- Keeley, J.E.; Syphard, A.D. Large California wildfires: 2020 fires in historical context. Fire Ecol. 2021, 17, 22. [Google Scholar] [CrossRef]
- Ihinegbu, C.; Ogunwumi, T. Multi-criteria modelling of drought: A study of Brandenburg Federal State, Germany. Model. Earth Syst. Environ. 2022, 8, 2035–2049. [Google Scholar] [CrossRef]
- Daşdemir, İ.; Aydın, F.; Ertuğrul, M. Factors Affecting the Behavior of Large Forest Fires in Turkey. Environ. Manag. 2021, 67, 162–175. [Google Scholar] [CrossRef]
- Parente, J.; Pereira, M.G.; Amraoui, M.; Fischer, E.M. Heat waves in Portugal: Current regime, changes in future climate and impacts on extreme wildfires. Sci. Total Environ. 2018, 631–632, 534–549. [Google Scholar] [CrossRef] [PubMed]
- Cochrane, M.A.; Bowman, D.M.J.S. Manage fire regimes, not fires. Nat. Geosci. 2021, 14, 455–457. [Google Scholar] [CrossRef]
- Kodandapani, N.; Parks, S.A. Effects of drought on wildfires in forest landscapes of the Western Ghats, India. Int. J. Wildland Fire 2019, 28, 431–444. [Google Scholar] [CrossRef]
- Turco, M.; Jerez, S.; Augusto, S.; Tarín-Carrasco, P.; Ratola, N.; Jiménez-Guerrero, P.; Trigo, R.M. Climate drivers of the 2017 devastating fires in Portugal. Sci. Rep. 2019, 9, 13886. [Google Scholar] [CrossRef]
- Margolis, E.; Woodhouse, C.A.; Swetnam, T.W. Drought, multi-seasonal climate, and wildfire in northern New Mexico. Clim. Change 2017, 142, 433–446. [Google Scholar] [CrossRef]
- Marín, P.-G.; Julio, C.J.; Dante Arturo, R.-T.; Daniel Jose, V.-N. Drought and spatiotemporal variability of forest fires across Mexico. Chin. Geogr. Sci. 2018, 28, 25–37. [Google Scholar] [CrossRef]
- Dowdy, A.J.; Ye, H.; Pepler, A.; Thatcher, M.; Osbrough, S.L.; Evans, J.P.; Di Virgilio, G.; McCarthy, N. Future changes in extreme weather and pyroconvection risk factors for Australian wildfires. Sci. Rep. 2019, 9, 10073. [Google Scholar] [CrossRef] [PubMed]
- Guttman, N.B. Accepting the standarized precipitaion index: A calculation algrithm. JAWRA J. Am. Water Resour. Assoc. 1999, 35, 311–322. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 179–183. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I.; Angulo, M.; El Kenawy, A. A New Global 0.5° Gridded Dataset (1901–2006) of a Multiscalar Drought Index: Comparison with Current Drought Index Datasets Based on the Palmer Drought Severity Index. J. Hydrometeorol. 2010, 11, 1033–1043. [Google Scholar] [CrossRef]
- Mega, N.; Medjerab, A. Statistical comparison between the standardized precipitation index and the standardized precipitation drought index. Model. Earth Syst. Environ. 2021, 7, 373–388. [Google Scholar] [CrossRef]
- Cabral-Alemán, C.; Villanueva-Díaz, J.; Quiñonez-Barraza, G.; Gómez-Guerrero, A.; Arreola-Ávila, J.G. Reconstruction of the Standardized Precipitation-Evapotranspiration Index for the Western Region of Durango State, Mexico. Forests 2022, 13, 1233. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, X.; Wang, Z.; Zhao, L.; Zhang, Q.-p. Time scale selection and periodicity analysis of grassland drought monitoring index in Inner Mongolia. Glob. Ecol. Conserv. 2022, 36, e02138. [Google Scholar] [CrossRef]
- He, B.; Chang, J.; Wang, Y.; Wang, Y.; Zhou, S.; Chen, C. Spatio-temporal evolution and non-stationary characteristics of meteorological drought in inland arid areas. Ecol. Indic. 2021, 126, 107644. [Google Scholar] [CrossRef]
- Yang, Q.; Li, M.; Zheng, Z.; Ma, Z. Regional applicability of seven meteorological drought indices in China. Sci. China Earth Sci. 2017, 60, 745–760. [Google Scholar] [CrossRef]
- Geng, G.; Yang, R.; Liu, L. Downscaled solar-induced chlorophyll fluorescence has great potential for monitoring the response of vegetation to drought in the Yellow River Basin, China: Insights from an extreme event. Ecol. Indic. 2022, 138, 108801. [Google Scholar] [CrossRef]
- Wells, N.; Goddard, S.; Hayes, M.J. A self-calibrating Palmer drought severity index. J. Clim. 2004, 17, 2335–2351. [Google Scholar] [CrossRef]
- Yang, S.; Zeng, A.; Tigabu, M.; Wang, G.; Guo, F. Investigating Drought Events and Their Consequences in Wildfires: An Application in China. Fire 2023, 6, 223. [Google Scholar] [CrossRef]
- Gond, S.; Gupta, N.; Patel, J.; Dikshit, P.K.S. Spatiotemporal evaluation of drought characteristics based on standard drought indices at various timescales over Uttar Pradesh, India. Environ. Monit. Assess. 2023, 195, 439. [Google Scholar] [CrossRef]
- Russo, A.; Gouveia, C.M.; Páscoa, P.; DaCamara, C.C.; Sousa, P.M.; Trigo, R.M. Assessing the role of drought events on wildfires in the Iberian Peninsula. Agric. For. Meteorol. 2017, 237–238, 50–59. [Google Scholar] [CrossRef]
- Wei, X.; He, W.; Zhou, Y.; Ju, W.; Xiao, J.; Li, X.; Liu, Y.; Xu, S.; Bi, W.; Zhang, X.; et al. Global assessment of lagged and cumulative effects of drought on grassland gross primary production. Ecol. Indic. 2022, 136, 108646. [Google Scholar] [CrossRef]
- Zhao, A.; Yu, Q.; Feng, L.; Zhang, A.; Pei, T. Evaluating the cumulative and time-lag effects of drought on grassland vegetation: A case study in the Chinese Loess Plateau. J. Environ. Manag. 2020, 261, 110214. [Google Scholar] [CrossRef]
- Dye, A.; Reilly, M.; McEvoy, A.; Lemons, R.; Riley, K.; Kim, J.; Kerns, B. Simulated Future Shifts in Wildfire Regimes in Moist Forests of Pacific Northwest, USA. J. Geophys. Res. Biogeosci. 2024, 129, e2023JG007722. [Google Scholar] [CrossRef]
- Zhang, F.; Biederman, J.A.; Dannenberg, M.P.; Yan, D.; Reed, S.C.; Smith, W.K. Five decades of observed daily precipitation reveal longer and more variable drought events across much of the western United States. Geophys. Res. Lett. 2021, 48, e2020GL092293. [Google Scholar] [CrossRef]
- Westerling, A.L.; Brown, T.J.; Schoennagel, T.; Swetnam, T.W.; Turner, M.G.; Veblen, T.T. Climate and wildfire in Western US Forests. For. Conserv. Anthr. Sci. Policy Pract. 2016, 43–55. [Google Scholar] [CrossRef]
- Williams, A.P.; Abatzoglou, J.T.; Gershunov, A.; Guzman-Morales, J.; Bishop, D.A.; Balch, J.K.; Lettenmaier, D.P. Observed impacts of anthropogenic climate change on wildfire in California. Earth’s Futur. 2019, 7, 892–910. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiang, Q.; Yu, C.; Bao, J.; Ho, H.C.; Sun, S.; Ding, Z.; Hu, K.; Zhang, L. Mortality risk and burden associated with temperature variability in China, United Kingdom and United States: Comparative analysis of daily and hourly exposure metrics. Environ. Res. 2019, 179, 108771. [Google Scholar] [CrossRef] [PubMed]
- Fang, S.; Yang, J.; Zou, C.B.; Krueger, E.S.; Ochsner, T.E.; Zhang, Q. Wildfire danger under changing climates in the southern Great Plains throughout the 21st century. Ecol. Indic. 2025, 170, 112994. [Google Scholar] [CrossRef]
- Liu, Y.; Feng, S.; Qian, Y.; Huang, H.; Berg, L.K. How do North American weather regimes drive wind energy at the sub-seasonal to seasonal timescales? Npj Clim. Atmos. Sci. 2023, 6, 100. [Google Scholar] [CrossRef]
- Sharma, S.; Carlson, J.; Krueger, E.S.; Engle, D.M.; Twidwell, D.; Fuhlendorf, S.D.; Patrignani, A.; Feng, L.; Ochsner, T.E. Soil moisture as an indicator of growing-season herbaceous fuel moisture and curing rate in grasslands. Int. J. Wildland Fire 2020, 30, 57–69. [Google Scholar] [CrossRef]
- Clark, S.; Mills, G.; Brown, T.; Harris, S.; Abatzoglou, J.T. Downscaled GCM climate projections of fire weather over Victoria, Australia. Part 2*: A multi-model ensemble of 21st century trends. Int. J. Wildland Fire 2021, 30, 596–610. [Google Scholar] [CrossRef]
- Krueger, E.S.; Ochsner, T.E.; Levi, M.R.; Basara, J.B.; Snitker, G.J.; Wyatt, B.M. Grassland productivity estimates informed by soil moisture measurements: Statistical and mechanistic approaches. Agron. J. 2021, 113, 3498–3517. [Google Scholar] [CrossRef]
- Krueger, E.S.; Ochsner, T.E.; Carlson, J.; Engle, D.M.; Twidwell, D.; Fuhlendorf, S.D. Concurrent and antecedent soil moisture relate positively or negatively to probability of large wildfires depending on season. Int. J. Wildland Fire 2016, 25, 657–668. [Google Scholar] [CrossRef]
- Perello, N.; Trucchia, A.; D’Andrea, M.; Degli Esposti, S.; Fiorucci, P.; Gollini, A.; Negro, D. An adaptable dead fuel moisture model for various fuel types and temporal scales tailored for wildfire danger assessment. Environ. Model. Softw. 2025, 183, 106254. [Google Scholar] [CrossRef]
- Asensio, M.I.; Cascón, J.M.; Laiz, P.; Prieto-Herráez, D. Validating the effect of fuel moisture content by a multivalued operator in a simplified physical fire spread model. Environ. Model. Softw. 2023, 164, 105710. [Google Scholar] [CrossRef]
- Lawson, B.D.; Armitage, O. Weather Guide for the Canadian Forest Fire Danger Rating System; Canadian Forest Service, Northern Forestry Centre: Edmonton, AB, Canada, 2008.
- Carlson, J.; Bradshaw, L.S.; Nelson, R.M.; Bensch, R.R.; Jabrzemski, R. Application of the Nelson model to four timelag fuel classes using Oklahoma field observations: Model evaluation and comparison with National Fire Danger Rating System algorithms. Int. J. Wildland Fire 2007, 16, 204–216. [Google Scholar] [CrossRef]
- Dowdy, A.J.; Mills, G.A.; Finkele, K.; De Groot, W. Australian Fire Weather as Represented by the McArthur Forest Fire Danger Index and the Canadian Forest Fire Weather Index. 2009. Available online: https://www.cawcr.gov.au/technical-reports/CTR_010.pdf (accessed on 18 March 2025).
- Yang, J.; Jiang, H.; Wang, S.; Ma, X. A Multi-Scale Deep Learning Algorithm for Enhanced Forest Fire Danger Prediction Using Remote Sensing Images. Forests 2024, 15, 1581. [Google Scholar] [CrossRef]
- Loupian, E.; Bartalev, S.; Ershov, D.; Kotel’nikov, R.; Balashov, I.; Bourtsev, M.; Egorov, V.; Efremov, V.Y.; Zharko, V.; Kovganko, K. Satellite data processing management in Forest Fires Remote Monitoring Information System (ISDM-Rosleskhoz) of the Federal Agency for Forestry. Sovrem. Probl. Distantsionnogo Zondirovaniya Zemli Iz Kosmosa 2015, 12, 222–250. [Google Scholar]
- Kotel’Nikov, R.; Lupyan, E.; Bartalev, S.; Ershov, D. Space monitoring of forest fires: History of the creation and development of ISDM-Rosleskhoz. Contemp. Probl. Ecol. 2020, 13, 795–802. [Google Scholar] [CrossRef]
- Llorens, R.; Sobrino, J.A.; Fernández, C.; Fernández-Alonso, J.M.; Vega, J.A. A methodology to estimate forest fires burned areas and burn severity degrees using Sentinel-2 data. Application to the October 2017 fires in the Iberian Peninsula. Int. J. Appl. Earth Obs. Geoinf. 2021, 95, 102243. [Google Scholar] [CrossRef]
- Kranz, J.; Bauer, K.; Pampanoni, V.; Zhao, L.; Marrs, C.; Mauder, M.; Poděbradská, M.; van der Maaten-Theunissen, M.; Yebra, M.; Forkel, M. Assessing predictors for fuel moisture content in Central European forests. Agric. For. Meteorol. 2025, 371, 110590. [Google Scholar] [CrossRef]
- Grishin, A.M. Mathematical Modeling of Forest Fires and New Methods of Fighting Them; Publishing House of the Tomsk State University: Tomsk, Russia, 1997. [Google Scholar]
- Grishin, A.M.; Golovanov, A.N.; Kataeva, L.Y.; Loboda, E.L. Formulation and solution of the problem of drying of a layer of combustible forest materials. Combust. Explos. Shock Waves 2001, 37, 57–66. [Google Scholar] [CrossRef]
- Grishin, A.; Filkov, A. A deterministic-probabilistic system for predicting forest fire hazard. Fire Saf. J. 2011, 46, 56–62. [Google Scholar] [CrossRef]
- Grishin, A.; Filkov, A. The forecast of ignition and spread of forest fires. Praktika 2005, 201. [Google Scholar]
- McNorton, J.R.; Di Giuseppe, F. A global fuel characteristic model and dataset for wildfire prediction. Biogeosciences 2024, 21, 279–300. [Google Scholar] [CrossRef]
- Grishin, A.M.; Zima, V.P.; Kuznetsov, V.T.; Skorik, A.I. Ignition of combustible forest materials by a radiant energy flux. Combust. Explos. Shock Waves 2002, 38, 24–29. [Google Scholar] [CrossRef]
- Castel-Clavera, J.; Pimont, F.; Opitz, T.; Ruffault, J.; Barbero, R.; Allard, D.; Dupuy, J.-L. A comparative analysis of fire-weather indices for enhanced fire activity prediction with probabilistic approaches. Agric. For. Meteorol. 2025, 361, 110315. [Google Scholar] [CrossRef]
- Boubeta, M.; Lombardía, M.J.; Marey-Pérez, M.; Morales, D. Poisson mixed models for predicting number of fires. Int. J. Wildland Fire 2019, 28, 237–253. [Google Scholar] [CrossRef]
- Pimont, F.; Fargeon, H.; Opitz, T.; Ruffault, J.; Barbero, R.; Martin-StPaul, N.; Rigolot, E.; RiviÉre, M.; Dupuy, J.-L. Prediction of regional wildfire activity in the probabilistic Bayesian framework of Firelihood. Ecol. Appl. 2021, 31, e02316. [Google Scholar] [CrossRef] [PubMed]
- Pimont, F.; Ruffault, J.; Opitz, T.; Fargeon, H.; Barbero, R.; Castel-Clavera, J.; Martin-StPaul, N.; Rigolot, E.; Dupuy, J.-L. Future expansion, seasonal lengthening and intensification of fire activity under climate change in southeastern France. Int. J. Wildland Fire 2023, 32, 4–14. [Google Scholar] [CrossRef]
- Wang, M.; Si, L.; Chen, F.; Shu, L.; Zhao, F.; Li, W. Simulation of Fire Occurrence Based on Historical Data in Future Climate Scenarios and Its Practical Verification. Fire 2024, 7, 346. [Google Scholar] [CrossRef]
- Chen, A. Evaluating the relationships between wildfires and drought using machine learning. Int. J. Wildland Fire 2022, 31, 230–239. [Google Scholar] [CrossRef]
- Riley, K.L.; Abatzoglou, J.T.; Grenfell, I.C.; Klene, A.E.; Heinsch, F.A. The relationship of large fire occurrence with drought and fire danger indices in the western USA, 1984–2008: The role of temporal scale. Int. J. Wildland Fire 2013, 22, 894–909. [Google Scholar] [CrossRef]
- Vilchis-Francés, A.Y.; Díaz-Delgado, C.; Becerril Piña, R.; Mastachi Loza, C.A.; Gómez-Albores, M.Á.; Bâ, K.M. Daily prediction modeling of forest fire ignition using meteorological drought indices in the Mexican highlands. Iforest-Biogeosciences For. 2021, 14, 437. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically weighted regression: A method for exploring spatial nonstationarity. Geogr. Anal. 1996, 28, 281–298. [Google Scholar] [CrossRef]
- Liu, X.; Feng, X.; Ciais, P.; Fu, B.; Hu, B.; Sun, Z. GRACE satellite-based drought index indicating increased impact of drought over major basins in China during 2002–2017. Agric. For. Meteorol. 2020, 291, 108057. [Google Scholar] [CrossRef]
- Su, J.; Liu, Z.; Wang, W.; Jiao, K.; Yu, Y.; Li, K.; Lü, Q.; Fletcher, T.L. Evaluation of the Spatial Distribution of Predictors of Fire Regimes in China from 2003 to 2016. Remote Sens. 2023, 15, 4946. [Google Scholar] [CrossRef]
- Zhao, L.; Li, L.; Li, Y.; Zhong, H.; Zhang, F.; Zhu, J.; Ding, Y. Monitoring vegetation drought in the nine major river basins of China based on a new developed Vegetation Drought Condition Index. J. Arid Land 2023, 15, 1421–1438. [Google Scholar] [CrossRef]
- Qing, G. Research on the Development of Climate Regionalization in China (1929–1966). Master’s Thesis, University of Science and Technology of China, Hefei, China, 2023. [Google Scholar]
- Fang, K.; Yao, Q.; Guo, Z.; Zheng, B.; Du, J.; Qi, F.; Yan, P.; Li, J.; Ou, T.; Liu, J.; et al. ENSO modulates wildfire activity in China. Nat. Commun. 2021, 12, 1764. [Google Scholar] [CrossRef] [PubMed]
- Vilar, L.; Garrido, J.; Echavarría, P.; Martínez-Vega, J.; Martín, M.P. Comparative analysis of CORINE and climate change initiative land cover maps in Europe: Implications for wildfire occurrence estimation at regional and local scales. Int. J. Appl. Earth Obs. Geoinf. 2019, 78, 102–117. [Google Scholar] [CrossRef]
- Thies, B. Machine learning wildfire susceptibility mapping for Germany. Nat. Hazards 2025. [Google Scholar] [CrossRef]
- Turco, M.; Marcos-Matamoros, R.; Castro, X.; Canyameras, E.; Llasat, M.C. Seasonal prediction of climate-driven fire risk for decision-making and operational applications in a Mediterranean region. Sci. Total Environ. 2019, 676, 577–583. [Google Scholar] [CrossRef]
- Chang, C.; Chang, Y.; Xiong, Z.; Ping, X.; Zhang, H.; Guo, M.; Hu, Y. Predicting Grassland Fire-Occurrence Probability in Inner Mongolia Autonomous Region, China. Remote Sens. 2023, 15, 2999. [Google Scholar] [CrossRef]
- Pike, R.J.; Evans, I.S.; Hengl, T. Chapter 1 Geomorphometry: A Brief Guide. Dev. Soil Sci. 2009, 33, 3–30. [Google Scholar]
- Zhang, Q.; Gao, C.; Shi, C. An improved machine-learning model for lightning-ignited wildfire prediction in Texas. Environ. Res. Lett. 2025, 20, 064026. [Google Scholar] [CrossRef]
- Oliveira, S.; Pereira, J.M.; San-Miguel-Ayanz, J.; Lourenço, L. Exploring the spatial patterns of fire density in Southern Europe using Geographically Weighted Regression. Appl. Geogr. 2014, 51, 143–157. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Cui, T.; Martz, L.; Guo, X. Grassland phenology response to drought in the Canadian prairies. Remote Sens. 2017, 9, 1258. [Google Scholar] [CrossRef]
- World Meteorological Organization. Standardized Precipitation Index User Guide; World Meteorological Organization: Geneva, Switzerland, 2012; 24p. [Google Scholar]
- Mishra, D.; Goswami, S.; Matin, S.; Sarup, J. Analyzing the extent of drought in the Rajasthan state of India using vegetation condition index and standardized precipitation index. Model. Earth Syst. Environ. 2022, 8, 601–610. [Google Scholar] [CrossRef]
- Hamarash, H.; Hamad, R.; Rasul, A. Meteorological drought in semi-arid regions: A case study of Iran. J. Arid Land 2022, 14, 1212–1233. [Google Scholar] [CrossRef]
- Won, J.; Kim, S. Ecological Drought Condition Index to Monitor Vegetation Response to Meteorological Drought in Korean Peninsula. Remote Sens. 2023, 15, 337. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, W.; Yang, B.; Xie, W.; Tao, C.; Hong, Z.; Xie, Y.; Li, J.; Li, L.; Meng, L. Long-term spatiotemporal characteristics of meteorological drought in China from a three-dimensional (longitude, latitude, time) perspective. Int. J. Appl. Earth Obs. Geoinf. 2024, 126, 103633. [Google Scholar] [CrossRef]
- Ben Mhenni, N.; Shinoda, M.; Nandintsetseg, B. Assessment of drought frequency, severity, and duration and its impacts on vegetation greenness and agriculture production in Mediterranean dryland: A case study in Tunisia. Nat. Hazards 2021, 105, 2755–2776. [Google Scholar] [CrossRef]
- Wei, W.; Yan, P.; Zhou, L.; Zhang, H.; Xie, B.; Zhou, J. A comprehensive drought index based on spatial principal component analysis and its application in northern China. Environ. Monit. Assess. 2024, 196, 193. [Google Scholar] [CrossRef]
- Wang, F.; Wang, Z.; Yang, H.; Zhao, Y. Study of the temporal and spatial patterns of drought in the Yellow River basin based on SPEI. Sci. China Earth Sci. 2018, 61, 1098–1111. [Google Scholar] [CrossRef]
- Zhang, P.; Cai, Y.; Cong, P.; Xie, Y.; Chen, W.; Cai, J.; Bai, X. Quantitation of meteorological, hydrological and agricultural drought under climate change in the East River basin of south China. Ecol. Indic. 2024, 158, 111304. [Google Scholar] [CrossRef]
- Guna, A.; Zhang, J.; Tong, S.; Bao, Y.; Han, A.; Li, K. Effect of climate change on maize yield in the growing season: A case study of the Songliao Plain Maize Belt. Water 2019, 11, 2108. [Google Scholar] [CrossRef]
- Yevjevich, V.M. An Objective Approach to Definitions and Investigations of Continental Hydrologic Droughts; Colorado State University: Fort Collins, CO, USA, 1967; Volume 23. [Google Scholar]
- Guo, H.; Bao, A.; Liu, T.; Jiapaer, G.; Ndayisaba, F.; Jiang, L.; Kurban, A.; De Maeyer, P. Spatial and temporal characteristics of droughts in Central Asia during 1966–2015. Sci. Total Environ. 2018, 624, 1523–1538. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A.; Kisi, O.; Khan, N.; Salih, S.Q.; Yaseen, Z.M. Analysis of dry and wet climate characteristics at Uttarakhand (India) using effective drought index. Nat. Hazards 2021, 105, 1643–1662. [Google Scholar] [CrossRef]
- Pang, Y.; Li, Y.; Feng, Z.; Feng, Z.; Zhao, Z.; Chen, S.; Zhang, H. Forest Fire Occurrence Prediction in China Based on Machine Learning Methods. Remote Sens. 2022, 14, 5546. [Google Scholar] [CrossRef]
- Wheeler, D.C. Diagnostic tools and a remedial method for collinearity in geographically weighted regression. Environ. Plan. A 2007, 39, 2464–2481. [Google Scholar] [CrossRef]
- Wang, N.; Sun, M.; Ye, J.; Wang, J.; Liu, Q.; Li, M. Spatial Downscaling of Forest Above-Ground Biomass Distribution Patterns Based on Landsat 8 OLI Images and a Multiscale Geographically Weighted Regression Algorithm. Forests 2023, 14, 526. [Google Scholar] [CrossRef]
- Stewart Fotheringham, A.; Charlton, M.; Brunsdon, C. The geography of parameter space: An investigation of spatial non-stationarity. Int. J. Geogr. Inf. Syst. 1996, 10, 605–627. [Google Scholar] [CrossRef]
- Cano-Crespo, A.; Traxl, D.; Prat-Ortega, G.; Rolinski, S.; Thonicke, K. Characterization of land cover-specific fire regimes in the Brazilian Amazon. Reg. Environ. Change 2023, 23, 19. [Google Scholar] [CrossRef]
- Huang, Z.; Li, S.; Peng, Y.; Gao, F. Spatial non-stationarity of influencing factors of China’s county economic development base on a multiscale geographically weighted regression model. ISPRS Int. J. Geo-Inf. 2023, 12, 109. [Google Scholar] [CrossRef]
- Lai, J.; Pan, J. China’s city network structural characteristics based on population flow during spring festival travel rush: Empirical analysis of “tencent migration” big data. J. Urban Plan. Dev. 2020, 146, 04020018. [Google Scholar] [CrossRef]
- Ma, L.; Yang, B.; Feng, Y.; Ju, L. Evaluation of provincial forest ecological security and analysis of the driving factors in China via the GWR model. Sci. Rep. 2024, 14, 14299. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Yang, S.; Wang, G.; Wang, W.; Xia, H.; Sun, S.; Guo, F.-T. Evaluation of geographically weighted logistic model and mixed effect model in forest fire prediction in northeast China. Front. For. Glob. Change 2022, 5, 1040408. [Google Scholar] [CrossRef]
- Tyas, S.W.; Puspitasari, L.A. Geographically weighted generalized poisson regression model with the best kernel function in the case of the number of postpartum maternal mortality in east java. MethodsX 2023, 10, 102002. [Google Scholar] [CrossRef] [PubMed]
- Cao, Q.; Zhang, L.; Su, Z.; Wang, G.; Sun, S.; Guo, F. Comparing four regression techniques to explore factors governing the number of forest fires in Southeast, China. Geomat. Nat. Hazards Risk 2021, 12, 499–521. [Google Scholar] [CrossRef]
- Zhang, W.; Dai, L.; Yan, Y.; Han, X.; Teng, Y.; Li, M.; Zhu, Y.; Zhang, Y. Multiscale geographically weighted regression-based analysis of vegetation driving factors and mining-induced quantification in the Fengfeng District, China. Ecol. Inform. 2024, 80, 102506. [Google Scholar] [CrossRef]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Bui, D.T.; Le, K.T.T.; Nguyen, V.C.; Le, H.D.; Revhaug, I. Tropical Forest Fire Susceptibility Mapping at the Cat Ba National Park Area, Hai Phong City, Vietnam, Using GIS-Based Kernel Logistic Regression. Remote Sens. 2016, 8, 15. [Google Scholar] [CrossRef]
- Al Moteri, M.; Alrowais, F.; Mtouaa, W.; Aljehane, N.O.; Alotaibi, S.S.; Marzouk, R.; Mustafa Hilal, A.; Ahmed, N.A. An enhanced drought forecasting in coastal arid regions using deep learning approach with evaporation index. Environ. Res. 2024, 246, 118171. [Google Scholar] [CrossRef]
- Samad Emamgholizadeh, S.S.; Mohamad Amin, E. Comparison of Artificial Neural Networks, Geographically Weighted Regression and Cokriging Methods for Predicting the Spatial Distribution of Soil Macronutrients (N, P, and K). Chin. Geogr. Sci. 2017, 27, 747–759. [Google Scholar] [CrossRef]
- Zong, X.; Tian, X.; Liu, X.; Shu, L. Drought threat to terrestrial gross primary production exacerbated by wildfires. Commun. Earth Environ. 2024, 5, 225. [Google Scholar] [CrossRef]
- Robbins, Z.J.; Loudermilk, E.L.; Mozelewski, T.G.; Jones, K.; Scheller, R.M. Fire regimes of the Southern Appalachians may radically shift under climate change. Fire Ecol. 2024, 20, 2. [Google Scholar] [CrossRef]
- Mallick, T.; Pandidurai, D.; Sharma, D.; Sharma, A.; Panda, S.K. A comparative assessment of meteorological drought characteristics in agro-climatic zones of Rajasthan (arid) and Tamil Nadu (humid), India. Nat. Hazards 2024, 120, 4181–4203. [Google Scholar] [CrossRef]
- González, M.E.; Gómez-González, S.; Lara, A.; Garreaud, R.; Díaz-Hormazábal, I. The 2010–2015 Megadrought and its influence on the fire regime in central and south-central Chile. Ecosphere 2018, 9, e02300. [Google Scholar] [CrossRef]
- Van der Kamp, D.; Bürger, G.; Werner, A. Evaluation of the Monthly Drought Code as a metric for fire weather in a region of complex terrain and un-certainties in future projections. Vic. Pac. Clim. Impacts Consort. 2013. Available online: https://www.pacificclimate.org/sites/default/files/publications/evaluation_of_the_monthly_drought_code.pdf (accessed on 18 March 2025).
- Chan, X.Y.; Robinne, F.-N.; Parisien, M.-A.; Wang, X.; Fleming, T.; Flannigan, M.D. Assessment of lake-level fluctuation as an indicator of fire activity in boreal Canada. Ecol. Indic. 2022, 145, 109611. [Google Scholar] [CrossRef]
- Yin, J.; He, B.; Fan, C.; Chen, R.; Zhang, H.; Zhang, Y. Drought-related wildfire accounts for one-third of the forest wildfires in subtropical China. Agric. For. Meteorol. 2024, 346, 109893. [Google Scholar] [CrossRef]
- Holden, Z.A.; Luce, C.H.; Crimmins, M.A.; Morgan, P. Wildfire extent and severity correlated with annual streamflow distribution and timing in the Pacific Northwest, USA (1984–2005). Ecohydrology 2012, 5, 677–684. [Google Scholar] [CrossRef]
- Dimitrakopoulos, A.; Vlahou, M.; Anagnostopoulou, C.; Mitsopoulos, I. Impact of drought on wildland fires in Greece: Implications of climatic change? Clim. Change 2011, 109, 331–347. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Cheng, L.; Cong, N.; Zheng, Z.; Huang, K.; Zhang, J.; Zhu, Y.; Gao, J.; Sun, Y. Have China’s drylands become wetting in the past 50 years? J. Geogr. Sci. 2023, 33, 99–120. [Google Scholar] [CrossRef]
- Zhao, C.; Feng, Y.; Liu, W.; Wang, H.; Wang, T.; Liu, Y.; Sun, F. Provincial-scale assessment of vulnerability and resilience to drought in China. Sci. Total Environ. 2024, 934, 173199. [Google Scholar] [CrossRef]
- Wei, W.; Zhang, J.; Zhou, J.; Zhou, L.; Xie, B.; Li, C. Monitoring drought dynamics in China using Optimized Meteorological Drought Index (OMDI) based on remote sensing data sets. J. Environ. Manag. 2021, 292, 112733. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Ge, Y.; Guo, S.; Li, H.; Li, X.; Sun, L.; Chen, J. Forest fire susceptibility mapping based on precipitation-constrained cumulative dryness status information in Southeast China: A novel machine learning modeling approach. For. Ecol. Manag. 2024, 558, 121771. [Google Scholar] [CrossRef]
- Hayes, J.P. Fire Suppression and the Wildfire Paradox in Contemporary China: Policies, Resilience, and Effects in Chinese Fire Regimes. Hum. Ecol. 2020, 1–14. [Google Scholar] [CrossRef]
- Zhao, F.; Liu, Y. Important meteorological predictors for long-range wildfires in China. For. Ecol. Manag. 2021, 499, 119638. [Google Scholar] [CrossRef]
- Yang, S.; Meng, D.; Li, X.; Wu, X. Multi-scale responses of vegetation changes relative to the SPEI meteorological drought index in North China in 2001–2014. Acta Ecol. Sin 2018, 38, 1028–1039. [Google Scholar]
- Su, B.; Huang, J.; Mondal, S.K.; Zhai, J.; Wang, Y.; Wen, S.; Gao, M.; Lv, Y.; Jiang, S.; Jiang, T.; et al. Insight from CMIP6 SSP-RCP scenarios for future drought characteristics in China. Atmos. Res. 2021, 250, 105375. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhang, X.; Li, C.; Xu, Y.; Fei, J. Compound ecological drought assessment of China using a Copula-based drought index. Ecol. Indic. 2024, 164, 112141. [Google Scholar] [CrossRef]
- Gupta, A.; Rico-Medina, A.; Caño-Delgado, A.I. The physiology of plant responses to drought. Science 2020, 368, 266–269. [Google Scholar] [CrossRef]
- Chen, C.; Zhu, L.; Tian, L.; Li, X. Spatial-temporal changes in vegetation characteristics and climate in the Qinling-Daba Mountains. Acta Ecol. Sin 2019, 39, 3257–3266. [Google Scholar]
- Zhang, Y.; Liu, L.-Y.; Liu, Y.; Zhang, M.; An, C.-B. Response of altitudinal vegetation belts of the Tianshan Mountains in northwestern China to climate change during 1989–2015. Sci. Rep. 2021, 11, 4870. [Google Scholar] [CrossRef]
- Qi, G.; Song, J.; Li, Q.; Bai, H.; Sun, H.; Zhang, S.; Cheng, D. Response of vegetation to multi-timescales drought in the Qinling Mountains of China. Ecol. Indic. 2022, 135, 108539. [Google Scholar] [CrossRef]
- Liu, P.; Chi, Y.; Huang, Z.; Zhong, D.; Zhou, L. Multidimensional response of China’s grassland stability to drought. Glob. Ecol. Conserv. 2024, 52, e02961. [Google Scholar] [CrossRef]
- Shi, X.; Ding, H.; Wu, M.; Shi, M.; Chen, F.; Li, Y.; Yang, Y. A comprehensive drought monitoring method integrating multi-source data. PeerJ 2022, 10, e13560. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zhang, B. The responses of natural vegetation dynamics to drought during the growing season across China. J. Hydrol. 2019, 574, 706–714. [Google Scholar] [CrossRef]
- Han, L.; Zhang, Q.; Zhang, Z.; Jia, J.; Wang, Y.; Huang, T.; Cheng, Y. Drought area, intensity and frequency changes in China under climate warming, 1961–2014. J. Arid Environ. 2021, 193, 104596. [Google Scholar] [CrossRef]
- Luo, M.; Meng, F.; Sa, C.; Duan, Y.; Bao, Y.; Liu, T.; De Maeyer, P. Response of vegetation phenology to soil moisture dynamics in the Mongolian Plateau. Catena 2021, 206, 105505. [Google Scholar] [CrossRef]
- Ding, Y.; Xu, J.; Wang, X.; Peng, X.; Cai, H. Spatial and temporal effects of drought on Chinese vegetation under different coverage levels. Sci. Total Environ. 2020, 716, 137166. [Google Scholar] [CrossRef]
- Ding, Y.; He, X.; Zhou, Z.; Hu, J.; Cai, H.; Wang, X.; Li, L.; Xu, J.; Shi, H. Response of vegetation to drought and yield monitoring based on NDVI and SIF. CATENA 2022, 219, 106328. [Google Scholar] [CrossRef]
- Reddy, A.R.; Chaitanya, K.V.; Vivekanandan, M. Drought-induced responses of photosynthesis and antioxidant metabolism in higher plants. J. Plant Physiol. 2004, 161, 1189–1202. [Google Scholar] [CrossRef]
- Xu, H.-J.; Wang, X.-P.; Zhao, C.-Y.; Yang, X.-M. Diverse responses of vegetation growth to meteorological drought across climate zones and land biomes in northern China from 1981 to 2014. Agric. For. Meteorol. 2018, 262, 1–13. [Google Scholar] [CrossRef]
- Liu, X.; Yu, S.; Yang, Z.; Dong, J.; Peng, J. The first global multi-timescale daily SPEI dataset from 1982 to 2021. Sci. Data 2024, 11, 223. [Google Scholar] [CrossRef] [PubMed]
- Deng, H.; Yin, Y.; Han, X. Vulnerability of vegetation activities to drought in Central Asia. Environ. Res. Lett. 2020, 15, 084005. [Google Scholar] [CrossRef]
- Parente, J.; Amraoui, M.; Menezes, I.; Pereira, M.G. Drought in Portugal: Current regime, comparison of indices and impacts on extreme wildfires. Sci. Total Environ. 2019, 685, 150–173. [Google Scholar] [CrossRef] [PubMed]
- Koutsias, N.; Martínez-Fernández, J.; Allgöwer, B. Do factors causing wildfires vary in space? Evidence from geographically weighted regression. GIScience Remote Sens. 2010, 47, 221–240. [Google Scholar] [CrossRef]
- Dormann, C.F.; McPherson, J.M.; Araújo, M.B.; Bivand, R.; Bolliger, J.; Carl, G.; Davies, R.G.; Hirzel, A.; Jetz, W.; Daniel Kissling, W. Methods to account for spatial autocorrelation in the analysis of species distributional data: A review. Ecography 2007, 30, 609–628. [Google Scholar] [CrossRef]
- Zhang, R.; Chen, Z.-Y.; Xu, L.-J.; Ou, C.-Q. Meteorological drought forecasting based on a statistical model with machine learning techniques in Shaanxi province, China. Sci. Total Environ. 2019, 665, 338–346. [Google Scholar] [CrossRef]
- Zhai, J.; Mondal, S.K.; Fischer, T.; Wang, Y.; Su, B.; Huang, J.; Tao, H.; Wang, G.; Ullah, W.; Uddin, M.J. Future drought characteristics through a multi-model ensemble from CMIP6 over South Asia. Atmos. Res. 2020, 246, 105111. [Google Scholar] [CrossRef]
- Yang, J.-Z.; Yang, Y.-C.; Li, Z.-H.; Liao, L.-P.; Gan, R.-M.; Wang, W.-Q.; Wang, T.-Y.; Liang, L.-Q. The regional characteristics of meteorological drought event and its multidimensional factors measurement by daily SPEI in Guangxi, China. Geomat. Nat. Hazards Risk 2023, 14, 117–142. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, R.; Wen, Z.; Khalifa, M.; Zheng, C.; Ren, H.; Zhang, Z.; Wang, Z. Assessing the impacts of drought on net primary productivity of global land biomes in different climate zones. Ecol. Indic. 2021, 130, 108146. [Google Scholar] [CrossRef]
- Ng, C.Y.; Wan Jaafar, W.Z.; Othman, F.; Lai, S.H.; Mei, Y.; Juneng, L. Assessment of Evaporative Demand Drought Index for drought analysis in Peninsular Malaysia. Sci. Total Environ. 2024, 917, 170249. [Google Scholar] [CrossRef]
- Migała, K.; Łupikasza, E.; Osuch, M.; Opała-Owczarek, M.; Owczarek, P. Linking drought indices to atmospheric circulation in Svalbard, in the Atlantic sector of the High Arctic. Sci. Rep. 2024, 14, 2160. [Google Scholar] [CrossRef] [PubMed]
- Gerberding, K.; Schirpke, U. Mapping the probability of forest fire hazard across the European Alps under climate change scenarios. J. Environ. Manag. 2025, 377, 124600. [Google Scholar] [CrossRef] [PubMed]
- Wickramasinghe, A.M.K.; Boer, M.M.; Cunningham, C.X.; Nolan, R.H.; Bowman, D.M.J.S.; Williamson, G.J. Modeling the Probability of Dry Lightning-Induced Wildfires in Tasmania: A Machine Learning Approach. Geophys. Res. Lett. 2024, 51, e2024GL110381. [Google Scholar] [CrossRef]
- Vissio, G.; Turco, M.; Provenzale, A. Testing drought indicators for summer burned area prediction in Italy. Nat. Hazards 2023, 116, 1125–1137. [Google Scholar] [CrossRef]
- Taylor, S.W.; Woolford, D.G.; Dean, C.; Martell, D.L. Wildfire prediction to inform fire management: Statistical science challenges. Stat. Sci. 2013, 28, 586–615. [Google Scholar] [CrossRef]
- Xu, Y.; Zhu, X.; Cheng, X.; Gun, Z.; Lin, J.; Zhao, J.; Yao, L.; Zhou, C. Drought assessment of China in 2002–2017 based on a comprehensive drought index. Agric. For. Meteorol. 2022, 319, 108922. [Google Scholar] [CrossRef]
- Qiu, M.-L.; Cao, X.-S.; Zhou, J.; Feng, X.-L.; Gao, X.-C. Spatial differentiation and impact factors of grain yield per hectare in Weibei Plateau based on GWR model: A case study of Binxian county, Shannxi. Sci. Agric. Sin. 2019, 52, 273–284. [Google Scholar]
- Wu, S.; Jiale, D.; Ruoxu, W.; Yige, W.; Ziyu, Y.; Bo, H.; Du, Z. Using an attention-based architecture to incorporate context similarity into spatial non-stationarity estimation. Int. J. Geogr. Inf. Sci. 2025, 39, 1460–1483. [Google Scholar] [CrossRef]


| SPEI | Degree of Drought |
|---|---|
| (−0.5,+∞) | No drought |
| (−1.0,−0.5] | Light drought |
| (−1.5,−1.0] | Mid-drought |
| (−2.0,−1.5] | Heavy drought |
| (-∞,−2.0] | Extraordinary drought |
| No. | Formula | Explanation | Variables Using This Formula |
|---|---|---|---|
| (1) | and are the values before and after data normalization, respectively; and are the maximum and minimum values of the full sample data, respectively. | Slope, terrain roughness, road density, stream density, settlements density, MDN, and MDD | |
| (2) | and are the values before and after data normalization, respectively; and are the maximum and minimum values of the full sample data, respectively. | MDS and MDI |
| Spatial Scale | Time Scale | MDN | MDD | MDS | MDI | Population Density | Terrain Roughness | Road Density | River Density | Slope |
|---|---|---|---|---|---|---|---|---|---|---|
| Grid | SPEI-1 | 473.515 | 735.083 | 785.057 | 516.373 | 1.995 | 4.42 | 2.429 | 1.838 | 4.737 |
| SPEI-3 | 93.778 | 250.833 | 270.608 | 101.432 | 2.019 | 4.412 | 2.433 | 1.863 | 4.713 | |
| SPEI-6 | 49.589 | 153.513 | 171.285 | 54.393 | 2.056 | 4.453 | 2.395 | 1.839 | 4.763 | |
| SPEI-12 | 19.768 | 64.058 | 70.288 | 17.068 | 2.089 | 4.393 | 2.494 | 1.748 | 4.684 | |
| Climate zone | SPEI-1 | 397.014 | 146.769 | 25,748.552 | 382.19 | 2.482 | 4.231 | 3.07 | 2.333 | 3.877 |
| SPEI-3 | 295.947 | 11,438.623 | 42.481 | 438.141 | 2.478 | 4.556 | 3.123 | 2.412 | 4.115 | |
| SPEI-6 | 317.43 | 12,263.315 | 15.759 | 396.97 | 2.5 | 4.849 | 3.015 | 2.42 | 4.087 | |
| SPEI-12 | 706.359 | 2788.144 | 2534.195 | 586.118 | 2.512 | 4.119 | 2.9 | 2.49 | 4.112 | |
| Vegetation zone | SPEI-1 | 413.698 | 21,402.356 | 89.097 | 658.156 | 3.049 | 3.362 | 4.328 | 2.737 | 3.438 |
| SPEI-3 | 5466.714 | 7715.038 | 6731.395 | 4685.985 | 2.769 | 3.778 | 3.861 | 3.205 | 3.329 | |
| SPEI-6 | 2932.186 | 5075.614 | 4503.222 | 2473.937 | 2.727 | 4.208 | 3.533 | 2.783 | 3.605 | |
| SPEI-12 | 1897.625 | 2881.682 | 2535.379 | 1564.443 | 2.69 | 3.622 | 3.335 | 3.398 | 3.991 |
| Spatial Scale | Time Scale | Forest Fire Regimes | Drought Characterization Selection | Correlation Coefficient (r) |
|---|---|---|---|---|
| Grid | SPEI-1 | Forest fires probability (FP) | MDD | 0.066 |
| SPEI-3 | Forest fires probability (FP) | MDD | 0.062 | |
| SPEI-6 | Forest fires probability (FP) | MDN | 0.118 | |
| SPEI-12 | Forest fires probability (FP) | MDN | 0.346 | |
| Climate zone | SPEI-1 | Forest fires number (AFN) | MDD | 0.274 |
| SPEI-3 | Forest fires number (AFN) | MDD | 0.301 | |
| SPEI-6 | Forest fires number (AFN) | MDD | 0.325 | |
| SPEI-12 | Forest fires number (AFN) | MDD | 0.337 | |
| SPEI-1 | Forest fires area (ABA) | MDD | 0.262 | |
| SPEI-3 | Forest fires area (ABA) | MDD | 0.278 | |
| SPEI-6 | Forest fires area (ABA) | MDD | 0.303 | |
| SPEI-12 | Forest fires area (ABA) | MDD | 0.323 | |
| Vegetation zone | SPEI-1 | Forest fires number (AFN) | MDN | 0.247 |
| SPEI-3 | Forest fires number (AFN) | MDN | 0.277 | |
| SPEI-6 | Forest fires number (AFN) | MDI | 0.317 | |
| SPEI-12 | Forest fires number (AFN) | MDN | 0.370 | |
| SPEI-1 | Forest fires area (ABA) | MDN | 0.281 | |
| SPEI-3 | Forest fires area (ABA) | MDN | 0.307 | |
| SPEI-6 | Forest fires area (ABA) | MDI | 0.358 | |
| SPEI-12 | Forest fires area (ABA) | MDN | 0.411 |
| Time Scale | Models | AUC (2020) | Significance Test | AUC (2021) | Significance Test | AUC (Average Value) | |
|---|---|---|---|---|---|---|---|
| 1 | GLR | 0.733 | p < 0.001 | 0.679 | p < 0.001 | 0.706 | 5557.885 |
| GWLR | 0.759 | p < 0.001 | 0.810 | p < 0.001 | 0.785 | 5075.387 | |
| 3 | GLR | 0.683 | p < 0.001 | 0.629 | p < 0.001 | 0.656 | 5549.720 |
| GWLR | 0.684 | p < 0.001 | 0.697 | p < 0.001 | 0.691 | 5015.870 | |
| 6 | GLR | 0.698 | p < 0.001 | 0.656 | p < 0.001 | 0.677 | 5621.884 |
| GWLR | 0.730 | p < 0.001 | 0.738 | p < 0.001 | 0.734 | 5079.253 | |
| 12 | GLR | 0.741 | p < 0.001 | 0.762 | p < 0.001 | 0.752 | 5552.902 |
| GWLR | 0.757 | p < 0.001 | 0.801 | p < 0.001 | 0.779 | 5100.363 |
| Time Scale | Spatial Scale | Forest Fire Regimes | Models | R2 | RMSE | MAE | |
|---|---|---|---|---|---|---|---|
| 1 | Vegetation zone | Forest fires number (AFN) | GPR | 0.5714 | 0.9142 | 0.6146 | 39.4522 |
| GWPR | 0.6684 | 0.8240 | 0.5312 | 38.4935 | |||
| Forest fires area (ABA) | GR | 0.4850 | 0.8141 | 1.4734 | 121.0521 | ||
| GWR | 0.5571 | 1.7304 | 1.3158 | 118.9629 | |||
| Climate zone | Forest fires number (AFN) | GPR | 0.1531 | 1.0093 | 0.8315 | 77.7203 | |
| GWPR | 0.3832 | 0.9215 | 0.7208 | 54.7073 | |||
| Forest fires area (ABA) | GR | 0.0230 | 2.0745 | 1.8009 | 190.6213 | ||
| GWR | 0.5020 | 2.1965 | 1.3348 | −172,435.9467 | |||
| 3 | Vegetation zone | Forest fires number (AFN) | GPR | 0.4777 | 0.9860 | 0.6488 | 39.2792 |
| GWPR | 0.6000 | 0.8884 | 0.5674 | 38.1480 | |||
| Forest fires area (ABA) | GR | 0.4673 | 1.8360 | 1.4195 | 119.7505 | ||
| GWR | 0.5285 | 1.7701 | 1.3347 | 116.8250 | |||
| Climate zone | Forest fires number (AFN) | GPR | 0.1665 | 1.0058 | 0.8116 | 75.5902 | |
| GWPR | 0.3702 | 0.9272 | 0.7175 | 53.8537 | |||
| Forest fires area (ABA) | GR | 0.0303 | 2.0792 | 1.7603 | 189.3072 | ||
| GWR | 0.1898 | 2.0248 | 1.6253 | 177.8480 | |||
| 6 | Vegetation zone | Forest fires number (AFN) | GPR | 0.5501 | 0.9312 | 0.6204 | 38.3726 |
| GWPR | 0.6473 | 0.8502 | 0.5488 | 37.8103 | |||
| Forest fires area (ABA) | GR | 0.4930 | 1.8016 | 1.4344 | 115.5250 | ||
| GWR | 0.5421 | 1.7385 | 1.3824 | −2859.9011 | |||
| Climate zone | Forest fires number (AFN) | GPR | 0.1832 | 0.9990 | 0.7966 | 75.5349 | |
| GWPR | 0.3623 | 0.9314 | 0.7176 | 53.7501 | |||
| Forest fires area (ABA) | GR | 0.0509 | 2.0669 | 1.7236 | 189.2227 | ||
| GWR | 0.1901 | 2.0267 | 1.6181 | 177.6037 | |||
| 12 | Vegetation zone | Forest fires number (AFN) | GPR | 0.5704 | 0.9142 | 0.6245 | 38.4794 |
| GWPR | 0.6480 | 0.8461 | 0.5492 | 37.5106 | |||
| Forest fires area (ABA) | GR | 0.4809 | 1.8246 | 1.4014 | 117.5047 | ||
| GWR | 0.5323 | 1.7675 | 1.3350 | 110.7712 | |||
| Climate zone | Forest fires number (AFN) | GPR | 0.2385 | 0.9852 | 0.7719 | 73.4857 | |
| GWPR | 0.3889 | 0.9211 | 0.6950 | 53.5372 | |||
| Forest fires area (ABA) | GR | 0.1035 | 2.0703 | 1.6436 | 187.6698 | ||
| GWR | 0.2095 | 2.0189 | 1.5895 | 177.3279 |
| Grid (FP) | Climate Zone (AFN) | Climate Zone (ABA) | Vegetation Zone (AFN) | Vegetation Zone (ABA) | ||
|---|---|---|---|---|---|---|
| SPEI-1 | Population density | −5.58 | −0.40 | 10.74 | −3.96 | −1.49 |
| Road density | 7.43 | 1.51 | 2.72 | 5.14 | 5.00 | |
| Surface roughness | 0.10 | −0.13 | 7.65 | −0.51 | −1.18 | |
| River density | 0.18 | 0.78 | 2.12 | 0.74 | 0.67 | |
| Slope | 1.82 | 0.21 | −12.28 | 0.77 | 2.04 | |
| Drought characteristics | −4.21 | 1.34 | −2.90 | 1.72 | 3.32 | |
| SPEI-3 | Population density | −5.69 | −0.31 | −1.14 | −3.87 | −1.92 |
| Road density | 8.10 | 1.48 | 1.88 | 5.03 | 4.97 | |
| Surface roughness | 0.75 | −0.49 | −1.40 | −0.64 | −1.40 | |
| River density | −0.37 | 0.79 | 0.84 | 0.50 | 0.30 | |
| Slope | 1.49 | 0.65 | 1.41 | 0.82 | 2.16 | |
| Drought characteristics | −4.44 | 1.71 | 2.26 | 1.44 | 3.10 | |
| SPEI-6 | Population density | −4.37 | −0.30 | −1.14 | −3.79 | −5.11 |
| Road density | 7.63 | 1.50 | 1.90 | 5.10 | 6.04 | |
| Surface roughness | 0.02 | −0.45 | −1.34 | −0.68 | −1.91 | |
| River density | 0.34 | 0.79 | 0.84 | 0.48 | 0.92 | |
| Slope | 2.54 | 0.63 | 1.37 | 0.88 | 2.50 | |
| Drought characteristics | −3.57 | 1.75 | 2.31 | 1.51 | 3.78 | |
| SPEI-12 | Population density | −4.87 | −0.21 | −1.07 | −3.66 | −2.05 |
| Road density | 6.92 | 1.49 | 1.89 | 5.03 | 4.90 | |
| Surface roughness | −0.24 | −0.49 | −1.41 | −0.73 | −1.45 | |
| River density | 1.11 | 0.86 | 0.94 | 0.27 | −0.15 | |
| Slope | 3.01 | 0.75 | 1.51 | 0.81 | 2.07 | |
| Drought characteristics | 0.87 | 1.64 | 2.19 | 1.58 | 4.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, X.; Li, C.; Chang, Y.; Xiong, Z.; Chen, H. Modeling Natural Forest Fire Regimes Based on Drought Characteristics at Various Spatial and Temporal Scales in P. R. China. Forests 2025, 16, 1041. https://doi.org/10.3390/f16071041
Shao X, Li C, Chang Y, Xiong Z, Chen H. Modeling Natural Forest Fire Regimes Based on Drought Characteristics at Various Spatial and Temporal Scales in P. R. China. Forests. 2025; 16(7):1041. https://doi.org/10.3390/f16071041
Chicago/Turabian StyleShao, Xianzhuang, Chunlin Li, Yu Chang, Zaiping Xiong, and Hongwei Chen. 2025. "Modeling Natural Forest Fire Regimes Based on Drought Characteristics at Various Spatial and Temporal Scales in P. R. China" Forests 16, no. 7: 1041. https://doi.org/10.3390/f16071041
APA StyleShao, X., Li, C., Chang, Y., Xiong, Z., & Chen, H. (2025). Modeling Natural Forest Fire Regimes Based on Drought Characteristics at Various Spatial and Temporal Scales in P. R. China. Forests, 16(7), 1041. https://doi.org/10.3390/f16071041








