Abstract
Understanding rainfall partitioning by shrub canopies is essential for assessing water balance and improving hydrological models in cold regions. From 2010 to 2012, field experiments were conducted in the Hulu catchment of the Qilian Mountains, focusing on Potentilla fruticosa and Caragana jubata during the growing season. Throughfall, stemflow, and interception loss were measured using rain gauges, stemflow collars, and a water balance approach. A total of 197 natural rainfall events were recorded, and precipitation partitioning characteristics were analyzed in relation to rainfall intensity, amount, and vegetation traits. One-way ANOVA and regression analyses were used to test differences and correlations. The results showed that the critical rainfall threshold for generating throughfall and stemflow was 1.9 mm. For P. fruticosa, throughfall, stemflow, and interception loss accounted for 66.96%, 3.51%, and 29.53% of gross rainfall, respectively; the corresponding values for C. jubata were 67.31%, 7.27%, and 25.42%. Significant differences (p < 0.05) in stemflow were observed between species. Partitioning components were positively correlated with rainfall amount and stabilized at ~4 mm h−1 intensity. Interception loss percentage decreased with intensity and plateaued at 2 mm h−1 for P. fruticosa and 5 mm h−1 for C. jubata. These findings provide empirical evidence for modeling shrub canopy rainfall redistribution in alpine environments.
1. Introduction
Vegetation-mediated rainfall partitioning—through the processes of throughfall (TF), stemflow (SF), and interception (IC)—is a critical component of the terrestrial water cycle and plays a fundamental role in regulating hydrological and ecological processes. Before precipitation reaches the ground, plant canopies redistribute incoming rainfall, thereby influencing soil moisture, surface runoff, infiltration, and groundwater recharge [1,2]. In cold alpine environments, where water availability is tightly linked to ecosystem stability, understanding rainfall partitioning is especially important due to the limited growing season, frequent low-intensity precipitation, and increasing shrub encroachment under climate change [3,4,5,6].
Rainfall partitioning varies greatly across ecosystems due to differences in climate, vegetation structure, and precipitation characteristics. Globally, the average interception loss across vegetation types is approximately 21.8%, with stemflow at 3.2% and throughfall at 73.0% of total precipitation [7]. These ratios are influenced by factors such as canopy density, leaf area index, branch architecture, and rainfall intensity or duration [8]. While trees generally intercept more rainfall due to their large canopies and complex structure, shrubs also play a significant role, especially in open landscapes where they dominate ground cover [9,10,11]. Previous research has highlighted notable differences between tree and shrub rainfall partitioning. Shrubs typically exhibit higher stemflow ratios relative to trees because of their compact form and higher stem density per unit area [12,13]. Moreover, in semi-arid or alpine ecosystems where shrubs are prevalent, their interception capacities can substantially affect water availability in shallow soils, with implications for plant competition, microbial activity, and hydrological connectivity [10,14].
Despite this, most rainfall partitioning studies have focused on forested ecosystems, and shrublands in cold, high-elevation regions remain understudied, particularly under natural precipitation regimes. Existing studies often rely on short-term experiments or artificial rainfall simulations, and many neglect stemflow entirely due to its perceived minor contribution or measurement difficulty (Table 1) [12,14,15,16,17,18]. Furthermore, limited attention has been paid to the combined influence of rainfall characteristics (e.g., depth and intensity) and shrub structural traits (e.g., canopy coverage and stem density) on rainfall partitioning processes in these environments [12,19,20]. These knowledge gaps hinder accurate estimation of effective rainfall inputs and limit our ability to model alpine ecohydrological processes.
The phenomenon of shrub expansion has been observed in cold regions [21]. After the expansion of shrubs, the high LAI and ET rates indicate that rainfall interception in forests is considerable in cold environments [22]. In cold regions, frequent phase transitions of precipitation occur [23]. The Qilian Mountains, located in northwestern China, are a critical ecological and hydrological barrier that feed major inland rivers such as the Heihe. The region’s cold alpine shrublands are dominated by alpine shrub, which form dense, low-stature vegetation across large areas [24]. Previous studies in the region have reported variable rainfall interception ratios for these shrubs: for instance, P. fruticosa intercepted 21.4% of rainfall at Qinghai Lake, 36.5% in the Shaliu River basin, and 34.6% in the Hulu catchment [16,24,25]. However, these values vary with site conditions, observation periods, and measurement techniques and lack standardized comparison with rainfall characteristics and vegetation traits.
To address these gaps, this study investigates the rainfall partitioning behavior of Potentilla fruticosa L. and Caragana jubata Poir. in the Hulu catchment of the Qilian Mountains using multi-year, in situ observations. Specifically, we aim to (1) quantify the throughfall, stemflow, and interception components of rainfall under natural conditions for both species; (2) analyze how rainfall amount and intensity influence partitioning outcomes; (3) assess the role of shrub canopy characteristics, particularly coverage, in modifying rainfall redistribution; (4) provide empirical parameters to inform hydrological modeling in alpine shrub-dominated ecosystems. This study contributes to a better understanding of shrub-mediated water regulation in cold regions and offers insights for ecohydrological modeling and regional water balance assessments under changing climate and vegetation dynamics.

Table 1.
Summary of rainfall partitioning in shrub canopy in cold regions.
Table 1.
Summary of rainfall partitioning in shrub canopy in cold regions.
| Shrubs | Study Area | Period | R/mm | TF% | SF% | IC% | References |
|---|---|---|---|---|---|---|---|
| Birch | Trail Valley Creek, Western Canadian Arctic | 22 June to 28 August 2018 | 90 | 76 | 8 | 16 | Zwieback et al. (2019) [12] |
| Alder | 72 | 17 | 11 | ||||
| Potentilla fruticosa | Qinghai Lake, Qilian Mountains, China | June to October 2012 | 531.0 | 29.3 | 49.3 | 21.4 | Zhang et al. (2018) [26] |
| Potentilla fruticose | Shaliu River, Qilian Mountains, China | June to September 2012 | 231.6 | 44.5 | 18.6 | 36.5 | Zhang et al. (2023) [16] |
| Potentilla fruticose | Hulu catchment, Qilian Mountains, China | June to October 2010 | 298.6 | 62.0 | 3.4 | 34.6 | Liu et al. (2012) [24] |
| Caragana jubata | 60.2 | 4.2 | 35.6 | ||||
| Hippophae rhamnoides | 52.3 | 8.0 | 39.7 | ||||
| Salix cupularis | 63.5 | 3.2 | 33.3 | ||||
| Potentilla fruticose | Xishui, Qilian Mountains, China | May to September 2014 | 483.3 | 64.76 | 2.85 | 32.39 | Liu et al. (2016) [15] |
| Salix cupularis | 540.7 | 58.70 | 4.05 | 37.25 | |||
| Caragana stenphylla | 388.1 | 66.38 | 4.28 | 29.34 | |||
| Berberis diaphana | 399.0 | 53.34 | 3.84 | 42.82 | |||
| Caragana jubata | 567.3 | 66.24 | 3.26 | 30.50 | |||
| Quercus aquifolioides | Wolong nature reserve, Southwest China | July to September 2011; June to August 2002 | 545.4 | 75.05 | NA | 24.9 | Li et al. (2006) [17] |
| Quercus aquifolioides | June to September 2007 | 486.7 | 82.6 | 0.9 | 16.5 | He et al. (2010) [27] | |
| Coyrlus heterpolal | Maoer Mountains, Northeast China | May to September 2004 | 352.6 | 75.2 | NA | 24.8 | Kong (2005) [28] |
| Sambucus mandehuriea | 78.7 | NA | 21.3 | ||||
| Sorbaira sorbfolia | 80.9 | NA | 19.1 | ||||
| Lespedeza bicolor | 88.1 | NA | 11.9 | ||||
| Spiraea ussrtiensis | 92.3 | NA | 7.7 | ||||
| Caragana jubata | Pailugou, Qilian Mountains, China | May 2007 to May 2008 | 410.6 | 83.3 | NA | 16.7 | Nie (2009) [25] |
| Salix gilashanica | 79.5 | NA | 20.5 | ||||
| Potentilla fruticosa | 89.5 | NA | 10.4 | ||||
| Berberis diaphana | 326.5 | 77.5 | NA | 22.4 | |||
| Caragana tangutica | 308.2 | 93.0 | NA | 7.0 | |||
| Caragana jubata | Tianlaochi, Qilian Mountains, China | July to September 2011; June to September 2012 | 674.7 | 58.9 | 0.9 | 40.2 | Liu (2013) [29] |
| Potentilla fruticosa | 697.6 | 69.8 | 1.3 | 28.9 | |||
| Myricaria squamosa | Qinghai Lake, Qilian Mountains, China | 6 July to 30 September 2010 | 156.6 | 48.40 | 4.04 | 47.5 | Ma et al. (2012) [30] |
TF% is throughfall percentage (%), SF% is stemflow percentage (%), and IC% is interception percentage (%). NA: indicates not measured in the literature.
2. Materials and Methods
2.1. Study Site
Field experiments were conducted at an alpine shrub site in the Hulu catchment, a representative cryospheric headwater basin located in the Qilian Mountains, northwestern China. The catchment spans an area of approximately 23.1 km2, between 38°12′ and 38°17′ N and 99°49′ to 99°54′ E, with elevations ranging from 2960 to 4800 m. The Hulu catchment was selected due to its hydrological significance as a typical alpine source region of the Heihe River Basin, China’s second-largest inland river. This region plays a crucial role in rainfall and snowmelt partitioning, representing typical cold-region eco-hydrological processes dominated by alpine shrubs and permafrost-affected soils.
In 2008, a Cryospheric Hydrometeorology Observation System (CHOICE) was established in the Hulu catchment [23,31], supporting long-term monitoring of precipitation, runoff, snow cover, and soil moisture. These conditions make it an ideal site for studying shrub-mediated rainfall redistribution in cold regions.
The climate is strongly continental, with a mean January temperature of −18.4 °C and a mean July temperature of 19.0 °C (2008–2021). The mean annual air temperature is −0.3 °C, and average annual precipitation is 599.8 mm, with approximately from 54.6 to 84.2% occurring as rainfall between June and October. The mean annual relative humidity is 54.2%, with peaks in July and August. The growing season, when vascular plants are active, typically spans late May to late September [32].
The Hulu catchment’s landscapes exhibit a gradient distribution with increasing elevation, including grassland, meadow, shrub, forest, marshy meadow, cushion plant, and so forth (Figure 1) [33]. The distribution of shrubs is primarily observed on the region’s shady, semi-shady, and semi-sunny slopes. The most prevalent shrub species in the study area include Potentilla fruticosa L., Caragana jubata Poir., Salix cupularis Rehd., and Salix oritrepha Schneid. Among them, P. fruticosa and C. jubata occur in patchy distributions across hillslopes and represent the dominant species in both the Hulu catchment and the broader Qilian Mountains region. These two alpine shrubs are ecologically important and hydrologically relevant as their distinct canopy structures and coverage patterns strongly influence rainfall partitioning, including throughfall, stemflow, and canopy interception. For this reason, P. fruticosa and C. jubata were selected as the focal species in this study.
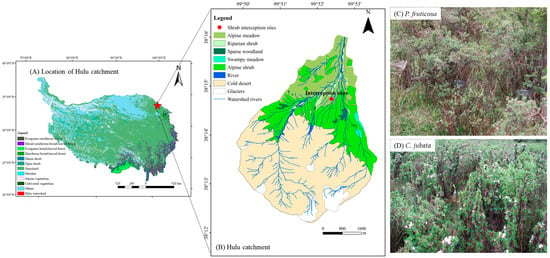
Figure 1.
Location of the study site and shrubland sample plots. (A) Map showing the location of the Hulu catchment within the Qilian Mountains; (B) vegetation distribution within the Hulu catchment based on remote sensing imagery; (C) Potentilla fruticosa (P. fruticosa) shrubland sample plot; (D) Caragana jubata (C. jubata) shrubland sample plot.
2.2. Shrubs Selection and Measurements
Following the field survey, representative P. fruticosa and C. jubata shrubs were selected, and standard plots measuring 10 m × 10 m were established for each species (Figure 1). This plot size has been widely used in alpine shrub studies to ensure adequate representation of canopy structure and shrub distribution patterns. The stem diameter of each shrub was measured at the base of the stem using a vernier caliper, and the stem angle was determined using a protractor [16]. The leaf area index (LAI) was estimated using a CI-110 Plant Canopy Imager (CID Bio-Science, Inc., Camas, WA, USA). The CI-110 uses a fisheye lens and a CCD image sensor to capture images of the plant canopy. Through specialized software analysis, it provides measurements of the leaf area index (LAI) and other canopy-related parameters. Shrub coverage was measured using the quadrat method. Several standard quadrats of 2 m × 2 m were established within the study area. The horizontal projected area of shrubs on the ground within each quadrat was recorded, and the proportion of this area relative to the total quadrat area was calculated [24]. Coverage was expressed as a percentage. The height of the shrub canopy was measured at its center. Canopy area was calculated by approximating it as an ellipse, with the east–west and north–south diameters measured at the fullest part of the canopy. The elliptical model provides a practical and effective method for estimating canopy area in field conditions and has been validated in previous ecological research [2]. The data collected for each shrub included (1) basal diameter (D: diameter 10 cm above ground, in cm) measured using a digital caliper; (2) height (H: height from ground level to the tallest point of the canopy, in cm); and (3) crown area (C: crown width multiplied by crown length at right angles, in cm2) (Table 2).

Table 2.
Descriptive characteristics of P. fruticose and C. jubata selected in the experiments.
2.3. Throughfall and Stemflow Measurements
Rainfall partitioning by the shrub canopy is typically divided into three components: interception loss (IC), stemflow (SF), and throughfall (TF). Since interception loss cannot be directly measured under field conditions, it was estimated indirectly using the water balance method based on simultaneous measurements of rainfall above the canopy (P), throughfall, and stemflow:
where IC is interception loss (mm), P is rainfall up the canopy (mm), TF is throughfall (mm), and SF is stemflow (mm).
This approach assumes negligible runoff and deep percolation during individual rainfall events, which is reasonable in the context of short-term precipitation on sloped shrubland. However, we acknowledge that this method may be affected by instrumental errors, evaporation from wet canopies, and unmeasured water storage on branches or leaves, which could introduce uncertainties in the estimation of interception loss. These factors are considered in the interpretation of results.
The P was measured by a DSJ2-type siphon self-counting rain gauge and S204 weighing self-counting rain gauge with a resolution of 0.1 mm, and a mini logger recording 10 min rainfall intensity values was installed in an open area approximately 60 m from the study plot. Rainfall events were discretized using a minimum inter-event time of 8 h, which allows adequate time for the shrub canopy to dry between events. This threshold is commonly adopted in interception studies to ensure that each rainfall event is hydrologically independent [6,26]. Air temperature, relative humidity, incoming solar radiation, and wind speed at 2 m were measured every 30 s, and 10 min averages were recorded by an automatic weather station with a CR1000 Logger (Campbell Scientific, Logan, UT, USA).
Throughfall (TF) was measured using 16 collecting bottles per plot (10 cm diameter, 15 cm height), each fitted with a funnel to minimize evaporation of collected water. After determining the canopy cover within each sample plot, nine throughfall collectors were strategically placed beneath varying canopy densities and depressions to capture spatial variability in throughfall. This sampling strategy improves the spatial representativeness of throughfall measurements and allows for more accurate estimation of rainfall partitioning under shrub canopies [26].
Stemflow (SF) was measured following the method of Han et al. (2018) [23]. In each shrub plot, six stemflow collectors were installed. For each selected shrub, a flexible polyethylene tube (inner diameter: 0.8 cm) was split longitudinally, wrapped around the main stem below the branching point, and sealed tightly using waterproof plastic tape to direct stemflow into a graduated collection bottle. The mouth of the bottle was closely fitted to the tubing to prevent the intrusion of rainfall or throughfall, ensuring that only stemflow was collected. The collected stemflow volume in each bottle was manually measured and divided by the projected area of the associated branch to obtain stemflow per unit area. The total stemflow of the shrub was then estimated by multiplying the per-branch value by the total number of similar branches. This setup was tested in the field to confirm accuracy and completeness of stemflow collection. However, we acknowledge that minor potential losses may occur due to leakage around the tape seals, evaporation from tubing, or clogging by debris, and these uncertainties were minimized through regular maintenance and inspection during the observation period [26].
Stemflow depth was calculated as
where SF is the stemflow depth (mm), VSF is the stemflow volume (L), and CA is the canopy area (m2).
In this study, only the rainfall partitioning process by shrub patches was considered, whereas in the interspaces, grass patches between shrub patches were not considered.
2.4. Statistical Analyses
To examine differences among data groups, we conducted one-way ANOVA followed by Least Significant Difference (LSD) tests. Prior to ANOVA, we tested the assumptions of normality (using the Shapiro–Wilk test) and homogeneity of variance (using Levene’s test). All assumptions were met before proceeding with the analysis. Pearson’s correlation coefficients were calculated to assess linear relationships between shrub morphological traits and rainfall partitioning metrics. A significance level of α = 0.05 was applied for all inferential statistics. Descriptive statistics were generated for both shrub structure parameters and rainfall characteristics, including rainfall depth and intensity.
To explore the influence of rainfall characteristics on partitioning components (throughfall, stemflow, and interception), we employed multiple linear regression analysis, which allows for quantifying the relative contribution of each explanatory variable. This method was selected due to its suitability in identifying multi-factor interactions under field conditions.
All statistical analyses were conducted using SPSS 22.0 software (SPSS Inc., Chicago, IL, USA). The regression models may be affected by potential multicollinearity among explanatory variables, and the limited number of rainfall events could constrain the generalizability of the statistical relationships. These limitations were considered in the interpretation of the results.
3. Results
3.1. Rainfall Characteristics During Growing Season
A total of 197 rainfall events were recorded during the experimental period, covering three growing seasons: 2010 (1 June–6 October), 2011 (2 June–2 October), and 2012 (5 May–3 October), with a cumulative rainfall of 1084.6 mm (Figure 2).
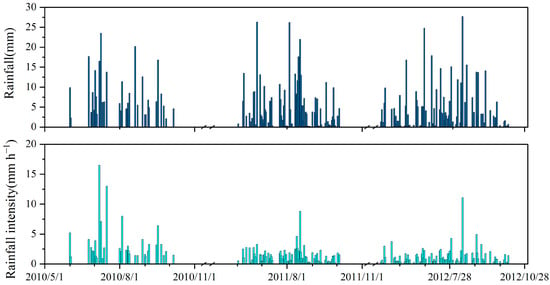
Figure 2.
Daily rainfall (in mm) and intensity (in mm h−1) on the Hulu catchment on growing season during 2010–2012.
Individual rainfall amounts ranged from 0.3 to 27.7 mm, with a multi-year average of 7.6 mm, while rainfall intensity ranged from 0.2 to 16.5 mm h−1, averaging 1.7 mm h−1.
One-way ANOVA indicated that mean daily rainfall amount and rainfall intensity varied significantly among the three years (p < 0.05), with 2012 showing the highest mean rainfall and intensity and 2011 the lowest. These interannual differences are relevant to understanding the variability in canopy rainfall partitioning. One-way ANOVA indicated that mean daily rainfall amount and rainfall intensity varied significantly among the three years (p < 0.05), with 2012 showing the highest mean rainfall and intensity and 2011 the lowest. These interannual differences are relevant to understanding the variability in canopy rainfall partitioning.
Rainfall events were further classified into six categories based on rainfall amount (Figure 3). The distribution of precipitation amounts was positively skewed: events in the 0–10 mm category were most frequent, making up 82.3% of all events. Among these, 32.5% were less than 2.0 mm, contributing only 4.6% of the total rainfall. Rainfall events exceeding 5 mm accounted for 76.7% of the total precipitation. Events greater than 10 mm constituted 16.8% of events but contributed 49.1% of the total rainfall (Figure 3). These findings highlight the dominance of small, frequent rainfall events in the study area, and the disproportionate contribution of larger events to the seasonal rainfall total.
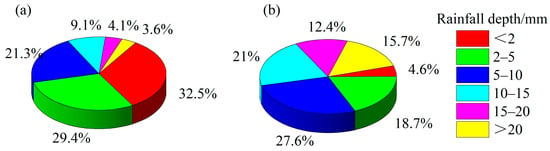
Figure 3.
Percentage distribution of rainfall events (a) and amount (b) under different rainfall class on the Hulu catchment during experimental period.
3.2. Rainfall Partitioning Percentage of Alpine Shrub
Among the 197 rainfall events, 61 were retained by the shrub canopy, while 136 were throughfall events. The threshold rainfall depth required to generate throughfall and stemflow was determined to be 1.9 mm.
Figure 4 presents the percentage distribution of stemflow (SF), throughfall (TF), and interception (IC) for alpine shrubs in the Hulu catchment. For P. fruticosa, the total throughfall depth was 726.2 mm, corresponding to an average of 66.96% ± 2.15% of total rainfall (95% CI). For C. jubata, throughfall totaled 729.0 mm, accounting for 67.31% ± 2.08%. A statistically significant difference was observed between the two species in terms of TF (p < 0.05). P. fruticosa produced a total stemflow of 36.6 mm (3.51% ± 0.46%), while C. jubata produced 44.6 mm (7.27% ± 0.52%), with the difference also being statistically significant (p < 0.05). However, no significant difference was found in the percentage of interception loss between the two species (p > 0.05) despite slight differences in absolute values (Figure 4). These results confirm species-specific partitioning patterns and variability within confidence bounds, increasing the reliability of the findings.
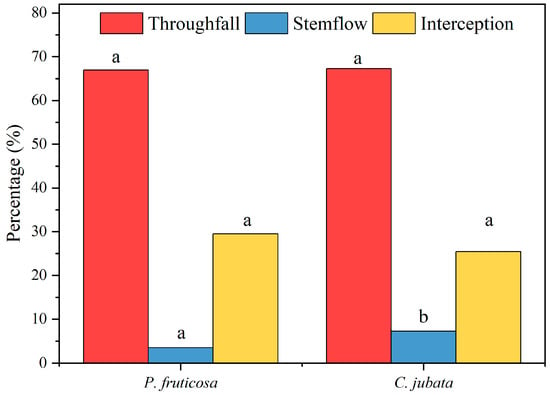
Figure 4.
The average percentages of stemflow, throughfall, and interception loss for P. fruticosa and C. jubata, respectively. Values with different letters in the percentages of stemflow, throughfall, and interception loss between P. fruticosa and C. jubata indicate significant differences at p < 0.05.
3.3. Rainfall Partitioning in Relation to Rainfall Amount
A significant positive correlation was found between individual rainfall amount and throughfall depth for both P. fruticosa and C. jubata (Figure 5a). Accordingly, regression models were fitted to describe the relationship (Figure 5b). The throughfall percentage increased with rainfall depth, eventually stabilizing at approximately 8 mm for C. jubata and 10 mm for P. fruticosa (Figure 5b). This stabilization suggests that the canopy water-holding capacity of each species had been exceeded, and drip formation and gravity-driven drainage began to dominate. The earlier stabilization for C. jubata may be attributed to its sparser canopy structure and lower leaf surface roughness, which reduce interception capacity compared to P. fruticosa.
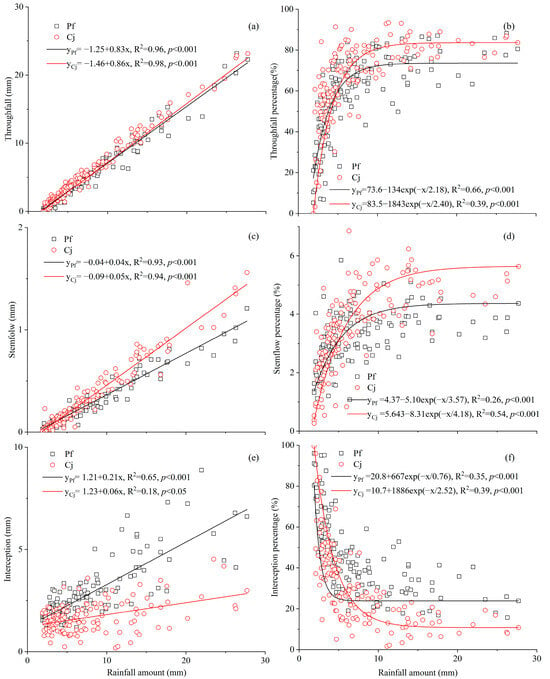
Figure 5.
Rainfall partitioning and its relationship with rainfall amount for P. fruticosa and C. jubata. (a) Throughfall (TF), (b) Stemflow (SF), (c) Interception (IC), (d) Throughfall percentage (TF%), (e) Stemflow percentage (SF%), and (f) Interception percentage (IC%).
Stemflow depth was significantly and positively correlated with rainfall (p < 0.001, Figure 5c). The stemflow percentage followed an exponential trend, increasing with rainfall before reaching an asymptote (Figure 5d). According to the fitted curves, stemflow stabilized when rainfall exceeded 10 mm. Interestingly, C. jubata produced a higher stemflow percentage under low rainfall conditions (<4.7 mm), likely due to its smooth stem surfaces and upright branching, which facilitate efficient water channeling. For interception loss, both species showed a positive linear relationship between rainfall depth and interception volume (Figure 5e), while the percentage of interception decreased exponentially with increasing rainfall (Figure 5f). This is consistent with the saturation behavior of the canopy: at low rainfall, a large fraction of precipitation is retained, but as rainfall continues, the canopy becomes saturated, and excess water is increasingly transferred as throughfall or stemflow. The interception loss percentage stabilized beyond 14 mm, indicating that additional rainfall no longer contributes proportionally to interception. P. fruticosa maintained higher interception percentages than C. jubata, which can be explained by its denser foliage, greater leaf area, and higher surface water storage potential.
3.4. Rainfall Partitioning in Relation to Rainfall Intensity
The individual amounts of throughfall, stemflow, and interception, as well as the percentages of throughfall and stemflow, increased with rainfall intensity up to approximately 4 mm h−1, after which they stabilized (Figure 6a–e). These relationships were best described by exponential saturation functions, which provided a better fit than linear or polynomial models. Model comparison using R2 and Root Mean Square Error (RMSE) indicated that the exponential function yielded superior goodness-of-fit across all partitioning components. For instance, the exponential model for stemflow depth produced an R2 of 0.84 with an RMSE of 0.32 mm, outperforming linear alternatives. Residual analysis confirmed no significant heteroscedasticity or systematic patterns, supporting the suitability of the exponential fit.
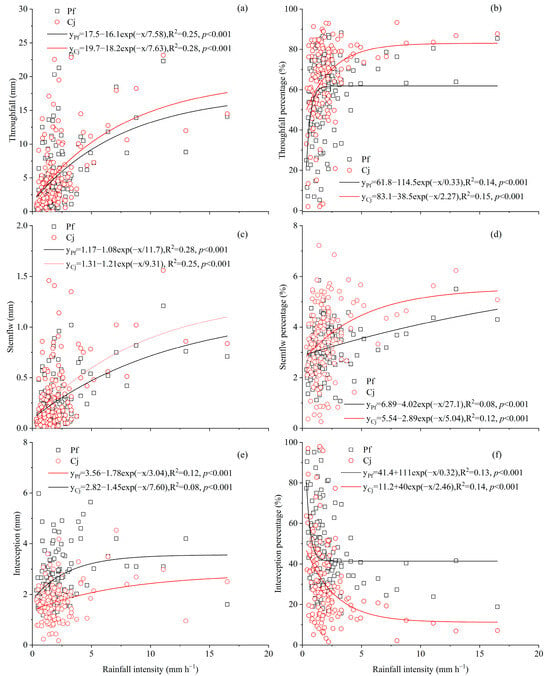
Figure 6.
Rainfall partitioning and its relationship with rainfall intensity for P. fruticosa and C. jubata. (a) Throughfall (TF), (b) Stemflow (SF), (c) Interception (IC), (d) Throughfall percentage (TF%), (e) Stemflow percentage (SF%), and (f) Interception percentage (IC%).
For P. fruticosa and C. jubata, the fitted models revealed the following asymptotic (stabilized) values: Stemflow depth: 1.17 mm (P. fruticosa) and 1.30 mm (C. jubata) (Figure 6a). Stemflow percentage: 6.89% and 5.54%, respectively (Figure 6b). Throughfall depth: 17.51 mm and 19.73 mm (Figure 6c). Throughfall percentage: 61.88% and 83.07% (Figure 6d). Interception loss depth: 3.56 mm and 2.82 mm (Figure 6e). Interception percentage: 41.42% and 11.26% (Figure 6f). Correlation analysis revealed that among all the meteorological variables assessed, only precipitation amount and intensity showed significant correlations with throughfall, stemflow, and interception (p < 0.05), while air temperature, relative humidity, and wind speed did not exhibit statistically significant effects.
This result is likely because rainfall partitioning occurs on short timescales, during which other meteorological factors remain relatively stable or have a secondary influence compared to direct rainfall input. Similar findings have been reported in other cold-region shrubland studies [34], where precipitation remains the dominant factor driving canopy water fluxes. Further insights may be gained in future studies by incorporating high-frequency micrometeorological data or controlled rainfall simulation experiments.
3.5. Correlations and Regression Analysis Between Rainfall Partitioning and Meteorological and Canopy Variables
The rainfall allocation variables for both P. fruticosa and C. jubata were analyzed for their correlation with air temperature, relative humidity, wind speed, radiation, and precipitation. No statistically significant correlations were found between these variables and the rainfall redistribution variables, except for precipitation. During our experimental periods, rainfall intensity showed a significant positive relationship with the increasing rainfall amount.
To better understand the combined influence of rainfall characteristics and vegetation structure, we incorporated canopy coverage (%) as an additional explanatory variable into the multiple linear regression models. The updated regression equations are presented in Table 3, showing improved model fits compared to rainfall-only models. The applicable range for the presented equations in Table 3 is when rainfall (RA) is greater than 1.9 mm.

Table 3.
Multiple linear regression analysis of rainfall partitioning and rainfall characteristics for P. fruticose and C. jubata.
Canopy coverage showed a significant negative effect on TF while positively affecting SF and IC, further confirming the structural role of vegetation in modifying rainfall partitioning. The updated models explained over 80% of the variance in TF and IC, and around 76% in SF, suggesting that combining meteorological and vegetation factors provides a more robust prediction of rainfall redistribution processes in alpine shrublands.
In addition to meteorological variables, we further analyzed the correlation between canopy coverage (%) and rainfall partitioning components (TF, SF, and IC) for both P. fruticosa and C. jubata. The results showed that canopy coverage was significantly negatively correlated with TF (p < 0.001) and positively correlated with both SF (p < 0.001) and IC (p < 0.01). This indicates that higher vegetation density enhances interception and stemflow, while reducing the proportion of direct throughfall. These patterns highlight the importance of shrub structural traits in regulating rainfall partitioning processes and support the view that TF, SF, and IC are jointly controlled by both rainfall characteristics and vegetation properties.
4. Discussions
4.1. Rainfall Partitioning by Shrubs in Cold Regions
Rainfall partitioning by shrub canopies varies significantly across biomes. Global meta-analyses suggest median values of rainfall interception (IC), stemflow (SF), and throughfall (TF) at 21.8%, 3.2%, and 73.0%, respectively [7]. However, the interception ratios for shrubs range widely—from 6.98% to as high as 68.3%—depending on vegetation type, climatic conditions, and rainfall characteristics [20]. Shrubs in cold, humid alpine regions tend to intercept more rainfall compared to those in arid or semi-arid regions due to higher precipitation input and denser canopy structures [2].
In our study, shrubs in the Hulu catchment exhibited interception values within the higher end of the global range. For example, P. fruticosa showed interception ratios of 34.6%, which is consistent with previous observations in the Qilian Mountains: 21.4% at Qinghai Lake, 36.5% at Shaliu River, and 10.4%–20.5% in the drier lower-altitude Gansu section [16,24]. High interception rates observed for Myricaria squamosa (47.5%) further highlight species-specific variability [30].
The observation duration also affects interception estimates. Interception percentages calculated over three growing seasons were generally lower than those from single-season studies, possibly due to seasonal variability and the inclusion of dry or non-growing periods [24]. Moreover, plant morphology plays a pivotal role: shrubs with dense branching and high leaf area index tend to exhibit higher interception efficiency [35]. These findings reinforce the importance of considering both climatic and biological factors when assessing the hydrological role of alpine shrubs.
4.2. Drivers of Rainfall Partitioning in Cold Environments
Among meteorological factors, precipitation amount and intensity exert the greatest influence on TF, SF, and IC [36]. Our results show that throughfall and stemflow increased with rainfall depth, while the percentage of interception decreased exponentially—a trend well captured by non-linear models (Figure 5). These findings are consistent with other studies in alpine regions [26,29,37] and highlight the existence of species-specific rainfall thresholds: TF stabilized above 10 mm for P. fruticosa and 8 mm for C. jubata, while IC percentage plateaued beyond 14 mm.
Rainfall intensity also significantly affected partitioning patterns. For P. fruticosa, interception sharply declined when intensity exceeded 2 mm·h−1, while C. jubata required over 5 mm·h−1 to reach a similar stabilization. These thresholds align with findings from Liu et al. (2012) [38], who reported that stemflow rate stabilized when the 10 min maximum rainfall intensity (I10) exceeded 6.0 mm·h−1 [24]. Hence, canopy saturation and drip/flow dynamics appear to regulate rainfall partitioning under varying storm intensities.
Stemflow dynamics are also influenced by canopy architecture and morphology [39,40]. P. fruticosa shrubs possess smooth, vertically oriented stems and high stem density (up to 385 stems/m2), facilitating stemflow under light rainfall [26]. In contrast, C. jubata has rougher stems and spiny twigs, which limit stemflow under light rain but allow more accumulation and flow during heavier events [24]. This morphological divergence explains why C. jubata exhibits greater stemflow volumes during intense rain, contributing to deep soil recharge—a critical ecological function under drought-prone conditions.
4.3. Structural and Ecological Implications
Beyond meteorological variables, vegetation structure, particularly canopy coverage, significantly influences rainfall partitioning [41,42]. Our correlation analysis showed that coverage was negatively correlated with throughfall and positively correlated with both interception and stemflow (Table 3). Denser shrub canopies increase storage capacity, reduce TF, and enhance water redistribution via SF and IC pathways.
This complex interaction between rainfall characteristics and vegetation traits underscores the need for integrating hydrological models with ecological structure parameters to better understand water cycling in alpine shrublands [4,32]. Moreover, considering the role of interception in total evapotranspiration (ET) remains a future research priority, especially under shifting precipitation regimes due to climate change [43].
5. Conclusions
No stemflow or throughfall was observed when rainfall amounts were below 1.9 mm, indicating complete interception by alpine shrub canopies under low-precipitation conditions. For P. fruticosa, the average proportions of throughfall, stemflow, and interception loss were 66.96%, 3.51%, and 29.53%, respectively. For C. jubata, the corresponding values were 67.31%, 7.27%, and 25.42%. These differences reflect species-specific morphological traits influencing rainfall partitioning. C. jubata exhibited higher stemflow production efficiency and lower interception loss than P. fruticosa, suggesting its greater potential in facilitating soil moisture recharge. The two shrubs showed distinct rainfall redistribution patterns, implying their unique roles in regulating local hydrological balance, particularly in seasonal permafrost environments. Rainfall partitioning was governed by both vegetation structure—such as canopy area, height, branch number, and stem basal area—and rainfall characteristics, including amount, intensity, and duration. While rainfall traits were the dominant driver within species, their hydrological impacts varied with plant morphology. These findings underscore the necessity of incorporating species-specific partitioning behavior into hydrological modeling in cold regions. Future studies should integrate detailed canopy traits and dynamic meteorological inputs to enhance understanding of shrub water regulation and improve predictive capacity under changing climatic conditions.
Author Contributions
Conceptualization, Z.L.; Data Curation, Y.T., J.Q. and Z.D.; Formal Analysis, Y.T. and C.H.; Funding Acquisition, Z.L. and R.C.; Investigation, Y.T.; Methodology, Z.L. and Y.Y.; Project Administration, Z.L. and R.C.; Resources, C.H.; Software, Z.L.; Supervision, Z.L.; Visualization, C.H.; Writing—Original Draft, Z.L.; Writing—Review and Editing, Z.L., R.C., C.H. and Y.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Gansu Provincial Science and Technology Planning Project (24ZD13FA004) and the National Natural Science Foundation of China (42171147).
Data Availability Statement
The data for this study are available by contacting Z.L. at zwliu@lzb.ac.cn.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Muzylo, A.; Llorens, P.; Valente, F.; Keizer, J.J.; Domingo, F.; Gash, J.H.C. A review of rainfall interception modelling. J. Hydrol. 2009, 370, 191–206. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuan, C.; Chen, N.; Levia, D.F. Rainfall partitioning by vegetation in China: A quantitative synthesis. J. Hydrol. 2023, 617, 128946. [Google Scholar] [CrossRef]
- Zhang, Y.-F.; Pan, Y.-X.; Hu, R.; Wang, X.-P. Differential intra-specific stemflow funnelling efficiencies of Caragana korshinskii within arid desert ecosystems. Hydrol. Res. 2017, 48, 1611–1623. [Google Scholar] [CrossRef]
- Shachnovich, Y.; Berliner, P.R.; Bar, P. Rainfall interception and spatial distribution of throughfall in a pine forest planted in an arid zone. J. Hydrol. 2008, 349, 168–177. [Google Scholar] [CrossRef]
- Li, X.-Y.; Liu, L.; Gao, S.; Ma, Y.; Yang, Z. Stemflow in three shrubs and its effect on soil water enhancement in semiarid loess region of China. Agric. For. Meteorol. 2008, 148, 1501–1507. [Google Scholar] [CrossRef]
- Yang, J.; Wang, A.; Shen, L.; Dai, G.; Liu, Y.; Zhang, Y.; Fei, W.; Wu, J. The Impact of Canopy on Nutrient Fluxes through Rainfall Partitioning in a Mixed Broadleaf and Coniferous Forest. Forests 2024, 15, 623. [Google Scholar] [CrossRef]
- Yue, K.; De Frenne, P.; Fornara, D.A.; Van Meerbeek, K.; Li, W.; Peng, X.; Ni, X.; Peng, Y.; Wu, F.; Yang, Y.; et al. Global patterns and drivers of rainfall partitioning by trees and shrubs. Glob. Change Biol. 2021, 27, 3350–3357. [Google Scholar] [CrossRef]
- Qian, Y.; Shi, C.; Zhao, T.; Lu, J.; Bi, B.; Luo, G. Canopy Interception of Different Rainfall Patterns in the Rocky Mountain Areas of Northern China: An Application of the Revised Gash Model. Forests 2022, 13, 1666. [Google Scholar] [CrossRef]
- Carlyle-Moses, D.E. Throughfall, stemflow, and canopy interception loss fluxes in a semi-arid Sierra Madre Oriental matorral community. J. Arid Environ. 2004, 58, 181–202. [Google Scholar] [CrossRef]
- Levia, D.F.; Germer, S. A review of stemflow generation dynamics and stemflow-environment interactions in forests and shrublands. Rev. Geophys. 2015, 53, 673–714. [Google Scholar] [CrossRef]
- Magliano, P.N.; Whitworth-Hulse, J.I.; Baldi, G. Interception, throughfall and stemflow partition in drylands: Global synthesis and meta-analysis. J. Hydrol. 2019, 568, 638–645. [Google Scholar] [CrossRef]
- Zwieback, S.; Chang, Q.; Marsh, P.; Berg, A. Shrub tundra ecohydrology: Rainfall interception is a major component of the water balance. Environ. Res. Lett. 2019, 14, 248. [Google Scholar] [CrossRef]
- Melo Neto, J.O.; Rodrigues, A.F.; Mello, C.R. On Canopy Rainfall Interception Modeling in a Eucalyptus Plantation. Forests 2024, 15, 1577. [Google Scholar] [CrossRef]
- Van Stan, J.T.; Gordon, D.A. Mini-Review: Stemflow as a Resource Limitation to Near-Stem Soils. Front. Plant Sci. 2018, 9, 248. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Zhang, X.; Zhao, W.; Chen, Z.; Yang, X.; Miao, Y.; Zhang, K. Comprehensive assessment of hydrological impacts of sub-alpine shrubs in Xishui Forest Area of Qilian Mountains. Arid. Land Geogr. 2016, 39, 86–94. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, X.; Zhang, S.; Wu, H.; Shi, F.; Li, W.; Yuan, C. Estimating rainfall interception of xerophytic deciduous shrubs by static- and variable-parameter Gash models with stem- and leaf-dominated canopy water storage. J. Hydrol. 2023, 625, 130031. [Google Scholar] [CrossRef]
- Li, Z.; Ouyang, Z.; Zheng, H.; Liu, X.; Su, Y. Comparison of rainfall redistribution in two ecosystems in Minjiang upper catchments, China. J. Plant Ecol. 2006, 30, 723–731. [Google Scholar]
- Garcia-Estringana, P.; Alonso-Blázquez, N.; Alegre, J. Water storage capacity, stemflow and water funneling in Mediterranean shrubs. J. Hydrol. 2010, 389, 363–372. [Google Scholar] [CrossRef]
- Klamerus-Iwan, A.; Błońska, E. Canopy storage capacity and wettability of leaves and needles: The effect of water temperature changes. J. Hydrol. 2018, 559, 534–540. [Google Scholar] [CrossRef]
- Zhong, F.; Jiang, S.; Koppa, A.; Ren, L.; Liu, Y.Y.; Wang, M.; Miralles, D.G. Multi-Decadal Dynamics of Global Rainfall Interception and Their Drivers. Geophys. Res. Lett. 2024, 19, e2024GL109295. [Google Scholar] [CrossRef]
- Myers-Smith, I.H.; Forbes, B.C.; Wilmking, M.; Hallinger, M.; Lantz, T.; Blok, D.; Tape, K.D.; Macias-Fauria, M.; Sass-Klaassen, U.; Lévesque, E.; et al. Shrub expansion in tundra ecosystems: Dynamics, impacts and research priorities. Environ. Res. Lett. 2011, 6, 045509. [Google Scholar] [CrossRef]
- Sadeghi, S.M.M.; Gordon, A.G.; Van Stan, J.T. A Global Synthesis of Throughfall and Stemflow Hydrometeorology. In Precipitation Partitioning by Vegetation: A Global Synthesis; Van Stan, I.J.T., Gutmann, E.D., Friesen, J., Eds.; Springer Nature: Cham, Switzerland, 2020; pp. 49–70. [Google Scholar] [CrossRef]
- Han, C.; Chen, R.; Liu, Z.; Yang, Y.; Liu, J.; Song, Y.; Wang, L.; Liu, G.; Guo, S.; Wang, X. Cryospheric Hydrometeorology Observation in the Hulu Catchment (CHOICE), Qilian Mountains, China. Vadose Zone J. 2018, 17, 180058. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, R.; Song, Y.; Han, C. Characteristics of rainfall interception for four typical shrubs in Qilian Mountain. Acta Ecol. Sin. 2012, 32, 1337–1346. [Google Scholar] [CrossRef][Green Version]
- Nie, X. Study on Water Conservation Function of Shrub in Qilian Mountains. Master’s Thesis, Gansu Agriculture University, Lanzhou, China, 2009. [Google Scholar]
- Zhang, S.Y.; Li, X.Y.; Jiang, Z.Y.; Li, D.Q.; Lin, H. Modelling of rainfall partitioning by a deciduous shrub using a variable parameters Gash model. Ecohydrology 2018, 11, e2011. [Google Scholar] [CrossRef]
- He, C.-Q.; Xue, J.-H.; Wu, Y.-B.; Zhang, L.-Y. Application of a revised Gash analytical model to simulate subalpine Quercus aquifolioides forest canopy interception in the upper reaches of Minjiang River. Acta Ecol. Sin. 2010, 30, 8. [Google Scholar]
- Kong, L. Assessment and Mechanism of the Shrub Water Conservation Function in East Mountainous Region of Heilongjiang Province. Master’s Thesis, Northeast Forestry University, Harbin, China, 2005. [Google Scholar]
- Liu, Y. Study on Rainfall Interception Characteristic of Vegetation in a Typical Small Watershed, Upper Reach of Heihe River Basin. Master’s Thesis, Lanzhou University, Lanzhou, China, 2013. [Google Scholar]
- Ma, Y.-J.; Gao, S.-Y.; Li, X.-Y.; Lu, R.-J.; Zhang, S.Y.; Li, G.-Y. Rainfall canopy partitioning and its influencing factors of Riparian shrub in the Alpine region. J. Desert Res. 2012, 32, 9. [Google Scholar]
- Chen, R.S.; Song, Y.X.; Kang, E.S.; Han, C.T.; Liu, J.F.; Yang, Y.; Qing, W.W.; Liu, Z.W. A Cryosphere-Hydrology Observation System in a Small Alpine Watershed in the Qilian Mountains of China and Its Meteorological Gradient. Arct. Antarct. Alp. Res. 2014, 46, 505–523. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, R.; Qi, J.; Dang, Z.; Han, C.; Yang, Y. Control of Mosses on Water Flux in an Alpine Shrub Site on the Qilian Mountains, Northwest China. Plants 2022, 11, 3111. [Google Scholar] [CrossRef]
- Tian, Y.; Liu, Z.; Fan, Y.; Li, Y.; Tao, H.; Han, C.; Ao, X.; Chen, R. Patterns and Drivers of Surface Energy Flux in the Alpine Meadow Ecosystem in the Qilian Mountains, Northwest China. Plants 2025, 14, 155. [Google Scholar] [CrossRef]
- Yaokui, C.; Li, J.; Guangcheng, H.; Jie, Z. Mapping of Interception Loss of Vegetation in the Heihe River Basin of China Using Remote Sensing Observations. IEEE Geosci. Remote Sens. Lett. 2015, 12, 23–27. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, C.; Liu, Y.; Chang, Y.; Huang, G.; Zang, F. Exploring the spatiotemporal distribution and driving factors of vegetation canopy rainfall interception in the Qilian Mountains, Northwest China. CATENA 2024, 237, 107829. [Google Scholar] [CrossRef]
- Chen, X.; Chen, L.; Yang, X.-g.; Li, M.; Yu, D.; Song, N. Rainfall partitioning characteristics by two sand-binding shrubs and their impact on shallow soil moisture replenishment in the Northwestern desert steppe of China. Ecohydrology 2024, 17, e2652. [Google Scholar] [CrossRef]
- Lu, S.; Yang, L.; Tang, W.; Tian, S.; Ma, R.; Sang, Y.; Zhang, J.; Zhang, Z.-H.; Shi, Y. Effects of plantations on rainfall redistribution in a rocky mountain area of North China. Hydrol. Process. 2024, 37, e14999. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, R.; Song, Y.; Han, C. Water holding capacity of mosses under alpine shrubs in Qilian Mountains. Arid Land Geogr. 2011, 37, 696–703. [Google Scholar]
- Yuan, C.; Gao, G.; Fu, B. Stemflow of a xerophytic shrub (Salix psammophila) in northern China: Implication for beneficial branch architecture to produce stemflow. J. Hydrol. 2016, 539, 577–588. [Google Scholar] [CrossRef]
- Yang, X.-G.; Chen, L.; Wang, L.; Wang, X.; Gu, J.-L.; Qu, W.-J.; Song, N.-P. Dynamic rainfall-partitioning relationships among throughfall, stemflow, and interception loss by Caragana intermedia. J. Hydrol. 2019, 574, 980–989. [Google Scholar] [CrossRef]
- Zhu, Z.; Shao, M.a.; Jia, X.; Zhao, C. Rainfall partitioning characteristics and simulation of typical shelter forest in Chinese Mu Us Sandy Land. Sci. Total Environ. 2024, 945, 174091. [Google Scholar] [CrossRef]
- Liu, X.; Jiao, L.; Bai, Y.; Li, Z.; Yuan, C.; Li, Z.; Gao, G. Rainfall partitioning in the Robinia pseudodcacia plantations with different thinning intensities in the semiarid Loess Plateau of China. Ecol. Front. 2025, 45, 257–267. [Google Scholar] [CrossRef]
- Gao, G.; Wang, D.; Zha, T.; Wang, L.; Fu, B. A global synthesis of transpiration rate and evapotranspiration partitioning in the shrub ecosystems. J. Hydrol. 2022, 606, 127417. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).