Stable Leaf Area Index Despite Shifts in Biomass Allocation and Leaf Traits: A Case Study in a Young European Beech Forest Under Intense Tree Competition
Abstract
1. Introduction
- (a)
- To study patterns in the long-term development of a dense beech stand originating from natural regeneration, focusing on key characteristics such as stand density, mean height, and mean diameter;
- (b)
- To observe tree mortality and mortality rate over time;
- (c)
- To develop stand-specific allometric models at two time points separated by a 10-year interval;
- (d)
- To quantify changes in biomass structure over the 10-year period;
- (e)
- To investigate leaf traits, with a particular emphasis on specific leaf area (SLA);
- (f)
- To compare the Leaf Area Index (LAI) and Leaf Area Ratio (LAR) between the two time points;
- (g)
- To examine how changes in these attributes are associated with increasing competition stress in young, naturally based European beech stands.
2. Materials and Methods
2.1. Site and Stand Conditions
2.2. Tree Measurements and Samplings
2.3. Calculations, Analyses, and Statistical Approaches
- LAij is the leaf area of the i-th tree in the j-th subplot, which is calculated as the product of the dry biomass of the leaves of the given tree and its specific leaf area derived depending on the diameter d0, i.e.,
- Wl is the leaf biomass;
- Sj is the area of the j-th subplot.
- TPLA is the total projected leaf area of all leaves of the trees present in the plot (tree projected leaf area);
- Wl is the dry biomass of tree leaves in the plot;
- Ww is the dry aboveground biomass of trees in the plot;
- SLAp is the mean one-sided specific leaf area, which expresses how much one-sided leaf area corresponds to one gram of dry leaf mass.
3. Results
4. Discussion
4.1. Dynamics in Basic Stand Properties and Mortality
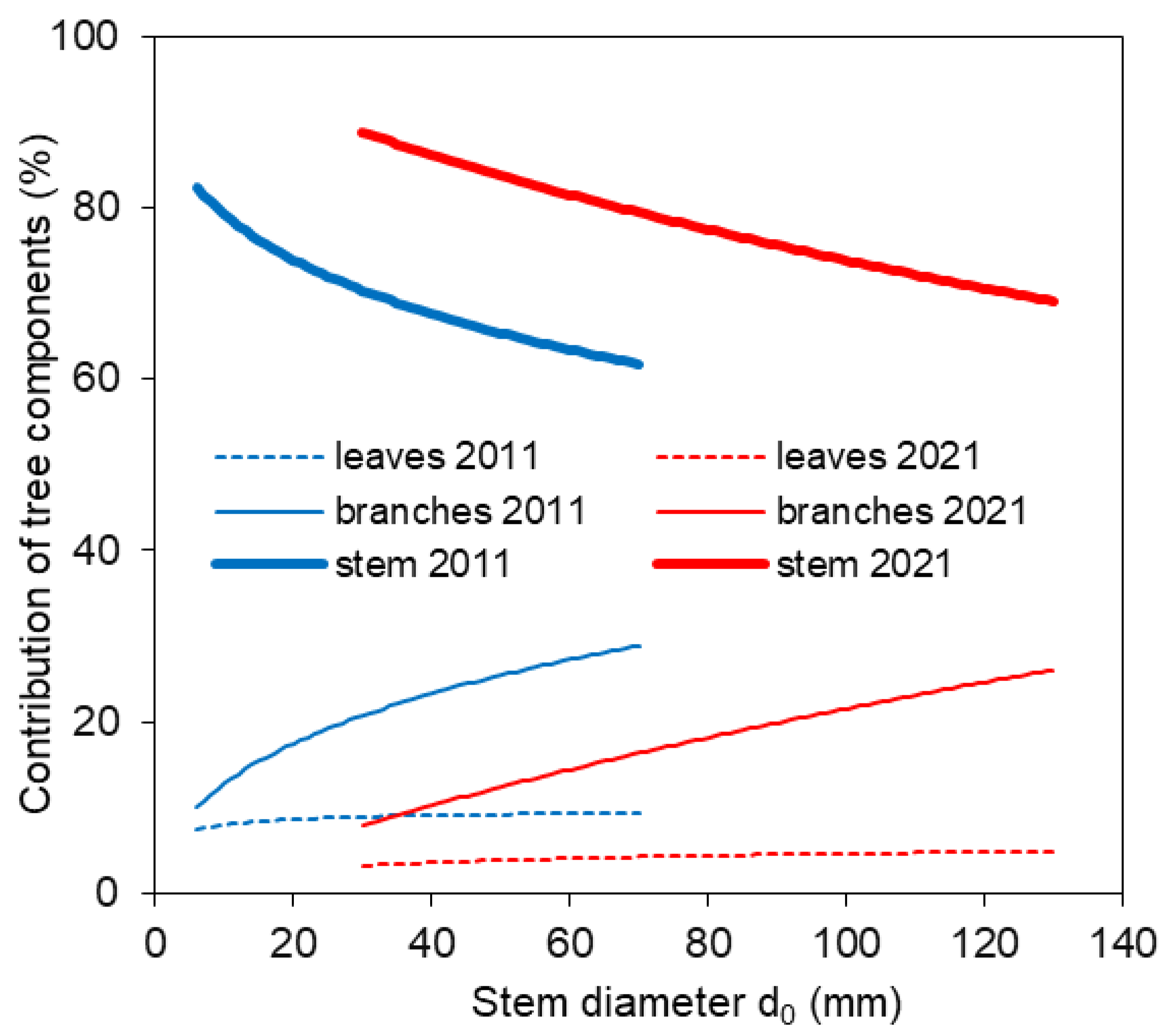
4.2. Changes in Biomass Allocation
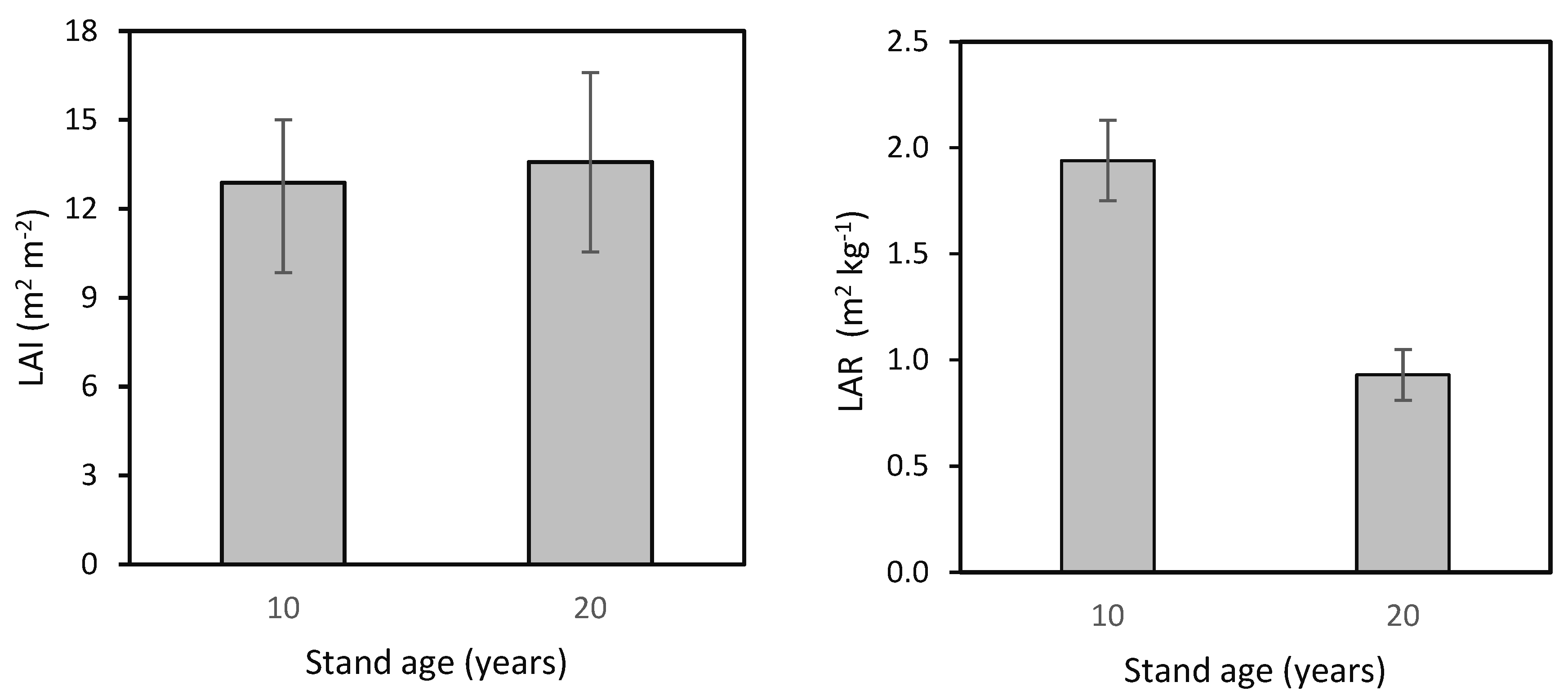
4.3. Changes in Leaf Traits
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Year | Eq. No | Tree Compartment | b0 | S.E. | p | b1 | S.E. | p | b2 | S.E. | p | R2 | MSE | λ | S.D. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2011 | (3) | Stem | −3.800 | 0.222 | <0.001 | 2.879 | 0.070 | <0.001 | 0.965 | 0.076 | 1.038 | 0.297 | |||
| Branches | −6.913 | 0.330 | <0.001 | 3.424 | 0.105 | <0.001 | 0.947 | 0.168 | 1.077 | 0.416 | |||||
| Leaves | −6.576 | 0.256 | <0.001 | 3.085 | 0.081 | <0.001 | 0.960 | 0.102 | 1.047 | 0.308 | |||||
| (4) | Stem | 2.569 | 0.116 | <0.001 | 2.787 | 0.110 | <0.001 | 0.914 | 0.189 | 1.093 | 0.476 | ||||
| Branches | 0.842 | 0.216 | <0.001 | 3.119 | 0.205 | <0.001 | 0.794 | 0.653 | 1.299 | 0.930 | |||||
| Leaves | 0.383 | 0.179 | 0.037 | 2.841 | 0.170 | <0.001 | 0.823 | 0.450 | 1.221 | 0.785 | |||||
| (5) | Stem | −1.763 | 0.216 | <0.001 | 1.905 | 0.093 | <0.001 | 1.069 | 0.093 | <0.001 | 0.989 | 0.024 | 1.011 | 0.152 | |
| Branches | −6.581 | −0.577 | <0.001 | 3.265 | 0.249 | <0.001 | 0.174 | 0.248 | 0.485 | 0.947 | 0.170 | 1.076 | 0.413 | ||
| Leaves | −5.943 | 0.439 | <0.001 | 2.783 | 0.190 | <0.001 | 0.332 | 0.189 | 0.083 | 0.962 | 0.098 | 1.045 | 0.305 | ||
| 2021 | (3) | Stem | −2.149 | 0.388 | <0.001 | 2.538 | 0.093 | <0.001 | 0.964 | 0.059 | 1.028 | 0.248 | |||
| Branches | −8.030 | 1.004 | <0.001 | 3.517 | 0.241 | <0.001 | 0.884 | 0.396 | 1.183 | 0.667 | |||||
| Leaves | −7.112 | 0.866 | <0.001 | 2.987 | 0.208 | <0.001 | 0.881 | 0.295 | 1.158 | 0.712 | |||||
| (4) | Stem | 0.887 | 0.531 | 0.106 | 3.425 | 0.241 | <0.001 | 0.879 | 0.198 | 1.094 | 0.465 | ||||
| Branches | −2.089 | 1.294 | 0.039 | 4.281 | 0.586 | <0.001 | 0.656 | 1.176 | 1.741 | 2.163 | |||||
| Leaves | −2.690 | 1.102 | 0.021 | 3.642 | 0.499 | <0.001 | 0.655 | 0.852 | 1.560 | 1.920 | |||||
| (5) | Stem | −1.682 | 0.220 | <0.001 | 1.785 | 0.106 | <0.001 | 1.215 | 0.150 | <0.001 | 0.989 | 0.018 | 1.008 | 0.126 | |
| Branches | −8.150 | 1.055 | <0.001 | 3.711 | 0.507 | <0.001 | −0.314 | 0.716 | 0.665 | 0.885 | 0.408 | 1.180 | 0.655 | ||
| Leaves | −7.205 | 0.911 | <0.001 | 3.137 | 0.437 | <0.001 | −0.242 | 0.618 | 0.698 | 0.881 | 0.304 | 1.158 | 0.707 |
References
- San-Miguel-Ayanz, J.; De Rigo, D.; Caudulo, G.; Durrant, T.H.; Mauri, A. European Atlas of Forest Tree Species; Publication Office of the European Union: Luxembourg, 2016; 200p. [Google Scholar]
- Walthert, L.; Graf Pannatier, E.; Meier, E.S. Shortage of nutrients and excess of toxic elements in soils limit the distribution of soil-sensitive tree species in temperate forests. For. Ecol. Manag. 2013, 297, 94–107. [Google Scholar]
- Barna, M.; Kulfan, J.; Bublinec, E. (Eds.) Beech and Beech Ecosystems of Slovakia; VEDA: Bratislava, Slovakia, 2011; 636p. [Google Scholar]
- Dieler, J.; Pretzsch, H. Morphological plasticity of European beech (Fagus sylvatica L.) in pure and mixed-species stands. For. Ecol. Manag. 2013, 295, 97–108. [Google Scholar] [CrossRef]
- Aleinikovas, M.; Linkevičius, E.; Kuliešis, A.; Rolhle, H.; Schroeder, J. The Impact of Competition for Growing Space on Diameter, Basal Area and Height Growth in Pine Trees. Balt. For. 2014, 20, 301–313. [Google Scholar]
- Schröter, M.; Härdtle, W.; von Oheimb, G. Crown plasticity and neighborhood interactions of European beech (Fagus sylvatica L.) in an old-growth forest. Eur. J. For. Res. 2012, 131, 787–798. [Google Scholar]
- Rubio, V.E.; Zambrano, J.; Iida, Y. Improving predictions of tropical tree survival and growth by incorporating measurements of whole leaf allocation. J. Ecol. 2021, 109, 1331–1343. [Google Scholar] [CrossRef]
- Le Goff, N.; Ottorini, J.M. Biomass distribution, allocation and growth efficiency in European beech trees of different ages in pure even-aged stands in northeast France. Cent. Eur. For. J. 2022, 68, 117–138. [Google Scholar]
- Wagner, S.; Collet, C.; Madsen, P.; Nakashizuka, T.; Nyland, R.D.; Sagheb-Talebi, K. Beech regeneration research: From ecological to silvicultural aspects. For. Ecol. Manag. 2010, 259, 2172–2182. [Google Scholar]
- Fichtner, A.; Sturm, K.; Rickert, C.; Härdtle, W.; Schrautezr, J. Competition response of European beech Fagus sylvatica L. varies with tree size and abiotic stress: Minimizing anthropogenic disturbances in forests. J. Appl. Ecol. 2012, 49, 1306–1315. [Google Scholar]
- Lifeng, P.; Wang, G.; Sharma, R.P.; Lu, J.; Tang, X.; Fu, L. Simulation of Thinning by Integrating Tree Competition and Species Biodiversity for Target Tree-Based Management of Secondary Forests. Forests 2023, 14, 1896. [Google Scholar] [CrossRef]
- Pajtík, J.; Konôpka, B.; Šebeň, V. Allometric models for estimating aboveground biomass of young Norway spruce trees in the Western Carpathians, Slovakia. Cent. Eur. For. J. 2022, 68, 154–162. [Google Scholar]
- Repáč, I.; Parobeková, Z.; Sendecký, M. Reforestation in Slovakia: History, current practice and perspectives. Reforesta 2017, 12, 53–88. [Google Scholar] [CrossRef]
- Konôpka, B.; Pajtík, J.; Šebeň, V.; Lukac, M. Decadal forest mensuration cycle significantly underestimates net primary production in dense young beech stands. For. Ecol. Manag. 2024, 555, 121711. [Google Scholar]
- Vile, D.; Garnier, E.; Shipley, B.; Laurent, G.; Navas, M.L.; Roumet, C.; Lavorel, S.; Díaz, S. Specific Leaf Area and Dry Matter Content Estimate Thickness in Laminar Leaves. Ann. Bot. 2005, 96, 1129–1136. [Google Scholar] [PubMed]
- Gao, J.; Wang, X.; Zhang, X. Patterns and drivers of community specific leaf area in China. Glob. Ecol. Conserv. 2022, 33, e01971. [Google Scholar]
- Poorter, H.; Niinemets, Ü.; Poorter, L.; Wright, I.J.; Villar, R. Causes and consequences of variation in leaf mass per area (LMA): A meta-analysis. New Phytol. 2009, 182, 565–588. [Google Scholar]
- Kozlowski, T.T.; Pallardy, S.G. Physiology of Woody Plants, 2nd ed.; Academic Press: Cambridge, UK, 1996; 469p. [Google Scholar]
- Anderson-Teixeira, K.J.; Herrmann, V.; Morgan, R.B.; Bond-Lamberty, J.; Cook-Patton, B.S.; Ferson, A.E.; Muller-Landau, H.C.; Wang, M.H. Carbon cycling in mature and regrowth forests globally. Environ. Res. Lett. 2021, 3, 053009. [Google Scholar]
- Fang, H.; Baret, F.; Plummer, S.; Schaepman-Strub, G. An Overview of Global Leaf Area Index (LAI): Methods, Products, Validation, and Applications. Rev. Geophys. 2019, 57, 739–799. [Google Scholar]
- Pokorný, R.; Tomášková, I.; Havránková, K. Temporal variation and efficiency of leaf area index in young mountain Norway spruce stand. Eur. J. For. Res. 2008, 127, 359–367. [Google Scholar]
- Larcher, W. Physiological Plant Ecology: Ecophysiology and Stress Physiology of Functional Groups, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2023; 513p. [Google Scholar]
- Nemani, R.R.; Running, S.W. Testing a theoretical climate–soil–leaf area hydrologic equilibrium of forests using satellite data and ecosystem simulation. Agric. For. Meteorol. 1989, 44, 245–260. [Google Scholar]
- Taugourdeau, S.; le Maire, G.; Avelino, J.; Jones, J.R.; Ramirez, L.G.; Quesada, M.J.; Charbonnier, F.; Gómez-Delgado, F.; Harmand, J.-M.; Rapidel, B.; et al. Leaf area index as an indicator of ecosystem services and management practices: An application for coffee agroforestry. Agric. Ecosyst. Environ. 2014, 192, 19–37. [Google Scholar] [CrossRef]
- Olamide, M. Estimation of Site-Specific Biomass and Leaf Area Index in a Young Scots pine Stand in Southern Sweden. Ph.D. Thesis, SLU Alnarp, Alnarp, Sweden, 2023; 42p. [Google Scholar]
- Konôpka, B.; Pajtík, J.; Šebeň, V.; Bošeľa, M.; Máliš, F.; Priwitzer, T.; Pavlenda, P. The research site Vrchslatina—An experimental design and the main aims. Lesn. Čas.—For. J. 2013, 59, 203–213. [Google Scholar] [CrossRef]
- Easlon, H.M.; Bloom, A.J. Easy Leaf Area: Automated digital image analysis for rapid and accurate measurement of leaf area. Appl. Plant Sci. 2014, 2, 1400033. [Google Scholar] [CrossRef] [PubMed]
- Pajtík, J.; Konôpka, B.; Lukac, M. Biomass functions and expansion factors in young Norway spruce (Picea abies [L.] Karst) trees. For. Ecol. Manag. 2008, 256, 1096–1103. [Google Scholar] [CrossRef]
- Opio, C.; Jacob, N.; Coopersmith, D. Height to diameter ratio as a competition index for young conifer plantations in northern British Columbia, Canada. For. Ecol. Manag. 2000, 137, 245–252. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, H.; Chhin, S.; Zhang, J. Effects of competition, age and climate on tree slenderness of Chinese fir plantations in southern China. For. Ecol. Manag. 2020, 485, 117815. [Google Scholar] [CrossRef]
- Zhang, B.; Sajjad, S.; Chen, K.; Zhou, L.; Zhang, Y.; Yong, K.K.; Sun, Y. Predicting Tree Height-Diameter Relationship from Relative Competition Levels Using Quantile Regression Models for Chinese Fir (Cunninghamia lanceolata) in Fujian Province, China. Forests 2020, 11, 183. [Google Scholar] [CrossRef]
- Xu, Q.; Lei, X.L.; Zang, H.; Zeng, W. Climate Change Effects on Height–Diameter Allometric Relationship Vary with Tree Species and Size for Larch Plantations in Northern and Northeastern China. Forests 2022, 13, 468. [Google Scholar] [CrossRef]
- Oliver, C.D.; Larson, B.C. Forest Stand Dynamics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1996; 520p. [Google Scholar]
- Pajtík, J.; Čihák, T.; Konôpka, B.; Merganičová, K.; Fabiánek, P. Annual tree mortality and felling rates in the Czech Republic and Slovakia over three decades. Cent. Eur. For. J. 2018, 64, 238–248. [Google Scholar]
- Larson, A.J.; Lutz, J.A.; Donato, D.C.; Freund, J.A.; Swanson, M.E.; Lambers, J.H.; Spruger, D.G.; Franklin, J.F. Spatial aspects of tree mortality strongly differ between young and old-growth forests. Ecology 2015, 96, 2855–2861. [Google Scholar] [CrossRef]
- Monserud, R.A.; Ledermann, T.; Sterba, H. Are Self-Thinning Constraints Needed in a Tree-Specific Mortality Model? For. Sci. 2004, 50, 848–858. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Z.; Chhin, S.; Wang, H.; Duan, A.; Zhang, J. Relative contributions of competition, stand structure, age, and climate factors to tree mortality of Chinese fir plantations: Long-term spacing trials in southern China. For. Ecol. Manag. 2020, 465, 118103. [Google Scholar] [CrossRef]
- Thorpe, H.C.; Astrup, R.; Trowbridge, A.; Coates, K.D. Competition and tree crowns: A neighborhood analysis of three boreal tree species. For. Ecol. Manag. 2010, 259, 1586–1596. [Google Scholar] [CrossRef]
- Yang, X.-Z.; Zhang, W.H.; He, Q.Y. Effects of intraspecific competition on growth, architecture and biomass allocation of Quercus liaotungensis. J. Plant Interact. 2018, 14, 284–294. [Google Scholar] [CrossRef]
- Jia, Q.; Luo, C.; Liu, Q.; Meng, S.; Zhou, G.; Zhuang, H. Biomass Allocation in Relation to Stand Age and Density in Natural Larix gmelinii Forests in Cold Temperate China. Nat. Environ. Pollut. Technol. 2016, 15, 1027–1033. [Google Scholar]
- Ma, S.H.; Eziz, A.; Tian, D.; Yan, Z.B.; Cai, Q.; Jiang, M.W.; Ji, C.J.; Fang, J.Y. Size- and age-dependent increases in tree stem carbon concentration: Implications for forest carbon stock estimations. J. Plant Ecol. 2020, 13, 233–240. [Google Scholar] [CrossRef]
- Goncalves, A.C. Effects of Forest Stand Structure in Biomass and Carbon. In Forest Biomass and Carbon; Shukla, G., Chakravarty, S., Eds.; IntechOpen: London, UK, 2018; pp. 28–42. [Google Scholar]
- Peralta, A.L.; Escudero, A.; de la Cruz, M.; Sanchez, A.M.; Luzuriaga, A.L. Functional traits explain both seedling and adult plant spatial patterns in gypsum annual species. Funct. Ecol. 2023, 37, 1170–1180. [Google Scholar] [CrossRef]
- Barna, M. Adaptation of European beech (Fagus sylvatica L.) to different ecological conditions: Leaf size variation. Pol. J. Ecol. 2024, 52, 34–45. [Google Scholar]
- Barna, M. Natural regeneration of Fagus sylvatica L.: A Review. Austrian J. For. Sci. 2011, 128, 71–91. [Google Scholar]
- Parker, G.G. Tamm review: Leaf Area Index (LAI) in both a determinant and a consequence of important processes in vegetation canopies. For. Ecol. Manag. 2020, 477, 118496. [Google Scholar] [CrossRef]
- Schlerf, M.; Atzberger, M.; Vohland, M.; Buddenbaum, H.; Seeling, S.; Hill, J. Derivation of forest leaf area index from multi- and hyperspectral remote sensing data. In New Strategies for European Remote Sensing; Oluic, M., Ed.; Millerpress: Rotterdam, The Netherlands, 2005; pp. 253–261. [Google Scholar]
- Marshall, J.D.; Waring, R.H. Comparison of methods of estimating leaf-area index in old-growth Douglas-fir. Ecology 1986, 40, 975–979. [Google Scholar] [CrossRef]
- Ramezani, M.R.; Bavani, A.R.; Jafari, M.; Peters, S. Investigating the leaf area index changes in response to climate change (case study: Kasilian catchment, Iran). SN Appl. Sci. 2020, 2, 501. [Google Scholar] [CrossRef]
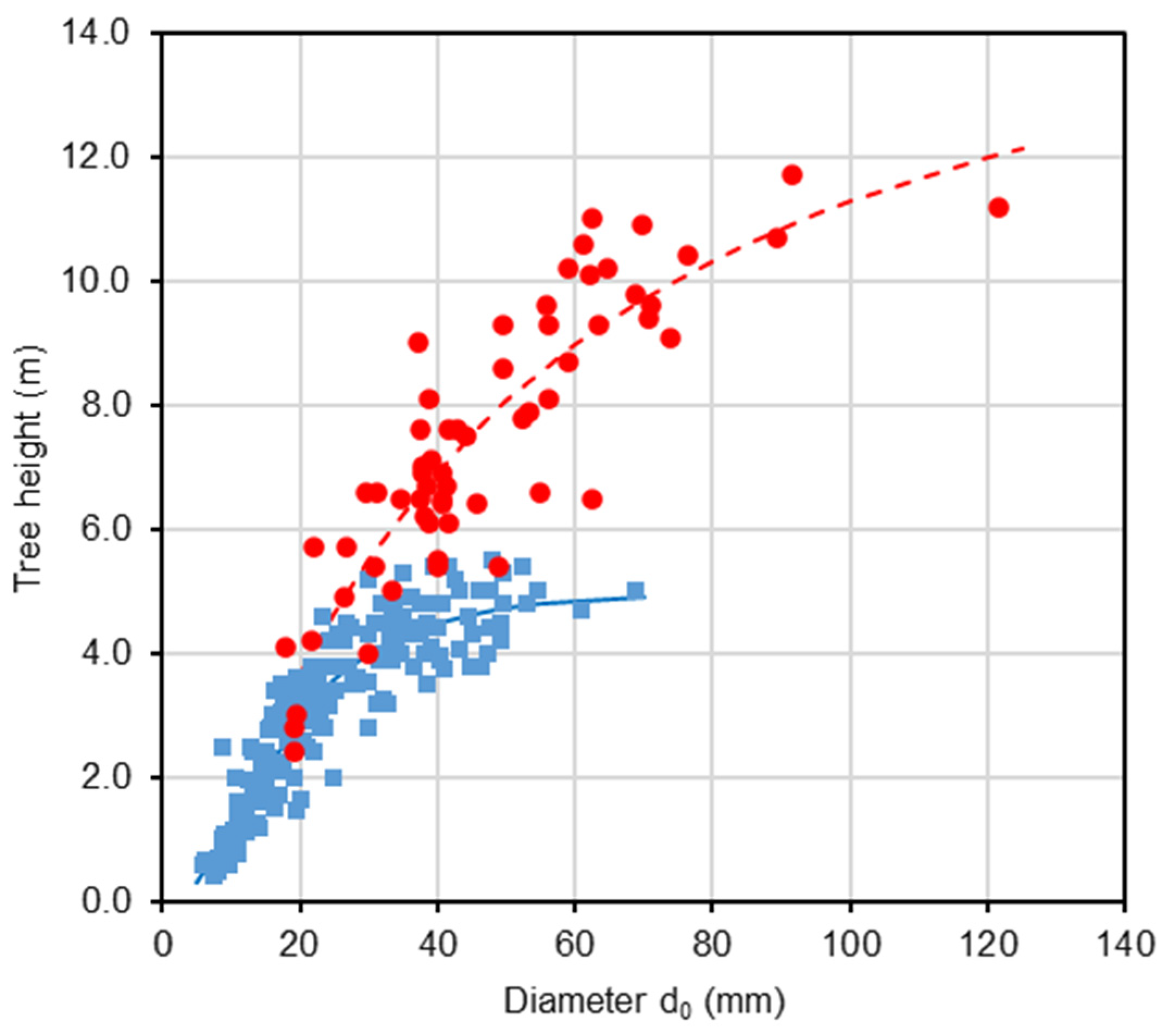
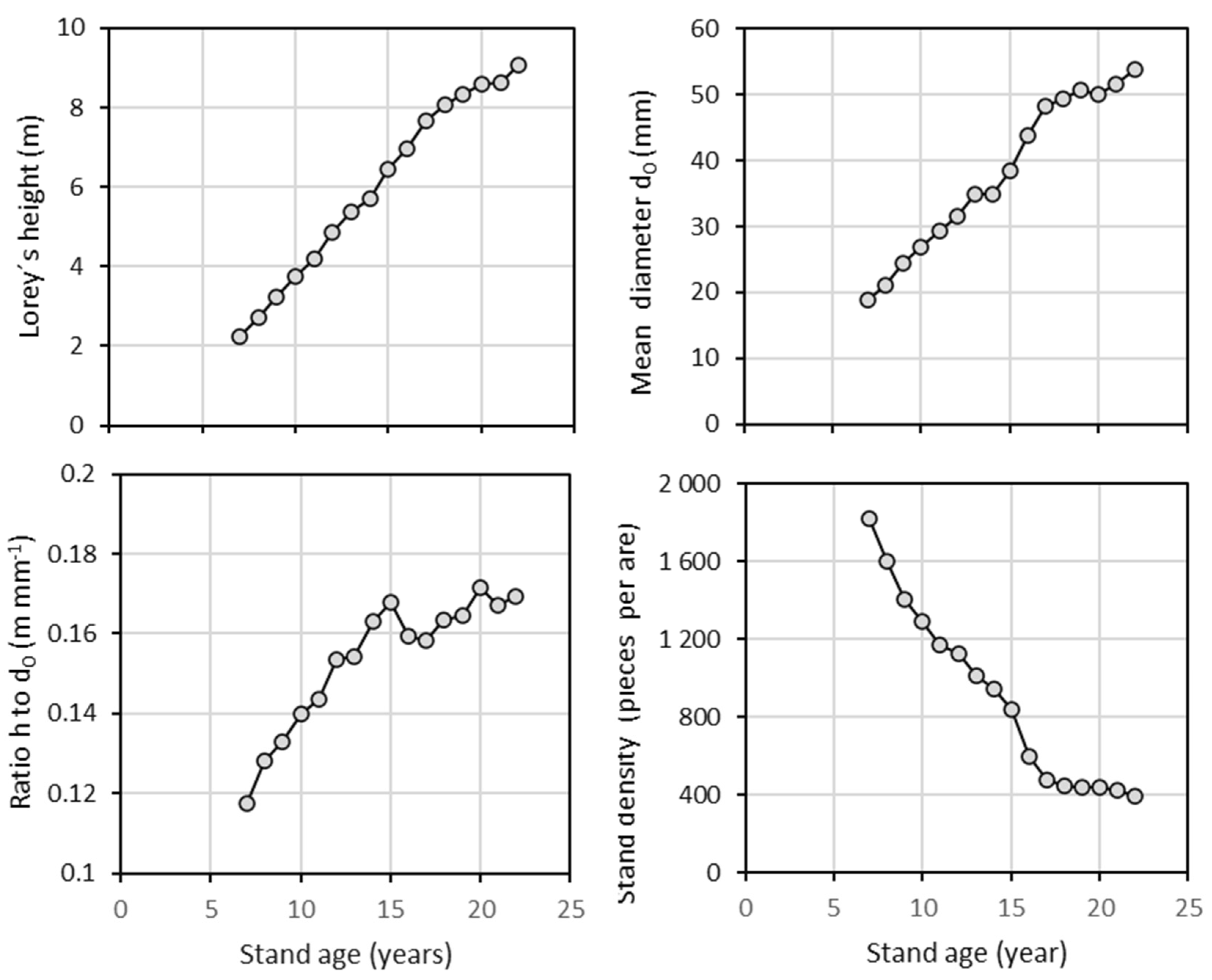
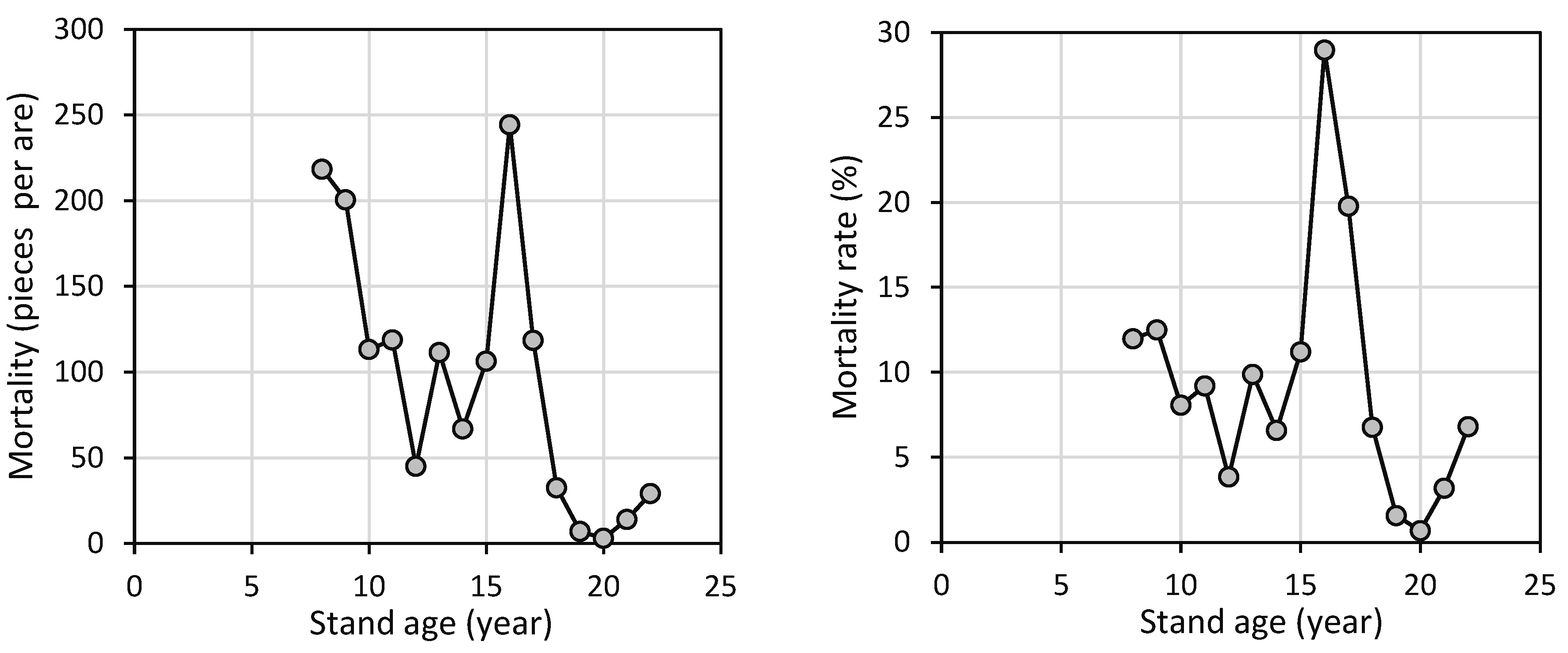
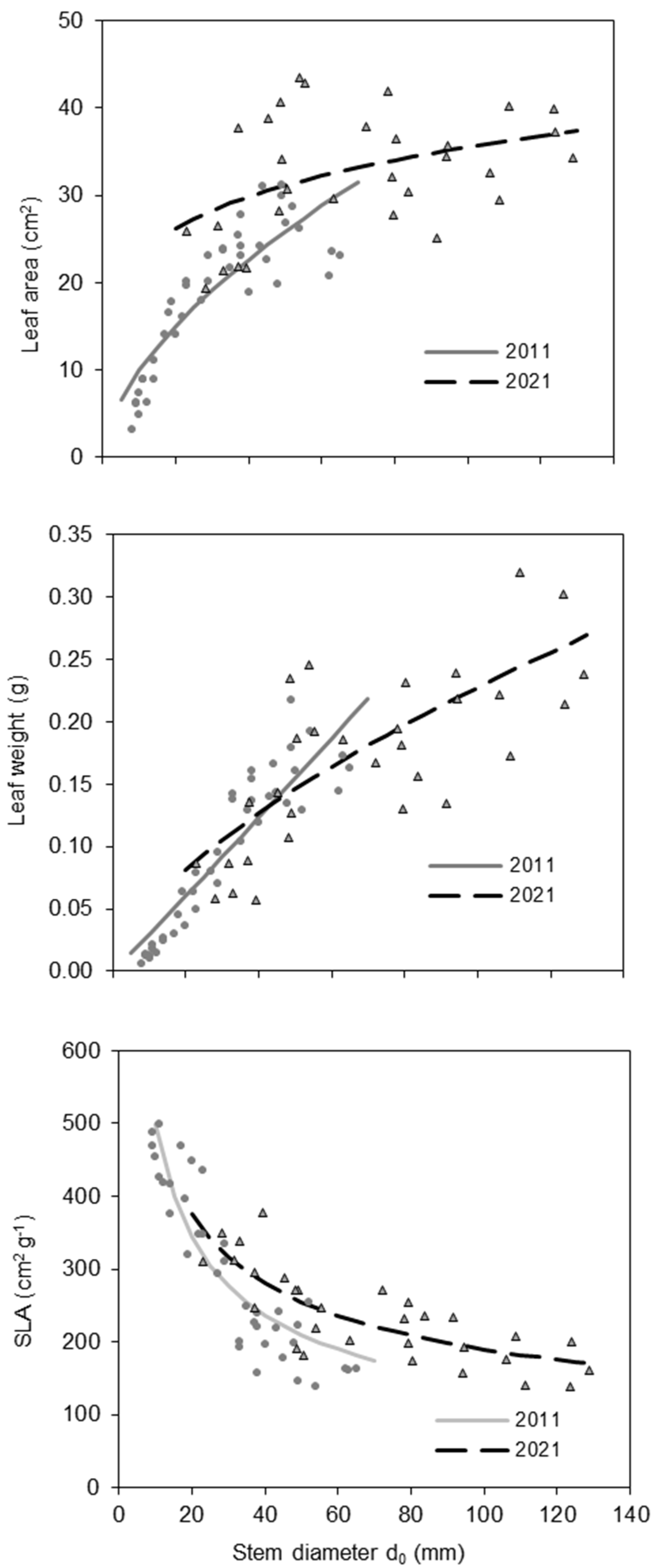
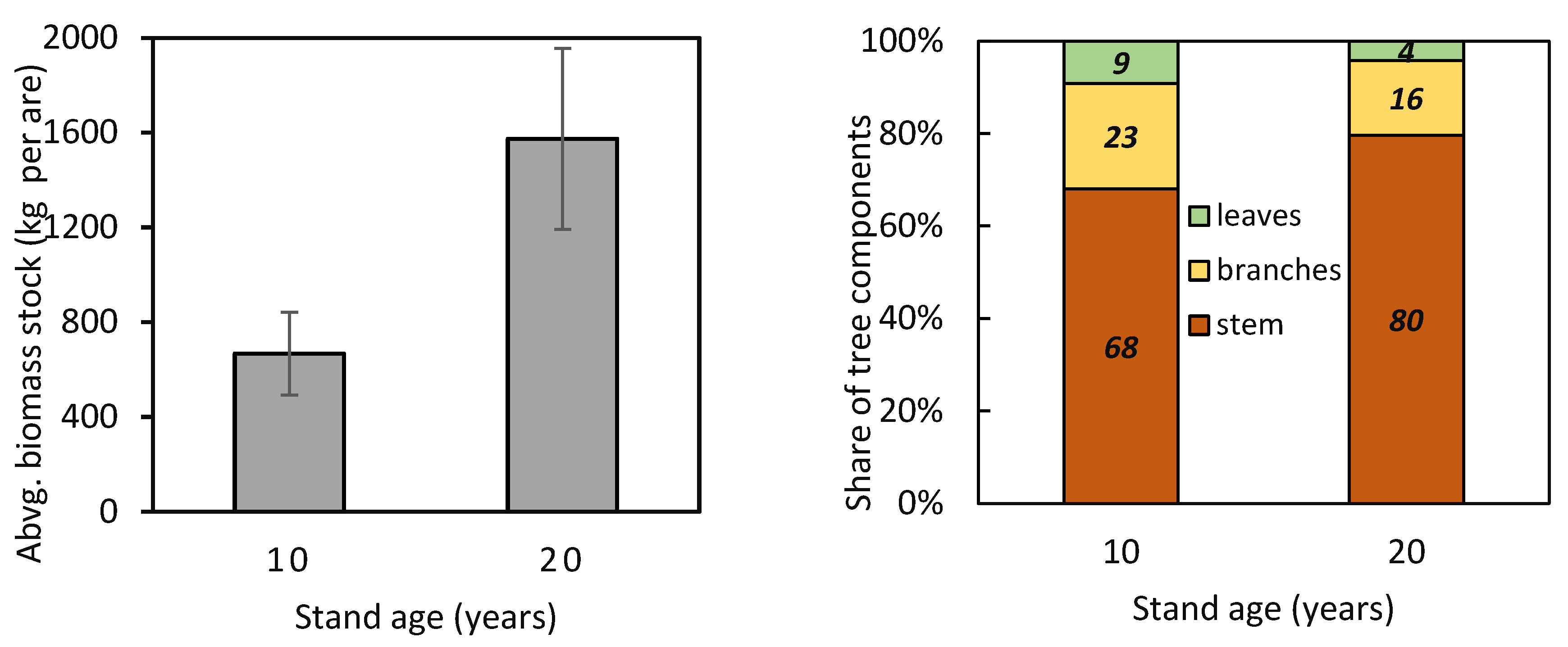
| Type of Data Set | Variable | Mean | SD | Min. | Max. |
|---|---|---|---|---|---|
| Plots 2011 | tree height | 2.87 | 1.23 | 0.45 | 5.5 |
| diameter d0 | 26.6 | 11.7 | 5.9 | 57.6 | |
| Sample trees 2011 | tree height | 2.81 | 1.17 | 0.51 | 5.11 |
| diameter d0 | 25.2 | 12.3 | 7.6 | 53.5 | |
| Plots 2021 | tree height | 7.42 | 2.22 | 2.40 | 11.70 |
| diameter d0 | 50.0 | 19.6 | 18.0 | 121.5 | |
| Sample trees 2021 | tree height | 9.32 | 2.65 | 3.74 | 13.5 |
| diameter d0 | 70.0 | 31.5 | 23.0 | 129.0 |
| Year | b0 | S.E. | p | b1 | S.E. | p | b2 | S.E. | p | R2 | MSE |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2011 | 83.112 | 14.315 | <0.001 | −1.539 | 1.150 | 0.182 | 0.209 | 0.021 | <0.001 | 0.851 | 0.288 |
| 2021 | 34.308 | 28.886 | 0.240 | 2.521 | 1.248 | 0.048 | 0.060 | 0.013 | <0.001 | 0.786 | 1.098 |
| Year | Leaf Trait (Unit) | b0 | (S.E.) | p | b1 | (S.E.) | p | R2 | MSE |
|---|---|---|---|---|---|---|---|---|---|
| 2011 | Leaf area (cm2) | 2.571 | (0.624) | <0.001 | 0.590 | (0.066) | <0.001 | 0.76 | 15.39 |
| Leaf mass, i.e., weight (g) | 0.0028 | (0.001) | 0.012 | 1.026 | (0.100) | <0.001 | 0.844 | 0.0006 | |
| Specific leaf area (cm2 g−1) | 1724.908 | (216.387) | <0.001 | −0.539 | (0.043) | <0.001 | 0.813 | 3122 | |
| 2021 | Leaf area (cm2) | 14.803 | (4.783) | 0.004 | 0.190 | (0.076) | 0.019 | 0.195 | 39.76 |
| Leaf mass, i.e., weight (g) | 0.012 | (0.006) | 0.068 | 0.639 | (0.120) | <0.001 | 0.558 | 0.0022 | |
| Specific leaf area (cm2 g−1) | 1349.087 | (325.820) | <0.001 | −0.426 | (0.061) | <0.001 | 0.637 | 1495 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konôpka, B.; Pajtík, J.; Šebeň, V. Stable Leaf Area Index Despite Shifts in Biomass Allocation and Leaf Traits: A Case Study in a Young European Beech Forest Under Intense Tree Competition. Forests 2025, 16, 557. https://doi.org/10.3390/f16040557
Konôpka B, Pajtík J, Šebeň V. Stable Leaf Area Index Despite Shifts in Biomass Allocation and Leaf Traits: A Case Study in a Young European Beech Forest Under Intense Tree Competition. Forests. 2025; 16(4):557. https://doi.org/10.3390/f16040557
Chicago/Turabian StyleKonôpka, Bohdan, Jozef Pajtík, and Vladimír Šebeň. 2025. "Stable Leaf Area Index Despite Shifts in Biomass Allocation and Leaf Traits: A Case Study in a Young European Beech Forest Under Intense Tree Competition" Forests 16, no. 4: 557. https://doi.org/10.3390/f16040557
APA StyleKonôpka, B., Pajtík, J., & Šebeň, V. (2025). Stable Leaf Area Index Despite Shifts in Biomass Allocation and Leaf Traits: A Case Study in a Young European Beech Forest Under Intense Tree Competition. Forests, 16(4), 557. https://doi.org/10.3390/f16040557







