Early- and Latewood vs. Stem Asymmetry: Which Is More Important for Dendrochemistry in Scots Pine?
Abstract
1. Introduction
- (i)
- Between the seasonal structure of a tree ring (early- and latewood) and stem asymmetry, which factor is more decisive for elemental allocation?
- (ii)
- Are the ratios of elements between early- and latewood significantly different in trees experiencing contrasting environmental conditions on opposite sides of the tree stem?
2. Materials and Methods
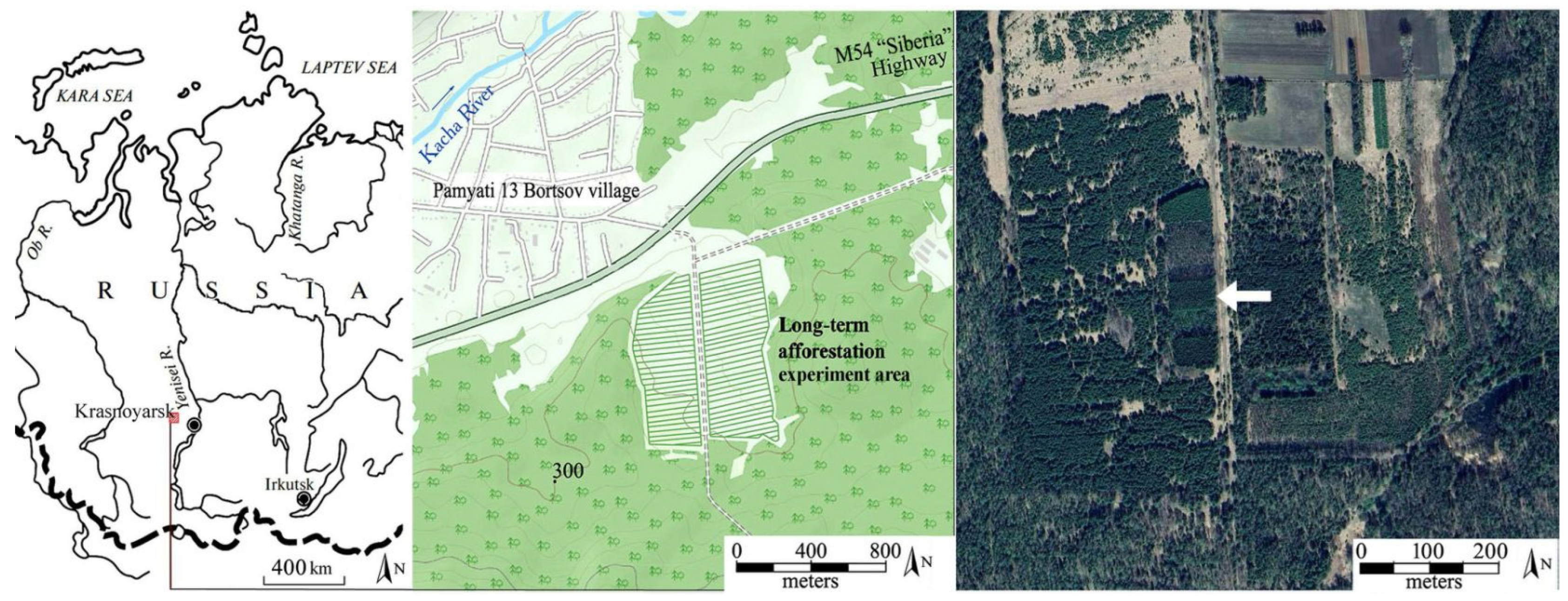
2.1. Area of Study
2.2. Experimental Design, Sampling
2.3. Treatment and the X-Ray Scanning of the Cores
2.4. Approach to Analyze the Relations of Elements
2.5. Statistical Treatment of Data
- Task A is the testing of differences in means—for the range of tree rings—of elemental content in latewood on the max-side vs. the min-side (Figure 5A).
- Task B is the testing of differences in means of elemental content in earlywood on the max-side vs. the min-side (Figure 5B).
- Task C is the testing of differences in means of elemental content of earlywood vs. latewood on the max-side (Figure 5C).
- Task D is the testing of differences in means of elemental content of earlywood vs. latewood on the min-side (Figure 5D).
3. Results
3.1. Evaluation of the Stem Asymmetry
3.2. Comparison of Elements’ Concentration Between Min-Side and Max-Side
3.3. Comparison of Element Concentrations Between Earlywood and Latewood
3.4. Comparison of Mean Element Ratios Between Min-Side/Max-Side and Earlywood/Latewood
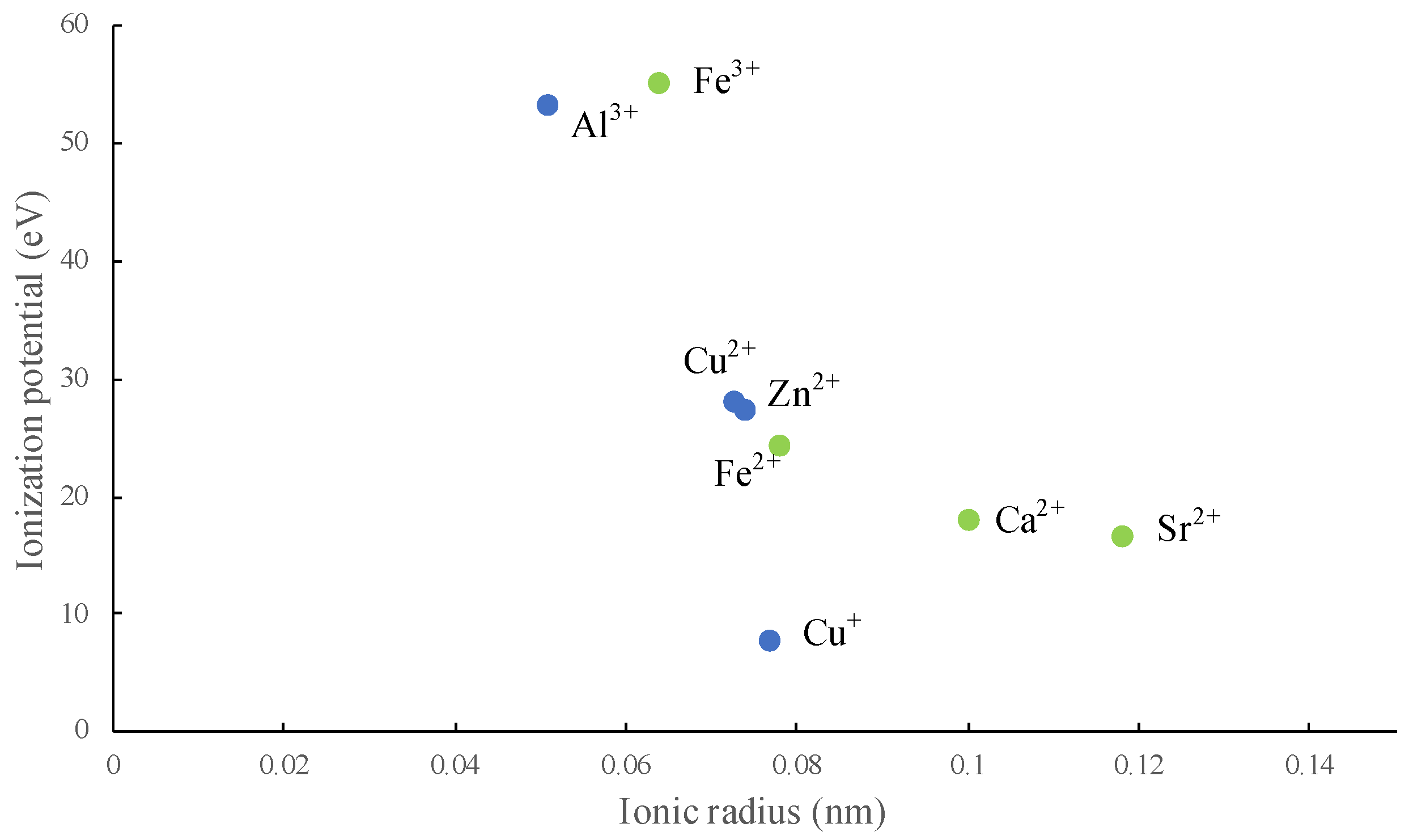
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hevia, A.; Sánchez-Salguero, R.; Camarero, J.J.; Buras, A.; Sangüesa-Barreda, G.; Galván, J.D.; Gutiérrez, E. Towards a better understanding of long-term wood-chemistry variations in old-growth forests: A case study on ancient Pinus uncinata trees from the Pyrenees. Sci. Total Environ. 2018, 625, 220–232. [Google Scholar] [CrossRef] [PubMed]
- Pearson, C.L.; Manning, S.W.; Coleman, M.; Jarvis, K. A dendrochemical study of Pinus sylvestris from Siljansfors Experimental Forest, central Sweden. Appl. Geochem. 2006, 21, 1681–1691. [Google Scholar] [CrossRef]
- Baes, C.F.; Ragsdale, H.L. Age-specific lead distribution in xylem rings of three tree genera in Atlanta, Georgia. Environ. Pollut—Ser. B Chem. Phys. 1981, 2, 21–35. [Google Scholar] [CrossRef]
- Baes, C.F.; McLaughlin, S.B. Trace elements in tree rings: Evidence of recent and historical air pollution. Science 1984, 224, 494–497. [Google Scholar] [CrossRef]
- Balouet, J.C.; Oudijk, G. The use of dendroecological methods to estimate the time frame of environmental releases. Environ. Claims J. 2006, 18, 35–52. [Google Scholar] [CrossRef]
- Abreu, S.N.; Soares, A.M.V.M.; Nogueira, A.J.A.; Morgado, F. Tree rings, Populus nigra L., as mercury data logger in aquatic environments: Case study of an historically contaminated environment. Bull. Environ. Contam. Toxicol. 2008, 80, 294–299. [Google Scholar] [CrossRef]
- Bondietti, E.A.; Baes, C.F., III; McLaughlin, S.B. Radial trends in cation ratios in tree rings as indicators of the impact of atmospheric deposition on forests. Can. J. For. Res. 1989, 19, 586–594. [Google Scholar] [CrossRef]
- Prohaska, T.; Stadlbauer, C.; Wimmer, R.; Stingeder, G.; Latkoczy, C.; Hoffmann, E.; Stephanowitz, H. Investigation of element variability in tree rings of young Norway spruce by laser-ablation-ICPMS. Sci. Total Environ. 1998, 219, 29–39. [Google Scholar] [CrossRef]
- Liu, Y.; Ta, W.; Bao, T.; Yang, Z.; Song, H.; Liu, N.; An, Z. Trace elements in tree rings and their environmental effects: A case study in Xi’an City. Sci. China Ser. D 2009, 52, 504–510. [Google Scholar] [CrossRef]
- De Vasconcellos, T.J.; dos Santos, R.S.; dos Anjos, M.J.; Tomazello-Filho, M.; Callado, C.H. Recording chemical changes in an urban environment: A dendrochemical study of Ceiba speciosa (A. St.-Hil.) Ravenna (Malvaceae) in the Atlantic Forest. Dendrochronologia 2025, 89, 126286. [Google Scholar] [CrossRef]
- Müller, R.O. Spectrochemical Analysis by X-Ray Fluorescence; Springer: New York, NY, USA, 1972; 326p. [Google Scholar] [CrossRef]
- Binda, G.; Di Iorio, A.; Monticelli, D. The what, how, why, and when of dendrochemistry: (paleo) environmental information from the chemical analysis of tree rings. Sci. Total Environ. 2021, 758, 143672. [Google Scholar] [CrossRef] [PubMed]
- Canning, C.M.; Laroque, C.P.; Muir, D. Critical Analysis of the Past, Present, and Future of Dendrochemistry: A Systematic Literature Review. Forests 2023, 14, 1997. [Google Scholar] [CrossRef]
- Silkin, P.P.; Ekimova, N.V. Relationship of strontium and calcium concentrations with the parameters of cell structure in Siberian spruce and fir tree-rings. Dendrochronologia 2012, 30, 189–194. [Google Scholar] [CrossRef]
- Scharnweber, T.; Hevia, A.; Buras, A.; van der Maaten, E.; Wilmking, M. Common trends in elements? Within- and be-tween-tree variations of wood-chemistry measured by X-ray fluorescence—A dendrochemical study. Sci. Total Environ. 2016, 566, 1245–1253. [Google Scholar] [CrossRef]
- Rowell, R.M. Handbook of Wood Chemistry and Wood Composites, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2013; 688p. [Google Scholar]
- Uprichard, J.M. Cellulose and lignin content in Pinus radiata D. Don. Within-tree variation in chemical composition, density, and tracheid length. Holzforschung 1971, 25, 97–105. [Google Scholar] [CrossRef]
- Czajka, M.; Fabisiak, E. Radial variation of the content of cellulose and lignin in selected softwood species. Ann. WULS-SGGW For. Wood Technol. 2017, 100, 233–238. [Google Scholar]
- Borukanlu, M.R.; Zadeh, O.H.; Moradpour, P.; Khedive, E. Effects of growth rate of eastern poplar trees on the chemical and morphological characteristics of wood fibers. Eur. J. Wood Wood Prod. 2021, 79, 1479–1494. [Google Scholar] [CrossRef]
- Bertaud, F.; Holmbom, B. Chemical composition of earlywood and latewood in Norway spruce heartwood, sapwood and transition zone wood. Wood Sci. 2004, 38, 245–256. [Google Scholar] [CrossRef]
- Fredriksson, M.; Pedersen, N.B.; Thygesen, L.G. The cell wall composition of Norway spruce earlywood and latewood revisited. Int. Wood Prod. J. 2018, 9, 80–85. [Google Scholar] [CrossRef]
- Antonova, G.F.; Zheleznichenko, T.V.; Stasova, V.V. Peculiarities of lignification in earlywood and latewood in Scots pine. In Proceedings of the Structure, Properties and Quality of Wood—Materials of VI B.N.Ugolev International Symposium Dedicated to 50th Anniversary of the Regional Coordination Committee on Modern Problems of Wood Science, Krasnoyarsk, Russia, 10–16 September 2018; pp. 46–58. (In Russian). [Google Scholar]
- Gavrikov, V.L.; Fertikov, A.I.; Sharafutdinov, R.A.; Vaganov, E.A. Properties of ions may explain elemental stoichiometry in late- and early-wood: A case study in Scots pine tree rings. J. For. Res. 2024, 35, 126. [Google Scholar] [CrossRef]
- Gavrikov, V.L.; Fertikov, A.I.; Sharafutdinov, R.A.; Tang, Z.; Vaganov, E.A. Early-Wood vs. Late-Wood in Scots Pine: Finding Stable Relationships in Elemental Distribution. Sci 2024, 6, 4. [Google Scholar] [CrossRef]
- Menyailo, O.V.; Hungate, B.A.; Zech, W. Tree species mediated soil chemical changes in a Siberian artificial afforestation experiment. Plant Soil 2002, 242, 171–182. [Google Scholar] [CrossRef]
- Schugalei, L.S. The Siberian afforestation experiment: History, methodology, and problems. In Tree Species Effects on Soils: Implications for Global Change; Binkley, D., Menyailo, O., Eds.; Springer: Dordrecht, The Netherlands, 2005; pp. 257–268. [Google Scholar]
- Balouet, J.C.; Burken, J.G.; Karg, F.; Vroblesky, D.; Smith, K.T.; Grudd, H.; Rindby, A.; Beaujard, F.; Chalot, M. Dendrochemistry of multiple releases of chlorinated solvents at a former industrial site. Environ. Sci. Technol. 2012, 46, 9541–9547. [Google Scholar] [CrossRef]
- Lide, D.R. (Ed.) Handbook of Chemistry and Physics, 83rd ed.; CRC Press: Boca Raton, FL, USA, 2002; 2664p. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023; Available online: https://www.R-project.org/ (accessed on 9 September 2023).
- Young, H.E.; Guinn, V.P. Chemical elements in complete mature trees of seven species in Maine. Tappi 1966, 49, 190–197. [Google Scholar]
- Saka, S.; Goring, D.A.I. The distribution of inorganic constituents in black spruce wood as determined by TEM-EDXA. Mokuzai Gakkaishi 1983, 29, 648–656. [Google Scholar]
- Speer, J.H. Fundamentals of Tree-Ring Research; University of Arizona Press: Tucson, AZ, USA, 2010; 509p. [Google Scholar]
- Cartenì, F.; Deslauriers, A.; Rossi, S.; Morin, H.; De Micco, V.; Mazzoleni, S.; Giannino, F. The Physiological Mechanisms Behind the Earlywood-To-Latewood Transition: A Process-Based Modeling Approach. Front. Plant Sci. 2018, 9, 1053. [Google Scholar] [CrossRef] [PubMed]
- Chave, J.; Coomes, D.; Jansen, S.; Lewis, S.L.; Swenson, N.G.; Zanne, A.E. Towards a worldwide wood economics spectrum. Ecol. Lett. 2009, 12, 351–366. [Google Scholar] [CrossRef]
- Antonova, G.F.; Varaksina, T.N.; Zheleznichenko, T.V.; Stasova, V.V. Lignin deposition during earlywood and latewood formation in Scots pine stems. Wood Sci. Technol. 2014, 48, 919–936. [Google Scholar] [CrossRef]
- O’Brien, J.J.; Oberbauer, S.F.; Clark, D.B. Whole tree xylem sap flow responses to multiple environmental variables in a wet tropical forest. Plant Cell Environ. 2004, 27, 551–567. [Google Scholar] [CrossRef]
- Li, W.; Wen, J.; Xiao, Z.; Xu, S. Application of ground-penetrating radar for detecting internal anomalies in tree trunks with irregular contours. Sensors 2018, 18, 649. [Google Scholar] [CrossRef]




| Tree Number | Mean Width of Tree Ring, mm | p-Value | |
|---|---|---|---|
| Min-Side | Max-Side | ||
| 1 | 2.06 | 3.30 | <0.0001 |
| 2 | 1.90 | 2.48 | 0.007 |
| 3 | 2.04 | 2.18 | 0.345 |
| 4 | 2.65 | 2.98 | 0.008 |
| 5 | 1.84 | 2.30 | 0.056 |
| 6 | 2.18 | 3.16 | <0.0001 |
| Element | Type of Wood | Concentration of Element: Min-Side > Max-Side | Concentration of Element: Min-Side < Max-Side | Significant |
|---|---|---|---|---|
| Al | Earlywood | always 1 | ||
| Latewood | mostly 2 | |||
| Si | Earlywood | mostly | mostly | |
| Latewood | mostly | mostly | ||
| P | Earlywood | mostly | ||
| Latewood | always | |||
| S | Earlywood | mostly | mostly | |
| Latewood | mostly | mostly | ||
| Cl | Earlywood | mostly | ||
| Latewood | mostly | |||
| Ca | Earlywood | mostly | ||
| Latewood | mostly | |||
| Fe | Earlywood | mostly | ||
| Latewood | mostly | |||
| Cu | Earlywood | |||
| Latewood | mostly | |||
| Zn | Earlywood | always | ||
| Latewood | always | |||
| Sr | Earlywood | mostly | ||
| Latewood | mostly | mostly |
| Element | Side of Tree | Concentration of Element: Earlywood > Latewood | Concentration of Element: Earlywood < Latewood | Significant |
|---|---|---|---|---|
| Al | Min-side | always 1 | always | |
| Max-side | always | always | ||
| Si | Min-side | always | always | |
| Max-side | always | always | ||
| P | Min-side | always | always | |
| Max-side | always | mostly 2 | ||
| S | Min-side | always | always | |
| Max-side | always | mostly | ||
| Cl | Min-side | always | always | |
| Max-side | always | mostly | ||
| Ca | Min-side | always | always | |
| Max-side | always | always | ||
| Fe | Min-side | always | always | |
| Max-side | always | always | ||
| Cu | Min-side | always | always | |
| Max-side | always | always | ||
| Zn | Min-side | always | always | |
| Max-side | always | always | ||
| Sr | Min-side | always | always | |
| Max-side | always | always |
| Ratio of Elements | Side of Tree | Mean Values of Ratios: Earlywood > Latewood | Mean Values of Ratios: Earlywood < Latewood | Significant |
|---|---|---|---|---|
| Ca/Sr | Min-side | always | always | |
| Max-side | always | mostly 2 | ||
| Fe/Ca | Min-side | always 1 | mostly | |
| Max-side | always | |||
| Fe/Sr | Min-side | always | always | |
| Max-side | always | mostly | ||
| Al/Cu | Min-side | always | ||
| Max-side | ||||
| Al/Zn | Min-side | always | always | |
| Max-side | always | mostly | ||
| Cu/Zn | Min-side | always | always | |
| Max-side | always | always |
| Ratio of Elements | Type of Wood | Mean Values of Ratios: Min-Side > Max-Side | Mean Values of Ratios: Min-Side < Max-Side | Significant |
|---|---|---|---|---|
| Ca/Sr | Earlywood | |||
| Latewood | mostly 2 | |||
| Fe/Ca | Earlywood | mostly | ||
| Latewood | mostly | |||
| Fe/Sr | Earlywood | |||
| Latewood | ||||
| Al/Cu | Earlywood | |||
| Latewood | mostly | |||
| Al/Zn | Earlywood | mostly | ||
| Latewood | always 1 | |||
| Cu/Zn | Earlywood | |||
| Latewood | mostly |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gavrikov, V.L.; Fertikov, A.I.; Sharafutdinov, R.A.; Vaganov, E.A. Early- and Latewood vs. Stem Asymmetry: Which Is More Important for Dendrochemistry in Scots Pine? Forests 2025, 16, 493. https://doi.org/10.3390/f16030493
Gavrikov VL, Fertikov AI, Sharafutdinov RA, Vaganov EA. Early- and Latewood vs. Stem Asymmetry: Which Is More Important for Dendrochemistry in Scots Pine? Forests. 2025; 16(3):493. https://doi.org/10.3390/f16030493
Chicago/Turabian StyleGavrikov, Vladimir L., Alexey I. Fertikov, Ruslan A. Sharafutdinov, and Eugene A. Vaganov. 2025. "Early- and Latewood vs. Stem Asymmetry: Which Is More Important for Dendrochemistry in Scots Pine?" Forests 16, no. 3: 493. https://doi.org/10.3390/f16030493
APA StyleGavrikov, V. L., Fertikov, A. I., Sharafutdinov, R. A., & Vaganov, E. A. (2025). Early- and Latewood vs. Stem Asymmetry: Which Is More Important for Dendrochemistry in Scots Pine? Forests, 16(3), 493. https://doi.org/10.3390/f16030493








