Optimizing UAV-LiDAR Point Density for Eucalyptus Height Estimation in Agroforestry
Abstract
1. Introduction
2. Materials and Methods
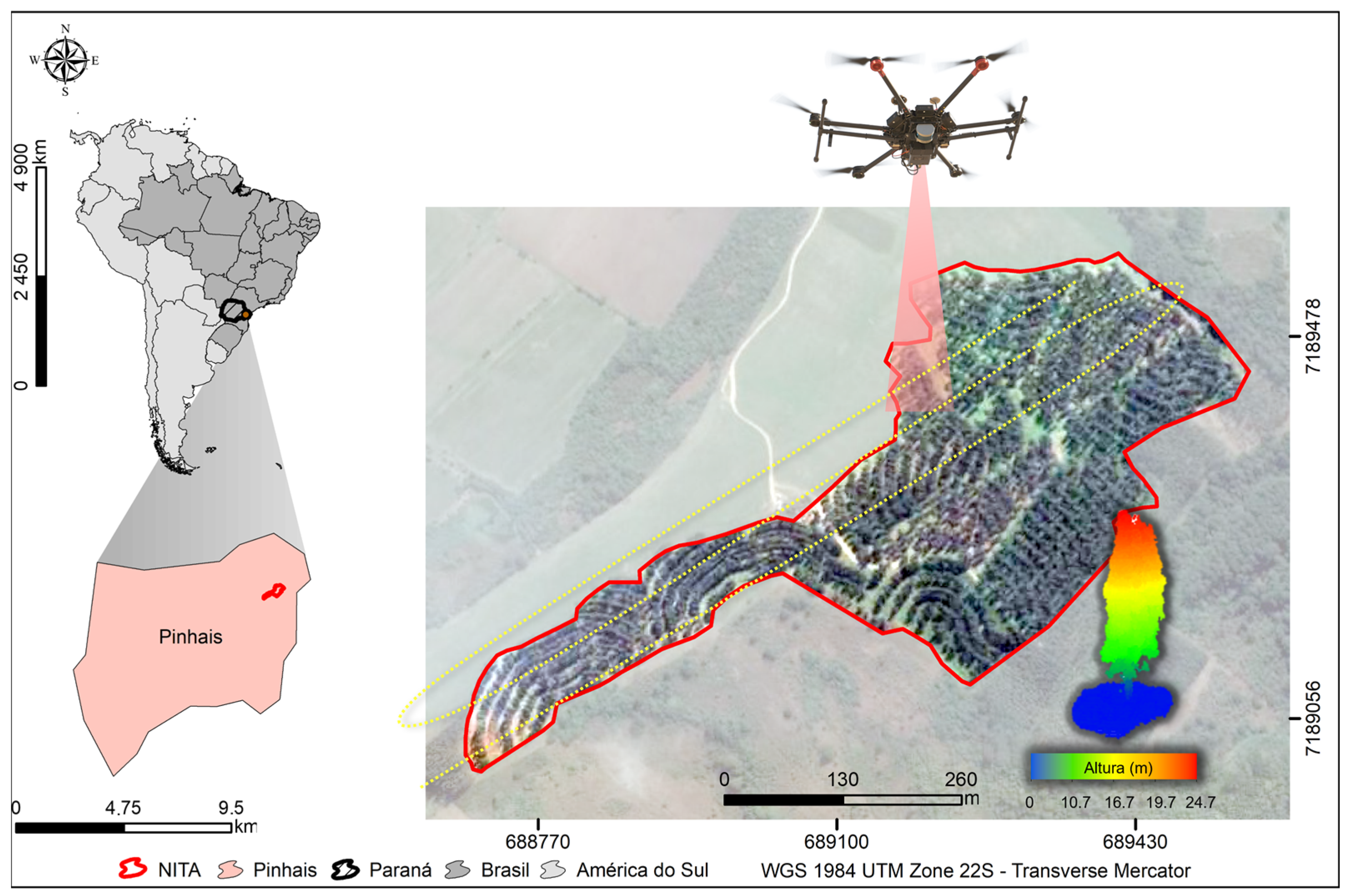
2.1. Study Area, Forest Inventory and UAV-LIDAR
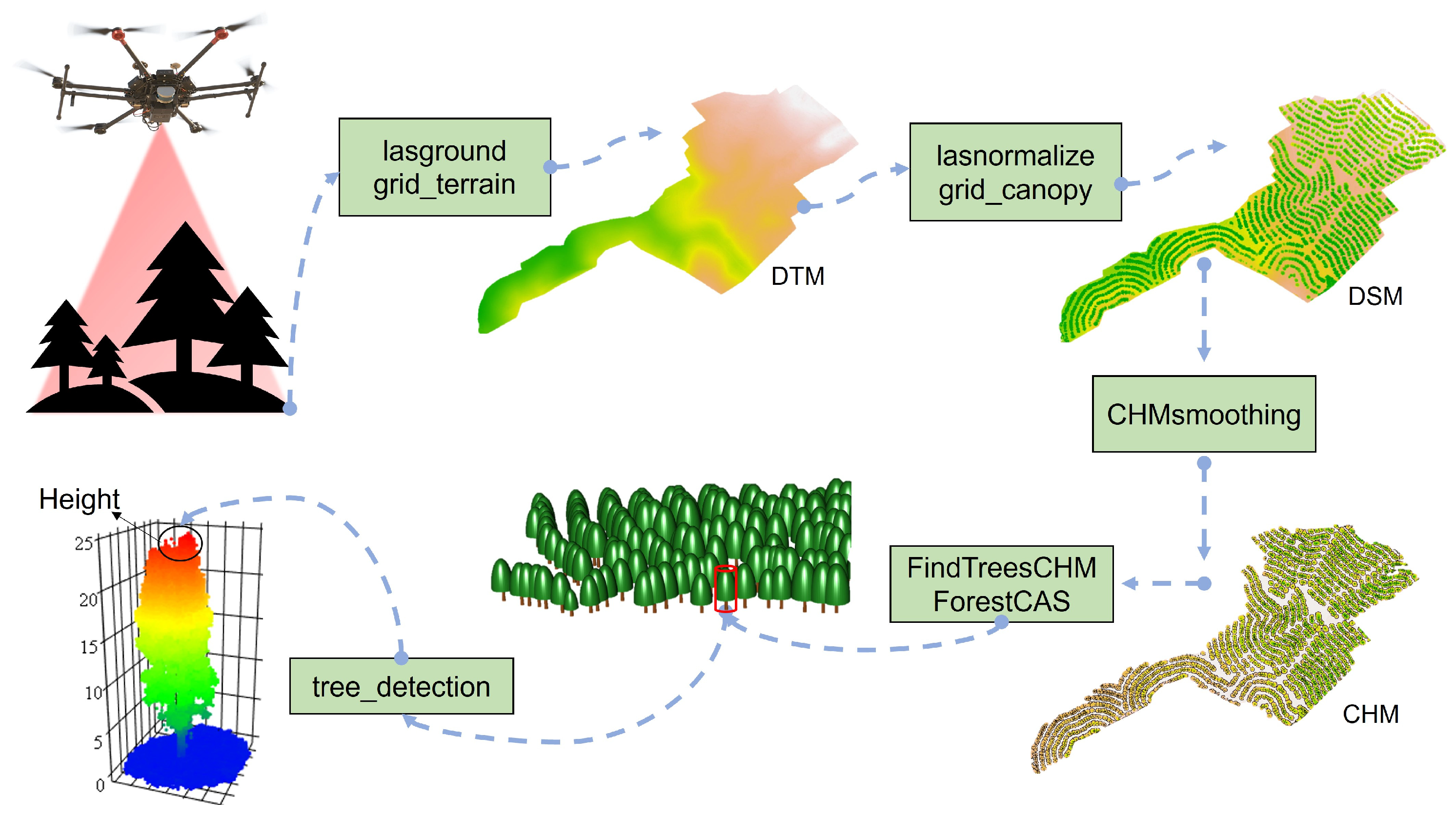
2.2. Comparison Between Heights Derived from the Point Cloud and Field Measures
3. Results
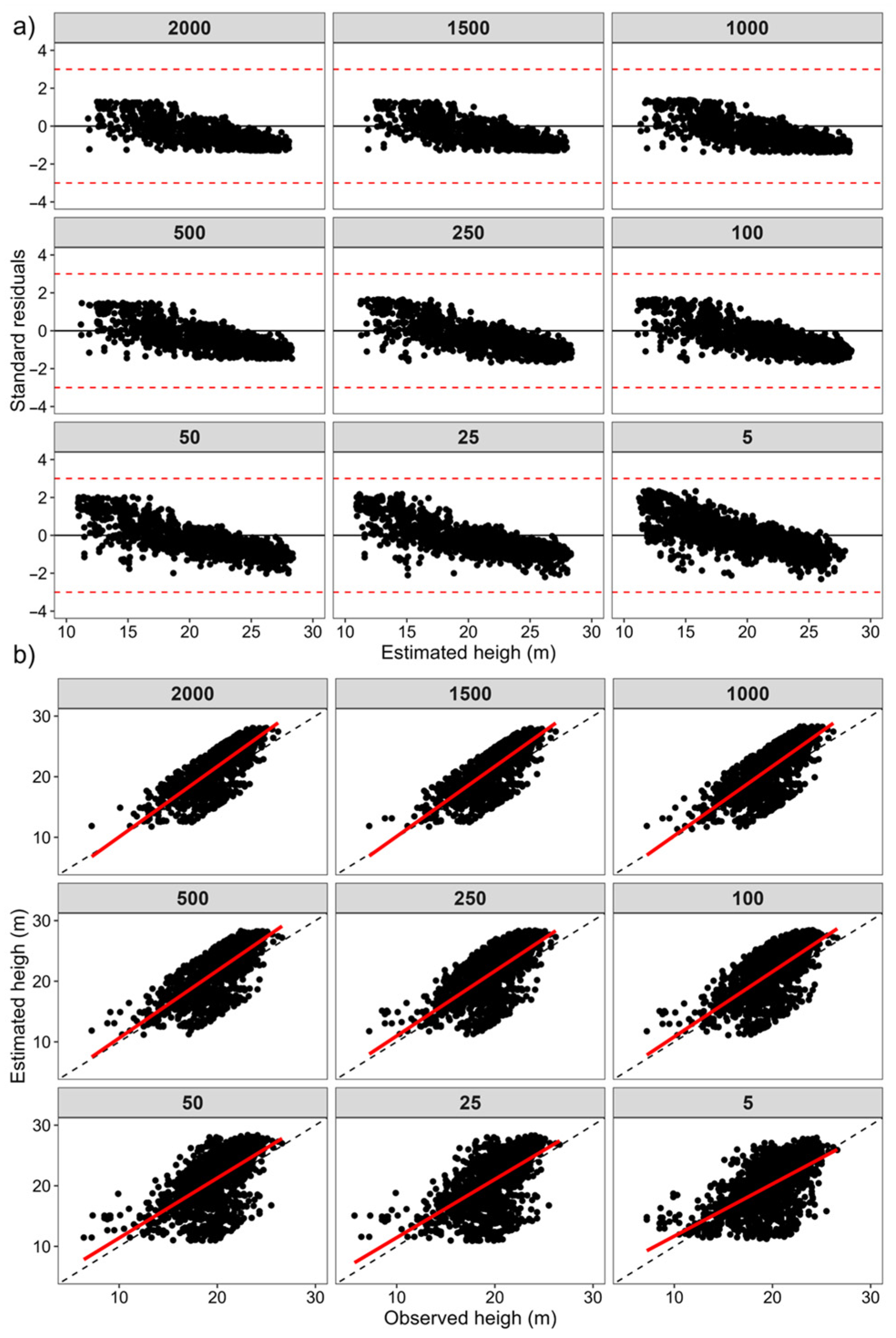
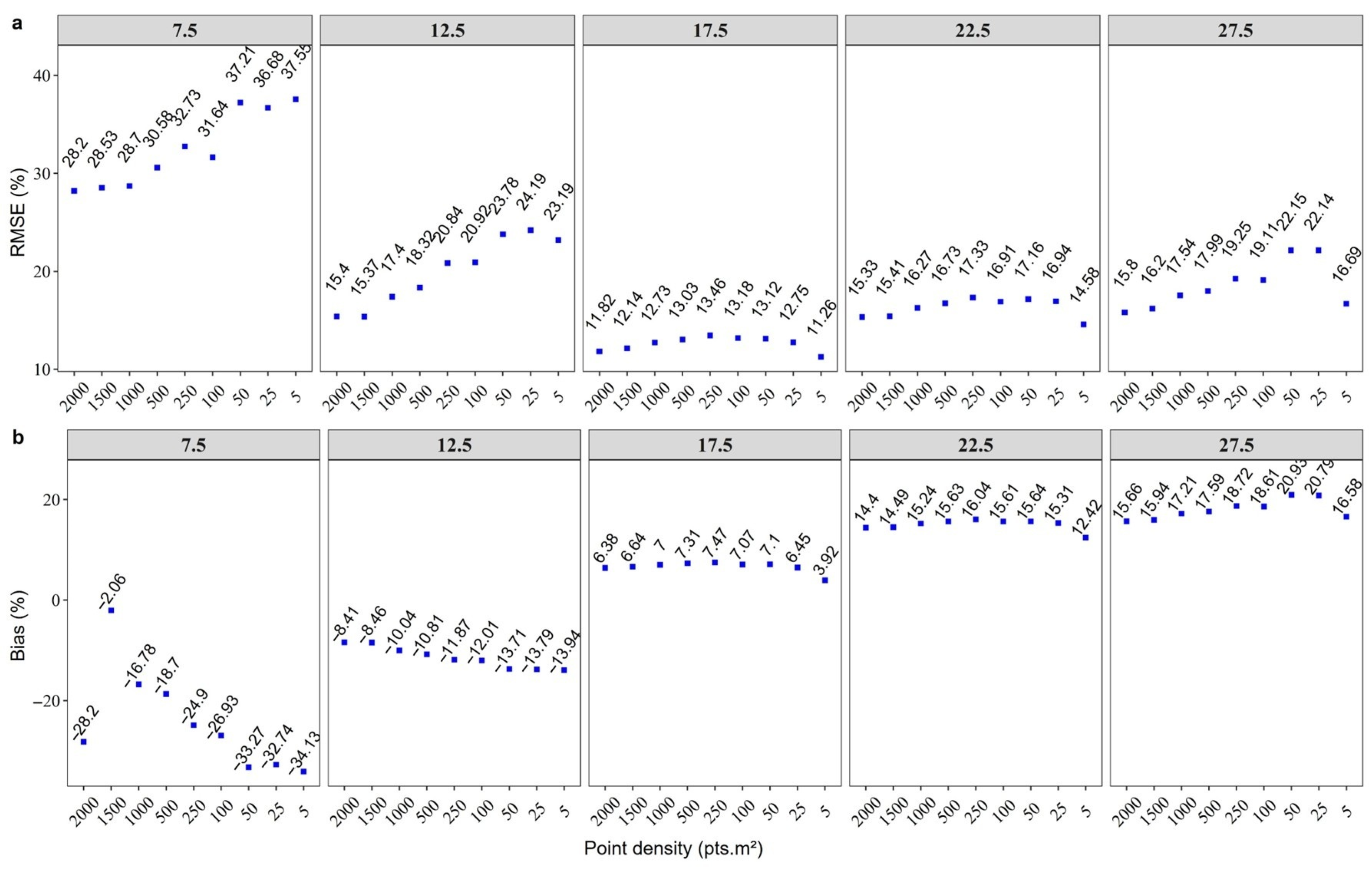
3.1. Evaluation of Height Estimated on Forest Inventory and UAV-Lidar
3.2. Comparison Between Heights Derived from the Point Cloud and Field Measures
4. Discussion
4.1. Forest Inventory and UAV-Lidar
4.2. Comparison Between Heights Derived from the Point Cloud and Field Measures
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hayashi, R.; Weiskittel, A.; Kershaw, J.A. Influence of Prediction Cell Size on LiDAR-Derived Area-Based Estimates of Total Volume in Mixed-Species and Multicohort Forests in Northeastern North America. Can. J. Remote Sens. 2016, 42, 473–488. [Google Scholar] [CrossRef]
- Yunjie, X. Wireless sensor monitoring system of Canadian Poplar Forests based on Internet of Things. Artif. Life Robot. 2019, 24, 471–479. [Google Scholar] [CrossRef]
- Fan, Y.; Feng, Z.; Mannan, A.; Khan, T.U.; Shen, C.; Saeed, S. Estimating tree position, diameter at breast height, and tree height in real-time using a mobile phone with RGB-D SLAM. Remote Sens. 2018, 10, 1845. [Google Scholar] [CrossRef]
- Corte, A.P.D.; Rex, F.E.; de Almeida, D.R.A.; Sanquetta, C.R.; Silva, C.A.; Moura, M.M.; Wilkinson, B.; Zambrano, A.M.A.; Cunha Neto, E.M.; Veras, H.F.P.; et al. Measuring individual tree diameter and height using gatoreye high-density UAV-lidar in an integrated crop-livestock-forest system. Remote Sens. 2020, 12, 863. [Google Scholar] [CrossRef]
- Parthiban, M.; Dharani, M.; Kathiga, S.; Keruthika, M. IOT based anti-poaching sensor system for trees in forest. Int. J. Innov. Technol. Explor. Eng. 2019, 8, 172–176. [Google Scholar] [CrossRef]
- Saikumar, S.T.; Sriramya, P. Iot enabled forest fire detection and altering the authorities. Int. J. Recent Technol. Eng. 2019, 7, 429–433. [Google Scholar]
- Rossit, D.A.; Olivera, A.; Viana Céspedes, V.; Broz, D. A Big Data approach to forestry harvesting productivity. Comput. Electron. Agric. 2019, 161, 29–52. [Google Scholar] [CrossRef]
- Shan, C.; Bi, H.; Watt, D.; Li, Y.; Strandgard, M.; Ghaffariyan, M.R. A new model for predicting the total tree height for stems cut-to-length by harvesters in Pinus radiata plantations. J. For. Res. 2021, 32, 21–41. [Google Scholar] [CrossRef]
- Alonzo, M.; McFadden, J.P.; Nowak, D.J.; Roberts, D.A. Mapping urban forest structure and function using hyperspectral imagery and lidar data. Urban For. Urban Green. 2016, 17, 135–147. [Google Scholar] [CrossRef]
- Veras, H.F.P.; Ferreira, M.P.; da Cunha Neto, E.M.; Figueiredo, E.O.; Corte, A.P.D.; Sanquetta, C.R. Fusing multi-season UAS images with convolutional neural networks to map tree species in Amazonian forests. Ecol. Inform. 2022, 71, 101815. [Google Scholar] [CrossRef]
- Yoga, S.; Bégin, J.; St-Onge, B.; Riopel, M. Modeling the effect of the spatial pattern of airborne lidar returns on the prediction and the uncertainty of timber merchantable volume. Remote Sens. 2017, 9, 808. [Google Scholar] [CrossRef]
- Ruiz, L.A.; Hermosilla, T.; Mauro, F.; Godino, M. Analysis of the influence of plot size and LiDAR density on forest structure attribute estimates. Forests 2014, 5, 936–951. [Google Scholar] [CrossRef]
- Campbell, M.J.; Dennison, P.E.; Hudak, A.T.; Parham, L.M.; Butler, B.W. Quantifying understory vegetation density using small-footprint airborne lidar. Remote Sens. Environ. 2018, 215, 330–342. [Google Scholar] [CrossRef]
- Kukunda, C.B.; Duque-Lazo, J.; González-Ferreiro, E.; Thaden, H.; Kleinn, C. Ensemble classification of individual Pinus crowns from multispectral satellite imagery and airborne LiDAR. Int. J. Appl. Earth Obs. Geoinf. 2018, 65, 12–23. [Google Scholar] [CrossRef]
- Kükenbrink, D.; Schneider, F.D.; Leiterer, R.; Schaepman, M.E.; Morsdorf, F. Quantification of hidden canopy volume of airborne laser scanning data using a voxel traversal algorithm. Remote Sens. Environ. 2017, 194, 424–436. [Google Scholar] [CrossRef]
- Wallace, L.; Lucieer, A.; Watson, C.; Turner, D. Development of a UAV-LiDAR system with application to forest inventory. Remote Sens. 2012, 4, 1519–1543. [Google Scholar] [CrossRef]
- Surový, P.; Ribeiro, N.A.; Panagiotidis, D. Estimation of positions and heights from UAV-sensed imagery in tree plantations in agrosilvopastoral systems. Int. J. Remote Sens. 2018, 39, 4786–4800. [Google Scholar] [CrossRef]
- Birdal, A.C.; Avdan, U.; Türk, T. Estimating tree heights with images from an unmanned aerial vehicle. Geomat. Nat. Hazards Risk 2017, 8, 1144–1156. [Google Scholar] [CrossRef]
- Nevalainen, O.; Honkavaara, E.; Tuominen, S.; Viljanen, N.; Hakala, T. Individual Tree Detection and Classification with UAV-Based Photogrammetric Point Clouds and Hyperspectral Imaging. Remote Sens. 2017, 9, 185. [Google Scholar] [CrossRef]
- Ota, T.; Ogawa, M.; Mizoue, N.; Fukumoto, K.; Yoshida, S. Forest Structure Estimation from a UAV-Based Photogrammetric Point Cloud in Managed Temperate Coniferous Forests. Forests 2017, 8, 343. [Google Scholar] [CrossRef]
- Dempewolf, J.; Nagol, J.; Hein, S.; Thiel, C.; Zimmermann, R. Measurement of Within-Season Tree Height Growth in a Mixed Forest Stand Using UAV Imagery. Forests 2017, 8, 231. [Google Scholar] [CrossRef]
- Simpson, J.E.; Smith, T.E.L.; Wooster, M.J. Assessment of errors caused by forest vegetation structure in airborne LiDAR-derived DTMs. Remote Sens. 2017, 9, 1101. [Google Scholar] [CrossRef]
- White, J.C.; Wulder, M.A.; Vastaranta, M.; Coops, N.C.; Pitt, D.; Woods, M. The utility of image-based point clouds for forest inventory: A comparison with airborne laser scanning. Forests 2013, 4, 518–536. [Google Scholar] [CrossRef]
- Ota, T.; Ogawa, M.; Shimizu, K.; Kajisa, T.; Mizoue, N.; Yoshida, S.; Takao, G.; Hirata, Y.; Furuya, N.; Sano, T.; et al. Aboveground biomass estimation using structure from motion approach with aerial photographs in a seasonal tropical forest. Forests 2015, 6, 3882–3898. [Google Scholar] [CrossRef]
- Cunha Neto, E.M.D.; Veras, H.F.P.; Moura, M.M.; Berti, A.L.; Sanquetta, C.R.; Pelissari, A.L.; Corte, A.P.D. Combining ALS and UAV to derive the height of Araucaria angustifolia in the Brazilian Atlantic Rain Forest. An. Acad. Bras. Cienc. 2023, 95, e20201503. [Google Scholar] [CrossRef]
- Sankey, T.; Donager, J.; Mcvay, J.; Sankey, J.B. Remote Sensing of Environment UAV lidar and hyperspectral fusion for forest monitoring in the southwestern USA. Remote Sens. Environ. 2017, 195, 30–43. [Google Scholar] [CrossRef]
- Wallace, L.; Lucieer, A.; Watson, C.S. Evaluating Tree Detection and Segmentation Routines on Very High Resolution UAV LiDAR Data. IEEE Trans. Geosci. Remote Sens 2014, 52, 7619–7628. [Google Scholar] [CrossRef]
- Jakubowski, M.K.; Guo, Q.; Kelly, M. Tradeoffs between lidar pulse density and forest measurement accuracy. Remote Sens. Environ. 2013, 130, 245–253. [Google Scholar] [CrossRef]
- Guo, Q.; Su, Y.; Hu, T.; Zhao, X.; Wu, F.; Liu, J.; Chen, L.; Xu, G.; Lin, G.; Zheng, Y.; et al. An integrated UAV-borne lidar system for 3D habitat mapping in three forest ecosystems across China. Int. J. Remote Sens. 2017, 38, 2954–2972. [Google Scholar] [CrossRef]
- Watt, M.S.; Meredith, A.; Watt, P.; Gunn, A. The influence of LiDAR pulse density on the precision of inventory metrics in young unthinned Douglas-fir stands during initial and subsequent LiDAR acquisitions. N. Z. J. For. Sci. 2014, 44, 18. [Google Scholar] [CrossRef]
- Cunha Neto, E.M.; Rex, F.E.; Veras, H.F.P.; Moura, M.M.; Sanquetta, C.R.; Käfer, P.S.; Sanquetta, M.N.I.; Zambrano, A.M.A.; Broadbent, E.N.; Corte, A.P.D. Using high-density UAV-Lidar for deriving tree height of Araucaria Angustifolia in an Urban Atlantic Rain Forest. Urban For. Urban Green. 2021, 63, 127197. [Google Scholar] [CrossRef]
- Alvares, C.A.; Stape, J.L.; Sentelhas, P.C.; De Moraes Gonçalves, J.L.; Sparovek, G. Köppen’s climate classification map for Brazil. Meteorol. Zeitschrift 2013, 22, 711–728. [Google Scholar] [CrossRef] [PubMed]
- Santos, H.G.; Jacomine, P.K.T.; Anjos, L.H.C.; Oliveira, V.Á.; Lumbreras, J.F.; Coelho, M.R.; Almeida, J.A.; Araújo Filho, J.C.; Oliveira, J.B.; Cunha, T.J.F. Sistema Brasileiro de Classificação de Solos, 5th ed.; Mattos, J.S.R., Ed.; Embrapa: Brasília, Brazil, 2018; ISBN 978-85-7035-800-4. [Google Scholar]
- De Moraes, A.; Pelissari, A.; Lustosa, S.B.C.; Portugal, T.B.; Schuster, M.Z.; Kruchelski, S.; Dominschek, R. Apresentação geral da área experimental do NITA. In Sistemas Integrados de Produção Agropecuária na Promoção da Intensificação Sustentável; Dominschek, R., Kruchelski, S., Deiss, L., Portugal, T.B., Denardin, L.G., Martins, A.P., Lang, C.R., Moraes, A.d., Eds.; Universidade Federal do Paraná: Curitiba, Brazil, 2018; pp. 54–67. ISBN 9788573353198. [Google Scholar]
- Wilkinson, B.; Lassiter, H.A.; Abd-Elrahman, A.; Carthy, R.R.; Ifju, P.; Broadbent, E.; Grimes, N. Geometric targets for UAS lidar. Remote Sens. 2019, 11, 3019. [Google Scholar] [CrossRef]
- Isenburg, M. Lastools—Efficient Lidar Processing Software, Version 2019; Rapidlasso GmbH: Gilching, Germany, 2019.
- Core Team. R: A Language and Environment for Statistical Computing, Version 3.6.2; R Foundation for Statistical Computing: Vienna, Austria, 2019.
- Roussel, J.-R.; Auty, D. lidR: Airborne LIDAR Data Manipulation and Visualization for Forestry Applications, Version 2.0.2; R-Lidar/Laval University: Quebec City, QC, Canada, 2019.
- Silva, C.A.; Crookston, N.L.; Hudak, A.T.; Vierling, L.A.; Klauberg, C.; Cardil, A. rLiDAR: LiDAR Data Processing and Visualization, Version 0.1.1; R Foundation for Statistical Computing: Vienna, Austria, 2017.
- Mohan, M.; Silva, C.A.; Klauberg, C.; Jat, P.; Catts, G.; Cardil, A.; Hudak, A.T.; Dia, M. Individual tree detection from unmanned aerial vehicle (UAV) derived canopy height model in an open canopy mixed conifer forest. Forests 2017, 8, 340. [Google Scholar] [CrossRef]
- Miranda, D.L.C.; Junior, V.B.; Gouveia, D.M. Fator de forma e equações de volume para estimativa volumétrica de árvores em plantio de Eucalyptus urograndis. Sci. PLENA 2015, 11, 1–8. [Google Scholar]
- Da Oliveira, J.T.S.; Hellmeister, J.C.; Simões, J.W.; Tomazello Filho, M. Characterization of seven eucalypt wood species to civil construction: 1-dendrometrics evaluations of the trees. Sci. For. 1999, 1, 113–124. [Google Scholar]
- Hamraz, H.; Contreras, M.A.; Zhang, J. Forest understory trees can be segmented accurately within sufficiently dense airborne laser scanning point clouds. Sci. Rep. 2017, 7, 6770. [Google Scholar] [CrossRef]
- Silva, C.A.; Hudak, A.T.; Vierling, L.A.; Klauberg, C.; Garcia, M.; Ferraz, A.; Keller, M.; Eitel, J.; Saatchi, S. Impacts of airborne lidar pulse density on estimating biomass stocks and changes in a selectively logged tropical forest. Remote Sens. 2017, 9, 1068. [Google Scholar] [CrossRef]
- Wannasiri, W.; Nagai, M.; Honda, K.; Santitamnont, P.; Miphokasap, P. Extraction of mangrove biophysical parameters using airborne LiDAR. Remote Sens. 2013, 5, 1787–1808. [Google Scholar] [CrossRef]
- Rex, F.E.; Corte, A.P.D.; Machado, S.D.A.; Silva, C.A.; Sanquetta, C.R. Estimating Above-Ground Biomass of Araucaria angustifolia (Bertol.) Kuntze Using LiDAR Data. Floresta E Ambiente 2019, 26, e20171107. [Google Scholar] [CrossRef]
- Rex, F.E.; Corte, A.P.D.; Machado, S.D.A.; Sanquetta, C.R. Identificação e extração de copas de Araucaria angustifolia (Bertol.) Kuntze a partir de dados LiDAR. Adv. For. Sci. 2018, 5, 319–323. [Google Scholar] [CrossRef]
- Sankey, T.; Shrestha, R.; Sankey, J.B.; Hardegree, S.; Strand, E. Lidar-derived estimate and uncertainty of carbon sink in successional phases of woody encroachment. J. Geophys. Res. Biogeosci. 2013, 118, 1144–1155. [Google Scholar] [CrossRef]
- Yin, D.; Wang, L. Individual mangrove tree measurement using UAV-based LiDAR data: Possibilities and challenges. Remote Sens. Environ. 2019, 223, 34–49. [Google Scholar] [CrossRef]
- Larjavaara, M.; Muller-landau, H.C. Measuring tree height: A quantitative comparison of two common field methods in a moist tropical forest. Methods Ecol. Evol. 2013, 4, 793–801. [Google Scholar] [CrossRef]
- Munroe, D.K.; Nagendra, H.; Southworth, J. Monitoring landscape fragmentation in an inaccessible mountain area: Celaque National Park, Western Honduras. Landsc. Urban Plan. 2007, 83, 154–167. [Google Scholar] [CrossRef]
- Southworth, J.; Tucker, C. The Influence of Accessibility, Local Institutions, and Socioeconomic Factors on Forest Cover Change in the Mountains of Western Honduras. Mt. Res. Dev. 2001, 21, 276–283. [Google Scholar] [CrossRef]
- Teixeira, A.M.G.; Soares-Filho, B.S.; Freitas, S.R.; Metzger, J.P. Modeling landscape dynamics in an Atlantic Rainforest region: Implications for conservation. For. Ecol. Manag. 2009, 257, 1219–1230. [Google Scholar] [CrossRef]
- Da Silva, G.F.; de Curto, R.A.; Soares, C.P.B.; de Piassi, L.C. Avaliação de métodos de medição de altura em florestas naturais. Rev. Arvore 2012, 36, 341–348. [Google Scholar] [CrossRef]
- da Silva, G.F.; de Oliveira, O.M.; de Souza, C.A.M.; Soares, C.P.B.; Lemos, R. Influência de diferentes fontes de erro sobre as medições de alturas de árvores. Cerne 2012, 18, 397–405. [Google Scholar] [CrossRef]
- Lauro, A.C.; Curto, R.D.A.; Tonini, H.; Biazatti, S.C.; Kohler, S.V. Operacionalidade de instrumentos na obtenção da altura total de árvores em sistema agrossilvipastoril. Adv. For. Sci. 2018, 5, 445–451. [Google Scholar] [CrossRef]
- Rahman, M.Z.A.; Bakar, M.A.A.; Razak, K.A.; Rasib, A.W.; Kanniah, K.D.; Kadir, W.H.W.; Omar, H.; Faidi, A.; Kassim, A.R.; Latif, Z.A. Non-destructive, laser-based individual tree aboveground biomass estimation in a tropical rainforest. Forests 2017, 8, 86. [Google Scholar] [CrossRef]
- Brede, B.; Calders, K.; Lau, A.; Raumonen, P.; Bartholomeus, H.M.; Herold, M.; Kooistra, L. Non-destructive tree volume estimation through quantitative structure modelling: Comparing UAV laser scanning with terrestrial LIDAR. Remote Sens. Environ. 2019, 233, 111355. [Google Scholar] [CrossRef]
- Silva, C.A.; Klauberg, C.; Hudak, A.T.; Vierling, L.A.; Liesenberg, V.; Carvalho, S.P.C.E.; Rodriguez, L.C.E. A principal component approach for predicting the stem volume in Eucalyptus plantations in Brazil using airborne LiDAR data. Forestry 2016, 89, 422–433. [Google Scholar] [CrossRef]
- Dube, T.; Mutanga, O.; Abdel-Rahman, E.M.; Ismail, R.; Slotow, R. Predicting Eucalyptus spp. stand volume in Zululand, South Africa: An analysis using a stochastic gradient boosting regression ensemble with multi-source data sets. Int. J. Remote Sens. 2015, 36, 3751–3772. [Google Scholar] [CrossRef]
- Liu, Y.; Noguchi, N.; Liang, L. Development of a positioning system using UAV-based computer vision for an airboat navigation in paddy field. Comput. Electron. Agric. 2019, 162, 126–133. [Google Scholar] [CrossRef]
- Wang, D.; Wan, B.; Liu, J.; Su, Y.; Guo, Q.; Qiu, P.; Wu, X. Estimating aboveground biomass of the mangrove forests on northeast Hainan Island in China using an upscaling method from field plots, UAV-LiDAR data and Sentinel-2 imagery. Int. J. Appl. Earth Obs. Geoinf. 2020, 85, 101986. [Google Scholar] [CrossRef]
- Brede, B.; Lau, A.; Bartholomeus, H.M.; Kooistra, L. Comparing RIEGL RiCOPTER UAV LiDAR derived canopy height and DBH with terrestrial LiDAR. Sensors 2017, 17, 2371. [Google Scholar] [CrossRef]
- Li, J.; Hu, B.; Noland, T.L. Classification of tree species based on structural features derived from high density LiDAR data. Agric. For. Meteorol. 2013, 171–172, 104–114. [Google Scholar] [CrossRef]
- Da Silva, M.N.; Tereza, A.; da Bezerra, D.S.B.; Pereira, L.; de Eloi, C.M.A.; dos Santos, A.L.S.S. A seca no Maranhão no período de 2010 a 2016 e seus impactos. Parcer. Estratégicas 2017, 22, 119–138. [Google Scholar]
- Aji, A.; Wang, F.; Vo, H.; Lee, H.; Liu, Q.; Zhang, X.; Saltz, J. Hadoop gis: A high performance spatial data warehousing system over mapreduce. Proc. VLDB Endow. 2013, 6, 1009–1020. [Google Scholar] [CrossRef]
- Hongchao, M.; Wang, Z. Distributed data organization and parallel data retrieval methods for huge laser scanner point clouds. Comput. Geosci. 2011, 37, 193–201. [Google Scholar] [CrossRef]
- Yang, G.; Liu, J.; Zhao, C.; Li, Z.; Huang, Y.; Yu, H.; Xu, B.; Yang, X.; Zhu, D.; Zhang, X.; et al. Unmanned aerial vehicle remote sensing for field-based crop phenotyping: Current status and perspectives. Front. Plant Sci. 2017, 8, 1111. [Google Scholar] [CrossRef] [PubMed]
- Jaakkola, A.; Hyyppä, J.; Kukko, A.; Yu, X.; Kaartinen, H.; Lehtomäki, M.; Lin, Y. A low-cost multi-sensoral mobile mapping system and its feasibility for tree measurements. ISPRS J. Photogramm. Remote Sens. 2010, 65, 514–522. [Google Scholar] [CrossRef]
- Paula, A.; Corte, D.; Ernandes, M.; Neto, C.; Rex, F.E.; Souza, D.; Behling, A.; Mohan, M.; Niroh, M.; Sanquetta, I.; et al. High-Density UAV-LiDAR in an Integrated Crop-Livestock-Forest System: Sampling Forest Inventory or Forest Inventory Based on Individual Tree Detection (ITD). Drones 2022, 6, 48. [Google Scholar]
- Leitold, V.; Keller, M.; Morton, D.C.; Cook, B.D.; Shimabukuro, Y.E. Airborne lidar-based estimates of tropical forest structure in complex terrain: Opportunities and trade-offs for REDD+. Carbon Balance Manag. 2015, 10, 3. [Google Scholar] [CrossRef]
- Veras, H.F.P.; da Cunha Neto, E.M.; Brasil, I.D.S.; Madi, J.P.S.; Araujo, E.C.G.; Camaño, J.D.Z.; Figueiredo, E.O.; de Almeida Papa, D.; Ferreira, M.P.; Corte, A.P.D.; et al. Estimating tree volume based on crown mapping by UAV pictures in the Amazon Forest. Sci. Electron. Arch. 2023, 16, 16720231742. [Google Scholar] [CrossRef]
- Goodbody, T.R.H.; Coops, N.C.; Marshall, P.L.; Tompalski, P.; Crawford, P. Unmanned aerial systems for precision forest inventory purposes: A review and case study. For. Chron. 2017, 93, 71–81. [Google Scholar] [CrossRef]
- Lin, J.; Wang, M.; Ma, M.; Lin, Y. Aboveground tree biomass estimation of sparse subalpine coniferous forest with UAV oblique photography. Remote Sens. 2018, 10, 1849. [Google Scholar] [CrossRef]
- Mascaro, J.; Detto, M.; Asner, G.P.; Muller-Landau, H.C. Evaluating uncertainty in mapping forest carbon with airborne LiDAR. Remote Sens. Environ. 2011, 115, 3770–3774. [Google Scholar] [CrossRef]
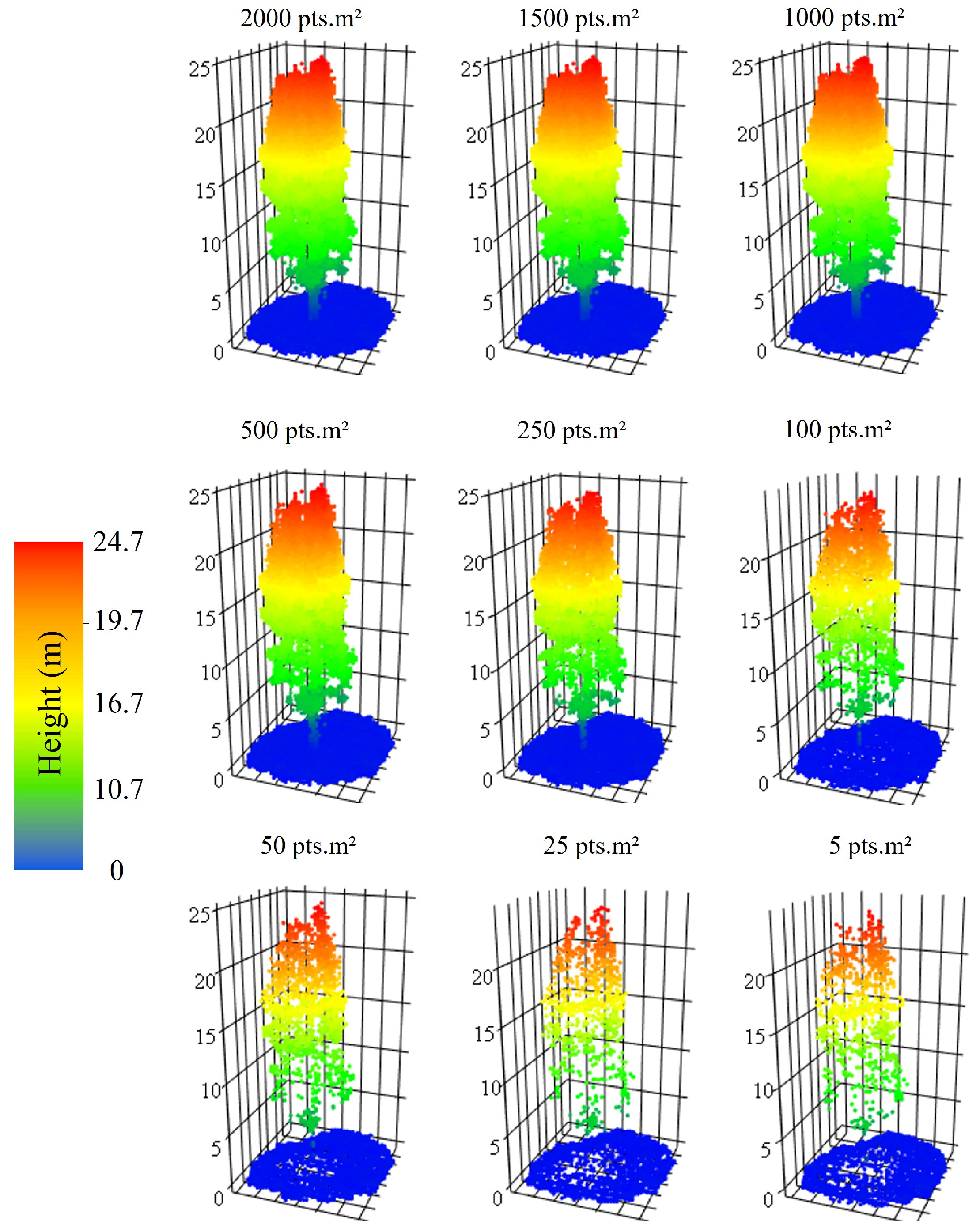

| Scenarios | Height (m) | Statistical Metric | ||||
|---|---|---|---|---|---|---|
| Min | ± SD | Max | SE | CV (%) | ||
| Field | 11.10 | 19.92 ± 2.65 | 26.20 | 0.0630 | 17.75 | |
| Point cloud density (pts/m2) | 2000 | 11.76 | 21.39 ± 3.66 | 28.06 | 0.1048 | 17.47 |
| 1500 | 11.76 | 21.62 ± 3.82 | 27.97 | 0.1047 | 17.67 | |
| 1000 | 11.35 | 21.64 ± 3.99 | 28.30 | 0.1044 | 18.43 | |
| 500 | 11.18 | 21.65 ± 4.02 | 28.30 | 0.1041 | 18.54 | |
| 250 | 11.25 | 21.55 ± 4.15 | 28.38 | 0.1044 | 19.26 | |
| 100 | 11.10 | 21.44 ± 4.17 | 28.44 | 0.1041 | 19.44 | |
| 50 | 10.95 | 21.12 ± 4.40 | 28.38 | 0.1077 | 20.85 | |
| 25 | 10.91 | 20.90 ± 4.45 | 28.30 | 0.1088 | 21.30 | |
| 5 | 11.23 | 20.12 ± 4.16 | 27.92 | 0.0886 | 20.65 | |
| Height’s Center Class (m) | Number of Individuals (n) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Field | Point Cloud Density (pts·m−2) | |||||||||
| 2000 | 1500 | 1000 | 500 | 250 | 100 | 50 | 25 | 5 | ||
| 7.5 | 13 | 4 | 18 | 20 | 20 | 20 | 23 | 21 | 32 | 60 |
| 12.5 | 87 | 208 | 206 | 214 | 207 | 211 | 225 | 248 | 281 | 438 |
| 17.5 | 788 | 395 | 401 | 404 | 391 | 386 | 400 | 392 | 394 | 646 |
| 22.5 | 974 | 623 | 632 | 642 | 642 | 670 | 691 | 703 | 708 | 1004 |
| 27.5 | 7 | 468 | 478 | 475 | 452 | 428 | 405 | 381 | 342 | 231 |
| Total | 1869 | 1698 | 1735 | 1755 | 1712 | 1715 | 1744 | 1745 | 1757 | 2379 |
| Difference (n) | 171 | 134 | 114 | 157 | 154 | 125 | 124 | 112 | −510 | |
| Difference (%) | 9.15 | 7.17 | 6.10 | 8.40 | 8.24 | 6.69 | 6.63 | 5.99 | −27.29 | |
| Point Cloud Density (pts·m−2) | r | RMSE (m) | RMSE (%) | Bias (m) | Bias (%) | t (p-Value) |
|---|---|---|---|---|---|---|
| 2000 | 0.792 | 2.904 | 14.547 | −1.675 | −8.389 | 0.839 |
| 1500 | 0.787 | 2.922 | 14.660 | −1.681 | −8.433 | 0.874 |
| 1000 | 0.757 | 3.141 | 15.763 | −1.713 | −8.598 | 0.891 |
| 500 | 0.736 | 3.241 | 16.270 | −1.737 | −8.720 | 0.849 |
| 250 | 0.690 | 3.440 | 17.315 | −1.673 | −8.418 | 0.846 |
| 100 | 0.690 | 3.405 | 17.129 | −1.568 | −7.889 | 0.869 |
| 50 | 0.617 | 3.693 | 18.609 | −1.277 | −6.433 | 0.868 |
| 25 | 0.598 | 3.726 | 18.791 | −1.073 | −5.412 | 0.878 |
| 10 | 0.578 | 3.724 | 18.811 | −0.484 | −2.447 | 0.297 |
| 5 | 0.579 | 3.426 | 17.314 | −0.334 | −1.688 | 0.839 |
| Scenario | Stands Variables | Difference (%) | |||||
|---|---|---|---|---|---|---|---|
| Vmi (m3·tree−1) | n | V (m3·ha−1) | Stock (m3) | Vmi | Stock | ||
| Field | 0.6963 | 1869 | 82.42 | 1301.38 | - | - | |
| Point cloud density (pts·m−2) | 2000 | 0.7616 | 1698 | 81.90 | 1293.24 | −9.38 | 0.63 |
| 1500 | 0.7595 | 1735 | 83.45 | 1317.70 | −9.07 | −1.25 | |
| 1000 | 0.7546 | 1755 | 83.87 | 1324.32 | −8.37 | −1.76 | |
| 500 | 0.7551 | 1712 | 81.87 | 1292.72 | −8.44 | 0.67 | |
| 250 | 0.7517 | 1715 | 81.64 | 1289.16 | −7.96 | 0.94 | |
| 100 | 0.7452 | 1744 | 82.31 | 1299.62 | −7.02 | 0.14 | |
| 50 | 0.7388 | 1745 | 81.64 | 1289.16 | −6.10 | 0.94 | |
| 25 | 0.7228 | 1757 | 80.43 | 1269.99 | −3.81 | 2.41 | |
| 5 | 0.6879 | 2379 | 103.64 | 1636.48 | 1.21 | −25.75 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cunha Neto, E.M.d.; Guaraná, E.; Moura, M.M.; Veras, H.F.P.; Zambrano, A.M.A.; Broadbent, E.N.; Maia, E.; Pelissari, A.L.; Lanssanova, L.R.; Sanquetta, C.R.; et al. Optimizing UAV-LiDAR Point Density for Eucalyptus Height Estimation in Agroforestry. Forests 2025, 16, 1747. https://doi.org/10.3390/f16111747
Cunha Neto EMd, Guaraná E, Moura MM, Veras HFP, Zambrano AMA, Broadbent EN, Maia E, Pelissari AL, Lanssanova LR, Sanquetta CR, et al. Optimizing UAV-LiDAR Point Density for Eucalyptus Height Estimation in Agroforestry. Forests. 2025; 16(11):1747. https://doi.org/10.3390/f16111747
Chicago/Turabian StyleCunha Neto, Ernandes Macedo da, Emmanoella Guaraná, Marks Melo Moura, Hudson Franklin Pessoa Veras, Angélica Maria Almeyda Zambrano, Eben North Broadbent, Emanuel Maia, Allan Libanio Pelissari, Luciano Rodrigo Lanssanova, Carlos Roberto Sanquetta, and et al. 2025. "Optimizing UAV-LiDAR Point Density for Eucalyptus Height Estimation in Agroforestry" Forests 16, no. 11: 1747. https://doi.org/10.3390/f16111747
APA StyleCunha Neto, E. M. d., Guaraná, E., Moura, M. M., Veras, H. F. P., Zambrano, A. M. A., Broadbent, E. N., Maia, E., Pelissari, A. L., Lanssanova, L. R., Sanquetta, C. R., & Dalla Corte, A. P. (2025). Optimizing UAV-LiDAR Point Density for Eucalyptus Height Estimation in Agroforestry. Forests, 16(11), 1747. https://doi.org/10.3390/f16111747










