Integrating Ecological Semantic Encoding and Distribution-Aligned Loss for Multimodal Forest Ecosystem
Abstract
1. Introduction
- Cross-level contrastive learning: We introduce a hierarchical contrastive learning paradigm that unifies aboveground vegetation and soil seed bank representations within a shared embedding space, explicitly addressing their asymmetric ecological dependencies beyond traditional linear (RDA, CCA) or symmetric contrastive models (SimCLR).
- Multi-channel ecological semantic encoder: A Transformer-based encoder integrates heterogeneous ecological features—species composition, functional traits, and environmental variables—into interpretable multi-scale embeddings, enabling cross-modal semantic fusion.
- Distribution-aligned contrastive loss: We combine InfoNCE with Maximum Mean Discrepancy (MMD) regularization to jointly optimize instance-level discrimination and distribution-level alignment. Although similar strategies exist in domain adaptation and cross-modal learning, this study is the first to extend them to ecological multimodal asymmetry, improving robustness under heterogeneous environmental conditions.
- Disturbance-aware attention: Unlike conditional or bias-gated attention used in environmental prediction, our mechanism dynamically reweights pairwise ecological alignments based on learned disturbance embeddings (e.g., grazing, burning, soil disturbance), allowing context-sensitive yet stable semantic coupling under variable disturbances.
- Mechanism–pattern–function integration: The framework incorporates land use/land cover (LULC) and ecosystem service indicators, linking ecological mechanisms and spatial patterns with functional outcomes to support large-scale ecosystem assessment and restoration.
2. Related Work
2.1. Modeling the Ecological Relationship Between Aboveground Vegetation and Seed Banks
2.2. Contrastive Learning and Ecological Multimodal Alignment
2.3. Land Use and Ecosystem Services Research
3. Materials and Method
3.1. Data Collection
3.2. Data Enhancement
3.3. Proposed Method
3.3.1. Overall
3.3.2. Ecological Semantic Encoder
3.3.3. Distribution-Aligned Contrastive Loss
3.3.4. Disturbance-Aware Attention Module
4. Results and Discussion
4.1. Evaluation Metrics
4.2. Experiment Settings
4.2.1. Hardware and Software Configuration
4.2.2. Hyperparameter Settings
4.2.3. Baseline Methods
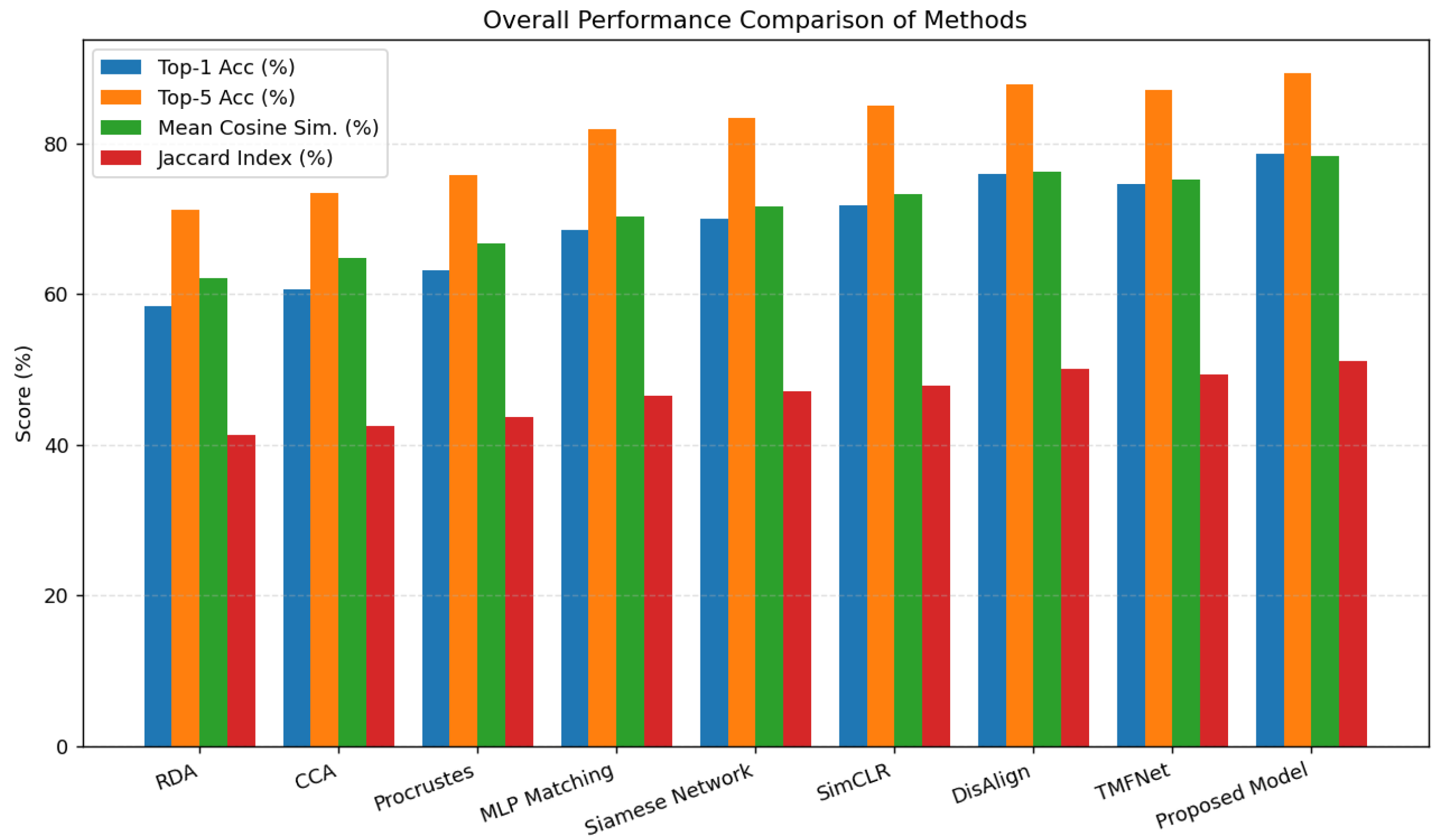
4.3. Overall Performance Comparison Between the Proposed Model and Baseline Methods
4.4. Comprehensive Evaluation Across Alignment, Distribution, and Structural Recovery Metrics
4.5. Ablation Study Evaluating the Contribution of Each Module in the Proposed Framework
4.6. Disturbance Sensitivity
4.7. Discussion
4.8. Limitations and Future Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Detailed Mathematical Derivations
Appendix A.1. Derivation of the Ecological Semantic Encoder
Appendix A.2. Distribution-Aligned Loss Derivation
Appendix A.3. Gradient Derivation for Optimization
References
- Sokol, N.W.; Slessarev, E.; Marschmann, G.L.; Nicolas, A.; Blazewicz, S.J.; Brodie, E.L.; Firestone, M.K.; Foley, M.M.; Hestrin, R.; Hungate, B.A.; et al. Life and death in the soil microbiome: How ecological processes influence biogeochemistry. Nat. Rev. Microbiol. 2022, 20, 415–430. [Google Scholar] [CrossRef]
- Birhanu, L.; Bekele, T.; Tesfaw, B.; Demissew, S. Soil seed bank composition and aboveground vegetation in dry Afromontane forest patches of Northwestern Ethiopia. Trees For. People 2022, 9, 100292. [Google Scholar] [CrossRef]
- Al-Huqail, A.A.; Al-Harbi, H.F.; Alowaifeer, A.M.; El-Sheikh, M.A.; Assaeed, A.M.; Alsaleem, T.S.; Kassem, H.S.; Azab, O.M.; Dar, B.A.; Malik, J.A.; et al. Correlation between aboveground vegetation composition and soil seed bank of Raudhat desert habitat: A case study of Raudhat Alkhafs, Saudi Arabia. BMC Plant Biol. 2025, 25, 136. [Google Scholar]
- Zhao, Y.; Li, M.; Deng, J.; Wang, B. Afforestation affects soil seed banks by altering soil properties and understory plants on the eastern Loess Plateau, China. Ecol. Indic. 2021, 126, 107670. [Google Scholar] [CrossRef]
- Chen, M.; Hussain, S.; Liu, Y.; Mustafa, G.; Hu, B.; Qin, Z.; Wang, X. Responses of soil seed bank and its above-ground vegetation to various reclamation patterns. Mar. Environ. Res. 2024, 196, 106436. [Google Scholar] [CrossRef] [PubMed]
- Ma, H.; Mo, L.; Crowther, T.W.; Maynard, D.S.; van den Hoogen, J.; Stocker, B.D.; Terrer, C.; Zohner, C.M. The global distribution and environmental drivers of aboveground versus belowground plant biomass. Nat. Ecol. Evol. 2021, 5, 1110–1122. [Google Scholar] [CrossRef] [PubMed]
- Larson, J.E.; Suding, K.N. Seed bank bias: Differential tracking of functional traits in the seed bank and vegetation across a gradient. Ecology 2022, 103, e3651. [Google Scholar] [CrossRef]
- Zhang, Y.; Wa, S.; Liu, Y.; Zhou, X.; Sun, P.; Ma, Q. High-accuracy detection of maize leaf diseases CNN based on multi-pathway activation function module. Remote Sens. 2021, 13, 4218. [Google Scholar] [CrossRef]
- Huanca-Nunez, N.; Chazdon, R.L.; Russo, S.E. Trait-mediated variation in seedling performance in Costa Rican successional forests: Comparing above-ground, below-ground, and allocation-based traits. Plants 2024, 13, 2378. [Google Scholar] [CrossRef]
- Lv, Y.; Shen, M.; Meng, B.; Zhang, H.; Sun, Y.; Zhang, J.; Chang, L.; Li, J.; Yi, S. The similarity between species composition of vegetation and soil seed bank of grasslands in Inner Mongolia, China: Implications for the asymmetric response to precipitation. Plants 2021, 10, 1890. [Google Scholar] [CrossRef]
- Lin, X.; Wa, S.; Zhang, Y.; Ma, Q. A dilated segmentation network with the morphological correction method in farming area image Series. Remote Sens. 2022, 14, 1771. [Google Scholar] [CrossRef]
- Haobo, W. Comparative learning leads weak label learning new SOTA, and Zhejiang University’s new research was selected as ICLR Oral. Heart 2022, 13, 58. [Google Scholar]
- Tang, Y.; Li, H. Comparing the performance of machine learning methods in predicting soil seed bank persistence. Ecol. Inform. 2023, 77, 102188. [Google Scholar] [CrossRef]
- Rosbakh, S.; Pichler, M.; Poschlod, P. Machine-learning algorithms predict soil seed bank persistence from easily available traits. Appl. Veg. Sci. 2022, 25, e12660. [Google Scholar] [CrossRef]
- Khan, R.W.A.; Shaheen, H.; Islam Dar, M.E.U.; Habib, T.; Manzoor, M.; Gillani, S.W.; Al-Andal, A.; Ayoola, J.O.; Waheed, M. A data-driven approach to forest health assessment through multivariate analysis and machine learning techniques. BMC Plant Biol. 2025, 25, 915. [Google Scholar] [CrossRef] [PubMed]
- Luo, S.; Ni, J.; Chen, S.; Yu, R.; Xie, Y.; Liu, L.; Jin, Z.; Yao, H.; Jia, X. Free: The foundational semantic recognition for modeling environmental ecosystems. arXiv 2023, arXiv:2311.10255. [Google Scholar]
- Plohák, P.; Švehláková, H.; Stalmachová, B.; Goňo, M.; Dvorskỳ, T. Combining extraction and cultivation methods for soil seed bank analysis increases number of captured species and their similarity to above-ground vegetation. Front. Plant Sci. 2025, 15, 1500941. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Yang, D.H.; Yi, T.H.; Zhang, G.H.; Han, J.G. Eliminating environmental and operational effects on structural modal frequency: A comprehensive review. Struct. Control Health Monit. 2022, 29, e3073. [Google Scholar] [CrossRef]
- Wang, L.; Jackson, D.A. Effects of sample size, data quality, and species response in environmental space on modeling species distributions. Landsc. Ecol. 2023, 38, 4009–4031. [Google Scholar] [CrossRef]
- Dou, X.; Li, W.; He, Y.; Zhao, Y.; Sang, Q.; Wang, Y.; Wang, C.; Yan, Y. Assessing the Future Effectiveness of Ecological Protection and Restoration by Compiling Ecological Patterns & Services Indicators and Multi-Scenario Simulation. Environ. Sustain. Indic. 2025, 28, 100939. [Google Scholar] [CrossRef]
- Borowiec, M.L.; Dikow, R.B.; Frandsen, P.B.; McKeeken, A.; Valentini, G.; White, A.E. Deep learning as a tool for ecology and evolution. Methods Ecol. Evol. 2022, 13, 1640–1660. [Google Scholar] [CrossRef]
- Pichler, M.; Hartig, F. Machine learning and deep learning—A review for ecologists. Methods Ecol. Evol. 2023, 14, 994–1016. [Google Scholar] [CrossRef]
- Wu, Y.; Gadsden, S.A. Machine learning algorithms in microbial classification: A comparative analysis. Front. Artif. Intell. 2023, 6, 1200994. [Google Scholar] [CrossRef]
- Luo, C.; Guo, X.; Feng, C.; Xiao, C. Soil seed bank responses to anthropogenic disturbances and its vegetation restoration potential in the arid mining area. Ecol. Indic. 2023, 154, 110549. [Google Scholar] [CrossRef]
- Sanou, L.; Savadogo, P.; Zida, D.; Thiombiano, A. Variation in soil seed bank and relationship with aboveground vegetation across microhabitats in a savanna-woodland of West Africa. Nord. J. Bot. 2022, 2022, e03304. [Google Scholar] [CrossRef]
- Luo, C.; Guo, X.P.; Feng, C.D.; Ye, J.P.; Li, P.F.; Li, Z.T. Spatial patterns of soil seed banks and their relationships with above-ground vegetation in an arid desert. Appl. Veg. Sci. 2021, 24, e12616. [Google Scholar] [CrossRef]
- Durkee, M.S.; Lleras, K.; Drukker, K.; Ai, J.; Cao, T.; Casella, G.; Ghosh, D.; Clark, M.R.; Giger, M.L. Generalizations of the Jaccard index and Sørensen index for assessing agreement across multiple readers in object detection and instance segmentation in biomedical imaging. J. Med. Imaging 2023, 10, 065503. [Google Scholar] [CrossRef]
- DeMalach, N.; Kigel, J.; Sternberg, M. The soil seed bank can buffer long-term compositional changes in annual plant communities. J. Ecol. 2021, 109, 1275–1283. [Google Scholar] [CrossRef]
- Borokini, I.T.; Weisberg, P.J.; Peacock, M.M. Quantifying the relationship between soil seed bank and plant community assemblage in sites harboring the threatened Ivesia webberi in the western Great Basin Desert. Appl. Veg. Sci. 2021, 24, e12547. [Google Scholar] [CrossRef]
- Ray, J.; Bordolui, S.K. Role of seed banks in the conservation of plant diversity and ecological restoration. J. Environ. Sci. 2021, 3, 1–16. [Google Scholar]
- Gao, J.; Yang, B.; Babu, S. Ecological links between aboveground and underground ecosystems under global change. Front. Ecol. Evol. 2024, 12, 1347653. [Google Scholar] [CrossRef]
- Zhang, W.; Stratos, K. Understanding hard negatives in noise contrastive estimation. arXiv 2021, arXiv:2104.06245. [Google Scholar] [CrossRef]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A simple framework for contrastive learning of visual representations. In Proceedings of the 37th International Conference on Machine Learning, ICML 2020, Virtual, 13–18 July 2020; pp. 1597–1607. [Google Scholar]
- Xiong, J.; Yu, H.; Li, L.; Yuan, M.; Yu, J. Asymmetry between ecosystem health and ecological quality from an Earth observation perspective. Sci. Rep. 2025, 15, 10143. [Google Scholar] [CrossRef]
- Zhou, X.; Chen, S.; Ren, Y.; Zhang, Y.; Fu, J.; Fan, D.; Lin, J.; Wang, Q. Atrous Pyramid GAN Segmentation Network for Fish Images with High Performance. Electronics 2022, 11, 911. [Google Scholar] [CrossRef]
- Mir, Y.H.; Mir, S.; Ganie, M.A.; Bhat, J.A.; Shah, A.M.; Mushtaq, M.; Irshad, I. Overview of land use and land cover change and its impacts on natural resources. In Ecologically Mediated Development: Promoting Biodiversity Conservation and Food Security; Springer: Singapore, 2025; pp. 101–130. [Google Scholar]
- Alemayehu, B.; Suarez-Minguez, J.; Rosette, J. The Implications of Plantation Forest-Driven Land Use/Land Cover Changes for Ecosystem Service Values in the Northwestern Highlands of Ethiopia. Remote Sens. 2024, 16, 4159. [Google Scholar] [CrossRef]
- Rana, S.; Gatti, M. Comparative Evaluation of Modified Wasserstein GAN-GP and State-of-the-Art GAN Models for Synthesizing Agricultural Weed Images in RGB and Infrared Domain. MethodsX 2025, 14, 103309. [Google Scholar] [CrossRef]
- Van Den Wollenberg, A.L. Redundancy analysis an alternative for canonical correlation analysis. Psychometrika 1977, 42, 207–219. [Google Scholar] [CrossRef]
- Ter Braak, C.J. Canonical correspondence analysis: A new eigenvector technique for multivariate direct gradient analysis. Ecology 1986, 67, 1167–1179. [Google Scholar] [CrossRef]
- Schönemann, P.H. A generalized solution of the orthogonal procrustes problem. Psychometrika 1966, 31, 1–10. [Google Scholar] [CrossRef]
- Huang, P.S.; He, X.; Gao, J.; Deng, L.; Acero, A.; Heck, L. Learning deep structured semantic models for web search using clickthrough data. In Proceedings of the 22nd ACM International Conference on Information & Knowledge Management, San Francisco, CA, USA, 27 October–1 November 2013; pp. 2333–2338. [Google Scholar]
- Bromley, J.; Guyon, I.; LeCun, Y.; Säckinger, E.; Shah, R. Signature verification using a “siamese” time delay neural network. Adv. Neural Inf. Process. Syst. 1993, 6, 737–744. [Google Scholar] [CrossRef]
- Zhang, S.; Li, Z.; Yan, S.; He, X.; Sun, J. Distribution alignment: A unified framework for long-tail visual recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 2361–2370. [Google Scholar]
- Liu, Y.; Gao, K.; Wang, H.; Yang, Z.; Wang, P.; Ji, S.; Huang, Y.; Zhu, Z.; Zhao, X. A Transformer-based multi-modal fusion network for semantic segmentation of high-resolution remote sensing imagery. Int. J. Appl. Earth Obs. Geoinf. 2024, 133, 104083. [Google Scholar] [CrossRef]


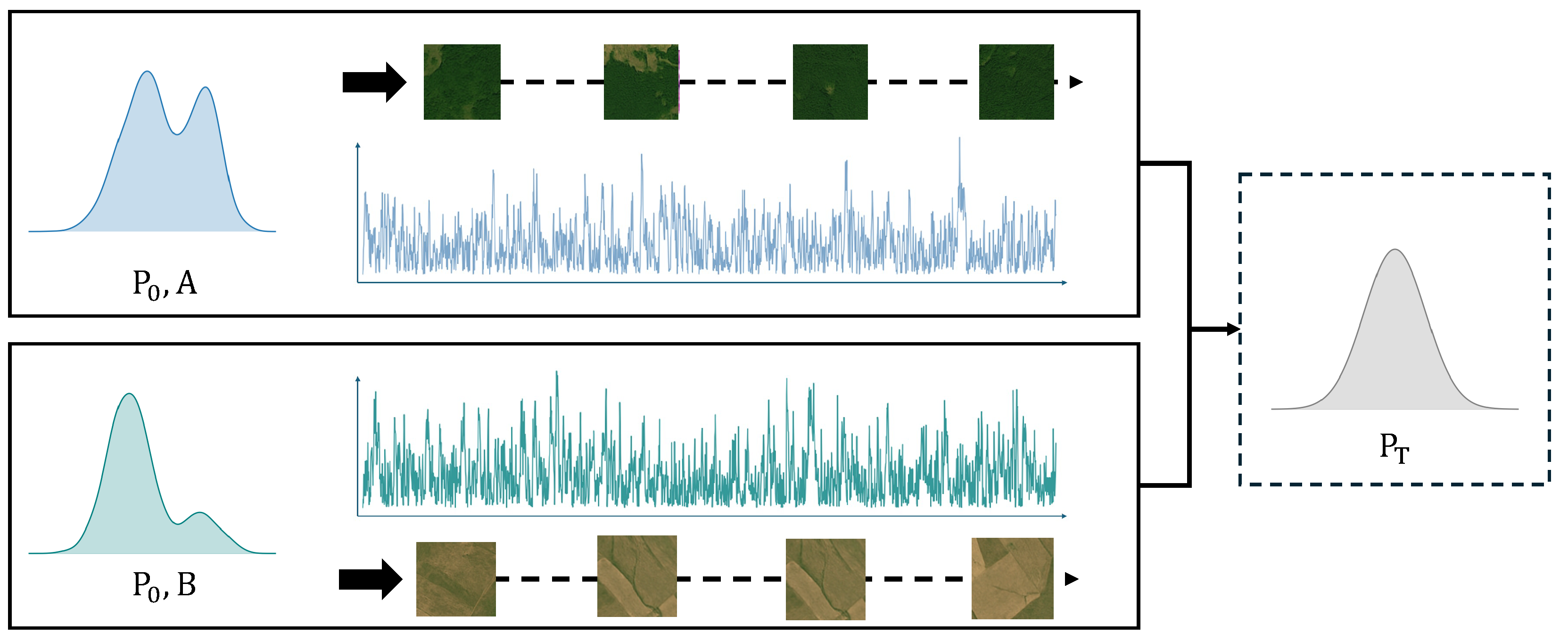

| Data Type | Quantity | Period | Source and Method |
|---|---|---|---|
| Aboveground vegetation records | 12,500 | 2022–2023 | Quadrat survey (1 m × 1 m) for species identification and abundance estimation |
| Soil seed bank samples | 2500 | 2022–2023 | 0–10 cm soil cores, laboratory germination test (90 days) |
| Environmental variables | 2500 | 2022–2023 | GPS/DEM, soil nutrients (N, P, K, OM), meteorological data |
| Disturbance history | 2500 | 2013–2023 | Field interviews, remote sensing (Landsat, Sentinel-2) |
| Total ecological pairs | 2022–2023 | Integrated aboveground–belowground paired dataset |
| Method | Top-1 Acc (%) | Top-5 Acc (%) | Mean Cosine Sim. | Jaccard Index |
|---|---|---|---|---|
| RDA [39] | 58.4 | 71.2 | 0.621 | 0.413 |
| CCA [40] | 60.7 | 73.5 | 0.648 | 0.425 |
| Procrustes [41] | 63.2 | 75.8 | 0.667 | 0.437 |
| MLP Matching [42] | 68.5 | 81.9 | 0.703 | 0.465 |
| Siamese Network [43] | 70.1 | 83.4 | 0.716 | 0.471 |
| SimCLR [33] | 71.8 | 85.0 | 0.733 | 0.479 |
| DisAlign [44] | 75.9 | 87.8 | 0.763 | 0.501 |
| TMFNet [45] | 74.6 | 87.1 | 0.752 | 0.493 |
| Proposed Model | 78.6 | 89.3 | 0.784 | 0.512 |
| Method | KL Div. ↓ | EMD ↓ | Sørensen Coeff. | NMDS Stress ↓ | Top-1 Acc (%) | Mean Cos. Sim. |
|---|---|---|---|---|---|---|
| RDA | 0.241 | 0.184 | 0.612 | 0.147 | 58.4 | 0.621 |
| CCA | 0.218 | 0.176 | 0.623 | 0.141 | 60.7 | 0.648 |
| Procrustes | 0.201 | 0.169 | 0.636 | 0.136 | 63.2 | 0.667 |
| MLP Matching | 0.176 | 0.158 | 0.652 | 0.127 | 68.5 | 0.703 |
| Siamese Network | 0.162 | 0.145 | 0.664 | 0.121 | 70.1 | 0.716 |
| SimCLR | 0.157 | 0.141 | 0.671 | 0.118 | 71.8 | 0.733 |
| DisAlign | 0.137 | 0.119 | 0.701 | 0.103 | 75.9 | 0.763 |
| TMFNet | 0.145 | 0.132 | 0.689 | 0.111 | 74.6 | 0.752 |
| Proposed Model | 0.128 | 0.107 | 0.713 | 0.094 | 78.6 | 0.784 |
| Model Variant | Top-1 Acc (%) | Mean Cosine Sim. | KL Div. ↓ | Jaccard Index |
|---|---|---|---|---|
| Without Ecological Semantic Encoder | 70.9 ** | 0.713 ** | 0.182 ** | 0.469 ** |
| Without Disturbance-Aware Attention | 72.4 ** | 0.731 ** | 0.168 ** | 0.478 * |
| Without Distribution-Aligned Loss | 74.3 * | 0.751 * | 0.152 * | 0.491 * |
| Full Model (Proposed) | 78.6 | 0.784 | 0.128 | 0.512 |
| Disturbance Type | Level | Mean Attention Activation | MMD (↓) | DSI (↑) |
|---|---|---|---|---|
| Grazing Intensity | Low | 0.421 | 0.017 | 0.864 |
| Medium | 0.457 | 0.014 | 0.879 | |
| High | 0.493 | 0.011 | 0.892 | |
| Fire Frequency | Low | 0.476 | 0.021 | 0.874 |
| Medium | 0.512 | 0.018 | 0.889 | |
| High | 0.549 | 0.016 | 0.901 | |
| Land-use Change | Low | 0.541 | 0.039 | 0.881 |
| Medium | 0.602 | 0.033 | 0.905 | |
| High | 0.665 | 0.032 | 0.918 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, J.; Fu, Z.; Zhou, H.; Liu, Y.; Zhang, Y.; Shi, R.; Li, J.; Dong, M. Integrating Ecological Semantic Encoding and Distribution-Aligned Loss for Multimodal Forest Ecosystem. Forests 2025, 16, 1697. https://doi.org/10.3390/f16111697
Peng J, Fu Z, Zhou H, Liu Y, Zhang Y, Shi R, Li J, Dong M. Integrating Ecological Semantic Encoding and Distribution-Aligned Loss for Multimodal Forest Ecosystem. Forests. 2025; 16(11):1697. https://doi.org/10.3390/f16111697
Chicago/Turabian StylePeng, Jing, Zhengjie Fu, Huachen Zhou, Yibin Liu, Yang Zhang, Rui Shi, Jiangfeng Li, and Min Dong. 2025. "Integrating Ecological Semantic Encoding and Distribution-Aligned Loss for Multimodal Forest Ecosystem" Forests 16, no. 11: 1697. https://doi.org/10.3390/f16111697
APA StylePeng, J., Fu, Z., Zhou, H., Liu, Y., Zhang, Y., Shi, R., Li, J., & Dong, M. (2025). Integrating Ecological Semantic Encoding and Distribution-Aligned Loss for Multimodal Forest Ecosystem. Forests, 16(11), 1697. https://doi.org/10.3390/f16111697





