Full Orthotropic Mechanical Characterization of Pinus radiata Plywood Through Tensile, Compression and Shear Testing with Miniaturized Specimens
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
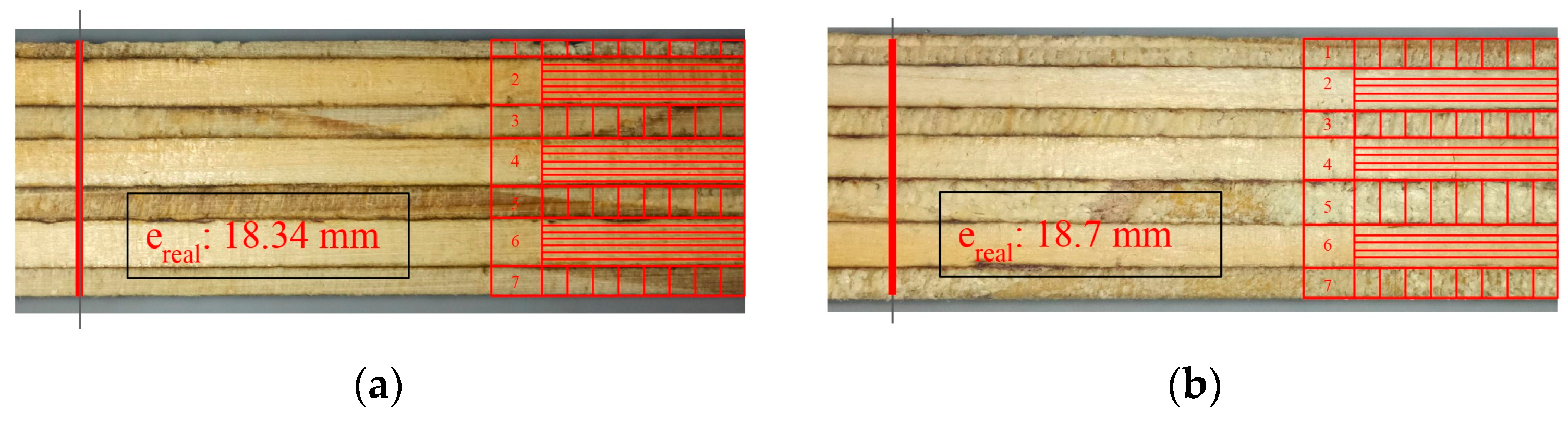
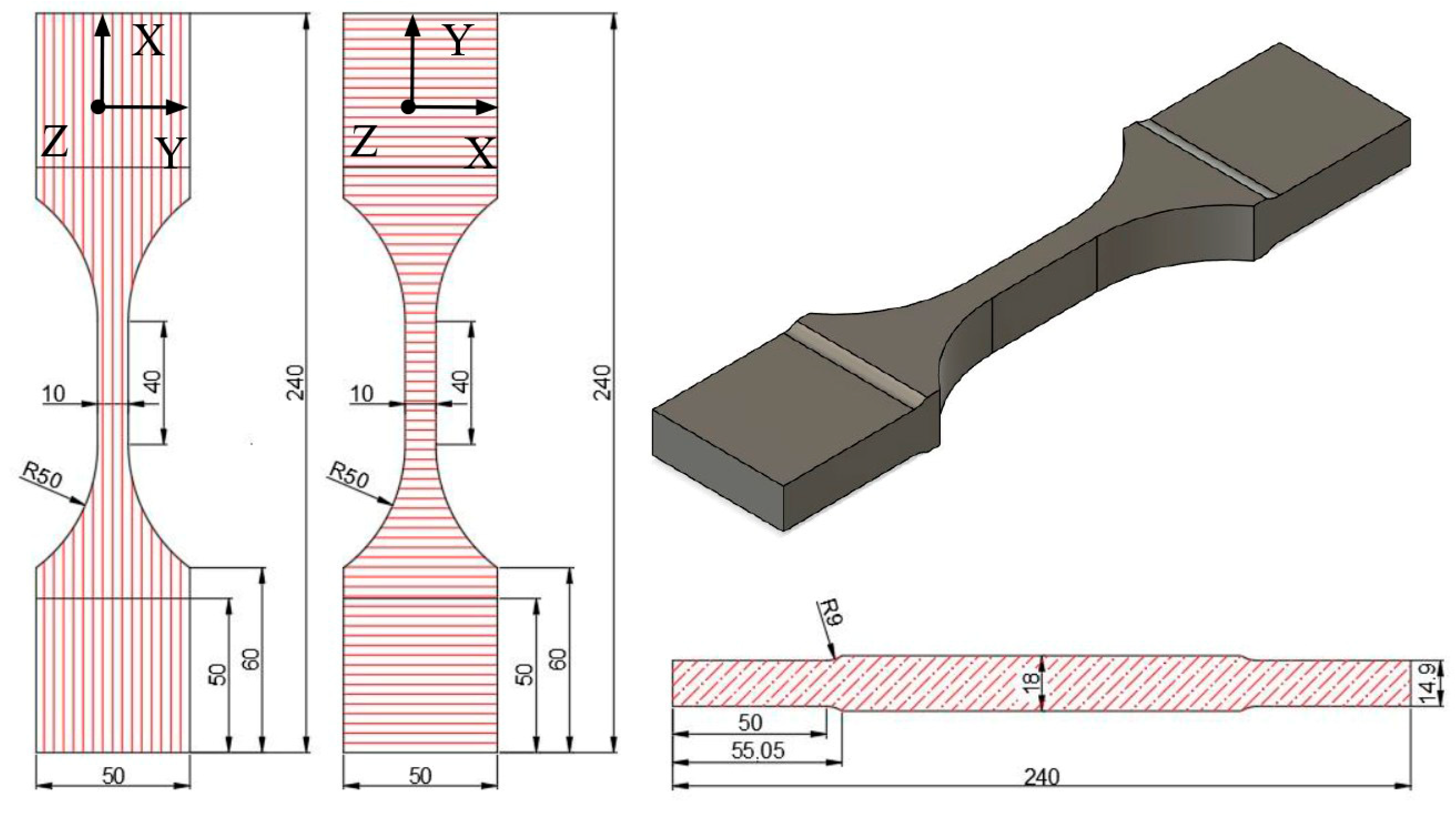
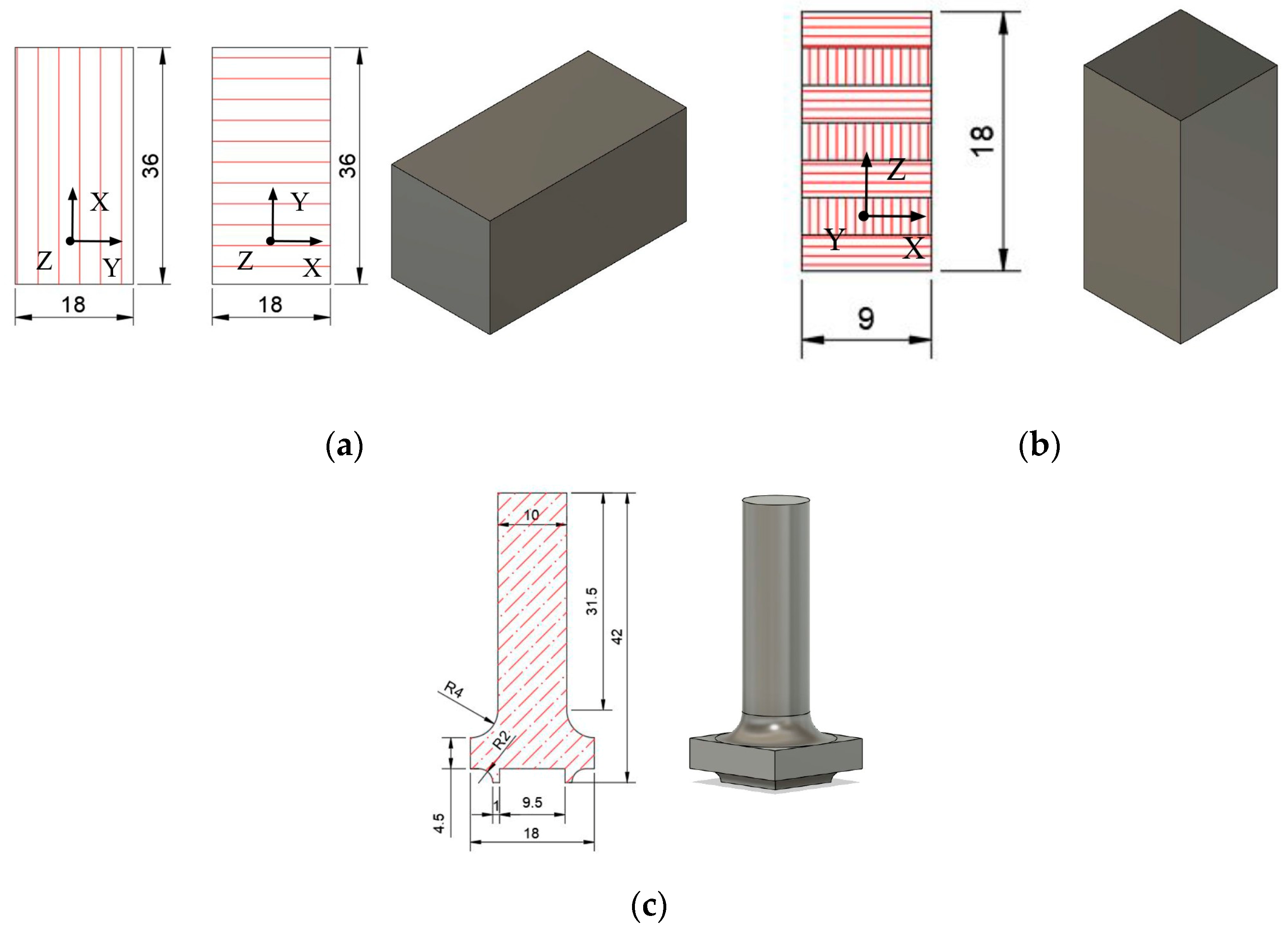
2.2. Samples Geometries and Manufacturing Toolpaths of Miniature Specimens
2.3. Mechanical Testing Procedures and Data Reduction
2.3.1. Test Speed
2.3.2. Tensile Tests
2.3.3. Compression Tests
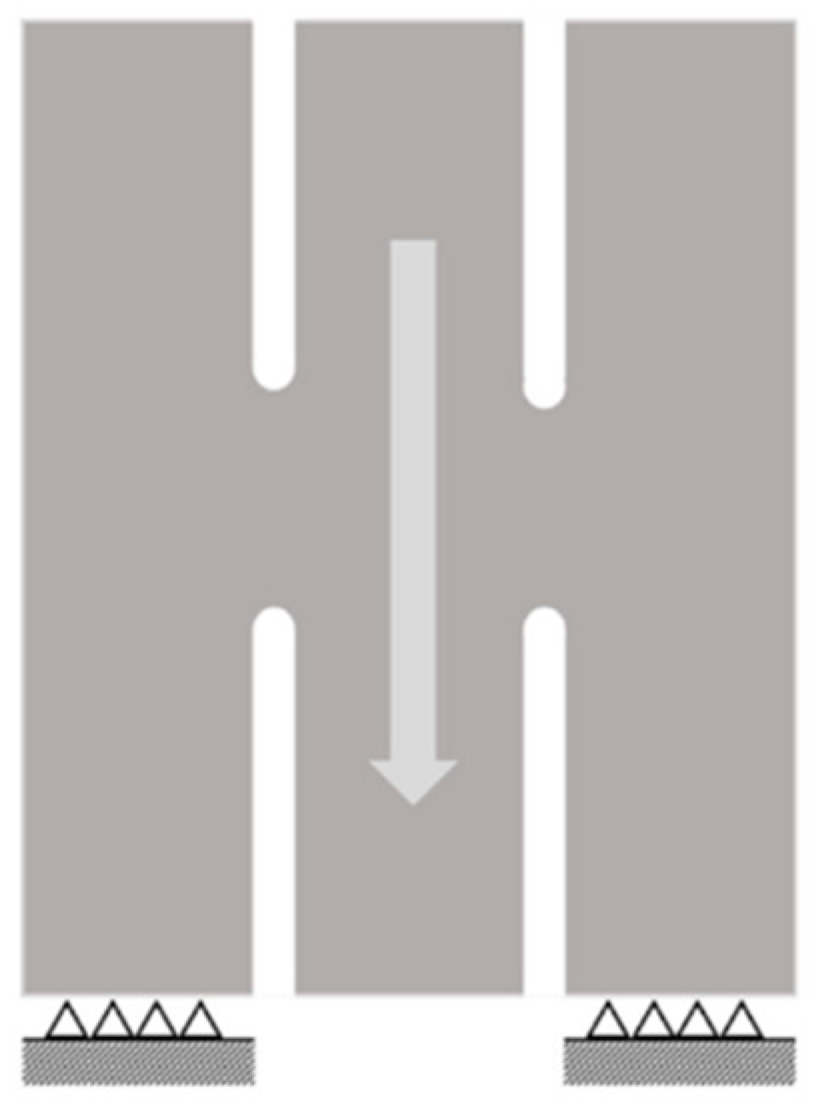
2.3.4. Shear Tests
3. Results: Orthotropic Properties Characterization in Plywood Panels
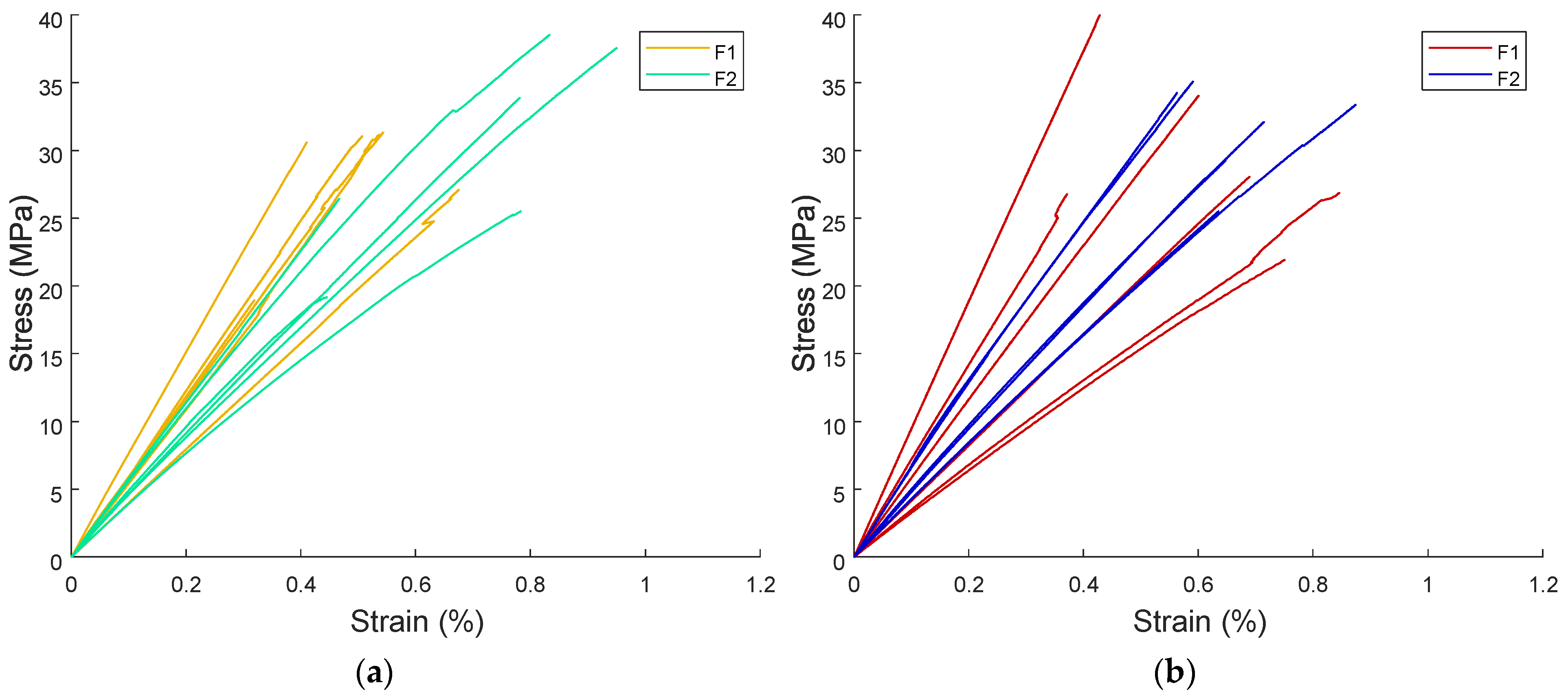
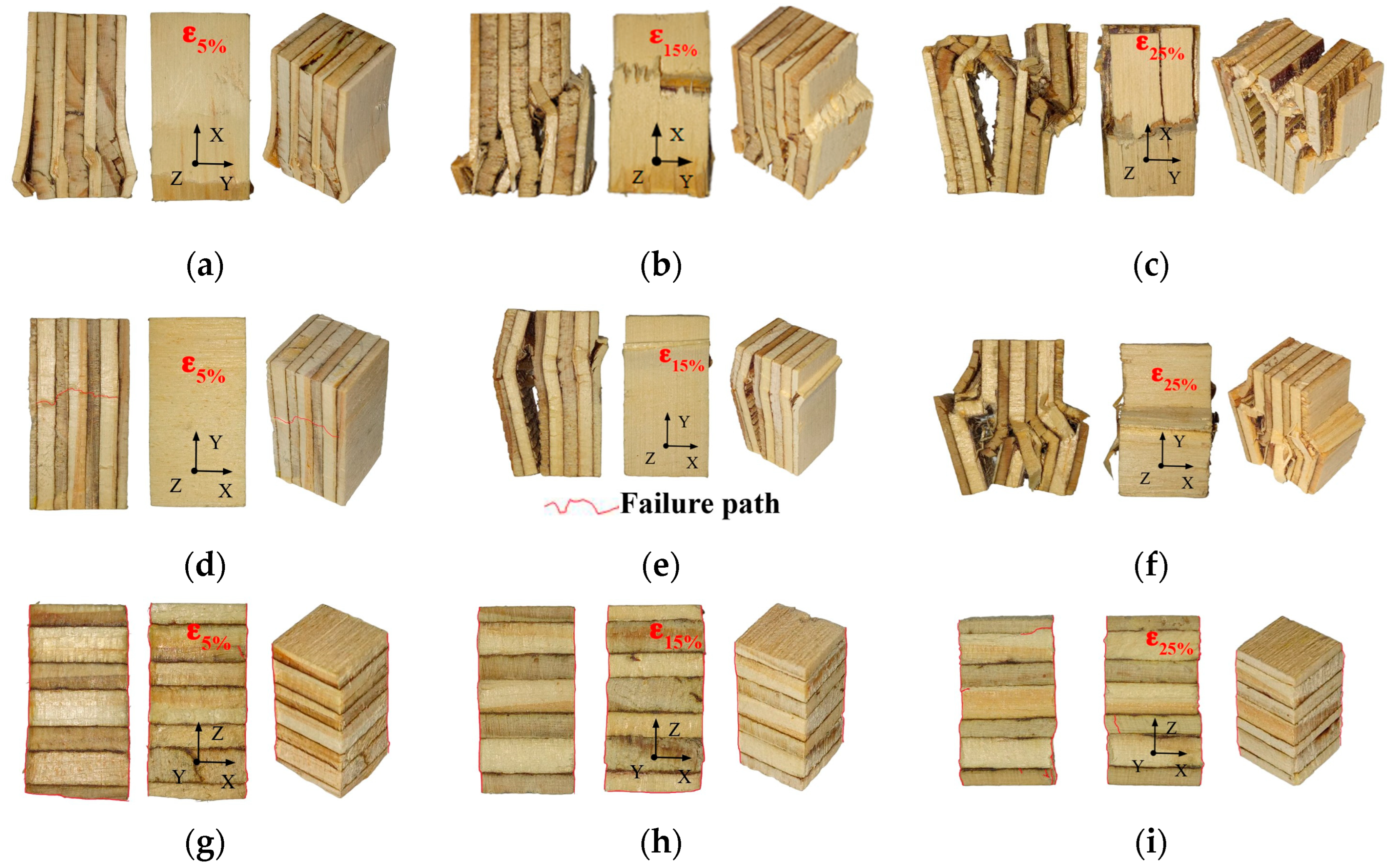
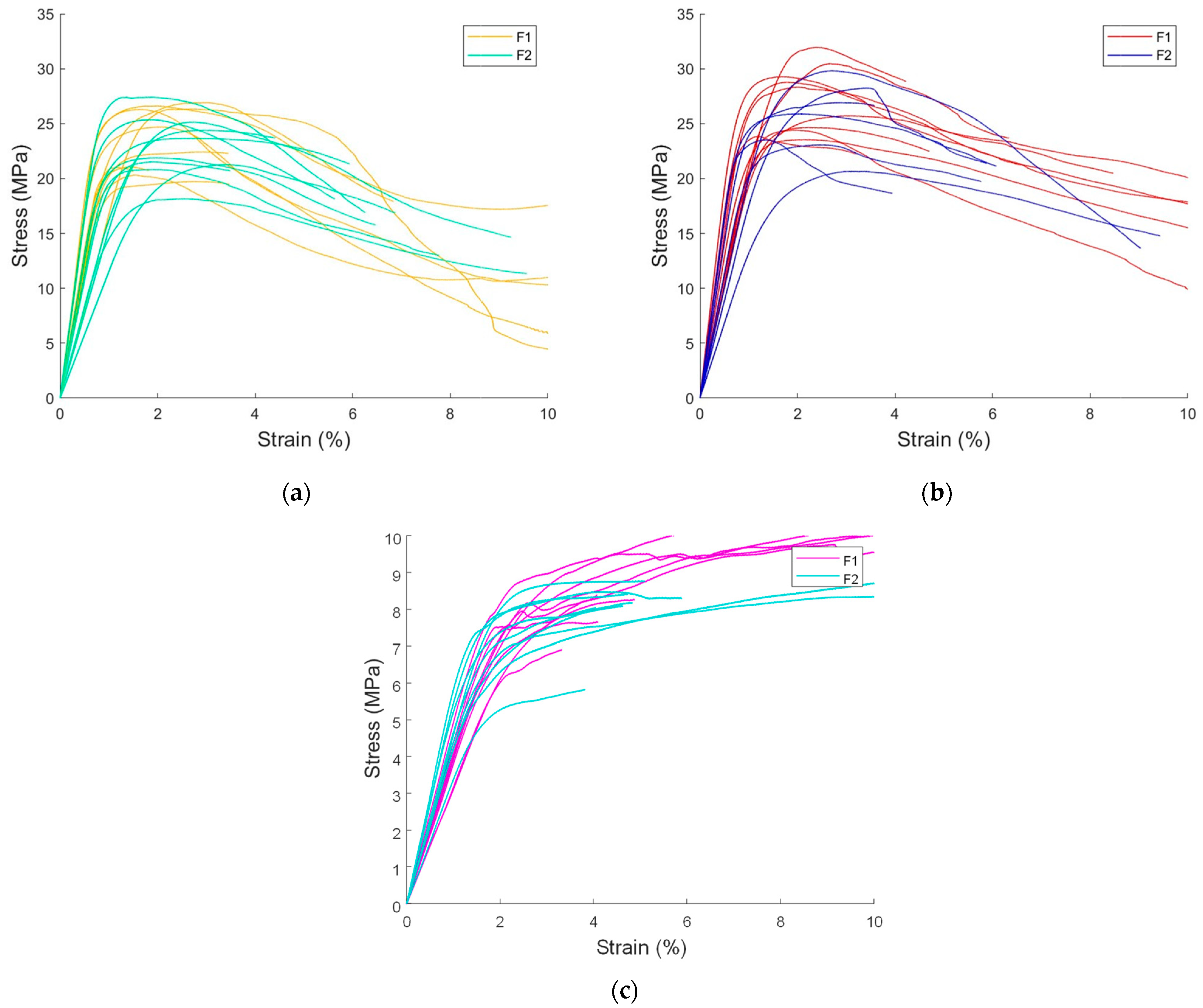
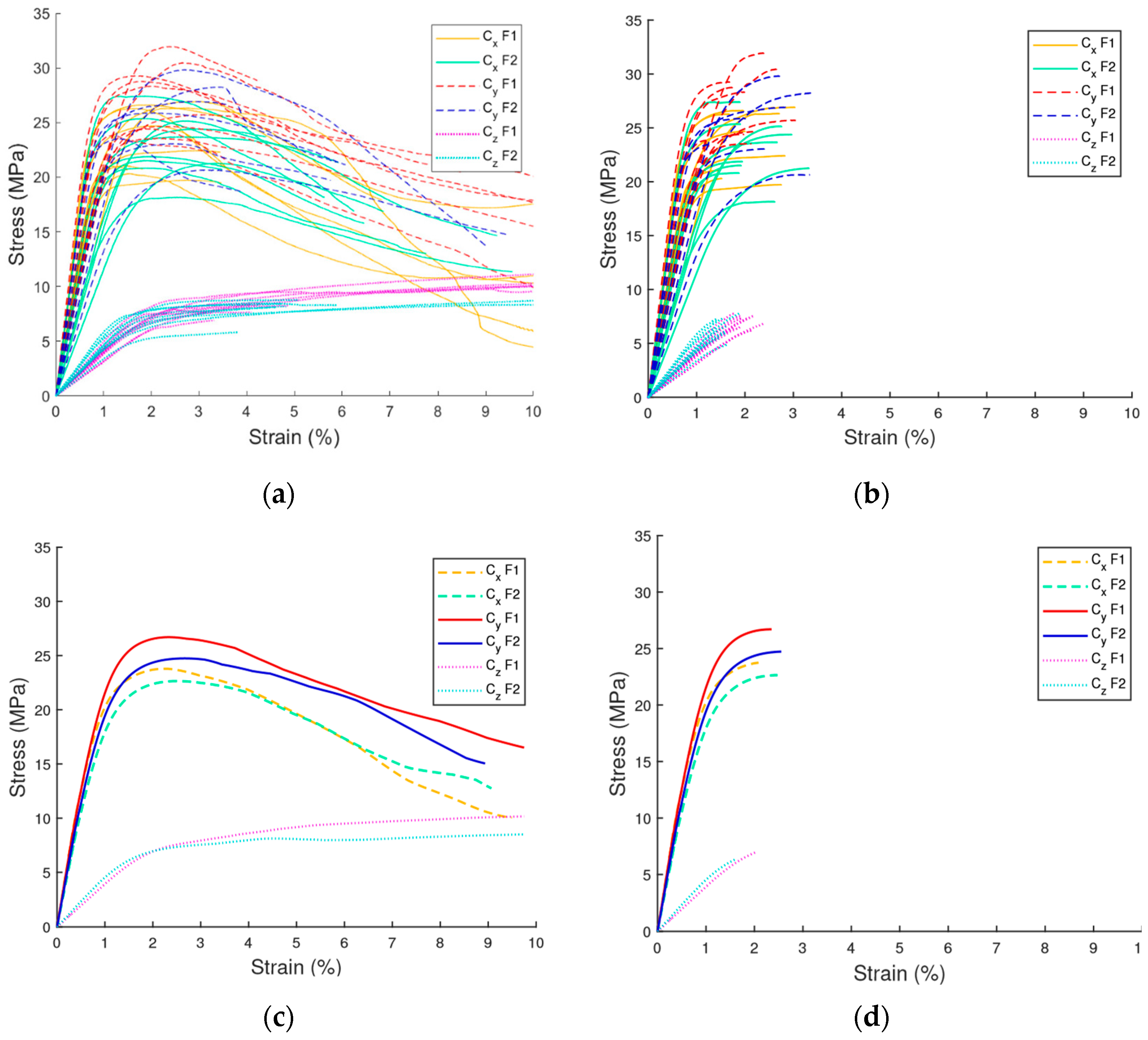
3.1. Tensile Test Results
3.2. Compression Test Results
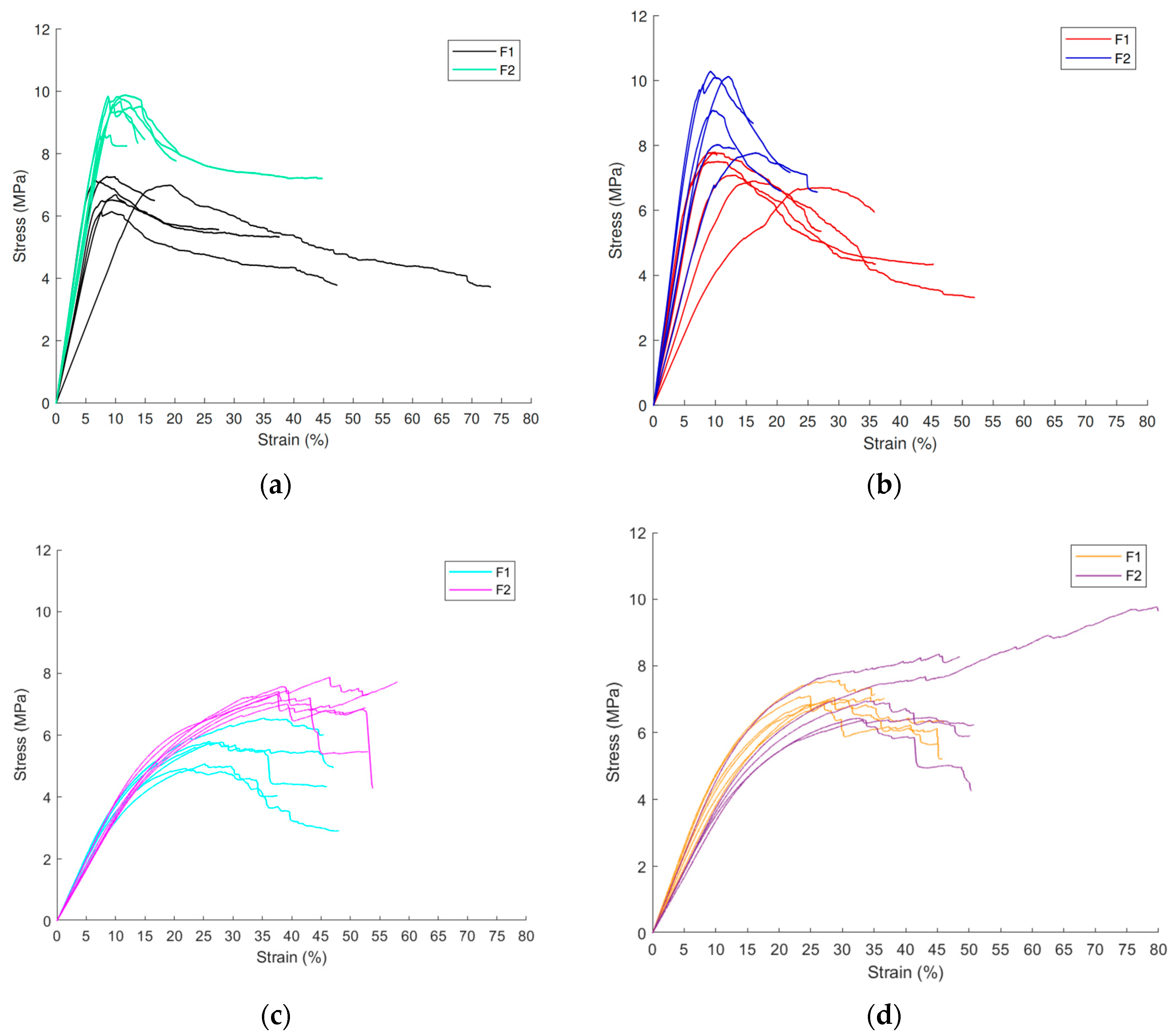
3.3. Shear Test Results
4. Discussion
- F1 consistently shows higher stiffness in both tension and compression, notably in Tx, Cy, and Cz, attributable to thicker perpendicular veneers and higher elastic moduli.
- F2 reaches superior maximum strengths in Tx, τxy, and τyx, benefitting from a more uniform veneer structure that reduces localized weaknesses.
- Out-of-plane orientations (Tz and Cz) display the lowest stiffness and strength, consistent with reduced load-bearing capacity perpendicular to grain and greater susceptibility to interlaminar shear failure.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Valenzuela, M.; Ciudad, G.; Cárdenas, J.P.; Medina, C.; Salas, A.; Oñate, A.; Pincheira, G.; Attia, S.; Tuninetti, V. Towards the Development of Performance-Efficient Compressed Earth Blocks from Industrial and Agro-Industrial by-Products. Renew. Sustain. Energy Rev. 2024, 194, 114323. [Google Scholar] [CrossRef]
- Miranda, A.; Muñoz, R.; Aedo, C.; Bustos, F.; Tuninetti, V.; Valenzuela, M.; Medina, C.; Oñate, A. High-Performance Concrete from Rubber and Shell Waste Materials: Experimental and Computational Analysis. Materials 2024, 17, 5516. [Google Scholar] [CrossRef]
- Kamali, M.; Hewage, K.; Sadiq, R. Conventional Versus Modular Construction Methods: A Comparative Cradle-to-Gate LCA for Residential Buildings. Energy Build. 2019, 204, 109479. [Google Scholar] [CrossRef]
- Pillai, R.G.; Gettu, R.; Santhanam, M.; Rengaraju, S.; Dhandapani, Y.; Rathnarajan, S.; Basavaraj, A.S. Service Life and Life Cycle Assessment of Reinforced Concrete Systems with Limestone Calcined Clay Cement (LC3). Cem. Concr. Res. 2019, 118, 111–119. [Google Scholar] [CrossRef]
- Cadavid-Giraldo, N.; Velez-Gallego, M.C.; Restrepo-Boland, A. Carbon Emissions Reduction and Financial Effects of a Cap and Tax System on an Operating Supply Chain in the Cement Sector. J. Clean. Prod. 2020, 275, 122583. [Google Scholar] [CrossRef]
- Chinzorigt, G.; Lim, M.K.; Yu, M.; Lee, H.; Enkbold, O.; Choi, D. Strength, Shrinkage and Creep and Durability Aspects of Concrete Including CO2 Treated Recycled Fine Aggregate. Cem. Concr. Res. 2020, 136, 106062. [Google Scholar] [CrossRef]
- Cuellar, S.; Grisales, S.; Castaneda, D.I. Constructing Tomorrow: A Multifaceted Exploration of Industry 4.0 Scientific, Patents, and Market Trend. Autom. Constr. 2023, 156, 105113. [Google Scholar] [CrossRef]
- Olawumi, T.O.; Chan, D.W.M.; Ojo, S.; Yam, M.C.H. Automating the Modular Construction Process: A Review of Digital Technologies and Future Directions with Blockchain Technology. J. Build. Eng. 2022, 46, 103720. [Google Scholar] [CrossRef]
- Lacey, A.W.; Chen, W.; Hao, H.; Bi, K. Structural Response of Modular Buildings–an Overview. J. Build. Eng. 2018, 16, 45–56. [Google Scholar] [CrossRef]
- Rasmussen, F.N.; Andersen, C.E.; Wittchen, A.; Hansen, R.N.; Birgisdóttir, H. Environmental Product Declarations of Structural Wood: A Review of Impacts and Potential Pitfalls for Practice. Buildings 2021, 11, 362. [Google Scholar] [CrossRef]
- Díaz, A.R.; Saavedra Flores, E.I.; Yanez, S.J.; Vasco, D.A.; Pina, J.C.; Guzmán, C.F. Multiscale Modeling of the Thermal Conductivity of Wood and Its Application to Cross-Laminated Timber. Int. J. Therm. Sci. 2019, 144, 79–92. [Google Scholar] [CrossRef]
- Thinley, J.; Hengrasmee, S. Innovating Bhutan’s Residential Construction with Mass Timber for Economic and Environmental Sustainability. J. Build. Eng. 2023, 78, 107763. [Google Scholar] [CrossRef]
- De Araujo, V.; Aguiar, F.; Jardim, P.; Mascarenhas, F.; Marini, L.; Aquino, V.; Santos, H.; Panzera, T.; Lahr, F.; Christoforo, A. Is Cross-Laminated Timber (CLT) a Wood Panel, a Building, or a Construction System? A Systematic Review on Its Functions, Characteristics, Performances, and Applications. Forests 2023, 14, 264. [Google Scholar] [CrossRef]
- Karacabeyli, E.; Douglas, B. CLT Handbook: Cross-Laminated Timber (U.S. Edition); FPInnovations and Binational Softwood Lumber Council: Pointe-Claire, QC, Canada, 2013; ISBN 978-0-86488-554-8. [Google Scholar]
- Nakano, K.; Karube, M.; Hattori, N. Environmental Impacts of Building Construction Using Cross-Laminated Timber Panel Construction Method: A Case of the Research Building in Kyushu, Japan. Sustainability 2020, 12, 2220. [Google Scholar] [CrossRef]
- Pina, J.C.; Saavedra Flores, E.I.; Saavedra, K. Numerical Study on the Elastic Buckling of Cross-Laminated Timber Walls Subject to Compression. Constr. Build. Mater. 2019, 199, 82–91. [Google Scholar] [CrossRef]
- Saavedra Flores, E.I.; Ajaj, R.M.; Dayyani, I.; Chandra, Y.; Das, R. Multi-Scale Model Updating for the Mechanical Properties of Cross-Laminated Timber. Comput. Struct. 2016, 177, 83–90. [Google Scholar] [CrossRef]
- Flores, E.I.S.; Dayyani, I.; Ajaj, R.M.; Castro-Triguero, R.; DiazDelaO, F.A.; Das, R.; Soto, P.G. Analysis of Cross-Laminated Timber by Computational Homogenisation and Experimental Validation. Compos. Struct. 2015, 121, 386–394. [Google Scholar] [CrossRef]
- Wang, T.; Wang, Y.; Crocetti, R.; Wålinder, M. In-Plane Mechanical Properties of Birch Plywood. Constr. Build. Mater. 2022, 340, 127852. [Google Scholar] [CrossRef]
- Tuninetti, V.; Sandoval, M.; Cárdenas-Ramírez, J.P.; Oñate, A.; Miranda, A.; Soto-Zúñiga, P.; Arnett, M.; Leiva, J.; Cancino, R. Miniaturized Shear Testing: In-Plane and Through-Thickness Characterization of Plywood. Materials 2024, 17, 5621. [Google Scholar] [CrossRef] [PubMed]
- Bekhta, P.; Pizzi, A.; Kusniak, I.; Bekhta, N.; Chernetskyi, O.; Nuryawan, A. A Comparative Study of Several Properties of Plywood Bonded with Virgin and Recycled LDPE Films. Materials 2022, 15, 4942. [Google Scholar] [CrossRef]
- Bekhta, P.; Chernetskyi, O.; Kusniak, I.; Bekhta, N.; Bryn, O. Selected Properties of Plywood Bonded with Low-Density Polyethylene Film from Different Wood Species. Polymers 2021, 14, 51. [Google Scholar] [CrossRef]
- Bekhta, P.; Pipíška, T.; Gryc, V.; Sedliačik, J.; Král, P.; Ráheľ, J.; Vaněrek, J. Properties of Plywood Panels Composed of Thermally Densified and Non-Densified Alder and Birch Veneers. Forests 2023, 14, 96. [Google Scholar] [CrossRef]
- Olenska, S.; Beer, P. Quality Evaluation of New Types of Core Layers Based on Different Thicknesses of Veneers for Flooring Materials. Materials 2024, 17, 5881. [Google Scholar] [CrossRef]
- Tuninetti, V.; Alzugaray, R.; González, J.; Valenzuela, M.; Jaramillo, A.; Diez, E. Root Cause and Vibration Analysis to Increase Veneer Manufacturing Process Efficiency: A Case Study on an Industrial Peeling Lathe. Eur. J. Wood Wood Prod. 2021, 79, 951–966. [Google Scholar] [CrossRef]
- Galdino, D.S.; Silva, M.F.F.; Arroyo, F.N.; Rangel, E.C.; Caraschi, J.C.; dos Santos, H.F.; de Freitas, L.; Christoforo, A.L.; de Campos, C.I. Properties of Plywood Made of Thermally Treated Veneers Bonded with Castor Oil-Based Polyurethane Adhesive. Forests 2023, 14, 1635. [Google Scholar] [CrossRef]
- Xiao, G.; Liang, J.; Li, D.; Tu, Y.; Zhang, B.; Gong, F.; Gu, W.; Tang, M.; Ding, X.; Wu, Z.; et al. Fully Bio-Based Adhesive from Tannin and Sucrose for Plywood Manufacturing with High Performances. Materials 2022, 15, 8725. [Google Scholar] [CrossRef] [PubMed]
- Birinci, E.; Kaymakci, A. Effect of Freeze–Thaw Cycling on the Screw Direct Withdrawal Resistance of Beech, Ozigo, and Okoume Plywoods. Forests 2023, 14, 1243. [Google Scholar] [CrossRef]
- Barboutis, I.; Kamperidou, V. Properties of Two Different Thicknesses 3-Ply Plywood of Tree-of-Heaven Veneers. In Proceedings of the 22nd International Scientific Conference, Zagreb, Croatia, 21 October 2011; Volume 2011, pp. 9–16. [Google Scholar]
- Koynov, D.; Antov, P.; Valyova, M.; Savov, V.; Dochev, I.; Lee, S.H. Properties of Hybrid Plywood Produced by Utilisation of Peeler Cores. Forests 2024, 15, 582. [Google Scholar] [CrossRef]
- Núñez-Decap, M.; Sandoval-Valderrama, B.; Opazo-Carlsson, C.; Moya-Rojas, B.; Vidal-Vega, M.; Opazo-Vega, A. Use of Carbon and Basalt Fibers with Adhesives to Improve Physical and Mechanical Properties of Laminated Veneer Lumber. Appl. Sci. 2023, 13, 10032. [Google Scholar] [CrossRef]
- Núñez-Decap, M.; Friz-Sánchez, C.; Opazo-Carlsson, C.; Moya-Rojas, B.; Vidal-Vega, M. A Potential Replacement to Phenol–Formaldehyde-Based Adhesives: A Study of Plywood Panels Manufactured with Bio-Based Wood Protein and Nanolignin Adhesives. Forests 2024, 15, 1345. [Google Scholar] [CrossRef]
- Papadopoulou, E.; Moutousidis, D.; Kountouras, S.; Argyropoulou, A.; Stathopoulos, P.; Skaltsounis, A.L.; Ioannidis, R.O.; Xanthopoulou, E.; Malletzidou, L.; Chrissafis, K. New Bio-Based Binding Systems for Plywood Panels. Appl. Sci. 2024, 14, 5862. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, C.; Du, Z.; Wang, H.; Du, G.; Essawy, H.; Lei, H.; Xi, X.; Zhou, X.; Cao, M. Soybean Meal–Oxidized Lignin as Bio-Hybridized Wood Panel Adhesives with Increased Water Resistance. Forests 2024, 15, 1036. [Google Scholar] [CrossRef]
- Jorda, J.; Cesprini, E.; Barbu, M.-C.; Tondi, G.; Zanetti, M.; Král, P. Quebracho Tannin Bio-Based Adhesives for Plywood. Polymers 2022, 14, 2257. [Google Scholar] [CrossRef] [PubMed]
- Sutiawan, J.; Syahfitri, A.; Purnomo, D.; Sudarmanto; Narto; Akbar, F.; Triwibowo, D.; Ismadi; Amanda, P.; Kusumah, S.S.; et al. Characterization and Application of Non-Formaldehyde Binder Based Citric Acid, Maleic Acid, and Molasses Adhesive for Plywood Composite. Polymers 2023, 15, 3897. [Google Scholar] [CrossRef]
- Shalbafan, A.; Thoemen, H. Development of Mineral-Bonded Plywood with Magnesium Oxychloride as a Binder Using the Hot-Pressing Process. Polymers 2023, 15, 805. [Google Scholar]
- Gonçalves, S.; Paiva, N.T.; Martins, J.; Magalhães, F.D.; Carvalho, L.H. Effect of Lignosulphonates on the Moisture Resistance of Phenol–Formaldehyde Resins for Exterior Plywood. Materials 2024, 17, 3715. [Google Scholar] [CrossRef]
- Chang, L.; Wang, Y.; Chen, X.; Ren, Y.; Luo, X. Effect of Grafting Conditions on the Interfacial Properties of Silane Modified Wood Veneer/PE Film Plywood. Polymers 2023, 15, 2957. [Google Scholar] [CrossRef] [PubMed]
- Gerrand, C. The Equivalent Orthotropic Elastic Properties of Plywood. Wood Sci. Technol. 1987, 21, 335–348. [Google Scholar] [CrossRef]
- Sudo, R.; Aoki, K.; Inayama, M. Investigation of Mechanical Properties and Elucidation of Factors Affecting Wood-Based Structural Panels under Embedment Stress with a Circular Dowel i: Analysis of the Influence of Various Conditions on the Embedment Properties. J. Wood Sci. 2023, 69, 18. [Google Scholar] [CrossRef]
- Krüger, R.; Buchelt, B.; Wagenführ, A. New Method for Determination of Shear Properties of Wood. Wood Sci. Technol. 2018, 52, 1555–1568. [Google Scholar] [CrossRef]
- Brabec, M.; Laga\v{n}a, R.; Milch, J.; Tippner, J.; Sebera, V. Utilization of Digital Image Correlation in Determining of Both Longitudinal Shear Moduli of Wood at Single Torsion Test. Wood Sci. Technol. 2017, 51, 29–45. [Google Scholar] [CrossRef]
- Guan, C.; Zhang, H.; Wang, X.; Miao, H.; Zhou, L.; Liu, F. Experimental and Theoretical Modal Analysis of Full-Sized Wood Composite Panels Supported on Four Nodes. Materials 2017, 10, 683. [Google Scholar] [CrossRef]
- Bachtiar, E.V.; Rüggeberg, M.; Hering, S.; Kaliske, M.; Niemz, P. Estimating Shear Properties of Walnut Wood: A Combined Experimental and Theoretical Approach. Mater. Struct. 2017, 50, 248. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, N. Evaluation of a Modified Iosipescu Shear Test Method for Determining the Shear Properties of Clear Wood. Wood Sci. Technol. 2017, 51, 323–343. [Google Scholar] [CrossRef]
- Krüger, R.; Wagenführ, A. Comparison of Methods for Determining Shear Modulus of Wood. Eur. J. Wood Wood Prod. 2020, 78, 1087–1094. [Google Scholar] [CrossRef]
- PS01-19; Structural Plywood. National Institute of Standards and Technology (NIST): Gaithersburg, MD, USA, 2019.
- EN 789:2004; Timber Structures-Test Methods-Determination of Mechanical Properties of Wood-Based Panels. European Committee for Standardization (CEN): Brussels, Belgium, 2004.
- EN 310:1993; Wood-Based Panels-Determination of Modulus of Elasticity in Bending and of Bending Strength. European Committee for Standardization (CEN): Brussels, Belgium, 1993.
- ASTM D1037-99; Standard Test Methods for Evaluating Properties of Wood-Base Fiber and Particle Panel Materials. ASTM International: West Conshohocken, PA, USA, 1999.
- ASTM D5456-03; Standard Specification for Evaluation of Structural Composite Lumber Products. ASTM International: West Conshohocken, PA, USA, 2003.
- ISO 12465:2007; Plywood–Specifications. International Organization for Standardization (ISO): Geneva, Switzerland, 2007.
- Dahl, K.B.; Malo, K.A. Nonlinear Shear Properties of Spruce Softwood: Experimental Results. Wood Sci. Technol. 2009, 43, 539–558. [Google Scholar] [CrossRef]
- Ostapska, K.; Malo, K.A. New Approach to Testing Shear in Wood on Structural Scale. Int. J. Solids Struct. 2021, 212, 46–60. [Google Scholar] [CrossRef]
- EN 314:1993; Plywood–Bonding Quality-Test Methods. European Committee for Standardization (CEN): Brussels, Belgium, 1993.
- Breyer, R.; Cannon, M.; Jennings, J.; Ashley, S. The Value of Transitioning from the Lap Shear to an Internal Bond for Testing Plywood. For. Prod. J. 2022, 72, 29–34. [Google Scholar] [CrossRef]
- Arriaga-Martitegui, F.; Peraza-Sánchez, F.; García-Esteban, L. Characteristic Values of the Mechanical Properties of Radiata Pine Plywood and the Derivation of Basic Values of the Layers for a Calculation Method. Biosyst. Eng. 2008, 99, 256–266. [Google Scholar] [CrossRef]
- Sugahara, E.; Casagrande, B.; Arroyo, F.; De Araujo, V.; Santos, H.; Faustino, E.; Christoforo, A.; Campos, C. Comparative Study of Plywood Boards Produced with Castor Oil-Based Polyurethane and Phenol-Formaldehyde Using Pinus taeda L. Veneers Treated with Chromated Copper Arsenate. Forests 2022, 13, 1144. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, T.; Crocetti, R.; Wålinder, M. Experimental Investigation on Mechanical Properties of Acetylated Birch Plywood and Its Angle-Dependence. Constr. Build. Mater. 2022, 344, 128277. [Google Scholar] [CrossRef]
- Valdivia, I.; Canales, C.; Tuninetti, V.; Flores, P.; Medina, C. Numerical Prediction of Failure in Unidirectional Fiber Reinforced Composite. Int. J. Appl. Mech. 2021, 13, 2150073. [Google Scholar] [CrossRef]
- Rojas-Ulloa, C.; Tuninetti, V.; Sepúlveda, H.; Betaieb, E.; Pincheira, G.; Gilles, G.; Duchêne, L.; Habraken, A.M. Accurate Numerical Prediction of Ductile Fracture and Micromechanical Damage Evolution for Ti6Al4V Alloy. Comput. Mech. 2024, 73, 177–198. [Google Scholar] [CrossRef]
- Romero, F.; Méndez, F.; González, J.; Tuninetti, V.; Medina, C.; Valin, M.; Valin, J.; Salas, A.; Vicuña, C. Acoustic Emission-Based Method for IFSS Characterization in Single-Fiber Fragmentation Tests. Appl. Sci. 2025, 15, 4517. [Google Scholar] [CrossRef]
- Wang, T.; Wang, Y.; Crocetti, R.; Wålinder, M. Influence of Face Grain Angle, Size, and Moisture Content on the Edgewise Bending Strength and Stiffness of Birch Plywood. Mater. Des. 2022, 223, 111227. [Google Scholar] [CrossRef]
- Zhao, C.; Liu, D.; Zhang, C.; Li, Y.; Wang, Y. Influence of Specimen Size on the Compressive Strength of Wood. Buildings 2024, 14, 1156. [Google Scholar] [CrossRef]
- Walley, S.M.; Rogers, S.J. Is Wood a Material? Taking the Size Effect Seriously. Materials 2022, 15, 5403. [Google Scholar] [CrossRef]
- NCh3617:2022; Madera Contrachapada Estructural-Requisitos y Ensayos. INN: Osaka, Japan, 2022.
- ASTM B831-98; Standard Test Method for Shear Testing of Thin Aluminum Alloy Products. ASTM International: West Conshohocken, PA, USA, 1998.
- Panchal, M.; Kaushik, L.; Khatirkar, R.; Choi, S.-H.; Singh, J. Recent Advances in the In-Plane Shear Testing of Mg Alloy Sheets. J. Magnes. Alloy. 2023, 11, 405–424. [Google Scholar] [CrossRef]
- Bitar, I.S.; Aboulkhair, N.T.; Leach, R. The Application of Composite Through-Thickness Assessment to Additively Manufactured Structures. In Proceedings of the 28th Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 7–9 August 2017. [Google Scholar]
- Tuninetti, V.; Flores, P.; Valenzuela, M.; Pincheira, G.; Medina, C.; Duchêne, L.; Habraken, A.M. Experimental Characterization of the Compressive Mechanical Behaviour of Ti6Al4V Alloy at Constant Strain Rates over the Full Elastoplastic Range. Int. J. Mater. Form. 2020, 13, 709–724. [Google Scholar] [CrossRef]
- Jakimovska Popovska, V.; Iliev, B.; Zlateski, G. Impact of Veneer Layouts on Plywood Tensile Strength. Drv. Ind. 2017, 68, 153–161. [Google Scholar] [CrossRef]
- Saavedra Flores, E.I.; DiazDelaO, F.A.; Friswell, M.I.; Sienz, J. A Computational Multi-Scale Approach for the Stochastic Mechanical Response of Foam-Filled Honeycomb Cores. Compos. Struct. 2012, 94, 1861–1870. [Google Scholar] [CrossRef]
- Weibull, W. A Statistical Distribution Function of Wide Applicability. J. Appl. Mech. 1951, 18, 293–297. [Google Scholar] [CrossRef]
- Bažant, Z.P. Scaling of Quasibrittle Fracture: Asymptotic Analysis. Int. J. Fract. 1997, 83, 19–40. [Google Scholar] [CrossRef]

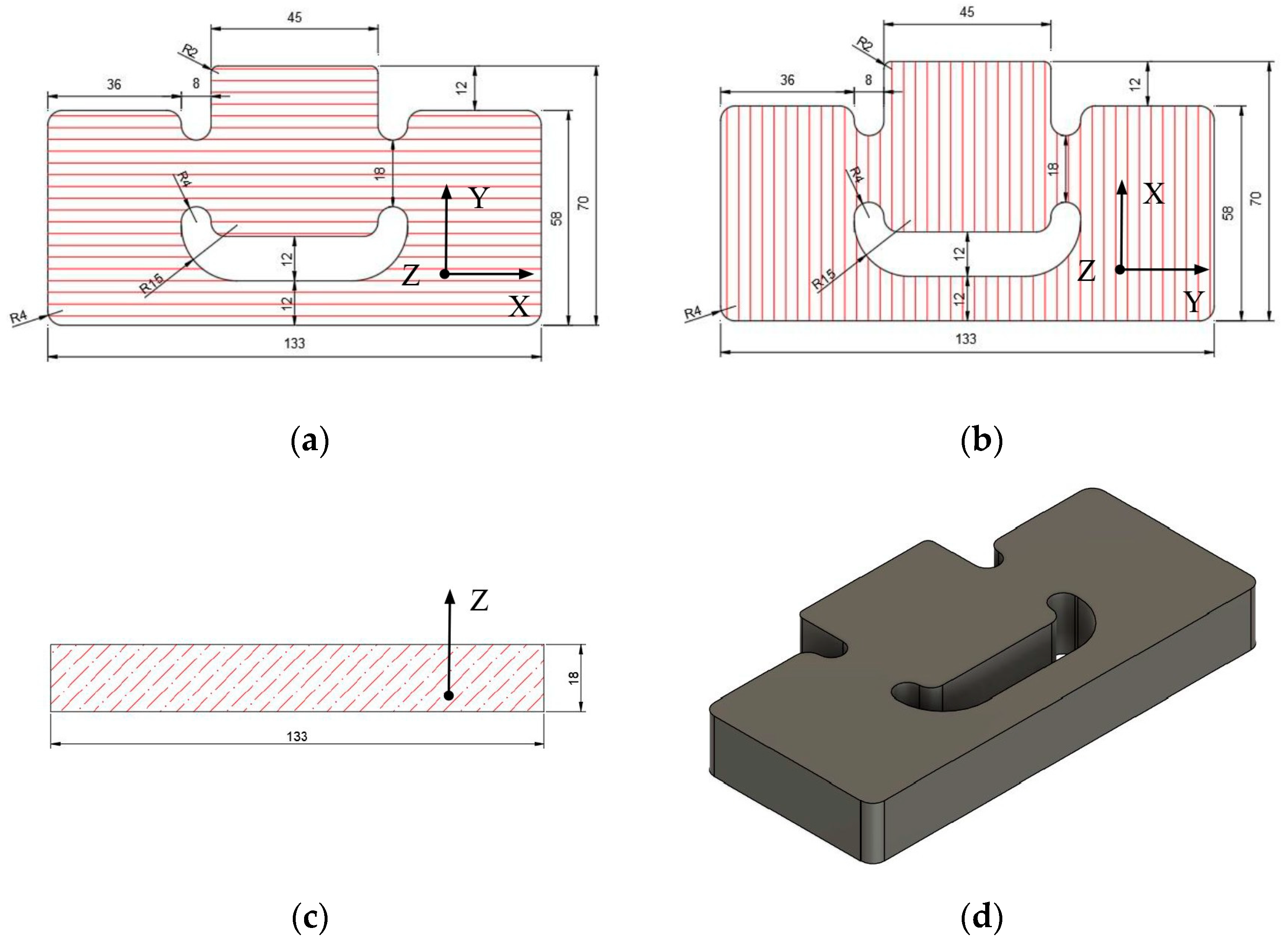
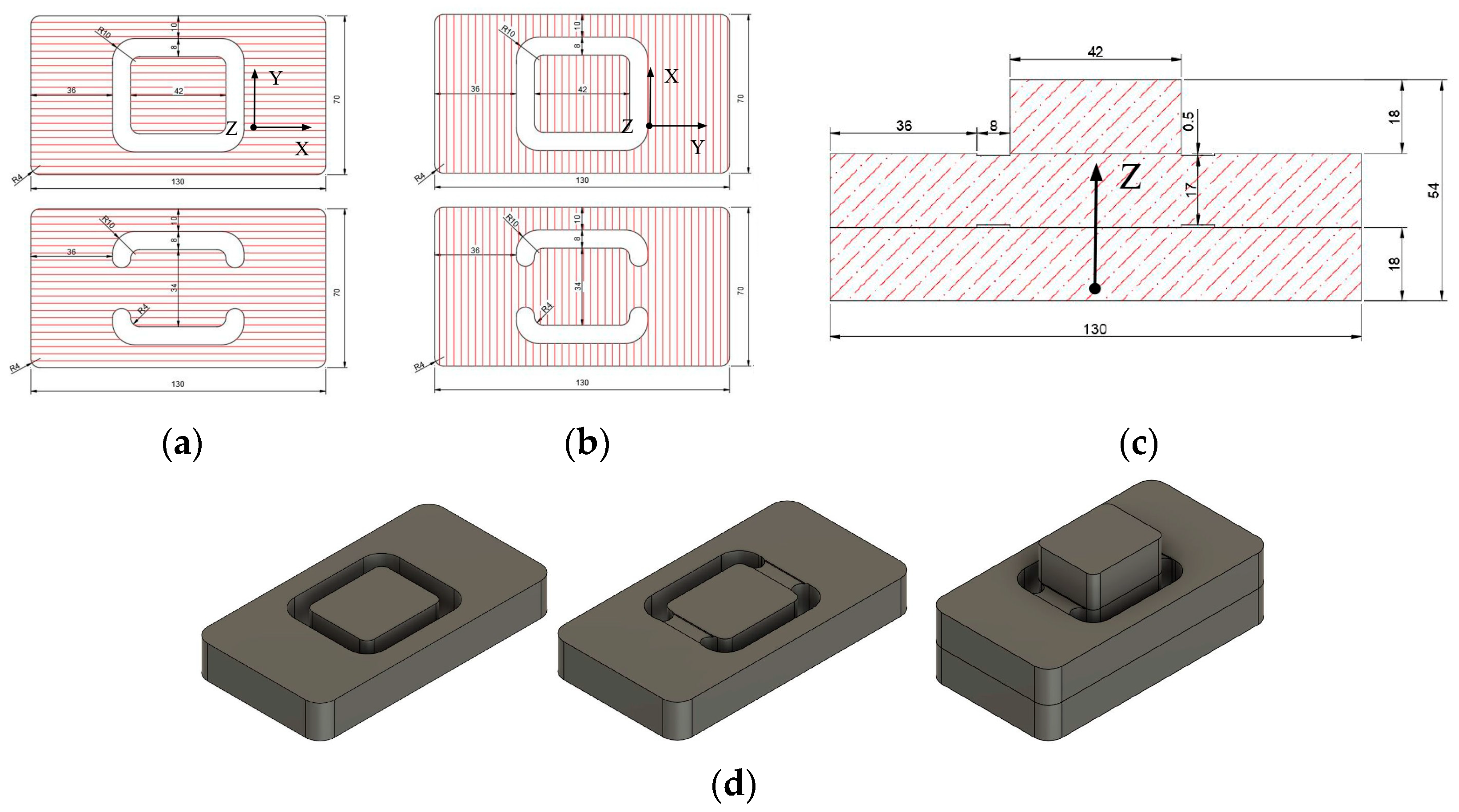










| Property | Detail | Unit |
|---|---|---|
| Printer | Ender 3 V3 KE | – |
| Material | PLA | – |
| Layer height | 0.2 | mm |
| Wall width | 0.4 | mm |
| Number of walls | 3 | – |
| Top layers | 2 | – |
| Bottom layers | 2 | – |
| Infill type | Lines | – |
| Infill density | 100 | % |
| Print temperature | 205 | °C |
| Bed temperature | 60 | °C |
| Print speed | 200 | mm/s |
| Orientation | Manufacturer | Number of Specimens. | ε10%Fmax (%) | ε40Fmax (%) | εFmax (%) | σFmax (MPa) | (GPa) |
|---|---|---|---|---|---|---|---|
| Tx | 1 | 6 | 0.051 ± 0.014 | 0.201 ± 0.051 | 0.498 ± 0.122 | 28.40 ± 4.89 | 5.83 ± 1.17 |
| 2 | 6 | 0.061 ± 0.016 | 0.259 ± 0.073 | 0.710 ± 0.206 | 30.22 ± 7.68 | 4.68 ± 0.73 | |
| Ty | 1 | 6 | 0.058 ± 0.016 | 0.238 ± 0.068 | 0.614 ± 0.185 | 29.66 ± 6.41 | 5.46 ± 2.49 |
| 2 | 6 | 0.061 ± 0.010 | 0.252 ± 0.041 | 0.641 ± 0.160 | 31.63 ± 3.60 | 5.08 ± 1.06 | |
| Tz | 1 | 5 | 0.015 ± 0.004 | 0.078 ± 0.025 | 0.417 ± 0.077 | 1.12 ± 0.26 | 0.59 ± 0.23 |
| 2 | 5 | 0.031 ± 0.019 | 0.194 ± 0.106 | 0.671 ± 0.295 | 1.30 ± 0.46 | 0.29 ± 0.16 |
| Orientation | Manufacturer | Number of Samples | ε10%ref (%) | ε40ref (%) | εref (%) | σref (MPa) | (GPa) |
|---|---|---|---|---|---|---|---|
| Cx | 1 | 10 | 0.092 ± 0.026 | 0.369 ± 0.104 | 2.120 ± 0.665 | 23.55 ± 2.92 | 2.67 ± 0.57 |
| 2 | 10 | 0.114 ± 0.038 | 0.457 ± 0.150 | 2.394 ± 0.540 | 22.97 ± 2.72 | 2.20 ± 0.73 | |
| Cy | 1 | 10 | 0.108 ± 0.028 | 0.433 ± 0.112 | 2.113 ± 0.517 | 27.11 ± 3.03 | 2.63 ± 0.64 |
| 2 | 7 | 0.116 ± 0.036 | 0.464 ± 0.146 | 2.593 ± 0.746 | 25.46 ± 3.21 | 2.37 ± 0.72 | |
| Cz | 1 | 9 | 0.181 ± 0.019 | 0.730 ± 0.079 | 2.028 ± 0.205 | 7.07 ± 0.57 | 0.39 ± 0.06 |
| 2 | 9 | 0.139 ± 0.015 | 0.558 ± 0.063 | 1.590 ± 0.147 | 6.46 ± 0.91 | 0.47 ± 0.08 |
| Orientation | Manufacturer | Specimen No. | ε10%τFmax (%) | ε40 τFmax (%) | ε τFmax (%) | τFmax (MPa) | (GPa) |
|---|---|---|---|---|---|---|---|
| τxy | 1 | 6 | 0.784 ± 0.324 | 3.145 ± 1.289 | 10.488 ± 4.348 | 6.79 ± 0.42 | 0.10 ± 0.03 |
| 2 | 6 | 0.803 ± 0.093 | 3.214 ± 0.374 | 10.105 ± 1.108 | 9.56 ± 0.49 | 0.12 ± 0.01 | |
| τyx | 1 | 6 | 0.949 ± 0.348 | 3.797 ± 1.393 | 14.495 ± 6.829 | 7.29 ± 0.46 | 0.09 ± 0.03 |
| 2 | 6 | 0.846 ± 0.148 | 3.384 ± 0.595 | 11.353 ± 2.715 | 9.23 ± 1.12 | 0.11 ± 0.03 | |
| τxz | 1 | 6 | 1.452 ± 0.116 | 5.809 ± 0.464 | 26.980 ± 4.481 | 5.64 ± 0.59 | 0.04 ± 0.00 |
| 2 | 6 | 2.073 ± 0.180 | 8.291 ± 0.718 | 42.260 ± 6.233 | 7.39 ± 0.28 | 0.04 ± 0.003 | |
| τyz | 1 | 6 | 1.541 ± 0.136 | 6.166 ± 0.545 | 28.147 ± 3.743 | 7.07 ± 0.26 | 0.05 ± 0.00 |
| 2 | 5 | 1.987 ± 0.366 | 7.950 ± 1.464 | 47.06 ± 19.111 | 7.59 ± 1.45 | 0.04 ± 0.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sandoval, M.; Javadi, M.; Soto-Zúñiga, P.; Cárdenas-Ramírez, J.P.; Arnett, M.; Oñate, A.; Cancino, R.; Saavedra Flores, E.I.; Tuninetti, V. Full Orthotropic Mechanical Characterization of Pinus radiata Plywood Through Tensile, Compression and Shear Testing with Miniaturized Specimens. Forests 2025, 16, 1676. https://doi.org/10.3390/f16111676
Sandoval M, Javadi M, Soto-Zúñiga P, Cárdenas-Ramírez JP, Arnett M, Oñate A, Cancino R, Saavedra Flores EI, Tuninetti V. Full Orthotropic Mechanical Characterization of Pinus radiata Plywood Through Tensile, Compression and Shear Testing with Miniaturized Specimens. Forests. 2025; 16(11):1676. https://doi.org/10.3390/f16111676
Chicago/Turabian StyleSandoval, Moisés, Masoud Javadi, Paula Soto-Zúñiga, Juan Pablo Cárdenas-Ramírez, Michael Arnett, Angelo Oñate, Rodrigo Cancino, Erick I. Saavedra Flores, and Víctor Tuninetti. 2025. "Full Orthotropic Mechanical Characterization of Pinus radiata Plywood Through Tensile, Compression and Shear Testing with Miniaturized Specimens" Forests 16, no. 11: 1676. https://doi.org/10.3390/f16111676
APA StyleSandoval, M., Javadi, M., Soto-Zúñiga, P., Cárdenas-Ramírez, J. P., Arnett, M., Oñate, A., Cancino, R., Saavedra Flores, E. I., & Tuninetti, V. (2025). Full Orthotropic Mechanical Characterization of Pinus radiata Plywood Through Tensile, Compression and Shear Testing with Miniaturized Specimens. Forests, 16(11), 1676. https://doi.org/10.3390/f16111676







