Effects of Cyclic Load Amplitude and Count on the Roughness and Friction Coefficient of the Round-End Wood Mortise–Tenon Joint

Abstract

The fatigue of wood mortise–tenon (M–T) joints commonly results from the looseness of the joints when subjected to long-term cyclic load. It is of critical importance to comprehensively understand the fatigue of M–T joints to know what occurs in M–T joints However, fatigue evolution progression (FEP) of M–T joints has been rarely studied. This study mainly aimed to investigate the FEP of the roughness of mortise (R_M) and tenon (R_T), and the friction coefficient of the non-glued round-end beech wood M–T joint when subjected to cyclic load to provide basic data for numerically modelling the FEP of the M–T joint. The effects of cyclic load amplitude (CLA) (150 N, 200 N, 250 N, and 300 N) and cyclic load count (CLC) (25%, 50%, 75%, and 100% fatigue life) on R_M, R_T, and the friction coefficient were investigated. The results demonstrate that the CLA and CLC have significant effects on R_M, R_T, and the friction coefficient of the M–T joint. The R_M, R_T, and friction coefficient of the M–T joint decrease non-linearly as the CLA and CLC increase, complying with the power law function. The R_M, R_T, and friction coefficient of M–T joints are reduced by a large margin within the CLC of the initial 25% fatigue life, and these reductions decelerate from a CLC of 75% to 100% for all CLAs. The relationships between the friction coefficient and R_M and R_T at each CLA can be well fitted by a quadratic model during FEP. This study provides a new insight to comprehensively understand the FEP of the round-end M–T joint and supplies basic data for numerically modelling the FEP of the M–T joint.

1. Introduction

Mortise–tenon (M–T) joints are widely used in solid wood frame furniture, contributing to their satisfactory strength and invisible appearance of joints [1,2]. The round-end M–T joint is the most commonly used joint as it is suitable for modern wood manufacturing machines [3,4,5]. It is known that the strengths of the round-end M–T joints mainly depend on the interference fit and frictional coefficient between mortise and tenon. The factors influencing the strength of the M–T joints have been widely investigated [6,7,8], such as the wood species, moisture content, tenon fit, and shape of the tenon. However, all these factors finally influence the interference fit, roughness, and frictional coefficient between mortise and tenon. In terms of the effect of fit on the strengths of M–T joints, an agreement was reached that the withdrawal and bending moment load resistances increased as the fit increased [9,10]. However, only limited studies have focused on roughness and the friction coefficient between mortise and tenon.

As is known, the friction coefficient between mortise and tenon depends on the surface roughness of the mortise and tenon. The roughness of the wood surface mainly depends on the manufacturing parameters of the wood machines, such as the feeding rate and cutting speed, the grit of the sandpaper, and the sanding process [11,12,13,14,15,16,17,18]. High feeding rate and cutting speed have negative effects on the roughness of the wood surfaces. Additionally, the factors of grain orientations, species, and moisture content also influenced the roughness of the wood [19,20,21,22,23]. Different coating and surface treatment methods can also affect the surface roughness of wood furniture, which finally impacts the aesthetic appearance and touch feeling [24,25,26,27,28,29,30,31,32]. To control the quality of wood furniture and improve the manufacturing steps, Zhong et al. [33] compared the surface roughness of 15 types of wood-based panels and 12 types of solid wood commonly used in furniture manufacturing. However, only a rare study was found on investigating the roughness of mortise (R_M) and tenon (R_T). Hu and Guan [34] used the cut-open mortise and tenon to obtain the friction coefficient between mortise and tenon. Furthermore, the effects of moisture content [35] and interference fit [8] on the withdrawal strengths of M–T joints were investigated in terms of the friction coefficient between the mortise and tenon. However, only a rare study was found on investigating the frictional coefficient relating to R_M and R_T.

The M–T joint is commonly considered the weakest part in wooden furniture frame construction [36,37,38,39]. The M–T joint failure is usually caused by long-term cyclic loading [40,41]. Previous studies carried out many experimental tests to investigate factors affecting the fatigue life of furniture constructed by M–T joints [42,43,44,45,46,47,48]. Some studies [46,47] reported that the tenon shape significantly influenced the fatigue life of M–T joints, finding that the M–T joint with a rectangular cross section had a longer fatigue life than ones with a diamond cross section, followed by dowels, and then a round cross section. Glued round and rectangular M–T joints had the highest cyclic load resistance. Ratnasingam et al. [49] reported that the fatigue strength of the PVAc adhesive M–T joints was much higher than that of UF adhesive joints. Allowable design stress for PVAc and UF adhesive M–T joints can be set at 30% and 25%, respectively, of their ultimate bending moment. Meanwhile, the M–T joints made of oil palm wood did not perform as well as with rubberwood. The fatigue life decreased with increasing load level [50,51]. Hu et al. [52] investigated the effects of cyclic load type, load amplitude, and joint fit (T-M clearance) on the fatigue life of round-end M–T joints. They suggested that cyclic load amplitude, cyclic load type, and joint fit had significant effects on the fatigue life of round-end M–T joints. The above studies indicate that the main factors influencing fatigue life of M–T joints are joint type (shape and dimension), wood material (wood species and moisture content), loading parameters (load amplitude and load frequency), and glue type (PVAc and UF). It is known that the fatigue of M–T joints does not occur instantly but has a damage evolution progression. Therefore, it can help us to understand comprehensively the fatigue of the M–T joint by knowing the changing laws of roughness, friction coefficient, and their relationships when subjected to long-term cyclic load. However, only a rare study has been found.

The preliminary aim of this study was to obtain the changing laws of R_M, R_T, and the friction coefficient between mortise and tenon during the fatigue of round-end M–T joints for numerically modeling the fatigue of the M–T joint. The specific aim was as follows: (1) investigate the effects of cyclic load amplitude (CLA) and cyclic load count (CLC) on R_M, R_T, and the friction coefficient between mortise and tenon; (2) reveal the relationships between R_M, R_T, and the friction coefficient of the round-end M–T joint when subjected to different CLA and CLC. The final objective was to provide a new insight for comprehensively understanding the FEP of the round-end M–T joint. Additionally, the changing laws presented basic data for the numerical models of the M–T joint, which can provide more details of the M–T joint during FEP.

2. Materials and Methods

2.1. Wood Materials

The wood species used to prepare M–T joint samples was beech (Fagus orientalis) purchased in a wood timber shop (Nanjing, China). The wood lumber had been stored in the wood processing laboratory for more than 5 years and had reached its air-dry condition. The density of the beech wood was 700 kg/m³ measured at a moisture content of 12%.

2.2. Experimental Design

A complete 4 × 4 factorial experiment was designed to investigate the effects of CLA (150 N, 200 N, 250 N, and 300 N) and CLC (25%, 50%, 75%, and 100% fatigue life) on the roughness of mortise (R_M) and tenon (R_T) as well as the friction coefficient between mortise and tenon.

Table 1. Arrangements and sample replications of cyclic load tests of mortise–tenon joints.

CLC	CLA (N)
	150	200	250	300
25%	3	3	3	3
50%	3	3	3	3
75%	3	3	3	3
100%	3	3	3	3

summarizes all the experimental combinations tested in this study. Three samples underwent cyclic load tests for each combination of CLA and CLC. Before loading and after completing specified cyclic load counts, the roughness and friction coefficient of each sample were measured 3 times. Therefore, there were 144 data points for each variable evaluated in this study—R_M, R_T, and friction coefficient. The fatigue lives of the M–T joints evaluated at each of the four CLA levels of 150 N, 200 N, 250 N, and 300 N were found to be 299,269, 37,345, 23,486, and 18,086 cycles, respectively, per our previous study [52].

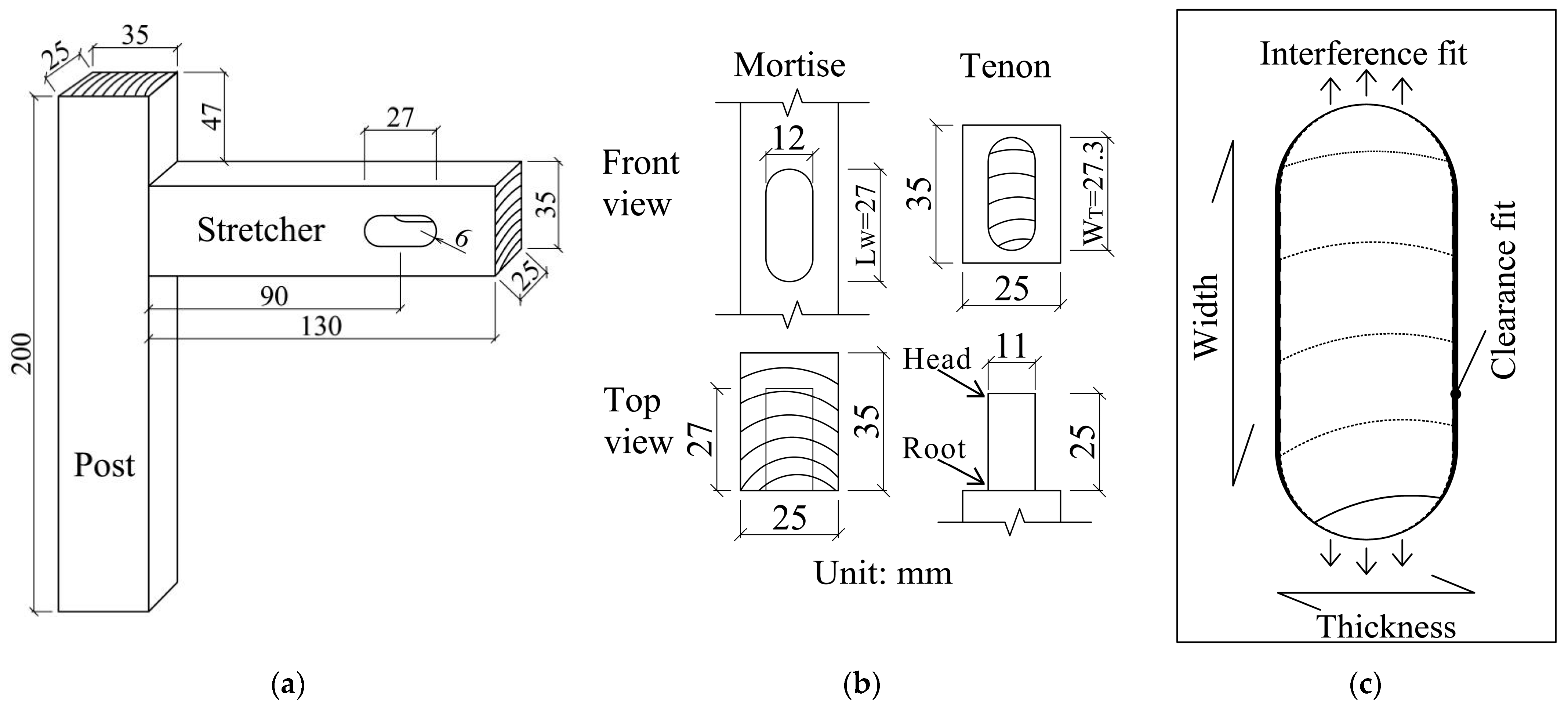
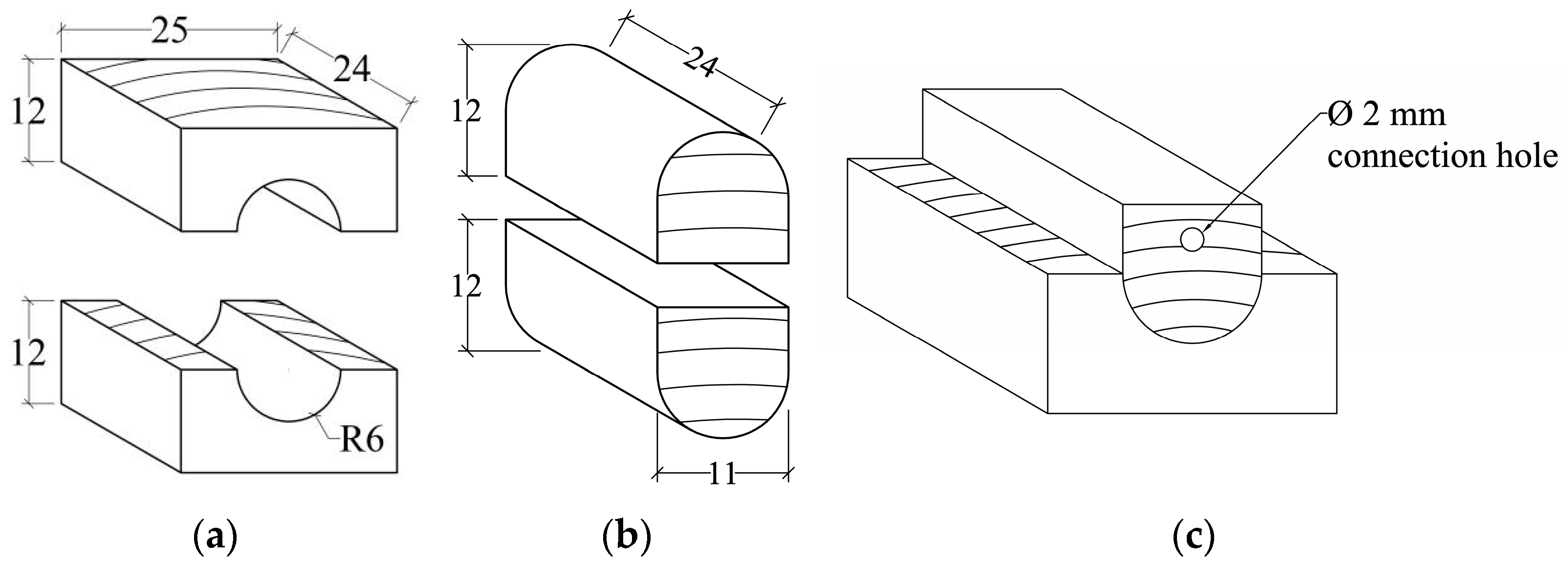
2.3. Sample Preparations

Figure 1a shows the dimensions of the L-shaped M–T joint sample tested in this study. It is composed of a tenon (horizontal) component and a mortise (vertical) component. The tenon and mortise components were machined by a computer numerical control (CNC) tenon machine (MDK3113B, New MAS Woodworking Machinery & Equipment Co., Ltd., Foshan, China) and a CNC horizontal double-end mortise machine (MS3112, New MAS Woodworking Machinery & Equipment Co., Ltd., Foshan, China), respectively. Figure 1b shows the configurations of the mortise and tenon in top and front views, indicating the head and root of the tenon. The nominal tenon width (W_T) measured 0.3 mm more than that of the mortise (W_M) to generate an interference fit between mortise and tenon (Figure 1c). In terms of tenon thickness, clearance fit was applied with a value of 1 m (Figure 1c). Based on this construction technique, the friction behavior between mortise and tenon is only in the curved part [53]. All mortise and tenon components were stored in sealed plastic bags to maintain a constant moisture condition. The mortise and tenon components were constructed without glue immediately before each fatigue test.

Figure 2a,b show the sizes of the cut-open mortise and tenon used to determine R_M and R_T, respectively. Figure 2c indicates the samples used to determine the friction coefficient between mortise and tenon. The connection hole was used to fix the steel wire for imposing loads.

2.4. Testing Methods

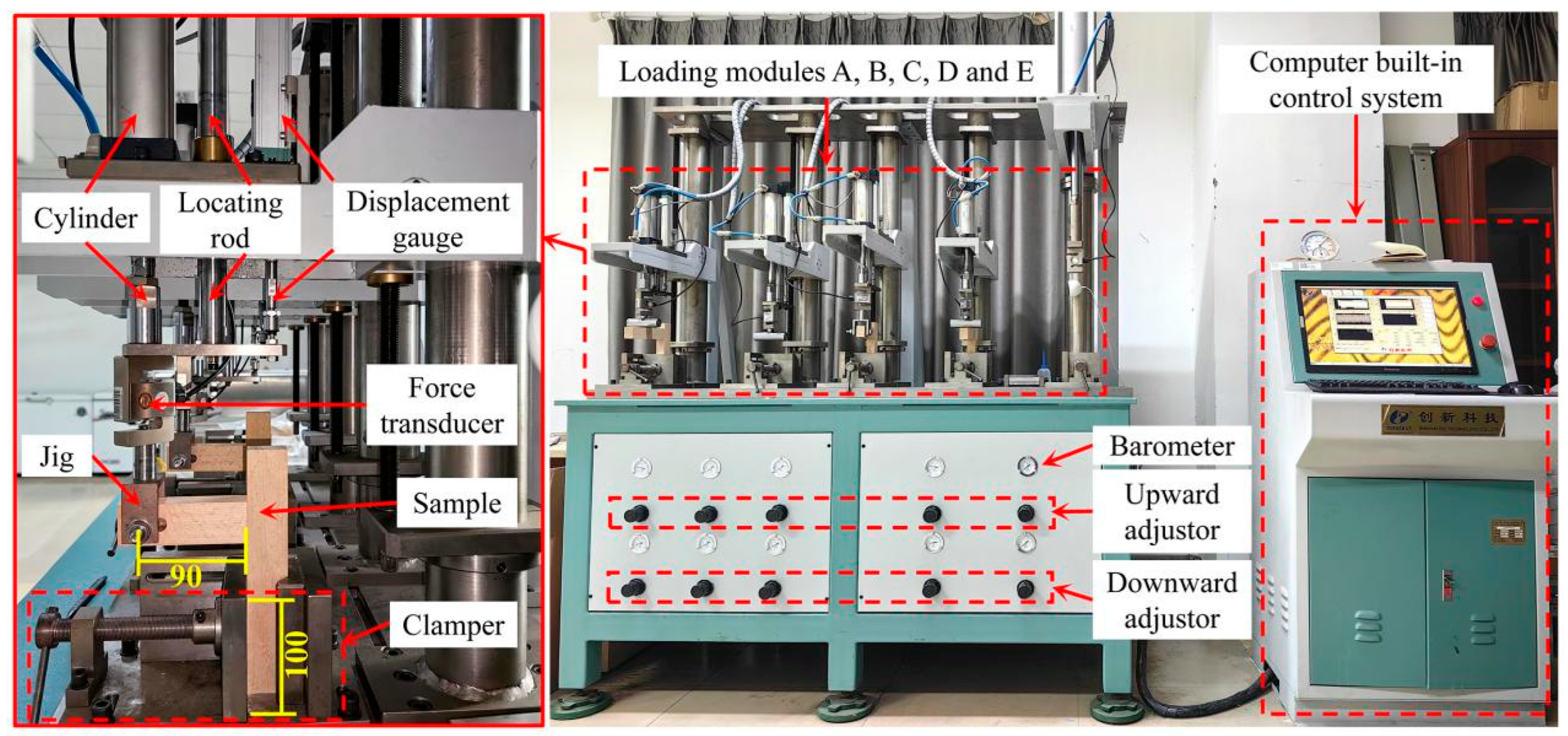
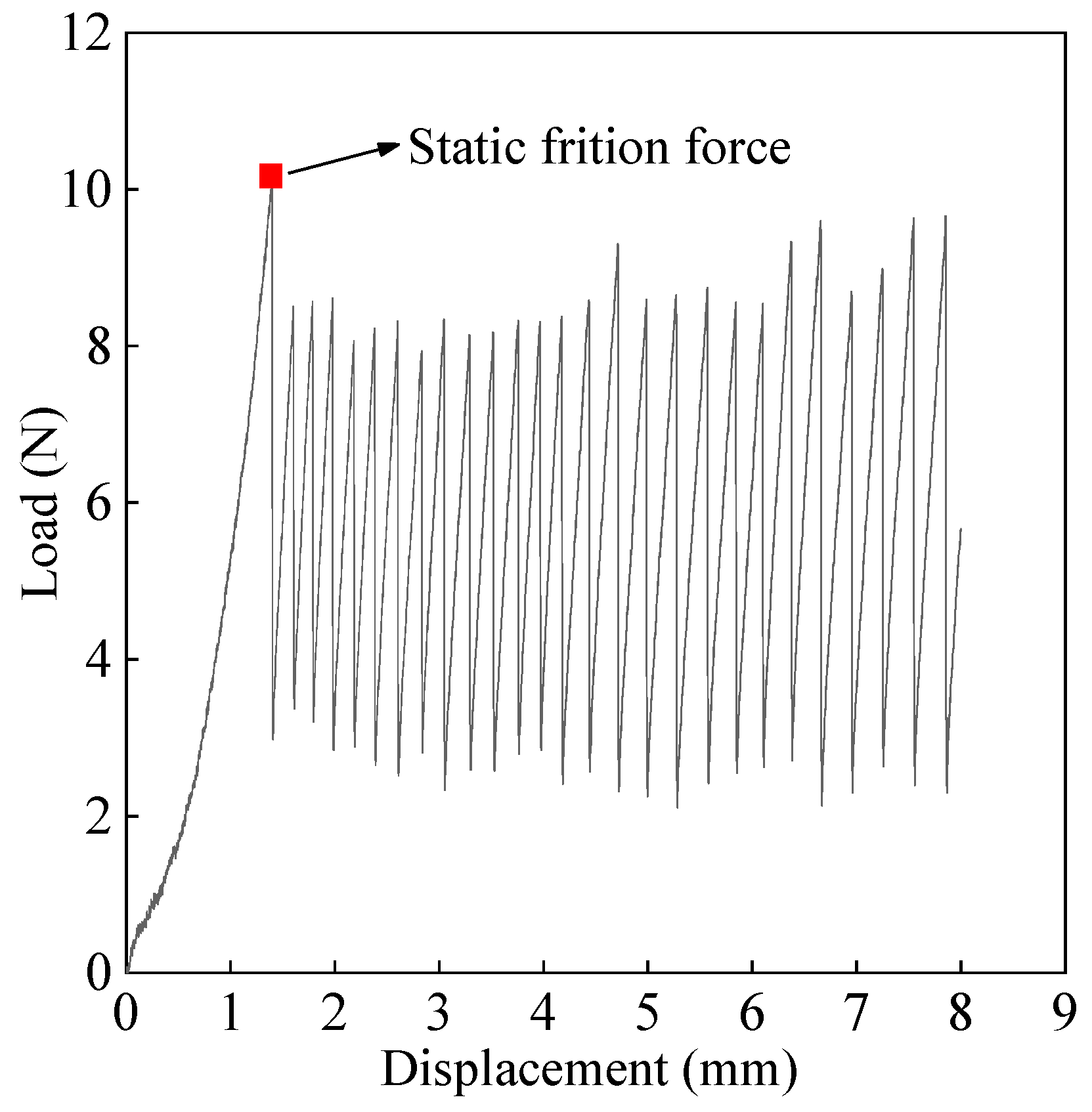
2.4.1. Cyclic Load Test

Figure 3 presents the testing machine and setup for conducting cyclic load tests of M–T joints. The setup was achieved by a self-designed air-operated multi-functional fatigue testing machine (CX-8392, Kunshan Innovation Testing Instruments Co., Ltd., Kunshan, China). It is composed of a computer control system for controlling and recording data. All load parameters were controlled by the software (Chunxin Technology system, version 1.13.0.36, Kunshan Innovation Testing Instruments Co., Ltd., Kunshan, China) built into the computer and connected with the test machine. It has 5 loading modules, allowing for conducting cyclic tests of 5 samples at the same time. Each loading module is composed of a cylinder, a loading rod, a displacement gauge, a force transducer connected to a jig, and a clamper for securing the sample. The applied load is adjusted by controlling the air pressure using the upward and downward adjustors. The air pressure is indicated by the barometers located above the adjustors. Operators only need to adjust the air pressure to the specified CLA, which can be seen on the computer screen, synchronizing with the air pressure adjustment. The laboratory temperature and humidity were 25 °C and 65% achieved by air conditioners.

Figure 4 shows the cyclic load spectrum indicating the main loading parameters. The up-and-down reversed load process within a cycle, T, involved the load reaching the specified positive value, F, and remaining at that value for t seconds. Then it reversed and reached the specified negative value, –F, and maintained that value for a further t seconds. The specified load, F, imposed was according to the CLA shown in the experimental design (Table 1). The frequency was set at 20 cycles per minute with each cycle lasting 3 s. Therefore, the value of T is 3 s, and t is 1 s. The roughness and friction coefficient were measured immediately when the CLC reached the specified values shown in Table 1.

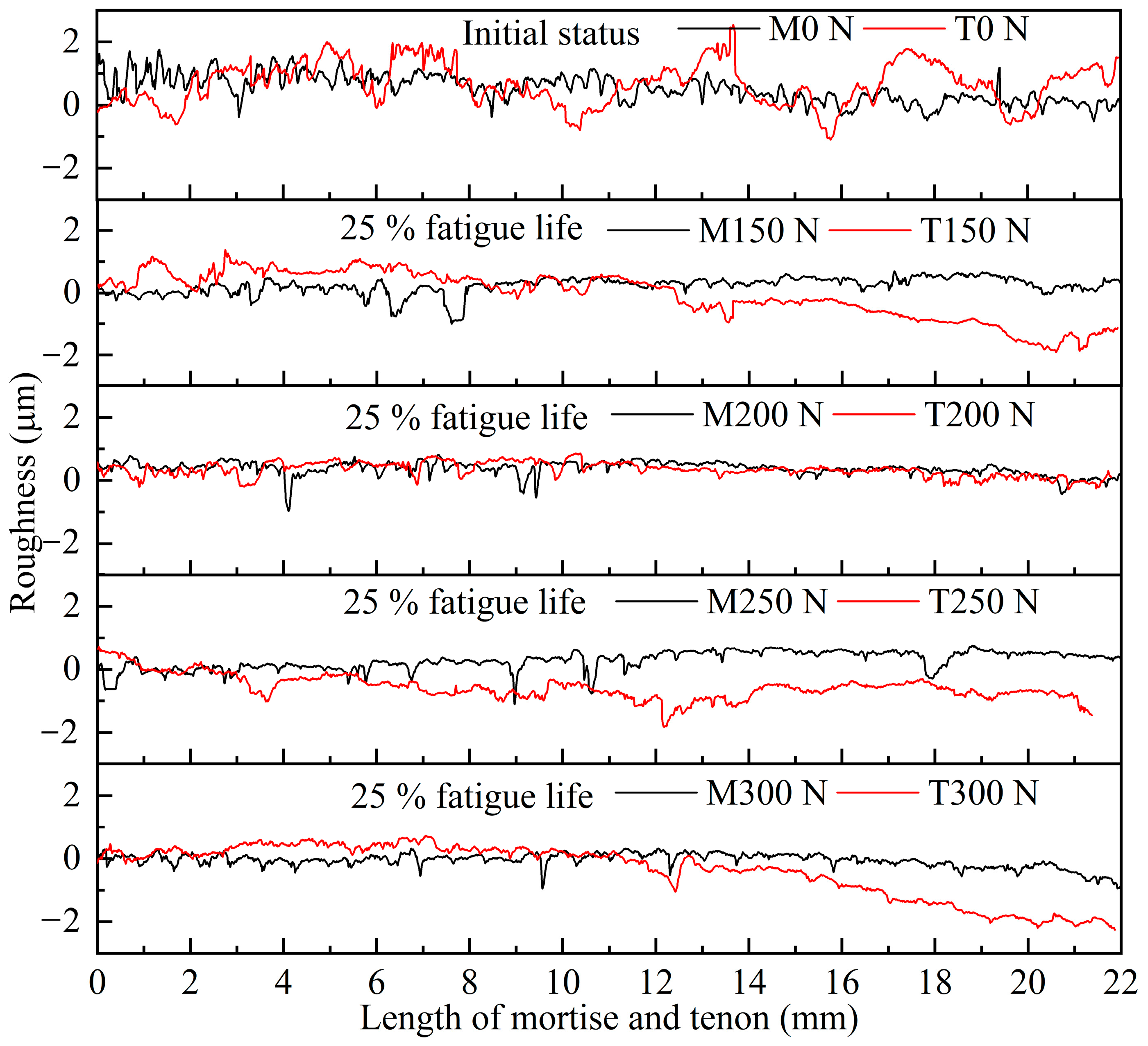
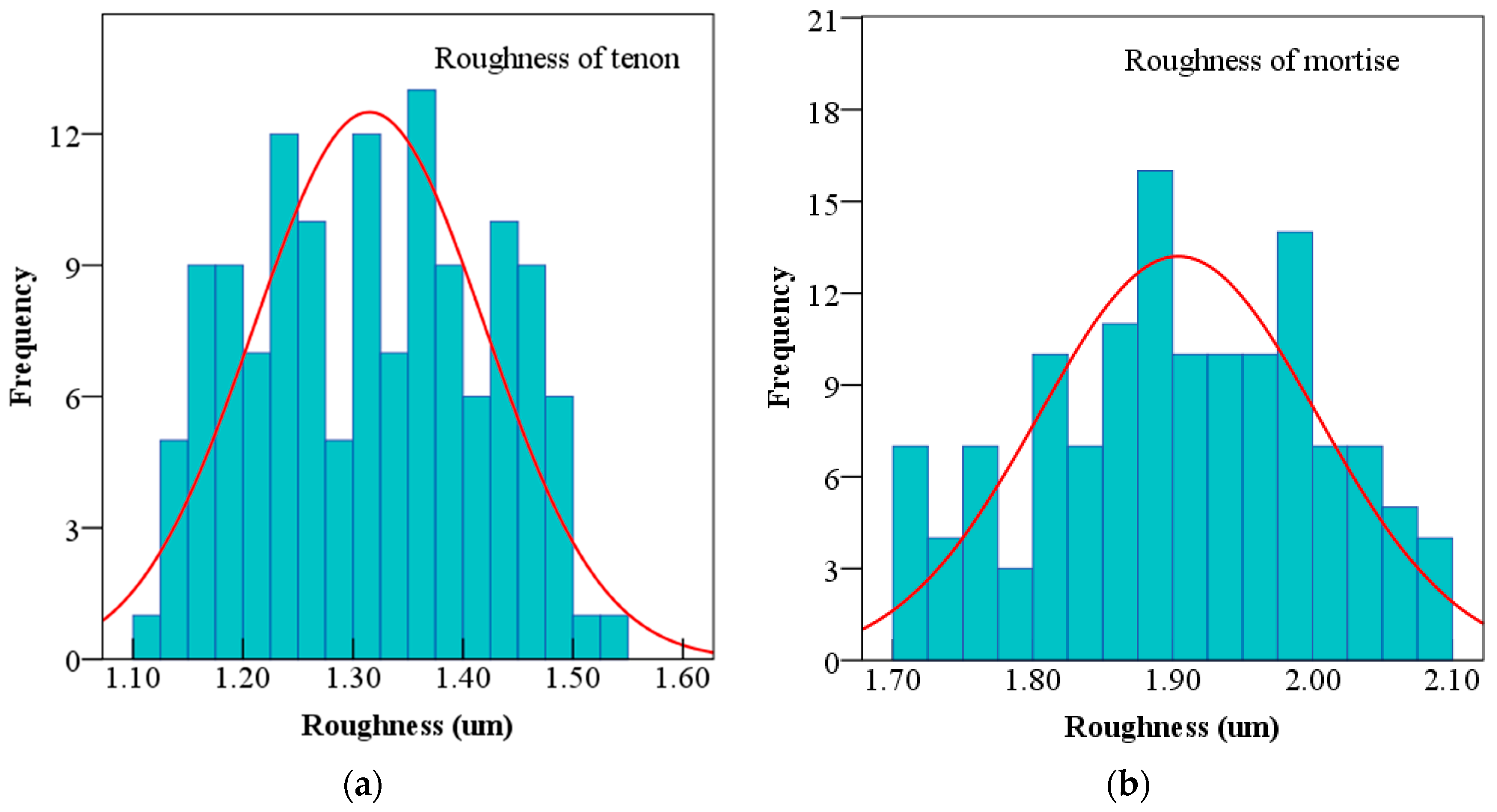
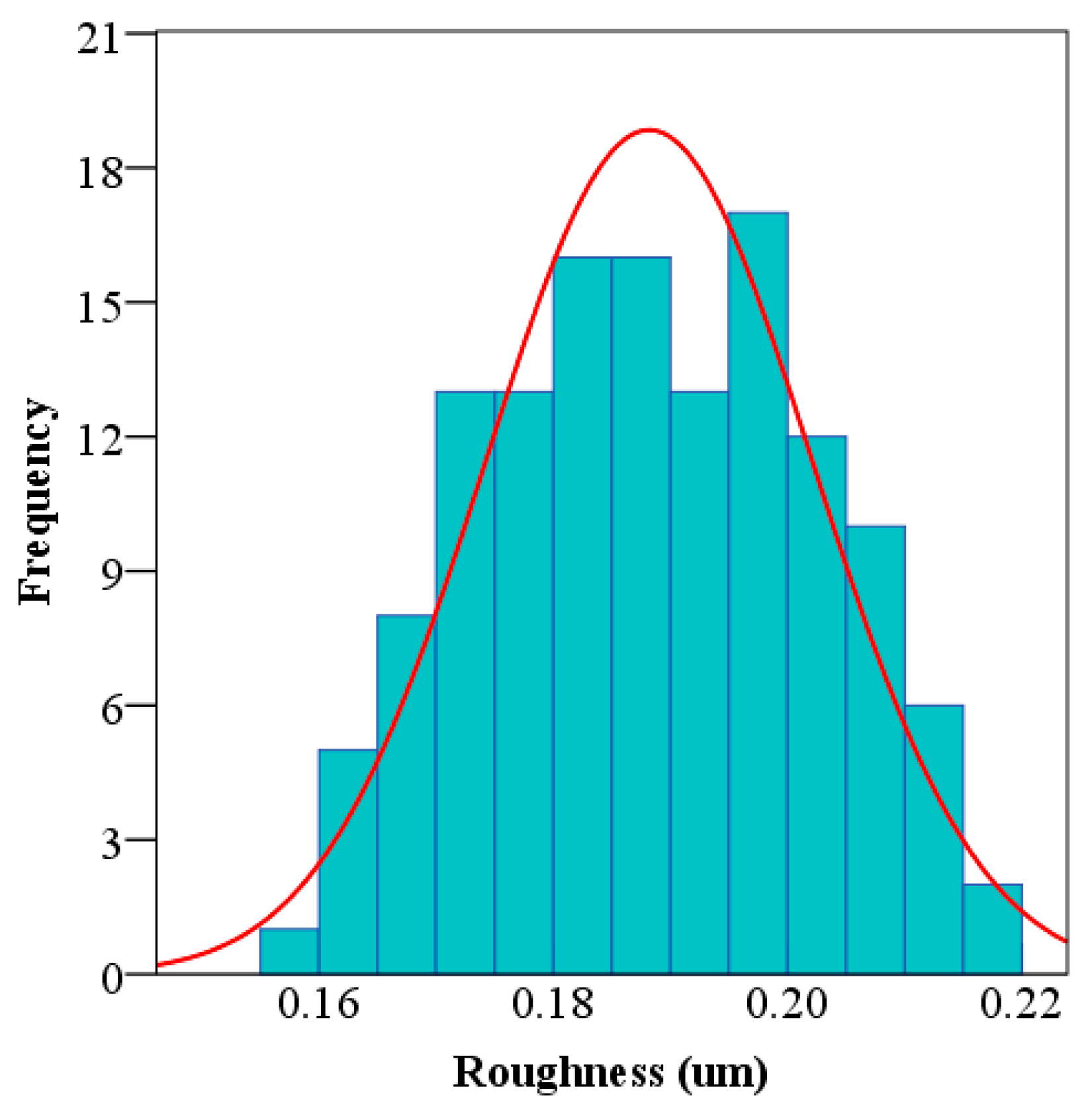
2.4.2. Roughness Measurement

Upon finishing each cyclic load test, the cut-open mortise and tenon components were cut from the fatiguing joints according to Figure 2, which was used for roughness measurement. Figure 5 presents the setup for determining the R_M and R_T by a profilometer (JB-4C, Shanghai Zhongheng Instrument Co., Ltd., Shanghai, China). The setup consisted of a probe, a control plate, and a computer with data analysis software built in. Upon conducting tests, the tested mortise and tenon were fixed on the measuring plate first. Then, the sample was adjusted to make it slightly contact the probe and the control plate was used to calibrate the initial condition to zero. Finally, the measuring was started. The measured position is at the middle line of the mortise and tenon. The measured length was 22 mm, starting and ending 1 mm from the two ends of the samples. The same procedure was repeated for all samples in terms of the experimental design. The parameter Ra, a common indicator [19,20] outputted by the profilometer, was used to characterize the roughness of the mortise and tenon.

2.4.3. Friction Coefficient Measurement

After completing roughness measurements, the tested samples were further tested for friction coefficient measurement. Figure 6 indicates the setup for determining the friction coefficient of the M–T joint using the universal test machine (AGS-X, SHIMADZU, Tokyo, Japan) and self-designed accessories. The cut-open mortise was fixed in the groove of a wooden baseboard. A dead weight was applied to the cut-open tenon. A horizontal load was applied to the tested cut-open tenon through a steel wire that was connected to the load head through a fixed pulley that changed the vertical displacement of the loading head to a horizontal movement on the tested cut-open tenon. The loading head speed was set to 3 mm/min to make the cut-open tenon slip in a stable manner on the cut-open mortise surface. The friction coefficient between mortise and tenon was calculated using Equation (1):

$$\mu ={\displaystyle \frac{F_{\mathrm{p}}}{(m_1+m_2)g}}$$

(1)

where μ is the friction coefficient between cut-open mortise and tenon surfaces, dimensionless; F_p is the static friction force (the horizontal load measured) in N; m₁ and m₂ are the mass of dead weight and half tenon applied onto a tested cut-open mortise in kg—the total mass of them is 1.6 kg; g is the gravitational acceleration—9.8 m/s².

2.5. Statistical Analysis

First, the normality of all variances were checked by the Shapiro–Wilk test. Subsequently, univariate and multivariate analysis of covariance (UNIANOVA) was conducted using a generalized linear model to evaluate the effects of CLA and CLC on the roughness and friction coefficient of the M–T joints. Then, mean comparison was conducted using the protected least squares difference multiple comparison procedure. All the above analyses were conducted at 5% significance level by SPSS software (22.0, IBM, USA). Finally, regression analyses were performed to explore the relationships among all evaluated variables.

3. Results and Discussion

3.1. Effects on the Roughness of Mortise and Tenon

Figure 7 indicates the representative curves of the roughness profiles of mortises and tenons at the initial status without cyclic load and having undergone each of four CLAs, following a CLC of 25% fatigue life of the M–T joints. From all the trends of these curves, both roughness profiles of mortise and tenon wave more seriously at the initial status than those at the CLC of 25% fatigue life, which indicates that the cyclic load imposed on the M–T joints makes the surface of the mortise and tenon smoother than at the initial status. The roughness of the tenons tends to decrease as the length increases from the head to the root of the M–T joint for each CLA. By contrast, the R_M in the length direction does not seem obvious. This may be caused by the larger compression on the root of the tenon compared to the mortise during the cyclic load, which makes the root part of the tenon smoother than the head. In addition, the grain orientation of the mortise and tenon in the compression direction is longitudinal and radial, respectively (Figure 2), making the tenon deform more than that of the mortise. Statistical analyses were conducted to further compare the mean roughness, Ra, of the mortise and tenon as the CLA and CLC increase.

Figure 8a,b show the results of normality tests of the roughness of mortise (R_M) and tenon (R_T) data, respectively, measured at each combination of CLA and CLC. There were 144 data points analyzed using SPSS software for each. The skewness and kurtosis of the R_T were 0.004 and −1.081, respectively, and those for R_M were −0.185 and −0.741, respectively, which indicate that the roughness data, R_T and R_M, suit for normal distributions, and these data can be used to conduct the UNIANOVA analysis.

Table 2. Two-way UNIANOVA results of effects of CLA, CLC, and their interaction on roughness, Ra, of mortise and tenon.

Sources	RT		RM
	F-Value	p-Value	F-Value	p-Value
CLA	679	<0.001 *	285	<0.001 *
CLC	202	<0.001 *	226	<0.001 *
CLA × CLC	3	0.003	1.5	0.16

* means the factor is significant at 5% significance level.

shows the results of the two-way UNIANOVA evaluating the effects of CLA and CLC on R_M and R_T. In terms of p-value, it demonstrates that the main effects of CLA and CLC on R_M and R_T are significant. Furthermore, CLA has a greater effect on R_M and R_T than CLC in terms of the F-value. The interaction effect of CLA and CLC on R_T is significant, but that on R_M is not significant. To further clarify these differences, post comparisons were conducted.

Table 3. Summaries of roughness, Ra, of tenon and mortise for cyclic load count at each cyclic load amplitude.

Component	CLA (N)	Roughness, Ra (μm)
		CLC (%)
		25%	50%	75%	100%
Tenon	150	1.479 (1.8) A,a	1.442 (1.4) B,a	1.403 (1.3) C,a	1.368 (1.0) D,a
	200	1.459 (1.5) A,b	1.366 (1.7) B,b	1.324 (1.5) C,b	1.295 (1.8) D,b
	250	1.350 (2.2) A,c	1.284 (2.3) B,c	1.233 (1.8) C,c	1.212 (2.6) C,c
	300	1.247 (1.5) A,d	1.195 (1.3) B,d	1.161 (1.1) C,d	1.141 (2.4) C,d
Mortise	150	2.055 (2.2) A,a	2.005 (2.5) B,a	1.952 (2.6) C,a	1.917 (2.1) D,a
	200	2.030 (2.7) A,b	1.969 (2.4) B,b	1.899 (2.1) C,b	1.858 (2.7) D,b
	250	1.985 (1.9) A,c	1.894 (2.2) B,c	1.835 (2.3) C,c	1.789 (2.9) D,c
	300	1.886 (2.4) A,d	1.815 (2.4) B,d	1.739 (2.6) C,d	1.724 (2.1) D,d

Note: The values in the parentheses are coefficients of variance (COV). The values within the same row not followed by a common upper-case letter are significantly different from one another. The values in the same column within a component, tenon or mortise, not followed by a common lower-case letter, are significantly different from one another.

summarizes the roughness, Ra, and the values of mortise and tenon after cyclic load at each combination of CLA and CLC. The initial values of R_M and R_T are 2.252 (4.9) and 2.171 (6.1) μm, respectively, with a coefficient of variance (COV) in brackets. In the case of the CLC, the R_M and R_T decrease as the CLC increases for each CLA, except 75% and 100% at CLAs of 250 N and 300 N. It may be caused because reductions of R_M and R_T have been nearly completed at higher CLA and CLC, which means that the M–T joint has approached its fatigue life. In terms of the CLA, the R_M and R_T consistently increase with increasing CLA for each CLC without any exception.

To further characterize the changing laws of R_M and R_T, Figure 9 shows the fitting lines of the roughness of tenon and mortise vs. CLC at each of four CLAs using the non-linear regression method. It indicates that the R_M is much higher than that of R_T during the whole cyclic load process with all fitting lines of the mortise (Equations (2)–(5)) beyond those of the tenons (Equations (6)–(9)). The power function was viable for fitting the relationships between roughness and CLC at each CLA, with r² higher than 0.99.

$${\mathrm{R}}_{\mathrm{M}-150\mathrm{N}}=7.47/(1+{(CLC/165852.23)}^{0.41})-5.22$$

(2)

$${\mathrm{R}}_{\mathrm{M}-200\mathrm{N}}=10.81/(1+{(CLC/117818.37)}^{0.46})-8.57$$

(3)

$${\mathrm{R}}_{\mathrm{M}-250\mathrm{N}}=1.1/(1+{(CLC/171.71)}^{0.59})+1.15$$

(4)

$${\mathrm{R}}_{\mathrm{M}-300\mathrm{N}}=0.94/(1+{(CLC/61.3)}^{0.52})+1.31$$

(5)

$${\mathrm{R}}_{\mathrm{T}-150\mathrm{N}}=5.34/(1+{(CLC/43594200)}^{0.13})-3.18$$

(6)

$${\mathrm{R}}_{\mathrm{T}-200\mathrm{N}}=1.04/(1+{(CLC/7.44)}^{0.65})+1.14$$

(7)

$${\mathrm{R}}_{\mathrm{T}-250\mathrm{N}}=1.93/(1+{(CLC/97.65)}^{0.22})+0.24$$

(8)

$${\mathrm{R}}_{\mathrm{T}-300\mathrm{N}}=2.32/(1+{(CLC/488.93)}^{0.14})-0.15$$

(9)

3.2. Effects on the Friction Coefficient Between Tenon and Mortise

Figure 10 presents a representative load–displacement curve when measuring the friction coefficient using the setup shown in Figure 6. In terms of the mechanical behavior of the curve, it can be found that the maximum value of each peak corresponds to the static friction force because sliding occurs when reaching the peak. Therefore, the static friction coefficient between mortise and tenon is made available using Equation (1). All friction coefficients of M–T joints when subjected to each combination of CLA and CLC were further analyzed using a statistical analysis method to clarify their differences.

Figure 11 indicates the normality test of the friction coefficient of the M–T joint determined at each combination of CLA and CLC based on 144 measurements. The skewness and kurtosis of the friction coefficient of the tenon are 0.007 and −0.755, respectively, which indicates that these data suit for the normal distribution and can be further used to conduct the UNIANOVA analysis.

Table 4. Two-way UNIANOVA results of effects of CLA, CLC, and their interaction on the friction coefficient of the round-end mortise–tenon joints.

Sources	Friction Coefficient
	F-Value	p-Value
CLA	48	<0.001 *
CLC	54	<0.001 *
CLA × CLC	1.3	0.24

* means the factor is significant at the 5% significance level.

shows the UNIANOVA results of the effects of CLA and CLC on the friction coefficient of the M–T joint. In terms of p-value, it indicates that CLA and CLC have significant effects on the friction coefficient between mortise and tenon, but the two-way interaction effect is not significant. To further clarify the differences between each combination of CLA and CLC, mean comparisons of friction coefficients were conducted.

Table 5. Mean comparisons of the friction coefficient between mortise and tenon after fatigue tests with each combination of cyclic load amplitude and cyclic load count.

CLA (N)	CLC in Percentage of Fatigue Life (%)
	0	25	50	75	100
150	0.365 (8.4) A	0.205 (3.7) B,a	0.202 (3.5) B,a	0.195 (4.1) C,a	0.192 (2.7) C,a
200	0.365 (8.4) A	0.204 (4.9) B,a	0.193 (5.1) C,b	0.187 (3.7) C,b	0.179 (5.1) D,b
250	0.365 (8.4) A	0.200 (5.0) B,a	0.184 (5.1) C,c	0.176 (2.8) D,c	0.172 (3.4) D,bc
300	0.365 (8.4) A	0.191 (3.2) B,b	0.181 (3.1) C,c	0.170 (4.0) D,d	0.165 (3.4) D,c

Note: The values in the parentheses are coefficients of variance (COV). The values within the same row not followed by a common upper-case letter are significantly different from one another. The values in the same column within a component, tenon or mortise, not followed by a common lower-case letter, are significantly different from one another.

compares the values of the friction coefficient measured at each combination of CLA and CLC. In terms of CLC, the friction coefficient significantly decreases as CLC increases for almost every CLA, especially from CLC of 0% to 25%. However, for the CLA of 150 N, the differences in friction coefficient between CLC of 25% and 50%, and 75% and 100% are not significant. This may result from the fact that 150 N is nearly the fatigue ultimate load [53], where the fatigue life is commonly regarded as infinite, which causes any two CLCs with a small increase not to have a significant difference. In the case of the CLA, the friction coefficients tend to decrease as the CLA increases. However, for CLC, not more than 25%, there is no significant difference as the CLA increases from 150 N to 250 N. This may be caused by a large margin of reduction from CLC of 0% to 25% for all CLAs.

Figure 12 shows the fitting lines of the friction coefficient of M–T joints relating to CLC using the nonlinear regression method. Equations (10)–(13) indicate that the power function was viable to regress the relationships between the friction coefficient and CLC at each CLA, with r² higher than 0.99. Fitting lines further demonstrate that the friction coefficient reduces by a large margin as CLC increases from 0% to 25% for each CLA, and a slight reduction is observed from 75% to 100%.

$${Fc}_{150\mathrm{N}}=0.58/(1+{(CLC/1212750)}^{0.09})-0.22$$

(10)

$${Fc}_{200\mathrm{N}}=0.62/(1+{(CLC/53253.42)}^{0.14})-0.26$$

(11)

$${Fc}_{250\mathrm{N}}=0.22/(1+{(CLC/4.32)}^{0.64})+0.15$$

(12)

$${Fc}_{300\mathrm{N}}=0.71/(1+{(CLC/75624.75)}^{0.14})-0.34$$

(13)

3.3. Relationships Between Roughness and Friction Coefficient

Figure 13 presents the relationships between the friction coefficient vs. R_M and R_T when subjected to each CLA during the cyclic load process. The regression formulas are shown in Equations (14)–(17) corresponding to CLA of 150 N, 200 N, 250 N, and 300 N, respectively, with r² higher than 0.95. It indicates that their relationships can be well fitted and described by a quadratic model during the fatigue evolution progression:

$$F_{150\mathrm{N}}=0.815-0.463{\mathrm{R}}_{\mathrm{T}}-0.372{\mathrm{R}}_{\mathrm{M}}+0.108{\mathrm{R}}_{\mathrm{T}}^2+0.06{\mathrm{R}}_{\mathrm{M}}^2+0.115{\mathrm{R}}_{\mathrm{T}}{\mathrm{R}}_{\mathrm{M}}$$

(14)

$$F_{200\mathrm{N}}=0.191-0.059{\mathrm{R}}_{\mathrm{T}}-0.075{\mathrm{R}}_{\mathrm{M}}+0.055{\mathrm{R}}_{\mathrm{T}}^2+0.034{\mathrm{R}}_{\mathrm{M}}^2+0.002{\mathrm{R}}_{\mathrm{T}}{\mathrm{R}}_{\mathrm{M}}$$

(15)

$$F_{250\mathrm{N}}=0.825-1.048{\mathrm{R}}_{\mathrm{T}}-0.08{\mathrm{R}}_{\mathrm{M}}+0.354{\mathrm{R}}_{\mathrm{T}}^2+0.005{\mathrm{R}}_{\mathrm{M}}^2+0.123{\mathrm{R}}_{\mathrm{T}}{\mathrm{R}}_{\mathrm{M}}$$

(16)

$$F_{300\mathrm{N}}=1.15-0.693{\mathrm{R}}_{\mathrm{T}}-0.757{\mathrm{R}}_{\mathrm{M}}+0.102{\mathrm{R}}_{\mathrm{T}}^2+0.131{\mathrm{R}}_{\mathrm{M}}^2+0.302{\mathrm{R}}_{\mathrm{T}}{\mathrm{R}}_{\mathrm{M}}$$

(17)

where F_150N, F_200N, F_250N, and F_300N indicate the friction coefficient when subjected to cyclic loads of 150 N, 200 N, 250 N, and 300 N, respectively. R_T and R_M mean roughness, Ra, of the tenon and mortise, respectively.

4. Limitations and Future Work

In this study, the M–T joint without glue was applied to investigate the roughness and the friction coefficient between the round-end mortise and tenon. It is known that the strengths of M–T joints mainly depend on the interference fit and frictional coefficient between mortise and tenon, while glue is commonly used synchronously to enhance the strengths of the M–T joints. When the mortise and tenon are assembled, in the width direction, the width of the tenon is greater than that of the mortise in order to generate an interference fit between the mortise and tenon. However, in the thickness direction, the thickness of the tenon is commonly equal to or smaller than that of the mortise. It is the most commonly used technique for constructing M–T joints in China and other countries [53,54]. In this context, even though glue is applied, it can be observed only in the thickness direction (clearance fit), but there is no glue in the width direction because of the interference fit. Previous studies [53,54] also proved this point. One of the aims of this study was to provide basic data for modeling the fatigue of the M–T joint. Therefore, the results of this study can also be used in the modeling of glued joints.

In future studies, the fatigue of glued M–T joints will be investigated when subjected to cyclic load and compared with the results of this study. Additionally, the fit between mortise and tenon can also change when subjected to cyclic load because of the deformations of the mortise and tenon. Therefore, the changing laws of M–T joint fit during fatigue evolution progression are also a critical factor that needs to be investigated in future studies. Then, the changing laws of the friction coefficient and M–T joint fit can be used to numerically model the fatigue of the M–T joint when subjected to cyclic load.

5. Conclusions

In this study, the effects of CLA and CLC on R_M, R_T, and the friction coefficient of the round-end M–T joint were investigated when subjected to cyclic load in order to explore the fatigue evolution progression of the beech wood M–T joint for modeling the fatigue of M–T joints. The following conclusions were drawn.

(1)

Both CLA and CLC have significant effects on R_M, R_T, and the friction coefficient of the round-end M–T joint, but the effect of CLA is much greater than that of CLC.

(2)

The R_M, R_T, and friction coefficient between mortise and tenon decrease non-linearly as the CLA and CLC increase, complying with the law of power function.

(3)

The relationships between the friction coefficient and R_M and R_T can be well fitted by a quadratic model during fatigue evolution progression at each of the four CLAs.

(4)

The fatigue evolution progressions of R_M, R_T, and the friction coefficient between mortise and tenon provide a new insight for understanding the fatigue of the round-end M–T joint, and supply basic data for numerically modeling the fatigue of the round-end M–T joint using FEM.