Comparative Study of Numerical Simulation on Short-Term Creep Behavior of Steam-Pretreated White Oak (Quercus alba L.) Wood
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Bending Creep Test
2.3. Mathematical Models
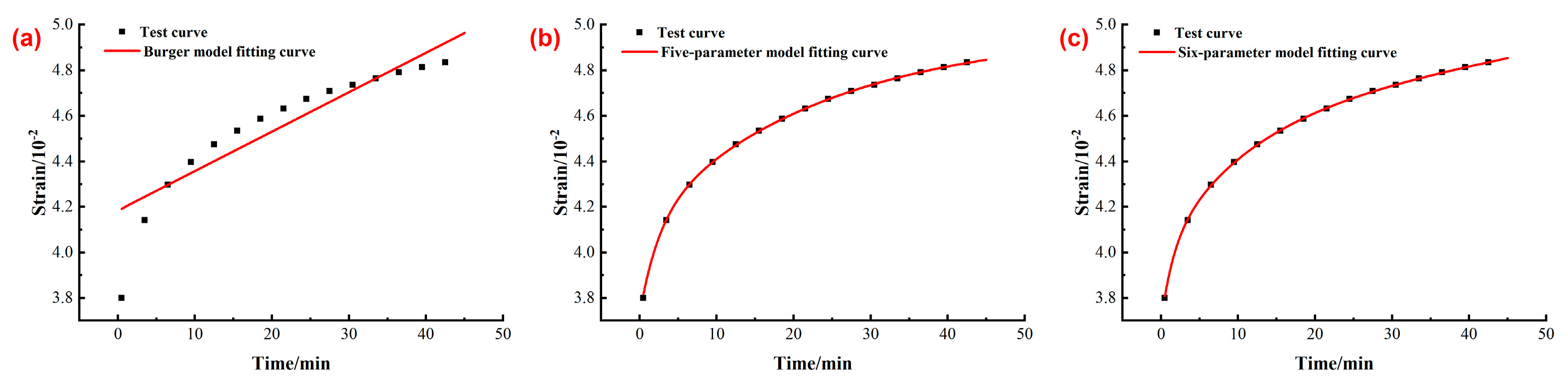
2.3.1. Burger Model
2.3.2. Five-Parameter Model
2.3.3. Six-Parameter Model
3. Results and Discussion
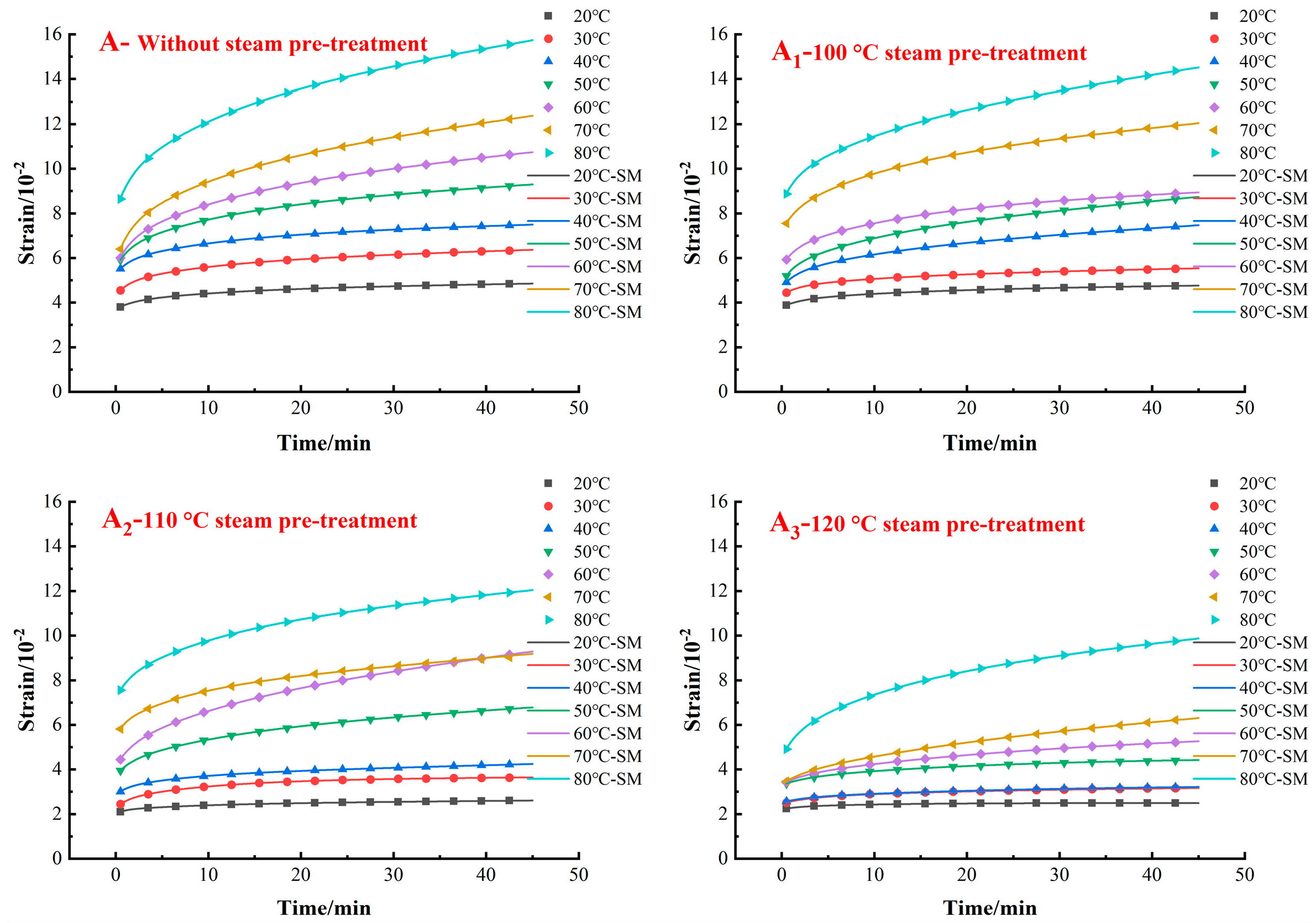
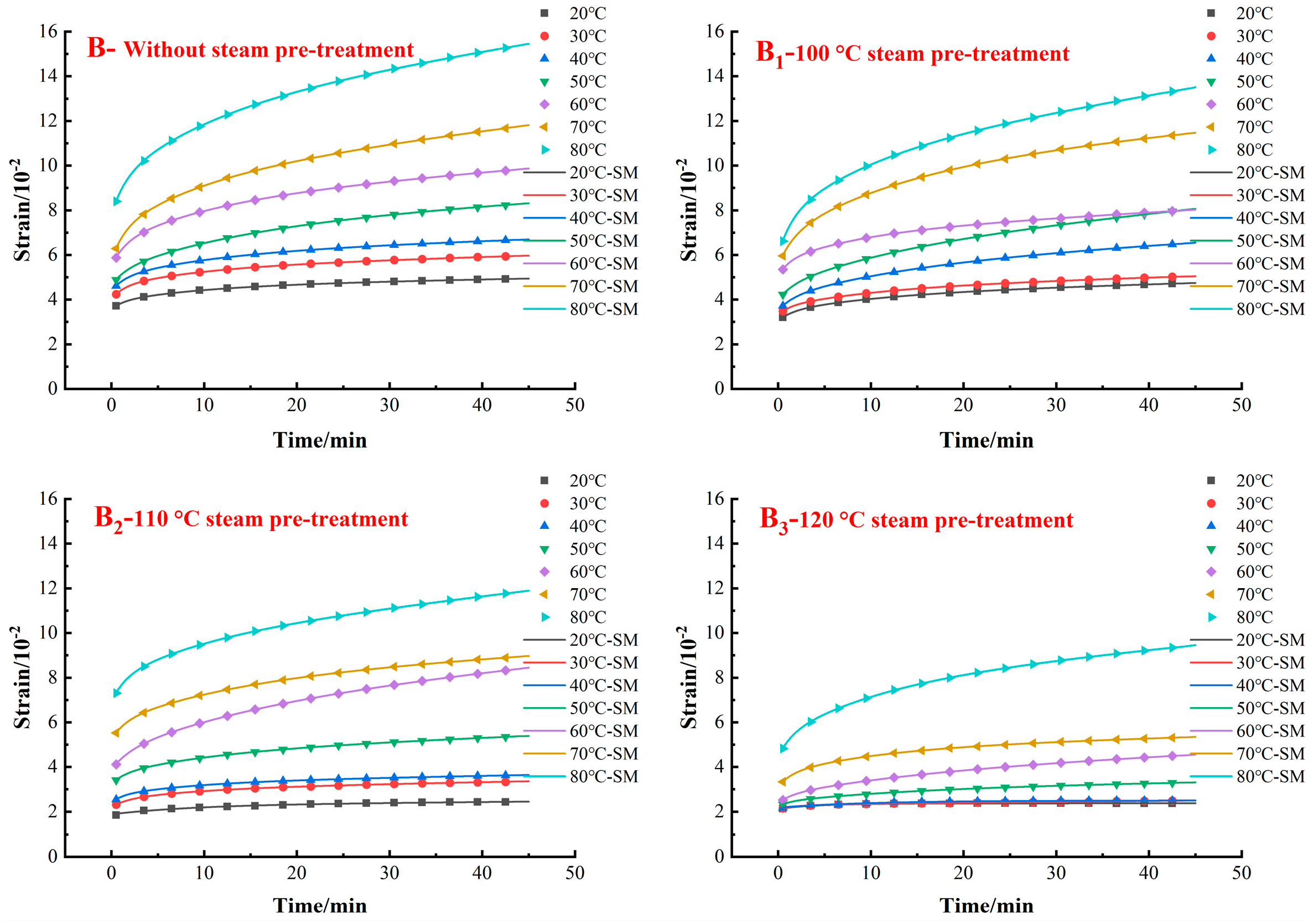
3.1. Effect of Steam Pretreatment on Creep Characteristics of White Oak Wood
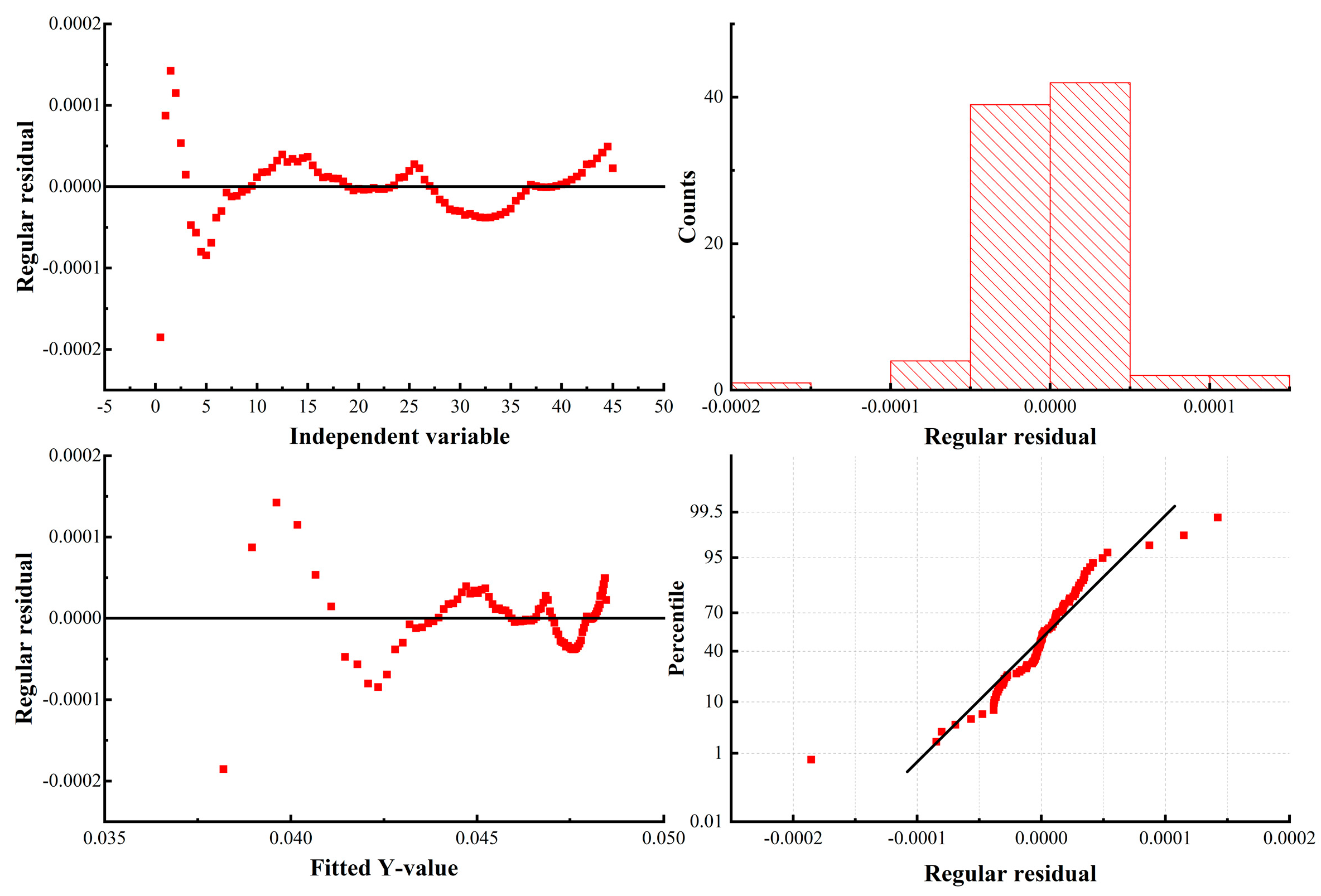
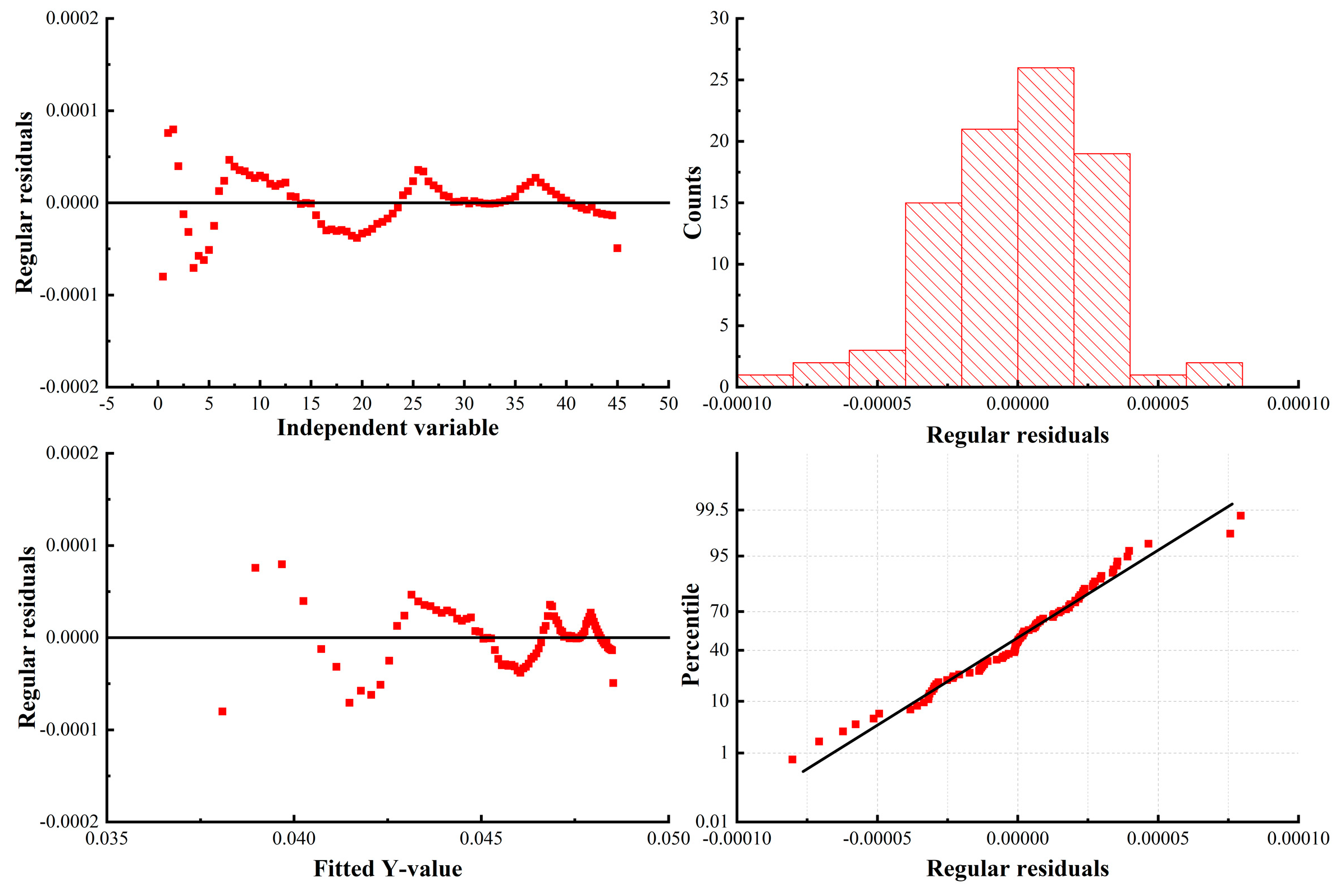
3.2. Viscoelastic Model Fitting Effect Evaluation
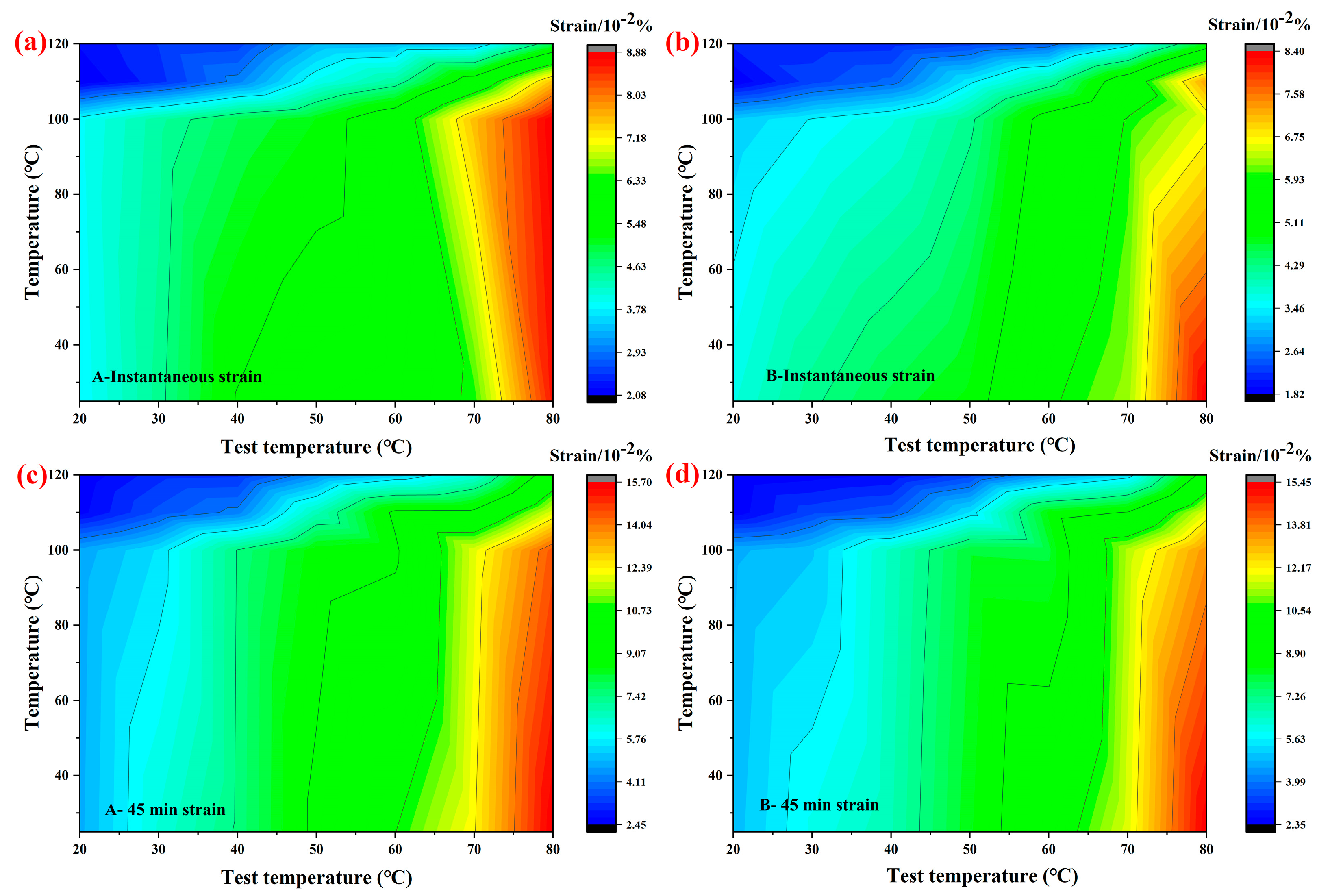
3.3. Analysis of Simulation Results
3.4. Effect of Testing Temperature on Creep Parameters
3.5. Effect of Steam Pretreatment on Creep Parameters
3.6. Effect of Earlywood Vessel Belt on Creep Parameters
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DBH | Diameter at breast height |
| MC | Moisture content |
| RH | Relative humidity |
| DMA | Dynamic thermo-mechanical analysis |
| ε(t) | Strain |
| σ0 | Stress |
| E1 | Generalized elastic module |
| E2 | High elastic module |
| η1 | Coefficient of viscosity |
| η2 | Bulk viscosity |
| t | Time |
| τ | E2/η2 |
| A | Coefficient |
| B | Parameter added additionally |
References
- Yoshida, M.; Harada, N.; Yoshida, K.; Nakagawa, T.; Shimohata, T.; Mawatari, K.; Takahashi, A.; Sakaue, H.; Nakaya, Y. High density lipoprotein inhibits the activation of sterol regulatory element-binding protein-1 in cultured cells. FEBS Lett. 2010, 584, 1217–1222. [Google Scholar] [CrossRef]
- Nakai, T.; Toba, K.; Yamamoto, H. Creep and stress relaxation behavior for natural cellulose crystal of wood cell wall under uniaxial tensile stress in the fiber direction. J. Wood Sci. 2018, 64, 745–750. [Google Scholar] [CrossRef]
- Peng, H.; Salmén, L.; Jiang, J.; Lu, J. Creep properties of compression wood fibers. Wood Sci Technol. 2020, 54, 1497–1510. [Google Scholar] [CrossRef]
- De Ligne, L.; Van Acker, J.; Baetens, J.M.; Omar, S.; De Baets, B.; Thygesen, L.G.; Van Den Bulcke, J.; Thybring, E.E. Moisture dynamics of wood-based panels and wood fibre insulation materials. Front. Plant Sci. 2022, 13, 951175. [Google Scholar] [CrossRef]
- Fridley, K.J.; Tang, R.C.; Soltis, L.A. Creep Behavior Model for Structural Lumber. J. Struct. Eng. 1992, 118, 2261–2277. [Google Scholar] [CrossRef]
- Nasir, V.; Cool, J. Cutting power and surface quality in sawing kiln-dried, green, andfrozen hem-fir wood. Wood Sci. Technol. 2021, 55, 505–519. [Google Scholar] [CrossRef]
- Grottesi, G.; Coelho, G.B.A.; Kraniotis, D. Heat and moisture induced stress and strain in wooden artefacts and elements in heritage buildings: A review. Appl. Sci. 2023, 13, 7251. [Google Scholar] [CrossRef]
- Wang, C.; Anupam, K.; Kasbergen, C.; Erkens, S. Frequency range optimization for linear viscoelastic characterization of Burger’s model. Int. J. Mech. Sci. 2024, 285, 109817. [Google Scholar] [CrossRef]
- Dong, C.; Zhang, S.; Wang, J.; Chui, Y.H. Static bending creep properties of furfurylated poplar wood. Constr. Build. Mater. 2021, 269, 121308. [Google Scholar] [CrossRef]
- Hu, W.G.; Guan, H.Y. Study on compressive stress relaxation behavior of beech based on the finite element method. Maderas Cienc. Tecnol. 2019, 21, 15–24. [Google Scholar] [CrossRef]
- Asyraf, M.R.M.; Ishak, M.R.; Sapuan, S.M.; Yidris, N. Comparison of static and long-term creep behaviors between balau wood and glass fiber reinforced polymer composite for cross-arm application. Fibers Polym. 2021, 22, 793–803. [Google Scholar] [CrossRef]
- Wang, C.; Wu, Q.; Lin, P.; Yang, D.; Yu, Y.M. Orthotropic creep performance of small flawless oak board. Sci. Silvae Sin. 2018, 54, 76–83. (In Chinese) [Google Scholar] [CrossRef]
- Huč, S.; Hozjan, T.; Svensson, S. Rheological behavior of wood in stress relaxation under compression. Wood Sci. Technol. 2018, 52, 793–808. [Google Scholar] [CrossRef]
- Yin, Y.Q.; Hou, J.F.; Jiang, Z.H.; Yu, Y.M. Effect of earlywood vessel distribution on creep characteristics of ring-porous oak wood. J. For. Eng. 2021, 6, 54–60. (In Chinese) [Google Scholar] [CrossRef]
- Bhangale, N.; Kachhia, K.B.; Gómez-Aguilar, J.F. Fractional viscoelastic models with Caputo generalized fractional derivative. Math Methods App Sci. 2023, 46, 7835–7846. [Google Scholar] [CrossRef]
- Wang, C.; Chen, X. A description of the isothermal ageing creep process in polymethyl methacrylate using fractional differential models. Polymers 2024, 16, 2725. [Google Scholar] [CrossRef]
- Hou, J.; Jiang, Y.; Yin, Y.; Zhang, W.; Chen, H.; Yu, Y.; Jiang, Z. Experimental study and comparative numerical modeling of creep behavior of white oak wood with various distributions of earlywood vessel belt. J. Wood Sci. 2021, 67, 57. [Google Scholar] [CrossRef]
- Chen, H.C. Numerical Simulation Analysis Asphaly Pavement Rutting Based on Creep Test. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2012. (In Chinese). [Google Scholar]
- Meena, S.; Biligiri, K.P. Binder rheological predictive models to evaluate rutting performance of asphalt mixtures. Constr Build Mater. 2016, 111, 556–564. [Google Scholar] [CrossRef]
- Wang, X.M. Wood Drying Dcience, 1st ed.; China Forestry Press: Beijing, China, 2007; ISBN 978-7-5038-4155-2. (In Chinese) [Google Scholar]
- Ma, S. Study on Improving Dimensional Stability of Wood after Saturated Steam Treatment. Wood Ind. 1998, 12, 36–37. [Google Scholar] [CrossRef]
- Chen, J.; Huang, X.; Feng, J.; Zhang, Y.; Yu, Y.; Hou, J. Investigation into the Long-Term Stress Relaxation Behaviors of White Oak (Quercus alba L.) Based on the Time–Temperature–Moisture Superposition Principle. Wood Mater. Sci. Eng. 2024, 19, 521–529. [Google Scholar] [CrossRef]
- Zhang, Y.; Hou, J.; Chen, H.; Cen, J.; Jiang, Z.; Yu, Y. Time-moisture superposition principle in creep behavior of white oak with various earlywood vessel locations. Maderas-Cienc. Tecnol. 2023, 26, 1–14. [Google Scholar] [CrossRef]
- Dinwoodie, J.M.; Higgins, J.A.; Robson, D.J.; Paxton, B.H. Creep in chipboard: Part 7: Testing the efficacy of models on 7–10 years data and evaluating optimum period of prediction. Wood Sci. Technol. 1990, 24, 181–189. [Google Scholar] [CrossRef]
- Liu, C.; Du, J.; Wu, C.; Liu, K.; Jiang, K. Low-temperature crack resistance of wood tar-based rejuvenated asphalt based on viscoelastic rheological method. Int. J. Pavement Res. Technol. 2022, 15, 1340–1353. [Google Scholar] [CrossRef]
- Tjeerdsma, B.F.; Militz, H. Chemical changes in hydrothermal treated wood: FTIR analysis of combined hydrothermal and dry heat-treated wood. Eur J Wood Wood Prod. 2005, 63, 102–111. [Google Scholar] [CrossRef]
- Michalak, L.; Knutsen, S.H.; Aarum, I.; Westereng, B. Effects of pH on steam explosion extraction of acetylated galactoglucomannan from Norway spruce. Biotechnol. Biofuels 2018, 11, 311. [Google Scholar] [CrossRef]
- Dussan, K.; Girisuta, B.; Lopes, M.; Leahy, J.J.; Hayes, M.H.B. Effects of soluble lignin on the formic acid-catalyzed formation of furfural: A case study for the upgrading of hemicellulose. ChemSusChem 2016, 9, 492–504. [Google Scholar] [CrossRef]
- Mohammadabadi, M.; Yadama, V.; Geng, J. Creep behavior of 3D core wood-strand sandwich panels. Holzforschung 2018, 72, 513–519. [Google Scholar] [CrossRef]
- Chang, F.-C.; Lam, F. Effects of temperature-induced strain on creep behavior of wood–plastic composites. Wood Sci. Technol. 2018, 52, 1213–1227. [Google Scholar] [CrossRef]
- Hsieh, T.-Y.; Chang, F.-C. Effects of moisture content and temperature on wood creep. Holzforschung 2018, 72, 1071–1078. [Google Scholar] [CrossRef]
- Furuta, Y.; Nakajima, M.; Nakanii, E.; Ohkoshi, M. The effects of lignin and hemicellulose on thermal-softening properties of water-swollen wood. Mokuzai Gakkaishi 2010, 56, 132–138. [Google Scholar] [CrossRef]
- Cui, C.; Sadeghifar, H.; Sen, S.; Argyropoulos, D.S. Toward thermoplastic lignin polymers; Part II: Thermal & polymer characteristics of kraft lignin & derivatives. Bioresources 2013, 8, 864–886. [Google Scholar] [CrossRef]
- Gao, Z.; Huang, R. Effects of pressurized superheated steam treatment on dimensional stability and its mechanisms in surface-compressed wood. Forests 2022, 13, 1230. [Google Scholar] [CrossRef]
- Stelte, W.; Clemons, C.; Holm, J.K.; Sanadi, A.R.; Ahrenfeldt, J.; Shang, L.; Henriksen, U.B. Pelletizing properties of torrefied spruce. Biomass Bioenergy 2011, 35, 4690–4698. [Google Scholar] [CrossRef]
- Tumen, I.; Aydemir, D.; Gunduz, G.; Uner, B.; Cetin, H. Changes in the chemical structure of thermally treated wood. Bioresources 2010, 5, 1936–1944. [Google Scholar] [CrossRef]
- Chai, H.; Xu, C.; Li, J.; Kong, F.; Cai, Y. Effects of pretreatment with saturated wet air and steaming on the high-frequency vacuum drying characteristics of wood. Bioresources 2019, 14, 9601–9610. [Google Scholar] [CrossRef]
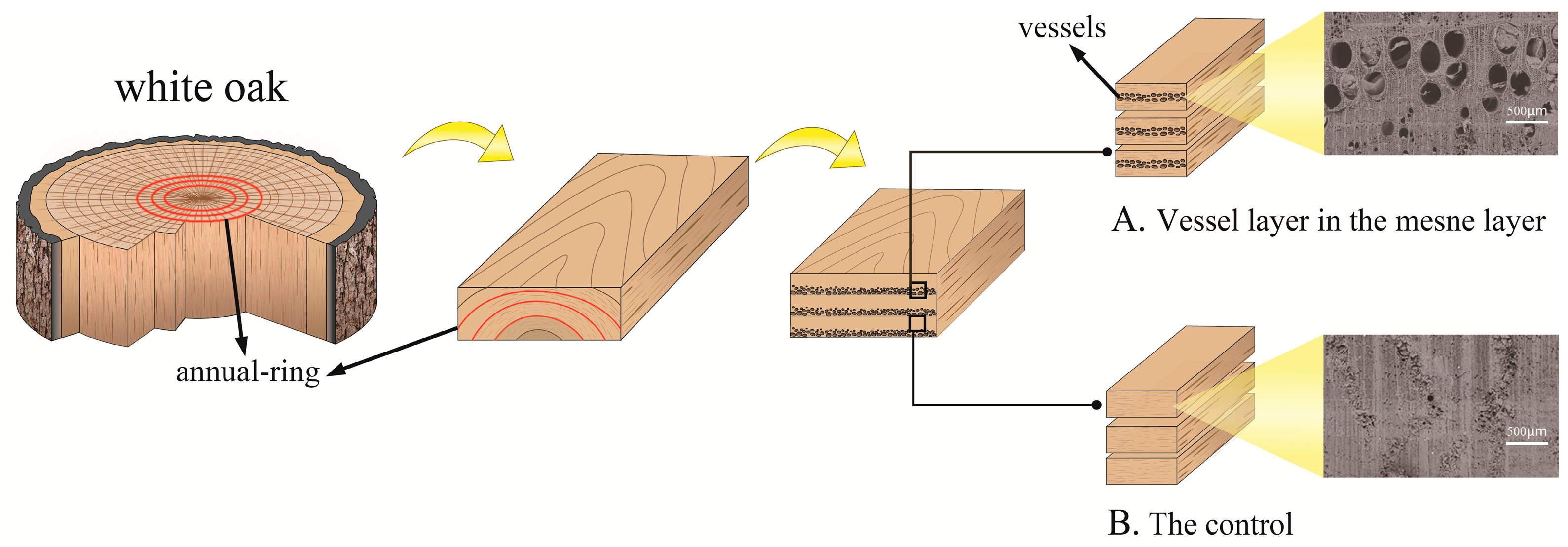

| Sample No. | Steam Pretreatment Temperature (°C) | Sample No. | Steam Pretreatment Temperature (°C) |
|---|---|---|---|
| A | The control | B | The control |
| A1 | 100 | B1 | 100 |
| A2 | 110 | B2 | 110 |
| A3 | 120 | B3 | 120 |
| Model Type | Parameter Value | ||||||
|---|---|---|---|---|---|---|---|
| E1 | E2 | η1 | η2 | A | B | R2 | |
| Burger model | 119.970 | −3.930 | −1.030 | 28,912.960 | - | - | 0.8624 |
| Five-parameter model | 134.100 | 1264.270 | - | 3116.350 | 13,863.250 | 0.040 | 0.9996 |
| Six-parameter model | 135.280 | 1646.960 | 80,775.850 | 2554.930 | 77.320 | 0.090 | 0.9998 |
| Specimen No. | A | B | E1 | E2 | η1 | η2 | R2 |
|---|---|---|---|---|---|---|---|
| 30 °C-A | 54.221 | 0.102 | 115.349 | 928.655 | 39,660.365 | 1248.809 | 0.99991 |
| 30 °C-B | 58.707 | 0.103 | 123.938 | 950.310 | 41,619.989 | 1266.289 | 0.99992 |
| 40 °C-A | 40.324 | 0.094 | 94.609 | 926.298 | 43,039.905 | 1185.257 | 0.99995 |
| 40 °C-B | 39.444 | 0.090 | 113.712 | 906.642 | 36,264.232 | 1253.568 | 0.99996 |
| 50 °C-A | 25.118 | 0.091 | 89.572 | 615.275 | 19,937.825 | 850.497 | 0.99996 |
| 50 °C-B | 15.946 | 0.068 | 107.352 | 832.009 | 21,678.822 | 1305.139 | 0.99997 |
| 60 °C-A | 21.004 | 0.093 | 89.298 | 489.570 | 11,631.957 | 682.544 | 0.99996 |
| 60 °C-B | 23.906 | 0.094 | 90.884 | 533.276 | 15,007.150 | 743.102 | 0.99995 |
| 70 °C-A | 18.498 | 0.097 | 85.191 | 369.137 | 8755.920 | 530.075 | 0.99995 |
| 70 °C-B | 19.588 | 0.097 | 86.332 | 393.385 | 9702.867 | 562.958 | 0.99995 |
| 80 °C-A | 13.730 | 0.090 | 61.824 | 360.487 | 7437.382 | 521.472 | 0.99997 |
| 80 °C-B | 14.046 | 0.091 | 63.859 | 356.03101 | 7422.394 | 515.261 | 0.99997 |
| Specimen No. | A | B | E1 | E2 | η1 | η2 | R2 |
|---|---|---|---|---|---|---|---|
| 30 °C-A1 | 88.371 | 0.090 | 115.656 | 1394.104 | 63523.791 | 2130.707 | 0.99948 |
| 30 °C-B1 | 54.045 | 0.094 | 150.630 | 1493.337 | 41425.351 | 1717.062 | 0.99995 |
| 40 °C-A1 | 37.787 | 0.085 | 106.214 | 892.708 | 20468.742 | 1349.896 | 0.99992 |
| 40 °C-B1 | 23.613 | 0.072 | 141.630 | 981.412 | 21318.088 | 1588.244 | 0.99994 |
| 50 °C-A1 | 33.626 | 0.103 | 102.441 | 776.486 | 13250.061 | 873.656 | 0.99994 |
| 50 °C-B1 | 22.667 | 0.077 | 125.285 | 889.201 | 11962.896 | 1353.927 | 0.99998 |
| 60 °C-A1 | 22.382 | 0.083 | 89.036 | 689.961 | 28068.007 | 886.611 | 0.99996 |
| 60 °C-B1 | 44.302 | 0.116 | 99.485 | 792.504 | 21194.137 | 820.351 | 0.99993 |
| 70 °C-A1 | 20.235 | 0.093 | 69.569 | 628.445 | 12563.810 | 839.819 | 0.99997 |
| 70 °C-B1 | 12.183 | 0.077 | 90.315 | 425.789 | 13085.048 | 680.247 | 0.99995 |
| 80 °C-A1 | 19.727 | 0.090 | 59.222 | 483.005 | 8036.453 | 661.361 | 0.99997 |
| 80 °C-B1 | 16.643 | 0.097 | 82.999 | 328.618 | 7326.137 | 474.600 | 0.99995 |
| Specimen No. | A | B | E1 | E2 | η1 | η2 | R2 |
|---|---|---|---|---|---|---|---|
| 30 °C-A2 | 54.349 | 0.098 | 218.461 | 1375.815 | 218,130.449 | 1811.668 | 0.99993 |
| 30 °C-B2 | 100.421 | 0.105 | 227.052 | 1642.013 | 67,339.245 | 2586.697 | 0.99971 |
| 40 °C-A2 | 116.430 | 0.141 | 175.692 | 1665.473 | 45,243.702 | 1706.100 | 0.99990 |
| 40 °C-B2 | 95.095 | 0.115 | 208.503 | 1644.112 | 66,145.565 | 1765.508 | 0.99988 |
| 50 °C-A2 | 31.138 | 0.089 | 134.120 | 958.909 | 19,786.005 | 1360.331 | 0.99996 |
| 50 °C-B2 | 42.137 | 0.088 | 153.891 | 1225.784 | 31,359.811 | 1736.174 | 0.99990 |
| 60 °C-A2 | 20.446 | 0.084 | 120.440 | 635.552 | 9549.612 | 1035.023 | 0.99997 |
| 60 °C-B2 | 15.286 | 0.066 | 128.369 | 739.032 | 12,217.617 | 1394.188 | 0.99996 |
| 70 °C-A2 | 43.110 | 0.136 | 92.535 | 843.326 | 13,949.481 | 641.1787 | 0.99818 |
| 70 °C-B2 | 18.8107 | 0.075 | 95.475 | 695.201 | 20,426.802 | 995.035 | 0.99996 |
| 80 °C-A2 | 20.235 | 0.093 | 69.569 | 628.445 | 12,563.890 | 839.819 | 0.99997 |
| 80 °C-B2 | 27.411 | 0.102 | 72.344 | 533.948 | 10,154.6310 | 715.915 | 0.99996 |
| Specimen No. | A | B | E1 | E2 | η1 | η2 | R2 |
|---|---|---|---|---|---|---|---|
| 30 °C-A3 | 45.723 | 0.042 | 202.249 | 1926.874 | 506,716.105 | 5558.816 | 0.99970 |
| 30 °C-B3 | 1001.920 | 0.328 | 242.935 | 5349.853 | 120,988.861 | 2562.949 | 0.99994 |
| 40 °C-A3 | 20.206 | 0.054 | 149.284 | 1338.580 | 16,331.660 | 2844.861 | 0.99997 |
| 40 °C-B3 | 42.588 | 0.098 | 172.036 | 994.782 | 98,701.955 | 1416.815 | 0.99987 |
| 50 °C-A3 | 23.363 | 0.044 | 151.130 | 1811.770 | 1,170,040.000 | 4670.174 | 0.99971 |
| 50 °C-B3 | 64.561 | 0.073 | 223.5934 | 2550.546 | 66,972.513 | 2975.074 | 0.99986 |
| 60 °C-A3 | 16.919 | 0.044 | 149.722 | 1479.720 | 48,032.780 | 3288.001 | 0.99993 |
| 60 °C-B3 | 34.025 | 0.067 | 209.185 | 1499.225 | 25,045.821 | 2191.718 | 0.99997 |
| 70 °C-A3 | 16.487 | 0.048 | 149.107 | 1281.165 | 17,652.804 | 2895.157 | 0.99996 |
| 70 °C-B3 | 40.548 | 0.094 | 160.328 | 919.413 | 41,665.421 | 1272.908 | 0.99988 |
| 80 °C-A3 | 16.333 | 0.084 | 110.180 | 541.136 | 11,931.507 | 813.383 | 0.99997 |
| 80 °C-B3 | 18.547 | 0.090 | 112.232 | 587.215 | 12,777.809 | 811.412 | 0.99998 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Cen, J.; Zhang, Y.; Han, S.; Gu, K.; Yu, Y.; Hou, J. Comparative Study of Numerical Simulation on Short-Term Creep Behavior of Steam-Pretreated White Oak (Quercus alba L.) Wood. Forests 2024, 15, 2166. https://doi.org/10.3390/f15122166
Zhang X, Cen J, Zhang Y, Han S, Gu K, Yu Y, Hou J. Comparative Study of Numerical Simulation on Short-Term Creep Behavior of Steam-Pretreated White Oak (Quercus alba L.) Wood. Forests. 2024; 15(12):2166. https://doi.org/10.3390/f15122166
Chicago/Turabian StyleZhang, Xingying, Junjie Cen, Yuge Zhang, Shenjie Han, Kongjie Gu, Youming Yu, and Junfeng Hou. 2024. "Comparative Study of Numerical Simulation on Short-Term Creep Behavior of Steam-Pretreated White Oak (Quercus alba L.) Wood" Forests 15, no. 12: 2166. https://doi.org/10.3390/f15122166
APA StyleZhang, X., Cen, J., Zhang, Y., Han, S., Gu, K., Yu, Y., & Hou, J. (2024). Comparative Study of Numerical Simulation on Short-Term Creep Behavior of Steam-Pretreated White Oak (Quercus alba L.) Wood. Forests, 15(12), 2166. https://doi.org/10.3390/f15122166






