Strengthening of Ancient Timber Beams during Restoration Operations: Effect of Wood Cutting on Modulus of Elasticity
Abstract
:1. Introduction
2. Materials and Methods
2.1. Timber Beams
2.2. Grooves
2.3. Mechanical Tests
2.4. Dynamic Tests
3. Results
3.1. MOE Reduction
Practical Consequences
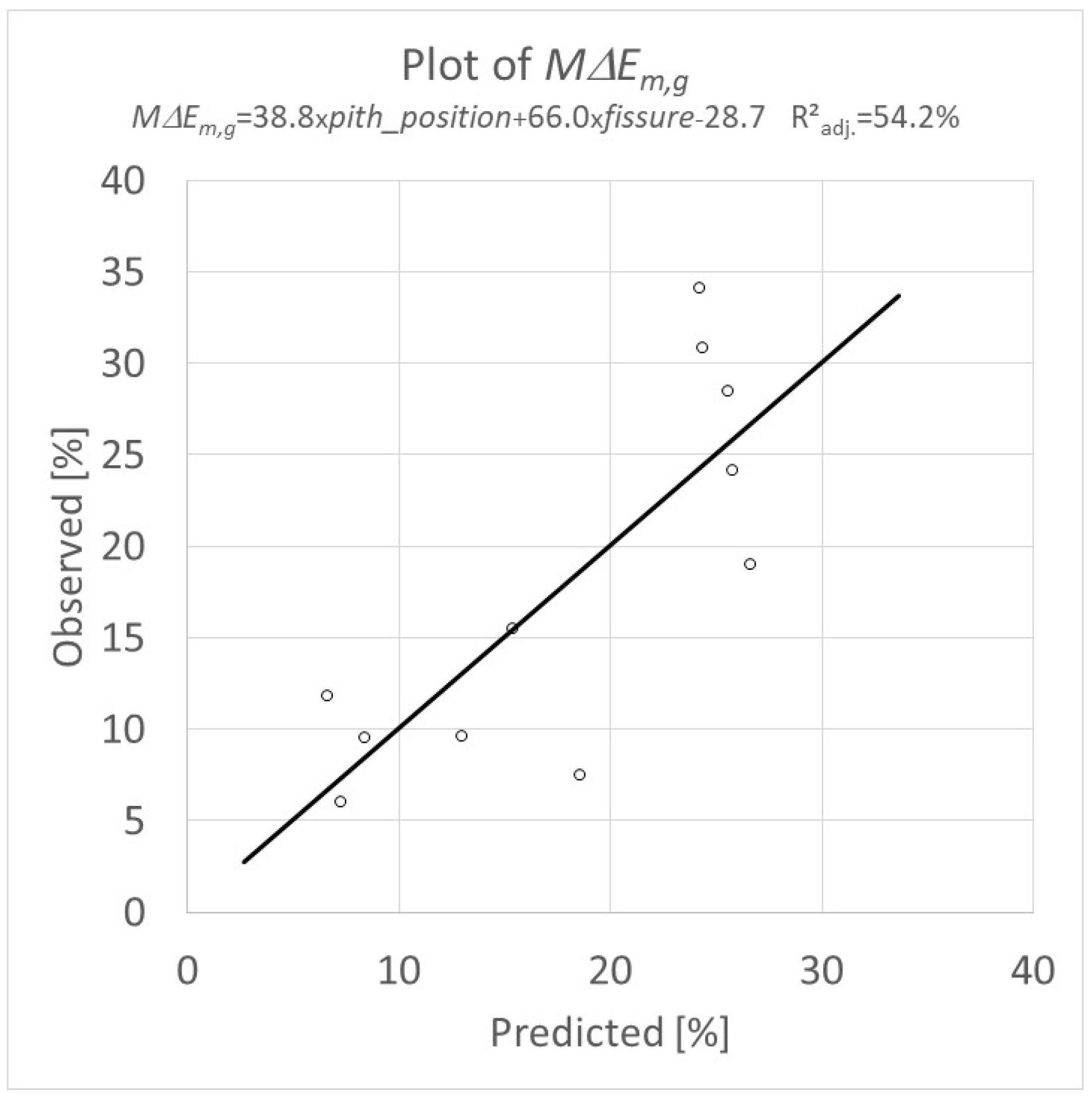
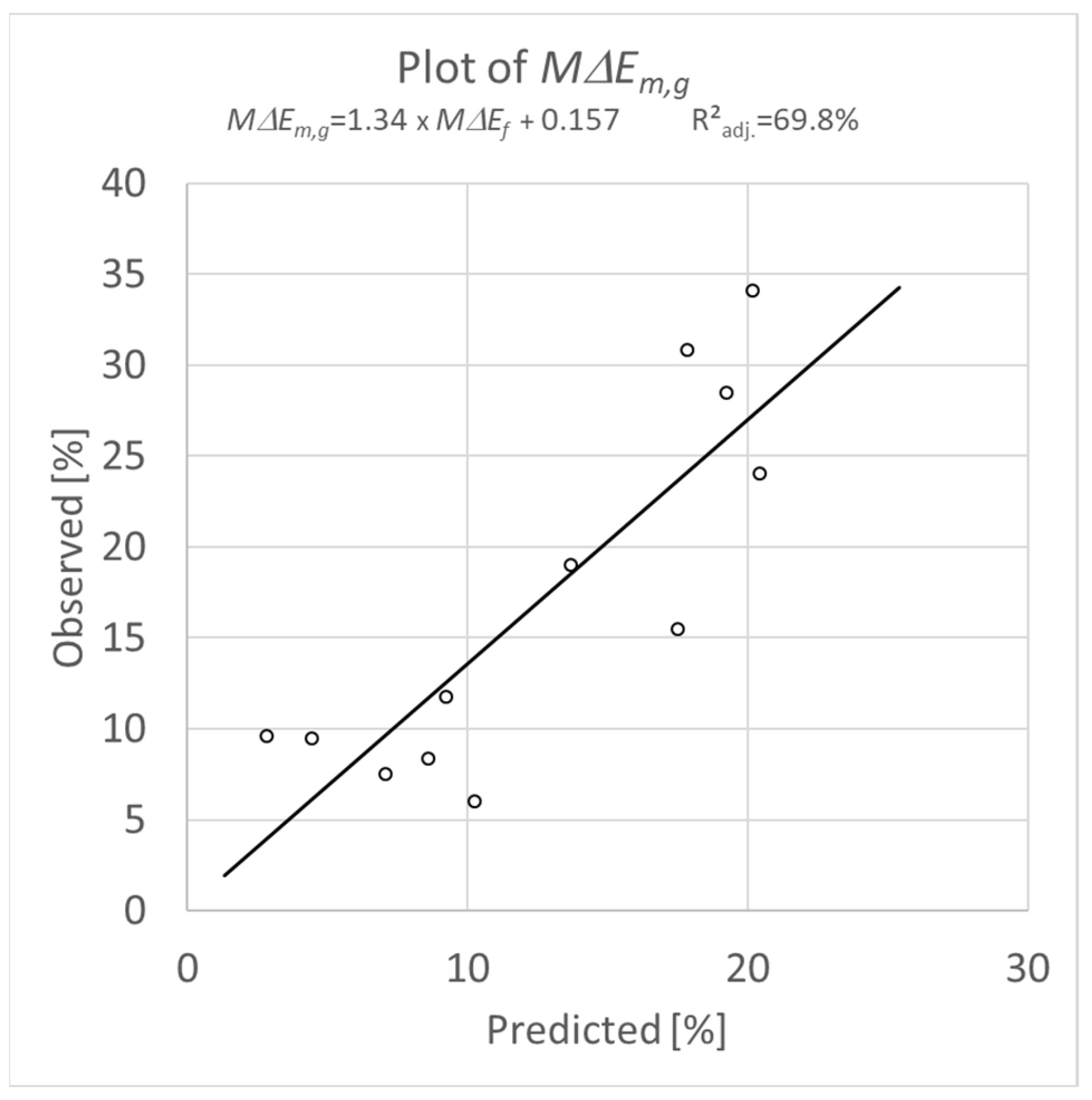
4. Assessment of Reduction in MOE
4.1. Dynamic Tests
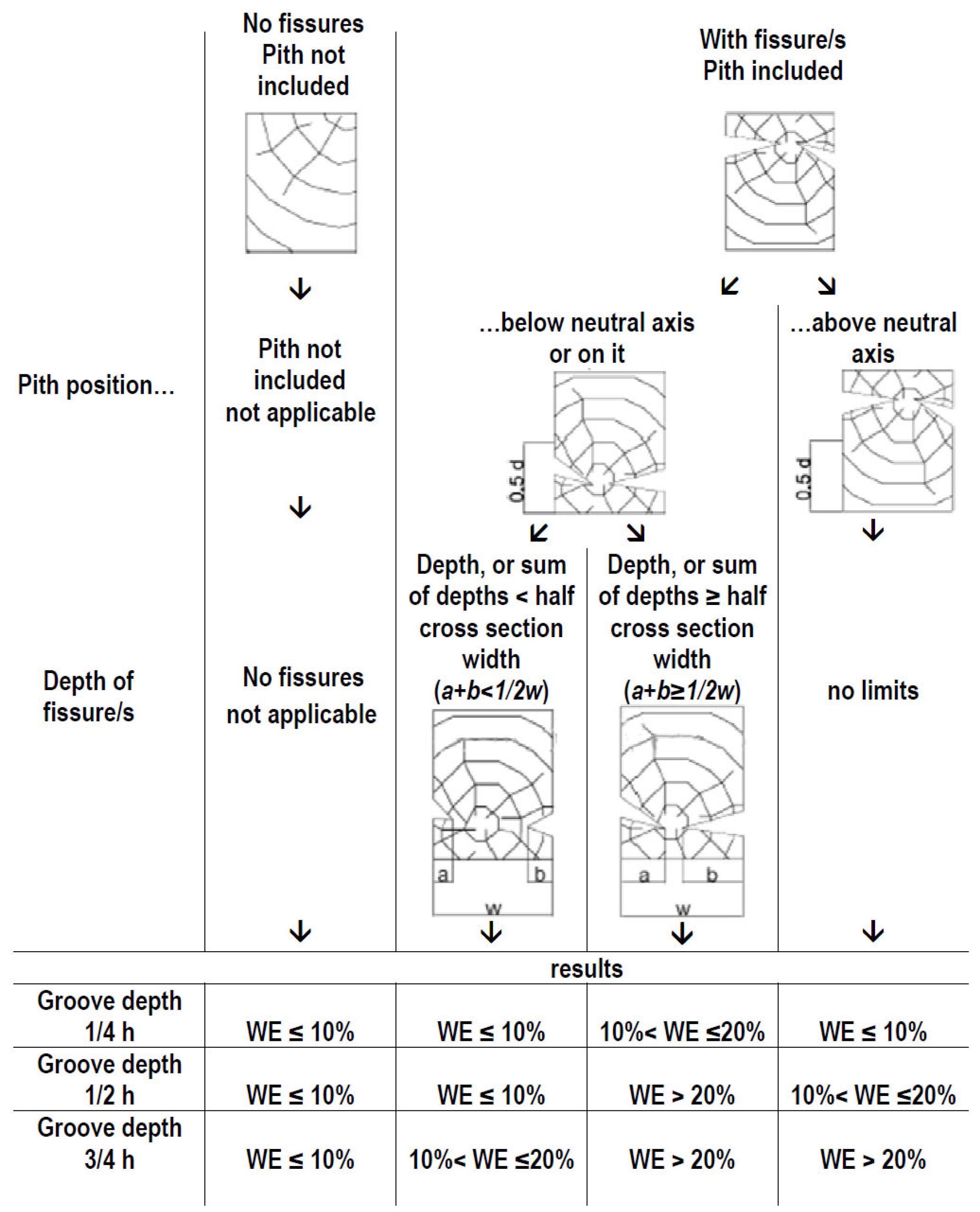
4.2. Visual Survey
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- IWC—ICOMOS Principles for the Preservation of Historic Timber Structures. 2017. Available online: https://www.icomos.org/images/DOCUMENTS/General_Assemblies/19th_Delhi_2017/Working_Documents-First_Batch-August_2017/GA2017_6-3-4_WoodPrinciples_EN_final20170730.pdf (accessed on 17 July 2023).
- Kasal, B.; Anthony, R.W. Advances in situ evaluation of timber structures. Prog. Struct. Eng. Mater. 2004, 6, 94–103. [Google Scholar] [CrossRef]
- Tampone, G. Mechanical Failures of the Timber Structural Systems. In From Material to Structure—Mechanical Behaviour and Failures of the Timber Structures; IIWC: Florence, Italy; Venice, Italy; Vicenza, Italy, 2007; p. 21. Available online: http://iiwc.icomos.org/assets/tampone.pdf (accessed on 16 April 2022).
- Palaia, L.; López, V.; Tormo, S.; Pérez, C.; Navarro, P. Assessment of Timber Structures in Service, by Using Combined Methods of Non-Destructive Testing Together with Traditional Ones. In Proceedings of the 9th International Conference on NDT of Art, Jerusalem, Israel, 25–30 May 2008; pp. 25–30. Available online: http://www.ndt.net/article/art2008/papers/060Palaia.pdf (accessed on 17 July 2023).
- Pinto, L. Inventory of Repair and Strengthening Methods Timber. Master‘s Thesis, University of Minho, Braga, Portugal, 2009. Available online: http://upcommons.upc.edu/pfc/bitstream/2099.1/7903/1/01.pdf (accessed on 17 July 2023).
- Stumes, P. Testing the Efficiency of Wood Epoxy Reinforcement Systems. Bull. Assoc. Preserv. Technol. 1975, 7, 2–35. [Google Scholar] [CrossRef]
- Piazza, M.; Riggio, M. Typological and Structural Authenticity in Reconstruction: The Timber Roofs of Church of the Pieve in Cavalese, Italy. Int. J. Archit. Herit. 2007, 1, 60–81. [Google Scholar] [CrossRef]
- Cavalli, A.; Cibecchini, D.; Togni, M.; Sousa, H.S. A review on the mechanical properties of aged wood and salvaged timber. Constr. Build. Mater. 2016, 114, 681–687. [Google Scholar] [CrossRef]
- Tampone, G. Il Restauro Delle Strutture di Legno; Hoepli: Milano, Italy, 1996; pp. 305–325. [Google Scholar]
- Gentile, C.; Svecova, D.; Rizkalla, S.H. Timber beams strengthened with GFRP bars: Development and applications. J. Compos. Constr. 2002, 6, 11–20. [Google Scholar] [CrossRef]
- Rotafix, Timber Resin Splice. 2018. Available online: http://rotafix.co.uk/wp-content/uploads/2016/09/TRS-Brochure.pdf (accessed on 17 July 2023).
- Alhayek, H.; Svecova, D. Flexural Stiffness and Strength of GFRP-Reinforced Timber Beams. J. Compos. Constr. 2012, 16, 245–252. [Google Scholar] [CrossRef]
- Arriaga, F.; Iñiguez-Gonzalez, G.; Esteban, M.; Fernandez-Cabo, J.L. Simplified model for strength assessment of timber beams joined by bonded plates. J. Mater. Civ. Eng. 2013, 25, 980–990. [Google Scholar] [CrossRef]
- Salčin, M.; Džubur, Ž.; Ćatović, F.; Džiho, E. Strengthening Timber Structure with Fiber Reinforced Polymer—An Overview. In New Technologies, Development and Application V. NT 2022; Lecture Notes in Networks and Systems; Karabegović, I., Kovačević, A., Mandžuka, S., Eds.; Springer: Cham, Switzerland, 2022; Volume 472. [Google Scholar] [CrossRef]
- Schober, K.U.; Rautenstrauch, K. Post-strengthening of timber structures with CFRP’s. Mater. Struct. 2007, 40, 27–35. [Google Scholar] [CrossRef]
- Duarte, A.; de Oliveira Negrão, J.; Cruz, H.; Balseiro, A. Bending strength of timber beams rehabilitated with reinforced epoxy mortar plates. J. Struct. Eng. 2008, 34, 792–800. [Google Scholar] [CrossRef]
- Alam, P.; Ansell, M.; Smedley, D. Mechanical repair of timber beams fractured in flexure using bonded-in reinforcements. Compositesb 2009, 40, 95–106. [Google Scholar] [CrossRef]
- Jankowski, L.J.; Jasieńko, J.; Nowak, T.P. Experimental assessment of CFRP reinforced wooden beams by 4-point bending tests and photoelastic coating technique. Mater. Struct. 2010, 43, 141–150. [Google Scholar] [CrossRef]
- Cavalli, A.; Togni, M. The influence of routed grooves on the bending behaviour of old timber beams. Adv. Mater. Res. 2013, 778, 393–401. [Google Scholar] [CrossRef]
- EN 408 Timber structures. Structural Timber and Glued Laminated Timber; Determination of Some Physical and Mechanical Properties; European Committee for Standardization: Brussels, Belgium, 2012. [Google Scholar]
- Giordano, G. Tecnologia del Legno, 2nd ed.; UTET: Torino, Italy, 1981; pp. 314–315. [Google Scholar]
- Kollman, F.; Krech, H. Dynamische Messung der elastischen Holzeigenschaften und der Dampfung. Holz Roh-Werkst. 1960, 18, 41–54. [Google Scholar] [CrossRef]
- Kolsky, H. Stress Waves in Solids; Dover Publication: New York, NY, USA, 1963; pp. 74–141. [Google Scholar]
- Arriaga, F.; Herrero, M.; Álvarez, R.; Maldonado, I. Efecto de las gemas en la resistencia a flexión de piezas enterizas de madera. The effect of wanes on the bending strength of solid timber beams. Mater. Construcc. 2007, 57, 61–76. [Google Scholar] [CrossRef]
- Togni, M.; Cavalli, A.; Mannozzi, D. Chestnut: From coppice to structural timber. The case study of “Uso Fiume” beams sampled in Liguria. J. Agric. Eng. 2013, 44, 1–9. [Google Scholar] [CrossRef]
- Ranta-Maunus, A. Round Small-Diameter Timber for Construction. Final Report of Project. 1999. Available online: https://www.vttresearch.com/sites/default/files/pdf/publications/1999/P383.pdf (accessed on 17 July 2023).
- Cavalli, A.; Togni, M. How to improve the on-site MOE assessment of old timber beams combining NDT and visual strength grading. J. Nondestruct. Test. Eval. 2013, 28, 252–262. [Google Scholar] [CrossRef]
- JCSS. Probabilistic Model Code Part 3: Resistance Models. 3.5.3.3. 2006, p. 7. Available online: https://www.jcss-lc.org/publications/jcsspmc/timber.pdf (accessed on 17 July 2023).
- Bodig, J.; Jayne, B.A. Mechanics of Wood and Wood Composites; Van Nostrand Reinhold: New York, NY, USA, 1982; pp. 103–104. [Google Scholar]
- Andrews, M. Which acoustic speed? In 13th International Symposium on Non-Destructive Testing of Wood; University of California: Berkeley, CA, USA, 2002; pp. 159–165. [Google Scholar]



| Beam No. | Height d (cm) | Width w (cm) | Fissure s | Pith Position h/d | Jy,25/Jy (%) | Jy,50/Jy (%) | Jy,75/Jy (%) | Em,g25/Em,g0 (%) | Em,g50/Em,g0 (%) | Em,g75/Em,g0 (%) | MΔEm,g (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 15.0 | 13.6 | 0.58 | 0.44 | 96.9 | 96.6 | 96.3 | 85.3 | 81.0 | 82.9 | 19.0 |
| 2 | 18.3 | 16.3 | 0.28 | 0.48 | 97.6 | 97.1 | 97.0 | 101.5 | 91.9 | 90.5 | 9.51 |
| 3 | 22.3 | 16.5 | 0.22 | 0.70 | 97.1 | 96.7 | 96.5 | 95.9 | 91.2 | 90.4 | 9.60 |
| 4 | 23.8 | 21.0 | 0.49 | 0.53 | 98.1 | 97.7 | 96.8 | 96.1 | 74.4 | 65.9 | 34.1 |
| 5 | 23.0 | 20.0 | 0.28 | 0.45 | 98.0 | 97.6 | 96.6 | 94.9 | 94.0 | 94.2 | 6.00 |
| 6 | 21.0 | 18.6 | 0.00 | no pith | 97.4 | 97.1 | 96.8 | 95.5 | 92.3 | 91.7 | 8.35 |
| 7 | 21.8 | 17.6 | 0.57 | 0.43 | 97.6 | 97.3 | 97.3 | 75.0 | 72.4 | 71.5 | 28.5 |
| 8 | 26.8 | 21.8 | 0.44 | 0.47 | 98.2 | 97.9 | 97.0 | 92.5 | 95.2 | 93.0 | 7.51 |
| 9 | 27.6 | 22.0 | 0.23 | 0.52 | 98.2 | 97.9 | 97.7 | 99.7 | 88.2 | 89.0 | 11.8 |
| 10 | 26.4 | 20.2 | 0.52 | 0.52 | 98.0 | 97.7 | 97.5 | 92.7 | 88.6 | 75.9 | 24.1 |
| 11 | 24.9 | 17.6 | 0.54 | 0.45 | 99.0 | 98.5 | 98.3 | 82.8 | 75.9 | 69.2 | 30.8 |
| 12 | 25.8 | 18.6 | 0.38 | 0.49 | 97.8 | 97.3 | 97.0 | 102.4 | 98.7 | 84.5 | 15.5 |
| average | 231 | 187 | 0.38 | 0.50 | 97.8 | 97.4 | 97.1 | 92.9 | 87.0 | 83.2 | 17.1 |
| minimum | 160 | 136 | 0 | 0.43 | 96.9 | 96.6 | 96.3 | 75.0 | 72.4 | 65.9 | 6.00 |
| maximum | 276 | 220 | 0.58 | 0.70 | 99.0 | 98.5 | 98.3 | 102.4 | 98.7 | 94.2 | 34.1 |
| stand. dev. | 3.52 | 2.50 | 0.18 | 0.08 | 0.56 | 0.54 | 0.56 | 8.10 | 8.84 | 10.07 | 9.98 |
| Ef0 | Ef25 | Ef50 | Ef75 | El0 | El25 | El50 | El75 | Esw0 | Esw25 | Esw50 | Esw75 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Em.g0 | 0.83 (11.8) | 0.70 (14.8) | 0.60 (18) | |||||||||
| Em.g25 | 0.84 (11.2) | 0.70 (17.2) | 0.63 (18.9) | |||||||||
| Em.g50 | 0.85 (10.5) | 0.66 (16.5) | 0.55 (18.7) | |||||||||
| Em.g75 | 0.81 (11.9) | 0.68 (15.8) | 0.50 (19.4) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cavalli, A.; Mazzanti, P.; Riparbelli, L.; Togni, M. Strengthening of Ancient Timber Beams during Restoration Operations: Effect of Wood Cutting on Modulus of Elasticity. Forests 2023, 14, 1854. https://doi.org/10.3390/f14091854
Cavalli A, Mazzanti P, Riparbelli L, Togni M. Strengthening of Ancient Timber Beams during Restoration Operations: Effect of Wood Cutting on Modulus of Elasticity. Forests. 2023; 14(9):1854. https://doi.org/10.3390/f14091854
Chicago/Turabian StyleCavalli, Alberto, Paola Mazzanti, Lorenzo Riparbelli, and Marco Togni. 2023. "Strengthening of Ancient Timber Beams during Restoration Operations: Effect of Wood Cutting on Modulus of Elasticity" Forests 14, no. 9: 1854. https://doi.org/10.3390/f14091854
APA StyleCavalli, A., Mazzanti, P., Riparbelli, L., & Togni, M. (2023). Strengthening of Ancient Timber Beams during Restoration Operations: Effect of Wood Cutting on Modulus of Elasticity. Forests, 14(9), 1854. https://doi.org/10.3390/f14091854







