Next Article in Journal
Phenological Changes of Woody Plants in the Southern and Northern Regions of Nanling Mountains and Their Relationship with Climatic Factors
Next Article in Special Issue
Short-Term Tree-Ring Series of Pinus hartwegii Lindl. Taken at Ground Level Correlate to Normalized Difference Vegetation Index Series
Previous Article in Journal
Climate Change-Driven Cumulative Mountain Pine Beetle-Caused Whitebark Pine Mortality in the Greater Yellowstone Ecosystem
Previous Article in Special Issue
Distinct Impact of Drought on Radial Growth at Different Heights and Parts of Populus euphratica in the Oasis at the Hinterland of the Taklimakan Desert
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Forests
Volume 14
Issue 12
10.3390/f14122362
forests-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Evaluating the Effect of Vegetation Index Based on Multiple Tree-Ring Parameters in the Central Tianshan Mountains

by
Jinghui Song
1,2,3,
Tongwen Zhang
4,*,
Yuting Fan
2,3,*,
Yan Liu
3,
Shulong Yu
2,3,
Shengxia Jiang
2,3,
Dong Guo
2,3,
Tianhao Hou
2,3,5 and
Kailong Guo
2,3,5
1
College of Geography and Remote Sensing Sciences, Xinjiang University, Urumqi 830046, China
2
Key Laboratory of Tree-Ring Physical and Chemical Research of China Meteorological Administration, Urumqi 830002, China
3
Institute of Desert Meteorology, China Meteorological Administration, Urumqi 830002, China
4
Xinjiang Climate Center, Urumqi 830002, China
5
School of Geography and Tourism, Xinjiang Normal University, Urumqi 830054, China
*
Authors to whom correspondence should be addressed.
Forests 2023, 14(12), 2362; https://doi.org/10.3390/f14122362
Submission received: 1 October 2023 / Revised: 26 November 2023 / Accepted: 28 November 2023 / Published: 30 November 2023
(This article belongs to the Special Issue Response of Tree Rings to Climate Change and Climate Extremes)
Browse Figures
Versions Notes

Abstract

:
Combining tree ring data with remote sensing data can help to gain a deeper understanding of the driving factors that influence vegetation change, identify climate events that lead to vegetation change, and improve the parameters of global vegetation index reconstruction models. However, it is currently not well understood how climate change at different elevations in the central Tianshan Mountains affects radial tree growth and the dynamics of forest canopy growth. We selected Schrenk spruce (Picea schrenkiana) tree core samples from different elevations in the central Tianshan Mountains. We analyzed the relationships of various tree-ring parameters, including tree-ring width, maximum latewood density (MXD), and minimum earlywood density (MID) chronologies, with 1982–2012 GIMMS (Global Inventory Modelling and Mapping Studies) NDVI (Normalized Difference Vegetation Index), 2001–2012 MODIS (moderate resolution imaging spectroradiometer) NDVI, and meteorological data. (1) There were strong correlations between tree-ring width chronologies and the lowest temperatures, especially in July. Tree-ring width chronologies at higher altitudes were positively correlated with temperature; the opposite pattern was observed at lower altitudes. MID chronologies were positively correlated with July temperature in high-altitude areas and mean temperature and highest temperature from May to September in low-altitude areas, and negatively correlated with precipitation during this period. MXD chronologies were mainly negatively correlated with precipitation. MXD chronologies were mainly positively correlated with temperature in April and May. (2) The correlations between MXD chronologies at each sampling point and NDVI in each month of the growing season were strong. Both MID and MXD chronologies were negatively correlated with GIMMS NDVI in July. The overall correlations between tree-ring parameters and MODIS NDVI were stronger than the correlations between tree-ring parameters and GIMMS NDVI in high-altitude areas; the opposite pattern was observed in low-altitude areas. Drought stress may be the main factor affecting tree ring parameters and NDVI. In the future, we should combine tree ring parameters with vegetation index to investigate a larger scale of forests.

1. Introduction

The normalized difference vegetation index (NDVI) and tree-ring parameters are often used markers in research on the ecology of forests and their reactions to climate change [1,2,3,4,5]. Tree-ring characteristics give long-term historical information on tree growth processes and their reactions to environmental changes at an annual time resolution by integrating both biological (ecophysiological responses) and non-biological (climate and site circumstances) components [6,7,8]. However, obtaining tree-ring data for a larger forest area requires a significant amount of effort and resources [9].
As remote sensing technology has advanced, satellite remote sensing data inversion of the vegetation index has become an effective means to quantitatively present global and regional vegetation coverage and growth changes [10]. Currently, there are more than 40 types of remote sensing vegetation indices and some types of product sets, such as NDVI, Enhanced Vegetation Index (EVI), etc. [11,12,13]. Among them, NDVI is a popular vegetation index for remote sensing and has been widely applied in research on regional vegetation coverage, vegetation growth status, vegetation productivity estimation, and extreme climate prediction [14,15,16,17]. MODIS (Moderate Resolution Imaging Spectroradiometer) NDVI is thought to be an enhancement of the AVHRR NDVI, with increased spatial resolution and chlorophyll sensitivity, elimination of atmospheric water vapor interference, and adjustment of synthesis methods. It is an advancement and continuation of the AVHRR NDVI. The main advantages of NDVI data obtained from remote sensing satellite imagery include their accessibility, wide coverage, and temporal resolution [18,19,20]. However, the collection of NDVI data via remote sensing has a short history [21,22].
Photosynthesis in the vegetation canopy affects the production of plant carbohydrates and controls carbon storage in the woody parts of trees. This consequently influences the plants’ radial growth. NDVI can accurately reflect vegetation greenness and photosynthetic activity [23,24]. The radial growth of trees reflects their growth status, and the width and density are the best indicators of radial growth [25,26]. The integration of tree-ring data with NDVI permits studies of tree-ring ecology from individual trees or forests to be conducted at a regional scale. This has ramifications for ecological research and forest management as well as improving our knowledge of how forests grow and adapt to climate change. Currently, many NDVI studies based on tree ring data have been carried out by researchers and yielded different results. The initial focus of the research was primarily on combining coarse-resolution NDVI with tree ring data. For instance, studies have shown a relationship in regions south of 40° latitude between tree ring width and the NDVI in the early spring and late autumn. Nonetheless, there is a relationship between summer NDVI and tree ring width in regions north of 40° latitude [27]. On a growing season scale in arid regions of Asia, approximately 77.4% of the variation in NDVI is found to be synchronous with changes in tree-ring width parameters [28]. However, coarse-resolution NDVI tends to overlook the heterogeneity of landscape patterns. It could cause the spatial scale of the NDVI and tree ring chronologies to diverge, thereby weakening the correlation between the two. Tree-ring growth and annual fluctuations in the high spatial resolution (1.21 km2) NDVI were found to be positively correlated [29]. Bhuyan et al. compared the response of tree growth using a random forest model between MODIS NDVI and GIMMS3g NDVI [30]. The findings demonstrated that the MODIS NDVI growth signal outperformed the GIMMS3g NDVI in coniferous forest areas. Vicente-Serrano et al. showed that while there may be variations in the association between tree rings and NDVI at different spatial resolutions, there are similarities in the patterns of correlation between tree rings and NDVI over a range of NDVI periods and months. The spatial resolution of the NDVI sequence is mostly insensitive to the consistency of tree rings and NDVI [31]. Furthermore, Brehaut et al. discovered that tree rings and the GIMMS3g NDVI (8 km) and the Alaska Composite (1 km) have a poor association, suggesting that elevation may be the cause of their erratic correlation [32].
Elevation primarily influences the relationship between tree ring and NDVI through temperature and precipitation. Coulthard et al. found that in high-elevation forest areas, there are no common climatic driving factors between the NDVI and tree ring chronologies. However, standardized tree ring chronologies and NDVI are closely correlated with low-elevation dry regions that are dominated by grasslands and shrublands [33]. In addition, Wen et al. found that as the altitude increases, the positive correlation between tree ring width and NDVI gradually decreases. The primary component causing this association could be drought stress [34]. Yuan et al. discovered that as altitude rises, the relationship between the canopy and trunk progressively becomes less significant. In high mountain regions, the correlation coefficient is 0.371; in valley regions, it is 0.413; in desert regions, it is 0.583 [35]. In conclusion, a variety of factors can affect how radial tree growth and vegetation canopy interact. Additionally, the indicators that show a significant relationship between tree ring and NDVI index vary in different regions. Therefore, it is necessary to use multiple tree ring parameters and NDVI with different spatial resolutions for research purposes.
To investigate how the middle Tianshan Mountains’ environment affects tree canopy and radial growth, we collected data from the Schrenk spruce (Picea schrenkiana) in Shawan Forest Farm. We established minimum earlywood density (MID), maximum latewood density (MXD), and tree-ring width using tree-ring samples gathered at eight distinct altitudes to explore how vegetation changes in response to climate change and how tree rings respond to it. Specifically, we aimed to (1) analyze the relationship between tree growth and the vegetation canopy, as well as the climate parameters that restrict tree growth, using climate variables related to tree-ring parameters; (2) evaluate differences in the relationships of vegetation index with different spatial resolutions with tree-ring width, MXD, and MID chronologies. Our findings provide new insights into ecological and environmental changes in the Tianshan Mountains’ center region and will aid predictions of future changes in this region.

2. Materials and Methods

2.1. Study Area

The study location is situated in Shawan County’s STG Forest location, in the middle of the Tianshan Mountains (Figure 1). In this region, the north has lower topography, while the south has higher terrain. The southern part is dominated by the Yilianhabierga Mountains, a branch of the Tianshan Mountains, and the northern part comprises the Gurban Tongut Desert. The area has a continental temperate arid climate, with cold winters, hot summers, short spring and autumn seasons, large temperature differences between winter and summer, abundant sunshine, low precipitation, and high evaporation. The primary forest is mainly concentrated on the windward slopes of the middle mountain belt at an elevation of 1700–2600 m. The vertical zonation of vegetation is quite distinct; grasses and shrubs are the main vegetation types in the forest. The soil is black-brown forest soil. P. schrenkiana forests are the predominant and extensively distributed type of forest on the Chinese northern slopes of the Tianshan Mountains.

2.2. Tree-Ring Data

We developed tree-ring width, MXD, and MID from P. schrenkiana. The sampling points were located in the STG Forest Area of Sha Wan City. The tree-ring samples were gathered during three separate periods from late August 2012 to August 2014. In 2012, one sample point was collected in the upper tree line area of the STG Forest Area. Samples were collected from five additional points at altitudes between 1740 and 2300 mm in the STG in late September 2013 considering the preliminary samples that had been collected at the top elevation of the STG in 2012 and the distribution of existing sampling points in Shaw Wan Forest Farm. The sampling points in STG had thin soil layers and steep slopes and lacked continuous slopes. The sampling points were mainly located on the steep slopes on the west side of the valley. High-altitude forests were covered in snow when samples were taken. The terrain in the STG Forest Area is steep; the thick snow, coupled with the slick roads, increases the difficulty of collecting tree samples between 2400 and 2500 m. Therefore, samples were taken from two further sites (stg 7 and stg 8) in the high-altitude forest area of STG in August 2014. The information on sampling points is shown in Table 1.
According to normal dendrochronological techniques, the core samples were transferred back to the laboratory for drying, fixing, grinding, and visual age determination [36]. With a Velmex Measuring System, the sanded cores were measured at a resolution of 0.001 mm while being viewed under a binocular microscope. We used the COFECHA application to ensure the quality of the cross-dating results, identify false rings and missing rings, eliminate errors in dating and measurement, remove unsuitable samples, ensure that the formation year of each tree ring is accurately determined, and keep the necessary documentation of this process [37].
The previously measured width samples were then desugared and defatted, and the samples were cut into trapezoidal blocks according to the angle of the wood fiber direction and fixed on the board. Using the DendroCut instrument, the core sample was cut into thin slices of 1 mm. Finally, X-ray transmission imaging was used to produce the film. The Dendro 2003 density measurement system was used to measure tree ring density values. When measuring the density of the overlapping sections, multiple tree rings were marked on the paper to indicate the overlapping part being measured and compared with the corresponding position on the test sample, in order to identify the overlapping tree rings and connect the segmented core samples. Finally, a data file is generated for each core sample [38,39].
Ultimately, the tree growth pattern was fitted and eliminated using the ARSTAN chronology development program by employing a negative exponential function in the fitting process. Ultimately, standardized chronologies (STD), differenced chronologies (RES), and autoregressive chronologies (ARS) for three tree ring parameters were established. This study is limited to a standardized tree-ring chronology of 8 sampling points. We further investigated using tree-ring width standardized chronologies, tree-ring maximum density standardized chronologies, and tree-ring minimum density standardized chronologies [40]. The sub-sample signal strength (SSS) greater than 0.85 was used to determine the reliable length of the chronology [41].

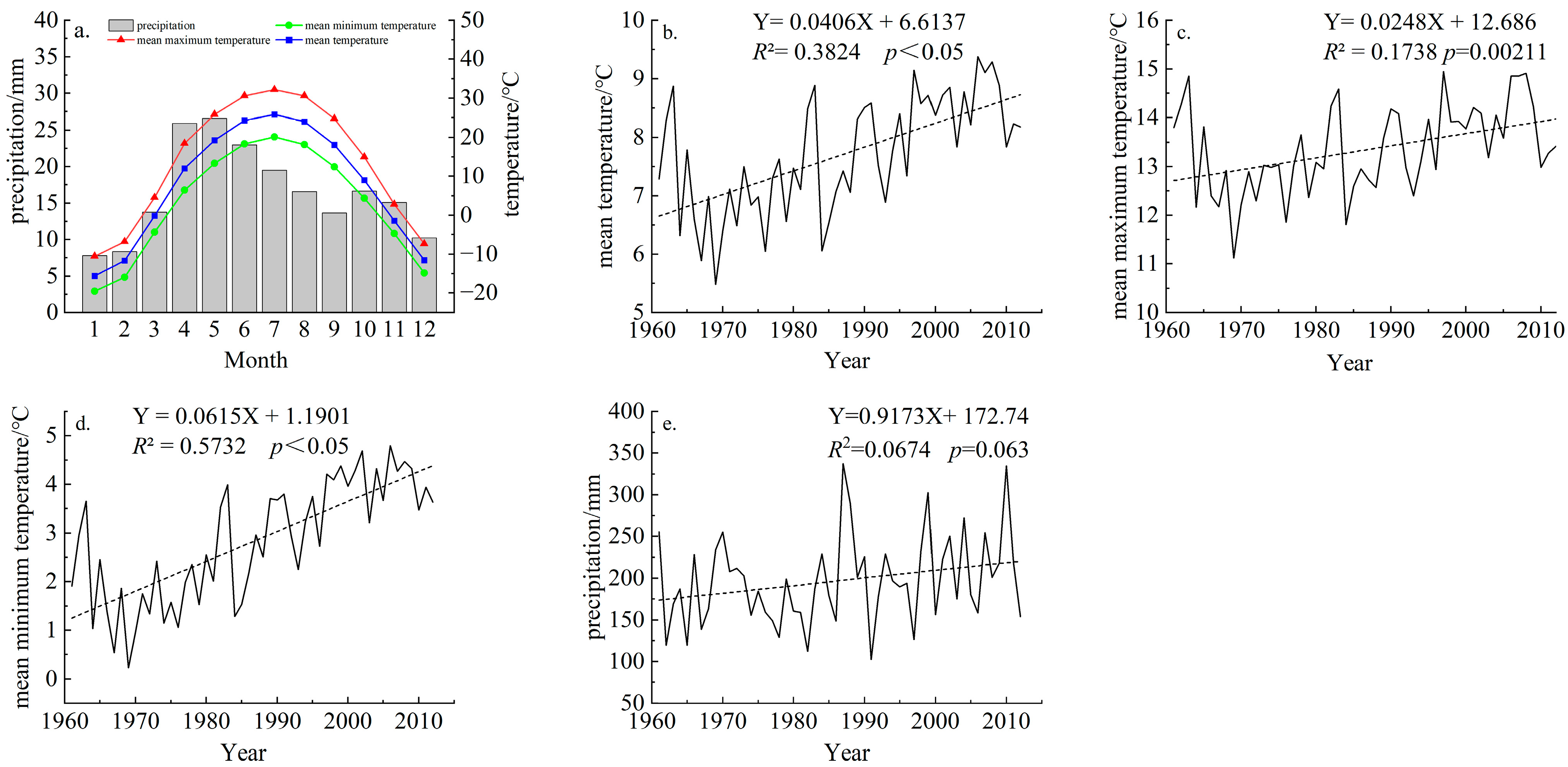
2.3. Meteorological Data

Shawan meteorological stations provided the meteorological data used in this study. (44°20′ N; 85°37′ E; altitude: 523 m a.s.l.; 48 km away from STG), which was close to the study area. We used precipitation (PCP), mean temperature (Tmean), mean maximum temperature (Tmax), and mean minimum temperature (Tmin) per month from 1961 to 2012. The above climatic data were from the Xinjiang Climate Center.
Analysis of changes in monthly PCP and average temperature at Shawan Meteorological Station (Figure 2) revealed that the average temperature in the region from 1961 to 2012 was approximately 7.69 °C. The average temperature of the hottest month (July) was 25.89 °C. The variation between the highest and lowest values for many years was only approximately 5 °C, indicating that the temperature was relatively stable. The average temperature in the coldest month (January) was −15.54 °C. The temperature difference was approximately 10 °C for many years, and changes in temperature over the years were significant. The average annual PCP was approximately 196 mm, and most PCP fell between April and July during the spring and summer seasons. Variation in PCP during the spring and summer seasons was much greater than that during the autumn and winter seasons.

2.4. NDVI Data

We employed the Moderate Resolution Imaging Spectroradiometer (MODIS) NDVI and the Global Inventory Modeling and Mapping Studies 3g (GIMMS3g) NDVI, two NDVI datasets with varying spatial resolutions.
MODIS data were obtained from the MODIS products (MOD13Q1 product in HDF format, 16 days, 250 m, strip number: h24v04, http://glovis.usgs.gov/, accessed on 16 October 2021). Compared with AVHRR, MODIS has a narrower spectral channel and lacks the water vapor absorption band in the near-infrared band, which reduces the effects of water vapor and improves the ability to detect sparse vegetation. We analyzed data from 2001 (the first complete year of NDVI data) until 2012, the last year of our assembled tree-ring dataset.
With a temporal resolution of 15 days and a spatial resolution of 8 km, GIMMS3g is produced with the Advanced Very High Resolution Radiometer (AVHRR). This yields two maximum-value composites per month and 24 observations annually (http://ecocast.arc.nasa.gov/data/pub/gimms/3g.v0/, accessed on 16 October 2021). These data have undergone radiation correction and geometric coarse correction. Compared with GIMMS NDVI data, the improved GIMMS NDVI3g data have undergone satellite orbit drift correction, which eliminates common associations between the solar zenith angle and NDVI time series and improves the calibration procedure. The GIMMS3g NDVI data were first collected in July 1981. We analyzed data from 1982 (the first complete year of NDVI data) to the end of 2012 to maximize the overlap with the assembled tree-ring dataset. The latitude and longitude of each of the tree-ring sites were used to select corresponding pixels from the GIMMS3g and MODIS NDVI datasets.
Figure 3 shows that the values of GIMMS NDVI were highest from May to September, with a June peak. The annual average change was relatively stable. The MODIS NDVI values were higher at each sampling point than the GIMMS NDVI values; MODIS NDVI values were highest from May to September and peaked in July. As the elevation increased, the MODIS NDVI values gradually decreased (Figure 3).

2.5. Statistical Analyses

The MOD13Q1 product first uses MRT V.4810 software to complete projection transformation and data format conversion and extract NDVI. The image output format is TIFF. Then, ArcGIS10.8 is used to batch clip the study area and exclude outliers, and finally, ArcGIS is used to synthesize monthly average NDVI values using the maximum synthesis method and extract the data to Excel v2019. The GIMMS NDVI3g product first uses Matlab R2022b to convert and project the downloaded NC data into a .tif format for image output. The study area is batch-cropped using ArcGIS, and the maximum composite method is used to extract the monthly average NDVI values of the study area. All data products use the Albers equal-area conic projection.
To analyze the relationships between connections between tree-ring at different altitudes and NDVI, using Pearson correlation analysis, the relationships between MXD, tree-ring width, and remote sensing vegetation index for all the sampling points were assessed. To determine whether climate had an impact on the relationship between tree-ring and NDVI, the relationships between climate and several tree growth indicators were examined. Given that the growth of trees might be affected by the climate conditions of the previous year, we conducted a monthly correlation analysis of the monthly Tmean, monthly mean Tmin, monthly mean Tmax, and PCP from April of the previous year to October of the current year, tree-ring width, MXD and MID, GIMMS NDVI, and MODIS NDVI.

3. Results

3.1. Statistical Characteristics of Chronologies

Table 2, Table 3 and Table 4 show that the tree-ring width normalized chronologies had mean sensitivity values ranging from 0.11 to 0.27. Below 2200 m, the average sensitivity is higher than the average sensitivity beyond this altitude. This indicates that tree-ring width chronologies in low-altitude regions are more sensitive to changes in climate factors. The mean sensitivity of MID was lower than that of tree-ring width chronologies. The MXD chronologies show a lower mean sensitivity and standard deviation in comparison to the MID chronologies. No significant changes in the mean sensitivity of the three chronologies with elevation were observed.
The first-order autocorrelation (AC1) between tree-ring width and MID chronologies was relatively high, and values were greater than 0.75 for all sampling points, with the exception of stg 4, stg 5, and stg 6. This suggests that the previous year’s climate had a significant impact on tree growth, with high-altitude locations experiencing a longer-lasting effect on tree growth than low-altitude ones. However, the AC1 of MXD chronologies was lower compared with that of the other two chronologies, and values were relatively small in stg 4, stg 5, and stg 6. This indicates that the MID and tree-ring width of this year’s tree rings are more influenced by changes in the previous year’s climate characteristics than by the MXD, and the effect on tree-ring maximum density was greater in low-altitude regions than in high-altitude regions.
The signal-to-noise ratio is a statistical measure of the amount of environmental information contained in a sample, and it is generally considered good if it is greater than 4 [41]. In this study, the signal-to-noise ratio of tree-ring width chronologies ranged from 7.8 to 20, the signal-to-noise ratio of MID ranged from 4.7 to 16.3, and the signal-to-noise ratio of MXD ranged from 5.1 to 13.4. These ranges indicate that the chronologies contain a significant amount of climate information and are suitable for dendroclimatology research.
Expressed population signals (EPSs) of all chronology samples were greater than 0.85, and the highest EPS value was observed at sampling point stg 1, indicating that the sampled cores provide an accurate representation of the study area.

3.2. Effects of Temperature and Precipitation on Forest Growth

Climate factors during the previous growing season have a major impact on tree-ring growth. Considering the physiological characteristics of trees and the fact that elevation results in a drop in temperature [42], we conducted a correlation analysis of Climate data from April of the previous year to October of the present one with the standardized tree-ring chronology (Figure 4, Figure 5 and Figure 6).
The response of tree-ring width to Tmean, Tmin, and Tmax varied at different elevations. Overall, there were strong correlations between tree-ring width and Tmin. Reaching an extremely significant level of Tmin in July. Specifically, tree-ring width at higher elevations was positively linked with temperatures; the opposite pattern was observed at lower elevations (Figure 7a–c). Tree-ring width at upper elevations (stg 1, stg 7, and stg 8) responded positively to temperature factors in the previous spring and current year. Low-altitude tree-ring width (stg 5 and stg 6) responded negatively to temperature factors in the fall of the prior year and in the summer and fall of the current year.
However, the responses of tree-ring width in the forested zone to different temperature factors vary, especially the responses to Tmax and Tmin. The responses of stg 2 and stg 4 to the Tmin during the growing seasons, and their response to Tmax mostly shifted from positive to negative. This proves that at the same height, the impact of various temperature parameters on tree-ring width varies.
The responses of tree-ring to PCP differed at high and low elevations. There was a high correlation between the width of the tree rings at the upper forest boundary (stg 1, stg 7, and stg 8) and July PCP. By contrast, there was a significant positive relationship between May and September PCP in the previous year and September precipitation in the previous year, as well as tree-ring width at lower elevations.
From December to March of the previous year, MID was significantly negatively linked to temperature, indicating that low temperatures before the growing season favor the formation of higher MID. From April to May, there was an upward relationship between MID and temperature and an adverse connection with PCP. There was a large and robust association between the May temperature and the tree-ring width of stg 8.
In high-altitude areas, MID chronologies had a negative correlation with PCP throughout this time and a positive correlation with July’s Tmean and Tmax. In low-altitude areas, from May to September, there was a positive correlation between MID and temperature, and a negative correlation between MID and PCP (Figure 8). At every sampling location, MID showed a positive correlation with PCP in April and November of the preceding year and a negative correlation with PCP in July of that same year, as well as in May and July–September of the current year. Specifically, the correlations between MID in high-altitude areas (stg 1, stg 7, and stg 8) and Tmean in July were significant, and the correlations between MID chronologies and average temperature were weaker at other altitudes. Between April of the previous year and February of the present year, there was a negative correlation between the MID at stg 2 and the Tmin; there was a positive correlation with the minimum temperature from April to October of the current year, this correlation was particularly significant for Tmin s in May and June. The MID of all sampling sites was negatively correlated with the Tmax in December of the previous year and positively correlated with the Tmax in July. With the exception of stg 3, MID was positively correlated with the Tmax from March to May of the current year. Specifically, MID in high-altitude areas was positively correlated with Tmax from March to October, and this correlation was significant in July; the correlations between MID in low-altitude areas and Tmax were weak (Figure 8).
Except for November, MXD was mainly negatively correlated with PCP (Figure 9a–c) and positively correlated with temperature factors in April and May of the current year, and negatively correlated with PCP during the same period. MXD chronologies at high altitudes were significantly positively correlated with the Tmean in April of the current year. MXD was negatively weakly correlated with the Tmean from November of the previous year to February of the current year and positively weakly correlated with the temperature from April to October of the current year (Figure 9).
Statistical analysis of NDVI and climate data (monthly Tmean, monthly Tmax, monthly Tmin, and monthly PCP) for the 12 months revealed variation in the correlations between NDVI and climate data (Figure 10 and Figure 11). Overall, the effect of temperature and PCP from the previous year on the GIMMS NDVI from April to July was weak and not statistically significant. In April, the GIMMS NDVI and temperature showed a strong positive association, with the Tmax showing an especially significant connection. In May and June, the influence of temperature on the GIMMS NDVI was low. A remarkable positive connection was seen between the May GIMMS NDVI and the April–May PCP. Both the July GIMMS NDVI and Tmean and Tmax in May, as well as the July GIMMS NDVI and Tmin in May and June, showed a highly significant negative connection. A statistically significant positive connection was seen between the July GIMMS NDVI and the May PCP. The GIMMS NDVI for August of the previous year showed a strong positive association with the April temperature, and significant negative correlations of GIMMS NDVI with temperature in April of the current year and PCP in November of the previous year. September GIMMS NDVI showed an important positive relationship with PCP of the current year in August and a significant negative correlation with the Tmin of the previous year in August. There were significant positive correlations between October NDVI and the temperature of the previous year from April to June and the temperature of the current year from February to March and August. Additionally, there was a significant opposite correlation between the October NDVI and the June and September PCP of the previous year. There were significant positive correlations between May to August GIMMS NDVI with the Tmean and Tmax of the previous year in August; there was also a highly significant positive correlation between May to August GIMMS NDVI and PCP in April.
MODIS NDVI at high altitudes (stg 1, stg 7, stg 8, and stg 2) was correlated with temperature and PCP (Figure 11). May MODIS NDVI was significantly positively correlated with April PCP. July MODIS NDVI was significantly negatively correlated with April and July temperatures of the previous year. For stg1 and stg 7, July MODIS NDVI was significantly positively correlated with October temperatures of the previous year and significantly negatively correlated with the highest temperature in May of the same year; July MODIS NDVI was also positively correlated with May PCP of the same year. Among high-altitude sampling points, August MODIS NDVI was weakly correlated with temperature but significantly positively correlated with June PCP. The correlation between May to August MODIS NDVI and temperature was weak. Only MODIS NDVI at stg 1 was significantly negatively correlated with Tmean and Tmin of April in the current year. In the low-altitude region, April MODIS NDVI was significantly negatively correlated with January average temperature and Tmin. The correlation between April MODIS NDVI and PCP was weak and not significant. October MODIS NDVI was highly significantly negatively correlated with May temperatures of the current year, and its correlation with PCP was weak.

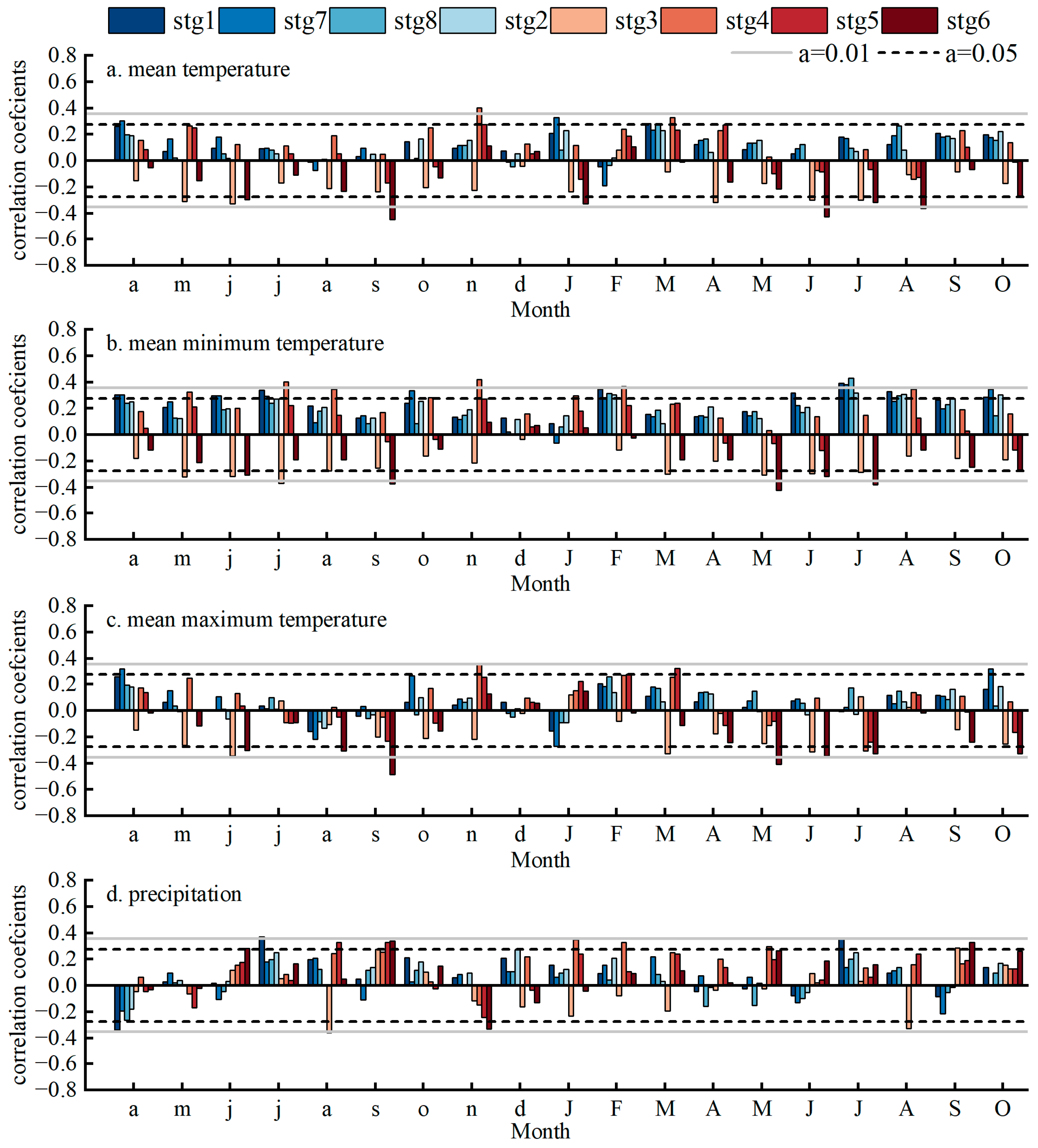
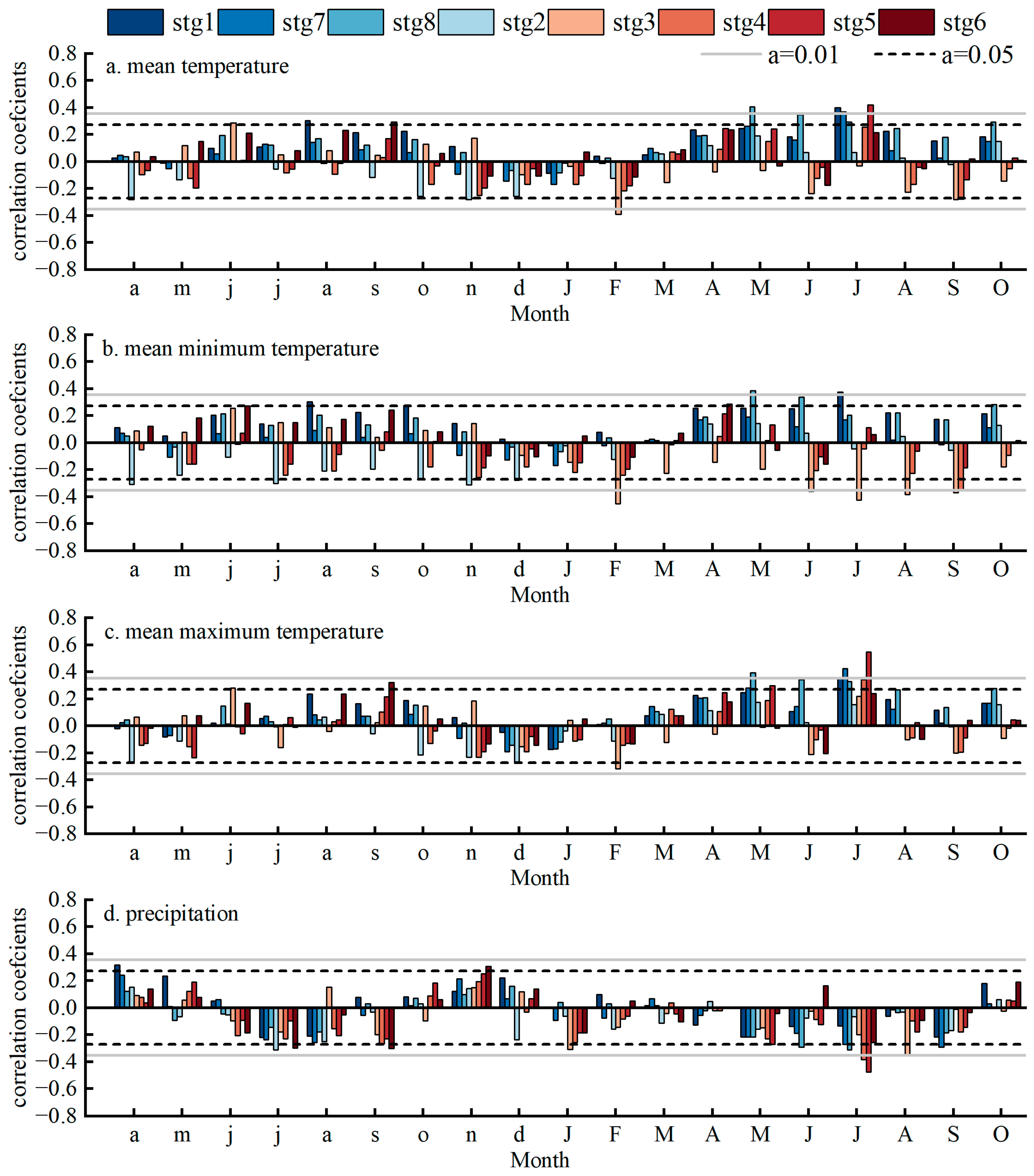
3.3. Relationships between Tree-Ring Parameters and NDVI

Figure 12 shows the correlations of tree-ring width, MXD, and MID chronologies with GIMMS NDVI and MODIS NDVI at different altitudes. Overall, the tree-ring width at all sampling sites was positively correlated with the GIMMS NDVI in July and December of the previous year and MODIS NDVI in February of the current year. The MID chronologies had a significant association with the MODIS NDVI of June of the past year and March of the current year, and a negative correlation with the GIMMS NDVI of October–December of the previous year and June to August of the current year. At each site, The GIMMS NDVI in January to February, July to August, and the growing season (May to August) showed negative correlations with the MXD chronologies, whereas the MODIS NDVI in June of both the prior and current year showed positive correlations.
There was a major positive association between tree-ring width at low altitudes (stg 4 and stg 5) and the GIMMS NDVI in October of that prior year, July of this present year, and during the growing period (May to August) of the current year. (Figure 12a). The response of tree-ring width to GIMMS NDVI at high altitudes (stg 1, stg 7, and stg 9) was not significant; however, in December of the prior year, there was a strong positive association between tree-ring width and GIMMS NDVI. Figure 12c illustrates the considerable negative correlation between GIMMS NDVI and MID chronologies at low altitudes in October of the preceding year and June to July of the current year. In January and February of this year, there was a substantial negative correlation between the MXD chronologies and the GIMMS NDVI (Figure 12e). MID and MXD chronologies at high altitudes responded weakly to GIMMS NDVI; highly significant correlations between MID chronology and GIMMS NDVI in April of the previous year and between MXD chronology and GIMMS in July of the current year were only observed at stg 1. Tree-ring parameters were more strongly correlated with MODIS NDVI than GIMMS NDVI at higher elevations. Tree-ring width at high altitudes (stg 1 and stg 7) was significantly positively correlated with MODIS NDVI in July (Figure 12b), and MID and MXD chronologies were significantly positively correlated with MODIS NDVI in June of the previous year (Figure 12d,f). However, the response of tree-ring parameters to MODIS NDVI and GIMMS NDVI differed in low-altitude areas. Tree-ring width and MID chronologies were significantly negatively correlated with MODIS NDVI in November of the previous year, and MXD chronologies were significantly positively correlated with MODIS NDVI in June of the current year. This indicates that the relationships between vegetation index with different spatial resolutions and tree-ring parameters varied with altitude. In high-altitude areas, the relationships between tree-ring parameters and MODIS NDVI were stronger than the relationships between tree-ring parameters and GIMMS NDVI; the opposite pattern was observed in low-altitude areas.

4. Discussion

4.1. Factors Affecting the Relationships between Tree-Ring Parameters and NDVI

This study revealed a correlation between monthly climatic parameters and the tree-ring width, MXD, and MID chronologies at various altitudes. The correlations between tree-ring width chronologies and Tmin were generally strong; the positive correlations between tree-ring width chronologies at high altitudes and Tmin in July were highly significant. The growth of tree rings requires suitable temperatures. In the research region, higher average low temperatures in July encourage photosynthesis in trees, which raises net nutrient accumulation, promotes cambial cell division, and ultimately causes the construction of larger tree rings. Higher temperatures during the growing season also accelerate the melting of ice and snow, which provides sufficient water for tree growth. Lower average temperatures in July can decrease the photosynthesis of trees, hinder the division of cambial cells, and even cause freezing or frost damage to trees, which results in narrower tree rings [43,44]. The tree-ring width chronology of stg 3 was negatively correlated with temperature. This might stem from the location of the sampling site in the PCP zone of the middle mountain belt on the northern slope of the Tianshan Mountains. The water and thermal conditions vary greatly in this region. Higher temperatures in this area lead to a decrease in soil moisture, an increase in the respiration of trees at night, a decrease in net photosynthesis, and ultimately the occurrence of narrower tree rings. MID and MXD chronologies were positively correlated with the temperature in the early growing season (April and May) and negatively correlated with PCP in April and May. April is a critical period for trees because it coincides with the transition from dormancy to an active state of growth. Moderate warming benefits trees by allowing them to break dormancy earlier, which stimulates the division of cells, improves photosynthetic efficiency, and promotes the buildup of carbohydrates. This gives plants enough energy to flourish. Additionally, higher temperatures in April can enhance snow melting, increase the soil moisture content, and thus improve the growth rate of plants during the growing season [45]. The MID shows a negative response to the temperature from December of the previous year to March of the current year. This negative response indicates that low temperatures have an adverse impact on tree growth and development. The higher temperatures during this period, from December to March, contribute to an accelerated photosynthesis process, which promotes the differentiation of cambial cells in trees and facilitates tree growth. As a result, the tree cells become larger and the cell walls thinner, leading to a smaller earlywood density value in the tree [46].

4.2. Relationships between Tree-Ring Parameters and NDVI with Different Spatial Resolutions

There is a mutual dependence between tree rings and tree crowns. Trees convert carbon dioxide, water, and mineral salts into organic compounds through photosynthesis in the canopy leaves, generating the nutrients necessary for their own growth and promoting radial tree growth. At various spatial resolutions, we detected inconsistencies in the connections between tree-ring characteristics and NDVI. This might be due to MODIS data’s high spatial resolution, which is superior to GIMMS data’s coarse spatial resolution (8 km) in capturing local climate and other information reflecting changes in vegetation or tree rings; at this resolution, the heterogeneity of vegetation landscape patterns, stand density, age structure, and other differences result in a spatial decoupling of NDVI and tree-ring chronology data, which weakens the relationship between the two [47,48]. Our research indicates that the correlations between tree-ring parameters and MODIS NDVI are generally stronger in high-altitude areas than the correlations between tree-ring parameters with GIMMS3g NDVI; however, the opposite pattern was observed in low-altitude areas. Bhuyan et al. [30] found similar results by comparing the response of tree growth to high spatial resolution (MODIS, 250 m) and coarse spatial resolution (GIMMS3g NDVI, 8 km) data using a random forest model. Specifically, they showed that the growth signal of MODIS NDVI was stronger than that of GIMMS3g NDVI in areas with coniferous forests. We analyzed the relationships between three tree-ring parameters and NDVI and found that the MXD chronologies of each sampling point were more strongly correlated with the NDVI of each month during the growing season than tree-ring width and MID chronologies. The MXD chronologies were negatively correlated with NDVI in July and August, which might stem from carbon allocation during the growing season to support bud growth (leaf area) and the initiation of cambial activity, given that cell division and expansion (resulting in wider tree rings) are prioritized over the thickening of the cell walls [49,50,51].
Although previous studies have demonstrated an increase in the strength of the correlation between NDVI and tree-ring width as the spatial resolution increases from 8 km to 250 m [32,52], our findings demonstrate the value of high-resolution dense time series for monitoring tree productivity and retrospective modeling. However, recent studies have observed correlation coefficients between tree-ring width and 30 m resolution NDVI ranging from −0.27 to 0.50. The use of 30 m resolution NDVI data did not enhance the correlations between tree-ring parameters and NDVI compared with 250 m resolution NDVI. Therefore, a 250 m spatial resolution might be sufficient for characterizing correlations between tree-ring and NDVI [53]. To improve our comprehension of the connection between the local canopy and cambial activity and evaluate the possible impacts of climate change on the development and productivity of forest trees, more research is required. Factors that might affect the NDVI signal such as soil moisture, topography, and vegetation type should be considered in future studies.
Compared with high elevations, there is a strong correlation between tree rings and GIMMS NDVI at low elevations; this is consistent with what Wen et al. found. According to research, it is possible to establish a mathematical relationship between tree rings and NDVI within the same region and period in order to effectively deduce historical changes in the NDVI when common external environmental factors influence the growth of trees and regional vegetation and when other non-climatic factors do not interfere [33]. In this study, the tree ring width chronology at higher altitudes is positively correlated with temperature, while at lower altitudes, it is the opposite. Due to its coarse spatial resolution, GIMMS NDVI fails to show the trend of altitude changes, but it is primarily positively correlated with temperature from April to August. The central part of the Tianshan Mountains may be a common environmental factor affecting tree ring parameters and NDVI under drought stress [54,55].

5. Conclusions

We analyzed the relationships between standardized tree-ring chronologies and NDVI in the central Tianshan Mountains. We found that the correlations between the two were generally weak, which might be explained by the lack of a consistent response of the radial growth of P. schrenkiana to climate factors. High-resolution tree-ring width data might not accurately reflect the changes in NDVI. Additional studies that use tree-ring parameters to reconstruct NDVI in this region are needed. Only eight sites were sampled in our study, and only climate factors, such as temperature and precipitation, were considered in our analysis. However, other factors, such as atmospheric CO2 concentrations, drought, fire, forest pests and diseases, volcanic eruptions, earthquakes, glacier movement, and human-induced environmental pollution, can also affect tree growth. Therefore, additional research examining the effects of a wider range of factors on the relationships between tree-ring and NDVI at large scales and over a long time would be particularly valuable.

Author Contributions

T.Z., Y.F., S.Y. and S.J. conceived and designed the experiments; J.S., D.G., T.H. and K.G. performed the experiments; J.S. and Y.L. analyzed the data; J.S. wrote the manuscript. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Natural Key Research and Development Program (Inter-governmental Key and Special Project, 2023YFE0102700), Natural Science Foundation of Xinjiang Uigur Autonomous Region-Science Fund for Distinguished Young Scholars (2022D01E105), Natural Science Foundation of China (41975095), Science and Technology Development Fund Project of Institute of Desert Meteorology, China Meteorological Administration (KJFZ202306).

Data Availability Statement

The data provided in this study are available from the authors upon request.

Conflicts of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

  1. Berner, L.T.; Beck, P.S.A.; Bunn, A.G.; Goetz, S.J. Plant response to climate change along the forest-tundra ecotone in northeastern Siberia. Glob. Chang. Biol. 2013, 19, 3449–3462. [Google Scholar] [CrossRef] [PubMed]
  2. Camarero, J.J.; Gutiérrez, E. Wood density of silver fir reflects drought and cold stress across climatic and biogeographic gradients. Dendrochronologia 2017, 45, 101–112. [Google Scholar] [CrossRef]
  3. Babst, F.; Bouriaud, O.; Papale, D.; Gielen, B.; Janssens, I.A.; Nikinmaa, E.; Ibrom, A.; Wu, J.; Bernhofer, C.; Kostner, B.; et al. Above-ground woody carbon sequestration measured from tree rings is coherent with net ecosystem productivity at five eddy-covariance sites. New Phytolodist. 2014, 201, 1289–1303. [Google Scholar] [CrossRef] [PubMed]
  4. Van Breugel, M.; Ransijn, J.; Craven, D.; Bongers, F.; Hall, J.S. Estimating carbon stock in secondary forests: Decisions and uncertainties associated with allometric biomass models. For. Ecol. Manag. 2011, 262, 1648–1657. [Google Scholar] [CrossRef]
  5. Miyeni, R.B.; Hall, F.G.; Sellers, P.J.; Marshak, A.L. The interpretation of spectral vegetation indexes. IEEE Trans. Geosci. Remote Sens. 1995, 33, 481–486. [Google Scholar]
  6. Erasmi, S.; Klinge, M.; Dulamsuren, C.; Schneider, F.; Hauck, M. Modelling the productivity of Siberian larch forests from Landsat NDVI time series in fragmented forest stands of the Mongolian forest-steppe. Environ. Monit. Assess. 2021, 193, 200. [Google Scholar] [CrossRef]
  7. Levesque, M.; Andreu-Hayles, L.; Smith, W.K.; Williams, A.P.; Hobi, M.L.; Allred, B.W.; Pederson, N. Tree-ring isotopes capture interannual vegetation productivity dynamics at the biome scale. Nat. Commun. 2019, 10, 742. [Google Scholar] [CrossRef]
  8. Zhang, T.; Zhang, R.; Lu, B.; Mambetov, B.T.; Kelgenbayev, N.; Dosmanbetov, D.; Maisupova, B.; Chen, F.; Yu, S.; Shang, H.; et al. Picea schrenkiana tree-ring chronologies development and vegetation index reconstruction for the Alatau Mountains, Central Asia. Geochronometria 2018, 45, 107–118. [Google Scholar] [CrossRef]
  9. Camarero, J.J.; Franquesa, M.; Sangüesa-Barreda, G. Timing of drought triggers distinct growth responses in holm oak: Implications to predict warming-induced forest defoliation and growth decline. Forests 2015, 6, 1576–1597. [Google Scholar] [CrossRef]
  10. Wang, M.Y.; Luo, Y.; Zhang, Z.Y. Recent advances in remote sensing of vegetation phenology: Retrieval algorithm and validation strategy. Natl. Remote Sens. Bull. 2020, 26, 431–455. [Google Scholar] [CrossRef]
  11. Rouse, J.W.; Haas, R.H.; Schell, J.A. Monitoring vegetation systems in the Great Plains with ERTS. In Third Earth Resources Technology Satellite-1 Symposium, Proceedings of a Symposium, Goddard Space Flight Center, Washington, DC, USA, 10–14 December 1973; NASA: Washington, DC, USA, 1974; Volume 351, pp. 309–317. [Google Scholar]
  12. Huete, A.; Didan, K.; Miura, T. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
  13. Kauth, R.J.; Thomas, G.S. The tasselled cap a graphic description of the spectra temporal development of agriculture crops as seen by Landsat. In Proceedings of the 2nd International Symposium on Machine Processing of Remotely Sensed Data, West Lafayette, IN, USA, 29 June–1 July 1976. [Google Scholar]
  14. Lopatin, E.; Kolström, T.; Spiecker, H. Determination of forest growth trends in Komi Republic (northwestern Russia): Combination of tree-ring analysis and remote sensing data. Boreal Environ. Res. 2006, 11, 341–353. [Google Scholar]
  15. Liang, E.Y.; Eckstein, D. Dendrochronological Potential of the Alpine Shrub Rhododendron nivale on the South-Eastern Tibetan Plateau. Ann. Bot. 2009, 104, 665–670. [Google Scholar] [CrossRef] [PubMed]
  16. Pettorelli, N.; Vik, J.O.; Mysterud, A.; Gaillard, J. Using the satellite-derived NDVI to assess ecological responses to environmental change. Trends Ecol. Evol. 2005, 20, 503–510. [Google Scholar] [CrossRef] [PubMed]
  17. Gamon, J.A.; Kovalchuck, O.; Wong, C.Y.S. Monitoring seasonal and diurnal changes in photosynthetic pigments with automated PRI and NDVI sensors. Biogeosciences 2015, 12, 4149–4159. [Google Scholar] [CrossRef]
  18. Furusawa, T.; Koera, T.; Siburian, R.; Wicaksono, A.; Matsudaira, K.; Yoshinori, I. Time-series analysis of satellite imagery for detecting vegetation cover changes in Indonesia. Sci. Rep. 2023, 13, 8437. [Google Scholar] [CrossRef]
  19. Mao, D.; Wang, Z.M.; Luo, L.; Ren, C.Y. Integrating AVHRR and MODIS data to monitor NDVI changes and their relationships with climatic parameters in Northeast China. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 528–536. [Google Scholar] [CrossRef]
  20. Vivar-Vivar, E.D.; Pompa-García, M.; Rodríguez-Trejo, D.A.; Leyva-Ovalle, A.; Wehenkel, C.; Carrillo-Parra, A.; García-Montiel, E.; Moreno-Anguiano, O. Drought responsiveness in two Mexican conifer species forming young stands at high elevations. For. Syst. 2021, 30, e012. [Google Scholar] [CrossRef]
  21. Fensholt, R.; Proud, S.R. Evaluation of Earth Observation based global long term vegetation trends Comparing GIMMS and MODIS global NDVI time series. Remote Sens. Environ. 2012, 199, 131–147. [Google Scholar] [CrossRef]
  22. Huang, S.; Tang, L.N.; Hupy, J.P.; Wang, Y.; Shao, G.F. A commentary review on the use of normalized difference vegetation index (NDVI) in the era of popular remote sensing. J. For. Res. 2020, 32, 1–6. [Google Scholar] [CrossRef]
  23. Decuyper, M.; Chávez, R.O.; Cufar, K.; Estay, S.A.; Clevers, J.G.P.W.; Prislan, P.; Gricar, J.; Crepinsek, Z.; Merela, M.; de Luis, M. Spatio-temporal assessment of beech growth in relation to climate extremes in Slovenia—An integrated approach using remote sensing and tree-ring data. Agric. For. Meteorol. 2020, 287, 107925. [Google Scholar] [CrossRef]
  24. Andreu-Hayles, L.; Gaglioti, B.V.; Berner, L.T.; Levesque, M.; Anchukaitis, K.J.; Goetz, S.; D’Arrigo, R. A narrow window of summer temperatures associated with shrub growth in Arctic Alaska. Environ. Res. Lett. 2020, 15, 105012. [Google Scholar] [CrossRef]
  25. Bonney, M.T.; He, Y.H. Temporal connections between long-term Landsat time-series and tree-rings in an urban–rural temperate forest. Int. J. Appl. Earth Obs. Geoinf. 2021, 103, 102523. [Google Scholar] [CrossRef]
  26. Tonelli, E.; Vitali, A.; Malandra, F.; Camarero, J.J.; Colangelo, M.; Nole, A.; Ripullone, F.; Carrer, M.; Urbinati, C. Tree-ring and remote sensing analyses uncover the role played by elevation on European beech sensitivity to late spring frost. Sci. Total Environ. 2023, 857, 159239. [Google Scholar] [CrossRef]
  27. Kaufmann, R.K.; D’arrigo, R.D.; Paletta, L.F.; Tian, H.Q.; Jolly, W.M.; Myneni, R.B. Identifying climatic controls on ring width: The timing of Correlations between The Timing Rings and NDVI. Earth Interact. 2008, 12, 114. [Google Scholar] [CrossRef]
  28. Wu, Q.Q.; Zhang, X.; Xu, S.X.; Yang, X.H.; Liu, Y.S.; Li, H.Z.; Shi, Z.J. Climatic responses of NDVI and tree growth in the arid areas of inland Asia and their influencing factors. J. Desert Res. 2022, 42, 1–10. [Google Scholar]
  29. Vicente-Serrano, S.M.; Martin-Hernandez, N.; Camarero, J.J.; Gazol, A.; Sanchez-Salguero, R.; Pena-Gallardo, M.; El Kenawy, A.; Dominguez-Castro, F.; Tomas-Burguera, M.; Gutierrez, E.; et al. Linking tree-ring growth and satellite-derived gross primary growth in multiple forest biomes. Tempor-Scale Matters. Ecol. Indic. 2020, 108, 105753. [Google Scholar] [CrossRef]
  30. Bhuyan, U.; Zang, C.; Vicente-Serrano, S.M.; Menzel, A. Exploring relationships among tree-ring growth, climate variability, and seasonal leaf activity on varying timescales and spatial resolutions. Remote Sens. 2017, 9, 526. [Google Scholar] [CrossRef]
  31. Vicente-Serrano, S.M.; Camarero, J.J.; Olano, J.M.; Martin-Hernandez, N.; Pena-Gallardo, M.; Tomas-Burguera, M.; Gazol, A.; Azorin-Molina, C.; Bhuyan, U.; El Kenawy, A.A. Diverse relationships between forest growth and the Normalized Difference Vegetation Index at a global scale. Remote Sens. Environ. 2016, 187, 14–29. [Google Scholar] [CrossRef]
  32. Brehaut, L.; Danby, R.K. Inconsistent relationships between annual tree ring-widths and satellite-measured NDVI in a mountainous subarctic environment. Ecol. Indic. 2018, 91, 698–711. [Google Scholar] [CrossRef]
  33. Coulthard, B.L.; Touchan, R.; Anchukaitis, K.J.; Meko, D.M.; Sivrikaya, F. Tree growth and vegetation activity at the ecosystem-scale in the eastern Mediterranean. Environ. Res. Lett. 2017, 12, 084008. [Google Scholar] [CrossRef]
  34. Wen, Y.; Jiang, Y.; Jiao, L.; Hou, C.X.; Xu, H. Inconsistent relationships between tree ring width and normalized difference vegetation index in montane evergreen coniferous forests in arid regions. Trees 2022, 36, 379–391. [Google Scholar] [CrossRef]
  35. Yuan, K.Y.; Xu, H.L.; Zhang, G.P. Is There Spatial and Temporal Variability in the Response of Plant Canopy and Trunk Growth to Climate Change in a Typical River Basin of Arid Areas. Water 2022, 14, 1573. [Google Scholar] [CrossRef]
  36. Speer, J.H. Fundamentals of Tree-Ring Research; The University of Arizona Press: Tucson, AZ, USA, 2010. [Google Scholar]
  37. Holmes, R.L. Computer-assisted quality control in tree-ring dating and measurement. Tree Ring Bull. 1983, 43, 68–78. [Google Scholar]
  38. Cook, E.R. A Time Series Analysis Approach to Tree-Ring Standardization; The University of Arizona: Tucson, AZ, USA, 1985. [Google Scholar]
  39. Fritts, H.C. Tree Rings and Climate; Academic Press: London, UK, 1976; p. 567. [Google Scholar]
  40. Cook, E.R.; Krusic, P.J. Program ARSTAN: A Tree-Ring Standardization Program Based on Detrending and Autoregressive Time Series Modeling, with Interactive Graphics; Lamont-Doherty Earth Observatory, Columbia University: New York, NY, USA, 2005; p. 5. [Google Scholar]
  41. Wigley, T.M.L.; Briffa, K.R.; Jones, P.D. On the average value of correlated time series, with applications in dendroclimatology and hydrometeorology. J. Clim. Appl. Meteorol. 1984, 23, 201–213. [Google Scholar] [CrossRef]
  42. Wang, Z. Plant Physiology; China Agriculture Press: Beijing, China, 2010; pp. 314–368. [Google Scholar]
  43. Jiao, L.; Ma, L.; Zhang, T.W.; Wang, S.J. Changes of mean minimum temperature in June–July since 1798 in central Altay Mountain recorded by tree rings. Acta Ecol. Sin. 2021, 41, 1944–1958. [Google Scholar]
  44. Shang, J.X.; Shi, Z.J.; Gao, J.X.; Xu, L.H.; Lü, S.H.; Feng, C.Y.; Wang, L.X. Response of tree-ring width of Pinus sylvestris var. mongolica to climate change in Hulunbuir sand land, China. Acta Ecol. Sin. 2012, 32, 1077–1084. [Google Scholar] [CrossRef]
  45. Zhang, Q.; Yu, R.D.; Zheng, H.W. Response Analysis of Larix sibirica to Climate Warming at Different Elevations in the Eastern Tianshan Mountains. Bull. Bot. Res. 2018, 38, 14–25. [Google Scholar]
  46. Chen, F.; Yuan, Y.; Wei, W. Chronology development and climate response analysis of Schrenk Spruce (Picea schrenkiana) tree-ring parameters in the Urumqi River basin, China. Geochronometria 2010, 36, 17–22. [Google Scholar] [CrossRef]
  47. Hauck, M.; Klinge, M.; Erasmi, S.; Dulamsuren, C. No Signs of Long-term Greening Trend in Western Mongolian Grasslands. Ecosystems 2023. [Google Scholar] [CrossRef]
  48. Xu, P.P.; Fang, W.; Zhou, T.; Zhao, X.; Luo, H.; Hendrey, G.; Yi, C.X. Spatial Upscaling of Tree-Ring-Based Forest Response to Drought with Satellite Data. Remote Sens. 2019, 11, 2344. [Google Scholar] [CrossRef]
  49. Correa-Díaz, A.; Gómez-Guerrero, A.; Vargas-Hernández, J.J.; Rozenberg, P.; Horwath, W.R. Long-term wood micro-density variation in alpine forests at Central México and their spatial links with remotely sensed information. Forests 2020, 11, 452. [Google Scholar] [CrossRef]
  50. Andreu-Hayles, L.; D’Arrigo, R.; Anchukaitis, K.J.; Beck, P.S.A.; Frank, D.; Goetz, S. Varying boreal forest response to Arctic environmental change at the Firth River, Alaska. Environ. Res. Lett. 2011, 6, 045503. [Google Scholar] [CrossRef]
  51. D’Arrigo, R.D.; Malmstrom, C.M.; Jacoby, G.C.; Jacoby, G.C.; Los, S.O.; Bunker, D.E. Correlation between Maximum Latewood Density of Annual Tree Rings and NDVI Based Estimates of Forest Productivity. Int. J. Remote Sens. 2000, 21, 2329–2336. [Google Scholar] [CrossRef]
  52. Bunn, A.G.; Hughes, M.K.; Kirdyanov, A.V.; Losleben, M.; Shishov, V.V.; Berner, L.; Oltchev, A.; Vaganov, E.A. Comparing forest measurements from tree rings and a space-based index of vegetation activity in Siberia. Environ. Res. Lett. 2013, 8, 035034. [Google Scholar] [CrossRef]
  53. Mašek, J.; Tumajer, J.; Lange, J.; Kaczka, R.; Fiser, P.; Treml, V. Variability in Tree-ring Width and NDVI Responses to Climate at a Landscape Level. Ecosystems 2023. [Google Scholar] [CrossRef]
  54. Huo, Y.X.; Gou, X.H.; Liu, W.H. Climate–growth relationships of Schrenk spruce (Picea schrenkiana) along an altitudinal gradient in the western Tianshan mountains, northwest China. Trees 2017, 31, 429–439. [Google Scholar] [CrossRef]
  55. Jiao, L.; Jiang, Y.; Wang, M.C. Responses to climate change in radial growth of Picea schrenkiana along elevations of the eastern Tianshan Mountains, northwest China. Dendrochronologia 2016, 40, 117–127. [Google Scholar] [CrossRef]
Forests 14 02362 g001
Figure 1. Map displaying the locations of meteorological stations and tree-ring collection sites in China’s Tianshan Mountains.
Figure 1. Map displaying the locations of meteorological stations and tree-ring collection sites in China’s Tianshan Mountains.
Forests 14 02362 g001
Forests 14 02362 g002
Figure 2. Climate data of the study area: (a) Precipitation, mean temperature, mean minimum temperature, and mean maximum temperature per month. Bars indicate precipitation (in mm), and curves with different colors indicate mean temperature (blue), mean minimum temperature (green), and mean maximum temperature (red) (in °C), (b–d) annual mean temperature, annual mean maximum temperature, and annual mean minimum temperature during 1961–2012, (e) annual precipitation during 1961–2012. Dashed lines indicate trends.
Figure 2. Climate data of the study area: (a) Precipitation, mean temperature, mean minimum temperature, and mean maximum temperature per month. Bars indicate precipitation (in mm), and curves with different colors indicate mean temperature (blue), mean minimum temperature (green), and mean maximum temperature (red) (in °C), (b–d) annual mean temperature, annual mean maximum temperature, and annual mean minimum temperature during 1961–2012, (e) annual precipitation during 1961–2012. Dashed lines indicate trends.
Forests 14 02362 g002
Forests 14 02362 g003
Figure 3. Two NDVI datasets with different spatial resolutions: (a) Monthly GIMMS3g NDVI (8 km, 1982–2012); (b) Annual mean NDVI during 1982–2012. Dashed lines indicate trends in GIMMS NDVI data. (c) Monthly MODIS NDVI (250 m, 2001–2012).
Figure 3. Two NDVI datasets with different spatial resolutions: (a) Monthly GIMMS3g NDVI (8 km, 1982–2012); (b) Annual mean NDVI during 1982–2012. Dashed lines indicate trends in GIMMS NDVI data. (c) Monthly MODIS NDVI (250 m, 2001–2012).
Forests 14 02362 g003
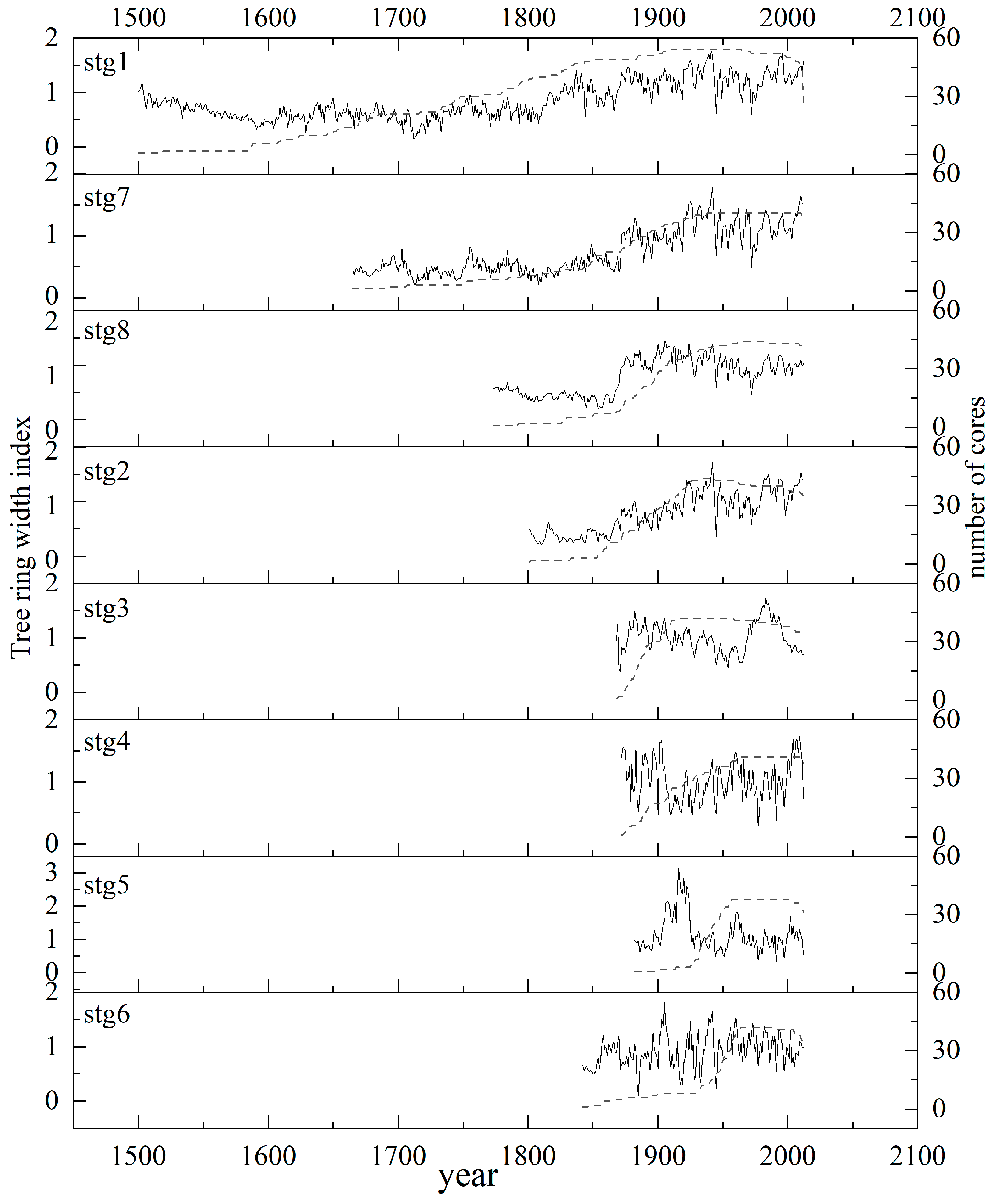
Forests 14 02362 g004
Figure 4. Tree-ring width standardized chronologies and sample depth. Solid line represents the tree ring width index; dashed line represents the sample size.
Figure 4. Tree-ring width standardized chronologies and sample depth. Solid line represents the tree ring width index; dashed line represents the sample size.
Forests 14 02362 g004
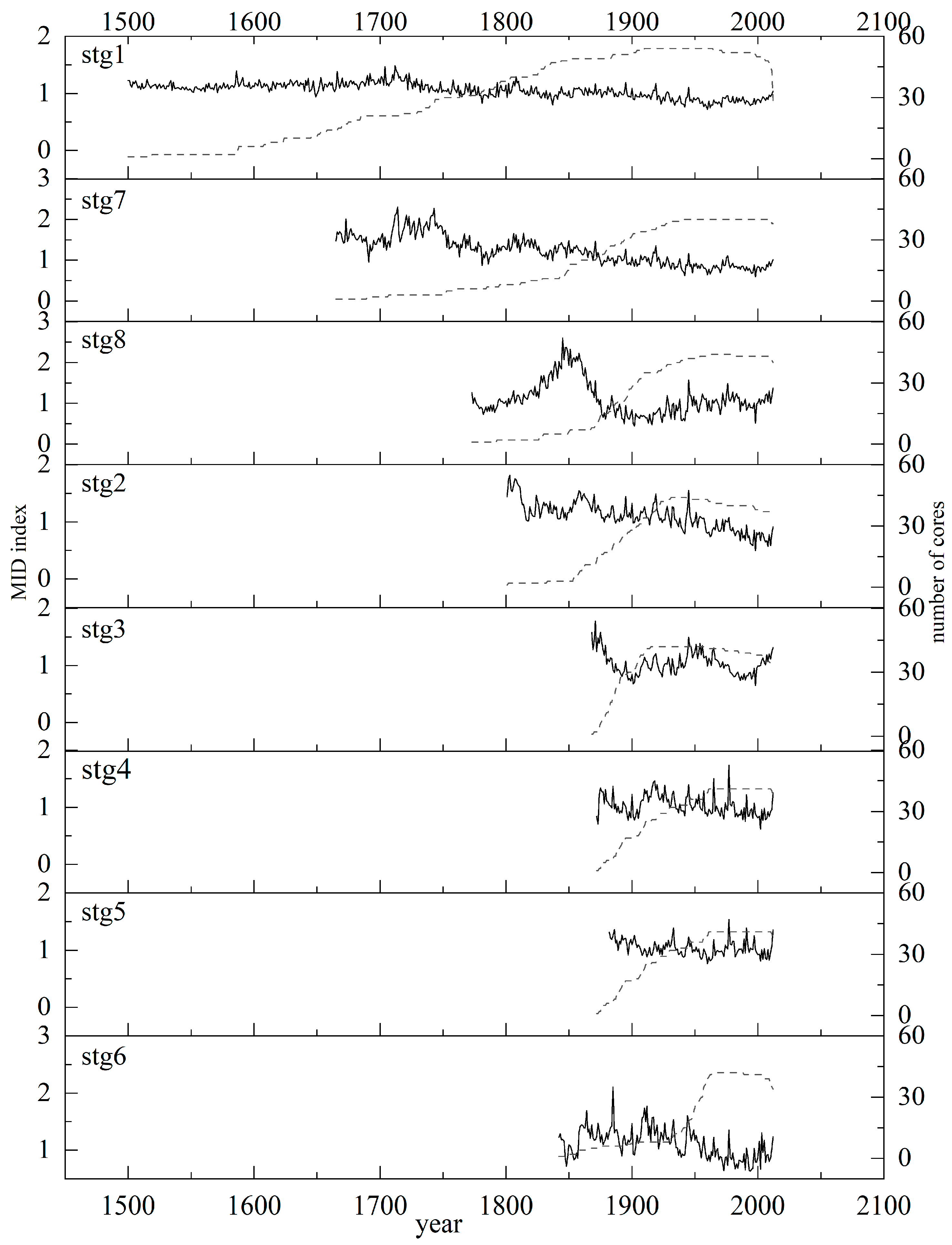
Forests 14 02362 g005
Figure 5. MID standardized chronologies and sample depth. Solid line represents the MID index; dashed line represents the sample size.
Figure 5. MID standardized chronologies and sample depth. Solid line represents the MID index; dashed line represents the sample size.
Forests 14 02362 g005
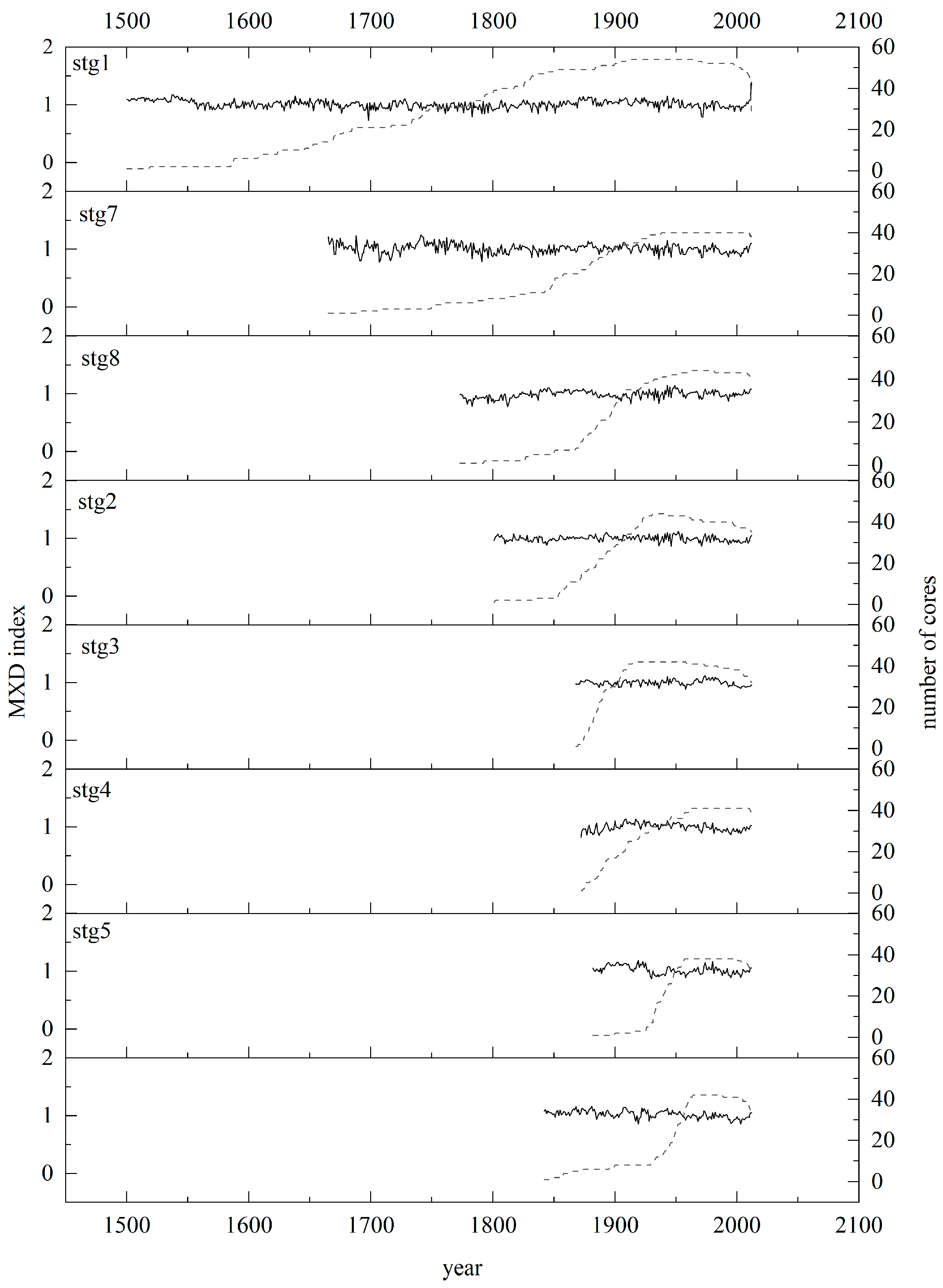
Forests 14 02362 g006
Figure 6. MXD standardized chronologies and sample depth. Solid line represents MXD index; dashed line represents the sample size.
Figure 6. MXD standardized chronologies and sample depth. Solid line represents MXD index; dashed line represents the sample size.
Forests 14 02362 g006
Forests 14 02362 g007
Figure 7. Pearson correlations between tree-ring width standardized chronologies and climatic data (monthly Tmean, monthly mean Tmin, monthly mean Tmax, and PCP). Lowercase and capital letters indicate months of the previous and current years, respectively.
Figure 7. Pearson correlations between tree-ring width standardized chronologies and climatic data (monthly Tmean, monthly mean Tmin, monthly mean Tmax, and PCP). Lowercase and capital letters indicate months of the previous and current years, respectively.
Forests 14 02362 g007
Forests 14 02362 g008
Figure 8. Pearson correlations between MID standardized chronologies and climatic data (monthly Tmean, monthly mean Tmin, monthly mean Tmax, and PCP). Lowercase and capital letters indicate months of the previous and current years, respectively.
Figure 8. Pearson correlations between MID standardized chronologies and climatic data (monthly Tmean, monthly mean Tmin, monthly mean Tmax, and PCP). Lowercase and capital letters indicate months of the previous and current years, respectively.
Forests 14 02362 g008
Forests 14 02362 g009
Figure 9. Pearson correlations between MXD standardized chronologies and climatic data (monthly Tmean, monthly mean Tmin, monthly mean Tmax, and PCP). Lowercase and capital letters indicate months of the previous and current years, respectively.
Figure 9. Pearson correlations between MXD standardized chronologies and climatic data (monthly Tmean, monthly mean Tmin, monthly mean Tmax, and PCP). Lowercase and capital letters indicate months of the previous and current years, respectively.
Forests 14 02362 g009
Forests 14 02362 g010
Figure 10. Correlations between GIMMS NDVI and climate factors (monthly Tmean, monthly mean Tmin, monthly mean Tmax, and PCP). The ordinate shows the monthly GIMMS NDVI from April to October, as well as the average NDVI from May to August. Lowercase and capital letters indicate months of the previous and current years, respectively. Deep red and deep blue indicate significance at p < 0.01; red and blue indicate significance at p < 0.05; light red and light blue indicate significance at p < 0.1.
Figure 10. Correlations between GIMMS NDVI and climate factors (monthly Tmean, monthly mean Tmin, monthly mean Tmax, and PCP). The ordinate shows the monthly GIMMS NDVI from April to October, as well as the average NDVI from May to August. Lowercase and capital letters indicate months of the previous and current years, respectively. Deep red and deep blue indicate significance at p < 0.01; red and blue indicate significance at p < 0.05; light red and light blue indicate significance at p < 0.1.
Forests 14 02362 g010
Forests 14 02362 g011
Figure 11. Correlations of MODIS NDVI with climate factors (monthly Tmean, monthly mean Tmin, monthly mean Tmax, and PCP). The ordinate shows the monthly MODIS NDVI from April to October, as well as the average NDVI from May to August. (a–h) shows the correlations between MODIS NDVI and climate factors at stg 1, stg 7, stg 8, stg 2, stg 3, stg 4, stg 5, and stg 6. Lowercase and capital letters indicate months of the previous and current years, respectively. Deep red and deep blue indicate significance at p < 0.01; red and blue indicate significance at p < 0.05; light red and light blue indicate significance at p < 0.1.
Figure 11. Correlations of MODIS NDVI with climate factors (monthly Tmean, monthly mean Tmin, monthly mean Tmax, and PCP). The ordinate shows the monthly MODIS NDVI from April to October, as well as the average NDVI from May to August. (a–h) shows the correlations between MODIS NDVI and climate factors at stg 1, stg 7, stg 8, stg 2, stg 3, stg 4, stg 5, and stg 6. Lowercase and capital letters indicate months of the previous and current years, respectively. Deep red and deep blue indicate significance at p < 0.01; red and blue indicate significance at p < 0.05; light red and light blue indicate significance at p < 0.1.
Forests 14 02362 g011
Forests 14 02362 g012
Figure 12. Relationships between tree-ring parameters and NDVI. (A) shows the correlations between tree-ring width standardized chronologies and NDVI. (B) shows the correlations between MID standardized chronologies and NDVI. (C) shows the correlations between MXD standardized chronologies and NDVI.
Figure 12. Relationships between tree-ring parameters and NDVI. (A) shows the correlations between tree-ring width standardized chronologies and NDVI. (B) shows the correlations between MID standardized chronologies and NDVI. (C) shows the correlations between MXD standardized chronologies and NDVI.
Forests 14 02362 g012
Table 1. Tree-ring sampling site information.
Table 1. Tree-ring sampling site information.
SiteLatitude (N)Longitude (E)Elevation (m)AspectSlope (°)Canopy DensityNo. of Trees/Cores
stg 143°52′59.5″85°30′56.1″2606N470.127/54
stg 743°53′02.7”85°31′11.7″2531NW400.320/40
stg 843°53′06.63”85°31′09.46″2400NE350.522/44
stg 243°53′11.5″85°31′4.4″2318NE350.322/44
stg 343°53′25.6″85°31′4.8″2206NE200.321/42
stg 443°53′54.7″85°31′0.8″2095ENE450.221/41
stg 543°54′10.3″85°31′11.4″1942NNW200.319/38
stg 643°54′42.2″85°31′17.2″1761N300.221/42
Table 2. Statistics of the STG tree-ring width standardized chronologies.
Table 2. Statistics of the STG tree-ring width standardized chronologies.
Statisticstg 1stg 7stg 8stg 2stg 3stg 4stg 5stg 6
Chronology length513350242213146142132172
Mean index (MI)0.8420.7440.7960.8011.0071.0391.1480.919
Mean sensitivity (MS)0.1590.1660.1210.1520.1190.2680.2360.262
Standard deviation (SD)0.3390.3680.3320.3770.2780.3840.5380.302
First-order autocorrelation (AC1)0.8780.9110.9310.9110.8490.5640.8180.556
Mean within-tree correlation0.4740.6450.6400.5330.5690.7190.6640.645
Signal-to-noise ratio (SNR)11.35710.69419.29512.30519.92114.7967.72117.032
Expressed population signal (EPS)0.9190.9140.9510.9250.9520.9370.8850.945
The first principal component (PC#1)30.338.648.958.147.741.029.649.5
First year of SSS > 0.8516461819185118611875188619321900
Table 3. Statistics of the STG MID standardized chronologies.
Table 3. Statistics of the STG MID standardized chronologies.
Statisticstg 1stg 7stg 8stg 2stg 3stg 4stg 5stg 6
Chronology length513350242213146142132172
Mean index (MI)1.0561.2281.1081.0991.0361.0291.0391.114
Mean sensitivity (MS)0.0640.1050.1490.1020.0970.1360.1010.141
Standard deviation (SD)0.1280.3520.4160.2600.2020.1850.1350.261
First-order autocorrelation (AC1)0.7550.8890.8830.8170.7430.4160.4340.669
Mean within-tree correlation0.3180.3680.3770.3210.3160.4060.4360.462
Signal-to-noise ratio (SNR)8.8915.6795.1404.7425.87916.2506.2355.645
Expressed population signal (EPS)0.8990.8500.8370.8260.8550.9420.8620.850
The first principal component (PC#1)30.929.230.726.333.242.425.025.4
First year of SSS > 0.8516511847187218741882188419331934
Table 4. Statistics of the STG MXD standardized chronologies.
Table 4. Statistics of the STG MXD standardized chronologies.
Statisticstg 1stg 7stg 8stg 2stg 3stg 4stg 5stg 6
Chronology length513350242213146142132172
Mean index (MI)4740353520452030
Mean sensitivity (MS)0.0570.0700.0510.0470.0360.0460.0450.044
Standard deviation (SD)0.0700.0830.0660.0530.0490.0650.0720.064
First-order autocorrelation (AC1)0.3920.3510.4800.2330.5430.5900.6700.595
Mean within-tree correlation0.4300.3980.4900.4120.3960.4050.3810.335
Signal-to-noise ratio (SNR)9.8849.2958.97913.39511.0089.4065.9015.157
Expressed population signal (EPS)0.9080.9030.9000.9310.9170.9040.8550.838
The first principal component (PC#1)29.430.537.338.537.133.823.925.0
First year of SSS > 0.8516511819187418581879188819331934
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Song, J.; Zhang, T.; Fan, Y.; Liu, Y.; Yu, S.; Jiang, S.; Guo, D.; Hou, T.; Guo, K. Evaluating the Effect of Vegetation Index Based on Multiple Tree-Ring Parameters in the Central Tianshan Mountains. Forests 2023, 14, 2362. https://doi.org/10.3390/f14122362

AMA Style

Song J, Zhang T, Fan Y, Liu Y, Yu S, Jiang S, Guo D, Hou T, Guo K. Evaluating the Effect of Vegetation Index Based on Multiple Tree-Ring Parameters in the Central Tianshan Mountains. Forests. 2023; 14(12):2362. https://doi.org/10.3390/f14122362

Chicago/Turabian Style

Song, Jinghui, Tongwen Zhang, Yuting Fan, Yan Liu, Shulong Yu, Shengxia Jiang, Dong Guo, Tianhao Hou, and Kailong Guo. 2023. "Evaluating the Effect of Vegetation Index Based on Multiple Tree-Ring Parameters in the Central Tianshan Mountains" Forests 14, no. 12: 2362. https://doi.org/10.3390/f14122362

APA Style

Song, J., Zhang, T., Fan, Y., Liu, Y., Yu, S., Jiang, S., Guo, D., Hou, T., & Guo, K. (2023). Evaluating the Effect of Vegetation Index Based on Multiple Tree-Ring Parameters in the Central Tianshan Mountains. Forests, 14(12), 2362. https://doi.org/10.3390/f14122362

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop