Experimental Study of Beam Stability Factor of Sawn Lumber Subjected to Concentrated Bending Loads at Several Points
Abstract
1. Introduction
2. Materials and Methods
2.1. Specimen Preparation
2.2. Small Specimen Bending Test
2.3. Full-Size Specimen Bending Test
2.4. Beam Stability Factor (CL) Value Calculation
3. Results and Discussion
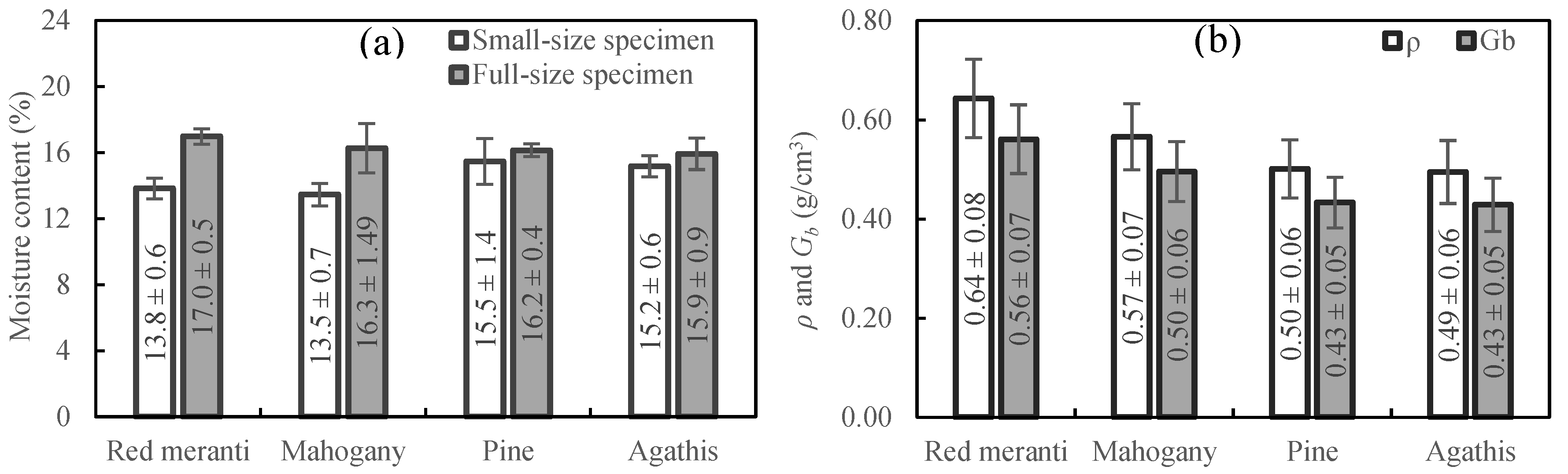
3.1. Moisture Content (Mc), Density (ρ), and Specific Gravity (Gb)
3.2. Flexural Properties of the Small Specimens
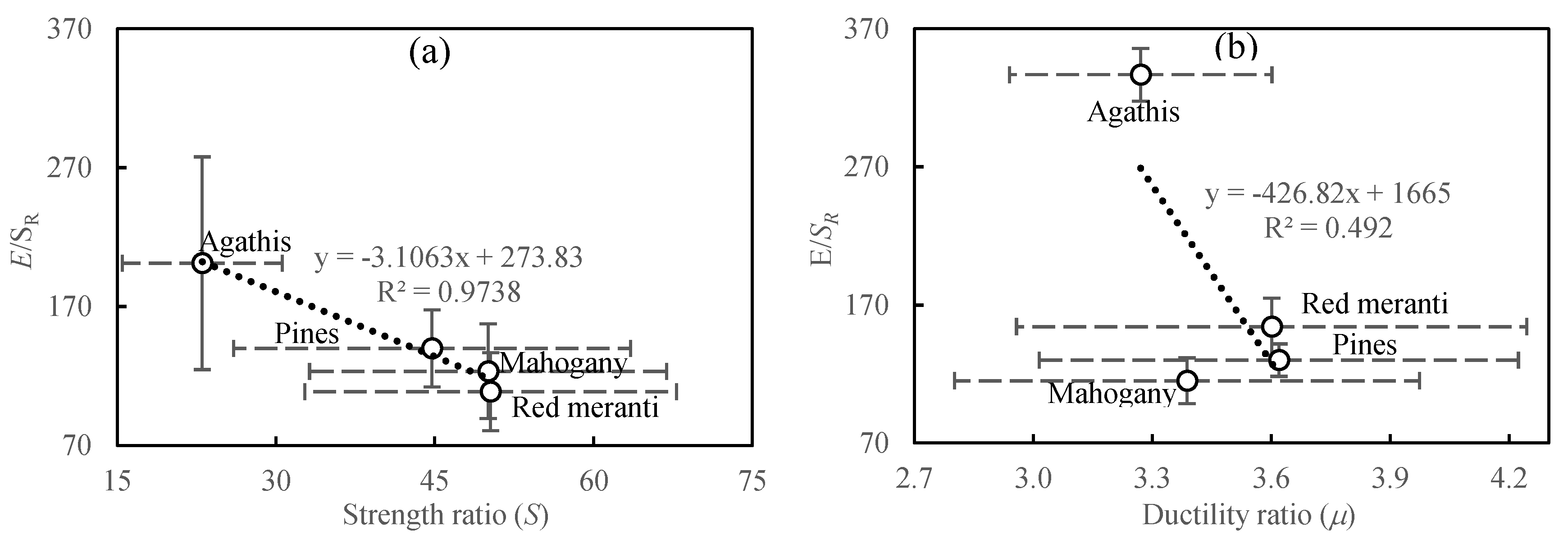
3.3. Strength Ratio of the Full-Size Specimens
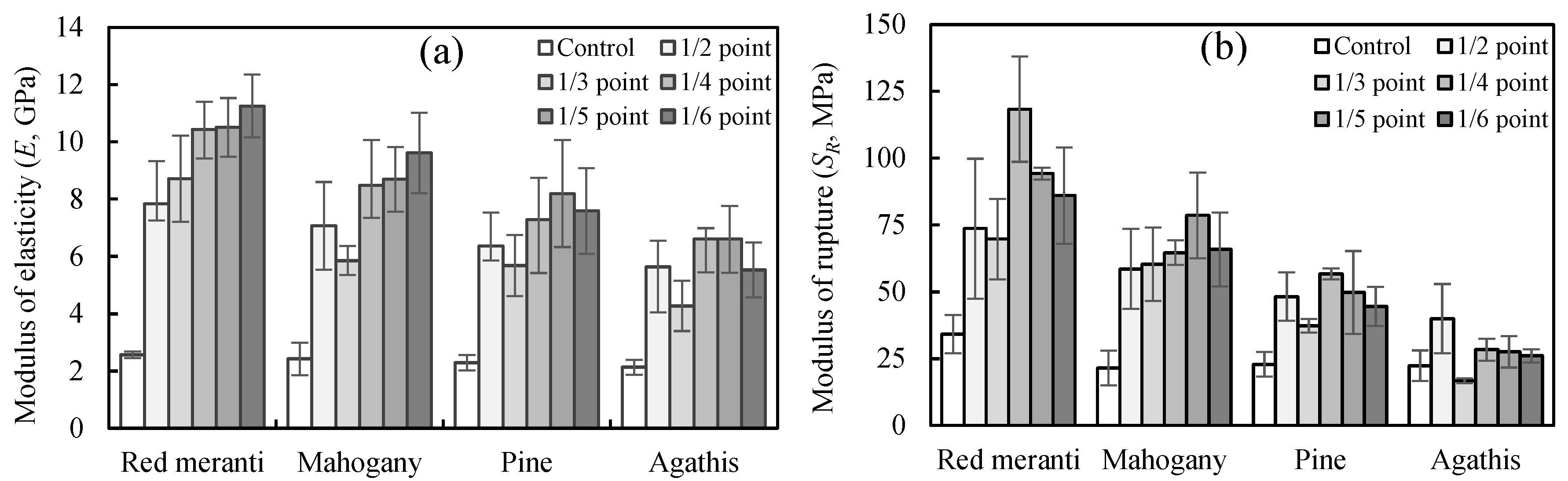
3.4. Flexural Properties of the Full-Size Specimens in Various Loading Configurations
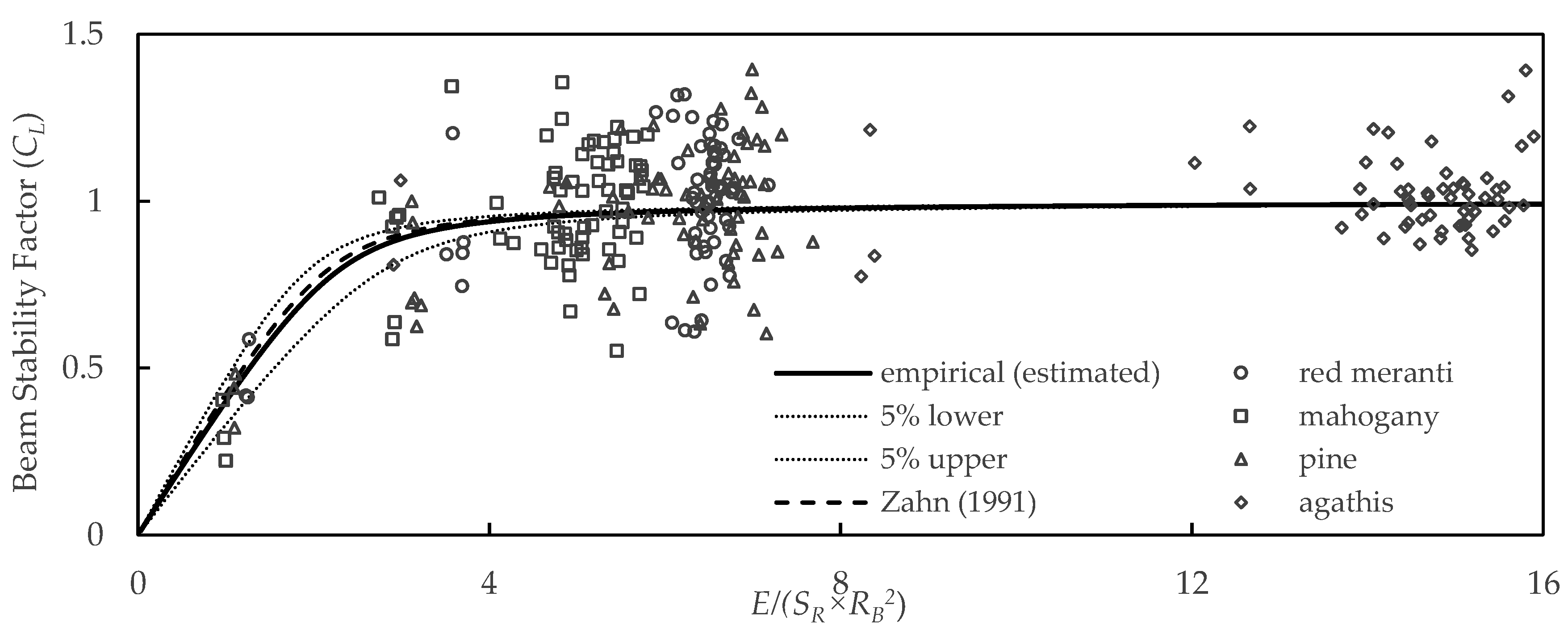
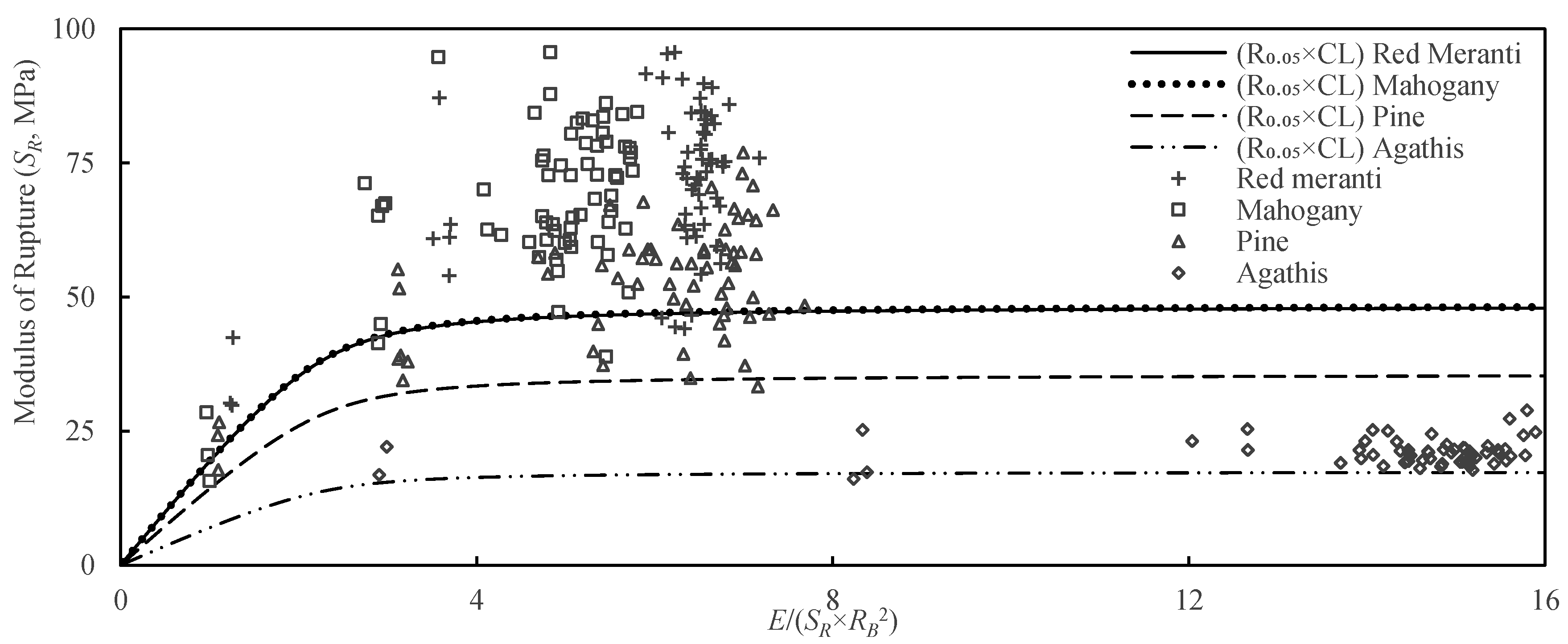
3.5. Beam Stability Factor (CL)
3.6. Beam Stability Factor (CL) Application in Beam Design
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| a | regression coefficient to estimate the KbE |
| b | specimen width (mm) |
| c | non-linear parameter for beam = 0.95 |
| CD | load duration factor |
| CF | size factor |
| Cfu | flat use factor |
| Ci | incising factor |
| Ck | beam stability factor limit |
| CL | beam stability factor |
| CLe | empirical beam stability factor |
| CM | wet service factor |
| Cr | repetitive member factor |
| Ct | temperature factor |
| d | specimen depth (mm) |
| E | modulus of elasticity (MPa) |
| Emin | 5% lower exclusion value of modulus elasticity (MPa) |
| Fb | reference bending design value (MPa) |
| Fb’ | adjusted reference bending design value |
| FbE | critical buckling design (MPa) |
| Fu | ultimate load (N) |
| Gb | specific gravity |
| KbE | Euler buckling coefficient |
| KbE’ | adjusted Euler buckling coefficient |
| L | specimen length (mm) |
| le | effective span length (mm) |
| lu | unsupported length (mm) |
| m0 | mass before the bending test (g) |
| m1 | mass after the bending test (g) |
| Mc | moisture content (%) |
| mot | mass after oven-drying (g) |
| R0.05 | 5% exclusion limit value |
| RB | beam slenderness ratio |
| Rk | characteristic value (MPa) |
| S | strength ratio (%) |
| SR | modulus of rupture (MPa) |
| Greek symbol | |
| μ | ductility ratio |
| Δu | ultimate displacement (mm) |
| Δy | yield displacement (mm) |
| ρ | density (g/cm3) |
References
- Lattke, F.; Lehmann, S. Multi-Storey Residential Timber Construction: Current Developments in Europe. J. Green Build. 2007, 2, 119–129. [Google Scholar] [CrossRef]
- Buchanan, A.; Deam, B.; Pampanin, S.; Fragiacomo, M.; Palermo, A. Multi-Storey Prestressed Timber Buildings in New Zealand. Struct. Eng. Int. J. Int. Assoc. Bridg. Struct. Eng. 2008, 18, 166–173. [Google Scholar] [CrossRef]
- Bahtiar, E.T.; Nugroho, N.; Hermawan, D.; Wirawan, W. Triangle bracing system to reduce the vibration level of cooling tower—Case study in PT Star Energy Geothermal (Wayang Windu) Ltd—Indonesia. Case Stud. Constr. Mater. 2018, 8, 248–257. [Google Scholar] [CrossRef]
- Bahtiar, E.T.; Nugroho, N.; Rahman, M.M.; Arinana; Sari, R.K.; Wirawan, W.; Hermawan, D. Estimation the remaining service-lifetime of wooden structure of geothermal cooling tower. Case Stud. Constr. Mater. 2017, 6, 91–102. [Google Scholar] [CrossRef]
- Bahtiar, E.T.; Nugroho, N.; Arinana, D.A. Pendugaan Sisa Umur Pakai Kayu Komponen Cooling Tower di Pembangkit Listrik Tenaga Panas Bumi (PLTP) Unit II Kamojang (Estimating the Remaining Life of Wood Cooling Tower Component in Geothermal Power Plant Unit II Kamojang). J. Tek. Sipil. 2012, 19, 103–113. [Google Scholar] [CrossRef]
- Lamar, D.M.; Schafer, B.W. Structural Analyses of Two Historic Covered Wooden Bridges. J. Bridg. Eng. 2004, 9, 623–633. [Google Scholar] [CrossRef]
- Firmanti, A.; Komatsu, K.; Kawai, S. Effective Utilization of Fast-Growing Acacia mangium Willd. Timber As a Structural Material. J. Trop. Wood Sci. Technol. 2007, 5, 29–37. [Google Scholar]
- Firmanti, A.; Bachtiar, E.T.; Surjokusumo, S.; Komatsu, K.; Kawai, S. Mechanical stress grading of tropical timbers without regard to species. J. Wood Sci. 2005, 51, 339–347. [Google Scholar] [CrossRef]
- Steffen, A.; Johansson, C.-J.; Wormuth, E.-W. Study of the relationship between flatwise and edgewise modull of elasticity of sawn timber as a means to improve mechanical strength grading technology. Holz als Roh-Werkst. 1997, 55, 245–253. [Google Scholar] [CrossRef]
- Oscarsson, J.; Olsson, A.; Enquist, B. Optimization of machine strength grading of structural timber by means of bending MOE profiles with high resolution. In Proceedings of the 18th International Nondestructive Testing and Evaluation of Wood Symposium, Madison, WI, USA, 24−27 September 2013. [Google Scholar]
- Bodig, J.; Jayne, B. Mechanics of Wood and Wood Composites; Van Nostrand Reinhold Company: New York, NY, USA, 1982. [Google Scholar]
- Bahtiar, E.T.; Malkowska, D.; Trujillo, D.; Nugroho, N. Experimental study on buckling resistance of Guadua angustifolia bamboo column. Eng. Struct. 2020, 228, 111548. [Google Scholar] [CrossRef]
- Nugroho, N.; Bahtiar, E.T. Buckling formulas for designing a column with Gigantochloa apus. Case Stud. Constr. Mater. 2021, 14, e00516. [Google Scholar] [CrossRef]
- Bahtiar, E.T.; Imanullah, A.P.; Hermawan, D.; Nugroho, N. Structural grading of three sympodial bamboo culms (Hitam, Andong, and Tali) subjected to axial compressive load. Eng. Struct. 2018, 181, 233–245. [Google Scholar] [CrossRef]
- Bahtiar, E.T.; Trujillo, D.; Nugroho, N. Compression resistance of short members as the basis for structural grading of Guadua angustifolia. Constr. Build. Mater. 2020, 249, 118759. [Google Scholar] [CrossRef]
- American Wood Council. 1997 NDS Commentary; American Wood Council: Leesburg, VA, USA, 1997. [Google Scholar]
- Pi, Y.-L.; Bradford, M.A. Thermoelastic lateral-torsional buckling of fixed slender beams under linear temperature gradient. Int. J. Mech. Sci. 2008, 50, 1183–1193. [Google Scholar] [CrossRef]
- Hindman, D.P.; Manbeck, H.B.; Janowiak, J.J. Measurement and prediction of lateral torsional buckling loads of composite wood materials: Rectangular sections. For. Prod. J. 2005, 55, 42. [Google Scholar]
- Hassan, O.A.; Johansson, C. Glued laminated timber and steel beams. J. Eng. Des. Technol. 2018, 16, 398–417. [Google Scholar] [CrossRef]
- ASTM D143; Standard Test Methods for Small Clear Specimens of Timber. ASTM: West Conshohocken, PA, USA, 2002.
- Jamil, A.M.; Zamin, J.M.; Omar, M.M. Relationship between mechanical properties of structural size and small clear specimens of timber. J. Trop. For. Sci. 2013, 25, 12–21. [Google Scholar]
- Bahtiar, E.T.; Nugroho, N.; Nandika, D. Daily Cycle of Air Temperature and Relative Humidity Effect to Creep Deflection of Wood Component of Low-cost House in Cibeureum-Bogor, West Java, Indonesia. Asian J. Sci. Res. 2014, 7, 501–512. [Google Scholar] [CrossRef][Green Version]
- Bahtiar, E.T.; Nugroho, N.; Surjokusumo, S. Estimating Young’s Modulus and Modulus of Rupture of Coconut Logs using Reconstruction Method. Civ. Eng. Dimens. 2010, 12, 65–72. [Google Scholar] [CrossRef][Green Version]
- BS 373:1957; Methods of Testing Small Clear Specimens of Timber. British Standards: London, UK, 1957.
- Bahtiar, E.T.; Nugroho, N.; Karlinasari, L.; Darwis, A.; Surjokusumo, S. Rasio Ikatan Pembuluh sebagai Substitusi Rasio Modulus Elastisitas pada Analisa Layer System pada Bilah Bambu dan Bambu Laminasi. J. Tek. Sipil 2014, 21, 147. [Google Scholar] [CrossRef]
- Veldman, S.; Bergsma, O.; Beukers, A. Bending of anisotropic inflated cylindrical beams. Thin-Walled Struct. 2005, 43, 461–475. [Google Scholar] [CrossRef]
- Manikandan, P.; Rao, G.S.; Srinath, J.; Sharma, V.; Narayanan, P.R.; Sharma, S.; George, K.M. Axial and Bending Fatigue Testing of AISI 304 L Plumbing Tubes Used for Launch Vehicles Control System. Mater. Sci. Forum 2015, 830–831, 187–190. [Google Scholar] [CrossRef]
- Trujillo, D.; Jangra, S.; Gibson, J.M. Flexural properties as a basis for bamboo strength grading. Proc. Inst. Civ. Eng.—Struct. Build 2017, 170, 284–294. [Google Scholar] [CrossRef]
- Nurmadina; Nugroho, N.; Bahtiar, E.T. Structural grading of Gigantochloa apus bamboo based on its flexural properties. Constr. Build. Mater. 2017, 157, 1173–1189. [Google Scholar] [CrossRef]
- Nugroho, N.; Bahtiar, E.T. Grading Development of Indonesian Bamboo Culm: Case Study on Tali Bamboo (Gigantochloa apus). In Proceedings of the 2018 World Conference on Timber Engineering, Seoul, Korea, 20 August 2018. [Google Scholar]
- Saoula, A.; Meftah, S.A.; Mohri, F.; Daya, E.M. Lateral buckling of box beam elements under combined axial and bending loads. J. Constr. Steel Res. 2016, 116, 141–155. [Google Scholar] [CrossRef]
- Galambos, T.V.; Surovek, A.E. Structural Stability of Steel; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2008. [Google Scholar]
- SNI 7973:2013; Spesifikasi Desain Untuk Konstruksi Kayu. Badan Standardisasi Nasional: Jakarta, Indonesia, 2013.
- Suryoatmono, B.; Tjondro, A. Lateral-torsional buckling of orthotropic rectangular section beams. In Proceedings of the 10th World Conference on Timber Engineering, Miyazaki, Japan, 2–5 June 2008. [Google Scholar]
- American National Standard Institution; American Wood Council. NDS, National Design Specification for Wood Construction, ASD/LRFD; American National Standard Institution: Washington, DC, USA, 2012. [Google Scholar]
- EN 1995-1-1:2004; Eurocode 5: Design of Timber Structures—Part 1-1: General—Common Rules and Rules for Buildings. The European Union: Brussels, Belgium, 2004.
- Zahn, J.J. Design of Wood Members Under Combined Load. J. Struct. Eng. 1986, 112, 2109–2126. [Google Scholar] [CrossRef]
- American Wood Council. National Design Specification (NDS) for Wood Construction; American Wood Council: Leesburg, VA, USA, 1986. [Google Scholar]
- Zahn, J. Combined-load Stability Criterion for wood-beam columns. J. Struct. Eng. 1988, 114, 22981. [Google Scholar] [CrossRef]
- American Forest and Paper Association. ANSI/NFoPA NDS-1991 National Design Specification for Wood Construction; American Forest and Paper Association: Washington, DC, USA, 1991. [Google Scholar]
- Zahn, J.J. Biaxial Beam-Column equation for Wood Members. In Proceedings of the 9th structures Congress Proceedings, New York, NY, USA, 29 April–1 May 1991; pp. 56–59. [Google Scholar]
- Kimble, R.E.; Bender, D.A. Stability of Built-Up Timber Beams and Columns: Accounting for Modulus of Elasticity Variability. Pr. Period. Struct. Des. Constr. 2010, 15, 272–277. [Google Scholar] [CrossRef]
- Du, Y.; Mohareb, M.; Doudak, G. Nonsway Model for Lateral Torsional Buckling of Wooden Beams under Wind Uplift. J. Eng. Mech. 2016, 142, 04016104. [Google Scholar] [CrossRef]
- Du, Y.; Mohareb, M.; Doudak, G.; Du, B.Y. Sway Model for the Lateral Torsional Buckling Analysis of Wooden Twin-beam-deck Systems. Structures 2019, 19, 19–29. [Google Scholar] [CrossRef]
- Hu, Y.; Mohareb, M.; Doudak, G. Lateral Torsional Buckling of Wooden Beams with Midspan Lateral Bracing Offset from Section Midheight. J. Eng. Mech. 2017, 143, 04017134. [Google Scholar] [CrossRef]
- Hu, Y.; Mohareb, M.; Doudak, G. Effect of Eccentric Lateral Bracing Stiffness on Lateral Torsional Buckling Resistance of Wooden Beams. Int. J. Struct. Stab. Dyn. 2018, 18, 1850027. [Google Scholar] [CrossRef]
- St-Amour, R.; Doudak, G. Experimental and numerical investigation of lateral torsional buckling of wood I-joists. Can. J. Civ. Eng. 2018, 45, 41–50. [Google Scholar] [CrossRef]
- Burow, J.R.; Manbeck, H.B.; Janowiak, J.J. Lateral Stability Considerations for Composite Wood I-Joists. In Proceedings of the ASAE Annual International Meeting, Tampa, FL, USA, 17–20 July 2005. [Google Scholar]
- Sahraei, A.; Pezeshky, P.; Mohareb, M.; Doudak, G. Simplified expressions for elastic lateral torsional buckling of wooden beams. Eng. Struct. 2018, 174, 229–241. [Google Scholar] [CrossRef]
- Xiao, Q.; Doudak, G.; Mohareb, M. Numerical and experimental investigation of lateral torsional buckling of wood beams. Eng. Struct. 2017, 151, 85–92. [Google Scholar] [CrossRef]
- Balaz, I. Lateral Torsional Buckling of Timber Beams. Wood Res. 2005, 50, 51–58. [Google Scholar]
- AFPA-TR14; Designing for Lateral-Torsional Stability in Wood Members. American Wood Council: Washington DC, USA, 2003.
- ASTM D2915; Standard Practice for Evaluating Allowable Properties for Grades of Structural Lumber. ASTM: West Conshohocken, PA, USA, 2002. [CrossRef]
- ASTM D5457; Standard specification for computing reference resistance of wood based materials and structural connections for load and resistance factor design. ASTM: West Conshohocken, PA, USA, 2002.
- Blaß, H.J.; Schädle, P. Ductility aspects of reinforced and non-reinforced timber joints. Eng. Struct. 2011, 33, 3018–3026. [Google Scholar] [CrossRef]
- Muñoz, W.; Salenikovich, A.; Mohammad, M.; Quenneville, P. Determination of yield point and ductility of timber assemblies: In search for a harmonised approach. In Proceedings of the 10th World Conference on Timber Engineering, Miyazaki, Japan, 2–5 June 2008. [Google Scholar]
- Jorissen, A.; Fragiacomo, M. General notes on ductility in timber structures. Eng. Struct. 2011, 33, 2987–2997. [Google Scholar] [CrossRef]
- Karacabeyli, E.; Ceccotti, A. Nailed Wood-Frame Shear Walls for Seismic Loads: Test Results and Design Considerations. In Structural Engineering World Wide; SCIRP: Wuhan, China, 1999; pp. 1–9. [Google Scholar]
- Yasumura, M.; Kawai, N. Estimating seismic performance of wood-framed structures. In Proceedings of the 5th World Conference on Timber Engineering, Montreux, Switzerland, 17–20 August 1998; Volume 2, pp. 564–571. [Google Scholar]
- Foliente, G.C. Issues in seismic performance testing and evaluation of timber structural systems. In Proceedings of the International Wood Engineering Conference, New Orleans, LA, USA, 28–31 October 1996; p. 8. [Google Scholar]
- EN 12512:2001/A1:2005; Timber Structures—Test methods—Cyclic Testing of Joints Made with Mechanical Fasteners. European Committee for Standardization: Bruxelles, Belgium, 2005.
- SIA 265:2003; Timber Structures. Swiss Society of Engineers and Architects: Zurich, Switzerland, 2003.
- Foliente, G.C.; Leicester, R.H. Evaluation of mechanical joint systems in timber structures. In Proceedings of the 25th Forest Products Research Conference, Melbourne, VIC, Australia, 18–21 November 1996; pp. 2–16. [Google Scholar]
- ASTM D245; Standard Practice for Establishing Structural Grades and Related Allowable Properties for Visually Graded Lumber. ASTM: West Conshohocken, PA, USA, 2000. [CrossRef]
- Bergou, E.H.; Diouane, Y.; Kungurtsev, V. Convergence and Complexity Analysis of a Levenberg–Marquardt Algorithm for Inverse Problems. J. Optim. Theory Appl. 2020, 185, 927–944. [Google Scholar] [CrossRef]
- Wistara, N.J.; Sukowati, M.; Pamoengkas, P. The properties of red meranti wood (Shorea leprosula Miq) from stand with thinning and shade free gap treatments. J. Indian Acad. Wood Sci. 2016, 13, 21–32. [Google Scholar] [CrossRef]
- Alokabel, K.; Lay, Y.E.; Wonlele, T. Penentuan Kelas Kuat Kayu Lokal di Pulau Timor Sebagai Bahan Konstruksi. JUTEKS J. Tek. Sipil 2018, 2, 139–148. [Google Scholar] [CrossRef]
- Lempang, M. Basic properties and uses of agathis (Agathis hamii M. Dr.) wood from South Sulawesi. J. Penelit. Kehutan. Wallacea 2017, 6, 157–167. [Google Scholar] [CrossRef]
- NI-5 PKKI 1961; Peraturan Konstruksi Kayu Indonesia. PKKI: Jakarta, Indonesia, 1961.
- Ong, C.B.; Ansell, M.P.; Chang, W.-S.; Walker, P. Bending properties of finger-jointed Malaysian dark red meranti. Int. Wood Prod. J. 2019, 10, 49–54. [Google Scholar] [CrossRef]
- Anoop, E.V.; Jijeesh, C.M.; Sindhumathi, C.R.; Jayasree, C.E. Wood physical, Anatomical and Mechanical properties of Big Leaf Mahogany (Swietenia macrophylla Roxb) a potential exotic for South India. Res. J. Agric. For. Sci. 2014, 2, 7–13. [Google Scholar]
- Darmawan, W.; Nandika, D.; Afaf, B.D.H.; Rahayu, I.; Lumongga, D. Radial Variation in Selected Wood Properties of Indonesian Merkusii Pine. J. Korean Wood Sci. Technol. 2018, 46, 323–337. [Google Scholar] [CrossRef]
- Ishiguri, F.; Wahyudi, I.; Iizuka, K.; Yokota, S.; Yoshizawa, N. Radial Variation of Wood Property in Agathis sp. and Pinus insularis Growing at Plantation in Indonesia. Wood Res. J. 2010, 1, 1–6. [Google Scholar]
- Eurocode 8; Design of structures for earthquake resistance. European Comission: Brussel, Belgium, 2005.
- Szabolcs, K.; Sandor, F.; Jozsef, A.; Taschner, R. Effect of knots on the bending strength and the modulus of elasticity of wood. Wood. Res. 2013, 58, 617–626. [Google Scholar]
- Pope, D.; Marcroft, J.; Whale, L. The effect of global slope of grain on the bending strength of scaffold boards. Holz als Roh- Werkst. 2005, 63, 321–326. [Google Scholar] [CrossRef]
- Bahtiar, E.T. Keandalan modulus of elasticity (MOE) untuk menduga kekuatan kayu bercacat akibat lubang bor. JTHH 2005, 18, 80–90. [Google Scholar]
- Mardikanto, T.R.; Karlinasari, L.; Bahtiar, E.T. Sifat Mekanis Kayu; IPB Press: Bogor, Indonesia, 2017. [Google Scholar]
- Rocha, M.F.V.; Costa, L.R.; Costa, L.J.; De Araújo, A.C.C.; Soares, B.C.D.; Hein, P. Wood Knots Influence the Modulus of Elasticity and Resistance to Compression. Floresta e Ambient. 2018, 25, e20170906. [Google Scholar] [CrossRef]
- Brunetti, M.; Nocetti, M.; Burato, P. Strength Properties of Chestnut Structural Timber with Wane. Adv. Mater. Res. 2013, 778, 377–384. [Google Scholar] [CrossRef]
- Brancheriau, L.; Bailleres, H.; Guitard, D. Comparison between modulus of elasticity values calculated using 3 and 4 point bending tests on wooden samples. Wood Sci. Technol. 2002, 36, 367–383. [Google Scholar] [CrossRef]
- Hein, P.R.G.; Silva, J.; Brancheriau, L. Correlations among microfibril angle, density, modulus of elasticity, modulus of rupture and shrinkage in 6-year-old Eucalyptus urophylla × E. grandis. Maderas Cienc Y Tecnol. 2013, 15, 171–182. [Google Scholar] [CrossRef]
- Sholadoye, I.O.; Abubakar, I.; Annafi, Q.B.; Ejeh, S.P. Evaluation of Some Wood Properties of Nigeria Timber Using Four-Point Bending Test. Adv. Multidiscip. Res. J. 2016, 2, 133–144. [Google Scholar]
- Divos, F.; Tanaka, T. Lumber Strength Estimation by Multiple Regression. Holzforschung 1997, 51, 467–471. [Google Scholar] [CrossRef]
- Machado, J.S.; Palma, P. Non-destructive evaluation of the bending behaviour of in-service pine timber structural elements. Mater. Struct. 2010, 44, 901–910. [Google Scholar] [CrossRef]
- Pelletier, B.; Doudak, G. Investigation of the lateral-torsional buckling behaviour of engineered wood I-joists with varying end conditions. Eng. Struct. 2019, 187, 329–340. [Google Scholar] [CrossRef]
- Hayatunnufus, A.; Nugroho, N.; Bahtiar, E.T. Faktor Stabilitas Balok Kayu pada Konfigurasi Pembebanan Terpusat. J. Tek. Sipil dan Lingkung. 2022, 7, 129–146. [Google Scholar] [CrossRef]
- Bahtiar, E.T. Experimental Study on Flexural Buckling of Timber, Mendeley Data V3; Elsevier Inc.: NY, USA, 2020. [Google Scholar] [CrossRef]


 = LVDT).
= LVDT).
 = LVDT).
= LVDT).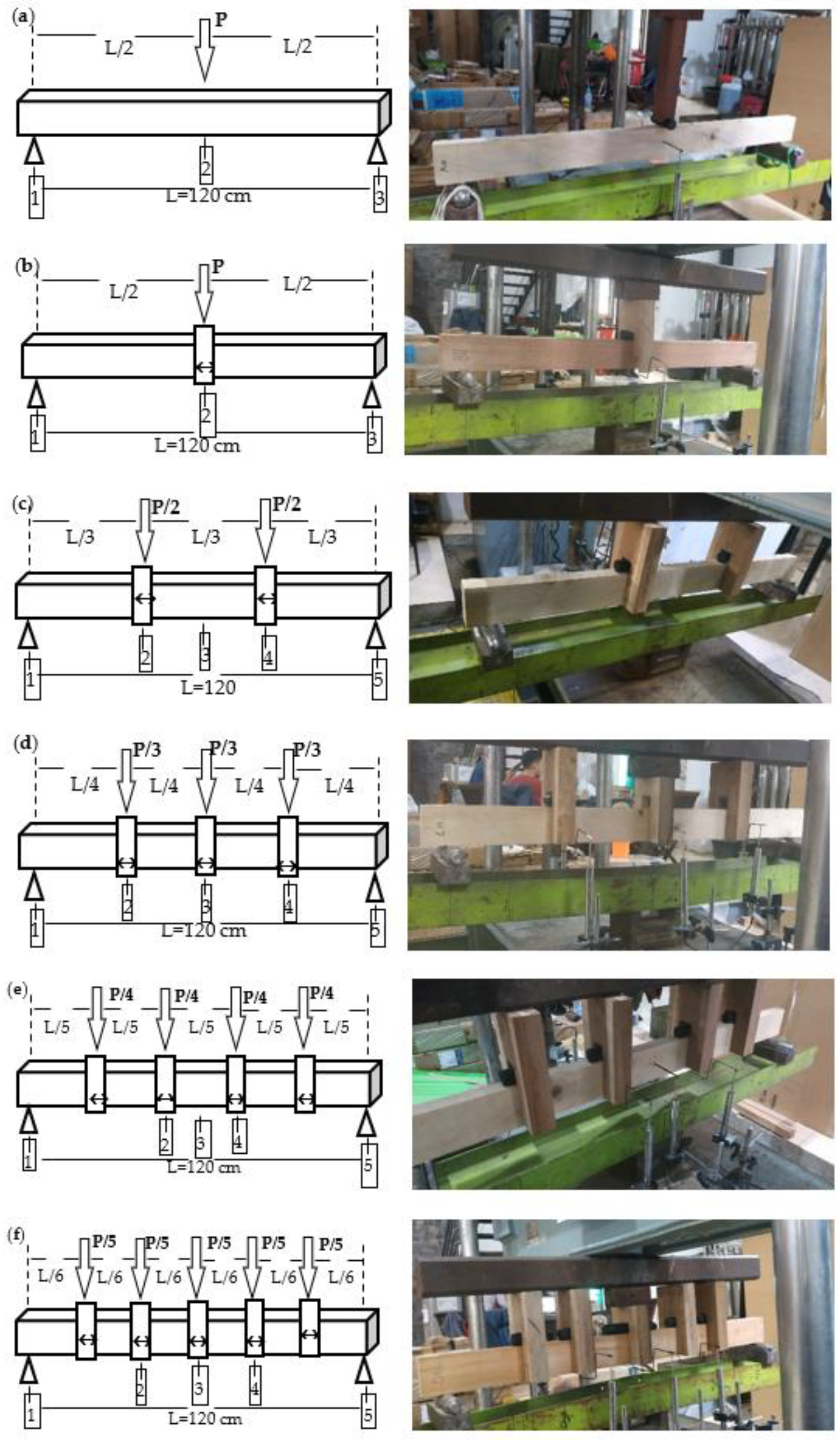


| Loading Configuration | Bending Formula | |
|---|---|---|
| center-point loading with or without lateral support | ||
| third point loading with lateral supports | ||
| fourth point loading with lateral supports | ||
| fifth point loading with lateral supports | ||
| sixth point loading with lateral supports | ||
| No | Single Span Beam | Effective Span Length (le) | |
|---|---|---|---|
| lu/d < 7 | lu/d ≥ 7 | ||
| 1. | center-point loading without lateral support | le = 1.8 lu | le = 1.37 lu + 3d |
| 2. | center-point loading with lateral support | le = 1.11 lu | |
| 3. | third point loading with lateral supports | le = 1.68 lu | |
| 4. | fourth point loading with lateral supports | le = 1.54 lu | |
| 5. | fifth point loading with lateral supports | le = 1.68 lu | |
| 6. | sixth point loading with lateral supports | le = 1.73 lu | |
| Modulus of Elasticity (E, MPa) | Modulus of Rupture (SR, MPa) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | Min | Max | Mean | s | CV (%) | Min | Max | Mean | s | CV (%) | ||
| Red meranti | 50 | 8346 | 13879 | 11001 | 1379 | 12.54 | 44.07 | 90.87 | 72.42 | 12.15 | 16.77 | 151.91 |
| Mahogany | 50 | 5275 | 10393 | 8033 | 1079 | 13.43 | 38.83 | 94.69 | 70.47 | 11.37 | 16.14 | 113.99 |
| Pine | 50 | 3460 | 10695 | 7218 | 1837 | 25.45 | 28.87 | 76.87 | 55.15 | 10.18 | 18.46 | 130.88 |
| Agathis | 50 | 6020 | 8604 | 6976 | 618 | 8.85 | 17.71 | 25.03 | 20.59 | 1.58 | 7.67 | 336.21 |
| Timber Species | Red Meranti | Mahogany | Pine | Agathis | ||||
|---|---|---|---|---|---|---|---|---|
| Parameter | E | SR | E | SR | E | SR | E | SR |
| Weibull | AD = 0.467 p = 0.244 | AD = 0.291 p > 0.250 | AD = 0.256 p > 0.250 | AD = 0.544 p = 0.172 | AD = 0.191 p > 0.250 | AD = 0.476 p > 0.250 | AD = 1.675 p < 0.010 | AD = 2.561 p < 0.010 |
| 5% PE | 8346 | 48.37 | 5949 | 48.56 | 3936 | 35.60 | 5784 | 17.44 |
| Lognormal | AD = 0.916 p = 0.018 | AD = 1.400 p < 0.005 | AD = 0.627 p = 0.097 | AD = 0.291 p = 0.053 | AD = 0.731 p = 0.093 | AD = 1.114 p = 0.006 | AD = 0.547 p = 0.151 | AD = 0.630 p = 0.095 |
| 5% PE | 8435 | 49.24 | 5993 | 49.25 | 4009 | 36.09 | 5843 | 17.65 |
| 5% TL (75%) | 8653 | 51.08 | 6164 | 50.97 | 4235 | 37.57 | 5945 | 17.92 |
| Normal | AD = 0.684 p = 0.070 | AD = 0.665 p = 0.078 | AD = 0.270 p = 0.663 | AD = 0.561 p = 0.139 | AD = 0.199 p = 0.880 | AD = 0.476 p = 0.229 | AD = 0.760 p = 0.045 | AD = 0.941 p = 0.016 |
| Mean | 11002 | 72.42 | 8033 | 70.47 | 7218 | 55.15 | 6977 | 27.28 |
| s | 1379 | 12.15 | 1079 | 11.37 | 1837 | 10.18 | 618 | 1.58 |
| 5% PE | 8228 | 48.00 | 5864 | 47.60 | 3524 | 34.68 | 5735 | 24.11 |
| 5% TL (75%) | 8504 | 50.42 | 6080 | 49.87 | 3891 | 36.71 | 5858 | 24.42 |
| Non-Parametric | ||||||||
| 5% PE | 8735 | 45.22 | 5670 | 50.96 | 3940 | 34.08 | 6164 | 18.25 |
| 5% TL (75%) | 8347 | 44.07 | 5276 | 38.83 | 3460 | 28.87 | 6020 | 17.71 |
| N | Min | Max | Mean | S | CV (%) | |
|---|---|---|---|---|---|---|
| Red meranti | 50 | 2.2 | 5.0 | 3.6 | 0.6 | 17.9 |
| Mahogany | 50 | 2.3 | 5.0 | 3.4 | 0.6 | 17.3 |
| Pine | 50 | 2.1 | 5.3 | 3.6 | 0.6 | 16.7 |
| Agathis | 50 | 2.6 | 4.0 | 3.3 | 0.3 | 10.1 |
| Timber Species | Properties | N | Min | Max | Mean | S | CV (%) |
|---|---|---|---|---|---|---|---|
| Red meranti | S due to slope of grain (%) | 18 | 40.00 | 84.50 | 60.62 | 14.85 | 24.49 |
| S due to knots (%) | 18 | 49.00 | 100.00 | 87.58 | 14.77 | 16.87 | |
| S due to shakes, checks, splits (%) | 18 | 50.00 | 100.00 | 94.44 | 16.17 | 17.12 | |
| S total value (%) | 18 | 16.80 | 84.50 | 50.27 | 17.56 | 34.94 | |
| Mahogany | S due to slope of grain (%) | 18 | 40.00 | 100.00 | 67.01 | 16.98 | 25.33 |
| S due to knots (%) | 18 | 62.00 | 100.00 | 73.36 | 10.34 | 14.09 | |
| S due to shakes, checks, splits (%) | 18 | 62.50 | 100.00 | 77.96 | 11.27 | 14.45 | |
| S total value (%) | 18 | 25.58 | 74.57 | 50.03 | 16.87 | 33.72 | |
| Pine | S due to slope of grain (%) | 18 | 40.00 | 92.50 | 68.26 | 12.29 | 18.00 |
| S due to knots (%) | 18 | 73.67 | 96.25 | 88.71 | 7.50 | 8.45 | |
| S due to shakes, checks, splits (%) | 18 | 50.00 | 100.00 | 83.33 | 24.25 | 29.10 | |
| S total value (%) | 18 | 14.74 | 75.50 | 44.74 | 18.75 | 41.91 | |
| Agathis | S due to slope of grain (%) | 18 | 40.00 | 45.98 | 40.40 | 1.42 | 3.53 |
| S due to knots (%) | 18 | 37.83 | 100.00 | 56.89 | 18.17 | 31.95 | |
| S due to shakes, checks, splits (%) | 18 | 100.00 | 100.00 | 100.00 | 0.00 | 0.00 | |
| S total value (%) | 18 | 15.13 | 40.00 | 23.03 | 7.56 | 32.80 |
| Parameter | Estimate | Standard Error | t-Value | p-Value | Lower Confident Limit | Upper Confident Limit |
|---|---|---|---|---|---|---|
| a ≅ KbE | 0.413 | 0.038 | 10.852 | 0.00 | 0.338 | 0.488 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bahtiar, E.T.; Erizal, E.; Hermawan, D.; Nugroho, N.; Hidayatullah, R. Experimental Study of Beam Stability Factor of Sawn Lumber Subjected to Concentrated Bending Loads at Several Points. Forests 2022, 13, 1480. https://doi.org/10.3390/f13091480
Bahtiar ET, Erizal E, Hermawan D, Nugroho N, Hidayatullah R. Experimental Study of Beam Stability Factor of Sawn Lumber Subjected to Concentrated Bending Loads at Several Points. Forests. 2022; 13(9):1480. https://doi.org/10.3390/f13091480
Chicago/Turabian StyleBahtiar, Effendi Tri, Erizal Erizal, Dede Hermawan, Naresworo Nugroho, and Rizky Hidayatullah. 2022. "Experimental Study of Beam Stability Factor of Sawn Lumber Subjected to Concentrated Bending Loads at Several Points" Forests 13, no. 9: 1480. https://doi.org/10.3390/f13091480
APA StyleBahtiar, E. T., Erizal, E., Hermawan, D., Nugroho, N., & Hidayatullah, R. (2022). Experimental Study of Beam Stability Factor of Sawn Lumber Subjected to Concentrated Bending Loads at Several Points. Forests, 13(9), 1480. https://doi.org/10.3390/f13091480







