Using a Vegetation Index-Based Mixture Model to Estimate Fractional Vegetation Cover Products by Jointly Using Multiple Satellite Data: Method and Feasibility Analysis
Abstract
:1. Introduction
- (i)
- analyzing the necessity of MODIS Vv and Vs downscaling for finer-resolution FVC estimation; and
- (ii)
- assessing uncertainty due to spectral response function differences for FVC estimation with different satellite data.
2. Materials and Methods
2.1. Study Areas and Field Measurements
2.2. Finer-Resolution NDVI
2.3. Spectral Library
2.4. Vv and Vs Downscaling
2.5. Spectral Normalization
2.6. FVC Production
3. Results
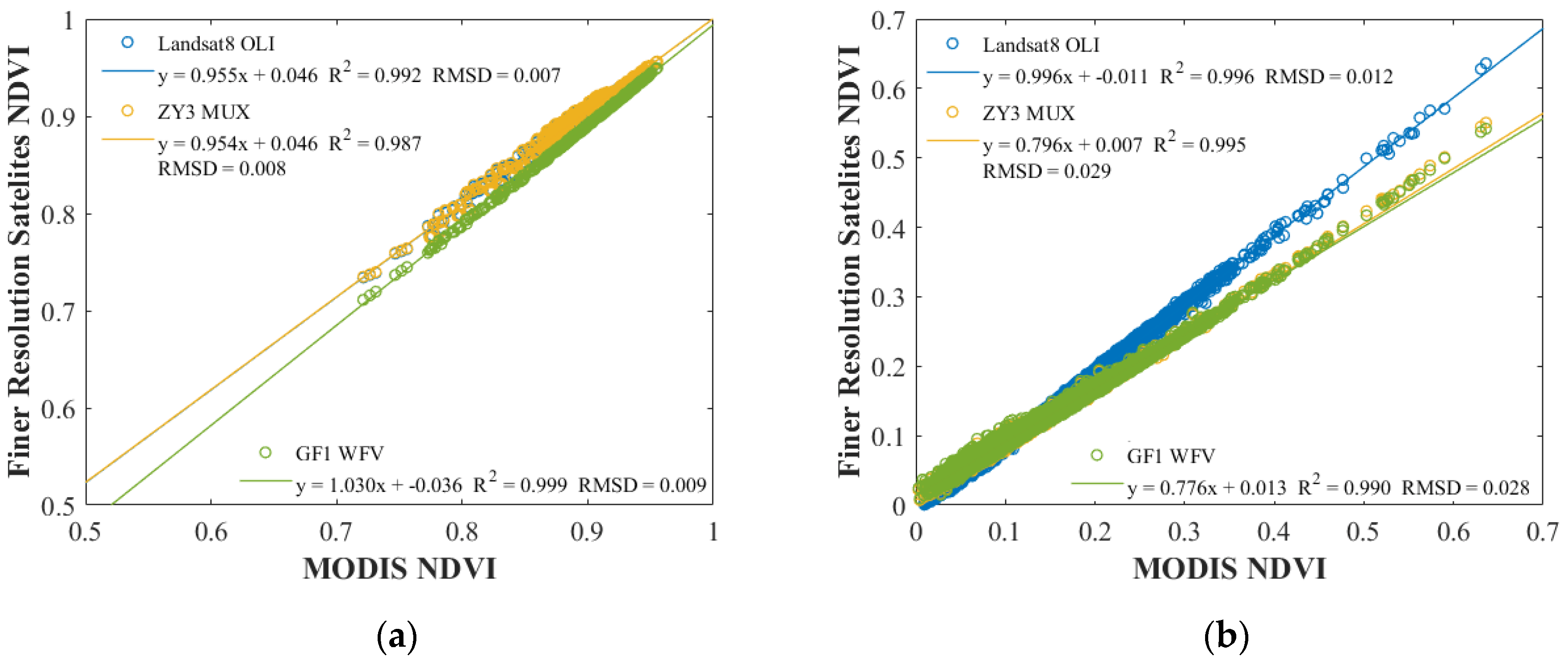
3.1. Necessity Analysis for Vv and Vs Downscaling
3.2. Uncertainty Analysis for Spectral Normalization
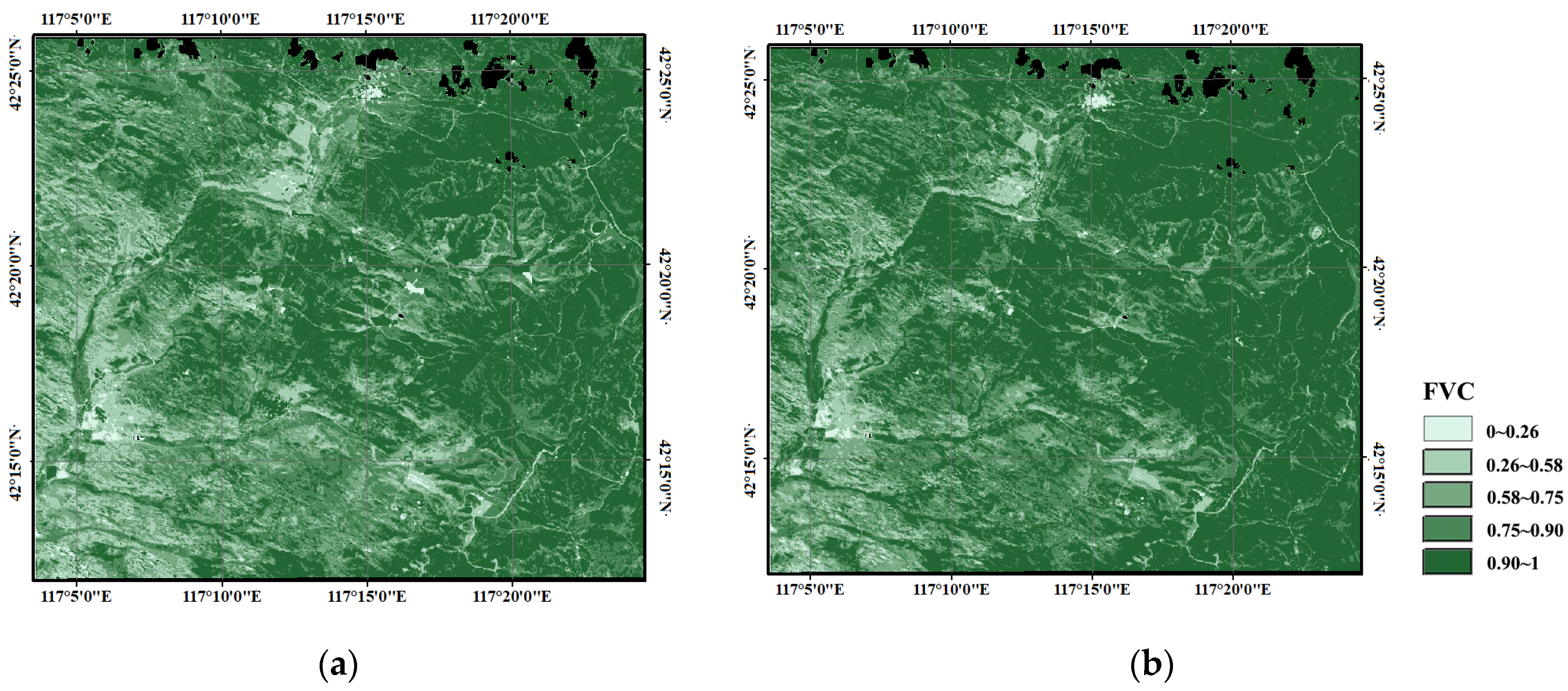
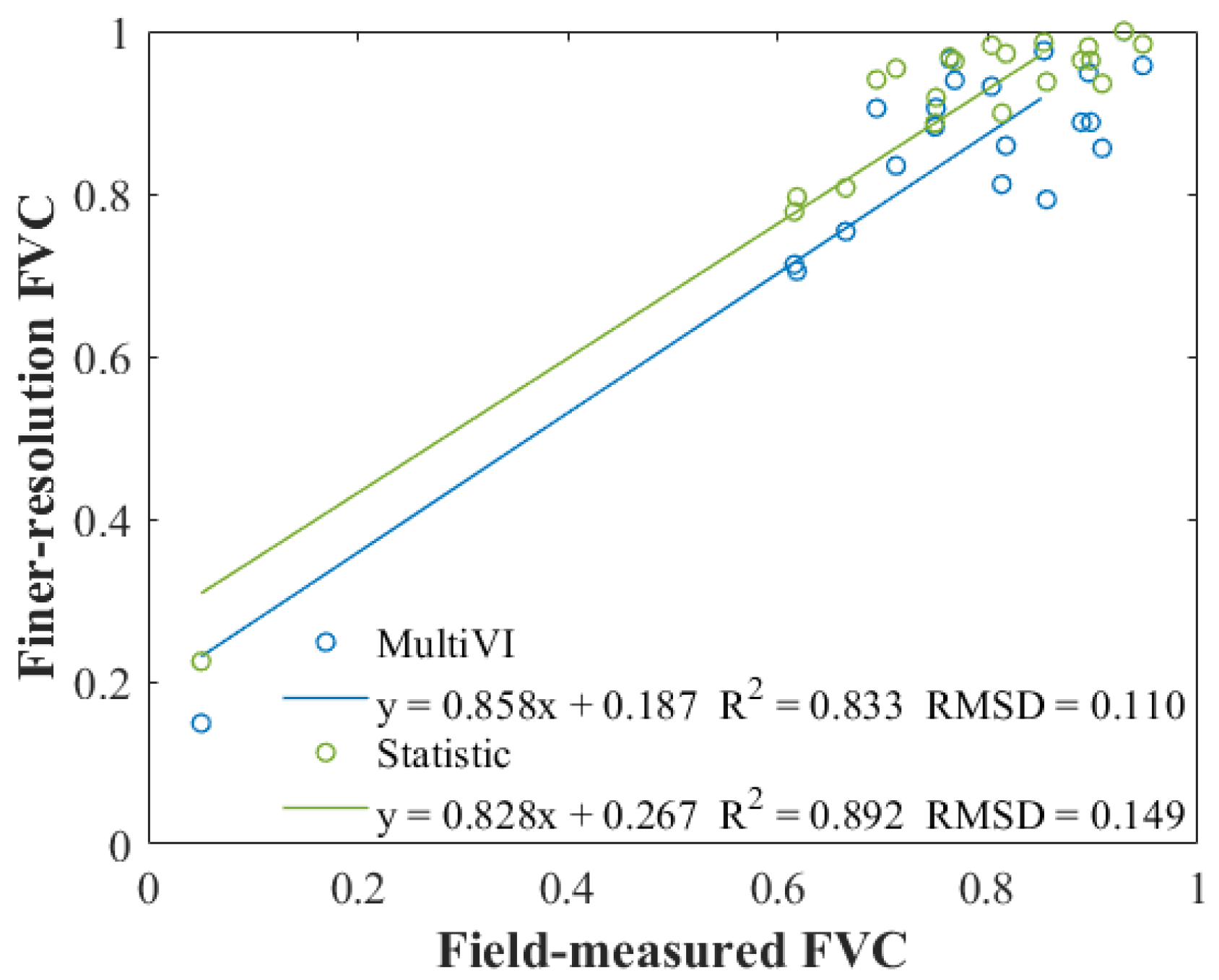
3.3. Accuracy Analysis for FVC by Comparing with Traditional VI-Based Linear Mixture Model
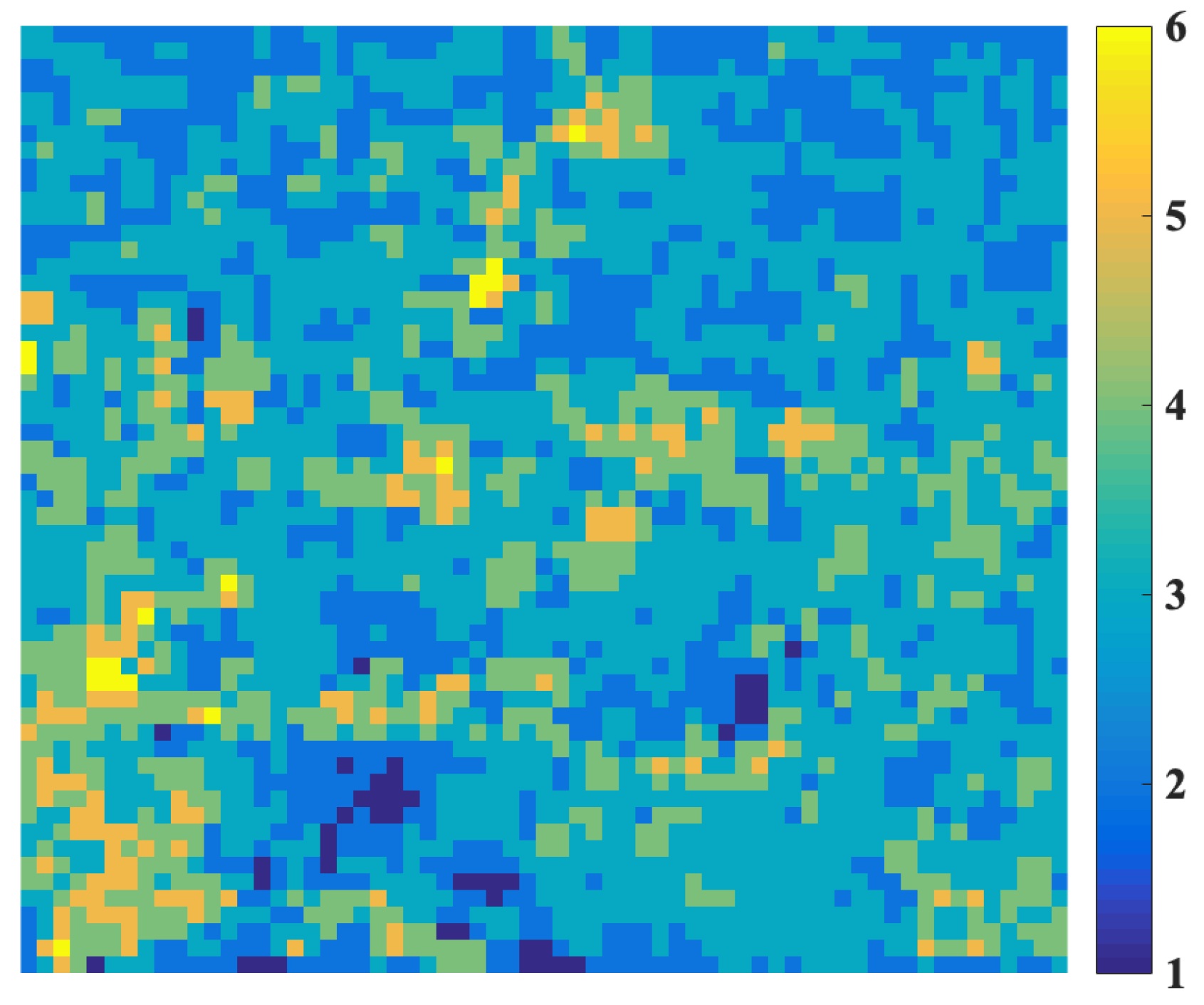
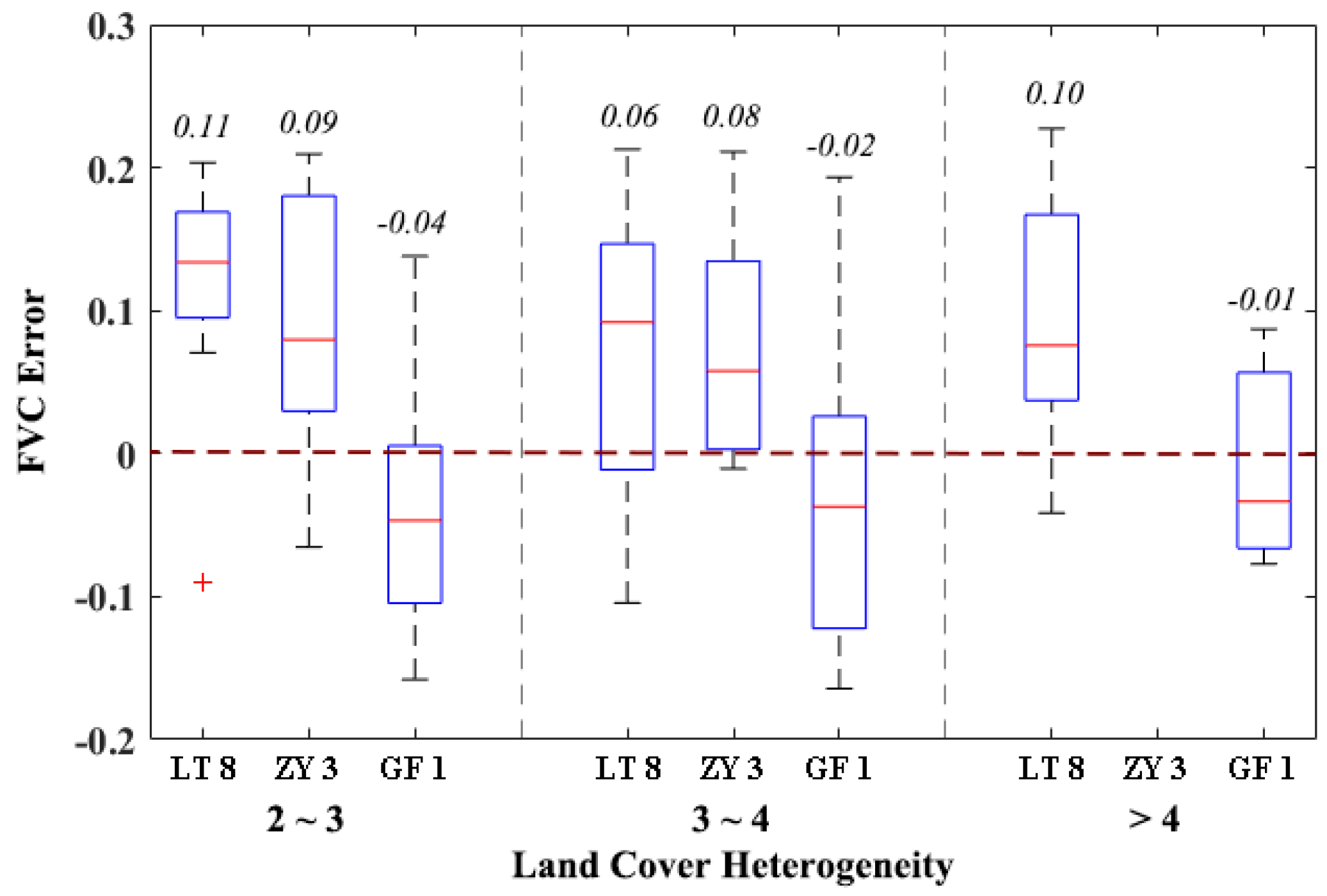
4. Discussion
4.1. Applicability of the Vv and Vs Downscaling Method
4.2. Spectral Analysis for Multiple Satellite Sensors
4.3. Prospect of FVC Estimation by Joint Using Multiple Satellite Data
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gutman, G.; Ignatov, A. The derivation of the green vegetation fraction from NOAA/AVHRR data for use in numerical weather prediction models. Int. J. Remote Sens. 1998, 19, 1533–1543. [Google Scholar] [CrossRef]
- Arneth, A. Climate science: Uncertain future for vegetation cover. Nature 2015, 524, 44–45. [Google Scholar] [CrossRef] [Green Version]
- Deardorff, J. Efficient prediction of ground surface temperature and moisture, with inclusion of a layer of vegetation. J. Geophys. Res. Ocean 1978, 83, 1889–1903. [Google Scholar] [CrossRef] [Green Version]
- Lu, H.; Raupach, M.R.; McVicar, T.R.; Barrett, D.J. Decomposition of vegetation cover into woody and herbaceous components using AVHRR NDVI time series. Remote Sens. Environ. 2003, 86, 1–18. [Google Scholar] [CrossRef]
- Ormsby, J.P.; Choudhury, B.J.; Owe, M. Vegetation spatial variability and its effect on vegetation indices. Int. J. Remote Sens. 1987, 8, 1301–1306. [Google Scholar] [CrossRef]
- Carlson, T.N.; Sanchez-Azofeifa, G.A. Satellite Remote Sensing of Land Use Changes in and around San José, Costa Rica. Remote Sens. Environ. 1999, 70, 247–256. [Google Scholar] [CrossRef]
- Sellers, P.J.; Tucker, C.J.; Collatz, G.J.; Los, S.O.; Justice, C.O.; Dazlich, D.A.; Randall, D.A. A Revised Land Surface Parameterization (SiB2) for Atmospheric GCMS. Part II: The Generation of Global Fields of Terrestrial Biophysical Parameters from Satellite Data. J. Clim. 1996, 9, 706–737. [Google Scholar] [CrossRef] [Green Version]
- Gan, M.; Deng, J.; Zheng, X.; Hong, Y.; Wang, K. Monitoring Urban Greenness Dynamics Using Multiple Endmember Spectral Mixture Analysis. PLoS ONE 2014, 9, e112202. [Google Scholar] [CrossRef]
- Pan, J.; Wen, Y. Estimation of soil erosion using RUSLE in Caijiamiao watershed, China. Nat. Hazards 2014, 71, 2187–2205. [Google Scholar] [CrossRef]
- Shao, Z.; Cai, J.; Fu, P.; Hu, L.; Liu, T. Deep learning-based fusion of Landsat-8 and Sentinel-2 images for a harmonized surface reflectance product. Remote Sens. Environ. 2019, 235, 111425. [Google Scholar] [CrossRef]
- Wang, X.; Jia, K.; Liang, S.; Li, Q.; Wei, X.; Yao, Y.; Zhang, X.; Tu, Y. Estimating Fractional Vegetation Cover From Landsat-7 ETM+ Reflectance Data Based on a Coupled Radiative Transfer and Crop Growth Model. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5539–5546. [Google Scholar] [CrossRef]
- Liu, M.; Yang, W.; Chen, J.; Chen, X. An Orthogonal Fisher Transformation-Based Unmixing Method Toward Estimating Fractional Vegetation Cover in Semiarid Areas. IEEE Geosci. Remote Sens. Lett. 2017, 14, 449–453. [Google Scholar] [CrossRef]
- Jia, K.; Liang, S.; Gu, X.; Baret, F.; Wei, X.; Wang, X.; Yao, Y.; Yang, L.; Li, Y. Fractional vegetation cover estimation algorithm for Chinese GF-1 wide field view data. Remote Sens. Environ. 2016, 177, 184–191. [Google Scholar] [CrossRef]
- Zeng, X.; Dickinson, R.E.; Walker, A.; Shaikh, M.; DeFries, R.S.; Qi, J. Derivation and Evaluation of Global 1-km Fractional Vegetation Cover Data for Land Modeling. J. Appl. Meteorol. 2000, 39, 826–839. [Google Scholar] [CrossRef]
- Yang, G.; Pu, R.; Zhang, J.; Zhao, C.; Feng, H.; Wang, J. Remote sensing of seasonal variability of fractional vegetation cover and its object-based spatial pattern analysis over mountain areas. ISPRS J. Photogramm. Remote Sens. 2013, 77, 79–93. [Google Scholar] [CrossRef]
- Waldner, F.; Canto, G.S.; Defourny, P. Automated annual cropland mapping using knowledge-based temporal features. ISPRS J. Photogramm. Remote Sens. 2015, 110, 1–13. [Google Scholar] [CrossRef]
- Gao, L.; Wang, X.; Johnson, B.A.; Tian, Q.; Wang, Y.; Verrelst, J.; Mu, X.; Gu, X. Remote sensing algorithms for estimation of fractional vegetation cover using pure vegetation index values: A review. ISPRS J. Photogramm. Remote Sens. 2020, 159, 364–377. [Google Scholar] [CrossRef]
- Mu, X.; Song, W.; Gao, Z.; McVicar, T.R.; Donohue, R.J.; Yan, G. Fractional vegetation cover estimation by using multi-angle vegetation index. Remote Sens. Environ. 2018, 216, 44–56. [Google Scholar] [CrossRef]
- Wang, L.; Yang, R.; Tian, Q.; Yang, Y.; Zhou, Y.; Sun, Y.; Mi, X. Comparative Analysis of GF-1 WFV, ZY-3 MUX, and HJ-1 CCD Sensor Data for Grassland Monitoring Applications. Remote Sens. 2015, 7, 2089. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Chen, Z.-x.; Jiang, Z.-w.; Wu, W.-b.; Ren, J.-q.; Liu, B.; Tuya, H. Comparative analysis of GF-1, HJ-1, and Landsat-8 data for estimating the leaf area index of winter wheat. J. Integr. Agric. 2017, 16, 266–285. [Google Scholar] [CrossRef]
- Song, W.; Mu, X.; Ruan, G.; Gao, Z.; Li, L.; Yan, G. Estimating fractional vegetation cover and the vegetation index of bare soil and highly dense vegetation with a physically based method. Int. J. Appl. Earth Obs. Geoinf. 2017, 58, 168–176. [Google Scholar] [CrossRef]
- Mu, X.; Huang, S.; Ren, H.; Yan, G.; Song, W.; Ruan, G. Validating GEOV1 fractional vegetation cover derived from coarse-resolution remote sensing images over croplands. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 439–446. [Google Scholar] [CrossRef]
- Mu, X.; Huang, S.; Chen, Y. HiWATER: Dataset of Fractional Vegetation Cover in the middle reaches of the Heihe River Basin. Heihe Plan Sci. Data Cent. 2013. [Google Scholar] [CrossRef]
- Song, W.; Mu, X.; Yan, G.; Huang, S. Extracting the Green Fractional Vegetation Cover from Digital Images Using a Shadow-Resistant Algorithm (SHAR-LABFVC). Remote Sens. 2015, 7, 10425. [Google Scholar] [CrossRef] [Green Version]
- Vermote, E.; Justice, C.; Claverie, M.; Franch, B. Preliminary analysis of the performance of the Landsat 8/OLI land surface reflectance product. Remote Sens. Environ. 2016, 185, 46–56. [Google Scholar] [CrossRef]
- Zhong, B.; Wu, S.; Yang, A.; Liu, Q. An Improved Aerosol Optical Depth Retrieval Algorithm for Moderate to High Spatial Resolution Optical Remotely Sensed Imagery. Remote Sens. 2017, 9, 555. [Google Scholar] [CrossRef] [Green Version]
- Qi, J.; Xie, D.; Yin, T.; Yan, G.; Gastellu-Etchegorry, J.-P.; Li, L.; Zhang, W.; Mu, X.; Norford, L.K. LESS: LargE-Scale remote sensing data and image simulation framework over heterogeneous 3D scenes. Remote Sens. Environ. 2019, 221, 695–706. [Google Scholar] [CrossRef]
- Féret, J.B.; Gitelson, A.A.; Noble, S.D.; Jacquemoud, S. PROSPECT-D: Towards modeling leaf optical properties through a complete lifecycle. Remote Sens. Environ. 2017, 193, 204–215. [Google Scholar] [CrossRef] [Green Version]
- Clark, B.E.; Fanale, F.P.; Salisbury, J.W. Meteorite-asteroid spectral comparison: The effects of comminution, melting, and recrystallization. Icarus 1992, 97, 288–297. [Google Scholar] [CrossRef]
- Batjes, N.H. A Globally Distributed Soil Spectral Library Visible Near Infrared Diffuse Reflectance Spectra; World Agroforestry Centre: Nairobi, Kenya, 2014. [Google Scholar]
- Chen, J.; Ban, Y.; Li, S. Open access to Earth land-cover map. Nature 2014, 514, 434. [Google Scholar] [CrossRef] [Green Version]
- Mu, X.; Zhao, T.; Ruan, G.; Song, J.; Wang, J.; Yan, G.; Mcvicar, T.R.; Yan, K.; Gao, Z.; Liu, Y.; et al. High Spatial Resolution and High Temporal Frequency (30-m/15-day) Fractional Vegetation Cover Estimation over China Using Multiple Remote Sensing Datasets: Method Development and Validation. J. Meteorol. Res. 2021, 35, 128. [Google Scholar] [CrossRef]
- Gao, F.; Anderson, M.C.; Zhang, X.; Yang, Z.; Alfieri, J.G.; Kustas, W.P.; Mueller, R.; Johnson, D.M.; Prueger, J.H. Toward mapping crop progress at field scales through fusion of Landsat and MODIS imagery. Remote Sens. Environ. 2017, 188, 9–25. [Google Scholar] [CrossRef] [Green Version]
- Yan, G.; Mu, X.; Jia, K.; Song, W.; Liu, Y.; Chen, J.; Gao, Z. Chapter 12—Fractional vegetation cover. In Advanced Remote Sensing, 2nd ed.; Liang, S., Wang, J., Eds.; Academic Press: Cambridge, MA, USA, 2020; pp. 477–510. [Google Scholar] [CrossRef]
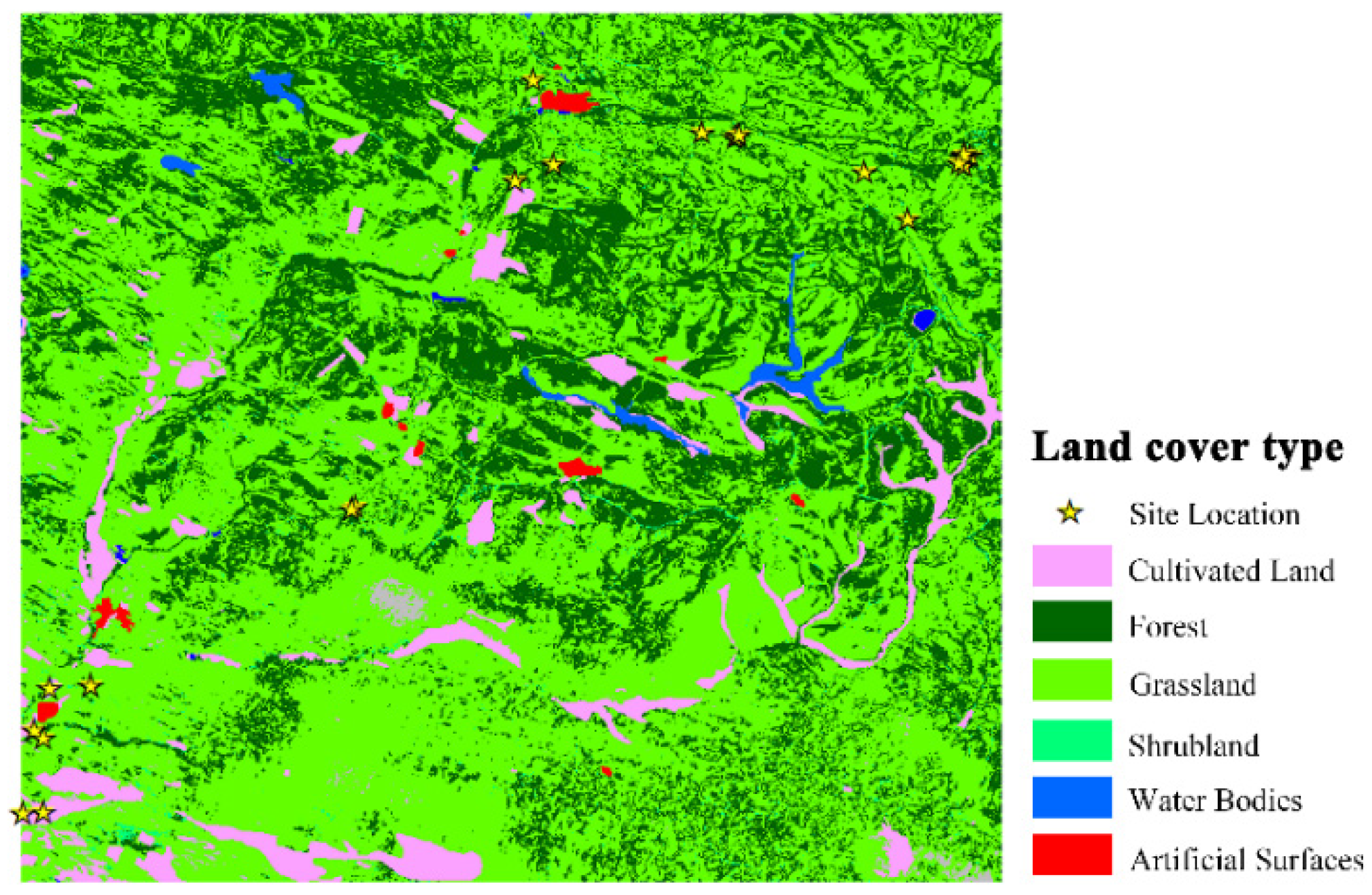
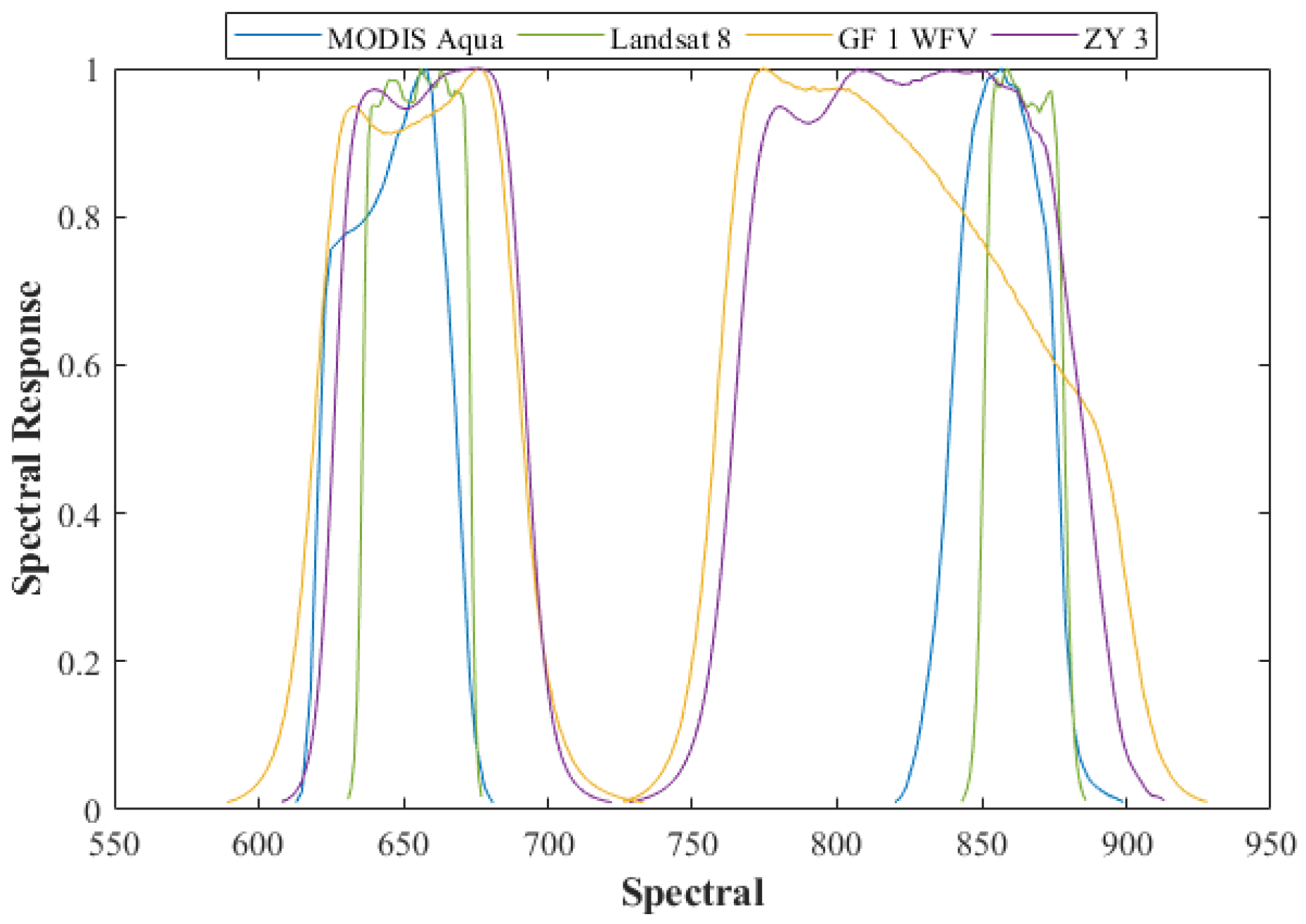
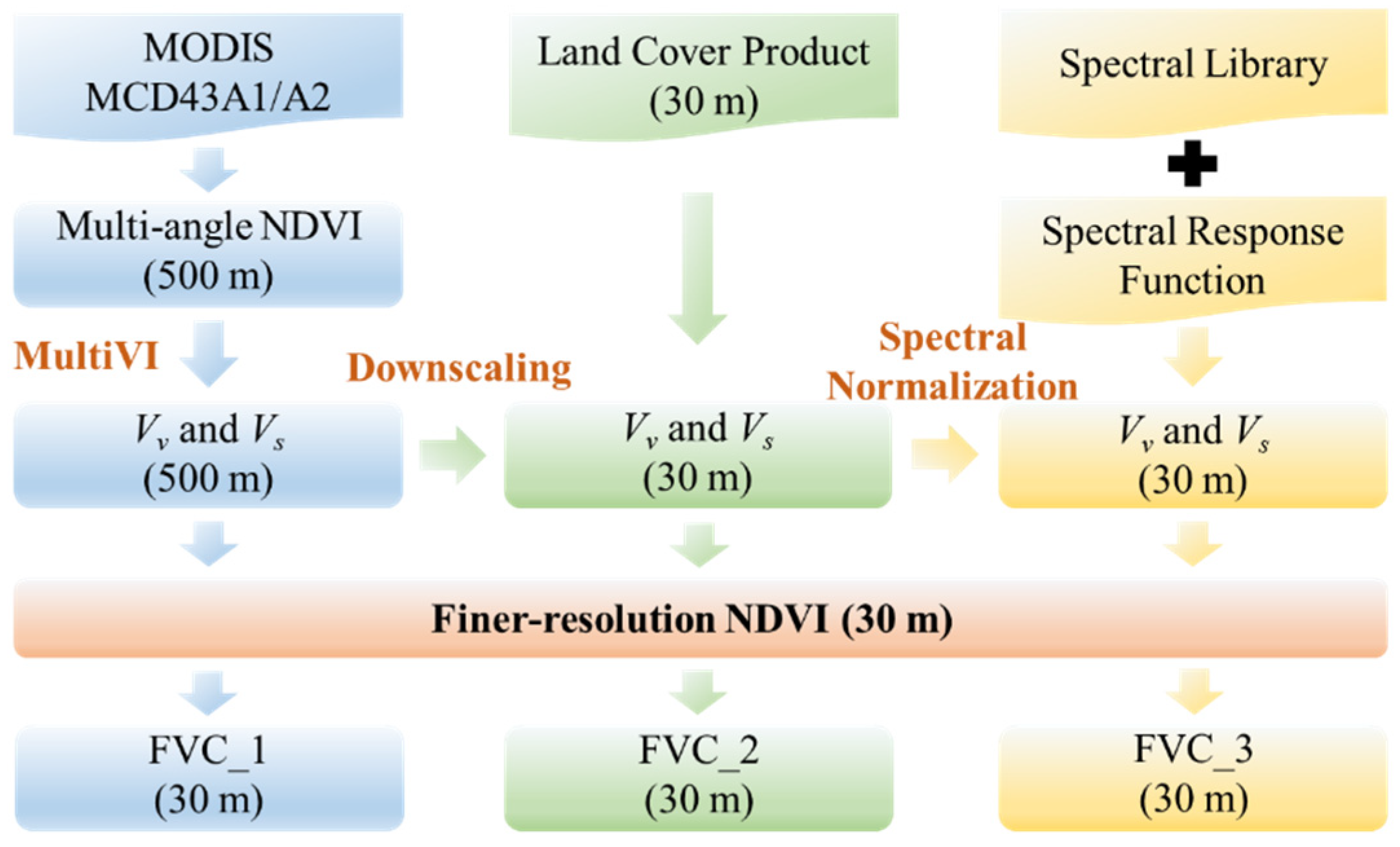
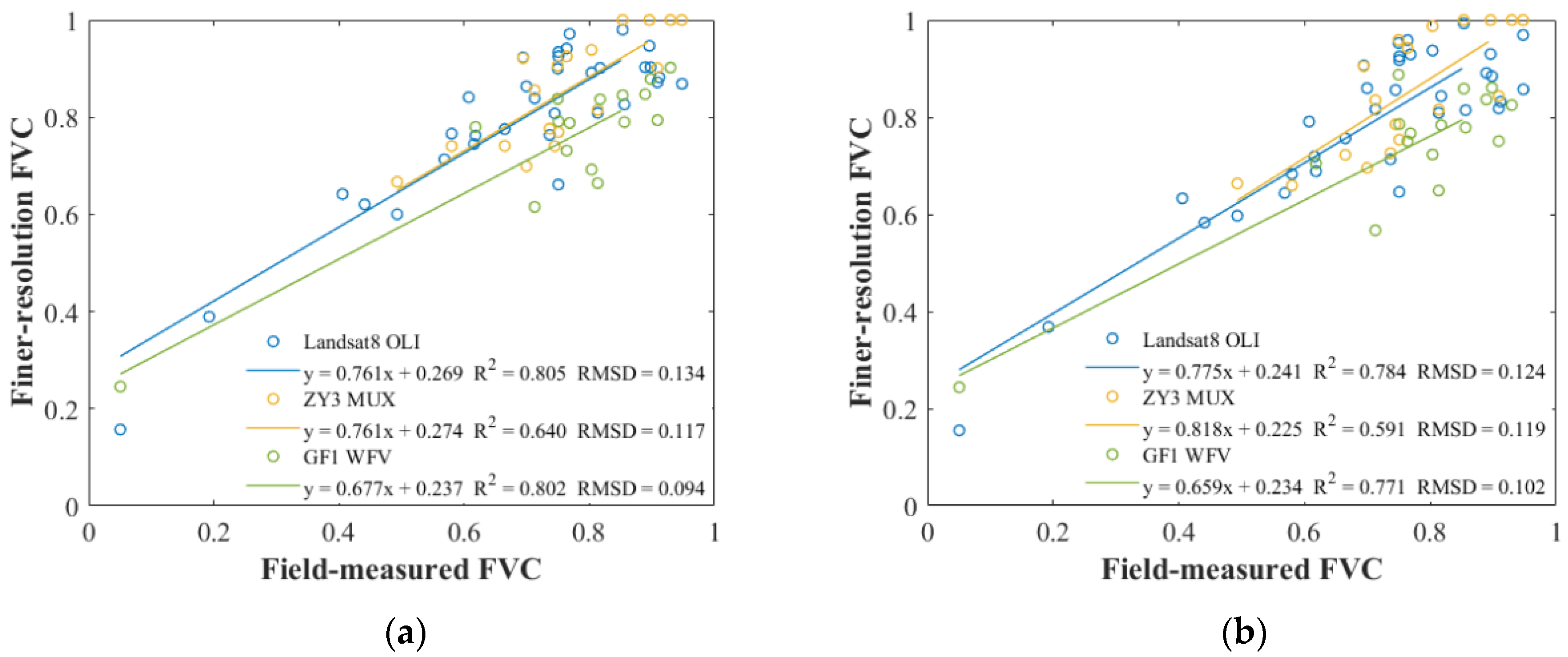
| Data | Landsat 8 | GF 1 | ZY 3 |
|---|---|---|---|
| Product Time | 19 June; 5 and 21 July; 6 August; 7 and 23 September | 30 June; 10 and 30 July; 8 September | 5 August; 3 September |
| Parameters | N | Cm (g/cm2) | Bp | Car (μg/cm2) | Cab (μg/cm2) | Anth (μg/cm2) | Cw (cm) |
|---|---|---|---|---|---|---|---|
| Values | 1.5 | 0.005; 0.01; 0.015 | 0 | 10 | 25 50 75 | 10 20 30 | 0.025 |
| Scene | Object | Object Radius | Object Height | LAD | Number of Soil Types | SZA |
|---|---|---|---|---|---|---|
| HOM | Leaf | 0.05 m | 0~15 m | UNI; SPH | 3 | 0°; 20°; 40° |
| HET | Sphere | 4 | 10~19 m | UNI; SPH | 3 | 0°; 20°; 40° |
| Satellite | Original | Normalized Vs | Normalized Vv | Normalized All |
|---|---|---|---|---|
| Landsat8 OLI | 0.124 | 0.126 | 0.119 | 0.121 |
| ZY3 MUX | 0.119 | 0.122 | 0.114 | 0.117 |
| GF1 WFV | 0.102 | 0.099 | 0.101 | 0.099 |
| Title 1 | MODIS | Landsat 8 | ZY 3 | GF 1 | |
|---|---|---|---|---|---|
| Vv | Ave. | 0.879 | 0.885 | 0.884 | 0.869 |
| Std. | 0.041 | 0.039 | 0.039 | 0.042 | |
| Vs | Ave. | 0.151 | 0.139 | 0.127 | 0.130 |
| Std. | 0.032 | 0.032 | 0.025 | 0.025 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, W.; Zhao, T.; Mu, X.; Zhong, B.; Zhao, J.; Yan, G.; Wang, L.; Niu, Z. Using a Vegetation Index-Based Mixture Model to Estimate Fractional Vegetation Cover Products by Jointly Using Multiple Satellite Data: Method and Feasibility Analysis. Forests 2022, 13, 691. https://doi.org/10.3390/f13050691
Song W, Zhao T, Mu X, Zhong B, Zhao J, Yan G, Wang L, Niu Z. Using a Vegetation Index-Based Mixture Model to Estimate Fractional Vegetation Cover Products by Jointly Using Multiple Satellite Data: Method and Feasibility Analysis. Forests. 2022; 13(5):691. https://doi.org/10.3390/f13050691
Chicago/Turabian StyleSong, Wanjuan, Tian Zhao, Xihan Mu, Bo Zhong, Jing Zhao, Guangjian Yan, Li Wang, and Zheng Niu. 2022. "Using a Vegetation Index-Based Mixture Model to Estimate Fractional Vegetation Cover Products by Jointly Using Multiple Satellite Data: Method and Feasibility Analysis" Forests 13, no. 5: 691. https://doi.org/10.3390/f13050691
APA StyleSong, W., Zhao, T., Mu, X., Zhong, B., Zhao, J., Yan, G., Wang, L., & Niu, Z. (2022). Using a Vegetation Index-Based Mixture Model to Estimate Fractional Vegetation Cover Products by Jointly Using Multiple Satellite Data: Method and Feasibility Analysis. Forests, 13(5), 691. https://doi.org/10.3390/f13050691








