Abstract
Biomass combustion is a major biogeochemical process, but uncertain in magnitude. We examined multiple levels of organization (twigs, branches, trees, stands, and landscapes) in large, severe forest fires to see how combustion rates for live aboveground woody parts varied with tree species, size, and fire severity in Ponderosa pine (Pinus ponderosa Dougl. ex Laws.) and mixed conifer-dominated forests of the Sierra Nevada, California, USA. In high severity fire patches, most combustion loss was from branches < 2 cm diameter; in low to moderate severity patches, most was from bole charring. Combustion rates decreased as fire severity declined and with increasing tree size. Pinus species had little branch combustion, leading them to have ≈50% the combustion rate of other taxa. Combustion rates could be 100% for small branch segments and up to 57% for small tree aboveground woody biomass in high severity fire patches. However, combustion rates are very low overall at the stand (0.1%–3.2%) and landscape level (0.6%–1.8%), because large trees with low combustion rates comprise the majority of biomass, and high severity fire patches are less than half of the area burned. Our findings of low live wood combustion rates have important implications for policies related to wildfire emissions and forest management.
1. Introduction
Combustion of biomass is a major biogeochemical process by which carbon is returned to the atmosphere from terrestrial ecosystems [1,2]. Fire has been an important process on Earth from at least the Silurian period over 400 million years ago [3]; since that period, this process has influenced the evolution of organisms [4,5], the successional state of ecosystems [6], and biogeochemical cycles including the concentration of oxygen and carbon dioxide in the atmosphere [7]. Although combustion is clearly a natural process that has occurred for much of Earth’s history, there is also a current concern that the incidence of wildfires, due to changes in fuel loads and climate, has and will continue to increase in the future [8,9]. Increased combustion could thus serve as a positive feedback to climate change. However, there is also a concern that past estimates of vegetation combustion have been biased upward, with one study indicating that the amount of carbon released by live tree combustion has likely been overestimated by 59% to 83% [10].
The fraction of a fuel combusted in wildfire depends on the interaction of particle size, packing, moisture, distance from heat source, and rate of energy release [11,12,13,14,15,16]. Although most studies of fuel combustion are on dead biomass, theoretically they can be applied to live fuels and suggest the following mechanisms. As fire intensity (i.e., rate of energy release) increases, so do the temperatures, combustion, and woody plant mortality rates associated with fires. Fine twigs are in close proximity to leaves and other twigs (i.e., within tens of centimeters), leading to more exchange of energy than more distant plant parts; hence, they are likely to be combusted. Moreover, their small diameter increases their surface area-to-volume ratio, allowing them to dry out and absorb energy faster than larger branches and stems. In contrast, large branch segments are not in such close proximity (i.e., separated by 10 to >100 cm), have a lower surface area-to-volume ratio, dry more slowly, and are less effective at absorbing energy from other burning particles. Tree stems or boles are separated by even more distance (i.e., often >1 m) and have a very low surface area-to-volume ratio when compared to twigs or branches; hence, they are the least likely to be combusted. As a result, the smallest diameter woody fuels are theoretically the most likely to be combusted in a wildfire [17].
Empirical estimates of the fraction of aboveground live woody vegetation combusted (as opposed to killed) by wildfires are highly uncertain, ranging from very little [10,17] to the majority [18]. It is unclear just how much of this variability in estimates is related to methodological differences as opposed to natural variation. We posit that smaller trees would have higher combustion rates than larger ones; moreover, high severity fire areas should have more combustion than low severity fire areas. Thus, natural variation in both vegetation structure and fire severity could lead to a large range in the combustion rate. However, when visual (either ground-based or remote) estimates of combustion after the fire are used, variation either among observers or methods can also introduce uncertainty.
Direct destructive methods are not practical, given the size of woody vegetation such as trees, and because combustion estimates require comparing biomass before and after a fire. Furthermore, there are hazards in working near an advancing fire front. Therefore, the most practical ways to estimate combustion rates are ground-based, post-fire estimates that can then be used to adjust existing biomass equations at the tree level (e.g., Miesel et al. [17]), make stand-level estimates of the proportion combusted (e.g., Campbell et al. [19]), and create similar types of estimates at larger spatial scales (e.g., Knorr et al. [1,2]). One challenge in making these estimates is to reconstruct the plant parts that were combusted. Another is to relate combustion estimates at one level (e.g., branches) to others (trees, stands, and landscapes); although there clearly has to be a relationship among these levels, most published estimates neither explicitly explore nor use this relationship.
Wildfires in California such as the Rim and Creek Fires have been used as an example of “fires of the future” in which wildfires become more intense, severe, and larger [20]. One of the many concerns related to such fires is the amount of carbon added to the atmosphere via combustion. Published estimates of combustion rates of aboveground live biomass from the Rim Fire, based on remote sensing, vary from 16% for low severity patches to 85% for high severity patches [18], whereas ground-based estimates from other fires [10], theoretical considerations (Figures S1 and S2), and ground-based observations (Figure S3) suggest much lower combustion rates. Therefore, our objective was to use ground-based methods to assess the fraction of aboveground woody carbon that is lost via combustion in low, moderate, and high severity patches in large fire complexes, and at multiple levels (twigs, branches and boles, individual trees, stands of trees, and the entire area in which a fire occurs), to test the following five hypotheses:
- Smaller woody structures (e.g., twigs) would more likely to be completely combusted than larger ones (e.g., boles);
- Combustion loss rates at the individual tree level would increase with fire severity and decrease with tree size (i.e., diameter and height);
- High combustion rates in small trees would be countered by lower rates in the largest trees, reducing stand-level average combustion rates, because at the stand-level, larger trees contribute substantially more biomass than small ones;
- Low and moderate severity patches are proportionally large enough and their combustion rates sufficiently low enough to reduce a fire’s average combustion rate at the landscape-level relative to that estimated for high severity patches.
- Given Hypotheses 1–4, aboveground woody combustion at the stand to landscape levels would be an order of magnitude less than previously estimated at the Rim Fire (e.g., Garcia et al. [18]).
To address these hypotheses, we developed a more robust ground-based method to determine the fraction of live aboveground woody biomass combusted during wildfire based on a reconstruction of the biomass that was combusted from branches and from the bole (i.e., main stem), as evidenced by charring. We examined a range of fire severities and tree sizes to determine the proportional loss of branch and bole carbon. We then developed species- and size-specific models of combustion rates and applied them to a range of stand diameter distributions and fire severity spatial databases to estimate carbon losses at the stand and landscape level for multiple large fires that have been described as either high severity or catastrophic.
2. Materials and Methods
2.1. Study Area
Our field study areas were composed of mixed-conifer and Pinus ponderosa (Dougl. ex Laws.), which dominated forests in the Rim Fire of 2013 and the Creek Fire of 2020 within the central and southern Sierra Nevada Mountains of California, USA (Figure 1). The 104,176 ha Rim Fire was active from 17 August through 4 November of 2013 on the Stanislaus National Forest, some private lands, and the western portion of Yosemite National Park. The 153,738 ha Creek Fire was active from 4 September through 24 December of 2020, mainly on the Sierra National Forest, but including some private lands. Our field data collection locations ranged from 1370 to 1490 m elevation in the Rim Fire, and from 1520 to 2180 m elevation in the Creek Fire.
Figure 1.
Location of study area in (a) western United States, (b) California, and (c) perimeters of 2020 Creek and 2013 Rim Fires in the Sierra Nevada Mountains, California.
At the lower elevations, these forests primarily consist of Ponderosa pine (P. ponderosa), white fir (Abies concolor (Gord. & Glend.) Lindl. ex Hildebr.), incense-cedar (Calocedrus decurrens (Torr.) Florin), Douglas-fir (Pseudotsuga menziesii (Mirbel) Franco), sugar pine (P. lambertiana Dougl.), and California black oak (Quercus kelloggii Newb.), with shrubs mainly consisting of mountain whitethorn (Ceanothus cordulatus Kellogg), deer brush (C. integerrimus Hook. & Arn.), and greenleaf manzanita (Arctostaphylos patula Greene). At the higher elevations in our study sites, the forests primarily consist of Jeffrey pine (P. jeffreyi Grev. & Balf.) and A. concolor, with some C. decurrens and occasional red fir (A. magnifica A. Murr.) at the highest elevations, and shrubs comprising mainly C. cordulatus.
2.2. Branch Models
Our branch models were based on branch orders, with first order branches representing the smallest twigs and second order branches representing branches where two first order branches joined, etc. (Figure S4). The benefit of this system is that it can be used to reconstruct the branch orders missing from those that remain given that higher order segments are more likely to remain than lower order ones.
2.2.1. Field Data for Branch Models
There were two phases of field data collection in the development of the branch models. First, branches from recently downed live trees or live tree tops of the main species present in the Rim and Creek Fires (A. concolor, C. decurrens, P. lambertiana, P. ponderosa, and P. menziesii) were dissected to determine the number, diameter, and length of the branch orders on individual branches. Mid-point diameter and the length were determined on a subsample of up to 10 of each branch order segments of each dissected branch; when there were <10, all segments were measured.
Second, we visually examined intact, standing trees of each of the five species listed above in each of six diameter at breast height (DBH) size classes (1.0–4.9, 5.0–9.9, 10.0–24.9, 25.0–49.9, 50.0–99.9, >100 cm) to determine branch structure, as defined by the highest branch order present on a tree, the maximum branch diameter, length of the highest branch order segment, and the total branch length of the highest branch order. Maximum branch order was determined by starting with the outmost twigs and visually assessing where they joined to form a second order, and where second orders joined to form third orders, and so on. Maximum branch diameter and lengths were estimated visually; however, these estimates were repeatedly checked against a caliper and meter stick when branches were low enough on the tree to be measured directly.
2.2.2. Branch-Level Models
The average maximum branch order, diameter, and length data, combined with the average bifurcation ratio (i.e., the number of lower order branches divided by the number of branches for the next higher order; see Figure S4), as well as segment diameter and length from the branch dissections, were used to develop tree species- and DBH size class-specific branch-level models. For lengths and diameters of orders not dissected, we interpolated between the highest order dissected and the highest order visually estimated. The volume of each branch order was calculated as the product of the branch segment area (as determined from the mid-length diameter), the length, and the number of segments. The total branch volume was determined by summing up all the branch order volumes and the relative branch order contribution was calculated as the ratio of the branch order volume to the total branch volume.
2.2.3. Tree-Level Branch Models
At the tree-level we developed three sets of models, with different weighting of the branches (Figure S5 The simplest used the relative contribution of orders found on the highest order branches of each species and DBH size class). We termed this the maximum branch order model. However, trees also contained branches that terminated at a lower order than those closest to the ground. We accounted for this by either using the total estimated volume of each branch for each DBH size class as a weighting factor (i.e., the volume-weighted model) or using an additional weighting factor related to the bole length each branch represented (i.e., the volume and length-weighted model).
2.3. Tree-Level Combustion Indicator Sampling
We collected field data in the spring of 2018 and 2021 for the Rim and Creek Fires, respectively. In both fire areas, we gathered data in each fire severity patch type (low, moderate, high) at five points separated by 50 m as determined by a laser hypsometer along straight-line transects through the middle of the patches. To determine the location of the fire severity categories, we used the U.S. Forest Service’s “Rapid Assessment of Vegetation Condition after Wildfire” (RAVG) fire severity mapping system (https://fsapps.nwcg.gov/ravg/data-access, accessed on 1 May 2021). If we encountered a point location along transects that was a different fire severity category than targeted in the specific sample area, we skipped that location and proceeded to the next location, 50 m further along. Additionally, if the transect came to the end of a patch within a particular fire severity category, we changed the direction of the transect 90 degrees to stay within the patch.
At each point location, we recorded the GPS coordinates and data on individual conifer trees in six size classes (see above), using the closest tree from each size class to the point location. This theoretically resulted in 30 trees being sampled per transect. However, in some cases, certain DBH size classes were not present near a plot center. To replace these “missing” trees, we sampled others as we traveled between points within the fire severity patch. Although we did not sample by species per se, we generally found the full range of DBH size classes for the main species we encountered. In the case of P. ponderosa, our method did not provide sufficient numbers of small DBH trees in high severity fire patches. We therefore sampled an additional transect in a high severity patch that was dominated by P. ponderosa in small DBH size classes to supplement the database. In addition, because trees >100 cm DBH were uncommon, some of our point locations did not include any trees of this DBH size class. In such cases, for the Creek Fire, we sampled >100 DBH trees as we traveled between point locations.
For each tree in the Rim fire, we recorded species, DBH, height, live/dead status, distance from point location, char depth of bole, maximum bole char height, whether there was any consumption of branches (yes or no), percentage of crown length killed, diameter of the smallest branches remaining, diameter of the largest branches consumed, and percentage consumption of each order of branches. The diameter of each tree was determined using either a DBH tape or a large caliper to the nearest 1 cm. The heights of DBH size classes 3–6 were visually estimated (with periodic checks using a clinometer and tape or hypsometer), whereas those of the smaller DBH size-classes were estimated using a meter stick. The maximum height or relative height (depending on the distance) of charring was determined, as we had assumed there would be a fixed relationship between the maximum and minimum char height. The char depth on the bole was visually estimated after a subset of trees had been examined by cutting into them with either a knife or hatchet. If crown consumption was noted we visually estimated the smallest branch diameter remaining and the largest one combusted, periodically checking these estimates with a caliper. The fraction of each branch order combusted was visually estimated when crown combustion had occurred as 5%, 10%, 25%, 50%, 75%, 90%, 95%, or 100% combustion. Given that the Rim Fire occurred several years before sampling, we distinguished between branches lost via decomposition-related fragmentation and combustion (Figure S6).
In the Creek Fire, we generally followed these same methods at each point with some changes to improve precision. At the Creek Fire, all tree heights were determined either using a clinometer and hypsometer or, if they were short enough, with a meter stick. We determined the minimum and maximum char height (percentage of tree height), given our observations on the Rim Fire that the char height often varied substantially on one side of the tree versus the other side. A detailed examination of char depth at the Rim Fire indicated that the char depth was variable enough that it needed to be determined on each tree. Therefore, at the Creek Fire we used a hatchet to chop into each bole on at least two places to determine the depth of char (generally in 0.5 cm increments).
2.4. Estimate of Wildfire Intensity
We used van Wagner’s scorch height model [21] to estimate I, the fire line intensity (kcals m−1 s−1) of the sampled areas:
with the maximum height of bole char (m) serving as the scorch height. For high severity fire patches, we used the maximum height observed on transects to indicate fire intensity. We did this for moderate and low severity fire patches as well; however, also we calculated the average fire intensity using all the trees in those transects because for these two severities it may be more representative than the maximum.
Scorch height = 0.385 × I 0.66
2.5. Tree-Level Combustion
The Jenkins et al. [22] general softwood equations were used to predict the proportion of aboveground woody mass in boles versus branches as a function of DBH (Figure S1). Data on the proportion of branch volume combusted were then combined with this to determine the fraction of each tree’s total aboveground woody biomass lost to branch combustion.
We also used the data on bole char height and depth to estimate proportion of aboveground woody biomass lost to combustion. For the Rim Fire we made several estimates, since only the maximum height of bole char was noted. First, we assumed that the minimum and maximum char heights were equal, giving a maximum bole combustion estimate. Second, we used the relationship between the minimum and maximum bole char height found for a subsample of trees examined in detail on the Rim Fire (Figure S15). This gave the minimum bole combustion estimate. The data on bark char depth collected at each fire were then used to estimate the volume of char, assuming that the char depth declined as one went up the tree, reaching zero where the char ended. We assumed that 46% of the bark’s C was lost via pyrolysis [23] during bole charring, based on the average of Czimczik et al. [24].
Individual tree estimates of the fraction combusted for each fire intensity class were used to develop non-linear regression models using SAS procedure NLIN with the Gauss method and parameter bounds [25] that would predict the proportion of branches, boles, and aboveground woody biomass consumed as a function of tree DBH. We estimated models for each fire severity class and species group (i.e., all species together, Pinus species, and other species). Species groups were based on a preliminary analysis, which indicated that species in the genus Pinus appeared to have substantially lower combustion rates (particularly of branches) than the other conifer species. Although we analyzed all six sets of estimates based on the branch and bole scorch models used, we largely present results for the estimates based on volume weighting of branches and maximum bole char height models.
The tree-level combustion models used were interrelated and based on negative exponential functions with multiple components. The most complicated was a negative exponential model with an asymptote that separated the response into three components:
where Combustion1, Combustion2, and Combustion3 pertain to the combustion maximums (percentage) for component 1, 2, and 3, respectively; k1 and k2 (cm−1) determine the rate the first two components decline with increasing DBH. We also ran simpler models including a dual component negative exponential (i.e., Combustion3 was zero):
a single component, negative exponential decline to an asymptote (i.e., k2 was zero):
and a single component negative exponential (i.e., Combustion2 was zero)
CombustionDBH = Combustion1 e−k1 + Combustion2 e−k2 + Combustion3
CombustionDBH = Combustion1 e−k1 + Combustion2 e−k2
CombustionDBH = Combustion1 e−k1 + Combustion2
CombustionDBH = Combustion1 e−k1
As Proc NLIN automatically reduced the number of parameters when a simpler model was sufficient to fit the data, the Akaike Information Criteria (AIC) was not necessary to select the simplest model. Therefore, our primary method to identify the “best” model was goodness of fit, which was calculated as:
where SS is the sums of squared deviations for either the error term or the corrected total. We also examined residuals to determine if there was a bias at any point in the DBH range examined and selected the model with the minimum bias.
r2 = 1 – SSerror/SScorrected total
2.6. Stand-Level Combustion
We estimated the total stand-level combustion losses for each of the fire severity classes from our combustion regression models and published data on DBH size class structure for mixed conifer forests in the California Sierra Mountains [20,26,27,28,29]. While some of the publications reported DBH size structure for species or Pinus versus other species, some did not [28,29]. However, the latter did report the relative contribution of species to basal area. We therefore apportioned the number of stems in each DBH size class by the proportion of basal area of species.
Total aboveground biomass was estimated from DBH using equations for species groups developed by Chojnacky et al. [30]. Biomass in branches and boles were calculated from total aboveground biomass using the Jenkins et al. [22] general softwood equations, predicting the proportion of aboveground woody mass in boles versus branches as a function of DBH. To calculate the combustion loss for each tree in a fire severity class (e.g., low severity) the appropriate biomass term (e.g., branch) was multiplied by the combustion rate, predicted from the corresponding combustion–DBH model (e.g., branch–low severity). We also estimated the fraction of combustion coming from branches versus boles.
2.7. Landscape-Level Combustion
To explore the consequences of the distribution of fire severities at the landscape-level (i.e., the entire area burned) we weighted the losses for each fire severity class at the stand-level by the abundance of the severity class on the landscape for the five largest Sierra Nevada fires occurring during 2011–2020 in conifer forests on national forest lands that were composed >50% by P. ponderosa, P. jeffreyi, and mixed-conifer forest types. In addition to the Creek Fire and Rim Fire, this included the 61386 ha Rough Fire of 2015, the 129068 ha Bear Fire of 2020, and the 70487 ha Castle Fire of 2020, all within the Sierra Nevada region. The Rapid Assessment of Vegetation Condition after Wildfire (RAVG) dataset (https://fsapps.nwcg.gov/ravg/data-access, accessed 15 November 2021) was used to determine distributions for conifer forests on national forest lands in three severity classes: low (<25% basal area mortality), moderate (25%–75% basal area mortality), and high (>75% basal area mortality).
3. Results
3.1. Tree Mortality
A total of 511 trees were examined on transects: 177 from the Creek Fire and 334 from the Rim Fire. For the high severity fire patches sampled, 99.4% of the 175 trees examined were killed by fire. For moderate severity fire patches, 68.4% of 165 the trees examined were killed, and for low severity fire patches, 47.9% of 171 trees were killed (mostly in the smallest size classes). Mortality rates, based on tree numbers, were quite similar between the two fires, with the maximum difference for low severity fire patches: 38–43% mortality of stems on the Creek Fire and 39%–52% on the Rim Fire (Table 1).

Table 1.
Mortality, maximum scorch and tree height, and estimated fire intensities for Creek and Rim fires in California’s Sierra Mountains.
3.2. Estimates of Fire Intensity
High severity fire patches had at least an order of magnitude higher intensity than moderate and low severity fire patches; however, for the most severe fire patches, the intensity estimate was limited by the heights of trees present at a site (Table 1; Figure S13). Specifically, for high severity fire patches, fire intensity estimates ranged from 735 to 1740 kcal m−1 s−1, but for most of these patches the maximum tree height and maximum scorch height were the same. Since maximum tree height ranged from 30 to 53 m, it is likely that fire intensity was considerably higher for some of the high severity patches that we examined. Fire intensity estimates based on maximum tree height ranged from 139–826 kcal m−1 s−1 to 139–557 kcal m−1 s−1 for moderate and low severity, respectively. Average fire intensity ranged from 38–156 kcal m−1 s−1 to 26–83 kcal m−1 s−1 for moderate and low severity fire patches, respectively.
3.3. Branch Models
Diameter and length of dissected branch segments increased with order for each species (Figure S7). First order branch segment diameters ranged from 2.0 ± 0.1 (mean ± standard error) to 12.3 ± 0.3 mm for A. concolor and P. ponderosa, respectively (Table S1). Diameters of the highest branch orders on the largest DBH size class ranged from 80 ± 33 to 150 ± 3 mm, for A. concolor and P. menziesii, respectively (Figure S8b). The length of first order branch segments also varied among species, ranging from 11.2 ± 0.7 (A. concolor) to 36.6 ± 2.5 cm (Pinus) (Table S1). Average length of the highest branch order segment for the largest two DBH size classes ranged from 110 ± 4 cm for C. decurrens to 330 ± 30 cm for P. lambertiana (Figure S8d). Based on these dimensions, the highest order branch segments contained 374–62,241 times more volume than first order ones.
The bifurcation ratio on dissected branches varied among branch orders within a species, ranging from 2 to 25 (Table S2). In some species (P. ponderosa and C. decurrens), the bifurcation ratio decreased as branch order increased; however, in others (A. concolor, P. lambertiana, and P. menziesii), the maximum bifurcation ratio occurred between orders two and three. The highest branch order on a tree significantly varied with DBH size class and species (Figure S8a). The maximum branch order observed also varied, the lowest being 3.8 ± 0.2 for P. ponderosa and the highest being 6.4 ± 0.2 for C. decurrens. Based on the bifurcation ratios observed, first order branch segments for the largest DBH size class were 52–2755 more numerous than the highest order segments.
The relative contribution of branch orders differed among species and DBH size classes with A. concolor and P. ponderosa exhibiting the most divergent patterns (Figure 2). In general, as DBH size class increased, the contribution of the highest order branches increased and that of order one decreased. Specifically, branch order one of DBH size class one comprised 25% to 55% of the branches; however, for DBH size class six, branch order one comprised 0.5%–8.6% of the branches.
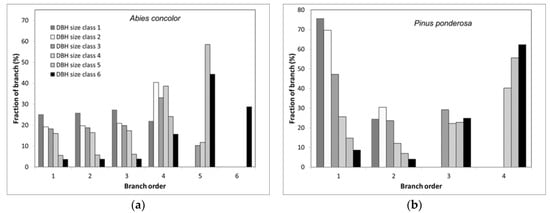
Figure 2.
Relative contribution of branch orders to branch volume for (a) Abies concolor (Gord. & Glend.) Lindl. ex Hildebr. and (b) Pinus ponderosa Dougl. ex Laws. for range of DBH size classes. These values are from the model that used the highest order branches found on a species-DBH size class combination.
The maximum order method estimated the lowest contribution of branch orders one to three in larger DBH size classes, whereas weighting by volume estimated the highest. However, the way that branches were weighted to produce tree-level branch models had limited effect on the relative contributions of branch orders and did not influence the overall pattern observed (Figure S9). For example, in the case of C. decurrens of DBH size class six, order one branch segments comprised 4% of the branches when the maximum order branch present model was used, but 5% when weighted by branch volume or when weighted by branch volume and bole length.
3.4. Branch Segment Sizes Combusted
Observations of the maximum branch segment diameter consumed by fire suggested that only the lowest few orders of branch segments were consumed even in the most severe fire patches, a finding consistent with Hypothesis 1. The largest diameter of branch segments consumed by fire was 2 cm and 1.5 cm at the Rim and Creek fires, respectively. However, the average maximum branch diameter consumed was 0.8 cm and 0.6 cm at the Rim and Creek fires, respectively. These observations of branch consumption were predominately in high severity fire patches (152 of a total of 197 branch consumption observations). Our findings suggest major limits on how much of a tree’s aboveground woody biomass can be combusted (Figures S10 and S11).
The smallest diameter branch segments remaining averaged 0.1 cm and 0.3 cm on the Rim Fire and Creek Fire, respectively. As with maximum diameter consumed, the majority of these observations were on high severity fire patches, given that consumption of branches was uncommon in low and moderate severity fire areas. Although very few small diameter branch segments remained on trees in high severity patches, there were always some to be found, particularly on larger trees. For example, in high severity fire patches, 90% of the first order branches of DBH size class one were combusted on average; in contrast, <50% of first order branch segments were combusted for DBH size classes five and six. This indicated that branch combustion was far from complete even in these extreme settings.
3.5. Bole Charring
The maximum char height on tree boles was a function of both DBH and fire severity (Figure S13). For high severity fire patches, the maximum char height generally followed tree height regardless of DBH. For low fire severity, char height was generally <10 m, although some exceptions occurred. This meant that the majority of trees in low severity patches had less than half of their bole length charred.
Although we had initially assumed that fire would have consumed some of the diameter at the trees’ base, we rarely saw evidence of this, except on very small diameter trees and a few large C. decurrens. Instead, we mostly found evidence of charring. At the Creek Fire, with a few exceptions, the range of char depth was from 0.1 to 2 cm (Figure S14); although the range was generally similar to that at the Rim Fire, more individuals in the low severity patches at the Rim Fire were assigned a char depth of zero. To some degree this may reflect the presence of unburned spots, but it also might reflect a bias caused by not chopping into each tree to distinguish between charring and surficial soot deposition. To estimate bole combustion, we therefore assigned a nominal char depth of 0.1 cm for any tree from the low severity patches of the Rim Fire that had bole scorch.
3.6. Branch Combustion
Combustion of branches declined substantially as fire severity decreased, with the maximum consumption of 100%, 71%, and 45% for the smallest DBH trees in high, moderate, and low severity fire patches, respectively (Figure S12). The average for the smallest DBH size class was lower: 71%, 11%, and 2.6% for high, moderate, and low severity fire patches, respectively. Consistent with Hypothesis 2, branch combustion declined as DBH increased, with the largest DBH size class having an average of 2% branch combustion for high severity fire patches. Pinus species had substantially less branch consumption than other species regardless of fire severity; this was likely due to their larger diameter in the lowest branch orders (i.e., 1–3) when compared to the other species.
Nonlinear regressions supported these conclusions, with the sum of the Combustion1–3 parameters being lower as fire severity decreased and lower for Pinus species than other species (Table S3). The combustion maximums of the regressions could be substantially lower than the highest combustion estimates reported above, as not all trees in the smaller DBH’s had high combustion rates. Although the majority of non-linear regressions were significant, the goodness of fit declined with fire severity from 0.3 to 0.6 and 0.06 to 0.08 for high and low severity fire patches, respectively. This was likely due to the fact that as fire severity decreased, the number of trees without branch consumption also increased. Pinus species in moderate to low severity patches had the only non-significant regressions; however, this was likely due to the fact that few branches on Pinus species were consumed at these two fire severity levels. In general, the number of parameters needed to fit the observations declined as fire severity decreased, with high severity best fit by a dual negative exponential, but low severity best fit by a single negative exponential or in some cases a constant.
3.7. Bole Combustion
Consistent with Hypothesis 2, combustion of boles also declined as fire severity decreased, with a maximum estimate of consumption of 24.6%, 13.5%, and 13.5% for the smallest DBH trees in high, moderate, and low severity fire patches, respectively (Figure S12). For the smallest DBH size class, the average bole combustion rate was 9.4%, 2.8%, and 2% in high, moderate, and low severity fire patches, respectively. For the largest DBH size class, bole combustion averaged 1.3% for high severity patches and 0.1% for low severity patches, indicating a decline by roughly an order of magnitude from the smallest to the largest trees. The differences between Pinus and other species in bole combustion rates was less evident than for branch combustion rates; however, the maximum bole combustion (as indicated by the sum of Combustion 1–3) for Pinus species was substantially lower than that of the other species, which was likely related to the thinner depth of char for P. ponderosa (Figure S15b).
The majority of non-linear regressions for bole combustion were highly significant, but as with branch consumption the goodness of fit declined as fire severity decreased (Table S4). Specifically, the goodness of fit for high severity patches was 0.66–0.75, whereas for low severity patches it was 0.14–0.34. As with branches, consumption was predicted to decrease as DBH increased. Pinus species regressions had higher maximum combustion values than the other species; however, the rate that combustion declined with increasing DBH was higher, leading to a prediction of lower combustion rates for Pinus species over most of the DBH range.
3.8. Tree-Level Combustion
Consistent with Hypothesis 2, combustion of aboveground woody parts declined as DBH increased and fire severity decreased, with the maximum consumption observed to be 56.7%, 57%, and 30.2% for the smallest DBH trees in high, moderate, and low severity fire patches, respectively (Figure 3). The average, as opposed to the maximum, consumption for the smallest DBH size class was 34.9%, 7.2%, and 2.3% in high, moderate, and low severity fire patches, respectively. As with branches and boles, there was a substantial decline in aboveground woody consumption as DBH increased, so much so that even for high severity patches the largest DBH size class averaged 1.4% consumption. Pinus species generally had lower consumption rates than the other tree species, with the largest differences for smaller DBH’s in high severity fire patches.
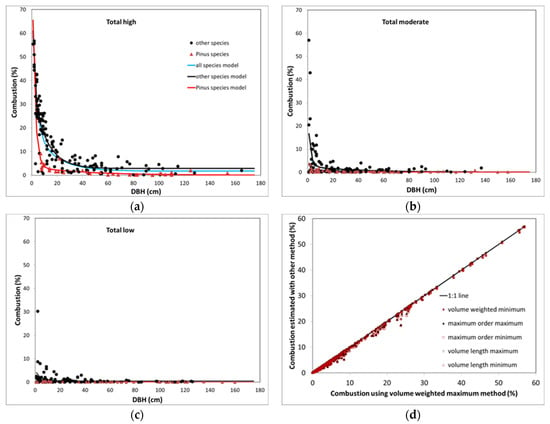
Figure 3.
Total aboveground consumption as a function of fire severity and diameter at breast height (DBH) at Rim and Creek fires in California’s Sierra Mountains: (a) high severity; (b) moderate severity; (c) low severity; and (d) estimates of total combustion using other methods when compared to estimates weighting branches by volume and assuming maximum bole scorch.
The non-linear regressions for the different species groups and fire severities were highly significant (Table 2). The sum of the Combustion1–3 parameters declined as fire severity declined; in the case of species other than Pinus it was 74.3%, 26.5%, and 5.3% for high, moderate, and low severity fire patches, respectively. Although these are higher than reported above, the regression equations predict a maximum of 58.7%, 16.7%, and 4.1% for trees with a DBH of 1 cm. Pinus species had lower combustion than the other species, but the Combustion1–3 parameter sums for Pinus species sometimes exceeded that of other species. However, Pinus species generally had steeper declines with an increase in DBH, leading to a lower predicted consumption rate for most of the diameter range. As with branches and boles, the goodness of fit declined as fire severity decreased; this was specifically from 0.72 to 0.80 and 0.07 to 0.20 for high and low severity fire patches, respectively.

Table 2.
Non-linear regressions predicting aboveground woody consumption in Creek and Rim Fires as a function of DBH for different fire severity classes and species groups.
Although Figure 3 displays the results for the volume weighted–maximum bole scorch method, the other five methods produced very similar, if somewhat lower estimates of combustion (Figure 3d). As anticipated, the maximum order–minimum bole scorch method produced the lowest estimates of combustion. The largest difference was 5% lower than the for volume weighted–maximum bole scorch method for intermediate levels of combustion, but for low and high combustion levels it was considerably less (<2%). Therefore, we conclude that the regression models in Table 2 predict the highest level of combustion of any of the methods used.
3.9. Stand-Level Combustion
Our stand-level results were consistent with Hypothesis 3. Applying the tree level combustion models to published DBH distributions indicated that stands within high severity fire patches combusts 1.2%–3.2% of the aboveground woody biomass (Figure 4a). In contrast, the same stand structure in a low severity fire patch combusted 0.1%–0.2%. The estimates for moderate fire patches were closer to low than high severity, with 0.2%–0.5% combusted. This indicates combustion rates do no correlate linearly with mortality rates.
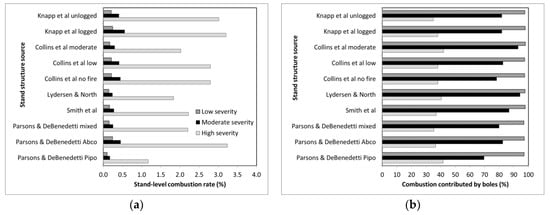
Figure 4.
Stand-level combustion for published DBH size distributions for mixed conifer forests in the Sierra Nevada Mountains, California: (a) total combustion for high, moderate, and low severity fires; and (b) portion of combustion contributed by boles for high, moderate, and low severity fires. Collins et al. moderate and low severity refers to stands than had been disturbed by moderate and low severity fires in the past, respectively.
For moderate and low severity patches the majority of combustion losses (70%–98%) were related to bole combustion (Figure 4b). For high severity patches, combustion losses were predicted to largely come from branch consumption, as bole consumption was 35%–42%. This non-linear transition in combustion sources as one proceeds from high to moderate severity patches is likely the cause of the response of stand-level combustion to changes in fire severity.
3.10. Landscape-Level Combustion
For the five large fires examined RAVG indicated high severity patches comprised 45%–52% of the area, being lowest for the Rim Fire and highest on the Bear Fire (Table 3). Low severity patches (37%–44%) were more abundant than moderate severity ones (11%–16%).

Table 3.
Distribution of fire severity classes as determined by RAVG for five large wildfires occurring between 2013 and 2020 in California’s Sierra Mountains.
When these severity distributions were used to estimate the landscape average, we found combustion rates ranged from 0.6% to 1.8% (Figure 5). Within a given fire, the difference between the minimum and maximum combustion rate associated with different DBH structures and species composition was 1.0%–1.1%. This difference increased as the proportion of high severity patches increased. Moreover, the lowest values were for older P. ponderosa dominated stands and the highest combustion rate was for logged mixed conifer stands. When the mid-point value was used to represent a mix of species and DBH structures, then the landscape combustion rate would have been 1.0%–1.2%, a result consistent with Hypothesis 4.
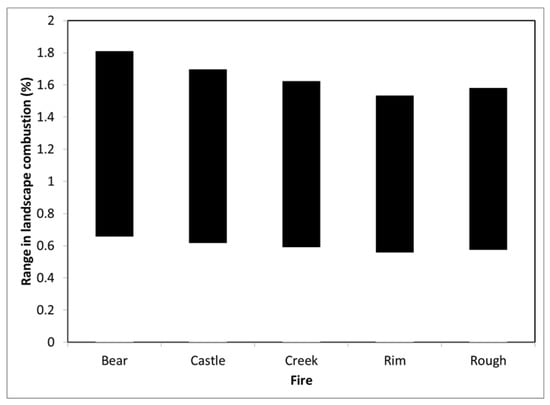
Figure 5.
Landscape-level estimates for aboveground woody biomass combustion for five large, severe fires in the California Sierra Mountains. The range presented is for the various stand structures presented in Figure 4.
4. Discussion
4.1. Evaluation of Hypotheses
We employed a novel, field-based method to estimate the fraction of aboveground woody biomass combusted in large wildfires and evaluated five hypotheses that span multiple levels, ranging from tree parts to landscapes. The advantage of our method is that findings at one level can be related to another. For example, although we did find high rates of biomass combustion for some portions of branches and for small trees in high severity fire patches, a number of factors led the average combustion rate at higher levels of organization (i.e., trees, stands, and landscapes) to be substantially lower. Below, we evaluate each of our hypotheses in turn.
4.1.1. Hypothesis 1
Our findings for branches and to some degree for boles were consistent with Hypothesis 1. We did not observe any live branches >2 cm diameter that were fully combusted in even the most severe fire patches; it is likely that 2 cm represents an approximate combustion threshold in terms of the proximity, surface area-to-volume ratio, and drying rates of branch segments. Moreover, the 2 cm diameter limit suggests that for the species we examined, only branch orders one to three are of potentially combustible size. This places significant constraints on how much of a branch or tree can be combusted (Figures S10 and S11).
We found that, while all sizes of trees had losses from bark charring, this loss was proportionally highest for the smallest diameter trees. However, this may have been more related to proximity to ground fuels and the distribution of energy release than diameter per se. This suggests that proximity to heat source is also important to consider.
4.1.2. Hypothesis 2
We found multiple lines of evidence to support Hypothesis 2. Specifically, our branch models predicted that as DBH increased the proportion of branches susceptible to combustion declined. Using A. concolor as an example, orders one to three (the most susceptible to combustion) comprise 78% and 11% of branches for DBH size classes one and six, respectively (Figure S10). At the level of trees, the proportion of branches in total aboveground woody biomass declined as DBH increased, which meant that even if the combustion rate of branches was constant, the fraction of total woody biomass combusted would be reduced 60% from the smallest to the largest DBH trees. Combining these two DBH-related effects suggests that 1.8%–31% of aboveground woody mass could be consumed for this species, with the highest value for the smallest trees (Figure S11). These estimates pertain to A. concolor in high severity fire patches; very little branch consumption occurred in low and moderate severity fire patches. Specifically, in moderate severity patches, only 17% of the trees had evidence of crown consumption. In low severity patches, even fewer trees (6%) had evidence of crown consumption. This suggests that on moderate and low severity fires, one could expect that 0.3%–5.3% and 0.1%–1.9% of aboveground woody biomass would be consumed at the level of trees, respectively, with the higher values pertaining to the smallest trees.
We found that the rate of bole combustion related to charring also declined as tree size increased. Although char depth increased to some degree with fire severity, the main effect was to char more of the bole length as fire severity increased (Figure S13). In contrast to Hypothesis 2, tree species had a larger effect on bole combustion than tree size. The differences in char depth among species seemed to be related to bark density, with less dense bark exhibiting a deeper char layer (Figure S15b).
4.1.3. Hypothesis 3
At the stand-level, consistent with Hypothesis 3, higher combustion rates (i.e., 34.9% in high severity fire patches) in the smallest trees were strongly offset by the lower ones (i.e., 1.4% also in high severity fire patches) in larger trees because biomass increases exponentially with DBH. Consider that it would take ≈190,000 1 cm DBH trees to equal the biomass of a single 100 cm DBH tree (or ≈30,000 to equal a 50 cm DBH tree). Thus, while small DBH trees might be orders of magnitude more abundant than larger ones, they are not sufficiently abundant to counter the effects that a few larger DBH trees have on stand-level combustion rates. In addition, increasing the proportion of biomass in Pinus species greatly decreased stand-level combustion rates, because branches of these species were rarely combusted. This suggests that estimates of stand level combustion rate need to account for differences in taxa as well as tree sizes.
4.1.4. Hypothesis 4
Consistent with Hypothesis 4, we found that, at the landscape level, the very low rates of combustion in low and moderate severity fire patches diluted the effects of higher combustion rates in high severity fire patches. The much lower rates of combustion observed in low and moderate severity fire patches is likely due to the fact that branch combustion in these two severity classes is extremely low. Despite being classified as high severity fires, a large share (48% to 58%) of the fires we examined was of low and moderate severity according to RAVG. Moreover, as noted below, the proportion of moderate severity fire patches is underestimated by RAVG, so it is highly likely that high severity fire patches comprise the minority of even “highly severe” wildfires. Thus, the overall combustion rate in “high” severity fires is likely to be less than half that observed in those portions that were actually high severity.
4.1.5. Hypothesis 5
Our estimates of stand- to landscape-level combustion rates are more than an order of magnitude less than reported by some remote sensing-based studies (Table 4). For example, Garcia et al. [18] estimated that 32%, 52%, and 85% of the aboveground biomass was consumed by the Rim fire in low, moderate, and high severity fire patches, respectively. De Santis et al. [31] estimated that conifers in low, moderate, and high severity fire patches had average biomass combustion rates of 25%, 47%, and 65%, respectively. Applied to the RAVG fire severity distribution for the Rim Fire, these values suggest a landscape average combustion rate of 45%–57% in contrast to the 1%–1.2% we found when our combustion models were applied to various stand structures. For high severity fire patches, we estimated that 1.2%–3.2% of aboveground woody biomass was combusted by fire. Even when foliage was accounted for (see below) our ranges were far below that of Garcia et al. [18] and De Santis et al. [31]. In contrast, our estimates are more in line with the 1%–3% that can be inferred from Miesel et al. [17] for a range of fire severities in mixed conifer forests of California. They are also consistent with field-based research of high-severity fire patches in multiple large fires in the Eastern Cascades of Oregon, where <3% of live conifer tree biomass was consumed [32]. Thus, we cannot reconcile Garcia et al.’s or De Santis et al.’s outcomes with our field data, or with that from other field-based studies, which also find that the vast majority of the carbon remains in trees, even in moderate- and high-severity fire patches in large wildfires [10,19,32,33].

Table 4.
Comparison of combustion rates (percentage) at stand- and landscape-level at Rim Fire.
4.2. Evaluation of Uncertainty
Our models predicting the relative volume of branch orders were preliminary and additional efforts should be made to improve them, particularly regarding estimates of bifurcation ratios. However, it is doubtful that these improvements would alter the relative relationships we found, specifically, that as tree DBH increases the maximum order present, diameter, and length of branches increases. Regardless of bifurcation ratios, these trends led to the highest order branch segments to be much larger than the lowest order ones. Hence, for the largest trees, the volume of the highest order branch segment was 374–62,241 times larger than for the first order ones. For the highest order and first order branch segments to have equal volume, then first order branch segments would have to be similarly more abundant than the highest order branch segments. Our models predicted that first order branch segments were less abundant than this by a factor of 5.5–66. It is highly unlikely that our estimates of bifurcation ratios could have been off by that much, but even if they were it may not have made a difference. In the case in which branch segment orders are equally abundant, the relative contribution of each order would be the reciprocal of the maximum order present; with six orders present, the contribution of the first three orders would be 50% to branches or 8% of aboveground woody mass of the largest trees. Therefore, given the limitations of branch mass on trees, even exceedingly high amounts of order one to three branch segments would not allow the majority of aboveground woody biomass to be consumed by fire.
Uncertainty was also introduced by our visual estimates of the fraction of branch orders consumed; however, this was unlikely to have altered our basic findings. In the case of small diameter trees in high fire severity patches, consumption of branch orders one to three were often complete, leading to little uncertainty in estimating the fraction consumed. Similarly, for trees in which no crown consumption occurred (the vast majority of trees), no uncertainty would have been introduced. Therefore, this source of uncertainty is highest for the largest trees in high severity fire patches, but even here it was unlikely to have been substantial. For example, if first order branch segments were 10% of branches and branches were 16% of aboveground woody mass (as is typical for large DBH trees), then estimating 50% consumption of first order branch segments would mean that 0.8% of aboveground woody biomass would have been consumed. Had 25 or 75% of the first order branch segments been consumed it would mean that 0.4% and 1.2% of the aboveground woody mass would have been consumed, respectively. Although these numbers certainly differ, all are small proportions of the aboveground woody biomass.
There were also uncertainties associated with combustion related to bole charring. We assumed that char thickness decreased as one proceeds up the stem. More needs to be learned about the longitudinal pattern of char depth. If the char depth is constant (which seems unlikely), then perhaps bole char losses would have been twice what we estimated. This would have had the largest impact on our estimates of combustion for low and moderate fire severity patches, because bole charring contributed to most of the combustion losses in these areas. However, char height was also limited in these patches. In addition to better understanding longitudinal variation in char depth, the amount of carbon lost via pyrolysis needs to be more precisely determined. Our use of a constant fraction of carbon loss of ≈46% likely overestimated losses from low severity fires and potentially underestimated it for high severity ones. As charring was the most important carbon loss mechanism in low to moderate severity fire patches, it is worthy of further attention.
Our stand-level estimates are preliminary, but additional DBH distribution data would be unlikely to alter our basic finding that combustion losses from the largest trees dominate stand-level calculations (Figure S16). Substantial improvements in stand-level estimates would most likely be related to better estimates of the proportion of stands comprised of Pinus versus other species, given that the former have ≈50% the combustion rates of the latter. Additionally, our analysis did not address interactions between stand structure and fire severity; however, while this interaction influences fire severity distributions, it would not change the fundamental relationships between tree size, biomass, and combustion rates.
At the level of entire fires (i.e., landscapes), uncertainty was related to the distribution of fire severity classes used. Specifically, we used RAVG to determine the areal extent of fire severity classes. Although RAVG provides an early (30–60 days) estimate of fire severities, it also tends to classify areas that eventually become moderate severity into the high severity class [34,35]. Therefore, our estimate of average landscape consumption rates may be higher than actually occurred. We can assess the degree this would have influenced our estimates of aboveground woody consumption for the Rim Fire. Potter [36] estimated that 33% of the Rim Fire was high severity; estimates based on MTBS (Monitoring Trends in Burn Severity) indicate that 20% was high severity. Using these fire severity distributions suggests that our landscape range for the Rim Fire would have been 0.5%–1.3% for Potter and 0.3%–0.9% for MTBS versus the 0.6%–1.5% we determined using RAVG.
4.3. Other Combustion Losses
We did not estimate fire consumption of either foliage or roots; however, the former, at least for high severity patches, could be substantial. If we assume that consumption of first order branch segments is the same as foliage consumption (Figure S17), then our stand level estimates of aboveground consumption for high severity patches would have been 3.2%–5.7%. At the landscape level, the average total aboveground consumption rate would have been much lower because there was very little foliage consumption for low and moderate severity patches. Specifically, the total aboveground biomass consumed at the landscape level, adjusted for foliage combustion, would have ranged from 1.4% to 3%. Although some of the fine roots in the lower portions of the organic soil horizons may have been consumed, particularly in high severity fire patches, there was little evidence that coarse roots of live trees were consumed. Assuming that combustion of live roots was minimal, and roots comprised 20% of total live biomass, the total stand-level live biomass combustion for high severity patches would be 2.6%–4.6%. Adjusting the landscape-level combustion rate to account for root biomass gives a range of 1.1%–2.4%. Although these combustion rates are low, they are 1.3–1.9 times our estimate for aboveground woody combustion and suggest that a more detailed accounting of foliage and root combustion is warranted in future studies.
We also did not evaluate combustion losses from either understory plants or aboveground, dead organic matter. During our field work in high severity fire patches, we observed that the forest floor and many downed tree boles, stumps, and associated dead coarse roots were largely consumed. In contrast, sound, large-standing dead trees could be deeply charred, but largely remained even in high severity fire patches. We can use the published distribution of carbon pools (e.g., found in Miesel et al. [17]) combined with our live woody biomass combustion rates, and assume the complete combustion of the understory plants and aboveground dead pools (i.e., coarse woody debris and the forest floor) to estimate pool-specific losses for high severity fire patches. This indicates that combustion of aboveground live woody biomass could account for 4%–10% of the total ecosystem combustion losses. Alternatively, if we assume that 50% of the coarse woody debris was combusted, then live aboveground woody biomass would have contributed 5%–12% of the total ecosystem combustion losses. These estimates contrast markedly with the live tree contribution if the values from Garcia et al. [18] were used: live combustion rates of 85% would mean 74% to 78% of the ecosystem combustion losses would have been associated with live tree combustion.
4.4. Policy Implications
Our findings have significant implications for a wide range of policy analyses related to wildfire combustion. The fraction of live woody biomass combusted varies not only with fire severity level; but also, depending on the organizational level being examined, a number of other factors, including the size structure of woody parts and trees, the species composition of trees present, and mixture of fire severity levels within fires. This suggests that great care must be taken in selecting the combustion rate(s) to be used in either modeling combustion or calibrating remote sensing-based estimates. Furthermore, until an improved multi-level (e.g., branches to landscapes) understanding of combustion rates has been attained, we recommend that such research be tied to field-based, level-relevant data to the extent possible. A key improvement includes determining the limits within which realistic combustion rates can be expected for a given level of analysis.
These findings also suggest that assumptions about combustion in past policy-related analyzes (e.g., [37,38]) should be re-evaluated. Based on our results and those of others [10], combustion-related emissions may have been overestimated. In contrast, fire-related losses via decomposition of fire-killed trees and the amount of fuel generated by fire disturbance may have been underestimated. Hence, the consequences of management actions may not be adequately understood until a more robust understanding of live woody combustion develops.
5. Conclusions
Our field-based examination of the amount of live aboveground woody biomass combusted indicated that while rates for small branch segments can be quite high (i.e., 100%), these rates do not translate in to major losses at the stand or landscape level. This is because high combustion rates in smaller structures are countered by other factors as one proceeds from branches to trees to stands, and to landscapes. The end result in the forests we examined is that even very severe fires combust <2% of live aboveground woody biomass on average. Our work as well as that of others [10] suggests that additional field research is needed to determine how wildfires release carbon to the atmosphere in a wide range of forest structures and fire-weather conditions. We suggest that researchers and policy makers avoid using estimators that are not field-based, because they currently appear to overstate the wildfire emissions used in carbon emissions reporting. As such, they have the potential to misdirect climate mitigation policy. The fact that the vast majority of aboveground woody biomass is not combusted raises the question of when fire-killed trees actually release their carbon. If dead trees are allowed to remain in place, the natural decomposition process could take many decades to centuries to release fire-killed carbon [39]. In contrast, if logged and removed for biomass energy, much of this carbon could be released relatively quickly [40]. Therefore, additional research is also needed to determine the degree that post-fire forest management influences the temporal profile of carbon release.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/f13030391/s1, Figure S1. Relationship for conifers between the proportion of aboveground woody parts in branches and tree diameter at breast height (based on equations in [22]; Figure S2. Amount of stem volume remaining for a given level of cumulative stem height lost or percentage of diameter lost along boles; Figure S3. Images of the Rim Fire from (a) December 2017 and (b) May 2018 indicate that substantial amounts of aboveground woody biomass remained even in high severity fire patches where all the trees were killed; Figure S4. Schematic depiction of branch orders and bifurcation ratios; Figure S5. Schematic depiction of branch weighting to create a whole tree estimate abundance of branch order segments for trees of different DBH size classes: (a) the maximum order method; (b) the volume weighed method; (c) the volume-length weighted method; and (d) the length weighted method; Figure S6. Examples of characteristics used to separate branches lost via combustion versus decomposition-related fragmentation: (a) branches with rectangular profiles without charring lost via decomposition-related fragmentation; (b) charring of branch stubs that had been broken off prior to fire; (c) thorn-like remnants of branches consumed in fire; Figure S7. Mean dimensions of branch orders of dissected branches for different tree species (a) mid-length diameter; and (b) segment length; Figure S8. Changes in branch structure among species and DBH size classes ((1: 1.0–4.9, 2: 5.0–9.9, 3: 10.0–24.9, 4: 25.0–49.9, 55: 0.0–99.9, 6: >100 cm)) adjacent to the Rim Fire, California: (a) highest branch order; (b) diameter of highest branch order present; (c) total length of highest order branches; and (d) length of highest order branch segment; Figure S9. Comparison of the different models used to estimate branch order contributions for C. decurrens. (a) maximum order model; (b) simple, unweighted average; (c) volume weighted model; and (d) volume and length weighted model; Figure S10 Theoretical maximum branch combustion possible based on: (a) branch orders observed to be consumed or (b) the maximum branch diameters to be consumed; Figure S11. Proportion of tree aboveground woody biomass in: (a) branch order segments 1–3; and (b) branch segments <2 cm diameter; Figure S12. Branch and bole consumption as a function of fire severity and diameter at breast height for the Creek and Rim Fires, California: (a) branch consumption for high severity fire patches; (b) bole consumption for high severity patches; (c) branch consumption moderate severity; (d) bole consumption moderate severity; (e) branch consumption low severity; and (f) bole consumption low severity; Figure S13. Bole char heights on trees compared to total tree height at: (a) Rim; and (b) Creek Fires; Figure S14. Radial char depth at base of tree bole based on: (a) chopping into and measuring char depth on each tree at Creek Fire; and (b) visual estimates from the Rim Fire; Figure S15. Bole char heights and depths for a subsample of trees on the Rim Fire: (a) the maximum versus minimum proportion of the bole charred; and (b) means depth of char at base of trees of three common species; Figure S16. Stand-level combustion for theoretical and published DBH size distributions: (a) total combustion of high severity fires for different DBH distribution types; and (b) total combustion of high severity fires for differing coefficients of variation for normal distribution (e.g., CV100= coefficient of variation of 100%); Figure S17. Relationship between diameter at breast height (DBH) of trees and the amount of foliage consumed by high severity fire patches in the Rim and Creek Fires; Table S1. Dimensions of dissected branch segments for five species in Rim Fire, Sierra Nevada Mountains, CA; Table S2. Bifurcation ratios for dissected tree branches for five species in Rim Fire, Sierra Nevada Mountains, CA; Table S3. Non-linear regressions predicting branch consumption as a function of DBH for different fire severity classes and species groups; Table S4. Non-linear regressions predicting bole consumption as a function of DBH for different fire severity classes and species groups.
Author Contributions
Conceptualization, M.E.H. and C.T.H.; methodology, M.E.H. and C.T.H.; software, M.E.H.; formal analysis, M.E.H.; investigation, M.E.H., D.A.D. and C.T.H.; resources, M.E.H., D.A.D. and C.T.H.; data curation, M.E.H. and C.T.H.; writing—original draft preparation, M.E.H.; writing—review and editing, M.E.H., D.A.D. and C.T.H.; project administration, M.E.H. and C.T.H.; funding acquisition, C.T.H. All authors have read and agreed to the published version of the manuscript.
Funding
C.T.H. and D.A.D. were funded by Environment Now foundation (#2021).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The underlying data used in this analysis is contained in Supplementary Materials.
Acknowledgments
We thank MarieClaire Egbert for assistance with note-taking during a portion of the Rim fire field work, and we thank GreenInfo Network for the GIS work pertaining to the study area figure.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Knorr, W.; Lehsten, V.; Arneth, A. Determinants and predictability of global wildfire emissions. Atmos. Chem. Phys. 2012, 12, 6845–6861. [Google Scholar] [CrossRef] [Green Version]
- Knorr, W.; Jiang, L.; Arneth, A. Climate, CO2 and human population impacts on global wildfire emissions. Biogeosciences 2016, 13, 267–282. [Google Scholar] [CrossRef] [Green Version]
- Glasspool, I.; Edwards, D.; Axe, L. Charcoal in the Silurian as evidence for the earliest wildfire. Geology 2004, 32, 381. [Google Scholar] [CrossRef]
- Pausas, J.; Keeley, J.E. A Burning Story: The Role of Fire in the History of Life. BioScience. 2009, 59, 593–601. [Google Scholar] [CrossRef] [Green Version]
- Keeley, J.E.; Pausas, J.; Rundel, P.W.; Bond, W.; Bradstock, R.A. Fire as an evolutionary pressure shaping plant traits. Trends Plant Sci. 2011, 16, 406–411. [Google Scholar] [CrossRef] [Green Version]
- McRae, D.J.; Duchesne, L.C.; Freedman, B.; Lynham, T.J.; Woodley, S. Comparisons between wildfire and forest harvesting and their implications in forest management. Environ. Rev. 2001, 9, 223–260. [Google Scholar] [CrossRef]
- Uhl, D.; Jasper, A.; Hamad, A.M.A.; Montenari, M. Permian and Triassic wildfires and atmospheric oxygen levels. Ecosystems 2008, 9, 179–187. [Google Scholar]
- Westerling, A.L.; Bryant, B.P. Climate change and wildfire in California. Clim. Chang. 2008, 87, 231–249. [Google Scholar] [CrossRef]
- Di Virgilio, G.; Evans, J.P.; Blake, S.A.P.; Armstrong, M.; Dowdy, A.J.; Sharples, J.; McRae, R. Climate Change Increases the Potential for Extreme Wildfires. Geophys. Res. Lett. 2019, 46, 8517–8526. [Google Scholar] [CrossRef]
- Stenzel, J.E.; Bartowitz, K.J.; Hartman, M.D.; Lutz, J.A.; Kolden, C.A.; Smith, A.M.S.; Law, B.E.; Swanson, M.E.; Larson, A.J.; Parton, W.J.; et al. Fixing a snag in carbon emissions estimates from wildfires. Glob. Chang. Biol. 2019, 25, 3985–3994. [Google Scholar] [CrossRef]
- Albini, F.A. A Model for Fire Spread in Wildland Fuels by-Radiation†. Combust. Sci. Technol. 1985, 42, 229–258. [Google Scholar] [CrossRef]
- Albini, F.; Reinhardt, E. Improved Calibration of a Large Fuel Burnout Model. Int. J. Wildland Fire 1997, 7, 21–28. [Google Scholar] [CrossRef]
- Catchpole, W.; Catchpole, E.; Butler, B.; Rothermel, R.C.; Morris, G.A.; Latham, D.J. Rate of Spread of Free-Burning Fires in Woody Fuels in a Wind Tunnel. Combust. Sci. Technol. 1998, 131, 1–37. [Google Scholar] [CrossRef]
- Hollis, J.J.; Anderson, W.R.; McCaw, W.L.; Cruz, M.; Burrows, N.D.; Ward, B.; Tolhurst, K.G.; Gould, J.S. The effect of fireline intensity on woody fuel consumption in southern Australian eucalypt forest fires. Aust. For. 2011, 74, 81–96. [Google Scholar] [CrossRef]
- Rossa, C.G. The effect of fuel moisture content on the spread rate of forest fires in the absence of wind or slope. Int. J. Wildland Fire 2017, 26, 24–31. [Google Scholar] [CrossRef]
- Rossa, C.G.; Fernandes, P.M. On the effect of live fuel moisture content on fire-spread rate. For. Syst. 2017, 26, eSC08. [Google Scholar] [CrossRef] [Green Version]
- Miesel, J.; Reiner, A.; Ewell, C.; Maestrini, B.; Dickinson, M. Quantifying Changes in Total and Pyrogenic Carbon Stocks Across Fire Severity Gradients Using Active Wildfire Incidents. Front. Earth Sci. 2018, 6, 41. [Google Scholar] [CrossRef] [Green Version]
- Garcia, M.; Saatchi, S.; Casas, A.; Koltunov, A.; Ustin, S.; Ramirez, C.; Garcia-Gutierrez, J.; Balzter, H. Quantifying biomass consumption and carbon release from the California Rim fire by integrating airborne LiDAR and Landsat OLI data. J. Geophys. Res. Biogeosciences 2017, 122, 340–353. [Google Scholar] [CrossRef]
- Campbell, J.; Donato, D.; Azuma, D.; Law, B. Pyrogenic carbon emission from a large wildfire in Oregon, United States. J. Geophys. Res. Earth Surf. 2007, 112, 04014. [Google Scholar] [CrossRef] [Green Version]
- Lydersen, J.; North, M. Topographic Variation in Structure of Mixed-Conifer Forests Under an Active-Fire Regime. Ecosystems 2012, 15, 1134–1146. [Google Scholar] [CrossRef]
- Van Wagner, C.E. Height of Crown Scorch in Forest Fires. Can. J. For. Res. 1973, 3, 373–378. [Google Scholar] [CrossRef] [Green Version]
- Jenkins, J.C.; Chojnacky, D.C.; Heath, L.S.; Birdsey, R.A. National-scale biomass estimators for United States tree species. For. Sci. 2003, 49, 12–35. [Google Scholar] [CrossRef]
- Santín, C.; Doerr, S.H.; Merino, A.; Bucheli, T.D.; Bryant, R.; Ascough, P.; Gao, X.; Masiello, C. Carbon sequestration potential and physicochemical properties differ between wildfire charcoals and slow-pyrolysis biochars. Sci. Rep. 2017, 7, 11233. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Czimczik, C.; Preston, C.M.; Schmidt, M.W.I.; Werner, R.A.; Schulze, E.-D. Effects of charring on mass, organic carbon, and stable carbon isotope composition of wood. Org. Geochem. 2002, 33, 1207–1223. [Google Scholar] [CrossRef] [Green Version]
- SAS Institute Inc. SAS/ACCESS® 9.4 Interface to ADABAS: Reference; SAS Institute Inc.: Cary, NC, USA, 2013; Available online: https://support.sas.com/software/94/ (accessed on 13 January 2022).
- Parsons, D.J.; DeBenedetti, S.H. Impact of fire suppression on a mixed-conifer forest. For. Ecol. Manag. 1979, 2, 21–33. [Google Scholar] [CrossRef]
- Smith, T.F.; Rizzo, D.M.; North, M. Patterns of mortality in an old-growth mixed-conifer forest of the southern Sierra Nevada, California. For. Sci. 2005, 51, 266–275. [Google Scholar] [CrossRef]
- Collins, B.M.; Everett, R.G.; Stephens, S.L. Impacts of fire exclusion and recent managed fire on forest structure in old growth Sierra Nevada mixed-conifer forests. Ecosphere 2011, 2, 1–14. [Google Scholar] [CrossRef]
- Knapp, E.E.; Skinner, C.N.; North, M.P.; Estes, B.L. Long-term overstory and understory change following logging and fire exclusion in a Sierra Nevada mixed-conifer forest. For. Ecol. Manag. 2013, 310, 903–914. [Google Scholar] [CrossRef]
- Chojnacky, D.C.; Heath, L.S.; Jenkins, J.C. Updated generalized biomass equations for North American tree species. For. Int. J. For. Res. 2014, 87, 129–151. [Google Scholar] [CrossRef] [Green Version]
- De Santis, A.; Asner, G.; Vaughan, P.J.; Knapp, D.E. Mapping burn severity and burning efficiency in California using simulation models and Landsat imagery. Remote Sens. Environ. 2010, 114, 1535–1545. [Google Scholar] [CrossRef]
- Meigs, G.W.; Donato, D.C.; Campbell, J.L.; Martin, J.G.; Law, B. Forest Fire Impacts on Carbon Uptake, Storage, and Emission: The Role of Burn Severity in the Eastern Cascades, Oregon. Ecosystems 2009, 12, 1246–1267. [Google Scholar] [CrossRef]
- Law, B.E.; Hudiburg, T.; Berner, L.T.; Kent, J.J.; Buotte, P.C.; HarmonM, E. Land use strategies to mitigate climate change in carbon dense temperate forests. Proc. Natl. Acad. Sci. USA 2018, 115, 3663–3668. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hanson, C.T.; North, M.P. Post-fire survival and flushing in three Sierra Nevada conifers with high initial crown scorch. Int. J. Wildland Fire 2009, 18, 857. [Google Scholar] [CrossRef]
- DellaSala, D.A.; Hanson, C.T. (Eds.) The Ecological Importance of Mixed—Severity Fires: Nature’s Phoenix; Elsevier Inc.: Waltham, MA, USA, 2015. [Google Scholar]
- Potter, C. Geographic Analysis of Burn Severity for the 2013 California Rim Fire. Nat. Resour. 2014, 05, 597–606. [Google Scholar] [CrossRef] [Green Version]
- Hurteau, M.D.; Koch, G.W.; Hungate, B.A. Carbon protection and fire risk reduction: Toward a full accounting of forest carbon offsets. Front. Ecol. Environ. 2008, 6, 493–498. [Google Scholar] [CrossRef] [Green Version]
- Liang, S.; Hurteau, M.D.; Westerling, A.L. Large-scale restoration increases carbon stability under projected climate and wildfire regimes. Front. Ecol. Environ. 2018, 16, 207–212. [Google Scholar] [CrossRef] [Green Version]
- Harmon, M.E.; Fasth, B.G.; Yatskov, M.; Kastendick, D.; Rock, J.; Woodall, C.W. Release of coarse woody detritus-related carbon: A synthesis across forest biomes. Carbon Balance Manag. 2020, 15, 1–21. [Google Scholar] [CrossRef]
- Hudiburg, T.W.; Law, B.E.; Moomaw, W.R.; Harmon, M.E.; Stenzel, J.E. Meeting GHG reduction targets requires accounting for all forest sector emissions. Environ. Res. Lett. 2019, 14, 095005. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).