Modeling Climatic Influences on Three Parasitoids of Low-Density Spruce Budworm Populations. Part 2: Meteorus trachynotus (Hymenoptera: Braconidae)
Abstract
1. Introduction
2. Materials and Methods
2.1. Model Description
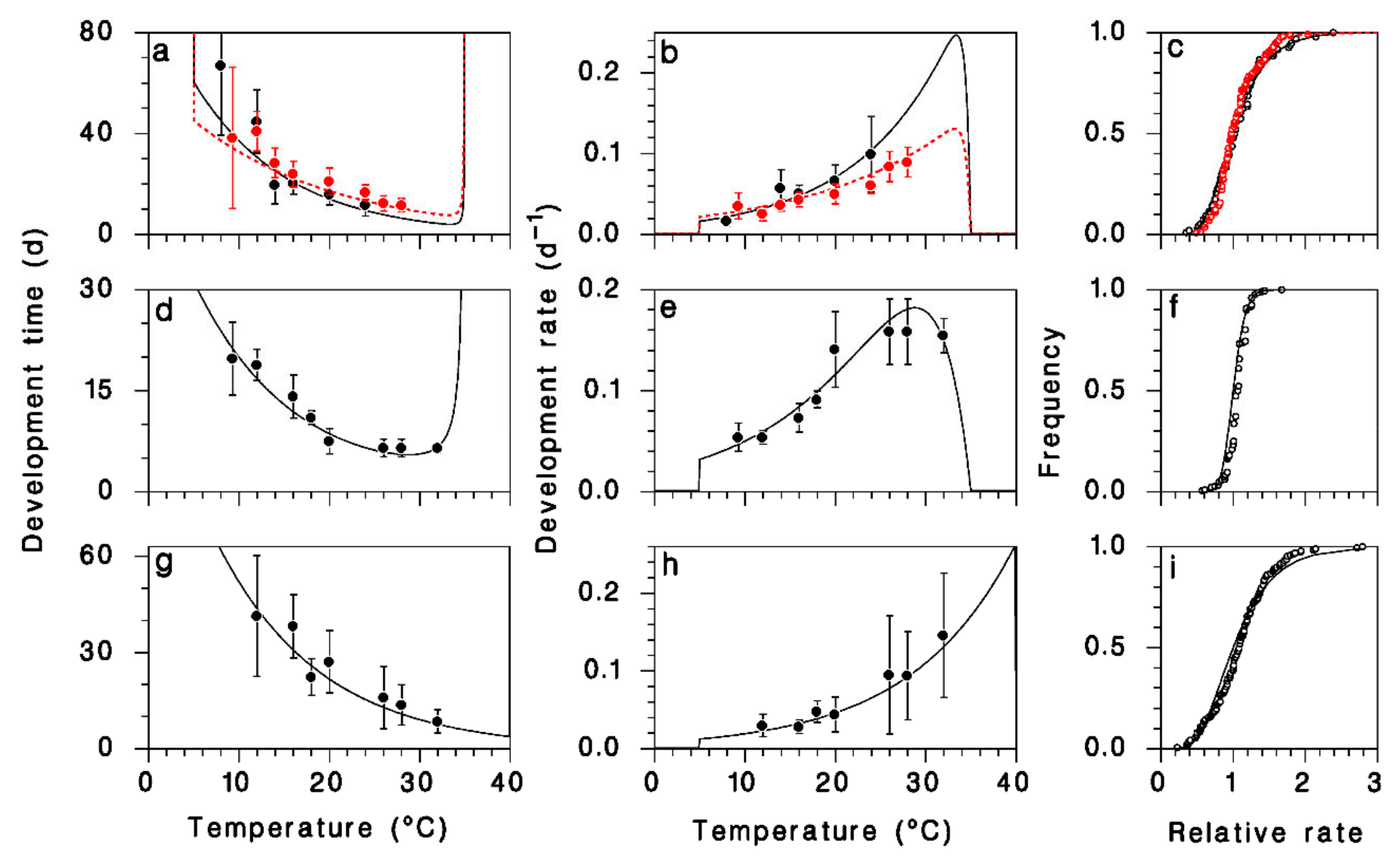
2.2. Parasitoid Development
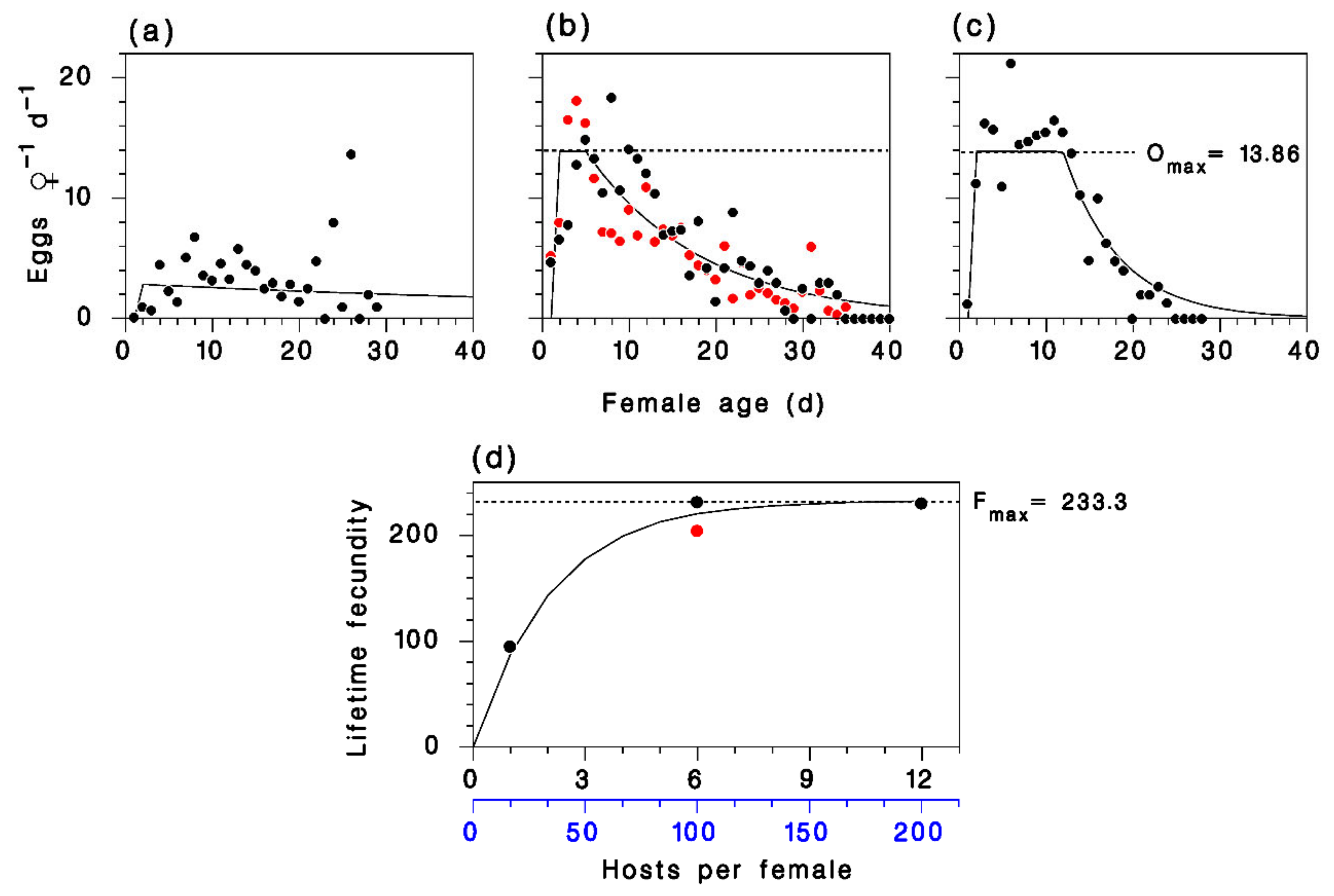
2.3. Parasitoid Reproduction
2.4. Model Calibration and Validation
2.5. Performance of the Parasitoid over Northeastern North America, Present and Future
3. Results
3.1. Development and Reproduction of M. trachynotus
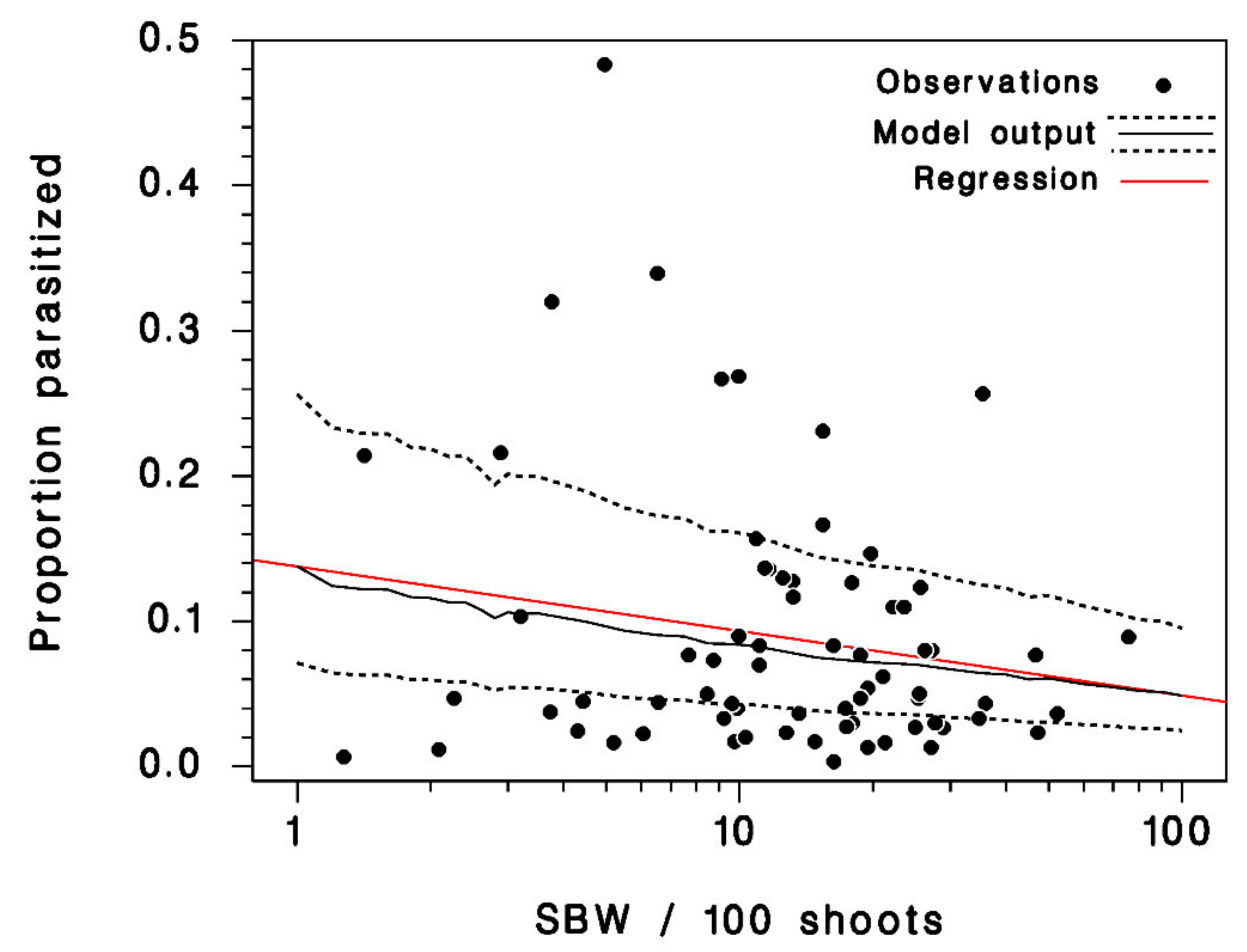
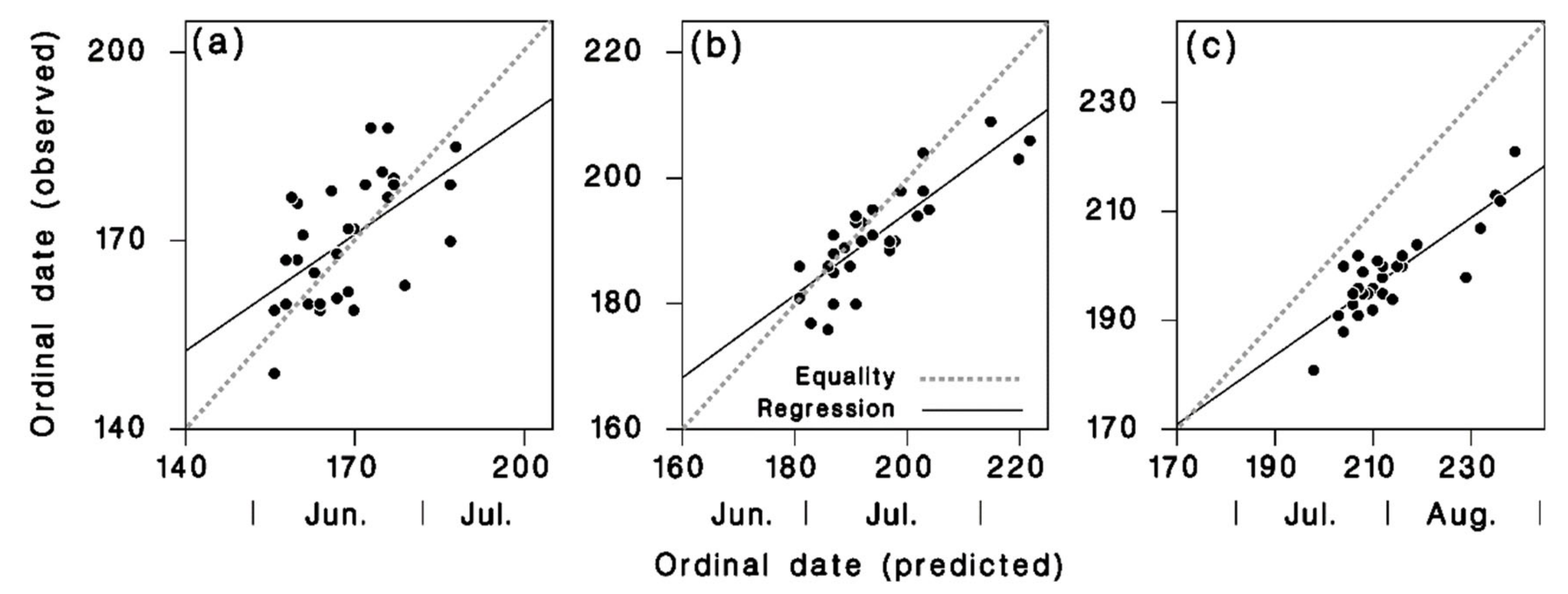
3.2. Model Calibration and Validation
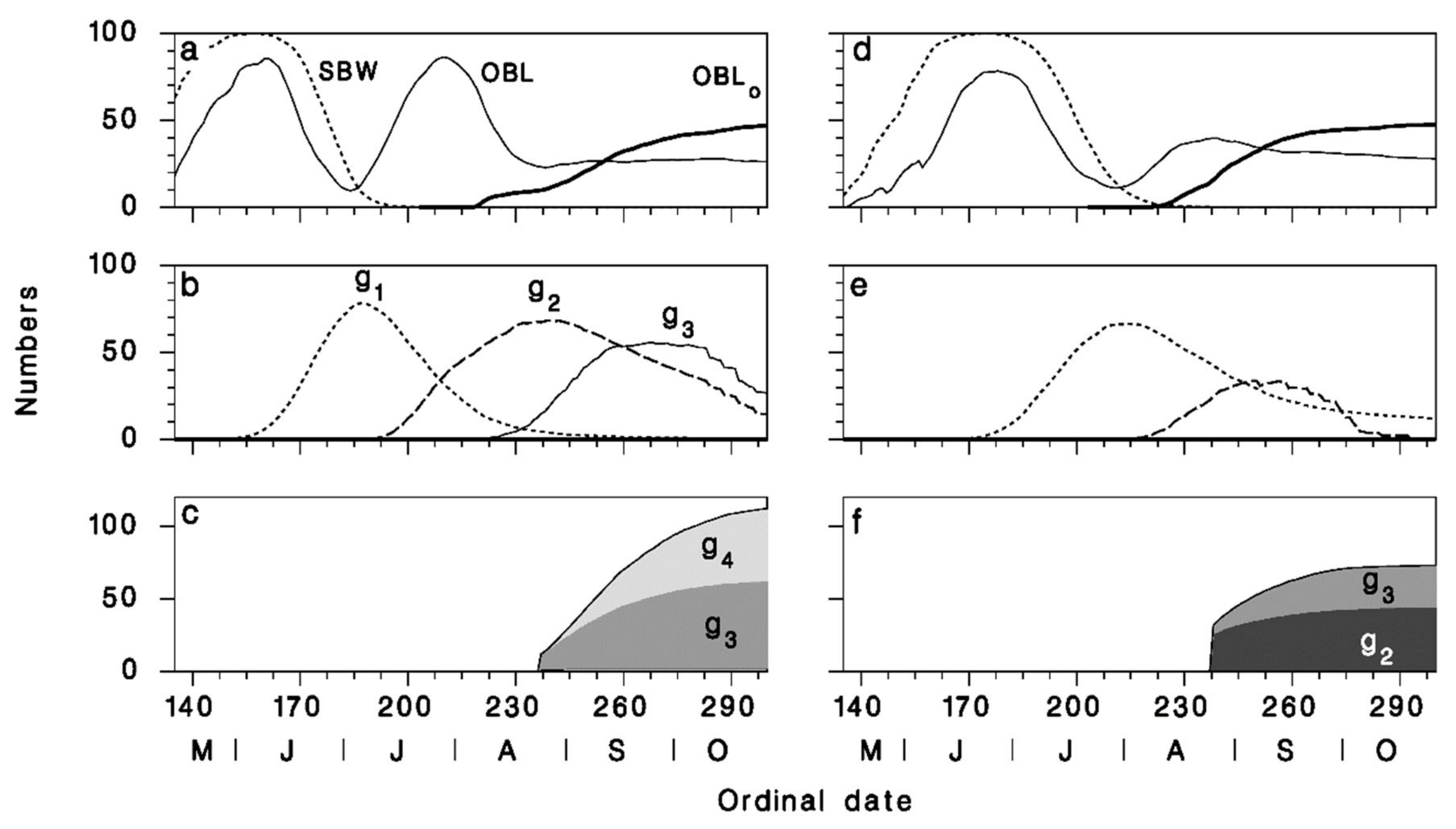
3.3. Seasonal Biology of Meteorus trachynotus and Its Hosts
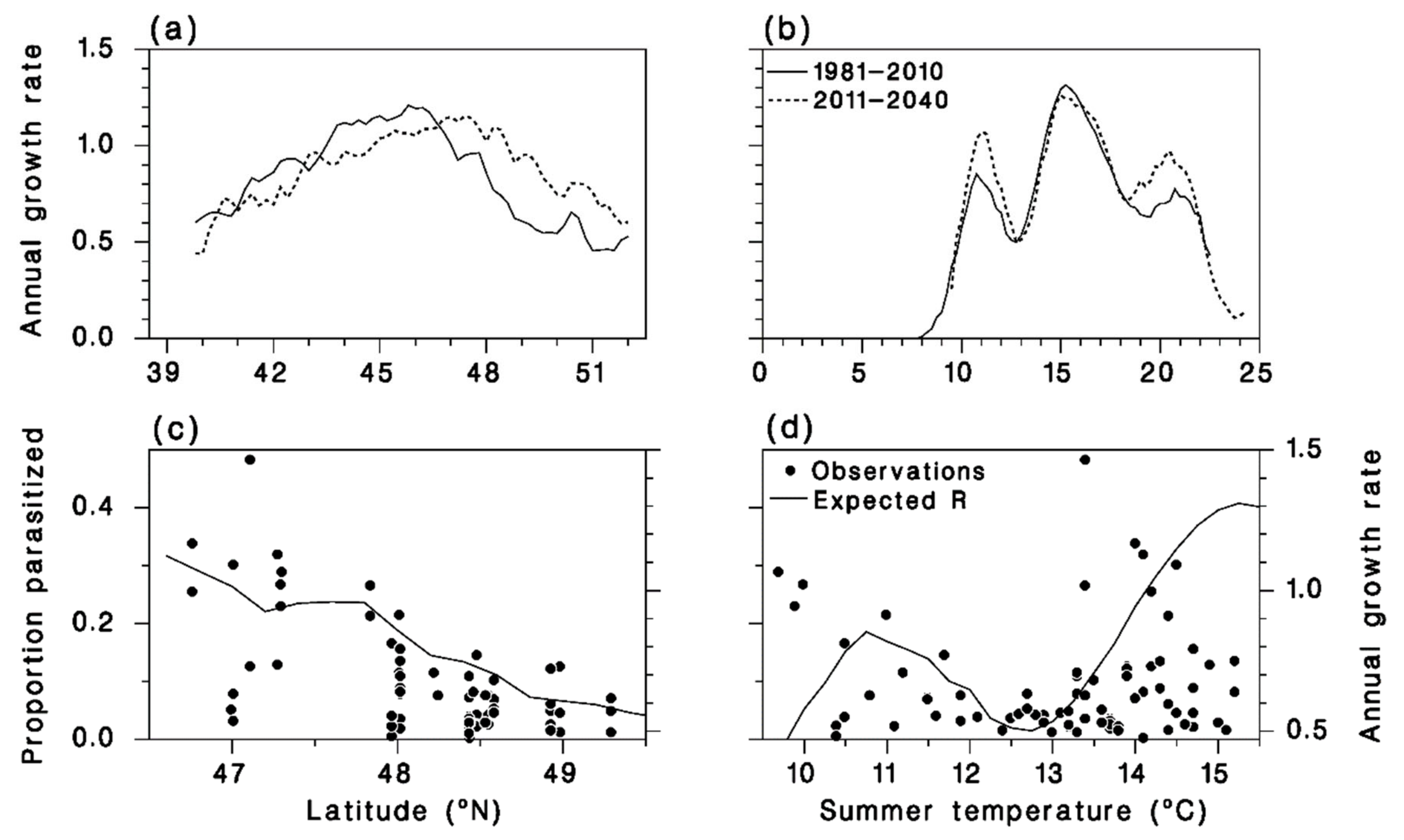
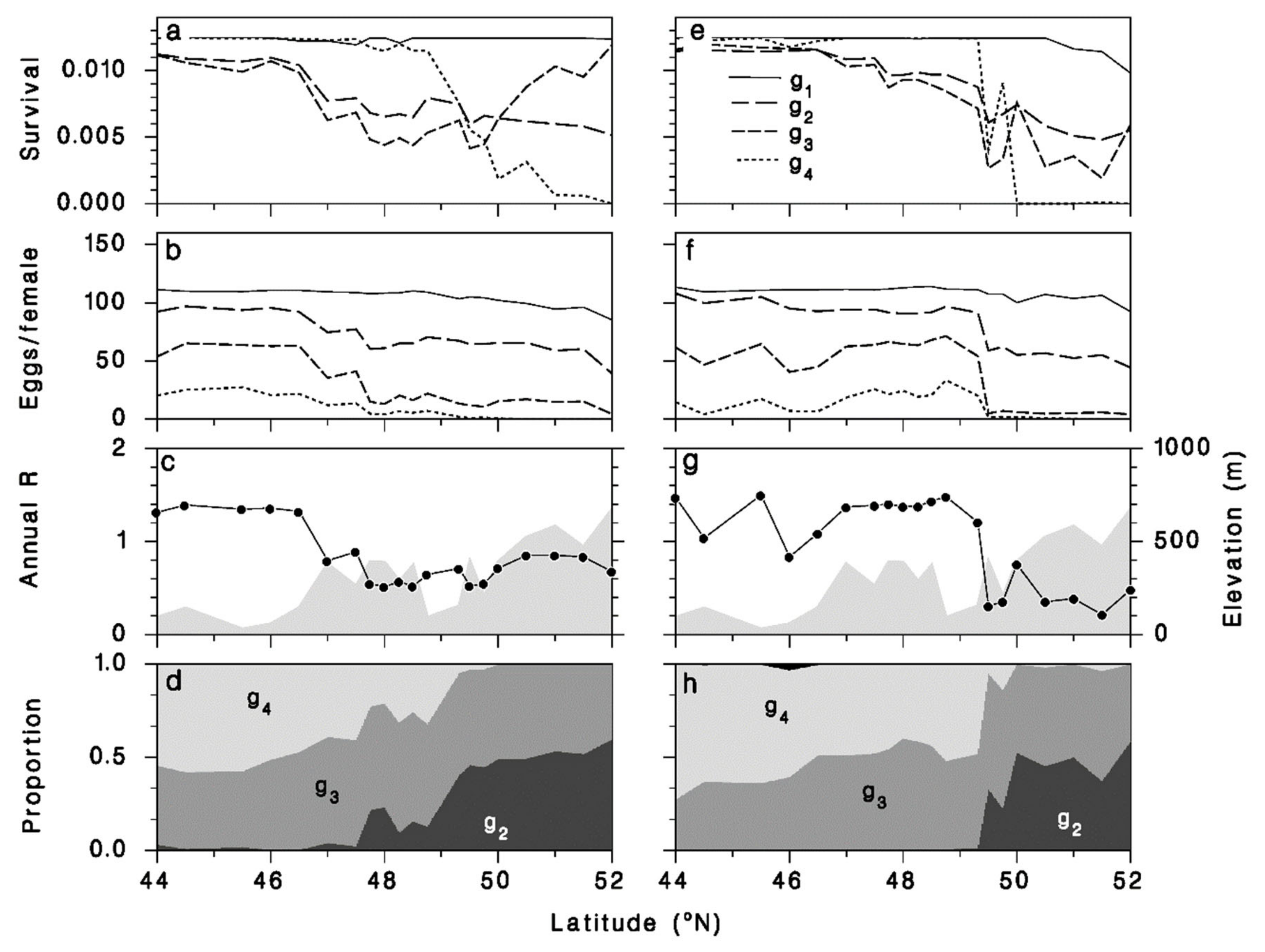
3.4. Meteorus trachynotus Performance Now and in the Future
3.5. Performance of M. trachynotus along a North-Nouth Transect
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nealis, V.G. Comparative ecology of conifer-feeding spruce budworms (Lepidoptera: Tortricidae). Can. Entomol. 2016, 148 (Suppl. 1), S33–S57. [Google Scholar] [CrossRef]
- Cooke, B.J.; Nealis, V.G.; Régnière, J. Insect defoliators as periodic disturbances in northern forest ecosystems. In Plant Disturbance Ecology: The Process and the Response, 2nd ed.; Johnson, E.A., Miyanishi, K., Eds.; Academic Press, Elsevier: London, UK, 2020; pp. 423–461. [Google Scholar]
- Régnière, J.; Nealis, V. Ecological mechanisms of population change during outbreaks of the spruce budworm. Ecol. Entomol. 2007, 32, 461–477. [Google Scholar] [CrossRef]
- Royama, T.; Eveleigh, E.S.; Miron, J.R.B.; Pollock, S.J.; McCarthy, P.C.; McDougall, G.A.; Lucarotti, C.J. Mechanisms underlying spruce budworm outbreak processes as elucidated by a 14-year study in New Brunswick, Canada. Ecol. Monogr. 2017, 87, 600–631. [Google Scholar] [CrossRef]
- Hawkins, B.A.; Cornell, H.V.; Hochberg, M.E. Predators, parasitoids, and pathogens as mortality agents in phytophagous insect populations. Ecology 1997, 78, 2145–2152. [Google Scholar] [CrossRef]
- Eveleigh, E.S.; McCann, K.S.; McCarthy, P.C.; Pollock, S.J.; Lucarotti, C.J.; Morin, B.; McDougall, G.A.; Strongman, D.B.; Huber, J.T.; Umbanhowar, J.; et al. Fluctuations in density of an outbreak species drive diversity cascades in food webs. Proc. Natl. Acad. Sci. USA 2007, 104, 16976–16981. [Google Scholar] [CrossRef]
- Greyson-Gaito, C.J.; McCann, K.S.; Fründ, J.; Lucarotti, C.J.; Smith, M.A.; Eveleigh, E.S. Parasitoid community responds indiscriminately to fluctuating spruce budworm and other caterpillars on balsam fir. Can. Entomol. (in Press), preprint bioRxiv. 2020. [CrossRef]
- Bouchard, M.; Martel, V.; Régnière, J.; Therrien, P.; Correa, D.L.P. Do natural enemies explain fluctuations in low-density spruce budworm populations? Ecology 2018, 99, 2047–2057. [Google Scholar] [CrossRef]
- Johns, C.R.; Bowden, J.B.; Carleton, R.D.; Cooke, B.J.; Edwards, S.; Emilson, E.J.S.; James, P.M.A.; Kneeshaw, D.; MacLean, D.A.; Martel, V.; et al. A conceptual framework for the spruce budworm early intervention strategy: Can outbreaks be stopped? Forests 2019, 10, 910. [Google Scholar] [CrossRef]
- Régnière, J.; Cooke, B.J.; Béchard, A.; Dupont, A.; Therrien, P. Dynamics and management of rising outbreak spruce budworm populations. Forests 2019, 10, 748. [Google Scholar] [CrossRef]
- LaSalle, J.; Gauld, I.D. Parasitic Hymenoptera and the biodiversity crisis. Redia 1991, 74, 315–334. [Google Scholar]
- Fidgen, J.G.; Eveleigh, E.S. Life history characteristics of Elachertus cacoeciae (Hymenoptera: Eulophidae), an ectoparasitoid of spruce budworm larvae, Choristoneura fumiferana (Lepidoptera: Tortricidae). Can. Entomol. 1998, 130, 215–229. [Google Scholar] [CrossRef]
- Fidgen, J.G.; Eveleigh, E.; Quiring, D.T. Influence of host size on oviposition behavior and fitness of Elachertus cacoeciae attacking a low-density populations of spruce budworm Choristoneura fumiferana larvae. Ecol. Entomol. 2000, 5, 156–164. [Google Scholar] [CrossRef]
- Régnière, J.; Seehausen, M.L.; Martel, V. Modeling Climatic influences on three parasitoids of low-density spruce budworm populations. Part 1: Tranosema rostrale (Hymenoptera: Ichneumonidae). Forests 2020, 11, 846. [Google Scholar] [CrossRef]
- Miller, C.A.; Renault, T.R. Incidence of parasitoids attacking endemic spruce budworm (Lepidoptera: Tortricidae) populations in New Brunswick. Can. Entomol. 1976, 108, 1045–1052. [Google Scholar] [CrossRef]
- Dowden, P.B.; Buchanan, W.D.; Carolin, V.M. Natural-control factors affecting the spruce budworm. J. Econ. Entomol. 1948, 41, 457–463. [Google Scholar] [CrossRef]
- Dowden, P.B.; Carolin, V.M.; Dirks, C.O. Natural control factors affecting the spruce budworm in the Adirondacks during 1946–1948. J. Econ. Entomol. 1950, 43, 774–783. [Google Scholar] [CrossRef]
- Jaynes, H.A.; Drooz, A.T. The importance of parasites in the spruce budworm infestations in New York and Maine. J. Econ. Entomol. 1952, 45, 1057–1061. [Google Scholar] [CrossRef]
- McGugan, B.M.; Blais, J.R. Spruce budworm parasite studies in northwestern Ontario. Can. Entomol. 1959, 91, 758–783. [Google Scholar] [CrossRef]
- Blais, J.R. Spruce budworm parasite investigations in the lower St-Lawrence and Gaspé régions of Quebec. Can. Entomol. 1960, 92, 384–396. [Google Scholar] [CrossRef]
- Blais, J.R. Parasite studies in two residual spruce budworm (Choristoneura fumiferana (Clem.)) outbreaks in Quebec. Can. Entomol. 1965, 97, 129–136. [Google Scholar] [CrossRef]
- Maltais, J.; Régnière, J.; Cloutier, C.; Hébert, C.; Perry, D. Seasonal biology of Meteorus trachynotus Vier. (Hymenoptera: Braconidae) and of its overwintering host Choristoneura rosaceana (Harr.) (Lepidoptera: Tortricidae). Can. Entomol. 1989, 121, 745–756. [Google Scholar] [CrossRef]
- Thireau, J.C.; Régnière, J.; Cloutier, C. Biology and morphology of immature stages of Meteorus trachynotus Vier. (Hymenoptera: Braconidae). Can. J. Zool. 1990, 68, 1000–1004. [Google Scholar] [CrossRef]
- Hébert, C.; Cloutier, C. Host instar as a determinant of preference and suitability for two parasitoids attacking lat instars of the spruce budworm (Lepidoptera: Tortricidae). Ann. Entomol. Soc. Am. 1990, 83, 734–741. [Google Scholar] [CrossRef]
- Thireau, J.C.; Régnière, J. Development, reproduction, voltinism and host synchrony of Meteorus trachynotus with its hosts Choristoneura fumiferana and C. rosaceana. Entomol. Exp. Appl. 1995, 76, 67–82. [Google Scholar] [CrossRef]
- Delisle, J. Monitoring the seasonal male flight activity of Choristoneura rosaceana (Lepidoptera: Tortricidae) in eastern Canada using virgin females and several different pheromone blends. Environ. Entomol. 1992, 21, 1007–1012. [Google Scholar] [CrossRef]
- Thomson, H.M. Some aspects of the epidemiology of a microsporidian parasite of the spruce budworm, Choristoneura fumiferana (Clem.). Can. J. Zool. 1958, 36, 309–316. [Google Scholar] [CrossRef]
- Wilson, G.G. Observations on the incidence of Nosema fumiferanae (Microsporidia) in a spruce budworm, Choristoneura fumiferana (Lepidoptera: Tortricidae) population. Proc. Entomol. Soc. Ont. 1977, 108, 144–145. [Google Scholar]
- Wilson, G.G. Observations on the Level Infection and Intensity of Nosema fumiferanae (microsporida) in Two Different Field Populations of Spruce Budworm, Choristoneura fumiferana; Info. Rep. FPM-X-79; Canadian Forest Service, Great Lakes Forestry Centre: Sault Ste. Marie, ON, Canada, 1987. [Google Scholar]
- Bauer, L.S.; Nordin, D.L. Effect of Nosema fumiferanae (Microsporida) on fecundity, fertility, and progeny performance of Choristoneura fumiferana (Lepidoptera: Tortricidae). Environ. Entomol. 1989, 18, 261–265. [Google Scholar] [CrossRef]
- Cusson, M.; Barron, J.R.; Goulet, H.; Régnière, J.; Doucet, D. Biology and status of Tranosema rostrale rostale (Hymenoptera: Ichneumonidae), a parasitoid of the spruce budworm (Lepidoptera: Tortricidae). Ann. Entomol. Soc. Am. 1998, 91, 87–97. [Google Scholar] [CrossRef]
- Régnière, J.; Saint-Amant, R.; Duval, P. Predicting insect distributions under climate change physiological responses: Spruce budworm as an example. Biol. Invasions 2012, 14, 1571–1586. [Google Scholar] [CrossRef]
- Régnière, J.; Powell, J.A. Animal life cycle models (Poikilotherms). In Phenology: An Integrative Environmental Science, 2nd ed.; Schwartz, M.D., Ed.; Springer: New York, USA, 2012; pp. 295–315. [Google Scholar] [CrossRef]
- RNCan/WeatherBasedSimulationFramework. Available online: https://github.com/RNCan/WeatherBasedSimulationFramework/tree/master/wbsModels/MeteorusTrachynotus (accessed on 28 January 2021).
- RNCan/WeatherBasedSimulationFramework. Available online: https://github.com/RNCan/WeatherBasedSimulationFramework/tree/master/wbsModels/MeteorusTrachynotus_OBL_SBW (accessed on 28 January 2021).
- Régnière, J. A process-oriented model of spruce budworm phenology (Lepidoptera: Tortricidae). Can. Entomol. 1982, 114, 811–825. [Google Scholar] [CrossRef]
- Régnière, J.; Saint-Amant, R.; Béchard, A. BioSIM 10 User’s Manual; Inf. Rep. LAU-X-137E; Natural Resources Canada, Canadian Forest Service, Laurentian Forestry Centre: Quebec, QC, Canada, 2014; Available online: https://d1ied5g1xfgpx8.cloudfront.net/pdfs/34818.pdf (accessed on 28 January 2021).
- Régnière, J.; Bolstad, P. Statistical simulation of daily air temperature patterns in eastern North America to forecast seasonal events in insect pest management. Environ. Entomol. 1994, 23, 1368–1380. [Google Scholar] [CrossRef]
- Régnière, J. A generalized approach to landscape-wide seasonal forecasting with temperature-driven simulation models. Environ. Entomol. 1996, 25, 869–881. [Google Scholar] [CrossRef]
- Régnière, J.; Saint-Amant, R. Stochastic simulation of daily air temperature and precipitation from monthly normals in North America north of Mexico. Int. J. Biometeorol. 2007, 51, 415–430. [Google Scholar] [CrossRef]
- Régnière, J.; Powell, J.; Bentz, B.; Nealis, V. Effects of temperature on development, survival and reproduction of insects: Experimental design, data analysis and modeling. J. Insect Physiol. 2012, 58, 634–647. [Google Scholar] [CrossRef]
- Anderson, T.W.; Darling, D.A. Asymptotic theory of certain “goodness-of-fit” criteria based on stochastic processes. Ann. Math. Stat. 1952, 23, 193–212. [Google Scholar] [CrossRef]
- Holling, C.S. Some characteristics of simple types of predation and parasitism. Can. Entomol. 1959, 91, 385–398. [Google Scholar] [CrossRef]
- Lethiecq, J.L.; Régnière, J. CFS Spruce Budworm Population Studies: Sites Descriptions; Info. Rep. LAU-X-83; Canadian Forest Service, Laurentian Forestry Centre: Quebec, QC, Canada, 1988. [Google Scholar]
- Thomas, A.W. Individual rearing of spruce budworm. Canadian Forest Service. Res. Notes 1984, 4, 23–25. Available online: https://cfs.nrcan.gc.ca/publications?id=8359.
- Tilles, D.A.; Woodley, N.E. Spruce budworm parasites in Maine: A reference manual for collection and identification of common species. In Agriculture Handbook; USDA Forest Service, Cooperative State Research Service: Washington DC, USA, 1984; Volume 616. [Google Scholar]
- Scinocca, J.F.; Kharin, V.V.; Jiao, Y.; Qian, M.W.; Lazare, M.; Solheim, L.; Flato, G.M. Coordinated global and regional climate modeling. J. Clim. 2016, 29, 17–35. [Google Scholar] [CrossRef]
- Arora, V.K.; Scinocca, J.F.; Boer, G.J.; Christian, J.R.; Denman, K.L.; Flato, G.M.; Kharin, V.V.; Lee, W.G.; Merryfield, W.J. Carbon emission limits required to satisfy future representative concentration pathways of greenhouse gases. Geophys. Res. Lett. 2011, 38, L05805. [Google Scholar] [CrossRef]
- Pachauri, R.K.; Allen, M.R.; Barros, V.R.; Broome, J.; Cramer, W.; Christ, R.; Church, J.A.; Clarke, L.; Dahe, Q.; Dasgupta, P.; et al. Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Pachauri, R.K., Meyer, L.A., Eds.; International Panel on Climate Change: Geneva, Switzerland, 2014; p. 151. Available online: https://www.ipcc.ch/report/ar5/syr (accessed on 3 August 2020).
- Canadian Centre for Climate Modelling and Analysis (CCCma) Climate Model Data, CanESM2/CGCM4 Model Output. 2018. Available online: http://climate-modelling.canada.ca/climatemodeldata/cgcm4/CanESM2/rcp45/ (accessed on 3 August 2020).
- Liebhold, A.M.; Rossi, R.E.; Kemp, W.P. Geostatistics and geographic information systems in applied insect ecology. Ann. Rev. Entomol. 1993, 38, 303–327. [Google Scholar] [CrossRef]
- Furlong, M.J.; Zalucki, M.P. Climate change and biological control: The consequences of increasing temperature on host-parasitoid interactions. Curr. Opin. Insect Sci. 2017, 20, 39–44. [Google Scholar] [CrossRef] [PubMed]
- Murdoch, W.W. Stabilizing effects of spatial heterogeneity in predator-prey systems. Theor. Popul. Biol. 1977, 11, 252–273. [Google Scholar] [CrossRef]
- Van Baalen, M.; Krivan, V.; van Rijn, P.C.J.; Sabelis, M.W. Alternative food, switching predators, and the persistence of predator-prey systems. Am. Nat. 2001, 175, 512–524. [Google Scholar] [CrossRef]
- Schenk, D.; Bacher, S. Functional response of a generalist insect predator to one of its prey species in the field. J. Anim. Ecol. 2002, 71, 524–531. [Google Scholar] [CrossRef]
- Charnov, E.L. Optimal foraging, the marginal value theorem. Theor. Popul. Biol. 1976, 9, 129–136. [Google Scholar] [CrossRef]
- Wajnberg, E.; Berhard, P.; Hamelin, F.; Boivin, G. Optimal patch time allocation for time-limited foragers. Behav. Ecol. Scociobiol. 2006, 60, 1–10. [Google Scholar] [CrossRef]
- Voigt, W.; Perner, J.; Davis, A.J.; Eggers, T.; Schumacher, J.; Bährmann, R.; Fabian, B.; Heinrich, W.; Köhler, G.; Lichter, D.; et al. Trophic levels are differentially sensitive to climate. Ecology 2003, 84, 2444–2453. [Google Scholar] [CrossRef]
- Hance, T.; van Baaren, J.; Vernon, P.; Boivin, G. Impact of extreme temperatures on parasitoids in a climate change perspective. Ann. Rev. Entomol. 2007, 52, 107–126. [Google Scholar] [CrossRef]
- Quicke, D.L.J. We know too little about parasitoid wasp distributions to draw any conclusions about latitudinal trends in species richness, body size and biology. PLoS ONE 2012, 7, e32101. [Google Scholar] [CrossRef]
- Harvey, J.A. Conserving host–parasitoid interactions in a warming world. Curr. Opin. Insect Sci. 2015, 12, 79–85. [Google Scholar] [CrossRef]
- Stireman, J.O.; Dyer, L.A.; Janzen, D.H.; Singer, M.S.; Lill, J.T.; Marquis, R.J.; Ricklefs, R.E.; Gentry, G.L.; Hallwachs, W.; Coley, P.D.; et al. Climatic unpredictability and parasitism of caterpillars: Implications of global warming. Proc. Natl. Acad. Sci. USA 2005, 102, 17384–17387. [Google Scholar] [CrossRef] [PubMed]
- De Souza, A.A.; Martins, S.G.F.; Zacarias, M.S. Computer simulation applied to the biological control of the insect Aphis gossypii for the parasitoid Lysiphlebus testaceipes. Ecol. Model. 2009, 220, 756–763. [Google Scholar] [CrossRef]
- Johnston, A.S.A.; Boyd, R.J.; Watson, J.W.; Paul, A.; Evans, L.C.; Gardner, E.L.; Boult, V.L. Predicting population responses to environmental change from indivual-level mechanisms: Towards a standardized mechanistic approach. R. Soc. Proc. B 2019, 286, 20191916. [Google Scholar] [CrossRef]
- Gherman, A.-L.M.; Hall, R.J.; Byers, J.E. Host and parasite thermal ecology jointly determine the effect of climate warming on epidemic dynamics. Proc. Natl. Acad. Sci. USA 2018, 115, 744–749. [Google Scholar] [CrossRef]
- Daugaard, U.; Petchey, O.L.; Pennekamp, F. Warming can destabilize predator-prey interactions by shifting the functional response from Type III to Type II. J. Anim. Ecol. 2019, 88, 1575–1586. [Google Scholar] [CrossRef] [PubMed]

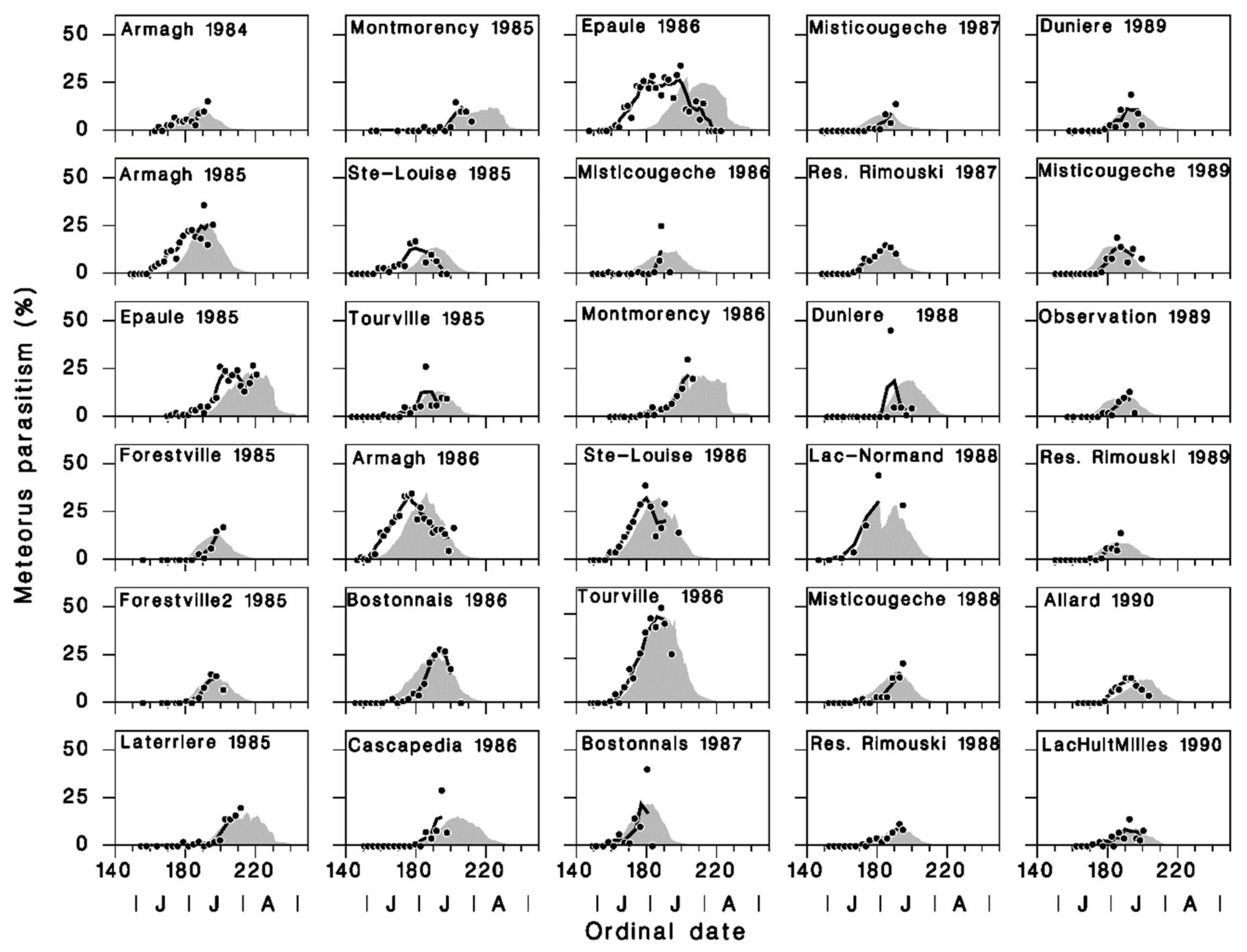
| Location | Coordinates | Observation Year | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| °N | °E | m | 84 | 85 | 86 | 87 | 88 | 89 | 90 | |
| Armagh | 46.7668 | −70.6575 | 277 | Y | Y | Y | ||||
| Laterriere | 47.9688 | −71.2205 | 815 | Y | ||||||
| Forestville | 48.9814 | −69.1938 | 250 | Y | ||||||
| Forestville 2 | 48.9257 | −69.1078 | 130 | Y | ||||||
| Epaule | 47.2997 | −71.1940 | 789 | Y | Y | |||||
| Tourville | 47.1140 | −69.9521 | 300 | Y | Y | |||||
| Sainte Louise | 47.2797 | −70.1203 | 70 | Y | Y | |||||
| Montmorency | 47.3220 | −71.1470 | 725 | Y | Y | |||||
| Cascapedia | 48.4787 | −65.9512 | 550 | Y | ||||||
| Bostonnais | 47.8396 | −72.4812 | 400 | Y | Y | |||||
| Misticougeche | 48.0198 | −68.3508 | 440 | Y | Y | Y | Y | |||
| Reserve Rimouski | 48.0630 | −68.1263 | 350 | Y | Y | Y | ||||
| Lac Normand | 47.0135 | −73.2025 | 335 | Y | ||||||
| Duniere | 48.4338 | −66.7805 | 475 | Y | Y | |||||
| Observation | 48.5851 | −65.1001 | 445 | Y | ||||||
| Lac Huit Milles | 48.4607 | −67.0853 | 345 | Y | ||||||
| Allard | 48.2217 | −66.4153 | 306 | Y | ||||||
| Parameter | Immatures | Pupa | Adult | |
|---|---|---|---|---|
| Spring | Summer | |||
| p1 | 0.0166 ± 0.0015 | 0.0222 ± 0.0009 | 0.0323 ± 0.0012 | 0.0124 ± 0.0010 |
| p2 | 2.9072 ± 0.2253 | 1.9227 ± 0.0878 | 2.7270 ± 0.1533 | 3.0574 ± 0.1567 |
| p3 | 0.0117 ± 0.5777 | 0.0117 ± 0.5777 | 0.1285 ± 0.0122 | 0.001 * |
| Tb * | 5 | 5 | 5 | 5 |
| Tm * | 35 | 35 | 35 | 40 |
| sε | 0.3608 | 0.2929 | 0.1328 ± 0.0066 | 0.4317 ± 0.0208 |
| Log likelihood | −1008.3 | −372.3 | −755.5 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Régnière, J.; Saint-Amant, R.; Thireau, J.-C.; Therrien, P.; Hébert, C.; Martel, V. Modeling Climatic Influences on Three Parasitoids of Low-Density Spruce Budworm Populations. Part 2: Meteorus trachynotus (Hymenoptera: Braconidae). Forests 2021, 12, 155. https://doi.org/10.3390/f12020155
Régnière J, Saint-Amant R, Thireau J-C, Therrien P, Hébert C, Martel V. Modeling Climatic Influences on Three Parasitoids of Low-Density Spruce Budworm Populations. Part 2: Meteorus trachynotus (Hymenoptera: Braconidae). Forests. 2021; 12(2):155. https://doi.org/10.3390/f12020155
Chicago/Turabian StyleRégnière, Jacques, Rémi Saint-Amant, Jean-Claude Thireau, Pierre Therrien, Christian Hébert, and Véronique Martel. 2021. "Modeling Climatic Influences on Three Parasitoids of Low-Density Spruce Budworm Populations. Part 2: Meteorus trachynotus (Hymenoptera: Braconidae)" Forests 12, no. 2: 155. https://doi.org/10.3390/f12020155
APA StyleRégnière, J., Saint-Amant, R., Thireau, J.-C., Therrien, P., Hébert, C., & Martel, V. (2021). Modeling Climatic Influences on Three Parasitoids of Low-Density Spruce Budworm Populations. Part 2: Meteorus trachynotus (Hymenoptera: Braconidae). Forests, 12(2), 155. https://doi.org/10.3390/f12020155






