Laminated Veneer Lumber with Non-Wood Components and the Effects of Selected Factors on Its Bendability
Abstract
1. Introduction
2. Materials and Methods
2.1. Material
2.2. Methods
2.2.1. Determining Selected Characteristics
2.2.2. Evaluation and Calculation of Kbend and Rmin
3. Results and Discussion
4. Conclusions
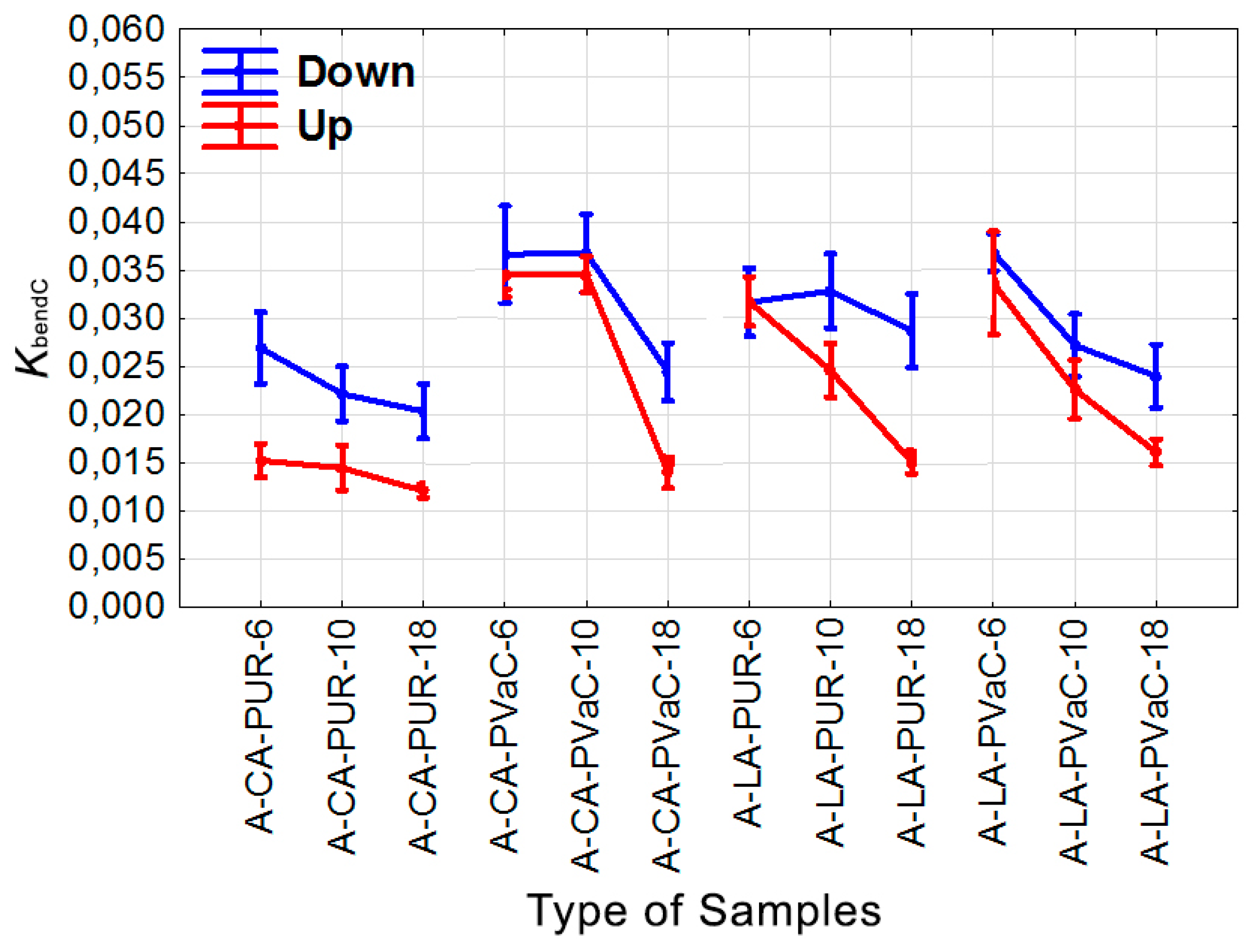
- The type and position of the non-wood component used in the laminated materials had a significant effect on all the observed characteristics: KbendC, KbendB, RminC, and RminB.
- Bending coefficient values based on the simple bending equation (KbendC) tended to be greater than bending coefficient values based on bending geometry (KbendB).
- The greatest values of the bending coefficient based on the simple bending equation (KbendC) and the bending coefficient based on bending geometry (KbendB) were generally found in materials of lower thickness.
- No rule was observed for the high or low measured values of the observed characteristics (KbendC, KbendB, RminC, and RminB) in relation to the wood species used.
Author Contributions
Funding
Conflicts of Interest
References
- Pokharel, R.; Grala, R.K.; Grebner, D.L. Woody residue utilization for bioenergy by primary forest products manufacturers: An exploratory analysis. For. Policy Econ. 2017, 85, 161–171. [Google Scholar] [CrossRef]
- Long, Z.; Wu, J.; Xu, W.; Lin, W. Study of the coordination mechanism of a wood processing residue-based reverse supply chain. BioResources 2018, 13, 2562–2577. [Google Scholar] [CrossRef]
- Bhoominathan, R.; Divyabarathi, P.; Manimegalai, R.; Nithya, T.; Shanmugapriya, S. Infra-red thermography based inspection of hybrid composite laminates under flexure loading. IJVSS 2018, 10, 6–9. [Google Scholar] [CrossRef]
- Silva, F.G.A.; de Moura, M.F.S.F.; Magalhães, A.G. Lowvelo city impact behaviour of a hybrid carbon-epoxy/corklaminate. Strain 2017, 53. [Google Scholar] [CrossRef]
- Abrate, S. Impact on laminated composite materials. Appl. Mech. Rev. 1991, 44, 155–190. [Google Scholar] [CrossRef]
- Bigg, D.M. The impact behavior of thermoplastic sheet composites. J Reinf. Plast. Comp. 1994, 13, 339–354. [Google Scholar] [CrossRef]
- Glos, P.; Denzler, J.K.; Linsenmann, P. Strength and stiffness behaviour of beech laminations for high strength glulam. In Proceedings of the Meeting 37 CIB Working Commission W18-Timber Structures, Edinburgh, Scotland, UK, August 2004. [Google Scholar]
- Frese, M.; Blaß, H.J. Characteristic bending strength of beech glulam. Mater. Struct. 2007, 40, 3–13. [Google Scholar] [CrossRef]
- Hill, C.A.S. Wood Modification: Chemical, Thermal and Other Processes; John Wiley & Sons: Chichester, UK, 2006. [Google Scholar] [CrossRef]
- Kubovský, I.; Babiak, M. Color changes induced by CO2 laser irradiation of wood surface. Wood Res. 2009, 54, 61–66. [Google Scholar]
- Hrčka, R.; Babiak, M. Some non-traditional factors influencing thermal properties of wood. Wood Res. 2012, 57, 367–374. [Google Scholar]
- Gašparík, M.; Barcík, Š. Impact of plasticization by microwave heating on the total deformation of beech wood. BioResources 2013, 8, 6297–6308. [Google Scholar] [CrossRef]
- Gašparík, M.; Barcík, Š. Effect of plasticizing by microwave heating on bending characteristics of beech wood. BioResources 2014, 9, 4808–4820. [Google Scholar] [CrossRef]
- Svoboda, T.; Ruman, D.; Gaff, M.; Gašparík, M.; Miftieva, E.; Dundek, L. Bending characteristics of multilayered soft and hardwood materials. BioResources 2015, 10, 8461–8473. [Google Scholar] [CrossRef][Green Version]
- Miftieva, E.; Gaff, M.; Svoboda, T.; Babiak, M.; Gašparík, M.; Ruman, D.; Suchopár, M. Effects of selected factors on bending characteristics of beech wood. BioResources 2016, 11, 599–611. [Google Scholar] [CrossRef]
- Fang, C.-H.; Mariotti, N.; Cloutier, A.; Koubaa, A.; Blanchet, P. Densification of wood veneers by compression combined with heat and steam. Eur. J. Wood Prod. 2012, 70, 155–163. [Google Scholar] [CrossRef]
- Gaff, M.; Vokatý, V.; Babiak, M.; Bal, B.C. Coefficient of wood bendability as a function of selected factors. Constr. Build Mater. 2016, 126, 632–640. [Google Scholar] [CrossRef]
- Blomberg, J.; Persson, B. Swelling pressure of semi-isostaticallydensified wood under different mechanical resraints. Wood Sci. Technol. 2007, 41, 401–415. [Google Scholar] [CrossRef]
- Plevris, N.; Triantafillou, T.C. CreepbehaviorofFRP-reinforcedwoodmembers. J. Struct. Eng. 1995, 121, 174–186. [Google Scholar] [CrossRef]
- Redon, C.; Li, V.C.; Wu, C.; Hoshiro, H.; Saito, T.; Ogawa, A. Measuring and modifying interface propertiesof PVA fibers in ECC matrix. J Mater. Civil Eng. 2001, 13, 399–406. [Google Scholar] [CrossRef]
- Sviták, M.; Ruman, D. Tensile-shear strength of layered wood reinforced by carbon materials. Wood Res. 2017, 62, 243–252. [Google Scholar]
- Gaff, M.; Babiak, M.; Vokatý, V.; Gašparík, M.; Ruman, D. Bending characteristics of hardwood lamellae in the elastic region. Compos. Part B-Eng. 2017, 116, 61–75. [Google Scholar] [CrossRef]
- Babiak, M.; Gaff, M.; Sikora, A.; Hysek, Š. Modulus of elasticity in three- and four-point bending of wood. Compos. Struct. 2018, 204, 454–465. [Google Scholar] [CrossRef]
- Gaff, M.; Gašparík, M.; Babiak, M.; Vokatý, V. Bendability characteristics of wood lamellae in plastic region. Compos. Struct. 2017, 163, 410–422. [Google Scholar] [CrossRef]
- Gaff, M.; Babiak, M. Methods for determining the plastic work in bending and impact of selected factors on its value. Compos. Struct. 2018, 202, 66–76. [Google Scholar] [CrossRef]
- Sikora, A.; Gaff, M.; Hysek, Š.; Babiak, M. The plasticity of composite material based on winter rapeseed as a function of selected factors. Compos. Struct. 2018, 202, 783–792. [Google Scholar] [CrossRef]
- Gaff, M.; Babiak, M. Tangent modulus as a function of selected factors. Compos. Struct. 2018, 202, 436–446. [Google Scholar] [CrossRef]
- Saracoglu, E. Finite-element Simulations of the Influence of Cracks on the Strength of Glulam Beams. Master’s Thesis, Blekinge Institute of Technology, Karlskrona, Sweden, 2011. [Google Scholar]
- Khorasan, S.R. Finite-element Simulations of Glulam Beams with Natural Cracks. Master’s Thesis, Blekinge Institute of Technology, Karlskrona, Sweden, 2012. [Google Scholar]
- Hýsek, Š.; Gaff, M.; Sikora, A.; Babiak, M. New composite material based on winter rapeseed and his elasticity properties as a function of selected factors. Compos. Part B-Eng. 2018, 153, 108–116. [Google Scholar] [CrossRef]
- Požgaj, A.; Chovanec, D.; Kurjatko, S.; Babiak, M. Štruktúra a Vlastnosti Dreva. In Structure and Properties of Wood; Príroda: Bratislava, Slovakia, 1997. [Google Scholar]
- Gaff, M.; Gašparík, M.; Borůvka, V.; Haviarová, E. Stress simulation in layered wood-based materials under mechanical loading. Mater. Des. 2015, 87, 1065–1071. [Google Scholar] [CrossRef]
- European Committee for Standardization, Wood-Based Panels. EN 310: Determination of Modulus of Elasticity in Bending and of Bending Strength; European Committee for Standardization: Brussels, Belgium, 1993. [Google Scholar]
- International Organization for Standardization. ISO 13061-1: Physical and Mechanical Properties of Wood—Test Methods for Small Clear Wood Specimens—Part 1: Determination of Moisture Content for Physical and Mechanical Tests; International Organization for Standardization: Geneva, Switzerland, 2014. [Google Scholar]
- International Organization for Standardization. ISO 13061-2: Physical and Mechanical Properties of Wood—Test Methods for Small Clear Wood Specimens—Part 2: Determination of Density for Physical and Mechanical Tests; International Organization for Standardization: Geneva, Switzerland, 2014. [Google Scholar]
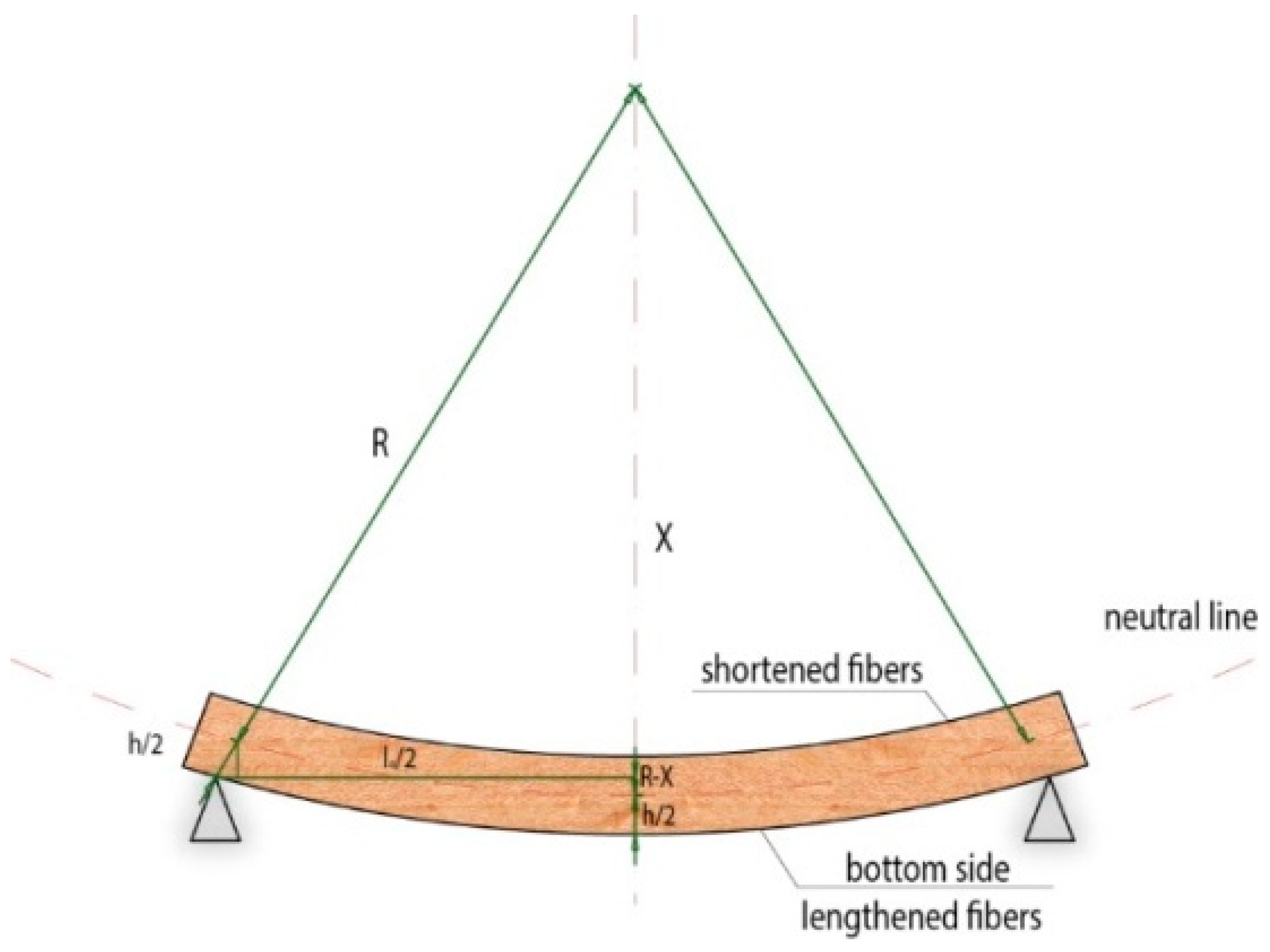
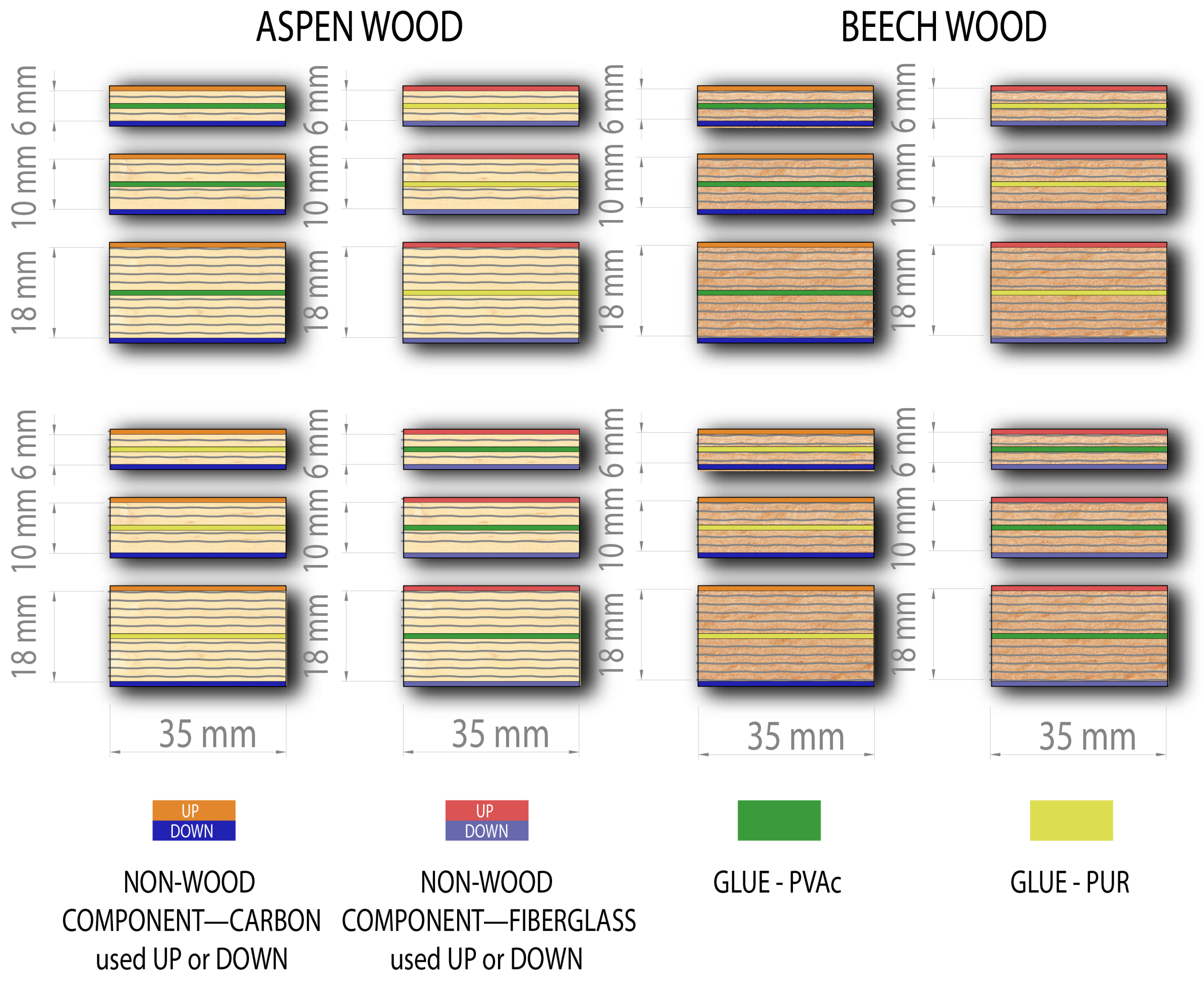
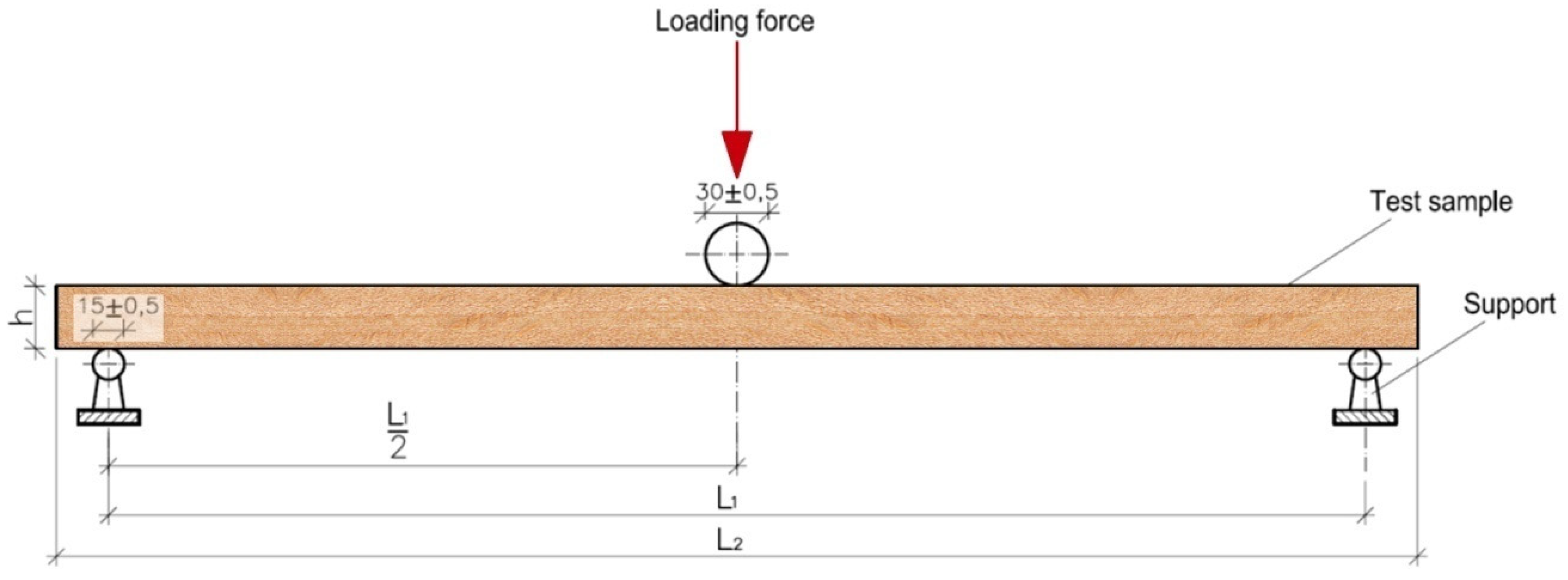
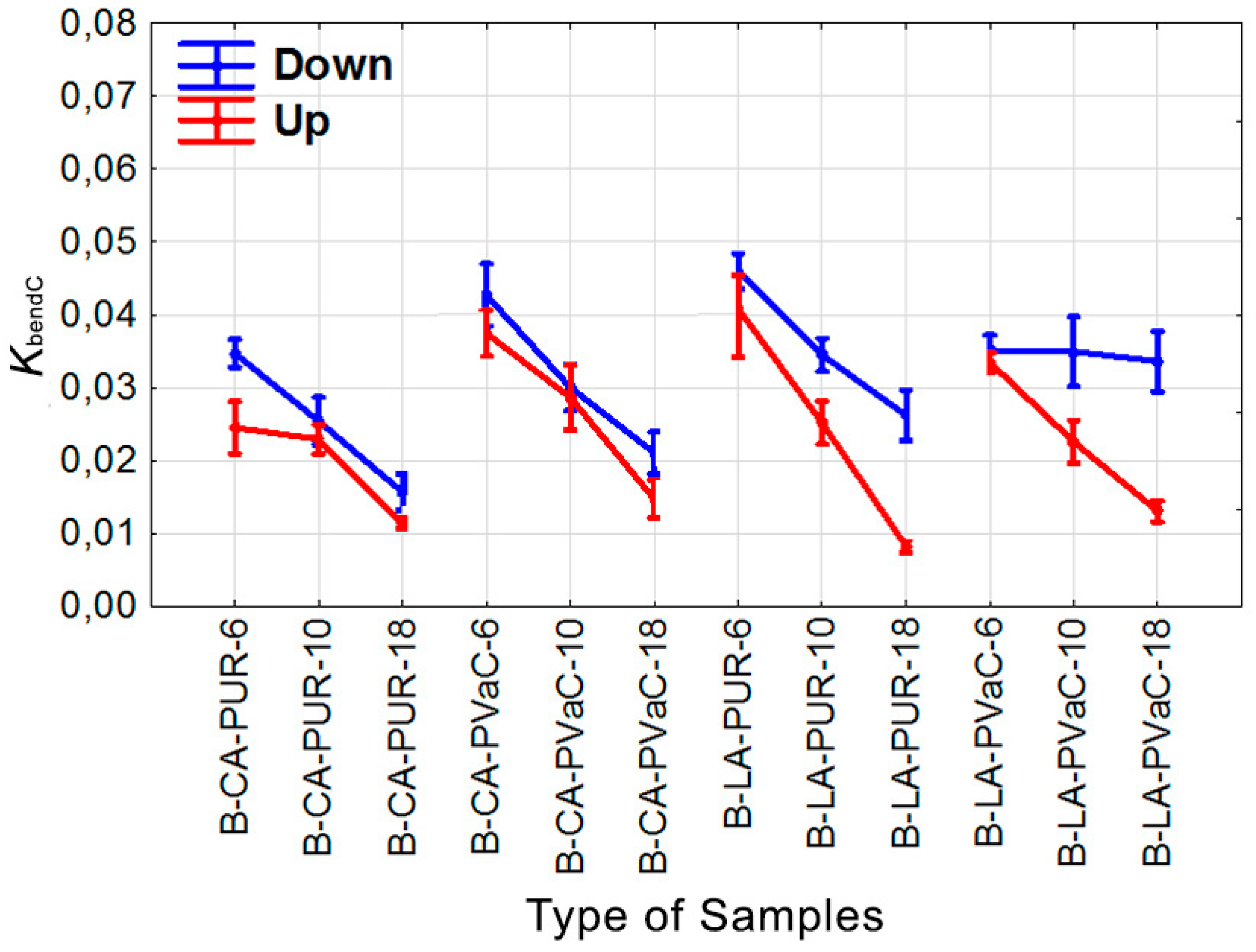
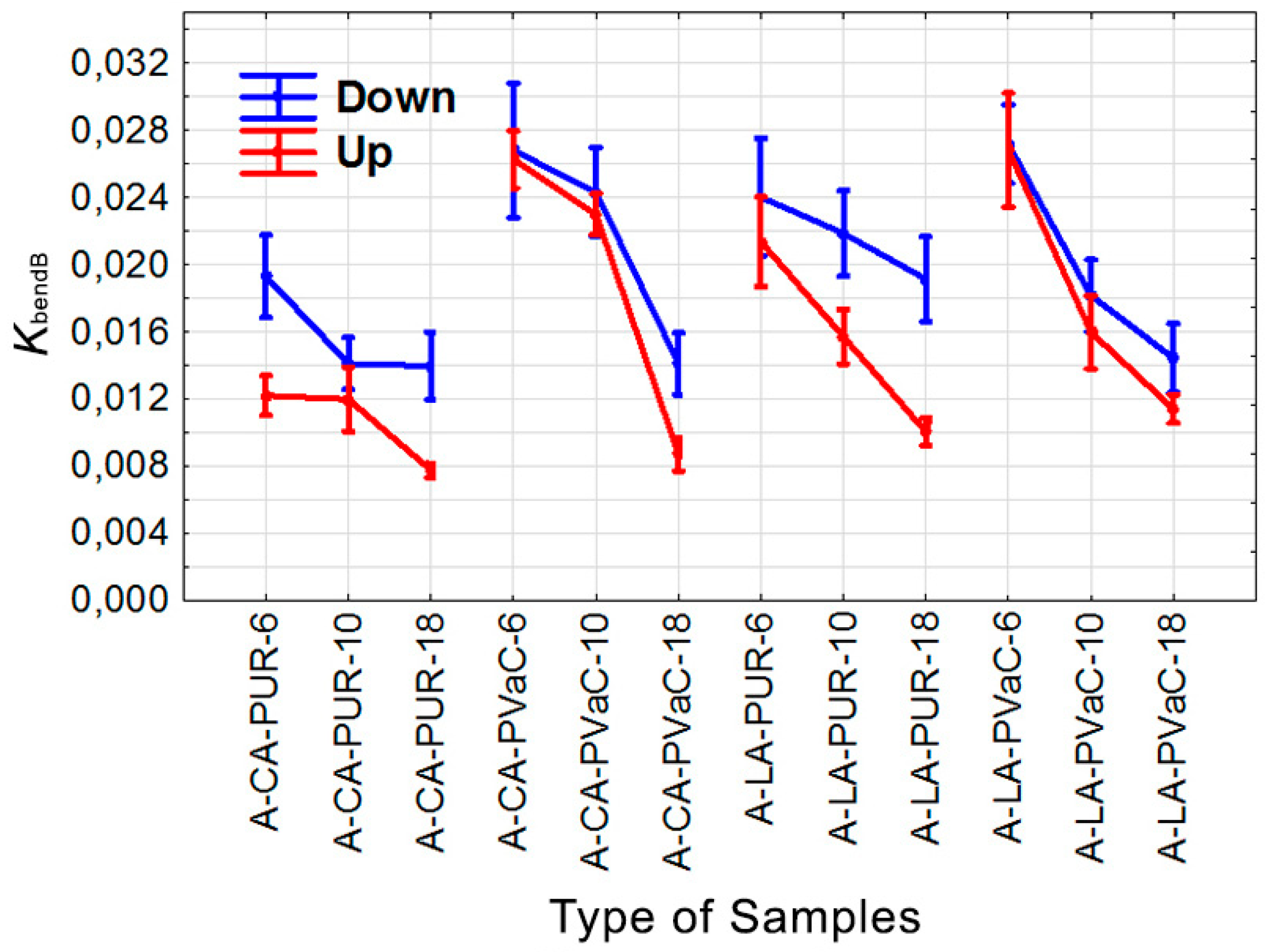
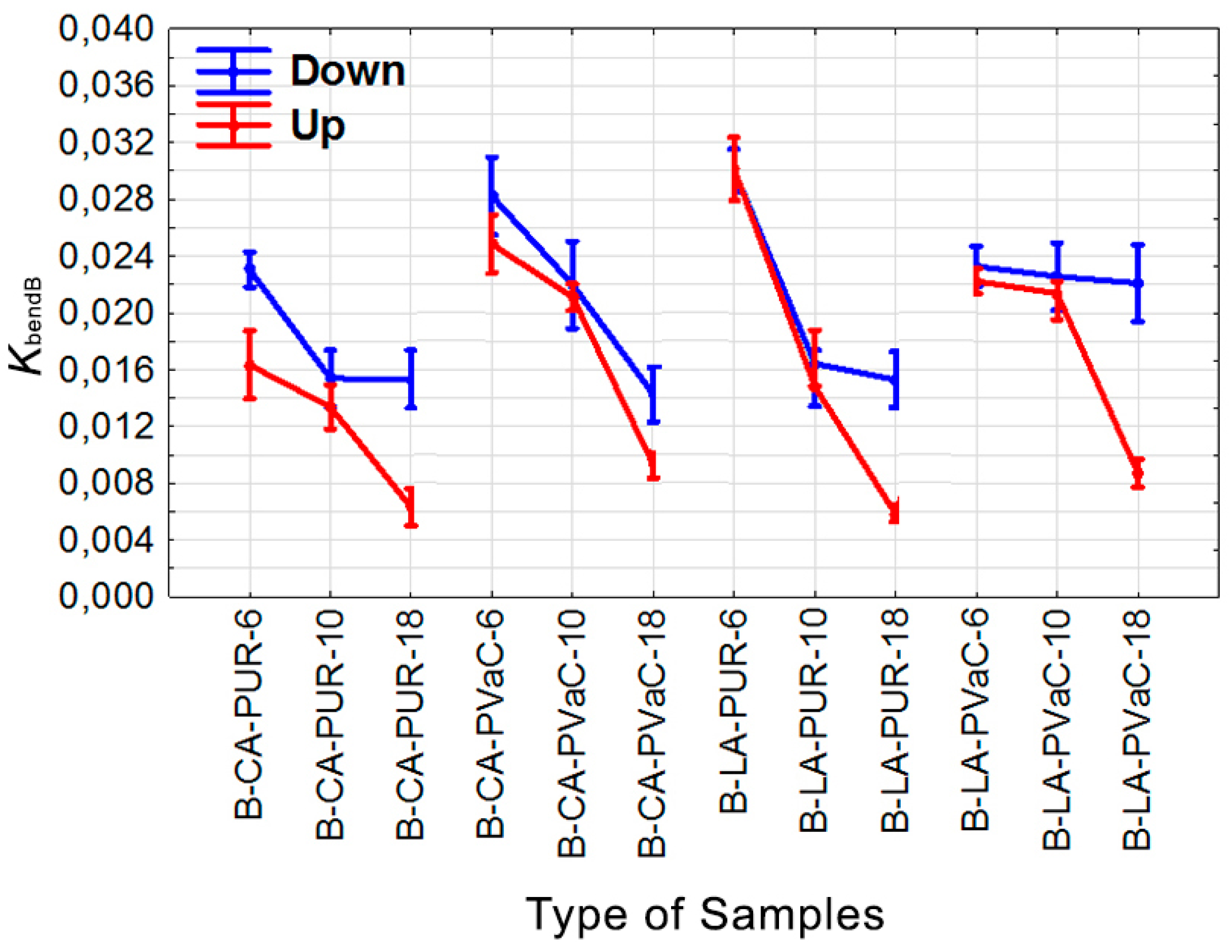
| WS | NWC | Location | Glue | T (mm) | Code of Test Sample | KbendC | KbendB | RminC (mm) | RminB (mm) |
|---|---|---|---|---|---|---|---|---|---|
| A | CA | U | PUR | 6 | A-CA-U-PUR-6 | 0.014 | 0.012 | 519.28 | 717.76 |
| (17.0) | (13.5) | (9.4) | (11.9) | ||||||
| A | CA | U | PUR | 10 | A-CA-U-PUR-10 | 0.024 | 0.015 | 526.38 | 693.13 |
| (13.3) | (16.8) | (14.9) | (20.4) | ||||||
| A | CA | U | PUR | 18 | A-CA-U-PUR-18 | 0.012 | 0.007 | 1616.03 | 2448.28 |
| (8.4) | (7.8) | (14.7) | (13.5) | ||||||
| A | CA | U | PVAc | 6 | A-CA-U-PVAc-6 | 0.039 | 0.026 | 150.72 | 227.08 |
| (4.1) | (4.1) | (3.3) | (3.3) | ||||||
| A | CA | U | PVAc | 10 | A-CA-U-PVAc-10 | 0.034 | 0.023 | 280.19 | 406.81 |
| (5.0) | (5.1) | (12.0) | (17.0) | ||||||
| A | CA | U | PVAc | 18 | A-CA-U-PVAc-18 | 0.013 | 0.008 | 1279.40 | 1651.62 |
| (14.0) | (13.6) | (15.5) | (11.4) | ||||||
| A | LA | U | PUR | 6 | A-LA-U-PUR-6 | 0.031 | 0.021 | 159.95 | 238.00 |
| (11.3) | (17.5) | (14.3) | (18.0) | ||||||
| A | LA | U | PUR | 10 | A-LA-U-PUR-10 | 0.024 | 0.015 | 511.83 | 671.01 |
| (16.0) | (14.4) | (18.5) | (16.6) | ||||||
| A | LA | U | PUR | 18 | A-LA-U-PUR-18 | 0.015 | 0.010 | 1233.71 | 1848.16 |
| (17.2) | (17.2) | (14.0) | (14.0) | ||||||
| A | LA | U | PVAc | 6 | A-LA-U-PVAc-6 | 0.043 | 0.028 | 134.11 | 202.81 |
| (14.7) | (14.1) | (11.4) | (11.0) | ||||||
| A | LA | U | PVAc | 10 | A-LA-U-PVAc-10 | 0.022 | 0.015 | 401.48 | 628.74 |
| (11.3) | (17.6) | (10.8) | (9.6) | ||||||
| A | LA | U | PVAc | 18 | A-LA-U-PVAc-18 | 0.016 | 0.011 | 1220.28 | 1688.32 |
| (10.3) | (8.9) | (10.8) | (13.4) | ||||||
| A | CA | D | PUR | 6 | A-CA-D-PUR-6 | 0.026 | 0.019 | 248.51 | 355.31 |
| (19.4) | (17.9) | (19.1) | (16.0) | ||||||
| A | CA | D | PUR | 10 | A-CA-D-PUR-10 | 0.022 | 0.014 | 379.73 | 570.20 |
| (17.9) | (15.4) | (18.4) | (18.3) | ||||||
| A | CA | D | PUR | 18 | A-CA-D-PUR-18 | 0.020 | 0.013 | 878.98 | 1365.45 |
| (19.6) | (20.4) | (13.2) | (18.2) | ||||||
| A | CA | D | PVAc | 6 | A-CA-D-PVAc-6 | 0.036 | 0.026 | 165.21 | 253.26 |
| (19.2) | (21.0) | (11.8) | (7.4) | ||||||
| A | CA | D | PVAc | 10 | A-CA-D-PVAc-10 | 0.037 | 0.024 | 280.82 | 427.67 |
| (15.7) | (15.3) | (16.4) | (15.8) | ||||||
| A | CA | D | PVAc | 18 | A-CA-D-PVAc-18 | 0.024 | 0.014 | 884.80 | 1454.81 |
| (17.2) | (18.3) | (12.0) | (11.9) | ||||||
| A | LA | D | PUR | 6 | A-LA-D-PUR-6 | 0.031 | 0.024 | 144.14 | 218.42 |
| (15.6) | (20.4) | (15.0) | (14.7) | ||||||
| A | LA | D | PUR | 10 | A-LA-D-PUR-10 | 0.032 | 0.021 | 330.58 | 495.74 |
| (16.5) | (16.3) | (16.3) | (16.2) | ||||||
| A | LA | D | PUR | 18 | A-LA-D-PUR-18 | 0.028 | 0.019 | 670.60 | 1004.97 |
| (18.7) | (18.5) | (21.4) | (21.3) | ||||||
| A | LA | D | PVAc | 6 | A-LA-D-PVAc-6 | 0.036 | 0.027 | 143.00 | 225.48 |
| (7.2) | (12.1) | (14.7) | (15.4) | ||||||
| A | LA | D | PVAc | 10 | A-LA-D-PVAc-10 | 0.027 | 0.018 | 402.30 | 602.38 |
| (16.6) | (16.5) | (18.6) | (18.5) | ||||||
| A | LA | D | PVAc | 18 | A-LA-D-PVAc-18 | 0.023 | 0.014 | 886.44 | 1322.03 |
| (19.2) | (19.9) | (17.9) | (18.0) |
| WS | NWC | Location | Glue | T (mm) | Code of Test Sample | KbendC | KbendB | RminC (mm) | RminB (mm) |
|---|---|---|---|---|---|---|---|---|---|
| B | CA | U | PUR | 6 | B-CA-U-PUR-6 | 0.024 | 0.016 | 231.20 | 340.25 |
| (17.6) | (17.6) | (12.9) | (8.4) | ||||||
| B | CA | U | PUR | 10 | B-CA-U-PUR-10 | 0.026 | 0.017 | 459.30 | 663.96 |
| (15.4) | (18.6) | (20.7) | (17.4) | ||||||
| B | CA | U | PUR | 18 | B-CA-U-PUR-18 | 0.011 | 0.006 | 2262.89 | 3288.95 |
| (6.0) | (19.4) | (18.2) | (16.4) | ||||||
| B | CA | U | PVAc | 6 | B-CA-U-PVAc-6 | 0.037 | 0.024 | 153.98 | 232.03 |
| (9.1) | (8.8) | (8.9) | (8.7) | ||||||
| B | CA | U | PVAc | 10 | B-CA-U-PVAc-10 | 0.031 | 0.021 | 354.65 | 531.16 |
| (9.6) | (9.6) | (9.5) | (9.5) | ||||||
| B | CA | U | PVAc | 18 | B-CA-U-PVAc-18 | 0.014 | 0.009 | 1416.71 | 1804.00 |
| (16.9) | (9.7) | (12.4) | (21.0) | ||||||
| B | LA | U | PUR | 6 | B-LA-U-PUR-6 | 0.044 | 0.030 | 134.43 | 169.19 |
| (5.1) | (0.8) | (11.2) | (8.5) | ||||||
| B | LA | U | PUR | 10 | B-LA-U-PUR-10 | 0.025 | 0.016 | 439.62 | 657.95 |
| (16.4) | (16.3) | (18.5) | (18.4) | ||||||
| B | LA | U | PUR | 18 | B-LA-U-PUR-18 | 0.008 | 0.005 | 2442.86 | 3391.53 |
| (19.3) | (17.2) | (20.3) | (14.3) | ||||||
| B | LA | U | PVAc | 6 | B-LA-U-PVAc-6 | 0.033 | 0.022 | 168.33 | 253.25 |
| (5.6) | (5.5) | (4.7) | (4.6) | ||||||
| B | LA | U | PVAc | 10 | B-LA-U-PVAc-10 | 0.032 | 0.022 | 317.76 | 476.68 |
| (11.8) | (10.8) | (16.7) | (16.4) | ||||||
| B | LA | U | PVAc | 18 | B-LA-U-PVAc-18 | 0.013 | 0.008 | 1451.32 | 2171.66 |
| (19.2) | (19.2) | (18.4) | (18.4) | ||||||
| B | CA | D | PUR | 6 | B-CA-D-PUR-6 | 0.034 | 0.023 | 166.27 | 250.18 |
| (7.7) | (7.6) | (8.6) | (8.4) | ||||||
| B | CA | D | PUR | 10 | B-CA-D-PUR-10 | 0.025 | 0.015 | 427.22 | 644.19 |
| (17.9) | (17.9) | (18.8) | (18.5) | ||||||
| B | CA | D | PUR | 18 | B-CA-D-PUR-18 | 0.015 | 0.015 | 1232.78 | 1488.03 |
| (12.3) | (18.5) | (15.1) | (17.2) | ||||||
| B | CA | D | PVAc | 6 | B-CA-D-PVAc-6 | 0.042 | 0.028 | 135.40 | 204.75 |
| (14.0) | (13.6) | (12.5) | (12.2) | ||||||
| B | CA | D | PVAc | 10 | B-CA-D-PVAc-10 | 0.030 | 0.021 | 296.37 | 489.47 |
| (14.9) | (19.5) | (16.9) | (19.4) | ||||||
| B | CA | D | PVAc | 18 | B-CA-D-PVAc-18 | 0.021 | 0.014 | 793.45 | 1248.23 |
| (18.9) | (18.8) | (18.4) | (11.0) | ||||||
| B | LA | D | PUR | 6 | B-LA-D-PUR-6 | 0.046 | 0.030 | 105.94 | 162.18 |
| (7.4) | (7.0) | (7.5) | (7.0) | ||||||
| B | LA | D | PUR | 10 | B-LA-D-PUR-10 | 0.024 | 0.015 | 426.66 | 683.36 |
| (13.0) | (17.9) | (13.0) | (19.0) | ||||||
| B | LA | D | PUR | 18 | B-LA-D-PUR-18 | 0.026 | 0.016 | 663.54 | 1209.10 |
| (18.4) | (16.7) | (18.5) | (14.0) | ||||||
| B | LA | D | PVAc | 6 | B-LA-D-PVAc-6 | 0.035 | 0.023 | 160.41 | 241.58 |
| (8.5) | (8.3) | (7.9) | (7.7) | ||||||
| B | LA | D | PVAc | 10 | B-LA-D-PVAc-10 | 0.034 | 0.024 | 296.34 | 459.85 |
| (19.3) | (13.5) | (19.6) | (13.9) | ||||||
| B | LA | D | PVAc | 18 | B-LA-D-PVAc-18 | 0.033 | 0.022 | 526.61 | 795.58 |
| (17.3) | (17.0) | (16.3) | (16.4) |
| Monitored Factor | Sum of Squares | Degrees of Freedom | Variance | Fisher’s F-Test | Significance Level |
|---|---|---|---|---|---|
| Intercept | 0.101015 | 1 | 0.101015 | 4182.484 | *** |
| 1) Type of Sample | 0.003778 | 11 | 0.000343 | 14.220 | *** |
| Error | 0.002608 | 108 | 0.000024 |
| Monitored Factor | Sum of Squares | Degrees of Freedom | Variance | Fisher’s F-Test | Significance Level |
|---|---|---|---|---|---|
| Intercept | 0.058817 | 1 | 0.058817 | 5814.366 | *** |
| 1) Type of Sample | 0.010364 | 11 | 0.000942 | 93.141 | *** |
| Error | 0.001022 | 101 | 0.000010 |
| Monitored Factor | Sum of Squares | Degrees of Freedom | Variance | Fisher’s F-Test | Significance Level |
|---|---|---|---|---|---|
| Intercept | 0.114036 | 1 | 0.114036 | 5587.265 | *** |
| 1) Type of Sample | 0.008469 | 11 | 0.000770 | 37.724 | *** |
| Error | 0.002204 | 108 | 0.000020 |
| Monitored Factor | Sum of Squares | Degrees of Freedom | Variance | Fisher’s F-Test | Significance Level |
|---|---|---|---|---|---|
| Intercept | 0.055837 | 1 | 0.055837 | 5566.564 | *** |
| 1) Type of Sample | 0.011935 | 11 | 0.001085 | 108.163 | *** |
| Error | 0.001144 | 114 | 0.000010 |
| Monitored Factor | Sum of Squares | Degrees of Freedom | Variance | Fisher’s F-Test | Significance Level |
|---|---|---|---|---|---|
| Intercept | 0.046953 | 1 | 0.046953 | 3654.379 | *** |
| 1) Type of Sample | 0.002775 | 11 | 0.000252 | 19.633 | *** |
| Error | 0.001388 | 108 | 0.000013 |
| Monitored Factor | Sum of Squares | Degrees of Freedom | Variance | Fisher’s F-Test | Significance Level |
|---|---|---|---|---|---|
| Intercept | 0.026766 | 1 | 0.026766 | 5122.907 | *** |
| 1) Type of Sample | 0.004369 | 11 | 0.000397 | 76.012 | *** |
| Error | 0.000528 | 101 | 0.000005 |
| Monitored Factor | Sum of Squares | Degrees of Freedom | Variance | Fisher’s F-Test | Significance Level |
|---|---|---|---|---|---|
| Intercept | 0.052061 | 1 | 0.052061 | 5814.871 | *** |
| 1) Type of Sample | 0.003206 | 11 | 0.000291 | 32.553 | *** |
| Error | 0.000967 | 108 | 0.000009 |
| Monitored Factor | Sum of Squares | Degrees of Freedom | Variance | Fisher’s F-Test | Significance Level |
|---|---|---|---|---|---|
| Intercept | 0.024553 | 1 | 0.024553 | 5158.266 | *** |
| 1) Type of Sample | 0.005388 | 11 | 0.000490 | 102.915 | *** |
| Error | 0.000543 | 114 | 0.000005 |
| Monitored Factor | Sum of Squares | Degrees of Freedom | Variance | Fisher’s F-Test | Significance Level |
|---|---|---|---|---|---|
| Intercept | 24436158 | 1 | 24436158 | 3264.754 | *** |
| 1) Type of Sample | 9717956 | 11 | 883451 | 118.032 | *** |
| Error | 808363 | 108 | 7485 |
| Monitored Factor | Sum of Squares | Degrees of Freedom | Variance | Fisher’s F-Test | Significance Level |
|---|---|---|---|---|---|
| Intercept | 44421882 | 1 | 44421882 | 2710.337 | *** |
| 1) Type of Sample | 28160468 | 11 | 2560043 | 156.197 | *** |
| Error | 1655370 | 101 | 16390 |
| Monitored Factor | Sum of Squares | Degrees of Freedom | Variance | Fisher’s F-Test | Significance Level |
|---|---|---|---|---|---|
| Intercept | 22802737 | 1 | 22802737 | 2892.018 | *** |
| 1) Type of Sample | 12097814 | 11 | 1099801 | 139.485 | *** |
| Error | 851549 | 108 | 7885 |
| Monitored Factor | Sum of Squares | Degrees of Freedom | Variance | Fisher’s F-Test | Significance Level |
|---|---|---|---|---|---|
| Intercept | 58491893 | 1 | 58491893 | 1178.097 | *** |
| 1) Type of Sample | 81191097 | 11 | 7381009 | 148.662 | *** |
| Error | 5660040 | 114 | 49649 |
| Monitored Factor | Sum of Squares | Degrees of Freedom | Variance | Fisher’s F-Test | Significance Level |
|---|---|---|---|---|---|
| Intercept | 57349324 | 1 | 57349324 | 2933.356 | *** |
| 1) Type of Sample | 24093243 | 11 | 2190295 | 112.031 | *** |
| Error | 2111481 | 108 | 19551 |
| Monitored Factor | Sum of Squares | Degrees of Freedom | Variance | Fisher’s F-Test | Significance Level |
|---|---|---|---|---|---|
| Intercept | 89797468 | 1 | 89797468 | 2744.915 | *** |
| 1) Type of Sample | 61286334 | 11 | 5571485 | 170.308 | *** |
| Error | 3304126 | 101 | 32714 |
| Monitored Factor | Sum of Squares | Degrees of Freedom | Variance | Fisher’s F-Test | Significance Level |
|---|---|---|---|---|---|
| Intercept | 51699287 | 1 | 51699287 | 2759.401 | *** |
| 1) Type of Sample | 22194201 | 11 | 2017655 | 107.690 | *** |
| Error | 2023455 | 108 | 18736 |
| Monitored Factor | Sum of Squares | Degrees of Freedom | Variance | Fisher’s F-Test | Significance Level |
|---|---|---|---|---|---|
| Intercept | 118241938 | 1 | 118241938 | 1681.398 | *** |
| 1) Type of Sample | 159214450 | 11 | 14474041 | 205.821 | *** |
| Error | 8016889 | 114 | 70324 |
| No. | Type of Sample | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.026 | 0.022 | 0.020 | 0.036 | 0.037 | 0.024 | 0.031 | 00.32 | 0.028 | 0.036 | 0.027 | 0.023 | ||
| 1. | A-CA-D-PUR-6 | ||||||||||||
| 2. | A-CA-D-PUR-10 | 0.048 | |||||||||||
| 3. | A-CA-D-PUR-18 | 0.007 | 0.414 | ||||||||||
| 4. | A-CA-D-PVAc-6 | 0.000 | 0.000 | 0.000 | |||||||||
| 5. | A-CA-D-PVAc-10 | 0.000 | 0.000 | 0.000 | 0.973 | ||||||||
| 6. | A-CA-D-PVAc-18 | 0.261 | 0.331 | 0.092 | 0.000 | 0.000 | |||||||
| 7. | A-LA-D-PUR-6 | 0.049 | 0.000 | 0.000 | 0.032 | 0.035 | 0.003 | ||||||
| 8. | A-LA-D-PUR-10 | 0.016 | 0.000 | 0.000 | 0.085 | 0.096 | 0.001 | 0.595 | |||||
| 9. | A-LA-D-PUR-18 | 0.445 | 0.008 | 0.001 | 0.001 | 0.001 | 0.077 | 0.182 | 0.078 | ||||
| 10. | A-LA-D-PVAc-6 | 0.000 | 0.000 | 0.000 | 0.943 | 0.965 | 0.000 | 0.036 | 0.100 | 0.001 | |||
| 11. | A-LA-D-PVAc-10 | 0.895 | 0.040 | 0.005 | 0.000 | 0.000 | 0.238 | 0.057 | 0.019 | 0.494 | 0.000 | ||
| 12. | A-LA-D-PVAc-18 | 0.213 | 0.403 | 0.120 | 0.000 | 0.000 | 0.840 | 0.002 | 0.000 | 0.056 | 0.000 | 0.187 |
| No. | Type of Sample | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.014 | 0.024 | 0.012 | 0.039 | 0.034 | 0.013 | 0.031 | 0.024 | 0.015 | 0.043 | 0.022 | 0.016 | ||
| 1. | A-CA-U-PUR-6 | ||||||||||||
| 2. | A-CA-U-PUR-10 | 0.000 | |||||||||||
| 3. | A-CA-U-PUR-18 | 0.198 | 0.000 | ||||||||||
| 4. | A-CA-U-PVAc-6 | 0.000 | 0.000 | 0.000 | |||||||||
| 5. | A-CA-U-PVAc-10 | 0.000 | 0.000 | 0.000 | 0.002 | ||||||||
| 6. | A-CA-U-PVAc-18 | 0.886 | 0.000 | 0.221 | 0.000 | 0.000 | |||||||
| 7. | A-LA-U-PUR-6 | 0.000 | 0.000 | 0.000 | 0.000 | 0.075 | 0.000 | ||||||
| 8. | A-LA-U-PUR-10 | 0.000 | 0.935 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |||||
| 9. | A-LA-U-PUR-18 | 0.603 | 0.000 | 0.086 | 0.000 | 0.000 | 0.535 | 0.000 | 0.000 | ||||
| 10. | A-LA-U-PVAc-6 | 0.000 | 0.000 | 0.000 | 0.011 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |||
| 11. | A-LA-U-PVAc-10 | 0.000 | 0.242 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.240 | 0.000 | 0.000 | ||
| 12. | A-LA-U-PVAc-18 | 0.264 | 0.000 | 0.022 | 0.000 | 0.000 | 0.228 | 0.000 | 0.000 | 0.502 | 0.000 | 0.000 |
| No. | Type of Sample | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.034 | 0.025 | 0.015 | 0.042 | 0.030 | 0.021 | 0.046 | 0.024 | 0.026 | 0.035 | 0.034 | 0.033 | ||
| 1. | B-CA-D-PUR-6 | ||||||||||||
| 2. | B-CA-D-PUR-10 | 0.000 | |||||||||||
| 3. | B-CA-D-PUR-18 | 0.000 | 0.000 | ||||||||||
| 4. | B-CA-D-PVAc-6 | 0.000 | 0.000 | 0.000 | |||||||||
| 5. | B-CA-D-PVAc-10 | 0.029 | 0.032 | 0.000 | 0.000 | ||||||||
| 6. | B-CA-D-PVAc-18 | 0.000 | 0.042 | 0.009 | 0.000 | 0.000 | |||||||
| 7. | B-LA-D-PUR-6 | 0.000 | 0.000 | 0.000 | 0.107 | 0.000 | 0.000 | ||||||
| 8. | B-LA-D-PUR-10 | 0.000 | 0.655 | 0.000 | 0.000 | 0.012 | 0.089 | 0.000 | |||||
| 9. | B-LA-D-PUR-18 | 0.000 | 0.702 | 0.000 | 0.000 | 0.061 | 0.020 | 0.000 | 0.438 | ||||
| 10. | B-LA-D-PVAc-6 | 0.861 | 0.000 | 0.000 | 0.000 | 0.025 | 0.000 | 0.000 | 0.000 | 0.000 | |||
| 11. | B-LA-D-PVAc-10 | 0.910 | 0.000 | 0.000 | 0.000 | 0.027 | 0.000 | 0.000 | 0.000 | 0.000 | 0.941 | ||
| 12. | B-LA-D-PVAc-18 | 0.592 | 0.000 | 0.000 | 0.000 | 0.078 | 0.000 | 0.000 | 0.000 | 0.001 | 0.516 | 0.544 |
| No. | Type of Sample | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.024 | 0.026 | 0.011 | 0.037 | 0.031 | 0.014 | 0.044 | 0.025 | 0.008 | 0.033 | 0.032 | 0.013 | ||
| 1. | B-CA-U-PUR-6 | ||||||||||||
| 2. | B-CA-U-PUR-10 | 0.174 | |||||||||||
| 3. | B-CA-U-PUR-18 | 0.000 | 0.000 | ||||||||||
| 4. | B-CA-U-PVAc-6 | 0.000 | 0.000 | 0.000 | |||||||||
| 5. | B-CA-U-PVAc-10 | 0.000 | 0.006 | 0.000 | 0.001 | ||||||||
| 6. | B-CA-U-PVAc-18 | 0.000 | 0.000 | 0.062 | 0.000 | 0.000 | |||||||
| 7. | B-LA-U-PUR-6 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||||||
| 8. | B-LA-U-PUR-10 | 0.689 | 0.296 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |||||
| 9. | B-LA-U-PUR-18 | 0.000 | 0.000 | 0.060 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||||
| 10. | B-LA-U-PVAc-6 | 0.000 | 0.000 | 0.000 | 0.017 | 0.304 | 0.000 | 0.000 | 0.000 | 0.000 | |||
| 11. | B-LA-U-PVAc-10 | 0.000 | 0.001 | 0.000 | 0.005 | 0.581 | 0.000 | 0.000 | 0.000 | 0.000 | 0.585 | ||
| 12. | B-LA-U-PVAc-18 | 0.000 | 0.000 | 0.313 | 0.000 | 0.000 | 0.333 | 0.000 | 0.000 | 0.006 | 0.000 | 0.000 |
| No. | Type of Sample | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.019 | 0.014 | 0.013 | 0.026 | 0.024 | 0.014 | 0.024 | 0.021 | 0.019 | 0.027 | 0.018 | 0.014 | ||
| 1. | A-CA-D-PUR-6 | ||||||||||||
| 2. | A-CA-D-PUR-10 | 0.004 | |||||||||||
| 3. | A-CA-D-PUR-18 | 0.003 | 0.936 | ||||||||||
| 4. | A-CA-D-PVAc-6 | 0.000 | 0.000 | 0.000 | |||||||||
| 5. | A-CA-D-PVAc-10 | 0.004 | 0.000 | 0.000 | 0.124 | ||||||||
| 6. | A-CA-D-PVAc-18 | 0.003 | 0.996 | 0.937 | 0.000 | 0.000 | |||||||
| 7. | A-LA-D-PUR-6 | 0.005 | 0.000 | 0.000 | 0.105 | 0.859 | 0.000 | ||||||
| 8. | A-LA-D-PUR-10 | 0.112 | 0.000 | 0.000 | 0.005 | 0.153 | 0.000 | 0.181 | |||||
| 9. | A-LA-D-PUR-18 | 0.918 | 0.005 | 0.004 | 0.000 | 0.003 | 0.004 | 0.005 | 0.110 | ||||
| 10. | A-LA-D-PVAc-6 | 0.000 | 0.000 | 0.000 | 0.808 | 0.093 | 0.000 | 0.074 | 0.003 | 0.000 | |||
| 11. | A-LA-D-PVAc-10 | 0.503 | 0.021 | 0.020 | 0.000 | 0.001 | 0.018 | 0.001 | 0.034 | 0.540 | 0.000 | ||
| 12. | A-LA-D-PVAc-18 | 0.005 | 0.844 | 0.795 | 0.000 | 0.000 | 0.837 | 0.000 | 0.000 | 0.006 | 0.000 | 0.022 |
| No. | Type of Sample | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.012 | 0.015 | 0.007 | 0.026 | 0.023 | 0.008 | 0.021 | 0.015 | 0.010 | 0.028 | 0.015 | 0.011 | ||
| 1. | A-CA-U-PUR-6 | ||||||||||||
| 2. | A-CA-U-PUR-10 | 0.002 | |||||||||||
| 3. | A-CA-U-PUR-18 | 0.000 | 0.000 | ||||||||||
| 4. | A-CA-U-PVAc-6 | 0.000 | 0.000 | 0.000 | |||||||||
| 5. | A-CA-U-PVAc-10 | 0.000 | 0.000 | 0.000 | 0.005 | ||||||||
| 6. | A-CA-U-PVAc-18 | 0.004 | 0.000 | 0.393 | 0.000 | 0.000 | |||||||
| 7. | A-LA-U-PUR-6 | 0.000 | 0.000 | 0.000 | 0.000 | 0.153 | 0.000 | ||||||
| 8. | A-LA-U-PUR-10 | 0.003 | 0.820 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |||||
| 9. | A-LA-U-PUR-18 | 0.071 | 0.000 | 0.056 | 0.000 | 0.000 | 0.242 | 0.000 | 0.000 | ||||
| 10. | A-LA-U-PVAc-6 | 0.000 | 0.000 | 0.000 | 0.024 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |||
| 11. | A-LA-U-PVAc-10 | 0.002 | 0.997 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.810 | 0.000 | 0.000 | ||
| 12. | A-LA-U-PVAc-18 | 0.480 | 0.000 | 0.003 | 0.000 | 0.000 | 0.024 | 0.000 | 0.000 | 0.226 | 0.000 | 0.000 |
| No. | Type of Sample | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.023 | 0.015 | 0.015 | 0.028 | 0.021 | 0.014 | 0.030 | 0.015 | 0.016 | 0.023 | 0.024 | 0.022 | ||
| 1. | B-CA-D-PUR-6 | ||||||||||||
| 2. | B-CA-D-PUR-10 | 0.000 | |||||||||||
| 3. | B-CA-D-PUR-18 | 0.000 | 0.973 | ||||||||||
| 4. | B-CA-D-PVAc-6 | 0.000 | 0.000 | 0.000 | |||||||||
| 5. | B-CA-D-PVAc-10 | 0.455 | 0.000 | 0.000 | 0.000 | ||||||||
| 6. | B-CA-D-PVAc-18 | 0.000 | 0.428 | 0.416 | 0.000 | 0.000 | |||||||
| 7. | B-LA-D-PUR-6 | 0.000 | 0.000 | 0.000 | 0.179 | 0.000 | 0.000 | ||||||
| 8. | B-LA-D-PUR-10 | 0.000 | 0.977 | 0.954 | 0.000 | 0.000 | 0.431 | 0.000 | |||||
| 9. | B-LA-D-PUR-18 | 0.000 | 0.524 | 0.521 | 0.000 | 0.000 | 0.178 | 0.000 | 0.514 | ||||
| 10. | B-LA-D-PVAc-6 | 0.863 | 0.000 | 0.000 | 0.001 | 0.382 | 0.000 | 0.000 | 0.000 | 0.000 | |||
| 11. | B-LA-D-PVAc-10 | 0.291 | 0.000 | 0.000 | 0.007 | 0.087 | 0.000 | 0.000 | 0.000 | 0.000 | 0.340 | ||
| 12. | B-LA-D-PVAc-18 | 0.473 | 0.000 | 0.000 | 0.000 | 0.935 | 0.000 | 0.000 | 0.000 | 0.000 | 0.405 | 0.094 |
| No. | Type of Sample | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.016 | 0.017 | 0.006 | 0.024 | 0.021 | 0.009 | 0.030 | 0.016 | 0.005 | 0.022 | 0.022 | 0.008 | ||
| 1. | B-CA-U-PUR-6 | ||||||||||||
| 2. | B-CA-U-PUR-10 | 0.398 | |||||||||||
| 3. | B-CA-U-PUR-18 | 0.000 | 0.000 | ||||||||||
| 4. | B-CA-U-PVAc-6 | 0.000 | 0.000 | 0.000 | |||||||||
| 5. | B-CA-U-PVAc-10 | 0.000 | 0.002 | 0.000 | 0.003 | ||||||||
| 6. | B-CA-U-PVAc-18 | 0.000 | 0.000 | 0.014 | 0.000 | 0.000 | |||||||
| 7. | B-LA-U-PUR-6 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||||||
| 8. | B-LA-U-PUR-10 | 0.682 | 0.621 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |||||
| 9. | B-LA-U-PUR-18 | 0.000 | 0.000 | 0.690 | 0.000 | 0.000 | 0.006 | 0.000 | 0.000 | ||||
| 10. | B-LA-U-PVAc-6 | 0.000 | 0.000 | 0.000 | 0.031 | 0.329 | 0.000 | 0.000 | 0.000 | 0.000 | |||
| 11. | B-LA-U-PVAc-10 | 0.000 | 0.000 | 0.000 | 0.032 | 0.303 | 0.000 | 0.000 | 0.000 | 0.000 | 0.902 | ||
| 12. | B-LA-U-PVAc-18 | 0.000 | 0.000 | 0.038 | 0.000 | 0.000 | 0.615 | 0.000 | 0.000 | 0.018 | 0.000 | 0.000 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Svoboda, T.; Sikora, A.; Záborský, V.; Gaffová, Z. Laminated Veneer Lumber with Non-Wood Components and the Effects of Selected Factors on Its Bendability. Forests 2019, 10, 470. https://doi.org/10.3390/f10060470
Svoboda T, Sikora A, Záborský V, Gaffová Z. Laminated Veneer Lumber with Non-Wood Components and the Effects of Selected Factors on Its Bendability. Forests. 2019; 10(6):470. https://doi.org/10.3390/f10060470
Chicago/Turabian StyleSvoboda, Tomáš, Adam Sikora, Vladimír Záborský, and Zuzana Gaffová. 2019. "Laminated Veneer Lumber with Non-Wood Components and the Effects of Selected Factors on Its Bendability" Forests 10, no. 6: 470. https://doi.org/10.3390/f10060470
APA StyleSvoboda, T., Sikora, A., Záborský, V., & Gaffová, Z. (2019). Laminated Veneer Lumber with Non-Wood Components and the Effects of Selected Factors on Its Bendability. Forests, 10(6), 470. https://doi.org/10.3390/f10060470





