Effect of Selected Factors on the Bending Deflection at the Limit of Proportionality and at the Modulus of Rupture in Laminated Veneer Lumber
Abstract
1. Introduction
2. Materials and Methods
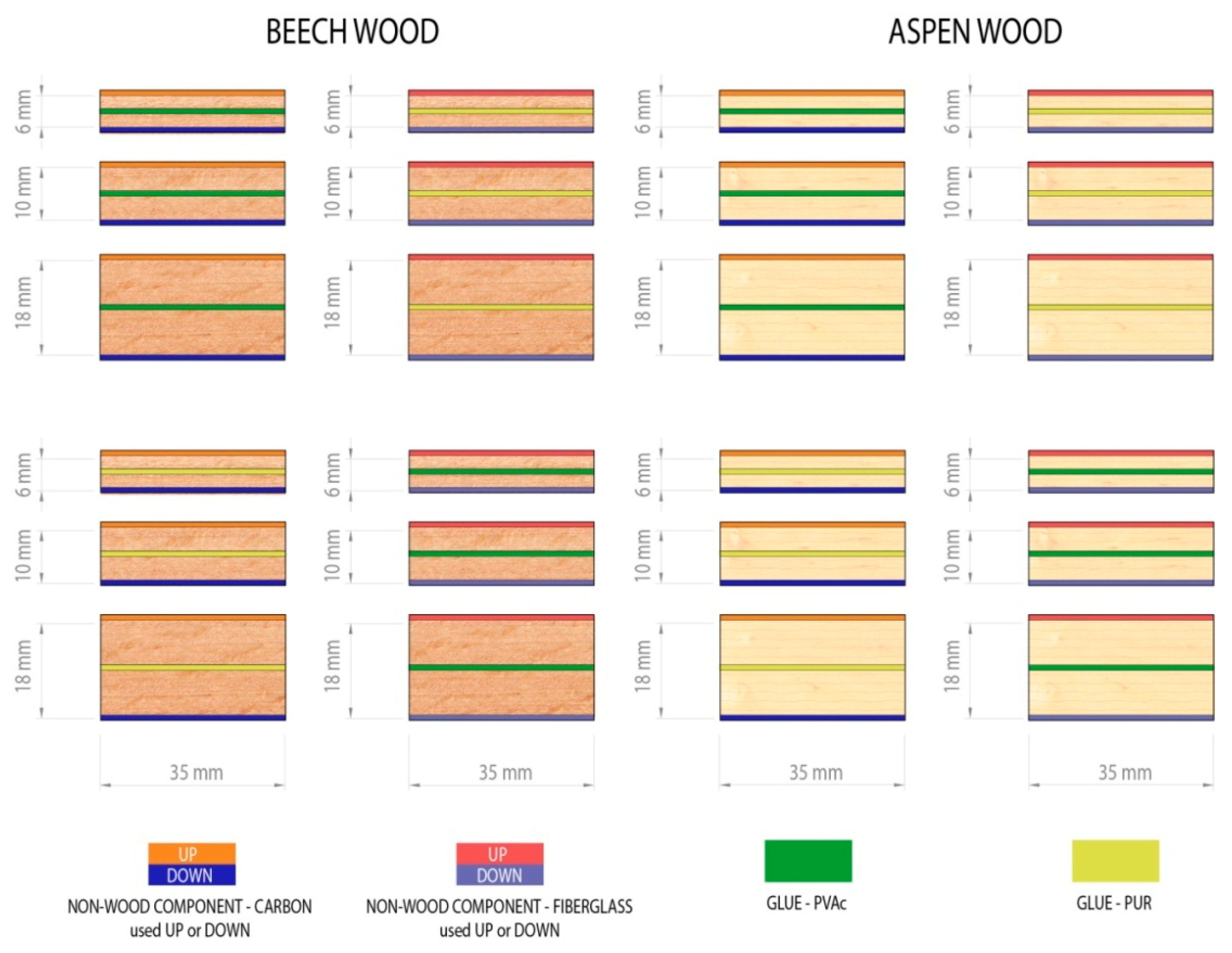
2.1. Material
2.2. Methods
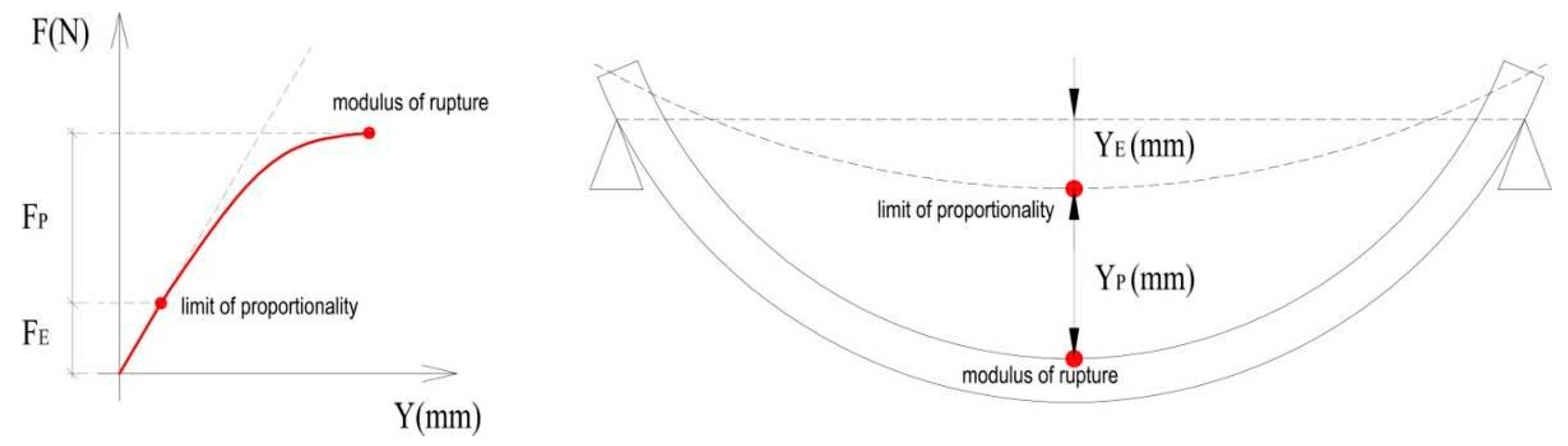
2.2.1. Determining Selected Characteristics
2.2.2. Evaluation and Calculation
3. Results and Discussion
4. Conclusions
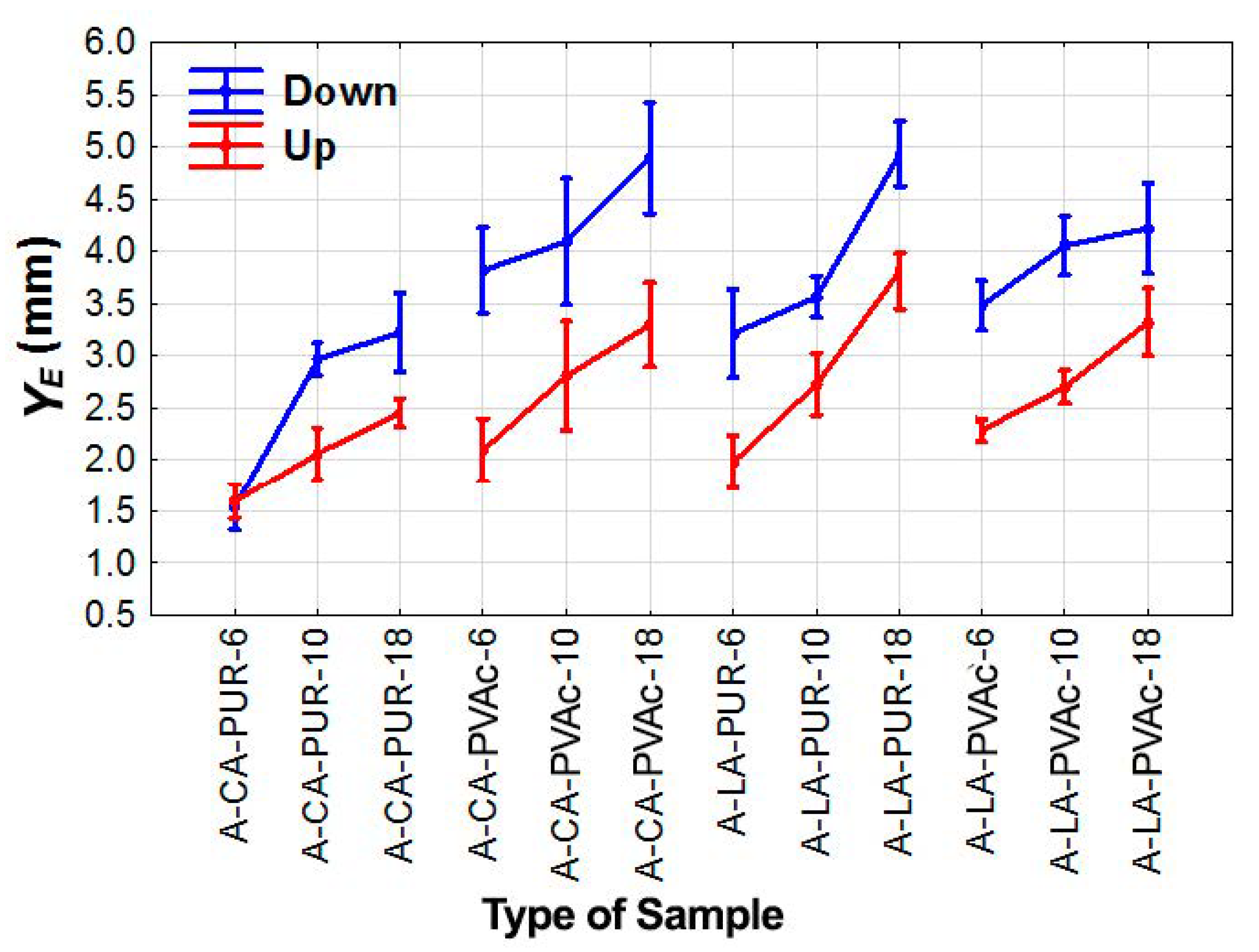
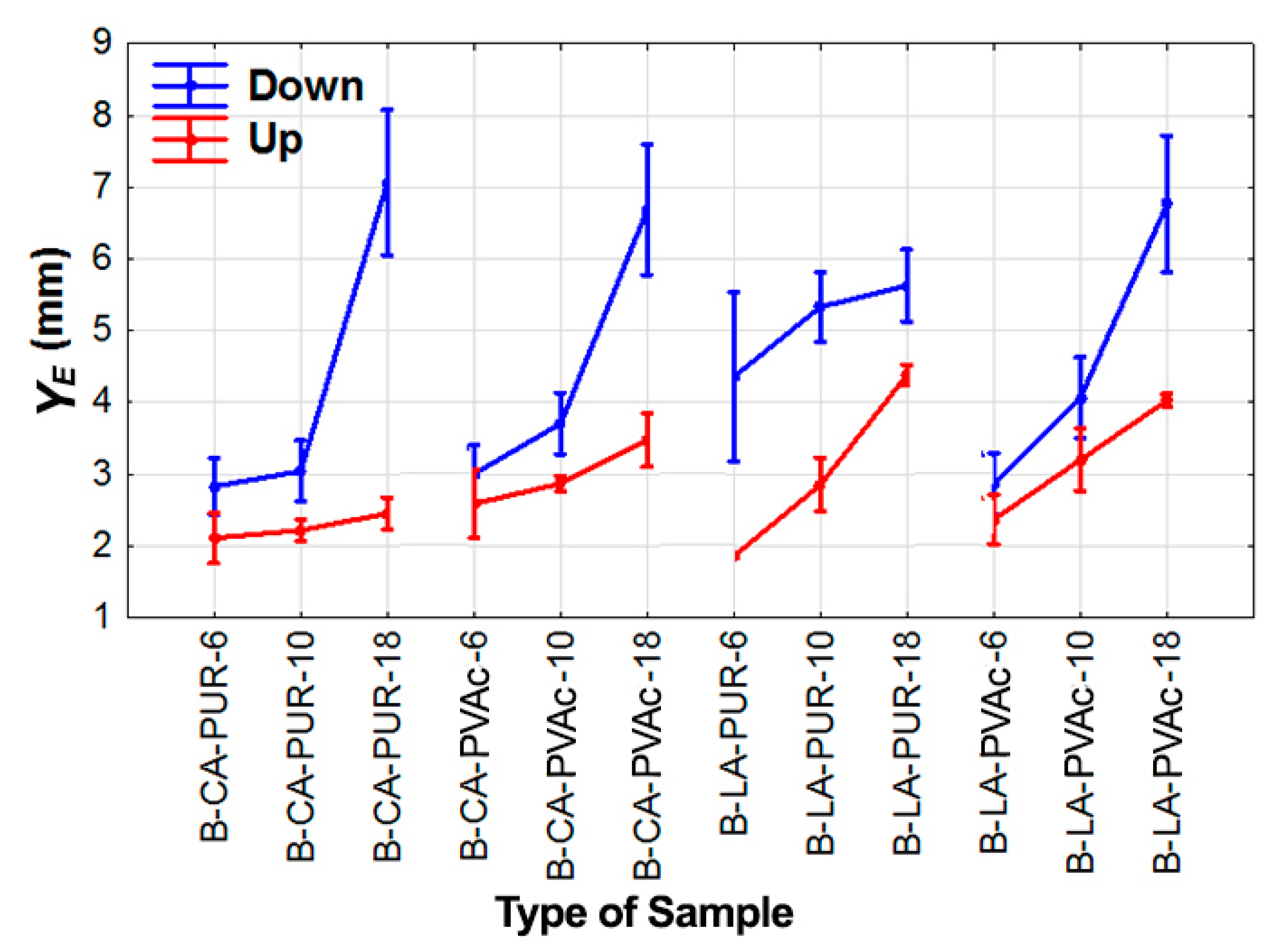
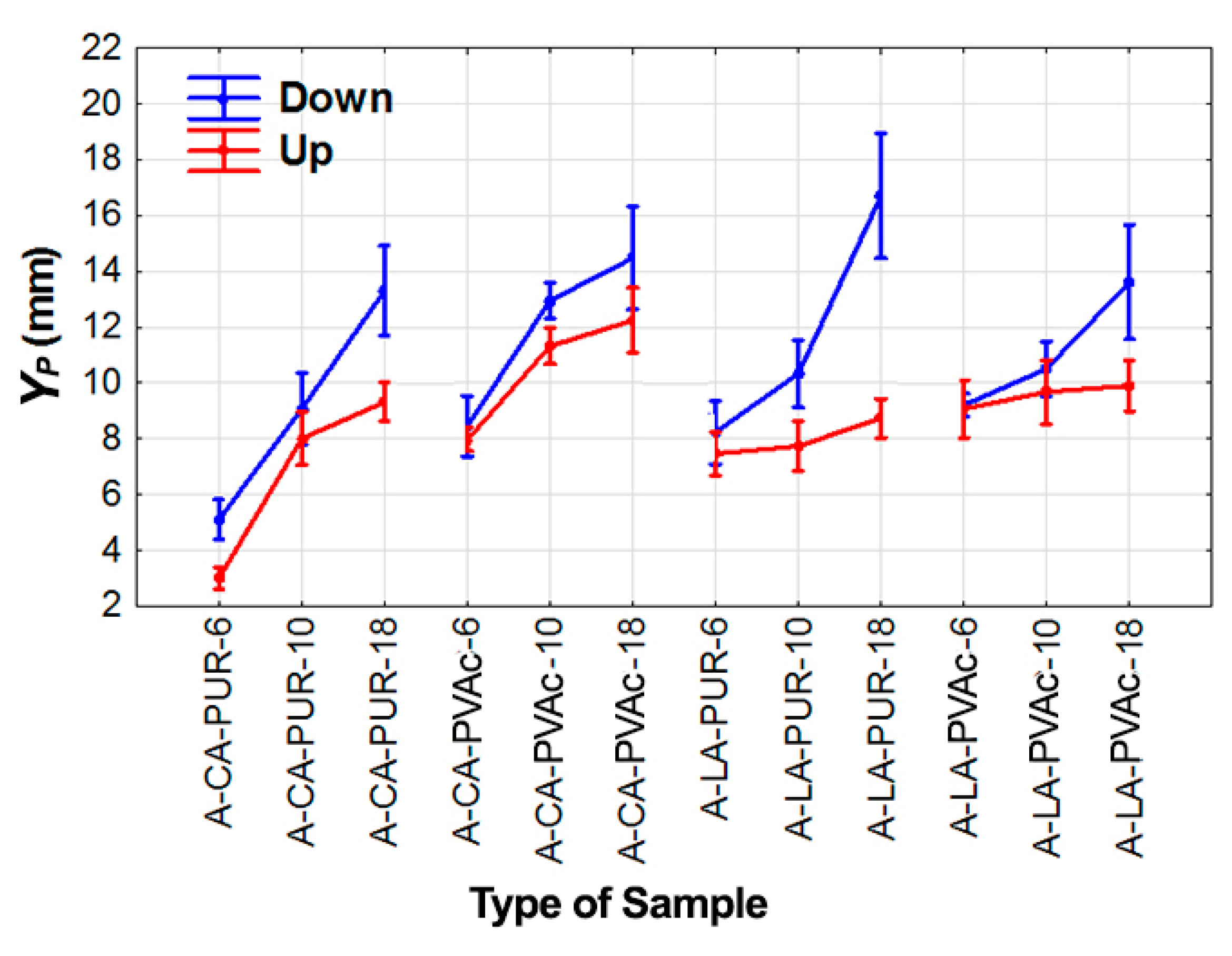
- For the laminated aspen and beech materials that were reinforced with non-wood components, the lowest deflection values were measured in the test specimens with the non-wood component on the up side with respect to the loading direction, and the highest deflection values were measured in the test specimens with the non-wood component on the down side with respect to the loading direction.
- Glass fiber was proven to be better non-wood component for both the laminated beech and aspen materials with regard to the deflection at the limit of proportionality and at the modulus of rupture in terms of the non-wood component itself.
- In the case of the adhesive used, it cannot be clearly stated which adhesive was the most effective. However, higher average values of deflection at the limit of proportionality and at the modulus of rupture were measured with the PVAc adhesive.
- As was expected, the thickness of the material proved to be an important factor that affected the deflection at both the limit of proportionality and at the modulus of rupture.
- In the case of aspen composition for better bendability, we suggest gluing with PUR adhesive and reinforcement with glass fiber on the down side with respect to the loading direction. In addition, in the case of beech composition, we suggest gluing with PVAc adhesive and reinforcement with glass fiber on the down side with respect to the loading direction.
Author Contributions
Funding
Conflicts of Interest
References
- Blomberg, J.; Persson, B. Swelling pressure of semi-isostatically densified wood under different mechanical restraints. Wood Sci. Technol. 2017, 41, 401–415. [Google Scholar] [CrossRef]
- Dai, L. Carbon Nanotechnology; Elsevier B.V.: Oxford, UK, 2006; p. 395s. [Google Scholar]
- Greason, W.D. Analysis of the Charge Transfer of Models for Electrostatic Discharge (EDS) and Semiconductor Devices. IEEE Trans. Ind. Appl. 1996, 32, 726–734. [Google Scholar] [CrossRef]
- Parvez, A.; Ansell, M.P.; Smedley, D. Mechanical repair of timber beams fractured in flexure using bonded-in reinforcements. Compos. Part B 2009, 40, 95–106. [Google Scholar]
- Brezovič, M.; Jambrekovič, V.; Pervan, S. Bending properties of carbon fibres in forced plywood. Wood Res. 2003, 48, 1336–4561. [Google Scholar]
- Bond, I.P.; Ansell, M.P. Fatigue properties of joined wood composites: Part I—Statistical analysis, fatigue master curves and constant life diagrams. J. Mater. Sci. 1998, 33, 2751–2762. [Google Scholar] [CrossRef]
- Kurjatko, S.; Čunderlík, I.; Dananajová, J.; Dibdiaková, J.; Dudas, J.; Gáborík, J.; Gaff, M.; Hrčka, R.; Hudec, J.; Kačík, F.; et al. Parametre Kvality Dreva Určujúce Jeho Finálne Použitie [Wood Quality Parameters Determining Its End Use]; Technical University in Zvolen: Zvolen, Slovakia, 2010. [Google Scholar]
- Bal, B.C. Flexural properties, bonding performance and splitting strength of LVL reinforced with woven glass fiber. Constr. Build. Mater. 2014, 51, 9–14. [Google Scholar] [CrossRef]
- Bao, F.; Fu, F.; Choong, E.T.; Hse, C.Y. Contribution factor of wood properties of three poplar clones to strength of laminated veneer lumber. Wood Fiber Sci. 2001, 33, 345–352. [Google Scholar]
- Guntekin, E.; Ozkan, S.; Yilmaz, T. Prediction of bending properties for beech lumber using stress wave method. Maderas. Cienc. Tecnol. 2014, 16, 93–98. [Google Scholar] [CrossRef]
- Požgaj, A.; Chovanec, D.; Kurjatko, S.; Babiak, M. Štruktúra a Vlastnosti Dreva [Structure and Properties of Wood]; Príroda, A.S.: Bratislava, Slovakia, 1997. [Google Scholar]
- Wagenführ, A.; Buchelt, B.; Pfriem, A. Material behaviour of veneer during multidimensional moulding. HolzRoh. Werkst. 2006, 64, 83–89. [Google Scholar] [CrossRef]
- Gaff, M.; Gašparík, M. Effect of cyclic loading on modulus of elasticity of aspen wood. BioResources 2015, 10, 290–298. [Google Scholar] [CrossRef][Green Version]
- Kamke, F.A. Densified radiata pine for structural composites. Maderas. Cienc. Technol. 2006, 8, 83–92. [Google Scholar] [CrossRef]
- Sandberg, D.; Navi, P. Introduction to Thermo-Hydro-Mechanical (THM) Wood Processing; Växjö University: Växjö, Sweden, 2007. [Google Scholar]
- Igaz, R.; Ružiak, I.; Krišťák, L.; Réh, R.; Iždinský, J.; Šiagiová, P. Optimization of pressing parameters of crosswise bonded timber formwork sheets. Acta Fac. Xylologiae 2015, 57, 83–88. [Google Scholar]
- Igaz, R.; Krišťák, L.; Ružiak, I.; Réh, R.; Danihelová, Z. Heat transfer during pressing of 3D moulded veneer plywood composite materials. Key Eng. Mat. 2016, 688, 131–137. [Google Scholar] [CrossRef]
- Mackes, K.H.; Lynch, D.L. The effect of aspen wood characteristics and properties on utilization. In Sustaining Aspen in Western Landscapes: Symposium Proceedings; Rocky Mountain Research Station: Grand Junction, CO, USA, 2001; pp. 429–440. [Google Scholar]
- Gaff, M.; Babiak, M.; Vokatý, V.; Ruman, D. Bending characteristics of hardwood lamellae in the elastic region. Compos. Part B Eng. 2017, 116, 61–65. [Google Scholar] [CrossRef]
- Gaff, M.; Babiak, M. Methods for determining the plastic work in bending and impact of selected factors on its value. Compos. Struct. 2018, 202, 66–76. [Google Scholar] [CrossRef]
- Hýsek, Š.; Gaff, M.; Sikora, A.; Babiak, M. New composite material based on winter rapeseed and his elasticity properties as a function of selected factors. Compos. Part B Eng. 2018, 153, 108–116. [Google Scholar] [CrossRef]
- Gaff, M.; Babiak, M. Tangent modulus as a function of selected factors. Compos. Struct. 2018, 202, 436–446. [Google Scholar] [CrossRef]
- Sikora, A.; Gaff, M.; Hysek, Š.; Babiak, M. The plasticity of composite material based on winter rapeseed as a function of selected factor. Compos. Struct. 2018, 202, 783–792. [Google Scholar] [CrossRef]
- Svoboda, T.; Gaffová, Z.; Rajnoha, R.; Šatanová, A.; Kminiak, R. Bending forces at the proportionality limit and the maximum—Technological innovations for better performance in wood processing companies. BioResources 2017, 12, 4146–4165. [Google Scholar] [CrossRef][Green Version]
- Corigliano, P.; Crupi, V.; Epasto, G.; Guglielmino, E.; Maugeri, N.; Marinò, A. Experimental and theoretical analyses of Iroko wood laminates. Compos. Part B Eng. 2013, 112, 251–264. [Google Scholar] [CrossRef]
- Plevris, N.; Triantafillou, T.C. Creep behavior of FRP-reinforced wood members. J. Struct. Eng. 1995, 121, 174–186. [Google Scholar] [CrossRef]
- Redon, C.; Li, V.C.; Wu, C.; Hoshiro, H.; Saito, T.; Ogawa, A. Measuring and modifying interface properties of PVA fibres in ECC matrix. J. Mater. Civil. Eng. 2001, 13, 399–406. [Google Scholar] [CrossRef]
- Sviták, M.; Ruman, D. Tensile-shear strength of layered wood reinforced by carbon materials. Wood Res. Slovakia 2017, 62, 243–252. [Google Scholar]
- Raftery, G.M.; Harte, A.M. Nonlinear numerical modelling of FRP reinforced glued laminated timber. Compos. Part B Eng. 2013, 52, 40–50. [Google Scholar] [CrossRef]
- Mosallam, A.S. Structural evaluation and design procedure for wood beams repaired and retrofitted with FRP laminates and honeycomb sandwich panels. Compos. Part B Eng. 2015, 87, 196–213. [Google Scholar] [CrossRef]
- Sandoz, J.L. Industrial Ultrasonic Grinding for Multi-glued Laminated Timber; Études& Constructions Bois, Concept Bois Technologie: Paris, France, 2009. [Google Scholar]
- Steiger, R.; Gehri, E. Quality control of glulam: Improved method for shear testing of glue lines. In Proceedings of the Final Conference of COST Action E53: The Future of Quality Control for Wood & Wood Products, Edinburgh, Scotland, 4–7 May 2010. [Google Scholar]
- Lorenzo, A. Numerical Tools for Moisture-stress and Fracture Analysis of Timber Structures. Ph.D. Dissertation, University of Calabria, Mendicino, Italy, 2010. [Google Scholar]
- Saracoglu, E. Finite-element Simulations of the Influence of Cracks on the Strength of Glulam Beams. Master’s Thesis, Blekinge Institute of Technology, Karlskrona, Sweden, 2011. [Google Scholar]
- EN 310. Wood-based panels: Determination of modulus of elasticity in bending and of bending strength; European Committee for Standardization: Brussels, Belgium, 1993. [Google Scholar]
- ISO 13061-1. Physical and Mechanical Properties of Wood—Test Methods for Small Clear Wood—Part 1: Determination of Moisture Content for Physical and Mechanical Tests; International Organization for Standardization: Geneva, Switzerland, 2014. [Google Scholar]
- ISO 13061-2. Physical and Mechanical Properties of Wood—Test Methods for Small Slear Wood Specimens—Part 2: Determination of Density for Physical and Mechanical Tests; International Organization for Standardization: Geneva, Switzerland, 2014. [Google Scholar]
- ISO 13061-3. Physical and Mechanical Properties of Wood—Test Methods for Small Clear Wood Specimens—Part 3: Determination of Density for Physical and Mechanical Tests; International Organization for Standardization: Geneva, Switzerland, 2014. [Google Scholar]
- Sikora, A.; Gaffová, Z.; Rajnoha, R.; Šatanová, A.; Kminiak, R. Deflection of densified beech and aspen woods as a function of selected factors. Bio Resour. 2017, 12, 3192–3210. [Google Scholar] [CrossRef][Green Version]
- Gáborík, J.; Gaff, M.; Ruman, D.; Záborský, V.; Kašíčková, V.; Sikora, A. Adhesive as a factor affecting the properties of laminated wood. Bio Resour. 2016, 11, 10565–10574. [Google Scholar] [CrossRef]

| Technical Data | AG-COLL 8761/L D3 | NEOPUR 2238R |
|---|---|---|
| Viscosity (mPa) | 5000 to 7000 by 23 °C | 2000 to 4500 by 25 °C |
| Working Time (min) | 15 to 20 | 60 |
| Density (g/cm3) | 0.9 to 1.1 by 23 °C | approx. 1.13 |
| NCO Content (%) | - | approx. 15.5 to 16.5 |
| Color | White, milk | Brown |
| Open Time (min) | 15 | approx. 20 to 25 |
| Dry Matter Content | 49 to 51 | 100 |
| pH | 3.8 to 4.5 | - |
| WS | NWC | NWC Location | Glue | T (mm) | Code | YE (mm) | YP (mm) |
|---|---|---|---|---|---|---|---|
| A | CA | U | PUR | 6 | A-CA-U-PUR-6 | 1.59 (14.0) | 3.00 (18.1) |
| A | CA | U | PUR | 10 | A-CA-U-PUR-10 | 2.06 (16.8) | 8.01 (16.6) |
| A | CA | U | PUR | 18 | A-CA-U-PUR-18 | 2.45 (13.0) | 9.32 (13.2) |
| A | CA | U | PVAc | 6 | A-CA-U-PVAc-6 | 2.10 (9.0) | 7.97 (3.3) |
| A | CA | U | PVAc | 10 | A-CA-U-PVAc-10 | 2.81 (17.7) | 11.32 (5.5) |
| A | CA | U | PVAc | 18 | A-CA-U-PVAc-18 | 3.29 (21.0) | 12.24 (16.8) |
| A | LA | U | PUR | 6 | A-LA-U-PUR-6 | 1.98 (17.9) | 7.46 (14.4) |
| A | LA | U | PUR | 10 | A-LA-U-PUR-10 | 2.73 (15.4) | 7.74 (15.9) |
| A | LA | U | PUR | 18 | A-LA-U-PUR-18 | 3.81 (8.0) | 8.74 (17.1) |
| A | LA | U | PVAc | 6 | A-LA-U-PVAc-6 | 2.28 (5.7) | 9.07 (13.6) |
| A | LA | U | PVAc | 10 | A-LA-U-PVAc-10 | 2.70 (7.7) | 9.68 (19.5) |
| A | LA | U | PVAc | 18 | A-LA-U-PVAc-18 | 3.32 (16.5) | 9.90 (11.0) |
| A | CA | D | PUR | 6 | A-CA-D-PUR-6 | 1.54 (20.2) | 5.11 (19.4) |
| A | CA | D | PUR | 10 | A-CA-D-PUR-10 | 2.97 (7.4) | 9.07 (19.9) |
| A | CA | D | PUR | 18 | A-CA-D-PUR-18 | 3.22 (16.4) | 13.30 (16.9) |
| A | CA | D | PVAc | 6 | A-CA-D-PVAc-6 | 3.82 (15.0) | 8.46 (20.4) |
| A | CA | D | PVAc | 10 | A-CA-D-PVAc-10 | 4.09 (20.6) | 12.95 (6.9) |
| A | CA | D | PVAc | 18 | A-CA-D-PVAc-18 | 4.89 (19.1) | 14.48 (17.9) |
| A | LA | D | PUR | 6 | A-LA-D-PUR-6 | 3.21 (18.5) | 8.23 (19.3) |
| A | LA | D | PUR | 10 | A-LA-D-PUR-10 | 3.56 (7.7) | 10.33 (16.4) |
| A | LA | D | PUR | 18 | A-LA-D-PUR-18 | 4.93 (8.8) | 16.70 (18.7) |
| A | LA | D | PVAc | 6 | A-LA-D-PVAc-6 | 3.48 (9.5) | 9.21 (6.2) |
| A | LA | D | PVAc | 10 | A-LA-D-PVAc-10 | 4.05 (12.9) | 10.51 (16.3) |
| A | LA | D | PVAc | 18 | A-LA-D-PVAc-18 | 4.22 (14.3) | 13.62 (21.1) |
| WS | NWC | NWC Location | Glue | T (mm) | Code | YE (mm) | YP (mm) |
|---|---|---|---|---|---|---|---|
| B | CA | U | PUR | 6 | B-CA-U-PUR-6 | 2.11 (20.1) | 5.13 (17.6) |
| B | CA | U | PUR | 10 | B-CA-U-PUR-10 | 2.22 (14.4) | 6.81 (19.8) |
| B | CA | U | PUR | 18 | B-CA-U-PUR-18 | 2.45 (8.7) | 7.38 (8.8) |
| B | CA | U | PVAc | 6 | B-CA-U-PVAc-6 | 2.59 (19.8) | 7.85 (9.3) |
| B | CA | U | PVAc | 10 | B-CA-U-PVAc-10 | 2.87 (8.1) | 9.48 (9.7) |
| B | CA | U | PVAc | 18 | B-CA-U-PVAc-18 | 3.48 (14.4) | 10.39 (9.5) |
| B | LA | U | PUR | 6 | B-LA-U-PUR-6 | 1.85 (12.6) | 5.42 (10.3) |
| B | LA | U | PUR | 10 | B-LA-U-PUR-10 | 2.85 (18.5) | 7.80 (17.0) |
| B | LA | U | PUR | 18 | B-LA-U-PUR-18 | 4.39 (18.7) | 9.25 (16.8) |
| B | LA | U | PVAc | 6 | B-LA-U-PVAc-6 | 2.37 (20.2) | 7.14 (4.8) |
| B | LA | U | PVAc | 10 | B-LA-U-PVAc-10 | 3.20 (17.6) | 10.25 (11.2) |
| B | LA | U | PVAc | 18 | B-LA-U-PVAc-18 | 4.03 (7.6) | 11.69 (19.3) |
| B | CA | D | PUR | 6 | B-CA-D-PUR-6 | 2.83 (19.5) | 7.26 (8.4) |
| B | CA | D | PUR | 10 | B-CA-D-PUR-10 | 3.04 (19.6) | 7.72 (14.9) |
| B | CA | D | PUR | 18 | B-CA-D-PUR-18 | 7.07 (20.1) | 15.12 (15.7) |
| B | CA | D | PVAc | 6 | B-CA-D-PVAc-6 | 3.00 (19.0) | 8.99 (12.9) |
| B | CA | D | PVAc | 10 | B-CA-D-PVAc-10 | 3.71 (16.1) | 10.07 (18.9) |
| B | CA | D | PVAc | 18 | B-CA-D-PVAc-18 | 6.69 (19.0) | 12.70 (16.1) |
| B | LA | D | PUR | 6 | B-LA-D-PUR-6 | 4.36 (17.9) | 11.38 (7.4) |
| B | LA | D | PUR | 10 | B-LA-D-PUR-10 | 5.33 (20.5) | 12.45 (17.4) |
| B | LA | D | PUR | 18 | B-LA-D-PUR-18 | 5.63 (12.4) | 15.33 (15.6) |
| B | LA | D | PVAc | 6 | B-LA-D-PVAc-6 | 2.87 (20.7) | 7.52 (8.1) |
| B | LA | D | PVAc | 10 | B-LA-D-PVAc-10 | 4.07 (19.3) | 11.84 (17.9) |
| B | LA | D | PVAc | 18 | B-LA-D-PVAc-18 | 6.77 (19.7) | 20.01 (18.9) |
| Deflection at the Limit of Proportionality of Aspen and NWC Down | |||||
| Monitored Factor | Sum of Squares | Degree of Freedom | Variance | Fisher’s F-test | Significance Level p |
| Intercept | 1469.556 | 1 | 1469.556 | 5410.635 | *** |
| (1) Type of Sample | 76.586 | 11 | 6.962 | 25.634 | *** |
| Error | 29.333 | 108 | 0.272 | - | |
| Deflection at the Limit of Proportionality of Aspen and NWC UP | |||||
| Monitored Factor | Sum of Squares | Degree of Freedom | Variance | Fisher’s F-test | Significance Level p |
| Intercept | 469.9151 | 1 | 469.9151 | 5033.475 | *** |
| (1) Type of Sample | 19.7016 | 11 | 1.7911 | 19.185 | *** |
| Error | 9.4292 | 101 | 0.0934 | - | |
| Deflection at the Modulus of Rupture of Aspen and NWC Down | |||||
| Monitored Factor | Sum of Squares | Degree of Freedom | Variance | Fisher’s F-test | Significance Level p |
| Intercept | 2373.329 | 1 | 2373.329 | 2497.682 | *** |
| (1) Type of Sample | 298.265 | 11 | 27.115 | 28.536 | *** |
| Error | 102.623 | 108 | 0.950 | - | |
| Deflection at the Modulus of Rupture of Aspen and NWC Up | |||||
| Monitored Factor | Sum of Squares | Degree of Freedom | Variance | Fisher’s F-test | Significance Level p |
| Intercept | 5186.339 | 1 | 5186.339 | 4235.214 | *** |
| (1) Type of Sample | 288.155 | 11 | 26.196 | 21.392 | *** |
| Error | 139.602 | 114 | 1.225 | - | |
| Deflection at the Limit of Proportionality of Beech and NWC Down | |||||
| Monitored Factor | Sum of Squares | Degree of Freedom | Variance | Fisher’s F-test | Significance Level p |
| Intercept | 13,863.51 | 1 | 13,863.51 | 3716.494 | *** |
| (1) Type of Sample | 1281.94 | 11 | 116.54 | 31.242 | *** |
| Error | 402.87 | 108 | 3.73 | - | |
| Deflection at the Limit of Proportionality of Beech and NWC Up | |||||
| Monitored Factor | Sum of Squares | Degree of Freedom | Variance | Fisher’s F-test | Significance Level P |
| Intercept | 6405.696 | 1 | 6405.696 | 4427.627 | *** |
| (1) Type of Sample | 373.911 | 11 | 33.992 | 23.495 | *** |
| Error | 146.122 | 101 | 1.447 | - | |
| Deflection at the Modulus of Rupture of Beech and NWC Down | |||||
| Monitored Factor | Sum of Squares | Degree of Freedom | Variance | Fisher’s F-test | Significance Level P |
| Intercept | 15,277.64 | 1 | 15,277.64 | 4198.613 | *** |
| (1) Type of Sample | 1739.17 | 11 | 158.11 | 43.451 | *** |
| Error | 392.98 | 108 | 3.64 | - | |
| Deflection at the Modulus of Rupture of Beech and NWC Up | |||||
| Monitored Factor | Sum of Squares | Degree of Freedom | Variance | Fisher’s F-test | Significance Level P |
| Intercept | 5186.339 | 1 | 5186.339 | 4235.214 | *** |
| (1) Type of Sample | 288.155 | 11 | 26.196 | 21.392 | *** |
| Error | 139.602 | 114 | 1.225 | - | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sikora, A.; Svoboda, T.; Záborský, V.; Gaffová, Z. Effect of Selected Factors on the Bending Deflection at the Limit of Proportionality and at the Modulus of Rupture in Laminated Veneer Lumber. Forests 2019, 10, 401. https://doi.org/10.3390/f10050401
Sikora A, Svoboda T, Záborský V, Gaffová Z. Effect of Selected Factors on the Bending Deflection at the Limit of Proportionality and at the Modulus of Rupture in Laminated Veneer Lumber. Forests. 2019; 10(5):401. https://doi.org/10.3390/f10050401
Chicago/Turabian StyleSikora, Adam, Tomáš Svoboda, Vladimír Záborský, and Zuzana Gaffová. 2019. "Effect of Selected Factors on the Bending Deflection at the Limit of Proportionality and at the Modulus of Rupture in Laminated Veneer Lumber" Forests 10, no. 5: 401. https://doi.org/10.3390/f10050401
APA StyleSikora, A., Svoboda, T., Záborský, V., & Gaffová, Z. (2019). Effect of Selected Factors on the Bending Deflection at the Limit of Proportionality and at the Modulus of Rupture in Laminated Veneer Lumber. Forests, 10(5), 401. https://doi.org/10.3390/f10050401




