Influence of Rainfall on Canopy Interception in Mixed Broad-Leaved—Korean Pine Forest in Xiaoxing’an Mountains, Northeastern China
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Site
2.2. Measurements of Precipitation (Rainfall), Throughfall, and Stemflow
2.3. Statistical Analysis
3. Results
3.1. Seasonal Pattern of Rainfall Amount and Intensity
3.2. Canopy Interception of Rainfall in a Mxed Broad-Leaved–Korean Pine Forest
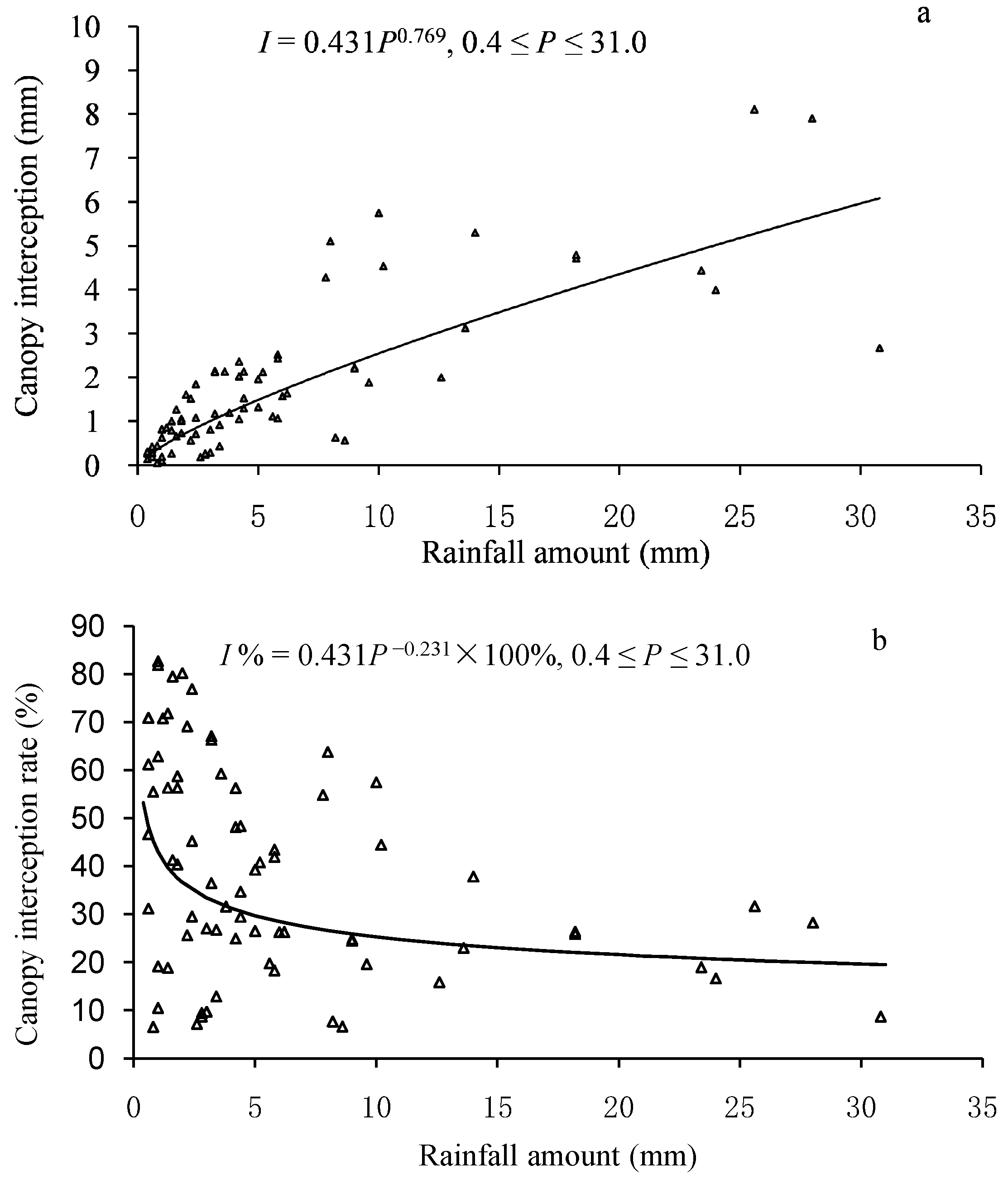
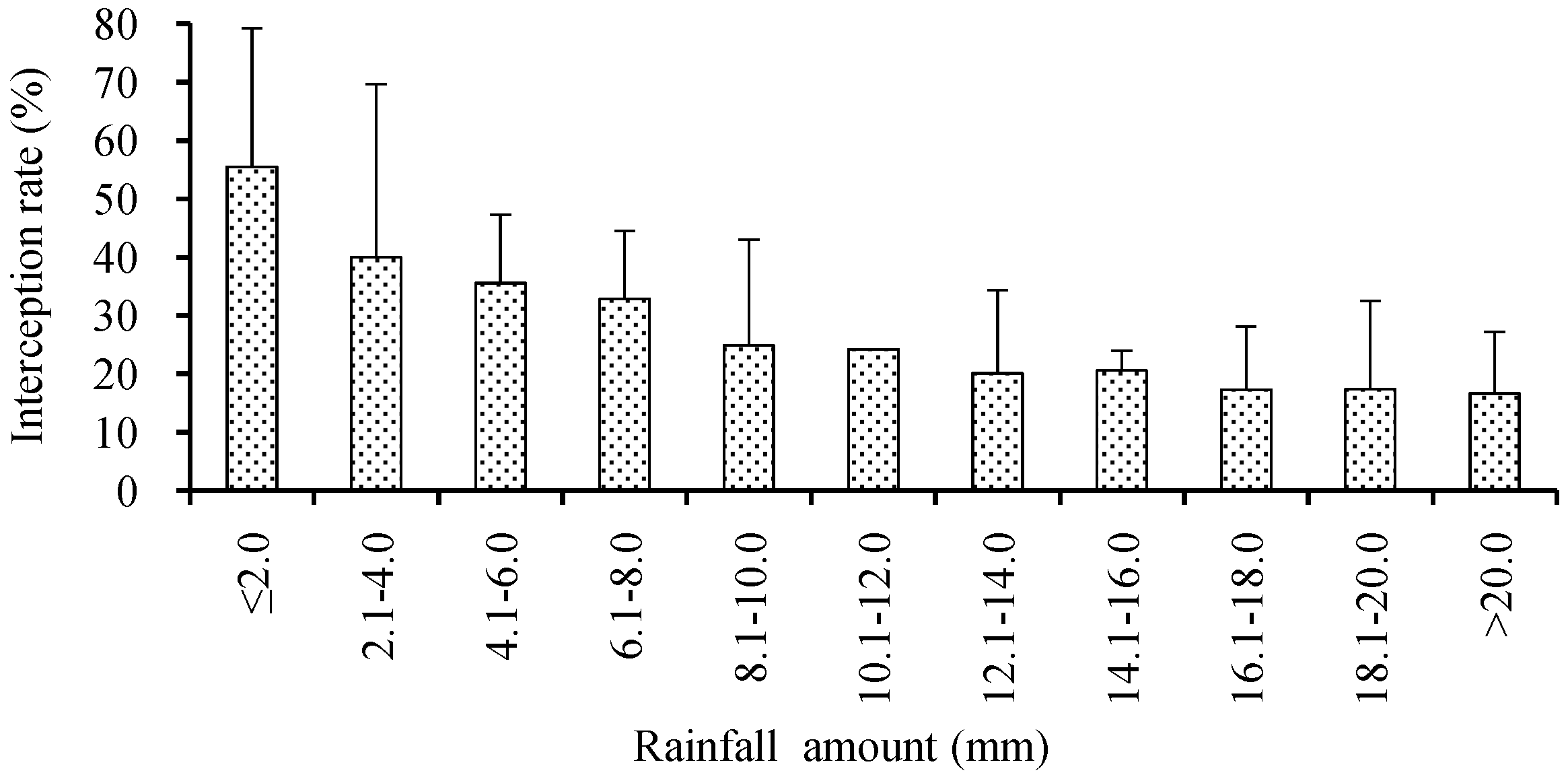
3.3. Canopy Interception Variation with Rainfall Characteristics
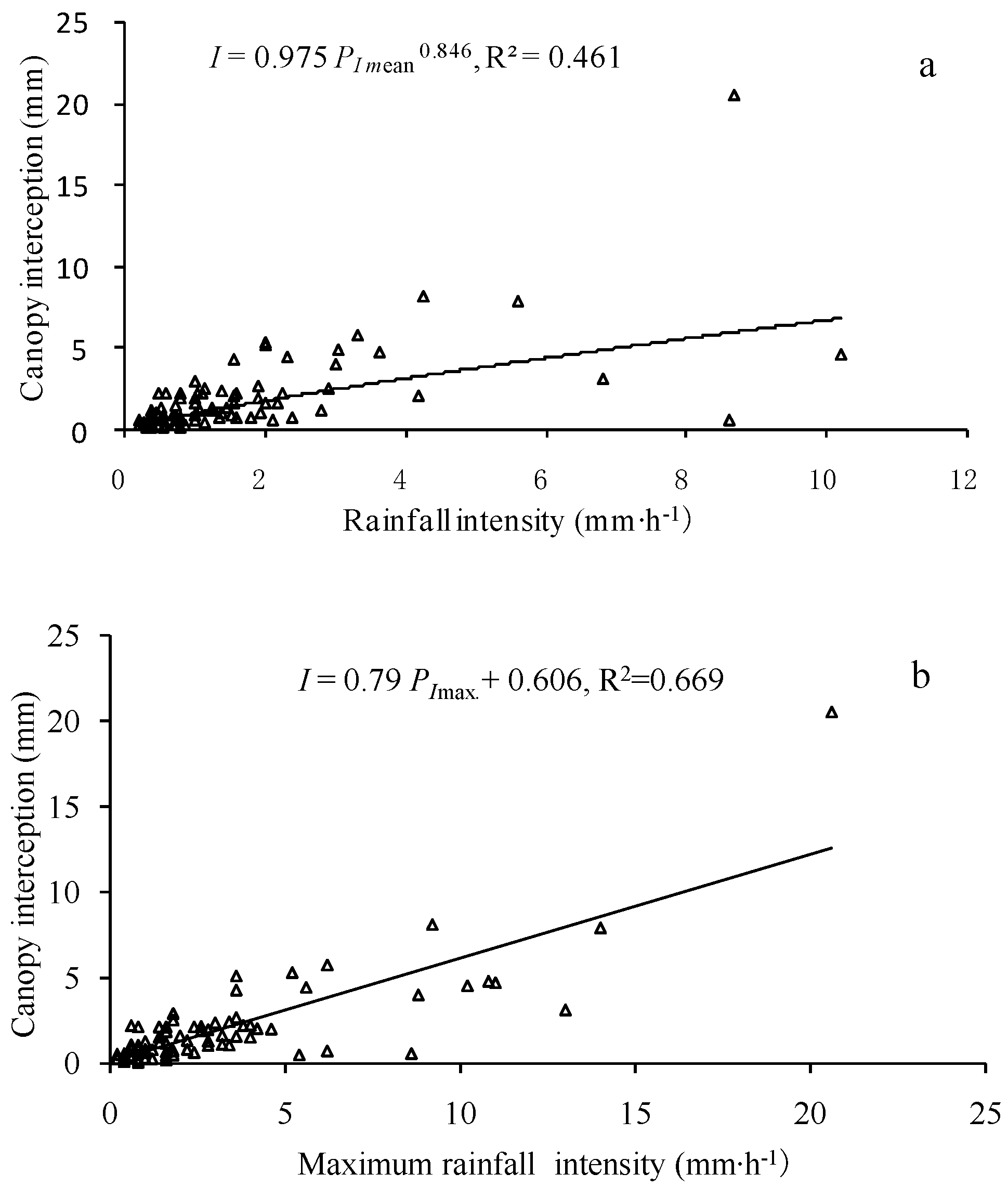
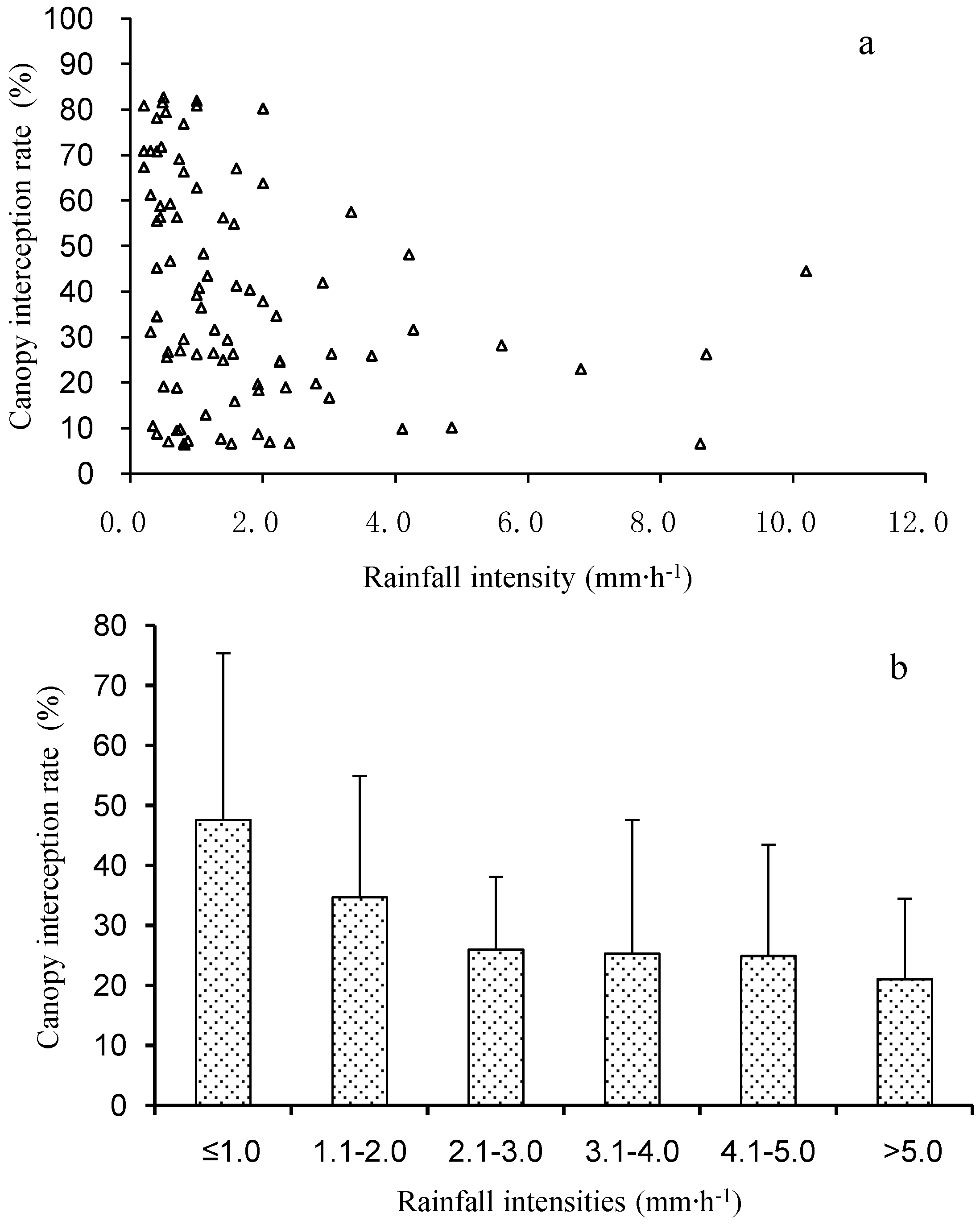
3.4. Influence of Rainfall Intensity on Canopy Interception
4. Discussion
4.1. Canopy Interception by the Mixed Forest of Broad-Leaved and Korean Pine
4.2. Effects of Rainfall Properties on Canopy Interception
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yan, W.; Deng, X.; Chen, X.; Tian, D.; Xiang, W.; Peng, Y. Long-term variations of rainfall interception in different growth stages of Chinese fir plantations. Hydrol. Sci. J. 2015, 60, 2178–2188. [Google Scholar] [CrossRef]
- Huber, A.; Iroumé, A. Variability of annual rainfall partitioning for different sites and forest covers in Chile. J. Hydrol. 2001, 248, 78–92. [Google Scholar] [CrossRef]
- Wei, X.H.; Liu, S.R.; Zhou, G.Y.; Wang, C.K. Hydrological processes in major types of Chinese forest. Hydrol. Processes 2005, 19, 63–75. [Google Scholar] [CrossRef]
- Llorens, P.; Domingo, F. Rainfall partitioning by vegetation under Mediterranean conditions. A review of studies in Europe. J. Hydrol. 2007, 335, 37–54. [Google Scholar] [CrossRef]
- Komatsu, H.; Shinohara, Y.; Kume, T.; Otsuki, K. Relationship between annual rainfall and interception ratio for forests across Japan. For. Ecol. Manag. 2008, 256, 1189–1197. [Google Scholar] [CrossRef]
- Nytch, C.J.; Meléndez-Ackerman, E.J.; Pérez, M.E.; Ortiz-Zayas, J.R. Rainfall interception by six urban trees in San Juan, Puerto Rico. Urban Ecosyst. 2019, 22, 103–115. [Google Scholar] [CrossRef]
- Carlyle-Moses, D.E.; Gash, J.H. Rainfall interception loss by forest canopies. In Forest Hydrology and Biogeochemistry; Springer: Dordrecht, The Netherlands, 2011; pp. 407–423. [Google Scholar]
- Livesley, S.J.; Baudinette, B.; Glover, D. Rainfall interception and stem flow by eucalypt street trees—The impacts of canopy density and bark type. Urban For. Urban Green. 2014, 13, 192–197. [Google Scholar] [CrossRef]
- Crockford, R.H.; Richardson, D.P. Partitioning of rainfall into throughfall, stemflow and interception: Effect of forest type, ground cover and climate. Hydrol. Processes 2000, 14, 2903–2920. [Google Scholar] [CrossRef]
- Xiao, Q.; McPherson, E.G.; Ustin, S.L.; Grismer, M.E.; Simpson, J.R. Winter rainfall interception by two mature open-grown trees in Davis, California. Hydrol. Processes 2000, 14, 763–784. [Google Scholar] [CrossRef]
- Barbier, S.; Balandier, P.; Gosselin, F. Influence of several tree traits on rainfall partitioning in temperate and boreal forests: A review. Ann. For. Sci. 2009, 66, 1–11. [Google Scholar] [CrossRef]
- Pérez-Suárez, M.; Arredondo-Moreno, J.T.; Huber-Sannwald, E.; Serna-Pérez, A. Forest structure, species traits and rain characteristics influences on horizontal and vertical rainfall partitioning in a semiarid pine–oak forest from Central Mexico. Ecohydrology 2014, 7, 532–543. [Google Scholar]
- Zabret, K.; Rakovec, J.; Šraj, M. Influence of meteorological variables on rainfall partitioning for deciduous and coniferous tree species in urban area. J. Hydrol. 2018, 558, 29–41. [Google Scholar] [CrossRef]
- Llorens, P.; Poch, R.; Latron, J.; Gallart, F. Rainfall interception by a Pinus sylvestris forest patch overgrown in a Mediterranean mountainous abandoned areaI. Monitoring design and results down to the event scale. J. Hydrol. 1997, 199, 331–345. [Google Scholar] [CrossRef]
- Levia, D.F.; Hudson, S.A.; Llorens, P.; Nanko, K. Throughfall drop size distributions: A review and prospectus for future research. Wiley Interdiscip. Rev.-Water 2017, 4, e1225. [Google Scholar] [CrossRef]
- Zabret, K.; Rakovec, J.; Mikoš, M.; Šraj, M. Influence of raindrop size distribution on throughfall dynamics under pine and birch trees at the rainfall event level. Atmosphere 2017, 8, 240. [Google Scholar] [CrossRef]
- Zabret, K.; Rakovec, J.; Šraj, M. Evaluation of drop size distribution impact on rainfall interception by trees. Presented at the 2nd International Electronic Conference on Atmospheric Sciences, Basel, Switzerland, 16–31 July 2017; Volume 1, p. 117. [Google Scholar]
- Liu, Y.Y.; Li, F.R.; Jin, G.Z. Spatial patterns and associations of four species in an old-growth temperate forest. J. Plant Interact. 2014, 9, 745–753. [Google Scholar] [CrossRef]
- Wang, W.H.; Zhang, S.L. Brief analysis of hydrological function of forest in Lesser Xing’an Mountains. J. North-East. For. Inst. 1985, 13, 42–47, (In Chinese with English abstract). [Google Scholar]
- Cai, T.J.; Zhu, D.G.; Sheng, H.C. Rainfall redistribution in virgin Pinus koaiensis forest and secondary Betula platyphylla forest in Northeast China. Sci. Soil Water Conserv. 2006, 4, 61–65, (In Chinese with English abstract). [Google Scholar]
- Zhu, J.W.; Shi, J.D. The hydrological effect of broad-leaved Korean pine forest in Xiaoxing’an Mountainous of North-eastern China. J. North-East. For. Inst. 1982, 4, 36–44, (In Chinese with English abstract). [Google Scholar]
- Wang, A.Z.; Pei, T.F.; Jin, C.J.; Guan, D.X. Estimation of rainfall interception by broad-leaved Korean pine forest in Changbai Mountains. Chin. J. Appl. Ecol. 2006, 17, 1403–1407, (In Chinese with English abstract). [Google Scholar]
- Chai, R.S.; Cai, T.J.; Man, X.L.; Wang, H.; Guan, J.Q. Simulation of rainfall interception process of primary Korean pine forest in Xiaoxing’an Mountains by using the modified Gash model. Acta Ecol. Sin. 2013, 33, 1276–1284, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Toba, T.; Ohta, T. An observational study of the factors that influence interception loss in boreal and temperate forests. J. Hydrol. 2005, 313, 208–220. [Google Scholar] [CrossRef]
- He, S.X.; Li, X.Y.; Mo, F.; Zhou, B.; Gao, G.L. The water conservation study of typical forest ecosystems in the forest transect of eastern China. Acta Ecol. Sin. 2011, 31, 3285–3295, (In Chinese with English abstract). [Google Scholar]
- Liu, Y.X.; Li, H.J.; Li, G.S.; Li, X.Y. A study on the interception of precipitation by the different kinds of forest in the East Mountain area, Liaoning. J. Shenyang Agric. Univ. 1993, 24, 298–301, (In Chinese with English abstract). [Google Scholar]
- Xiao, Y.H.; Dai, L.M.; Niu, D.K.; Tong, F.C.; Chen, G.; Deng, H.B. Influence of canopy on precipitation and its nutrient elements in broad-leaved/Korean pine forest on the northern slope of Changbai Mountain. J. For. Res. 2002, 13, 201–204. [Google Scholar]
- Zhang, H.R.; Li, C.; Dong, X.B. Influence of forest canopy in low-quality stands in Lesser Xing’an Mountains on rainfall interception. J. Northeast For. Univ. 2012, 4, 90–91, (In Chinese with English abstract). [Google Scholar]
- Ji, Y.; Cai, T.J. Canopy interception in original Korean pine forest: Measurement and dividual simulation in Xiaoxing’an Mountains, northeastern China. J. Beijing For. Univ. 2015, 37, 41–49, (In Chinese with English abstract). [Google Scholar]
- Zhang, Z.S.; Zhao, Y.; Li, X.R.; Huang, L.; Tan, H.J. Gross rainfall amount and maximum rainfall intensity in 60-minute influence on interception loss of shrubs: A 10-year observation in the TenggerDesert. Sci. Rep. 2016, 6, 26030. [Google Scholar] [CrossRef] [PubMed]
- Fathizadeh, O.; Hosseini, S.M.; Keim, R.F.; Darvishi Boloorani, A. A seasonal evaluation of the reformulated Gash interception model for semi-arid deciduous oak forest stands. For. Ecol. Manag. 2018, 409, 601–613. [Google Scholar] [CrossRef]
- Chen, S.J.; Chen, C.G.; Cao, T.J.; Zhao, X.T.; Hao, H.K.; Pang, J.Z.; Zhang, S.X. Effects of rainfall size class and intensity on canopy interception of Pinus tabulaeformis forest in the Qinling Mountains, China. J. Basic Sci. Eng. 2015, 23, 41–55, (In Chinese with English abstract). [Google Scholar]
- Sheng, H.C.; Cai, T.J.; Li, Y.; Liu, Y.J. Rainfall redistribution in Larix gmelinii forest on northern of Daxing’an Mountains, north-east China. J. Soil Water Conserv. 2014, 28, 101–105, (In Chinese with English abstract). [Google Scholar]
- Sun, X.Y.; Wang, G.X.; Li, W.; Liu, G.S.; Lin, Y. Measurements and modeling of canopy interception in the Gongga Mountain subalpine succession forest. Adv. Water Sci. 2011, 22, 23–29. [Google Scholar]
- Alan, M.; Ali, F. Throughfall characteristics in three non-native Hawaiian forest stands. Agric. For. Meteorol. 2010, 150, 1453–1466. [Google Scholar]
- Kermavnar, J.; Vilhar, U. Canopy precipitation interception in urban forests in relation to stand structure. Urban Ecosyst. 2017, 20, 1373–1387. [Google Scholar] [CrossRef]
- Li, Z.X.; Ouyang, Z.Y.; Zheng, H.; Liu, X.L.; Su, Y.M. Comparison of rainfall redistribution in two ecosystems in Minjiang upper catchments, China. J. Plant Ecol. 2006, 30, 723–731, (In Chinese with English abstract). [Google Scholar]
- Peng, H.H.; Zhao, C.Y.; Zhao, D.F.; Xu, Z.L.; Wang, C.; Zhao, Y. Canopy interception by a spruce forest in the upper reach of Heihe River Basin, Northwestern China. Hydrol. Processes 2014, 28, 1734–1741. [Google Scholar] [CrossRef]
- Chen, L.H.; Zhang, Y.; Yu, X.X.; Shi, Y.; Huang, Z.Y. Characteristics and Simulation on Canopy Interception of Typical Forest Vegetation in Beijing West Mountain Area. J. Basic Sci. Eng. 2013, 21, 423–431, (In Chinese with English abstract). [Google Scholar]
- Li, X.; Xiao, Q.F.; Niu, J.Z.; Dymond, S.; van Doorn, N.S.; Yu, X.X.; Xie, B.Y.; Lv, X.Z.; Zhang, K.B.; Li, J. Process-based rainfall interception by small trees in Northern China: The effect of rainfall traits and crown structure characteristics. Agric. For. Meteorol. 2016, 218–219, 65–73. [Google Scholar] [CrossRef]
- Zhang, J.; Bruijnzeel, L.A.; van Meerveld, H.I.; Ghimire, C.P.; Tripoli, R.; Pasa, A.; Herbohn, J. Typhoon-induced changes in rainfall interception loss from a tropical multi-species ‘reforest’. J. Hydrol. 2019, 568, 658–675. [Google Scholar] [CrossRef]
- Cisneros Vaca, C.; Tol, C.V.D.; Ghimire, C.P. The influence of long-term changes in canopy structure on rainfall interception loss: A case study in Speulderbos, the Netherlands. Hydrol. Earth Syst. Sci. 2018, 22, 3701–3719. [Google Scholar] [CrossRef]
| Tree Species | Total Number of Trees | Basal Area (m2 ha−1) | Mean DBH ± SD (cm) | Mean Height ± SD (m) | Max Height (m) |
|---|---|---|---|---|---|
| P. koraiensis | 241 | 22.7 | 39.8 ± 15.8 | 22.5 ± 5.8 | 32.0 |
| T. amurensis | 102 | 3.0 | 15.4 ± 12.0 | 14.2 ± 6.4 | 27.6 |
| T. mandshurica | 68 | 2.1 | 12.4 ± 10.0 | 12.5 ± 6.8 | 25.3 |
| B. costata | 61 | 2.1 | 12.2 ± 10.4 | 12.0 ± 5.4 | 24.0 |
| Rainfall Intensity (mm h−1) | Frequency (%) | Percentage Amount (%) | ||||
|---|---|---|---|---|---|---|
| 2010 | 2011 | 2010–2011 | 2010 | 2011 | 2010–2011 | |
| ≤1.0 | 50.0 | 44.2 | 46.9 | 16.5 | 10.7 | 13.2 |
| 1.1–2.0 | 21.7 | 34.6 | 28.8 | 22.5 | 33.6 | 28.7 |
| 2.1–3.0 | 13.0 | 13.5 | 13.3 | 14.8 | 35.7 | 26.4 |
| 3.1–4.0 | 2.2 | 1.9 | 2.0 | 3.1 | 4.5 | 3.8 |
| 4.1–5.0 | 6.5 | 1.9 | 4.1 | 12.3 | 6.3 | 8.9 |
| >5.0 | 6.5 | 3.9 | 5.1 | 30.9 | 9.3 | 18.9 |
| Summary Interval | Statistical Variable | 2010 | 2011 | ||||
|---|---|---|---|---|---|---|---|
| P (mm) | I (mm) | I (%) | P (mm) | I (mm) | I (%) | ||
| Growing season | Total | 325.2 | 71.6 | 22.0 | 409.2 | 89.8 | 21.9 |
| Single Rainfall Event | Mean | 7.1 | 1.8 | 34.4 | 7.9 | 2.0 | 34.2 |
| Minimum | 0.4 | 0.1 | 6.6 | 0.4 | 0.1 | 6.7 | |
| Maximum | 78.2 | 20.5 | 82.7 | 30.8 | 8.1 | 80.2 | |
| Standard deviation | 11.7 | 3.2 | 27.8 | 8.8 | 2.0 | 25.9 | |
| Location | Precipitation/mm | Time | Interception | Throughfall | Stemflow | References | |||
|---|---|---|---|---|---|---|---|---|---|
| mm | % | mm | % | mm | % | ||||
| Changbai Mountain Range | 599.1 | May to Oct.—2005 to 2007 | 190.0 | 31.7 | 314.0 | 52.4 | 95.2 | 15.9 | He et al. 2011 |
| 743.1 | Jan. to Dec.—1993 | 179.1 | 24.1 | 558.8 | 75.2 | 5.2 | 0.7 | Liu et al. 1993 | |
| 469.2 | Jun. to Sep.—2001 | 109.7 | 23.4 | 322.1 | 68.7 | 37.4 | 8.0 | Xiao et al. 2002 | |
| Xiaoxing’an Mountains | 763.7 | Jan. to Dec.—1957 | 288.3 | 37.8 | Wang and Zhang 1985 | ||||
| 648.2 | Jan. to Dec.—1958 | 190.5 | 29.4 | ||||||
| 792.8 | Jan. to Dec.—1962 to 1963 | 271.3 | 34.2 | ||||||
| 643.2 | Jan. to Dec.—1963 to 1964 | 199.6 | 31.0 | ||||||
| 712.2 | Jan. to Dec.—1964 to 1965 | 195.2 | 27.4 | ||||||
| 716.0 | Jan. to Dec.—1962 to 1965 | 222.0 | 31.0 | Zhu and Shi 1982 | |||||
| 503.2 | May to Oct.—2005 | 98.7 | 19.6 | 395.8 | 78.7 | 8.8 | 1.7 | Cai et al. 2006 | |
| 828.5 | May to Sep.—2006 May to Sep.—2007 | 177.8 | 21.5 | 636.0 | 76.8 | 14.6 | 1.8 | Ji and Cai 2015 | |
| 354.8 | Jun. to Aug.—2010 | 69.5 | 19.6 | 248.4 | 70.0 | 37.0 | 10.4 | Zhang et al. 2012 | |
| 514.1 | Jul. to Oct.—2010 May to Oct.—2011 | 132.4 | 25.8 | 373.2 | 72.6 | 8.0 | 1.6 | Chai et al. 2013 | |
| 325.2 | May to Sep.—2010 | 71.6 | 22.0 | 252.6 | 77.7 | 1.0 | 0.3 | This study | |
| 409.2 | May to Sep.—2011 | 89.8 | 21.9 | 318.0 | 77.7 | 1.4 | 0.3 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheng, H.; Cai, T. Influence of Rainfall on Canopy Interception in Mixed Broad-Leaved—Korean Pine Forest in Xiaoxing’an Mountains, Northeastern China. Forests 2019, 10, 248. https://doi.org/10.3390/f10030248
Sheng H, Cai T. Influence of Rainfall on Canopy Interception in Mixed Broad-Leaved—Korean Pine Forest in Xiaoxing’an Mountains, Northeastern China. Forests. 2019; 10(3):248. https://doi.org/10.3390/f10030248
Chicago/Turabian StyleSheng, Houcai, and Tijiu Cai. 2019. "Influence of Rainfall on Canopy Interception in Mixed Broad-Leaved—Korean Pine Forest in Xiaoxing’an Mountains, Northeastern China" Forests 10, no. 3: 248. https://doi.org/10.3390/f10030248
APA StyleSheng, H., & Cai, T. (2019). Influence of Rainfall on Canopy Interception in Mixed Broad-Leaved—Korean Pine Forest in Xiaoxing’an Mountains, Northeastern China. Forests, 10(3), 248. https://doi.org/10.3390/f10030248




