Iterative Models for Early Detection of Invasive Species across Spread Pathways
Abstract
1. Introduction
2. Materials and Methods
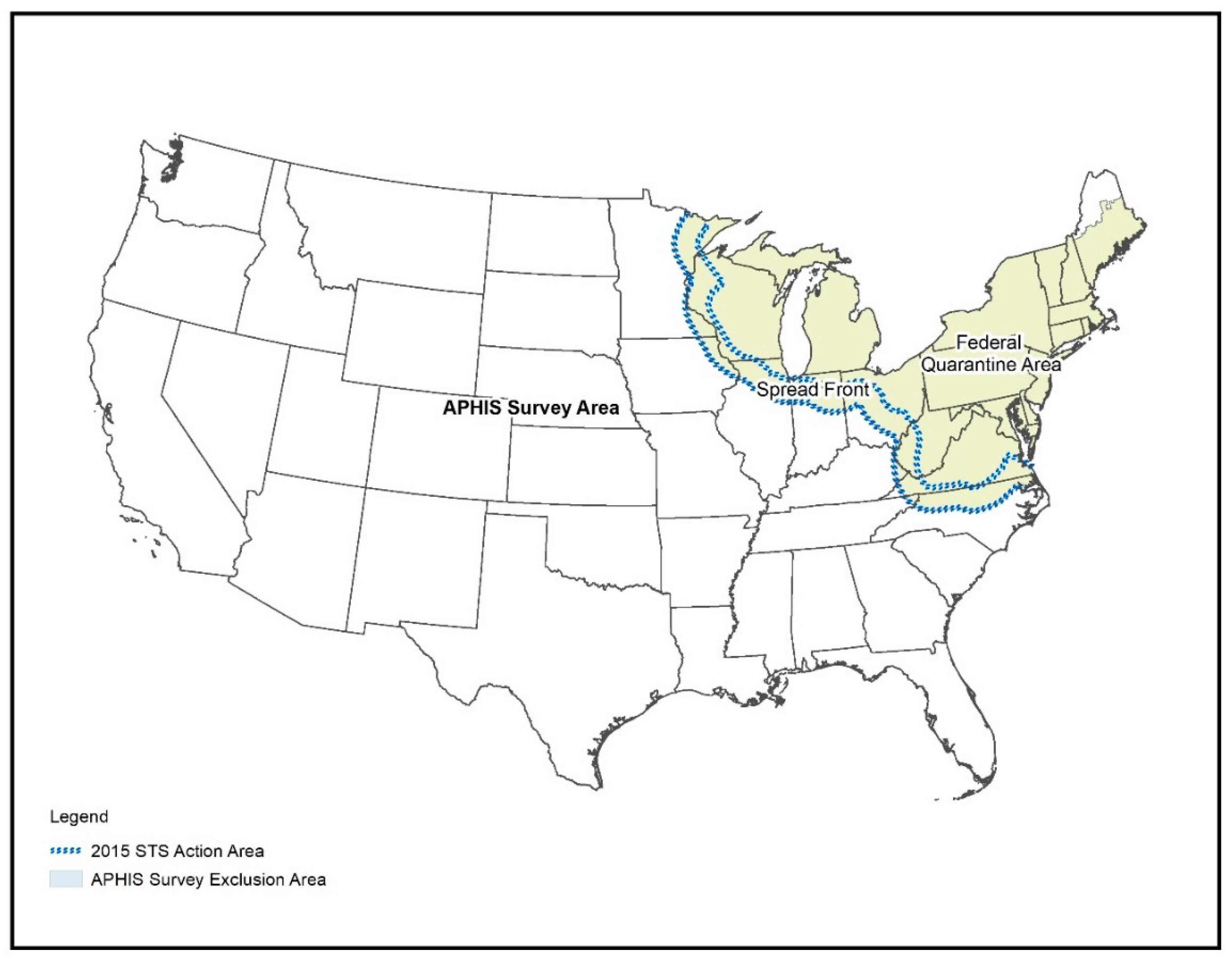
2.1. Study Area
2.2. Survey Data Acquisition and Preparation
2.3. Predictor Variables
2.4. Model Development
2.5. Survey Design
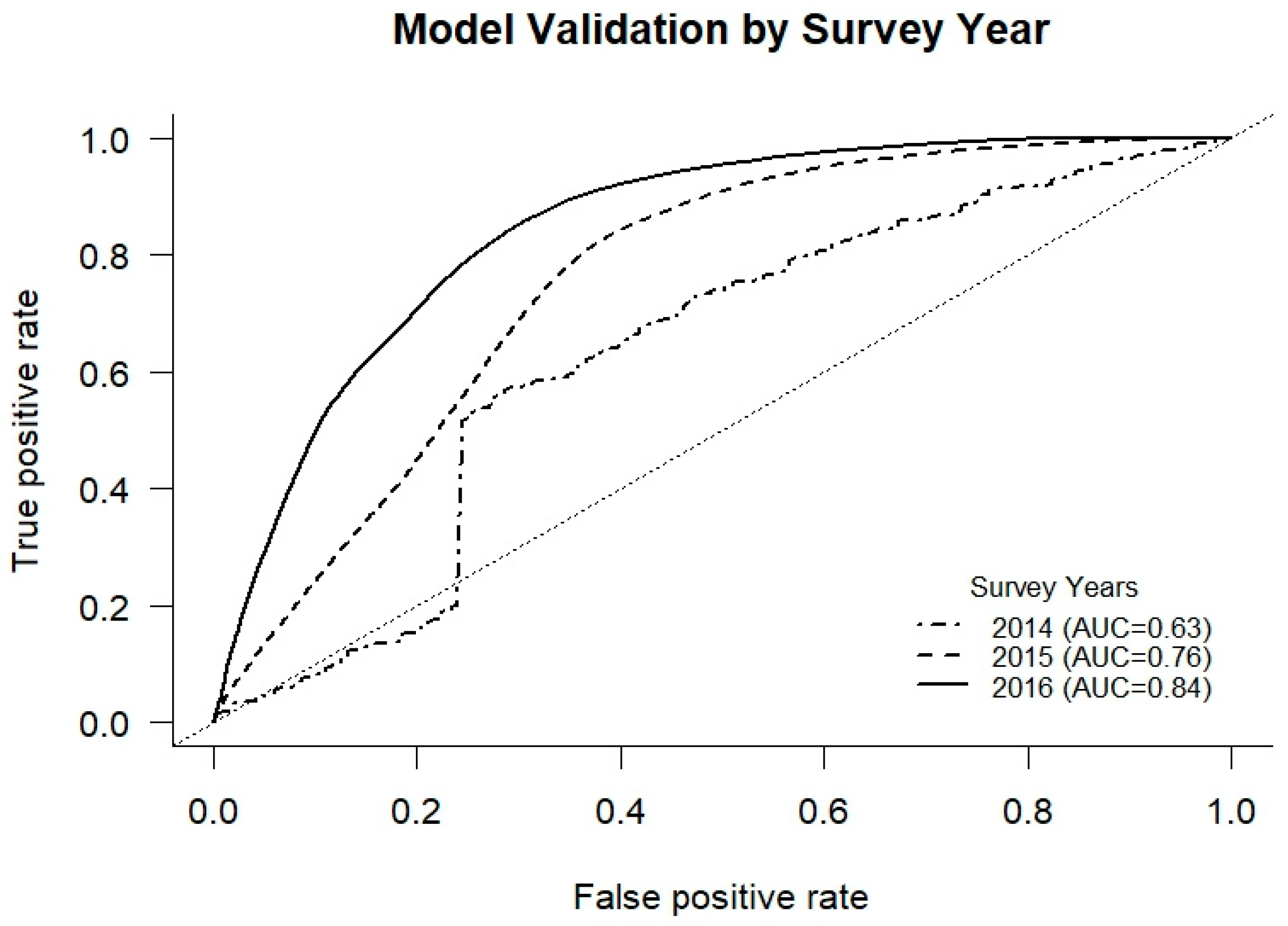
2.6. Model Validation
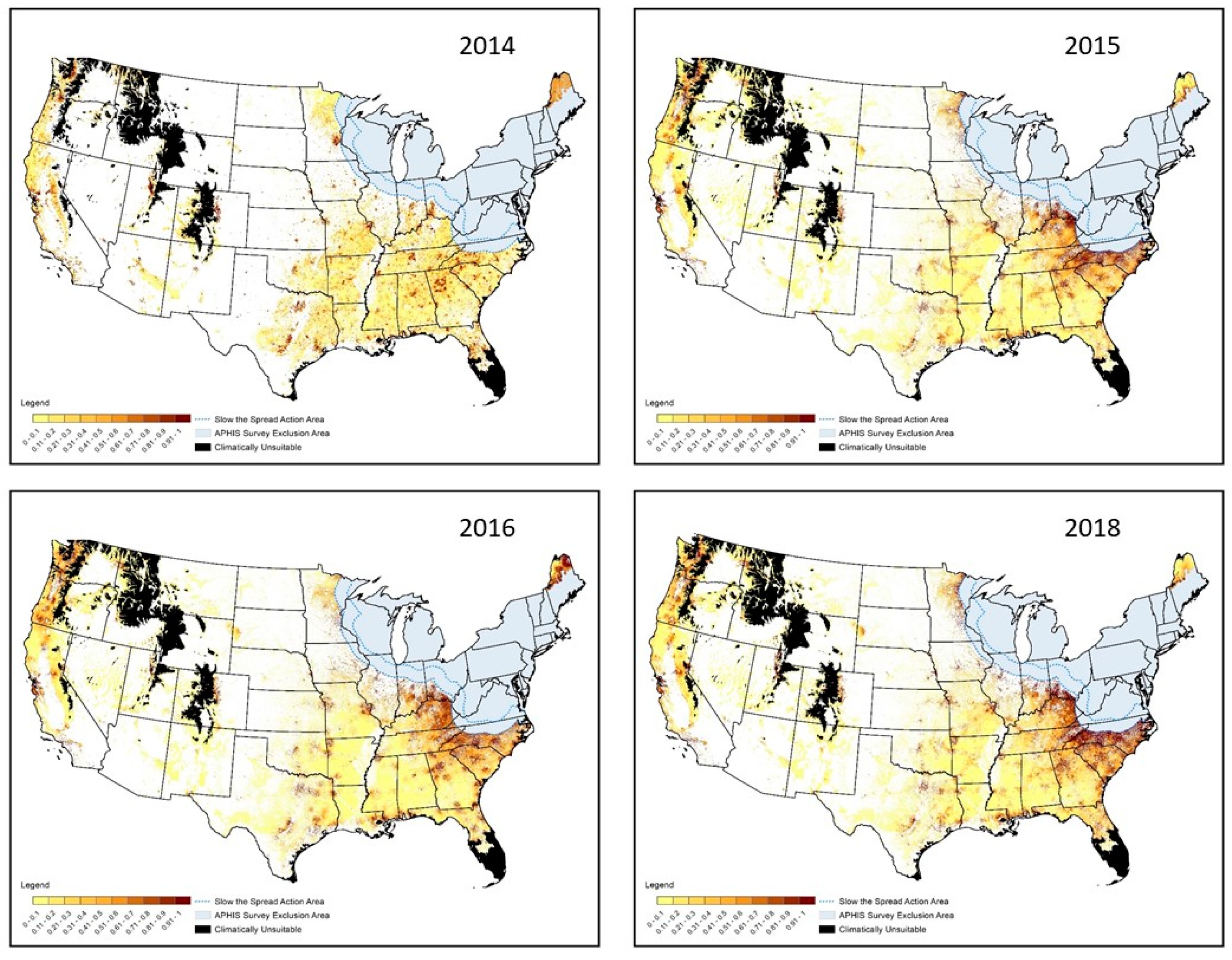
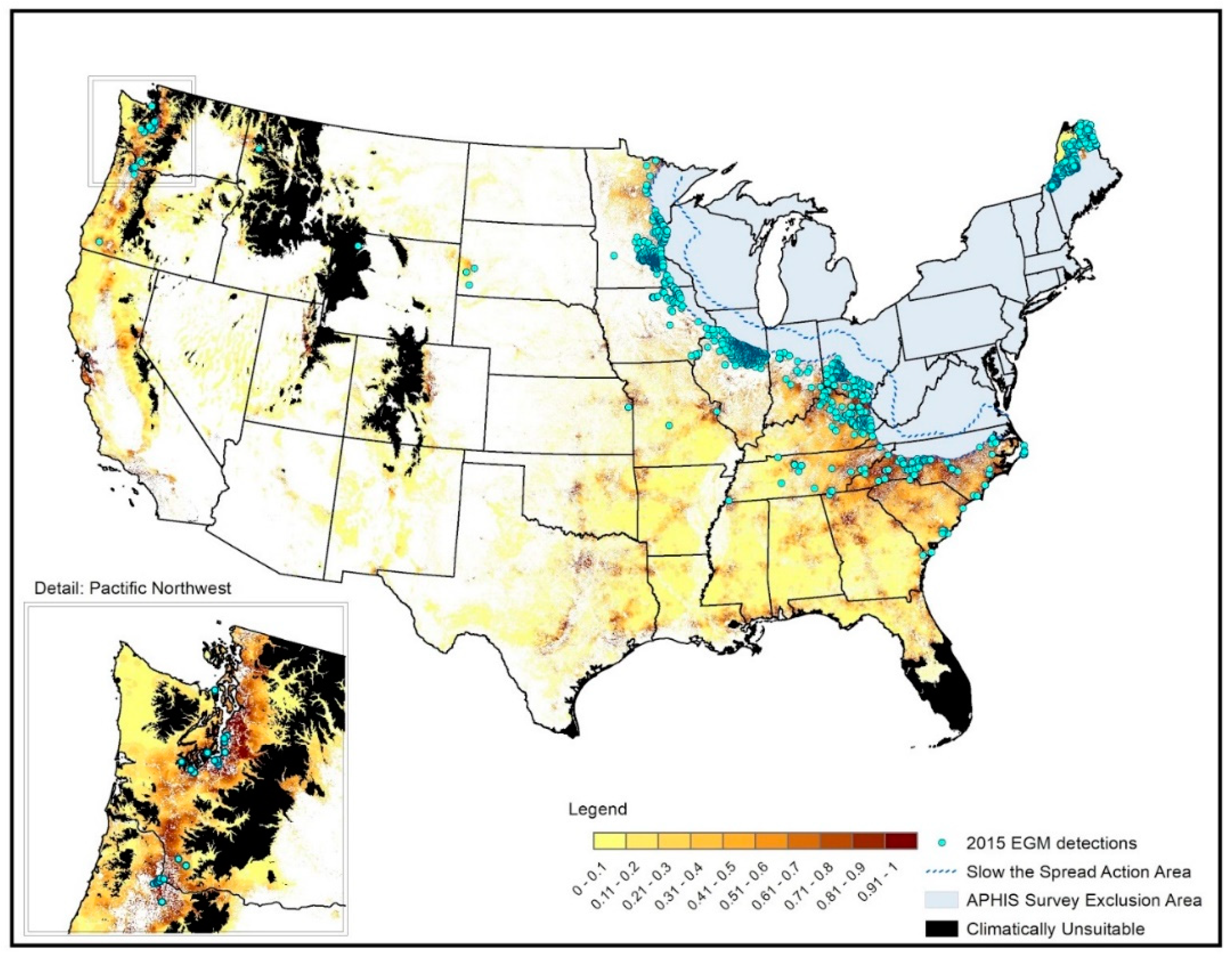
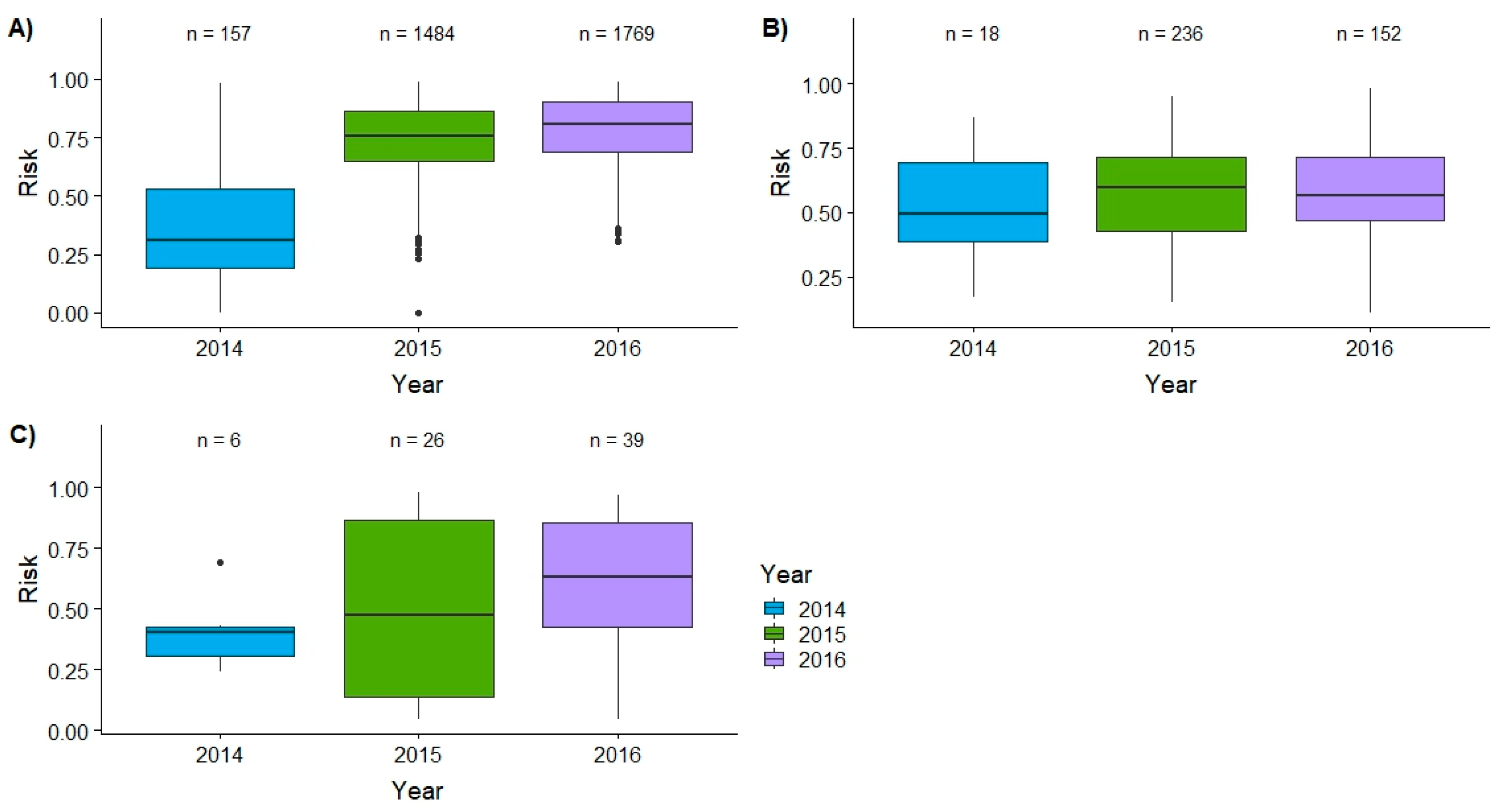
3. Results
3.1. Spatial Targeting
3.2. Temporal Targeting
3.3. Pathways Predictor Performance
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mehta, S.V.; Haight, R.G.; Homans, F.R.; Polasky, S.; Venette, R.C. Optimal detection and control strategies for invasive species management. Ecol. Econ. 2007, 61, 237–245. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R. Species distribution models: Ecological explanation and prediction across space and time. Annu. Rev. Ecol. Evol. Syst. 2009, 40, 677–697. [Google Scholar] [CrossRef]
- Václavík, T.; Meentemeyer, R.K. Invasive species distribution modeling (iSDM): Are absence data and dispersal constraints needed to predict actual distributions? Ecol. Model. 2009, 220, 3248–3258. [Google Scholar] [CrossRef]
- Soberón, J.; Nakamura, M. Niches and distributional areas: Concepts, methods, and assumptions. Proc. Natl. Acad. Sci. USA 2009, 106, 19644–19650. [Google Scholar] [CrossRef] [PubMed]
- Peterson, A.T.; Soberón, J.; Pearson, R.G.; Anderson, R.P.; Martínez-Meyer, E.; Nakamura, M. Ecological Niches and Geographic Distributions (MPB-49); Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Hardin, G. The competitive exclusion principle. Science 1960, 131, 1292–1297. [Google Scholar] [CrossRef]
- Pollock, L.J.; Tingley, R.; Morris, W.K.; Golding, N.; O’Hara, R.B.; Parris, K.M.; Vesk, P.A.; McCarthy, M.A. Understanding co-occurrence by modelling species simultaneously with a Joint Species Distribution Model (JSDM). Methods Ecol. Evol. 2014, 5, 397–406. [Google Scholar] [CrossRef]
- Trainor, A.M.; Schmitz, O.J.; Ivan, J.S.; Shenk, T.M. Enhancing species distribution modeling by characterizing predator–prey interactions. Ecol. Appl. 2014, 24, 204–216. [Google Scholar] [CrossRef] [PubMed]
- Feldman, R.E.; Peers, M.J.L.; Pickles, R.S.A.; Thornton, D.; Murray, D.L. Climate driven range divergence among host species affects range-wide patterns of parasitism. Glob. Ecol. Conserv. 2017, 9, 1–10. [Google Scholar] [CrossRef]
- Crystal-Ornelas, R.; Lockwood, J.L.; Cassey, P.; Hauber, M.E. The establishment threat of the obligate brood-parasitic pin-tailed whydah (Vidua macroura) in North America and the Antilles. Condor 2017, 119, 449–458. [Google Scholar] [CrossRef]
- Barve, N.; Barve, V.; Jiménez-Valverde, A.; Lira-Noriega, A.; Maher, S.P.; Peterson, A.T.; Soberón, J.; Villalobos, F. The crucial role of the accessible area in ecological niche modeling and species distribution modeling. Ecol. Model. 2011, 222, 1810–1819. [Google Scholar] [CrossRef]
- McNeely, J.A. As the world gets smaller, the chances of invasion grow. Euphytica 2006, 148, 5–15. [Google Scholar] [CrossRef]
- Tatem, A.J.; Hay, S.I.; Rogers, D.J. Global traffic and disease vector dispersal. Proc. Natl. Acad. Sci. USA 2006, 103, 6242–6247. [Google Scholar] [CrossRef]
- Floerl, O.; Inglis, G.J.; Dey, K.; Smith, A. The importance of transport hubs in stepping-stone invasions. J. Appl. Ecol. 2009, 46, 37–45. [Google Scholar] [CrossRef]
- Hastings, A.; Cuddington, K.; Davies, K.F.; Dugaw, C.J.; Elmendorf, S.; Freestone, A.; Harrison, S.; Holland, M.; Lambrinos, J.; Malvadkar, U.; et al. The spatial spread of invasions: New developments in theory and evidence. Ecol. Lett. 2005, 8, 91–101. [Google Scholar] [CrossRef]
- Koch, F.H.; Yemshanov, D.; Haack, R.A.; Magarey, R.D. Using a network model to assess risk of forest pest spread via recreational travel. PLoS ONE 2014, 9, 10. [Google Scholar] [CrossRef] [PubMed]
- Colunga-Garcia, M.; Magarey, R.A.; Haack, R.A.; Gage, S.H.; Qi, J.Q. Enhancing early detection of exotic pests in agricultural and forest ecosystems using an urban-gradient framework. Ecol. Appl. 2010, 20, 303–310. [Google Scholar] [CrossRef] [PubMed]
- Thomas, S.M.; Moloney, K.A. Combining the effects of surrounding land-use and propagule pressure to predict the distribution of an invasive plant. Biol. Invasions 2015, 17, 477–495. [Google Scholar] [CrossRef]
- Hulme, P.E.; Bacher, S.; Kenis, M.; Klotz, S.; Kuhn, I.; Minchin, D.; Nentwig, W.; Olenin, S.; Panov, V.; Pergl, J.; et al. Grasping at the routes of biological invasions: A framework for integrating pathways into policy. J. Appl. Ecol. 2008, 45, 403–414. [Google Scholar] [CrossRef]
- Simberloff, D. The role of propagule pressure in biological invasions. Annu. Rev. Ecol. Evol. Syst. 2009, 40, 81–102. [Google Scholar] [CrossRef]
- Lockwood, J.L.; Cassey, P.; Blackburn, T. The role of propagule pressure in explaining species invasions. Trends Ecol. Evol. 2005, 20, 223–228. [Google Scholar] [CrossRef] [PubMed]
- Hulme, P.E. Trade, transport and trouble: Managing invasive species pathways in an era of globalization. J. Appl. Ecol. 2009, 46, 10–18. [Google Scholar] [CrossRef]
- Paini, D.R.; Yemshanov, D. Modelling the arrival of invasive organisms via the international marine shipping network: A khapra beetle study. PLoS ONE 2012, 7, 9. [Google Scholar] [CrossRef]
- Wilson, C.E.; Castro, K.L.; Thurston, G.B.; Sissons, A. Pathway risk analysis of weed seeds in imported grain: A Canadian perspective. NeoBiota 2016, 30. [Google Scholar] [CrossRef]
- Leung, B.; Bossenbroek, J.M.; Lodge, D.M. Boats, pathways, and aquatic biological invasions: Estimating dispersal potential with gravity models. Biol. Invasions 2006, 8, 241–254. [Google Scholar] [CrossRef]
- Meentemeyer, R.K.; Anacker, B.L.; Mark, W.; Rizzo, D.M. Early detection of emerging forest disease using dispersal estimation and ecological niche modeling. Ecol. Appl. 2008, 18, 377–390. [Google Scholar] [CrossRef] [PubMed]
- Sullivan, M.J.P.; Davies, R.G.; Reino, L.; Franco, A.M.A. Using dispersal information to model the species-environment relationship of spreading non-native species. Methods Ecol. Evol. 2012, 3, 870–879. [Google Scholar] [CrossRef]
- Dullinger, S.; Kleinbauer, I.; Peterseil, J.; Smolik, M.; Essl, F. Niche based distribution modelling of an invasive alien plant: Effects of population status, propagule pressure and invasion history. Biol. Invasions 2009, 11, 2401–2414. [Google Scholar] [CrossRef]
- Mędrzycki, P.; Jarzyna, I.; Obidziński, A.; Tokarska-Guzik, B.; Sotek, Z.; Pabjanek, P.; Pytlarczyk, A.; Sachajdakiewicz, I. Simple yet effective: Historical proximity variables improve the species distribution models for invasive giant hogweed (Heracleum mantegazzianum s.l.) in Poland. PLoS ONE 2017, 12, e0184677. [Google Scholar] [CrossRef]
- Liu, X.; Rohr, J.R.; Li, Y. Climate, vegetation, introduced hosts and trade shape a global wildlife pandemic. Proc. R. Soc. B Biol. Sci. 2013, 280. [Google Scholar] [CrossRef]
- Davis, A.J.S.; Singh, K.K.; Thill, J.-C.; Meentemeyer, R.K. Accounting for residential propagule pressure improves prediction of urban plant invasion. Ecosphere 2016, 7, e01232. [Google Scholar] [CrossRef]
- U.S. Department of the Interior. Safeguarding America’s Lands and Waters from Invasive Species: A National Framework for Early Detection and Rapid Response; U.S. Department of the Interior: Washington, DC, USA, 2016; 55p.
- McGeoch, M.A.; Genovesi, P.; Bellingham, P.J.; Costello, M.J.; McGrannachan, C.; Sheppard, A. Prioritizing species, pathways, and sites to achieve conservation targets for biological invasion. Biol. Invasions 2016, 18, 299–314. [Google Scholar] [CrossRef]
- U.S. Department of Agriculture. Hungry Pests: Leave Hungry Pests Behind. Available online: https://www.aphis.usda.gov/aphis/resources/pests-diseases/hungry-pests/What-You-Can-Do (accessed on 9 November 2018).
- Araujo, M.B.; Guisan, A. Five (or so) challenges for species distribution modelling. J. Biogeogr. 2006, 33, 1677–1688. [Google Scholar] [CrossRef]
- Dormann, C.F.; Schymanski, S.J.; Cabral, J.; Chuine, I.; Graham, C.; Hartig, F.; Kearney, M.; Morin, X.; Römermann, C.; Schröder, B.; et al. Correlation and process in species distribution models: Bridging a dichotomy. J. Biogeogr. 2012, 39, 2119–2131. [Google Scholar] [CrossRef]
- Barry, S.; Elith, J. Error and uncertainty in habitat models. J. Appl. Ecol. 2006, 43, 413–423. [Google Scholar] [CrossRef]
- Gallien, L.; Douzet, R.; Pratte, S.; Zimmermann, N.E.; Thuiller, W. Invasive species distribution models—How violating the equilibrium assumption can create new insights. Glob. Ecol. Biogeogr. 2012, 21, 1126–1136. [Google Scholar] [CrossRef]
- Sullivan, M.J.P.; Franco, A.M.A. Changes in habitat associations during range expansion: Disentangling the effects of climate and residence time. Biol. Invasions 2018, 20, 1147–1159. [Google Scholar] [CrossRef]
- Václavík, T.; Meentemeyer, R.K. Equilibrium or not? Modelling potential distribution of invasive species in different stages of invasion. Divers. Distrib. 2012, 18, 73–83. [Google Scholar] [CrossRef]
- Andow, D.A.; Kareiva, P.M.; Levin, S.A.; Okubo, A. Spread of invading organisms. Landsc. Ecol. 1990, 4, 177–188. [Google Scholar] [CrossRef]
- Shigesada, N.; Kawasaki, K. Biological Invasions: Theory and Practice; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Merow, C.; Smith, M.J.; Silander, J.A. A practical guide to MaxEnt for modeling species’ distributions: What it does, and why inputs and settings matter. Ecography 2013. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef]
- Guillera-Arroita, G.; Lahoz-Monfort, J.J.; Elith, J.; Gordon, A.; Kujala, H.; Lentini, P.E.; McCarthy, M.A.; Tingley, R.; Wintle, B.A. Is my species distribution model fit for purpose? Matching data and models to applications. Glob. Ecol. Biogeogr. 2015, 24, 276–292. [Google Scholar] [CrossRef]
- Jarnevich, C.S.; Stohlgren, T.J.; Kumar, S.; Morisette, J.T.; Holcombe, T.R. Caveats for correlative species distribution modeling. Ecol. Inform. 2015, 29, 6–15. [Google Scholar] [CrossRef]
- Uden, D.R.; Allen, C.R.; Angeler, D.G.; Corral, L.; Fricke, K.A. Adaptive invasive species distribution models: A framework for modeling incipient invasions. Biol. Invasions 2015, 17, 2831–2850. [Google Scholar] [CrossRef]
- Wang, O.; Zachmann, L.J.; Sesnie, S.E.; Olsson, A.D.; Dickson, B.G. An iterative and targeted sampling design informed by habitat suitability models for detecting focal plant species over extensive areas. PLoS ONE 2014, 9, e101196. [Google Scholar] [CrossRef] [PubMed]
- Williams, J.N.; Seo, C.; Thorne, J.; Nelson, J.K.; Erwin, S.; O’Brien, J.M.; Schwartz, M.W. Using species distribution models to predict new occurrences for rare plants. Divers. Distrib. 2009, 15, 565–576. [Google Scholar] [CrossRef]
- Rinnhofer, L.J.; Roura-Pascual, N.; Arthofer, W.; Dejaco, T.; Thaler-Knoflach, B.; Wachter, G.A.; Christian, E.; Steiner, F.M.; Schlick-Steiner, B.C. Iterative species distribution modelling and ground validation in endemism research: An Alpine jumping bristletail example. Biodivers. Conserv. 2012, 21, 2845–2863. [Google Scholar] [CrossRef]
- Guisan, A.; Broennimann, O.; Engler, R.; Vust, M.; Yoccoz, N.G.; Lehmann, A.; Zimmermann, N.E. Using niche-based models to improve the sampling of rare species. Conserv. Biol. 2006, 20, 501–511. [Google Scholar] [CrossRef] [PubMed]
- Lauzeral, C.; Grenouillet, G.; Brosse, S. The iterative ensemble modelling approach increases the accuracy of fish distribution models. Ecography 2015, 38, 213–220. [Google Scholar] [CrossRef]
- Crall, A.W.; Jarnevich, C.S.; Panke, B.; Young, N.; Renz, M.; Morisette, J. Using habitat suitability models to target invasive plant species surveys. Ecol. Appl. 2013, 23, 60–72. [Google Scholar] [CrossRef]
- Liebhold, A.M.; Gottschalk, K.W.; Muzika, R.-M.; Montgomery, M.E.; Young, R.; O’Day, K.; Kelley, B. Suitability of North American Tree Species to Gypsy Moth: A Summary of Field and Laboratory Tests; General Technical Report NE-211; USDA Forest Service, Northeastern Forest Experiment Station: Radnor, PA, USA, 1995; 34p.
- Gottschalk, K.W. Gypsy moth effects on mast production. In Proceedings of the Workshop: Southern Appalachian Mast Management, Knoxville, TN, USA, 14–16 August 1989; McGee, C.E., Ed.; University of Tennessee: Knoxville, TN, USA, 1989; pp. 42–50. [Google Scholar]
- Kessler, K.R.; Labosky, P., Jr. Pulp and papermaking properties of gypsy moth-killed trees. Wood Fiber Sci. 2007, 20, 386–396. [Google Scholar]
- Gale, G.A.; DeCecco, J.A.; Marshall, M.R.; McClain, W.R.; Cooper, R.J. Effects of gypsy moth defoliation on forest birds: An assessment using breeding bird census data. J. Field Ornithol. 2001, 72, 291–304. [Google Scholar] [CrossRef]
- Thurber, D.K.; McClain, W.R.; Whitmore, R.C. Indirect effects of gypsy moth defoliation on nest predation. J. Wildl. Manag. 1994, 58, 493–500. [Google Scholar] [CrossRef]
- Lovett, G.M.; Christenson, L.M.; Groffman, P.M.; Jones, C.G.; Hart, J.E.; Mitchell, M.J. Insect defoliation and nitrogen cycling in forests. BioScience 2002, 52, 335–341. [Google Scholar] [CrossRef]
- Etkind, P.H.; Odell, T.M.; Canada, A.T.; Shama, S.K.; Finn, A.M.; Tuthill, R. The gypsy moth caterpillar: A significant new occupational and public health problem. J. Occup. Med. Off. Publ. Ind. Med. Assoc. 1982, 24, 659–662. [Google Scholar] [CrossRef]
- Aukema, J.E.; Leung, B.; Kovacs, K.; Chivers, C.; Britton, K.O.; Englin, J.; Frankel, S.J.; Haight, R.G.; Holmes, T.P.; Liebhold, A.M.; et al. Economic impacts of non-native forest insects in the continental United States. PLoS ONE 2011, 6, e24587. [Google Scholar] [CrossRef] [PubMed]
- Liebhold, A.; Bascompte, J. The Allee effect, stochastic dynamics and the eradication of alien species. Ecol. Lett. 2003, 6, 133–140. [Google Scholar] [CrossRef]
- Liebhold, A.M.; Sharov, A.A.; Tobin, P.C. Population biology of gypsy moth spread. In Slow the Spread: A National Program to Manage the Gypsy Moth; General Technical Report NRS-6; Tobin, P.C., Blackburn, L.M., Eds.; USDA Forest Service, Northern Research Station: Newtown Square, PA, USA, 2007; pp. 15–32. [Google Scholar]
- Logan, J.A.; Regniere, J.; Gray, D.R.; Munson, A.S. Risk assessment in the face of a changing environment: Gypsy moth and climate change in Utah. Ecol. Appl. 2007, 17, 101–117. [Google Scholar] [CrossRef]
- Regniere, J.; Nealis, V. Modelling seasonality of gypsy moth, Lymantria dispar (Lepidoptera: Lymantriidae), to evaluate probability of its persistence in novel environments. Can. Èntomol. 2002, 134, 805–824. [Google Scholar] [CrossRef]
- Regniere, J.; Sharov, A. Simulating temperature-dependent ecological processes at the sub-continental scale: Male gypsy moth flight phenology as an example. Int. J. Biometeorol. 1999, 42, 146–152. [Google Scholar] [CrossRef]
- Bigsby, K.M.; Tobin, P.C.; Sills, E.O. Anthropogenic drivers of gypsy moth spread. Biol. Invasions 2011, 13, 2077–2090. [Google Scholar] [CrossRef]
- Tobin, P.C.; Blackburn, L.M. Long-distance dispersal of the gypsy moth (Lepidoptera: Lymantriidae) facilitated its initial invasion of Wisconsin. Environ. Entomol. 2008, 37, 87–93. [Google Scholar] [CrossRef]
- Tobin, P.C.; Van Stappen, J.; Blackburn, L.M. Human visitation rates to the Apostle Islands National Lakeshore and the introduction of the non-native species Lymantria dispar (L.). J. Environ. Manag. 2010, 91, 1991–1996. [Google Scholar] [CrossRef] [PubMed]
- Gray, D.R. Hitchhikers on trade routes: A phenology model estimates the probabilities of gypsy moth introduction and establishment. Ecol. Appl. 2010, 20, 2300–2309. [Google Scholar] [CrossRef] [PubMed]
- Lippitt, C.D.; Rogan, J.; Toledano, J.; Sangermano, F.; Eastman, J.R.; Mastro, V.; Sawyer, A. Incorporating anthropogenic variables into a species distribution model to map gypsy moth risk. Ecol. Model. 2008, 210, 339–350. [Google Scholar] [CrossRef]
- Taylor, R.A.J.; McManus, M.L.; Pitts, C.W. The absolute efficiency of gypsy moth, Lymantria dispar (Lepidoptera: Lymantriidae), milk-carton pheromone traps. Bull. Èntomol. Res. 1991, 81, 111–118. [Google Scholar] [CrossRef]
- Tobin, P.C.; Zhang, A.; Onufrieva, K.; Leonard, D.S. Field evaluation of effect of temperature on release of disparlure from a pheromone-baited trapping system used to monitor gypsy moth (Lepidoptera: Lymantriidae). J. Econ. Entomol. 2011, 104, 1265–1271. [Google Scholar] [CrossRef]
- Sharov, A.A.; Liebhold, A.M.; Roberts, A.E. Optimizing the use of barrier zones to slow the spread of gypsy moth (Lepidoptera: Lymantriidae) in North America. J. Econ. Entomol. 1998, 91, 165–174. [Google Scholar] [CrossRef]
- Sharov, A.A.; Liebhold, A.M. Bioeconomics of managing the spread of exotic pest species with barrier zones. Ecol. Appl. 1998, 8, 833–845. [Google Scholar] [CrossRef]
- Epanchin-Niell, R.S.; Haight, R.G.; Berec, L.; Kean, J.M.; Liebhold, A.M. Optimal surveillance and eradication of invasive species in heterogeneous landscapes. Ecol. Lett. 2012, 15, 803–812. [Google Scholar] [CrossRef]
- Gray, D.R. The gypsy moth life stage model: Landscape-wide estimates of gypsy moth establishment using a multi-generational phenology model. Ecol. Model. 2004, 176, 155–171. [Google Scholar] [CrossRef]
- Downing, M.C.; Withrow, J.R.; Leinwand, I.I.F.; Cook, G.L.; Kennaway, L.F.; Jarnevich, C.; Sapio, F.J. European Gypsy Moth Lymantria Dispar Dispar Establishment Suitability for 2014; USDA Forest Service, Forest Health Assessment and Applied Sciences Team: Fort Collins, CO, USA, 2014. Available online: https://www.fs.fed.us/foresthealth/technology/pdfs/European_Gyspy_Moth_Establishement_Map_Summary.pdf (accessed on 10 November 2018).
- McManus, M.L. The Role of Behavior in the Disperal of Newly Hatch Gypsy Moth Larvae; Research Paper NE-267; USDA Forest Service, Northeastern Forest Experiment Station: Upper Darby, PA, USA, 1973.
- McFadden, M.W.; McManus, M.E. An insect out of control? The potential for spread and establishment of the gypsy moth in new forest areas in the United States. In Insect Guilds: Patterns of Interaction with Host Trees; Baranchikov, Y.N., Mattson, W.J., Hain, F.P., Payne, T.L., Eds.; USDA Forest Service, Northeastern Forest Experiment Station: Radnor, PA, USA, 1991; pp. 172–186. [Google Scholar]
- Frank, K.L.; Tobin, P.C.; Thistle, H.W.; Kalkstein, L.S. Interpretation of gypsy moth frontal advance using meteorology in a conditional algorithm. Int. J. Biometeorol. 2013, 57, 459–473. [Google Scholar] [CrossRef] [PubMed]
- Tobin, P.; Blackburn, L.M. Slow the Spread: A National Program to Manage the Gyspy Moth; Gen. Tech. Rep. NRS-6; US Department of Agriculture, Forest Service, Northern Research Station: Newton Square, PA, USA, 2007.
- Tobin, P.C.; Onufrieva, K.S.; Thorpe, K.W. The relationship between male moth density and female mating success in invading populations of Lymantria dispar. Èntomol. Exp. Appl. 2013, 146, 103–111. [Google Scholar] [CrossRef]
- Tobin, P.C.; Robinet, C.; Johnson, D.M.; Whitmire, S.L.; Bjørnstad, O.N.; Liebhold, A.M. The role of Allee effects in gypsy moth, Lymantria dispar (L.), invasions. Popul. Ecol. 2009, 51, 373–384. [Google Scholar] [CrossRef]
- Sharov, A.A.; Liebhold, A.M.; Ravlin, F.W. Prediction of Gypsy Moth (Lepidoptera: Lymantriidae) mating success from pheromone trap counts. Environ. Èntomol. 1995, 24, 1239–1244. [Google Scholar] [CrossRef]
- Onufrieva, K.; Thorpe, K.; Hickman, A.; Leonard, D.; Roberts, E.; Tobin, P. Persistence of the gypsy moth pheromone, disparlure, in the environment in various climates. Insects 2013, 4, 104–116. [Google Scholar] [CrossRef] [PubMed]
- Dormann, C.F.; McPherson, J.M.; Araujo, M.B.; Bivand, R.; Bolliger, J.; Carl, G.; Davies, R.G.; Hirzel, A.; Jetz, W.; Kissling, W.D.; et al. Methods to account for spatial autocorrelation in the analysis of species distributional data: A review. Ecography 2007, 30, 609–628. [Google Scholar] [CrossRef]
- USDA, Animal and Plant Health Inspection Service. Gypsy Moth Program Manual. First Edition ed. Plant Protection and Quarantine; 2010. Available online: http://www.aphis.usda.gov/import_export/plants/manuals/domestic/downloads/gypsy_moth.pdf (accessed on 10 November 2018).
- Liebhold, A.M.; Tobin, P. Growth of newly established alien populations: Comparison of North American gypsy moth colonies with invasion theory. Popul. Ecol. 2006, 48, 253–262. [Google Scholar] [CrossRef]
- Tobin, P.C.; Bai, B.B.; Eggen, D.A.; Leonard, D.S. The ecology, geopolitics, and economics of managing Lymantria dispar in the United States. Int. J. Pest Manag. 2012, 58, 195–210. [Google Scholar] [CrossRef]
- Armstrong, K.; McHugh, P.; Chinn, W.; Frampton, E.R.; Walsh, P. Tussock moth species arriving on imported used vehicles determined by DNA analysis. N. Z. Plant Prot. 2003, 56, 16–20. [Google Scholar]
- Sharov, A.A.; Liebhold, A.M. Model of slowing the spread of gypsy moth (Lepidoptera: Lymantriidae) with a barrier zone. Ecol. Appl. 1998, 8, 1170–1179. [Google Scholar] [CrossRef]
- Morisette, J.T.; Jarnevich, C.S.; Holcombe, T.R.; Talbert, C.B.; Ignizio, D.; Talbert, M.K.; Silva, C.; Koop, D.; Swanson, A.; Young, N.E. VisTrails SAHM: Visualization and workflow management for species habitat modeling. Ecography 2013, 36, 129–135. [Google Scholar] [CrossRef]
- Elith, J.; Phillips, S.J.; Hastie, T.; Dudík, M.; Chee, Y.E.; Yates, C.J. A statistical explanation of MaxEnt for ecologists. Divers. Distrib. 2011, 17, 43–57. [Google Scholar] [CrossRef]
- Phillips, S.J.; Anderson, R.P.; Schapire, R.E. Maximum entropy modeling of species geographic distributions. Ecol. Model. 2006, 190, 231–259. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J. Predicting species distributions from museum and herbarium records using multiresponse models fitted with multivariate adaptive regression splines. Divers. Distrib. 2007, 13, 265–275. [Google Scholar] [CrossRef]
- Friedman, J.H. Multivariate adaptive regression splines. Ann. Stat. 1991, 1–67. [Google Scholar] [CrossRef]
- McCullagh, P.; Nelder, J.A. Generalized Linear Models; CRC Press: Boca Raton, FL, USA, 1989; Volume 37. [Google Scholar]
- Friedman, J.; Hastie, T.; Tibshirani, R. Additive logistic regression: A statistical view of boosting (with discussion and a rejoinder by the authors). Ann. Stat. 2000, 28, 337–407. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Merow, C.; Smith, M.J.; Edwards, T.C.; Guisan, A.; McMahon, S.M.; Normand, S.; Thuiller, W.; Wüest, R.O.; Zimmermann, N.E.; Elith, J. What do we gain from simplicity versus complexity in species distribution models? Ecography 2014, 37, 1267–1281. [Google Scholar] [CrossRef]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Marquéz, J.R.G.; Gruber, B.; Lafourcade, B.; Leitão, P.J.; et al. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography 2013, 36, 027–046. [Google Scholar] [CrossRef]
- Freeman, E.A.; Moisen, G. PresenceAbsence: An R package for presence absence analysis. J. Stat. Softw. 2008, 23, 1–31. [Google Scholar] [CrossRef]
- USDA Forest Service, Forest Health Assessment and Applied Sciences Team. Invasive Species Sample Design Tool (ArcGIS 10.0). Available online: http://www.fs.fed.us/foresthealth/technology/invasives_sample_design_tool.shtml (accessed on 10 November 2018).
- Stevens, D.L., Jr.; Olsen, A.R. Spatially balanced sampling of natural resources. J. Am. Stat. Assoc. 2004, 99, 262–278. [Google Scholar] [CrossRef]
- Theobald, D.M.; Stevens, D.L.; White, D.; Urquhart, N.S.; Olsen, A.R.; Norman, J.B. Using GIS to generate spatially balanced random survey designs for natural resource applications. Environ. Manag. 2007, 40, 134–146. [Google Scholar] [CrossRef] [PubMed]
- Government of Canada, Canadian Food Inspection Agency, and Plant Health and Biosecurity Directorate. “Appendix 1: List of North American Gypsy Moth Infested or Suspected Infested Areas of Canada and the United States.” D-98-09: Comprehensive Policy to Control the Spread of North American Gypsy Moth, Lymantria Dispar in Canada and the United States. 23 June 2017. Available online: www.inspection.gc.ca/plants/plant-pests-invasive-species/directives/forestry/d-98-09/appendix-1/eng/1343832991660/1343834043533 (accessed on 13 December 2018).
- Regniere, J.; Nealis, V.; Porter, K. Climate suitability and management of the gypsy moth invasion into Canada. Biol. Invasions 2009, 11, 135–148. [Google Scholar] [CrossRef]
- Andresen, J.; McCullough, D.; Potter, B.; Koller, C.; Bauer, L.; Lusch, D.; Ramm, C. Effects of winter temperatures on gypsy moth egg masses in the Great Lakes region of the United States. Agric. For. Meteorol. 2001, 110, 85–100. [Google Scholar] [CrossRef]
- Bossenbroek, J.M.; Johnson, L.E.; Peters, B.; Lodge, D.M. Forecasting the expansion of zebra mussels in the United States. Conserv. Biol. 2007, 21, 800–810. [Google Scholar] [CrossRef] [PubMed]
- Pyšek, P.; Hulme, P.E. Spatio-temporal dynamics of plant invasions: Linking pattern to process. Écoscience 2005, 12, 302–315. [Google Scholar] [CrossRef]
- Stohlgren, T.J.; Schnase, J.L. Risk analysis for biological hazards: What we need to know about invasive species. Risk Anal. 2006, 26, 163–173. [Google Scholar] [CrossRef] [PubMed]
- Thompson, L.M.; Faske, T.M.; Banahene, N.; Grim, D.; Agosta, S.J.; Parry, D.; Tobin, P.C.; Johnson, D.M.; Grayson, K.L. Variation in growth and developmental responses to supraoptimal temperatures near latitudinal range limits of gypsy moth Lymantria dispar (L.), an expanding invasive species. Physiol. Èntomol. 2017, 42, 181–190. [Google Scholar] [CrossRef]
- Bell, R.A. Manipulation of diapause in the gypsy moth, Lymantria dispar L., by application of KK-42 and precocious chilling of eggs. J. Insect Physiol. 1996, 42, 557–563. [Google Scholar] [CrossRef]
- Campbell, R.W. The role of disease and desiccation in the population dynamics of the gypsy moth Porthetria dispar (L.) (Lepidoptera: Lymantriidae). Can. Èntomol. 1963, 95, 426–434. [Google Scholar] [CrossRef]
- Tobin, P.C.; Diss-Torrance, A.; Blackburn, L.M.; Brown, B.D. What does “local” firewood buy you? Managing the risk of invasive species introduction. J. Econ. Èntomol. 2010, 103, 1569–1576. [Google Scholar] [CrossRef] [PubMed]
- Muirhead, J.R.; Leung, B.; van Overdijk, C.; Kelly, D.W.; Nandakumar, K.; Marchant, K.R.; MacIsaac, H.J. Modelling local and long-distance dispersal of invasive emerald ash borer Agrilus planipennis (Coleoptera) in North America. Divers. Distrib. 2006, 12, 71–79. [Google Scholar] [CrossRef]
- Koch, F.H.; Yemshanov, D.; Magarey, R.D.; Smith, W.D. Dispersal of invasive forest insects via recreational firewood: A quantitative analysis. J. Econ. Èntomol. 2012, 105, 438–450. [Google Scholar] [CrossRef] [PubMed]
- Anderson, L.G.; Rocliffe, S.; Haddaway, N.R.; Dunn, A.M. The role of tourism and recreation in the spread of non-native species: A systematic review and meta-analysis. PLoS ONE 2015, 10, e0140833. [Google Scholar] [CrossRef] [PubMed]
- Drescher, M.; Perera, A.H.; Johnson, C.J.; Buse, L.J.; Drew, C.A.; Burgman, M.A. Toward rigorous use of expert knowledge in ecological research. Ecosphere 2013, 4, 1–26. [Google Scholar] [CrossRef]
- Jarnevich, C.S.; Esaias, W.E.; Ma, P.L.A.; Morisette, J.T.; Nickeson, J.E.; Stohlgren, T.J.; Holcombe, T.R.; Nightingale, J.M.; Wolfe, R.E.; Tan, B. Regional distribution models with lack of proximate predictors: Africanized honeybees expanding north. Divers. Distrib. 2014, 20, 193–201. [Google Scholar] [CrossRef]
- Leung, B.; Lodge, D.M.; Finnoff, D.; Shogren, J.F.; Lewis, M.A.; Lamberti, G. An ounce of prevention or a pound of cure: Bioeconomic risk analysis of invasive species. Proc. R. Soc. Lond. Ser. B-Biol. Sci. 2002, 269, 2407–2413. [Google Scholar] [CrossRef] [PubMed]
- American Moving and Storage Association. Gypsy Moths: Remove before You Move. Available online: https://www.moving.org/home/moving-101/gypsy-moths-remove-before-you-move/ (accessed on 29 November 2018).
- U.S. Department of Agriculture, Animal and Plant Health Inspecton Service. Your Move Gypsy Moth Free. Available online: https://www.aphis.usda.gov/aphis/resources/pests-diseases/hungry-pests/the-threat/gypsy-moth-free/ (accessed on 29 November 2018).
| Predictor | Description | Value Range | Source |
|---|---|---|---|
| Distance from STS 1 | Euclidean distance from a historical merge of STS action areas dating from 2005–2016. “Distance from the spread front”. | 0–1,032,550 m | Slow the Spread |
| Distance From Prior Year Source Population 1 | Euclidean distance of current year detection from previous year’s population source (≥3 moths in a trap). Functions as a basic spread kernel. | 0–1,097,132 m | APHIS PPQ |
| Traffic Volume (20-mile moving window) 2 | Traffic volume was selected for highways/interstates and queried on directionality of gypsy moth spread (west/south). Within quarantine bounds, the maximum traffic volume was used regardless of direction. Volumes were interpolated over a 20-mile moving window to represent multiple highway introduction potential within urban areas. “NoData” values were reclassed to zero. | 0–207,028 AADT (or equivalent metric) | TrafficMetrix |
| Road Density 2 | Developed from rasterized 2003 TeleAtlas Dynamap /Transportation v. 5.2 for each state at 100 m. Density was calculated by summing the number of 100 m road pixels within a 1 km pixel and standardized to a 0–100 scale. | 0–100 | US Forest Service FHAAST |
| Address Forwards 2 | Summary of the number of United States Postal Service (USPS) address forwards originating from zipcodes within the gypsy moth quarantine area to that destination census tracts for a two-year period. Forwarding data was compiled by USPS from January 2012–December 2014, and provided to USDA/APHIS under a memorandum of understanding. “NoData” values were reclassed to zero. | 0–14,332 forwards per census tract | US Postal Service |
| Median Household Income 2 | 12 months (2012) median household income reported on census tract level and joined to 2011 U.S. Census TIGER tracts boundaries. “NoData” values were reclassed to zero. | $0–$250,000 | US Census Bureau, American Commodity Survey. |
| Population Density 2 | Population density reported by block group, and joined to 2010 TIGER census block boundaries. | 0–732,314 people/ square mile | 2010 Census, US Census Bureau |
| Distance From Campgrounds 2 | Euclidean distance from campgrounds identified by federal and state cooperators, or compiled by APHIS from federal, state, and private data sources. | 0–83,451 m | ReserveAmerica, APHIS PPQ, USCampgrounds.info |
| Distance From Nurseries 2 | Euclidean distance from regulated nurseries (wholesale and retail). | 0–1,080,628 m | APHIS PPQ |
| Distance From Intermodal Facilities 2 | Euclidean distance from intermodal facilities, where commodities exchange modes of transportation (road, rail, sea port, etc.) | 0–1,081,072 m | Bureau of Transportation Statistics, NTAD 2012 |
| Distance From Weigh Stations 2 | Euclidean distance from weigh stations. | 0 – 1,128,904 m | POI-Factory.com |
| Distance From Military Bases 2 | Euclidean distance from military bases. | 0–1,079,191 m | Bureau of Transportation Statistics, NTAD 2012 |
| Distance From Rest Stops 2 | Euclidean distance from rest stops. | 0–1,111,864 m | POI-Factory.com |
| Distance From Saw Mills 2 | Euclidean distance from primary sawmills. | 0–1,356,683 m | US Forest Service, Southern Research Station 2005 |
| Distance From Universities 2 | Euclidean distance from universities. | 0–1,085,964 m | ArcGIS Online, 2010 |
| Distance From Wood Pallet Manufacturers 2 | Euclidean distance from wood pallet manufacturers. | 0–1,079,592 m | Hoovers, NAICS code 321920, pulled December 2013 |
| Year | Relative Importance | Variable Rank | Accumulated Data (# Years) |
|---|---|---|---|
| 2015 | 5.9% | 6 | 3 |
| 2016 | 17.36% | 2 | 4 |
| 2018 | 35.76% | 1 | 5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cook, G.; Jarnevich, C.; Warden, M.; Downing, M.; Withrow, J.; Leinwand, I. Iterative Models for Early Detection of Invasive Species across Spread Pathways. Forests 2019, 10, 108. https://doi.org/10.3390/f10020108
Cook G, Jarnevich C, Warden M, Downing M, Withrow J, Leinwand I. Iterative Models for Early Detection of Invasive Species across Spread Pathways. Forests. 2019; 10(2):108. https://doi.org/10.3390/f10020108
Chicago/Turabian StyleCook, Gericke, Catherine Jarnevich, Melissa Warden, Marla Downing, John Withrow, and Ian Leinwand. 2019. "Iterative Models for Early Detection of Invasive Species across Spread Pathways" Forests 10, no. 2: 108. https://doi.org/10.3390/f10020108
APA StyleCook, G., Jarnevich, C., Warden, M., Downing, M., Withrow, J., & Leinwand, I. (2019). Iterative Models for Early Detection of Invasive Species across Spread Pathways. Forests, 10(2), 108. https://doi.org/10.3390/f10020108





