Estimating Fine Root Production from Ingrowth Cores and Decomposed Roots in a Bornean Tropical Rainforest
Abstract
1. Introduction
2. Materials and Methods
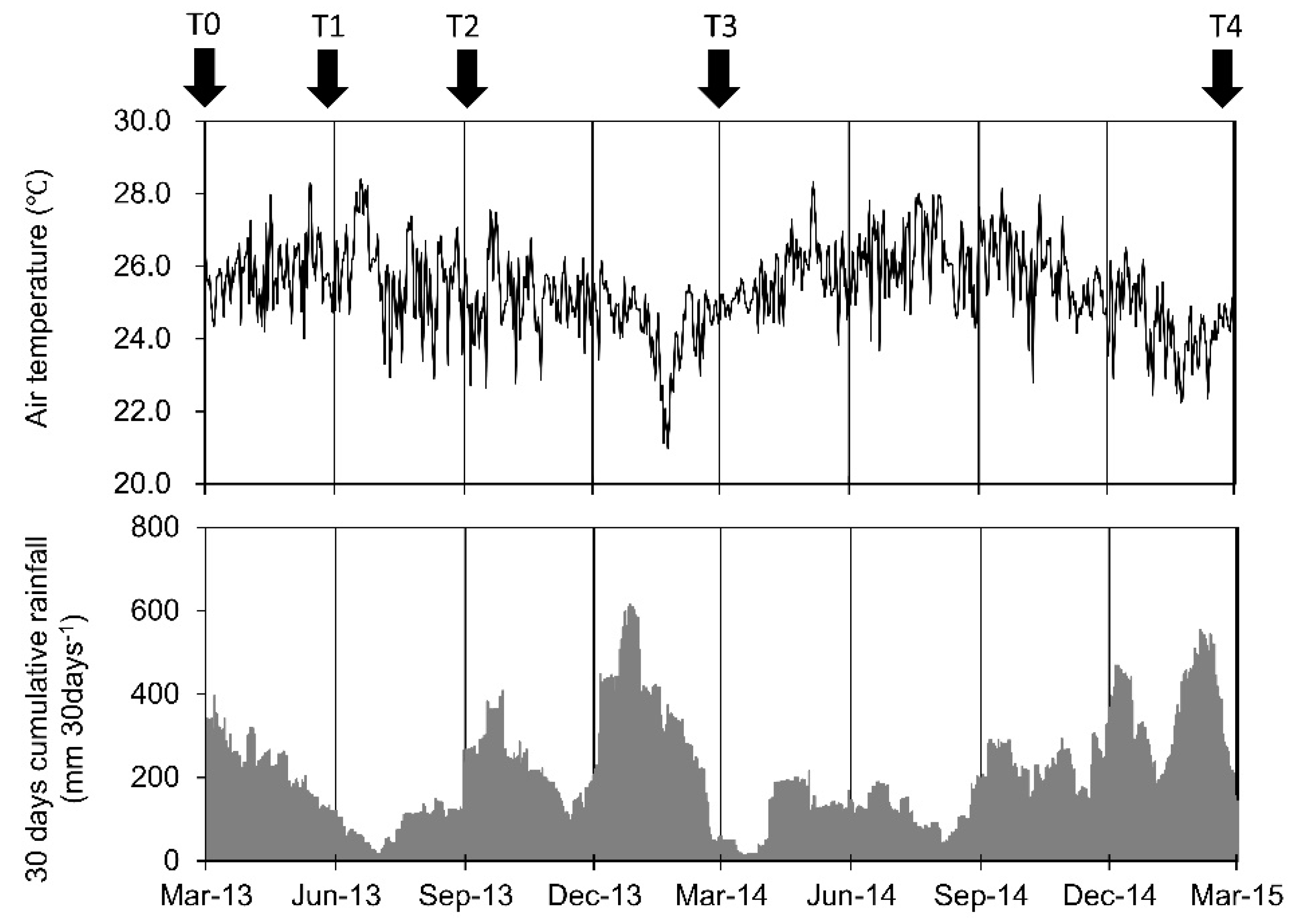
2.1. Study Site
2.2. Measurements
2.3. Methods of calculating FRP
2.4. NPPfr Estimates
2.5. Statistical Analyses
3. Results
3.1. FRP Taking Decomposed Roots into Account
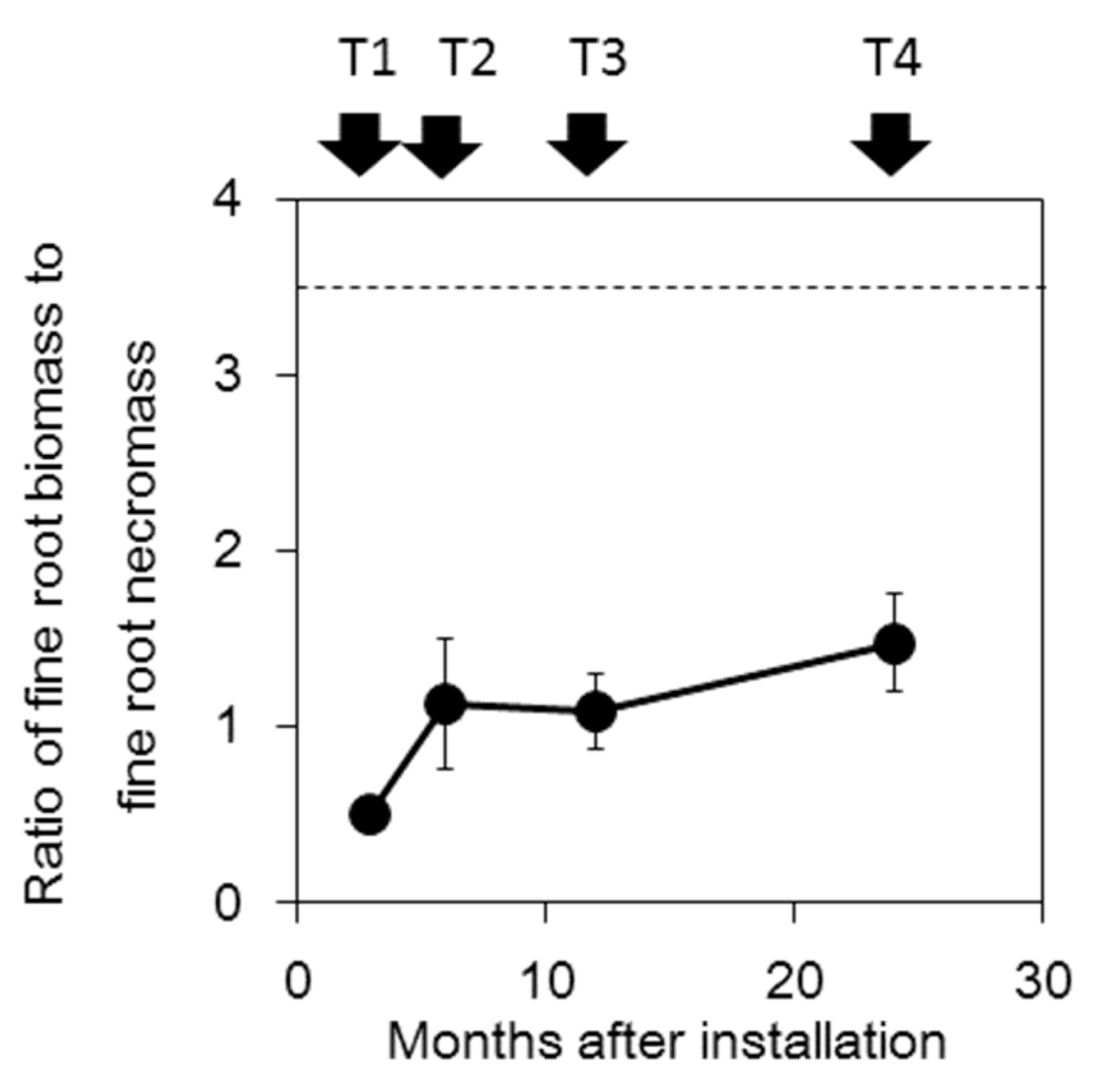
3.2. Biomass Outside and Inside the Cores
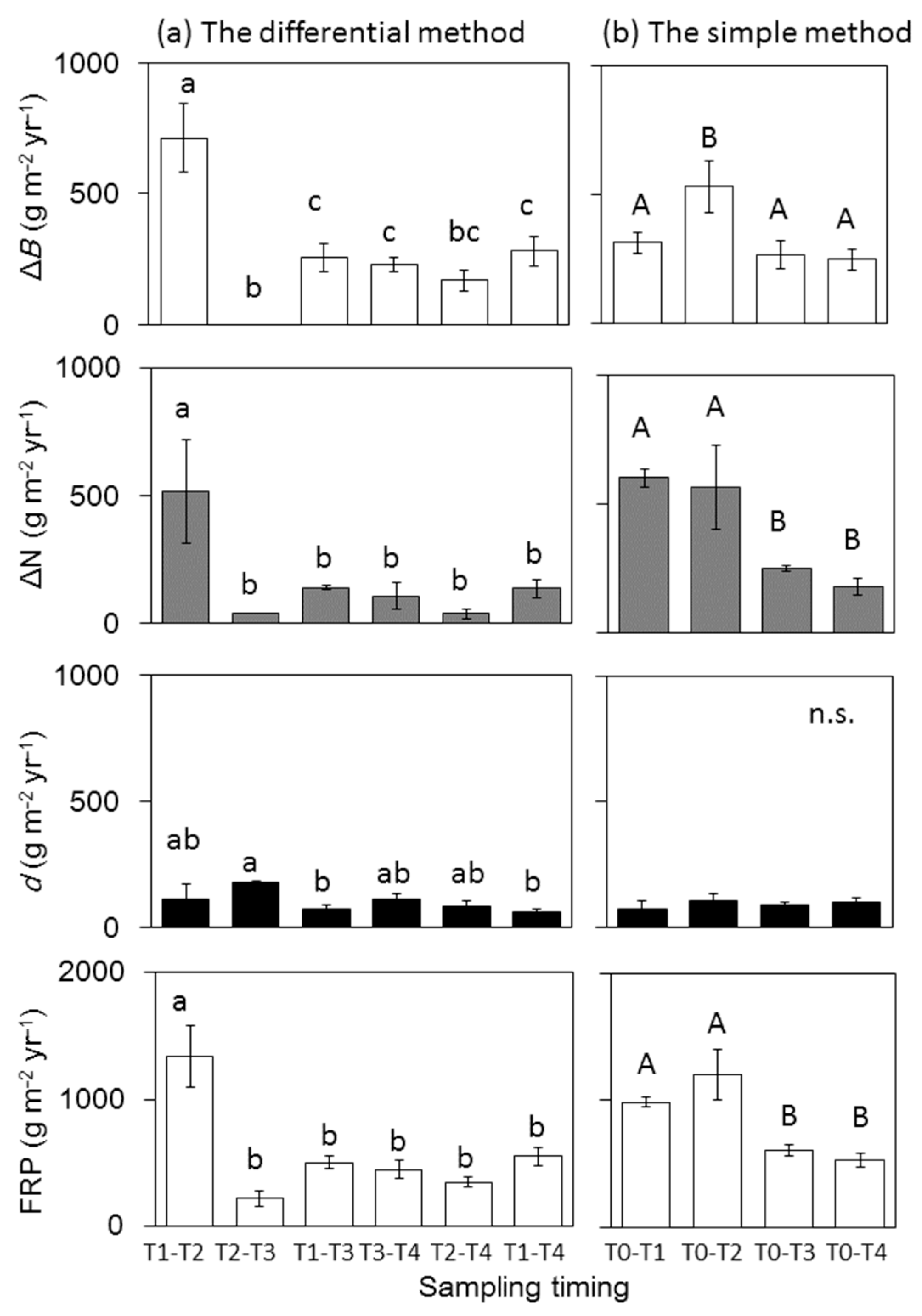
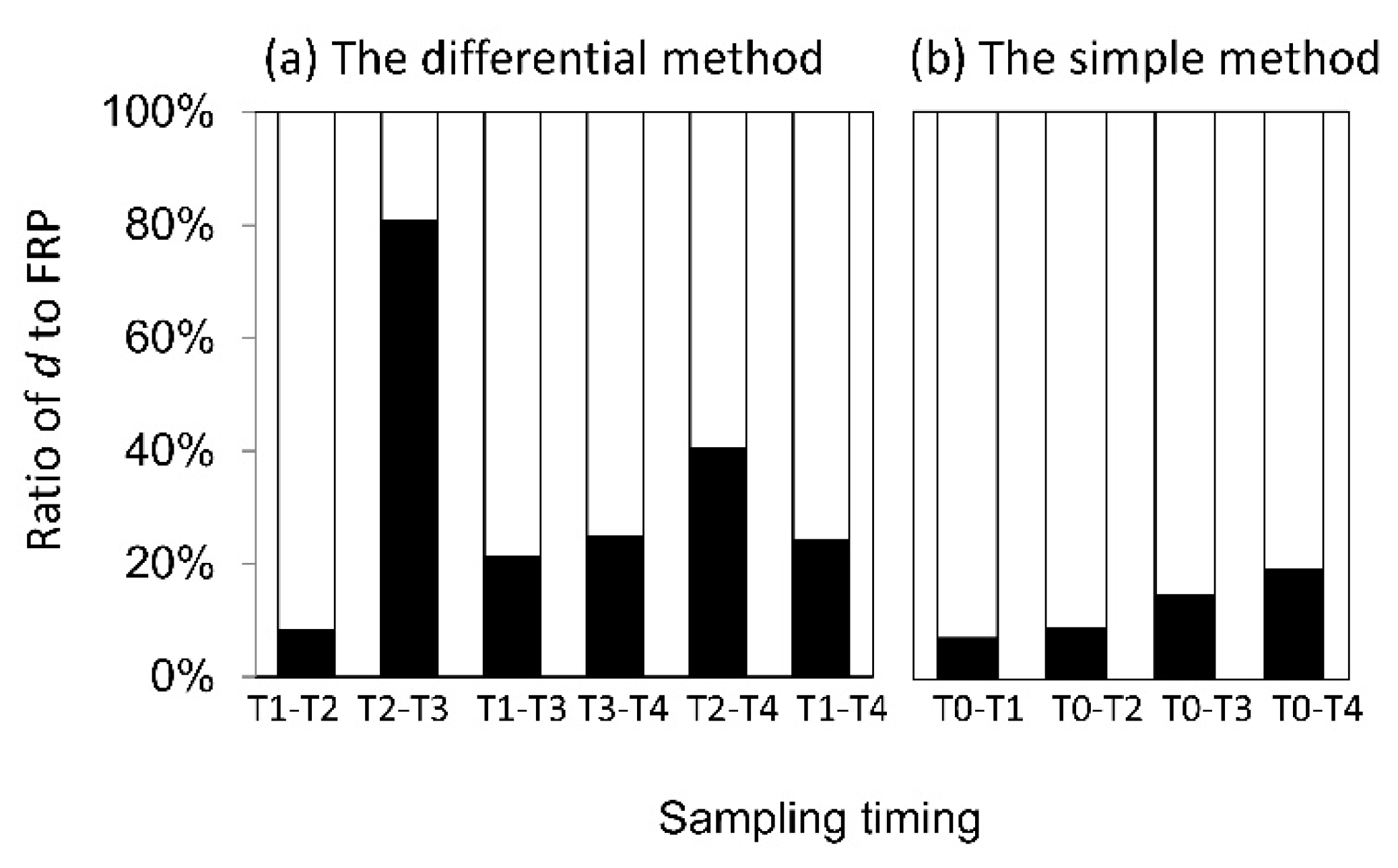
3.3. FRP Estimates Based on Different Sampling Intervals and Calculation Methods
4. Discussion
4.1. Characteristics of d and FRP in the Study Forest
4.2. Impact of Decomposed Fine Roots on FRP Estimates
4.3. Impact of Sampling Interval on FRP Estimates
4.4. Impact of the Calculation Methods on FRP Estimates
4.5. Uncertainties
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Luyssaert, S.; Inglima, I.; Jung, M.; Richardson, A.D.; Reichstein, M.; Papale, D.; Piao, S.L.; Schulze, E.D.; Wingate, L.; Matteucci, G.; et al. CO2 balance of boreal, temperate, and tropical forests derived from a global database. Glob. Change Biol. 2007, 13, 2509–2537. [Google Scholar] [CrossRef]
- Malhi, Y. The productivity, metabolism and carbon cycle of tropical forest vegetation. J. Ecol. 2012, 100, 65–75. [Google Scholar] [CrossRef]
- Finér, L.; Ohashi, M.; Noguchi, K.; Hirano, Y. Fine root production and turnover in forest ecosystems in relation to stand and environmental characteristics. For. Ecol. Manag. 2011, 262, 2008–2023. [Google Scholar] [CrossRef]
- Metcalfe, D.B.; Meir, P.; Aragão, L.E.O.C.; Da Costa, A.C.L.; Braga, A.P.; Gonçalves, P.H.L.; De Athaydes Silva, J., Jr.; de Almeida, S.S.; Dawson, L.A.; Malhi, Y.; et al. The effects of water availability on root growth and morphology in an Amazon rainforest. Plant Soil. 2008, 311, 189–199. [Google Scholar] [CrossRef]
- Kho, L.K.; Malhi, Y.; Tan, S.K.S. Annual budget and seasonal variation of aboveground and belowground net primary productivity in a lowland dipterocarp forest in Borneo. J. Geophys. Res. Biogeosci. 2013, 118, 1282–1296. [Google Scholar] [CrossRef]
- Steele, S.J.; Gower, S.T.; Vogel, J.G.; Norman, J.M. Root mass, net primary production and turnover in aspen, jack pine and black spruce forests in Saskatchewan and Manitoba, Canada. Tree Physiol. 1997, 17, 577–587. [Google Scholar] [CrossRef] [PubMed]
- Ostonen, I.; Lõhmus, K.; Pajuste, K. Fine root biomass, production and its proportion of NPP in a fertile middle-aged Norway spruce forest: Comparison of soil core and ingrowth core methods. For. Ecol. Manag. 2005, 212, 264–277. [Google Scholar] [CrossRef]
- Hendricks, J.J.; Hendrick, R.L.; Wilson, C.A.; Mitchell, R.J.; Pecot, S.D.; Guo, D. Assessing the patterns and controls of fine root dynamics: An empirical test and methodological review. J. Ecol. 2006, 94, 40–57. [Google Scholar] [CrossRef]
- Osawa, A.; Aizawa, R. A new method to estimating fine root production, mortality, and decomposition using litterbag experiments and soil core. Plant Soil. 2012, 355, 167–181. [Google Scholar] [CrossRef]
- Li, X.; Zhu, J.; Lange, H.; Han, S. A modified ingrowth core method for measuring fine root production, mortality and decomposition in forests. Tree Physiol. 2013, 33, 18–25. [Google Scholar] [CrossRef]
- Parton, W.; Silver, W.L.; Burke, I.C.; Grassens, L.; Harmon, M.E.; Currie, W.S. Global-scale similarities in nitrogen release patterns during long-term decomposition. Science 2007, 315, 361–364. [Google Scholar] [CrossRef] [PubMed]
- Vogt, K.A.; Vogt, D.J.; Bloomfield, J. Analysis of some direct and indirect methods for estimating root biomass and production of forests at an ecosystem level. Plant Soil. 1998, 200, 71–89. [Google Scholar] [CrossRef]
- Jourdan, C.; Silva, E.V.; Gonçalves, J.L.M.; Ranger, J.; Moreira, R.M.; Laclau, J.-P. Fine root production and turnover in Brazilian Eucalyptus plantations under contrasting nitrogen fertilization regimes. For. Ecol. Manag. 2008, 256, 396–404. [Google Scholar] [CrossRef]
- Kumagai, T.; Saitoh, T.M.; Sato, Y.; Takahashi, H.; Manfroi, O.J.; Morooka, T.; Kuraji, K.; Suzuki, M.; Yasunari, T.; Komatsu, H. Annual water balance and seasonality of evapotranspiration in a Bornean tropical rainforest. Agric. For. Meteorol. 2005, 128, 81–92. [Google Scholar] [CrossRef]
- Paoli, G.D.; Curran, L.M.; Slik, L.W.F. Soil nutrients affect spatial patterns of aboveground biomass and emergent tree density in southwestern Borneo. Oecologia 2008, 155, 287–299. [Google Scholar] [CrossRef] [PubMed]
- Katayama, A.; Kume, T.; Ohashi, M.; Matsumoto, K.; Nakagawa, M.; Saito, T.; Kumagai, T.; Otsuki, K. Characteristics of wood CO2 efflux in a Bornean tropical rainforest. Agric. For. Meteorol. 2016, 220, 190–199. [Google Scholar] [CrossRef]
- Malhi, Y.; Doughty, C.; Galbraith, D. The allocation of ecosystem net primary productivity in tropical forests. Philos. Trans. Roy. Soc. B 2011, 366, 3225–3245. [Google Scholar] [CrossRef]
- Katayama, A.; Kume, T.; Komatsu, H.; Ohashi, M.; Nakagawa, M.; Yamashita, M.; Otsuki, K.; Suzuki, M.; Kumagai, T. Effect of forest structure on the spatial variation in soil respiration in a Bornean tropical rain forest. Agric. For. Meteorol. 2009, 149, 1666–1673. [Google Scholar] [CrossRef]
- Katayama, A.; Kume, T.; Komatsu, H.; Saitoh, T.; Ohashi, M.; Nakagawa, M.; Suzuki, M.; Otsuki, K.; Kumagai, T. Carbon allocation in a Bornean tropical rainforest without dry seasons. J. Plant Res. 2013, 126, 505–515. [Google Scholar] [CrossRef]
- Ashton, P.S.; Hall, P. Comparisons of structure among mixed dipterocarp forests of north-western Borneo. J. Ecol. 1992, 80, 459–481. [Google Scholar] [CrossRef]
- King, D.A.; Davies, S.J.; Tan, S.; Nur Supardi, M.N. Trees approach gravitational limits to height in tall lowland forests of Malaysia. Funct. Ecol. 2009, 23, 284–291. [Google Scholar] [CrossRef]
- Lee, H.S.; Davies, S.J.; LaFrankie, J.V.; Tan, S.; Yamakura, T.; Itoh, A.; Ohkubo, T.; Ashton, O. Floristic and structural diversity of mixed dipterocarp forests in Lambir Hills National Park, Sarawak, Malaysia. J. Trop. For. Sci. 2002, 14, 379–400. [Google Scholar]
- Ishizuka, S.; Tanaka, S.; Sakurai, K.; Hirai, H.; Hirotani, K.; Ogino, K.; Lee, H.S.; Kedawang, J.J. Characterization and distribution of soils at Lambir Hills National Park in Sarawak, Malaysia, with special reference to soil hardness and soil texture. Tropics 1998, 8, 31–44, (In Japanese with English summary). [Google Scholar] [CrossRef]
- Sakurai, K. Soils and agriculture in Borneo. Tropics 1999, 9, 27–40, (In Japanese with English summary). [Google Scholar] [CrossRef]
- Kume, T.; Tanaka, N.; Kuraji, K.; Komatsu, H.; Yoshifuji, N.; Saitoh, T.M.; Suzuki, M.; Kumagai, T. Ten-year evapotranspiration estimates in a Bornean tropical rainforest. Agric. For. Meteorol. 2011, 151, 1183–1192. [Google Scholar] [CrossRef]
- Makkonen, K.; Helmisaari, H.S. Assessing fine-root biomass and production in a Scots pine stand-comparison of soil core and root ingrowth core methods. Plant Soil. 1999, 210, 43–50. [Google Scholar] [CrossRef]
- Addo-Danso, S.D.; Prescott, C.E.; Smith, A.R. Methods for estimating root biomass and production in forest and woodland ecosystem carbon studies: A review. For. Ecol. Manag. 2016, 359, 332–351. [Google Scholar] [CrossRef]
- Da Costa, A.C.L.; Metcalfe, D.B.; Doughty, C.E.; de Oliveira, A.A.R.; Neto, G.F.C.; da Costa, M.C.; de Athaydes Silva Junior, J.; Aragão, L.E.O.C.; Almeida, S.; Galbraith, D.R.; et al. Ecosystem respiration and net primary productivity after 8–10 years of experimental through-fall reduction in an eastern Amazon forest. Plant Ecol. Div. 2013, 7, 7–24. [Google Scholar] [CrossRef]
- Doughty, C.E.; Metcalfe, D.B.; da Costa, M.C.; de Oliveira, A.A.R.; Neto, G.F.C.; Silva, J.A.; Aragão, L.E.O.C.; Almeida, S.A.; Quesada, C.A.; Girardin, C.A.J.; et al. The production, allocation and cycling of carbon in a forest on fertile terra preta soil in eastern Amazonia compared with a forest on adjacent infertile soil. Plant Ecol. Div. 2013, 7, 41–53. [Google Scholar] [CrossRef]
- Doughty, C.E.; Malhi, Y.; Araujo-Murakami, A.; Metcalfe, D.B.; Silva-Espejo, J.E.; Arroyo, L.; Heredia, J.P.; Pardo-Toledo, E.; Mendizabal, L.M.; RojasLandivar, V.D.; et al. Allocation trade-offs dominate the response of tropical forest growth to seasonal and interannual drought. Ecology 2014, 95, 2192–2201. [Google Scholar] [CrossRef] [PubMed]
- Malhi, Y.; Amezquita, F.F.; Doughty, C.E.; Silva-Espejo, J.E.; Girardin, C.A.J.; Metcalfe, D.B.; Aragao, L.E.O.C.; Huaraca-Quispe, L.P.; Alzamora-Taype, I.; Eguiluz-Mora, L.; et al. The productivity, metabolism and carbon cycle of two lowland tropical forest plots in south-western Amazonia, Peru. Plant. Ecol. Div. 2014, 7, 85–105. [Google Scholar] [CrossRef]
- Malhi, Y.; Doughty, C.E.; Goldsmith, G.R.; Metcalfe, D.B.; Girardin, C.A.; Marthews, T.R.; del Aguila-Pasquel, J.; Aragão, L.E.; Araujo-Murakami, A.; Brando, P.; et al. The linkages between photosynthesis, productivity, growth and biomass in lowland Amazonian forests. Glob. Change Biol. 2015, 21, 2283–2295. [Google Scholar] [CrossRef] [PubMed]
- Malhi, Y.; Aragão, L.E.O.C.; Metcalfe, D.B.; Paiva, R.; Quesada, C.A.; Almeida, S.; Anderson, L.; Brando, P.; Chambers, J.Q.; Costa, A.C.L.; et al. Comprehensive assessment of carbon productivity, allocation and storage in three Amazonian forests. Glob. Change Biol. 2009, 15, 1255–1274. [Google Scholar] [CrossRef]
- Van Do, T.; Sato, T.; Kozan, O. A new approach for estimating fine root production in forests: A combination of ingrowth core and scanner. Trees 2015, 30, 545–554. [Google Scholar] [CrossRef]
- Silver, W.L.; Miya, R.K. Global patterns in root decomposition: Comparisons of climate and litter quality effects. Oecologia 2001, 129, 407–419. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Wang, W. The decomposition of fine and coarse roots: Their global patterns and controlling factors. Sci. Rep. 2015, 5, 9440. [Google Scholar] [CrossRef]
- Litton, C.M.; Giardina, C.P. Below-ground carbon flux and partitioning: Global patterns and response to temperature. Funct. Ecol. 2008, 22, 941–954. [Google Scholar] [CrossRef]
- Hishi, T.; Takeda, H. Life cycles of individual roots in fine root system of Chamaecyparis obtusa Sieb. et Zucc. J. For. Res. 2005, 10, 181–187. [Google Scholar] [CrossRef]
- Cheng, X.; Bledsoe, C.S. Contrasting seasonal patterns of fine root production for blue oaks (Quercus douglasii) and annual grasses in California oak woodland. Plant Soil. 2002, 240, 263–274. [Google Scholar] [CrossRef]
- Ichie, T.; Hiromi, T.; Yoneda, R.; Kamiya, K.; Kohira, M.; Ninomiya, I.; Ogino, K. Short-term drought causes synchronous leaf shedding and flushing in a lowland mixed dipterocarp forest; Sarawak; Malaysia. J. Trop. Ecol. 2004, 20, 697–700. [Google Scholar] [CrossRef]
- Sakai, S.; Harrison, R.D.; Momose, K.; Kuraji, K.; Nagamasu, H.; Yasunari, T.; Chong, L.; Nakashizuka, T. Irregular droughts trigger mass flowering in aseasonal tropical forests in Asia. Am. J. Bot. 2006, 93, 1134–1139. [Google Scholar] [CrossRef] [PubMed]
- Ohashi, M.; Kumagai, T.; Kume, T.; Gyokusen, K.; Saitoh, T.M.; Suzuki, M. Characteristics of soil CO2 efflux variability in a seasonal tropical rainforest in Borneo Island. Biogeochemistry 2008, 90, 275–289. [Google Scholar] [CrossRef]
- Kochsiek, A.; Tan, S.; Russo, S.E. Fine root dynamics in relation to nutrients in oligotrophic Bornean rain forest soils. Plant Ecol. 2013, 214, 869–882. [Google Scholar] [CrossRef]

| NPPfr | NPPacw | NPPlitterfall | NPPtotal | NPPfr/NPPtotal | Reference | |
|---|---|---|---|---|---|---|
| Malaysia, Lambir | 4.25 ± 0.84 | 3.74 ± 0.29 | 3.02 ± 0.36 | 11.01 ± 0.96 | 0.39 | This study, [19] |
| Malaysia, Lambir | 1.96–1.96 | 2.87–4.17 | 5.99–7.89 | 10.82 | 0.18 | [5] |
| Brazil, Caxiuana | 3.89 ± 0.80 | 2.55 ± 0.06 | 2.94 ± 0.04 | 9.38 ± 0.80 | 0.41 | [28] |
| Brazil, Cax06 | 3.68 ± 0.52 | 3.02 ± 0.30 | 5.03 ± 0.07 | 11.73 ± 0.60 | 0.31 | [29] |
| Bolivia, KEN01 | 4.03 ± 0.47 | 5.27 ± 0.31 | 6.20 ± 1.09 | 15.5 ± 1.23 | 0.26 | [30] |
| KEN02 | 3.04 ± 0.34 | 3.61 ± 0.23 | 4.62 ± 0.90 | 11.27 ± 0.99 | 0.27 | |
| Peru, TAM05 | 4.54 ± 0.71 | 2.41 ± 0.24 | 5.39 ± 0.35 | 12.34 ± 0.83 | 0.37 | [31] |
| TAM06 | 2.11 ± 0.31 | 2.49 ± 0.25 | 4.94 ± 0.40 | 9.54 ± 0.56 | 0.22 | |
| ALP01 | 3.02 ± 0.29 | 2.54 ± 0.25 | 4.70 ± 0.86 | 10.26 ± 0.94 | 0.37 | [32] |
| ALP30 | 3.50 ± 0.38 | 2.76 ± 0.28 | 6.42 ± 0.81 | 12.68 ± 0.94 | 0.34 | |
| Average | 3.40 ± 0.87 | 3.13 ± 0.88 | 4.93 ± 1.20 | 11.45 ± 1.79 | 0.31 ± 0.08 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Katayama, A.; Kho, L.K.; Makita, N.; Kume, T.; Matsumoto, K.; Ohashi, M. Estimating Fine Root Production from Ingrowth Cores and Decomposed Roots in a Bornean Tropical Rainforest. Forests 2019, 10, 36. https://doi.org/10.3390/f10010036
Katayama A, Kho LK, Makita N, Kume T, Matsumoto K, Ohashi M. Estimating Fine Root Production from Ingrowth Cores and Decomposed Roots in a Bornean Tropical Rainforest. Forests. 2019; 10(1):36. https://doi.org/10.3390/f10010036
Chicago/Turabian StyleKatayama, Ayumi, Lip Khoon Kho, Naoki Makita, Tomonori Kume, Kazuho Matsumoto, and Mizue Ohashi. 2019. "Estimating Fine Root Production from Ingrowth Cores and Decomposed Roots in a Bornean Tropical Rainforest" Forests 10, no. 1: 36. https://doi.org/10.3390/f10010036
APA StyleKatayama, A., Kho, L. K., Makita, N., Kume, T., Matsumoto, K., & Ohashi, M. (2019). Estimating Fine Root Production from Ingrowth Cores and Decomposed Roots in a Bornean Tropical Rainforest. Forests, 10(1), 36. https://doi.org/10.3390/f10010036





