Plant Electrical Signal Classification Based on Waveform Similarity
Abstract
:1. Introduction
2. Related Works
2.1. Plant Electrical Signal Recognition and Classification
2.2. Time Series Waveform Recognition and Classification
2.2.1. Artifacts Reduction
2.2.2. Recognition of Waveform in Time Series
2.2.3. Features Extraction and Classification
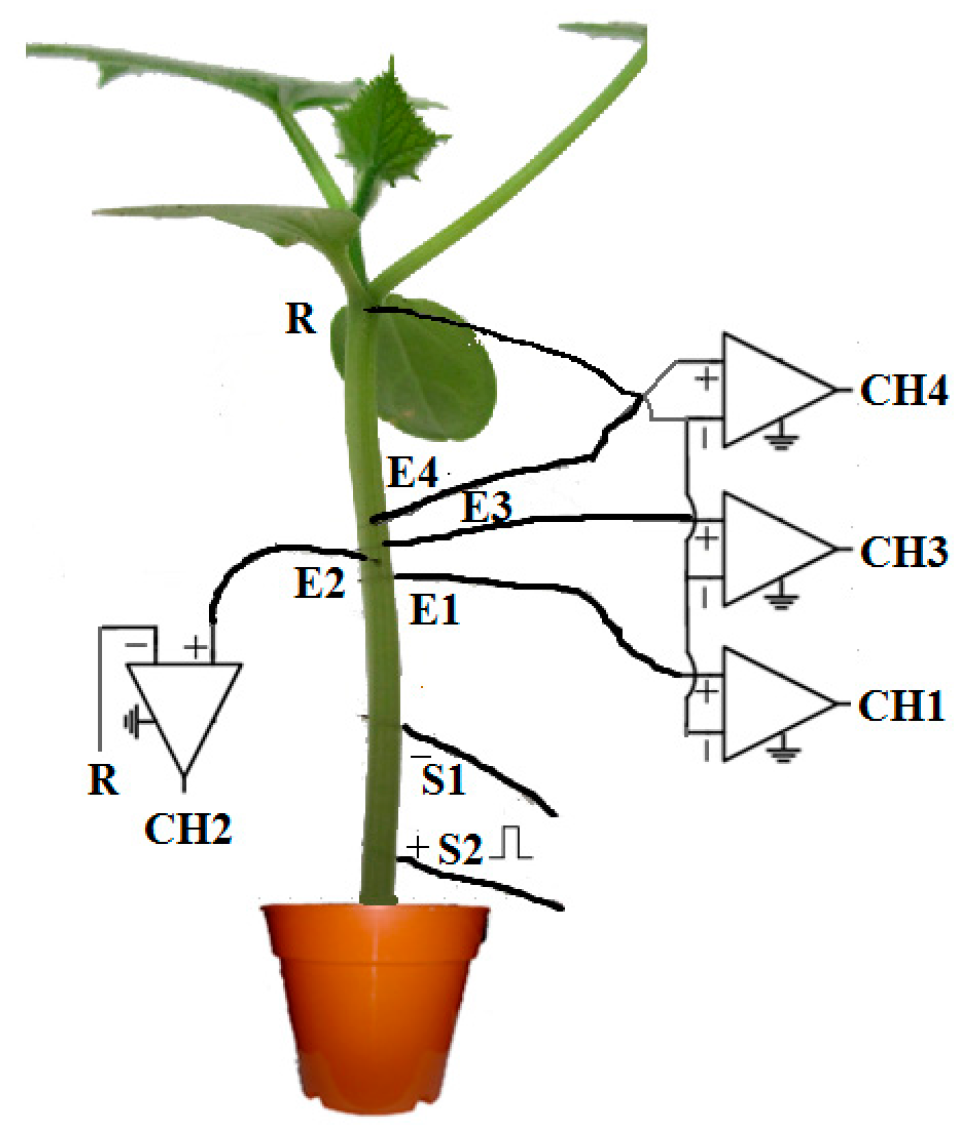
3. Materials and Methods
3.1. Our Proposed Method
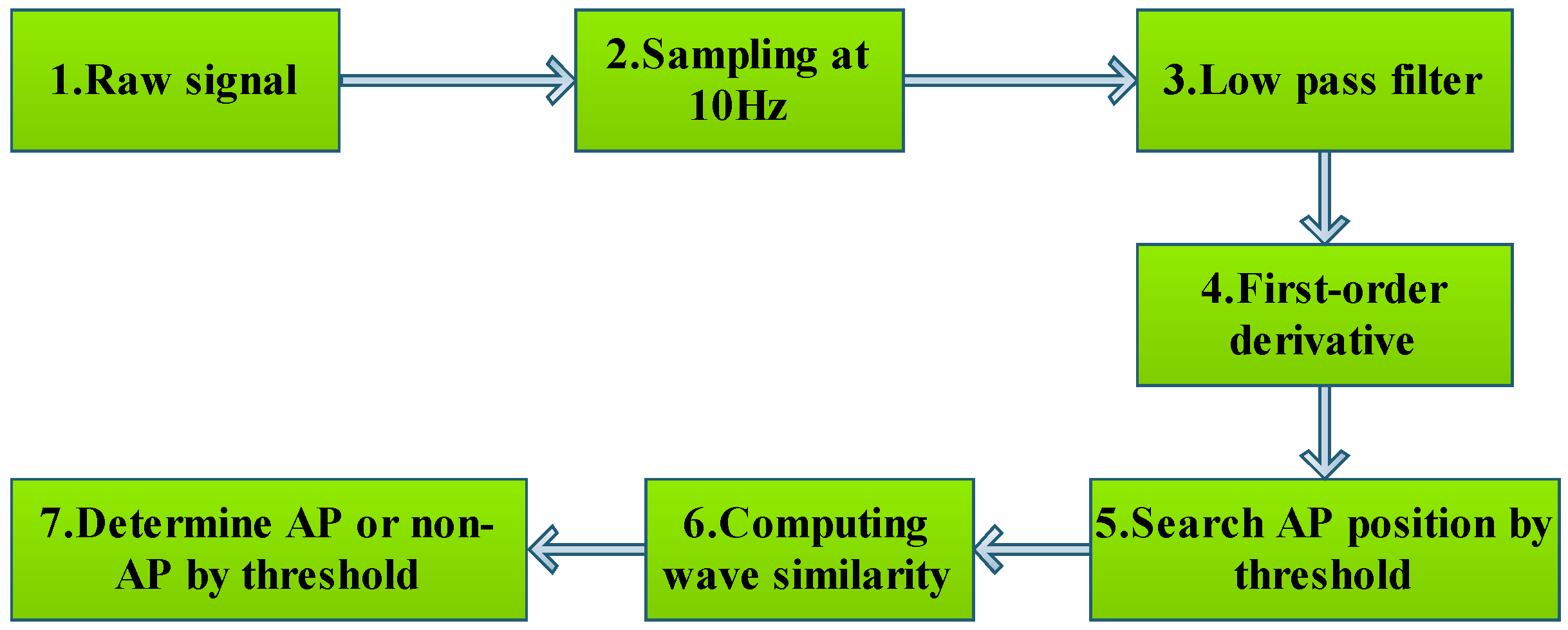
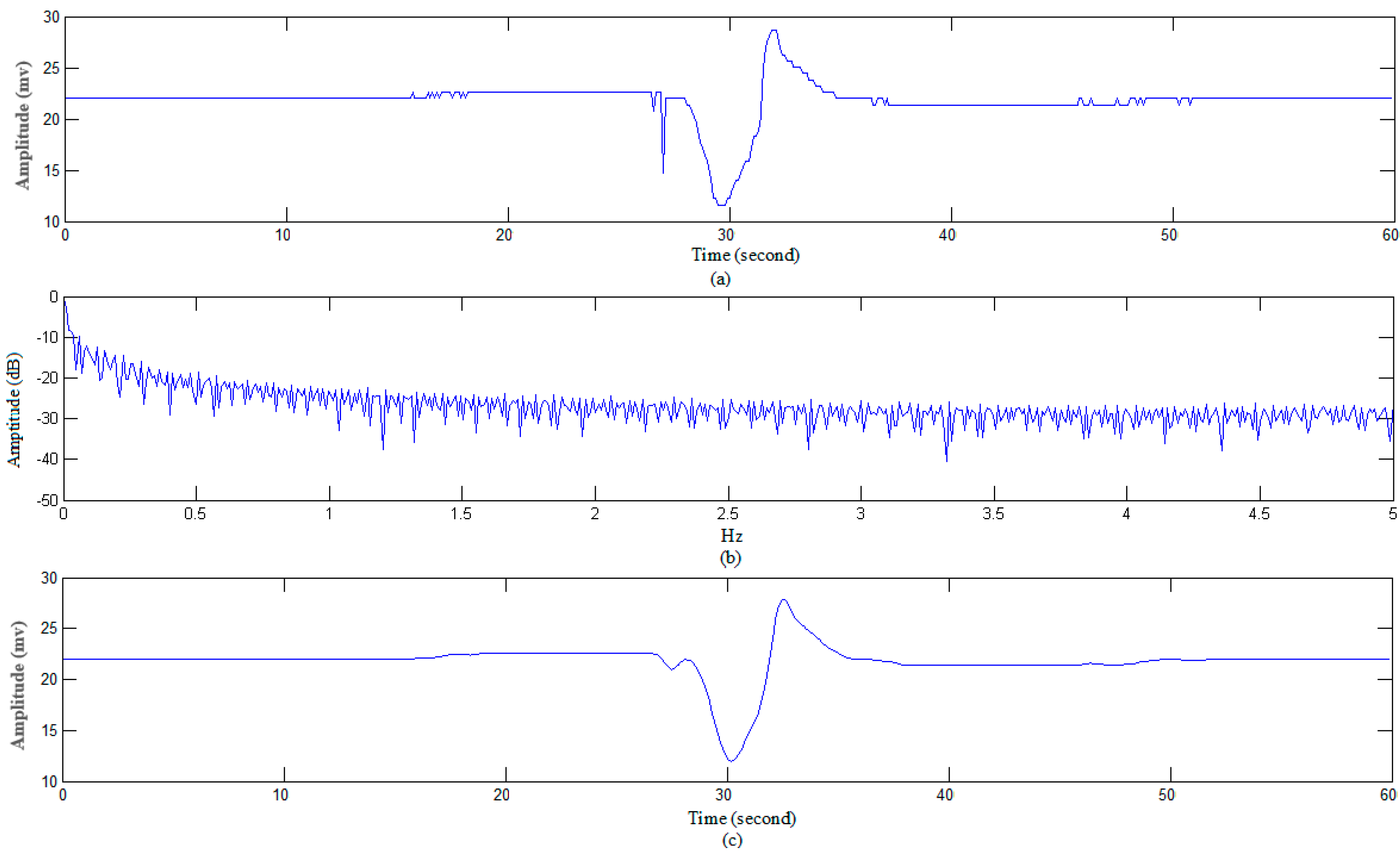
3.1.1. Data Preprocessing
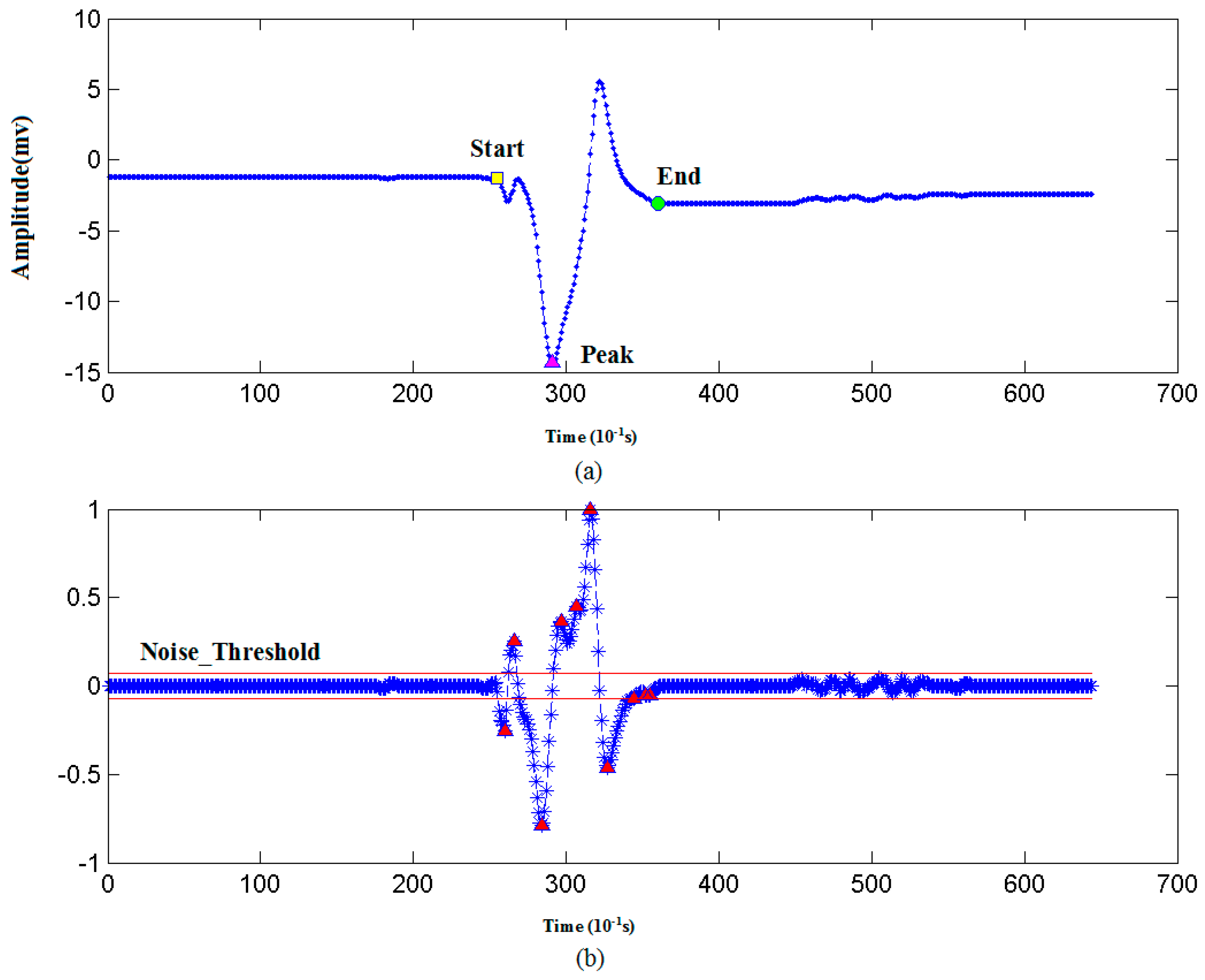
3.1.2. Recognizing Algorithm for Plant Electrical Signals
| Algorithm 1: AP extraction. |
| Input: Raw signal is represented by ST Output: Waveforms similar to AP |
| BEGIN |
| 1. DS = Take derivative of ST by a five order central difference algorithm // Derivative. |
| 2. Noise_Threshold = 0.1 // Initialize noise threshold. |
| 3. PV = findpeaks(DS) // A search algorithm to find the peaks and valleys in DS. |
| 4. For i=1:N // N is the number of peaks or valleys in PV. |
| 5. IF amplitude of PV(i) < Noise_Threshold THEN N_Peaks = PV(i); // If peak amplitude is below Noise_Threshold, then add it into N_Peaks. |
| 6. Else S_Peaks = PV(i); // If peak amplitude is above Noise_Threshold, then add it into S_Peaks. |
| 7. ENDIF |
| 8. END |
| 9. Noise_Threshold = 0.75×Noise_Threshold + 0.25×mean(N_Peaks) // Update noise threshold |
| 10. For i=1:NS //NS is the number of peaks in S_Peaks |
| 11. S_Peaks_left_Position(i) = Search the left part of S_Peaks(i) //Search for start point on the left of S_Peaks(i) |
| 12. S_Peaks_right_Position(i) = Search the right part of S_Peaks(i) // Search for end point on the right of S_Peaks(i) |
| 13. END |
| 14. For i=1:NS-1 //NS is the number of peaks in S_Peaks |
| 15. IF S_Peaks_left_Position(i+1) < S_Peaks_right_Position(i) // For overlap AP signals, separate them by resetting the end position of last AP and start position of next AP. . |
| 16. THEN L = S_Peaks_right_Position(i) - S_Peaks_left_Position(i+1); L1 = L –; L2 = ; S_Peaks_right_Position(i) = S_Peaks_right_Position(i) − L1; S_Peaks_left_Position(i+1) = S_Peaks_left_Position(i+1) + L2 ; |
| 17. ENDIF |
| 18. END |
| 19. For i=1:NS-1 //NS is the number of peaks in S_Peaks |
| 20. IF Amplitude(S_Peaks(i)) < 5 mv&&Duration(S_Peaks(i))<1s // remove the s_peak point if they meet these conditions |
| 21. THEN Remove S_Peaks(i) |
| 22. ENDIF |
| 23. END |
| 24. For i=1:NS’-1 // NS’ is the number of peaks in S_Peaks |
| 25. IF S_Peaks_left_Position(i+1) == S_Peaks_right_Position(i)|| S_Peaks_left_Position(i+1) == S_Peaks_right_Position(i) + 1 // For adjacent monophasic AP signals, merge them into one APs. |
| 26. THEN // Merge the two APs into one AP S_Peaks_right_Position(i) = S_Peaks_right_Position(i+1); Delete S_Peaks(i+1), S_Peaks_left_Position(i+1) and S_Peaks_right_Position(i+1). |
| 27. ENDIF |
| 28. END |
| 29. END |
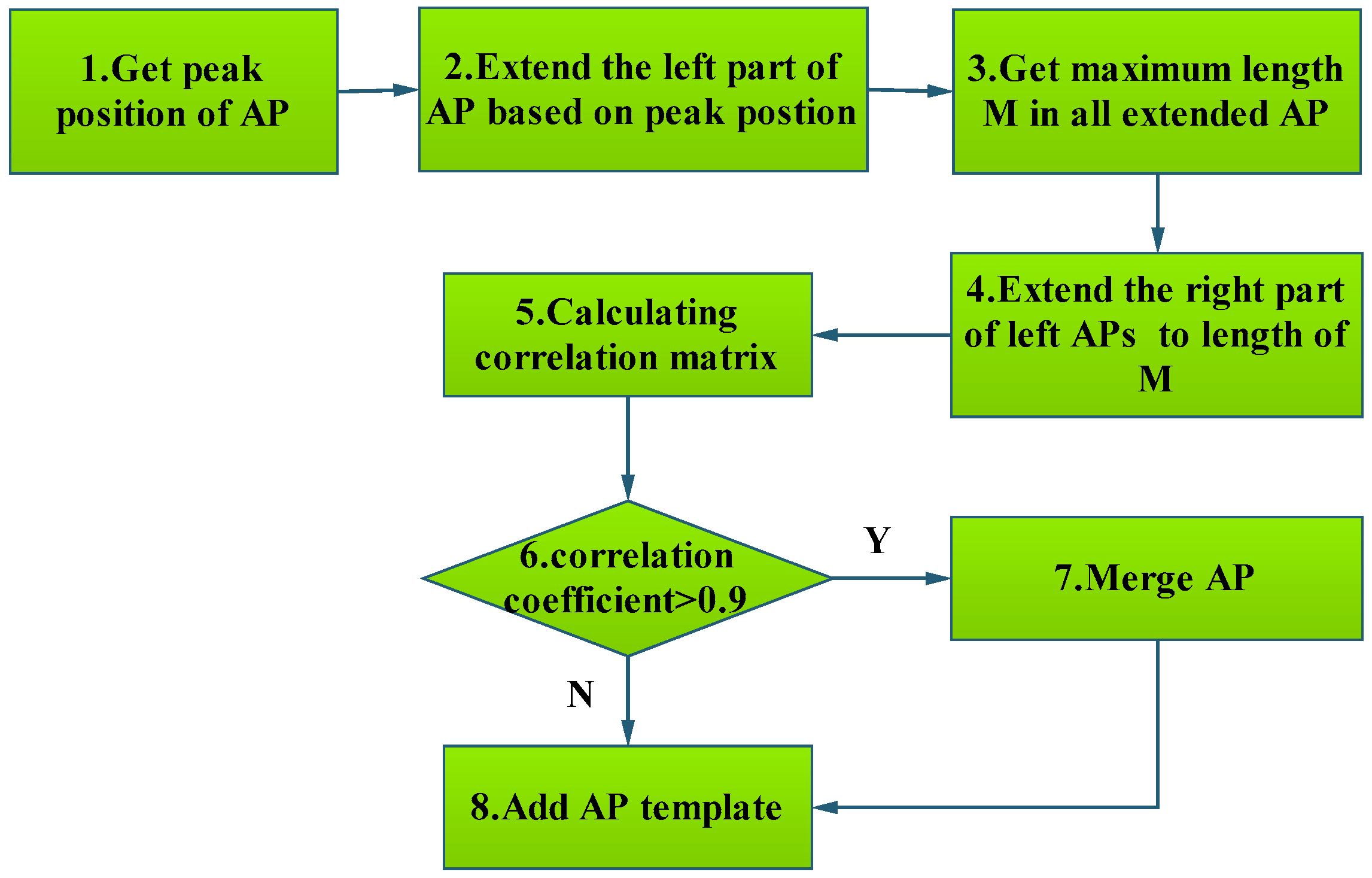
3.1.3. Template Matching Algorithm to Classify AP
| Algorithm 2: Template matching algorithm to classify AP. |
| Input: Raw signal represented by ST, AP template represented by AT in database |
| Output: AP, non-AP |
| 1. Normalize ST and AT // Normalize ST and AT by Equation (2) |
| 2. Align ST with AT // STs are properly aligned with templates |
| Append-Threshold = 0.91; // |
| Update-threshold = 0.95; // |
| 3. corr = Pearson correlation coefficient between ST and AT // Computing PCC |
| 4. IF corr < Append-Threshold |
| ST is not an AP signal, reject it. |
| Return FALSE; |
| ENDIF |
| 5. IF corr> = Append-Threshold && corr < Update-threshold |
| Add ST into APTemp // Add ST into AP Template library |
| Return TURE; |
| ENDIF |
| 6.IF corr >Update-threshold |
| Merge ST with APTemp; |
| Return TURE; |
| ENDIF |
3.1.4. Features Extraction from AP
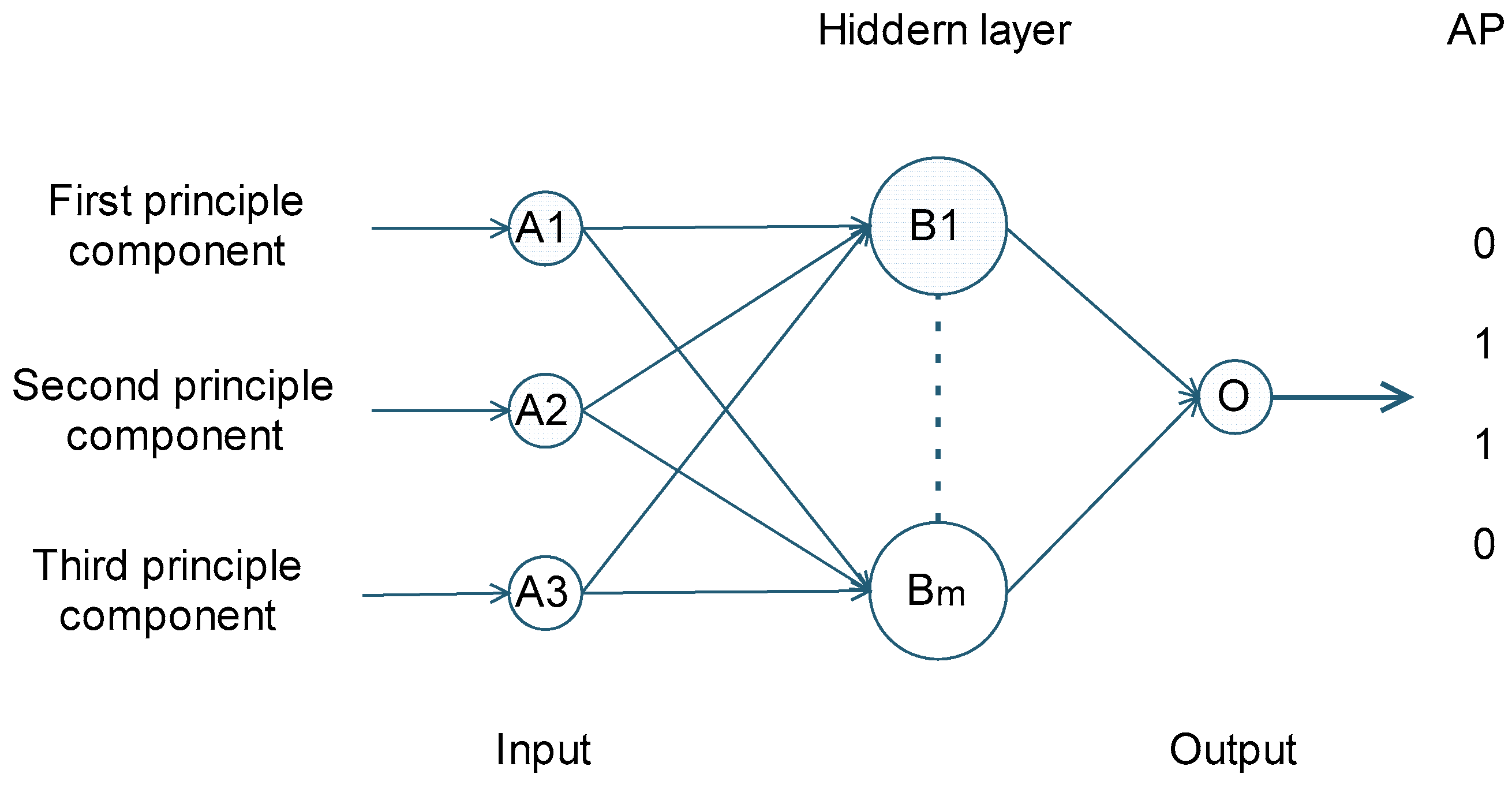
3.2. BP-ANNs
3.3. SVM
3.4. Deep Learning Algorithm
4. Results
4.1. Classification Results of Our Proposed Method
4.1.1. Experimental Data
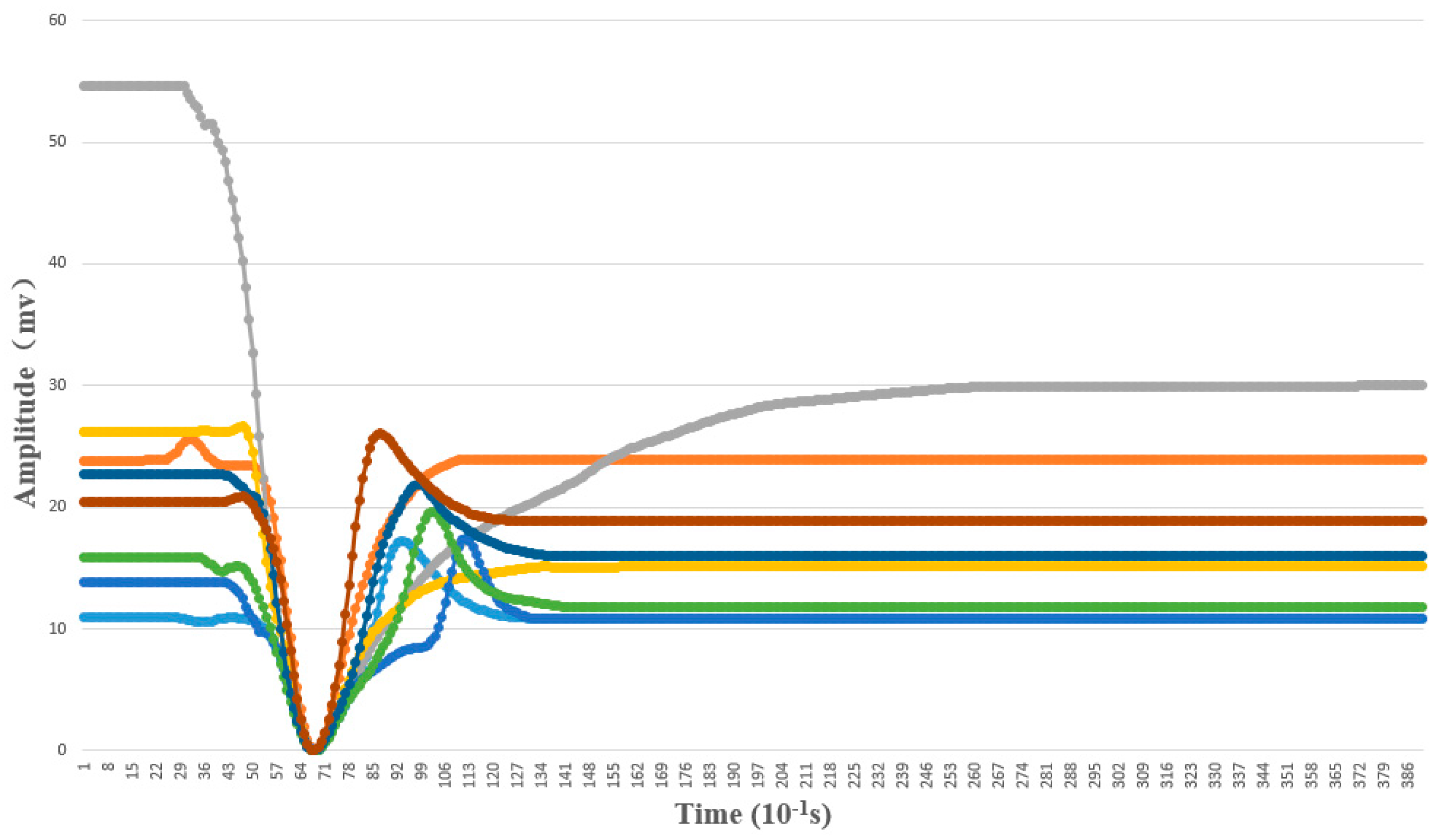
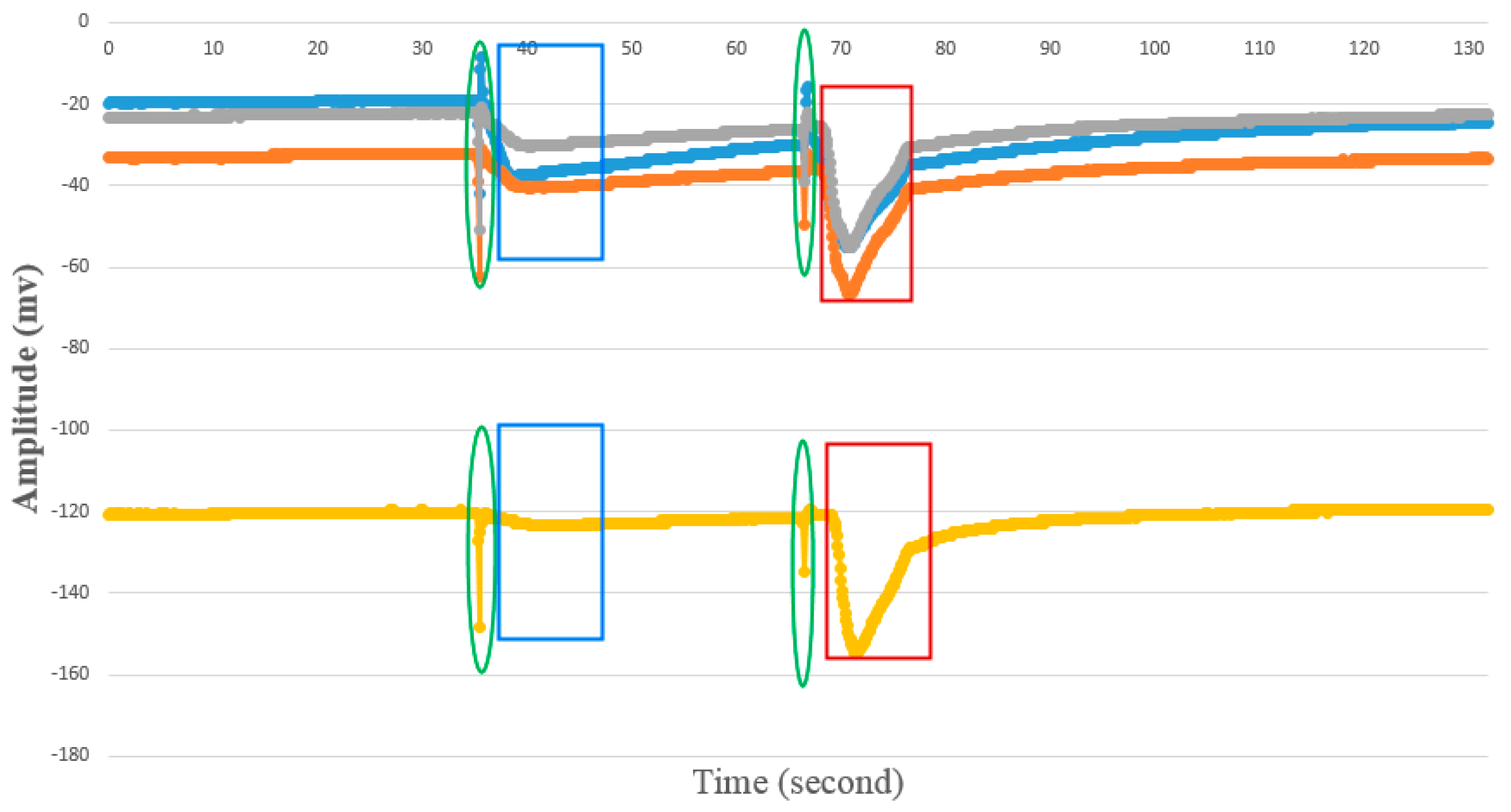
4.1.2. AP Waveform Recognition Results
4.1.3. Template Matching Results
4.1.4. Features of AP waveforms
4.2. Classification Results of BP-ANNs
4.3. Classification Results of SVM
4.4. Classification Results of Deep Learning Method
5. Discussion
6. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Trebacz, K.; Dziubinska, H.; Krol, E. Electrical signals in long-distance communication in plants. In Communication in Plants; Baluska, F., Mancuso, S., Volkmann, D., Eds.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2006; pp. 277–290. [Google Scholar]
- Yan, X.; Wang, Z.; Huang, L.; Wang, C.; Hou, R.; Xu, Z.; Qiao, X. Research progress on electrical signals in higher plants. Prog. Nat. Sci. 2009, 19, 531–541. [Google Scholar] [CrossRef]
- Król, E.; Dziubinska, H.; Trebacz, K. What do plants need action potentials? In Action Potential: Biophysical and Cellular Context, Initiation, Phases and Propagation; Dubois, M.L., Ed.; Nova Science Publisher: New York, NY, USA, 2010; pp. 1–26. [Google Scholar]
- Fromm, J.; Lautner, S. Generation, Transmission, and Physiological Effects of Electrical Signals in Plants. In Plant Electrophysiology-Signaling and Responses; Volkov, A.G., Ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2012; pp. 207–232. [Google Scholar]
- Gallé, A.; Lautner, S.; Flexas, J.; Fromm, J. Environmental stimuli and physiological responses: The current view on electrical signalling. Environ. Exp. Bot. 2015, 114, 15–21. [Google Scholar] [CrossRef]
- Vodeneev, V.A.; Katicheva, L.A.; Sukhov, V.S. Electrical signals in higher plants: Mechanisms of generation and propagation. Biophysical 2016, 61, 505–512. [Google Scholar] [CrossRef]
- Zimmermann, M.R.; Maischak, H.; Mithoefer, A.; Boland, W.; Felle, H.H. System potentials, a novel electrical long-distance apoplastic signal in plants, induced by wounding. Plant Physiol. 2009, 149, 1593–1600. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Sukhov, V.; Nerush, V.; Orlova, L.; Vodeneev, V. Simulation of action potential propagation in plants. J. Theor. Biol. 2011, 291, 47–55. [Google Scholar] [CrossRef] [PubMed]
- Sukhov, V.; Akinchits, E.; Katicheva, L.; Vodeneev, V. Simulation of Variation Potential in Higher Plant Cells. J. Membr. Biol. 2013, 246, 287–296. [Google Scholar] [CrossRef] [PubMed]
- Davies, E. New functions for electrical signals in plants. New Phytol. 2004, 161, 607–610. [Google Scholar] [CrossRef]
- Fromm, J.; Lautner, S. Electrical signals and their physiological significance in plants. Plant. Cell Environ. 2007, 30, 249–257. [Google Scholar] [CrossRef] [PubMed]
- Stahlberg, R.; Stephens, N.R.; Cleland, R.E.; Volkenburgh, E.V. Shade-Induced Action Potentials in Helianthus annuus L. Originate Primarily from the Epicotyl. Plant Signal Behav. 2006, 1, 15–22. [Google Scholar] [CrossRef] [PubMed]
- Favre, P.; Greppin, H.; Agosti, R.D. Accession-dependent action potentials in Arabidopsis. J. Plant Physiol. 2011, 168, 653–660. [Google Scholar] [CrossRef] [PubMed]
- Pavlovic, A.; Slovakova, L.; Pandolfi, C.; Mancuso, S. On the mechanism underlying photosynthetic limitation upon trigger hair irritation in the carnivorous plant Venus flytrap (Dionaea muscipula Ellis). J. Exp. Bot. 2011, 62, 1991–2000. [Google Scholar] [CrossRef] [PubMed]
- Sukhov, V.; Surova, L.; Sherstneva, O.; Katicheva, L.; Vodeneev, V. Variation potential influence on photosynthetic cyclic electron flow in pea. Front. Plant Sci. 2015, 5. [Google Scholar] [CrossRef] [PubMed]
- Krupenina, N.A.; Bulychev, A.A. Action potential in a plant cell lowers the light requirement for non-photochemical energydependent quenching of chlorophyll fluorescence. Biochim. Biophys. Acta 2007, 1767, 781–788. [Google Scholar] [CrossRef] [PubMed]
- Sukhov, V.; Sherstneva, O.; Surova, L.; Katicheva, L.; Vodeneev, V. Proton cellular influx as a probable mechanism of variation potential influence on photosynthesis in pea. Plant. Cell Environ. 2014, 37, 2532–2541. [Google Scholar] [CrossRef] [PubMed]
- Sukhov, V.; Surova, L.; Morozova, E.; Sherstneva, O.; Vodeneev, V. Changes in H+-ATP synthase activity, proton electrochemical gradient, and pH in pea chloroplast can be connected with variation potential. Front. Plant Sci. 2016, 7. [Google Scholar] [CrossRef] [PubMed]
- Lautner, S.; Stummer, M.; Matyssek, R.; Fromm, J.; Grams, T.E.E. Involvement of respiratory processes in the transient knockout of net CO2 uptake in Mimosa pudica upon heat stimulation. Plant. Cell Environ. 2014, 37, 254–260. [Google Scholar] [CrossRef] [PubMed]
- Surova, L.; Sherstneva, O.; Vodeneev, V.; Katicheva, L.; Semina, M.; Sukhov, V. Variation potential-induced photosynthetic and respiratory changes increase ATP content in pea leaves. J. Plant Physiol. 2016, 202, 57–64. [Google Scholar] [CrossRef] [PubMed]
- Grams, T.E.E.; Koziolek, C.; Lautner, S.; Matyssek, R.; Fromm, J. Distinct roles of electric and hydraulic signals on the reaction of leaf gas exchange upon re-irrigation in Zea mays L. Plant. Cell Environ. 2007, 30, 79–84. [Google Scholar] [CrossRef] [PubMed]
- Sukhov, V.; Surova, L.; Sherstneva, O.; Bushueva, A.; Vodeneev, V. Variation potential induces decreased PSI damage and increased PSII damage under high external temperatures in pea. Funct. Plant Biol. 2015, 42, 727–736. [Google Scholar] [CrossRef]
- Maffei, M.E.; Mithofer, A.; Boland, W. Before gene expression: Early events in Plant-insect interaction. Trends Plant Sci. 2007, 12, 310–316. [Google Scholar] [CrossRef] [PubMed]
- Hedrich, R.; Salvador-Recatala, V.; Dreyer, I. Electrical Wiring and Long-Distance Plant Communication. Trends Plant Sci. 2016, 21, 376–387. [Google Scholar] [CrossRef] [PubMed]
- Großkinsky, D.K.; Svensgaard, J.; Christensen, S.; Roitsch, T. Plant phenomics and the need for physiological phenotyping across scales to narrow the genotype-to-phenotype knowledge gap. J. Exp. Bot. 2015, 66, 5429–5440. [Google Scholar]
- Fiorani, F.; Schurr, U. Future Scenarios for Plant Phenotyping. Annu. Rev. Plant Biol. 2013, 64, 267–291. [Google Scholar] [CrossRef] [PubMed]
- Mousavi, S.A.; Chauvin, A.; Pascaud, F.; Kellenberger, S.; Farmer, E.E. Glutamate Receptor-Like genes mediate leaf-to-leaf wound signalling. Nature 2013, 500, 422–426. [Google Scholar] [CrossRef] [PubMed]
- Felle, H.H.; Zimmermann, M.R. Systemic signalling in barley through action potentials. Planta 2007, 226, 203–214. [Google Scholar] [CrossRef] [PubMed]
- Agosti, R.D. Touch-induced action potentials in Arabidopsis thaliana. Arch. Des. Sci. J. 2014, 67, 125–138. [Google Scholar]
- Macedo, F.C.O.; Dziubinska, H.; Trebacz, K.; Oliveira, R.F.; Moral, R.A. Action potentials in abscisic acid-deficient tomato mutant generated spontaneously and evoked by electrical stimulation. Acta Physiol. Plant 2015, 37, 1–9. [Google Scholar] [CrossRef]
- Mancuso, S. Hydraulic and electrical transmission of wound-induced signals in Vitis vinifera. Aust. J. Plant Physiol. 1999, 26, 55–61. [Google Scholar] [CrossRef]
- Stahlberg, R.; Cosgrove, D.J. A reduced xylem pressure altered the electric and growth responses in cucumber hypocotyls. Plant Cell Environ. 2008, 20, 101–109. [Google Scholar] [CrossRef]
- Volkov, A.G.; Adesina, T.; Jovanov, E. Closing of Venus flytrap by electrical stimulation of motor cells. Plant Signal. Behav. 2007, 3, 139–145. [Google Scholar] [CrossRef]
- Van Bel, A.J.E.; Ehlers, K. Electrical Signalling via Plasmodesmata. In Plasmodesmata; Oparka, K.J., Ed.; Blackwell Publishing Ltd.: Oxford, UK, 2005; pp. 263–278. [Google Scholar] [CrossRef]
- Huang, L.; Wang, Z.Y.; Xu, Z.L.; Liu, Z.C.; Zhao, Y.; Hou, R.F.; Wang, C. Design of Multi-channel Monitoring System for Electrical Signals in Plants. Mod. Sci. Instrum. 2006, 4, 45–47. (In Chinese) [Google Scholar]
- Zhao, D.J.; Chen, Y.; Wang, Z.Y.; Xue, L.; Mao, T.L.; Liu, Y.M.; Wang, Z.Y.; Huang, L. High-resolution non-contact measurement of the electrical activity of plants in situ using optical recording. Sci. Rep. 2015, 5, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Parisot, C.; Agosti, R.D. Fast acquisition of action potentials in Arabidopsis thaliana. Arch. Des. Sci. J. 2014, 67, 139–148. [Google Scholar]
- Masi, E.; Ciszak, M.; Stefano, G.; Renna, L.; Azzarello, E.; Pandolfi, C.; Mugnai, S.; Baluška, F.; Arecchi, F.T.; Mancuso, S. Spatiotemporal dynamics of the electrical network activity in the root apex. Proc. Natl. Acad. Sci. USA 2009, 106, 4048–4053. [Google Scholar] [CrossRef] [PubMed]
- Kalovrektis, K.; Th, G.; Antonopoulos, J.; Gotsinas, A.; Shammas, N.Y.A. Development of Transducer Unit to Transmit Electrical Action Potential of Plants to A Data Acquisition System. Am. J. Bioinform. Res. 2013, 3, 21–24. [Google Scholar]
- Gil, P.M.; Gurovich, L.; Schaffer, B.; Alcayaga, J.; Rey, S.; Iturriaga, R. Root to leaf electrical signaling in avocado in response to light and soil water content. J. Plant Physiol. 2008, 165, 1070–1078. [Google Scholar] [CrossRef] [PubMed]
- Salvador-Recatala, V.; Tjallingii, W.F.; Farmer, E.E. Real-time, in vivo recordings of caterpillar-induced waves in sieve elements using aphid electrodes. New Phytol. 2014, 203, 674–684. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.H.; Yu, N.M.; Xi, G.; Meng, X. Changes in the power spectrum of electrical signals in maize leaf induced by osmotic stress. Chin. Sci. Bull. 2012, 57, 413–420. [Google Scholar] [CrossRef]
- Huang, L.; Wang, Z.Y.; Zhao, L.L.; Zhao, D.J.; Wang, C.; Xu, Z.L.; Hou, R.F.; Qiao, X.J. Electrical signal measurement in plants using blind source separation with independent component analysis. Comput. Electron. Agric. 2010, 71, S54–S59. [Google Scholar] [CrossRef]
- Zhao, D.J.; Wang, Z.Y.; Li, J.; Wen, X.; Liu, A.; Huang, L.; Wang, X.D.; Hou, R.F.; Wang, C. Recording extracellular signals in plants: A modeling and experimental study. Math. Comput. Model. 2013, 58, 556–563. [Google Scholar] [CrossRef]
- Aditya, K.; Chen, Y.L.; Kim, E.H.; Udupa, G.; Lee, Y.K. Development of Bio-machine based on the plant response to external stimuli. In Proceedings of the 2011 IEEE International Conference on Robotics and Biomimetics (ROBIO), Shanghai, China, 9–13 May 2011; pp. 1218–1223.
- Yang, R.; Lenaghan, S.C.; Li, Y.F.; Oi, S.; Zhang, M.J. Mathematical Modeling, Dynamics Analysis and Control of Carnivorous Plants. In Plant Electrophysiology; Alexander, G.V., Ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2012; pp. 63–83. [Google Scholar]
- Chatterjee, S.; Das, S.; Maharatna, K.; Masi, E.; Santopolo, L.; Mancuso, S.; Vitaletti, A. Exploring strategies for classification of external stimuli using statistical features of the plant electrical response. J. R. Soc. Interface 2015, 12. [Google Scholar] [CrossRef] [PubMed]
- Chatterjee, S.K.; Ghosh, S.; Das, S.; Manzella, V.; Vitaletti, A.; Masi, E.; Santopolo, L.; Mancuso, S.; Maharatna, K. Forward and Inverse Modelling Approaches for Prediction of Light Stimulus from Electrophysiological Response in Plants. Measurement 2014, 53, 101–116. [Google Scholar] [CrossRef]
- Lanata, A.; Guidi, A.; Baragli, P.; Valenza, G.; Scilingo, E.P. A Novel Algorithm for Movement Artifact Removal in ECG Signals Acquired from Wearable Systems Applied to Horses. PLoS ONE 2015, 10, e0140783. [Google Scholar] [CrossRef] [PubMed]
- Khatun, S.; Mahajan, R.; Morshed, B.I. Comparative Study of Wavelet-Based Unsupervised Ocular Artifact Removal Techniques for Single-Channel EEG Data. IEEE J. Transl. Eng. Health Med. 2016, 4, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Manikandan, M.S.; Soman, K.P. A novel method for detecting R-peaks in electrocardiogram (ECG) signal. Biomed. Signal Process. 2012, 7, 118–128. [Google Scholar] [CrossRef]
- Satija, U.; Ramkumar, B.; Manikandan, M.S. A simple method for detection and classification of ECG noises for wearable ECG monitoring devices. In Proceedings of the Second IEEE International Conference on Signal Processing and Integrated Networks (SPIN), Greater Noida, India, 19–20 February 2015.
- Liu, S.H. Motion artifact reduction in electrocardiogram using adaptive filter. J. Med. Biol. Eng. 2011, 31, 67–72. [Google Scholar] [CrossRef]
- Wessel, J.R. Testing Multiple Psychological Processes for Common Neural Mechanisms Using EEG and Independent Component Analysis. Brain Topogr. 2016. [Google Scholar] [CrossRef] [PubMed]
- Poungponsri, S.; Yu, X.H. An adaptive filtering approach for electrocardiogram (ECG) signal noise reduction using neural networks. Neurocomputing 2013, 117, 206–213. [Google Scholar] [CrossRef]
- Arbateni, K.; Bennia, A. Sigmoidal radial basis function ANN for QRS complex detection. Neurocomputing 2014, 145, 438–450. [Google Scholar] [CrossRef]
- Kabir, M.A.; Shahnaz, C. Denoising of ECG signals based on noise reduction algorithms in EMD and wavelet domains. Biomed. Signal Process. 2012, 7, 481–489. [Google Scholar] [CrossRef]
- Bhateja, V.; Verma, R.; Mehrotra, R.; Urooj, S. A Non-linear Approach to ECG Signal Processing using Morphological Filters. Int. J. Meas. Technol. Instrum. Eng. (IJMTIE) 2013, 3, 46–59. [Google Scholar] [CrossRef]
- Zhang, F.; Lian, Y. QRS Detection Based on Multiscale Mathematical Morphology for Wearable ECG Devices in Body Area Networks. IEEE Trans. Biomed. Circuits Syst. 2009, 3, 220–228. [Google Scholar] [CrossRef] [PubMed]
- Arzeno, N.M.; Deng, Z.D.; Poon, C.S. Analysis of first-derivative based QRS detection algorithms. IEEE Trans. Biomed. Eng. 2008, 55, 478–484. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Shin, H. Simple and Robust Realtime QRS Detection Algorithm Based on Spatiotemporal Characteristic of the QRS Complex. PLoS ONE 2016, 11. [Google Scholar] [CrossRef] [PubMed]
- Riedl, M.; Müller, A.; Wessel, N. Practical considerations of permutation entropy: A tutorial review. Eur. Phys. J. Spec. Top. 2013, 222, 249–262. [Google Scholar] [CrossRef]
- Richman, J.S.; Lake, D.E.; Moorman, J.R. Sample Entropy. Method Enzymol. 2004, 384, 172–184. [Google Scholar]
- Silva, C.; Pimentel, I.R.; Andrade, A.; Foreid, J.P.; Ducla-Soares, E. Correlation Dimension Maps of EEG from Epileptic Absences. Brain Topogr. 1999, 11, 201–209. [Google Scholar] [CrossRef] [PubMed]
- Kocarev, L.; Tasev, Z. Lyapunov exponents, noise-induced synchronization, and Parrondo’s paradox. Phys. Rev. E 2002, 65, 046215. [Google Scholar] [CrossRef] [PubMed]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Stefański, A. Determining Thresholds of Complete Sychronization and Application; World Scientific: Singapore, 2009. [Google Scholar]
- Martinis, M.; Knezević, A.; Krstacić, G.; Vargović, E. Changes in the Hurst exponent of heartbeat intervals during physical activity. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2002, 70, 127–150. [Google Scholar] [CrossRef] [PubMed]
- Martis, R.J.; Acharya, U.R.; Min, L.C. ECG beat classification using PCA, LDA, ICA and Discrete Wavelet Transform. Biomed. Signal Process. 2013, 8, 437–448. [Google Scholar] [CrossRef]
- Mario, S.; Roberta, F.; Alessandro, P.; Sansone, C. Electrocardiogram pattern recognition and analysis based on artificial neural networks and support vector machines: A review. J. Healthc. Eng. 2013, 4, 465–504. [Google Scholar]
- Luz, E.J.S.; Schwartz, W.R.; Cámara-Chávez, G.; Menotti, D. ECG-based heartbeat classification for arrhythmia detection: A survey. Comput. Meth. Prog. Biol. 2016, 127, 144–164. [Google Scholar] [CrossRef] [PubMed]
- Özbay, Y.; Tezel, G. A new method for classification of ECG arrhythmias using neural network with adaptive activation function. Digit. Signal Process. 2010, 20, 1040–1049. [Google Scholar] [CrossRef]
- Shadmand, S.; Mashoufi, B. A new personalized ECG signal classification algorithm using Block-based Neural Network and Particle Swarm Optimization. Biomed. Signal Process. 2016, 25, 12–23. [Google Scholar] [CrossRef]
- Nakai, Y.; Izumi, S.; Nakano, M.; Yamashita, K.; Fujii, T.; Kawaguchi, H.; Yoshimoto, M. Noise tolerant QRS detection using template matching with short-term autocorrelation. In Proceedings of the 36th IEEE Annual International Conference on Engineering in Medicine and Biology Society (EMBC), Chicago, IL, USA, 26–30 August 2014.
- Baumert, M.; Starc, V.; Porta, A. Conventional QT variability measurement vs. template matching techniques: Comparison of performance using simulated and real ECG. PLoS ONE 2012, 7, e41920. [Google Scholar] [CrossRef] [PubMed]
- Saini, I.; Singh, D.; Khosla, A. QRS detection using K -Nearest Neighbor algorithm (KNN) and evaluation on standard ECG databases. J. Adv. Res. 2013, 4, 331–344. [Google Scholar] [CrossRef] [PubMed]
- Das, S.; Ajiwibawa, B.J.; Chatterjee, S.K.; Ghosh, S.; Maharatna, K.; Dasmahapatra, S.; Vitaletti, A.; Masi, E.; Mancuso, S. Drift removal in plant electrical signals via IIR filtering using wavelet energy. Comput. Electron. Agric. 2015, 118, 15–23. [Google Scholar] [CrossRef]
- Pan, J.; Tompkins, W.J. A Real-Time QRS Detection Algorithm. IEEE Trans. Biomed. Eng. 1985, 32, 230–236. [Google Scholar] [CrossRef] [PubMed]
- Favre, P.; Degli Agosti, R. Voltage-dependent action potentials in Arabidopsis thaliana. Physiol. Plant 2007, 131, 263–272. [Google Scholar] [CrossRef] [PubMed]
- Zawadzki, T.; Davies, E.; Bziubinska, H.; Trebacz, K. Characteristics of action potentials in Helianthus annuus. Physiol. Plant 1991, 83, 601–604. [Google Scholar] [CrossRef]
- Dziubinska, H.; Trebacz, K.; Zawadzki, T. Transmission route for action potentials and variation potentials in Helianthus annuus L. J. Plant Physiol. 2001, 158, 1167–1172. [Google Scholar] [CrossRef]
- Salvador, S.; Chan, P. Toward accurate dynamic time warping in linear time and space. Intell. Data Anal. 2007, 11, 561–580. [Google Scholar]
- Sedgwick, P. Pearson’s correlation coefficient. BMJ 2012, 345, e4483. [Google Scholar] [CrossRef]
- Cilimkovic, M. Neural Networks and Back Propagation Algorithm; Institute of Technology Blanchardstown, Blanchardstown Road: North Dublin, Ireland, 2015; Volume 15. [Google Scholar]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Chen, K.; Yang, S.J.; Batur, C. Effect of multi-hidden-layer structure on performance of BP neural network: Probe. In Proceedings of the 2012 Eighth IEEE International Conference on Natural Computation (ICNC), Chongqing, China, 29–31 May 2012.
- Noble, W.S. What is a support vector machine? Nat. Biotechnol. 2006, 24, 1565–1567. [Google Scholar] [CrossRef] [PubMed]
- Lee, L.H.; Wan, C.H.; Rajkumar, R.; Isa, D. An enhanced Support Vector Machine classification framework by using Euclidean distance function for text document categorization. Appl. Intell. 2012, 37, 80–99. [Google Scholar] [CrossRef]
- Chau, A.L.; Li, X.; Yu, W. Support vector machine classification for large datasets using decision tree and Fisher linear discriminant. Future Gener. Comput. Syst. 2014, 36, 57–65. [Google Scholar] [CrossRef]
- Lauzon, F.Q. An introduction to deep learning. In Proceedings of the International Conference on Information Science, Signal Processing and Their Applications, Montreal, QC, Canada, 2–5 July 2012; pp. 1438–1439.
- Längkvist, M.; Karlsson, L.; Loutfi, A. A review of unsupervised feature learning and deep learning for time-series modeling. Pattern Recogn. Lett. 2014, 42, 11–24. [Google Scholar] [CrossRef]
- Hinton, G.E. A Practical Guide to Training Restricted Boltzmann Machines. Momentum 2010, 9, 599–619. [Google Scholar]
- Stankovic, B.; Witters, D.L.; Zawadzki, T.; Davies, E. Action potentials and variation potentials in sunflower: An analysis of their relationship and distinguishing characteristics. Physiol. Plant 1998, 103, 51–58. [Google Scholar] [CrossRef]
| Expression | Definition | Advantages | Disadvantages |
|---|---|---|---|
| Euclidean distance | Calculating the distance of two time series in N-dimensional space | Simple, and supports high-dimensional data | Sensitive to data shift and noise. The length of two time series must be same |
| DTW | DTW is an algorithm for measuring the similarity between two temporal sequences with different length | Estimate the similarity of two time series with unequal length | O(N2) for computing complexity |
| Classification | Feature Parameters |
|---|---|
| Time-domain features (seven items) | Amplitude, Duration, Rising duration, Decline duration, Rising slope, Decline slope, Area |
| Statistics characteristics (five items) | Skewness, Kurtosis, Hjorth: Hjorth activity, Hjorth mobility, Hjorth complexity |
| Frequency-domain features (two items) | Average power, Energy |
| Nonlinear features (five items) | Permutation entropy, Sample entropy, Correlation dimension (CD), LLE, Hurst exponent |
| Append-Threshold | Update-Threshold | Accuracy | The Number of New Templates |
|---|---|---|---|
| 0.89 | 0.95 | 95.4% | 38 |
| 0.9 | 0.95 | 95.4% | 27 |
| 0.91 | 0.95 | 96.0% | 24 |
| 0.92 | 0.95 | 95.7% | 21 |
| 0.93 | 0.95 | 92.1% | 19 |
| 0.94 | 0.95 | 87.5% | 13 |
| 0.95 | 0.96 | 85.4% | 13 |
| Features | Non-AP (Mean ± S.E.M.) | AP (Mean ± S.E.M.) |
|---|---|---|
| Amplitude * (mV) | 14.33 ± 9.90 | 20.57 ± 12.55 |
| Durations * (s) | 8.01 ± 4.35 | 9.75 ± 5.05 |
| Rising duration * (s) | 2.36 ± 1.31 | 3.00 ± 1.62 |
| Decline duration * (s) | 5.75 ± 3.61 | 6.85 ± 4.22 |
| Rising slope * (mv/s) | 6.78 ± 6.19 | 8.42 ± 7.47 |
| Decline slope (mv/s) | 2.64 ± 2.13 | 2.90 ± 2.61 |
| Area | 4749.01 ± 7728.3 | 6078.16 ± 11,038.49 |
| Skewness | −0.57 ± 0.71 | −0.50 ± 0.65 |
| Kurtosis | 2.80 ± 1.33 | 2.70 ± 0.82 |
| Hjorth activity * | 27.27 ± 34.44 | 48.82 ± 54.37 |
| Hjorth mobility * | 0.16 ± 0.10 | 0.14 ± 0.07 |
| Hjorth complexity * | 1.89 ± 0.71 | 2.17 ± 0.91 |
| Energy * | 740,601.4 ± 1,415,709 | 1,207,443 ± 2,076,630 |
| Average power * | 8065.49 ± 15,968.75 | 11,440.17 ± 18,881.54 |
| Permutation entropy | 0.83 ± 0.25 | 0.82 ± 0.19 |
| Sample entropy | 0.05 ± 0.05 | 0.05 ± 0.05 |
| Correlation dimension | 0.75 ± 0.24 | 0.74 ± 0.22 |
| LLE * | −0.07 ± 0.07 | −0.05 ± 0.04 |
| Hurst | 0.99 ± 0.07 | 0.99 ± 0.04 |
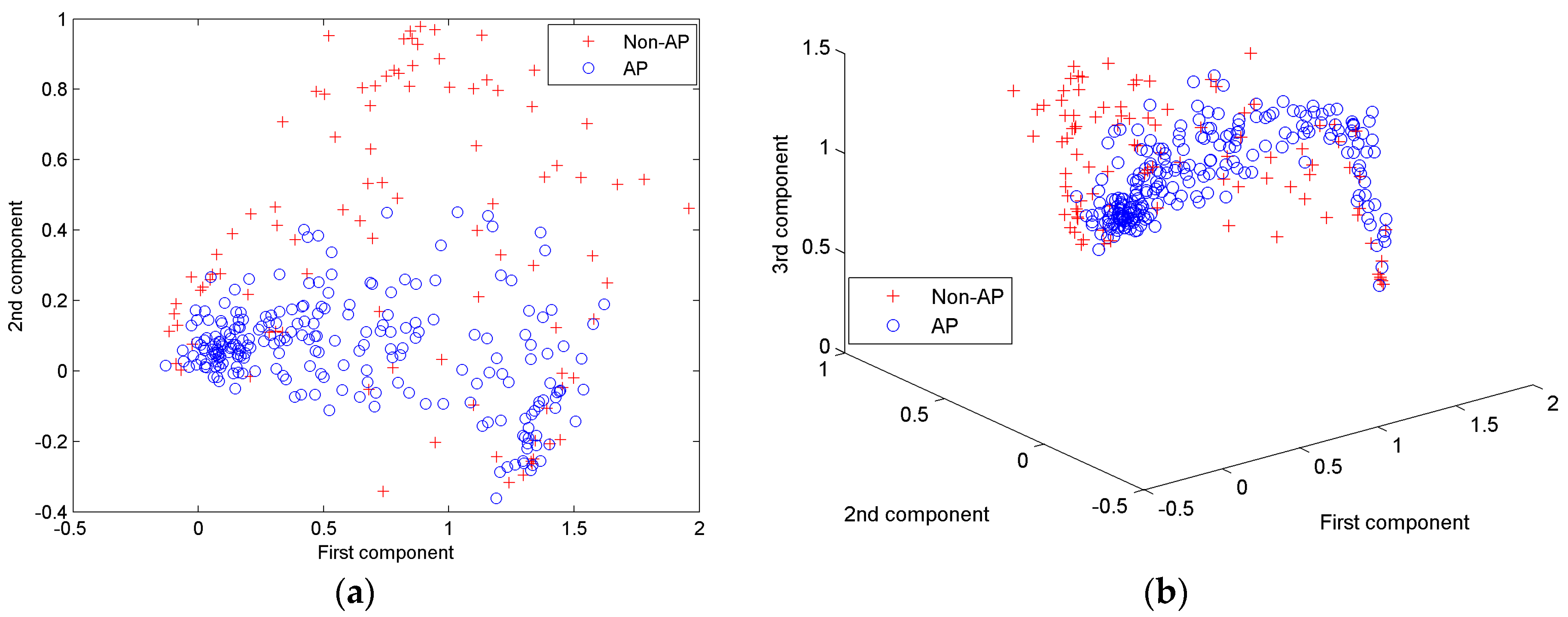
| First Principle Component | Second Principle Component | Third Principle Component | Fourth Principle Component | Fifth Principle Component | |
|---|---|---|---|---|---|
| Eigenvalue | 0.2700 | 0.0770 | 0.0285 | 0.0128 | 0.0078 |
| Percentage | 65.89% | 18.80% | 6.96% | 3.13% | 1.91% |
| Accumulated percentage | 65.89% | 84.68% | 91.65% | 94.78% | 96.69% |
| Units Number | Accuracy | Run Time |
|---|---|---|
| 20 | 79.7% | 2704 s |
| 16 | 84.8% | 5340 s |
| 12 | 81.5% | 34,727 s |
| 8 | 84.1% | 65,664 s |
| 4 | 83.5% | 20,687 s |
| First Principle Component | Second Principle Component | Third Principle Component | Fourth Principle Component | Fifth Principle Component | |
|---|---|---|---|---|---|
| Accuracy | 55.6% | 66.7% | 75.8% | 76.7% | 77.3% |
| Kernel Function | Range of Parameters | Interval | Selected Parameters | Highest Accuracy |
|---|---|---|---|---|
| Quadratic kernel | b = 2 | 0 | b = 2 | 62.96% |
| Polynomial kernel | b = 3 | 0 | b = 3 | 74.07% |
| Gaussian Radial Basis Function | 0.1 | 77.59% | ||
| Sigmoid kernel | 0.1 | c = −0.3 | 78.17% |
| Number of Second Hidden Units | Number of Third Hidden Units | Number of Fourth Hidden Units | Selected Parameters | Highest Accuracy | |
|---|---|---|---|---|---|
| Range | [40, 200] | [8, 24] | [4, 8] | Multiple selections | 77.4% (3 hidden layers) |
| Interval | 40 | 4 | 4 | Multiple selections | 77.4% (4 hidden layers) |
| Classifier | Accuracy | Average Running Time | Sensitivity | Specificity | Positive Predictive Value (PPV) | Negative Predictive Value (NPV) |
|---|---|---|---|---|---|---|
| Template matching | 96.0% | 3.20 s | 96.6% | 94.8% | 97.8% | 91.9% |
| BP neural network | 84.8% | 5340 s | 74.9% | 52% | 89.7% | 27.1% |
| SVM | 78.2% | 2.1 s | 89.5% | 95.8% | 98.7% | 7.2% |
| DBN | 77.4% | 112.06 s | 100% | 0 | 70.8% | 0 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Zhao, D.-J.; Wang, Z.-Y.; Wang, Z.-Y.; Tang, G.; Huang, L. Plant Electrical Signal Classification Based on Waveform Similarity. Algorithms 2016, 9, 70. https://doi.org/10.3390/a9040070
Chen Y, Zhao D-J, Wang Z-Y, Wang Z-Y, Tang G, Huang L. Plant Electrical Signal Classification Based on Waveform Similarity. Algorithms. 2016; 9(4):70. https://doi.org/10.3390/a9040070
Chicago/Turabian StyleChen, Yang, Dong-Jie Zhao, Zi-Yang Wang, Zhong-Yi Wang, Guiliang Tang, and Lan Huang. 2016. "Plant Electrical Signal Classification Based on Waveform Similarity" Algorithms 9, no. 4: 70. https://doi.org/10.3390/a9040070
APA StyleChen, Y., Zhao, D.-J., Wang, Z.-Y., Wang, Z.-Y., Tang, G., & Huang, L. (2016). Plant Electrical Signal Classification Based on Waveform Similarity. Algorithms, 9(4), 70. https://doi.org/10.3390/a9040070






