A New Fuzzy Harmony Search Algorithm Using Fuzzy Logic for Dynamic Parameter Adaptation

Abstract

In this paper, a new fuzzy harmony search algorithm (FHS) for solving optimization problems is presented. FHS is based on a recent method using fuzzy logic for dynamic adaptation of the harmony memory accepting (HMR) and pitch adjustment (PArate) parameters that improve the convergence rate of traditional harmony search algorithm (HS). The objective of the method is to dynamically adjust the parameters in the range from 0.7 to 1. The impact of using fixed parameters in the harmony search algorithm is discussed and a strategy for efficiently tuning these parameters using fuzzy logic is presented. The FHS algorithm was successfully applied to different benchmarking optimization problems. The results of simulation and comparison studies demonstrate the effectiveness and efficiency of the proposed approach.

1. Introduction

In the literature, there is a wide variety of metaheuristic algorithms and this paper focuses on one of them, the harmony search algorithm (HS), which, as its name suggests, is inspired by music. In particular, it refers to jazz behavior of a musical orchestra, where the goal is to compose the most harmonious melody, as measured by aesthetic standards [1]. The HS method considers the following mathematical form that basically consists of three steps: harmony memory accepting (HMR), pitch adjusting (PArate) and randomization. The model is inspired by a musical orchestra. Musicians have three options to play tunes: the first is to play any melody that is already known in the memory; the second is to start playing a song that already exists and to adjust the tone as the melody progresses; and the third option is to play a tune at random that was never played before. The three steps mentioned above are essential to achieve optimal results for addressing a particular problem since each of them has a specific function, whether it is to explore or exploit the search space, thereby avoiding local optima and finding the global optimum. HS has many advantages over other algorithms: (a) it does not require complex calculations; (b) because the HS algorithm uses stochastic random search, derivative information is also unnecessary, although HS uses different concept derivatives based on human experiences [2]; and (c) it can be used in linear and nonlinear functions. The harmony search algorithm has been very successful in a wide variety of optimization problems, presenting several advantages with respect to traditional optimization techniques, as outlined in the following [3,4,5]. However, HS also has disadvantages, as is the case for all algorithms that move the parameters by trial and error—they can fall into local optima. Therefore, this paper presents a new method called fuzzy harmony search algorithm (FHS), which uses fuzzy logic for dynamically changing the algorithm parameters and thereby exploring and exploiting the search space at the right time in order to obtain the global optimum in the shortest possible time. Several fuzzy systems are used to perform dynamical parameter adaptation. The main scientific contribution in this paper is that currently there are methods and variants on the harmony search algorithm that use techniques to move its parameters, such as linear functions, statistical methods and other methods that help improve the convergence of the algorithm among others, but there is no method in the literature which adjusts the parameters using fuzzy logic. This is therefore the main scientific contribution, which is based on the study of parameters and performing experiments by trial and error, and in this way finding the best ranges for the outputs of the membership functions and fuzzy rules.

In addition, a set of experiments was carefully performed to reveal the impact of control parameters when applied to benchmark mathematical functions, and a comparison with another method called the fuzzy bat algorithm [6] is presented.

Similarly, there are papers on harmony search algorithm (HS) applications that use this algorithm to solve real world problems. To mention a few: self-adaptive harmony search algorithm for optimization [7] and a tabu harmony search-based approach to fuzzy linear regression [8], two improved harmony search algorithms for solving engineering optimization problems [9], combined heat and power economic dispatch by harmony search algorithm [5], a novel hybrid bat algorithm with harmony search for global numerical optimization [10], a hybrid Taguchi-harmony search algorithm for solving engineering optimization problems [11], and a dynamic multi-swarm particle swarm optimizer with harmony search [12].

There are also papers of different metaheuristic algorithms that could be considered as related work, including the firefly algorithm [13,14], the bat-inspired algorithm [15], differential evolution [16], virtual bee algorithms [17], hybridization of Particle swarm optimization (PSO) and Genetic Algorithms (GA) [18], fuzzy Particle swarm algorithm—a generalization of particle swarm optimization [19], and design of PSO-based fuzzy classification system [20].

The rest of the paper is organized as follows: Section 2 shows the methodology for parameter adaptation and describes the proposed methods. Section 3 shows the experimentation with the fuzzy system and benchmark mathematical functions. Section 4 presents simulation results and a comparison of the harmony search algorithm with fuzzy harmony search algorithm. Section 5 presents simulation results and a comparison of the fuzzy harmony search algorithm with the fuzzy bat algorithm. Section 6 offers a statistical comparison. Finally, Section 7 describes the conclusions.

2. Methodology for Parameter Adaptation

Harmony search is relatively a new metaheuristic optimization algorithm inspired by music and was first proposed by Geem et al. in 2001 [1,21,22]. The HS algorithm is defined by Equations (1)–(3), which are the equations to control the exploitation and exploration of the search domain, respectively [10].

$$HMR\in \left[0,1\right]$$

(1)

$$x_{new}=x_{old}+b_p\left(2 rand-1\right)$$

(2)

$$P_a= P_{lower limit}+P_{range}\times rand$$

(3)

The HMR and PArate parameters introduced in the improvisation process help the algorithm to find globally and locally improved solutions. The traditional HS algorithm uses fixed values for the HMR and PArate parameters whereas the improvement suggested in [23] varies the PArate and bandwidth (bw) parameters throughout the iterations. Inspired by their modification, the paper presents a new fuzzy harmony search algorithm (FHS).

Mathematical Description of the Fuzzy Harmony Search (FHS) Algorithm

The mathematical description for FHS is defined as follows: Equation (1) shows the fundamental part of the traditional HS algorithm; where the harmony memory accepting (HMR) is represented by a constant value. Equation (2) shows the fundamental part of the traditional HS algorithm, where the pitch adjusting (PArate) is represented by a constant value. Equations (1) and (2) describe the different ways the basic equations of HS are modified for achieving the goal, and then, convert part of it into fuzzy parameters. The differences between both equations are that HMR in Equation (1) and PArate in Equation (2) are those that change, because an essential part of the proposed method lies in these two parameters. Traditionally, these two parameters are constant; in this case, due to the importance of these two parameters, they are converted into fuzzy parameters. Therefore, for designing the fuzzy systems, which dynamically adjust the HMR and PArate parameters, the measure of percentage of iterations is considered as the input. All the fuzzy systems are of Mamdani type because it is more common to use them in this type of fuzzy control and the defuzzification method is the centroid. In this case, this type of defuzzification was used because other researchers have achieved good results with this method.

In this case, these values are considered fuzzy because they are changing dynamically when the FHS is running, and are defined by Equations (4) and (5), where HMR and PArate are changing values in the range [0,1].

$$HMR= \frac{{{\displaystyle \sum }}_{i=1}^{r_{hmr}}{\mu }_i^{hmr} \left(hm{r}_{1i}\right)}{{{\displaystyle \sum }}_{i=1}^{r_{hmr}}{\mu }_i^{hmr}}$$

(4)

where HMR is the harmony memory accepting rate; $r_{hmr}$ is the number of rules of the fuzzy system corresponding to hmr; $hm{r}_{1i}$ is the output result for rule i corresponding to hmr; ${\mu }_i^{hmr}$ is the membership function of rule i corresponding to hmr.

$$PArate= \frac{{{\displaystyle \sum }}_{i=1}^{r_{PArate}}{\mu }_i^{PArate} \left(PArat{e}_{1i}\right)}{{{\displaystyle \sum }}_{i=1}^{r_{PArate}}{\mu }_i^{PArate}}$$

(5)

where PArate is the pitch adjusting; $r_{PArate}$ is the number of rules of the fuzzy system corresponding to PArate; $PArat{e}_{1i}$ is the output result for rule i corresponding to PArate; ${\mu }_i^{PArate}$ is the membership function of rule i corresponding to PArate.

Fuzzy logic is based on fuzzy set theory proposed by Zadeh in 1965, which helps us in modeling knowledge, through the use of if-then fuzzy rules. The fuzzy set theory provides a systematic calculus to deal with linguistic information, and that improves the numerical computation by using linguistic labels stipulated by membership functions [19,20].

The parameters of HMR and PArate are selected to be modified using fuzzy logic, since these parameters account for controlling the exploitation and exploration of the search domain. The HMR and PArate parameters in the HS algorithm are very important to fine-tuning the optimized solution vectors, and can be potentially useful in adjusting the convergence rate of the algorithm to find the optimal solution Therefore, the adjustment of these parameters is of great interest.

There are three variants of the algorithm that have been applied to achieve better results and they are briefly explained in the following: The improved harmony search algorithm (IHS) [13] is a novel method for generating new solution vectors that enhance accuracy and convergence rate of harmony search (HS) algorithm; the global best harmony search (GHS) [24] is proposed in this paper where concepts from swarm intelligence are borrowed to enhance the performance of HS; and the new global harmony search (NGHS) [25] is a proposed new algorithm that includes two important operations—position updating and genetic mutation with a small probability. The former enables the worst harmony of the harmony memory to move to the global best harmony rapidly in each iteration, and the latter can effectively prevent the NGHS from trapping into the local optimum. It should be noted that none of these methods use fuzzy logic techniques to achieve their goals.

The harmony search algorithm has been applied so far to various optimization problems: optimization of functions [9,14], the distribution of water, groundwater modeling, energy-saving clearance, structural design [26], vehicle routing, and others. The possibility of combining harmony search with other algorithms, such as particle swarm optimization and genetic algorithms has also been investigated.

The parameter harmony memory accepting (HMR) represents the exploitation, and this will ensure that the best harmonies will be transferred to the new harmony memory.

The parameter pitch adjustment (PArate) represents the exploration of this algorithm, and is similar to the mutation operator in genetic algorithms. A pitch adjustment rate (PArate) was used to control the degree of adjustment. The literature suggests the range of pitch adjustment to be between 0 and 1; this parameter in the original algorithm does not change during the iterations and some authors use this parameter in a range between 0.1 and 0.7. In the proposed model, the parameters change during iterations in the range 0.7 to 1 through the use of a fuzzy system to give diversity algorithm and finding the global optimum.

Parameter randomization is used to increase the diversity of the solutions, and the use of randomization can further push the system to explore various regions with high diversity solutions in order to find the global optimum.

The main difference between FHS and the traditional HS method is in the way they perform the adjusting of the HMR and PArate parameters. To improve the performance of the HS algorithm, the FHS algorithm considers the HMR and PArate as dynamic parameters in the improvisation step. FHS uses a fuzzy system to be responsible for dynamically changing the HMR and PArate parameters in the range from 0 to 1 and 0.7 to 1; this range is based on a detailed study of the behavior of the algorithm parameters after performing a series of experiments applied to optimization problems, since some items used different ranges in the original method [22] in each iteration number. In this case, the rules are used in increasing and decreasing form as shown in Figure 1.

This method includes the input iterations of the algorithm, because other studies have found it favorable to consider this measure that can control the execution of the algorithm.

In addition, it is also found that an algorithm performance measure, such as the iterations, needs to be considered in the parameter adaptation. In this work, all the above are taken into consideration for the fuzzy systems to modify the HMR and PArate parameters by dynamically changing these parameters in each iteration of the algorithm.

In this phase, the percentage of elapsed iterations is considered to determine the values of HMR and PArate. If a low percentage of iterations elapses, the HMR and PArate parameters would take a low value in the range in order to enable a wide search in the search space, as a kind of exploration. On the contrary, if a high percentage of iterations have occurred, it would give the HMR and PArate parameters a high value in the indicated range in order to draw a more intense exploitation within the search space in advanced iterations. Subsequently, if the percentage of elapsed iterations is medium, then a medium value for HMR and PArate would occur, with the aim of expanding the above criteria. The following equation represents this idea [27]:

$$\mathrm{Iteration}=\frac{\mathrm{Current}\mathrm{Iteration}}{\mathrm{Maximun}\mathrm{of}\mathrm{iterations}}$$

(6)

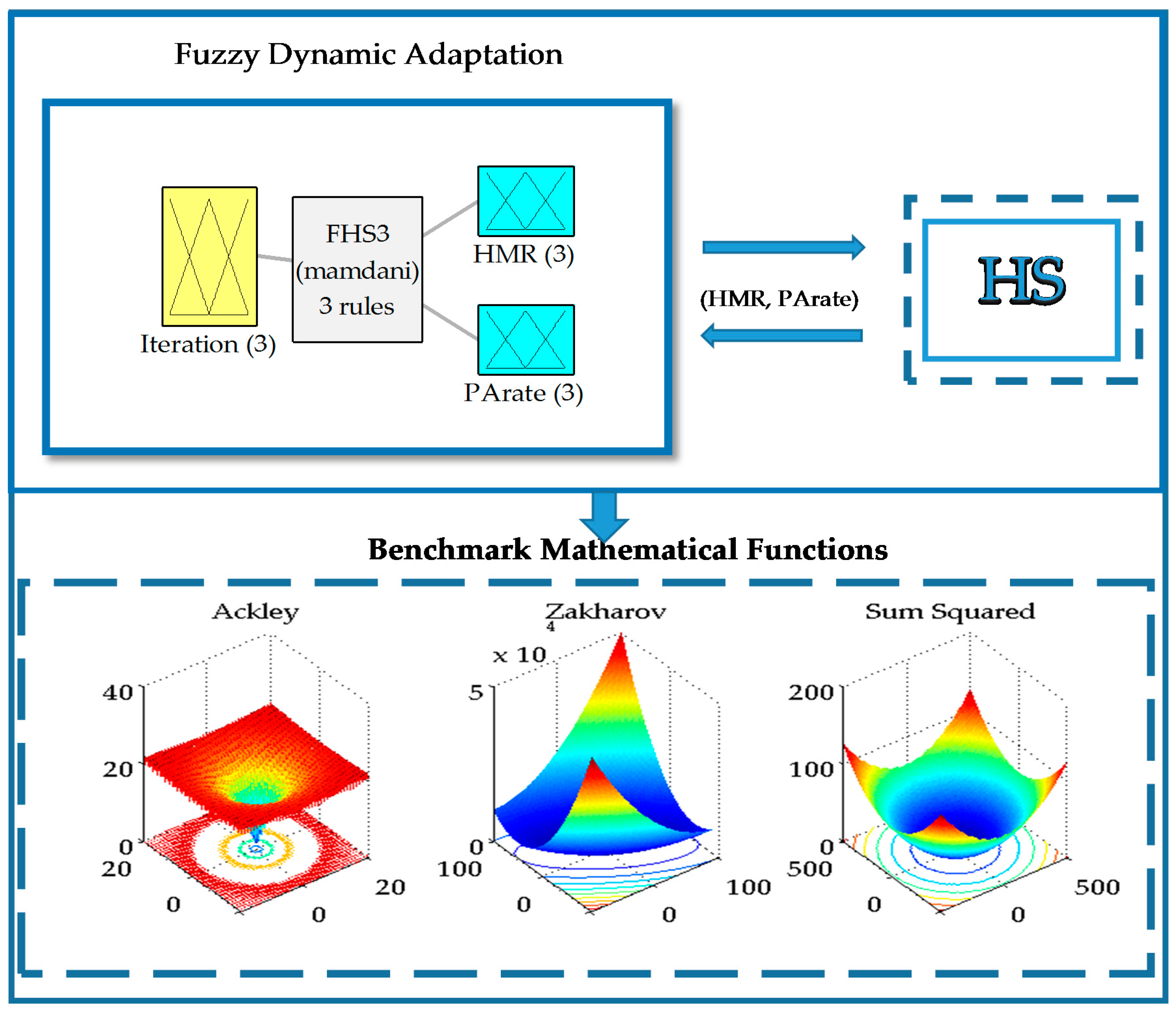
Therefore, for designing the fuzzy systems, which dynamically adjust the HMR and PArate parameters, the measure described above was considered as the input. Experiments were performed to test each parameter separately in order to check their behavior when applied to optimization problems with different fuzzy rules to increase or decrease, and eventually the two parameters in the output were put together to test the effectiveness of the method. The first proposed output of the fuzzy system is the HMR parameter, the second proposed output of the fuzzy system is the PArate parameter and for the third proposed fuzzy system, the outputs are both HMR and PArate parameters. The fuzzy systems use rules with increment and decrement and with ranges from 0 to 1 and from 0.7 to 1, respectively, for the experiments.

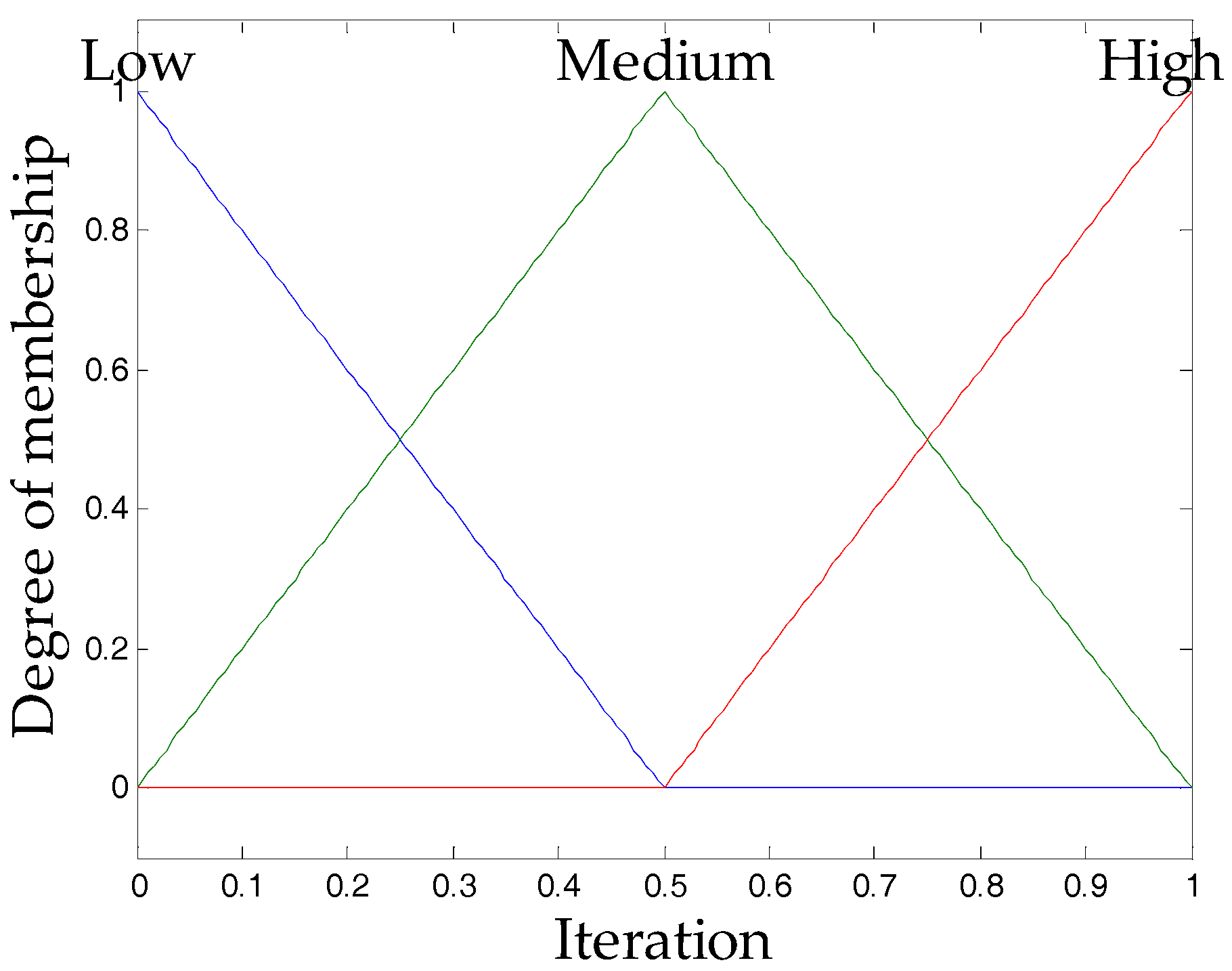
The design of the input variable in all fuzzy systems can be found in Figure 2, which shows the input called “iteration”, and this input is granulated into three triangular membership functions.

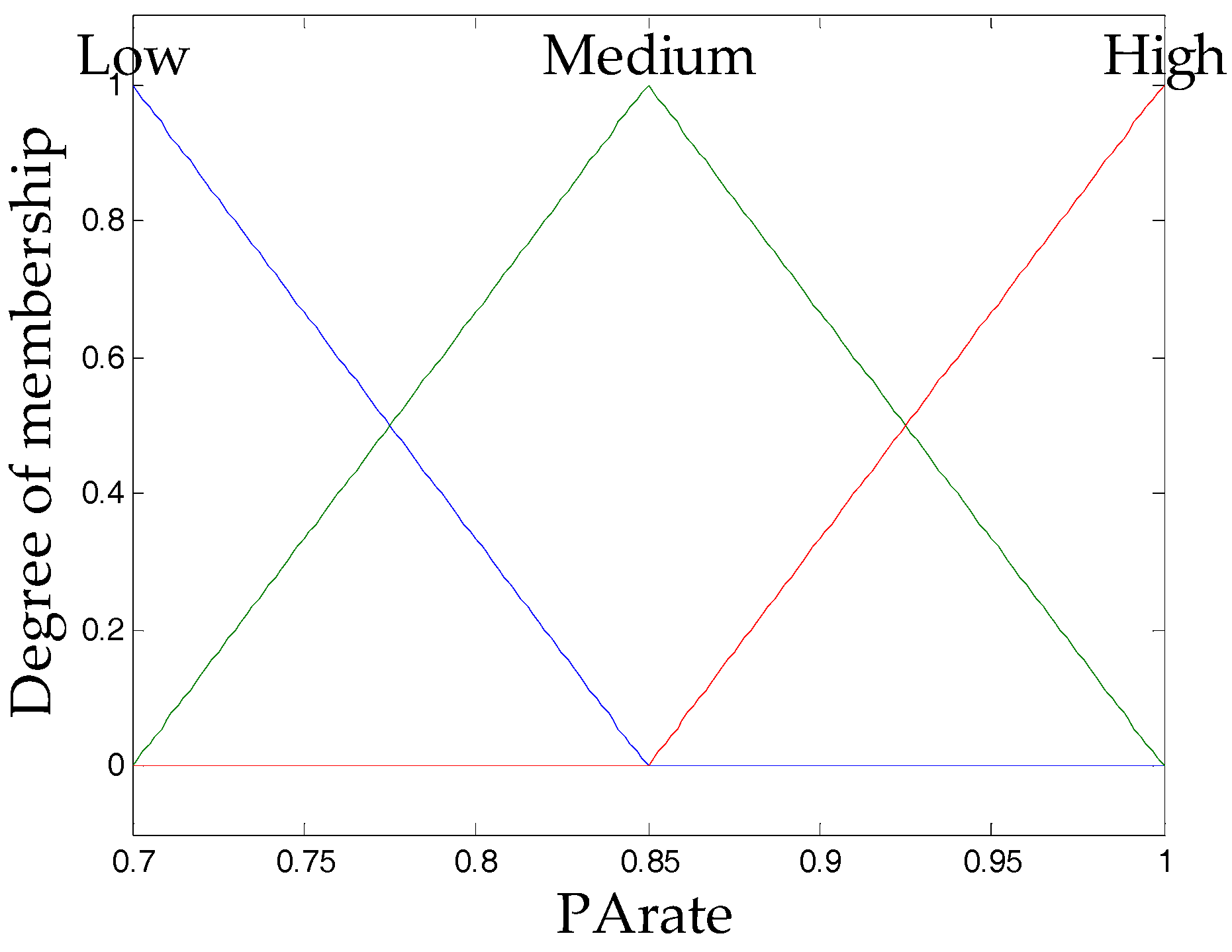
For the output variables, as mentioned above, the recommended values for HMR and PArate are from 0 to 1 and 0.7 to 1, so the output variables are designed using these ranges of values. Each output is granulated into three triangular membership functions which are low, medium and high, and the design of the HMR and PArate output variables can be found in Figure 3 and Figure 4.

Having defined the possible output variables, it was decided to combine them to generate different fuzzy systems for the dynamic adjustment of HMR and PArate. Based on the literature the recommended values for the parameters are from 0 to 1, so in this case the range 0 to 1 and 0.7 to 1 were used for the outputs in the fuzzy system. There are 12 possible fuzzy systems, in this case only the three fuzzy systems using a range 0.7 to 1 are presented, using rules to increase because these algorithms achieve better results, which are defined below.

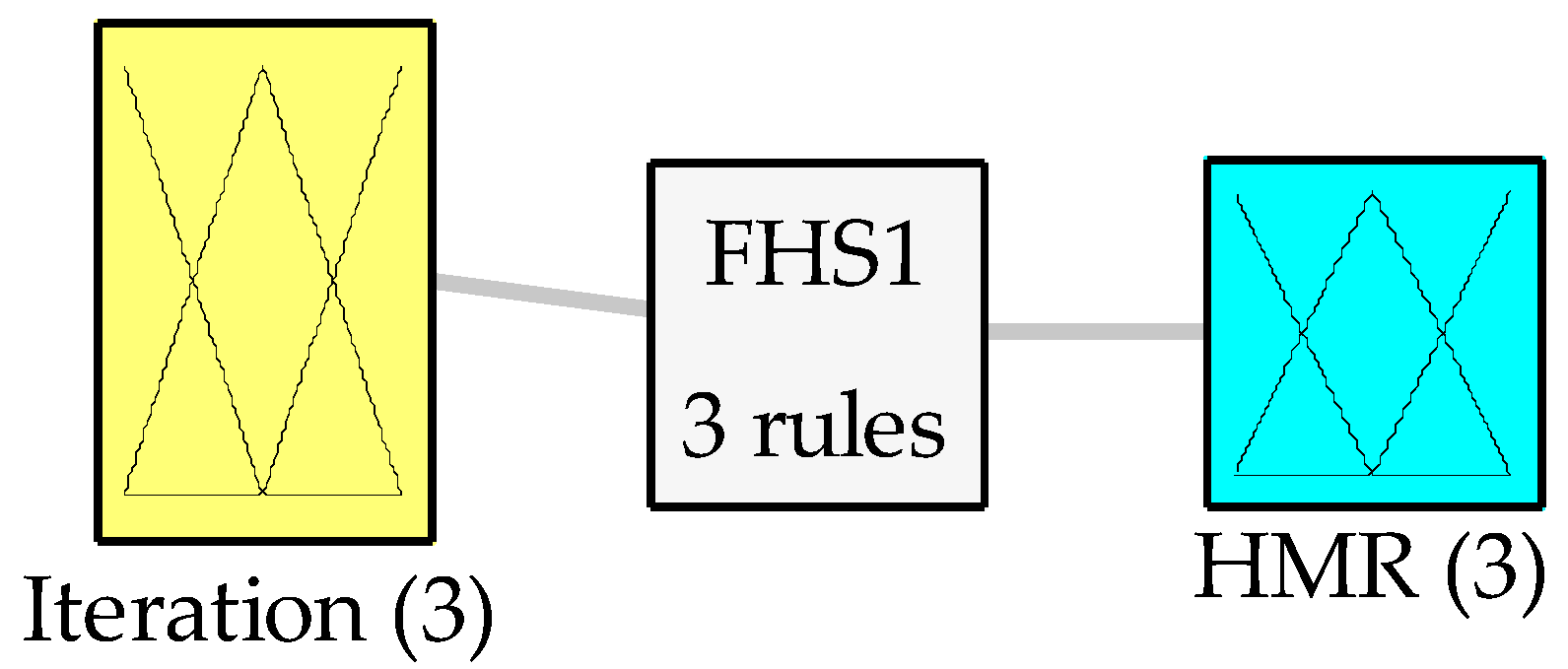
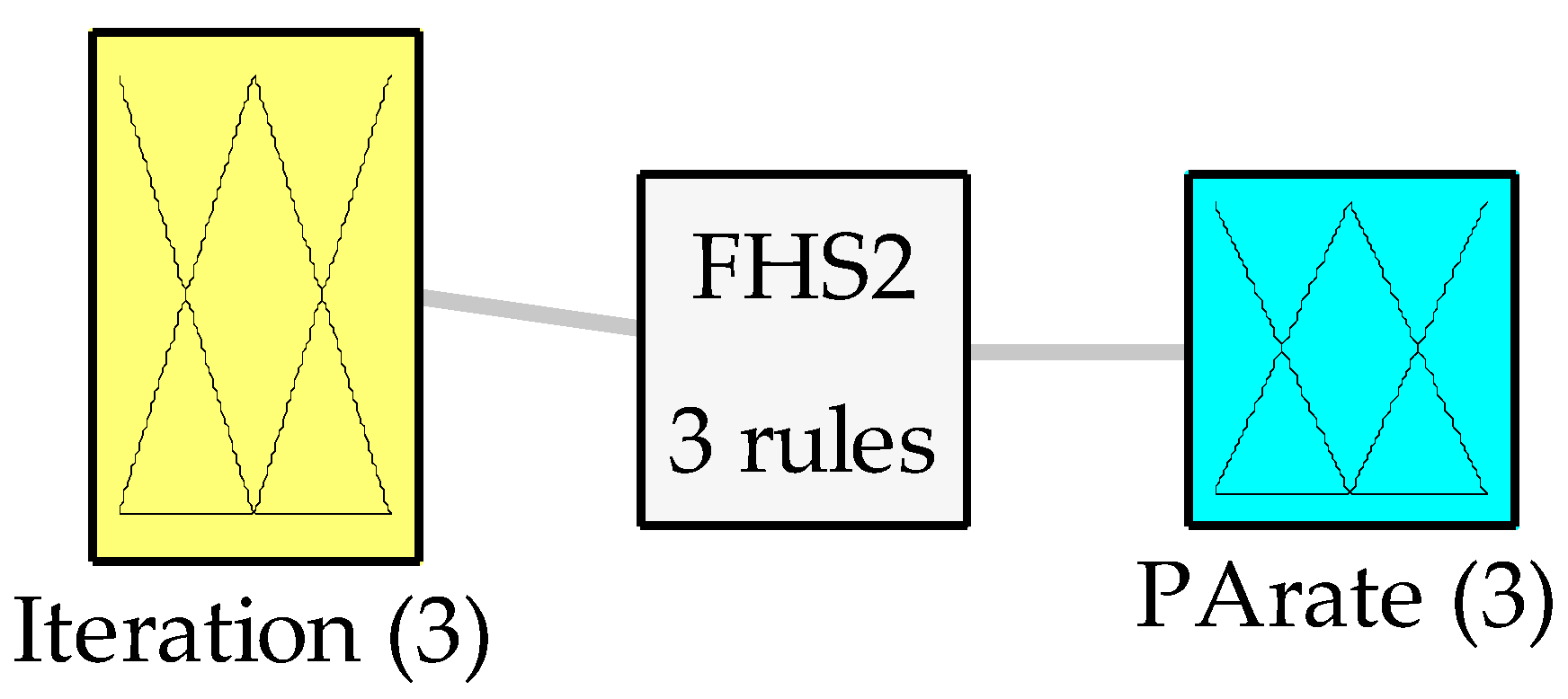
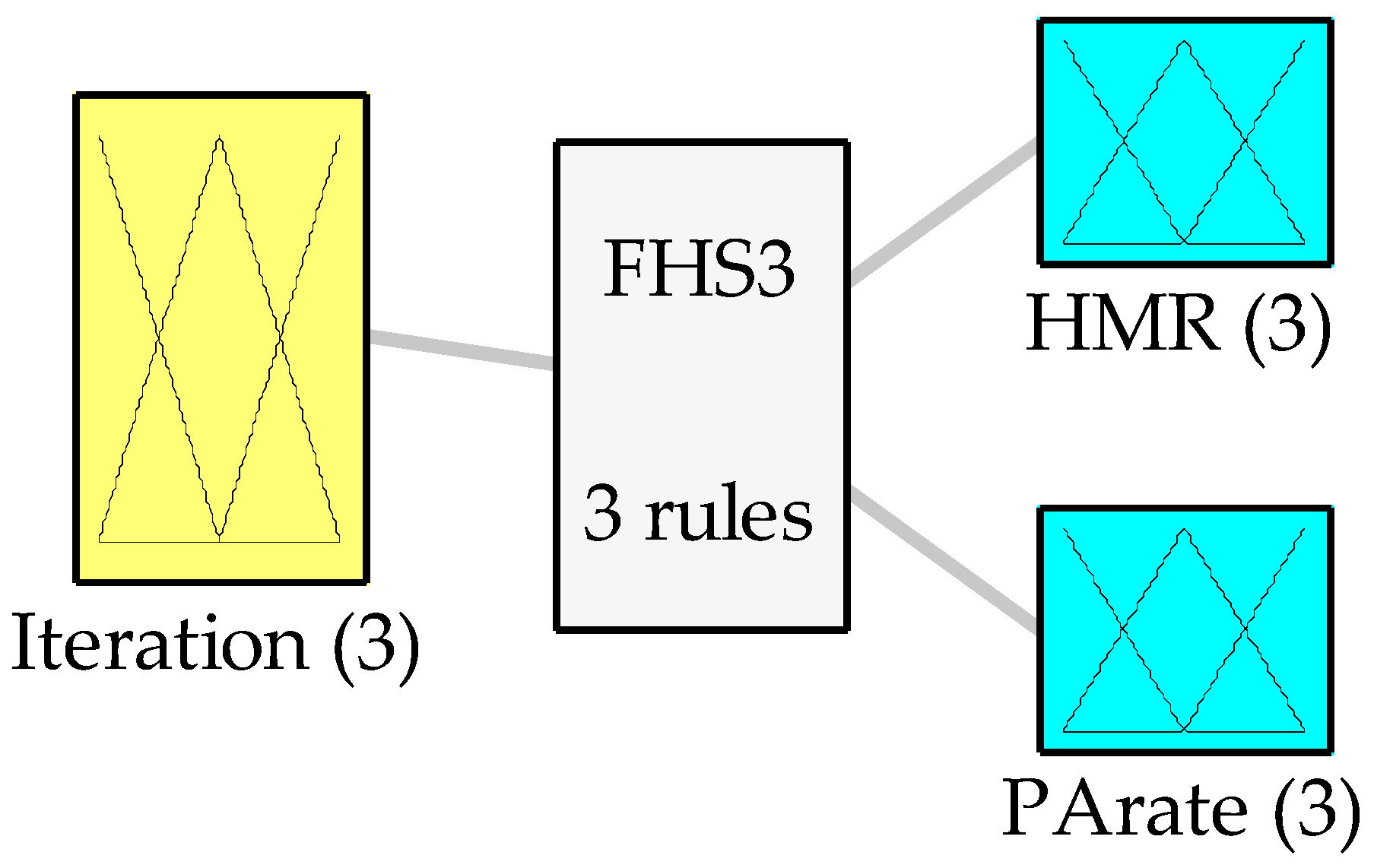
The first fuzzy system has iteration as input and HMR as output, which is shown in Figure 5. The second fuzzy system has iteration as input and PArate as output and is shown in Figure 6. The third fuzzy system has iteration as input and the outputs are HMR and PArate, as shown in Figure 7.

The first fuzzy system is defined by the following design, using as input the iterations and as output in this case the harmony memory accepting (HMR) to dynamically vary the first parameter that within the algorithm represents the exploitation, which is the number of solutions that will be considered for the subsequent iteration, as shown in Figure 5.

The second fuzzy system is defined by the following design, using as input the iterations and as output the pitch adjusting (PArate) to dynamically vary the second parameter that represents the exploration in the algorithm, which can be viewed as a refinement of local solutions, as shown in Figure 6.

The third fuzzy system, which is composed of the following design, uses as input the iterations and as outputs the HMR and PArate parameters to move both parameters dynamically. For this case, a combination of rules based on the results of the two previous fuzzy systems is made, as illustrated in Figure 7.

To design the rules of each fuzzy system, it was decided that in early iterations the HS algorithm must explore and eventually exploit.

The rules for the fuzzy system number 1 are shown in Figure 8 and Figure 9, the rules for the fuzzy system number 2 are shown in Figure 10 and Figure 11 and the rules for the fuzzy system number 3 are shown in Figure 12 and Figure 13, respectively.

The rules given in Figure 8 are those used in the fuzzy system 1, and are defined to increase the HMR parameter according to the iterations to achieve better exploration and exploitation of the search space.

The rules given in Figure 9 are those used also for the fuzzy system 1, which are defined for decreasing the HMR parameter to achieve exploitation and exploration of the search space.

The rules given in Figure 10 are those used in the fuzzy system 2, in this case for increasing the PArate parameter to achieve exploration and exploitation of the search space.

The rules given in Figure 11 are those used in the fuzzy system 2, but now for decreasing the PArate parameter to achieve exploitation and exploration of the search space.

The rules given in Figure 12 are used in the fuzzy system 3, which are a combination of the two parameters in increase to first explore and then exploit the search space.

The rules given in Figure 13 are used in the third fuzzy system, which are another combination of the two parameters in decrease to first exploit and then explore the search space.

3. Experimentation with the Fuzzy Systems in Harmony Search for Benchmark Mathematical Functions

For all the experiments used, the parameters are presented in

Table 1. Parameters for each of the methods.

Parameter	Simple HS	FHS1	FHS2	FHS3
Harmonies	4 to 40	4 to 40	4 to 40	4 to 40
Iterations	1000	1000	1000	1000
HMR	0.95	Dynamic	0.95	Dynamic
PArate	0.7	0.7	Dynamic	Dynamic

. For all the functions, the global minimum is zero. The proposed method used six mathematical functions—some simple and some more complicated—in order to test the algorithm and measure its effectiveness. In this case, ten dimensions in each problem were used, as the literature suggests this number for the first tests. We then compare it with the bat algorithm method which also uses ten dimensions. Once you validate the performance of the method it will apply to problems of control.

Table 1 shows the parameters of the methods to be considered in the comparison; in this case, the comparison of the proposed method (FHS) and the simple HS algorithm.

Also for the comparison of the proposed method with respect to the HS without parameter adaptation, parameters that give the global minimum of each of the six benchmark mathematical functions have to be found. In Figure 14, there is a sample of the functions that are used [28,29].

As indicated in Figure 14, functions of ten dimensions for the experiments were considered. Once the fuzzy systems that dynamically adjust the parameters of HS are defined, and the problem to which this is applied is defined (benchmark mathematical functions), the proposal is as shown in Figure 1, where it can be observed that the harmony memory accepting (HMR) and pitch adjustment (PArate) parameters are adjusted by a fuzzy system, and in turn this “fuzzy HS” searches for the optimal parameters for the benchmark mathematical functions [30].

4. Experiment Results Comparison of the Simple Harmony Search Algorithm with Fuzzy Harmony Search

In this section, the experimental results obtained by the Harmony Search algorithm and fuzzy harmony search are shown in separate tables of the 12 proposed fuzzy systems.

The results obtained using the original method, with six benchmark mathematical functions, are presented in

Table 2. Results obtained using the harmony search algorithm.

Simple Harmony Search
Function	Best	Worst	Average
Spherical	$2.36\mathrm{E}-05$	$1.49\mathrm{E}-04$	$6.57\mathrm{E}-05$
Rosenbrock	$1.47\mathrm{E}-11$	$1.31\mathrm{E}-02$	$4.88\mathrm{E}-04$
Rastrigin	$9.31\mathrm{E}-12$	$2.24\mathrm{E}-07$	$2.26\mathrm{E}-08$
Ackley	$8.72\mathrm{E}-06$	$4.54\mathrm{E}-04$	$1.18\mathrm{E}-04$
Zakharov	$7.33\mathrm{E}-05$	$1.80\mathrm{E}-03$	$2.71\mathrm{E}-04$
Sum Square	$4.82\mathrm{E}-06$	$1.05\mathrm{E}-04$	$3.59\mathrm{E}-05$

. It should be noted that the best, worst and average of 30 experiments are shown for each mathematical function.

In Table 2, the overall averages obtained for each mathematical function are presented. The first column represents the best values of the experiments, the second column represents the worst values of the experiments and the third column represents the averages of the experiments with the original harmony search algorithm.

The first proposal made by this method was to perform the dynamic adjustment of parameters applied to the first parameter of the algorithm, which is the harmony memory accepting (HMR). This was created to dynamically change this parameter in the range that indicates the literature, which is from 0 to 1. This methodology was applied to the six benchmark mathematical functions previously mentioned and 30 experiments were performed with each of these functions.

Table 3. Comparison of results obtained with the FHS1 using fuzzy logic to increase and decrease of the HMR parameter in the range 0 to 1.

FHS1 Rules Increase in Range 0 to 1				FHS1 Rules Decrease in Range 0 to 1
Function	Best	Worst	Average	Function	Best	Worst	Average
Spherical	$1.22\mathrm{E}-04$	$1.31\mathrm{E}-01$	$4.71\mathrm{E}-03$	Spherical	$2.10\mathrm{E}-03$	$4.90\mathrm{E}-01$	$1.19\mathrm{E}-01$
Rosenbrock	$1.18\mathrm{E}-12$	$9.24\mathrm{E}-06$	$3.04\mathrm{E}-07$	Rosenbrock	$4.46\mathrm{E}-16$	$2.01\mathrm{E}-09$	$1.18\mathrm{E}-10$
Rastrigin	$2.65\mathrm{E}-07$	$2.00\mathrm{E}+00$	$5.69\mathrm{E}-02$	Rastrigin	$4.70\mathrm{E}-10$	$3.23\mathrm{E}-06$	$3.35\mathrm{E}-07$
Ackley	$8.23\mathrm{E}-05$	$4.35\mathrm{E}-01$	$1.72\mathrm{E}-01$	Ackley	$6.64\mathrm{E}-05$	$1.80\mathrm{E}-03$	$6.50\mathrm{E}-04$
Zakharov	$2.00\mathrm{E}-03$	$1.38\mathrm{E}+02$	$2.04\mathrm{E}+00$	Zakharov	$1.01\mathrm{E}+00$	$1.47\mathrm{E}+01$	$6.67\mathrm{E}+00$
Sum Square	$4.30\mathrm{E}-04$	$1.00\mathrm{E}+00$	$3.33\mathrm{E}-02$	Sum Square	$3.70\mathrm{E}-02$	$9.08\mathrm{E}+00$	$2.38\mathrm{E}+00$

shows the results.

In Table 3, the overall averages, as well as best and worst results obtained for each mathematical function and method can be found. The results obtained with the FHS1 using the range of 0 to 1 using rules increment and decrement are presented.

Based on the previous experiments, the range of 0.7 to 1 for the HMR output was used. In the literature, it is recommended to use this parameter in the range from 0.7 to 0.95 to obtain better results, but in many existing works they use the range up to 0.99 and 1, hence the experiments were performed by trial and error.

Table 4. Results obtained with FHS1 using fuzzy logic to increase and decrease HMR with a range from 0.7 to 1, applied to six benchmark mathematical functions.

FHS1 Rules Increase in Range 0.7 to 1				FHS1 Rules Decrease in Range 0.7 to 1
Function	Best	Worst	Average	Function	Best	Worst	Average
Spherical	$2.45\mathrm{E}-09$	$3.52\mathrm{E}-04$	$5.28\mathrm{E}-05$	Spherical	$4.94\mathrm{E}-04$	$2.91\mathrm{E}-01$	$5.12\mathrm{E}-02$
Rosenbrock	$2.95\mathrm{E}-11$	$6.88\mathrm{E}-05$	$6.33\mathrm{E}-07$	Rosenbrock	$1.81\mathrm{E}-13$	$1.35\mathrm{E}-08$	$1.88\mathrm{E}-09$
Rastrigin	$1.06\mathrm{E}-11$	$9.32\mathrm{E}-08$	$1.36\mathrm{E}-08$	Rastrigin	$1.32\mathrm{E}-09$	$2.07\mathrm{E}-06$	$1.88\mathrm{E}-07$
Ackley	$1.00\mathrm{E}-09$	$5.09\mathrm{E}-04$	$7.87\mathrm{E}-05$	Ackley	$3.31\mathrm{E}-05$	$1.40\mathrm{E}-03$	$4.60\mathrm{E}-04$
Zakharov	$1.30\mathrm{E}-13$	$9.54\mathrm{E}-04$	$1.25\mathrm{E}-04$	Zakharov	$3.55\mathrm{E}-01$	$1.27\mathrm{E}+01$	$3.41\mathrm{E}+00$
Sum Square	$2.30\mathrm{E}-09$	$5.70\mathrm{E}-05$	$3.72\mathrm{E}-06$	Sum Square	$1.58\mathrm{E}-02$	$5.47\mathrm{E}+00$	$9.28\mathrm{E}-01$

shows the results obtained with this modification.

In Table 4, the averages of the 30 experiments for each mathematical function are shown, in addition to the best and worst results obtained for each mathematical function and the overall average obtained in each function. The results of these experiments suggest the use of the range of 0.7 to 1 with the proposed method as shown in

Table 5. Comparison of results obtained with FHS1 and the harmony search algorithm.

Simple Harmony Search				FHS1 Rules Increase in Range 0.7 to 1
Function	Best	Worst	Average	Function	Best	Worst	Average
Spherical	$2.36\mathrm{E}-05$	$1.49\mathrm{E}-04$	$6.57\mathrm{E}-05$	Spherical	$2.45\mathrm{E}-09$	$3.52\mathrm{E}-04$	$5.28\mathrm{E}-05$
Rosenbrock	$1.47\mathrm{E}-11$	$1.31\mathrm{E}-02$	$4.88\mathrm{E}-04$	Rosenbrock	$2.95\mathrm{E}-11$	$6.88\mathrm{E}-05$	$6.33\mathrm{E}-07$
Rastrigin	$9.31\mathrm{E}-12$	$2.24\mathrm{E}-07$	$2.26\mathrm{E}-08$	Rastrigin	$1.06\mathrm{E}-11$	$9.32\mathrm{E}-08$	$1.36\mathrm{E}-08$
Ackley	$8.72\mathrm{E}-06$	$4.54\mathrm{E}-04$	$1.18\mathrm{E}-04$	Ackley	$1.00\mathrm{E}-09$	$5.09\mathrm{E}-04$	$7.87\mathrm{E}-05$
Zakharov	$7.33\mathrm{E}-05$	$1.80\mathrm{E}-03$	$2.71\mathrm{E}-04$	Zakharov	$1.30\mathrm{E}-13$	$9.54\mathrm{E}-04$	$1.25\mathrm{E}-04$
Sum Square	$4.82\mathrm{E}-06$	$1.05\mathrm{E}-04$	$3.59\mathrm{E}-05$	Sum Square	$2.30\mathrm{E}-09$	$5.70\mathrm{E}-05$	$3.72\mathrm{E}-06$

.

In Table 5, the averages of the 30 experiments for each mathematical function are shown, as well as the best and worst results for each mathematical function and the overall average. The results are with the original algorithm and the best fuzzy system, in this case FHS1, with rules and increase in the output range from 0.7 to 1. The best results obtained are of the proposed method.

The second proposal made by this method was to perform the dynamic adjustment of parameters applied to the second parameter of the algorithm, which is the pitch adjustment (PArate). This was created to dynamically change this parameter in the range indicated in the literature, which is from 0 to 1. This methodology was applied to the six previously mentioned benchmark mathematical functions of which 30 experiments are performed.

Table 6. Results obtained with FHS2 using fuzzy logic to increase and decrease PArate with 0 to 1 range applied to six benchmark mathematical functions.

FHS2 Rules Increase in Range 0 to 1				FHS2 Rules Decrease in Range 0 to 1
Function	Best	Worst	Average	Function	Best	Worst	Average
Spherical	$1.19\mathrm{E}-04$	$1.01\mathrm{E}-02$	$1.14\mathrm{E}-03$	Spherical	$3.02\mathrm{E}-05$	$1.54\mathrm{E}-02$	$9.06\mathrm{E}-04$
Rosenbrock	$1.20\mathrm{E}-12$	$1.51\mathrm{E}-08$	$7.31\mathrm{E}-10$	Rosenbrock	$7.01\mathrm{E}-13$	$1.58\mathrm{E}-09$	$1.34\mathrm{E}-10$
Rastrigin	$3.66\mathrm{E}-11$	$6.40\mathrm{E}-07$	$6.42\mathrm{E}-08$	Rastrigin	$1.62\mathrm{E}-10$	$2.76\mathrm{E}-06$	$2.86\mathrm{E}-07$
Ackley	$6.86\mathrm{E}-06$	$7.98\mathrm{E}-04$	$2.30\mathrm{E}-04$	Ackley	$1.49\mathrm{E}-05$	$9.57\mathrm{E}-04$	$2.36\mathrm{E}-04$
Zakharov	$3.40\mathrm{E}-03$	$3.29\mathrm{E}+00$	$7.89\mathrm{E}-01$	Zakharov	$2.40\mathrm{E}-03$	$3.86\mathrm{E}+00$	$7.74\mathrm{E}-01$
Sum Square	$2.20\mathrm{E}-03$	$1.26\mathrm{E}-01$	$2.00\mathrm{E}-02$	Sum Square	$7.08\mathrm{E}-04$	$1.26\mathrm{E}-01$	$1.33\mathrm{E}-02$

shows the results obtained with this modification.

In Table 6, the overall averages, best and worst obtained for each mathematical function and each method can be found. The results obtained with the FHS2 using the range of 0 to 1 and rules increment or decrement are presented.

In

Table 7. Results obtained with FHS2 using fuzzy logic to increase and decrease PArate with a range from 0.7 to 1, applied to 6 benchmark mathematical functions.

FHS2 Rules Increase in Range 0.7 to 1				FHS2 Rules Decrease in Range 0.7 to 1
Function	Best	Worst	Average	Function	Best	Worst	Average
Spherical	$1.54\mathrm{E}-09$	$2.64\mathrm{E}-04$	$1.38\mathrm{E}-05$	Spherical	$5.15\mathrm{E}-14$	$7.60\mathrm{E}-03$	$9.08\mathrm{E}-04$
Rosenbrock	$5.44\mathrm{E}-14$	$2.80\mathrm{E}-10$	$1.76\mathrm{E}-11$	Rosenbrock	$4.14\mathrm{E}-14$	$8.64\mathrm{E}-10$	$7.31\mathrm{E}-11$
Rastrigin	$1.20\mathrm{E}-11$	$1.28\mathrm{E}-07$	$1.08\mathrm{E}-08$	Rastrigin	c$1.44\mathrm{E}-10$	$2.58\mathrm{E}-06$	$2.22\mathrm{E}-07$
Ackley	$1.07\mathrm{E}-08$	$4.28\mathrm{E}-04$	$9.55\mathrm{E}-06$	Ackley	$4.31\mathrm{E}-05$	$2.00\mathrm{E}-03$	$4.98\mathrm{E}-04$
Zakharov	$1.10\mathrm{E}-10$	$7.55\mathrm{E}-04$	$4.72\mathrm{E}-05$	Zakharov	$6.91\mathrm{E}-04$	$3.54\mathrm{E}+00$	$5.94\mathrm{E}-01$
Sum Square	$2.06\mathrm{E}-08$	$5.50\mathrm{E}-06$	$2.53\mathrm{E}-06$	Sum Square	$1.00\mathrm{E}-03$	$5.70\mathrm{E}-03$	$3.13\mathrm{E}-03$

, the averages of the 30 experiments for each mathematical function are shown. The best and worst results obtained for each mathematical function, and the overall averages obtained in each function are also shown. The results of these experiments are the best ones in the range of 0.7 to 1 and rules increment with the proposed method is as shown in

Table 8. Comparison results obtained with FHS2 and the harmony search algorithm.

Simple Harmony Search				FHS2 Rules Increase in Range 0.7 to 1
Function	Best	Worst	Average	Function	Best	Worst	Average
Spherical	$2.36\mathrm{E}-05$	$1.49\mathrm{E}-04$	$6.57\mathrm{E}-05$	Spherical	$1.54\mathrm{E}-09$	$2.64\mathrm{E}-04$	$1.38\mathrm{E}-05$
Rosenbrock	$1.47\mathrm{E}-11$	$1.31\mathrm{E}-02$	$4.88\mathrm{E}-04$	Rosenbrock	$5.44\mathrm{E}-14$	$2.80\mathrm{E}-10$	$1.76\mathrm{E}-11$
Rastrigin	$9.31\mathrm{E}-12$	$2.24\mathrm{E}-07$	$2.26\mathrm{E}-08$	Rastrigin	$1.20\mathrm{E}-11$	$1.28\mathrm{E}-07$	$1.08\mathrm{E}-08$
Ackley	$8.72\mathrm{E}-06$	$4.54\mathrm{E}-04$	$1.18\mathrm{E}-04$	Ackley	$1.07\mathrm{E}-08$	$4.28\mathrm{E}-04$	$9.55\mathrm{E}-06$
Zakharov	$7.33\mathrm{E}-05$	$1.80\mathrm{E}-03$	$2.71\mathrm{E}-04$	Zakharov	$1.10\mathrm{E}-10$	$7.55\mathrm{E}-04$	$4.72\mathrm{E}-05$
Sum Square	$4.82\mathrm{E}-06$	$1.05\mathrm{E}-04$	$3.59\mathrm{E}-05$	Sum Square	$2.06\mathrm{E}-08$	$5.50\mathrm{E}-06$	$2.53\mathrm{E}-06$

.

In Table 8, the averages of the 30 experiments for each mathematical function are shown, in addition to the best and worst results obtained for each mathematical function and the overall averages obtained in each function for each method. The results are with the original algorithm and the best fuzzy system, in this case FHS2 with rules and increase in the output range from 0.7 to 1. The best results obtained are of the proposed method.

The third proposal was proposed to make dynamic the HMR and PArate parameters in the range from 0.7 to 1, both for increasing and decreasing the parameters.

In

Table 9. Comparison of results obtained with FHS 3 using fuzzy logic rules for increasing and decreasing using the range 0 to 1 for the two outputs.

FHS3 Rules Increase in Range 0 to 1				FHS3 Rules Decrease in Range 0 to 1
Function	Best	Worst	Average	Function	Best	Worst	Average
Spherical	$1.44\mathrm{E}-05$	$2.33\mathrm{E}+00$	$4.96\mathrm{E}-01$	Spherical	$1.30\mathrm{E}-03$	$4.60\mathrm{E}-01$	$1.23\mathrm{E}-01$
Rosenbrock	$5.20\mathrm{E}-11$	$5.28\mathrm{E}-06$	$1.34\mathrm{E}-07$	Rosenbrock	$2.14\mathrm{E}-12$	$6.50\mathrm{E}-09$	$5.46\mathrm{E}-10$
Rastrigin	$1.66\mathrm{E}-06$	$1.13\mathrm{E}+00$	$1.28\mathrm{E}-01$	Rastrigin	$6.60\mathrm{E}-10$	$2.63\mathrm{E}-06$	$2.80\mathrm{E}-07$
Ackley	$1.70\mathrm{E}-03$	$4.04\mathrm{E}+00$	$8.59\mathrm{E}-01$	Ackley	$1.50\mathrm{E}-03$	$4.86\mathrm{E}-01$	$1.32\mathrm{E}-01$
Zakharov	$5.00\mathrm{E}-05$	$8.30\mathrm{E}-01$	$6.35\mathrm{E}-02$	Zakharov	$8.77\mathrm{E}-01$	$2.23\mathrm{E}+01$	$7.02\mathrm{E}+00$
Sum Square	$8.42\mathrm{E}-05$	$9.40\mathrm{E}-04$	$3.40\mathrm{E}-04$	Sum Square	$1.74\mathrm{E}-02$	$6.79\mathrm{E}+00$	$1.34\mathrm{E}+00$

, the overall averages, as well as best and worst obtained for each mathematical function and method, are presented. The results were obtained with the FHS3 using the range of 0 to 1 and rules increment or decrement are shown.

In

Table 10. Comparison of results obtained with FHS 3 using fuzzy logic rules for increasing and decreasing using the range 0.7 to 1 for the two outputs.

FHS3 Rules Increase in Range 0.7 to 1				FHS3 Rules Decrease in Range 0.7 to 1
Function	Best	Worst	Average	Function	Best	Worst	Average
Spherical	$3.74\mathrm{E}-06$	$1.11\mathrm{E}-04$	$3.39\mathrm{E}-05$	Spherical	$2.03\mathrm{E}-06$	$5.68\mathrm{E}-05$	$1.59\mathrm{E}-05$
Rosenbrock	$3.55\mathrm{E}-15$	$1.08\mathrm{E}-10$	$9.52\mathrm{E}-12$	Rosenbrock	$2.55\mathrm{E}-14$	$8.56\mathrm{E}-11$	$9.30\mathrm{E}-12$
Rastrigin	$3.52\mathrm{E}-11$	$1.62\mathrm{E}-07$	$2.52\mathrm{E}-08$	Rastrigin	$7.60\mathrm{E}-12$	$3.66\mathrm{E}-07$	$3.51\mathrm{E}-08$
Ackley	$1.12\mathrm{E}-05$	$6.40\mathrm{E}-04$	$1.73\mathrm{E}-04$	Ackley	$1.53\mathrm{E}-06$	$6.25\mathrm{E}-04$	$1.68\mathrm{E}-04$
Zakharov	$9.73\mathrm{E}-05$	$1.14\mathrm{E}-01$	$1.69\mathrm{E}-03$	Zakharov	$3.46\mathrm{E}-05$	$1.80\mathrm{E}+00$	$8.79\mathrm{E}-02$
Sum Square	$6.43\mathrm{E}-05$	$2.00\mathrm{E}-03$	$6.33\mathrm{E}-04$	Sum Square	$2.87\mathrm{E}-05$	$9.26\mathrm{E}-04$	$2.52\mathrm{E}-04$

, the averages of the 30 experiments for each mathematical function are shown; also the best and worst results for each mathematical function and the overall average in each function are shown. The results of these experiments use the range of 0.7 to 1 and rules in increment with the proposed method.

In

Table 11. Comparison results obtained with FHS3 and the harmony search algorithm.

Simple Harmony Search				FHS3 Rules Increase in Range 0.7 to 1
Function	Best	Worst	Average	Function	Best	Worst	Average
Spherical	$2.36\mathrm{E}-05$	$1.49\mathrm{E}-04$	$6.57\mathrm{E}-05$	Spherical	$3.74\mathrm{E}-06$	$1.11\mathrm{E}-04$	$3.39\mathrm{E}-05$
Rosenbrock	$1.47\mathrm{E}-11$	$1.31\mathrm{E}-02$	$4.88\mathrm{E}-04$	Rosenbrock	$3.55\mathrm{E}-15$	$1.08\mathrm{E}-10$	$9.52\mathrm{E}-12$
Rastrigin	$9.31\mathrm{E}-12$	$2.24\mathrm{E}-07$	$2.26\mathrm{E}-08$	Rastrigin	$3.52\mathrm{E}-11$	$1.62\mathrm{E}-07$	$2.52\mathrm{E}-08$
Ackley	$8.72\mathrm{E}-06$	$4.54\mathrm{E}-04$	$1.18\mathrm{E}-04$	Ackley	$1.12\mathrm{E}-05$	$6.40\mathrm{E}-04$	$1.73\mathrm{E}-04$
Zakharov	$7.33\mathrm{E}-05$	$1.80\mathrm{E}-03$	$2.71\mathrm{E}-04$	Zakharov	$9.73\mathrm{E}-05$	$1.14\mathrm{E}-01$	$1.69\mathrm{E}-03$
Sum Square	$4.82\mathrm{E}-06$	$1.05\mathrm{E}-04$	$3.59\mathrm{E}-05$	Sum Square	$6.43\mathrm{E}-05$	$2.00\mathrm{E}-03$	$6.33\mathrm{E}-04$

, the averages of the 30 experiments for each mathematical function are shown. The best and worst results for each mathematical function and the overall average obtained in each function for each method are also shown. The results are with the original algorithm and the best fuzzy system, in this case FHS3 with rules in increase in the output range from 0.7 to 1. The results obtained in this case are better only in two benchmark functions; other evidence is not significant since similar results are obtained.

The results of an analysis of Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10 and Table 11 applying the three proposed fuzzy systems to benchmark mathematical functions using the output range of 0 to 1 with increment and decrement rules, as well as the range of 0.7 to 1 with rules in increment and decrement, are compared in

Table 12. Comparison of results obtained with all the proposed methods.

Function	Simple HS	FHS1	FHS2	FHS3
Spherical	$6.57\mathrm{E}-05$	$5.28\mathrm{E}-05$	$1.38\mathrm{E}-05$	$3.39\mathrm{E}-05$
Rosenbrock	$4.88\mathrm{E}-04$	$6.33\mathrm{E}-07$	$1.76\mathrm{E}-11$	$9.52\mathrm{E}-12$
Rastrigin	$2.26\mathrm{E}-08$	$1.36\mathrm{E}-08$	$1.08\mathrm{E}-08$	$2.52\mathrm{E}-08$
Ackley	$1.18\mathrm{E}-04$	$7.87\mathrm{E}-05$	$9.55\mathrm{E}-06$	$1.73\mathrm{E}-04$
Zakharov	$2.71\mathrm{E}-04$	$1.25\mathrm{E}-04$	$4.72\mathrm{E}-05$	$1.69\mathrm{E}-03$
Sum Square	$3.59\mathrm{E}-05$	$3.72\mathrm{E}-06$	$2.53\mathrm{E}-06$	$6.33\mathrm{E}-04$
Average	$1.63\mathrm{E}-04$	$4.35\mathrm{E}-05$	$1.22\mathrm{E}-05$	$4.22\mathrm{E}-04$

.

In Table 12, the overall averages obtained for each mathematical function of the three proposed fuzzy methods can be found. Figure 15 shows the data plot of the three proposals; it is noteworthy that the best algorithm is the fuzzy harmony search with dynamic adjustment of the PArate parameter (FHS2).

Based on these experiments of the proposed methods and the original method (with parameters by trial and error), the conclusion is that, for the best results, the most effective range is from 0.7 to 1 and with the rules in increase.

5. Comparison between of Fuzzy Harmony Search Algorithm (FHS) and of Fuzzy Bat Algorithm (FBA)

This section presents a comparison between two metaheuristic algorithms that apply fuzzy logic to dynamically adapt some of its parameters. In this case it was decided to choose the fuzzy harmony search algorithm with increasing parameters of pitch adjustment since, according to the three proposals that made in this paper, this one obtained better results. This was tested with six benchmark mathematical functions and ten dimensions in each of its harmonies (number of vector solution) or bats that were used; note that the results of the fuzzy bat algorithm was taken from the literature [6]. The following tables show the behavior of each of the methods.

Table 13. Experiment results obtained for the sphere function with FBA and FHS algorithms.

FBA				FHS
Num. Bats	Best	Worst	Average	Num. Harmonies	Best	Worst	Average
2	$3.47\mathrm{E}-03$	$1.54\mathrm{E}+00$	$1.10\mathrm{E}-01$	2	$1.01\mathrm{E}-07$	$2.64\mathrm{E}-04$	$5.84\mathrm{E}-05$
5	$1.09\mathrm{E}-04$	$9.37\mathrm{E}-01$	$1.28\mathrm{E}-01$	5	$1.54\mathrm{E}-09$	$1.19\mathrm{E}-05$	$9.28\mathrm{E}-07$
10	$5.53\mathrm{E}-06$	$1.60\mathrm{E}-04$	$1.20\mathrm{E}-04$	10	$1.10\mathrm{E}-06$	$9.42\mathrm{E}-05$	$1.63\mathrm{E}-05$
20	$2.77\mathrm{E}-06$	$2.30\mathrm{E}-04$	$9.82\mathrm{E}-05$	20	$1.86\mathrm{E}-08$	$2.48\mathrm{E}-05$	$4.17\mathrm{E}-06$
30	$9.31\mathrm{E}-06$	$4.50\mathrm{E}-04$	$9.99\mathrm{E}-05$	30	$1.57\mathrm{E}-08$	$1.99\mathrm{E}-05$	$2.65\mathrm{E}-06$
40	$2.74\mathrm{E}-06$	$6.10\mathrm{E}-04$	$9.34\mathrm{E}-05$	40	$1.92\mathrm{E}-08$	$2.47\mathrm{E}-06$	$3.46\mathrm{E}-07$

shows the overall averages for each method according to the number of bats or harmonies used, as well as the best and the worst results obtained for the sphere function.

In

Table 14. Experiment results obtained for the Ackley function with the FBA and FHS algorithms.

FBA				FHS
Num. Bats	Best	Worst	Average	Num. Harmonies	Best	Worst	Average
2	$3.81\mathrm{E}-05$	$9.52\mathrm{E}-01$	$4.60\mathrm{E}-01$	2	$2.64\mathrm{E}-08$	$1.67\mathrm{E}-04$	$1.94\mathrm{E}-05$
5	$1.07\mathrm{E}-05$	$6.69\mathrm{E}-01$	$2.23\mathrm{E}-01$	5	$1.07\mathrm{E}-08$	$1.38\mathrm{E}-04$	$5.53\mathrm{E}-06$
10	$2.76\mathrm{E}-07$	$2.00\mathrm{E}+00$	$1.13\mathrm{E}+00$	10	$8.46\mathrm{E}-08$	$4.28\mathrm{E}-04$	$1.62\mathrm{E}-05$
20	$4.41\mathrm{E}-07$	$3.45\mathrm{E}+00$	$9.60\mathrm{E}-01$	20	$1.98\mathrm{E}-08$	$6.08\mathrm{E}-05$	$4.05\mathrm{E}-06$
30	$3.19\mathrm{E}-06$	$2.05\mathrm{E}+00$	$9.22\mathrm{E}-01$	30	$2.63\mathrm{E}-08$	$5.99\mathrm{E}-06$	$1.50\mathrm{E}-06$
40	$3.91\mathrm{E}-06$	$1.56\mathrm{E}+00$	$4.17\mathrm{E}-01$	40	$1.40\mathrm{E}-08$	$9.02\mathrm{E}-05$	$1.05\mathrm{E}-05$

, the overall averages for each method according to the number of bats or harmonies used can be observed, as well as the best and the worst results obtained for the Ackley function.

In

Table 15. Experiment results obtained for the Rosenbrock function with the FBA and FHS algorithms.

FBA				FHS
Num. Bats	Best	Worst	Average	Num. Harmonies	Best	Worst	Average
2	$0.00\mathrm{E}+00$	$5.29\mathrm{E}-01$	$1.11\mathrm{E}-01$	2	$1.00\mathrm{E}-12$	$2.80\mathrm{E}-10$	$2.38\mathrm{E}-11$
5	$1.67\mathrm{E}-03$	$1.71\mathrm{E}+00$	$6.60\mathrm{E}-01$	5	$8.86\mathrm{E}-14$	$1.20\mathrm{E}-10$	$1.42\mathrm{E}-11$
10	$0.00\mathrm{E}+00$	$1.40\mathrm{E}-03$	$6.13\mathrm{E}-04$	10	$4.58\mathrm{E}-13$	$6.50\mathrm{E}-11$	$1.12\mathrm{E}-11$
20	$1.83\mathrm{E}-02$	$1.00\mathrm{E}+00$	$5.09\mathrm{E}-01$	20	$2.33\mathrm{E}-13$	$8.56\mathrm{E}-11$	$1.85\mathrm{E}-11$
30	$2.39\mathrm{E}-02$	$8.69\mathrm{E}-01$	$5.31\mathrm{E}-01$	30	$2.33\mathrm{E}-13$	$8.56\mathrm{E}-11$	$1.85\mathrm{E}-11$
40	$3.32\mathrm{E}-02$	$1.00\mathrm{E}+00$	$3.94\mathrm{E}-01$	40	$5.44\mathrm{E}-14$	$1.35\mathrm{E}-10$	$1.96\mathrm{E}-11$

, the overall averages for each method according to the number of bats or harmonies used can be observed, as well as the best and the worst results obtained for the Rosenbrock function.

In

Table 16. Experiment results for the Zakharov function with the FBA and FHS algorithms.

FBA				FHS
Num. Bats	Best	Worst	Average	Num. Harmonies	Best	Worst	Average
2	$7.84\mathrm{E}-06$	$7.81\mathrm{E}-01$	$3.42\mathrm{E}-01$	2	$1.40\mathrm{E}-07$	$7.55\mathrm{E}-04$	$1.59\mathrm{E}-04$
5	$8.21\mathrm{E}-06$	$6.38\mathrm{E}-01$	$2.71\mathrm{E}-01$	5	$1.20\mathrm{E}-10$	$7.15\mathrm{E}-04$	$4.46\mathrm{E}-05$
10	$2.31\mathrm{E}-06$	$2.15\mathrm{E}-01$	$1.07\mathrm{E}-01$	10	$1.10\mathrm{E}-09$	$6.94\mathrm{E}-04$	$2.58\mathrm{E}-05$
20	$4.44\mathrm{E}-06$	$1.55\mathrm{E}+00$	$7.01\mathrm{E}-01$	20	$1.10\mathrm{E}-10$	$9.95\mathrm{E}-05$	$2.73\mathrm{E}-05$
30	$2.58\mathrm{E}-07$	$8.83\mathrm{E}-01$	$3.88\mathrm{E}-01$	30	$1.40\mathrm{E}-09$	$9.02\mathrm{E}-05$	$1.95\mathrm{E}-05$
40	$2.61\mathrm{E}-07$	$7.77\mathrm{E}-01$	$3.84\mathrm{E}-01$	40	$9.60\mathrm{E}-09$	$9.61\mathrm{E}-05$	$7.56\mathrm{E}-06$

, the overall averages for each method according to the number of bats or harmonies used can be observed, as well as the best and the worst results obtained for the Zakharov function.

In

Table 17. Experiment results for the Rastrigin function with the FBA and FHS algorithms.

FBA				FHS
Num. Bats	Best	Worst	Average	Num. Harmonies	Best	Worst	Average
2	$1.63\mathrm{E}-05$	$9.34\mathrm{E}-01$	$3.50\mathrm{E}-01$	2	$1.06\mathrm{E}-10$	$6.60\mathrm{E}-08$	$9.62\mathrm{E}-09$
5	$4.63\mathrm{E}-05$	$9.95\mathrm{E}-01$	$5.29\mathrm{E}-01$	5	$1.90\mathrm{E}-11$	$2.95\mathrm{E}-08$	$2.46\mathrm{E}-09$
10	$1.43\mathrm{E}-06$	$7.29\mathrm{E}-01$	$3.64\mathrm{E}-01$	10	$1.08\mathrm{E}-10$	$1.28\mathrm{E}-07$	$1.91\mathrm{E}-08$
20	$1.06\mathrm{E}-05$	$3.54\mathrm{E}-01$	$1.77\mathrm{E}-01$	20	$1.85\mathrm{E}-10$	$3.62\mathrm{E}-08$	$4.86\mathrm{E}-09$
30	$6.21\mathrm{E}-06$	$8.73\mathrm{E}-01$	$2.39\mathrm{E}-01$	30	$1.20\mathrm{E}-11$	$9.32\mathrm{E}-08$	$1.59\mathrm{E}-08$
40	$2.98\mathrm{E}-06$	$6.86\mathrm{E}-01$	$3.32\mathrm{E}-01$	40	$1.43\mathrm{E}-10$	$7.42\mathrm{E}-08$	$1.27\mathrm{E}-08$

, the overall averages for each method according to the number of bats or harmonies used can be found, as well as the best and the worst results obtained for the Rastrigin function.

In

Table 18. Experiment results for the function sum squared with FBA and FHS algorithms.

FBA				FHS
Num. Bats	Best	Worst	Average	Num. Harmonies	Best	Worst	Average
2	$8.67\mathrm{E}-03$	$8.39\mathrm{E}-01$	$5.20\mathrm{E}-01$	2	$2.60\mathrm{E}-08$	$4.20\mathrm{E}-06$	$1.74\mathrm{E}-06$
5	$9.40\mathrm{E}-03$	$7.50\mathrm{E}-01$	$4.43\mathrm{E}-01$	5	$2.00\mathrm{E}-07$	$5.50\mathrm{E}-06$	$2.51\mathrm{E}-06$
10	$3.92\mathrm{E}-02$	$9.17\mathrm{E}-01$	$6.12\mathrm{E}-01$	10	$4.00\mathrm{E}-08$	$5.00\mathrm{E}-06$	$1.55\mathrm{E}-06$
20	$1.39\mathrm{E}-02$	$8.51\mathrm{E}-01$	$4.46\mathrm{E}-01$	20	$3.10\mathrm{E}-07$	$5.10\mathrm{E}-06$	$3.12\mathrm{E}-06$
30	$1.50\mathrm{E}-02$	$9.45\mathrm{E}-01$	$3.21\mathrm{E}-01$	30	$3.60\mathrm{E}-07$	$4.70\mathrm{E}-06$	$3.02\mathrm{E}-06$
40	$1.82\mathrm{E}-03$	$8.31\mathrm{E}-01$	$2.97\mathrm{E}-01$	40	$3.40\mathrm{E}-07$	$5.40\mathrm{E}-06$	$3.24\mathrm{E}-06$

, the overall averages for each method according to the number of bats or harmonies used can be observed, as well as the best and the worst results obtained for the sum squared function.

6. Statistical Comparison

A statistical comparison is also made between the fuzzy bat algorithm (FBA) and the fuzzy harmony search algorithm (FHS), to evaluate the efficiency of each method on each of the six mathematical functions applied.

The statistical test for comparison is the Wilcoxon matched pairs test, which can be used to analyze the data, and whose parameters are given in

Table 19. Parameters for the Wilcoxon statistical test.

		F1	F2
Function	No.	FBA	FHS	Difference	abs(Difference)	Rank	Sign	Signed Rank(+)
Spherical	1	$3.97\mathrm{E}-02$	$1.38\mathrm{E}-05$	$3.97\mathrm{E}-02$	$3.97\mathrm{E}-02$	1	1	1
Rosenbrock	2	$6.85\mathrm{E}-01$	$1.76\mathrm{E}-11$	$6.85\mathrm{E}-01$	$6.85\mathrm{E}-01$	6	1	6
Rastrigin	3	$3.68\mathrm{E}-01$	$1.08\mathrm{E}-08$	$3.68\mathrm{E}-01$	$3.68\mathrm{E}-01$	4	1	4
Ackley	4	$3.66\mathrm{E}-01$	$9.55\mathrm{E}-06$	$3.65\mathrm{E}-01$	$3.65\mathrm{E}-01$	3	1	3
Zakharov	5	$3.32\mathrm{E}-01$	$4.72\mathrm{E}-05$	$3.32\mathrm{E}-01$	$3.32\mathrm{E}-01$	2	1	2
Sum Square	6	$4.40\mathrm{E}-01$	$1.38\mathrm{E}-05$	$4.40\mathrm{E}-01$	$4.40\mathrm{E}-01$	5	1	5

.

The alternative hypothesis states that the average of the results of the fuzzy harmony search algorithm is different than the average performance of the fuzzy bat algorithm, and therefore the null hypothesis tells us that the average of the results of the fuzzy harmony search algorithm is equal to the average of the fuzzy bat algorithm.

To test the hypothesis, first the absolute values │$Z_i$│…│$Z_n$│ are sorted and assigned their range rank; the sign column indicates that all values obtained are positive; the signed rank column indicates the order of these values from lowest to highest.

The formula of the statistical test is applied:

$$W^{+}={\displaystyle \sum }_{\approx i>0}{R}_i$$

(7)

That is, the sum of the ranges $R_i$ corresponding to positive values $Z_i$.

The value of $W^{+}$ is the sum of the positive ranks, the value W⁻ is the sum of the negative ranks, W is the differences between two data samples, and W0 indicates the value of the table for a two-tailed test using 30 samples.

The test to evaluate is as follows:

If W ≤ W0, then reject Ho.

Table 20. Values of parameters for the statistical test.

${\mathit{W}}^{-}$	${\mathit{W}}^{+}$	W	Level Significance	m = Degrees of Freedom	W0 = W α, m
0	21	0	0.05	6	1

shows a statistical test applied to the two fuzzy methods. In applying the Wilcoxon statistic, with a confidence level of 95% and a value of W = 0 and W0 = 1, the W ≤ W0 condition is satisfied, so the statistical test results are as follows: for the fuzzy harmony search, there is significant evidence to reject the null hypothesis and the alternative hypothesis is accepted stating that the average fuzzy harmony search algorithm is different than the average performance of the fuzzy bat algorithm. In summary, one can state that the fuzzy harmony search outperforms the fuzzy bat algorithm for this set of benchmark functions.

7. Conclusions

The harmony search (HS) algorithm is a relatively new method which can solve various kinds of problems in an easy and effective manner, as it requires many complex calculations. HS can handle the discrete and continuous variables and can be applied to linear and nonlinear functions.

Currently, the parameters of the algorithms are set by trial and error. In this paper, a new algorithm was proposed to achieve better convergence and not stay in local optima.

This paper presents a new algorithm to search for harmony with adjustable fuzzy parameters, in order for the fuzzy system to dynamically move the parameters of this algorithm and subsequently obtain a faster convergence and better results than the original method and others existing in the literature.

The paper proposed three different fuzzy systems to initially move each parameter independently of the algorithm. The harmony memory accepting (HMR) parameter provides exploitation ability to the algorithm, and pitch adjustment (PArate) is controlled by the scanning algorithm; it has a combination of both parameters and each of the changes make mathematical functions applied it to benchmark to test the efficiency of the algorithm.

Finally, an analysis of the results of each of the proposed methods led to the conclusion that when using a range between 0.7 and 1 in each of the parameters, and moving them dynamically using a fuzzy system, better results are achieved with the original method and the other existing methods in the literature applied, in this case, to six mathematical functions benchmarks. However, more variations with the rules of the FHS3 are needed to obtain a significant advantage in all function benchmarks. In the future, when the method is applied to more complex math functions and more dimensions, it is expected to achieve good results in the same number of iterations. Future work includes testing the proposed fuzzy harmony search with other functions and real world applications. In addition, type-2 fuzzy logic could be used instead of type-1, as is done in this paper.