Robust Hessian Locally Linear Embedding Techniques for High-Dimensional Data
Abstract
:1. Introduction
- (1)
- We reformulate the original HLLE algorithm through the truncation function from differential manifold [24]. As far as we know, we are the first to explicitly relate the truncation function from differential manifold to a classical manifold learning method, i.e., HLLE, to explain the connection between the local geometric object and the global geometric object of the manifold. With the help of this reformulation, we explicitly propose a weighted global functional to reduce the influence of outliers and noises.
- (2)
- We propose a fast outlier detection method based on robust statistics [25]. In contrast to the traditional RPCA-based algorithms, our method is much more efficient for high-dimensional datasets. Our proposed method can be successfully applied to the existing manifold learning algorithms to improve their robustness.
- (3)
- As reviewed in this section, the related works are suitable for either the outlier or noise problem. In contrast, our RHLLE algorithm is robust against both outliers and noises.
2. Reformulating HLLE through Truncation Function from Differential Manifold
2.1. Brief Review of Hessian LLE
- (1)
- Find nearest neighbors: For each data point , find the indices corresponding to the k-nearest neighbors in Euclidean distance. Let denote the collection of those neighbors.
- (2)
- Obtain tangent coordinates: Perform a singular value decomposition on the points in , getting their tangent coordinates.
- (3)
- Develop Hessian estimator: Develop the infrastructure for least-squares estimation of the local Hessian operator .
- (4)
- Develop quadratic form: Build a symmetric matrix having, in coordinate pair , the entry . approximates the continuous operator .
- (5)
- Compute the embedding from the estimated functional: Perform an eigenanalysis of and choose Y to be the eigenvectors corresponding to the d smallest eigenvalues, excluding the constant eigenvector.
2.2. Reformulating Hessian LLE
3. Sensitivity of Hessian LLE to Outliers and Noise
4. Robust Hessian Locally Linear Embedding
4.1. Robust PCA
- (1)
- Perform PCA to compute the orthonormal basis matrix and displacement of the local tangent space. Set .
- (2)
- Repeat until convergence:
- (a)
- Compute ;
- (b)
- Compute according to (16), where
- (c)
- Compute the weighted least squares estimates and according to (14 15), where
- (d)
- if , return;else .
4.2. Fast Outlier Identifying Algorithm
Step 1
- (1)
- Set the initial mean . Set .
- (2)
- Repeat until convergence:
- (a)
- Compute according to Equation (17);
- (b)
- update the mean
- (c)
- if (we set in our experiments), return;else .
Step 2
4.3. Noise Reduction Using Local Linear Smoothing
- (1)
- For each sample , find the k nearest neighbors of including itself:
- (2)
- Compute the weights using an iterative weight selection procedure.
- (3)
- Compute an approximation of the tangent space at by a weighted PCA according to Equation (13);
- (4)
- Project to the approximate tangent subspace to obtain:
4.4. Robust Hessian Locally Linear Embedding
- (1)
- Perform the fast outlier identifying algorithm described in Section 4.2 on the dataset , and obtain the ddataset whose outliers have been removed.
- (2)
- Perform the local smoothing procedure described in Section 4.3 on the dataset , and obtain the noise reduction dataset .
- (3)
- (a)
- Find the k nearest neighbors for each point as the HLLE algorithm does.
- (b)
- Compute the total reliability scores for each local patch , and determine the reliable local patch subset .
- (c)
- Compute the local tangent coordinates and the local Hessian operator for each local patch as described in Section 2.2.
- (d)
- Compute the weighted global functional instead of the global functional in Equation (11) which measures the average “curviness” of the manifold :
- (4)
- Perform an eigenanalysis of and choose the low-dimensional embedding coordinates Y to be the eigenvectors of with d smallest eigenvalues, excluding the constant eigenvector.
5. Experiments
5.1. Synthetic Data
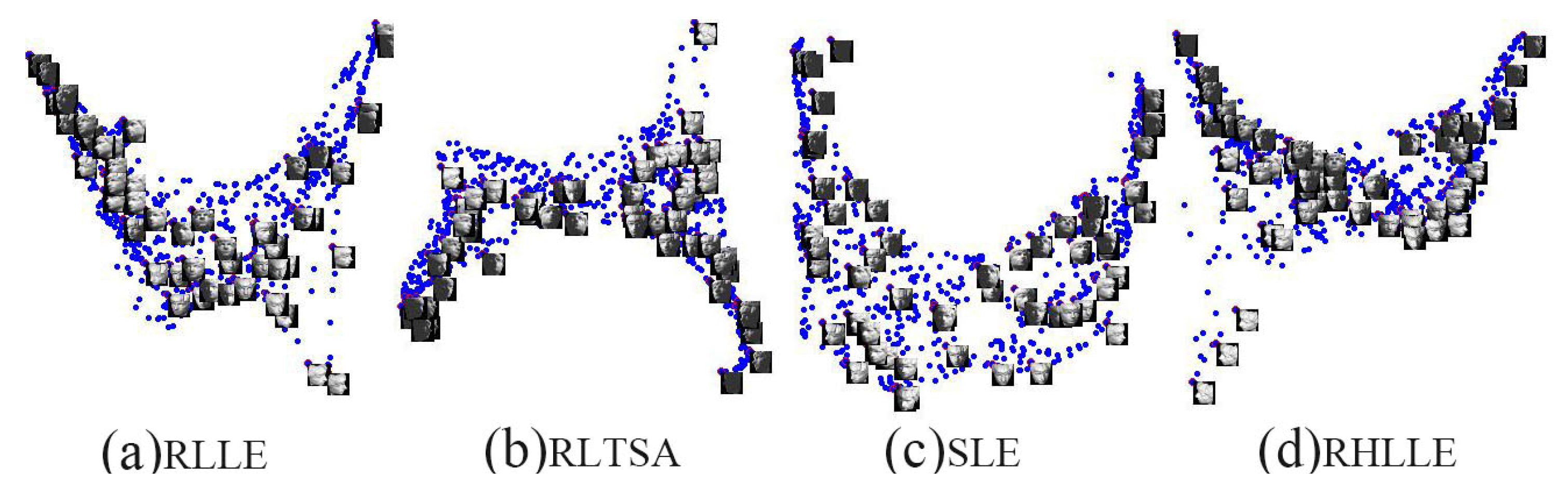
5.2. High-Dimensional Image Datasets
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tenenbaum, J.B.; de Silva, V.; Langford, J.C. A global geometric framework for nonlinear dimensionality reduction. Science 2000, 290, 2319–2323. [Google Scholar] [CrossRef] [PubMed]
- Roweis, S.T.; Saul, L.K. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef] [PubMed]
- Belkin, M.; Niyogi, P. Laplacian eigenmaps and spectral techniques for embedding and clustering. In Advances in Neural Information Processing Systems 14 (NIPS); Dietterich, T.G., Becker, S., Ghahramani, Z., Eds.; Neural information processing systems foundation: Vancouver, BC, Canada, 2001; Volume 14, pp. 585–591. [Google Scholar]
- Zhang, Z.Y.; Zha, H.Y. Principal manifolds and nonlinear dimensionality reduction via tangent space alignment. J. Shanghai Univ. (Engl. Ed.) 2004, 8, 406–424. [Google Scholar] [CrossRef]
- Donoho, D.L.; Grimes, C. Hessian eigenmaps: Locally linear embedding techniques for high-dimensional data. Proc. Natl. Acad. Sci. 2003, 100, 5591–5596. [Google Scholar] [CrossRef] [PubMed]
- Weinberger, K.Q.; Saul, L.K. Unsupervised learning of image manifolds by semidefinite programming. Int. J. Comput. Vis. 2006, 70, 77–90. [Google Scholar] [CrossRef]
- Lin, T.; Zha, H. Riemannian manifold learning. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 796–809. [Google Scholar] [PubMed]
- Wang, R.; Shan, S.; Chen, X.; Chen, J.; Gao, W. Maximal linear embedding for dimensionality reduction. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 1776–1792. [Google Scholar] [CrossRef] [PubMed]
- Xing, X.; Wang, K.; Lv, Z.; Zhou, Y.; Du, S. Fusion of Local Manifold Learning Methods. IEEE Signal Process. Lett. 2015, 22, 395–399. [Google Scholar] [CrossRef]
- Seung, H.S.; Lee, D.D. The manifold ways of perception. Science 2000, 290, 2268–2269. [Google Scholar] [CrossRef] [PubMed]
- Belkin, M.; Niyogi, P.; Sindhwani, V. Manifold regularization: A geometric framework for learning from labeled and unlabeled examples. J. Mach. Learn. Res. 2006, 7, 2399–2434. [Google Scholar]
- Xing, X.; Yu, Y.; Jiang, H.; Du, S. A multi-manifold semi-supervised Gaussian mixture model for pattern classification. Pattern Recognit. Lett. 2013, 34, 2118–2125. [Google Scholar] [CrossRef]
- Souvenir, R.; Pless, R. Manifold clustering. In Proceeding of the Tenth IEEE International Conference on Computer Vision, ICCV 2005, Beijing, China, 17–21 October 2005; Volume 1, pp. 648–653.
- Hawkins, D.M. Identification of Outliers; Springer: New York, NY, USA, 1980; Chapter 1. [Google Scholar]
- Chang, H.; Yeung, D.Y. Robust locally linear embedding. Pattern Recognit. 2006, 39, 1053–1065. [Google Scholar] [CrossRef]
- De La Torre, F.; Black, M.J. A framework for robust subspace learning. Int. J. Comput. Vis. 2003, 54, 117–142. [Google Scholar] [CrossRef]
- Zhan, Y.; Yin, J. Robust local tangent space alignment via iterative weighted PCA. Neurocomputing 2011, 74, 1985–1993. [Google Scholar] [CrossRef]
- Zhang, Z.; Zha, H. Local Linear Smoothing for Nonlinear Manifold Learning; Technical Report; CSE, Penn State University: Old Main, PA, USA, 2003. [Google Scholar]
- Park, J.; Zhang, Z.; Zha, H.; Kasturi, R. Local smoothing for manifold learning. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 27 June–2 July 2004; Volume 2, pp. 445–452.
- Hein, M.; Maier, M. Manifold denoising. In Advances in Neural Information Processing Systems 19 (NIPS); Schölkopf, B., Platt, J.C., Hoffman, T., Eds.; Neural Information Processing System Foundation: Vancouver, BC, Canada, 2006; Volume 19, pp. 561–568. [Google Scholar]
- Zhou, D.; Bousquet, O.; Lal, T.N.; Weston, J.; Schölkopf, B. Learning with Local and Global Consistency. In Advances in Neural Information Processing Systems 16 (NIPS); Thrun, S., Saul, L.K., Schölkopf, B., Eds.; Neural Information Processing Systems Foundation: Vancouver, BC, Canada, 2003; Volume 16, pp. 321–328. [Google Scholar]
- Xing, X.; Du, S.; Jiang, H. Semi-Supervised Nonparametric Discriminant Analysis. IEICE Trans. Inf. Syst. 2013, 96, 375–378. [Google Scholar] [CrossRef]
- Gashler, M.; Martinez, T. Robust manifold learning with CycleCut. Connect. Sci. 2012, 24, 57–69. [Google Scholar] [CrossRef]
- Chern, S.S.; Chen, W.H.; Lam, K.S. Lectures on Differential Geometry; World Scientific Pub Co Inc.: Singapore, 1999; Volume 1. [Google Scholar]
- Huber, P.J. Robust Statistics; Springer: Berlin, Germany, 2011. [Google Scholar]
- Kim, K.I.; Steinke, F.; Hein, M. Semi-Supervised Regression Using Hessian Energy with an Application to Semi-Supervised Dimensionality Reduction. In Advances in Neural Information Processing Systems 22 (NIPS); Bengio, Y., Schuurmans, D., Lafferty, J.D., Williams, C.K.I., Culotta, A., Eds.; Neural Information Processing Systems Foundation: Vancouver, BC, Canada, 2009; Volume 22, pp. 979–987. [Google Scholar]
- Lin, B.; He, X.; Zhang, C.; Ji, M. Parallel vector field embedding. J. Mach. Learn. Res. 2013, 14, 2945–2977. [Google Scholar]
- Lin, B.; Zhang, C.; He, X. Semi-Supervised Regression via Parallel Field Regularization. In Advances in Neural Information Processing Systems 24 (NIPS); Shawe-Taylor, J., Zemel, R.S., Bartlett, P.L., Pereira, F., Weinberger, K.Q., Eds.; Neural Information Processing Systems Foundation: Granada, Spain, 2011; Volume 24. [Google Scholar]
- Turk, M.; Pentland, A. Eigenfaces for recognition. J. Cognit. Neurosci. 1991, 3, 71–86. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Qiao, H.; Zhang, B. An improved local tangent space alignment method for manifold learning. Pattern Recognit. Lett. 2011, 32, 181–189. [Google Scholar] [CrossRef]
- De la Torre, F.; Black, M.J. Robust principal component analysis for computer vision. In Proceeding of the Eighth IEEE International Conference on Computer Vision, 2001. ICCV 2001, Vancouver, BC, USA; 2001; Volume 1, pp. 362–369. [Google Scholar]
- Holland, P.W.; Welsch, R.E. Robust regression using iteratively reweighted least-squares. Commun. Stat. Theory Methods 1977, 6, 813–827. [Google Scholar] [CrossRef]
- Huber, P.J. Robust regression: Asymptotics, conjectures and Monte Carlo. Ann. Stat. 1973, 1, 799–821. [Google Scholar] [CrossRef]
- Cleveland, W.S.; Loader, C. Smoothing by Local Regression: Principles and Methods. In Statistical Theory and Computational Aspects of Smoothing; Springer: Heidelberg, Germany, 1996; pp. 10–49. [Google Scholar]
- Hou, C.; Zhang, C.; Wu, Y.; Jiao, Y. Stable local dimensionality reduction approaches. Pattern Recognit. 2009, 42, 2054–2066. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Q.; He, L.; Zhou, Z.H. Quantitative analysis of nonlinear embedding. IEEE Trans. Neural Netw. 2011, 22, 1987–1998. [Google Scholar] [CrossRef] [PubMed]
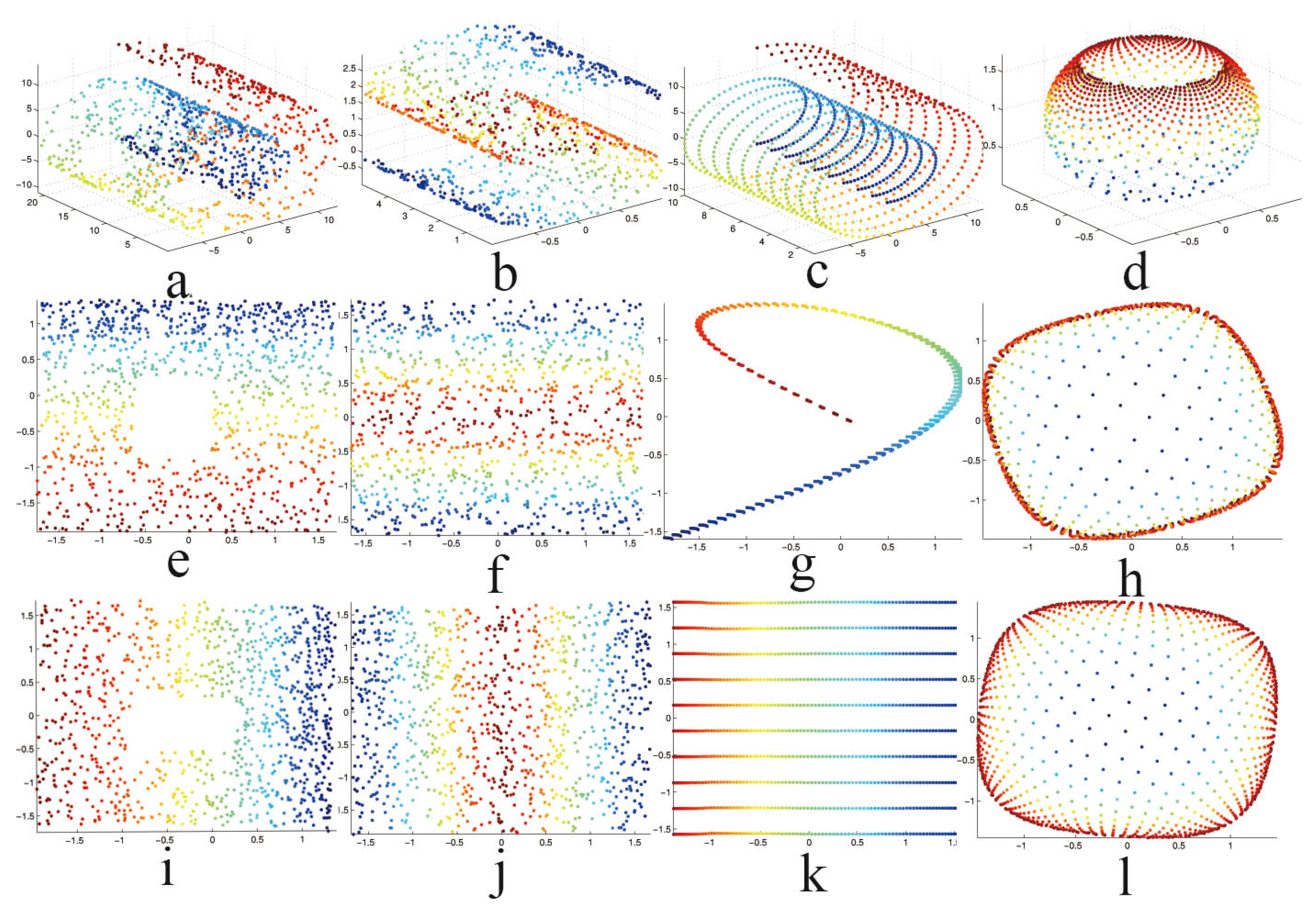
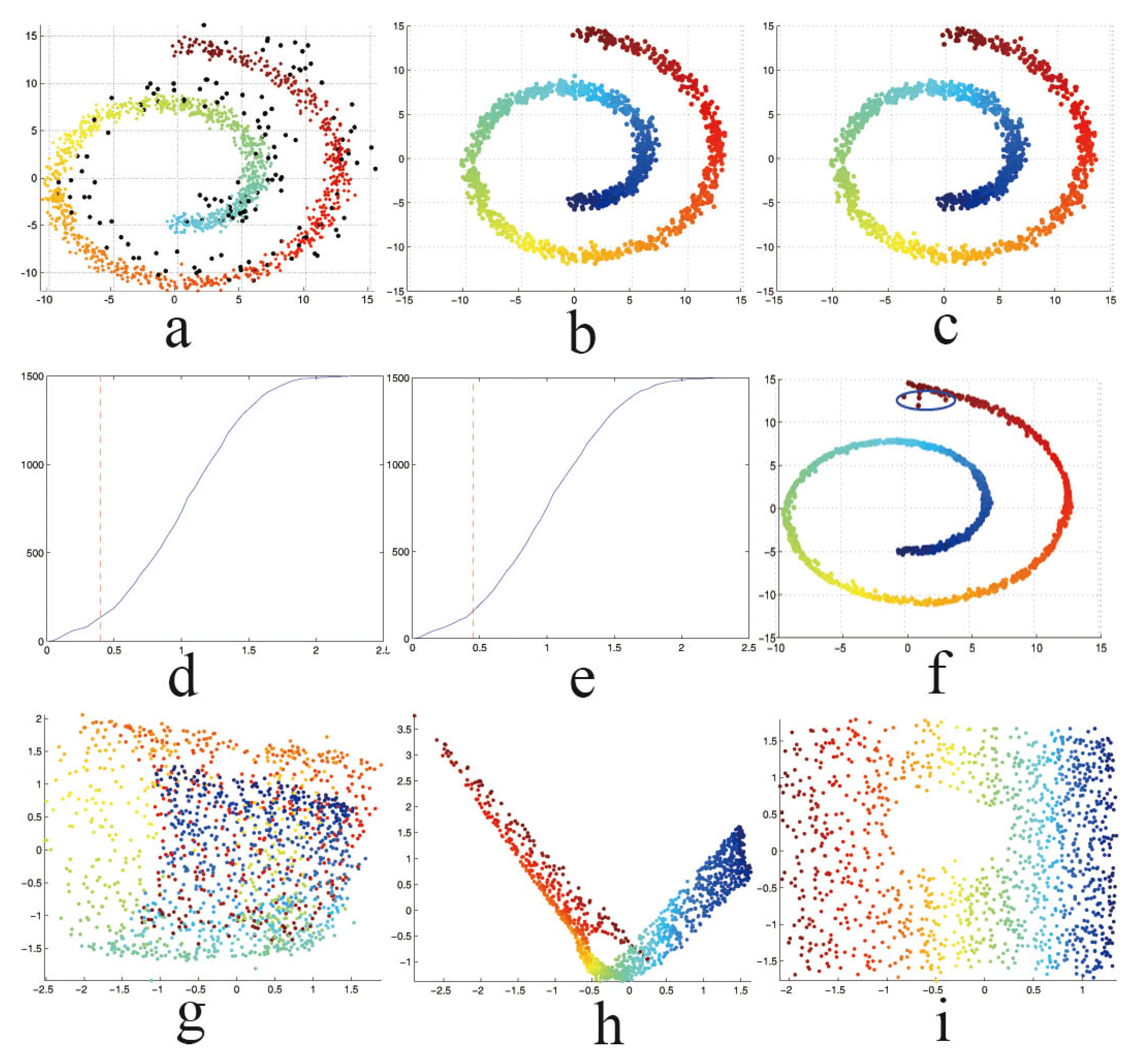
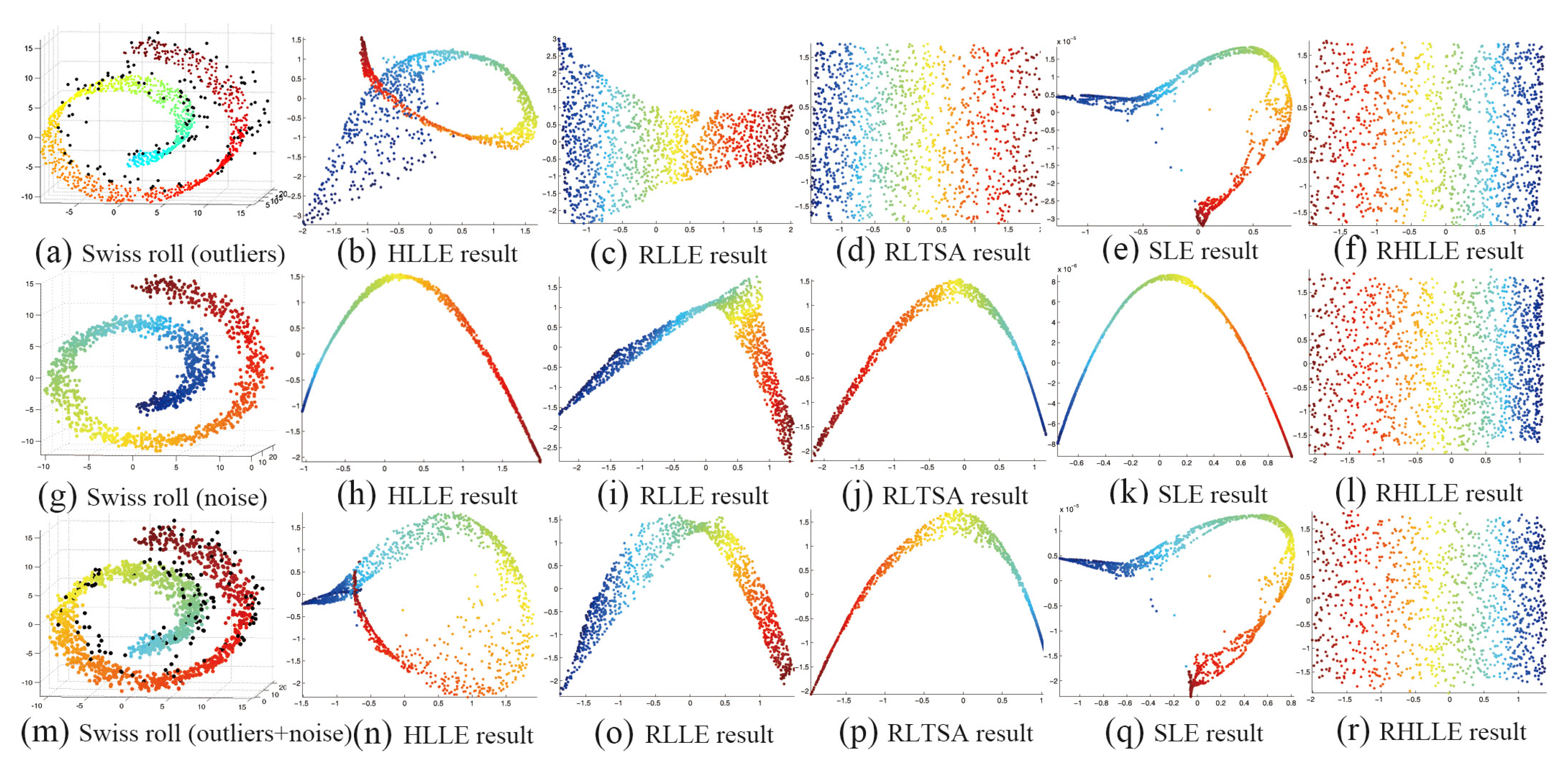
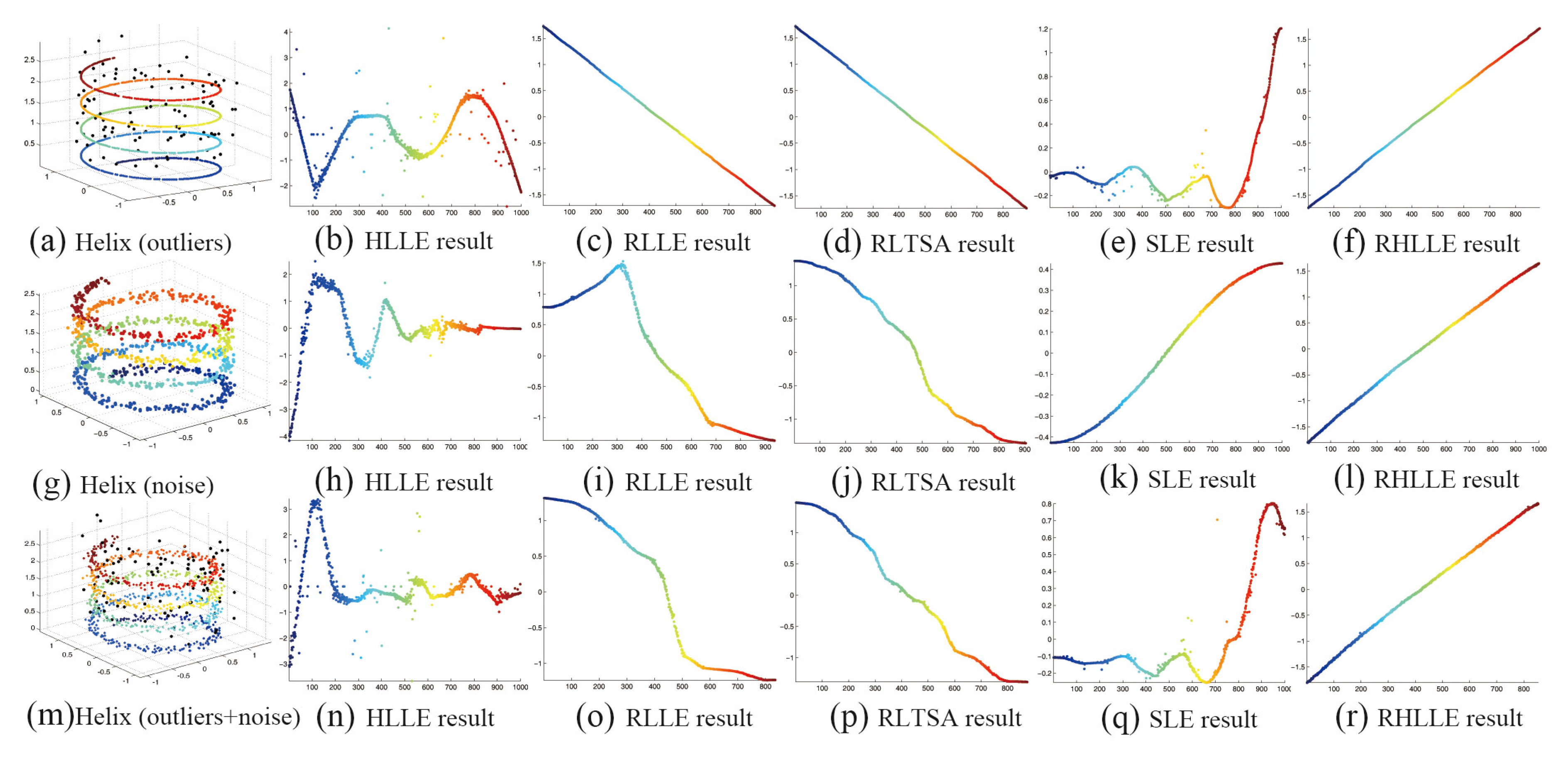

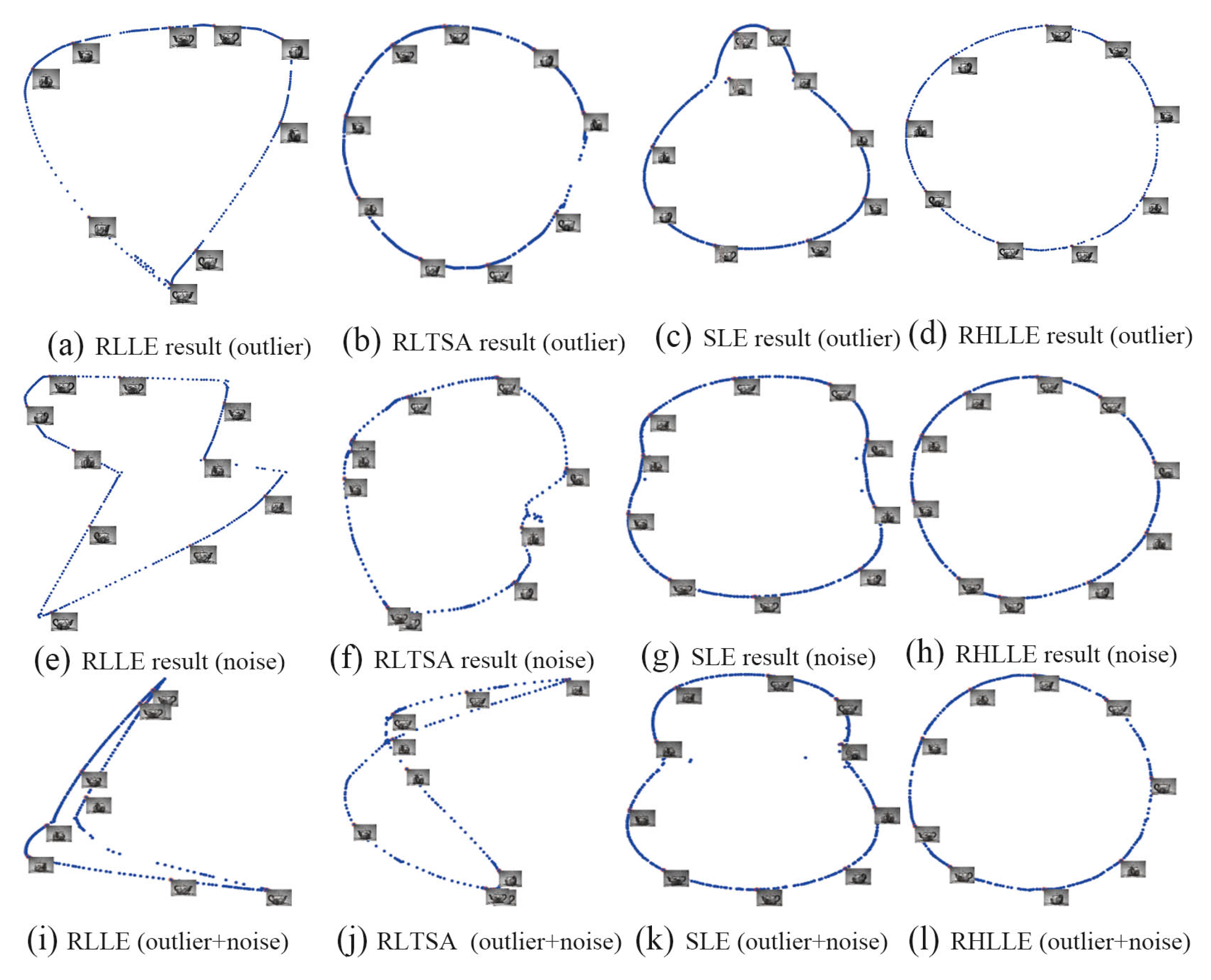
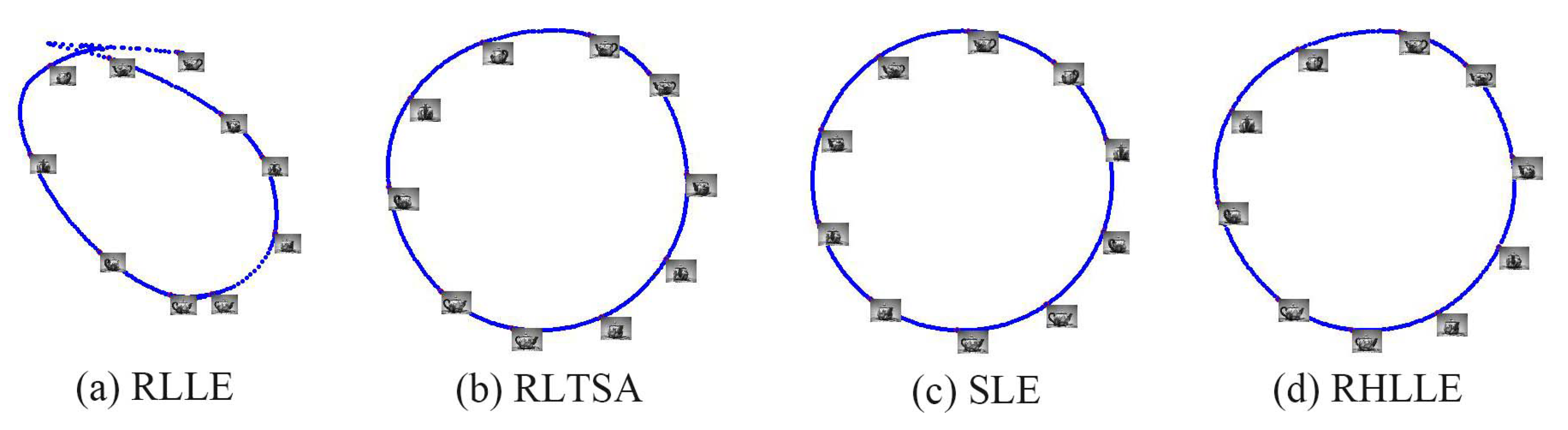

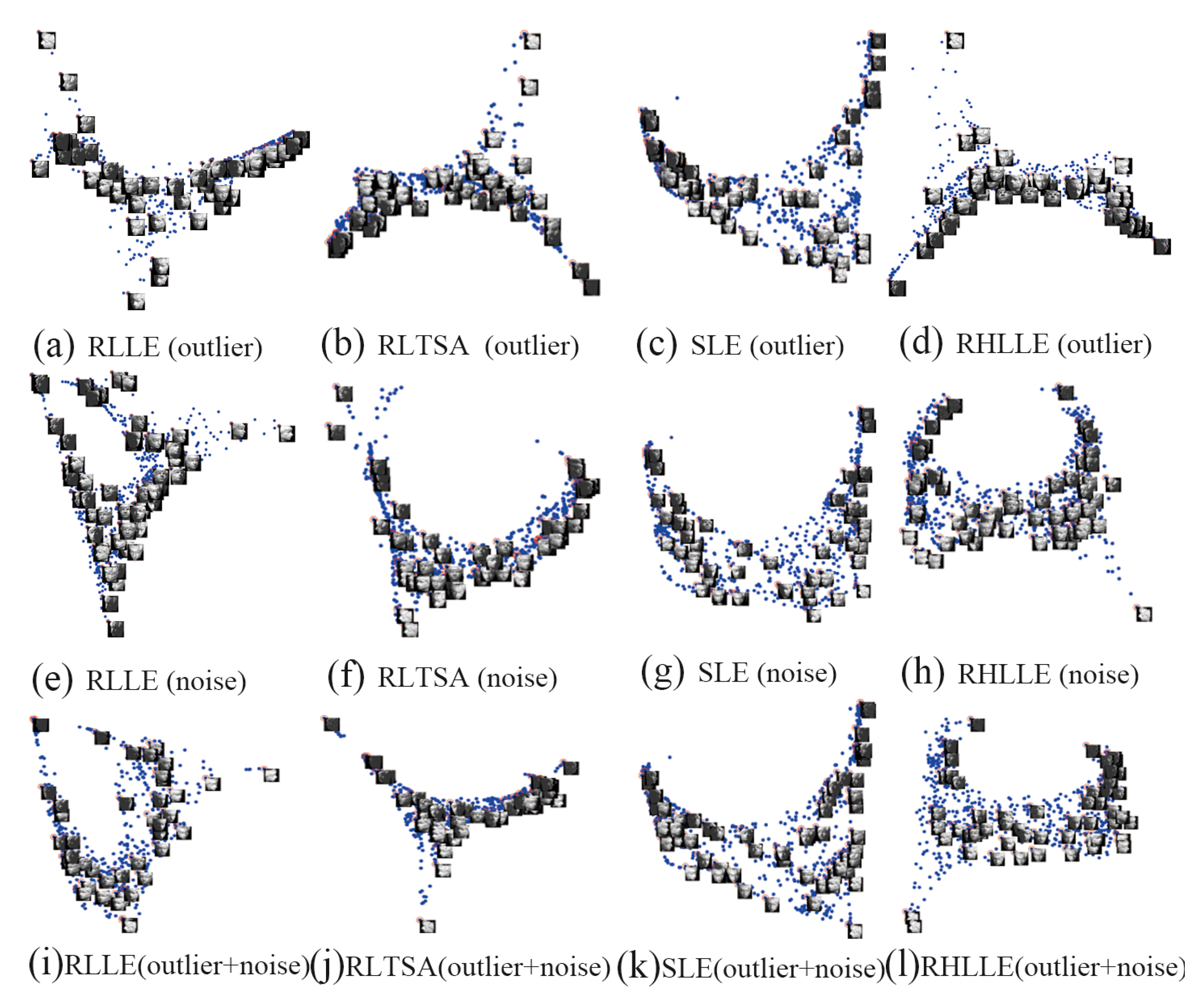
| Parameters | Swiss Roll | S-Curve | Helix |
|---|---|---|---|
| Dimensionality of ambient space (D) | 3 | 3 | 3 |
| Dimensionality of embedding space (d) | 2 | 2 | 1 |
| Number of nearest neighbors (k) | 15 | 15 | 10 |
| Number of the data points | 1500 | 1500 | 1000 |
| Percentage of outlier points | 10% | 10% | 10% |
| Amplitude of the outliers | 3 | 0.5 | 0.5 |
| Percentage of noise-corrupted points | 90% | 90% | 90% |
| Standard deviation of the Gaussian noise | 0.5 | 0.1 | 0.05 |
| Method | RLLE | RLTSA | SLE | Our RHLLE |
|---|---|---|---|---|
| Outlier | 0.2865 | 0.2411 | 0.2332 | 0.2294 |
| Noise | 0.3322 | 0.2771 | 0.1942 | 0.1843 |
| Outlier+Noise | 0.3747 | 0.3020 | 0.2148 | 0.2036 |
| Method∖Data | Swiss Roll | S Curve | Helix | Teapot | Isoface |
|---|---|---|---|---|---|
| RLLE | 1.378 | 0.976 | 0.421 | 1999.3 | 1248.7 |
| RLTSA | 1.482 | 1.081 | 0.511 | 2006.1 | 1253.9 |
| SLE | 463.2 | 477.8 | 218.5 | 10.83 | 42.65 |
| our RHLLE | 1.572 | 1.256 | 0.792 | 514.8 | 263.3 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, X.; Du, S.; Wang, K. Robust Hessian Locally Linear Embedding Techniques for High-Dimensional Data. Algorithms 2016, 9, 36. https://doi.org/10.3390/a9020036
Xing X, Du S, Wang K. Robust Hessian Locally Linear Embedding Techniques for High-Dimensional Data. Algorithms. 2016; 9(2):36. https://doi.org/10.3390/a9020036
Chicago/Turabian StyleXing, Xianglei, Sidan Du, and Kejun Wang. 2016. "Robust Hessian Locally Linear Embedding Techniques for High-Dimensional Data" Algorithms 9, no. 2: 36. https://doi.org/10.3390/a9020036
APA StyleXing, X., Du, S., & Wang, K. (2016). Robust Hessian Locally Linear Embedding Techniques for High-Dimensional Data. Algorithms, 9(2), 36. https://doi.org/10.3390/a9020036





