Abstract
The nonlinear unconditionally stable energy-conserving integration method (ECM) is a new method for solving a continuous equation of motion. To our knowledge, there is still no report about its application on a hybrid test. Aiming to explore its effect on hybrid tests, the nonlinear beam-column element program is developed for computation. The program contains both the ECM and the average acceleration method (AAM). The comparison of the hybrid test results with thesetwo methods validates the effectiveness of the ECM in the hybrid simulation. We found that the energy error of hybrid test by using ECM is less than that of AAM. In addition, a new iteration strategy with reduction factor is presented to avoid the overshooting phenomena during iteration process with the finite element program.
1. Introduction
As an effective testing technique, hybrid simulation is widely utilized in the experimental research of seismic behavior of large-scale structures. In a hybrid simulation, the whole structure is divided into numerical substructures modeled in computers and physical substructures loaded by actuators in laboratories. To obtain the seismic responses of the structure, the whole equations of motion must be solved through explicit or implicit integration algorithms. When an explicit method, such as the central difference method, is applied to the structures with high frequency, time increment must be limited within a very small critical one due to its conditional stability [1]. Then the displacement increment might be too small to be controlled by the actuator with limited resolution.
The limitation of explicit algorithms may be overcome by most classical implicit integration methods [2,3,4,5] due to their unconditional stability. However, the so-called unconditional stability was rigorously proved only for linear structures, and it could be lost in nonlinear cases [6,7], especially those with geometric nonlinearity [8]. To avoid iteration in implicit methods, some scholars proposed unconditional explicit methods [9,10,11,12]. However, the stability of all these methods was investigated with linear theory, and hence it is suspicious if it is valid for nonlinear systems.
Deng discussed a relationship between the concepts of B-stability and unconditional stability and showed that the numerical response of a nonlinear structure with B-stability is also unconditionally stable [13]. However, Deng proved that an SDOF structure with nonlinear damping is B-stable. An alternative approach to investigating the numerical stability of nonlinear structures is the energy approach. With the energy approach, the stabilities of the average acceleration method and midpoint rule for structures with nonlinear damping have been proved unconditionally stable in [14,15]. For other types of nonlinearities, the discussion on the stability of these classical integration methods was not reported.
Because the unconditional stability of classic time-stepping algorithms such as the Newmark average method holds only for linear structures in a strict mathematical sense, significant concerns have been raised on the numerical reliability for nonlinear structures since the 1970s in the circle of computational mechanics. For more general nonlinear structures, the energy-conserving method (ECM) with unconditional stability was proposed by Simo [16] and has been developed into different styles [17,18,19,20]. The local finite difference scheme at element or material point level is adopted for ECM; this is different from the global scheme in classical integration methods. The ECM can be used not only for numerical analyses of structural dynamics with geometric nonlinearity but also hybrid simulation.
Although many ECMs are available, the one by Galvanetto and Crisfield [17] is proposed for hybrid simulation in this paper because of its clarity and concise form. In the remainder of the paper, an overview of the ECM is given in Section 2, an improved approach of iteration is proposed to avoid the overshooting in hybrid simulation, and a hybrid test for validation is described in Section 3.
2. Theory of Energy Conserving Integration
2.1. Integration Method
The equation of motion for a nonlinear structure can be written as
where M and C are the mass and damping matrixes, respectively; u, v, a, qin and qex represent the vectors of displacement, velocity, acceleration, internal force and external load, respectively. With implicit midpoint rule [21], the discretized solution to Equation (1) at the n + 1 step can be expressed as
in which vm, um, and qex,m are the average velocity, displacement, and external load, respectively, i.e.,
Letting
then Equation (2) becomes
As a modified format of the implicit midpoint method, the ECM was firstly proposed for nonlinear dynamics by Simo and Tarnow [16]. Galvanetto and Crisfield presented an implementation of energy conserving method for structures with beam elements [17]. The difference of the ECM and implicit midpoint algorithm is the calculation of internal force. With Crisfield’s approach, the average internal force of a plane beam element is expressed as
in which, Nav and Mav are average value of axial force and end bending moments in a basic (simply supported) system, respectively; bm, Bm and B0 are nonlinear transformation matrices of midpoint internal forces from basic to global systems (see Figure 1), and they are expressed as
where l and ∆α are the length and rigid-body rotation angle of the beam element, respectively; s = sine(∆α), and c = cosine(∆α). The parameters featuring energy conserving in Equation (9) are θa and θb, which can be expressed by
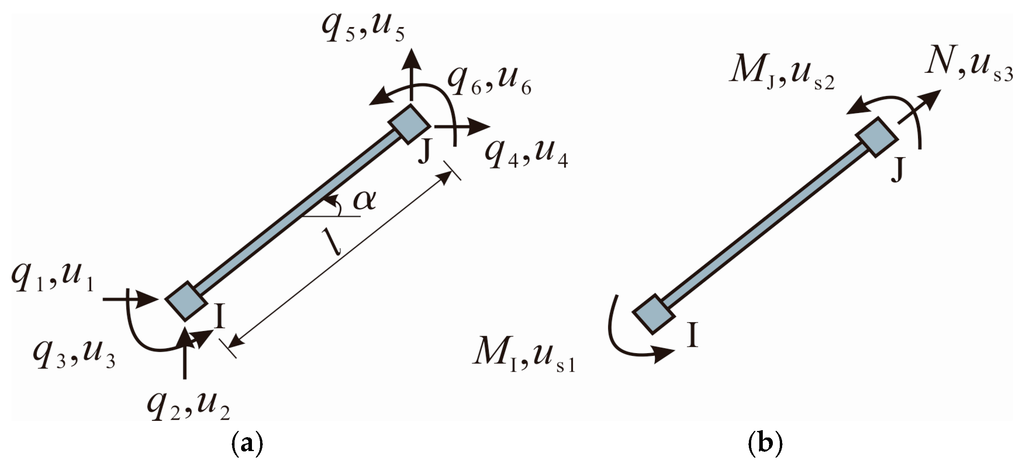
Figure 1.
Beam element in different coordinate systems, (a) global system; (b) basic (simply supported) system.
2.2. Improved Iteration for Hybrid Simulation
Substituting Equations (3)–(7) into Equation (8) yields a nonlinear algebraic equation expressed as
The above equation can be considered as an equivalent static equation written as
in which R(un+1) and Fn+1 are the equivalent internal and external forces respectively. With Newton-type iteration, the displacement increment from ti to ti+1 can be obtained as
where K is the equivalent initial or tangent stiffness matrix; subscript i represents the number of iterative step. Defining the exact secant stiffness Ksec as the stiffness with which the exact solution is obtained with just one iteration, we have
In each iterative step, the overshoot can be identified by a difference vector written as
in which | | denotes absolute value of a vector. If some components of K are smaller than those of Ksec, the relevant component of Φ could be negative, which indicates overshoot taking place.
For hybrid tests, a possible significant problem arising from iteration is the overshooting with which the displacement exceeds the true value and then goes back, approaching the true value. The overshoot would bring artificial hysteresis for inelastic materials, and hence should be avoided or at least confined at an acceptable level. In a hybrid simulation with Newton-type iteration algorithm, the stiffness matrix used for the iteration consists of two parts: one from the numerical substructure and the other from the experimental substructure. The former is assembled and updated from the FE program, while the latter is usually fixed and the initial stiffness is quite often an option. In some cases, this iterative stiffness could be “smaller” than exact secant stiffness, and hence produce the reciprocating iterative phenomenon [22]. This iteration will lead to artificial numerical dissipation and inaccurate structure response. The authors of [22] presented a solution of introducing a reducing parameter in every iteration, which can reduce the possibility of spurious loading/unloading cycles. However, in the same condition of convergence criterion, it takes much more computation time to reach a satisfactory equilibrium, and the uniform displacement increment cannot be ensured.
In general, the application of the iterative stiffness matrix always makes the overshooting phenomenon take place in the first or second iteration and disappear in the following iterations of each time step. Thus, the current paper presents a solution of increment reduction factor θ only for the first one or two iterations. The reduction factor θ of displacement increment is used in first or first two iterations for the balance of overshoot remedy and computation efficiency. For the ith iteration, displacement increment with modified Newton iteration can be expressed as
By suppressing the displacement increment of first or first two iterations with the parameter θ < 1, the total displacement increment can be expressed as
The value of θ is determined according to the amount of overshooting: the more the overshoot, the less the value of θ is needed.
2.3. FE Program
Based on the above theory, a nonlinear fiber beam element program is compiled with Matlab as the computational tool for the hybrid simulation in this paper. The material nonlinearity of elasto-plasticity is taken into account, as is geometric nonlinearity. The return-mapping algorithm is performed in calculating the stress and stiffness of each fiber [23]. Through using the co-rotation technique, the internal forces can only be calculated in a simply supported system. For comparison, both energy conserving and the average acceleration method (AAM) are incorporated in this FE program.
3. Hybrid Test
3.1. Experimental Setup
The test facilities were located at the Structural and Seismic Testing Center, Harbin Institute of Technology. The hardware of the test system mainly consisted of a PC, dSpace-DS1104 RD controller board, servo-hydraulic controller and three MTS actuators (1000 kN, ±500 mm), as shown in Figure 2. The displacement command calculated from the FE program described in Section 2.3 was transmitted to dSpace through OpenFresco software [24]. To make the actuators run smoothly, the displacement command was interpolated in dSpace, and then passed to Servo-Hydraulic Controller to drive the actuators. The forces of actuators were measured and sent back to the FE program for the iteration of the next step.
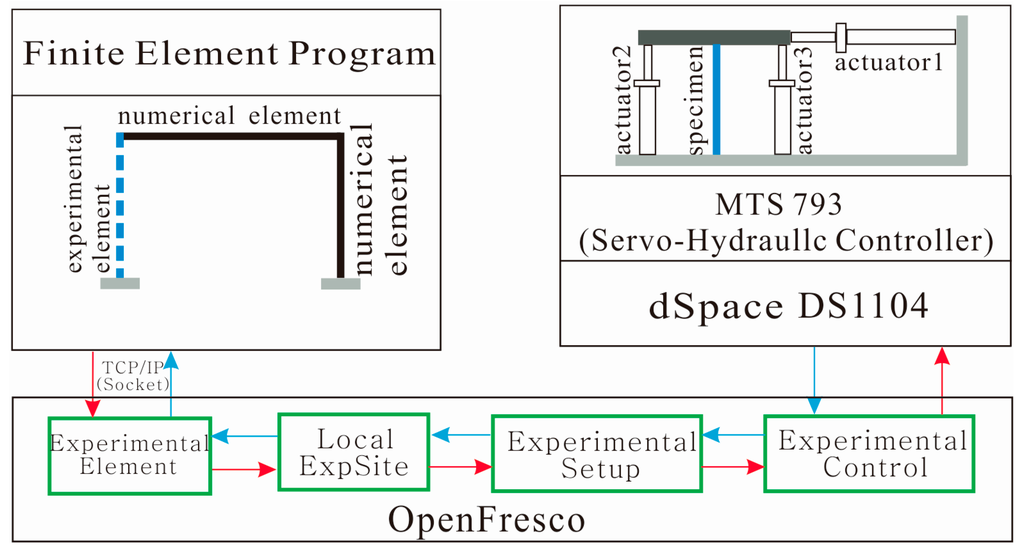
Figure 2.
Block diagram of data communication and hardware for hybrid simulation.
The structure to be emulated was a steel frame with single floor and single bay as shown in Figure 3. The mass was lumped at the top of the columns. The Rayleigh damping matrix was determined based on the damping ratio of 5% for the first two modes. Before seismic analysis, the structure was subjected to static gravity load in the form of concentrated force. The numerical substructure in the FE program contains two beam-column elements with six DOFs, and the physical substructure was the left column as shown in Figure 3. There are three DOFs, i.e., two translational and one rotational, on the top of the tested column. Three actuators were used to achieve the three DOFs of the column as shown in Figure 4: two vertically placed actuators for the vertical displacement and rotation, and the horizontal actuator for the horizontal displacement. The actuators were connected to the column through a rigid loading girder. The bottom of the column was fixed on the ground. The displacements of the actuators were related to those at the DOFs of the specimen through
where ua, uc were displacement vectors of the actuators and specimen, respectively; Tca was the transformation matrix which was expressed as
in which L = 2 m is half length of the loading girder. The transpose of Tca was used for force transformation backwards.
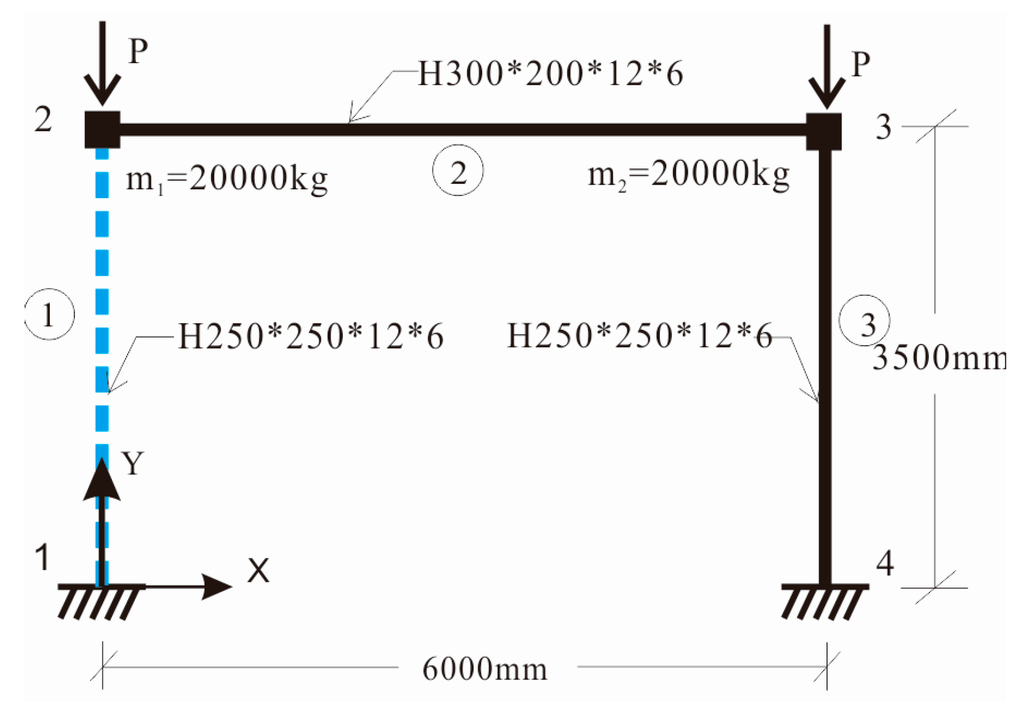
Figure 3.
Schematic of one-story and one bay steel frame.
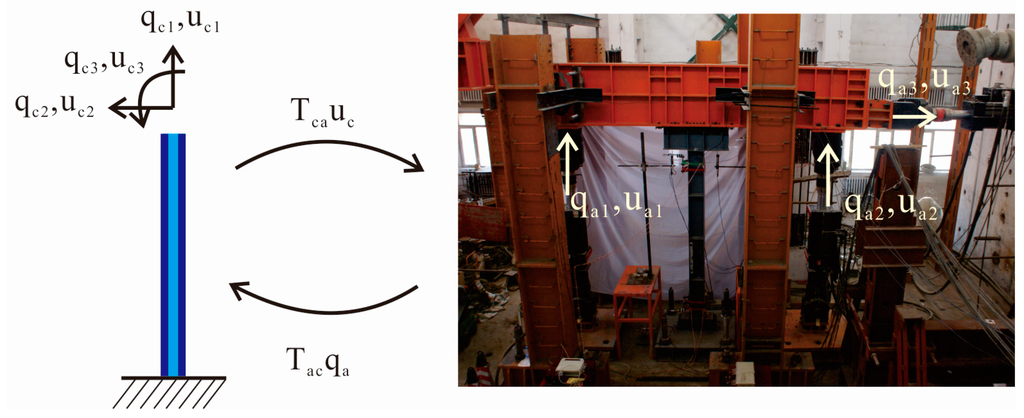
Figure 4.
The coordinate transformation between specimen and three actuators.
3.2. Software Validation
The software including the nonlinear FE program described in Section 2.3 and OpenFresco should be validated before actual hybrid simulation. The seismic responses of the steel frame of the last subsection are evaluated with the energy conserving method and average acceleration method encoded in the FE program written in Matlab. The earthquake input is El Centro (NS, 1940) with peak ground acceleration scaled to 220 Gal. The results are shown in Figure 5, where we see that the two are almost identical, as they should be, since the responses are not large enough to cause significant energy imbalance for the average acceleration method. The result with OpenSees is also shown in Figure 5. The three results matched each other perfectly. Then the steel frame was divided into two parts just as in a hybrid simulation: the left column is modeled in OpenSees and, through OpenFresco, connected to the rest that is modeled in the FE program. Figure 5 shows that the result with OpenFresco agreed very well with all the others.
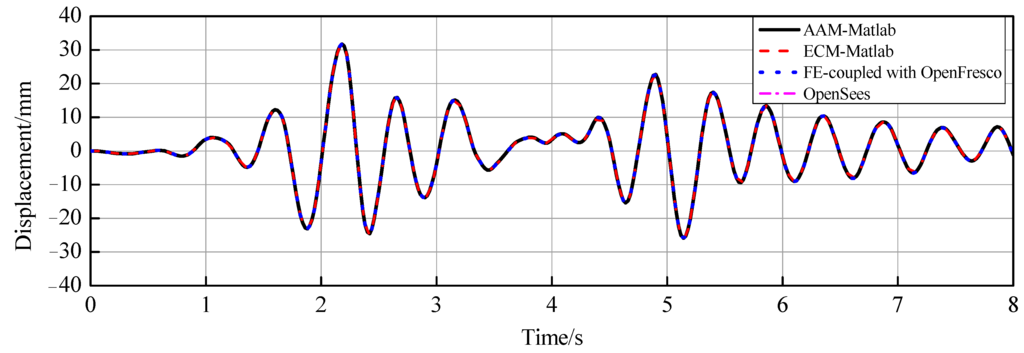
Figure 5.
Displacement on top of column.
3.3. Analysis of Reduction Factor for Iteration
In the case studied in Section 3.2, no treatment for overshooting is employed, i.e., the reduction factor θ takes the value of unity. In this subsection, the effects of different value of θ are investigated. The results with θ used for the first and first two iterations are shown in Figure 6a,b, respectively. For comparison, the result of θ = 0.85 for all iterations is also included. From Figure 6, it is seen that overshooting is almost eliminated for all θ < 1, and the number of iterations with θ used for first or first two iterations is much less than the case in which θ = 0.85 is employed for each iteration. The results also indicate that θ = 0.85, which is used only for the first iteration, is optimal in the sense that the overshooting is effectively suppressed and the iteration times are the least. So the strategy of θ = 0.85 for the first iteration is adopted for the hybrid test in this paper.
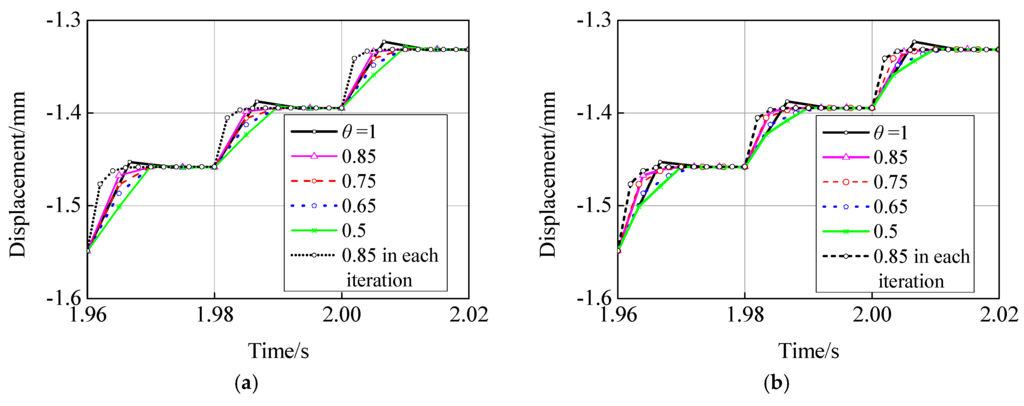
Figure 6.
Iterative vertical displacement on the top of column. (a) Reduction factor used in the first iteration; (b) Reduction factor used in the first two iterations
3.4. Test Results and Discussions
The hybrid simulations were conducted on the steel frame, which has been shown in Figure 3. Prior to hybrid simulation, the stiffness matrix of specimen used for iteration was obtained based on the data of the static loading test. For comparison, both the ECM and the AAM were used in the hybrid simulation. The integration time step was 0.02 s. Figure 7 shows the horizontal displacement responses of the experimental column when the frame was subjected to the El Centro (NS, 1940) earthquake scaled to a PGA of 35 Gal. The results with two integration methods were almost identical. Figure 8 and Figure 9 show the force-displacement responses of the experimental and numerical columns. It is seen that the numerical column was in elastic range, while the experimental one exhibited slight hysteretic behavior.
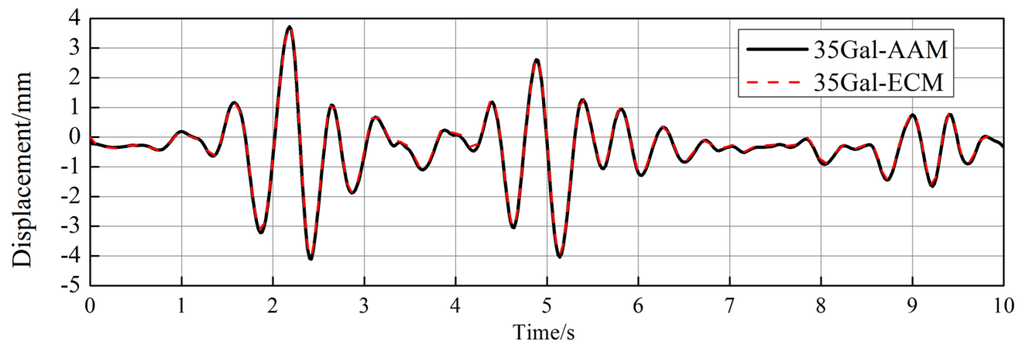
Figure 7.
Horizontal displacement on the top of experimental column (35 Gal).
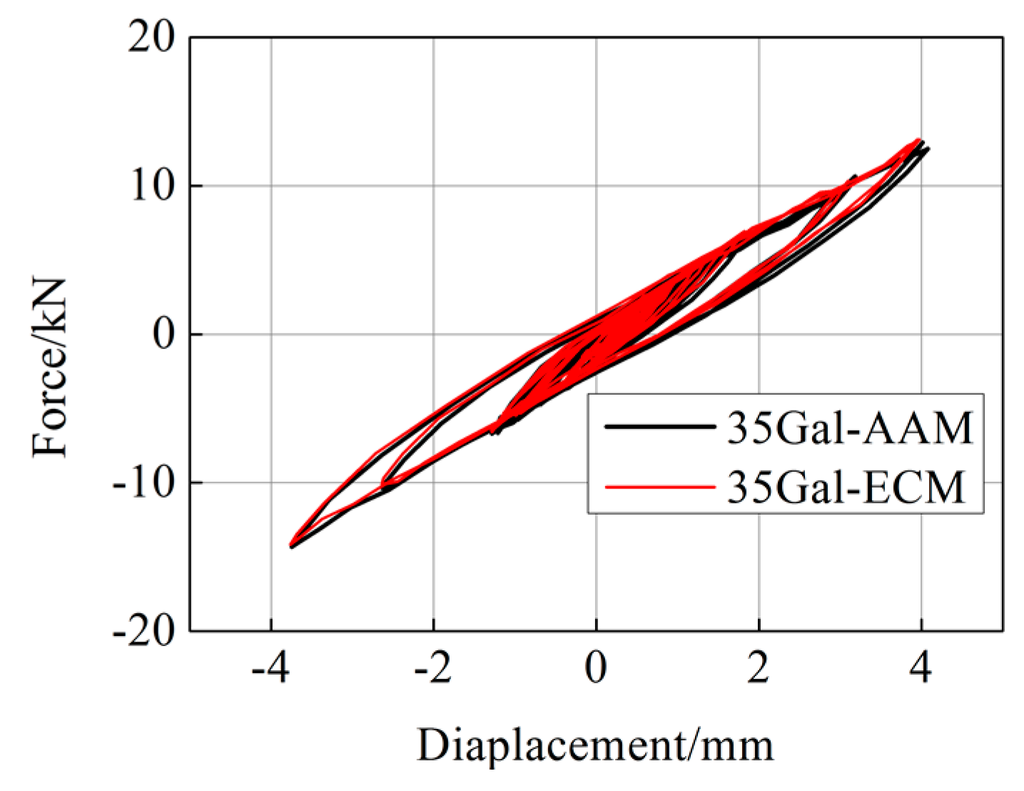
Figure 8.
Hysteretic loops of specimen (35 Gal).
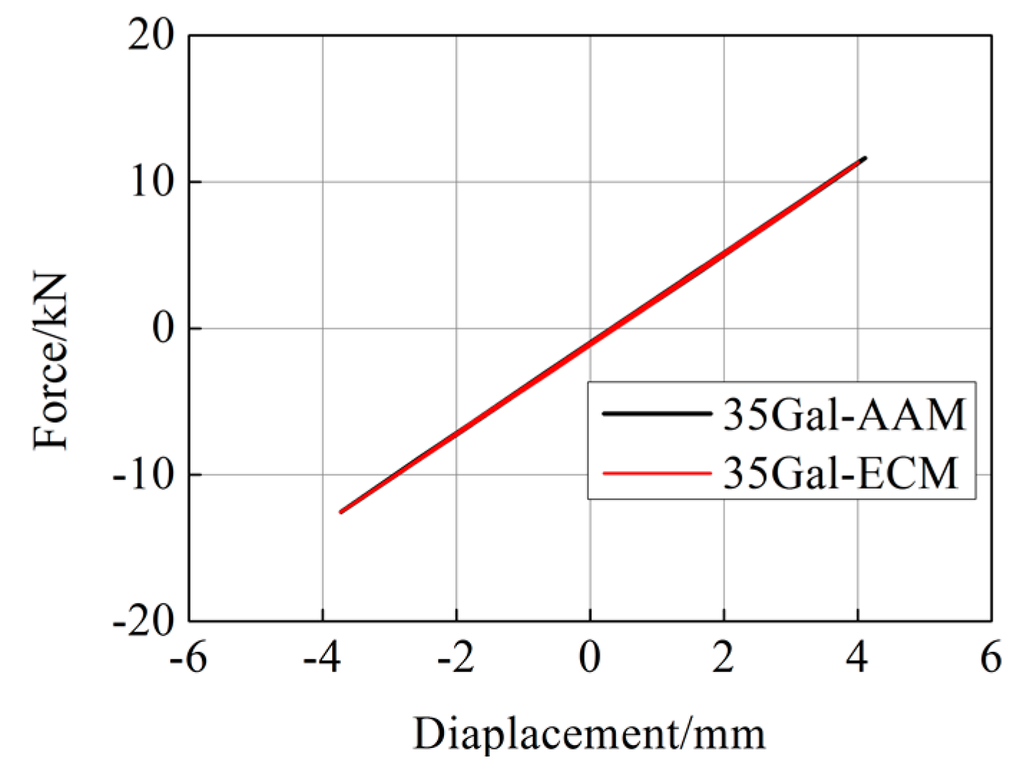
Figure 9.
Hysteretic loops of numerical column (35 Gal).
Figure 10, Figure 11 and Figure 12 show the responses subjected to the El Centro (NS, 1940) earthquake with a PGA of 220 Gal, where it is seen that the difference between the two integration methods appeared slightly more significant than the case of 35 Gal. The result of pure numerical analysis with the ECM is also shown in Figure 10, from which we see that the numerical result basically agreed with that of hybrid simulation.
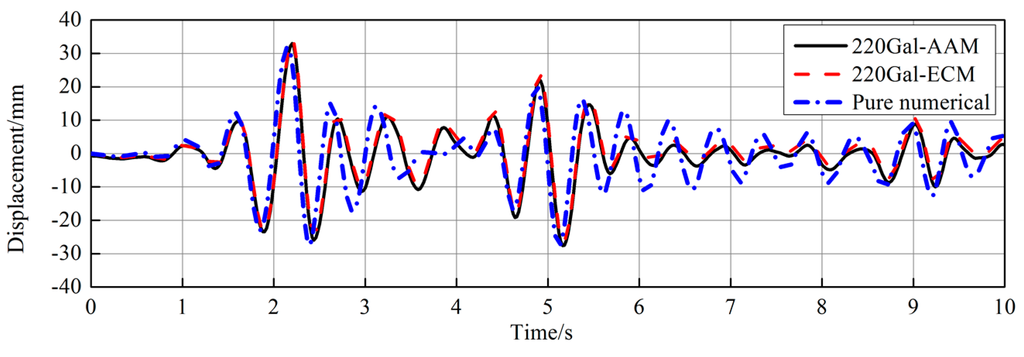
Figure 10.
Horizontal displacement on the top of experimental column (220 Gal).
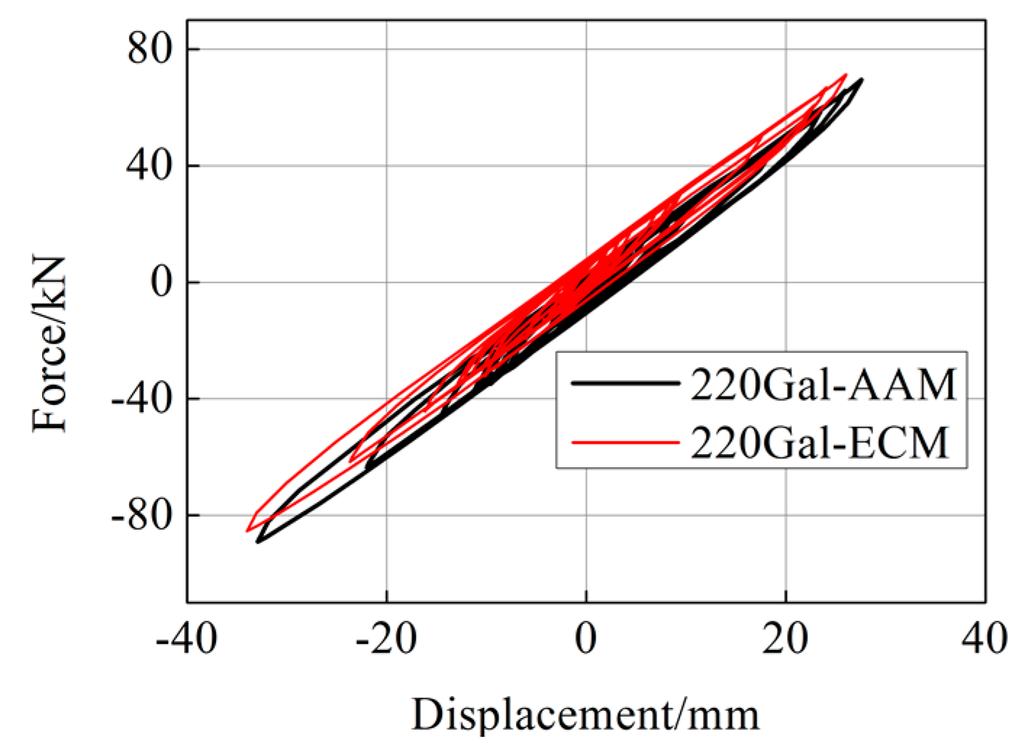
Figure 11.
Hysteretic loops of specimen (220 Gal).
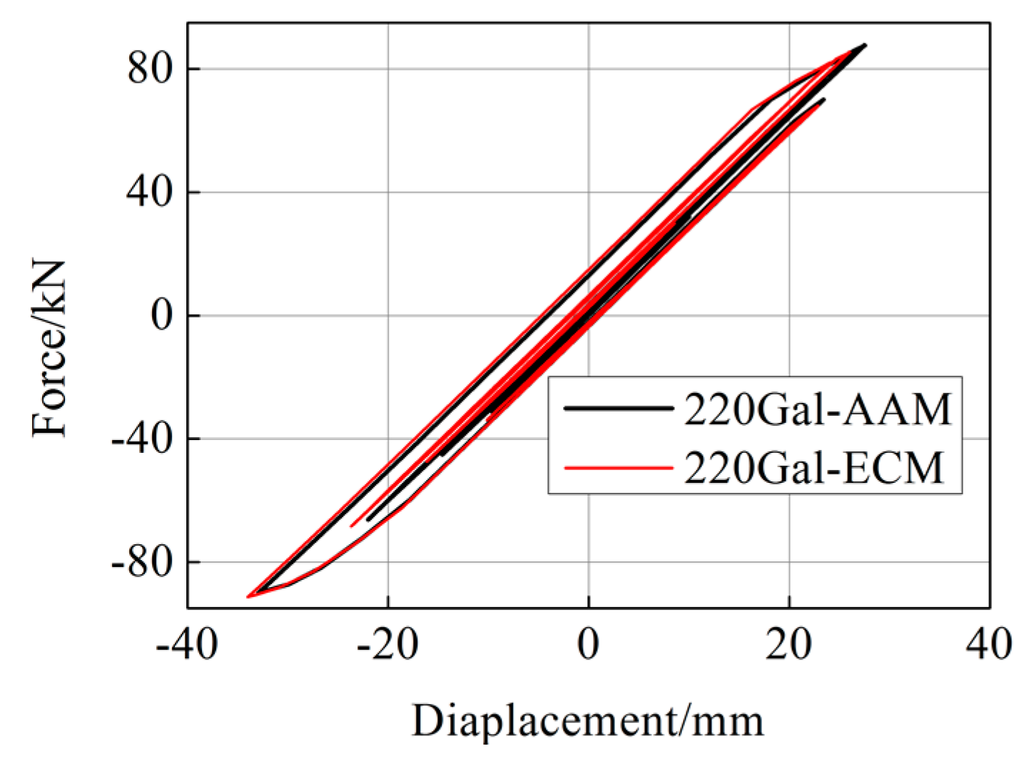
Figure 12.
Hysteretic loops of numerical column (220 Gal).
In the hybrid simulations, the factor θ = 0.75 was adopted for the first iteration in every time step. Part of the responses during iteration for the case of 220 Gal with the ECM is shown in Figure 13, where no overshooting can be observed in all three DOFs.
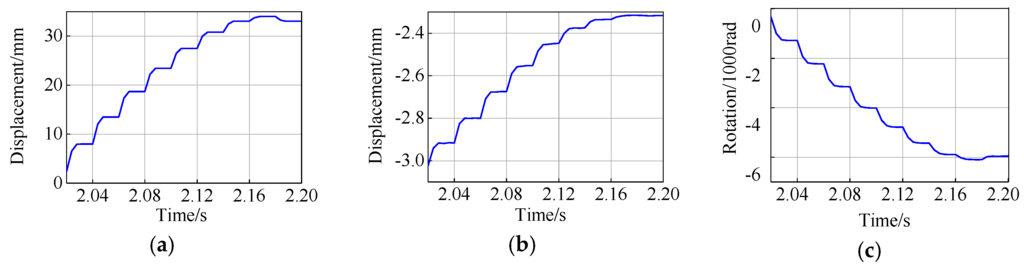
Figure 13.
Displacement response in iteration (220 Gal), (a) Horizontal displacement; (b) Vertical displacement; (c) Rotation.
To further reveal the difference of the two integration methods, the energy errors are shown in Figure 14. The energy error is defined as the difference of external work and the sum of internal, damping and kinetic energy. It is seen from the energy errors from the hybrid simulation as shown in Figure 14a,b that the ECM was not shown to be advantageous compared to AAM. The reason for this may be attributed to the small response which resulted in insignificant geometric nonlinearity, and the small advantage of the ECM was covered by the experimental errors. Unfortunately, the specimen was used for another test, and hence no further hybrid simulation with higher PGA was carried out to reveal the advantage of the ECM experimentally. Due to this, we have to rely on the results of pure numerical analysis which is shown in in Figure 14c for the case of 400 Gal. It is clearly seen that the energy error of the ECM is much lower than that of the AAM.
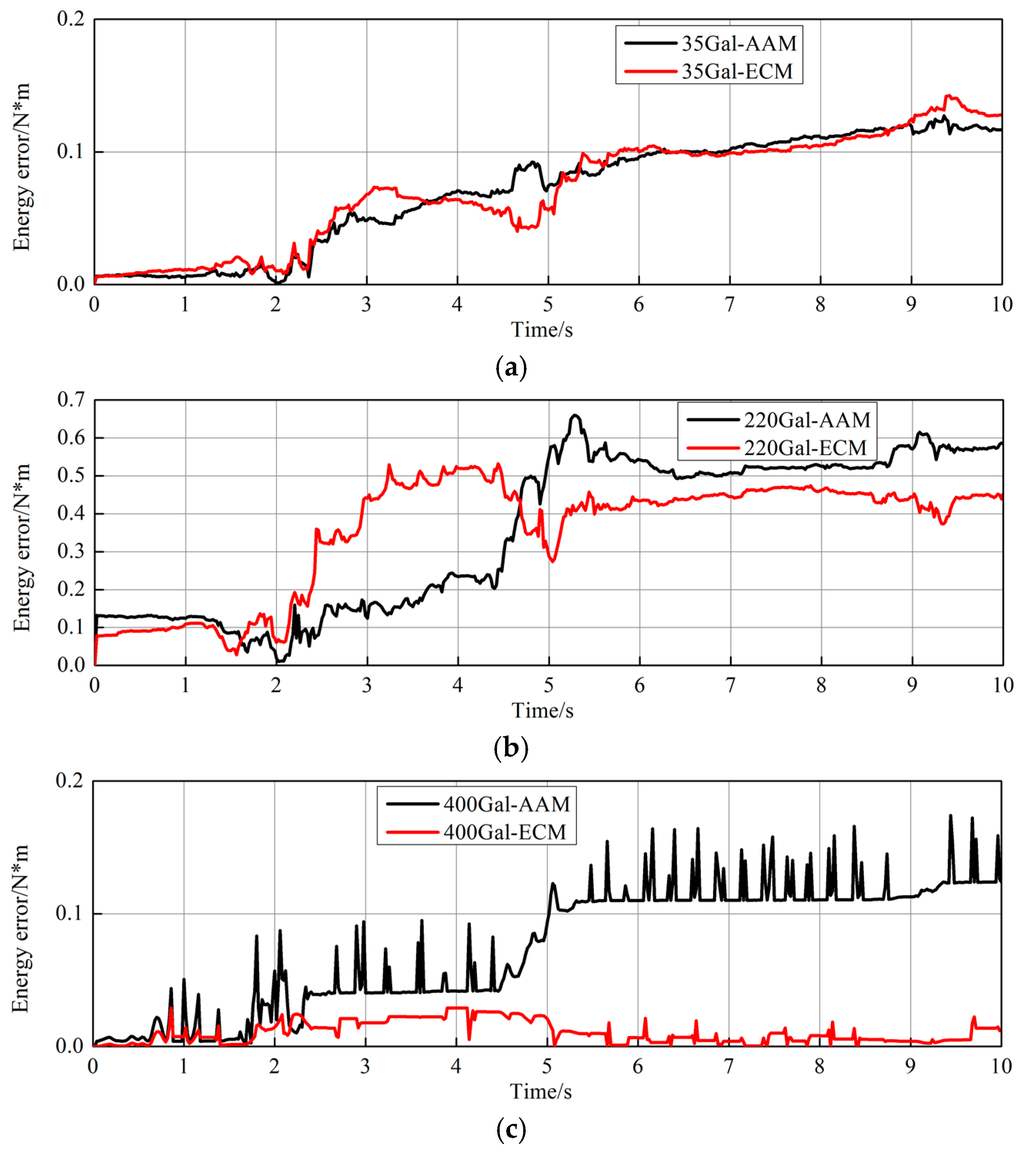
Figure 14.
Energy errors of ECM and AAM, (a) 35 Gal; (b) 220 Gal; (c) 400 Gal.
4. Conclusions
In this paper, the ECM is applied to hybrid simulation of structures with both geometrical and material nonlinearities. The method was validated by numerical analysis using OpenSees and hybrid simulation of a steel frame structure. The simulation and experimental results show that the ECM has less energy error than traditional average acceleration method. The energy error of AAM becomes larger with increasing response, while the energy error of ECM is still in limited range.
Furthermore, we presented a new iteration strategy to avoid overshooting phenomenon in the hybrid test. A reduction factor that was introduced only in the first or first two iterations could avoid artificial dissipation. The effect of the new strategy is also validated by hybrid simulation and test.
Acknowledgments
The National Science Foundation of China (51161120360, 91315301-09) provided the financial support for this experimental research. The authors greatly acknowledge L. Ni for her patient assistance with the operation of the MTS testing system.
Author Contributions
Tianlin Pan conceived and designed the experiments and analyzed the data; Yongsheng Chen and Guoshan Xu performed the experiments; Bin Wu wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wu, B.; Deng, L.; Yang, X. Stability of central difference method for dynamic real-time substructure testing. Earthq. Eng. Struct. Dyn. 2009, 38, 1649–1663. [Google Scholar] [CrossRef]
- Mosqueda, G.; Ahmadizadeh, M. Iterative implicit integration procedure for hybrid simulation of large nonlinear structures. Earthq. Eng. Struct. Dyn. 2011, 40, 945–960. [Google Scholar] [CrossRef]
- Mosqueda, G.; Ahmadizadeh, M. Implicit numerical integration in hybrid simulation with iteration strategy for experimental substructures. In Proceedings of the 2009 American Control Conference, ACC09, St. Louis, MO, USA, 10–12 June 2009; pp. 5241–5246.
- Chang, S.Y.; Sung, Y.C. Nonlinear error propagation analysis of implicit pseudodynamic algorithm. J. Chin. Inst. Eng. 2006, 29, 639–653. [Google Scholar] [CrossRef]
- Gomez, H.P.; Hughes, T.J.R. Provably unconditionally stable, second-order time-accurate, mixed variational methods for phase-field models. J. Comput. Phys. 2011, 230, 5310–5327. [Google Scholar] [CrossRef]
- Yang, J.S.; Xia, P.Q. Energy conserving and decaying algorithms for corotational finite element nonlinear dynamic responses of thin shells. Sci. China Technol. Sci. 2012, 55, 3311–3321. [Google Scholar] [CrossRef]
- Pan, T.L.; Wu, B.; Guo, L.N.; Chen, Y.S. Application of energy conserving step-by-step integration algorithm in dynamic analysis of engineering structures. Eng. Mech. 2014, 21–27. (In Chinese) [Google Scholar]
- Krenk, S.; Nielsen, M.B. Hybrid state-space time integration of rotating beams. Comput. Methods Appl. Mech. Eng. 2012, 213, 243–254. [Google Scholar] [CrossRef]
- Nakashima, M.; Kaminosono, T.; Ishida, M.; Ando, K. Integration techniques for substructure pseudo-dynamic test. In Proceedings of the 4th US National Conference on Earthquake Engineering, Palm Springs, CA, USA, 20–24 May 1990.
- Ghaboussi, J.; Yun, G.J.; Hashash, Y.M.A. A novel predictor–corrector algorithm for sub-structure pseudo-dynamic testing. Earthq. Eng. Struct. Dyn. 2006, 35, 453–476. [Google Scholar] [CrossRef]
- Chang, S.Y.; Yang, Y.S.; Hsu, C.W. A family of explicit algorithms for general pseudodynamic testing. Earthq. Eng. Eng. Vib. 2011, 10, 51–64. [Google Scholar] [CrossRef]
- Chen, C.; Ricles, J.M.; Marullo, T.M.; Mercan, O. Real time hybrid testing using the unconditionally stable explicit CR integration algorithm. Earthq. Eng. Struct. Dyn. 2009, 38, 23–44. [Google Scholar] [CrossRef]
- Deng, L. Numerical Stability Analysis of Substructure Testing; Harbin Institute of Technology: Harbin, China, 2011. [Google Scholar]
- Li, Y.; Wu, B.; Ou, J. Stability of average acceleration method for structures with nonlinear damping. Earthq. Eng. Eng. Vib. 2006, 5, 87–92. [Google Scholar] [CrossRef]
- Tianlin, P.; Bin, W. Stability of implicit midpoint algorithm applied to nonlinear damping structure. J. Vib. Shock 2013, 32, 38–42. (In Chinese) [Google Scholar]
- Simo, J.C.; Tarnow, N. The discrete energy-momentum method. Conserving algorithms for nonlinear elastodynamics. Z. Angew. Math. Phys. ZAMP 1992, 43, 757–792. [Google Scholar] [CrossRef]
- Galvanetto, U.; Crisfieldm, M.A. An Energy-Conserving Co-Rotational Procedure for the Dynamics of Planar Beam Structures. Int. J. Numer. Methods Eng. 1996, 39, 2265–2282. [Google Scholar] [CrossRef]
- Almeida, F.S.; Awruch, A.M. Corotational nonlinear dynamic analysis of laminated composite shells. Finite Elem. Anal. Des. 2011, 47, 1131–1145. [Google Scholar] [CrossRef]
- Romero, I. An analysis of the stress formula for energy-momentum methods in nonlinear elastodynamics. Comput. Mech. 2012, 50, 603–610. [Google Scholar] [CrossRef]
- Noels, L.; Stainier, L.; Ponthot, J.P. A first-order energy-dissipative momentum-conserving scheme for elasto-plasticity using the variational updates formulation. Comput. Methods Appl. Mech. Eng. 2008, 197, 706–726. [Google Scholar] [CrossRef]
- Lambert, J.D. Numerical Methods for Ordinary Differential Systems; John Willey&Son: London, UK, 1997. [Google Scholar]
- Shing, P.S.B.; Vannan, M.T. Implicit time integration for pseudo-dynamic tests: Convergence and energy dissipation. Earthq. Eng. Struct. Dyn. 1991, 20, 809–819. [Google Scholar] [CrossRef]
- Simo, J.C.; Hughes, T.J.R. Computational Inelasticity; Springer Science & Business Media: New York, NY, USA, 2006. [Google Scholar]
- Schellenberg, A.; Kim, H.K.; Takahashi, Y.; Fenves, G.L.; Mahin, S.A. OpenFresco Command Language Manual; Version: 2.6; University of California at Berkeley: Berkeley, CA, USA, 2009. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).