We present an algorithm to extract a hidden structure, called a co-occurrence relation, from a ZDD. Our algorithm constructs a co-occurrence partition while traversing a ZDD. We first explain how to traverse a ZDD and then how to manipulate a partition efficiently in the traversal. We furthermore introduce the notion of a conditional co-occurrence relation and present an extraction algorithm.
3.1. Traversal Part
Let us first consider a naive method to compute a co-occurrence partition. Suppose that a ZDD represents a collection
C of subsets of a set
S. The co-occurrence partition is incrementally constructed as follows. We start with the partition
consisting of the single block
S. For each path
P from the root to ⊤, we obtain a new partition from the current partition by separating each block
b into the two parts
and
if both parts are nonempty, where
denotes the set in
C corresponding to
P. This can be done by checking which arc is selected at each node of
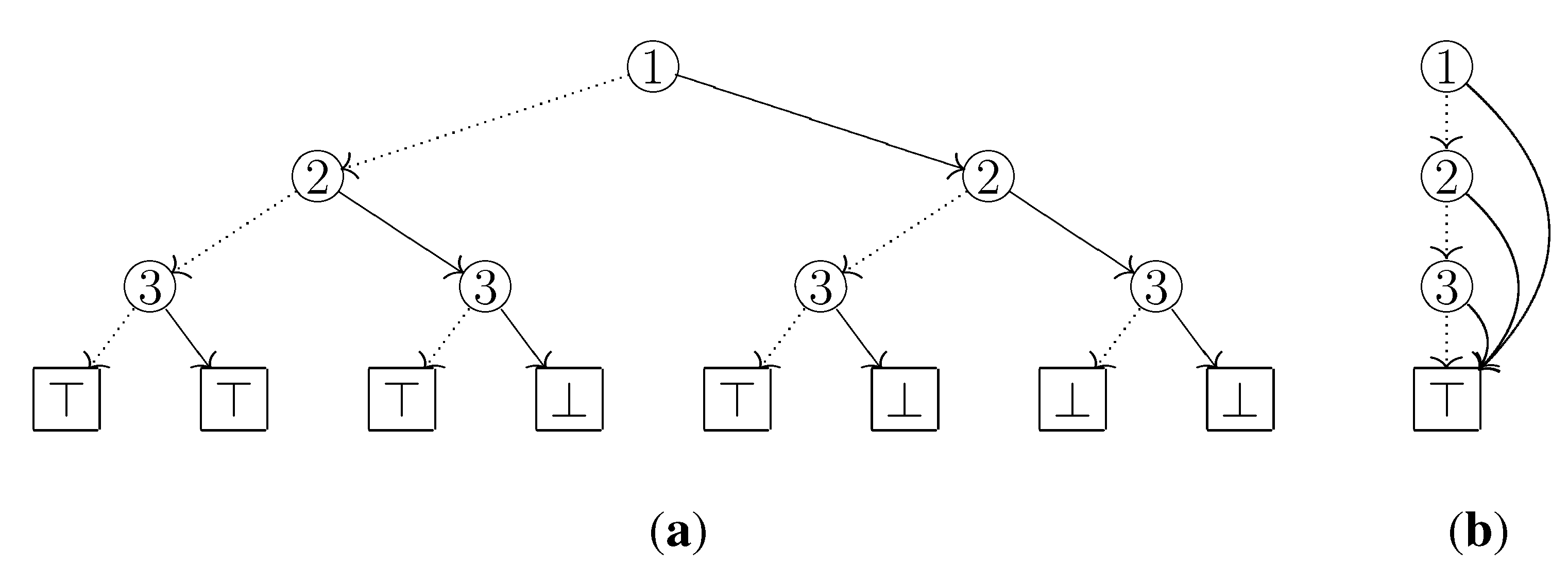
P. For example, let us see the ZDD given in
Figure 3: If we first examine the path
, then the block
S of the initial partition splits into the two parts
and
, since HI arc is selected only at the label 4 node. It can be easily verified that after all paths are examined, the co-occurrence partition induced by
C is constructed. However, since this method depends on the number of paths (thus the size of
C), this is not effective for ZDDs which efficiently compress a large number of sets. It would be desirable if we could construct a co-occurrence partition directly from a ZDD.
Figure 3.
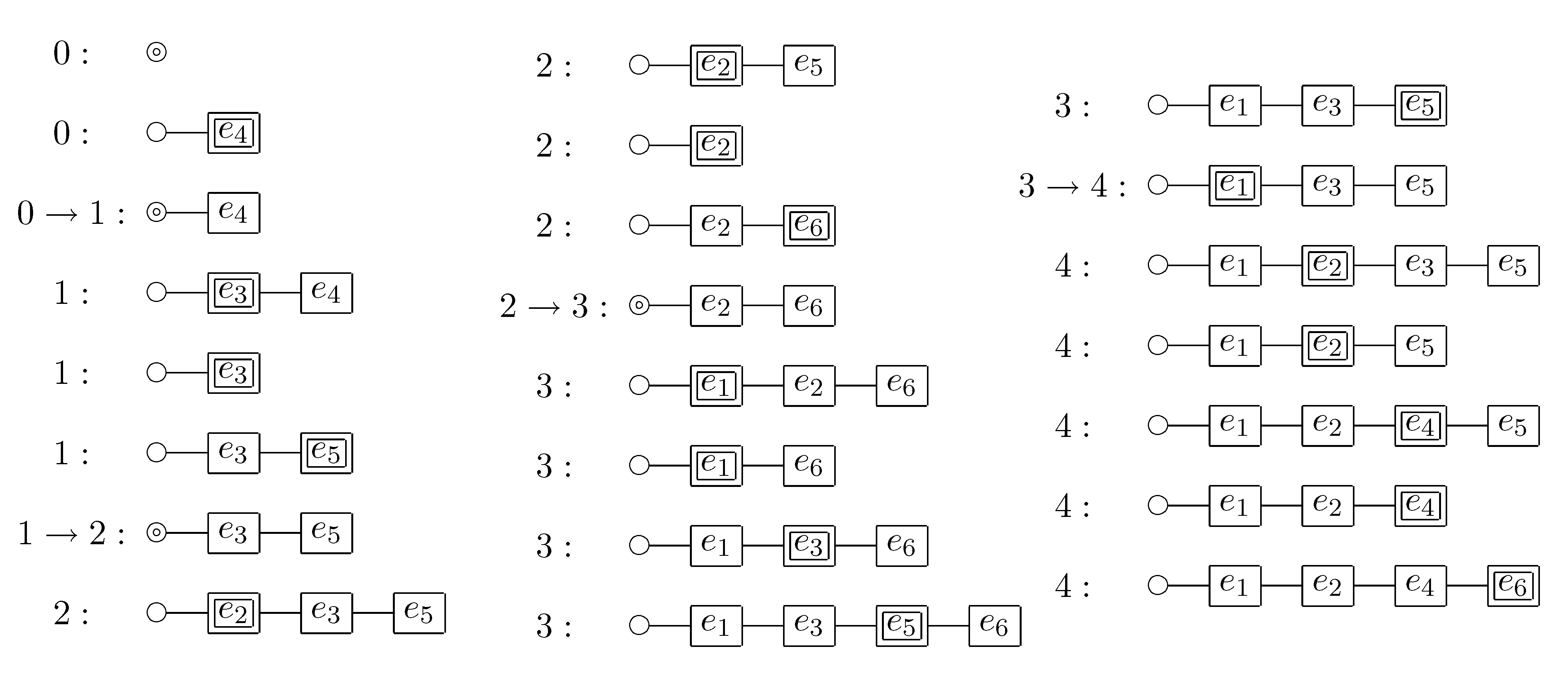
The computing process of our algorithm for the ZDD that represents the set family is shown below. For example, in the third line from the bottom of the left column, the number 2 on the left side means that ⊤ was visited twice; the right arrow means that the state of changed from LO to HI; the left arrow means that the state of changed from HI to LO. In the bottom of the right column, the co-occurrence partition is obtained.
Figure 3.
The computing process of our algorithm for the ZDD that represents the set family is shown below. For example, in the third line from the bottom of the left column, the number 2 on the left side means that ⊤ was visited twice; the right arrow means that the state of changed from LO to HI; the left arrow means that the state of changed from HI to LO. In the bottom of the right column, the co-occurrence partition is obtained.
Our algorithm improves the naive method above by avoiding as many useless visits of nodes as possible. We traverse a ZDD basically in a depth-first order. In each node, we select the next node in a LO arc first order,
i.e., the LO child if the LO child is not ⊥; otherwise, the HI child. After we arrive at ⊤, we go back to the most recent branch node and select the HI arc. Note that we need not go back to the root, since arc types do not change until the most recent branch node. For example, in
Figure 3, after the first visit of ⊤, we go back to the label 3 node and go ahead along the path
.
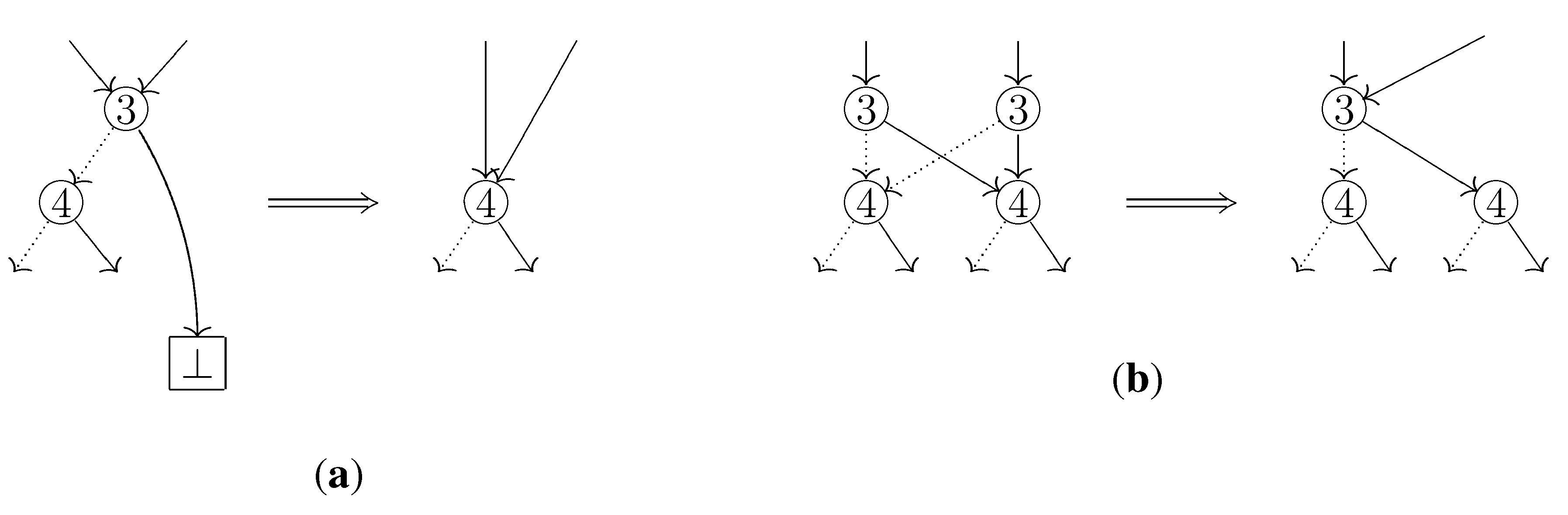
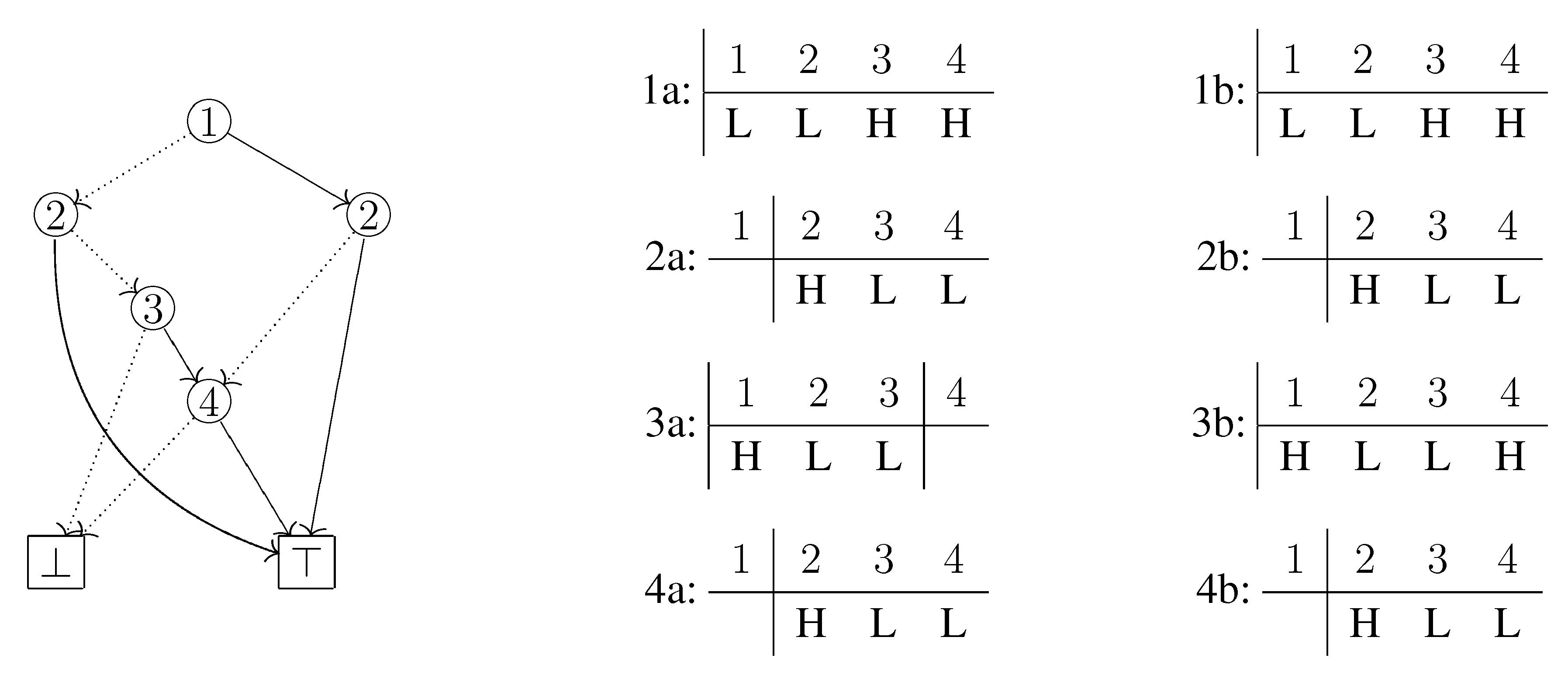
The difference from the usual depth-first search is that when we visit an already visited node, we go down from the node to ⊤ by selecting only HI-arcs. This is essential because the usual depth-first search may fail to detect separable elements. For example, in
Figure 4, the two elements
and
are separable, and in our traversal the third and fourth columns in the table 3b have different arc types thus we can know that they are really separated. On the other hand, in the usual depth-first search they are observed as if they had a common arc type: Since an already visited node is no longer visited, the arc type of
in the
table 3a is not updated, which means the type remains LO.
Figure 4.
Each table on the center shows the change of selected arc types when the ZDD is traversed by the usual depth-first search. Similarly, the tables on the right correspond to the changes when traversed by our algorithm.
Figure 4.
Each table on the center shows the change of selected arc types when the ZDD is traversed by the usual depth-first search. Similarly, the tables on the right correspond to the changes when traversed by our algorithm.
Unlike the usual depth-first search, we do not skip necessary paths as the following lemma implies.
Lemma 3.1. In each visit of a node g after the first, two elements get separated when traversing the subgraph whose root is g if and only if they get separated when going from g to ⊤ with only HI-arcs.
Proof. Since the sufficiency is immediate, we only show the necessity. Suppose for contradiction that two elements and get separated when visiting all nodes below g, while they are not separated when only selecting HI-arcs. Let denote the element corresponding to g. For the case , there are two paths from g such that they have different arc types at . However, in the first visit of g, we could trace both paths and know that and are separated, which is a contradiction. For the other case , there is a path from g with different arc types at and , and we could trace this path in the first visit of g and reach a contradiction.
The traversal part is formally described in Algorithm 1. We here explain some notation and terminology. Recall that in each internal node f, the next node of f in a LO arc first order is the LO child if f is a branch node, i.e., an internal node whose two children have paths leading to ⊤; otherwise, the HI child. In order to traverse a ZDD, branch nodes are pushed onto the stack BRANCH, and visited nodes are contained in . The ⊤ is contained in in the initialization part, which reduces an exceptional case in the traversal part, i.e., the loop block. For each step of the traversal, by invoking the function Update, we update the current partition p according to which arc is selected at the currently visited node f and whether there exist nodes hidden between f and the next node g due to the node elimination rule. To do this efficiently, we need the following things: The graph structure G defined on the blocks of p, the set of blocks which have been created since the last visit of ⊤, and the set of elements whose arc types are HI. The set is refreshed for each visit of ⊤. The function Update is explained in detail in the next subsection.
| Algorithm 1 Calculate a co-occurrence partition from a ZDD defined on a set |
Require: ZDD is neither ⊥ nor ⊤, and
the partition ;
the digraph with no arc and one vertex corresponding to the unique block S of p;
; ; Initialize BRANCH as an empty stack;
the root of ZDD;
the next node of f in a LO arc first order;
;
if f is a branch node then
push f onto BRANCH;
end if
loop
;
if then
;
the next node of f in a LO arc first order;
;
if f is a branch node then
push f onto BRANCH;
end if
else
while do
;
;
;
end while
if BRANCH is empty then
return p; // End of the traversal
end if
;
the node popped from BRANCH;
;
end if
end loop |
3.2. Manipulation Part
In the traversal described in the previous subsection, whenever we visit a node f and select the next node g, we update the current partition p by invoking the function Update. Namely, when we find an element which is separable from the other elements in the same block, we move to an appropriate block so that each block consists of inseparable elements with respect to the information up to this time.
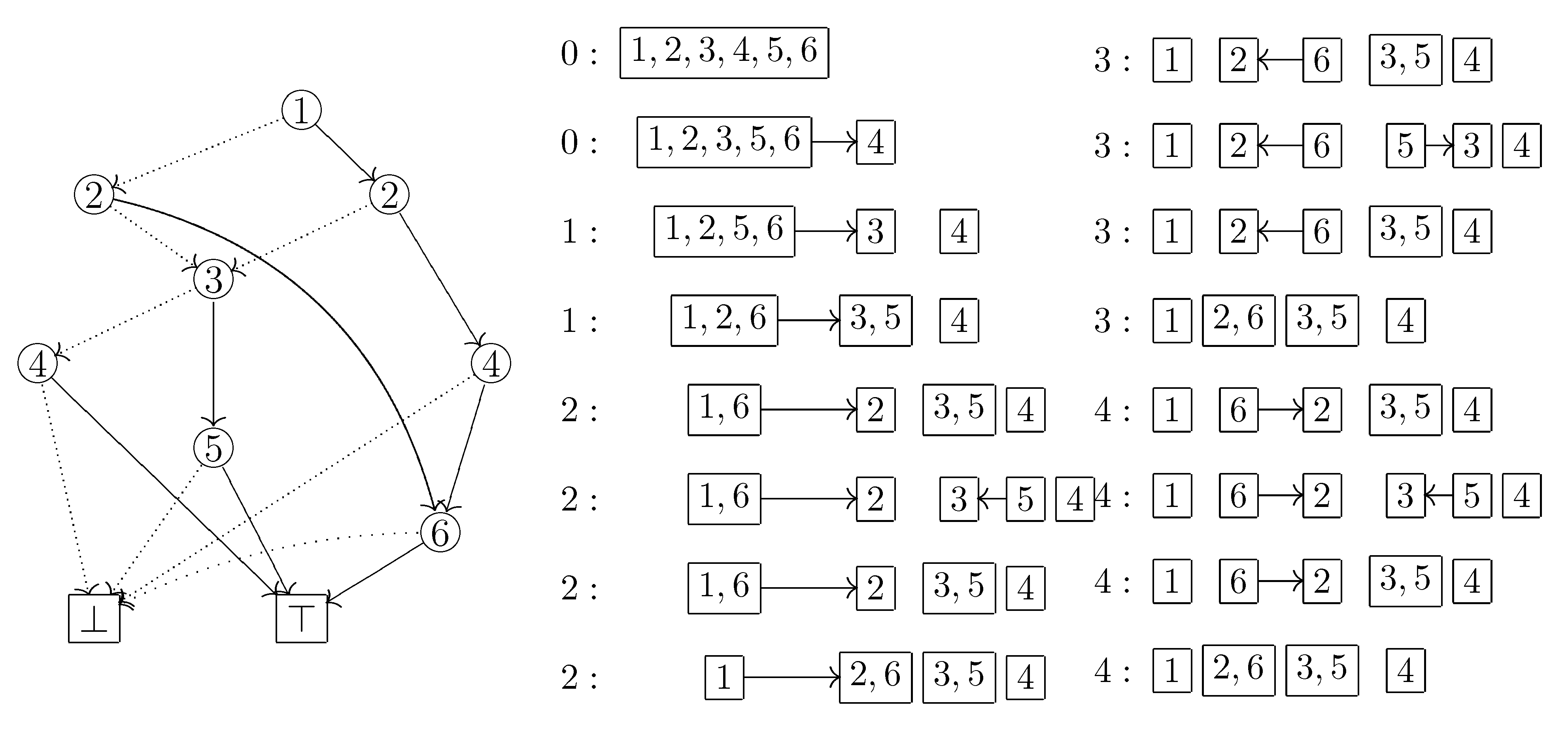
For example, let us see the computing process in
Figure 3 step by step. Suppose that we arrive at the label 3 node after the first visit of ⊤. At this time
. When we go to the label 5 node along the HI arc, the element
becomes in a HI state while the other elements are in a LO state. Thus we create a new block and move
into it. We furthermore memorize the arc from the previous block
b, which
was in, to the new block
, which now consists of only
. This is necessary because
soon becomes in a HI state and we have to insert
into
, not a new block. We then reach ⊤ and go back to the label 2 node on the left side. The element
becomes in a HI state, but we never insert
into
, since insertion is allowed only within the period from the creation of
until the arrival at ⊤. Therefore, we create a new block
and move
into it. We furthermore redirect the outgoing arc of
b to the new block
. In this way, we update the current partition
p, the graph structure
G on the blocks of
p, and the set
of blocks created since the last visit of ⊤.
The function Update is formally described in Algorithm 2. Let and be the elements corresponding to the current node f and the next node g, respectively. We move to another block only if the arc type of changes from LO to HI or from HI to LO. Note that we need not move in the other cases. This move operation for is done in the former part of the function Update by invoking the function Move. The destination block of is determined by means of the auxiliary data structures G and . The G defines a parent-child relation between the blocks of the current partition p. That a block b is a parent of a block implies that is formed by elements which most recently went out from b. Moving elements of b to is allowed only within the period from the creation of until the arrival at ⊤, which can be decided by using .
There may be some nodes hidden between the current node f and the next node g due to the node elimination rule. Let be the element corresponding to such a hidden node. Since is now in a LO state, it suffices to move only if the previous arc type is HI. This computation is done in the latter part of the function Update.
We are now ready to state the time complexity of our algorithm. Recall that a branch node is an internal node whose two children have paths leading to ⊤.
Theorem 3.2 Let k be the maximum number of HI arcs in a path from the root to ⊤. Let m be the number of branch nodes. Let n be the size of a ground set. Algorithm 1 correctly computes a co-occurrence partition. It can be implemented to run in time proportional to .
Proof. From Lemma 3.1 and the observations up to here, we can easily verify that Algorithm 1 correctly computes a co-occurrence partition. Throughout this proof, we mean by a period the time period from a visit of ⊤ to the next visit.
The time necessary to create the initial partition is proportional to
n. We show that the function Update can be implemented so that the total time in a period is proportional to
k. Partitions can be manipulated so that the function Move runs in constant time. Thus the latter part of the function Update is the computational bottleneck. To compute this part efficiently, we implement
as a doubly linked list (see
Figure 5). For each step of the traversal, we memorize the position of the most recently inserted element into
. Note that when we arrive at ⊤ and go back to the most recent branch node, we have to recover the corresponding position in some way e.g., by means of a stack. When we insert an element
into
, we put
in the next position of the most recently inserted element. It can be easily verified that all elements placed before (respectively, after) the most recently inserted element are sorted in increasing order of their indices. Thus, in order to scan all elements
with
, it suffices to search from the position of the most recently inserted element until the condition breaks. Since the total number of elements searched in a period is proportional to
k, we obtain the time necessary to compute the function Update through a period.
| Algorithm 2 Update the current partition p and the auxiliary data structures according to the current node f, the selected arc type of f, and the next node g |
function Update(f, g, p, G, ,
; ;
if the HI arc of f is selected and then
; ;
else if the LO arc of f is selected and then
; ;
end if
for all with do
; ;
end for
end function
function Move(, p, G, )
the block of p which contains ;
if the child of b is not in then
Add a new empty block to p;
Add to G in such a way that has no child and the child of b is ;
;
end if
Move to the block corresponding to the child of b;
Delete b from p and G if b is empty;
end function |
Let us consider the number of traversed nodes with repetition during the computation. Clearly the number of periods is . For each , let denote the path traced in the i-th period, which starts with a branch node and ends with ⊤. The number of HI arcs in is bounded above by k. The head of each LO arc in is a branch node, since the LO arc of a non-branch node is not selected in our traversal. The LO arc of any branch node is traversed exactly once. Thus the total number of LO arcs traversed during the computation is m. Therefore, . We conclude that the time necessary to execute Algorithm 1 is proportional to .
Figure 5.
For each step of the traversal of the ZDD given in
Figure 3, the doubly linked list of HI-state elements is shown below, where the index denotes the number of times ⊤ was visited and the double box or circle denotes the position after which an element is inserted.
Figure 5.
For each step of the traversal of the ZDD given in
Figure 3, the doubly linked list of HI-state elements is shown below, where the index denotes the number of times ⊤ was visited and the double box or circle denotes the position after which an element is inserted.
3.3. Conditional Co-occurrence Relations
Given a ZDD where every two elements are separable, Algorithm 1 cannot extract any useful information from the ZDD, but even so, we want to find some structural information hidden in the ground set. In this subsection we focus on the condition that enforces some elements always to be in a HI state and some elements always to be in a LO state.
Let (ON, OFF) be a pair of subsets of the ground set S of a ZDD. Two elements are conditionally inseparable with respect to (ON, OFF) if they co-occur with each other for all paths that satisfy the condition: the HI arcs are always selected for all elements in ON; The LO arcs are always selected for all elements in OFF.
Before extracting this relation, we need a preprocessing so that we can trace only paths that satisfy the condition above. Recall that the cardinality of a node
f is the number of paths from
f to ⊤. It is known (see also Algorithm C and Exercise 208 in [
12]) that given a ZDD, the cardinalities of all nodes in the ZDD can be computed in time proportional to the size of
f. This computation can be done in a bottom-up fashion: The cardinalities of ⊥ and ⊤ are 0 and 1, respectively; the cardinality of each internal node is the sum of the cardinalities of the two children. Given a pair (ON, OFF), it is easy to change to be able to compute the numbers of paths from all internal nodes
f to ⊤ that satisfy the condition concerning (ON, OFF). For convenience we call these numbers conditional cardinalities with respect to (ON, OFF).
To construct a conditional co-occurrence partition, change Algorithm 1 as follows.
Return the initial partition if the conditional cardinality of the root is zero.
The next node g of the current node f is the LO child if the conditional cardinalities of the two children are nonzero; else if the conditional cardinality of the LO child is zero, the HI child; else, the LO child.
In the while block of Algorithm 1, the next node g is the LO child if the conditional cardinality of the HI child is zero; otherwise, the HI child.
Theorem 3.3 Let m be the number of branch nodes. Let n be the size of a ground set. The computation for a conditional co-occurrence partition can be done in time proportional to mn.
Proof. This theorem can be proved in a similar way to the proof in Theorem 3.2, but an upper bound for the number of the traversed nodes cannot be similarly calculated. Indeed, because of the change in the while block, we may have to select many LO arcs. At least we can say that the size of each path is at most n and the number of periods is at most . Thus the time is proportional to .
Thanks to this theorem, when selecting a pair (ON, OFF), there is no need to worry about a rapid increase of computation time. This is in contrast to the case where we arbitrarily select paths and compute a co-occurrence partition from the selected paths. These paths are no longer compressed, and even if they can be compressed in some way, the size is generally irrelevant to the size of the original ZDD, and thus we cannot give a similar guarantee.