Maximum Disjoint Paths on Edge-Colored Graphs: Approximability and Tractability

Abstract

The problem of finding the maximum number of vertex-disjoint uni-color paths in an edge-colored graph has been recently introduced in literature, motivated by applications in social network analysis. In this paper we investigate the approximation and parameterized complexity of the problem. First, we show that, for any constant $\epsilon >0$, the problem is not approximable within factor $c^{1-\epsilon }$, where c is the number of colors, and that the corresponding decision problem is W[1]-hard when parametrized by the number of disjoint paths. Then, we present a fixed-parameter algorithm for the problem parameterized by the number and the length of the disjoint paths.

1. Introduction

Social networks are usually represented and studied as graphs. Vertices represent the elements analyzed (e.g., individuals), while edges represent a binary relation between the considered elements. Among the different properties considered to study such graphs, one of the most relevant is the vertex connectivity of two given vertices. Vertex connectivity is a measure of the information flowing from one vertex to the other, and it has many applications. For example, it is used for the identifications of important structural properties of a social network, like group cohesiveness and centrality [1,2]. A classical result of graph theory, known as Menger’s theorem, states that vertex connectivity is equivalent to the maximum number of disjoint paths between two given vertices.

While a lot of interest has been put in the study of networks that represent a single type of relation, a natural extension that has been recently introduced in literature [3] is to consider multi-relational social networks, that is social networks where more than one kind of relation between elements of the network is considered. In order to investigate vertex connectivity in multi-relational social networks, the combinatorial problem known as Maximum Colored Disjoint Paths (MAX CDP) has been introduced in [3]. MAX CDP asks for the maximum number of vertex-disjoint uni-color paths in an edge-colored graph, where the different edge-colors represent different kinds of relation.

The computational and approximation complexity of MAX CDP has been investigated in [3]. When the input graph contains exactly one color, MAX CDP is polynomial time solvable (it can be reduced to the maximum flow problem), while it has been shown to be NP-hard when the edges of the graph are colored. Moreover, MAX CDP is shown to be approximable within factor c, where c is the number of colors of the edges of the input graph, but not approximable within factor $2-\epsilon$, for any $\epsilon >0$, even when c is a fixed constant.

In [3], it is also investigated a variant of the problem, denoted as ℓ-LCDP, where the length of the paths in the solution are (upper) bounded by an integer $\ell \ge 1$. The ℓ-LCDP problem is NP-hard, for $\ell \ge 4$, while it admits a polynomial time algorithm when $\ell \le 3$. This variant of the problem can be approximated in polynomial time within factor $(\ell -1)/2+\epsilon$.

In this paper we investigate the approximation and parameterized complexity of MAX CDP and ℓ-LCDP. First, we show in Section 3 that MAX CDP is not approximable within factor $c^{1-\epsilon }$, for any constant $\epsilon >0$, and that the corresponding decision problem (CDP) is W[1]-hard when parametrized by the number p of disjoint uni-color paths. Then, in Section 4, we give a fixed-parameter algorithm for ℓ-LCDP, when ℓ and the number of disjoint uni-color paths are considered as parameters. Table 1 summarizes the results known about the complexities of these problems along with the new results presented in this work.

Table 1. Complexity status of MAX CDP.

Problem	Parameter	Status	Ref.
MAX CDP	c	NP-hard for any $c\ge 2$,	[3]
		c-approximable
		Inapprox. within $c^{1-\epsilon }$	new
CDP	p	W[1]-hard	new
ℓ-LCDP	ℓ	NP-hard for $\ell \ge 4$	[3]
		Poly-time for $\ell \le 3$	[3]
ℓ-LCDPp	$(\ell ,p)$	FPT	new

Table 1. Complexity status of MAX CDP.

Problem	Parameter	Status	Ref.
MAX CDP	c	NP-hard for any $c\ge 2$,	[3]
		c-approximable
		Inapprox. within $c^{1-\epsilon }$	new
CDP	p	W[1]-hard	new
ℓ-LCDP	ℓ	NP-hard for $\ell \ge 4$	[3]
		Poly-time for $\ell \le 3$	[3]
ℓ-LCDPp	$(\ell ,p)$	FPT	new

2. Definitions

In this section we give some preliminary definitions that will be useful in the rest of the paper. First, in this paper, we will consider only undirected graphs. Consider a set of colors $C=\{1,\cdots ,c\}$. In the paper we denote by c the cardinality of C. A C-edge-colored graph (or simply an edge-colored graph when the set of colors is clear from the context) is defined as $G=(V,\mathcal{E})$, where V denotes the set of vertices of G and $\mathcal{E}=\{E_1,\cdots ,E_c\}$ denotes a collection of edge sets, where the set $E_i$, with $i\in C$, represents the set of edges colored with color i. Notice that, for a given pair of vertices $v_i$, $v_j$, there may exist more than one edge between $v_i$ and $v_j$ (each of these edges is associated with a distinct color of C).

A path π in G is called a uni-color path if all the edges of π have the same color, that is they belong to the same set $E_i$ (for some $i\in C$). Given two vertices $x,y\in V$, an $xy$-path is a path between vertices x and y. Two paths ${\pi }^{\prime }$ and ${\pi }^{″}$ are internally disjoint (or, simply, disjoint) if they do not share any internal vertex, while a set of paths are internally disjoint if they are pairwise internally disjoint.

Next, we introduce the formal definitions of the problems we deal with in this paper, namely the optimization problem MAX CDP, the decision problem (CDP) naturally associated with MAX CDP, and the corresponding length-bounded variants ℓ-LCDP and ℓ-LCDP_p.

Problem 1. MAXIMUM COLORED DISJOINT PATHS (MAX CDP).

Input: a set C of colors, a C-edge-colored graph $G=(V,\mathcal{E})$, and two vertices $s,t\in V$.

Output: the maximum number of disjoint uni-color $st$-paths.

Problem 2. COLORED DISJOINT PATHS (CDP).

Input: a set C of colors, a C-edge-colored graph $G=(V,\mathcal{E})$, a non-negative integer p, and two vertices $s,t\in V$.

Output: Do there exist at least p disjoint uni-color $st$-paths in G?

The ℓ-LENGTH COLORED DISJOINT PATHS (ℓ-LCDP) problem is a variant of MAX CDP where the length of the paths in the solution is bounded by an integer $\ell \ge 1$. The ℓ-LCDP problem is the decision version of ℓ-LCDP which asks if there exists a solution of ℓ-LCDP with cardinality at least p.

3. Approximation and Parameterized Complexity of

In this section, we present a reduction from MAXIMUM INDEPENDENT SET to MAX CDP. Since the reduction preserves the solution cost, it implies that MAX CDP is not approximable within factor $c^{1-\epsilon }$, for any $\epsilon >0$, and that CDP is W[1]-hard when the parameter is the size p of the solution.

Given an undirected graph $G_I=(V_I,E_I)$, the MAXIMUM INDEPENDENT SET (MAX INDSET) problem asks for an independent set $I\subseteq V_I$ of maximum cardinality, i.e., a maximum-cardinality set I such that if $v^{\prime },v^{″}\in I$ then $\{v^{\prime },v^{″}\}\notin E_I$. In the following, starting from a graph $G_I$, we construct a gadget (an edge-colored graph) $G_C$, such that finding an independent set I of cardinality k in $G_I$ is equivalent to finding k disjoint uni-color $st$-paths in $G_C$. First, we describe the edge-colored graph $G_C$ associated with a generic graph $G_I$, then we prove some properties of the computed gadget.

Description of the gadget. Let $G_I=(V_I,E_I)$ be an undirected graph, with $V=\{v_1,\dots ,v_n\}$ and $E_I=\{e_1,\dots ,e_m\}$. Without loss of generality, we assume that $G_I$ is connected, since a maximum independent set of a non-connected graph is the union of the maximum independent sets of its connected components. Let ${\Pi }_{E_I}$ be an ordered list of the edges of $G_I$, based on some ordering. We construct an edge-colored graph $G_C=(V_C,E_1,\dots ,E_n)$ associated with $G_I$ as follows. Informally, the vertex set $V_C$ is composed by two distinguished vertices s and t and a vertex for each edge of $G_I$, while each set $E_i$, $1\le i\le c$, is composed connecting the vertices associated with edges of $G_I$ incident to $v_i$ in the same order as they appear in ${\Pi }_{E_I}$. Formally, the set of colors is:

$$C=\{1,\cdots ,n\}$$

Now, we define the vertex set $V_C$:

$$V_C=\{s,t\}\cup \{u_{i,j}\mid \{v_i,v_j\}\in E_I\}$$

Finally, we define the edge set $E_i$, $1\le i\le n$:

$$\begin{array}{cc}\hfill E_i=& \left\{\{u_{i,x},u_{i,y}\}\mid \text{no}\text{edge}\{v_i,v_z\}\text{appears}\text{between}\{v_i,v_x\}\text{and}\{v_i,v_y\}\text{in}\text{the}\text{list}{\Pi }_{E_I}\right\}\cup \hfill \\ & \left\{\{s,u_{i,j}\}\mid u_{i,j}\text{is}\text{the}\text{first}\text{edge}\text{incident}\text{in}{v}_i\text{of}\text{the}\text{list}{\Pi }_{E_I}\right\}\cup \hfill \\ & \left\{\{u_{i,j},t\}\mid u_{i,j}\text{is}\text{the}\text{last}\text{edge}\text{incident}\text{in}{v}_i\text{of}\text{the}\text{list}{\Pi }_{E_I}\right\}\hfill \end{array}$$

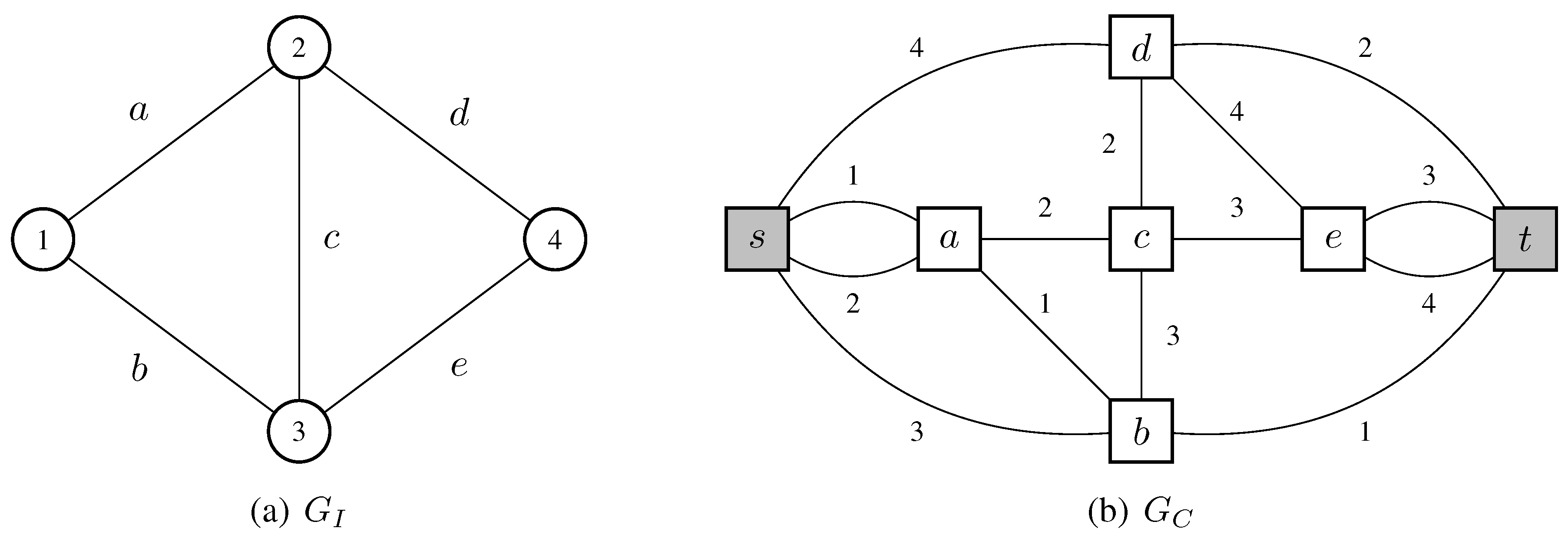
Figure 1 represents an example of an undirected graph $G_I$ and of the edge-colored graph $G_C$ associated with it.

Figure 1. An example of a graph $G_I$ and the edge-colored graph $G_C$ associated with it. For convenience, we labelled the edges of $G_I$ such as they correspond to the vertices in $G_C$. The colors of the edges in $G_C$ are indicated by numbers placed near the edges, while the two distinguished vertices s and t are highlighted in grey. The order ${\Pi }_{E_I}$ of the edges of $G_I$ is simply the lexicographic order of their labels.

Figure 1. An example of a graph $G_I$ and the edge-colored graph $G_C$ associated with it. For convenience, we labelled the edges of $G_I$ such as they correspond to the vertices in $G_C$. The colors of the edges in $G_C$ are indicated by numbers placed near the edges, while the two distinguished vertices s and t are highlighted in grey. The order ${\Pi }_{E_I}$ of the edges of $G_I$ is simply the lexicographic order of their labels.

Given a graph $G_I$ with n vertices and m edges, the associated edge-colored graph $G_C$ has $m+2$ vertices, $O\left(mn\right)$ edges, and n colors, i.e., $c=n$.

Properties of the gadget. First, we introduce the following properties of the gadget.

Remark 1. A uni-color $st$-path of color i, with $1\le i\le c$, contains each vertex $u_{i,x}$ of $G_C$ associated with an edge incident in $v_i\in V_I$.

Proof.

The proof follows by construction, since the edges of color i, with $1\le i\le c$, induce a $st$-path that contains each vertex $u_{i,x}$ of $G_C$ associated with an edge incident in $v_i\in V_I$ ordered as in list ${\Pi }_{E_I}$.

Next, we prove the two main results of the reduction from to MAX INDSET to MAX CDP.

Lemma 2.

Let $G_I=(V_I,E_I)$ be an undirected graph and $I\subseteq V_I$ be an independent (vertex) set for $G_I$. Then, we can compute in polynomial time (at least) |I| disjoint uni-color $st$-paths in the edge-colored graph $G_C$ associated with $G_I$.

Lemma 3.

Let $G_I=(V_I,E_I)$ be an undirected graph and $G_C$ be the edge-colored graph associated with $G_I$. If there exist k disjoint uni-color $st$-paths in $G_C$, then we can compute in polynomial time an independent set $I\subseteq V_I$ for $G_I$, with $\left|I\right|=k$.

The first lemma is easily proved by showing that the uni-color $st$-paths associated with the vertices of the independent set I are pairwise disjoint. Conversely, the second lemma can be proved by showing that the vertices of $G_I$ associated with the k uni-color $st$-paths of $G_C$ form an independent set for $G_I$.

Proof of Lemma 2.

By construction, in $G_C$ there exists a uni-color $st$-path associated with each vertex v of the original graph $G_I$. We will show that the set P of paths of $G_C$ associated with each vertex $v\in I$ are internally disjoint. Let ${\pi }_i$ and ${\pi }_j$ be two paths of P associated with vertices $v_i$ and $v_j$, respectively, of I. Notice that the two paths ${\pi }_i$ and ${\pi }_j$ connect the vertices which represent the edges of $G_I$ incident to $v_i$ and $v_j$, respectively. Since I is an independent set in $G_I$, no edge $e^{\prime }\in E_I$ is incident to both $v_i$ and $v_j$ ($u_{i,j}\notin E_I$), thus ${\pi }_i$ and ${\pi }_j$ are (internally) disjoint.

Proof of Lemma 3.

Let P be the set of k disjoint uni-color $st$-paths of $G_C$. Since each color is (bi-univocally) associated with a single path in $G_C$ which, in turn, is (bi-univocally) associated with a single vertex of $G_I$, we can define a set $I\subseteq V_I$ that consists of the vertices of $G_I$ associated with a path of P. Clearly, $\left|I\right|=\left|P\right|=k$. We claim that I is an independent vertex set for $G_I$. Suppose that I is not an independent set, thus there exist two vertices $v_i,v_j\in I$ such that $\{v_i,v_j\}\in E_I$. Let $u_{i,j}$ be the vertex of $G_C$ representing edge $\{v_i,v_j\}$. Since $v_i,v_j\in I$, then there exist two paths ${\pi }_i,{\pi }_j$ in P associated with $v_i$ and $v_j$. By Remark 1, both paths must contain vertex $u_{i,j}$ as an internal vertex, since edge $\{v_i,v_j\}$ is incident to both $v_i$ and $v_j$. Hence paths ${\pi }_i$ and ${\pi }_j$ are not internally disjoint, which contradicts our assumption and thus I is an independent set for $G_I$.

Consequences. Lemmas 2 and 3 prove the existence of an L-reduction [4] from MAX INDSET to MAX CDP with constants $\beta =\gamma =1$. Hence, considering that, unless $\text{P}=\mathrm{NP}$, MAX INDSET cannot be approximated in polynomial time within factor ${\left|V_I\right|}^{1-\epsilon }$ for any constant $\epsilon >0$ [5], and that $\left|V_I\right|=c$, the following theorem holds.

Theorem 4.

For any constant $\epsilon >0$, MAX CDP cannot be approximated within factor $c^{1-\epsilon }$ in polynomial time unless $\text{P}=\mathrm{NP}$.

This result greatly improves the previous inapproximability factor $2-\epsilon$ for MAX CDP [3] and, given the c-approximation algorithm presented in [3], it is the asymptotically optimal inapproximability ratio for MAX CDP. However, notice that the inapproximability factor $2-\epsilon$ for MAX CDP given in [3] holds even if c is a fixed constant, while in our reduction c is not fixed.

From the parameterized complexity point of view, the reduction also implies the W[1]-hardness of the decision problem CDP, as stated in the following theorem.

Theorem 5.

CDP is W[1]-hard when parameterized by the number p of disjoint uni-color $st$-paths.

Proof.

The reduction presented by Lemmas 2 and 3 is also a parameterized reduction [6] from INDEPENDENT SET (the decision problem naturally associated with MAX INDSET) to CDP (indeed the size of an independent set of $G_I$ is identical to the number of disjoint uni-color $st$-path in $G_C$). Since INDEPENDENT SET is W[1]-hard when the parameter is the size of the required independent set [7], then also CDP is W[1]-hard when parametrized by number p of disjoint uni-color $st$-paths. ☐

4. A Fixed-Parameter Algorithm for

In this section, we study ℓ-LCDP_p, the length-bounded (decision) version of MAX CDP, which asks if there exist p uni-color disjoint $st$-paths of length at most ℓ. We show that ℓ-LCDP_p is fixed-parameter tractable when the parameters are ℓ and p by presenting a parameterized algorithm based on the color coding technique [8]. For an introduction to parameterized complexity see [6]. Notice that ℓ-LCDP_p is unlikely to admit fixed-parameter tractable algorithms when parameterized only by p or only by ℓ. Indeed in the latter case, ℓ-LCDP_p is already -hard when $\ell =4$ [3]. In the former case, we have proved in the previous section that CDP (hence ℓ-LCDP_p, when $\ell =n$) is W[1]-hard when parameterized by p.

Color coding is a technique initially introduced to design fixed-parameter algorithms for various restrictions of the subgraph isomorphism problem. It then gained popularity and it has been successfully applied to tackle the computational hardness of various problems on networks and graphs [9,10,11], on strings [12,13], and problems of subset selection [14,15]. The basic idea of the color coding technique applied on graph problems is, first, to “color” the vertices of the graph from a set of k colors (for an appropriate choice of the number k of colors), and, then, to find a solution of the given problem with the additional constraint that the vertices of the solution are colored with distinct colors (called a “colorful” or “color coded” solution), if such a solution exists. The process is re-iterated with a different coloring if a colorful solution is not found.

The key theoretical result, which allows to obtain deterministic algorithms based on the color coding technique, is the deterministic construction of k-perfect families of hash functions. A family F of hash functions from a set U (the vertex set in the traditional applications of color coding) to the set $\{1,\dots ,k\}$ of colors is k-perfect if, for each subset $U^{\prime }$ of U such that $\left|U^{\prime }\right|=k$, there exists a hash function f in F such that $U^{\prime }$ is colorful w.r.t. f, i.e., f assigns a distinct label to each element of $U^{\prime }$. In fact, if the given problem has a solution S of size k, then there exists a hash function in F such that solution S is colorful. Hence, it suffices to test if there exists a colorful solution for one of the colorings given by the hash functions of the k-perfect family in order to guarantee the existence of a solution of the original problem, if such a solution exists. Crucial to the overall running time is the size of a k-perfect family and the time required to enumerate and evaluate the hash functions of the family. Currently, the best bounds (such as [8,16,17]) are, in general, explicit constructions of families of size $2^{O\left(k\right)}{log}^{O\left(1\right)}\left(\right|U\left|\right)$ in time proportional to their size.

The description of the parameterized algorithm for the ℓ-LCDP_p problem is divided into two parts. First, we present a procedure that, given an edge-colored graph $G_C$ and a vertex-coloring function λ, verifies if in $G_C$ there exist p disjoint uni-color $st$-paths long at most ℓ and with the additional constraint that the inner vertices of the p paths are colored with distinct colors. Then, we show that, by exploiting well-known properties of families of perfect hash functions, the previous procedure can be used to solve the ℓ-LCDP_p problem in polynomial time (if p and ℓ are parameters). In the following, to avoid ambiguities between vertex’s and edge’s colors, function λ will be called vertex-labelling function (or, simply, a labelling function) instead of the traditional term of coloring function.

A dynamic-programming procedure for the $\mathcal{L}$-labelled problem. Let $G_C=(V,E_1,\dots ,E_c)$ be a C-edge-colored graphs with two distinguished vertices s and t, and let λ be a labelling function which maps each vertex v of $V\backslash \{s,t\}$ to a label $\lambda \left(v\right)$ belonging to a set $\mathcal{L}$ (we assume that λ assigns a distinct label to each vertex of a solution of ℓ-LCDP_p). Let $L\subseteq \mathcal{L}$ be a fixed set of labels. A simple path π in $G_C$ is L-labelled if and only if the labels of its vertices (with the exclusion of s and t) are contained in L and are pairwise distinct. A set $\{{\pi }_1,\dots ,{\pi }_k\}$ of simple paths is L-labelled if and only if there exists a partition $\{L_1,\dots ,L_k\}$ of L such that each ${\pi }_i$ is $L_i$-labelled. We say that a path π is g-colored, with $g\in C$, if all of its edges belong to set $E_g$. The $\mathcal{L}$-labelled ℓ-LCDP_p problem, given $G_C$ and $\lambda :V\to \mathcal{L}$ with $\left|\mathcal{L}\right|=(\ell -1)p$, asks if there exists an $\mathcal{L}$-labelled solution for the ℓ-LCDP_p problem on $G_C$. We solve the $\mathcal{L}$-labelled ℓ-LCDP_p problem by combining two dynamic-programming recurrences. The first one, $M[L,v,g]$, tests if, for a set of labels $L\subseteq \mathcal{L}$, there exists an L-labelled g-colored path from vertex s to a vertex v different from t. The second one, $P\left[L\right]$, tests if, for a set of labels $L\subseteq \mathcal{L}$ such that $\left|L\right|=(\ell -1)q$ for some integer $q\in [0,p]$, there exists a partition $\{L_1,\dots ,L_q\}$ of L in q subsets such that each set $L_i$ labels a $g_i$-colored $st$-path of length $l\le \ell$.

Recurrence for $M[L,v,g]$ is defined as follows (where ⊎ represents the disjoint union operator):

$$M[L,v,g]=\left\{\begin{array}{cc}1\hfill & \text{if}v=s\hfill \\ 0\hfill & \text{if}L=\varnothing \text{and}v\ne s\hfill \\ max\left\{M[L^{\prime },u,g]\mid L=|L^{\prime }\uplus \left\{\lambda \left(v\right)\right\}\wedge \{u,v\}\in E_g\right\}\hfill & \text{otherwise}\hfill \end{array}\right.$$

(4.1)

Correctness of the previous recurrence is proved by the following lemma.

Lemma 6.

$M[L,v,g]$ is true if and only if there exists an L-labelled g-colored path from s to v.

proof.

The proof is by induction on the cardinality of L. If $\left|L\right|=0$, the base cases apply and a path which does not use any label exits if and only if $v=s$. Now, assume that $M[L,v,g]$ is correct for any L such that $\left|L\right|\le k$ (for some k) and we will prove the correctness of $M[L^{\prime },v,g]$ for all $L^{\prime }$ such that $\left|L^{\prime }\right|=k+1$. Moreover, assume that $v\ne s$, since, otherwise, the first base case applies which is clearly correct. Then, an $L^{\prime }$-labelled g-colored path from s to $v\ne s$ exists if and only if $\lambda \left(v\right)\in L$ and (ii) there exists an $L^{″}$-labelled g-colored path π from s to a vertex u such that $\{u,v\}\in E_g$ and $L^{″}=L^{\prime }\backslash \left\{\lambda \left(v\right)\right\}$. Since $\left|L^{″}\right|=\left|L^{\prime }\right|-1=k$, path π exists if and only if $M[L^{″},u,g]$ is true. The inductive case of Equation 4.1 tests the above mentioned conditions, hence $M[L^{\prime },v,g]$ is correct also for sets of labels L such that $\left|L\right|=k+1$, concluding the proof.

Clearly, M can be used to test if there exists an $\mathcal{L}$-labelled g-colored $st$-path, as illustrated by the following corollary.

Corollary 7.

The existence of an $\mathcal{L}$-labelled g-colored $st$-path can be tested in time $O\left(2^{\left|\mathcal{L}\right|}\right|E_g\left|\right)$.

Proof.

By Lemma 6, to test the existence of an $\mathcal{L}$-labelled g-colored $st$-path, it suffices to test the existence of a vertex v such that $\{v,t\}\in E_g$ and $M[\mathcal{L},v,g]$ is true. For a fixed color g and a fixed set L of labels, the time needed to evaluate $M[L,v,g]$ for all $v\in V$ is $O\left(\right|E_g\left|\right)$ since each edge is considered only a constant number of times (twice, indeed). Since there exist $2^{\left|\mathcal{L}\right|}$ distinct subsets of $\mathcal{L}$, the overall time is $O\left(2^{\left|\mathcal{L}\right|}\right|E_g\left|\right)$.

The second recurrence, $P\left[L\right]$, which, given an integer $q\in [0,p]$ and a subset $L\subseteq \mathcal{L}$ such that $L=(\ell -1)q$, solves the L-labelled ℓ-LCDP_p problem, is defined as follows:

$$P\left[L\right]=\left\{\begin{array}{cc}1\hfill & \text{if}L=\varnothing \hfill \\ \begin{array}{cc}\hfill max& \{P\left[L^{\prime }\right]\wedge M[L^{″},v,g]\mid \hfill \\ & L=L^{\prime }\uplus \left|L^{″}\right|\wedge L^{″}=(\ell -1)\wedge g\in C\wedge \{v,t\}\in E_g\}\hfill \end{array}\hfill & \text{otherwise}\hfill \end{array}\right.$$

(4.2)

Notice that we implicitly assume that the solution of the ∅-labelled ℓ-LCDP₀ problem is always Yes (i.e., $P\left[\varnothing \right]=1$).

Correctness of Equation 4.2, as proved in the following lemma, derives from Corollary 7, from the bound on the cardinality of $L^{″}$, and from the disjointness of $L^{\prime }$ and $L^{″}$.

Lemma 8.

Given an edge-colored graph $G_C$ and a vertex-labelling function $\lambda :V\to \mathcal{L}$ with $\left|\mathcal{L}\right|=(\ell -1)p$, then there exists an $\mathcal{L}$-labelled set S of p disjoint uni-color $st$-paths of length at most ℓ if and only if $P\left[\mathcal{L}\right]$ is true.

To prove this lemma, we first prove some intermediate results.

Property 9.

Let $L_i$ and $L_j$ be two disjoint subsets of $\mathcal{L}$, let $v_i$ and $v_j$ be two distinct vertices, and $g_i$ and $g_j$ be two (possibly equal) colors. Then $M[L_i,v_i,g_i]$ and $M[L_j,v_j,g_j]$ are both true if and only if there exist two disjoint uni-color paths ${\pi }_i$ and ${\pi }_j$ from s to $v_i$ and $v_j$, respectively.

Proof.

By Lemma 6, since both $M[L_i,v_i,g_i]$ and $M[L_j,v_j,g_j]$ are true, paths ${\pi }_i$ and ${\pi }_j$ exist labelled with set $L_i$ and $L_j$, respectively. Since $L_i$ and $L_j$ are disjoint, there could not exist a common vertex v (different from s), otherwise $\lambda \left(v\right)$ would belong to both $L_i$ and $L_j$. Hence, ${\pi }_i$ and ${\pi }_j$ are disjoint.

Property 10.

The length of an L-labelled path π from s to a vertex $v\ne t$ is, at most, |L|.

Proof.

All the vertices (but s, which is not labelled) of π are labelled with distinct labels in L, hence there could be at most $\left|L\right|+1$ vertices in π.

Proof of Lemma 8.

We prove the correctness of P by induction on the number of paths p. If $p=0$, then $\left|\mathcal{L}\right|=(\ell -1)p=0$. Thus, the base case applies and, since we assume that 0 paths always exist, it is also correct. Let us assume that P is correct for any $p\le k$ and let us prove its correctness for $p=k+1$. First, we prove that if $P\left[\mathcal{L}\right]$ is true, then a solution S for ℓ-LCDP_p can be built. Notice that the second case of Equation 4.2 tries every possible bi-partition of set $\mathcal{L}$ in two sets $L^{\prime }$ and $L^{″}$ of cardinality $\left|\mathcal{L}\right|-(\ell -1)$ and $\ell -1$, respectively. If function $P\left[\mathcal{L}\right]$ is true, then at least one of the bi-partitions verifies the given conditions. Notice that $\left|L^{\prime }\right|=\left|\mathcal{L}\right|-(\ell -1)=(\ell -1)(k+1)-(\ell -1)=(\ell -1)k$. Hence, by induction hypothesis, since $P\left[L^{\prime }\right]$ is true, there exists an $L^{\prime }$-labelled set $S^{\prime }$ of k disjoint uni-color $st$-paths. The other conditions, as shown in the proof of Corollary 7, test the existence of an $L^{″}$-labelled g-colored $st$-path π for some color $g\in C$. Thus, if there exists a bi-partition which satisfies all the conditions, then there exits an L-labelled set $S=S^{\prime }\uplus \left\{\pi \right\}$ of $k+1$ uni-color $st$-paths. Moreover, since $L^{\prime }$ and $L^{″}$ are disjoint, by Property 9, path π and any path of S are disjoint. Furthermore, since $\left|L^{″}\right|=\ell -1$, by Property 10, the length of π is, at most, ℓ (in particular, $\ell -1$ from s to vertex v, plus 1 from v to t). As a consequence, S is an $\mathcal{L}$-labelled set of $p=k+1$ disjoint uni-color $st$-paths of length, at most, ℓ.

Now, we prove that if there exists an $\mathcal{L}$-labelled set S of $(k+1)$ disjoint uni-color $st$-paths, then $P\left[\mathcal{L}\right]$ is true. For each path $\pi \in S$, let $L_i$ be the set of labels labelling ${\pi }_i$. Since the paths in S are disjoint, also the sets $L_1,\dots ,L_{k+1}$ are disjoint. Moreover, since the length of each path is at most ℓ, we have that $\left|L_i\right|\le (\ell -1)$. Notice that |$\mathcal{L}$| is $(\ell -1)(k+1)$, thus it is possible to find a partition of $\mathcal{L}$ in p sets $L_1^{\prime },\dots L_{k+1}^{\prime }$ of cardinality $\ell -1$ such that each $L_i$ is a subset of $L_i^{\prime }$. Let us consider a generic path ${\pi }_i$. Since ${\pi }_i$ is a uni-color $st$-path (of length at most ℓ), then there exists a vertex v and a color g such that $M[L_i^{\prime },v,g]$ is true and $\{v,t\}\in E_g$ (Corollary 7). Finally, since $\overline{L_i^{\prime }}=L\backslash L_i^{\prime }$ is a set of labels of cardinality $(\ell -1)k$ and $S\backslash \left\{{\pi }_i\right\}$ is an $\overline{L_i^{\prime }}$-labelled set of k disjoint uni-color $st$-paths of length at most ℓ, by induction hypothesis we have that $P\left[\overline{L_i^{\prime }}\right]$ is true. Therefore, the bi-partition $\{L_i^{\prime },\overline{L_i^{\prime }}\}$ satisfies all the condition of Equation 4.2 and $P\left[\mathcal{L}\right]$ is true.

An immediate consequence is that the $\mathcal{L}$-labelled ℓ-LCDP_p problem can be solved in polynomial time when ℓ and p are parameters.

Corollary 11.

The $\mathcal{L}$-labelled problem can be solved in time $O(2^{2\ell p}m)$, where $m={\sum }_{g\in C}\left|E_g\right|$.

Proof.

The evaluation of M needs $O(2^{\left|\mathcal{L}\right|}m)$ time. For a fixed $L\subseteq \mathcal{L}$, the evaluation of $P\left[L\right]$ requires $O(2^{\left|L\right|}m)$ and, since there are $2^{\left|\mathcal{L}\right|}$ possible subsets of $\mathcal{L}$, the time needed to evaluate P is $O(2^{\left|\mathcal{L}\right|})+O(2^{\left|\mathcal{L}\right|}{2}^{\left|\mathcal{L}\right|}m)=O(2^{2\ell p}m)$. ☐

The algorithm for ℓ-LCDP_p. As explained before, it is possible to explicitly construct a k-perfect family F of hash functions, that is a set F of hash functions from a universal set U to the set of integers $\{1,\dots ,k\}$ such that for each $U^{\prime }\subseteq U$ of cardinality k there exists a hash function $f\in F$ which assigns distinct integers to the elements of $U^{\prime }$. It has been shown (see, for example, [8,16,17]) that a k-perfect family of hash functions of size $2^{O\left(k\right)}{log}^{O\left(1\right)}\left|U\right|$ can be explicitly constructed in time proportional to its size. As a consequence, the ℓ-LCDP_p problem can be solved by solving the $\mathcal{L}$-labelled ℓ-LCDP_p problem for all the labelling functions given by the hash functions of a $(\ell -1)p$-perfect family (where $U=V$) in time $2^{O\left(\ell p\right)}O(m{log}^{O\left(1\right)}|V_C|)$. We remark that this algorithm is mainly of theoretical interest, since the running times are impractical even with modest choices of the parameters ℓ and p. However, as formalized by the following theorem, it settles the parameterized complexity of the ℓ-LCDP_p problem for the parameters ℓ and p.

Theorem 12.

The problem parameterized by the bound on the path length ℓ and the number p of disjoint uni-color $st$-paths is in FPT.

5. Conclusions

In this paper we have considered the MAX CDP problem, a combinatorial problem motivated by applications in social network analysis that, given an edge-colored graph $G_C$, asks for the maximum number of disjoint uni-color paths in $G_C$. We have shown that the problem is not approximable within factor $c^{1-\epsilon }$, for any constant $\epsilon >0$, and that the corresponding decision problem (CDP) is W[1]-hard when parametrized by the number p of disjoint uni-color paths. Then, we have given a fixed-parameter algorithm for ℓ-LCDP_p, a restriction of the problem where the length of the disjoint paths are bounded by a parameter. An interesting open problem is to improve the time complexity of the fixed-parameter algorithm for ℓ-LCDP_p. Moreover, kernelization complexity issues are still completely unexplored.