Interactive Compression of Digital Data

Abstract

If we can use previous knowledge of the source (or the knowledge of a source that is correlated to the one we want to compress) to exploit the compression process then we can have significant gains in compression. By doing this in the fundamental source coding theorem we can substitute entropy with conditional entropy and we have a new theoretical limit that allows for better compression. To do this, when data compression is used for data transmission, we can assume some degree of interaction between the compressor and the decompressor that can allow a more efficient usage of the previous knowledge they both have of the source. In this paper we review previous work that applies interactive approaches to data compression and discuss this possibility.

1. Introduction

Data Compression is crucial for the transmission and storage of digital data. It is possible to improve the compression performance when we can use previous knowledge of the emitting source in the compression process. In this case in the fundamental source coding theorem we can substitute entropy with conditional entropy and we have a new theoretical limit that allows for better compression.

When data compression is used for data transmission we might assume some degree of interaction between the compressor and the decompressor that allows a more efficient usage of the previous knowledge of the source they both might have. The price we accept to pay, in some cases, is a negligible probability of errors.

In this paper we review recent work that applies previous knowledge of the emitting source to data compression and interactive approaches and discuss these possibilities. We will concentrate on lossless, dictionary based, compression algorithms.

In the next section we review relevant concepts about the theoretical limits of data compression and about the dictionary based compression methods. Section 3 discusses how to use the previous knowledge of the source when the shared knowledge is represented by common, identical files that both sides have available but there is no possibility of interaction between the Sender and the Receiver that need to communicate. Section 4 reviews the situation in which both Sender and Receiver have knowledge of the source, but do not share necessarily the same, identical, files. In this case, by taking advantage of the interaction between the two communication sides, Sender and Receiver can improve the compression process by using the shared knowledge if they accept a small possibility of communication errors. Section 5 presents our conclusions and points to new research directions.

2. Compression, Entropy and Dictionaries

Data and information today are digital. We need data compression to deal with digital data: without compression we cannot store and/or transmit the huge amount of data we treat every day. The theoretical background of data compression techniques is strong and well established. It dates back to the seminal work of Claude Elwood Shannon (see [1]). In the late 1940s, he gave a formal definition of the notion of information content or randomness of a source, which he called entropy. This theoretical background gives precise limits on the performance of a compression algorithm.

Any process that generates information can be viewed as a source that emits a sequence of symbols from a finite alphabet. The source output can be seen as a sequence of words: i.e., finite length sequences of alphabet symbols. From the practical point of view to divide the source outputs into words might involve a semantic analysis that depends on the source and that it is possible only if the output of the source is interpreted in a determinate context. For example, a word of a source that emits English sentences can be a sequence of one or more common English words, including blanks, punctuation marks, etc. If we consider a first-order source S, in which successive symbols are statistically independent, Shannon and Weaver in [1] showed that, given the set of probabilities P = {p₁, p₂, ..., p_n) for the source symbols, the optimal expected number of code bits is:

$$\sum _{i=1}^n–p_i{\mathit{log}}_2(p_i)$$

a quantity which they called the Entropy of the source S, usually denoted by H(S). Conditional entropy H(S₁|S₂) is the natural analogue of the entropy H(S) but it is based on the conditional probability. It can be shown that: H(S₁|S₂) ≤ H(S₁).

Entropy is a measure of uncertainty about an event: it has a zero value if and only if there is absolute certainty and it is maximal when all the events are equiprobable: i.e., there is absolute uncertainty. The “fundamental source-coding theorem” can be stated as in Storer [2]: “Let S be a first-order source over an alphabet Σ and let Γ be an alphabet of r > 1 characters. Then encoding the characters of S with characters of Γ requires an average of H_r(s) characters of Γ per character of Σ. Furthermore, for any real number ε > 0 there exists a coding scheme that uses an average of H_r(s) + ε characters of Γ per character of Σ”. Because of the fundamental source coding theorem entropy is a limit to the length of the string that we can use to lossless code a message.

Today lossless compressors are very efficient. While it is not possible to prove that they always achieve the theoretical limit, the performances of the state of the art compressors for specific types of data, like natural language text, are certainly very close to this theoretical limit. Current research on lossless compression focuses on developing compressors for new types of digital data or on improving, often only by small amounts, existing compressors for a specific class of data. Even a small improvement is an important achievement, given the economical impact it can have on data transmission and storage. Many data compression methods are based on the notion of “dictionary”. In this paper we will primarily consider dictionary based compression methods.

Dictionaries can be static, i.e., built at the beginning of the compression/communication process and never updated and in this case the compression method is called static dictionary method. Otherwise, if the dictionaries are consistently and independently built, maintained, and updated by both compressor and decompressor, then the compression method is called dynamic dictionary method. We can use static dictionary methods when the source is known in advance. When we use data compression to communicate, the Sender and the Receiver use the same (static) dictionary and eventually, at the beginning of the communication, the Sender needs to send the dictionary to the Receiver.

For example, in vector quantization algorithms the compressor builds up a dictionary on a training set of images and it uses this dictionary to compress the new data. The decompressor needs the same dictionary to decompress; therefore the compressor shall transmit this dictionary to the decompressor.

The cost of making this dictionary available depends on its dimensions. Generally this cost is not considered in the analysis of a static dictionary compression method by using the argument that the constant cost can be amortized over time by compressing a large amount of data. In real life situations this is not always true. Frequently we have as compression target only small or medium size files, that represent computer programs, images, text data, music, videos, etc. For example it is often necessary to send only a few computer programs or a few images from a source to a destination, possibly via a telephone line by using a modem or via a fast internet connection. In these cases the cost of sending the dictionary might have an important impact on the total cost of the communication, making static compression methods unpractical.

Dynamic dictionary methods build up the Sender and the Receiver dictionary at run time, by starting with empty dictionaries and by building up the dictionaries in terms of the already compressed data. If the files we want to compress are small, the empty dictionary might initially bias the compression process: it is not equally effective to compress data by using a dictionary that contains only the alphabet symbols instead of a dictionary that is complete. It would be obviously more effective to start up the compression/decompression process with an appropriate, fully loaded, dictionary instead of an empty one. Mainstream methods that are based on dictionaries are almost always dynamic dictionary methods: this adaptive technique is flexible and can be easily used in practical situations. All the optimality proofs for this technique use asymptotic arguments and do not take into account the (theoretically constant) cost of filling up the dictionary.

3. Conditional Compression

One option we have to increase compression is to use the knowledge of similar messages that Sender and Receiver have compressed in the past from the same source and to design algorithms that efficiently compress and decompress given this previous knowledge: by doing this the conditional entropy is the new theoretical limit and it allows for better compression.

3.1. A simple experiment

It is not easy to determine the behavior of a source by looking at a finite, small number of consecutive messages. In real life we often update our personal computers with new versions of existing software products: internet browsers, word processors, anti-viruses, messengers, etc. Generally the new software distribution includes large parts of the previous one. If we identify these repeated parts we can avoid their re-transmission when both the encoder and the decoder maintain a copy of the old distribution.

To study the amount of shared knowledge that is retained by successive software distributions, we can extend the logical operator eor to compute the differences between two binary files. We indicate with ⊕ this difference operator: if A and B are two binary files of equal length then: C = A ⊕ B, where C will be a new binary file such that C[i], i.e., the i-th bit of C, will be one if and only if the i-th bits of A and B are not equal.

Therefore, given that the operator is associative and commutative:

A ⊕ B ⊕ A = B and A ⊕ B ⊕ B = A. Moreover A ⊕ A = 000…0.

Suppose that M and N are two large and strictly correlated files (for example they are two subsequent distribution versions of the same software) and that we compute M ⊕ N. If we can identify and remove from N the sequences of bits that are unchanged with respect to its old version M the resulting, smaller, file will be hopefully easier to compress. In a simple experiment (see [3]) we consider two consecutive distribution versions of the Internet browser Netscape for Mac:

• MacNS6FullInstaller.sea.bin (about 17.7 Mb),
• MacNS6FullInstaller2.sea.bin (about 17.7 Mb),

These two files are self-extracting files that are already partially compressed. Part of the correlation between the files is therefore probably lost. We compress (by using the standard Unix utility gzip) the first file, then we split the files into consecutive segments of 2,000 bytes each and compare the compressed size of the first file with the size of the compressed Net(i) files, where each Net(i) of the second file is obtained from the first file by operating a bitwise eor difference in the first i segments.

The intuition is that, when considering two consecutive distribution versions of the same software, we might expect to see the parts of the files that are similar at the beginning of the files after which the two files will probably differentiate.

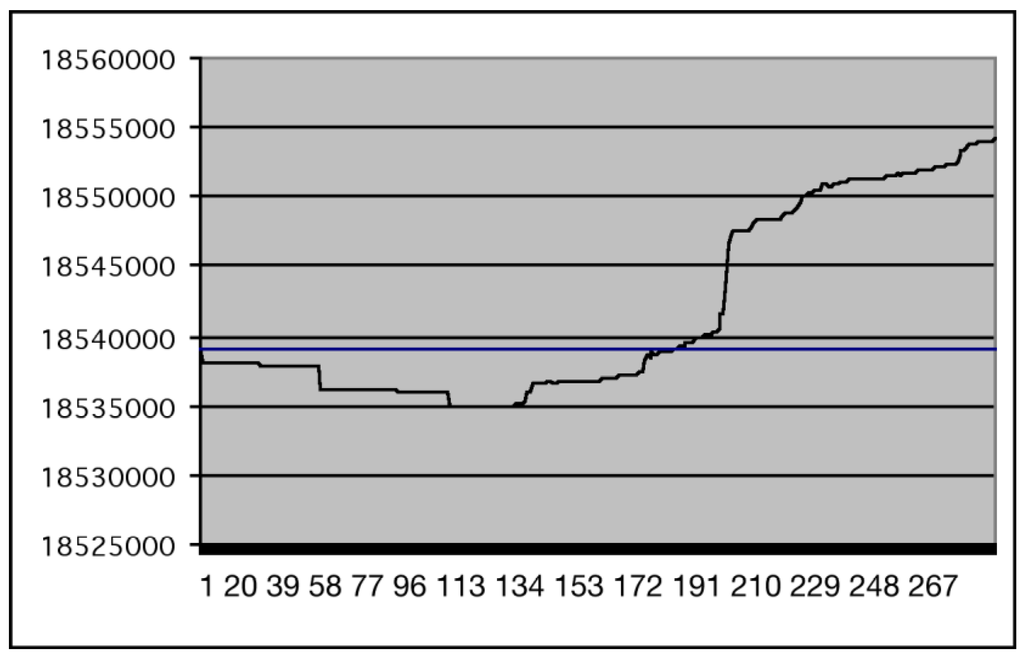
Figure 1. Applying the difference operator between file 1. and the Net(i) files from file 2.

Figure 1. Applying the difference operator between file 1. and the Net(i) files from file 2.

Figure 1 (from [3]) shows the results of this approach for MacNS6FullInstaller.sea.bin. We have plotted on the x-axis the number of 2,000 bytes segments on which we apply the difference operator (between this file and MacNS6FullInstaller2.sea.bin) and on the y-axis the size of the compressed file. For convenience we have also reported the size of the gzip compressed version of MacNS6FullInstaller.sea.bin (the straight line).

We see in the figure that the first part of the first file and the first part of the second file (up to about the first two hundreds 2,000 bytes segments) are strictly correlated. By operating a difference between the actual distribution of the software and the previous version we have used previous knowledge of the source (or the knowledge of a source that is correlated to the one we want to compress) to exploit the compression process. The savings we have obtained are limited because of the original nature and correlation of the files we are experimenting, but it is significant that even with this type of data and at least in this case, this approach works.

In the experiment we have used a segmentation of the two files in fixed size segments. This implies a sort of alignment of the two files we are comparing. While it has been proven that the related “optimal vector alignment problem” is NP complete (see Carpentieri and Storer [4]), we can expect to be able to find heuristically good approximations of this optimal alignment and therefore to further improve the compression obtained in similar experiments by a careful alignment of the files.

Cilibrasi in [10] and Cilibrasi and Vitany in [11] studied the Normalized Compression Distance (NCD) a parameter-free, universal, similarity measure based on a data compressor. NCD is a non-negative number representing how different two files are. NCD is a new way of looking at data compression that allows us to use compression programs for a wide variety of problems, such as learning, clustering and classification, data mining, etc.

NCD gives a different way of looking at the problem we deal with in this paper, the intuition is that if two files are close (in the NCD sense) then probably we can do a better job in sending one of them to a destination that already has the other file if we can use interaction.

3.2. Compression in the presence of shared data

Factor, Sheinwald and Yassour [5] and Factor and Sheinwald [6] exploit the performance of dictionary based compressors in the case of pre-existing shared data by including in the dictionary the pre-existing strings. They consider real life situations in which a Sender and a Receiver have to communicate and they share knowledge of data, as it is common for example in a client-server environment where the server manages pervasive devices, or when a product distributor has to ship a new release of a software package to clients that hold an older release. Their idea is to extend the dictionary used by the dictionary based compression algorithm by using the shared data. This will produce longer matches during the compression process and will avoid starting the compression process with an almost empty dictionary.

The dictionary words are sent from the encoder to the decoder by triples, called segment specifiers. The triples have the form (file-id; offset: length) and indicate clearly to the decoder the id of the shared file from which the dictionary word has to be retrieved. This scheme is appropriate when the Sender has strong computational resources and no time constraints in compressing the data: the Sender has to find an effective way to use the dictionary (that is distributed also into the shared files) to compress the file. The Receiver is instead fast and simple: it just copies and pastes strings by using the Sender’s instructions.

They experimentally show that there is a gain in compression (ranging from a 1–2% and in some cases up to 6–7% in the size of the compressed file) that is due to the fact that the compressed file does not contain the whole dictionary but rather parts of this dictionary are already available at no cost: they are known as shared data.

4. Interactive Compression

If we assume some degree of interaction between the compressor and the decompressor then we can exploit the previous knowledge they both have of the source when data compression is used for data transmission. The price we accept to pay, in some cases, is a low probability of communication errors.

The solution of the communication problem, in this case, is an interactive protocol that allows Sender and Receiver to take advantage of the knowledge they have of the source and that exploits the interaction to minimize the communication cost. In real life this could be used in situations in which finite size files are transmitted over a bidirectional communication line, like a telephone line, internet, a satellite link or any other line between two systems that have already available a large number of files of the same type.

As an example consider an internet user that has to frequently download the same kind of file (a newsletter, an image, a report, etc.) from the same source, or a system manager that has to download repetitively an update file for a program or for an antivirus, or an ftp mirroring site that has to be periodically brought up to date, etc. The compression algorithms involved in the communication might be static or dynamic dictionary methods or, in the case of images, Vector Quantization.

4.1. Interactive data compression

El Gamal and Orlistky in [7] consider the following problem: “Given two random variables X and Y with entropies H(X) and H(Y) and joint entropy H(X,Y), and two persons P_X and P_Y, such that P_X knows X and P_Y knows Y, suppose that the two persons wish to communicate over a noiseless two-way channel so that at the end of the communication process they both know X and Y. How many bits on the average must they exchange and what are the optimal codes?”

They prove that at least H(X|Y) + H(Y|X) bits must be exchanged on the average and that H(X,Y) + 2 bits are sufficient and that if the joint probability p(x,y) is uniform then the average number of bits needed is close to H(X|Y) + H(Y|X). They also discuss randomized protocols that can reduce the amount of communication if some probability of communication error is acceptable.

4.2. An interactive communication protocol

An efficient communication protocol that allows a Sender and a Receiver to communicate via dictionaries that are built independently from previous (and may be discordant) examples of communication messages that each of the two sides has available is presented by Carpentieri in [8]. This communication protocol results in an improvement in compression paid with a negligible or almost null possibility of communication errors.

Consider an information source U that emits words over a certain alphabet and for which it is possible to partition the words emitted by the source into two sets: one D of cardinality m that has probability P(D) = 1 − α and another D_comp with probability P(D_comp) = α, where α << 1/2, and the words w ∊ D have probability p_w such that |(1 − α)/m − p_w| < ε for an appropriately chosen ε. The set D might be viewed as the ideal “Dictionary” for the source.

It is possible to recognize this property in many real life situations. As an example consider a source that outputs programs. For this source an ideal set D might include all the keywords and reserved words of the programming language and the set of the most common identifiers.

Consider now a situation in which Sender and Receiver have access to different corpora of the same language: for example different sets of books and/or web pages and/or newspapers, etc. They can use these different corpora to independently construct their own dictionaries.

If the Sender and the Receiver have both knowledge of the source in the form of a large number of messages that are recorded in two files of length approximately n, if n is big enough and n_w is the number of occurrences of w in the file and δ is an opportunely chosen number in [0, 1/2], then we have that for each word w, (P|n_w/n− p_w| < ε) > (1− δ).

The Sender and the Receiver build up, respectively, dictionaries D_S and D_R of size m. They can estimate the probability of each word w by counting the number of its appearances in the file of length n. Now consider the possibility that a word is in D_S but not in D_R. This could happen if the frequency count of w done by the Sender does not reflect the probability p_w, and therefore w belongs to D_S incorrectly and w does not belong to D_R correctly, or if the Receiver has a wrong estimate of p_w and therefore w belongs to D_S correctly but incorrectly does not belong to D_R or, finally, if both Sender and Receiver have a wrong estimate of p_w. Therefore, if n is big enough the probability of a word w in D_S but not in D_R is: P(w belongs to D_S but does not belong to D_R) < 2δ − δ².

In a practical situation the Sender has to transmit to the Receiver a message that comes from a source whose behavior is well known by both Sender and Receiver: they have available a large number of messages from the source, but not necessarily the same messages. Based on the messages each of them knows, Sender and Receiver independently construct dictionaries D_S and D_R by including in the dictionaries what they assume are the m most common words of the source.

The Sender transmits the compressed message to the Receiver by using dictionary D_S and the Receiver decodes the message by using dictionary D_R. The communication line between Sender and Receiver is a bidirectional line: the Receiver has the possibility of sending acknowledgment messages to the Sender, participating actively to the compression/ transmission process.

The Sender will send dictionary words by using Karp and Rabin’s fingerprints (see [9]) to improve the compression by allowing a small possibility of communication errors. If the current input word is in the Sender’s dictionary than the Sender either sends a previously assigned codeword (if Sender and Receiver have already agreed on that word) or it sends a fingerprint of the current word.

In this second case the Receiver either acknowledges its understanding of the dictionary word (if the Receiver has a single word that matches that fingerprint in its dictionary), or it tells the Sender that there is more than one word in its dictionary for that fingerprint and then invites the Sender to send another, different, fingerprint for the same word, or finally it communicates to the Sender that it does not recognize the word and that the word has to be sent explicitly through a standard compression method. The Sender shall act accordingly.

The Sender will not send more than two fingerprints to identify a word: after two unsuccessful fingerprint trials it sends the word by entropy coding. Every time a new word is acknowledged by the Receiver then a new codeword is independently, but consistently, assigned to that word by both Sender and the Receiver. If the current input word is not in the Sender’s dictionary than the Sender switches to a standard lossless compressor and entropy codes the input word.

This approach exploits compression by taking into account shared data and interaction. It is possible to analyze, as in [8], the possibility of a communication error, i.e., the possibility that the Receiver decodes a word incorrectly, and to prove that this probability is very low.

As an example, if we assume that the length in bits of the dictionary words is n = 250, and that t = |D| = 4,000, M = nt² = 4 × 109, δ = 0.01 then by using this protocol the probability of a false match for the fingerprinting algorithm is less than 2 × 10⁻⁸, and the overall communication error probability is less than 4 × 10⁻¹⁰.

The Sender with probability higher than 0.98 will send a word w to the Receiver by using only fingerprints (and it will spend less than 70 bits for word), or otherwise it will send the word by entropy coding (by spending more than 70 + 125 bits per word) with probability less than 0.0199.

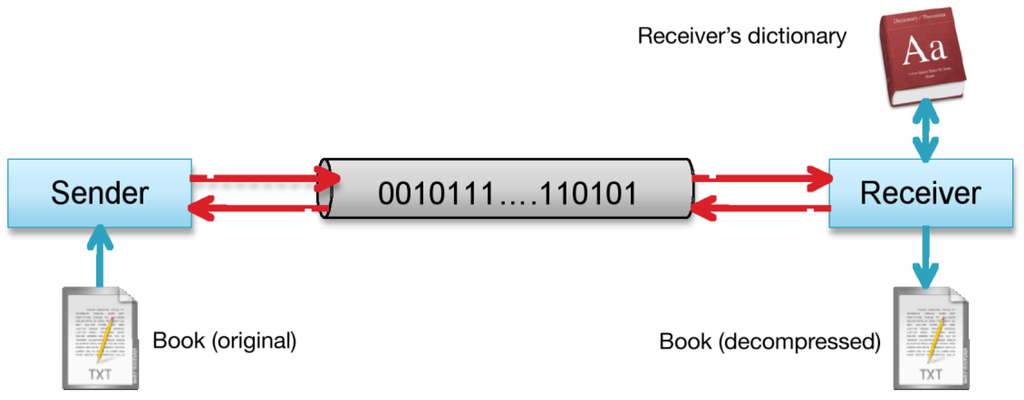
Figure 2. Sender and Receiver communicate a book.

Figure 2. Sender and Receiver communicate a book.

In [8] the protocol is experimentally tested for the compression of source programs in the C programming language. These experimental results show an average improvement of 5–6% with respect to the standard, dictionary based, lossless compressors.

4.3. Interactive compression of books.

A possible application of interactive data compression is in the transmission of natural language textual data, for example electronic newspapers or books, which can be sent from a remote source to a client destination. In this case we can improve the transmission/compression process by taking into account the common rules of the specific natural language (i.e., the set of common words of the natural language, the syntax, etc.). All these rules might be considered as shared knowledge between the Sender (that sends the book) and the Receiver (that receives the data).

For example, when the Receiver receives the book it can use a standard on line dictionary of the language in which the book is written to decode the Sender’s messages. The Sender does not know which static dictionary the Receiver is using. It might try to send the words as pointers that the Receiver could decode by using its dictionary. We have experimented with this dictionary based approach by digitizing ten books: five of them are in the Italian language and the other five are in English.

The Sender sends a book to the Receiver a word at a time. If the word is long enough, instead of the raw word, the Sender sends a token including the initial character of that word, the length of the word and a hash value (for example a Karp and Rabin hash) for that word. The Receiver will receive the token and will try to decode the word by using its local dictionary.

If the token sent by the Sender cannot be decoded because for the hash value that the Sender has sent there is a collision in the Receiver’s dictionary, then the Receiver asks the Sender to send a new token for the same word but with a different letter (may be the middle letter of the word) and a different hash.

Table 1. Compression results.

Book Title	Original Dimensions	Interactive Protocol (12 bits hash)			Zip		Gzip
		Compresed size	Compression ratio	Compresed size	Compression ratio	Compresed size	Compression ratio
Angeli e demoni	948.3 KB	334.7 KB	2.83	353.3 KB	2.68	339.1 KB	2.78
Decamerone	1,638.2 KB	544.6 KB	3.00	577.2 KB	2.83	551.7 KB	2.96
Gomorra	663.0 KB	240.2 KB	2.76	251.4 KB	2.63	241.3 KB	2.74
Promessi Sposi	1,394.9 KB	490.1 KB	2.84	520.2 KB	2.68	498.5 KB	2.79
Uomini che odiano le donne	1,093.5 KB	373.9 KB	2.92	405.6 KB	2.69	388.1 KB	2.81
20,000 Leagues Under The Sea	875,5 KB	306.2 KB	2.85	336.1 KB	2.60	323.4 KB	2.70
The Wealth Of Nations	2,273.1 KB	602.9 KB	3.77	688.1 KB	3.30	652.8 KB	3.48
Catcher in the Rye	384.3 KB	122.4 KB	3.13	131.5 KB	2.92	125.6 KB	3.05
For Whom The Bell Tolls	937.4 KB	288.2 KB	3.25	326.3 KB	2.87	310.1 KB	3.02
The Grapes Of Wrath	935.3 KB	310.8 KB	3.00	342.3 KB	2.73	324.8 KB	2.87

Table 1. Compression results.

Book Title	Original Dimensions	Interactive Protocol (12 bits hash)			Zip		Gzip
		Compresed size	Compression ratio	Compresed size	Compression ratio	Compresed size	Compression ratio
Angeli e demoni	948.3 KB	334.7 KB	2.83	353.3 KB	2.68	339.1 KB	2.78
Decamerone	1,638.2 KB	544.6 KB	3.00	577.2 KB	2.83	551.7 KB	2.96
Gomorra	663.0 KB	240.2 KB	2.76	251.4 KB	2.63	241.3 KB	2.74
Promessi Sposi	1,394.9 KB	490.1 KB	2.84	520.2 KB	2.68	498.5 KB	2.79
Uomini che odiano le donne	1,093.5 KB	373.9 KB	2.92	405.6 KB	2.69	388.1 KB	2.81
20,000 Leagues Under The Sea	875,5 KB	306.2 KB	2.85	336.1 KB	2.60	323.4 KB	2.70
The Wealth Of Nations	2,273.1 KB	602.9 KB	3.77	688.1 KB	3.30	652.8 KB	3.48
Catcher in the Rye	384.3 KB	122.4 KB	3.13	131.5 KB	2.92	125.6 KB	3.05
For Whom The Bell Tolls	937.4 KB	288.2 KB	3.25	326.3 KB	2.87	310.1 KB	3.02
The Grapes Of Wrath	935.3 KB	310.8 KB	3.00	342.3 KB	2.73	324.8 KB	2.87

If the Receiver finds a unique word that matches the token in the dictionary then it decodes the word and eventually acknowledges the Sender. If the Receiver does not find any word that matches the token in the dictionary, then it sends a request to have the word (entropy coded and) sent directly as raw data to the Sender. Figure 2 shows the communication line between Sender and Receiver. This communication protocol could introduce errors, i.e., situations in which the Receiver believes it can decode correctly the word but the word that it finds in its dictionary is not the correct one.

If the probability of an error is very low, as shown in subsection 4.2, then the Receiver might accept to have a few words incorrectly decoded: it will be still possible to read and understand the book. If we assume that the dictionary used by the Receiver is the correct dictionary for that specific book language, then the probability of an error depends on the choice and length of the hash value.

In Table 1 we show the results obtained by compressing ten books by using, Karp and Rabin, hashes of length 12 bits. The results obtained are compared with the “off of the shelves” standard dictionary based compressors Zip and Gzip.

Table 2. Compression errors.

Angeli e demoni	Deca-merone	Gomorra	Promessi Sposi	Uomini che odiano le donne	20000 Legues Under The Sea	The Wealth Of Nations	Catcher in the Rye	For Whom The Bell Tolls	The Grapes Of Wrath
0.031%	0.047%	0.096%	0.087%	0.083%	0.036%	0.004%	0.012%	0.032%	0.025%

Table 2. Compression errors.

Angeli e demoni	Deca-merone	Gomorra	Promessi Sposi	Uomini che odiano le donne	20000 Legues Under The Sea	The Wealth Of Nations	Catcher in the Rye	For Whom The Bell Tolls	The Grapes Of Wrath
0.031%	0.047%	0.096%	0.087%	0.083%	0.036%	0.004%	0.012%	0.032%	0.025%

In our experiments the running time of the program that simulates the interaction (if we do not visualize on the computer monitor the messages describing the interaction) is fast enough to be of the same order of the gzip running time on the same input.

These results are very encouraging: with this approach we have implicitly set a strong limit on the length of any matched string that is copied into the output stream (the maximum length of a match will be the length of the longest word in the static Receiver’s dictionary) but nevertheless the results are competitive with respect to the standard zip and gzip compressors. Possible improvements are therefore foreseen if we allow the matches to have longer lengths. The price we pay is the possibility of communication errors.

With the above settings we have a very limited communication error: i.e., only a very few words (often less than ten) are mismatched in a whole book which therefore maintains its readability. Table 2 shows the communication error percentage for each book in the previous experiment when the hash value is Karp and Rabin’s hash of length 12 bits. There is a strong relationship between the length of the hash value, the compression results, and the compression errors. With a longer hash we have less compression errors but a worst compression, with a shorter hash we improve compression but we pay the price of more compression errors.

Figure 3 depicts the relationship between the length of the hash value, the size of the compressed file and the error percentage for the book “Uomini che odiano le donne”. In the left part of the picture we have on the x-axis the lengths of the hash value in bits and on the y-axis the corresponding sizes in Kb of the compressed file. In the right part of the picture on the x-axis we have again the lengths of the hash value in bits but on the y-axis we have the corresponding error percentages. The figure shows that the compression results are better for a hash value that has a length of 9 bits, but also that this length is not good enough to cope with transmission errors. Instead a hash of length 15 bits gives a compression that is almost lossless but the compression obtained is not competitive. The right compromise for the hash length here might be 12 bits. The behavior for the other books is very similar to the one in Figure 3.

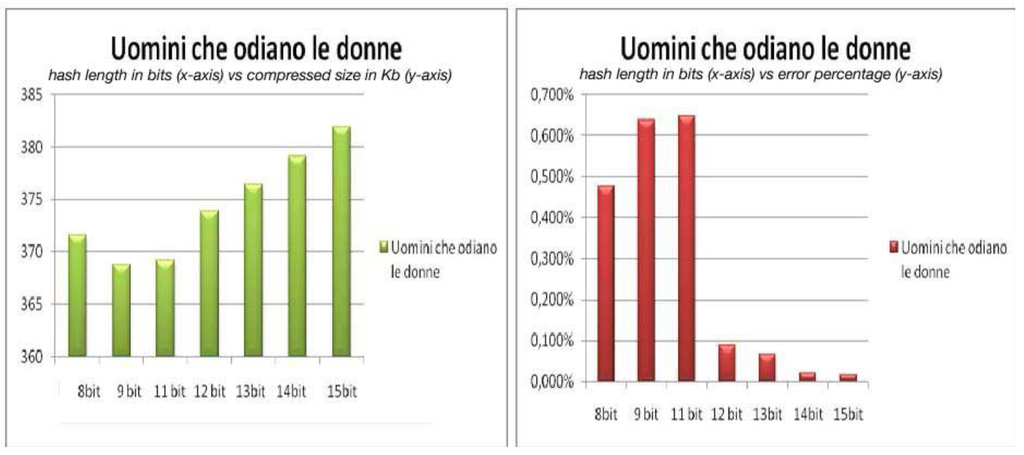
Figure 3. Compression and hash length for “Uomini che odiano le donne”.

Figure 3. Compression and hash length for “Uomini che odiano le donne”.

5. Conclusions and Future Work

The interaction between a Sender and a Receiver that have to communicate over a bidirectional line can improve the transmission process if both Sender and Receiver share previous knowledge about the data they want to communicate.

By doing this in the fundamental source coding theorem we can substitute entropy with conditional entropy and therefore we have a new theoretical limit that allows for better compression. In this paper we have reviewed recent work that applies interactive approaches to data compression and discussed this possibility. Future work will focus on the improvement of the algorithms presented and on a wider testing of the approaches described.

There are points of contacts between part of the work described in this paper and the transfer learning techniques studied in machine learning and data mining. Future work might also include a wider analysis of this relationship between the techniques that are described in this paper to improve the interaction between the Sender and the Receiver and the transfer learning techniques.