Abstract
Given a sequence of size , with symbols from a fixed alphabet Σ, , the suffix array provides a listing of all the suffixes of T in a lexicographic order. Given T, the suffix sorting problem is to construct its suffix array. The direct suffix sorting problem is to construct the suffix array of T directly without using the suffix tree data structure. While algorithims for linear time, linear space direct suffix sorting have been proposed, the actual constant in the linear space is still a major concern, given that the applications of suffix trees and suffix arrays (such as in whole-genome analysis) often involve huge data sets. In this work, we reduce the gap between current results and the minimal space requirement. We introduce an algorithm for the direct suffix sorting problem with worst case time complexity in , requiring only bits in memory space. This implies bytes for total space requirment, (including space for both the output suffix array and the input sequence T) assuming , and 4 bytes per integer. The basis of our algorithm is an extension of Shannon-Fano-Elias codes used in source coding and information theory. This is the first time information-theoretic methods have been used as the basis for solving the suffix sorting problem.
1. Introduction
The suffix array provides a compact representation of all the n suffixes of T in a lexicographic order. The sequence of positions in T of the first symbols from the sorted suffixes in this lexicographic order is the suffix array for the sequence. The suffix sorting problem is to construct the suffix array of T. Mamber and Myers [1] were the first to propose an algorithm to construct the suffix array with three to five times less space than the traditional suffix tree. Other methods for fast suffix sorting in time have been reported in [2], while memory efficient constructions were considered in [3]. Puglisi et al. [4] provide a detailed comparison of different recently proposed linear time algorithms for suffix sorting.
Suffix trees and suffix arrays have drawn a significant attention in recent years due to their theoretical linear time and linear space construction, and their logarithmic search performance. Gusfield [5] provides a detailed study on the use of suffix trees in the analysis of biological sequences. Suffix sorting is also an important problem in data compression, especially for compression schemes that are based on the Burrows-Wheeler Transform [6,7]. In fact, it is known that the suffix sorting stage is a major bottleneck in BWT-based compression schemes[6,7,8]. The suffix array is usually favored over suffix trees due to its smaller memory footprint. This is important given that the applications of suffix trees and suffix arrays (such as in whole-genome sequence analysis) often involve huge data sets. An important problem therefore is to construct suffix arrays in linear time, while requiring space for the input sequence, in addition to bits, the minimal space required to hold the suffix array. This translates to bytes of total space requirment, assuming = 256, and 4 bytes per integer. Existing algorithms, such as the KS Algorithm [9] require bytes, while the KA Algorithm [10] requires bytes.
This paper presents a space-efficient linear time algorithm for solving the direct suffix sorting problem, using only bytes. The basis of the algorithm is an extension of the Shannon-Fano-Elias codes pupularly used in arithmetic coding. In the next section, we provide a background to the problem, and briefly describe related work. Section 3 presents our basic algorithm for suffix sorting. Section 4 improves the complexity of the basic algorithm using methods from source coding and information theory.
2. Background
The BWT [6,7] performs a permutation of the characters in the input sequence, such that characters in lexically similar contexts will be near to each other. Thus, the BWT is very closely related to the suffix tree and suffix array - two important data structures used in pattern matching, analysis of sequence redundancy, and in data compression. The major link is the fact the BWT provides a lexicographic sorting of the contexts as part of the permutation of the input sequence. The recent book [7] provides a detailed treatment of the link between the BWT and suffix arrays and suffix trees. Apart from the BWT, other popular compression schemes have also been linked with the suffix tree data structure. For instance, the PPM* compression was implemented using suffix trees and suffix tries in [11]. The sequence decomposition step required for constructing the dictionary in LZ-based schemes can be performed by the use of tree structures, such as binary search trees, or suffix tries [12]. A detailed analysis on the use of suffix trees in data compression is provided in Szpankowski [13]. When decorated with the array of longest common prefixes, the suffix array can be used in place of the suffix tree in almost any situation where a suffix tree is used [14]. This capability is very important for applications that require huge storage, given the smaller memory requirement of the suffix array. An important issue is how to devise efficient methods for constructing the suffix array, without the suffix tree.
Some methods for constructing suffix arrays first build the suffix tree, and then construct the suffix array by performing an inorder traversal of the suffix tree. Farach al.[15] proposed a divide and conquer method to construct the suffix tree for a given sequence in linear time. The basic idea is to divide the sequence into odd and even sequences, based on the position of the symbols. Then, the suffix tree is constructed recursively for the odd sequence. Using the suffix tree for the odd sequence, they construct the suffix tree for the even sequence. The final step merges the suffix tree from the odd and even sequences into one suffix tree using a coupled depth-first search. The result is a linear time algorithm for sufix tree construction. This divide and conquer approach is the precursor to many recent algorithms for direct suffix sorting.
Given the memory requirement and implementation difficulty of the suffix tree, it is desirable to construct the suffix array directly, without using the suffix tree. Also, for certain applications such as in data compression where only the suffix array is needed, avoiding the construction of the suffix tree will have some advantages, especially with respect to memory requirements. More importantly, direct suffix sorting without the suffix tree raises some interesting algorithmic challenges. Thus, more recently, various methods have been proposed to construct the suffix array directly from the sequence [9,10,16,17,18], without the need for a suffix tree.
Kim et al. [16] followed an approach similar to Farach’s above, but for the purpose of constructing the suffix array directly. They introduce the notion of equivalent classes between strings, which they use to perform coupled depth-first searches at the merging stage. In [9] a divide and conquer approach similar to Farach’s method was used, but for direct construction of the suffix array. Here, rather than dividing the sequence into two symmetric parts, the sequence was divided into two unequal parts, by considering suffixes that begin at positions in the sequence. These suffixes are recursively sorted, and then the remaining suffixes are sorted based on information in the first part. The two sorted suffixes are then combined using a merging step to produce the final suffix array. Thus, a major difference is in the way they divided the sequences into two parts, and in the merging step.
Ko and Aluru [10] also used recursive partitioning, but following a fundamentally different approach to construct the suffix array in linear space and linear time. They use a binary marking strategy whereby each suffix in T is classified as either an S-suffix or an L-suffix, depending on its relative order with its next neighbor. Let denote the suffix of sequence T starting at position i. An S-suffix is a suffix that is lexicographically smaller than its right neighbor in T, while an L-suffix is one that is lexicographically larger than its right neighbor. That is, is an S-suffix if , otherwise is an L-suffix. This classification is motivated by the observation that an S-suffix is always lexicographically greater than any L-suffix that starts with the same first character. The two types of suffixes are then treated differently, whereby the S-suffixes are sorted recursively by performing some special distance computations. The L-suffixes are then sorted using the sorted order of the S-suffixes. The classification scheme is very similar to the approach earlier used by Itoh and Tanaka [19]. But the algorithm in [19] runs in time on average.
Lightweight suffix sorting algorithms [3,17,20,21] have also been proposed which pay more attention on the extra working space required. Working space excludes the space for the output suffix array. In general, the suffix array requires bit space, while the input text requires another bits, or in the worst case bits. In [22], an algorithm that runs in worst case time, requiring working space was proposed, while Hon et al. [20] constructed suffix arrays for integer alphabets in time, using -bit space. Nong and Zhang [17] combined ideas from the KS algorithm [9] and the KA algorithm [10] to develop a method that works in time, using -bit working space (without the output suffix array). In [23,24] they extended the method to use bytes of working space (or a total space of bytes, including space for the suffix array, and the original sequence), by exploiting special properties of the L and S suffixes used in the KA algorithm, and of the leftmost S-type substrings. In-place suffix sorting was considered in [25], where suffix sorting was performed for strings with symbols from a general alphabet using working space in time. In some other related work [2,26], computing the BWT was viewed as a suffix sorting problem. Okanohara and Sadakane [26] modified a suffix sorting algorithm to compute the BWT using a working space of bits. There has also been various efforts on compressed suffix arrays and compressed suffix trees as a means to tackle the space problem with suffix trees and suffix arrays. (See [27,28,29] for examples). We do not consider compressed data structures in this work. A detailed survey on suffix array construction algorithms is provided in [4].
2.1. Main Contribution
We propose a divide-and-conquer sort-and-merge algorithm for direct suffix sorting on a given input string. Given a string of length n, our algorithm runs in worst case time and space. The algorithm recursively divides an input sequence into two parts, performs suffix sorting on the first part, then sorts the second part based on the sorted suffix from the first. It then merges the two smaller sorted suffixes to provide the final sorted array. The method is unique in its use of Shannon-Fano-Elias codes in efficient construction of a global partial order for the suffixes. To our knowledge, this is the first time information-theoretic methods have been used as the basis for solving the suffix sorting problem.
Our algorithm also differs from previous approaches in the use of a simple partitioning step, and how it exploits this simple partitioning scheme for conflict resolution. The total space requirement for the proposed algorithm is bits, including the space for the output suffix array, and for the original sequence. Using the standard assumption of 4 bytes per integer, with , we get a total space requirement of bytes, including the n bytes for the original string and the bytes for the output suffix array. This is a significant improvement when compared with other algorithms, such as the bytes required by the KA algorithm [10], or the bytes required by the KS algorithm [9].
3. Algorithm I: Basic Algorithm
3.1. Notation
Let be the input sequence of length n, with symbol alphabet . Let denote the suffix of T starting at position . Let denote the i-th symbol in T. For any two strings, say α and β, we use to denote that the α preceeds β in lexicographic order. (Clearly, α and β could be individual symbols, from the same alphabet, i.e. .) We use $ as the end of sequence symbol, where and . Further, we use to denote the suffix array of T, and S to denote the sorted list of first characters in the suffixes. Essentially, . Given , we use to denote its inverse. We define as follows: . That is, . We use to denote the probability of symbol , and the probability of the substring , the m-length substring starting at position i.
3.2. Overview
We take the general divide and conquer approach:
- Divide the sequence into two groups;
- Construct the suffix array for the first group;
- Construct the suffix array for the second group;
- Merge the suffix arrays from the two groups to form the suffix array for the parent sequence;
- Perform the above steps recursively to construct the complete suffix array for the entire sequence.
Figure 1 shows a schematic diagram for the working of the basic algorithm using an example sequence, . The basic idea is to recursively partition the input sequence in a top-down manner into two equal-length subsequences according the odd and even positions in the sequence. After reaching the subsequences with length , the algorithm then recursively merges and sorts the subsequences using a bottom-up approach, based on the partial suffix arrays from the lower levels of the recursion. Thus, the algorithm does not start the merging procedure until it reaches the last partition on a given branch.
Each block in the figure contains two rows. The first row indicates the position of the current block of symbols in the original sequence T. The second row indicates the current symbols. The current symbols are unsorted in the downstream dividing block and sorted in the upstream merging block. To see how the algorithm works, starting from the top left block follow the solid division arrow, the horizontal trivial sort arrow (dotted arrow), and then the dashed merge arrows. The procedure ends at the top right block. We briefly describe each algorithmic step in the following. Later, we modify this basic algorithm for improved complexity results.
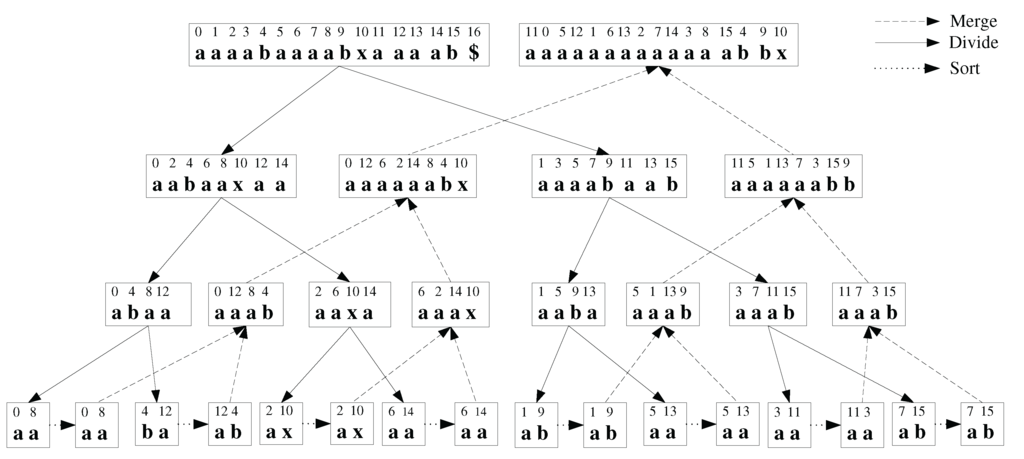
Figure 1.
Basic working of the proposed algorithm using an example. The original sequence is indicated at the top left. The sorted sequence and the suffix array are indicated in the top right box.
3.3. Algorithm I
3.3.1. Divide T
If , divide T into 2 subsequences, and . contains all the symbols at the even positions of T. contains all the symbols at the odd positions of T. That is, ,
3.3.2. Merge SA of and SA of
Let and be the suffix array of and respectively. Let be the suffix array of T. If and have been sorted to obtain their respective suffix arrays and , then we can merge and in linear time on average, to form the suffix array . Without loss in generality, we assume , and are the sorted indices of , and T respectively. Given , we use to denote its corresponding position in T. That is, . Similarly, for . and are easily obtained from , based on the level of recursion, and whether we are on a left branch or a right branch. For , we compare the partially ordered subsequences using and , viz.
Whenever we compare two symbols, from and from , we might get into the ambiguous situation whereby the two symbols are the same (i.e., ). Thus, we cannot easily decide which suffix precedes the other, (i.e., whether , or ), based on the individual symbols. We call this situation a conflict. The key to the approach is how efficiently we can resolve potential conflicts as the algorithm progresses. We exploit the nature of the division procedure, and the fact that we are dealing with substrings (suffixes) of the same string, for efficient conflict resolution. Thus, the result of the merging step will be a partially sorted subsequence, based on the sorted order of the smaller child subsequences. An important difference here is that unlike in other related approaches [9,10,16], our sort-order at each recursion level is global with respect to T, rather than being local to the subsequence at the current recursion step. This is important, as it significantly simplifies the subsequent merging step.
3.3.3. Recursive Call
Using the above procedure, we recursively construct the suffix array of from its two children and . Similarly, we obtain the suffix array for from its children and . We follow this recursive procedure until the base case is reached (when the length of the subsequence is ).
3.4. Conflict Resolution
We use the notions of conflict sequence or conflict pairs. Two suffixes and form a conflict sequence in T if , (that is, ) for some . Thus, the two suffixes can not be assigned a total order after considering their first k symbols. We say that the conflict between and is resolved whenever , and . Here, is called the conflict length. We call the triple a conflict pair, or conflict sequence. We use the notation to denote a conflict pair and with a conflict length of . We also use to denote a conflict pair where the conflict length is yet to be determined, or is not important given the context of the discussion.
The challenge, therefore, is how to resolve conflicts efficiently given the recursive partitioning framework proposed. Obviously, , the sequence length. Thus, the minimum distance from the start of each conflicting suffix to the end of the sequence (), or the distance from an already sorted symbol can determine how long it will take to resolve a conflict. Here, we consider how the previously resolved conflicts can be exploited for a quick resolution of other conflicts. We maintain a traceback record on such previously resolved conflicts in a conflict tree, or a conflict table.
Figure 2 shows the conflict tree for the example sequence, . Without loss in generality and for easier exposition of the basic methodology, we assume that , for some positive integer x. Our conflict resolution strategy is based on the following properties of conflict sequences and conflict trees.
- Given the even-odd recursive partitioning scheme, at any given recursion level, conflicts can only occur between specific sets of positions in the original sequence T. For instance, at the lowest level, conflicts can only occur between , and , or more generally, between , and . See Figure 2.
- Given the conflict sequence, and the corresponding conflict pair is unique in T. That is, only one conflict pair can have the pair of start positions . Thus the conflict pairs and are equivalent. Hence, we represent both and as , where, .
- Consider at level in the tree. We define its neighbors as the conflict pairs: , with , or , where , with , and . Essentially, neighboring conflicts are found on the same level in the conflict tree, from the leftmost node to the current node. For example, for at , the neighbor will be: . We notice that, by our definition, not all conflicts in the same node are neighbors.
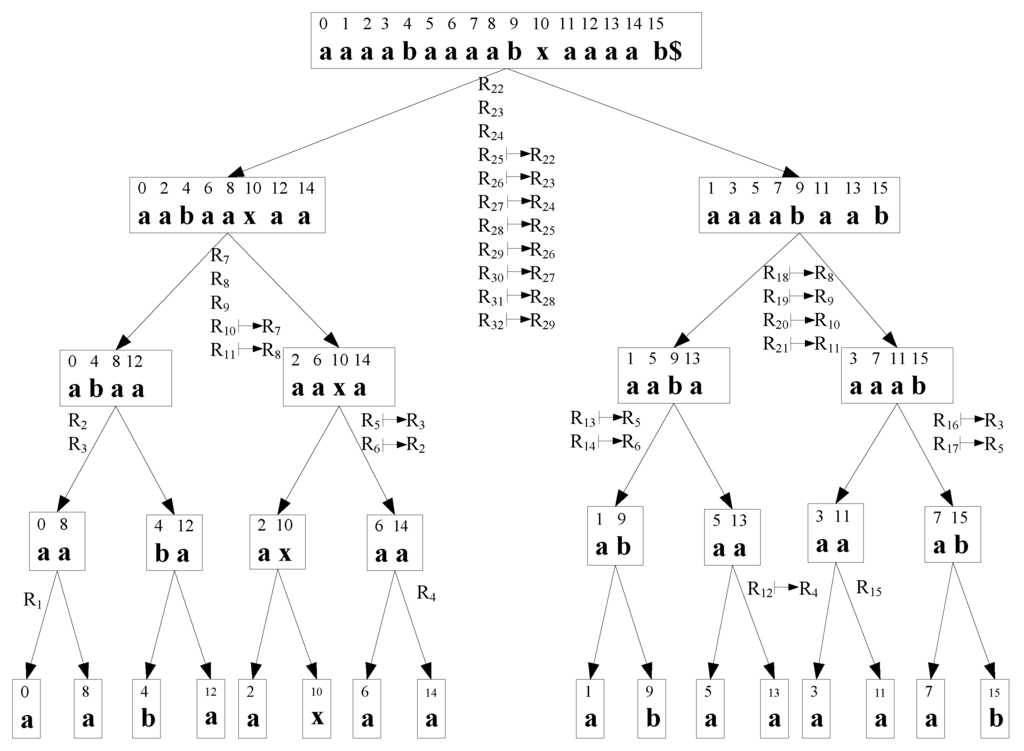
Figure 2.
Conflict tree for the example sequence . The original sequence is indicated at the root node. The notation indicates that conflict pair is resolved by after a certain number of steps, given that has been resolved. Conflict pairs are labeled following a depth-first traversal on the tree.
Given the conflict tree, we can determine whether a given conflict pair can be resolved based on previous trace back information (i.e., previously resolved conflicts). From the conflict tree, we see that this determination can be made by checking only a fixed number of neighboring conflict pairs. In fact, from the definition above, we see that the size of the neighborhood is at most 6. For , the neighbors will be the conflict pairs in the set , with ; ; ; ; ; and . Some of these pair of indices may not be valid indices for a conflict pair. For example, using the previous example, has only one valid neighbor, . Also, given that we resolve the conflicts based on the depth first traversal order, neighbors of that are located on a node to the right of in the conflict tree cannot be used to resolve conflict . Therefore, in some cases, less than six probes may be needed.
Let be the current conflict. Let be a previously resolved neighboring conflict. We determine whether can be resolved based on using a simple check: Let . If Δ is negative, then can be resolved with iff: Conversely, if Δ is positive, then can be resolved with iff: If any of the two conditions holds, we say that is resolved by , after Δ steps. Essentially, this means that after Δ comparison steps, becomes equivalent to . We denote this equivalence using the notation: . The following algorithm shows how we can resolve a given conflict pair, .
| ResolveConflict |
| Generate neighbors for |
| Remove invalid neighbors |
| Probe the valid neighbors for previously resolved conflict pairs |
| for each valid neighbor, compute the quantity ; end for |
| Select the neighbor with maximum value for d |
| if ( and ), then /* no extra work is needed */ |
| Compute . |
| else if ( and ), then |
| Perform at most () extra comparison steps |
| if (conflict is not resolved after the comparisons), then |
| /*Resolve conflict using */ |
| Compute |
| end if |
| end if |
| else /* conflict cannot be resolved using earlier conflicts */ |
| Resolve conflict using direct symbol-wise comparisons |
| end if |
The complexity of conflict resolution (when it can be resolved using previous conflicts) thus depends on the parameter Δ. Table 1 shows the conflict pairs for the example sequence used to generate the conflict tree of Figure 2. That table includes the corresponding Δ value where a conflict can be resolved based on a previous conflict.
The final consideration is how to store the conflict tree to ensure constant-time access to the resolved conflict pairs. Since for a given , the pair is unique, we can use these for direct access to the conflict tree. We can store the conflict tree as a simple linear array, where the positions in the array are determined based on the values, and hence the height in the tree. To avoid the sorting that may be needed for fast access using the indices, we use a simple hash function, where each hash value can be computed in constant time. The size of this array will be in the worst case, since there are at most conflicts (see analysis below). The result will be an time access to any given conflict pair, given its index in T.

Table 1.
Conflict pairs for . indicates that conflict pair is resolved by a previously resolved conflict pair , after a fixed number of steps. That is, after the fixed number of steps Δ, conflict pair becomes equivalent to conflict pair .
| R | ↦ | Δ | R | ↦ | Δ | R | ↦ | Δ | R | ↦ | Δ | ||||
| − | − | − | − | ||||||||||||
| − | − | ||||||||||||||
| − | − | ||||||||||||||
| − | − | ||||||||||||||
| − | − | ||||||||||||||
| − | − | ||||||||||||||
| − | − | − | − | ||||||||||||
| − | − | − | − |
3.5. Complexity Analysis
Clearly, the complexity of the algorithm depends on the overall number of conflicts, the number of conflicts that require explicit symbol-wise comparisons, the number that can be resolved using earlier conflicts, and how much extra comparsions are required for those. We can notice that we require symbol-wise comparison mainly for the conflicts at the leftmost nodes on the conflict tree, and the first few conflicts in each node. For the sequence used in Figure 2 and Table 1, with , we have the following: 32 total number of conflict pairs; 20 can be resolved with only look-ups based on the neighbors (with no extra comparisons); 1 requires extra comparisons after lookup (a total of 6 extra comparisons); 11 cannot be resolved using lookups, and thus requires direct symbol-wise; comparisons (a total of 20 such comparisons in all). This gives 44 overall total comparisons, and 21 total lookups.
This can be compared with the results for the worst case sequence with the same length, . Here we obtain: 49 total number of conflict pairs; 37 can be resolved with only look-ups based on the neighbors (with no extra comparisons); 8 requires extra comparisons after lookup (a total of 12 extra comparisons); 4 cannot be resolved using lookups, and thus require direct symbol-wise; comparisons (a total of 19 such comparisons in all). This results in 41 overall total comparisons and 45 total lookups. While the total number of comparisons is similar for both cases, the number of lookups is significantly higher for , the worst case sequence.
The following lemma establishes the total number of symbol comparisons and the number of conflicts that can be encountered using the algorithm.
Lemma 1: Given an input sequence , with length n, the maximum number of symbol comparisons and the maximum number of conflict pairs are each in .
Proof. Deciding on whether we can resolve a given conflict based on its neigbors requires only constant time, using Algorithm ResolveConflict(). Assume we are sorting the worst case sequence, . Consider level h in the conflict tree. First, we resolve the left-most conflict at this level, say conflict . This will require at most symbol comparisons. For example, at , the level just before the lowest level, the leftmost conflict will be , requiring comparsions. However, each conflict on the same level with can be resolved with at most comparisons, plus constant time lookup using the earlier resolved neighbors. A similar analysis can be made for conflict pairs , where both i and j are odd. There are are at most conflicts for each node at level h of the tree. Thus, the total number of comparisons required to resolve all conflicts will be . In the worst case, each node in the tree will have the maximum number of conflicts. Thus, similar to the overall number of comparisons, the worst case total number of conflicts will be in . □
We state our complexity results in the following theorem:
Theorem 1: Given an input sequence , with symbols from an alphabet Σ, Algorithm I solves the suffix sorting problem in time and space, for both the average case and the worst case.
Proof. The worst case result on required time follows from Lemma 1 above. Now consider the random string with symbols in Σ unifomly distributed. Here, the probablity of encountering one symbol is . Thus, the probability of matching two substrings from T will decrease rapidly as the length of the substrings increase. In fact, the probability of a conflict of length will be . Following [30], the maximum value of , the length of the longest common prefix for a random string is given by . Thus, the average number of matching symbol comparisons for a given conflict will be:
This gives:
For each conflict pair, there will be exactly one mismatch, requiring one comparison. Thus, on average, we require at most 3 comparisons to resolve each conflict pair.
The probability of a conflict is just the probablity that any two randomly chosen symbols will match. This is simply . However, we still need to make at least one comparison for each potential conflict pair. The number of this potential conflict pairs is exacty the same as the worst case number of conflicts. Thus, although the average number of comparisons per conflict is constant, the total time required to resolve all conflicts is still in .
We can reduce the space required for conflict resolution as follows. A level-h conflict pair can be resolved based on only previous conflicts (its neighbors), all at the same level, h. Thus, rather than the current depth-first traversal, we change the traversal order on the tree, and use a bottom-up breadth-first traversal. Then, starting with the lowest level, , we resolve all conflicts at a given level (starting from the leftmost), before moving up to the next level. Then, we re-use the space used for the lower levels in the tree. This implies a maximum of entries in the hash table at any given time, or space.
We make a final observation about the nature of the algorithm above. It may be seen that, in deed, we do not need to touch , the odd tree at all, until the very last stage of final merging. Since we can sort to obtain without reference to , we can therefore use to sort using radix sort, since positions in and are adjacent in T. This will eliminate consideration of the worst case conflicts at level , and all the conflicts in . This will however not change the complexity results, since the main culprit is the total number of conflicts in the worst case. We make use of this observation in the next section, to develop an time and space algorithm for suffix sorting.
4. Algorithm II: Improved Algorithm
The major problem with Algorithm I is the time taken for conflict resolution. Since the worst case number of conflicts is in , an algorithm that performs a sequential resolution of each conflict can do no better than time in the worst case. We improve the algorithm by modifying the recursion step, and the conflict resolution strategy. Specifically, we still use binary partitioning, but we use a non-symmetric treatment of the two branches at each recursion step. That is, only one branch will be sorted, and the second branch will be sorted based on the sorted results from the first branch. This is motivated by the observation at the end of the last section. We also use a preprocessing stage inspired by methods in information theory to facilitate fast conflict resolution.
4.1. Overview of Algorithm II
In Algorithm I, we perform symmetric division of T into two subsequences and , and then merge their respective suffix arrays and to form , the suffix array of T. and in turn are obtained by recursive division of and and subsequent merging of the suffix arrays of their respective children. The improvement in Algorithm II is that when we divide T into and , the division is no longer symetric. Similar to the KS Algorithm [9], here we form and as follows: , . This is a 1:2 asymetric partitioning. The division schemes are special cases of the general partitioning, where in the above, while in the symetric partitioning scheme of Algorithm I. An important parameter is α, defined as: . In the current case, .
Further, the recursive call is now made on only one branch of T, namely . After we obtain the suffix array for , we radix sort based on the values in to construct . This radix sorting step only takes linear time. The merging step remains similar to Algorithm I, though with some important changes to accomodate the above non-symetric partitioning of T. We also now use an initial ordering stage for faster conflict resolution.
4.2. Sort to Form
After dividing T into and , we need to sort each child sequence to form its own smaller suffix array. Consider . We form by performing the required sorting recursively, using a non-symmetric treatment of each branch. is thus sorted by a recursive subdivision, and local sorting at each step. The suffix arrays of the two children are then merged to form the suffix array of their parent. Figure 3 shows this procedure for the example sequence . Merging can be performed as before (with changes given the non-symetric nature of and ). The key to the algorithm is how to obtain the sorted array of the left child from that of the right child at each recursion step.
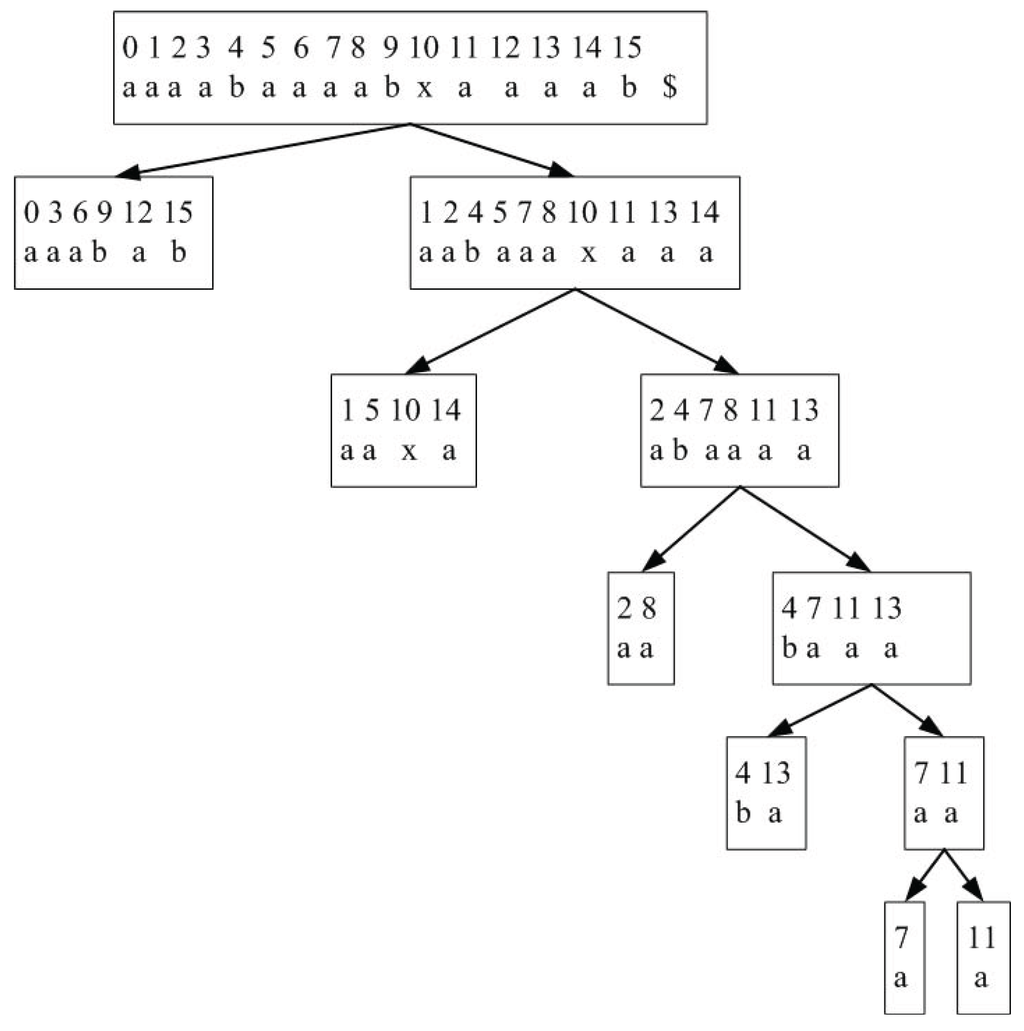
Figure 3.
Asymmetric recursive partitioning for improved algorithm, using . Recursive partitioning is performed on the right branch.
4.3. Sort by Inducing from
Without loss in generality, we assume is unsorted and has been sorted to form . Given the partitioning scheme, we have that for any , . There must exist an ordering of , since the indices in are unique. For each k, we construct the set of pairs P, given by . Each pair in P is unique. Then, we radix sort P to generate the suffix array of . This step can thus be accomplished in linear time. This only works for the highest level (i.e., obtaining from ). However, we can use a similar procedure, but with some added work, at the other levels of recursion.
Consider a lower level of recursion, say at level h. See Figure 3. We can append the values in the from the right tree so that we can perform successive bucket sorts. Thus, we use the from the right tree as the tie breaker, after a certain number of steps. In general, this will not change the number of comparisons at the lowest level of the tree. However, for the general case, this will ensure that at most bucket sorts are performed, involving symbols in each bucket sort, where is the lowest level of recursion. For instance, using the example in Figure 3, at , we will have , and (for convenience, we have used superscripts to denote the respective positions in the original sequence T). Assume has been sorted to obtain . Using , we now form the sequences:
where symbol ’∘’ denotes concatenation. The last symbol in each sequence is obtained from , the suffix array of the right tree. These sequences are then bucket-sorted to obtain . Since bucket sorting is linear in the number of input symbols, in the worst case, this will result in a total of time at each level. Thus, the overall time for this procedure will still be in worst case.
We can also observe that with the asymetric partitioning, and by making the recursive call on only one partition at each level, we reduce both the overall number of conflicts and number of comparisons to . But the number of lookups could still be in worst case.
4.4. Improved Sorting - Using Shannon-Fano-Elias Codes
The key to improved sorting is to reduce the number of bucket sorts in the above procedure. We do this by pre-computing some information before hand, so that the sorting can be performed based on a small block of symbols, rather than one symbol at a time. Let m be the block size. With the precomputed information, we can perform a comparison involving an m-block symbol in time. This will reduce the number of bucket sorts required at each level h from to , each involving symbols. By an appropriate choice of m, we can reduce the complexity of the overall sorting procedure. For instance, with , this will lead to an overall worst case complexity in time for determining the suffix array of from that of . With , this gives time. We use in subsequent discussions.
The question that remains then is how to perform the required computations, such that all the needed block values can be obtained in linear time. Essentially, we need a pair-wise global partial ordering of the suffixes involved in each recursive step. First, we observe that we only need to consider the ordering between pairs of suffixes at the same level of recursion. The relative order between suffixes at different levels is not needed. For instance, using the example sequence of Figure 3, the sets of suffixes for which we need the pair-wise orderings will be those at positions: . Each subset corresponds to a level of recursion, from to . Notice that we don’t necessarily need those at level , as we can directly induce the sorted order for these suffixes from , after sorting .
We need a procedure to return the relative order between each pair of suffix positions in constant time. Given that we already have an ordering from the right tree in , we only need to consider the prefixes of the suffixes in the left tree up to the corresponding positions in , such that we can use entries in to break the tie, after a possible bucket sorts. Let be the m-length prefix of the suffix : . We can use a simple hash function to compute a representative of , for instance using the polynomial hash function:
where , if x is the k-th symbol in , and is the nearest prime number . The problem is that the ordering information is lost in the modulus operation. Although order-preserving hash functions exist (see [31]), these run in time on average, without much guarantees on their worst case. Also, with the m-length blocks, this may require time on average.
We use an information theoretic approach to determine the ordering for the pairs. We consider the required representation for each m-length block as a codeword that can be used to represent the block. The codewords are constrained to be order preserving: That is, iff and iff , where is the codeword for sequence x. Unlike in traditional source coding where we are given one long sequence to produce its compact representation, here, we have a set of short sequences, and we need to produce their respective compact representations, and these representations must be order preserving.
Let be the probability of , the m-length block starting at position i in T. Let be the probability of symbol . If necessary, we can pad T with a maximum of ’$’ symbols, to form a valid m-block at the end of the sequence. We compute the quantity: . Recall that , and . For a given sequence T, we should have: . However, since T may not contain all the possible length blocks in , we need to normalize the product of probabilities to form a probability space:
To determine the code for , we then use the cumulative distribution function (cdf) for the ’s, and determine the corresponding position for each in this cdf. Essentially, this is equivalent to dividing a number line in the range [0 1], such that each is assigned a range proportional to its probability, . See Figure 4. The total number of divisions will be equal to the number of unique m-length blocks in T. The problem then is to determine the specific interval on this number line that corresponds to , and to choose a tag to represent .
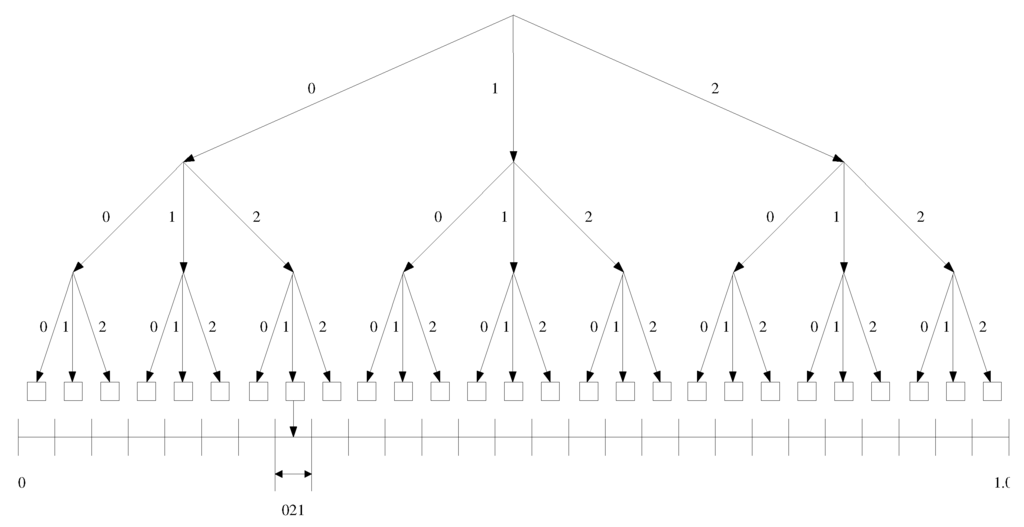
Figure 4.
Code assignment by successive partitioning of a number line.
We use the following assignment procedure to compute the tag, . First we determine the interval for the tag, based on which we compute the tag. Define the cumulative distribution function for the symbols in : . The symbol probabilities, ’s are simply obtained based on the ’s. For each symbol in Σ, we have an open interval in the cdf: . Now, given the sequence , , the procedure steps through the sequence. At each step along the sequence, we can compute and , the respective current upper and lower ranges for the tag using the following relations:
The procedure stops at , and the values of and at this final step will be the range of the tag, . We can choose the tag as any number in the range: . Thus we chose as the mid point of the range at the final step: . Figure 5(a) shows an example run of this procedure for a short sequence: with a simple alphabet, , and where each symbol has an equal probability . This gives .
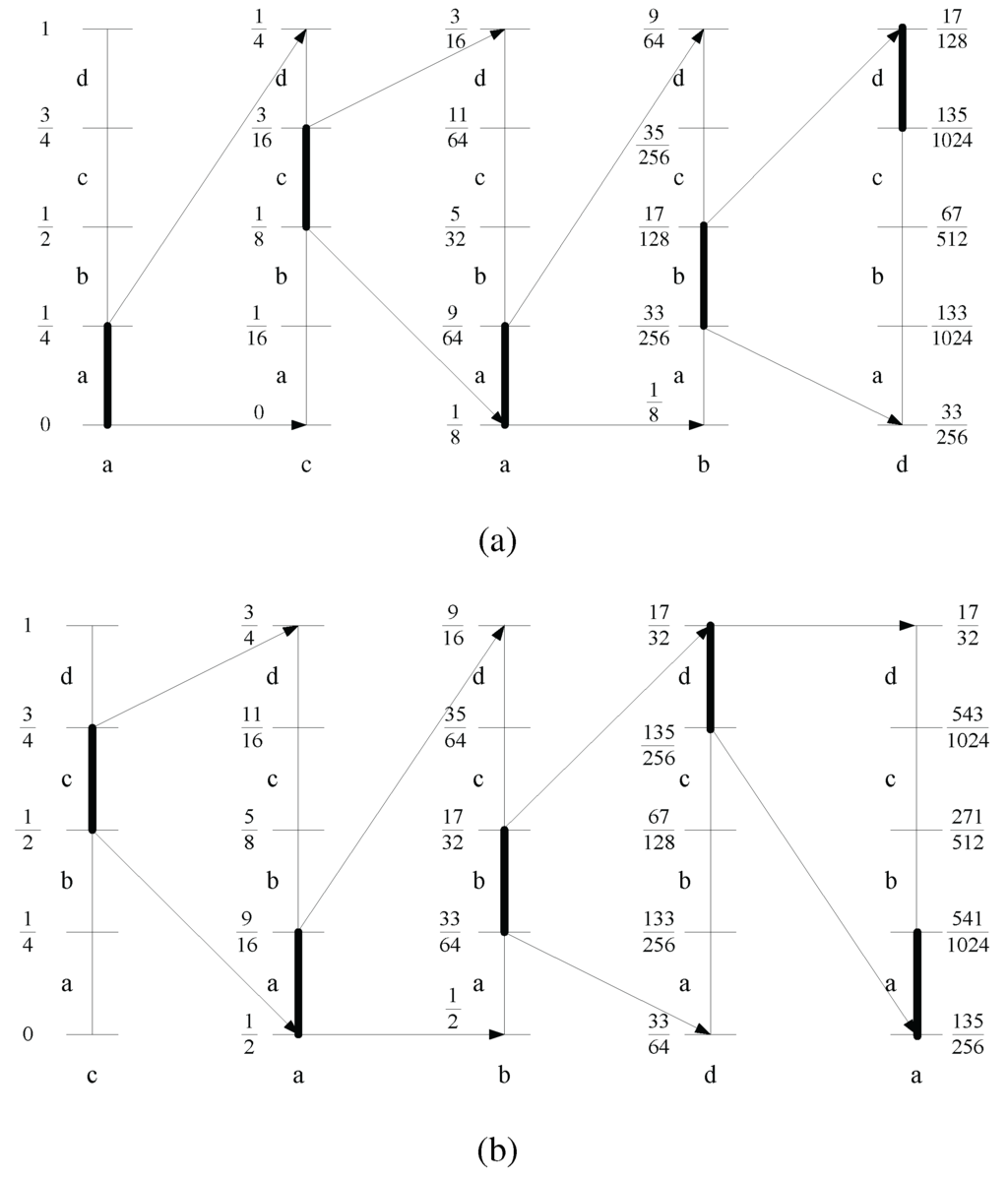
Figure 5.
Code assignment procedure, using an example sequence. The vertical line represents the current state of the number line. The current interval at each step in the procedure is shown with a darker shade. The symbol considered at each step is listed under their respective number lines (a) Using the sequence . (b) Evolution of code assignment procedure, after removing the first symbol (in previous sequence acabd), and bringing in a new symbol a to form a new sequence: .
Lemma 2: The tag assignment procedure results in a tag that is unique to .
Proof. The procedure described can be seen as an extension of the Shanon-Fano-Elias coding procedure used in source coding and information theory [32]. Each tag is analogous to an arithmetic coding sequence of the given m-length block, . The open interval defined by for each m-length sequence is unique to the sequence.
To see this uniqueness, we notice that the final number line at step m represents the cdf for all m-length blocks that appeared in the original sequence T. Denote this cdf for the m-blocks as . Given , the i-th m-block in T, the size of its interval is given by . Since all probabilities are positive, we see that whenever . Therefore, determines uniquely. Thus, serves as a unique code for . Choosing any number within the upper and lower bounds for each define a unique tag for . Thus the chosen tag defined by the midpoint of this interval is unique to . □
Lemma 3: The tags generated by the assignment procedure are order preserving.
Proof. Consider the ordering of the tags for different m-length blocks. Each step in the assignment procedure uses the same fixed order of the symbols on a number line, based on their order in Σ. Thus, the position of the upper and lower bounds at each step depends on the previous symbols considered, and the position of the current symbol in the ordered list of symbols in Σ. Therefore the ’s are ordered with respect to the lexicographic ordering of the ’s: , and . □
Lemma 4: Given , all the required tags , can be computed in time.
Proof. Suppose we have already determined and for the m-block as described above. For efficient processing, we can compute and the tag in the number line, using the previous values for and . This is based on the fact that and are consecutive positions in T (In practice, we need only a fraction of the positions in T, which will mean less time and space are required. But here we describe the procedure for the entire T since the complexity remains the same.). In particular, given , and . We compute as:
Then, we compute using Equation (1). Thus, all the required ’s can be computed in = time.
Similarly, given the tag for , and its upper and lower bounds and , we can compute the new tag for the incoming m-block, based on the structure of the assignment procedure used to compute , (see Figure 5(b)). We compute the new tag by first computing it’s upper and lower bounds. Denote the respective upper and lower bounds for as: . Similarly, we use for the respective bounds for . Let be the first symbol in . Its probability is given by . Also, let be the new symbol that is shifted in. Its probability is given by , and we also know it’s position in the cdf. We first compute the intermediate bounds at step when using , namely:
Multiplying by changes the probability space from the previous range of to . After the computations, we can then perform the last step in the assignment procedure to determine the final range for the new tag:
The tag is then computed as the average of the two bounds as before. The worst case time complexity of this procedure is in . The component comes from the time needed to sort the unique symbols in T before computing the cdf. This can be performed in linear time using counting sort. Since , this gives a worst case time bound of to compute the required codes for all the m-length blocks. □
Figure 5(b) shows a continuation of the previous example, with the old m-block: , and a new m-block . That is, the new symbol a has been shifted in, while the first symbol in the old block has been shifted out. We observe that the general structure in Figure 5(a) is not changed by the incoming symbol, except only at the first step and last step. For the running example, the new value will be . Table 2 shows the evolution of the upper and lower bounds for the two adjacent m-blocks. The bounds are obtained from the figures.

Table 2.
Upper and lower bounds on the current interval on the number line.
| a | c | a | b | d | c | a | b | d | a | |
| 1 | 1 | |||||||||
| 0 | 0 | 0 | ||||||||
| 1 | 1 |
Having determined , which is fractional, we can then assign the final code for by mapping the tags to an integer in the range . This can be done using a simple formula:
where , and . Notice that here, the ’s computed will not necessarily be consecutive. But they will be ordered. Also, the number of distinct ’s is at most n. The difference between and will depend on and . The floor function, however, could break down the lexicographic ordering. A better approach is to simply record the position where each fell on the number line. We then read off these positions from 0 to 1, and use the count at which each is encountered as its code. This is easily done using the cummulative count of occurence of each distinct . Since the ’s are implicitly sorted, so are the ’s. We have thus obtained an ordering of all the m-length substrings in T. This is still essentially a partial ordering of all the suffixes based on their first m symbols, but a total order on the distinct m-length prefixes of the suffixes.
We now present our main results in the following theorems:
Theorem 2: Given the sequence , from a fixed alphabet Σ, , all the m-length prefixes of the suffixes of T can be ordered in linear time and linear space in the worst case.
Proof. The theorem follows from Lemmas 2 to 4. The correctness of the ordering follows from Lemma 2 and Lemma 3. The time complexity follows from Lemma 3. What remains is to prove is the space complexity. We only need to maintain two extra arrays, one for the number line at each step, and the other to keep the cumulative distribution function. Thus, the space needed is also linear in . □
Theorem 3: Given the sequence , with symbols from a fixed alphabet Σ, , Algorithm II computes the suffix array of T in worst case time and space.
Proof. At each iteration, the recursive call applies only to the suffixes in . Thus, the running time for the algorithm is given by the solution to the recurrence : . This gives . Combined with Theorem 2, this establishes the linear time bound for the overall algorithm.
We improve the space requirement using an alternative merging procedure. Since we now have and , we can modify the merging step by exploiting the fact that any conflict that can arise during the merging can be resolved by using only . To resolve a conflict between suffix in and suffix in , we need to consider two cases:
- Case 1: If , we compare versus , since the relative order of both and are available from .
- Case 2: If , we compare versus . Again, for this case, the tie is broken using the triplet, since the relative order of both and are also available from .
Consider the step just before we obtain from as needed to obtain the final . We needed the codes for the m-blocks in sorting to obtain . Given the 1:2 non-symetric partitioning used, at this point, the number of such m-blocks needed for the algorithm will be . These require integers to store. We need integers to store . At this point, we also still have the inverse SA used to merge the left and right suffix arrays to form . This requires integers for storage. Thus, the overall space needed at this point will be integers, in addition to the space for T. However, after getting , we no longer need the integer codes for the m-length blocks. Also, the merging does not involve , so this need not be computed. Thus, we compute , and re-use the space for the m-block codes. requires integers. Further, since we are merging and from the same direction, we can construct the final SA in-place, by re-using part of the space used for the already merged sections of and . (See for example [33,34]). Thus, the overall space requirement in bits will be , where we need bits to store T, bits for the output suffix array, and bits for . □
The above translates to a total space requirement of bytes, using standard assumptions of 4 bytes per integer, and 1 byte per symbol.
Though the space above is , the bits used to store could further be reduced. We do this by by making some observations in the above two cases encountered during merging. We can notice that after obtaining and , we do not really need to store the text T anymore. The key observation is that, merging of and proceeds in the same direction for each array, for instance, from the least to the largest suffix. Thus, at the k-th step, the symbol at position (that is, ) can easily be obtained using , and two arrays, namely, : which stores the symbols in Σ in lexicographic order, and that stores the cummulative count for each symbol in .
For , we compute and use the value as index into . We then use the position in the arrray to determine the symbol value from . Similarly we obtain the symbol , using a second set of arrays. For symbol we do not have . However, we can observe that symbol will be some symbol in . Hence, we can use and to determine the symbol, as described above.
Thus, we can now release the space currently used to store T and use this in part to store , and then merge and using and the two sets of arrays. The space saving gained in doing this will be: ( bits. Using this in the previous space analysis leads to a final space requirement of bits. This gives bytes, assuming at 4 bytes per integer.
Finally, since we do not need anymore, we can release the space it is occupying. Compute a new set of and arrays (in place) for the newly computed SA. The second set of arrays are no longer needed. Using SA and the new and arrays, we now recover the original sequence T, at no extra space cost.
5. Conclusion and Discussion
We have proposed two algorithms for solving the suffix sorting problem. The first algorithm runs in time and space, for both the averge case and worst case. Using ideas from Shannon-Fano-Elias codes used in infomation theory, the second algorithm improved the first to an worst case time and space complexity. The algorithms proposed perform direct suffix sorting on the input sequence, circumventing the need to first construct the suffix tree.
We mention that the proposed algorithms are generally independent of the type of alphabet, Σ. The only requirement is that Σ be fixed during the run of the algorithm. Any given fixed alphabet can be mapped to a corresponding integer alphabet. Also, since practically the number of unique symbols in cannot be more than n, the size of T, it is safe to say that .
For practical implementation, one will need to consider the problem of practical code assignment, since the procedure described may involve dealing with very small fractions, depending on m, the block length, and . This is a standard problem in practical data compression. With , , we have ,and thus we may need to store values as small as while computing the tags. This translates to , or about . In most implementations, a variable of type can store values as small as . For the case of 1:2 asymetric partitioning used above, we need only only of the m-blocks, and hence, the overall space needed to store them will still be n integers, since the size of double is typically twice that of integers. To use the approach for much larger sequences, periodic re-scaling and re-normalization schemes can be used to address the problem. Another approach will be to consider occurrence counts, rather than occurrence probabilities for the m-blocks. Here, the final number line will be a cummulative count, rather than a cdf, with the total counts being n. Then, the integer code for each m-block can easily be read off this number line, based on its overall frequency of occurrence. Therefore, we will need space for at most integers in computing the integer codes for the positions needed. Moffat et al. [35] provide some ideas on how to address practical problems in arithmetic coding.
Overall, by a careful re-use of previously allocated space, the algorithm requires bits, including the n bytes needed to store the original string. This translates to bytes, using standard assumptions of 4 byte per integer, and 1 byte for each symbol. This is a significant improvement over the bytes required by the KA algorithm [10], or the bytes required by the KS algorithm [9]. Our algorithm is also unique in its use of Shannon-Fano-Elias codes, traditionally used in source coding, for efficient suffix sorting. This is the first time information-theoretic methods have been used as the basis for solving the suffix sorting problem. We believe that this new idea of using an information theoretic approach to suffix sorting could shed a new light on the problems of suffix array construction, their analysis, and applications.
Acknowledgements
This work was partially supported by a DOE CAREER grant: No: DE-FG02-02ER25541, and an NSF ITR grant: IIS-0228370. A short version of this paper was presented at the 2008 IEEE Data Compression Conference, Snowbird, Utah.
References
- Manber, U.; Myers, G. Suffix arrays: A new method for on-line string searches. SIAM J. Comput. 1993, 22, 935–948. [Google Scholar] [CrossRef]
- Larsson, N.J.; Sadakane, K. Faster suffix sorting. Theoret. Comput. Sci. 2007, 317, 258–272. [Google Scholar] [CrossRef]
- Manzini, G.; Ferragina, P. Engineering a lightweight suffix array construction algorithm. Algorithmca 2004, 40, 33–50. [Google Scholar] [CrossRef]
- Puglisi, S.J.; Smyth, W.F.; Turpin, A. A taxonomy of suffix array construction algorithms. ACM Comput. Surv. 2007, 39, 1–31. [Google Scholar] [CrossRef]
- Gusfield, D. Algorithms on Strings, Trees and Sequences: Computer Science and Computational Biology; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Burrows, M.; Wheeler, D.J. A Block-Sorting Lossless Data Compression Algorithm; Research Report 124; Digital Equipment Corporation: Palo Alto, CA, USA, 1994. [Google Scholar]
- Adjeroh, D.; Bell, T.; Mukherjee, A. The Burrows-Wheeler Transform: Data Compression, Suffix Arrays and Pattern Matching; Springer-Verlag: New York, NY, USA, 2008. [Google Scholar]
- Seward, J. On the performance of BWT sorting algorithms. In Proceedings of IEEE Data Compression Conference, Snowbird, UT, USA, March 28–30, 2000; Volume 17, pp. 173–182.
- Kärkkäinen, J.; Sanders, P.; Burkhardt, S. Linear work suffix array construction. J. ACM 2006, 53, 918–936. [Google Scholar] [CrossRef]
- Ko, P.; Aluru, A. Space-efficient linear time construction of suffix arrays. J. Discrete Algorithms 2005, 3, 143–156. [Google Scholar] [CrossRef]
- Cleary, J.G.; Teahan, W.J. Unbounded length contexts for PPM. Comput. J. 1997, 40, 67–75. [Google Scholar] [CrossRef]
- Bell, T.; Cleary, J.; Witten, I. Text Compression; Prentice-Hall: Englewood Cliffs, NJ, USA, 1990. [Google Scholar]
- Szpankowski, W. Asymptotic properties of data compression and suffix trees. IEEE Trans. Inf. Theory 1993, 39, 1647–1659. [Google Scholar] [CrossRef]
- Abouelhoda, M.I.; Kurtz, S.; Ohlebusch, E. Replacing suffix trees with enhanced suffix arrays. J. Discrete Algorithms 2004, 2, 53–86. [Google Scholar] [CrossRef]
- Farach-Colton, M.; Ferragina, P.; Muthukrishnan, S. On the sorting-complexity of suffix tree construction. J. ACM 2000, 47, 987–1011. [Google Scholar] [CrossRef]
- Kim, D.K.; Sim, J.S.; Park, H.; Park, K. Constructing suffix arrays in linear time. J. Discrete Algorithms 2005, 3, 126–142. [Google Scholar] [CrossRef]
- Nong, G.; Zhang, S. Optimal lightweight construction of suffix arrays for constant alphabets. In Proceedings of Workshop on Algorithms and Data Structures, Halifax, Canada, August 15–17, 2007; Volume 4619, pp. 613–624.
- Maniscalco, M.A.; Puglisi, S.J. Engineering a lightweight suffix array construction algorithm. In Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data, Vancouver, BC, Canada, June 10–12, 2008.
- Itoh, H.; Tanaka, H. An efficient method for in memory construction of suffix arrays. In Proceedings of String Processing and Information Retrieval Symposium and International Workshop on Groupware, Cancun, Mexico, September 22–24, 1999; pp. 81–88.
- Hon, W.; Sadakane, K.; Sung, W. Breaking a time-and-space barrier in constructing full-text indices. In Proceedings of IEEE Symposium on Foundations of Computer Science, Cambridge, MA, USA, October 11–14, 2003.
- Na, J.C. Linear-time construction of compressed suffix arrays using O (n log n)-bit working space for large alphabets. In Proceedings of 16th Annual Symposium on Combinatorial Pattern Matching 2005, LNCS, Jeju Island, Korea, June 19–22, 2005; Volume 3537, pp. 57–67.
- Burkhardt, S.; Kärkkäinen, J. Fast lightweight suffix array construction and checking. In Proceedings of the 14th Annual ACM-SIAM Symposium on Discrete Algorithms, Baltimore, MD, USA, January 12–14, 2003.
- Nong, G.; Zhang, S.; Chan, W.H. Linear time suffix array construction using D-critical substrings. In CPM; Kucherov, G., Ukkonen, E., Eds.; Springer: New York, NY, USA, 2009; Volume 5577, pp. 54–67. [Google Scholar]
- Nong, G.; Zhang, S.; Chan, W.H. Linear suffix array construction by almost pure induced-sorting. In DCC; Storer, J.A., Marcellin, M.W., Eds.; IEEE Computer Society: Hoboken, NJ, USA, 2009; pp. 193–202. [Google Scholar]
- Franceschini, G.; Muthukrishnan, S. In-place suffix sorting. In ICALP; Arge, L., Cachin, C., Jurdzinski, T., Tarlecki, A., Eds.; Springer: New York, NY, USA, 2007; Volume 4596, pp. 533–545. [Google Scholar]
- Okanohara, D.; Sadakane, K. A linear-time Burrows-Wheeler Transform using induced sorting. In SPIRE; Karlgren, J., Tarhio, J., Hyyrö, H., Eds.; Springer: New York, NY, USA, 2009; Volume 5721, pp. 90–101. [Google Scholar]
- Ferragina, P.; Manzini, G. Opportunistic data structures with applications. In Proceedings of the 41st Annual Symposium on Foundations of Computer Scienc, Redondo Beach, CA, USA, November 12–14, 2000; pp. 390–398.
- Grossi, R.; Vitter, J.S. Compressed suffix arrays and suffix trees with applications to text indexing and string matching. In Proceedings of the 32nd Annual ACM Symposium on Theory of Computing, Baltimore, MD, USA, May 22–24, 2005.
- Sirén, J. Compressed suffix arrays for massive data. In SPIRE; Karlgren, J., Tarhio, J., Hyyrö, H., Eds.; Springer: New York, NY, USA, 2009; Volume 5721, pp. 63–74. [Google Scholar]
- Karlin, S.; Ghandour, G.; Ost, F.; Tavare, S.; Korn, L. New approaches for computer analysis of nucleic acid sequences. Proc. Natl. Acad. Sci. USA 1983, 80, 5660–5664. [Google Scholar] [CrossRef] [PubMed]
- Fox, E.A.; Chen, Q.F.; Daoud, A.M.; Heath, L.S. Order-preserving minimal perfect hash functions and information retrieval. ACM Trans. Inf. Syst. 1991, 9, 281–308. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley Interscience: Malden, MA, USA, 1991. [Google Scholar]
- Symvonis, A. Optimal stable merging. Comput. J. 1995, 38, 681–690. [Google Scholar] [CrossRef]
- Huang, B.; Langston, M. Fast stable sorting in constant extra space. Comput. J. 1992, 35, 643–649. [Google Scholar] [CrossRef]
- Moffat, A.; Neal, R.M.; Witten, I.H. Arithmetic coding revisited. ACM Trans. Inf. Syst. 1995, 16, 256–294. [Google Scholar] [CrossRef]
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).