PISI: Physical Information Based Solver-Interactive Network Structure Reconstruction

Abstract

Inference of the interactive network structure of the physical world that is captured by nonlinear dynamic systems is a long-standing goal for machine learning. Existing inference methods have shown limited incorporation of physical system information and solver interaction capabilities. We present a comprehensive Physical Information based Solver-Interactive (PISI) network structure identification framework that incorporates network topology, physical constraints, and bidirectional solver interaction in nonlinear dynamical systems. To this end, we first develop a physical information-based graphical neural network (PIGNN). The PIGNN cells are embedded as the basic integration units to iterative interact with dynamical solver. The dynamical systems’s physical information can be flexibly added to the iterative interaction for PIGNN training. The above stages are trained end-to-end using a Runge–Kutta solver. The network structure inferring capability of the proposed framework is demonstrated through two kuramoto systems. Our PISI methodology, integrating graph topology, physical constraints, and solver interactivity shows advantages in trajectory prediction and structure reconstruction compared to state-of-the-art methods.

1. Introduction

A wide range of dynamical systems in ecology [1], power systems [2], social networks [3], epidemics [4], and other areas can be seen as groups of interaction components. The interaction patterns among individual components give rise to complex dynamic behaviors at the component level, while also inducing emergent complexity at the holistic system level. The classical approach to modeling interactions between individuals is through complex networks [5]. In reality, we can only access the component observations through sensors, with the underlying interaction as a black box. However, the unknown interactions, i.e., the network structure, are of great importance in dynamic evolution. For example, identifying synaptic adjacency relationships between neurons can reveal abnormal discharge propagation pathways in epileptic seizures [6]. Accurately identifying physical adjacency relationships among generator nodes is critical for predicting cascading failures. Also, adjacency relationship identification based on social contact networks enables precise prediction of virus transmission hot spots [7]. Thus arises the problem of network structure inference in nonlinear dynamical systems.

Classic structure identification methods primarily rely on observations to reconstruct network topology. This approach fails to fully exploit the inherent physical properties of the underlying dynamical systems. In fact, the dynamical evolution process embodies substantial physical information, including but not limited to initial conditions, boundary conditions, and the governing equations themselves. Moreover, the numerical solvers of dynamical evolution are intrinsically coupled with network structure, where each iteration can be viewed as an interaction among initial conditions, network topology, and individual dynamics. Certain numerical solvers inherently generate physical information during iterative computations, such as automatic differentiation of parameters. However, such critical information remains underutilized in traditional identification paradigms.

The advancement of artificial intelligence algorithms has given rise to diverse methodologies capable of exploiting physical system information from multiple perspectives [8]. First, regarding observational data, whereas classic approaches require extensive sampling to predict short-term system states, contemporary neural network-based methods demand significantly fewer samples while aiming for extended temporal prediction horizons [9]. Secondly, from the dynamic solver interaction perspective, parameter estimation methods with solver interactivity have been developed for individual physical oscillators [10]. However, for network structure identification in systems composed of multiple oscillators, the parameter dimensionality escalates from a fixed number to a quadratic problem, rendering solver-interactive network structure identification exceptionally challenging. Thirdly, from the perspective of physical information, Physics-Informed Neural Networks (PINNs) have emerged in recent years [11]. These networks aim to integrate physical knowledge by embedding physical constraints into the loss function, thereby combining the learning capacity of neural networks with physical principles to enhance learning efficiency and identification accuracy. However, in the context of network structure identification, PINNs face challenges similar to those encountered in solver-interactive methods specifically. How to extend their advantages in single-oscillator parameter identification to network topology inference still remains a challenge.

In response to these challenges, we propose an integrated physical information-based solver-interactive network structure reconstruction framework (PISI). Specifically, our framework employs a physical information based graph neural network (PIGNN) as the foundational component and embeds PIGNN into each solver iteration. By leveraging automatic differentiation (AD) information generated during the solving process, the proposed framework achieves end-to-end network structure learning. We validate the effectiveness of the PISI method in state prediction and structure reconstruction using an Runge–Kutta (RK) solver for two Kuramoto systems. The primary innovations and contributions of this research are outlined as follows.

• The proposed PISI is solver-interactive, enabling simultaneous estimation of network topology and system states.
• By integrating multiple information sources, PISI dramatically reduces the required sample size for a high network structure identification accuracy.
• The proposed PISI method realizes extending from single-node parameter identification to multi-agent system structure reconstruction by leveraging the interaction between graph neural networks and solvers.

The rest of this study is organized as follows. Section 2 reviews related works in three aspects. Section 3 describes the methodology module of this study. Section 4 presents the results of this study and discusses the state of the art of the methodology. Section 5 concludes this study.

2. Related Work

In this section, we present research related to our work in three aspects: (1) graph neural network (GNN)-based structure reconstruction, (2) PINN-based parameter estimation of nonlinear dynamics, and (3) solver-interactivity parameter estimation of single oscillators.

2.1. GNN Based Network Structure Reconstruction

GNN was initially designed to process data with known graph structures by employing message-passing mechanisms to predict or estimate node states [12]. Subsequent research has gradually expanded to infer or reconstruct unknown network structures from observed data (such as node states or interaction behaviors), forming several important branches in this direction [13]. Thomas [14] et al. took the form of a variational auto-encoder, in which the latent code represents the underlying interaction graph and the reconstruction is based on graph neural networks. Zang [15] et al. proposed combining Ordinary Diferential Equation Systems (ODEs) and GNNs to learn continuous-time dynamics on complex networks in a data-driven manner. Rakshit [16] et al. presented DyRep, a novel modeling framework for dynamic graphs that posits representation learning as a latent mediation process bridging two observed processes, namely the dynamics of the network (realized as topological evolution) and dynamics on the network (realized as activities between nodes). Zhang [17] et al. proposed an LLM-based robust graph structure inference framework, LLM4RGNN, which distills the inference capabilities of GPT-4 into a local LLM for identifying malicious edges and an LM-based edge predictor for finding missing important edges, so as to recover a robust graph structure. Although GNNs are capable of handling structure estimation and state prediction tasks, their lack of physics-informed mechanisms compared to our PISI results in a high demand for training data. For example, in [14], to reconstruct a system consisting of five oscillators, more than 50,000 samples are needed.

2.2. PINN Based Parameter Estimation of Nonlinear Dynamics

PINN integrates neural networks with physical equations by using automatic differentiation to compute PDE residuals, which are incorporated as part of the loss function. The usage of physical information requires no large training datasets, due to the fact that the neural network can be trained solely based on PDE constraints [18]. Raissi et al. devised a new family of data efficient spatio-temporal function approximators for continuous systems; for discrete systems, the model allows the use of arbitrarily accurate implicit Runge–-Kutta time stepping schemes with an unlimited number of stages. Ji [19] et al. investigated the performance of the PINN in solving stiff chemical kinetic problems with governing equations of stiff ordinary differential equations. The results elucidate the challenges of utilizing the PINN in stiff ODE systems. However, the loss function of PINN faces difficulties when solving network structure reconstruction compared to our PISI. The aforementioned applications of PINNs have primarily focused on individual systems, with insufficient research on network structure identification.

2.3. Solver-Interactivity Parameter Estimation of Nonlinear Dynamics

In both dynamical evolution and inverse problem parameter estimation, differential equation solvers for dynamical systems invariably play a crucial and inescapable role [20]. In all of the literature reviewed in Section 2.1 and Section 2.2 above, iterative solvers have been consistently employed. Therefore, the integration of parameter estimation and structure reconstruction with solver iterations is of critical importance. Kiwon [21] et al. integrated the solver into the training loop and thereby allowed the model to interact with the PDE during training. Philipp [22] et al. presented a novel hierarchical predictor-corrector scheme enabling neural networks to learn to understand and control complex nonlinear physical systems over long time frames, in which the predictor network plans optimal trajectories and the control network infers the corresponding control parameters. Drawing inspiration from classical numerical integration solution rules for differential equations, Zhai [10] et al. proposed a new recurrent neural network architecture, taking PINN cells as the basic integration units of the architecture to introduce prior physics-based biases. Although existing research has explored the integration of solver-in-the-loop approaches with PINNs, the insufficient understanding of graph properties in network structure identification tasks compared to our PISI hinders their ability to effectively address such problems.

3. Methodology

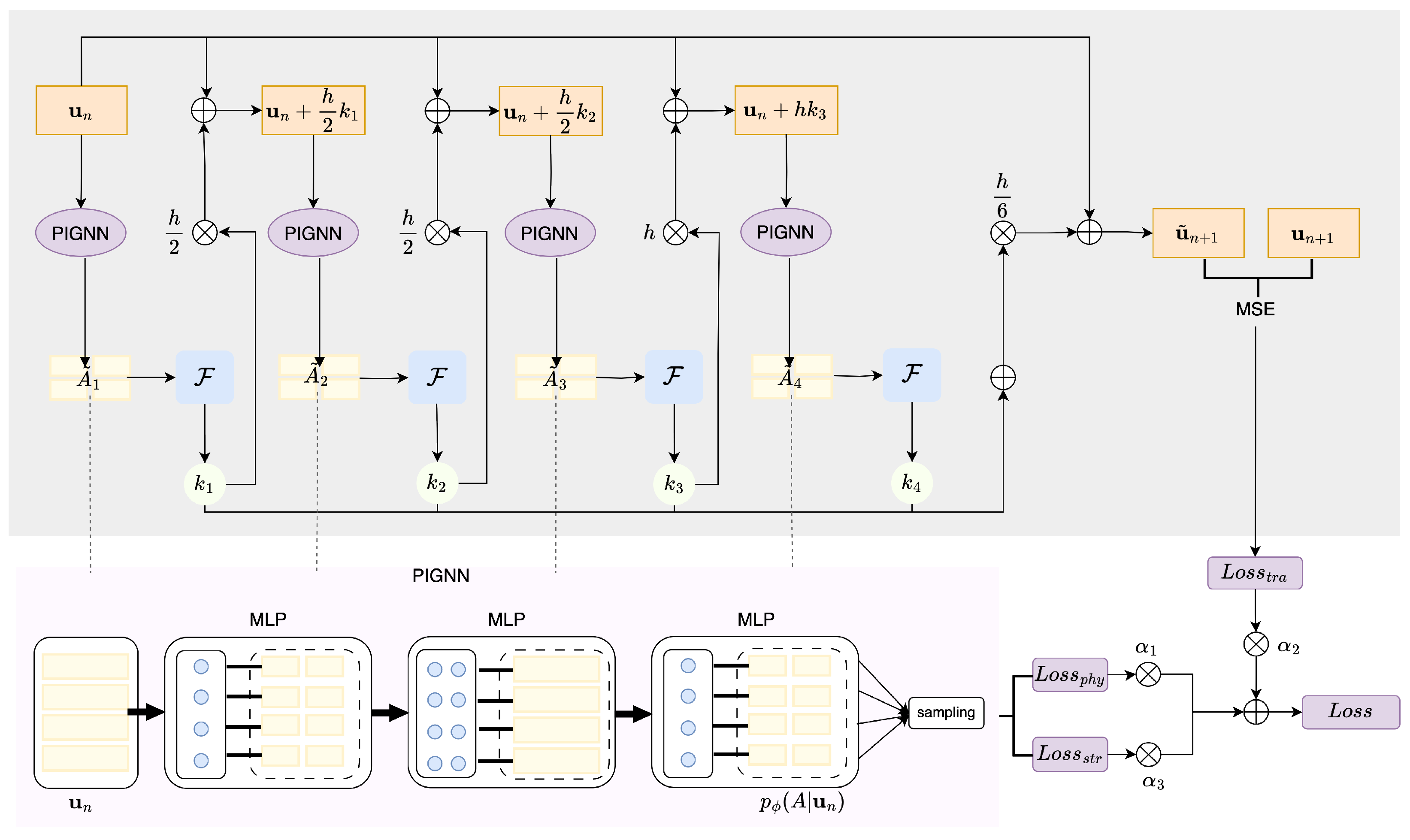
In this study, we propose a unified neural network framework that integrates neural graph, physical, and solver information, aiming to reconstruct the network structure of nonlinear dynamics systems and at the same time predict the system state. The framework comprises two modules: a physical information-based GNN, and an iterative solver. We propose an end-to-end network structure reconstruction solution. The method employs the fourth-order Runge–Kutta (RK4) method for differential equation solving as its backbone. We employ RK4 as an illustrative example, while other differential equation solvers are equally applicable. The PIGNN takes the observation data as input and outputs, with edge type posterior $p_{\varphi }(A|\mathbf{u})$. With a sampling module, we obtain the estimated network structure $\tilde{A}$. $\tilde{A}$ will compensate for the unknown terms in the dynamical system, thereby enabling the operation of the RK4 solver. The PIGNN and RK4 module interact as follows. At each stage of RK4, the PIGNN provide structure estimation value and the receive the stage node state to obtain the physical loss. At the end of each RK4 iteration, state loss is provided to PIGNN, thereby achieving end-to-end training across all four involved PIGNNs.

3.1. Modeling of the Network Structure Reconstruction Problem

Consider a system composed of n coupled oscillators, captured by parametrized and nonlinear differential equations of the general form

$$\begin{array}{c}\hfill \dot{\overrightarrow{u}}+\mathcal{F}[\overrightarrow{u};A]=0,\end{array}$$

(1)

where $\overrightarrow{u}(·,t)$ consists of solutions $u_i,i=1,\dots N$ defined in Banach space $\mathcal{X}$, and $\dot{\overrightarrow{u}}=({\dot{u}}_1,\dots ,{\dot{u}}_N)$ denotes the time derivative term of each oscillators. $\mathcal{F}(\overrightarrow{u};A)\in {\mathcal{X}}^N\to {\mathcal{X}}^N$ is a parametrized nonlinear operator, and $A\in R^{N\times N}$ represents system coupling strength parameters, where $A_{ij}\in [0,1]$ is a discrete categorical variable representing the edge type between oscillators $u_i$ and $u_j$.

Without loss of generality, for each oscillator i, the nonlinear operator $\mathcal{N}[·,·]$ consists of three parts

$$\begin{array}{c}\hfill {\dot{u}}_i+\mathcal{L}{u}_i+\mathcal{G}(u;A)+\mathcal{D}{u}_i=0\end{array}$$

(2)

with $\mathcal{L}{u}_i$ describing the intrinsic oscillatory linear properties, $\mathcal{G}(u_i;A)$ describing the phase interaction between oscillators, and $\mathcal{D}{u}_i$ describing the spatial diffusion/dissipation of the phase field. This decomposition represents many scenarios in mathematical physics, including the extended Kuramoto model describing power grid frequency synchronization [23], the XY model [24], and the theta-gamma coupled oscillation model [25] for brain rhythm synchronization [26]. As an important model that we will focus on in the following discussion, the Kuramoto model corresponds to the case when $\mathcal{L}{u}_i=D_i{\dot{u}}_i$, $\mathcal{G}(u_i;A)=-K{A}_{ij}{\displaystyle \sum _{j\ne i}}sin(u_j-u_i)$, $\mathcal{D}{u}_i=M_i{\ddot{u}}_i$, with $D_i,M_i$, and K as the time-independent constant. The first problem we focus on is: how to incorporate the solver with the network inferring procedure thus to improve the state predict accuracy? The second problem we focus on is: how can we infer the coupling strength, i.e., the network structure A from as less as observed data?

3.2. Runge–Kutta Methods

The inputs consist of trajectories of the N oscillators. We denote the observed trajectories of the oscillator $u_i$ at time t as ${\mathbf{u}}_i^t$. All observed data for N oscillators from time $t=1:T$ are denoted as $\mathbf{u}=\{{\mathbf{u}}^1,\dots ,{\mathbf{u}}^T\}$, with the ${\mathbf{u}}^t=\{{\mathbf{u}}_1^t,\dots ,{\mathbf{u}}_N^t\}$ as all trajectories of N oscillator at time t. We denote the trajectories of node $u_i$ as ${\mathbf{u}}_i=\{{\mathbf{u}}_i^1,\dots ,{\mathbf{u}}_i^T\}$.

To solve the considered two problems, we first introduce one of the most widely used differential equation solvers. The Runge–Kutta method can advance temporal solutions for non-stiff ordinary differential equations and semi-discretion partial differential equations. The flexible and extensible framework accommodates both explicit and implicit formulations for temporal discretizations. The RK4 is self-starting and eliminates the dependency on historical data required by multi-step methods. The Runge–-Kutta methods are linear extrapolations based on Taylor series expansion. Since A is unknown during the iteration, we explicitly represent A in $\mathcal{F}$. Next, we employ the fourth-order Runge–Kutta (RK4) method for temporal discretization as an illustrative example. For time step $\Delta t$, from time $t_n$ to $t_{n+1}=t_n+\Delta t$, the solution can be written as

$$\begin{array}{c}\hfill {\mathbf{u}}_i^{n+1}={\mathbf{u}}_i^n+{\displaystyle \frac{h}{6}}(k_1+2k_2+2k_3+k_4)\end{array}$$

(3)

where

$$\begin{array}{cc}\hfill & k_1=\mathcal{F}({\mathbf{u}}_i^n,t^n,A),\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & k_2=\mathcal{F}({\mathbf{u}}_i^n+{\displaystyle \frac{k_1}{2}},t^n+{\displaystyle \frac{h}{2}},A),\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill & k_3=\mathcal{F}({\mathbf{u}}_i^n+{\displaystyle \frac{k_2}{2}},t^n+{\displaystyle \frac{h}{2}},A),\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & k_4=\mathcal{F}({\mathbf{u}}_i^n+k_3,t^n+h,A).\hfill \end{array}$$

(7)

3.3. Design of PISI

It should be noticed that among the RK4 procedure, the discretization of phase interaction $\mathcal{G}(\overrightarrow{u},A)$ encodes the underlying reconstructed A, thus leading to the underlying inferred $\mathcal{F}(u_i,t,A)$. During the RK4 procedure, the unknown vector field $\mathcal{F}(u_i,t,A)$ is evaluated four times at distinct intermediate stages. Higher-order Runge–Kutta methods require progressively more evaluations of the vector field. Thus, the key of structure reconstruction and states prediction lies in the refer of $\mathcal{F}(u_i,t,A)$. Our basic idea is to approximate $\mathcal{F}$ with a graph based neural network during the RK4 procedure. The designed neural network undergoes four invocations during a single RK4 iteration while maintaining parameter sharing across all calls. In designing the neural network, we prioritize three key considerations. First, the architecture should effectively utilize intermediate RK iteration data and physical information. Second, the PISI should effectively incorporate graph attributes of the identifiable matrix A. Finally, the network’s input and output data should maintain compatibility with the RK4 iterative procedure.

3.3.1. The Physic Information Based Graph Neural Network

Overall, we adopt the graph neural network structure from [14], but redesign the loss function to satisfy the aforementioned three requirements for our neural network. The PIGNN supports the RK4 procedure as follows by predicting the interaction graph given the trajectories.

First, we state the graph neural network part of PIGNN, then we present how the traditional GNN incorporates the physical information. The physical information-based graph neural network can be denoted as edge type posterior $p_{\varphi }(A|\mathbf{u})=PIGNN(\mathbf{u},\varphi )$ with $\varphi$ the shared parameter of the four PIGNNs. The PIGNN returns a factorized distribution of A.

We state a brief introduction of GNN, which operates directly on graph-structured data by passing local messages [27]. We define a single node-to-node message passing operation in a GNN as follows:

$$\begin{array}{ccc}\hfill & \mathrm{Node}\mathrm{Pair}\mathrm{Embedding}\hfill & \hfill {\mathbf{h}}_{ij}=f_{{\varphi }_1}({\mathbf{h}}_i,{\mathbf{h}}_{\mathbf{j}},\mathbf{u},A)\end{array}$$

(8)

$$\begin{array}{ccc}& \mathrm{Node}\mathrm{Embedding}\hfill & \hfill {\mathbf{h}}_i^{\prime }=f_{{\varphi }_2}(\sum _{j\ne i}{\mathbf{h}}_j,\mathbf{u},A).\end{array}$$

(9)

in which the ${\mathbf{h}}_i$ and ${\mathbf{h}}_{ij}$ are the embedding of node i and edge between nodes i and j. The function $f_{{\varphi }_1}$ denotes a neural network like MLP [28], CNN [29] with under trainable parameter ${\varphi }_1$. Equation (8) enables iterative bidirectional mapping between edge and node representations through successive message-passing operations.

Adopting the GNN structure from [14], we design a message passing procedure consists of two messages passing from nodes to edges as in Figure 1, with the first passing encoding the information of local node pairs and the second passing encoding global information corresponding to the considered nodes pair. Specifically, starting from a fully-connected graph without self-loop, the two nodes to edges message passing for $A_{ij}$ of the graph neural network is as follows

$$\begin{array}{ccc}& \mathrm{Node}\mathrm{Embedding:}\hfill & \hfill {\mathbf{h}}_j^1=ML{P}_1({\mathbf{u}}_j)\end{array}$$

(10)

$$\begin{array}{ccc}& \mathrm{Node}\mathrm{Pair}\mathrm{Embedding:}\hfill & \hfill {\mathbf{h}}_{(ij)}^1=ML{P}_2([{\mathbf{h}}_i^1,{\mathbf{h}}_i^1])\end{array}$$

(11)

$$\begin{array}{ccc}& \mathrm{Global}\mathrm{Node}\mathrm{Embedding:}\hfill & \hfill {\mathbf{h}}_j^2=ML{P}_3(\sum _{j\ne i}{\mathbf{h}}_{(ij)}^1)\end{array}$$

(12)

$$\begin{array}{ccc}& \mathrm{Global}\mathrm{Pair}\mathrm{Embedding:}\hfill & \hfill {\mathbf{h}}_{(ij)}^2=ML{P}_4([{\mathbf{h}}_i^2,{\mathbf{h}}_j^2]).\end{array}$$

(13)

Then, from the global feature ${\mathbf{h}}_{(ij)}^2$, we can calculate the edge type posterior $p_{\varphi }(A_{ij}|\mathbf{u})=\mathrm{softmax}({\mathbf{h}}_{(ij)}^2)$.

To bridge the gap between the PIGNN and the RK4 procedure, we sample from the edge type posterion and obtain ${\tilde{A}}_{ij}$ (into Appendix A for sampling method). The resulting edge value should be substituted into the partial unknown vector field $\mathcal{F}$ feeding to Equations (4)–(7).

Above all, the interaction between the PIGNN and RK4 is as follows. In the n-th time period of RK4, from trajectories input ${\mathbf{u}}^n$, run the first $\mathrm{PIGNN}(\mathbf{u},\varphi )$ and obtain ${\tilde{A}}_1$. Substitute ${\tilde{A}}_1$ into the RK4 procedure, and oobtain the evolution function $\mathcal{F}({\mathbf{u}}^n,t^n,{\tilde{A}}_1)$. Calculate the second intermediate variable $k_2$. The process is then iterated cyclically until reaching the fourth stage of RK4. From Equation (3), we can then obtain the estimated trajectories ${\tilde{\mathbf{u}}}^{n+1}$. Within a time step of RK4, we employ adjacency matrices ${\tilde{A}}_n,n=1,2,3,4$ at four stages to enhance the model’s learning capacity. To ensure the numerical stability of the RK4 algorithm, we introduce a consistency loss term for the adjacency matrices within each time step, guaranteeing evolutionary continuity between stages. The specific design of the penalty term is detailed in next subsection.

3.3.2. Loss Function

The four PIGNNs share parameter $\varphi$, and the training loss consists of three components: (1) physical information: automatic differentiation of the structure, (2) the trajectory prediction loss term, and (3) the structure reconstruction loss. The incorporation of tri-dimensional information endows our method with sampling efficiency.

Automatic differentiation is a numerical method for computing derivatives of functions with respect to the input, serving as the core operation in PINNs. Its fundamental principle involves decomposing complex functions into elementary operations and systematically applying the chain rule, making it inherently compatible with most modern neural network training frameworks. The underlying structure can be calculated from the k-th PIGNN as

$$\begin{array}{c}\hfill A_{\mathrm{phy},k}^n=AD({\mathbf{u}}^n,PIGN{N}_k(\mathbf{u},\varphi )),k=1,2,3,4.\end{array}$$

(14)

with $AD(·,·)$ the automatic differentiation calculation in the PIGNN training procedure. As the four PIGNN shares parameter and the ground truth of the structure A is time-invariant among the four stages in RK4, we take coefficient of variation as physic information loss

$$\begin{array}{cc}\hfill {\mathrm{Loss}}_{phy}=& c_v^2(A_{\mathrm{phy}})\hfill \end{array}$$

(15)

$$\begin{array}{ccc}\hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}& \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=& \hfill {\displaystyle \frac{1}{4T}}\sum _{n=1}^T\sum _{k=1}^4{(A_{\mathrm{phy},k}^n-{\overline{A}}_{\mathrm{phy}}^n)}^2/{({\overline{A}}_{\mathrm{phy}}^n)}^2\end{array}$$

(16)

where $c_v^2$ is the coefficient of variation and ${\overline{A}}_{\mathrm{phy}}$ the mean of ${\overline{A}}_{\mathrm{phy},k},k=1,2,3,4$.

For the trajectory prediction, we focus on the end-to-end loss. In one iteration of RK4, the end-to-end loss uses the sample ${\mathbf{u}}^{n+1}$ and the output ${\tilde{\mathbf{u}}}^{n+1}$. The PIGNN parameter is trained via the MSE of the trajectories as follows

$$\begin{array}{c}\hfill {\mathrm{Loss}}_{tra}={\displaystyle \frac{1}{T}}\sum _{n=1}^{T-1}{({\mathbf{u}}^{n+1}-{\tilde{\mathbf{u}}}^{n+1})}^2\end{array}$$

(17)

For the structure reconstruction loss, we delve into the four stages of RK4 while maintaining an end-to-end learning process. For each stage, the Kullback–Leibler (KL) divergence is employed. Across different stages, we constrain the overall distribution matching by averaging the KL divergences, thereby compelling all stages to jointly optimize the alignment between latent variables and priors, rather than focusing on any single network. The resulting structure reconstruction loss of the k-th step at the n-th time period $A_k^n$ is as follows:

$$\begin{array}{c}\hfill {\mathrm{Loss}}_{str}={\displaystyle \frac{1}{4T}}\sum _{n=1}^T\sum _{k=1}^4\mathrm{KL}(p(A_k^n|\mathbf{u})\left|\right|p(A))\end{array}$$

(18)

The prior $P(A)$ is a factorized uniform distribution over edge types. The core assumption of the factorized uniform prior is that edge types are independent and unbiased.

The total loss function of the total training loss combines the above three losses, using the weighting parameters ${\alpha }_1$, ${\alpha }_2$ and ${\alpha }_3$ to control the relative importance of each part of the optimization process. We define the total training $Los{s}_{\mathrm{total}}$ as follows:

$$\begin{array}{c}\hfill {\mathrm{Loss}}_{total}={\alpha }_1{\mathrm{Loss}}_{phy}+{\alpha }_2{\mathrm{Loss}}_{tra}+{\alpha }_3{\mathrm{Loss}}_{str}\end{array}$$

(19)

By employing the combined loss function ${\mathrm{Loss}}_{total}$, the model can optimize state prediction and structure estimation. Now that we have described all the elements in the framework in Figure 2, the training goes as follows.

4. Experiment

We used PyTorch (version 2.7.0) to implement our network. All models in the experiment were trained for 300 epochs. We train the framework with Adam [30], using an initial learning rate of 3 × ${10}^{-5}$ that is halved every 10 epochs. The entire network was trained and evaluated using an NVIDIA GeForce RTX 4090 GPU with a batch size of 64. The grid search method was utilized to find the proper values of weights of the three loss terms.

4.1. Kuramoto Model

The Kuramoto model was independently introduced in the context of power grids in [31] and has a long history of study there. We use the following notation:

$$\begin{array}{c}\hfill M_i{\displaystyle \frac{d^2{\theta }_i}{d{t}^2}}+D_i{\displaystyle \frac{d{\theta }_i}{dt}}=P_i+K\sum _{j=1}^N{A}_{ij}sin({\theta }_j-{\theta }_i)\end{array}$$

(20)

where ${\theta }_i$ denotes the phase angle of oscillator i, and the first-order and second derivative of ${\theta }_i$ denote voltage angle ${\omega }_i$ and its time derivatives, respectively. The injected power $P_i$ is selected in $\{1,-1\}$. $K=9$ is the uniform coupling coefficient [32]. The classical Kuramoto model can be transformed into an equivalent state-space representation for trajectories sampling:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \frac{d{\theta }_i}{dt}}={\omega }_i\hfill \\ {\displaystyle \frac{d{\omega }_i}{dt}}={\displaystyle \frac{1}{M_i}}(P_i-D_i{\omega }_i+K{\displaystyle \sum _{j=1}^N}{A}_{ij}sin({\theta }_j-{\theta }_i)).\hfill \end{array}\right.\end{array}$$

(21)

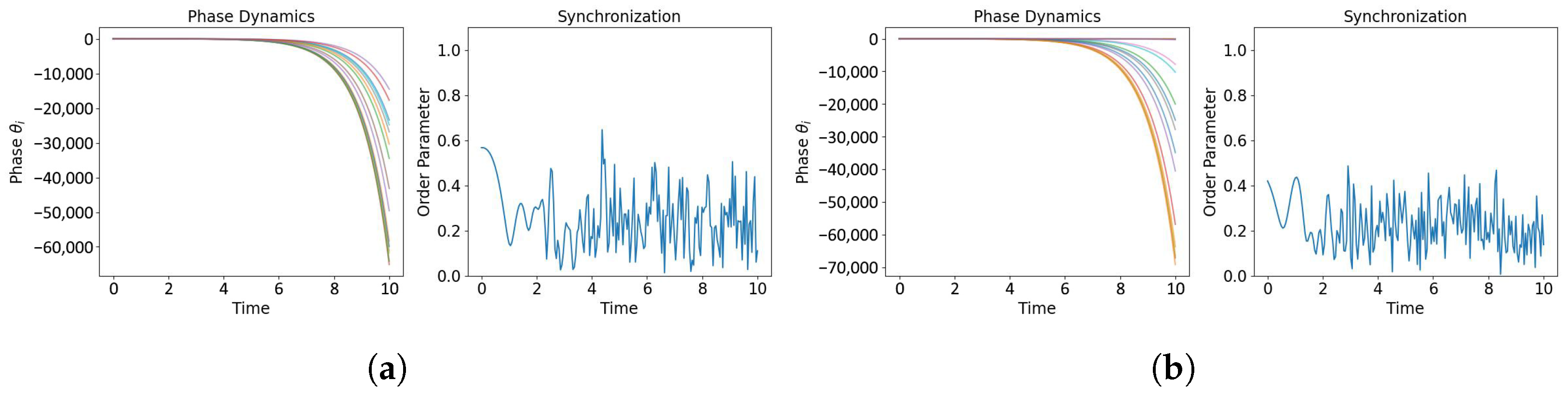
The initial voltage angle is a random vector from $[-5,5]$. The initial phase angle is sampled from a Logistic map to generate highly dispersed initial phase angles. We introduce the outlier value to prevent the system from reaching synchronization prematurely, as synchronization can significantly interfere with structural identification [33,34]. Specifically, we multiply an outlier parameter with the logistic map during the generation of initial values. We present the order parameter in sampling time period to quantify the level of synchronization in Figure 3. The outlier value is selected from $[3.5,4]$.

4.2. System Structure

Given the initial conditions, we can simulate the trajectories by solving Equation (21) by RK4 method. The time step is set to 0.01 in the RK4. By default, training and validation trajectories takes length 49 while test trajectories continue for another 20 time steps. We explicitly hard-coded the first edge type as a “non-edge”, i.e., no messages are passed along edges of this type. The MLPs have hidden and output dimensions of 256. The overall input/output dimension of our model is 2 for the Kuramoto model experiments. During training, we use teacher forcing in every 10th time step (i.e., every 10th time step, the model receives a ground truth input; otherwise, it receives its previous prediction as input). The detailed PIGNN structure is in Figure 1. To characterize the small-world [35] properties of smart grids and demonstrate the applicability of our method to diverse network topologies, we employ two distinct small-world networks. Small-world networks are characterized by high clustering coefficients and short average path lengths. We simulate two networks with $N\in \{10,20\}$ nodes, representing the small world network structure in Figure 4. The generator nodes are connected by a global connection strength of 0.01. We implement the classical Watts–Strogatz model using the NetworkX library [36]. The network parameters are as in

Table 1. The small world parameters of synthetic networks.

Node Number	Neighbors Number	Rewire Rate
10	4	0.3
20	6	0.4

.

4.3. Physic Information

According to Equation (21), we will derive the automatic differentiation information for the Kuramoto system. We dnote

$$\begin{array}{c}\hfill g({\dot{\omega }}_i,{\omega }_i)={\displaystyle \frac{1}{K}}(M_i{\dot{\omega }}_i-P_i+D_i{\omega }_i).\end{array}$$

(22)

Then, we have

$$\begin{array}{c}\hfill AD(({\theta }_i,{\omega }_i),PGINN(({\theta }_i,{\omega }_i),\varphi ))={\displaystyle \frac{\partial g({\dot{\omega }}_i,{\omega }_i)}{\partial sin({\theta }_j-{\theta }_i)}}.\end{array}$$

(23)

In PIGNN training, $g(·,·)$ does not directly depend on the variable $sin({\theta }_j-{\theta }_i)$ in PyTorch’s automatic differentiation. Therefore, we introduce an intermediate variable ${\theta }_j-{\theta }_i$, and obtain the AD information as follows:

$$\begin{array}{c}\hfill AD(({\theta }_i,{\omega }_i),PGINN(({\theta }_i,{\omega }_i),\varphi ))={\displaystyle \frac{\partial g({\dot{\omega }}_i,{\omega }_i)}{\partial ({\theta }_j-{\theta }_i)}}·{\displaystyle \frac{\partial ({\theta }_j-{\theta }_i)}{\partial sin({\theta }_j-{\theta }_i)}}\end{array}$$

(24)

Here, ${\dot{\omega }}_i$ is from the teacher forcing ${\displaystyle \frac{\omega -\omega }{\Delta t}}$ (i.e., the ground truth of next time step).

4.4. Experimental Results

We compare our model with the state-of-the-art structure reconstruction method and evaluate it on the two Kuramoto systems with node size 10 and 20 both in the trajectory prediction and structure reconstruction. To demonstrate our method’s sample efficiency as stated in Section 3.3.2, we conduct comparative Mean Squared Error (MSE) tests across different models with varying sample quantities.

Table 2. The state prediction MSE for 20 prediction steps with node size 20.

Sample Size	Static	LSTM (Single)	LSTM (Joint)	PISI (Local)	PISI (Global)
Node Size 20
50 K	2.26	1.35	2.24 × ${10}^{-1}$	7.34 × ${10}^{-1}$	1.56 × ${\mathbf{10}}^{-\mathbf{1}}$
60 K	1.87	8.94 × ${10}^{-1}$	5.11 × ${10}^{-1}$	6.25 × ${10}^{-2}$	4.31 × ${\mathbf{10}}^{-\mathbf{2}}$
70 K	1.13	1.57 × ${10}^{-1}$	2.49 × ${\mathbf{10}}^{-\mathbf{2}}$	7.13 × ${10}^{-2}$	2.57 × ${10}^{-2}$
90 K	9.88 × ${10}^{-1}$	9.86 × ${10}^{-2}$	2.46 × ${10}^{-2}$	4.83 × ${10}^{-2}$	2.41 × ${\mathbf{10}}^{-\mathbf{2}}$
100 K	4.01 × ${10}^{-1}$	9.20 × ${10}^{-2}$	2.21 × ${\mathbf{10}}^{-\mathbf{2}}$	4.31 × ${10}^{-2}$	2.29 × ${10}^{-2}$

compares the state prediction MSE of single LSTM, joint LSTM [37], the global PISI, the local PISI, and static under different sample sizes for systems with 20 nodes. The best result under each sample size is highlighted in bold. We run all the methods with $T=50$ time steps, and predict the following 20 time steps. The LSTM baseline labeled “single” employs separate but weight-shared LSTMs for each object. The alternative “joint” approach concatenates all state vectors as input to a single LSTM trained for simultaneous multi-object state prediction. The global PISI corresponds to the two message passing GNN in Equation (10). The local PISI corresponds to the classic GNN in Equation (8). The static baseline uses ${\mathbf{u}}^{t+1}={\mathbf{u}}^t$. In RK4PINN [10], a total of 6K samples are required for estimating three parameters in the Lorenz system. We set the minimum sampling size to 50 K, as the neural relational inference (NRI) [14] model reconstructs 10-node graphs with only graph information at this sample size. The results demonstrate that our method exhibits advantages when the sample size is limited. When the sample size is over 60 K, our global PISI reaches 0.01 level MSE.

Table 3. The state prediction MSE for 100 K sample size with 20 nodes.

Prediction Steps	Static	LSTM (Single)	LSTM (Joint)	PISI (Local)	PISI (Global)
Node Size 20
1	5.75 × ${10}^{-3}$	1.41 × ${10}^{-3}$	7.23 × ${10}^{-4}$	9.96 × ${10}^{-4}$	4.80 × ${\mathbf{10}}^{-\mathbf{4}}$
10	9.33 × ${10}^{-1}$	9.27 × ${10}^{-2}$	4.41 × ${\mathbf{10}}^{-\mathbf{3}}$	6.90 × ${10}^{-2}$	8.71 × ${10}^{-3}$
20	4.25 × ${10}^{-1}$	8.56 × ${10}^{-2}$	2.58 × ${10}^{-2}$	5.59 × ${10}^{-2}$	2.26 × ${\mathbf{10}}^{-\mathbf{2}}$

studies the MSE of state prediction with node size 20 and sample size 100 K when the prediction steps are increasing. For one-step prediction, the joint LSTM, local PISI, and the global PISI reaches a 1 × ${10}^{-4}$ level. Our global PISI shows advantages for prediction steps 1 and 20.

For the structure reconstruction accuracy, we compare our PISI with correlation LSTM, the correlation path method, and the NRI in

Table 4. The structure reconstruction accuracy (in %).

	Correlation LSTM		Correlation Path		NRI		PISI (Global)
Node Size	10	20	10	20	10	20	10	20
50 K	52.4	50.6	57.4	54.0	96.1	95.7	96.3	96.2
60 K	52.7	51.2	57.1	54.2	96.3	95.7	96.2	96.3
70 K	52.5	51.5	57.9	54.9	96.3	95.8	96.4	96.4
80 K	52.0	51.4	57.9	54.8	96.4	95.6	96.3	96.3
100 K	53.1	51.8	57.8	54.8	96.4	95.8	96.5	96.3

with node sizes of 10 and 20 and sample size increasing. The final accuracy is the average over all batches, and the accuracy for each batch is calculated as ${\displaystyle \frac{1}{N\times N}}{\sum }_{i,j=1}^N\delta ({\tilde{A}}_{ij},A_{ij})$ with $\delta (·,·)$ the Kronecker delta function. The correlation LSTM method trains an LSTM network with shared parameters [38] to individually model each trajectory, computes correlations between the final hidden states, and generates an interaction matrix through thresholding. The correlation path method estimates the interaction graph by applying thresholding to the correlation matrix between trajectory feature vectors. Table 4 demonstrates a slight improvement in reconstruction accuracy as the sample size increases. Our global PISI demonstrates superior performance with 20 nodes, outperforming state-of-the-art methods by 0.5% with sample size 100 K.

Table 5. The structure reconstruction accuracy with three outlier values and evolution time steps for the 20 nodes network.

	Outlier Value			Evolution Time Step
Method	0.5	3	3.5	10	50	100
Correlation LSTM	32.4	32.8	62.7	29.4	62.7	62.5
Correlation Path	31.6	31.0	62.3	28.6	62.3	63.0
NRI	50.7	54.7	96.9	49.3	96.9	97.9
Ours	50.5	53.9	97.8	50.7	97.6	97.7

investigates the impact of outlier values and the dynamic evolution time step on the recognition results. As stated in Section 4.1, the system synchronization has significant drawbacks for network structure identification. We set the outlier values 0.5, 3, and 3.8 with an evolution time step of 50. When the outlier value is 0.5, the network achieves synchronization at time step 10. The considered four methods all fail to reconstruct the structure. When the outlier reaches 3.5, the system fails to achieve synchronization. Compared to baseline methods, our approach shows improved reconstruction accuracy. The evolution time scales linearly with the sampling size, where the scaling factor is the sampling interval. We set it to 10, 50, and 100 to maintain consistency with the state prediction experiment.

4.5. Ablation Studies

Finally, we set ${\alpha }_1=100$, ${\alpha }_2=1$, and ${\alpha }_3=100$ to balance the loss terms for different tasks. In this subsection, we will first perform an ablation study on weight parameters ${\alpha }_1$, ${\alpha }_2$, and ${\alpha }_3$ to verify the effect of each loss term in Equation (19). Among the three weight parameters, ${\alpha }_1$ and ${\alpha }_3$ capture the structure importance. ${\alpha }_2$ captures the trajectory importance. 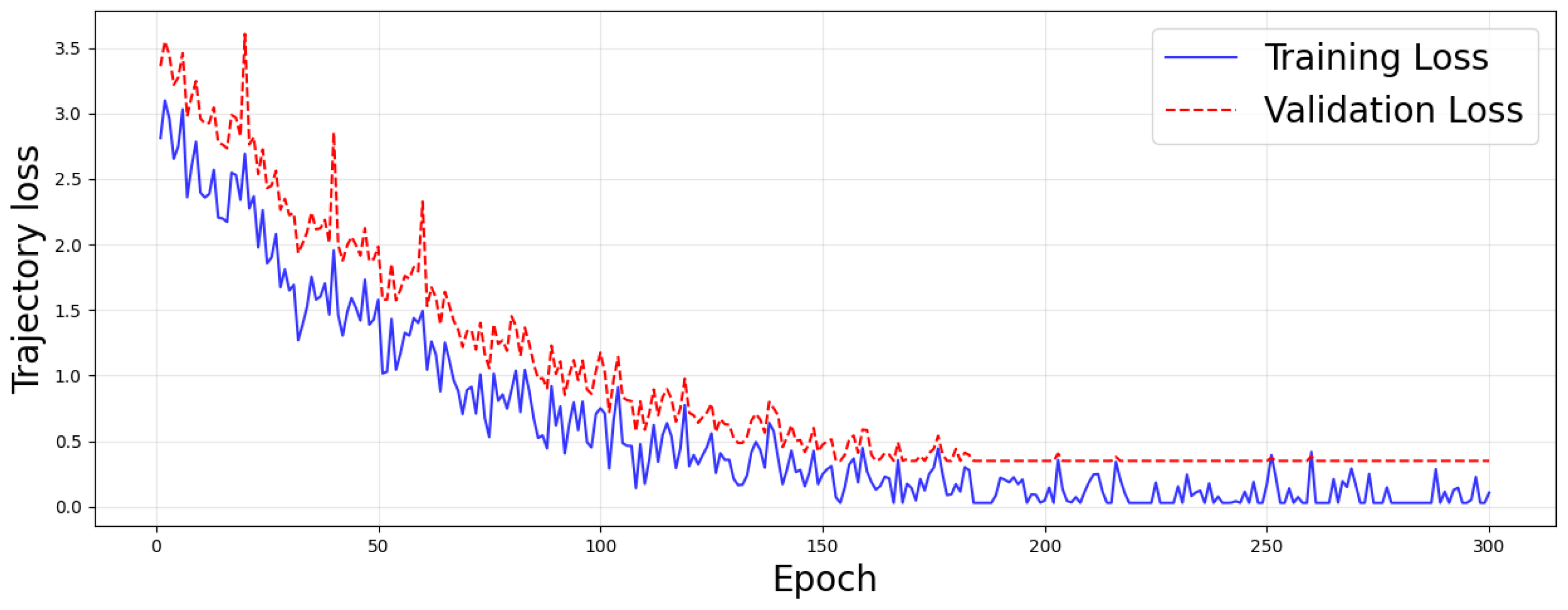Increasing the weight parameter ${\alpha }_2$ accelerates the convergence of loss term of trajectory. Figure 5 shows the trajectory loss convergence with ${\alpha }_2=1$, ${\alpha }_1=100$, and ${\alpha }_3=100$.

When ${\alpha }_1=0$, PISI degenerates into a structure identification algorithm that does not rely on physical information but depends on the graph neural network and solver iteration. In

Table 6. The structure reconstruction accuracy with increasing ${\alpha }_1$ for node size 10 and 20.

${\mathit{\alpha }}_1$	Accuracy
	Node Size 10	Node Size 20
0	52.9	52.6
100	96.1	96.3
500	57.7	57.4

, we investigate the impact of physical information on structural identification for networks with $N\in \{10,20\}$. It can be observed that when ${\alpha }_1=0$, the structural identification accuracy decreases. This is due to insufficient utilization of physical information from the adjacency matrix. When ${\alpha }_1$ is too large (relative to ${\alpha }_2$), the structural identification accuracy also declines, as excessive physical information loss leads to slower convergence in fitting node states.

5. Conclusions

In this study, we propose a physical information-based solver-interactive network structure reconstruction method. The PISI effectively predicts the system trajectory. Furthermore, it is able to output the system structure adjacent matrix. The core concept of PISI lies in employing neural networks to approximate the unknown dynamic functions during the solution process of dynamic systems, thereby integrating physical information, system structure, and trajectory data. Specifically, PISI comprises two main modules: the structure reconstruction PIGNNs and the dynamic solver RK4. For the input observation, the RK4 modular evolves the state, thus providing the trajectory loss for PIGNN. At the end of each RK4 iteration, we obtain a trajectory loss. PIGNN provides the estimated structure for each RK4 stage. We employ four parameter-shared PIGNNs to approximate the unknown dynamic function in RK4. The four PIGNNs are trained end-to-end in a RK4 iteration. Each PIGNN internally consists of a global GNN. The global GNN consists of node-to-edge and edge-to-node message passing operations to enable more efficient exploitation of global structural information. Each information channel is processed by an MLP. Finally, the PISI loss function comprises three components: trajectory loss from RK4 output, physics-informed loss derived from physical constraints at each RK4 stage, and estimated structural loss for stage-wise topology reconstruction. We evaluate our method in two Kuramoto systems. Compared to the baseline, the global PISI shows advantage in the trajectory prediction and the structure reconstruction. Ablation studies demonstrate that the balance among the three loss terms significantly impacts recognition performance.