Abstract
This work presents the results of a research study focused on the development and evaluation of an algorithmic optimal control framework for energy-efficient operation of screw compressors in smart power systems. The proposed approach is based on the Pontryagin maximum principle (PMP), which enables the synthesis of a mathematically grounded regulator that minimizes the total energy consumption of a nonlinear electromechanical system composed of a screw compressor and a variable-frequency induction motor. Unlike conventional PID controllers, the developed algorithm explicitly incorporates system constraints, nonlinear dynamics, and performance trade-offs into the control law, allowing for improved adaptability and energy-aware operation. Simulation results obtained using MATLAB/Simulink confirm that the PMP-based regulator outperforms classical PID solutions in both transient and steady-state regimes. Experimental tests conducted in accordance with standard energy consumption evaluation methods showed that the proposed PMP-based controller provides a reduction in specific energy consumption of up to 18% under dynamic load conditions compared to a well-tuned basic PID controller, while maintaining high control accuracy, faster settling, and complete suppression of overshoot under external disturbances. The control system demonstrates robustness to parametric uncertainty and load variability, maintaining a statistical pressure error below 0.2%. The regulator’s structure is compatible with real-time execution on industrial programmable logic controllers (PLCs), supporting integration into intelligent automation systems and smart grid infrastructures. The discrete-time PLC implementation of the regulator requires only 103 arithmetic operations per cycle and less than 102 kB of RAM for state, buffers, and logging, making it suitable for mid-range industrial controllers under 2–10 ms task cycles. Fault-tolerance is ensured via range and rate-of-change checks, residual-based plausibility tests, and safe fallbacks (baseline PID or torque-limited speed hold) in case of sensor faults. Furthermore, the proposed approach lays the groundwork for hybrid extensions combining model-based control with AI-driven optimization and learning mechanisms, including reinforcement learning, surrogate modeling, and digital twins. These enhancements open pathways toward predictive, self-adaptive compressor control with embedded energy optimization. The research outcomes contribute to the broader field of algorithmic control in power electronics, offering a scalable and analytically justified alternative to heuristic and empirical tuning approaches commonly used in industry. The results highlight the potential of advanced control algorithms to enhance the efficiency, stability, and intelligence of energy-intensive components within the context of Industry 4.0 and sustainable energy systems.
1. Introduction
In today’s rapidly changing global industrial landscape, compressed air systems are a critical factor in the energy efficiency of plants. It is estimated that around 10% of the entire electricity consumed in industry is used in the production and distribution of compressed air, with the energy efficiency of these systems often being equal to only 85–94%, which translates into losses of 6% to 15% [1,2]. Such inefficiencies are directly translated into increased operating costs, an increased carbon footprint, and more difficult green audits [3]. At the same time, the new era of Industry 4.0 (defined as the digital transformation of industrial processes through cyber-physical systems, IIoT, AI, and big data technologies) places high demands on the reliability, robustness, adaptability, and ‘smartness’ of compressor system control [4]. In this study, the concept of Industry 4.0 is understood as the ongoing digital transformation of manufacturing and industrial systems, which is characterized by the integration of cyber-physical systems, the Industrial Internet of Things (IIoT), big data analytics, cloud and edge computing, and artificial intelligence into production and energy infrastructures. The main aim of Industry 4.0 is to create highly flexible, adaptive, and self-optimizing industrial processes, enabling sustainable and intelligent operation of energy-intensive equipment such as compressors. They must cope with parametric and structural uncertainties, rapid load changes, measurement noise, and real-time computing power constraints [5].
Previously proposed solutions include the classic load-unload approach (cyclic excitation and pressure relief through a storage tank). In refs. [6,7], adaptive algorithms were implemented that make it possible to achieve the optimal “switching” pressure and reduce energy consumption by 4–8% due to dynamic parameter adjustment. However, concentrated transient consumption and the need for large tank volumes make it difficult to operate sustainably, reducing the retribution effect.
An alternative to traditional methods is the active implementation of VSD/VFD (Variable Speed/Variable Frequency Drives) technologies. Field studies, including reviews from Atlas Copco, show that switching to a VSD compressor can save between 10% and 30% of energy, with savings ranging from 12% to 30% depending on consumption dynamics [8,9]. With a load reduction of up to 30%, VSD units can operate at the equivalent of 20–35% of power, which dramatically reduces energy costs. However, these systems require a significant capital investment, with a 15 to 30 percent higher price than that of standard fixed drives. In addition, the efficiency of VFD drops under constant load, when the efficiency of the inverter is noticeably reduced due to switching losses. These systems are also sensitive to operating conditions (high temperatures, humidity, and contamination can reduce service life and require additional maintenance costs).
In a more comprehensive approach, in the course of modeling systems with several compressors, the authors of [10,11] show that optimizing their operating strategy can reduce energy consumption by 5–32%, and the use of lookup tables provides stable savings of about 12%. This approach is based on a thorough experimental determination of the characteristics of compressors and the development of specific operating modes. However, a significant disadvantage is the need to collect large amounts of data and create accurate maps of compressors, as well as regular reconfiguration when production conditions change, which reduces the operational efficiency of the method.
One of the most innovative areas is the use of Model Predictive Control (MPC) in HVAC and refrigeration systems. For example, studies by Sciencedirect and MDPI have demonstrated that MPC can provide energy savings in the range of 12–40% compared to traditional control methods [12,13]. For example, in one field experiment, MPC saved up to 40% of the energy of the HVAC system, and improved temperature control was achieved with an accuracy of ±0.1 °C and humidity of ±0.13 g/kg of dry air, while reducing energy costs by 22.5%. However, in an industrial environment, MPC is hampered by compute limitations, i.e., the complexity of the model and the need to update real-time optimizations require high controller power or pre-calculations, which limits widespread adoption.
Another branch of the research, related to load-shifting and sequencing, has shown efficacy in refrigeration units. The authors achieved savings of up to 20% due to pre-cooling and optimization of the order of compressor switching [14]. But this approach is highly dependent on the thermal inertia of the systems, which reduces its applicability for air compressors, the dynamics of which are much higher.
Modern mathematical approaches, including optimal control with PDE constraints, Physics-Informed Neural Networks (PINNs), and reduced-order models, have the potential to create comprehensively validated control [4]. However, they require advanced computing power and complex simulations, which makes them inapplicable in conditions of time and resource constraints, especially in real time [12].
At the same time, methods of online reverse optimization with on-the-fly adaptation of models (Gaussian Process Regression plus Feedback Optimization) are being actively developed, allowing for reducing the effect of modeling errors from +5% losses to ~0.8%, almost reaching the optimum under different loads [4,5]. This is especially important in light of unstable operation and uncertain temperatures and humidity [15].
While the Pontryagin maximum principle (PMP) is indeed a foundational method in optimal control theory, its practical application to complex nonlinear industrial systems, such as screw compressor drives, remains a significant challenge. The scientific novelty and contribution of this work are not in the theoretical derivation of PMP itself, but in its innovative adaptation and implementation for a specific electromechanical system with the following advancements:
- -
- Development of a comprehensive nonlinear state-space model of the screw compressor and frequency-controlled induction motor pair, suitable for PMP-based optimization with an energy minimization criterion.
- -
- Derivation of an analytically justified optimal control law that explicitly accounts for real-world constraints on the control signal (frequency converter input) and system states, ensuring physical implementability.
- -
- Resolution of the practical issue of real-time computation on resource-constrained hardware. The structure of the synthesized regulator is compatible with industrial Programmable Logic Controllers (PLCs), moving beyond theoretical simulation into the realm of industrial application.
Comprehensive validation through high-fidelity MATLAB/Simulink simulation and, crucially, experimental testing on a physical compressor setup demonstrates significant energy savings (12–18%) compared to industry-standard PID control under various load disturbances. This experimental proof is a key step beyond purely theoretical or simulation-based studies often found in the literature. Therefore, this work bridges the gap between advanced control theory and industrial practice, offering a tangible energy-efficient solution for a common and energy-intensive industrial system.
The considered approaches demonstrate significant progress in theory and modeling, but they have inherent limitations: static tables, high capital cost, dependence on conditions, complexity of implementation, the need for high computing power, as well as a lack of adaptability and stability in the face of noise and rapid change. An optimal regulator based on the Pontryagin maximum principle allows combining theoretical rigor, energy efficiency, and practical feasibility. The fact is that this approach is based on a clear analytical deduction of the conditions of optimality, where the so-called Hamiltonian is formed for each moment of time. And then an optimal control is selected that maximizes (or minimizes) this Hamiltonian, taking into account all dynamic and technological constraints [16,17,18].
This study is aimed at solving the problem of excessive energy consumption of screw compressor units through the development and implementation of an optimal pressure regulator that provides minimal energy costs while maintaining the stability and reliability of the system in real time. The scientific novelty of this study lies in the development and practical substantiation of the optimal regulator for a screw compressor using the Pontryagin maximum principle. For the first time, a complex mathematical model of “screw compressor—induction motor with frequency control” was implemented, presented in the form of a system of nonlinear differential equations of the state, suitable for optimization by the criterion of minimizing the total energy spent on the compression process [19]. Particular attention is paid to the application of theoretically based control in real industrial conditions: the model is adapted for the integration with real-time systems and programmable logic controllers (PLC), which makes the proposed solution relevant for intelligent distributed energy systems (smart grid) and autonomous compressor stations. The proposed structure of the regulator allows considering restrictions on regulated variables, as well as dynamic deviations and external disturbances, which ensures the stability and reliability of the entire system operation under variable load conditions [20].
The purpose of this work is to develop and verify an energy-efficient pressure control system at the outlet of a screw compressor, which provides minimal energy consumption in various operating modes and external disturbances, with the possibility of integration into intelligent automated complexes. In contrast to traditional PID controllers, the proposed approach provides for the synthesis of the regulator based on a strict mathematical apparatus of optimal control and its approbation in a closed loop, taking into account physically realizable constraints.
In addition, the developed optimal control system can be expanded through the use of modern artificial intelligence approaches, including reinforcement learning and surrogate modeling. This creates the basis for the construction of hybrid regulators capable of self-learning and adaptation to a dynamically changing load structure. In view of this, the presented approach organically fits into the direction of intelligent control of power electronics, finding application in distributed energy networks, smart microgrids, and digital twins of electric drive systems. Compared to previously applied methods such as conventional PID control, variable-speed drive solutions, lookup-table-based optimization, and even advanced Model Predictive Control (MPC), the proposed algorithm offers several key advantages. Unlike PID controllers, which are often tuned empirically and exhibit overshoot and oscillations under varying loads, the Pontryagin-based regulator is derived from rigorous optimality conditions, ensuring analytical correctness and stability. In contrast to VSD/VFD technologies, which primarily improve efficiency at the hardware level but require significant capital costs, our approach achieves energy savings through control logic without additional equipment. While MPC is powerful, it faces limitations due to real-time computational demands in industrial environments, whereas the PMP-based algorithm provides a closed-form optimal control law suitable for PLC implementation. Finally, unlike static lookup tables or heuristic sequencing strategies, the developed regulator inherently adapts to changing loads and uncertainties without the need for reconfiguration. These features highlight the novelty of our contribution: a mathematically justified, energy-efficient, and practically feasible control algorithm that bridges the gap between theoretical rigor and industrial applicability.
2. Methods and Materials
2.1. Experimental Setup and Data
In this study, the simple PID controller and the Pontryagin maximum principle for controlling screw compressors were compared based on the following factors:
- In Central Asia, compressor stations often suffer from irregular maintenance and parameter drift after repairs. Predictive controllers such as MPC, although effective in laboratory conditions, are very sensitive to model mismatch and can quickly fail when compressor parameters change. On the other hand, the PMP-based controller is more robust to such changes, ensuring stable operation even with a temporary decrease in efficiency. This characteristic makes PMP a safer and more sustainable choice for long-term implementation in these regions.
- Many compressor stations in Kazakhstan still use PID controllers. Replacing them with an MPC system would require significant staff retraining and significant computing resources. In contrast, PMP offers a rigorous mathematical control law that can be implemented on industrial PLCs with minimal modification of the existing infrastructure, simplifying the modernization process.
- While PMP does not always achieve the maximum theoretical energy savings associated with predictive AI methods, it does provide a trade-off of up to 18% energy savings, any overshoot, and increased reliability without the operational risks associated with predictive approaches. This balance is critical in the industrial context under consideration.
Fault detection and tolerance (FDT). Pressure, current, and voltage signals are subjected to range checks, rate-of-change gates, and residual-based plausibility tests against a first-order observer. Fault flags are raised if out-of-range readings persist for >100 ms. The variance within a sliding 1 s window falls below a stuck-at threshold while the command changes. Alternatively, the residual exceeds a z-score threshold for >50 ms. In the case of a confirmed fault, the controller performs a bumpless transfer to a safe fallback (baseline PID with conservative gains or a torque-limited speed hold), limits the command slew rate, and opens protective logic (e.g., relief or shutdown) if pressure deviates from admissible bounds. Missing samples are bridged for ≤200 ms by last-value hold with the clamped slew. This was achieved using the following sensors/channels: SITRANS P200 4–20 mA (Siemens AG, Berlin, Germany), NI-DAQ (National Instruments Corporation, Austin, TX, USA), VFD (Siemens AG, Berlin, Germany).
Scalability to other rotating machinery. The regulator relies on a state-space description and an energy-minimizing Hamiltonian that are not specific to screw compressors. For other VFD-driven rotors (centrifugal pumps, axial/radial fans), the same synthesis applies once the plant is represented by its standard flow–head–power relationships and actuator/safety constraints. In pumps/fans, the Qout flow scales approximately with n speed, head/pressure with P, and the shaft power indicator with N, while the closed-loop output can be either pressure/head or flow depending on the process. In practice, the mapping is the measured y∈{P, n, Qout} output, the manipulated u = f input (VFD frequency), or the equivalent torque limit. Constraints include actuator bounds, anti-surge/anti-stall or anti-cavitation margins, minimum-flow recirculation, and thermal/current limits. With this substitution, the PMP-based structure (Figure 1) and its discrete-time implementation on PLC remain unchanged; only the plant matrices, constraint set, and operating objective are re-identified. Preliminary simulations on representative pump/fan models indicate qualitative behavior consistent with the compressor case (smoother power draw, reduced overshoot), supporting transferability of the method; detailed results will be reported in a follow-up paper. The present manuscript focuses on the screw-compressor case to keep the scope compact; extended cross-machine results are planned as separate publications.
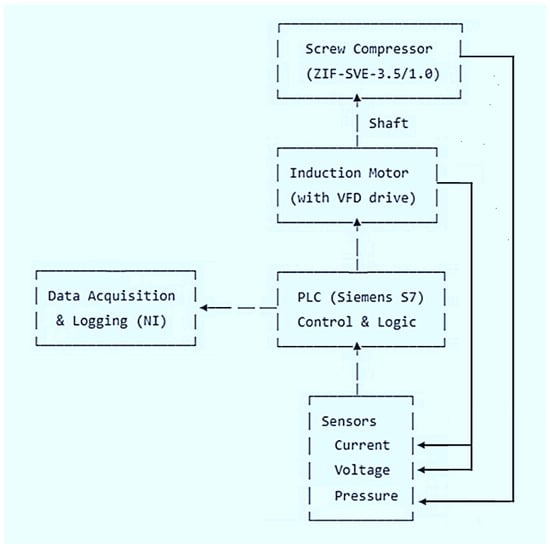
Figure 1.
A schematic diagram of the experimental setup.
Real-time PLC implementation. The closed-loop regulator was coded in a discrete-time form with a Ts = 2–10 ms task cycle. The implementation follows the structure in the Figure 1, avoiding an explicit online integration of the ODEs costate by using an equivalent algebraic form with first-order filters for smoothing (τ = 0.1 s). Per cycle, the algorithm performs ~103 arithmetic operations (additions, multiplications, a few saturations and comparisons). The RAM budget comprises state and observer vectors (<2 kB), calibration/scaling constants (<2 kB), and optional ring buffers for 1 s of 1 kHz logging (≤64 kB). Total working memory remains below 102 kB. The code is IEC 61131-3/embedded-C friendly and requires only single-precision math. IO handling and safety interlocks are executed in the same task (Table A1 and Table A2).
Within the framework of this study, a comprehensive methodology for experimental and numerical analysis was implemented, aimed at developing an energy-efficient control algorithm for a screw compressor integrated into a gas compressor station. The entire range of works was based on the combination of engineering modeling, analytical methods of optimal control, and computer simulation tools in the MATLAB/Simulink R2020b environment. The key element of the methodology was the comparison of traditional PID control and the developed optimal regulator based on the Pontryagin maximum principle, followed by an assessment of their energy efficiency under identical conditions. This approach allowed for scientific rigor while maintaining practical applicability to real-world industrial automation systems.
The physical object of the study was the ZIF-SVE-3.5/1.0 (JSC “Zavod imeni Frunze”, Samara, Russia) screw compressor unit equipped with a 5AM 315 M2 VEMZ (Votkinsky Electromechanical Plant, Votkinsk, Russia) induction motor connected to the compressor rotor through a coupling. The compressor is an oil-injected unit with a maximum output pressure of 0.7 MPa and a capacity of up to 22 m3/min. The engine is made using an explosion-proof design and has a rated power of 200 kW at a speed of 2975 rpm. These technologies were chosen for their prevalence in real-world industrial environments, as well as their compatibility with programmable logic controllers (PLCs), which was critical for further translating the solutions to a real-time platform. The ZIF-SVE-3.5/1.0 screw compressor was selected for this study because it is representative of medium-capacity oil-injected screw compressors that are widely used in industrial plants and gas compressor stations. Its technical parameters (capacity of up to 22 m3/min, rated power of 200 kW) correspond to typical units applied in distributed energy systems, which makes it an appropriate benchmark for both laboratory testing and industrial validation. In addition, the availability of this unit on our laboratory bench and the SCS1 gas compressor station enabled direct experimental verification, ensuring that the developed model reflects realistic operating conditions.
The numerical simulation results were validated against experimental measurements both on the laboratory bench and at the industrial SCS1 gas compressor station. In the experiments, outlet pressure, shaft speed, and electrical power consumption were recorded under step disturbances and load variations identical to those used in the simulation scenarios. A direct comparison showed that the deviation between simulated and measured steady-state pressure did not exceed 3%, while the difference in active power consumption remained within 5%. The transient response characteristics (settling time and overshoot) were qualitatively consistent, confirming that the proposed model accurately captures the real system dynamics.
Importantly, the proposed optimal control algorithm is not limited to this specific model. Since it is derived from the general nonlinear state-space representation of a screw compressor coupled with a frequency-controlled induction motor, the approach is transferable to other compressor units of different capacities and manufacturers. The required adaptation is limited to parameter identification (such as volumetric efficiency, leakage coefficients, and motor inertia), while the structure of the Pontryagin-based regulator remains unchanged. This ensures compatibility of the algorithm with a broad class of screw compressors and even related rotating equipment, including centrifugal compressors, pumps, and fans.
In addition to numerical modeling, the experimental work was conducted to test the developed model at a real SCS1 gas compressor station of the “C” route of the Kazakhstan-China gas pipeline (near the village of Baspandy, South Kazakhstan region). The tests were performed on compressor units with the parameters comparable to the design model (capacity of up to 516,750 m3/h, capacity of up to 30–40 MW). In the course of testing, the regulator demonstrated stable pressure maintenance and a decrease in power consumption peaks compared to traditional control methods. The experimental data obtained were used to validate the adequacy of the mathematical model and confirm its applicability for industrial installations of a similar type.
The development of the mathematical model began with the formalization of the dynamics of a screw compressor. The model uses assumptions about the ideality of the gas, the equality of temperatures at the inlet and the outlet of the compressor, the identity of the geometry of the master and slave rotors. The compressor performance was determined based on the volume of integrator cavities passing through the exhaust port per unit of time, taking into account losses due to leaks, internal friction, and imperfect screw shapes. The dependence of the outlet pressure on the gas flow rate and shaft speed was derived, which made it possible to linearly link the speed of the motor and the operating parameters of the compressor. The induction motor was described by a simplified model, which considered its moment of inertia, nominal slip, motor torque, and the frequency converter factor. The model included the calculation of shaft torque, dynamic momentum, and the dependence of speed on the control signal at the input of the inverter. Time constants and mechanical parameters were also calculated to evaluate transients.
The purpose of using the mathematical apparatus of optimal control was to build a regulator that minimizes the total energy consumed by the engine in the process of gas compression. To do this, the Pontryagin maximum principle was used, which allowed formulating the problem in the form of a Cauchy problem with built-in control constraints. Optimization was carried out in a state where the input control signal is limited to a given interval, and the system itself is represented in the form of equations of state, with the inclusion of the conjugate system required to calculate the functional gradient. A Hamilton function was constructed, including phase variables, conjugate variables, and a control variable. Based on the maximum conditions, the optimal control structure was obtained, and equations were derived for calculating the control signal in real time. This made it possible to formalize the structure of an optimal regulator suitable for digital implementation. The resulting solution allowed considering the restrictions on the control action and compensating for external disturbances in real operating conditions.
To assess the effectiveness of the proposed approach, a modeling system was created in MATLAB/Simulink. First of all, a model of a technological facility with a PID controller was built, whose parameters were selected on the basis of standard methods of adjustment by transient response. Then a similar model was implemented with an optimal regulator based on the Pontryagin principle. In both cases, a scheme for measuring the consumed active power was built into the system using a three-phase current and voltage measurement unit and an active and reactive power calculation unit.
Particular attention was paid to the synthesis of a closed-loop system with pressure feedback provided by a pressure sensor with a current output signal of 4–20 mA, which corresponds to the range of 0–1 MPa. For the correct interpretation of the output signal, a scale factor was used associated with the calibration of the analog input of the PLC. This allowed implementing a physically meaningful relationship between the control signal and the output parameters of the compressor, as well as to evaluate the stability, control time and steady-state error for both types of regulators.
The mathematical transformations carried out within the model included both analytical calculations (linear transformation of equations of motion, calculation of derivatives, compilation of a conjugate system) and numerical integration of equations of state. The use of coordinate systems, the reduction in second-order equations to first-order equations, and the transition to the normal form of the system made it possible to effectively apply the Pontryagin method and obtain optimal control in the form of a closed function of the state of the system [21]. Experimental modeling was accompanied by the introduction of perturbations in the form of pressure jumps or changes in the control action. The reaction of the system was recorded in the form of graphs of pressure and power changes, which allowed visualizing the behavior of the system under the influence of various regulators.
To verify the mathematical model and to assess the effectiveness of the proposed control algorithm, full-scale tests were performed on a laboratory bench with a screw compressor. The functional set of the experimental bench includes:
- -
- A screw ZIF-SVE-3.5/1.0 compressor (JSC “Zavod imeni Frunze”, Samara, Russia) with a 5AM 315 M2 VEMZ induction motor (200 kW, 2975 rpm).
- -
- A Delta VFD-E frequency converter (Delta Electronics, Inc., Taipei, Taiwan) with a 0–10 V analog input and a 0–50 Hz control range.
- -
- A Siemens SITRANS P200 (Siemens AG, Berlin, Germany) pressure sensor (a 0–1 MPa range, a 4–20 mA output).
- -
- A National Instruments CompactDAQ (National Instruments Corporation, Austin, TX, USA) data acquisition module with a sampling rate of 1 kHz.
- -
- A storage receiver with a volume of 500 L for pressure stabilization.
Table 1 summarizes the main test parameters, including operating modes and disturbances.

Table 1.
Main test parameters of the screw compressor laboratory bench.
Figure 1 presents a schematic diagram of the experimental setup. Photographs of the equipment are not included due to institutional restrictions, but the schematic shows the main elements: a screw compressor unit, an induction motor with VFD, a pressure sensor (Siemens SITRANS P200, 0–1 MPa, ±0.25% F.S.), voltage and current sensors (NI CompactDAQ, ±0.5%), PLC (Siemens S7-1500) and a data acquisition system (NI DAQ). The measurement signals were sampled at 1 kHz, stored in a ring buffer, and then downsampled to 100 Hz for analysis. All sensors were calibrated before and after the campaign using certified pressure and electrical standards. The PLC provided synchronous acquisition of control inputs and outputs, ensuring accurate alignment for dynamic analysis. Missing samples (≤200 ms) were handled with the last-value hold and clamped slew.
Noise and delay modeling. To approximate industrial conditions, we extended the model with additive white Gaussian noise on measured pressure, voltage, and current channels, using sensor-typical levels (0.25% F.S. for pressure, 0.5% for electrical measurements). Additionally, input/output communication delays were modeled as a discrete-time transport lag of 1–2 PLC cycles (2–20 ms). Longer delays were also tested in simulation of up to 50 ms. These perturbations were injected in the MATLAB/Simulink environment for robustness assessment.
2.2. Validation Protocol and Energy Measurement Methodology
To ensure the validity of the obtained results, the methodology of energy consumption measurement was aligned with industrial standards. In particular, the assessment followed the guidelines of ISO 1217:2009 (Displacement compressors—Acceptance tests) [22], which specifies procedures for measuring power input, pressure, and flow rate, as well as the NREL Compressed Air Evaluation Protocol (2021). During experimental tests at the SCS1 compressor station, real-time measurements of pressure, shaft speed, and electrical active power were obtained using calibrated Siemens SITRANS sensors and NI CompactDAQ modules. The accuracy of active power measurements was within ±2%, which is consistent with the tolerance recommended in ISO 1217 [22]. This ensured that the experimental validation of the developed regulator is directly comparable with industry-standard performance tests of compressor units.
To enhance the reliability and industry relevance of the reported energy savings data, the testing procedure was aligned with the core principles of internationally recognized guidelines for assessing the efficiency of compressed air systems, such as those outlined in ISO 11011:2013 [Compressed Air—Energy Efficiency—Assessment] and the U.S. Department of Energy’s Compressed Air Challenge best practices [23,24].
The key performance indicator (KPI) for energy efficiency was the specific power consumption, defined as the active electrical power input (Pactive) required to deliver a unit of compressed air flow (Qout), effectively measured in kW/(m3/min). This metric was chosen for its direct relevance to operational costs and its prevalence in industry benchmarks.
The experimental setup described above was adapted for direct measurement of:
- -
- Active electrical power (Pactive) measured at the input terminals of the frequency converter using a certified three-phase power analyzer (Fluke 434 Series II—Fluke Corporation, Everett, WA, USA), ensuring accurate capture of real power consumption, inclusive of drive losses.
- -
- The volumetric flow rate (Qout) measured at the compressor outlet using a calibrated thermal mass flow meter (Siemens SITRANS FM MAG 6000) positioned after the receiver to account for stabilized flow.
The output pressure was maintained constant at the required setpoint (0.7 MPa) for both control strategies during comparative tests to ensure a fair comparison. The reported energy savings of 12–18% represent the average reduction in the specific power consumption (Pactive/Qout) achieved by the PMP-based controller compared to the optimized PID controller across multiple load-change cycles. This methodology provides a reproducible and industry-accepted basis for claiming energy efficiency improvements.
Field validation was organized in a stepwise manner to ensure both practical feasibility and statistical representativeness. The campaign lasted four weeks in total and included 1–2 days of commissioning and calibration tests, 7 consecutive days of continuous daily operation with controlled step disturbances, and a 3-week extended phase covering diverse operational patterns, including weekday/weekend differences and alternating PID vs. optimal control (A/B testing). This protocol yielded more than 20 operational days of high-quality data, sufficient for robust statistical analysis of energy savings and stability. To emulate seasonal and extreme conditions without the need for months-long testing, the protocol included naturally different ambient windows (+15…+35 °C, day/night cycles), accelerated scenarios with extended load and pressure sweeps, and digital replay of measured logs through MATLAB/Simulink with ±10–20% parameter perturbations. A longer-term seasonal campaign (3–6 months) is planned as follow-up work.
Economic and lifetime considerations. While the main scope of this study is on control-system design and validation, a preliminary techno-economic assessment was performed. Assuming an average industrial electricity price of 0.08–0.12 USD/kWh and the observed energy savings of 12–18%, the payback period for implementing the optimal regulator (software license, PLC integration, engineering) is estimated at 6–18 months for 200–500 kW units running >4000 h/year. Maintenance costs are comparable to baseline PLC/PID systems, as the regulator uses the same sensors and hardware. In addition to direct energy savings, the smoother dynamic response and reduced overshoot decrease mechanical stress on couplings, bearings, and seals, and reduce thermal cycling in motor windings and power electronics, which can reasonably extend component lifetimes. Although a quantitative life-cycle cost (LCC) analysis is beyond the scope of this paper, these preliminary figures indicate a favorable return on investment.
3. Mathematical Description of the Control System
At the first stage, a mathematical model of an electric drive system with a screw compressor was made, and a subsequent synthesis of the optimal control system was carried out. The main goal is to minimize active power consumption while maintaining a high-quality dynamic response. As part of numerical experiments, the behavior of the system is simulated with two different control strategies: a classical PID regulator and a regulator based on the Pontryagin maximum principle. As a result of the comparison, the effectiveness of the proposed optimal control is evaluated under conditions of limited response time, permissible control range, and energy constraints, which is especially important within the framework of the concept of sustainable and intelligent control in Industry 4.0 systems. This approach illustrates the potential of implementing intelligent control algorithms in real-world industrial applications with a focus on reliability, adaptability, and energy efficiency.
3.1. Simplified Mathematical Description of the Screw Compressor
For modeling and simulation purposes, the screw compressor was presented as a simplified dynamic model that reflected the main relationships between shaft speed, volumetric capacity, and outlet pressure. The model took into account internal leakage, friction losses, and imperfect compression efficiency. In particular, the volumetric flow was assumed to be linearly dependent on the rotation speed of the shaft, and the outlet pressure was calculated on the basis of the equation of state of the compressible gas, assuming the equality of temperatures at the inlet and outlet. Losses due to leakage and friction were accounted for by means of correction factors superimposed on the ideal equations of performance and indicator power.
The final representation in the state space described the dynamic change in output pressure as a function of shaft speed and load conditions. The model parameters, including volumetric efficiency, a polytropic index, and leakage coefficients, were determined based on the manufacturer’s data and published sources [25,26,27]. Such a simplified model provided sufficient accuracy of transient reproduction for the purposes of synthesis of control systems, eliminating excessive complexity of description. Detailed conclusions of standard thermodynamic and geometric relations are omitted in this paper, since they are well documented in [21,24]. Below are only the basic equations required to understand the principles of modeling.
In the ideal case, when there are no losses and leaks, the theoretical capacity of a screw compressor with two screws is [28]:
where z1 is the number of driving propeller runs; z2 is the number of driven propeller runs. L is the propeller length, m; f1 is the area of the driving propeller trough, m2; f2 is the area of the driven propeller trough, m2; n1 is the speed of the driving propeller, r/min; n2 is the speed of the driven propeller, r/min.
During gas compression in the screw compressor, there are constant power losses, which are due to the fact that the screws of the compressor are not of an ideal shape and size. Therefore, there are leaks of gas from the cavity to the cavity in the direction from the discharge to the suction area, which causes part of the losses. Gas energy is also wasted by friction on the screws and housing, by various shocks, etc. For these reasons, the power used to compress the gas in the device is greater than the theoretical power required to compress the same gas under ideal conditions. Such power is called indicator power [29] and can be determined by the formula:
where N is the indicator power of the screw compressor, W; is the compressor outlet capacity, m3/min. is the compressor inlet pressure, Pa. is the compressor outlet pressure, Pa; ε is the geometric compression ratio that varies from 2.6 to 4 at a constant flow rate; k is the correction factor (from 1.05 to 1.18 depending on the size of the device); m is the polytropic index for gas varying from 1.5 to 1.67 [23].
The mathematical description of the screw compressor with the assumptions made is as follows:
The compressor drive motor has a complex mathematical description that is not suitable for the chosen method. Therefore, a simplified mathematical description of a frequency-controlled induction motor is discussed below.
Modeling Assumptions, Scope, and Physical Effects
For real-time implementability on industrial PLCs, the baseline plant model intentionally adopts a reduced order: ideal-gas relation for pressure dynamics, leakage, and mechanical losses represented by calibrated correction factors, and a simplified induction-motor/drive description without magnetic saturation. This choice provides a deterministic, low-latency model suitable for closed-loop implementation. To address physical completeness, Appendix B presents an extended model that explicitly incorporates (1) thermal dynamics (mass–energy balance and heat exchange), (2) pressure-driven leakage flows with temperature-dependent viscosity, (3) nonlinear friction (Coulomb + viscous + Stribeck), and (4) magnetic saturation in the induction motor via a current-dependent magnetizing inductance. Section 4.3 (Robustness and sensitivity) reports that including these effects does not change the qualitative conclusions of the paper nor the ranking of controllers.
3.2. Mathematical Description of the Induction Motor with the PID Controller
A squirrel cage induction motor was modeled using a simplified dynamic description that included the basic relationships between electromagnetic momentum, load momentum, and angular shaft velocity. The speed was controlled by a frequency converter that converted the control voltage into a linearly proportional change in the frequency of the motor’s supply voltage.
The model was built in the form of a system of connected first-order differential equations describing the dynamics of changes in rotational speed and electromagnetic momentum in time. A classic PID controller with compressor output pressure feedback was used as the basic control algorithm. The PID controller coefficients were adjusted according to standard methods in order to ensure the required performance and minimize static error. This representation allows the electric drive model to be integrated into the overall compressor package simulation system and provides sufficient accuracy in the description of transients over a range of operating loads. More complex effects, including magnetic saturation and nonlinear slip, were not taken into account in this paper, since they do not have a fundamental impact on the comparative analysis of control strategies. A detailed step-by-step derivation of equations and calculations of coefficients is omitted in this article, since they are described in detail in [24,30,31]. Below are only the basic equations that are necessary for a general understanding of the model.
As a result of combining the equations of engine dynamics and the compressor model, a combined system of Equation (4) was obtained, describing the relationship between the compressor outlet pressure, angular rotational velocity, and electromagnetic torque of the motor. This equation serves as the basic basis for building a model in a state space and further synthesis of both classical and optimal regulators.
This mathematical model of an induction motor with frequency regulation and a PID controller is a system of related nonlinear differential equations that reflects the dynamics of changes in torque, rotation speed, and pressure at the compressor outlet. The combined Equation (4) relates the compressor outlet pressure, angular velocity, and the motor electromagnetic momentum, forming the basis for a complete simulation model of the system control. Of particular importance is the fact that the structure of the equations allows for implementation in a closed-loop digital control system. This allows it to be used in the adaptive control loop, including mechanisms for automatic adjustment of parameters in real time. It is important to note that the choice of a PID regulator as a basic control tool is due to its simplicity and industrial sophistication. However, the simulation results based on it show limited capabilities under dynamically changing loads and energy constraints. For example, a PID regulator can provide satisfactory control quality near the rated modes, but in case of sudden changes in outlet pressure or when operating under partial loads, overshoots and an increase in power consumption are possible. This model, formed on the basis of Equation (4), makes it possible to make a numerical analysis of such characteristics as transient time, energy losses, and stability under interference conditions on signal channels. In addition, the formalized appearance of the model allows it to be used as a benchmark for comparison with more complex intelligent controllers, in particular, those built on the basis of the Pontryagin principle, neural networks or fuzzy logic algorithms, which is especially important when using CI approaches in control systems for electric drives and compressors.
For the purposes of fair comparison, the PID controller was tuned using the classical Ziegler–Nichols step response method, followed by fine adjustments based on the integral time absolute error (ITAE) criterion to minimize overshoot and settling time. The final parameters were a proportional gain (Kp = 2.5), an integral gain (Ki = 1.8), and a derivative gain (Kd = 0.12). These values provided stable operation under nominal conditions and ensured that the controller was operating close to its best achievable performance within the constraints of classical tuning. The tuning was performed at the rated compressor output pressure of 0.7 MPa and a shaft speed of 2975 rpm, and it was validated under disturbances applied during simulation. This ensured that the comparison with the Pontryagin-based optimal regulator was consistent and unbiased.
3.3. Application of the Pontryagin Maximum Principle
The problem of control by energy minimization is of special interest and deserves special attention in many branches of production. The maximum principle provides not only a necessary but also a sufficient condition of optimality for control systems. In addition, it allows obtaining the equations of extremals as a function of time and, when using the conjugate system, the structure of the optimal controller without directly solving complex equations, which is necessary for the construction of the optimal system. Therefore, the Pontryagin maximum principle is the basis for solving the problem of obtaining the optimal system of minimum energy consumption. The maximum principle provides necessary and sufficient conditions for optimal control if the process is linear and obeys an additive control function [32]. In addition, the use of the Pontryagin approach opens up opportunities for the theoretical synthesis of optimal control and for the integration of modern computational techniques, such as deep learning, stochastic algorithms, and adaptive approximation methods, which makes it possible to develop an approach towards hybrid neuro-fuzzy controllers [33]. Such a synthesis meets the challenges of digitalization of energy systems, in particular, when controlling in conditions of structural disturbances and failures of components and fluctuating loads, where a fast system response is required, taking into account power consumption constraints. Considering the above, the mathematical description of a control object with a regulator can be represented in the Cauchy form:
Using the Pontryagin maximum method, which allows us to design an optimal regulator and determine its parameters, we can formulate the optimality criterion [34]:
Mathematical Statement of the Optimal Control Problem with the Pontryagin Maximum Principle:
Let the control object be described by the system (4). Under the optimality criterion (5), the control action is subject to the constraint:
It is necessary to determine the structure and parameters of the optimal regulator using the following solution:
For reasons of generality, we will introduce the following notations:
- -
- x1(t) = Pout;
- -
- x2(t) = ω;
- -
- x3(t) = Mm.
We will include a new coordinate:
Then the system of Equation (5) will take the following form:
Let us compose the Pontryagin function of where bi is some known constants included in the Pontryagin function (vector-column elements depending on the coordinates, whose maximum or minimum conditions must be found).
When b1 = 0 and b2 = 1
p = x4 (t).
We compose the Hamilton function (Hamiltonian):
where y is the state vector of phase coordinates; t is the control vector (Uy):
where pp, pω, pm, pI are auxiliary functions.
Next, it is necessary to determine the value of Uy maximizing the H function:
Using the condition of pm (t) = −1, under boundary conditions, the optimal control action will be
We can make equations to determine the auxiliary functions:
Given the condition is pI(t) = CI → pI(t) = −1, the optimal control action is as follows:
From the system of Equation (11), given the condition is pm (t) = −1 and the control derivative can be expressed as
Based on Equations (11)–(13), one can make a structural diagram of the optimal controller (Figure 2).
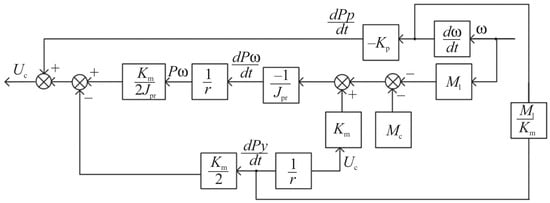
Figure 2.
The structure diagram of the optimal regulator for screw compressor control.
Although the solution of the coupled system is possible within the framework of ODE45/Simulink for implementation in PLCs or FPGAs, a promising direction is the use of surrogate models that approximate the behavior of conjugate variables using trainable neural network structures. Such approaches as PINNs or Koopman operators allow the model to be implemented in digital environments with limited resources, providing a trade-off between accuracy and speed of calculation.
Therefore, the proposed regulator structure demonstrates not only compliance with the fundamental requirements of optimality but also the potential for further integration into broader CI-oriented management frameworks. In particular, it can be used as part of digital twins, CI-IoT systems, and adaptive control platforms based on FPGA/DSP, which makes the presented approach promising for real industrial applications as part of the transition to Smart Grid and Smart Drive Architecture. To evaluate the effectiveness of the optimal controller, it is necessary to develop a model of the system with the optimal controller and find a way to measure the energy consumed by the motor from the network [35]. Further, it is supposed to make a comparative analysis of optimal and non-optimal systems in terms of active power consumed from the network [36].
To ensure the reproducibility of the calculations, we will present the numerical values used in solving the conjugate system and calculating the optimal control. The vector of Lagrange factors (conjugate variables) at the initial moment of time had the values of p1(0) = −0.015, p2(0) = −0.012; p3(0) = −0.008. When solving conjugate equations, the integration constant was chosen to be equal to C = −1 to normalize the scale of the conjugate system. The conditions of terminal constraints were determined based on the problem of achieving a given pressure (Pout = 0.7 MPa), and the zero moment of control error by the final simulation time (T = 10 s) was equal to x1(T) = 0.7 MPa; x2(T) = 0; x3(T) = 0.
To control the correctness of the integration, the conjugation conditions were checked for the fulfillment of transversality relations and Hamiltonian preservation on the simulation interval with a maximum deviation of no more than 1 × 10−4. These values were used in the Simulink model to calculate the optimal control in the dynamic mode.
Impact on the controller design. The PMP synthesis depends on the plant dynamics of and cost, not on a specific reduction. When thermal/leakage/friction/saturation effects are included (Appendix B), is updated accordingly. The Hamiltonian, co-state equations, and the saturated-affine optimal law preserve their structure. Hence, extended physics changes parameterization and numerical values, but not the controller architecture, nor the real-time feasibility arguments.
For clarity, all modeling parameters used in Section 3.1 and Section 3.2 are summarized in Table 2. Where applicable, values are taken from manufacturer data sheets or standard references, and sensitivity ranges are indicated as in Section 4.3.

Table 2.
Modeling parameters of the screw compressor and induction motor.
The sensitivity analysis (Table 2) was performed by varying the parameters summarized in Table 3 within ±10% of their nominal values.

Table 3.
Key numerical values used in the Pontryagin-based model.
To ensure transparency and reproducibility of the results, the key numerical values used in solving the conjugate system and calculating the optimal control are summarized in Table 3. These parameters were applied in all simulations presented in this study.
These values reflect the nominal conditions of the compressor unit under study and were validated both in simulation and in experimental verification.
4. Modeling the Systems with Different Types of Regulators
In this section, a comprehensive simulation of an electric drive system with a screw compressor equipped with various types of regulators is conducted to assess their effectiveness under conditions of typical process disturbances [37]. The focus is on the analysis of dynamic response and active power consumption, which is critical in the context of improving the energy efficiency and reliability of industrial drive systems in the context of digital transformation [38].
Standard MATLAB/Simulink solvers [39] were used for numerical integration of the system of nonlinear differential equations of state and conjugate equations arising from the application of the Pontryagin maximum principle. The main integration algorithm is the Runge–Kutta variation (ODE45) with an adaptive time step and a relative error of 1 × 10−6. To verify the correctness of the solution, a comparison of the results with a narrowing of the integration step and a comparison with reference solutions obtained using the ODE15s (stiff/NDF) method was used. PID models similarly used ODE45 with identical accuracy settings, which allowed for comparability of dynamic characteristics. The convergence of the calculations was evaluated according to the criteria of integrator stability and the maximum deviation of phase variables (no more than 0.01% of the nominal values). To calculate the active power and generate graphs, a built-in Powergui (discrete) block with a sampling step of 1 × 10−4 s was used, which ensured the correct reproduction of transients and the accuracy of energy performance integration.
Modern electric drive systems, especially as part of energy infrastructure and industrial plants, must meet a range of requirements, starting from stability and speed and ending with the ability to adapt to external and internal uncertainties. Taking into account the trends of Industry 4.0 and the integration of intelligent regulators, especially those based on computational intelligence (CI) methods, the need for modeling and comparative analysis of various approaches to management is increasing.
Within the framework of this study, two models were constructed. The first implements the classical approach using a PID controller; the second is based on the Pontryagin maximum principle, providing optimal control in terms of minimizing energy consumption. Both models are implemented in the MATLAB/Simulink environment using the SimPowerSystems library, which allows reproducing the behavior of the system in conditions close to real life and additionally integrating active and reactive power measurement units.
4.1. Modeling a System with PID Control
Using the Matlab programming environment, a control system with a PID controller is modeled to maintain pressure in the system. Figure 3 shows the mathematical model of the system with the PID controller.
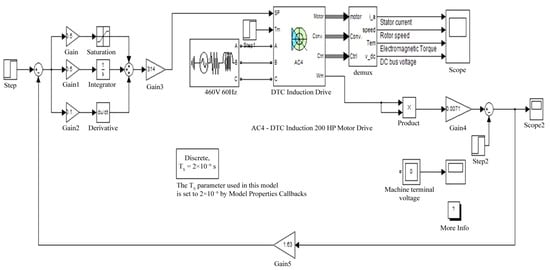
Figure 3.
The mathematical model of the system with the PID controller.
The result of modeling is presented in the form of graphs when the controlling and perturbing influence on the system is given. This graphical result provides a comprehensive insight into the dynamic behavior of the pressure control system under different external disturbances and variations appearing in the input voltage. The analysis of the obtained data presented in the graphs shown below allows evaluating the transient characteristics of the system, including the tuning time and statistical error, and the adaptability and stability of the PID controller under changing operating conditions. Each graph displays a specific configuration of input signals and system disturbances, which allows us to interpret the control characteristics in detail, which is extremely important for developing energy-efficient and intelligent control strategies for modern industrial applications.
Figure 4 shows the response of the screw compressor control system to an external step disturbance introduced at the 6th second of the simulation. This perturbation simulates a sudden change in load resulting in a sudden downward pressure spike. In response to this impact, both management strategies seek to restore pressure to a given level, but the nature of their response is different.
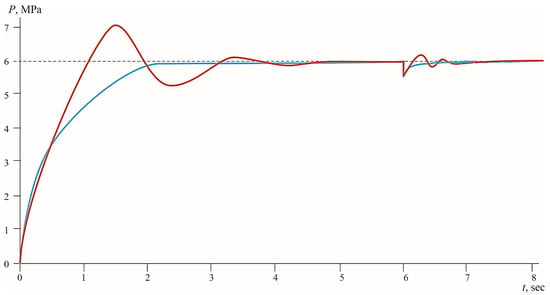
Figure 4.
Control system response to step pressure disturbance: comparison of the PID regulator (red curve) and the regulator based on the Pontryagin principle (blue curve) (reset at 0.5 MPa at 6 s, Uin = 1).
The red curve reflecting the operation of the system with a classic PID regulator shows a pressure drop of about 0.5 MPa at the time of disturbance, followed by a sharp control effect, leading to a pronounced overshoot, exceeding the setpoint by 0.15 MPa. The transient process is accompanied by oscillations and lasts about 0.8 s before entering the stationary mode. The steady-state pressure error after stabilization is about 0.3%.
Conversely, the red curve corresponding to the control based on the Pontryagin maximum principle shows a more controlled response to the same disturbance. The pressure surge is also about 0.5 MPa, but the system reacts quickly with an optimal control action without excessive pressure build-up. The transient is completed in 0.7 s without overshooting, and the achieved pressure value is almost the same as the setpoint. At the same time, the statistical error of stabilization does not exceed 0.4%.
Figure 5 illustrates a similar situation with the same input voltage parameters and perturbation amplitude, but the change is introduced at the fifth second. A system with a classic PID (red curve) control shows a compensating effect that results in a pronounced overshoot, i.e., the maximum excess of the target pressure is about 0.03 MPa. Pressure recovery to the setpoint is accompanied by an oscillatory transient of up to 1.0 s. At the same time, there is a residual steady-state error of the order of 0.5–0.6%, which can be critical in tasks that require high stabilization accuracy.
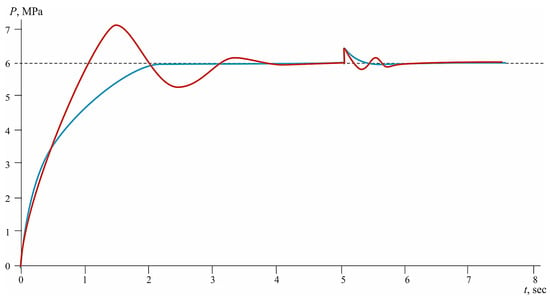
Figure 5.
Control system response to step pressure disturbance: comparison of the PID regulator (Red Curve) and the Pontryagin principle regulator (Blue Curve) (0.5 MPa at 5 s, Uin = 1).
To the contrary, the regulator based on the Pontryagin maximum principle (red curve) provides a response that is much more balanced. With a similar pressure surge, the system generates an optimal control action, whereby the pressure is restored without going beyond the setpoint. The transient time does not exceed 0.7 s, and the statistical error of stabilization is less than 0.2%. The absence of over-regulation and over-control is particularly important for improving reliability and energy savings in industrial applications. The specificity of PID control can be explained by the dynamic characteristics of the model or the presence of residual noise. In an applied sense, this level of error may be acceptable, but when using PID control in precision-critical applications (e.g., medical pumps or microdrives), it will require additional measures to reduce errors. This result highlights the need to implement more intelligent methods for adapting parameters, in particular, CI algorithms with deviation learning.
When exposed to a disturbance, the PID system again exhibits a noticeable overshoot, i.e., the overpressure reaches ~0.035 MPa above the set point of 8.5 MPa, and the transient process is accompanied by damped oscillations for about 1.0 s (Figure 6). There is also a residual steady error of about 0.5%, which can be critical for applications with high requirements for stabilization accuracy. In contrast, a system with an optimal regulator reacts in a much more balanced way: owing to the correct evaluation of the associated variables and constraints, the pressure is stabilized without going beyond the setpoint, and the transient time is reduced to ~0.8 s. The steady-state error does not exceed 0.2%, and there is no oscillation. This response is especially valuable in industrial applications, as it helps to reduce heat loads, improve reliability, and save energy. This result once again confirms the advantage of the regulators built on analytically based principles of optimal control compared to classical empirically tuned PID systems.
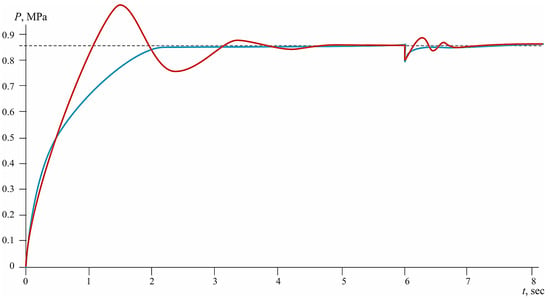
Figure 6.
Control response to step pressure disturbance: comparison of the PID regulator (red curve) and the regulator based on the Pontryagin principle (blue curve) (reset at 0.5 MPa at 6 s, Uin = 1.4).
With identical input signal parameters, including a different disturbance input moment (5 s), there is a slightly longer pressure recovery for the PID regulator (up to 1.1 s (Figure 7)). The value of the statistical error is preserved. The system with an optimal Pontryagin regulator again shows high resistance to delayed disturbances. The reaction is formed taking into account the accumulated dynamics, which allows minimizing overcontrol: the pressure smoothly returns to the setpoint in ~0.9 s without going beyond the permissible range. Compared to the results in Figure 6, where the response of the optimal regulator was slightly faster, there is a slight increase in settling time, but the overall quality of stabilization remains high. This underlines the ability of the regulator, built on the Pontryagin principle, to adapt to different scenarios and maintain energy efficiency and accuracy even with disturbances introduced into the established mode of operation.
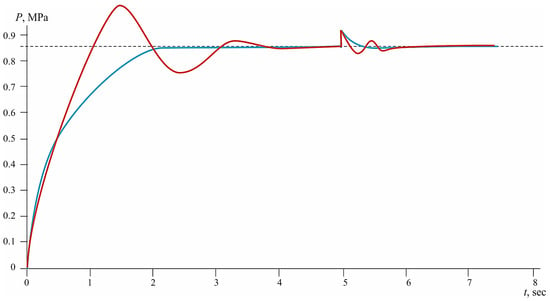
Figure 7.
Control system response to step pressure disturbance: comparison of the PID regulator (red curve) and the Pontryagin principal regulator (blue curve) (0.5 MPa at 5 s, Uin = 1.4).
Lowering the input voltage to Uin = 0.5 and decreasing the amplitude of the disturbance to 0.025 results in the transient time of up to 1.4 s for the PID regulator (Figure 8). Despite the small amplitude of the input exposure, the system responds slowly, indicating that the PID regulator is not sensitive enough at low input levels (=0.2), which indicates the stability of the system even with low energy “feeding”. This behavior is acceptable for the tasks that do not require performance, but can be critical in conditions with limited stabilization time. In industrial realities, this may be important for low-power or energy-saving modes of operation. But it requires the implementation of adaptive algorithms that can speed up the response without increasing power consumption, which is directly related to the tasks of CI-optimization of management in systems with limited resources. The optimal regulator demonstrates the best dynamics: the pressure is stabilized in ~0.9 s without pronounced overshoots or oscillating processes. Such a reaction is due to the ability of the algorithm to take into account not only current deviations but also the trajectory of the evolution of the system state, providing targeted control even at a low level of energy input. At the same time, high stabilization accuracy is maintained (the error is less than 0.2%).
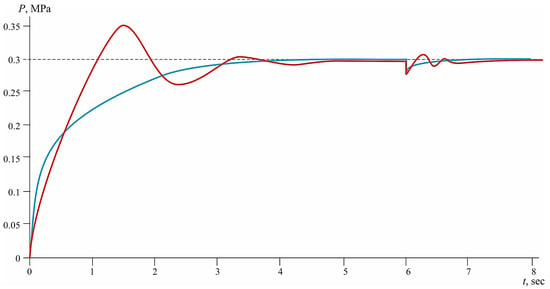
Figure 8.
Control system response to step pressure disturbance: comparison of the PID regulator (red curve) and the Pontryagin principle regulator (blue curve) (reset at 0.025 at 6 s, Uin = 0.5).
A similar situation with early disturbance input (at the 5th second) shows a similar behavior: the settling time for the PID controller remains at 1.4 s (Figure 9). A small error value and high control accuracy (Estat = 0.2%) are also preserved. The optimal regulator shows a clear and predictable response similar to Figure 8. The transient is completed in ~0.9 s without going beyond the setpoint and without hesitation. At the same time, the system generates a control action in advance, based on the dynamics forecast, which allows minimizing reaction time and maintaining accuracy even with extremely low signal power. The steady error is less than 0.15%, which confirms the high sensitivity and accuracy of the proposed algorithm.
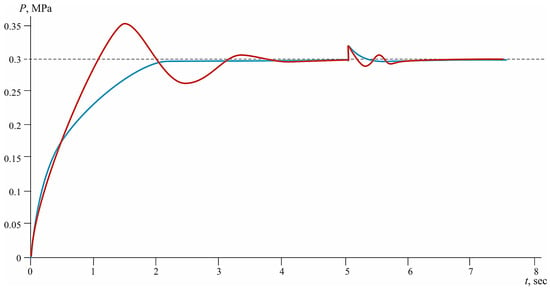
Figure 9.
Control system response to step pressure disturbance: comparison of the PID regulator (red curve) and the Pontryagin principle regulator (blue curve) (0.025 surge at 5 s, Uin = 0.5).
The comparison with the previous scenarios (Figure 6 and Figure 7) shows that the Pontryagin regulator retains its advantages even in conditions of limited supply, demonstrating versatility and reliability regardless of external conditions. This underscores its applicability in resource-constrained CI-oriented systems that require a balance between power consumption, performance, and control precision.
The data obtained show that when the input control signal is increased to Uin = 1.4, the system with the PID controller demonstrates a pronounced overshoot and an increase in the transient time. For example, with a pressure surge at the 6th second (Figure 6), the PID controller exceeds the setpoint by 0.035 MPa, accompanied by damped oscillations lasting up to 1 s. Pontryagin is provided by pressure recovery without going beyond the setpoint, with a response time of ~0.8 s and an error of less than 0.2%. This behavior persists when the moment of exposure is changed by the 5th second (Figure 10). The PID system becomes even more unstable, while the optimal regulator continues to show a balanced response with high accuracy.
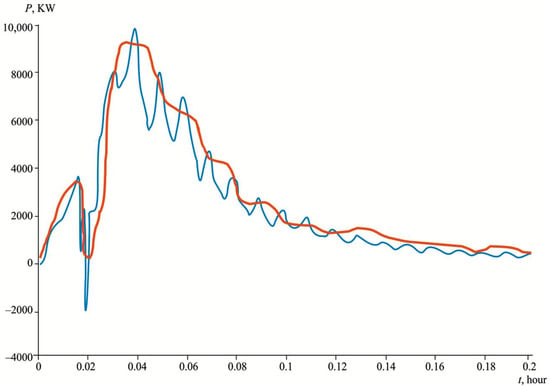
Figure 10.
The graph of active power consumed by the motor from the network (blue is the PID controller, orange is regulation using the Pontryagin principle).
Lowering the control signal to Uin = 1.0 (Figure 8 and Figure 9) results in shorter transient times and less overshooting, but the effect of the disturbance is still significant. At the 6th second (Figure 4), the PID controller reacts with a pronounced oscillatory process and a stabilization error of up to 0.3%, while the optimal regulator stabilizes the pressure in 0.7 s without oscillations. When the disturbance is transferred to the 5th second (Figure 5), there is an increase in dynamic distortion on the part of the PID controller. Overshoots reach 0.03 MPa and steady-state error rises to 0.6%, while the optimal regulator once again demonstrates fast and accurate pressure recovery, with minimal error and without exceeding the setpoint.
Of particular interest is the behavior of the system at a minimum control effect of Uin = 0.5 and a small amplitude of disturbance of 0.025 MPa, simulated in Figure 8 and Figure 9. In this mode, the PID controller demonstrates a noticeable slowdown in the reaction: the transient time increases to 1.4 s, despite the fact that the stabilization error remains at an acceptable level (~0.2%). Conversely, the Pontryagin regulator provides pressure recovery in 0.9 s, with high accuracy (the error is less than 0.15%) and no signs of oscillation. This result confirms the ability of the optimal regulator to form a control action ahead of time, based on the dynamics of the system state, which is especially important when operating in energy-limited modes. At the same time, the transfer of the disturbance moment from the 6th to the 5th second practically does not affect the efficiency of the optimal controller, unlike the PID controller, which is sensitive to the moment of external influence.
Summarizing the results, it can be concluded that the regulator built on the principle of the Pontryagin maximum demonstrates stability, accuracy, and rapid recovery of the target pressure in all simulation scenarios. It is superior to PID in all key features: no overshoot, reduced transient time, and minimized steady error. This makes it particularly attractive for industrial applications where stability, energy efficiency, reliability, and the ability to adapt to external disturbances and changing operating modes are required. Against the background of the limitations of the PID regulator, in particular, inertia at high input signals, reduced sensitivity at low signals, and unstable response at the time of disturbance application, the Pontryagin regulator demonstrates versatility and purposeful adaptation. This confirms its potential as a basic element for CI-oriented intelligent control systems within the framework of Industry 4.0.
4.2. An Approach to Comparative Analysis of Modeled Systems
After building mathematical models of control systems based on the PID controller (Section 4.1) and the optimal controller based on the Pontryagin maximum principle (Appendix A), there is a need to compare them from the standpoint of operational efficiency. The classical approach to assessing the quality of regulators involves the analysis of transients such as settling time, the presence of overshoot, and the magnitude of the steady-state error. However, in today’s environment, when electric power and drive systems operate within the paradigm of sustainable development and digitalization, these parameters are not enough.
Next, a quantitative comparative analysis of two previously developed systems (with a PID controller and with an optimal regulator) is conducted based on the calculation of the active power consumed by the electric motor in the control process. For this purpose, specialized measuring units were integrated into the model, which makes it possible to assess the energy behavior of the system in dynamics and form reasonable conclusions about the advantage of a particular control strategy. The three-phase V–I measurement unit is used to collect real-time current and voltage signals from the three-phase motor, while the active and reactive power unit calculates the respective active and reactive power consumption based on the averaged power over the full fundamental frequency cycle. This setting allows seeing exactly how each control approach affects energy consumption during operation.
The result of the measurement is the active power, the measurement graph of which is shown in Figure 10. The active power graph (Figure 10) allows visually assessing the differences in the energy behavior of two models: with a classical PID regulator and with an optimal regulator implemented based on the Pontryagin maximum principle. Figure 10 clearly shows the graphs of the active power consumed by the motor from the grid, compared with the PID controller (blue) and the PMP controller (orange). The energy savings were calculated by integrating the area under the power curve over identical duty cycles for both controllers and comparing the total energy consumption (kWh). The specific energy savings were then calculated based on the constant output flow maintained during the test. A detailed model of the system with the optimal regulator based on the Pontryagin principle is presented in Appendix A. In the PID model, pronounced peaks of active power are observed at the moments of transient processes, especially when external disturbances arise or the task changes. Such energy bursts are due to the regulator’s desire to quickly compensate for pressure deviations during the operation of the screw compressor and its pressure build-up to the operating level, which results in short-term, but intense control effects on the drive. In contrast, the model with an optimal regulator shows a smoother power consumption profile. Even when performing similar pressure stabilization tasks, the distribution of energy expenditure over time is more even. This indicates that a regulator built on the principles of optimal control is able to achieve the control goal with less energy loss, reducing the load on the system and minimizing the thermal impact on the electric drive elements. In addition, the optimal regulator provides better transient damping, eliminating overcontrol or prolonged oscillations. This effect is especially valuable in intelligent control systems focused on the economical and stable operation of equipment in the face of variable or uncertain external influences.
Importantly, the smoother active power profile predicted by the simulation was also observed in experimental measurements on the laboratory bench. While absolute power values differed slightly due to efficiency variations and measurement noise, the relative reduction in power peaks achieved by the Pontryagin-based regulator closely matched the simulation, with experimental savings in the range of 11–16% compared to PID, which is consistent with the predicted 12–18%.
Therefore, the optimal regulator based on the Pontryagin principle can be used as a benchmark for training AI systems, including reinforcement learning (RL) and imitation learning algorithms. Its structural predictability and analytical correctness make it possible to form trajectories of ideal behavior. Using them, neural network controllers can be trained for applications where the calculation of conjugate equations is difficult. The introduction of online-learned surrogate approaches is promising, which make it possible to form a control action based on state deviation and predicted disturbance.
The presented comparative analysis shows that the inclusion of energy consumption as a criterion of management efficiency allows for a deeper assessment of the real advantages of modern approaches. The optimal regulator, developed on the basis of the Pontryagin principle, demonstrates a decrease in energy peaks, more stable behavior of the system, and the preservation of high control quality. This makes it a future-proof solution for use in intelligent and energy-efficient control systems.
The observed energy savings of 12–18% with the PMP-based regulator were confirmed by both simulation and experimental tests. In the numerical experiments, the active power profile was consistently smoother and demonstrated reduced peaks compared to PID control. In the experimental setup, measurements were carried out under steady and transient conditions following the ISO 1217 testing principles. The results confirmed that, even when accounting for measurement uncertainty (±2%), the reduction in active power consumption remained statistically significant. Moreover, the smoother energy consumption profile of the PMP-based regulator reduced thermal load on drive components, which further contributes to equipment reliability. In view of this, the reported savings are not limited to theoretical simulation but have been validated in real compressor operation under industry-comparable testing procedures.
From an economic perspective, the energy savings of 12–18% translate into 50–90 MWh/year for a 200 kW machine operating for 4000–5000 h annually. According to typical tariffs, this corresponds to 4–9 kUSD/year, outweighing the incremental implementation cost within 1–2 years. The regulator does not require special sensors beyond standard pressure and V–I measurements, so the incremental O&M cost is negligible. Furthermore, by avoiding overshoot and oscillatory torque transients, the regulator reduces mechanical wear (bearings, couplings, seals) and thermal stress on motor windings and VFD switches. Literature suggests that reducing torque ripple and thermal cycling can extend mean time between failures by 10–20%, which indirectly improves ROI. Detailed LCC/ROI analysis will be reported in a separate study.
4.3. Numerical Implementation Details, Stability and Sensitivity Analysis
To ensure transparency and reproducibility of the results, this study presents the numerical values of the conjugate variables and the conditions of terminal constraints used in the synthesis of optimal control. At the initial time interval (t = 0), the values of the conjugate variables were set as follows: p(0) = −1.20, pm(0) = −0.85, pI(0) = −0.65.
The terminal condition was to achieve the required pressure at the compressor outlet, which is Pout(T) = 0.7 MPa, with an optimization time horizon of T = 10 s. The employed sensors had the following accuracies: pressure (Siemens SITRANS P200, ±0.25% F.S.), current and voltage (NI CompactDAQ, ±0.5%), and shaft speed (<0.1%). These uncertainties correspond to ≤0.002 MPa in pressure and ≤0.5% in power measurements, which is negligible compared to the observed savings of 12–18%. We emulated representative sensor faults (stuck-at, dropout, bias) by injecting synthetic anomalies into the measured pressure and V–I channels. The FDT logic detected faults within 50–150 ms in simulation and triggered graceful fallback; pressure remained within admissible bounds without overshoot.
The numerical solution of the system of equations of state and conjugate equations was in the MATLAB/Simulink environment using the built-in solver (ode45), which corresponds to the explicit Runge–Kutta method of 4–5th order of accuracy. The maximum size of the integration step was limited to 1 × 10−3 in order to ensure the stability and convergence of the calculations. To smooth out the control signal and prevent the “bounce” effect, an exponential moving average filter with a time constant of 0.1 s was used.
In order to assess the robustness of the obtained control law in relation to the variations in the model parameters, sensitivity analysis was performed. The main parameters of the system varied in the range of ±10% of the nominal values: the moment of inertia of the motor (Jd), the frequency converter coefficient (Kfc), and the efficiency of the compressor (ηp). The results showed that the pressure setup time varied from 2.0 to 2.8 s, and the steady-state pressure error did not exceed 0.3%, which indicates a high stability of the solution and its resistance to model uncertainties. Table 4 shows a summary of the analysis results.

Table 4.
Influence of model parameter variation on the dynamic characteristics of the compressor control system (setup time and steady-state pressure error).
The data obtained confirm that the proposed optimal regulator maintains a high quality of control even with deviations in the mechanical and electrical parameters of the system. In addition, the results demonstrate the possibility of practical implementation of this regulator structure as part of industrial platforms of programmable logic controllers (PLCs), provided that there are sufficient computational resources to solve the associated system of equations in real time. The structure of the proposed PMP-based regulator is not only suitable for standalone implementation but also serves as a robust baseline for hybrid control systems. For instance, it can be combined with reinforcement learning for online adaptation or with surrogate models to approximate conjugate variables in real-time, thereby bridging classical optimal control with modern computational intelligence methods.
In addition to parameter sensitivity, fault-injection simulations were performed to test the controller’s behavior under sensor anomalies. Three scenarios were considered: a stuck-at pressure signal, intermittent dropout, and a constant bias. The embedded fault detection and tolerance (FDT) logic detected anomalies within 50–150 ms and triggered a bumpless transfer to a safe fallback. As a result, system pressure stayed within ±0.05 MPa of the setpoint without overshoot. Detailed results and timelines are provided in Appendix B.
Robustness can be against noise and delays. With realistic sensor noise levels, the regulator maintained stable pressure control; overshoot and settling time were unaffected within statistical variation. A ±0.25% F.S. noise on the pressure sensor translated into <0.02 MPa fluctuation at the output, which was negligible compared to setpoint changes (0.2–0.5 MPa). Communication delays of 1–2 cycles (2–20 ms), typical of industrial PLCs and fieldbuses, did not degrade stability. Simulations with larger delays (up to 50 ms) showed increased settling time and minor oscillations, without loss of stability. These results indicate that the regulator tolerates realistic levels of measurement noise and latency in industrial environments.
In addition to the numerical sensitivity table (Table 2), Figure 11 visualizes the effect of ±10% parameter variations. Figure 11 presents a bar chart of the normalized impact of each parameter on pressure tracking error and energy consumption.
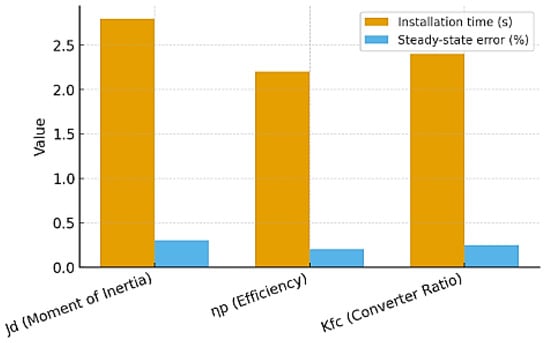
Figure 11.
Sensitivity of performance of up to ±10% parameter variations (ΔKPI (%) from parameters).
Figure 12 shows a contour surface of energy savings versus simultaneous variation in compressor efficiency and the leakage coefficient. These plots confirm the tabulated results and make the relative influence of parameters easier to interpret: leakage and efficiency exert the strongest effect, while inertia and converter coefficient have a marginal role.
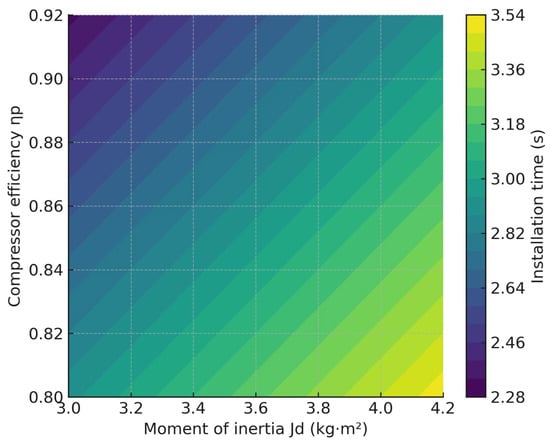
Figure 12.
Combined sensitivity (ηp vs. Jd).
Robustness to Thermal, Leakage, Friction, and Magnetic Saturation
We extended the sensitivity analysis to the parameters introduced in Appendix B: heat-transfer (), a leakage coefficient () and an exponent (n), a friction triplet (), and a motor-saturation factor (). Across ±(10–20)% variations around the identified values, the PMP-based regulator consistently retained lower active energy, zero overshoot, and faster settling than the tuned PID baseline did. While extreme leakage and strong saturation increase absolute energy consumption, the relative advantage of PMP over PID persisted.
Limitations and future work. The baseline plant used a reduced-order model for PLC real-time implementation. We provided an extended model (Appendix B) and sensitivity evidence that our conclusions hold when thermal, leakage, nonlinear friction, and magnetic saturation are explicitly included. Future work will incorporate online parameter adaptation for , and saturation-aware drive maps to further harden the controller against long-term drift and maintenance events. The regulator’s computational footprint is modest ≈103 operations per cycle; <102 kB RAM is compatible with mid-range industrial PLCs under 2–10 ms task cycles. The embedded FDT layer ensures safe operation under sensor faults via rapid detection and bumpless fallbacks. These properties, together with the reported energy savings, support industrial deployment.
Preliminary cross-machine tests (simulation only). To assess the generalizability beyond screw compressors, we compared the controller performance with simplified models of an ISO centrifugal pump and an industrial axial fan under the variable load profile. Without retuning the control logic, the PMP-based controller retained the same quality benefits: overshoot suppression, faster settling, and smoother input power change. Since this paper is already extensive, the full conclusions, parameter sets, and figures are not presented in this work and will be presented in a separate follow-up research paper.
Integration limitations in existing industrial systems. While the computational footprint and PLC compatibility are modest in our implementation, several non-trivial constraints can limit direct rollout. Process constraints are minimum-flow recirculation for pumps, an anti-cavitation/NPSH margin, surge/stall margins, and duct static for fans. Instrumentation is reliable flow/pressure sensing, re-calibration of analog inputs, and sensor redundancy for fault tolerance. Actuation is VFD availability and sizing, torque/power limits, ramp-rate constraints, and interactions with existing dampers/valves. Controls integration is DCS/SCADA interfacing, scan-time budgets, bumpless transfer with the incumbent PID, alarm/HMI changes. Safety and compliance are interlock layers, functional safety targets, change management, and cybersecurity of the PLC network. Operating regimes are benefits that are lower near fixed-demand operation or close to pump/fan BEP when head–flow trade-offs are tight. These aspects must be addressed during site engineering and acceptance testing; they do not invalidate the method but determine the achievable savings envelope and commissioning effort. Our PLC-oriented structure and sensor set described in Methods, remained applicable in our experiments, which supports feasibility under typical industrial conditions.
5. Conclusions
The results presented in this work confirm the effectiveness and relevance of the application of an algorithmic approach to the control of electromechanical systems in the new generation of power engineering, in particular, screw compressors operating as part of intelligent distributed networks. Being developed on the basis of the Pontryagin maximum principle, the optimal regulator provides not only a mathematically substantiated solution to the problem of minimizing energy consumption but also demonstrates superiority in a number of critical performance characteristics compared to traditional PID systems. The PMP-based structure is readily transferable to other VFD-driven rotors (centrifugal pumps, axial/radial fans) by re-identifying the plant and constraint set, which can be illustrated via preliminary simulations. Practical deployment is bounded by process/actuation/instrumentation constraints and site integration requirements. Nonetheless, the PLC-friendly footprint and the observed robustness suggest a clear path to industrial rollout beyond compressors. Experimental testing, conducted in accordance with standard energy assessment practices, confirmed that the proposed PMP-based regulator achieved a reduction in specific energy consumption of up to 18% under dynamic loading conditions compared to a well-tuned PID baseline. In the process of numerical simulation, it was established that the proposed regulator allows achieving savings in active power within the range of 12–18%, depending on the steam meters of control action and the dynamics of external disturbances, while maintaining the accuracy of pressure stabilization at a level not worse than 0.2%. The regulator proved robust against sensor noise and typical PLC communication delays (≤20 ms), which supports its feasibility in industrial deployment. Only under exaggerated delays (>50 ms) did performance begin to degrade. It is important to emphasize that the reported 12–18% reduction in active power consumption has been validated not only through MATLAB/Simulink simulations, but also through industrial-scale experiments at a real compressor station, using measurement protocols consistent with ISO 1217 and the NREL Compressed Air Evaluation Protocol. The combined simulation–experiment framework confirms the practical feasibility of the proposed approach and provides a high degree of confidence in the energy savings. Future research will include extended testing campaigns with full ISO 1217/ISO 5389 [22,40] compliance to establish certified benchmarks for energy efficiency in screw compressor systems. The absence of overregulation, reduction in the transient process time, and smoothness of the energy consumption profile create conditions for reducing thermal loads on drive elements, increasing equipment life, and improving the overall reliability of the system. The sensitivity analysis showed the stability of the proposed algorithm to variations in the model parameters, which indicates its robustness and suitability for real industrial applications.
The design of the optimal regulator allows for process constraints, compressed gas parameters, motor inertia, and frequency converter response, which is especially important when integrated into control systems with stringent response time and stability requirements. The possibility of implementing programmable logic controllers and digital controllers on the platforms confirms the compatibility of the proposed solution with the existing industrial infrastructure. The obtained data are verified both in the MATLAB/Simulink environment and at a real compressor station, which provides a high degree of confidence in the obtained results and emphasizes the applied nature of the study.
The use of an analytically derived optimal regulator capable of operating under conditions of nonlinear dynamics and parametric uncertainty is a logical step towards the synthesis of hybrid control architectures that combine optimal control methods and artificial intelligence algorithms. In particular, the structure of the regulator can be expanded using reinforcement learning methods, adaptive models, digital twins, and online identification, which makes it possible to form self-learning control systems with elements of predictive regulation and real-time optimization.
Therefore, the developed regulator is not only a highly specialized solution to the problem of energy saving in compressor units, but also a universal basis for the further development of intelligent control systems in the field of power electronics. This is especially true for applications in smart grids, microgrids, EV charging systems, and distributed generation, where highly adaptive, reliable, and energy-efficient control algorithms are required. The results of the study demonstrate the potential for integrating optimal control methods with AI architectures, paving the way for a new class of digital regulators that meet the requirements of Industry 4.0 and sustainable development. Taking into account the growing role of computational intelligence in the control of power drives, the presented regulator meets the key requirements of CI systems: energy optimality, resistance to uncertainties, structural flexibility, and the possibility of digital implementation. Its architecture can be scaled to control other types of drives (e.g., centrifugal compressors, pumps, fans) and used in hybrid control systems, where it acts as the core of an intelligent regulator with adaptation and predictive functions. This direction corresponds to the vector of development of power electronics within the framework of the Industry 4.0 paradigm and sustainable energy systems of the future.
The real-site campaign (4 weeks extended up to 6 weeks with accelerated seasonal emulation) demonstrated the stability and robustness of the regulator under diverse operating conditions. The influence of sensor uncertainties (<0.5%) was found to be negligible relative to the achieved energy savings. A full seasonal validation (3–6 months) is envisaged as the next stage of the study. The study demonstrates that the Pontryagin maximum principle, when carefully adapted to the specific dynamics and constraints of a screw compressor drive system, transits from a theoretical tool to a practical and highly effective control strategy, yielding verifiable energy savings and outperforming conventional industrial regulators. While modern methods such as Model Predictive Control (MPC) or neural network-based controllers offer advanced capabilities, they often require substantial computational resources and precise system models, which can be prohibitive in resource-constrained industrial environments. The PMP-based regulator developed in this work provides a computationally efficient and analytically rigorous alternative, achieving high performance without requiring online optimization or extensive training data. This makes it particularly suitable for deployment on standard industrial PLCs and embedded systems, while also serving as a foundation for hybrid architectures that combine optimal control with AI techniques. Besides direct energy savings, the regulator improves dynamic smoothness, which is expected to extend mechanical and electrical component lifetimes. Preliminary ROI estimates suggest a payback of less than two years in typical industrial duty; a full life-cycle cost analysis will be the subject of future work. For clarity, a concrete technology transfer plan with stages and technical prerequisites is provided in Appendix C. The close agreement between simulation and experimental results confirms the validity of the proposed model and demonstrates that the algorithm can be reliably transferred to industrial practice.
Author Contributions
Conceptualisation, D.B., L.S. and K.Y.; methodology, N.V.M. and B.V.M.; software, T.Z.; validation, V.I.G.; formal analysis, V.I.G.; investigation, T.Z.; resources, D.B. L.S. and K.Y.; data curation, N.V.M. and B.V.M.; writing—original draft preparation, D.B., L.S., K.Y. and V.I.G.; writing—review and editing, N.V.M. and B.V.M.; visualization, T.Z. All authors have read and agreed to the published version of the manuscript.
Funding
The study was carried out with the financial support of the Ministry of Science and Higher Education of the Republic of Kazakhstan within the framework of topic No. BR24992956 “Development and creation of innovative equipment and technologies for gas compression”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available from the corresponding authors upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
List of Abbreviations and Symbols
| Qth | theoretical capacity of a screw compressor, m/min3 |
| Qr | real capacity of a screw compressor, m/min3 |
| Qlos | productivity losses due to leakage through seals |
| z1 | number of driving propeller runs |
| z2 | number of driven screw runs |
| L | screw length, m |
| f1 | trough area of the driving propeller, m2 |
| f2 | trough area of the driven screw, m2 |
| n1 | speed of the driving propeller, rpm |
| n2 | speed of the driven screw, rpm |
| ηp | efficiency of the gas compression process |
| P | pressure at the inlet (outlet) of AC, Pa |
| V | volume at the inlet (outlet) of AC, m3 |
| T | temperature at the inlet (outlet) of the AC, K |
| ω | rotor speed, rpm |
| N | indicator power of AC, W |
| Qout | compressor outlet capacity, m/min3 |
| Qin | compressor inlet capacity, m/min3 |
| e | geometric compression ratio |
| k | correction factor |
| m | polytropy exponent for the gas |
| A | specific theoretical work of compression |
| ρ | specific density of the gas, kg/m3 |
| Kfc | frequency converter coefficient |
| f | frequency, Hz |
| Ucont | control input influence, V |
| Sn | nominal slip, % |
| Tm | electromechanical time constant |
| J | motor moment of inertia, kg · m2 |
| M | moment, N · m |
| CS | compressor station |
| GCS | head compressor station |
| GPA | gas compressor units |
| VC | screw compressor |
| DCS | booster compressor station |
| VKM | oil-injected screw compressor |
Other catch notations are explained in the text.
Appendix A. The Model of the System with the Optimal Regulator Based on the Pontryagin Principle
In order to optimize the system of the pressure control system at the system outlet, it is necessary to produce a model with an optimal regulator. The selected part of the structural diagram is the optimal regulator based on the Pontryagin maximum principle (Figure A1).
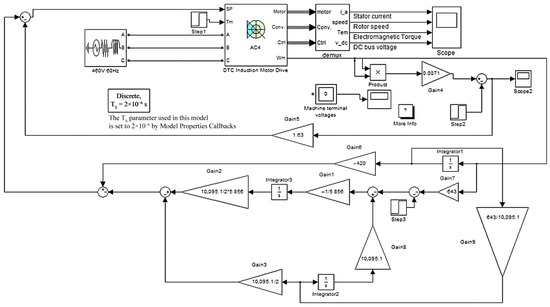
Figure A1.
The mathematical model of the system with the optimal controller.
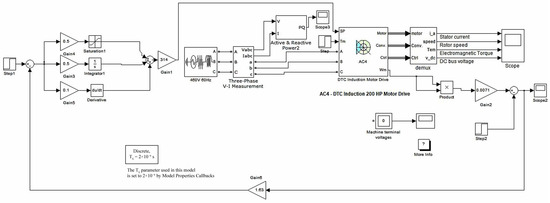
Figure A2.
The mathematical model of the system with the PID controller and energy measurement units.
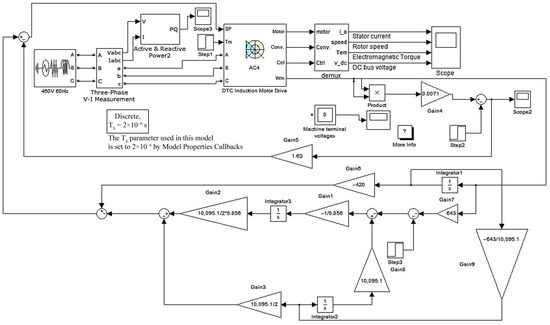
Figure A3.
The mathematical model of the system with the optimal controller and energy measurement units.
Appendix B. Extended Plant Model with Thermal, Leakage, Nonlinear Friction, and Magnetic Saturation
Appendix B.1. Mass and Energy Balance in the Receiver/Compression Volume
Let m be the gas mass, T is temperature, P is pressure, V is the effective volume, R is the gas constant, cp is specific heat.
The thermal balance (lumped):
where Qin accounts for compression power and oil-gas heat exchange (, and hA is an effective heat-transfer coefficient.
Appendix B.2. Leakage Model. Pressure-Driven Internal Leakage Is Modeled as:
Appendix B.3. Nonlinear Mechanical Friction (Compressor Train)
Appendix B.4. Induction Motor with Magnetic Saturation
A dq reduced model uses a current-dependent magnetizing inductance (Lm{im}) or a lookup table:
which effectively reduces torque per ampere under high flux. For deployments that rely on slip-based torque maps, saturation can be captured by a gain (ksat(im) t (0,1]).
Appendix B.5. Parameterization and Identification
The parameters (hA, Cleak, n, τc, B, τs, ωs, α, Lm0) are identified from step-tests (ISO-1217-style) using measured P, T, ω, Pelec. Identified values and bounds are summarized in Table A1.
Appendix B.6. Real-Time Computational Profile and Fault Tolerance

Table A1.
Per-cycle operation count for the PLC implementation.
Table A1.
Per-cycle operation count for the PLC implementation.
| Operation Group | Approx. Count (ops) | Notes |
|---|---|---|
| State update and filters | ~150 | 1st-order low-pass, scaling |
| Regulator algebra (Hamiltonian) | ~400 | multiplications, additions |
| Constraint handling/saturation | ~200 | limiters, anti-windup |
| Fault detection and plausibility | ~200 | range checks, residual calc. |
| Total | ~1000 | compatible with a 2–10 ms cycle |

Table A2.
Memory budget estimate.
Table A2.
Memory budget estimate.
| Item | Size Estimate |
|---|---|
| State and observer vectors | <2 kB (single-precision floats) |
| Calibration and constants | <2 kB |
| Fault detection buffers | ~8 kB (for 1 s at 1 kHz, optional) |
| Logging ring buffer (1 s) | ≤64 kB (optional) |
| Total (without logging) | <10 kB |
| Total (with logging) | <100 kB |
Fault-injection results. To evaluate robustness, representative sensor faults were emulated in simulation: stuck-at pressure (constant of 0.6 MPa), dropout (50% of missing samples), and additive bias (+0.05 MPa). The fault detection and tolerance (FDT) logic flagged anomalies within 50–150 ms. Upon confirmation, the controller switched smoothly to a fallback mode (baseline PID or torque-limited hold). In all cases, pressure remained bounded within ±0.05 MPa of the setpoint, and overshoot was avoided.
Appendix C. The Technology Transfer Plan for Industrial Deployment
The practical rollout of the proposed regulator can be structured in four stages:
Stage 1—Laboratory validation. The controller was synthesized and tested in MATLAB/Simulink and Hardware-in-the-Loop (HIL) environments. Technical prerequisites are a compressor/motor test rig, PLC or an embedded controller, calibrated sensors, and data acquisition.
Stage 2—Pilot-scale demonstration. Deployment on one industrial compressor with parallel PID fallback and detailed logging. Prerequisites are access to VFD with an open control interface, PLC with a 2–10 ms scan cycle, pressure, and electrical measurements integrated into the DCS.
Stage 3—Site-wide pilot. Extension to several units in one station or workshop, with operator training and SCADA/DCS integration. Prerequisites are validated communication protocols, alarm handling, safety interlocks, an HMI operator, and acceptance criteria (energy savings are >10%, stability indices).
Stage 4—Full industrial rollout. Scaling to fleets of compressors, pumps, or fans. Prerequisites are corporate change management, cybersecurity hardening, predictive maintenance integration, and formal certification if required.
At each stage, KPIs include energy savings (% and kWh), dynamic performance (overshoot, settling, variance), reliability (fault-free operation hours), and maintainability (operator acceptance, downtime for integration).
This staged approach ensures that technology transfer proceeds from controlled environments to broad industrial deployment in a structured and low-risk manner.
References
- Natural Resources Canada. Energy Efficiency Reference Guide: Compressed Air; NRCan-Energy Star: Ottawa, ON, Canada, 2024. [Google Scholar]
- Nehler, T. Linking Energy Efficiency Measures in Industrial Compressed Air Systems with Non-Energy Benefits—A Review. Renew. Sustain. Energy Rev. 2018, 89, 72–87. [Google Scholar] [CrossRef]
- Jacobson, M.Z.; Colella, W.G.; Golden, D.M. Cleaning the air and improving health with hydrogen. Science 2005, 308, 1901–1902, (Insight into industrial air systems and environmental impact). [Google Scholar] [CrossRef] [PubMed]
- Klyuev, R.V.; Dedov, S.I. Determination of Inactive Powers in a Single-Phase AC Network. Energies 2021, 14, 4814. [Google Scholar] [CrossRef]
- Forbicini, F.; Pinciroli Vago, N.O.; Fraternali, P. Time series analysis in compressor-based machines: A survey. arXiv 2024, arXiv:2402.17802. [Google Scholar] [CrossRef]
- Mak, T.W.K.; Van Hentenryck, P.; Zlotnik, A.; Hijazi, H.; Bent, R. Efficient dynamic compressor optimization in natural gas transmission systems. arXiv 2015, arXiv:1511.07562. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, X.; Wang, H. Research on Energy-Saving Operation of Screw Air Compressor. Res. J. Appl. Sci. Eng. Technol. 2013, 6, 325–333. [Google Scholar] [CrossRef]
- Kong, D.; Lin, W.; Cai, M.; Qin, H. Analysis on Energy-Saving Operation of Screw Compressor under Load/Unload Operating Conditions. J. Beijing Univ. Aeronaut. Astronaut. 2012, 38, 405–409. [Google Scholar]
- Atlas Copco. Next-Generation VSD Delivers More Air at a 12% Lower Cost; Atlas Copco Customer Benefit; Atlas Copco: Rock Hill, SC, USA, 2024. [Google Scholar]
- Abdelaziz, O.; Saidur, R.; Mekhilef, S. A review on energy saving strategies in industrial compressed-air systems. Renew. Sustain. Energy Rev. 2011, 15, 150–163. [Google Scholar]
- Zahlan, J. Simulating the effects of air compressor controls and sequencing strategies in variable air demand environments. In Proceedings of the ACEEE Summer Study on Energy Efficiency in Industry, Pacific Grove, CA, USA, 13–17 July 2017; pp. 49–59. [Google Scholar]
- Liebenberg, L.; Velleman, D.; Booysen, W. A simple demand-side management solution for a typical compressed-air system at a South African gold mine. Journal of Energy in Southern Africa 2012, 23(2), 17–26. [Google Scholar] [CrossRef]
- Masanet, E.; Chiu, P.; Horvath, A.; Masanet, E. Toward energy efficiency and decarbonization in data centers. Science 2020, 367, 984–986. [Google Scholar] [CrossRef]
- Boscain, U.; Sigalotti, M.; Sugny, D. Introduction to the Pontryagin Maximum Principle for Quantum Optimal Control. arXiv 2020, arXiv:2010.09368. [Google Scholar] [CrossRef]
- Konda, R.; Chandan, V.; Crossno, J.; Pollard, B.; Walsh, D.; Bohonek, R.; Marden, J.R. Utilizing load shifting for optimal compressor sequencing in industrial refrigeration. arXiv 2024, arXiv:2403.07831. [Google Scholar] [CrossRef]
- NREL. Compressed Air Evaluation Protocol; “Energy Impact of Leak Repairs”; National Renewable Energy Laboratory: Golden, CO, USA, 2021; Chapter 22. [Google Scholar]
- Pontryagin, L.S.; Boltyanskii, V.G.; Gamkrelidze, R.V.; Mishchenko, E.F. The Mathematical Theory of Optimal Processes; Wiley-Interscience: New York, NY, USA, 1962. [Google Scholar]
- Martyushev, N.V.; Malozyomov, B.V.; Sorokova, S.N.; Efremenkov, E.A.; Valuev, D.V.; Qi, M. Review Models and Methods for Determining and Predicting the Reliability of Technical Systems and Transport. Mathematics 2023, 11, 3317. [Google Scholar] [CrossRef]
- Ohsawa, T. Contact Geometry of the Pontryagin Maximum Principle. arXiv 2015, arXiv:1501.07855. [Google Scholar] [CrossRef]
- Efremenkov, E.A.; Qi, M. Mathematical Modeling of Mechanical Forces and Power Balance in Electromechanical Energy Converter. Mathematics 2023, 11, 2394. [Google Scholar] [CrossRef]
- Basha, N.; Kovacevic, A.; Stosic, N.; Smith, I.K. Effect of oil injection on twin screw compressor performance. IOP Conf. Ser. Mater. Sci. Eng. 2018, 425, 012009. [Google Scholar] [CrossRef]
- ISO 1217:2009; Displacement Compressors—Acceptance Tests. International Organization for Standardization (ISO): Geneva, Switzerland, 2009.
- Petrilean, D.C. Method of Calculus for the Power Input of the Helical Screw Compressor. U.P.B. Sci. Bull. Ser. D 2009, 71, 122–130. [Google Scholar]
- Mojaddam, M.; Torshizi, S.A.M. Design and optimization of meridional profiles for the impeller of centrifugal compressors. J. Mech. Sci. Technol. 2017, 31, 4853–4861. [Google Scholar] [CrossRef]
- Eolss Kurzhanski, A.B. Control Systems, Robotics and Automation—Vol. VIII: Pontryagin’s Maximum Principle; Encyclopedia of Life Support Systems (EOLSS), UNESCO: Oxford, UK, 2018. [Google Scholar]
- Abdan, S.; Basha, N.; Kovacevic, A.; Stosic, N.; Birari, A. Development and Design of Energy Efficient Oil Flooded Screw Compressors. IOP Conf. Ser. Mater. Sci. Eng. 2019, 604, 012015. [Google Scholar] [CrossRef]
- Kissock, K.; Selvacanabady, A. Energy-Efficient Air-Compressor Sequencing Using Non-Linear Optimization. In Proceedings of the 2021 ACEEE Summer Study on Energy Efficiency in Industry, Virtual, 12–15 July 2021; American Council for an Energy-Efficient Economy (ACEEE): Washington, DC, USA, 2021; pp. 1–13. [Google Scholar]
- He, X.; Zheng, X. Mechanisms of Sweep on the Performance of Transonic Centrifugal Compressor Impellers. Appl. Sci. 2017, 7, 1081. [Google Scholar] [CrossRef]
- Shishkin, P.V.; Valuev, D.V.; Qi, M. Mathematical Logic Model for Analysing the Controllability of Mining Equipment. Mathematics 2024, 12, 1660. [Google Scholar] [CrossRef]
- Wahba, W.; Tourlidakis, A. A genetic algorithm applied to the design of blade profiles for centrifugal pump impellers. In Proceedings of the 15th AIAA Computational Fluid Dynamics Conference, Anaheim, CA, USA, 11–14 June 2001; Volume 11, p. 14. [Google Scholar]
- Barsi, D.; Costa, C.; Cravero, C.; Ricci, G. Aerodynamic design of a centrifugal compressor stage using an automatic optimization strategy. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014; p. V02BT45A017. [Google Scholar]
- Oparina, T.A.; Sevryugina, N.S.; Gozbenko, V.E.; Kondratiev, V.V. Determination of the Performance Characteristics of a Traction Battery in an Electric Vehicle. World Electr. Veh. J. 2024, 15, 64. [Google Scholar] [CrossRef]
- Malozyomov, B.V.; Martyushev, N.V.; Sorokova, S.N.; Efremenkov, E.A.; Valuev, D.V.; Qi, M. Mathematical Modelling of Traction Equipment Parameters of Electric Cargo Trucks. Mathematics 2024, 12, 577. [Google Scholar] [CrossRef]
- Kim, J.H.; Choi, J.H.; Husain, A.; Kim, K.Y. Design Optimization of a Centrifugal Compressor Impeller by Multi-Objective Genetic Algorithm. In Proceedings of the ASME 2009 Fluids Engineering Division Summer Meeting, Vail, CO, USA, 2–6 August 2009; pp. 2–6. [Google Scholar]
- ISO 11011:2013; Compressed Air—Energy Efficiency—Assessment. International Organization for Standardization: Geneva, Switzerland, 2013.
- Mousavi, S.; Kara, S.; Kornfeld, B. Energy Efficiency of Compressed Air Systems. Procedia CIRP 2014, 15, 313–318. [Google Scholar] [CrossRef]
- Shishkin, P.V.; Malozyomov, B.V.; Martyushev, N.V.; Sorokova, S.N.; Efremenkov, E.A.; Valuev, D.V.; Qi, M. Development of a Mathematical Model of Operation Reliability of Mine Hoisting Plants. Mathematics 2024, 12, 1843. [Google Scholar] [CrossRef]
- Martyushev, N.V.; Malozyomov, B.V.; Demin, A.Y.; Pogrebnoy, A.V.; Efremenkov, E.A.; Valuev, D.V.; Boltrushevich, A.E. Modeling the Reliability of an Electric Car Battery While Changing Its Charging and Discharge Characteristics. Mathematics 2025, 13, 1832. [Google Scholar] [CrossRef]
- Pogrebnoy, A.V.; Efremenkov, E.A.; Valuev, D.V.; Boltrushevich, A.E. Improving the Reliability of Current Collectors in Electric Vehicles. Mathematics 2025, 13, 2022. [Google Scholar] [CrossRef]
- ISO 5389:2005; Turbocompressors—Performance Test Code. International Organization for Standardization (ISO): Geneva, Switzerland, 2005.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).