Abstract
The accurate segmentation of pigmented skin lesions is a critical prerequisite for reliable melanoma detection, yet approximately 30% of lesions exhibit fuzzy or poorly defined borders. This ambiguity makes the definition of a single contour unreliable and limits the effectiveness of computer-assisted diagnosis (CAD) systems. While clinical assessment based on the ABCDE criteria (asymmetry, border, color, diameter, and evolution), dermoscopic imaging, and scoring systems remains the standard, these methods are inherently subjective and vary with clinician experience. We address this challenge by reframing segmentation into three distinct regions: background, border, and lesion core. These regions are delineated using superpixels generated via the Simple Linear Iterative Clustering (SLIC) algorithm, which provides meaningful structural units for analysis. Our contributions are fourfold: (1) redefining lesion borders as regions, rather than sharp lines; (2) generating superpixel-level embeddings with a transformer-based autoencoder; (3) incorporating these embeddings as features for superpixel classification; and (4) integrating neighborhood information to construct enhanced feature vectors. Unlike pixel-level algorithms that often overlook boundary context, our pipeline fuses global class information with local spatial relationships, significantly improving precision and recall in challenging border regions. An evaluation on the HAM10000 melanoma dataset demonstrates that our superpixel–RAG–transformer (region adjacency graph) pipeline achieves exceptional performance (100% F1 score, accuracy, and precision) in classifying background, border, and lesion core superpixels. By transforming raw dermoscopic images into region-based structured representations, the proposed method generates more informative inputs for downstream deep learning models. This strategy not only advances melanoma analysis but also provides a generalizable framework for other medical image segmentation and classification tasks.
1. Introduction
Melanoma is an aggressive malignant tumor that originates from melanocytic cells, which are primarily located in the skin. The development of melanoma is influenced by several key risk factors, including a history of excessive sun exposure and sunburns, Fitzpatrick skin types I and II, and the presence of atypical nevi.
According to epidemiological data, the incidence rate of melanoma in the United States was reported at 21.2 cases per 100,000 individuals in 2022 [1]. Projections from the American Cancer Society estimate that 104,960 new cases will be diagnosed in 2025 [2]. Despite significant advancements in therapeutic approaches, melanoma continues to exhibit a mortality rate of approximately 8% [3,4].
The determination of whether a pigmented lesion is benign or malignant has been approached from multiple perspectives. Clinically, physicians rely on visual inspection guided by the ABCDE criteria and dermoscopic patterns, often supported by scoring systems, though these remain highly dependent on expertise and prone to subjectivity. To reduce variability, computer-assisted diagnosis (CAD) systems have emerged, initially using handcrafted, feature-based methods to quantify asymmetry, border irregularity, color, and diameter and more recently advancing toward deep learning models, including convolutional neural networks and transformer-based architectures. While these approaches have improved diagnostic accuracy, both clinical assessment and CAD systems face limitations related to subjectivity in lesion boundaries and variability across datasets. A more detailed discussion of these methodologies is provided in Section 2.
A comprehensive meta-analysis conducted within the medical community evaluated the effectiveness of AI models in skin cancer detection. Following the PRISMA methodology, the review included 272 publications from an initial pool of 14,224 studies, spanning the years 2000 to 2021. The analysis reported a mean F1 score of 0.807 for melanoma detection, with scores ranging from 0.732 to 0.882 [5].
Despite significant advancements in deep learning-based melanoma detection, current AI methods remain insufficient for widespread clinical adoption, largely due to limitations in data quality, particularly regarding melanoma subtypes, patient demographics, image quality, dataset provenance, and the tendency for DL systems to use such data without sufficient contextual consideration. This study bridges computer science and medical perspectives to address these shortcomings by investigating biases arising from annotated lesion borders, especially in irregular or ambiguous cases, and introducing a region-based analysis using superpixels, rather than the traditional pixel-by-pixel approach employed in CAD systems.
Contributions
Although AI models have significantly advanced in recent years, delineating lesions remains a subjective task even for specialists. We propose that the lesion border should not be treated as a single, well-defined line but, rather, as a transitional region that separates the background from the core of the lesion. Figure 4b presents a blended image composed of the ground truth mask overlaid on the original lesion. In our work, the border region is defined as the area between the outer edge of the mask and the visible boundary of the lesion. This region can be more precisely delineated using superpixels, which provide a spatially coherent segmentation aligned with local image features. Our objective is to develop a model capable of accurately identifying all three regions. In this paper, we propose a new method called SPADE (Superpixel Adjacency Driven Embedding) for three-class melanoma segmentation. The main contributions of SPADE are as follows.
- Definition of three anatomical zones: we define three distinct zones in dermoscopy images, the background, the border, and the core of the lesion.
- Transformer-based superpixel embedding: we train a transformer autoencoder to generate embeddings for each superpixel, enabling the model to capture contextual relationships between spatially distant regions belonging to the same class.
- Context-Aware Region Adjacency Graph (RAG): we construct a region adjacency graph using superpixels obtained via the SLIC algorithm to model spatial relationships.
- Input definition based on the region adjacency graph: each input vector consists of the embedding of a given superpixel, along with the embeddings of its immediate neighbors, effectively capturing the local spatial context.
- Semantic representation of dermoscopy images: the system effectively captures the semantic content of dermoscopy images, supporting improved lesion characterization.
2. Assessing the Malignancy of Pigmented Lesions
The determination of whether a pigmented skin lesion is benign or malignant is a critical step in melanoma detection. Several approaches exist, spanning traditional clinical examination, computer-assisted diagnostic (CAD) tools, and modern machine learning–based systems. While clinical methods remain the standard in practice, CAD systems have evolved from handcrafted feature extraction to advanced deep learning models, each offering distinct advantages and limitations. This section outlines these approaches in detail.
2.1. Clinical Assessment Methods
Clinical examination of melanoma relies on the assessment of lesion characteristics based on the ABCDE criteria, as depicted in Figure 1, which evaluate asymmetry, border irregularity, color variation, diameter greater than 6 mm, and evolution over time [6]. Other than the diameter, the ABC criteria are subject to subjective interpretation. Furthermore, physicians with more clinical experience tend to demonstrate higher diagnostic accuracy [7].
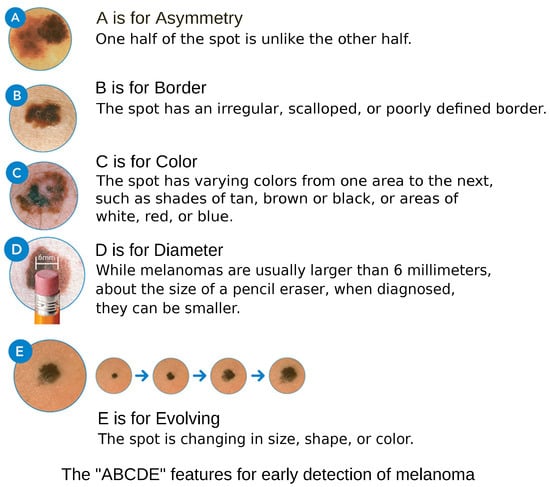
Figure 1.
ABCD Features. Courtesy of American Academy of Dermatology Association.
Dermoscopy is a non-invasive diagnostic technique widely used by general practitioners (GPs) and dermatologists to improve the detection of skin lesions suspected of malignancy. A dermatoscope, in simple terms, is a magnifying lens equipped with illumination and, in many cases, digital imaging capabilities. It facilitates the visualization of subsurface skin structures that are not visible to the unaided eye, as shown in Figure 2a. Studies have demonstrated that the incorporation of dermoscopy into the diagnostic workflow enhances accuracy; it increases accuracy from 54% to between 76% and 79%, compared to visual inspection alone [8]. Dermoscopy captures unique and mixed basic structural patterns such as reticular, streaked, globular, and homogeneous, as illustrated in Figure 2b.
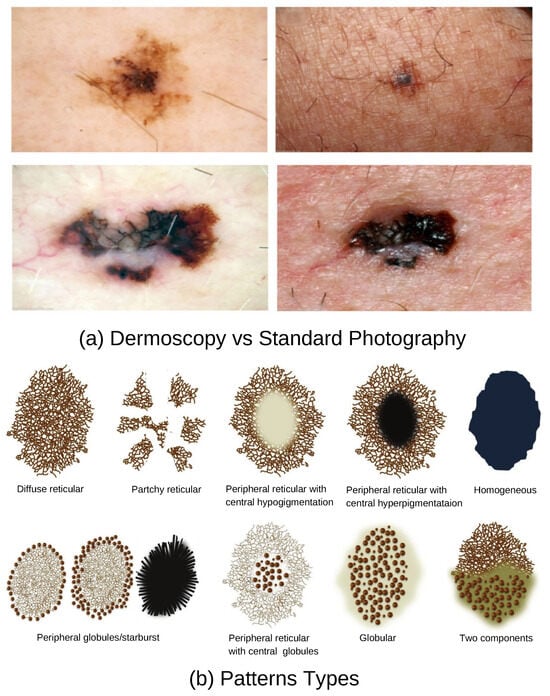
Figure 2.
Dermoscopy Patterns. Courtesy American Family Physician.
For GPs, the initial step involves distinguishing melanocytic lesions from non-melanocytic ones through clinical evaluation to ensure accurate preliminary classification. The second step focuses on differentiating nevi from melanoma by applying clinical criteria such as the ABCDE rules, interpreting dermoscopic findings, and utilizing scoring systems. Suspicious lesions are typically referred to a specialist (dermatologist) for further assessment. We have described how human intelligence, through visual inspection, dermoscopic tools, and scoring systems, is used to determine whether a lesion is benign or malignant. Nonetheless, these evaluation methods rely heavily on human judgment, whether through clinical assessment, the use of tools such as dermoscopy, or the application of clinician-derived scoring systems, making them inherently prone to subjectivity.
2.2. CAD Systems
The diagnostic subjectivity and inter-observer variability associated with melanoma underscore the need for automated and objective computer-assisted diagnosis (CAD) systems.
2.2.1. Classification Based on the ABCD Rule
Two primary approaches have been developed for melanoma classification using CAD. The first approach aligns with the clinical methodology and employs scoring systems based on the ABCD rule. To ensure objectivity, automated methods have been proposed for detecting shape asymmetry, color variegation, and lesion diameter. Among these, Fourier descriptors are considered the most robust techniques for quantifying asymmetry due to their mathematically rigorous formulation and demonstrated alignment with expert dermatological assessments, achieving up to 92% concordance with dermatologist evaluations [9,10]. For border irregularity, combined shape descriptors including fractal dimension, Zernike moments, and convexity coupled with convolutional neural network (CNN) classifiers have achieved state-of-the-art results, with reported classification accuracies reaching 93.6% [11]. In assessing color variegation, the CIELAB color space combined with the Minkowski distance metric has proven the most effective, offering perceptual uniformity that closely matches human color vision and handling wide color variations reliably [12]. Regarding lesion diameter, Feret’s diameter has been identified as the most accurate and consistent measure, particularly for lesions with irregular boundaries [12].
2.2.2. Classification Based on Direct Feature Extraction
The second approach focuses on direct skin lesion classification, which can be performed using either full images or segmented lesion regions. Studies have shown that classifiers trained on segmented images generally outperform those trained on whole images [13]. In classical CAD systems, lesion segmentation is typically performed using three main approaches: edge-based, region-based, and threshold-based methods [14]. For classification, methods such as score averaging (AVGSC), linear SVM, and non-linear SVM using a histogram intersection kernel have demonstrated acceptable performance levels [15].
The advent of deep learning has significantly enhanced both segmentation and classification accuracy by leveraging CNNs and transformer-based architectures [16]. Deep supervised learning has led to the development of increasingly sophisticated architectures beyond traditional CNNs.
Popular CNN-based models for melanoma classification include ResNet [17], VGG16 [18], MobileNet [19], DenseNet [19], and Inception [20]. Transformer-based architectures have also demonstrated strong performance [21,22,23]. Reported classification performance across these models varies, with accuracy ranging from 80% to 98%, sensitivity from 60% to 90%, and specificity from 86% to 98%. Among these, EfficientNet-B7 [24] and transformer-based models [21,22,23] exhibit the highest diagnostic accuracy.
Models based solely on CNNs have been increasingly outperformed by architectures incorporating encoder–decoder frameworks, reflecting a shift towards more effective hierarchical feature representations. CNN-based segmentation models fall into two primary categories: pixel-wise upsampling techniques, such as fully convolutional networks (FCNs), and spatial and pyramidal upsampling approaches, such as the DeepLab family of models [25]. Notably, DeepLabV3+ introduces a decoder module designed to enhance segmentation accuracy and refine feature extraction, particularly at object boundaries [26]. An encoder–decoder architecture like U-Net and V-Net utilize symmetric upsampling at each layer to preserve spatial resolution during reconstruction. This improves the fidelity of the segmented output [27,28,29]. Further advancements have been realized through attention-based models, which improve both feature selection and contextual awareness. Prominent architectures in this category include the vision transformer (ViT) [30,31] and visual attention networks [32], which leverage self-attention mechanisms to capture long-range dependencies within an image. The segmentation accuracy of deep learning models for skin lesion analysis ranges from 80% to 98%, with recent architectures consistently surpassing their predecessors in both precision and generalization capacity.
Accurate lesion segmentation is essential for the reliable extraction of ABCD features and for effective classification. In most publicly available datasets, lesion boundaries are manually annotated by dermatologists, residents, medical students, or trained personnel. This process is not only time-consuming but also inherently subjective. For lesions with fuzzy or ambiguous boundaries, substantial inter-annotator variability exists. A study by Kittler et al. reported discrepancies of up to 20–30% due to ambiguous lesion edges and variations in annotator expertise [33,34,35]. To address this, some organizations provide standardized segmentation protocols. For instance, the ISIC archive employs multi-rater consensus in cases with ambiguous lesion boundaries [15]. These practices underscore the degree of subjectivity that remains embedded in CAD systems dependent on manual segmentation for classification or ABCD rule application.
3. Related Work
Fine-tuning AI models for accurate border delineation in blurry or low-contrast dermoscopic images has been addressed through methods that identify and label regions adjacent to lesions. Adegun et al. employ probabilistic models in which each pixel is assigned a value between 0 and 1, representing the likelihood of belonging to the lesion [36]. The algorithm ultimately produces a lesion boundary represented as a line. Halil et al. utilize region of interest (ROI) bounding, where an initial bounding box or elliptical region is drawn around the lesion, followed by consensus among multiple annotators [37]. Although the initial stage localizes the lesion broadly, the final boundary is refined using the GrabCut algorithm, resulting in a sharply delimited line. Zahra et al. propose an approach based on multiple expert-generated masks, from which a consensus mask is derived through fusion [38]. The final output is again a single mask outlined by a distinct boundary line. Li et al. [39,40] introduce a method that explicitly marks regions of uncertainty, rather than enforcing a hard boundary. They use class activation maps to generate pseudo-labels and apply binary thresholding to create segmentation masks. This approach allows the model to learn from ambiguous regions, thereby improving robustness in uncertain contexts. In contrast to these methods, which ultimately produce a line-based lesion boundary, our approach focuses on defining lesion regions, providing a more granular and context-aware representation.
Graph-based methods also commonly leverage superpixels by constructing an RAG, where each node represents a superpixel and edges encode similarity metrics between neighboring regions such as color, texture, or boundary strength. Once the graph is constructed, segmentation is performed using algorithms such as spectral clustering, normalized cuts, or min-cut/max-flow, and neural networks, which partition the graph into semantically meaningful regions [41]. RAGs naturally integrate with graph neural networks (GNNs) and have been employed for image classification tasks. Nazir et al. applied graph convolutional neural networks (GCNNs) using both spatial and spectral convolution techniques, demonstrating that spectral-based models outperform spatial-based models and classical CNNs while requiring less computational cost [42]. Avelar et al. explored attention-based GNNs for classification and showed that the feature space can be enhanced by weighting the edges of a superpixel graph using a learned function based solely on geometric information [41]. Nowosad et al. apply graph-based segmentation to non-imagery geospatial data by grouping superpixels based on dissimilarity measures and pruning the resulting graph to a minimum spanning tree (MST) [43]. Additionally, Qin et al. propose a superpixel-based and boundary-sensitive CNN model specifically designed for liver segmentation, demonstrating the effectiveness of combining region-based pre-processing with deep learning techniques [44]. Similar to our work, these studies employed superpixels and RAG to construct graph representations. However, unlike prior work, the current phase of our study does not incorporate graph neural networks or edge attributes for classification.
4. Methods and Algorithm Design
The SPADE pipeline proceeds as follows: the images are first resized; superpixels are then generated using the Simple Linear Iterative Clustering (SLIC) algorithm; a region adjacency graph is constructed; each superpixel is labeled by class (background, border, and lesion); class-specific embeddings are generated using a transformer; and finally, a transformer is trained to predict the three classes.
4.1. Resizing Images
All images were initially adjusted to a landscape orientation and resized to a width of 1024 pixels and a height of 768 pixels using a bilinear interpolation algorithm from the OpenCV framework.
4.2. Superpixel Generation Strategy
Superpixel segmentation partitions an image into regions composed of similar and spatially connected pixels, providing perceptually meaningful atomic regions.
SLIC is classified as a neighborhood-based clustering algorithm. SLIC is an adaptation of the k-means clustering algorithm, specifically designed for efficient superpixel generation. It introduces two key parameters: a search radius that limits the number of distance computations, and a weighted distance metric that balances color similarity and spatial proximity, S. The distance function is defined as follows:
where is the Euclidean distance in the RGB color space, is the geometric distance between pixels, and m is a compactness parameter that controls the trade-off between color and spatial proximity. These parameters enable control over the size and compactness of the resulting superpixels. Furthermore, SLIC’s linear computational complexity contributes to its widespread adoption in superpixel generation tasks [45].
Each pixel in SLIC is represented by a five-dimensional feature vector consisting of three components for color and two for spatial coordinates . The algorithm employs the CIELAB color space, which offers a perceptually uniform representation of color, ensuring a more meaningful similarity measure. The segmentation process in SLIC involves three main steps. First, clusters are initialized based on the desired number of superpixels. Second, an iterative clustering process assigns pixels to the nearest cluster using a distance function that incorporates both color and spatial information. Finally, a post-processing step enforces spatial connectivity to ensure that each superpixel forms a contiguous region [45,46].
SLIC superpixels effectively capture low-level image features like color, position, and depth while preserving fine-grained boundary details. This is essential for detecting subtle background transitions around lesions, which clinicians often rely on. Moreover, superpixels reduce noise by averaging local pixel variations within each region and help focus computational resources on meaningful structures since larger segments often carry more semantic information than individual pixels.
The SLIC algorithm was applied to each image to obtain its segmented regions. Specifically, we employed the SuperpixelSLIC algorithm from OpenCV with the following parameters: a desired number of superpixels k set to 600, an area size of 1320, , and a ruler value (m) of 19220, producing the segmentations shown in Figure 3. The software suite provides three different algorithms, SLIC, SLICO, and MSLIC, among which SLIC was chosen due to its balance between algorithmic compactness, boundary recall, and computational efficiency. Each superpixel was assigned a unique identifier, which was used to track and analyze the segmented regions [47]. At the beginning of the algorithm, each superpixel is assigned a unique identifier (ID) when the initial centroids are defined. This ID is stored as an integer value in the database and remains constant throughout the duration of the experiment.
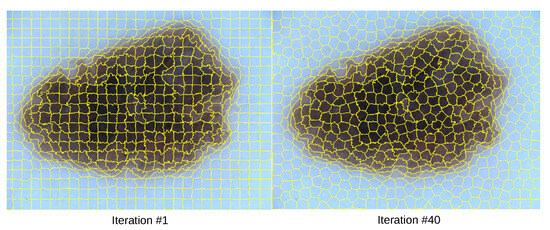
Figure 3.
SLIC Superpixels Image Sequences.
4.3. Constructing the Region Adjacency Graph (RAG)
The RAG was constructed by traversing the labeled superpixel matrix and establishing undirected edges between adjacent superpixels with differing labels based on 4-and 8-connected neighborhood criteria, capturing spatial connectivity through horizontal, vertical, and diagonal adjacency, as depicted in Figure 4a [48].
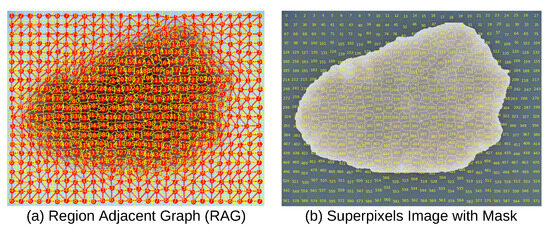
Figure 4.
Dermoscopy Image, Superpixels, RAG, and Mask.
We hypothesize that, similar to how transformers leverage the sequential ordering of words to learn language structure, our region adjacency graph (RAG) explicitly defines “neighbor” relationships among superpixels. Unlike vision transformers, where all patches are included as input tokens, our RAG-based approach provides meaningful context to the transformer. In this framework, the transformer’s self-attention mechanism operates over graph nodes, attending preferentially to adjacent regions that share meaningful boundaries or semantic relationships. In contrast to vision transformers, which may waste computational resources attending to regions lacking relevant context, our RAG-based model focuses attention on superpixels containing semantically relevant information.
For instance, consider an image with a size of pixels, with patch sizes of ; this results in a total of 196 patches. In a vision transformer, each transformer layer computes self-attention with a complexity of , where N is the number of patches and D is the embedding dimension. In our superpixel-based approach, we observe that each superpixel has, on average, 7 neighbors (ranging from (2–19)), leading to a significantly reduced complexity of .
4.4. Creating Features
For each image, we extracted metadata including the filename, height, and width. We also computed the mean and standard deviation for each RGB channel. For each superpixel, we computed the mean, standard deviation, kurtosis, and skewness per RGB channel. Using the segmented region as a binary mask in a 2D image, where pixels belonging to the superpixel were set to 1 and all others to 0, we calculated the area , centroid , centroid , and second central moments using the OpenCV moments function. Additionally, neighboring superpixels were identified and included as part of the superpixel-level information.
To facilitate further analysis, the superpixels were categorized into three classes (background, border, and core lesion) for a subset of 2000 images from the HAM10000 dataset (“Human Against Machine with 10,000 training images”) [49]. A custom annotation tool was developed to allow manual labeling of superpixels. The supplementary video (Video S1) provides a visual demonstration of how the annotator selects the “border in” and “border out” regions on dermoscopic images. The “border out” class includes superpixels marking the transition between the lesion and the surrounding skin, whereas the “border in” class contains superpixels located just inside the lesion boundary.
To delineate the lesion interior, a concave hull algorithm was applied to enclose all superpixels within the “border in” region. Unlike the convex hull, which may encompass unrelated background superpixels, the concave hull prevents the inclusion of superpixels that do not belong to the lesion, as illustrated in Figure 5b.
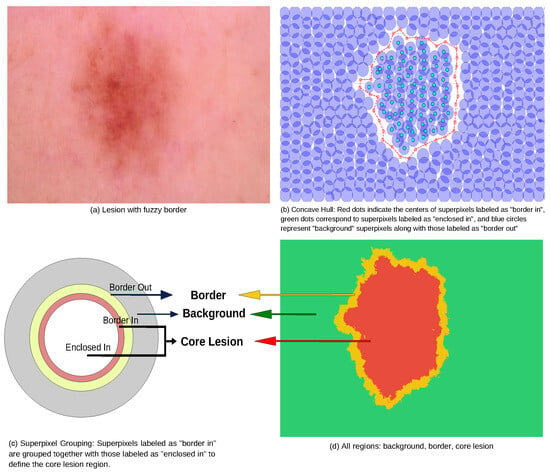
Figure 5.
Grouping superpixels on classes.
Based on the proposed classification scheme, we define the core lesion as the union of superpixels labeled as “border in” and those enclosed by them. The border class corresponds to the “border out” superpixels, and all the remaining superpixels are assigned to the background class, as shown in Figure 5c.
Table 1 presents the total number of superpixels per category, where class labels 0, 1, and 2 correspond to background, core lesion, and border, respectively. We use these regions because they encode clinically meaningful cues: the background region supports estimation of the Fitzpatrick skin type, while the lesion border and core inform assessment of the ABCD features, enabling dermatologists to form a coherent mental map of the lesion.

Table 1.
Superpixel class statistics.
4.5. Transformer Autoencoders for Generating Embeddings
To generate embeddings for each superpixel, we train a transformer autoencoder independently for each semantic class (background, border, or core). Each superpixel is resized to contain 700 pixels per channel, and the latent space dimensionality is set to 256. The model architecture is illustrated in Figure 6. The encoder consists of four multi-head self-attention layers (with four heads each), interleaved with four feed-forward linear layers. This encoder maps the input patch tokens to a 256-dimensional latent vector. The decoder is symmetric, consisting of four self-attention layers and four linear layers, and it reconstructs the original input from the latent representation. Each attention and feed-forward sub-layer is followed by residual connections and layer normalization to stabilize training and improve gradient flow.
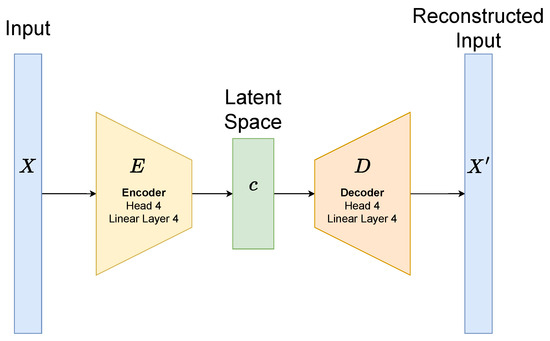
Figure 6.
Transformer autoencoder.
We train a separate autoencoder for each class using only superpixels labeled accordingly. The reconstruction loss is measured using the mean squared error (MSE) between the original input and the decoder’s output. Optimization is performed using the Adam optimizer with early stopping, based on an 80/20 training-validation split (random seed = 40).
By leveraging the transformer’s self-attention mechanism, these autoencoders effectively learn to encode irregular, shape-conforming superpixels. This allows them to capture not only intra-region content but also inter-region semantic patterns—capabilities that fixed grid patches or traditional CNN encoders cannot achieve as efficiently. We hypothesize that combining these learned embeddings with our region adjacency graph (RAG) structure (Section 4.3) enables a context-aware segmentation framework built upon semantically meaningful, spatially grounded building blocks.
We also trained a vanilla autoencoder to obtain embeddings; however, it yielded a higher training loss and required longer training time than the transformer autoencoder.
The extracted information was stored in a Neo4j graph database [50], where the data was structured into three main entities, images, superpixels, and centroids, as shown in Figure 7a,b. The image entity contained all image-related properties, while the superpixel entity stored superpixel-specific characteristics, including the embeddings generated via the latent space. The centroid entity recorded the centroid’s x and y coordinates. Within the database, IN_IMAGE relationships linked each image entity to its corresponding superpixel entities. NEIGHBOR_OF relationships connected superpixel entities with their neighboring superpixels, such that edge weights represented the Euclidean distance between RGB mean values. Finally, CENTER_AT relationships associated each Superpixel entity with its respective Centroid.
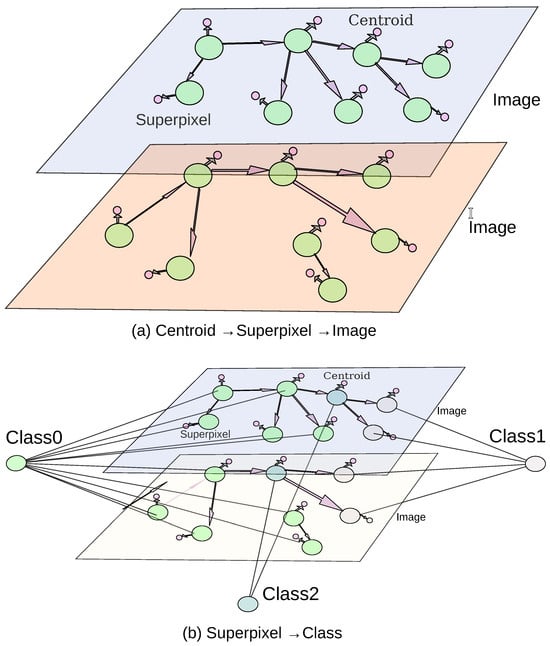
Figure 7.
Graph representation of RAG.
PyTorch version 2.2.2 and CUDA 12 were used to create and run the deep learning models for training and inference. The data was normalized and split amongst training and validation sets, 80% and 20%, respectively. We set the random seed to 40 for all experiments.
The described steps to obtain the embeddings are clearly depicted on the Algorithm 1.
| Algorithm 1: Obtain embeddings from superpixels and neighbors. |
 |
5. Results
5.1. Experiments Phase One
HAM10000 dataset contains dermatoscopic images of both malignant and benign pigmented lesions, with diagnoses confirmed through histopathology, dermatologist consensus, and clinical evolution.
The features can be originated solely from basic statistics extracted from each superpixel, or from a combination of basic statistics and learned embeddings, as illustrated in Figure 8a. Additionally, feature vectors were constructed using information either from a single superpixel or from its neighboring superpixels, as shown in Figure 8b. In the latter case, the order of concatenation was determined by sorting the superpixels according to their ID numbers in ascending order. The combination of these features and their spatial origin forms the basis for constructing our input vectors.
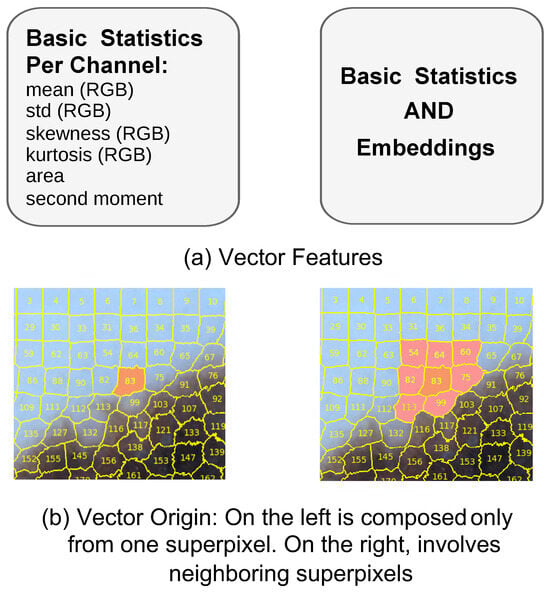
Figure 8.
Building vectors.
In the first phase of our experiments, we constructed four distinct types of input–output feature vectors to support different modes of training and inference:
- Type I: The input vector consists of basic region descriptors mean, standard deviation, skewness, and kurtosis of the RGB channels, area, centroid, and shape moments extracted from the target superpixel. The output is the class label associated with the target superpixel.
- Type II: The input vector includes the basic descriptors of the target superpixel, as well as those of its neighboring superpixels. The output remains the class label of the target superpixel.
- Type III: Similar to Type II, the input concatenates descriptors of both the target and neighboring superpixels. However, the output vector extends to predict the class label for every superpixel included in the input group, encompassing both the target and its neighbors.
- Type IV: This configuration consists of two sets of input–output vectors. The first input vector encodes the statistical descriptors of the neighboring superpixels, with the corresponding output vector specifying their class labels. The second input vector captures the descriptors of the target superpixel alone, with a dedicated output vector indicating its class.
The following neural architectures were used to model these input–output relationships:
- Linear neural network: a fully connected feed-forward network with three hidden layers of sizes 128, 64, and 32 applied to the Type I and Type II feature vectors.
- GRU RNN (many-to-one): A recurrent neural network utilizing four gated recurrent units (GRUs), applied to the sequential embedding of neighbor features (Type II). The final hidden state is passed to a softmax classifier for target class prediction.
- Transformer encoder–decoder (many-to-one): The encoder, composed of four self-attention heads, processes the sequence of target and neighbor superpixels (Type IV). A decoder with four attention heads attends to the encoded context and predicts the target superpixel’s class.
- Transformer encoder (many-to-many): A transformer encoder block (with four self-attention heads) jointly processes the concatenated feature set from multiple superpixels (Type III). It outputs class predictions for each region simultaneously.
In our first experiment, we trained a linear neural network on the first vector type to predict the class of each superpixel. As shown in Table 2, the linear neural network performs adequately, given the limited feature set, particularly for Classes 0 and 1 with F1 scores of 0.8333 and 0.8077, respectively. Class 1 exhibits better differentiation from other classes, with the highest accuracy (0.9091) and competitive recall (0.7915). The model performs poorly on class 2 with an F1 score of 0.2937.

Table 2.
Model performance.
In the second experiment, we trained a linear neural network on the second vector type to predict the class of the target superpixel. As depicted in Table 2, compared to the previous model, the values are higher; however, the behavior is similar. The model is good enough for classes 0 and 1, but it underperforms for class 2. Class 1 is better differentiated than the other classes. These results suggest that incorporating neighboring superpixel properties enhances classification, especially for classes 0 and 1.
In the third experiment, we modeled the data as a sequential input of superpixels in ascending order, and we trained an RNN, specifically a GRU, on the second vector type to predict the class of the target superpixel. As illustrated in Table 2, this model, compared to the previous linear neural network experiments, performs marginally lower for classes 0 and 1, implying that sequential modeling may not fully exploit the contextual dependencies in the third vector type.
In the fourth experiment, we implemented a many-to-one RNN architecture using a transformer model with encoder–decoder components, trained on the fourth vector type to predict the class of the target superpixel. The encoder processes multiple superpixels (including their class information), while the decoder focuses on the target superpixel to generate its predicted class. As portrayed in Table 2, Class 0 achieves exceptional performance, with an F1 score of 0.9377, precision of 0.9229, and recall of 0.9529, indicating highly reliable predictions. Class 1 demonstrates strong results (F1: 0.8828; precision: 0.8823) and the highest accuracy (0.9432), suggesting the effective utilization of contextual information from neighboring superpixels. Class 2, however, continues to underperform, with an F1 score of 0.3572 and remarkably low recall (0.2976), despite moderate precision (0.4468).
In the fifth experiment, we employed a many-to-many RNN architecture, specifically a transformer model, trained on the third vector type to predict the classes of all superpixels simultaneously. As detailed in Table 2, Class 0 achieves near-perfect performance, with an F1 score of 0.9816, precision of 0.9753, and recall of 0.9880, demonstrating robust alignment between predictions and ground truth. Class 1 also exhibits strong performance (F1: 0.9196; precision: 0.9199; recall: 0.9193), with accuracy peaking at 0.9812. However, Class 2 remains a challenge, with an F1 score of 0.4816 and a low recall (0.4011), despite moderate precision (0.6026). These results underscore the efficacy of many-to-many transformers in leveraging global dependencies for multi-superpixel classification tasks, though Class 2 may require targeted architectural or data-centric interventions.
5.2. Experiment Phase Two
In the second phase of our experiments, we selected the best-performing model from the initial evaluation, the transformer encoder model, as the basis for further analysis. To enhance the feature representation, we expanded the Type III input vectors by incorporating additional embeddings generated via the transformer autoencoders. This augmentation resulted in a total of 270 features per input instance.
The updated feature vectors were trained using a many-to-many transformer encoder architecture, consisting of a single encoder block with four self-attention heads. The model demonstrated perfect classification performance, achieving an accuracy and F1 score of 1.0 across all semantic classes.
To assess the robustness and generalizability of this performance, we conducted a five-fold cross-validation. The model consistently produced the same results across all folds, confirming the stability and reliability of the learned representations.
As observed in the transformer many-to-many encoder model, using input vectors without embeddings yields strong classification performance for class 0 and class 1, with F1 scores of 0.98 and 0.91, and accuracies of 0.96 and 0.97, respectively. These results suggest that simple statistical features are sufficient for accurately identifying superpixels corresponding to the background and core of the lesion. In other words, distinguishing these two classes is not particularly challenging for the model. Therefore, incorporating embeddings naturally aligns with the goal of maintaining or improving performance.
In contrast, the classification of class 2 (the lesion border) proves significantly more difficult, with an F1 score of 0.48 despite a high accuracy of 0.97, showing the class imbalance and mis-classification When embeddings are added and the input is expanded to include information from neighboring superpixels, performance improves substantially.
These findings strongly suggest that the border superpixels carry the most significant information in the entire image. Moreover, the border regions may be crucial for distinguishing between benign and malignant lesions.
We acknowledge that our dataset consists of 2000 images, and it is likely that the variation in lesion morphology across diverse skin types and racial backgrounds is limited, an inherent limitation of the dataset.
6. Discussion
At this stage of our research, achieving high performance in either lesion classification (benign vs. malignant), or segmentation is not our primary objective. For the medical community to adopt AI in clinical settings, it is essential to address several challenges related to data quality, methodological rigor, and, most importantly, interpretability [5].
In our study, unlike previous approaches that focus on segmentation or disease classification, the primary role of superpixels is to capture the semantics of the superpixels. Each superpixel is labeled as a background, border, or lesion, corresponding to the classes identified in the image. Superpixels from each class are used to train transformer-based autoencoders in order to produce meaningful embeddings that capture the context of all superpixels of each class, regardless of distance between them. We proved that these embeddings capture the semantic content of the classes more effectively than relying solely on the statistical properties of the superpixels.
To enhance classification performance, we not only utilize the embedding of the target superpixel but also incorporate embeddings from its neighboring superpixels as an input to the classifier. The transformer captures the context of the near superpixels (spatial locality). We consider our approach to be novel, with the main contribution being a model that learns to interpret the semantic structure of an image through superpixel-based embeddings.
We hypothesize that superpixels provide more natural and semantically meaningful context for the classification transformer compared to the fixed square patches used in the vision transformer (ViT) while maintaining the same number of features [51].
We establish the originality of our methodology in several key aspects:
- Defining the border as a region instead of a well-defined line.
- Generating embeddings for every superpixel using a transformer autoencoder.
- Incorporating those embeddings as features for further training.
- Taking into account the neighborhood to create the input vectors.
However, our study involved several limitations. These include the dependency on SLIC segmentation quality, the need for manual annotations, and the requirement of training the transformer autoencoder as a separate task for embedding generation. The algorithm is not simple and requires several steps for inference; however, it offers the advantage of requiring minimal computational power on both CPU and GPU. The dataset also presents limitations, including demographic imbalances, uneven diagnostic representation, and variable image quality.
The proposed approach converts raw dermoscopic images into structured, region-based representations, thereby producing enhanced input data for subsequent deep learning architectures. This methodology not only contributes to improved melanoma diagnostic capabilities but also establishes a transferable framework applicable to broader medical image segmentation and classification challenges. Future research could extend this approach by exploring its integration with multimodal data, such as clinical metadata or genomic profiles, to improve diagnostic accuracy across diverse patient populations.
7. Conclusions
The objective of our work is to classify superpixels extracted from natural skin images to identify background, border, and core lesion regions. An RAG is constructed from the superpixels to determine neighboring relationships for each individual superpixel. We first constructed input vectors based on the image statistics of each superpixel and used them to train linear neural networks. In our second approach, we expanded the input vectors to include features from both the superpixel and its neighbors, and trained RNNs, specifically GRUs and transformers. Finally, we generated embeddings for each superpixel using transformer-based autoencoders, and we used these embeddings as inputs to train transformer-based RNNs. The best results were achieved using the autoencoder-generated embeddings. We proved that these embeddings capture the semantic characteristics of each class more effectively than raw statistical features.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/a18090551/s1, Video S1: Labeling Superpixels.
Author Contributions
P.O. was responsible for the study design, data collection and analysis, software tool development, experiment execution, manuscript drafting, and revisions. S.A. contributed to software development, image annotation, and manuscript revisions. I.G. participated in software tool development and image annotation. Y.X. contributed to the study design and provided critical revisions of the manuscript. C.Y.X. and X.Z. both contributed to the critical revision of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
We use ISIC (HAM) dataset: https://dataverse.harvard.edu/dataset.xhtml?persistentId=doi:10.7910/DVN/DBW86T (accessed on 20 August 2025).
Conflicts of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- SEER. Melanoma of the Skin–Cancer Stat Facts. 2025. Available online: https://seer.cancer.gov/statfacts/html/melan.html (accessed on 19 January 2025).
- ACS (American Cancer Society). Melanoma Skin Cancer Statistics. 2025. Available online: https://www.cancer.org/cancer/types/melanoma-skin-cancer/about/key-statistics.html (accessed on 19 January 2025).
- Siegel, R.L.; Miller, K.D.; Fuchs, H.E.; Jemal, A. Cancer statistics, 2022. CA Cancer J. Clin. 2022, 72, 7–33. [Google Scholar] [CrossRef]
- Society, A.C. Cancer Facts and Figures 2022. 2025. Available online: https://www.cancer.org/research/cancer-facts-statistics/all-cancer-facts-figures/cancer-facts-figures-2022.html (accessed on 19 January 2025).
- Jones, O.T.; Matin, R.N.; van der Schaar, M.; Prathivadi Bhayankaram, K.; Ranmuthu, C.K.I.; Islam, M.S.; Behiyat, D.; Boscott, R.; Calanzani, N.; Emery, J.; et al. Artificial intelligence and machine learning algorithms for early detection of skin cancer in community and primary care settings: A systematic review. Lancet Digit. Health 2022, 4, e466–e476. [Google Scholar] [CrossRef] [PubMed]
- Hassel, J.C.; Enk, A.H. Fitzpatrick’s Dermatology, 9e; Kang, S., Amagai, M., Bruckner, A.L., Enk, A.H., Margolis, D.J., McMichael, A.J., Orringer, J.S., Eds.; McGraw-Hill Education: New York, NY, USA, 2019; Chapter 116. [Google Scholar]
- Boiko, P.E.; Koepsell, T.D.; Larson, E.B.; Wagner, E.H. Skin cancer diagnosis in a primary care setting. J. Am. Acad. Dermatol. 1996, 34, 608–611. [Google Scholar] [CrossRef]
- Soyer, H.P.; Smolle, J.; Kerl, H.; Stettner, H. Early diagnosis of malignant melanoma by surface microscopy. Lancet 1987, 330, 803. [Google Scholar] [CrossRef]
- Zahn, C.T.; Roskies, R.Z. Fourier descriptors for plane closed curves. IEEE Trans. Comput. 1972, C-21, 269–281. [Google Scholar] [CrossRef]
- Toureau, V.; Bibiloni, P.; Talavera-Martínez, L.; González-Hidalgo, M. Automatic Detection of Symmetry in Dermoscopic Images Based on Shape and Texture. In Proceedings of the Information Processing and Management of Uncertainty in Knowledge-Based Systems (IPMU 2020), Lisbon, Portugal, 15–19 June 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 591–603. [Google Scholar] [CrossRef]
- Ali, A.M.; Li, J.; Yang, G.; O’Shea, S. A Novel Fuzzy Multilayer Perceptron (F-MLP) for the Detection of Border Irregularity in Skin Lesions. Front. Med. 2020, 7, 297. [Google Scholar] [CrossRef] [PubMed]
- Ali, A.R.; Li, J.; O’Shea, S.J. Towards the automatic detection of skin lesion shape asymmetry, color variegation and diameter in dermoscopic images. PLoS ONE 2020, 15, e0234352. [Google Scholar] [CrossRef]
- Samuel, N.E.; Anitha, J. Melanoma Detection and Classification based on Dermoscopic Images using Deep Learning Architectures-A Study. In Proceedings of the 2022 4th International Conference on Inventive Research in Computing Applications (ICIRCA), Coimbatore, India, 21–23 September 2022; pp. 993–1000. [Google Scholar] [CrossRef]
- Alsahafi, Y.S.; Elshora, D.S.; Mohamed, E.R.; Hosny, K.M. Multilevel threshold segmentation of skin lesions in color images using Coronavirus Optimization Algorithm. Diagnostics 2023, 13, 2958. [Google Scholar] [CrossRef]
- Codella, N.C.F.; Gutman, D.; Celebi, M.E.; Helba, B.; Marchetti, M.A.; Dusza, S.W.; Kalloo, A.; Liopyris, K.; Mishra, N.; Kittler, H.; et al. Skin Lesion Analysis Toward Melanoma Detection: A Challenge at the 2017 International Symposium on Biomedical Imaging (ISBI), Hosted by the International Skin Imaging Collaboration (ISIC). arXiv 2018, arXiv:1710.05006. [Google Scholar] [CrossRef]
- Patel, R.H.; Foltz, E.A.; Witkowski, A.; Ludzik, J. Analysis of Artificial Intelligence-Based Approaches Applied to Non-Invasive Imaging for Early Detection of Melanoma: A Systematic Review. Cancers 2023, 15, 4694. [Google Scholar] [CrossRef]
- Rosas-Lara, M.; Mendoza-Tello, J.C.; Flores, A.; Zumba-Acosta, G. A Convolutional Neural Network-Based Web Prototype to Support Melanoma Skin Cancer Detection. In Proceedings of the 2022 Third International Conference on Information Systems and Software Technologies (ICI2ST), Quito, Ecuador, 8–10 November 2022; pp. 1–7. [Google Scholar] [CrossRef]
- Subramanian, B.; Muthusamy, S.; Thangaraj, K.; Panchal, H.; Kasirajan, E.; Marimuthu, A.; Ravi, A. A new method for detection and classification of melanoma skin cancer using deep learning based transfer learning architecture models. Res. Sq. 2022. [CrossRef]
- Sagar, A.; Jacob, D. Convolutional Neural Networks for Classifying Melanoma Images. bioRXiv 2020. [Google Scholar] [CrossRef]
- Gangwani, D.; Liang, Q.; Wang, S.; Zhu, X. An Empirical Study of Deep Learning Frameworks for Melanoma Cancer Detection using Transfer Learning and Data Augmentation. In Proceedings of the 2021 IEEE International Conference on Big Knowledge (ICBK), Auckland, New Zealand, 7–8 December 2021; pp. 38–45. [Google Scholar] [CrossRef]
- Cirrincione, G.; Cannata, S.; Cicceri, G.; Prinzi, F.; Currieri, T.; Lovino, M.; Militello, C.; Pasero, E.; Vitabile, S. Transformer-Based Approach to Melanoma Detection. Sensors 2023, 23, 5677. [Google Scholar] [CrossRef]
- Khan, S.; Khan, A. SkinViT: A transformer based method for Melanoma and Nonmelanoma classification. PLoS ONE 2023, 18, e0295151. [Google Scholar] [CrossRef]
- Xie, J.; Wu, Z.; Zhu, R.; Zhu, H. Melanoma Detection based on Swin Transformer and SimAM. In Proceedings of the 2021 IEEE 5th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Xi’an, China, 15–17 October 2021; Volume 5, pp. 1517–1521. [Google Scholar] [CrossRef]
- Tan, M.; Le, Q.V. EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks. arXiv 2020, arXiv:1905.11946. [Google Scholar] [CrossRef]
- Hosny, K.M.; Elshoura, D.; Mohamed, E.R.; Vrochidou, E.; Papakostas, G.A. Deep Learning and Optimization-Based Methods for Skin Lesions Segmentation: A Review. IEEE Access 2023, 11, 85467–85488. [Google Scholar] [CrossRef]
- Zafar, M.; Amin, J.; Sharif, M.; Anjum, M.A.; Mallah, G.A.; Kadry, S. DeepLabv3+-Based Segmentation and Best Features Selection Using Slime Mould Algorithm for Multi-Class Skin Lesion Classification. Mathematics 2023, 11, 364. [Google Scholar] [CrossRef]
- Chen, B.; Liu, Y.; Zhang, Z.; Lu, G.; Kong, A.W.K. TransAttUnet: Multi-Level Attention-Guided U-Net With Transformer for Medical Image Segmentation. IEEE Trans. Emerg. Top. Comput. Intell. 2024, 8, 55–68. [Google Scholar] [CrossRef]
- Akyel, C.; Arıcı, N. LinkNet-B7: Noise Removal and Lesion Segmentation in Images of Skin Cancer. Mathematics 2022, 10, 736. [Google Scholar] [CrossRef]
- Shreshth, S.; Divij, G.; Anil, K.T. Detector-SegMentor Network for Skin Lesion Localization and Segmentation. arXiv 2020, arXiv:2005.06550. [Google Scholar]
- Zhang, L. FITrans: Skin Lesion Segmentation Based on Feature Integration and Transformer. In Proceedings of the 2023 3rd International Conference on Neural Networks, Information and Communication Engineering (NNICE), Guangzhou, China, 24–26 February 2023; pp. 324–329. [Google Scholar] [CrossRef]
- Dong, Y.; Wang, L.; Li, Y. TC-Net: Dual coding network of Transformer and CNN for skin lesion segmentation. PLoS ONE 2022, 17, e0277578. [Google Scholar] [CrossRef]
- Liu, S.; Zhuang, Z.; Zheng, Y.; Kolmaniè, S. A VAN-Based Multi-Scale Cross-Attention Mechanism for Skin Lesion Segmentation Network. IEEE Access 2023, 11, 81953–81964. [Google Scholar] [CrossRef]
- Kittler, H.; Pehamberger, H.; Wolff, K.; Binder, M. Diagnostic accuracy of dermoscopy. Lancet Oncol. 2002, 3, 159–165. [Google Scholar] [CrossRef]
- Wighton, P.; Lee, T.K.; Lui, H.; McLean, D.I.; Atkins, M.S. Generalizing Common Tasks in Automated Skin Lesion Diagnosis. IEEE Trans. Inf. Technol. Biomed. 2011, 15, 622–629. [Google Scholar] [CrossRef]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-Decoder with Atrous Separable Convolution for Semantic Image Segmentation. arXiv 2018, arXiv:1802.02611. [Google Scholar] [CrossRef]
- Adegun, A.A.; Viriri, S.; Yousaf, M.H. A Probabilistic-Based Deep Learning Model for Skin Lesion Segmentation. Appl. Sci. 2021, 11, 3025. [Google Scholar] [CrossRef]
- Ünver, H.M.; Ayan, E. Skin Lesion Segmentation in Dermoscopic Images with Combination of YOLO and GrabCut Algorithm. Diagnostics 2019, 9, 72. [Google Scholar] [CrossRef] [PubMed]
- Mirikharaji, Z.; Abhishek, K.; Izadi, S.; Hamarneh, G. D-LEMA: Deep Learning Ensembles from Multiple Annotations—Application to Skin Lesion Segmentation. arXiv 2021, arXiv:2012.07206. [Google Scholar]
- Li, X.; Peng, B.; Hu, J.; Ma, C.; Yang, D.; Xie, Z. USL-Net: Uncertainty Self-Learning Network for Unsupervised Skin Lesion Segmentation. arXiv 2024, arXiv:2309.13289. [Google Scholar] [CrossRef]
- Lu, W.; Gong, D.; Fu, K.; Sun, X.; Diao, W.; Liu, L. Boundarymix: Generating pseudo-training images for improving segmentation with scribble annotations. Pattern Recognit. 2021, 117, 107924. [Google Scholar] [CrossRef]
- Avelar, P.H.C.; Tavares, A.R.; da Silveira, T.L.T.; Jung, C.R.; Lamb, L.C. Superpixel Image Classification with Graph Attention Networks. In Proceedings of the 2020 33rd SIBGRAPI Conference on Graphics, Patterns and Images (SIBGRAPI), Ipojuca, Brazil, 7–10 November 2020; pp. 203–209. [Google Scholar] [CrossRef]
- Nazir, U.; Wang, H.; Taj, M. Survey of Image Based Graph Neural Networks. arXiv 2021, arXiv:2106.06307. [Google Scholar] [CrossRef]
- Nowosad, J.; Stepinski, T.F. Extended SLIC superpixels algorithm for applications to non-imagery geospatial rasters. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102935. [Google Scholar] [CrossRef]
- Qin, W.; Wu, J.; Han, F.; Yuan, Y.; Zhao, W.; Ibragimov, B.; Gu, J.; Xing, L. Superpixel-based and boundary-sensitive convolutional neural network for automated liver segmentation. Phys. Med. Biol. 2018, 63, 095017. [Google Scholar] [CrossRef]
- Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Süsstrunk, S. SLIC Superpixels Compared to State-of-the-Art Superpixel Methods. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 34, 2274–2282. [Google Scholar] [CrossRef]
- Gaur, U.; Manjunath, B.S. Superpixel Embedding Network. IEEE Trans. Image Process. 2020, 29, 3199–3212. [Google Scholar] [CrossRef]
- OpenCV Team. OpenCV (Open Source Computer Vision Library). Version 4.9.0.2023. Available online: https://opencv.org/ (accessed on 19 January 2025).
- Jaworek-Korjakowska, J.; Kleczek, P. Region Adjacency Graph Approach for Acral Melanocytic Lesion Segmentation. Appl. Sci. 2018, 8, 1430. [Google Scholar] [CrossRef]
- Tschandl, P.; Rosendahl, C.; Kittler, H. The HAM10000 dataset, a large collection of multi-source dermatoscopic images of common pigmented skin lesions. Sci. Data 2018, 5, 180161. [Google Scholar] [CrossRef]
- Neo4j, Inc. Neo4j: Graph Data Platform. 2023. Available online: https://neo4j.com/ (accessed on 19 January 2025).
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).