Abstract
The Minimum Spanning Tree with Conflicting Edge Pairs is a generalization that adds conflict constraints to a classical optimization problem on graphs used to model several real-world applications. In recent years, several heuristic and exact approaches have been proposed to tackle this problem. In this paper, we present a mixed-integer linear program not previously applied to this problem, and we solve it with an open-source solver. Computational results for the benchmark instances commonly adopted in the literature of the problem are reported. The results indicate that the approach we propose obtains results aligned with those of the much more sophisticated approaches available, notwithstanding it being much simpler to implement. During the experimental campaign, six instances were closed for the first time, with nine improved best-known lower bounds and sixteen improved best-known upper bounds over a total of two hundred thirty instances considered.
1. Introduction
The Minimum Spanning Tree Problem with Conflicting Edge Pairs (MSTC) is a variant of the classical minimum spanning tree (MST) problem recently introduced [1]. Given a connected undirected graph with costs on the edges and a set of edge pairs in conflict with each other, the MSTC consists of finding the spanning tree with the minimum total cost that uses at most one of the edges of each conflicting pair. The MSTC was first introduced by Darmann et al. [2]. It was shown that under general settings, the problem cannot be solved in polynomial time, although some special cases are shown to be polynomially solvable. Several heuristic methods were subsequently proposed in [3], while a branch-and-cut based on a mathematical programming model and some valid inequalities was presented in [4]. More recently, a metaheuristic method was designed and presented in [5], while some new methods based on Lagrangian relaxations, able to produce high-quality lower bounds and heuristic solutions, were introduced in [6]. Finally, a new branch-and-cut approach based on some new valid inequalities was discussed in [7] and shown to represent the current state-of-the-art exact solving methods.
In the literature of graph theory and algorithms, several classic optimization problems have been studied in one or more variants involving conflict constraints, witnessing increasing popularity of the topic due to the number of related real-world applications. For example, for the Assignment Problem with Conflicts, theoretical results on the computational complexity, together with some approximation results, can be found in [2]. Further results for special polynomially solvable settings were presented in [8], together with some heuristics and lower-bounding schema. More contributions can be found in [9,10], where some Mixed-Integer Linear Programming models, exact Branch-and-Bound methods, and heuristic ideas are introduced. The concepts of the last two papers were later summarized and extended in [11]. For the Knapsack Problem with Conflicts, a local-search heuristic and a branch-and-bound method based on Lagrangian relaxation are discussed in [12]. In [13], the authors proposed some preprocessing techniques and a different branch-and-bound algorithm. Heuristic methods for this problem were discussed in [14,15]. Metaheuristic approaches were finally presented in [16,17]. Finally, a branch-and-bound exact method, based on binary branching, was proposed in [18], while another branch-and-bound schema, based on n-ary branching, was developed and tested in [19]. Different Set-Covering Problems with Conflicts were proposed in [20,21], together with approximation algorithms and computational complexity results. Different families of valid inequalities for a model representing the problem were presented in [22], together with some preprocessing and speed-up routines. A specialization of the same problem in geometric settings was discussed in [23], where some approximation results were presented. The Shortest Path Problem with Conflicts can be found in [24], where critical variants of the shortest path problem arising in the automatic generation of test paths for programs were introduced, and in [25], where the first definition of conflict pairs was presented, although nodes instead of arcs were a part of the conflicts. A procedure to solve the problem was discussed in [26]. A polyhedral study of the problem was presented in [27], while branch-and-bound and dynamic programming approaches were recently proposed in [28,29]. The Maximum Flow Problem with Conflicts was first studied in [30], where the NP-hardness of the problem is shown. Later, some mixed-integer linear programming formulations and exact methods, such as a Benders Decomposition, a Branch-and-Bound, and a Russian Doll Search were presented in [31]. More recently, the authors of [32] proposed a heuristic approach for the problem called Kernousel, obtained by merging two metaheuristic approaches, one based on Carousel Greedy [33] and the other on Kernel Search [34].
The MSTC can be used to represent real applications arising in different domains. For example, the design of an offshore wind farm network, where the wind turbines have to be connected together, and the different possible point-to-point connections are characterized by different costs. Technical reasons prevent the use of overlapped cables in such a context [35], and this generates conflict constraints. Other practical applications are in the design and installation of long-distance pipelines, where conflicts typically represent the impossibility of using infrastructures owned by competitor service providers or, alternatively, the impossibility of crossing countries with reciprocal political issues with the same line [36].
In this paper, a compact mixed-integer linear programming model for the MSTC is introduced in the context of the MSTC. It is based on multi-commodity flow concepts and extends known formulations for the MST problem ([37,38]) to the case with conflicts. Notice that multi-commodity flow models are common for problems related to the MST problem (see, for example, [39] for the Min-degree Constrained MST and [40] for the Diameter-Constrained MST). The model we propose is solved by the open-source solver CP-SAT, which is a part of the Google OR-Tools [41] optimization suite. Normally, models based on multi-commodity flow are not very effective in the context of integer programming, due to the poor linear relaxation, but we believe such a formulation might perform well when solved with CP-SAT. Successful application of this solver on optimization problems with characteristics similar to the problem under investigation, such as the Parallel Drone-Scheduling Traveling Salesman Problem and Vehicle Routing Problems [42,43], the Maximum Flow Problem with Conflict Constraints [44], and the Home Healthcare-Routing and Scheduling Problem [45], motivated this study. A comprehensive experimental campaign is conducted and reported on the benchmark instances previously used in the literature.
The overall organization of the paper can be summarized as follows: Section 2 is dedicated to the formal introduction and definition of the Minimum Spanning Tree Problem with Conflicting Edge Pairs. Section 3 presents a compact mixed-integer linear programming model to represent the problem. In Section 4, the new model is validated through an extensive experimental perspective. After the description of the benchmark instances considered and of the methods used for comparison purposes, the detailed results obtained by solving the new model are reported. Some conclusions about the work presented and the results achieved are drawn in Section 5 to close the paper.
2. Problem Description
The Minimum Spanning Tree Problem with Additional Conflicts can be defined on an undirected graph (), with V denoting the set of nodes and E the set of edges. Each edge () is associated with a cost (). The following feature differentiates the problem from the classic Minimum Spanning Tree Problem and increases the theoretical computational complexity of the problem to –hard [2]: Two edges () are said to be in conflict if, at most, one of them can be included in a feasible solution. The set of edges in conflict with the edge () is contained in the set . The goal of the MSTC is to find the minimum-cost-spanning tree that satisfies all the conflict constraints.
An example of an MFPC instance and the optimal solution for the same instance are provided in Figure 1.
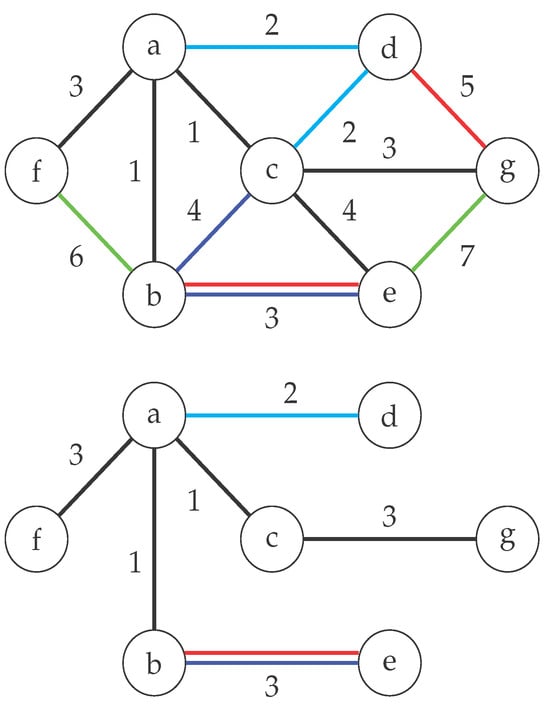
Figure 1.
(Top) An example of a small MSTC instance is shown, where the edge costs are placed by the edges. Edges in black are not affected by conflicts, while any two edges sharing the same red, cyan, blue, or green color are in conflict. According to the notation , , , , , , , and . (Bottom) the optimal solution that does not violate any conflict is reported. Note that no edge of the green conflict is included.
3. A Mixed-Integer Linear Programming Model
In this section, a model for the MSTC—obtained by extending a classical model for the Minimum Spanning Tree Problem [37]—is proposed. The compact model is based on multi-commodity flow, characterized by the number of variables in the order of O() and the number of constraints in the order of O(), making it compact and suitable to be attacked directly by a solver. Conversely, the approaches previously considered in the literature rely on models with an exponential number of constraints [4,7], which require a more complex implementation of dynamic and iterative mechanisms to generate violated constraints during the solving process. Our approach is expected to have a weaker linear relaxation than the exponential models, but we believe it has potential when approached with solvers able to do logical inferences, as is done herein. The new model uses a set (A) of (directed) arcs, obtained by including the two arcs ( and () for each edge (). A node (s) is arbitrarily selected as the root (node 0 in our implementation), and the model aims to send one unit of flow from the source to each other node.
The new model can be formally defined as follows: A variable () is introduced for each and takes the value of the flow transiting the arc (). An additional set of variables is introduced to link the multi-commodity flow formulation to the MSTC. Then, a binary variable () is defined for each edge (). It takes a value of 1 if the edge is a part of the solution and 0 otherwise. The resulting compact model, characterized by a polynomial number of variables and constraints, is as follows:
The objective function (1) minimizes the cost of the spanning tree. Constraints (2) implement a classical multi-commodity flow model on the directed network and impose that one unit of the commodity has to exit the source (s) for each other node of V (case ) and that each node different from s has to retain exactly one unit of the commodity (case ). An example of the flow associated with the solution reported in Figure 1 is available in Figure 2.
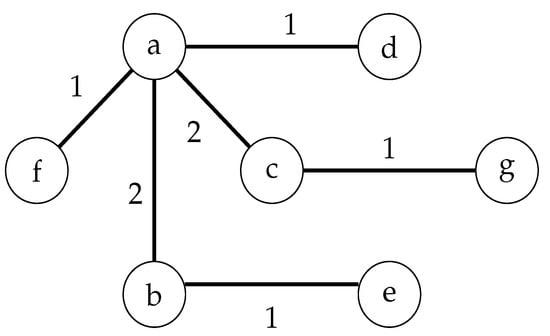
Figure 2.
Assignment of flow variables (f) for the solution reported in Figure 1, assuming node a is designed to be the source node (s).
Inequalities (3) and (4) connect the x and y variables by imposing that has to take a value of 1 as soon as either or takes a positive value. Constraints (5) encode conflict constraints by ensuring that conflicting edges are not selected simultaneously. Finally, the domains of the variables are specified in constraints (6) and (7) for the x and y variables, respectively.
4. Computational Experiments
This section is devoted to the experimental validation of the new compact model introduced in Section 3. The model’s results are compared to those of existing methods for the standard benchmark instances from the literature. In detail, Section 4.1 is devoted to the description of the benchmark instances previously introduced in the literature and used in the present study. An extensive comparison between the results achieved in this work and the results previously published is presented in Section 4.2.
4.1. Benchmark Instances
The benchmark sets originally proposed in [3,7], which have been widely used in the previous literature to validate and compare solving methods, are adopted for the experiments reported in the present work.
From the benchmark set proposed in [3], the 50 most challenging instances are considered, since the other ones can easily be solved to optimality by any recent method. The instances are generated at random and have a number of nodes that ranges between 50 and 300 and a number of edges between 200 and 1000. The edge costs are between 0 and 500, and different densities for the conflict graph are considered. We refer the interested reader to [3] for full details on instance generation.
A newer set of benchmark instances was recently introduced in [7] and is formed by random instances with the number of nodes between 25 and 100 and the edge density equal to 0.2, 0.3, or 0.4 (notice that the previous set of benchmarks was characterized by lower densities). Costs are between 1 and 30, and the density of the conflict graph is 0.01, 0.04, or 0.07. All 180 instances of the set are considered for the experiments reported in the present work. We refer the reader interested in the generation process of the instances to [7] for full details.
4.2. Experimental Results
The model discussed in Section 3 has been solved with the Google OR-Tools CP-SAT solver [41] version 9.12. The CP-SAT solver is designed to work in a multi-thread environment (compatible with all new processors) and implements a portfolio strategy with effective data exchange among the different threads. The main process runs a Constraint-Programming Solver based on Lazy Clause Generation (LCG) [46]. The concept behind LCG involves the (incremental) transformation of the problem to an SAT formula, subsequently employing an SAT solver to seek a solution (or prove bounds for infeasibility). The input model is also linearized, the corresponding linear program is (partially) solved with the (dual) simplex algorithm, and other classical MILP techniques are run to enhance bounds and retrieve new solutions, aiming at supporting the satisfiability model. Finally, instances of metaheuristic methods, seeking high-quality feasible solutions, are executed.
We believe a compact model heavily based on binary variables, like those discussed in Section 3, might be very suitable to be attacked with a solver with the characteristics of CP-SAT.
The experiments have been run on a computer equipped with an Intel Core i7 12700F CPU, but the computational times were normalized using the Intel Core i7-3770 CPU used for the experiments reported in [5,6,7], as a baseline. This ensures fair comparisons across methods. The normalization of the computation times has been carried out according to the conversion ratios inferred from [47]. Notice that ref. [47] is commonly used in the community to compare results obtained on different machines (see, for example, [32,44]). In accordance with the tests previously reported in [7], a maximum computation time of 5010 s is allowed for all the methods for which a computation time is reported in the tables that follow.
The first experiments have been carried out on the instances proposed in [3] and are summarized in Table 1. The first columns identify each instance (n is the number of nodes, m is the number of edges, and p is the number of conflicts, following the parameters used to generate the instances), while the rest of the table summarizes all the relevant results presented in the previous literature. The (not necessarily) optimal results obtained by solving a Mixed-Integer Linear Programming (MILP) model and two lower-bounding procedures (LB-MST and LB-MI) are taken from [3] (with no computation time). The lower and upper bounds (HDA and HDA+, respectively) from [6] are reported together with the upper bounds obtained with the multi-ethnic genetic metaheuristic method that appeared in [5] (Mega) and the lower and upper bounds obtained by the two branch-and-cut approaches discussed in [4] (unfortunately, without computation times) and [7], respectively (BC). Finally, the results obtained by the method presented in this paper are presented in the last five columns (CP-SAT). On top of the lower and upper bounds obtained and the relative computation time, the percentage deviation (Dev%) against the best lower and upper bounds is also reported to better position the new approach. These deviations are calculated as and , respectively, where and are the best-known lower and upper bounds available from the previous literature, and and are the values provided by CP-SAT. Negative deviations (corresponding to improved best-known results) are highlighted in bold.

Table 1.
Computational results for the instances introduced in [3].
The results in Table 1 suggest that the approach we propose (CP-SAT) is particularly effective in identifying infeasible instances: Five such instances were identified for the first time in this study by the powerful feasibility checker provided by the adopted solver (notice that infeasible instances are marked as Infeas in the table). This corroborates the intuition that the logical inference carried out by CP-SAT can be effective on the compact model we propose. Moreover, another best-known upper bound has been improved. In general, the new approach has a performance comparable with those of the other state-of-the-art methods available, with deviation gaps remaining below 8.5% (and, in general, substantially below) from best-known bounds (taken as the best of the results obtained by several different algorithms). We observe that the average deviations reported are not very significant because they are heavily affected by the figures for the infeasibility proofs. Notably, CP-SAT consistently provides meaningful lower and upper bounds, demonstrating a level of robustness—especially on the upper bounds—that is uncommon among other methods. On the other hand, the lower bounds found by CP-SAT appear sometimes worse than those of BC (from [7]) in some of the most challenging instances. This might indicate scalability issues. When observing computation times, CP-SAT often appears slower than the other methods. This likely depends on the model we propose, which is characterized by a poor linear relaxation, which, in turn, means that no strong lower bound from linear programming is available to the solver. CP-SAT effectively compensates for this lack of information by applying logical inference, although this takes a longer time, showing that the solver is suitable for the new model, and the combination leads to very good results.
The percentage deviations from the best-known (before the present study) lower and upper bounds are plotted for all the methods considered and for each instance of the first benchmark set in Figure 3 and Figure 4. The plots help to position the new approach even more clearly. A plot representing the computation times required to close each instance by the two exact methods for which such information is available (BC [7] and CP-SAT) is provided in Figure 5. A negative value is plotted when no result is available for the solver BC. The plot suggests how CP-SAT is often generally slower in the instances solved by the two methods, but, on the other hand, the number of instances solved by such an approach is higher.
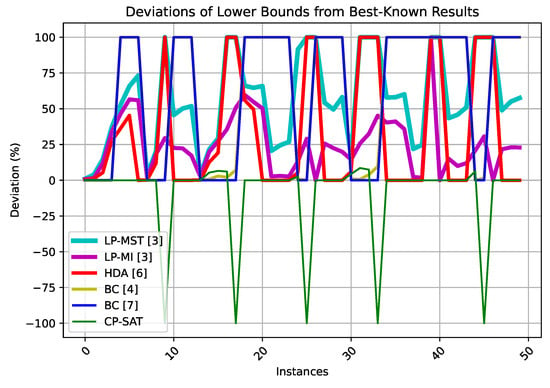
Figure 3.
Percentage deviations from the best-known lower bounds in the instances of the first benchmark set.
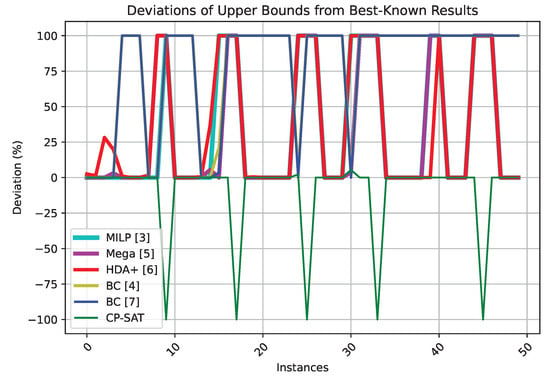
Figure 4.
Percentage deviations from the best-known upper bounds in the instances of the first benchmark set.
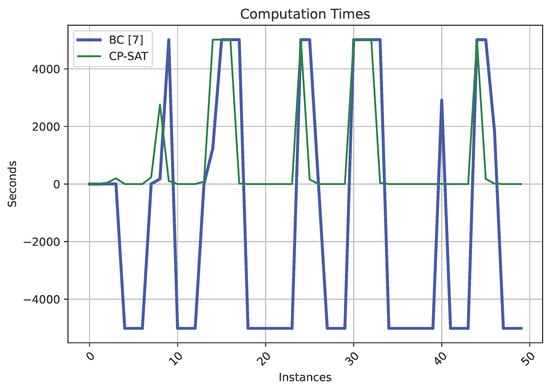
Figure 5.
Computation times for two exact methods in the instances of the first benchmark set.
A second set of experiments has been carried out on the instances proposed in [7], and the results are summarized in Table 2. The meaning of the column matches that of the column in Table 1, with the addition of parameter s, which is the seed used to generate the instances and helps to distinguish among instances with the same characteristics. The results of all the methods for which results are available in this dataset (namely, the most recent approaches) are reported. Computational times are available for all the methods reported.

Table 2.
Computational results for the instances introduced in [7].
The comparison proposed in Table 2 shows that the approach we propose (CP-SAT) also performs well in this second set of benchmark instances, with average deviations from the previously best-known results of 0.4% concerning the lower bounds and 0.8% concerning the upper bounds. These figures are very good, considering the abundance of methods considered while calculating the (previous) best-known results. The maximum deviation is negligible for most of the instances, with only a few cases above 10% for upper bounds and never above 2.2% for lower bounds. Notice that for some of the instances of this benchmark set, CP-SAT suffers on the heuristic solution side (upper bounds). This indicates that several tailored heuristics presented for the problem were well motivated. A total of four new best-known lower bounds and ten new best-known upper bounds have been produced during the experimental campaign, with one instance (50-245-2093-349) closed for the first time during this experimental campaign. The same conclusion drawn for computation times in Table 1 also applies to these experiments too.
Analogous to what was done for the first benchmark set, the percentage deviations from the best-known (before the present study) lower and upper bounds are plotted for all the methods considered and for each instance of the first benchmark set in Figure 6 and Figure 7. The plots help to position the new approach even more clearly, although the dominance of CP-SAT here is not as clear as in Figure 3 and Figure 4. We plot the computation times required to close each instance by the two exact methods for which such information is available in Figure 8. The plot suggests that for the second benchmark set, BS converges faster (and closes a few more instances) than CP-SAT.
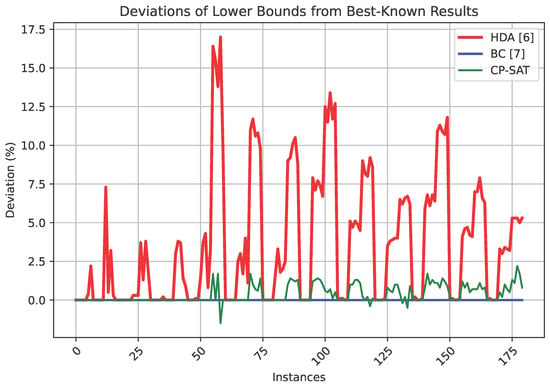
Figure 6.
Percentage deviations from the best-known lower bounds in the instances of the second benchmark set.
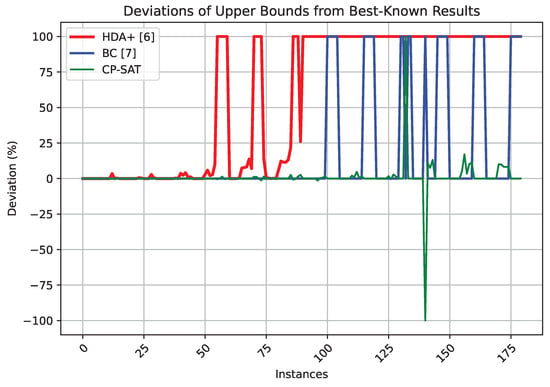
Figure 7.
Percentage deviations from the best-known upper bounds in the instances of the second benchmark set.
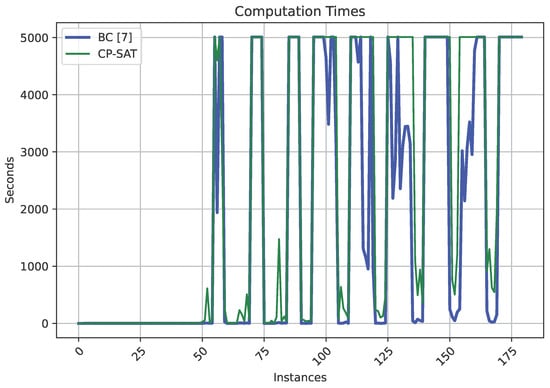
Figure 8.
Computation times for two exact methods in the instances of the second benchmark set.
As a general conclusion, the proposed model closely matches or improves upon the best-known results available prior to this work. The proposed method also demonstrates consistent robustness across the entire dataset, although its convergence times appear slower than those of some of the methods previously proposed.
5. Conclusions
A compact mixed-integer linear formulation for the Minimum Spanning Tree Problem with Conflicting Edge Pairs was proposed for the first time in the context of this problem and solved via an open-source solver.
The results of a vast experimental campaign run on the benchmark instances adopted in the previous literature are reported. The results indicate that the proposed approach achieves computational results comparable with the best of those achieved by the substantially more complex methods that appeared in the prior literature, although, sometimes, the computation times are longer due to the mechanics of the solver. A total of six instances were closed for the first time, with nine best-known lower bounds and sixteen best-known upper bounds improved out of the two hundred thirty instances considered. In some of the instances, the new approach still performs slightly worse than some among the other methods it is compared against, but overall, it guarantees robust results, with improvements in instances attacked and solved in the research community for more than a decade.
Future research directions might be twofold. On the one hand, compact models, like the one we propose, might be employed on problems with conflicts similar to the one treated in this paper or employ soft constraints (that can be violated at the price of a penalty), which, by their nature, would pose new challenges. On the other hand, variants of the Minimum Spanning Tree, characterized by soft constraints, with penalties to be paid if violated, might be considered.
Author Contributions
Conceptualization, R.M. and D.H.S.; methodology, R.M.; software, R.M.; validation, R.M. and D.H.S.; formal analysis, R.M. and D.H.S.; investigation, R.M.; resources, R.M.; data curation, R.M.; writing—original draft preparation, R.M.; writing—review and editing, R.M. and D.H.S.; visualization, R.M. and D.H.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the Google Cloud Research Credits Program.
Data Availability Statement
The instances used for the experiments, originally introduced in [3,7], are available upon request to the corresponding author.
Acknowledgments
The authors have reviewed and edited the output and take full responsibility for the content of this publication.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Prim, R.C. Shortest connection networks and some generalizations. Bell Syst. Tech. J. 1957, 6, 1389–1401. [Google Scholar] [CrossRef]
- Darmann, A.; Pferschy, U.; Schauer, J.; Woeginger, G.J. Paths, trees and matchings under disjunctive constraints. Discret. Appl. Math. 2011, 16, 1726–1735. [Google Scholar] [CrossRef]
- Zhang, R.; Kabadi, S.; Punnen, A. The minimum spanning tree problem with conflict constraints and its variations. Discret. Optim. 2011, 2, 191–205. [Google Scholar] [CrossRef]
- Samer, P.; Urrutia, S. A branch and cut algorithm for minimum spanning trees under conflict constraints. Optim. Lett. 2014, 1, 41–55. [Google Scholar] [CrossRef]
- Carrabs, F.; Cerrone, C.; Pentangelo, R. A multi-ethnic genetic approach for the minimum conflict weighted spanning tree problem. Networks 2019, 2, 134–147. [Google Scholar] [CrossRef]
- Carrabs, F.; Gaudioso, M. A Lagrangian approach for the minimum spanning tree problem with conflicting edge pairs. Networks 2021, 1, 32–45. [Google Scholar] [CrossRef]
- Carrabs, F.; Cerulli, R.; Pentangelo, R.; Raiconi, A. Minimum spanning tree with conflicting edge pairs: A branch-and-cut approach. In Annals of Operations Research; Springer: Berlin/Heidelberg, Germany, 2019; pp. 65–78. [Google Scholar]
- Öncan, T.; Zhang, R.; Punnen, A.P. The minimum cost perfect matching problem with conflict pair constraints. Comput. Oper. Res. 2013, 40, 920–930. [Google Scholar] [CrossRef]
- Öncan, T.; Altınel, I.K. Iterated exact and heuristic algorithms for the minimum cost bipartite perfect matching problem with conflict constraints. In Proceedings of the 2017 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Singapore, 10–13 December 2017; pp. 1032–1036. [Google Scholar]
- Öncan, T.; Altınel, I.K. A Branch-and-Bound Algorithm for the Minimum Cost Bipartite Perfect Matching Problem with Conflict Pair Constraints. Electron. Notes Discret. Math. 2018, 64, 5–14. [Google Scholar] [CrossRef]
- Öncan, T.; Şuvak, Z.; Akyüz, M.H.; Altınel, I.K. Assignment problem with conflicts. Comput. Oper. Res. 2019, 111, 214–229. [Google Scholar] [CrossRef]
- Yamada, T.; Kataoka, S.; Watanabe, K. Heuristic and exact algorithms for the disjunctively constrained knapsack problem. Informs J. Comput. 2002, 43, 2864–2870. [Google Scholar]
- Hifi, M.; Michrafy, M. Reduction strategies and exact algorithms for the disjunctively constrained knapsack problem. Comput. Oper. Res. 2007, 34, 2657–2673. [Google Scholar] [CrossRef]
- Hifi, M.; Michrafy, M. A reactive local search-based algorithm for the disjunctively constrained knapsack problem. J. Oper. Res. Soc. 2006, 57, 718–726. [Google Scholar] [CrossRef]
- Akeb, H.; Hifi, M.; Ould Ahmed Mounir, M.E. Local branching-based algorithms for the disjunctively constrained knapsack problem. Comput. Ind. Eng. 2011, 60, 811–820. [Google Scholar] [CrossRef]
- Hifi, M.; Omani, N. An algorithm for the disjunctively constrained knapsack problem. Int. J. Oper. Res. 2012, 13, 22–43. [Google Scholar] [CrossRef]
- Hifi, M. An iterative rounding search-based algorithm for the disjunctively constrained knapsack problem. Eng. Optim. 2014, 46, 1109–1122. [Google Scholar] [CrossRef]
- Bettinelli, A.; Cacchiani, V.; Malaguti, E. A Branch-and-Bound Algorithm for the Knapsack Problem with Conflict Graph. INFORMS J. Comput. 2017, 29, 457–473. [Google Scholar] [CrossRef]
- Coniglio, S.; Furini, F.; San Segundo, P. A new combinatorial branch-and-bound algorithm for the Knapsack Problem with Conflicts. Eur. J. Oper. Res. 2021, 289, 435–455. [Google Scholar] [CrossRef]
- Carrabs, F.; Cerulli, R.; Mansini, R.; Moreschini, L.; Serra, D. Solving the Set Covering Problem with Conflicts on Sets: A new parallel GRASP. Comput. Oper. Res. 2024, 166, 106620. [Google Scholar] [CrossRef]
- Jacob, A.; Majumdar, D.; Raman, V. Parameterized complexity of conflict-free set cover. Lect. Notes Comput. Sci. 2019, 11532, 191–202. [Google Scholar]
- Saffari, S.; Fathi, Y. Set covering problem with conflict constraints. Comput. Oper. Res. 2022, 143, 105763. [Google Scholar] [CrossRef]
- Banik, A.; Panolan, F.; Raman, V.; Sahlot, V.; Saurabh, S. Parameterized Complexity of Geometric Covering Problems Having Conflicts. Algorithmica 2020, 82, 1–19. [Google Scholar] [CrossRef]
- Gabow, H.; Maheshwari, S.; Osterweil, L. On Two Problems in the Generation of Program Test Paths. IEEE Trans. Softw. Eng. 1976, SE-2, 227–231. [Google Scholar] [CrossRef]
- Krause, K.W.; Goodwin, M.A.; Smith, R.W. Optimal Software Test Planning Through Automated Network Analysis; TRW Systems Group: Redondo Beach, CA, USA, 1973; pp. 18–22. [Google Scholar]
- Srimani, P.K.; Sinha, B.P. Impossible pair constrained test path generation in a program. Inf. Sci. 1982, 28, 87–103. [Google Scholar] [CrossRef]
- Blanco, M.; Borndörfer, R.; Brückner, M.; Hoàng, N.D.; Schlechte, T. On the Path Avoiding Forbidden Pairs Polytope. Electron. Notes Discret. Math. 2015, 50, 343–348. [Google Scholar] [CrossRef]
- Ferone, D.; Festa, P.; Salani, M. Branch and Bound and Dynamic Programming Approaches for the Path Avoiding Forbidden Pairs Problem. In Optimization and Decision Science: ODS, Virtual Conference, November 19, 2020; Cerulli, R., Dell’Amico, M., Guerriero, F., Pacciarelli, D., Sforza, A., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 227–235. [Google Scholar]
- Cerulli, R.; Guerriero, G.; Scalzo, E.; Sorgente, C. Shortest paths with exclusive-disjunction arc pairs conflicts. Comput. Oper. Res. 2023, 152, 106158. [Google Scholar] [CrossRef]
- Pferschy, U.; Schauer, J. The maximum flow problem with disjunctive constraints. J. Comb. Optim. 2013, 26, 109–119. [Google Scholar] [CrossRef]
- Şuvak, Z.; Altınel, I.K.; Aras, N. Exact solution algorithms for the maximum flow problem with additional conflict constraints. Eur. J. Oper. Res. 2020, 287, 410–437. [Google Scholar] [CrossRef]
- Carrabs, F.; Cerulli, R.; Mansini, R.; Serra, D.; Sorgente, C. Hybridizing Carousel Greedy and Kernel Search: A new approach for the maximum flow problem with conflict constraints. Eur. J. Oper. Res. 2025, 324, 414–435. [Google Scholar] [CrossRef]
- Cerrone, C.; Cerulli, R.; Golden, B. Carousel greedy: A generalized greedy algorithm with applications in optimization. Comput. Oper. Res. 2017, 85, 97–112. [Google Scholar] [CrossRef]
- Angelelli, E.; Mansini, R.; Speranza, M.G. Kernel search: A new heuristic framework for portfolio selection. Comput. Optim. Appl. 2012, 51, 345–361. [Google Scholar] [CrossRef]
- Klein, A.; Haugland, D.; Bauer, J.; Mommer, M. An integer programming model for branching cable layouts in offshore wind farms. In Advances in Intelligent Systems and Computing; Springer: Berlin/Heidelberg, Germany, 2015; pp. 27–36. [Google Scholar]
- Darmann, A.; Pferschy, U.; Schauer, J. Determining a minimum spanning tree with disjunctive constraints. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2009; pp. 414–423. [Google Scholar]
- Magnanti, T.L.; Wolsey, L. Optimal trees. In Handbook in Operations Research and Management Science; Ball, M.O., Magnanti, T.L., Monma, C.L., Nemhauser, G.L., Eds.; North Holland Publishing: Amsterdam, The Netherlands, 1995; pp. 503–615. [Google Scholar]
- Abdelmaguid, T.F. An Efficient Mixed Integer Linear Programming Model for the Minimum Spanning Tree Problem. Mathematics 2018, 6, 183. [Google Scholar] [CrossRef]
- de Almeida, A.M.; Martins, P.; de Souza, M.C. Min-degree constrained minimum spanning tree problem: complexity, properties, and formulations. Int. Trans. Oper. Res. 2012, 19, 323–352. [Google Scholar] [CrossRef]
- Gouveia, L.; Magnanti, T.L. Network flow models for designing diameter-constrained minimum-spanning and Steiner trees. Networks 2003, 41, 159–173. [Google Scholar] [CrossRef]
- Perron, L.; Didier, F. Google OR-Tools-CP-SAT. 2025. Available online: https://developers.google.com/optimization/cp/cp_solver/ (accessed on 9 July 2025).
- Montemanni, R.; Dell’Amico, M. Solving the parallel drone scheduling traveling salesman problem via constraint programming. Algorithms 2023, 16, 40. [Google Scholar] [CrossRef]
- Montemanni, R.; Dell’Amico, M.; Corsini, A. Parallel drone scheduling vehicle routing problems with collective drones. Comput. Oper. Res. 2024, 163, 106514. [Google Scholar] [CrossRef]
- Montemanni, R.; Smith, D.H. On Solving the Maximum Flow Problem with Conflict Constraints. In Proceedings of the 2025 Industrial Electronics and Applications Conference, Sabah, Malaysia, 8–9 September 2025. [Google Scholar]
- Montemanni, R. Solving a Home Healthcare Routing and Scheduling Problem with Real-World Features. In Machine Learning and Soft Computing, Proceedings of International Conference on Machine Learning and Soft Computing, Tokyo, Japan, 24–26 January 2025; Springer: Singapore, 2025; pp. 111–119. [Google Scholar]
- Stuckey, P.J. Lazy Clause Generation: Combining the Power of SAT and CP (and MIP?) Solving. In Proceedings of the International Conference on Integration of Artificial Intelligence and Operations Research Techniques in Constraint Programming (CPAIOR), Bologna, Italy, 14–18 June 2010; pp. 5–9. [Google Scholar]
- GEne Network Expansion. CPU Performance. 2025. Available online: https://gene.disi.unitn.it/test/cpu_list.php (accessed on 9 July 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).