Abstract
Parkinson’s disease (PD) is a chronic neurodegenerative disorder that progressively impairs motor functions. Clinical assessments have traditionally relied on rating scales such as the Movement Disorder Society Unified Parkinson Disease Rating Scale (MDS-UPDRS); however, these evaluations are susceptible to rater-dependent variability and may miss subtle motor changes. This study explored objective and quantitative methods for assessing motor function in PD patients using the Quantum Metaglove, a sensory glove produced by MANUS®, which was used to record finger movements during three tasks: finger tapping, hand gripping, and pronation–supination. Classic and geometric motor features (the latter based on Clifford algebra, an advanced approach for trajectory shape analysis) were extracted. The resulting data were used to train various machine learning algorithms (k-NN, SVM, and Naive Bayes) to distinguish healthy subjects from PD patients. The integration of traditional kinematic and geometric approaches improves objective hand movement analysis, providing new diagnostic opportunities. In particular, geometric trajectory analysis provides more interpretable information than conventional signal processing methods. This study highlights the value of wearable technologies and Clifford algebra-based algorithms as tools that can complement clinical assessment. They are capable of reducing inter-rater variability and enabling more continuous and precise monitoring of hand motor movements in patients with PD.
1. Introduction
Sensory gloves (SGs) represent a versatile and impactful technology for objectively capturing fine-grained hand and finger motion data [1,2]. In particular, in the medical field SGs have been successfully adopted for surgical training of medical doctors (by tracking hand motions in virtual surgical environments [3] to capture and classify performance metrics [4] like tremor, precision, and timing) and motor assessment of the hand capabilities [5] of patients (by tracking fine motor functions when performing everyday or standard hand motor tasks [6]), which is useful for diagnostics [7], rehabilitation [8,9], monitoring [10], training [11], and beyond [12,13].
Parkinson’s disease (PD) is a chronic and progressive neurodegenerative disorder that impacts motor and non-motor functions [14,15]. Its cardinal motor symptoms—bradykinesia, rigidity, and tremor—significantly impair mobility and interfere with everyday activities [16]. Clinical assessment in PD relies on standardized clinical scales, such as the Movement Disorder Society Unified Parkinson Disease Rating Scale (MDS-UPDRS) [17]. A large section of the MDS-UPDRS motor evaluation (in particular part III [18]) is focused on assessing hand bradykinesia by means of finger tapping (FT), hand gripping (HG), and hand prono-supination (PS) motor tasks administered to patients (subitems 3.4, 3.5, and 3.6, respectively) [19]. However, when assessing hand bradykinesia, the MDS-UPDRS relies on visual inspections performed by movement-disorder experts [20]. Moreover, some subtle hand movements [21] (that produce signals with harmonic frequencies due to nonlinear movements) can be hard to quantify [22] or even undetectable with the human eye.
Within this frame, among wearable electronics [23,24,25,26], an SG can be a valid support when quantifying hand bradykinesia in PD [27,28], which is particularly important in clinical practice, as it occurs during PD motor impairment evaluation [29].
In this study, we enrolled 71 subjects (41 subjects with PD and 30 healthy subjects) and directed them to perform hand movements according to MDS-UPDRS subitems 3.4, 3.5, and 3.6, which are used to assess hand bradykinesia. Hand movements were clinically evaluated by experienced neurologists and instrumentally acquired by means of an SG termed a Quantum Metaglove® (by Manus, Baanhoek, The Netherlands) [30]. All patients were clinically and instrumentally examined while receiving therapy (e.g., levodopa treatment). Our movement analysis primarily focused on hand bradykinesia for two main reasons: (i) an SG practically allows the objective detection of hand movements and (ii) hand bradykinesia is commonly used to clinically estimate global bradykinesia in patients with PD in telemonitoring scenarios.
We realized a comprehensive analysis of the spatiotemporal features extracted from the measurements obtained by means of the SG. As a novelty, we adopted a geometric algebra-based approach to highlight the geometrical meaning of the extracted features, thereby enhancing data interpretability. Moreover, for comparison purposes, we also adopted a standard approach based on three machine learning algorithms, i.e., k-Nearest Neighbors (k-NN) [31,32], Support Vector Machine (SVM) [33,34], and Naive Bayes (NB) [35,36] (which are among the most commonly adopted algorithms [37]), and a new approach based on geometric algebra capable of accounting for the geometrical meaning of the extracted features, in order to improve data interpretability and classification performance using the same machine learning algorithms.
The rest of this paper is organized as follows: Section 2 details the participants and the sensory glove; Section 3 describes the study methodology; Section 4 presents and discusses the results, highlighting the contributions of geometric features to classification performance; and Section 5 provides the conclusions and outlines potential directions for future research.
2. Related Work
In [20], the authors acquired objective data from hand motor tasks using an optical-based motion capture device termed Leap Motion, from which motion features were extracted. Features were then selected using a random forest algorithm and were later adopted for SVM-based classification to determine the akinesia in the hands of 45 PD patients. However, in [38] the authors revealed the Leap Motion suffers from a systematic error that must be considered during finger tapping.
In [6], the authors investigated hand movement capabilities by measuring straight lines drawn on the surface of a pad and evaluating the velocity and trajectory of the pen for 24 PD patients. Interestingly, the authors considered the geometry aspect related to the physics of the movements but with a standard approach to the geometry.
In [39], the authors focused on finger tapping data acquired by means of video recordings on which they performed index finger motion segmentation, signal normalization, feature extraction, and SVM-based classification for 13 PD patients. However, this procedure can only be realized in an environment prepared with cameras.
In [40], the authors considered hand gripping, hand prono-supination, and finger tapping, as these three motor tasks demand unequal forces. The finger tapping was the most difficult to perform for 33 PD patients. Interestingly, this work underlined the importance of focusing on hand dexterity as one of the fundamental aspects when dealing with PD patients.
Although there are many interesting works, as far as we know, there is a lack of research considering data gathered by wearable electronics processed to evidence geometrical aspects related to asymmetries between the two hands in PD patients. Therefore, we adopted an SG and an ad hoc-developed geometric algebra algorithm never previously adopted in the medical domain, as well as a standard procedure to evidence possible improvements.
3. Materials
3.1. Participants
This study involved a total of 71 subjects, who were divided into two groups: 41 patients affected by PD (21 males and 20 females, aged 71.8 ± 7.9 years old) and 30 healthy subjects (with comparable ages and physical characteristics) as a control group (HC hereafter) (16 males and 14 females, aged 63.1 ± 10.5 years old).
The patients with PD included in this study were in an intermediate stage of the disease and receiving stable pharmacological treatments, mainly levodopa and dopaminergic agonists, and were therefore considered to be in the ‘ON’ phase.
The PD patients were enrolled according to the following inclusion criteria: a diagnosis of idiopathic PD based on current consensus criteria and clinical follow-up evaluations [41], an absence of dementia (Montreal cognitive assessment (MoCA) > 23) [42], and comorbidities affecting arm or hand movements. All patients underwent clinical assessments using standardized clinical scales such as the Hoehn and Yahr scale (H&Y) [43] and MDS-UPDRS part III [19]. All patients were evaluated in the ‘ON’ state of their medication (i.e., around one hour after taking their usual dopaminergic treatment).
The HC group consisted of healthy subjects without diagnoses of neurological pathologies. They were cognitively intact and of ages comparable to the PD group.
All participants provided written informed consent, and this study was approved by the institutional review board in accordance with the Declaration of Helsinki.
3.2. Sensory Glove
The Quantum Metaglove® (Figure 1) hosts one source of electromagnetic (EM) signals on the dorsal aspect of the hand and five EM sensors hosted on hoods worn on the tips of the fingers. As such, the EM sensors measure the dynamic distances between the fingertips and the EM source during finger flexion/extension and adduction/abduction (according to the EM field variations), and, accounting for the fingers’ physical constraints, proprietary Manus software extrapolates the relative rotations of all the joints of the fingers. For completeness, an inertial measurement unit (IMU), hosted together with the EM source, provides data related to the movements of the hand in space.
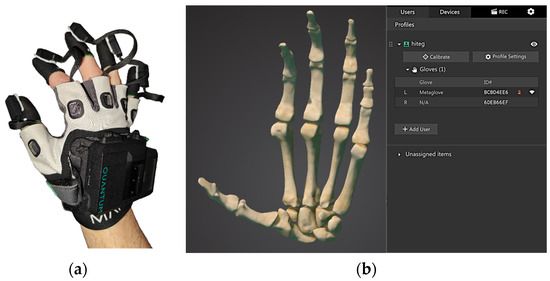
Figure 1.
(a) The Quantum Metaglove and (b) the graphical interface provided by Manus.
The Quantum Metaglove®, which is specifically designed for real-time tracking, is made of an antibacterial-treated fabric composed of a polyester and spandex blend, and it features a fingerless design. At the finger joints, including the metacarpophalangeal (MCP) and interphalangeal (IP) joints, there are five tunnels through which sensor cables can pass, allowing signals to be conducted to the fingertips.
The glove is designed for ergonomic and biomechanical compatibility. Sensors are mounted on elastic thimbles of various sizes that fit snugly on the fingers, while braided flat ribbons manage the wiring to minimize the bulk and mechanical interference. The angular rotations of the finger joints are indirectly obtained based on an ad hoc-developed proprietary algorithm.
4. Methods
4.1. SG Calibration
For reliability measurements a three-step calibration procedure was adopted and individually performed by each subject before recording data related to any motor tasks. The procedure consisted of initially holding the hand in a flat position, then a closed-fist position, and finally repeatedly opening and closing the fingertips as far away from the proximal joints as possible. This calibration functionally defined the reference coordinate system and allowed the correct distances to be detected between each EM sensor (on the fingertips) and the EM source (on the back of the hand) in both static and dynamic conditions.
4.2. Hand Motor Tasks
According to the MDS-UPDRS protocol and the experience of the physicians, we considered three hand motor tasks as the most relevant: finger tapping (FT), hand gripping (HG), and hand prono-supination (PS) [44]. In particular, FT consists of tapping the index finger and thumb together, HG consists of opening and closing the hand, and PS consists of alternating pronation and supination of the hand with the forearm fully extended.
For all tasks, in turn, each subject was asked to perform the movement as quickly and widely as possible for a short period (typically 10–15 s as practice) while keeping the shoulder flexed forward at 90° and minimizing other body movements.
We accounted for asymmetries between the two hands, discriminating between the most affected hand and the less affected hand for the PD group and between the dominant and non-dominant hands for the HC group. More specifically, in the PD patients we defined the “most affected” side as the one with the higher upper-limb MDS-UPDRS score, calculated as the sum of subitems 3.3 (rigidity), 3.4–3.6 (bradykinesia), and 3.15–3.17 (tremor), all referring to the upper limb.
4.3. Measurement Protocol
Before the hand motor tasks, each patient was informed of the procedure and gave signed informed consent. Then, each patient underwent a preliminary clinical evaluation, which included collection of demographic data and medical history and administration of the MDS-UPDRS scale, with particular focus on section III (motor examination), to obtain a reference score for the severity of the observed symptoms.
Then, in turn, each patient wore the SG (under the supervision of a neurologist to ensure a proper fit) and performed the three motor tasks (FT, HG, and PS) in order, with breaks between them to avoid fatigue, under the supervision of a neurologist to ensure adherence to the protocol. Each task was performed for both hands, according to the MDS-UPDRS protocol, and the SG furnished the related motor data as spatial coordinates, joint rotations, relative angles, and interphalangeal distances.
4.4. Data Processing
4.4.1. Classic Feature Extraction
For each task, different kinematic features were extracted to determine their biomechanical relevance, signal quality, and clinical importance, specifically:
- The FT task: the thumb–index distance (cm);
- The HG task: the flex/extension of the PIP joints (degrees) for the index, middle, ring, and little fingers (the thumb was excluded since, due to its anatomy, it does not fully synergistically support hand closing and showed a less stable signal);
- The PS task: the 3D spatial coordinates (cm) assumed by the most distal phalanx of the thumb, which is capable of reflecting overall motion (the other fingers were considered too, but no relevant information was added).
In particular, for the PS task, by means of Principal Component Analysis (PCA) [45], 3D values were reduced to 2D projections, but the informative content was maintaining. These projections were easier to interpret and compare across subjects.
The raw data were pre-processed: application of the Gaussian smoothdata routine in MATLAB® v.2024a [46] reduced high-frequency spurious oscillations (possibly due to micro-movements, electromagnetic disturbances, or imperfect glove–skin contact), and a time of 15 s windowed the signals (Figure 2 shows the procedure for the thumb–index distance over a 15 s period). We used the smoothdata routine with a smoothing window length of 20 (empirically determined), which given the sampling rate of 120 Hz, corresponded to a time window of approximately 167 ms.
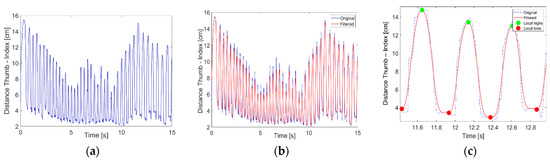
Figure 2.
Thumb–index distance measured during FT task: (a) raw data, (b) Gaussian smoothed data, and (c) zoomed-in with local maxima (green dots) and minima (red dots).
From the pre-processed data for each motor task, for each participant, and for both hands, some features were calculated, such as the frequency (, to compute which local maxima and minima were identified, as represented in Figure 2c); the range of motion (RoM, averaged during the 15 s of task repetition); the coefficient of variation of the RoM (); the mean velocities (calculated as derivatives of the filtered signal accounting for the local maxima and minima averages) of both the opening () and closing () movements; the coefficient of variation of (, calculated as the mean velocity and its standard deviation ratio); and a performance index () that we created to combine the frequency and the average RoM, since these are the main parameters observed by doctors for medical assessment but, when observed individually, can be ambiguous (for example, a high frequency may be due to a reduced ROM, and conversely, a high ROM may result in a reduced frequency).
In particular, the can be rich in information since PD patients typically exhibit greater variability relative to the mean compared to healthy subjects, and the is correlated with the ability to perform the movement both widely and quickly, as specifically required by the UPDRS protocol.
In general, given that PD commonly manifests with asymmetric motor signs [47], to account for asymmetries (if any) between hands, a further feature, asym, was calculated as the ratio between the homogeneous features of the two hands for both the PD and HC groups to account for differences.
4.4.2. A Geometric Algebra-Based Approach
As a novelty, we adopted so-called Clifford geometric algebra (GA), which allows spatial trajectories (as in Figure 3) to be handled in a geometrically consistent and robust manner to compare complex movements, such as those of the fingers across the three motor tasks addressed thus far [48]. In such a manner, geometrical features were obtained.
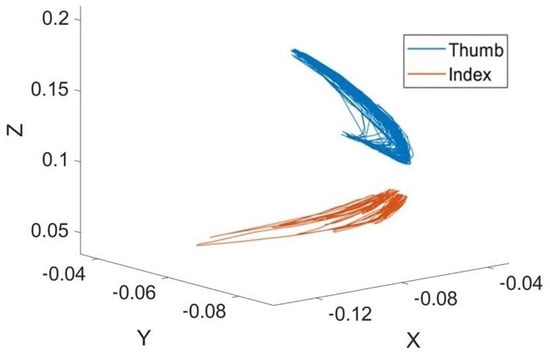
Figure 3.
The three-dimensional trajectory of thumb and index finger movement during the FT task.
Specifically, geometric algebra (GA) [49] is a powerful extension of vector algebra that provides a framework for representing and manipulating geometric objects such as points, lines, planes, and volumes in space. It combines a set of operations between vectors (such as addition, the scalar product, the geometric vector product, and the exterior product) into a single associative product called the geometric product and allows for the representation of multidimensional objects such as planes, bivectors, trivectors, etc., as elements of a unique finite dimensional vector algebra.
GA is used to represent and interpret gesture trajectories in a more transparent and interpretable manner compared to traditional machine learning techniques, which can often behave like a “black box”. Each gesture is seen as a sequence of points in space (2D or 3D), where each point represents a position in space at a given moment in time. GA is therefore useful for analyzing how these trajectories evolve over time and for precisely characterizing their shapes and directions.
In a recent work [48], GA was successfully applied in the context of hand gesture recognition, where movements were represented as sequences of 3D points (P = (xP, yP, zP)) over time, and GA allows us to calculate and compare the shapes and directions of related trajectories. Distance metrics, such as those based on bivectors and trivectors, can quantify the similarity between hand movements (performed by different individuals or by the same individual at different times), while geometric distances can be employed to detect asymmetries between the right and left hand (as occurs in PD).
Geometric algebra is, to the best of our knowledge, entirely unknown in biomedical engineering applications related to PD. For this reason, a comparative study using the numerous existing approaches that rely on conventional geometric features (vectorial and scalar) would require dedicated research efforts that fall outside the scope of the present article. Precisely due to the novelty of our approach and the use of geometric algebra, misunderstandings may arise. In this section, we aim to highlight potential sources of confusion.
The first possible misunderstanding concerns the abbreviation “GA,” which in other mathematical contexts commonly refers to a “Genetic Algorithm”. Since our work does not involve genetic algorithms, we have chosen to retain “GA” as an abbreviation for “Geometric Algebra”. This decision is based on two reasonable considerations: (i) within the geometric algebra community, the abbreviation “GA” is standard and unambiguous, and (ii) adopting the alternative abbreviation “CGA” for “Clifford Geometric Algebra” would likely introduce even greater confusion, as “CGA” is widely recognized to refer to “Conformal Geometric Algebra,” a distinct branch of geometric algebra not related to our approach.
In this article, we have deliberately minimized explanations regarding the multivector quantity that encodes the “shape of an oriented triangle.” Providing more detailed or intuitive explanations of geometric algebra, while certainly valuable for educational purposes, lies beyond the scope of this research article. For further reading, we refer interested readers to the book [49] and the article [50].
Another potential misunderstanding, stemming from limited familiarity with geometric algebra, is the assumption that it merely reformulates concepts already expressible within conventional vector calculus. This is not the case. For example, in standard vector calculus, the ratio between two vectors cannot be defined in a general, dimension-independent way due to Frobenius’s theorem on real division vector algebras. In contrast, this notion is elementary in geometric algebra. Moreover, it is precisely the Clifford ratio between two vectors that encodes the shape of an oriented triangle—where two ordered and oriented sides form the pair of vectors to be divided—which we use in this work.
A further misunderstanding might arise from observing that the modulus of the Clifford ratio between two vectors approximates the curvature of a continuous and differentiable trajectory in the limit of infinitesimal lengths. The issue here is underestimation of the novelty of our approach: while curvature is a scalar quantity, the Clifford ratio is a multivector (in our case, of four dimensions). Finally, although the ratio between two 3D vectors is isomorphic to the Hamilton quaternion, it is important to note that our GA-based approach allows for the division of vectors in arbitrary dimensions, making it applicable to far more general contexts than those addressed by quaternions.
4.4.3. Geometric Feature Extraction
The main operations used in Clifford GA for gesture recognition are the dot product, the geometric vector product, and calculating the geometric distances between trajectories.
The distance between two points (P and Q) in a three-dimensional space is
This is fundamental for measuring the separation between two positions in a 3D space and is used to analyze the variation in a position between two points along a trajectory in order to perform a uniform sampling of 3D finger trajectories.
The dot product of two three-dimensional vectors ( and ) is defined as follows:
as a measure of the alignment between the two vectors.
The cross product of a and b is given by
the result being a 3D vector perpendicular to a and b.
To start, the data were subjected to a downsample routine in MATLAB®, where they were downsampled by a factor of 3, reducing the signal frequency from 120 Hz to 40 Hz (still above the Nyquist rate for human finger movement kinematics) to lower the computational load for feature extraction and classification but preserving information integrity. Then the data were uniformly resampled to obtain points evenly spaced along the trajectory curve (Figure 4) to allow the comparison of gestures performed at different speeds and to ensure that all resampled trajectories had the same number of points.
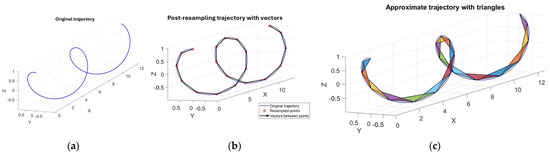
Figure 4.
(a) A 3D trajectory, (b) the trajectory resampled with equidistant points connected by 3D vectors, and (c) the trajectory divided into triangles.
Later, the trajectory (which could be complex, with continuous variations in direction and speed) was approximated using consecutive triangles to reduce its geometric complexity while preserving key information for analysis.
Each triangle was formed by two consecutive vectors whose ratio in GA represented the “shape” of the trajectory in a particular region, which served the following functions:
- It provided information about the direction of motion via the vectors that defined it;
- It served as a local approximation of the curve, enabling analysis of the overall shape without the need to examine every point along the path;
- It used simple geometric shapes (i.e., GA ratios) that were easy to manipulate and compare with other triangles (e.g., between two movements) with lower computational effort than comparing individual points, especially for complex trajectories.
According to GA, the dot product and cross product can be used to efficiently and compactly describe the shapes of segments and, thus, triangles.
This process can be mathematically described as follows:
- Consider two consecutive points, and , along the trajectory, and compute the vector between them.
- Construct an oriented triangle using two consecutive vectors, and , by “joining” the head of with the tail of . This is repeated across the entire trajectory, yielding a sequence of consecutive triangles (Figure 4b,c).
- Consider two consecutive vectors, and , to compute their dot product and cross product, which provide information about their relative orientations and angular difference.
In GA the shape of such an oriented triangle is coded as the geometric ratio of vectors and , which in our case is a 4D vector with dimensionless coordinates:
At this stage, a series of 4D points (, coding the orientation and shape of each oriented triangle in a trajectory) was obtained. With an ad hoc routine in MATLAB and the recorded motion signals, we extracted the shapes of the triangles—and therefore the trajectory forms—for both hands.
Such GA coding of shapes as 4D points allowed us to measure the asymmetry between two shapes, S and S′ (corresponding to the fingers’ trajectories), by simply computing the corresponding 4D Euclidean distance:
As a result of applying GA, we determined the dimensionless geometrical features coding the shapes of the trajectories of the fingers’ movements, and we evaluated the asymmetries between the two hands in terms of the distances between 4D points. These distances were named according to the fingers and motor tasks as follows: a-Thumb FT, a-Index FT, a-Thumb HG, a-Index HG, a-Middle HG, a-Ring HG, a-Little HG, a-Thumb PS, a-Index PS, a-Middle PS, a-Ring PS, and a-Little PS.
4.4.4. Feature Selection
Among all features, some were selected as the most informative ones from previously obtained datasets of both classic and geometric features. This selection was based on their statistical significance (aimed at a meaningful classification) and the non-parametric Mann–Whitney U test [51], which does not assume data normality when comparing two independent groups of data that do not follow a normal or Gaussian distribution.
4.4.5. Classification
To compare improvements in the geometric features with respect to the classical ones, we tested the performances of three different machine learning algorithms that were fed one group of features at a time. In particular, we adopted MATLAB’s Classification Learner. The k-NN, SVM, and NB classifiers were fed classic and geometric features one at a time and split into a training set comprising 75% of the data and a testing set comprising 25%, as suggested in [28,52]. Our choice of these three classifiers was due to their known balance between accuracy and training speed when dealing with small sample sizes, as in our work. During the training phase the performances were optimized by varying k for k-NN and varying the kernel (tested as linear, polynomial, and Radial Basis Function (RBF)) for SVM. The classification performance of each classifier was evaluated in terms of its accuracy; training time; prediction speed; confusion matrix; Receiver Operating Characteristic (ROC); and Area Under the Curve (AUC) values [53,54]. In particular, the training time represented the time required to train the model on the training dataset provided, including internal parameter optimization, cross-validation procedures, and execution of other operations necessary to build the final model. Moreover, the prediction speed was the rate at which the trained model could generate predictions for new data, expressed as the number of observations predicted per second. The AUC assessed the classifiers’ ability to distinguish between classes, especially for the partially imbalanced distribution of the dataset we had (41 PD and 30 HC).
5. Results and Discussion
5.1. Classic Features Selected
Table 1 reports the measured values of the classic features related to the movements of the most affected hand for the PD group and the right (dominant) hand for the HC group.

Table 1.
The measured values of the classic features related to the most affected hand in the PD group and the right hand in the HC group for the three motor tasks (FT: finger tapping, HG: hand gripping, and PS: prono-supination) and the related p-values (<0.05 in bold) obtained using the Mann–Whitney U test.
According to the Mann–Whitney U test, 13 of the 24 classic features had significance (p < 0.05) across the three motor tasks (FT, HG, and PS) for classifying PD vs. HC. Interestingly, the FT and PS tasks produced relevant features concerning, in particular, the velocity and (ir)regularity of the movement ( and for FT and for PS out of the meaningful ones), while the HG results had poor significance when differentiating PD vs. HC.
Moreover, to evidence motor asymmetries (if any), we calculated the ratios of the homologous features of the most affected hand with respect to the less affected hand for the PD group and the ratios of the homologous features of the right hand with respect to the left hand for the HC group (Table 2). Among all of the features, the statistical analysis using the Mann–Whitney U test identified 4 out of 24 as significant features (p < 0.05) (they were considered later for classification purposes).

Table 2.
The statistical significance assessment using the independent-sample Mann–Whitney U test. Features with p-values lower than 0.05 are highlighted in bold.
5.2. Geometric Features Selected
Using the Mann–Whitney U test for independent samples (as before), we determined that 4 of the 12 features were statistically significant (and therefore usable for later classification). As shown in Table 3, a-Thumb demonstrated relevance for both the FT and HG tasks, a-Index was relevant for FT and PS, and a-Ring was only relevant for PS.

Table 3.
The statistical significance evaluation according to the Mann–Whitney U test for independent samples based on geometric features. Features with p-values lower than 0.05 are highlighted in bold.
Figure 5 shows the dispersion densities of the significant features that graphically evidence how the PD group exhibited greater asymmetry compared to the HC group, who consistently appeared more clustered around zero.
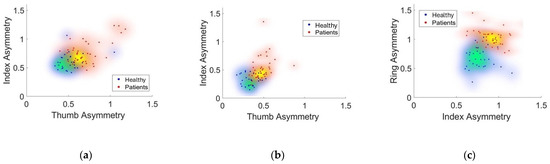
Figure 5.
The dispersion densities of the asymmetries in the geometric feature spaces as a result of the (a) FT, (b) HG, and (c) PS tasks.
It is worth recalling that the asymmetry between the trajectories traced by the fingers of both hands was calculated by evaluating the difference between the shapes of the triangles constructed along those trajectories. Therefore, the more similar the movements of the two hands, the smaller the distance between the corresponding points.
5.3. Machine Learning
Different classifiers, such as k-NN, SVM, and Naive Bayes, were adopted, first for distinguishing the PD and HC groups using only the selected classical features, then to evidence asymmetries between the hands using both the selected classical features and the selected geometric features.
5.3.1. Classification with Classic Features
The results obtained based only on the classical features show moderate testing accuracy (Table 4). The Naive Bayes model achieved the best accuracy on the training dataset (83.26%) but had the highest training time (6.58 s) and the lowest rate of prediction (591/s). The SVM proved to be the most efficient in terms of the computational cost (2681 predictions/s), and k-NN performed similarly in terms of the training time (1.23 s) and prediction rate (1415/s).

Table 4.
Performances of classifiers fed classical features.
Figure 6 shows the ROC curves of each classifier, with the corresponding AUC values (useful for accounting for unbalanced datasets (41 PD and 30 HC)). k-NN performed best (AUC = 0.8429), and the SVM was very similar (AUC = 0.8286), while Naive Bayes was the lowest (AUC = 0.7643).
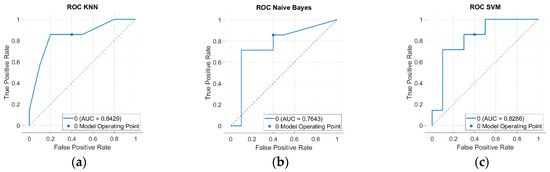
Figure 6.
The ROC curves of the (a) KNN, (b) Naive Bayes, and (c) SVM classifiers trained with the selected classical features. The AUC value is reported in the bottom right corner of each image.
5.3.2. Classification with Mixed Features
To evidence the relevance of geometric features (if any) to enhancing the classification performance, we fed the k-NN, SVM, and Naive Bayes algorithms four classic (Table 2) and five geometric (Table 3) features, as previously selected. Table 5 summarizes the results.

Table 5.
Performances of classifiers fed mixed features to evidence asymmetries.
Here, we decided not to perform a standalone classification analysis with only the geometric algebra-based features for methodological reasons [55,56]. Specifically, after statistical testing, only a limited subset of the geometric features showed significant differences between the PD and HC groups. Given the relatively small size of our dataset (41 PD and 30 HC), training a classification model with such a reduced and highly specific feature set would have increased the risk of overfitting and produced unstable, non-generalizable results. Preliminary exploratory tests confirmed that the classification accuracy using only the statistically significant geometric features was substantially lower compared to using the mixed features, and their independent discriminative power was limited. For these reasons, we integrated the geometric features with the classical ones to capture both the kinematic and spatial-trajectory aspects of the movements. This combination yielded robust and reproducible classification performance, as detailed later.
Specifically, for k-NN the testing accuracy (82.67 vs. 73.76%) and prediction speed (1766.66 vs. 1415 predictions/s) were greatly increased, with an interesting reduction in the training time (0.376 vs. 1.23 s), so the training time and prediction speed were somewhat balanced. For Naive Bayes, the testing accuracy was reduced (73.56 vs. 77.58%), but the prediction speed significantly increased (4628.36 vs. 591 predictions/s) at the cost of less than 2 s of training time. Moreover, for the SVM, the testing accuracy meaningfully increased (79.22 vs. 68.14%), with a lower prediction speed (1676.55 vs. 2681 predictions/s) and a similar training time (1.52 vs. 1.20 s).
As a result, adopting only five geometric features increased the classification performance.
The ROC curves (Figure 7) reveal how the SVM reached the highest AUC (0.9286), indicating good discrimination between the two classes, despite a slightly lower overall accuracy.
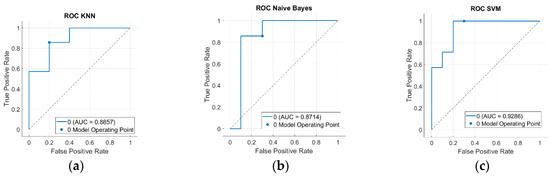
Figure 7.
The ROC curves of the (a) KNN, (b) Naive Bayes, and (c) SVM classifiers fed with a combination of classical and geometric features. The AUC value is reported in the bottom right corner of each image.
6. Conclusions
Assessment of bradykinesia in Parkinson’s disease (PD) is a complex task, but it is fundamental to optimizing treatments. Currently bradykinesia is evaluated by means of standardized rating scales that assign scores based on visual inspection. Accordingly, some subtle motor impairments cannot be evaluated since they are undetectable by the human eye (as are the frequency harmonic contents in the movement signals).
Conversely, wearable electronics, such as sensory gloves (SGs), can allow objective evaluation of hand movements. Therefore, here we adopted an SG, termed the Quantum Metaglove®, to measure the three main hand motor tasks (as indicated by UPDRS part III items 3.4, 3.5, and 3.6), which are finger tapping, opening/closing, and prono-supination hand motor tasks. For this purpose, 71 subjects were enrolled in this study, 41 with PD and 30 healthy controls.
As a novelty, the values we extracted from the measurements consisted of both classical features and so-called geometric features. The latter, in particular, resulted in dimensionless values that were determined by means of geometric algebra (GA), which allowed spatial trajectories, such as hand movements, to be handled consistently in a geometric manner to analyze and compare complex movements.
The meaningful extracted features were used for classification purposes by means of k-Nearest Neighbors (k-NN), Support Vector Machine (SVM), and Naive Bayes classifiers. In particular, our focus was devoted to evidencing asymmetries between the most affected and less affected hands related to PD.
Our results indicate that combined usage of both classical and geometric features, with respect to using only classic features, increases classification performance. In particular k-NN, as the best classifier among the three, had a training accuracy of 86.67% and a testing accuracy of 82.67% when adopting both classic and geometric features, compared to a training accuracy of 78.54% and a testing accuracy of 73.76% when only adopting classic features.
This work can represent a first step in adopting GA in signal analysis, especially using data acquired by wearable electronics aimed at detecting subtle motor issues not visible to the human eye. In particular, the feature extraction method based on geometric algebra aligns with so-called explainable AI, that is, the pursuit of recognition and classification methodologies capable of providing interpretable information about the nature of the results. For this reason, we believe that adopting geometric algebra in signal analysis can make a significant contribution to clinical research, as it enriches the obtained results with interpretable meaning. Moreover, the results show that a classifier trained using geometric features achieves faster training and classification, suggesting that this type of feature would be particularly suitable in contexts where training and classification require real-time responses, such as in telemedicine environments.
When considering the present findings, several points should be carefully considered. First, our study sample consisted of patients in an intermediate stage of the disease. Hence, the present findings should not be generalized to the whole population of patients with PD. Second, our cohort included patients examined only when receiving therapy. Accordingly, our data does not allow us to reveal the effect of dopaminergic treatment on the instrumental measures and analyses reported here. Future studies with larger cohorts including patients in the early stage of the disease and those examined when receiving and not receiving therapy will further expand the clinical utility of SG-based technologies in the objective monitoring of PD. Nevertheless, this work can represent a first step in adopting GA for signals acquired by wearable electronics aimed to evidence subtle motor issues not evident to human eyes.
Author Contributions
Conceptualization, G.S., P.R. and A.S.; methodology, G.S., P.R., L.P., A.R., N.A., M.P. and A.S.; software, P.R., L.P., A.R. and N.A.; validation, G.S., P.R. and A.S.; formal analysis, G.S., P.R., L.P. and A.R.; investigation, G.S., L.P., A.R. and M.P.; resources, G.S. and A.S.; data curation, P.R., L.P., A.R. and M.P.; writing—original draft preparation, G.S. and A.R.; writing—review and editing, G.S., P.R., L.P., A.R., M.P. and A.S.; visualization, G.S. and A.R.; supervision, G.S., P.R. and A.S.; project administration, G.S.; funding acquisition, G.S. and A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The authors will provide data upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SG | sensory glove |
| PD | Parkinson’s disease |
| MDS-UPDRS | Movement Disorder Society Unified Parkinson Disease Rating Scale |
| HC | healthy control |
| k-NN | k-Nearest Neighbors |
| SVM | Support Vector Machine |
| NB | Naive Bayes |
| EM | electromagnetic |
| IMU | inertial measurement unit |
| MCP | metacarpophalangeal |
| IP | interphalangeal |
| FT | finger tapping |
| HG | hand gripping |
| PS | prono-supination |
| PCA | Principal Component Analysis |
| RoM | range of motion |
| PI | performance index |
| GA | geometric algebra |
| RBF | Radial Basis Function |
| ROC | Receiver Operating Characteristic |
| AUC | Area Under the Curve |
References
- Saggio, G.; Orengo, G.; Leggieri, A. Sensory Glove and Surface EMG with Suitable Conditioning Electronics for Extended Monitoring and Functional Hand Assessment. In Proceedings of the 9th International Joint Conference on Biomedical Engineering Systems and Technologies, Rome, Italy, 21–23 February 2016; SCITEPRESS—Science and and Technology Publications: Setúbal, Portugal, 2016; pp. 206–213. [Google Scholar]
- Mohan, A.; Tharion, G.; Kumar, R.K.; Devasahayam, S.R. An Instrumented Glove for Monitoring Hand Function. Rev. Sci. Instrum. 2018, 89, 105001. [Google Scholar] [CrossRef] [PubMed]
- Saggio, G.; Lazzaro, A.; Sbernini, L.; Carrano, F.M.; Passi, D.; Corona, A.; Panetta, V.; Gaspari, A.L.; Di Lorenzo, N. Objective Surgical Skill Assessment: An Initial Experience by Means of a Sensory Glove Paving the Way to Open Surgery Simulation? J. Surg. Educ. 2015, 72, 910–917. [Google Scholar] [CrossRef]
- Saggio, G.; Santosuosso, G.L.; Cavallo, P.; Pinto, C.A.; Petrella, M.; Giannini, F.; Di Lorenzo, N.; Lazzaro, A.; Corona, A.; D’Auria, F.; et al. Gesture Recognition and Classification for Surgical Skill Assessment. In Proceedings of the 2011 IEEE International Symposium on Medical Measurements and Applications, Bari, Italy, 30–31 May 2011; IEEE: New York, NY, USA, 2011; pp. 662–666. [Google Scholar]
- Oess, N.P.; Wanek, J.; Curt, A. Design and Evaluation of a Low-Cost Instrumented Glove for Hand Function Assessment. J. Neuroeng. Rehabil. 2012, 9, 2. [Google Scholar] [CrossRef]
- Kotsavasiloglou, C.; Kostikis, N.; Hristu-Varsakelis, D.; Arnaoutoglou, M. Machine Learning-Based Classification of Simple Drawing Movements in Parkinson’s Disease. Biomed. Signal Process Control 2017, 31, 174–180. [Google Scholar] [CrossRef]
- Dutta, D.; Modak, S.; Kumar, A.; Roychowdhury, J.; Mandal, S. Bayesian Network Aided Grasp and Grip Efficiency Estimation Using a Smart Data Glove for Post-Stroke Diagnosis. Biocybern. Biomed. Eng. 2017, 37, 44–58. [Google Scholar] [CrossRef]
- Saggio, G.; Sbernini, L.; De Leo, A.; Awaid, M.; Di Lorenzo, N.; Gaspari, A.L. Assessment of Hand Rehabilitation after Hand Surgery by Means of a Sensory Glove. In Proceedings of the 9th International Joint Conference on Biomedical Engineering Systems and Technologies, Rome, Italy, 21–23 February 2016; SciTePress: Science and Technology Publications: Setúbal, Portugal, 2016; pp. 187–194. [Google Scholar]
- Zhu, Y.; Gong, W.; Chu, K.; Wang, X.; Hu, Z.; Su, H. A Novel Wearable Soft Glove for Hand Rehabilitation and Assistive Grasping. Sensors 2022, 22, 6294. [Google Scholar] [CrossRef]
- Henderson, J.; Condell, J.; Connolly, J.; Kelly, D.; Curran, K. Review of Wearable Sensor-Based Health Monitoring Glove Devices for Rheumatoid Arthritis. Sensors 2021, 21, 1576. [Google Scholar] [CrossRef]
- Meng, F.; Liu, C.; Li, Y.; Hao, H.; Li, Q.; Lyu, C.; Wang, Z.; Ge, G.; Yin, J.; Ji, X.; et al. Personalized and Safe Soft Glove for Rehabilitation Training. Electronics 2023, 12, 2531. [Google Scholar] [CrossRef]
- Caeiro-Rodríguez, M.; Otero-González, I.; Mikic-Fonte, F.A.; Llamas-Nistal, M. A Systematic Review of Commercial Smart Gloves: Current Status and Applications. Sensors 2021, 21, 2667. [Google Scholar] [CrossRef] [PubMed]
- Demolder, C.; Molina, A.; Hammond, F.L.; Yeo, W.-H. Recent Advances in Wearable Biosensing Gloves and Sensory Feedback Biosystems for Enhancing Rehabilitation, Prostheses, Healthcare, and Virtual Reality. Biosens. Bioelectron. 2021, 190, 113443. [Google Scholar] [CrossRef]
- Bloem, B.R.; Okun, M.S.; Klein, C. Parkinson’s Disease. Lancet 2021, 397, 2284–2303. [Google Scholar] [CrossRef]
- Leite Silva, A.B.R.; Gonçalves de Oliveira, R.W.; Diógenes, G.P.; de Castro Aguiar, M.F.; Sallem, C.C.; Lima, M.P.P.; de Albuquerque Filho, L.B.; Peixoto de Medeiros, S.D.; Penido de Mendonça, L.L.; de Santiago Filho, P.C.; et al. Premotor, Nonmotor and Motor Symptoms of Parkinson’s Disease: A New Clinical State of the Art. Ageing Res. Rev. 2023, 84, 101834. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Jenkins, M.E.; Naish, M.D.; Trejos, A.L. The Measurement and Analysis of Parkinsonian Hand Tremor. In Proceedings of the 2016 IEEE-EMBS International Conference on Biomedical and Health Informatics (BHI), Las Vegas, NV, USA, 24–27 February 2016; IEEE: New York, NY, USA, 2016; pp. 414–417. [Google Scholar]
- Goetz, C.G.; Choi, D.; Guo, Y.; Stebbins, G.T.; Mestre, T.A.; Luo, S. It Is as It Was: MDS-UPDRS Part III Scores Cannot Be Combined with Other Parts to Give a Valid Sum. Mov. Disord. 2023, 38, 342–347. [Google Scholar] [CrossRef] [PubMed]
- Trundell, D.; Davies, E.W.; Barrett, L.; Zanigni, S.; Shariati, N.; Rogers, R.; Monnet, A.; Moore, E.; Pross, N.; Pagano, G.; et al. Estimation of and Clinical Consensus on the Meaningful Motor Progression Threshold on MDS-UPDRS Part III. J. Park. Dis. 2025, 15, 97–110. [Google Scholar] [CrossRef]
- Goetz, C.G.; Tilley, B.C.; Shaftman, S.R.; Stebbins, G.T.; Fahn, S.; Martinez-Martin, P.; Poewe, W.; Sampaio, C.; Stern, M.B.; Dodel, R.; et al. Movement Disorder Society-sponsored Revision of the Unified Parkinson’s Disease Rating Scale (MDS-UPDRS): Scale Presentation and Clinimetric Testing Results. Mov. Disord. 2008, 23, 2129–2170. [Google Scholar] [CrossRef]
- Shin, J.; Matsumoto, M.; Maniruzzaman, M.; Hasan, M.A.M.; Hirooka, K.; Hagihara, Y.; Kotsuki, N.; Inomata-Terada, S.; Terao, Y.; Kobayashi, S. Classification of Hand-Movement Disabilities in Parkinson’s Disease Using a Motion-Capture Device and Machine Learning. IEEE Access 2024, 12, 52466–52479. [Google Scholar] [CrossRef]
- Maetzler, W.; Mirelman, A.; Pilotto, A.; Bhidayasiri, R. Identifying Subtle Motor Deficits Before Parkinson’s Disease Is Diagnosed: What to Look For? J. Park. Dis. 2024, 14, S287–S296. [Google Scholar] [CrossRef]
- Martinez, F.; Contreras-Corredor, S.A.; Salazar-Acosta, I. Parkinsonian Hand Tremor Characterization from Magnified Video Sequences. In Proceedings of the 14th International Symposium on Medical Information Processing and Analysis, Mazatlán, Mexico, 24–26 October 2018; Romero, E., Lepore, N., Brieva, J., Eds.; SPIE: Bellingham, WA, USA, 2018; p. 43. [Google Scholar]
- Aich, S.; Youn, J.; Chakraborty, S.; Pradhan, P.M.; Park, J.; Park, S.; Park, J. A Supervised Machine Learning Approach to Detect the On/Off State in Parkinson’s Disease Using Wearable Based Gait Signals. Diagnostics 2020, 10, 421. [Google Scholar] [CrossRef] [PubMed]
- Bhavana, C.; Gopal, J.; Raghavendra, P.; Vanitha, K.M.; Talasila, V. Techniques of Measurement for Parkinson’s Tremor Highlighting Advantages of Embedded IMU over EMG. In Proceedings of the 2016 International Conference on Recent Trends in Information Technology (ICRTIT), Chennai, India, 8–9 April 2016; IEEE: New York, NY, USA, 2016; pp. 1–5. [Google Scholar]
- Li, H.; Zecca, M.; Huang, J. Evaluating the Utility of Wearable Sensors for the Early Diagnosis of Parkinson Disease: Systematic Review. J. Med. Internet Res. 2025, 27, e69422. [Google Scholar] [CrossRef]
- Rovini, E.; Maremmani, C.; Cavallo, F. How Wearable Sensors Can Support Parkinson’s Disease Diagnosis and Treatment: A Systematic Review. Front. Neurosci. 2017, 11, 555. [Google Scholar] [CrossRef]
- Dong, Y.; Liu, J.; Yan, W. Dynamic Hand Gesture Recognition Based on Signals from Specialized Data Glove and Deep Learning Algorithms. IEEE Trans. Instrum. Meas. 2021, 70, 2509014. [Google Scholar] [CrossRef]
- Huang, Q.; Jiang, Y.; Duan, Z.; Yuan, Z.; Wu, Y.; Peng, J.; Xu, Y.; Li, H.; He, H.; Tai, H. A Finger Motion Monitoring Glove for Hand Rehabilitation Training and Assessment Based on Gesture Recognition. IEEE Sens. J. 2023, 23, 13789–13796. [Google Scholar] [CrossRef]
- Li, Y.; Yin, J.; Liu, S.; Xue, B.; Shokoohi, C.; Ge, G.; Hu, M.; Li, T.; Tao, X.; Rao, Z.; et al. Learning Hand Kinematics for Parkinson’s Disease Assessment Using a Multimodal Sensor Glove. Adv. Sci. 2023, 10, 2206982. [Google Scholar] [CrossRef] [PubMed]
- Manuri, F.; Decataldo, F.; Sanna, A.; Brizzi, P. A Comparison of Two Interaction Paradigms for Training Low Cost Automation Assembly in Virtual Environments. Information 2023, 14, 340. [Google Scholar] [CrossRef]
- Halder, R.K.; Uddin, M.N.; Uddin, M.A.; Aryal, S.; Khraisat, A. Enhancing K-Nearest Neighbor Algorithm: A Comprehensive Review and Performance Analysis of Modifications. J. Big Data 2024, 11, 113. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, R.; Lei, Y.; Liao, W.-H.; Cao, H.; Cao, J. Severity Level Diagnosis of Parkinson’s Disease by Ensemble K-Nearest Neighbor under Imbalanced Data. Expert Syst. Appl. 2022, 189, 116113. [Google Scholar] [CrossRef]
- Guido, R.; Ferrisi, S.; Lofaro, D.; Conforti, D. An Overview on the Advancements of Support Vector Machine Models in Healthcare Applications: A Review. Information 2024, 15, 235. [Google Scholar] [CrossRef]
- Bhattacharya, I.; Bhatia, M.P.S. SVM Classification to Distinguish Parkinson Disease Patients. In Proceedings of the Proceedings of the 1st Amrita ACM-W Celebration on Women in Computing in India, Coimbatore, India, 16–17 September 2010; ACM: New York, NY, USA, 2010; pp. 1–6. [Google Scholar]
- Hemachandran, K.; Tayal, S.; George, P.M.; Singla, P.; Kose, U. (Eds.) Bayesian Reasoning and Gaussian Processes for Machine Learning Applications; Chapman & Hall/CRC Press: Boca Raton, FL, USA, 2022; ISBN 9781003164265. [Google Scholar]
- Langarizadeh, M.; Moghbeli, F. Applying Naive Bayesian Networks to Disease Prediction: A Systematic Review. Acta Inform. Med. 2016, 24, 364–369. [Google Scholar] [CrossRef]
- Bourouhou, A.; Jilbab, A.; Nacir, C.; Hammouch, A. Comparison of Classification Methods to Detect the Parkinson Disease. In Proceedings of the 2016 International Conference on Electrical and Information Technologies (ICEIT), Tangiers, Morocco, 4–7 May 2016; IEEE: New York, NY, USA, 2016; pp. 421–424. [Google Scholar]
- Moshkova, A.; Bukin, V.; Samorodov, A. The Error Evaluation of the Amplitude of Finger Tapping and Pronation/Supination of the Palm Exercises Recorded by Leap Motion. In Proceedings of the 2023 Systems and Technologies of the Digital HealthCare (STDH), Tashkent, Uzbekistan, 4–6 October 2023; IEEE: New York, NY, USA, 2023; pp. 81–83. [Google Scholar]
- Khan, T.; Nyholm, D.; Westin, J.; Dougherty, M. A Computer Vision Framework for Finger-Tapping Evaluation in Parkinson’s Disease. Artif. Intell. Med. 2014, 60, 27–40. [Google Scholar] [CrossRef]
- Agostino, R.; Berardelli, A.; Currà, A.; Accornero, N.; Manfredi, M. Clinical Impairment of Sequential Finger Movements in Parkinson’s Disease. Mov. Disord. 1998, 13, 418–421. [Google Scholar] [CrossRef] [PubMed]
- Postuma, R.B.; Berg, D.; Stern, M.; Poewe, W.; Olanow, C.W.; Oertel, W.; Obeso, J.; Marek, K.; Litvan, I.; Lang, A.E.; et al. MDS Clinical Diagnostic Criteria for Parkinson’s Disease. Mov. Disord. 2015, 30, 1591–1601. [Google Scholar] [CrossRef] [PubMed]
- Carson, N.; Leach, L.; Murphy, K.J. A Re-examination of Montreal Cognitive Assessment (MoCA) Cutoff Scores. Int. J. Geriatr. Psychiatry 2018, 33, 379–388. [Google Scholar] [CrossRef] [PubMed]
- Bhidayasiri, R.; Tarsy, D. Parkinson’s Disease: Hoehn and Yahr Scale. In Movement Disorders: A Video Atlas; Humana Press: Totowa, NJ, USA, 2012; pp. 4–5. [Google Scholar]
- Sacristán, H.E.; Serra Fulles, J.A. The Essentials in Parkinson’s Disease. EC Neurol. 2023, 15, 36–67. [Google Scholar]
- Gupta, I.; Sharma, V.; Kaur, S.; Singh, A.K. PCA-RF: An Efficient Parkinson’s Disease Prediction Model Based on Random Forest Classification. arXiv 2022, arXiv:2203.11287. [Google Scholar]
- Shin, J.H.; Ong, J.N.; Kim, R.; Park, S.; Choi, J.; Kim, H.-J.; Jeon, B. Objective Measurement of Limb Bradykinesia Using a Marker-Less Tracking Algorithm with 2D-Video in PD Patients. Park. Relat. Disord. 2020, 81, 129–135. [Google Scholar] [CrossRef] [PubMed]
- Djaldetti, R.; Ziv, I.; Melamed, E. The Mystery of Motor Asymmetry in Parkinson’s Disease. Lancet Neurol. 2006, 5, 796–802. [Google Scholar] [CrossRef] [PubMed]
- Calado, A.; Roselli, P.; Errico, V.; Magrofuoco, N.; Vanderdonckt, J.; Saggio, G. A Geometric Model-Based Approach to Hand Gesture Recognition. IEEE Trans. Syst. Man. Cybern. Syst. 2022, 52, 6151–6161. [Google Scholar] [CrossRef]
- Dorst, L.; Fontijne, D.; Mann, S. Geometric Algebra for Computer Science (Revised Edition); Morgan Kaufmann: Burlington, MA, USA, 2009; ISBN 9780123749420. [Google Scholar]
- Luzzi, L.; Roselli, P. The Shape of Planar Smooth Gestures and the Convergence of a Gesture Recognizer. Aequ. Math. 2020, 94, 219–233. [Google Scholar] [CrossRef]
- MacFarland, T.W.; Yates, J.M. Mann–Whitney U Test. In Introduction to Nonparametric Statistics for the Biological Sciences Using R; Springer International Publishing: Cham, Switzerland, 2016; pp. 103–132. [Google Scholar]
- Avuçlu, E.; Elen, A. Evaluation of Train and Test Performance of Machine Learning Algorithms and Parkinson Diagnosis with Statistical Measurements. Med. Biol. Eng. Comput. 2020, 58, 2775–2788. [Google Scholar] [CrossRef]
- Ricci, M.; Di Lazzaro, G.; Pisani, A.; Mercuri, N.B.; Giannini, F.; Saggio, G. Assessment of Motor Impairments in Early Untreated Parkinson’s Disease Patients: The Wearable Electronics Impact. IEEE J. Biomed. Health Inform. 2020, 24, 120–130. [Google Scholar] [CrossRef]
- Eskofier, B.M.; Lee, S.I.; Daneault, J.-F.; Golabchi, F.N.; Ferreira-Carvalho, G.; Vergara-Diaz, G.; Sapienza, S.; Costante, G.; Klucken, J.; Kautz, T.; et al. Recent Machine Learning Advancements in Sensor-Based Mobility Analysis: Deep Learning for Parkinson’s Disease Assessment. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; IEEE: New York, NY, USA, 2016; pp. 655–658. [Google Scholar]
- Nan, T.; Zheng, S.; Qiao, S.; Quan, H.; Gao, X.; Niu, J.; Zheng, B.; Guo, C.; Zhang, Y.; Wang, X.; et al. Deep Learning Quantifies Pathologists’ Visual Patterns for Whole Slide Image Diagnosis. Nat. Commun. 2025, 16, 5493. [Google Scholar] [CrossRef] [PubMed]
- Hu, D.; Dong, Z.; Liang, K.; Yu, H.; Wang, S.; Liu, X. High-Order Topology for Deep Single-Cell Multiview Fuzzy Clustering. IEEE Trans. Fuzzy Syst. 2024, 32, 4448–4459. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).