Abstract
The representation of binary data in a compact, printable, efficient, and often human-readable format is essential in numerous computing applications, mainly driven by the limitations of systems and communication protocols not designed to handle arbitrary 8-bit binary data. This paper provides a comprehensive survey and an extensive characterization of printable encoding schemes, tracing their evolution from historical methods to contemporary solutions for representing, storing, and transmitting binary data using restricted character sets. The review includes a foundational analysis of fundamental character encodings, proposes a layered model for the classification of printable encodings, and examines various schemes based on their numerical bases, alphabets, and functional characteristics. Algorithms, key design trade-offs, the impact of relevant standards, security implications, performance considerations, and human factors are systematically discussed, aiming to offer a detailed understanding of the current context and open challenges.
1. Introduction
Many applications require the ability to represent binary data in a compact, printable, and/or human-readable form.
Among the earliest examples of a measure efficiently encoded for human readability, the printout from the Ohio State University’s Big Ear radio telescope [1] is definitely a good example. This system, which enabled the 1977 discovery of the Wow! signal [1], employed a concise 36-symbol alphabet (comprising a blank, the decimal digits 1–9, and the 26 capital letters from the Latin alphabet) to facilitate the compact and easily decipherable representation of its considerable data volume [2].
As an example of an inefficient but nonetheless useful printable encoding of binary data, we mention the easy-to-read decimal system used to represent numbers with numerals using ten symbols. Single octets can be expressed with three decimal characters from 000 to 255, while double octets can be represented over five characters with sequences from 00000 to 65535 (with the obvious alphabet ). Considering one octet to encode every decimal character, e.g., ASCII, then the increase factor of space occupation is 3 when representing single octets and when encoding pairs of octets.
In the present paper, we will give an extensive characterization of the printable encodings developed through the years and their use in various computing operations. To this aim, the next section will introduce the notation and the nomenclature used throughout the paper to establish a common ground of terms. All acronyms can be found at the end of the paper.
Section 3 lists and comments on the characteristics of the main character encodings, given that some of them are used by printable encodings to represent the symbols in their alphabets. In Section 4, we introduce a layer model useful to present a taxonomy aimed at classifying and describing the properties of the different printable encodings. Section 5 surveys the numerical bases, the associated alphabets, and the characteristics that define the developed printable encodings used to represent and transmit information through systems that do not transparently process binary data. In Section 6, some well-known and used applications of printable encodings are discussed. Section 7 will draw some conclusions and possible further developments of the presented or foreseen methods for printable encoding of binary strings.
Finally, Appendix A will present a tutorial on the main principles and frequently used algorithms related to procedures for the encoding and decoding of binary data into a printable/human-readable form: the readers familiar with these topics may ignore this section and consider the heart of the paper exploring, a taxonomy of the various printable encoding proposals.
2. Notation and Nomenclature
2.1. Notation
In this paper, we will indicate
- scalar variables with italicized lowercase letters, like ; to ease reading; some variables may be named with longer strings of letters, e.g., to indicate a length;
- program variables with lowercase and uppercase letters, both italics or not, e.g., , v, Z;
- a range of values comprised between a and b with ;
- sets and alphabets with boldface uppercase letters, like A, B, and T;
- numerals S in base b (in the present work b will always be written in base 10) with , with where A is an alphabet (see Section 2.2) of b symbols, ;
- an element, that with others belongs to a set or an alphabet, with a lowercase letter and possibly a subscript, like ;
- Unicode code points identified by a number are written in hexadecimal notation (with alphabet ) with four or six characters prefixed by the string “U+”;
- unless differently stated, all numbers are written in the decimal base;
- the floor and ceiling functions are indicated with and , respectively.
2.2. Nomenclature
This subsection establishes the meaning of the following terms when used throughout this paper; the terms are sorted alphabetically in ascending order for convenience.
- 8-bit cleanness property of a system that is able to store, transmit, and process 8-bit data without requiring data formatted in 7-bit units or relying on a possible use of the 8 th bit of an octet for its own processing; alternatively, it is the quality of a system that is capable of processing octets without assigning specific meanings to some binary configurations; thus, a not-8-bit-clean system may interpret in a misleading way or modify the Most Significant Bit (MSB);
- alphabet an ordered set of n symbols, each one associated, in order, to an integer number from 0 to ;
- ASCII armor a technique used by OpenPGP (see the OpenPGP Message Format [3]) to encode any kind of data (i.e., binary) in a form that is not modified by intermediate not-8-bit clean systems: it uses Radix-64, i.e., a printable encoding based on Base64 [4], to represent with printable ASCII characters the data and the relative checksum encapsulating them into header and trailer lines;
- base b positional numeral system a numeral representation system using b symbols from an alphabet ( represents the natural number i) where the numeral expresses the number , that is, every symbol is weighted according to its position in the numeral; the number b is called the base of the positional numeral system;
- big endian referred to the transmission or storage order of octets, meaning that a data object composed of many octets is sent starting from its Most Significant Octet (MSO), and in its memory area, it is stored by putting the MSO towards lower memory addresses and the Least Significant Octet (LSO) at higher memory addresses;
- bit (binary digit) the fundamental unit of information that can assume one of two values with the same probability; mathematically, it is the information (or entropy) of a source that produces as an outcome one of two equiprobable events (i.e., each one having probability );
- Byte Order Mark the byte order mark (BOM) is a special block of octets (i.e., bytes) prefixed to an octet sequence useful in the decoding of data. In particular, the BOM (the term byte order mark comes from the name of this character, BYTE ORDER MARK, in Unicode 1.0; if this character is present in the following part of a data stream, it should be interpreted as a word joiner, i.e., the character string must not be separated at that point, but since Unicode 3.2, it is recommended to use the character WORD JOINER U+2060 for this purpose) is the Unicode character ZERO WIDTH NO-BREAK SPACE (ZWNBSP) with code point U+FEFF: when this character is the first of a sequence, the decoder can establish the endianness of the data encoding; moreover, the presence of this character at the beginning allows the decoder, with a high probability, to be confident that the data stream is Unicode encoded and to determine the type of encoding. In fact, UTF-8 does not allow the octets and to be present as first data, excluding this kind of encoding. In the case of UTF-16 and UTF-32, the BOM allows us to determine if the data has been saved in big-endian or little-endian mode: given that the octet sequence does not represent any character in Unicode, then its presence as the first character signals the decoder that the data has been recorded in little-endian mode, allowing it to correctly interpret the data stream and to save it with the local machine’s endianness.To sum up, the BOM for UTF-16 encoded in big endian mode is the octet sequence , and in little endian mode it is ; for UTF-32, the BOM for big endian systems is , and for little endian systems it is .Other UTF encodings have a header, called BOM, used to specify the type of encoding:
- UTF-1 has the octet sequence ;
- UTF-7 has the sequence followed by another octet whose value depends on the next symbol;
- UTF-8 has a sequence whose usage is not recommended by Unicode, corresponding to .
- C0 control codes compose a set of 32 characters found in ASCII and other encodings used to represent printing, character set switch, communication, alert, power, and formatting commands. The values of the C0 control codes range from to . In some contexts, also the space character (ASCII value ) and the delete (DEL) character (ASCII value ) are also considered control codes but are not part of the C0 set;
- C1 control codes compose the “twin” set of the C0 control codes when considering an extended ASCII character set (i.e., over 8 bits): The C1 set is made up of the characters in the range to , that is, the C0 characters with the eighth (most significant) bit set;
- character an elementary piece of information that can be associated with a symbol and that, with others, composes an alphabet;
- code page a table specifying the association between a graphic character, like ‘A’, or a control character, like newline, and a number, thus defining an encoding; this name was introduced by IBM, which numbered many possible code pages, and many other vendors and software producers aligned or produced their own numbering;
- code point the address (label) of an element in a multi-dimensional matrix containing heterogeneous entities; in the context of the present paper, an integer number that uniquely identifies a (part of a) character in an encoding system like ASCII or Unicode;
- endianness refers to the octet ordering and can be little-endian or big-endian;
- G0, G1, G2, G3 working sets of graphic characters that can be loaded and accessed using particular special sequences of control characters;
- GL, GR the primary code area for graphic characters in 7-bit environments is called GL (Graphic Left), while in 8-bit environments, the additional code area is called GR (Graphic Right);
- glyph the graphical representation of a symbol; a symbol may be represented with many glyphs, e.g., a, a, a, a;
- grapheme an elementary object of a writing system that in the computer science field has the same meaning as character;
- little endian referred to the transmission or storage order of octets, meaning that a data object composed of many octets is sent starting from its LSO and in its memory area is stored by putting the LSO towards lower memory addresses and the MSO at higher memory addresses;
- nibble a sequence of four bits, i.e., half an octet;
- number the measure of a quantity, or of an amount, defining a concept perceived by an entity;
- numeral the expression of a number, that is, a symbol, a signal, or a sequence of symbols or signals instantiating the concept of a number. For example, the sequence 12 from the decimal numeral system using Arabic digits expresses the concept of the number of months in the year of the Gregorian calendar, but the same number can be expressed with the Roman numerals as XII or in the English language as twelve;
- octet a sequence of eight bits;
- percent encoding (also called URL-encoding) is a method to encode octets of arbitrary value using only ASCII characters that are not reserved for representing URIs; more details on this encoding are in the dedicated section;
- sequence an ordered list of homogeneous (i.e., having the same type) objects;
- shellcode a portion of code that has the purpose of letting a hacker or a cracker gain control over a machine, in some cases launching a command shell (thus the name);
- string a sequence of characters;
- symbol the representation of a concept; in the context of this paper, it generally identifies a computer character;
- URL-encoding see percent encoding;
- URL-safe URLs can be written according to the specifications [5,6]; even if printable, some characters are reserved for coding or due to possible misinterpretation by other protocols or systems and, as such, must not be used in URLs. A character is considered URL-safe if it is printable and is not reserved; a character string is URL-safe if all its characters are URL-safe;
- wide character a data type having a size of one or more octets aimed at containing a character. The necessity of a char data type larger than 8 bits became clear when character sets having more than 256 symbols were defined. For example, UTF-8 and UTF-16 encodings of UCS require up to four octets to represent a character. In general, language implementations define a wide character as two octets, for example, if UTF-16 is used (but surrogate pairs require two of them), or four octets to contain all the UTF-32 code points. Note that, being compiler-specific the size of a wide character can also be a single octet.
3. Character Encodings
Printable encodings are strictly related to character encodings: in fact, a printable encoding relies upon a representation of characters, namely a code, which has a subset that is recognized as a collection of printable characters by all the systems involved in the transmission and processing of the considered data. For this reason and due to the fact that many printable encodings refer to a character code, this section will survey the most widely used character encodings. The evolution from 7/8-bit fixed-width encodings to variable-width Unicode Transformation Formats (UTFs) directly reflects the increasing complexity of data and the need for a universal representation, introducing more complex challenges in making sure that characters are printable and displayed properly on different systems.
- ASCII: the American Standard Code for Information Interchange [7,8] is a method for encoding a set of characters. Standard ASCII uses 7 bits to portray code points, which are associated with printable and non-printable symbols. The 95 code points having values from to designate printable characters comprising the letters of the Latin (and English) alphabet, both uppercase and lowercase, the ten decimal digits, the space, and 32 punctuation, mathematical, and special characters, like ampersand and tilde. The remaining 33 code points associated with non-printable characters (code points from to , called C0 control codes, and ) are associated with control characters corresponding to commands for printers, disks, modems, or other peripherals.
- EBCDIC: the Extended Binary Coded Decimal Interchange Code is an 8-bit character code developed by IBM in the sixties and, as its name says, extends the 6-bit code BCDIC (Binary Coded Decimal Interchange Code) used for punched cards having two groups of rows (named zone and number) [9]. Due to the mechanical constraints of BCDIC, the EBCDIC encoding inherits some character representations, and for this reason, in the invariant part of the code alphabet, letters, both uppercase and lowercase, are not assigned to consecutive binary configurations; for example, the letter R is represented with , and S is encoded with . Control codes are represented with codes from to plus . Space, special characters, digits, and letters occupy a part from to , but many codes are left free and assigned by each code page for each world language. Moreover, code pages for languages not using the Latin alphabet may also reassign the codes for the Latin letters.
- ISO/IEC 646: a 7-bit encoding strictly related to ASCII is ISO/IEC 646 [10]. ISO/IEC 646 consists of multiple 7-bit standard character sets sharing a common Basic Character Set composed of the ten decimal digits, the space, some basic punctuation and mathematical characters, and the uppercase and lowercase letters of the ISO Basic Latin alphabet (which coincides with the English alphabet); the first 32 codes are the same control codes of ASCII, as well as code , which is DEL (the code associated with DEL is a legacy of punched cards: given that the presence of a hole represented a 1-valued bit, the solution adopted to delete, i.e., mark as unusable, a previously punched 7-bit character was to overwrite it with seven 1 bits, transforming any character into DEL; zeroing a bit was not practical because it required shutting a hole in the card). Twelve (12) codes are free to be used by national variants to represent their language characters (for example, è, à, etc. of the Italian language). Code is allowed to be £ or #, and code must be $ or the character for international unspecified currency ¤; nonetheless, some national variants change these two characters.
- ISO/IEC 8859 [11]: this family of encoding standards was developed with the objective of enriching the ASCII standard with symbols present in alphabets based on the Latin alphabet but that also contain new characters or modifications of the ones already present (e.g., accented characters or diacritics). These standards use an 8-bit encoding; given that the added configurations are not able to cover all the alphabets, many parts have been developed inside ISO/IEC 8859: for example, ISO/IEC 8859-4 is called Latin-4 North European and covers Estonian, Latvian, Lithuanian, Greenlandic, and Sami alphabets.
- ISO/IEC 10646 is a family of standards defining the Universal Coded Character Set (UCS) that evolved in time and converged with Unicode in 1991 for the representation of characters (see next list point about Unicode); nonetheless, Unicode adds other attributes and procedures tied to the use of the defined characters (e.g., writing direction). The characters (i.e., code points) represented by ISO/IEC 10646 are those encoded by UTF-16, namely those in the range : these code points are represented with 2 or 4 octets (see UTF-16 in the following). Also, ISO/IEC 10646 allows an encoding over 4 octets called UTF-32, simply expressing the code point over 32 bits.
- Unicode [12] is a standard that defines a unique number, called a code point, for every character in the world, regardless of the language, script, or system. There are currently almost code points in Unicode, covering alphabets, symbols, emojis, and more. Note that Unicode does not define an encoding method but a unique correspondence between code point and character. Different Unicode encodings (Unicode Transformation Formats) have been defined, as described in the following.
- ▶
- UTF-7 [13] (Unicode Transformation Format 7-bit) is an obsolete character encoding scheme that was created to represent and transmit Unicode characters through systems that only handle 7-bit ASCII data. The UTF-7 encoding scheme uses base64 to encode non-ASCII characters into ASCII characters. The Unicode Consortium never approved UTF-7 as an official standard. It has security problems that made software developers stop using it. HTML 5 does not allow it. In UTF-7, escaping is used to encode non-ASCII characters, using the character “+” to indicate the start of an escaped sequence, followed by a base64 encoding of the non-ASCII character, and terminated by a “-” character or the end of the string. For example, the character é (U+00E9) is encoded as +AOk- in UTF-7: the “+” at the beginning signals the start of the escape, the AOk is the base64 encoding of é, and the “-” at the end indicates the end of the escape.
- ▶
- UTF-8 [14] is a way of representing any Unicode character using one to four octets. It was invented by Ken Thompson and Rob Pike in 1992 as a coding method that is simple, efficient, and backward compatible with ASCII. UTF-8 was soon adopted by the Internet Engineering Task Force (IETF) and the Unicode Consortium as a standard for Unicode encoding. Features of UTF-8 are as follows:
- ○
- It can encode any Unicode character using one to four octets, depending on its value. The first 128 characters, which correspond to ASCII, are encoded using one octet. The higher the value of the character, the more octets it requires.
- ○
- It is self-synchronizing, meaning that it is possible to find the start of a character by looking at the prefix bits of each octet. The first octet of a multi-octet sequence has a certain number of prefix bits (110, 1110, or 11110) that indicate the number of octets in the sequence. The continuation octets have a prefix bit of 10. This makes it easy to parse and manipulate UTF-8 strings.
- ○
- It is error-resistant, meaning that it can detect and recover from invalid or corrupted sequences. If an octet does not match the expected pattern, it can be skipped or replaced with a replacement character. This prevents the propagation of errors and the loss of data.
- ○
- It is compact, meaning that it uses less space than other Unicode encodings for most texts. This is especially true for texts that contain mostly ASCII characters, such as English or HTML.
- ▶
- UTF-16 [15] is a standard encoding format that is capable of representing all the Unicode code points, from U+000000 to U+10FFFF, using 2 or 4 octets. The code points in the Basic Multilingual Plane (BMP) have an associated value in the range , i.e., , and are encoded by UTF-16 with their representation in 2 octets, except the range of values , called surrogate range: This range of values is reserved (i.e., these values do not represent any symbol) to also encode the symbols not belonging to the BMP, corresponding to the code points from U+010000 to U+10FFFF. Given a code point having a value v greater than , the exceeding part from is computed: the resulting value can be expressed with 20 bits; this quantity is split into two parts of 10 bits: the most significant part is added (more efficiently, OR-ed) to (where the digits in italics are the less significant 10 bits), producing the high surrogate, and the less significant part is OR-ed to , resulting in the low surrogate. In this case, a code point is encoded with four octets.The result is that all the Unicode code points can be unequivocally encoded with two or four octets, and the first pair of octets allows one to immediately distinguish the presence of a surrogate pair; moreover, the most significant six bits of each surrogate pair distinguish a high surrogate from a low surrogate, allowing a correct reconstruction of the original code point.When not already specified by the encoding, the endianness may be detected by representing the BOM (Byte Order Mark) U+FEFF (representing the Unicode zero-width no-break space) that, if encoded with , reveals a little-endian encoding, whilst if left unaltered, specifies a big-endian encoding.
- ▶
- UTF-32: UTF-32 [16] is an encoding format for Unicode that uses 4 octets to represent all the Unicode code points (from U+0000 to U+10FFFF): this leaves, for every code point, the 11 Most Significant Bits zeroed. Due to the use of 4 octets for every symbol, it is less space efficient than UTF-8 and UTF-16 but has the advantages of a fixed-length encoding: In a stream of UTF-32 encoded data, the i-th code point starts at the -th octet. Note that given that a complex character may be represented using more than one code point, then the previous direct access formula may be applied to a sequence of code points but not to the characters they represent (requiring a linear reading of all the code points to arrive at the one(s) of character under examination). The endianness is detected by the encoding of the BOM U+FEFF.
- ▶
- UTF-EBCDIC (originally called EBCDIC-Friendly UCS Transformation Format, EF-UTF) is a transformation format specified in [17] that may represent all the Unicode points up to plane 16 (from U+0000 to U+10FFFF) with 1 to 5 octets; moreover, UTF-8-Mod, the encoding used by UTF-EBCDIC, may represent all the UCS-4 code points, namely up to U+7FFFFFFF, encoding them with a maximum of 7 octets.The UTF-EBCDIC encoding goes through two reversible steps: a Unicode code point is first converted into what is called an I8-sequence (of octets) obtained from an adapted UTF-8 encoding, and then the derived octets are singularly remapped with a reversible transformation. The objective of this transformation format is to map the code points from U+0000 to U+009F to a single octet of the same value and then to remap these octet values to match the value of the corresponding character in the EBCDIC encoding. Moreover, the values from to never appear in any octet that is part of a sequence encoding code points greater than U+009F.
- ▶
- UTF-1 (“ISO IR 178: UCS Transformation Format One (UTF-1)”, [18,19]) is an encoding method for Unicode and ISO/IEC 10646 characters. It is capable of representing the UCS characters from to (even if Unicode is upper limited to ). Every character is encoded with one, two, three, or five octets, depending on its value. The objective of this encoding is to generate octet sequences that do not contain the octets in the sets of the C0 or C1 control codes, along with space () and DEL (), obviously apart from the octet representing the control code itself. This leaves usable octet representations, leading to an alphabet for a Base190 encoding that is saved in a variable-length octet sequence as previously mentioned: this alphabet is selected by means of a function and its inverse ( and in [18,19]) that filter the allowed subset of octet configurations (namely, all but the C0 or C1 control codes, the space, and DEL).
- ▶
- UTF-5 was proposed in the year 2000 with an Internet Draft [20], now expired, as a transformation format for ISO/IEC 10646 and Unicode.The objective of UTF-5 was to develop a format alternative to UTF-7, UTF-8, and UTF-16 for systems, applications, and protocols unable to process 7-bit or 8-bit strings. Examples of proposed applications are the representation of names used in the Domain Name System (DNS) and addresses in the Simple Mail Transfer Protocol (SMTP).In [20], a sequence of 5 bits is called quintet, whose value is represented with the 32 characters of the alphabet0123456789ABCDEFGHIJKLMNOPQRSTUV(as noted in [20], each character can be encoded in binary with any code, typically ASCII).Considering a UCS-4 Unicode 32-bit representation of a symbol, UTF-5 encodes the nibbles (four-bit aggregations) from left to right, starting from the first non-zero-valued nibble (the UCS value 0 is considered as a single nibble). The sequence of nibbles is represented as a sequence of quintets, one nibble in the four rightmost bits of each quintet: the first (most significant) quintet will have its leftmost (most significant) bit (MSB) set (i.e., valued 1), and the other quintets will have the MSB reset (valued 0). For example, the UCS-4 value will be represented in UTF-5 as G, while the UCS-4 symbol will be encoded as QBCDE.
- ▶
- UTF-6 was proposed in the (now expired) Internet Draft [21]. This encoding augments UTF-5 (hence the name UTF-6), adding compression by leveraging the intrinsic redundancy of UTF-16 encoded host names for the DNS. The compressed data distinguishes a redundant octet using the Y character and a redundant nibble with the Z character; in addition to these two characters, the alphabet is composed of the same 32 (lowercase) symbols of UTF-5, namely0123456789abcdefghijklmnopqrstuvThe resulting string is prefixed by the sequence of characters wp--
- ▶
- UTF-9 and UTF-18 are introduced in [22] as an April Fools’ Day RFC from IETF whose application is possible even with reduced time/space efficiency for present architectures having 8-bit bytes (note that in the past the term byte referred to sequences of bits with different lengths; thus, we prefer the term octet when dealing with 8-bit bytes). RFC 4042 describes a Unicode transformation format aimed at architectures using 9-bit addressable units, called nonets. The code points from U+0000 to U+00FF are encoded in one nonet with the MSB unset. The code points from U+0100 to U+10FFFF are encoded with two (for code points in the BMP) or three nonets depending on the required space to save the meaningful bits in the eight bits of each nonet, setting the MSB to indicate continuation on the next nonet and leaving the last nonet MSB unset (note that in [22] the code points outside the BMP are identified in the range U+1000–U+10FFFF instead of U+10000–U+10FFFF, presumably due to a typo). With this technique, also the remaining UCS-4 code points (from U+110000 to U+7FFFFFFF) are UTF-9 encoded with three or four nonets.UTF-18 encodes the Unicode planes 0, 1, 2, and 14 only. The first three plane code points map directly to the 18 bits of UTF-18, whilst plane 14 code points are stored in UTF-18 after subtracting (it seems that this value is reported as in [22], apparently due to a typo) from the code point value.In [23], a comparison between Unicode encodings requiring a zeroed most significant bit in each octet and those that are 8-bit clean is reported.
- UCS-2: this definition is now superseded and should not be used anymore; originally, it referred to a character representation over 2 octets for symbols now located in the Basic Multilingual Plane [24].
- UCS-4: the ISO/IEC 10646 standard originally defined the Universal Character Set to represent characters in 4 octets in the range but subsequently limited the range to , and currently UCS-4 and UTF-32 indicate the same set [24].
- ISO/IEC 2022: the ISO/IEC 2022 standard [25] is a framework developed for encoding character sets in a way that enables switching between multiple character sets within a single data stream. Originally published in 1986 and known as “Information technology – Character code structure and extension techniques”, ISO/IEC 2022 supports the use of multiple national and international character encodings, particularly in contexts where 7-bit or 8-bit communication channels are used. At its core, ISO/IEC 2022 provides mechanisms for code extension by defining escape sequences (starting with the ESC octet, ) that designate or invoke various character sets. It defines four working sets of graphic characters, referred to as G0, G1, G2, and G3 [26], where different graphic character sets can be loaded and then accessed. In particular, special sequences of control characters (escape sequences) are used to designate which specific character set is loaded into each of the G0, G1, G2, or G3 slots, while other control characters (shift functions) are then used to invoke or load one of these designated G-sets to be the currently used set for interpreting subsequent octet values. The standard also defines code areas within the 7-bit or 8-bit code spaces where these graphic character sets are invoked (made active for interpreting subsequent octets): for 7-bit environments, the primary code area for graphic characters is called GL (Graphic Left), while in 8-bit environments, an additional code area called GR (Graphic Right) is used. This enables compatibility with legacy systems and multilingual text processing, especially in East Asian languages, which require large character sets. ISO/IEC 2022 underpins several regional and application-specific standards, such as ISO-2022-JP (for Japanese [27]), ISO-2022-KR (for Korean [28]), and ISO-2022-CN (for Chinese [29]), which are still used in specific contexts like e-mail transmission (per MIME specifications) despite being largely supplanted by Unicode in modern applications. While flexible, ISO/IEC 2022 has been criticized for its complexity, especially in parsing and rendering text streams. Its stateful encoding model, requiring the interpretation of escape sequences to know which character set is active in which code area, makes it error-prone and challenging to implement compared with stateless encodings like UTF-8. Nonetheless, its historical significance and influence on character encoding architectures remain substantial.
4. The Printable Encoding Model
In this section, we propose a model that structures the information that encodes the binary data.
The model is composed of four layers, where each layer exposes elements and functionalities to the upper layer to perform a step towards the production of a sequence of printable characters that may be decoded into the original binary sequence.
The four layers are as follows (from the lower to the higher):
- Representation level: This level provides the alphabet symbols used to encode the binary values and eventually other symbols (e.g., CR, LF, =) that are used to format the resulting sequence of characters;
- Coding level: This level uses the symbols provided by the Representation level to encode and decode blocks of binary data sequences of possibly various lengths; it may provide the upper level with means to signal the end of the encoded sequence;
- Stream level: This level composes and formats the encoded blocks and reversibly extracts them from and to the Coding level;
- Application level: The encoded stream is encapsulated into a larger object (like an e-mail or a file), possibly enveloped into a structure that determines its format.
These layers help classify the encoding schemes, since all the encodings presented throughout this paper possess the lower levels (representation and coding), but some of them lack the higher levels because they leave those functions to the software using them, while others also specify how the encoded data stream should be managed (stream) and integrated into application contexts (application).
5. Binary to Printable Encodings
This section presents the developed base encodings and some special printable encodings. Note that at this Wikipedia page [30], an overview of some binary-to-text encoding formats and protocols is presented.
At the end of Section 5.1, a table summarizes the main characteristics of each printable encoding.
5.1. Base Printable Encodings
This subsection describes various encoding schemes that convert binary data into a printable form using a defined numerical base and an associated alphabet of symbols. The choice of a base encoding often involves a trade-off between efficiency, the size and nature of the alphabet, and computational complexity.
- The Base64, Base32, and Base16 defined in [4] are amongst the most widely known representations of binary data in printable form.Base64 may use different alphabets, but the canonical one defined in [4] is the following:ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/=This alphabet is composed of 65 symbols: the first 64 are used for representing the octet strings, as will be explained, and the equal sign “=” is used for padding. This alphabet does not care about using human-distinguishable glyphs because the encoding is principally reserved for data transmission between computer systems.The encoding (called base64) is easily performed considering the binary expression of octets: a sequence of 3 octets is divided into 4 sextets (i.e., 6 bits), and the value of each sextet is used as an index in the alphabet to get a character. In case the input octet length is not a multiple of 3, then two cases may happen:
- An ending single octet: The input is padded with 4 zero-valued bits, the two sextets are encoded, and two equal signs are appended (“==”);
- Two ending octets: The input is padded with 2 zero-valued bits, the three sextets are encoded, and one equal sign is appended (“=”).
At the application level, it may be required to write the output stream with Carriage Return/Line Feed to limit the length of the lines of Base64 encoded data (see, for example, MIME [31] and PEM [32]).A variant of the previous alphabet, called base64url ([4] sec. 5), was proposed for URL and filename safe encodings. In particular, the new alphabet substitutes the last two symbols with “-” (minus symbol) and “_” (underline, or underscore symbol). The new alphabet isABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789-_=and if padding is used in URIs, then the equal sign should be percent encoded.Base32 performs an encoding (called base32) analogous to Base64 but using an alphabet of 33 symbols, namely the 26 letters of the Latin alphabet, the decimal digits from 2 to 7, and the padding equal sign “=”. Extensionally the alphabet isABCDEFGHIJKLMNOPQRSTUVWXYZ234567=Input sequences of 5 octets are re-interpreted as sequences of 8 quintets (i.e., a group of five bits), and the value of each quintet is used as an index for a character in the Base32 alphabet vector.When the input octet length is not a multiple of 5, then four cases requiring padding may happen:- An ending single octet: the input is padded with 2 c, the two quintets are encoded, and six equal signs are appended (“======”);
- Two ending octets: the input is padded with 4 zero-valued bits, the four quintets are encoded, and four equal signs are appended (“====”);
- Three ending octets: the input is padded with 1 zero-valued bit, the five quintets are encoded, and three equal signs are appended (“===”);
- Four ending octets: the input is padded with 3 zero-valued bits, the seven quintets are encoded, and one equal sign is appended (“=”).
In ([4] sec. 7), a Base32 encoding with an Extended Hex Alphabet called base32hex is proposed. The alphabet used in this case is0123456789ABCDEFGHIJKLMNOPQRSTUV=The encoding method is the same as the base32 one, but the resulting printable strings keep the sort order of the input binary data from which they were computed.Base16 encoding, called base16 or hex, is based on the classical sixteen symbols of the alphabet0123456789ABCDEFand represents each octet with two characters using each nibble value as an index in the alphabet vector. - Base36: The Base36 is made available in many programming languages and is based on an alphabet composed of the ten decimal digits and the 26 letters (in general, case insensitive) of the Latin alphabet; that is,0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZIn particular, JavaScript has the methods Number.prototype.toString() [33] and Number.parseInt() [34], Python has the functions numpy.base_repr() [35] and int() [36], and PHP uses the function base_convert() [37] to support conversions to and from base 2 to Base36. Also, spreadsheets have the function BASE(), which converts a number into a base from 2 to 36, and the function DECIMAL(), which interprets a string in a base from 2 to 36, converting it into a number.
- Base41: the base 41 was chosen in the work [38] (a related web page with sample code is available at [39]) because 41 is the minimum number of symbols that must be used over three symbol positions to represent all binary configurations of 16 bits (i.e., a pair of octets).The main objectives of [38] are the use of an alphabet containing only uppercase and lowercase Latin alphabet letters, avoiding special character symbols to have the widest possible applicability (for example, the printable strings produced by the conversion are URL-safe); moreover, letters that can lead to human visual misinterpretation (e.g., uppercase I and lowercase l) are not present in the proposed 41-letter alphabet.ABCDFGHJKLMNQRSTUVXZabcdefhikmnopqrstuvxzThe method [38] allows the printable encoding of octet and bit strings of any length.In 2014, [40] proposed a method for binary-to-text encoding using an alphabet of 41 characters for encoding pairs of octets with three symbols. The intensional definition of the symbol’s alphabet is the set of ASCII characters from code to code , that is, extensionally,)*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNOPQThe work in [40] allows the conversion of octet strings of even length only.
- Base45: an encoding based on 45 symbols is proposed in [41]. The number of alphabet symbols is chosen according to the QR code alphanumeric encoding that is based on the following 45 symbols (note the ‘space’ character between Z and $):0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ $%*+-./:Using this alphabet, octet strings to be stored in a QR code are represented in printable form, and then pairs of Base45 characters are saved in strings of 11 bits (6 bits only to represent a possible single final character).Pairs of octets are encoded in Base45 with three Base45 symbols; if a single octet is present at the end of an odd-length octet string, then it is converted to Base45 with two symbols. Decoding performs Base45 to binary conversion, and care must be taken to signal an error in case of decoded values greater than when starting from three characters or greater than if decoding two characters.Due to the alphabet employed, this encoding may produce strings that are not URL-safe, requiring, in some cases, an additional percent encoding.
- Base56: At this web resource [42], Python functions for encoding and decoding in a base with 56 symbols are available. The alphabet used is23456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnpqrstuvwxyzThis set of characters avoids visual ambiguity for characters 1, lowercase L, uppercase I, and uppercase and lowercase O. The encoding function performs the classical conversion between bases (see Appendix A.1).
- Base58: the use of a base using 58 symbols is proposed in two works, namely [43,44].In [43], the objective of binary representation is oriented towards the human interpretation of binary data, avoiding mistakes due to confusing zero (0) with capital O or capital I and lowercase L (l); moreover, the used alphabet avoids characters having special meanings for operating systems like slash (/) in file pathnames. Note that this is an expired Internet Engineering Task Force Internet Draft; nonetheless, it is used for encoding Bitcoin addresses [44]. In the Bitcoin context, Base58Check [44] is used to represent Bitcoin addresses or any other octet sequence. The object to be converted is prefixed by an octet indicating its type, then the Secure Hash Algorithm is applied twice on the obtained sequence, producing a cryptographic hash: the first 4 octets of this hash are appended as a checksum to the sequence, and the result is converted into Base58. The aim of this checksum is to improve security by detecting typing errors or maliciously modified addresses/keys, making evident even small differences from the intended address/key.The alphabet’s extensional definition is123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyzThe same alphabet intensional specification is the decimal digits apart from 0, the Latin alphabet uppercase letters except I and O, and the Latin alphabet lowercase letters apart from l (lowercase L).Other systems, namely Ripple [45] and Flickr [46], use the same characters in this alphabet but with a different order. Ripple’s order seems to be used to ease the recognition of the type of data encoded, whilst Flickr simply swaps uppercase and lowercase letters.
- Base62: Sixty-two printable characters are adopted in the works [47,48].The paper [47] uses a Base62 encoding as a final step of a compression algorithm. The alphabet used isABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789This alphabet’s intensional definition is the Latin alphabet’s uppercase and lowercase letters and the ten decimal digits. The bit stream is divided into blocks of 6 bits and the decimal value of each block is used as an index in the alphabet to define its encoding character. In case the 6 bits, have a value greater than 59 (thus, having values , , , or ), then only the first 5 bits, having binary value or , are encoded with the characters 8 or 9, respectively, assigning the leftover bit to the following block of 6 bits. The last block of bits is zero-padded to have a correct length for the encoding with one of the 62 characters; the decoder will discard the exess zero bits to have a length compatible with an octet string.In [48], an alphabet of 62 characters, namely0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyzis used to define a transformation format, called UTF-62, for ISO 10646 UCS, a collection of standards that define an international set of characters. Code values representing characters can be expressed with 16 bits or 31 bits. In the case of 16 bit (UCS-2) code values, the number is converted to Base62 (employing the previously mentioned alphabet) using three symbols, where the most significant does not exceed V; on the other hand 31-bit code values (UCS-4) require six Base62 symbols. Moreover, to distinguish from UCS-2 encoded values, the first (most significant) symbol is shifted (increased) by 32 positions (due to the maximum UCS-4 value, no overflow may happen with this shift), leading to a most significant symbol not less than W.
- Base85: an encoding using 85 printable characters was first introduced by P. E. Rutter for the utility btoa: this program originally used an alphabet composed of the ASCII charater from code (space) to code (character “t”), but to avoid problems with programs that skipped white spaces (ASCII code ), the alphabet was shifted by one position from code (special character “!”) to code (character “u”). The btoa utility added a header (made by the string xbtoa Begin) and a trailer (composed of the string xbtoa End, the original data length in decimal and in Base16, and three checksums). The coding level considers the case of four binary octets 0-valued returning the character “z” instead of the five Base85 symbols “!!!!!”, and in a subsequent release of the btoa utility, also four input octets valued at (space) are encoded as the character “y”.Adobe Systems Incorporated developed functions documented in [49] that perform encoding and decoding in Base85, starting from chunks of four binary octets, interpreting them as a number to be converted into Base85 and returning five printable characters for each chunk (adding 33 to each value returned from the Base85 conversion). Thus, the alphabet used is!"#$%&’()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ[\]^_‘abcdefghijklmnopqrstuThat is, the ASCII characters from code (special character “!”) to code (character “u”).At the coding level, in the case of four binary octets 0-valued, the character “z” substitutes the five Base85 symbols “!!!!!”; moreover, at the stream level, if the octet string has a length not a multiple of 4, then it is completed with 0-valued octets, converted into Base85, and the same number of (less significant) symbols added is discarded from the result: this allows the decoder to restore the correct length of the original octet string. At the application level, the Base85 encoded sequence is terminated with the two-character string “∼>”.The RFC 1924 [50] proposes a compact Base85 encoding of IPv6 addresses. These addresses are 128 bits long, and 85 is the minimum base to write them in 20 characters. The extensional expression of the alphabet used is0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz!#$%&()*+-;<=>?@^_‘{|}~Also, the patch system of the Git version control system employs a Base85 encoding to store diff binary data.
- Base91: coding efficiency was the motivation in [51] for the development of a binary-to-text code based on the following 91 ASCII symbol alphabet:!"#$%&’()*+,/0123456789:;<>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ[\]^_‘abcdefghijklmnopqrstuvwxyz{|}~That is, the 95 printable characters purged of the space character, the dot, the dash, and the equal sign. The binary data to be encoded is divided into chunks of 13 bits that can be represented with two Base91 characters, leaving unused Base91 pairs. Among these 89 configurations, twelve (from 8192 to 8203) are used to specify how many filling bits (if any) were added to the last chunk to make it 13 bits long: this allows the method to encode bit strings of arbitrary length (this is managed at the stream level). A Base91 code has a data expansion factor of , lower than those of Base 64 () and Base85 ().Different software using a 91-character alphabet was developed and made available at [52]ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789!#$%&()*+,./:;<=>?@[]^_‘{|}~"In this case, the encoding uses all the two-letter configurations to represent 13-bit chunks; in addition, the 13-bit chunks with decimal values from 0 to 88 are also associated with the 89 unused configurations, allowing to encode one more bit (for a total of 14 bits) with the net result of not wasting any configuration but requiring a higher level of encoding to establish the right length of the original bit string at the decoding stage (thus, the stream level is empty and does not control the data length, whose management is left to the application level).
- Base94: In [53,54], a space efficiency analysis of the bases from 2 to 94 is presented, computing an optimal ratio between the number of input octets and output characters. The maximum base 94 is chosen, restricting the possible output alphabet symbols to the printable ASCII characters (), i.e., without the C0 control codes, also excluding the space (ASCII code ) and DEL (ASCII code ) characters (leading to ).
- Base122: the use of 122 symbols to encode binary data for HTML pages is proposed in [55]. The idea is to store binary data into the free bits of one and two octets of UTF-8 encoded data. Recalling UTF-8, the code points up to are represented with the single octet binary string 0BBBBBBB (where the seven bits B can assume the value 0 or 1), and the remaining code points up to are expressed with the two-octet string 110BBBBB 10BBBBBB (eleven free bits).Given that web browsers cannot deal transparently with all single-octet UTF-8 representations, among the 128 configurations, six are unused, namely NUL, Line Feed, Carriage Return, backslash, ampersand, and double quotes. This leaves 122 possible single-octet UTF-8 configurations and requires the use of two UTF-8 octets for encoding the remaining six configurations. The eleven free bits of these octets are employed in the following way:
- ▶
- Three bits encode one of the six configurations that were not possible to store in a single octet;
- ▶
- One bit is forced to 1 to avoid the possible illegal UTF-8 encoding of a code point less than over two UTF-8 octets;
- ▶
- Seven bits store the following input binary data; note that in the second octet (10BBBBBB of the UTF-8 encoding), any binary sequence does not create any problem).
In the case of encoding of bit strings of any length, then the stream level can manage the termination in many ways: a proposal is to always pad with a bit string beginning with 1 and add as many zeros as required to complete the UTF-8 characters.
To ease reading Table 1, Figure 1 reports the printable ASCII characters sorted according to their codes.

Table 1.
Summary of Base encodings.
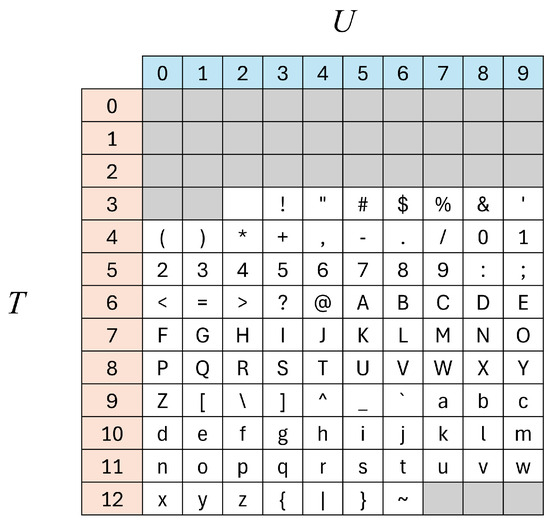
Figure 1.
The printable ASCII characters, namely the characters with ASCII codes from to . At each intersection there is the character having code .
The columns of Table 1 refer to the base considered, the alphabet used and possibly other characters used for encoding the binary stream and defining borders in data, the Asymptotic Inflation Ratio (AIR), which represents the factor of data increase (eventually when long binary strings are encoded), the minimum block size encoded in bits, the operating level of the proposed encoding algorithm, and the bibliographic reference(s) to the encoding proposal. Then, the last two columns report possible applications and observations related to the encoding.
The alphabet, defined at the representation level, reflects the encoding’s utility and constraints. The alphabets listed in Table 1 can be classified as (a) standard alphabets, (b) URL and filename-safe alphabets (e.g., Base64url), (c) human-readable alphabets (e.g., Base58, used in Bitcoin), and (d) constrained alphabets (e.g., Base45, used in QR codes).
The column “Asymptotic Inflation Ratio” of Table 1 quantifies the overhead of the listed methods, giving an indication of their efficiency. As derived in the paper’s appendix, the AIR for a given base b can be calculated as . This formula shows that as the size of the alphabet (the base b) increases, the inflation ratio decreases, meaning the encoding becomes more efficient. Figure 2 highlights this relation between alphabet size and asymptotic inflation ratio. However, the AIR represents a theoretical limit for infinitely large data streams. Practical efficiency is also influenced by other factors, particularly the encoded block size.
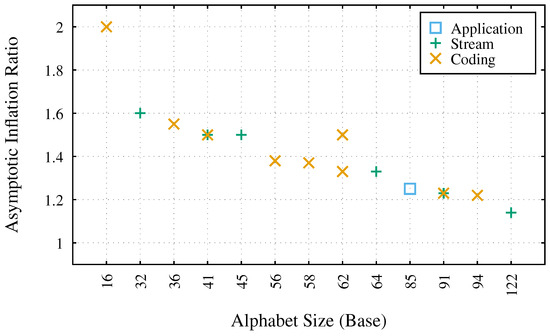
Figure 2.
Base encodings from Table 1 sorted by alphabet size with their respective asymptotic inflation ratios. When more than one asymptotic inflation ratio is present, only the “best” one is considered for this plot. The different colors (and point types) represent the highest level (see Section 4) on which each encoding is involved in.
To perform the conversion into a particular base alphabet, data is first grouped into fixed-size blocks. If the input data size is not a multiple of the block size, a padding scheme is required, generally appending a number of padding characters to the output. This mechanism can operate at the coding and/or stream level. In addiction, the application level may impose additional rules, e.g., the line length limit imposed by MIME, where Base64 encoded data must be broken into lines of no more than 76 characters.
Different implementations of atob() and btoa() use the Base64 or the Base85 alphabets. The encoding operations are different for the two bases. In particular, Base64 encodes three octets with four characters: this operation can be performed using only shift and logical operations on octets. On the other hand, the conversion into Base85 requires divisions, which are more computationally intensive operations; nonetheless, efficiency may be improved using algorithms devised for the division by a constant that, in general, leverage multiplications and shifts [62,63].
5.2. Special Printable Encodings for Data Representation
This subsection covers encoding methods that do not strictly rely on numerical bases but serve specific data representation purposes. These encodings are often highly context-specific, designed to solve a particular problem rather than being general-purpose binary-to-text solutions.
5.2.1. Bootstring and Punycode
Punycode is an application of the Bootstring [64] algorithm developed to provide a transfer encoding for Internationalized Domain Names (IDNs) with the protocol IDNA (Internationalizing Domain Names in Applications) [65] that allows the reversible translation of sequences of characters from Unicode [12] to strings composed of characters from a subset of standard ASCII [7].
The provided algorithm converts ASCII and non-ASCII symbols (both represented as Unicode code points) into a string composed of basic code points, namely the ASCII symbols having hexadecimal values in the range to .
At large, the Bootstring algorithm is general and can be used to reversibly convert a string (called the extended string) composed of characters (code points) from a set U to a string (called the basic string) made up of characters (called the basic code points) from a subset A of U. The algorithm requires that each code point can be distinctively identified by a numerical value (as is the case of Unicode) and that the first n values are associated with the basic code points.
The encoding operation of the Bootstring algorithm firstly copies, in order, to the (output) basic string all the characters in the (input) extended string that belong to A, if any are present: in that case a hyphen, i.e., minus character (“-”, ASCII decimal code 45), is postponed to the output string computed so far (see Figure 3).
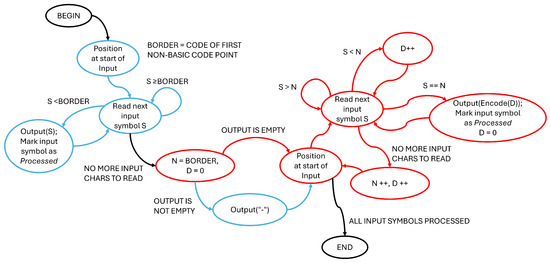
Figure 3.
A high-level scheme of the Bootstring encoding algorithm operation and main data involved. (Blue elements refer to basic code points processing, whilst red elements are related to the non-basic code points encoding.)
After that, the encoder prepares a list of numbers to be used in an operation called insertion unsort coding. Starting from the first non-basic code of U, which becomes the current code N (see Figure 3), the extended input string is scanned from left to right searching for an occurrence of this code, increasing a counter D for every symbol less than N, and encoding D (as it will be shown later) if a symbol equal to N is met, in which case D is zeroed. When the end of the input string is reached, then N is increased by one, D is also increased by one, and the input string scanning process is restarted: this searches for the next code in the input string. With this procedure the variable D stores the distance of the code to be inserted from the previously inserted symbol, both in terms of code number and of position in the input string (considering only the codes examined so far). This process is terminated when all the codes of the extended input string have been encoded into the basic code output string. The procedures available in [64] perform these operations efficiently using integer division and modulo operations.
The encoding of the distance D, representing a new non-basic code point when the preceding one is known, is made using a numeral format called generalized variable-length integers in [64].
The generalized variable-length integers encoding (see Algorithm 1) represents numbers with a little variation on the classical base b positional numeral system
where is the number of symbols composing the numeral representing n. A variable-length integer representation uses a set of thresholds with the following application:
where and have the same meaning as in the previous case, and to have a self-delimiting numeral, .
| Algorithm 1 Algorithm for converting a number to base b with generalized variable-length integers using symbols and thresholds . |
|
The expression in (2) has the advantage of giving rise to a single representation for any number (no leading zeros) and a self-delimiting numeral: this means that concatenating a sequence of numerals with this representation, it is always possible to uniquely separate them from one another. Note also that the thresholds must be known for every numeral to perform a correct decoding (also, the s need not be the same for different numerals; moreover, changing the set of s used to represent a number produces, in general, a different numeral).
The generalized variable-length integers representation is employed by Punycode with the thresholds computed for every number using a different parameter (see [64]) and limited to the range . The base used is , and the alphabet is composed of the letters of the English alphabet from “a” (or “A”, case is not considered) to “z” (or “Z”), having values from 0 to 25, and the digits from 0 to 9 (having values from 26 to 35). As already said, this alphabet is extended with one more symbol used by Punycode to separate different parts of the encoding, namely the hyphen (or minus, “-”).
We report two Punycode encoding examples. To highlight the encoding of non-basic code points and to keep the example manageable and clear, we chose two similar names containing only standard ASCII characters except for one. The names encoded are Lætitia and Laëtitia. In the first case, the basic code points are output followed by the hyphen symbol: Ltitia-. After that, the input string is scanned searching for the smallest non-basic code point, in this case, æ that has Unicode code U+00E6 (). When found, its code distance from the previously encoded non-basic code point is computed (the first one is considered code ), thus . Given that in the string Ltitia there are 7 possible insertion points and that æ must be inserted in position 1, then this symbol will be represented by . This value will be encoded with variable-length integers with (Punycode) thresholds , corresponding to weights : , which corresponds to the Base36 string pua (the 0 exploits the generalized variable-length property of self-limitation). To sum up, the Punycode encoding of Lætitia is Ltitia-pua. Similarly, Laëtitia will be encoded with Latitia- along with the encoding of ë (Unicode U+00EB, ). Given that there are 8 possible insertion points and ë will be in the second position, the distance to be encoded is , which, according the previous weights, will be expressed as , corresponding to the Base36 string sya. This leads to the representation of Latitia-sya.
5.2.2. Quoted Printable
Quoted printable is a binary-to-text encoding defined in [31] to protect the transmission of arbitrary octet values through systems that are not 8-bit clean.
In general, the method uses the symbol equal (“=”) as a prefix to escape the hexadecimal representation of an octet value (the alphabet used is 0123456789ABCDEF; capital letters are mandatory, but it is suggested to also accept lowercase letters when decoding). For example, the Carriage Return (CR), having decimal value 13, can be encoded with =0D; obviously, the equal sign (that has ASCII decimal value 61) must be escaped, leading to =3D.
The ASCII printable characters (i.e., those having decimal code values from 33 to 126), except the equal symbol, may be represented with the character itself, but escaping their hexadecimal representation with “=” is also acceptable.
A (hard) line break (i.e., a Carriage Return/Line Feed pair of octets) in a text is mapped to the output as is. Instead, octets encoding a CR, an LF, or a CR/LF sequence in a binary stream must be escaped with the equal sign followed by the corresponding hexadecimal representations (=0D for CR and =0A for LF).
Given that encoded lines have a maximum length of 76 characters, if a source line is longer than a soft line break, represented as an equal symbol, it must be inserted at the end of the encoded line to indicate the continuation on the next line.
White spaces (ASCII decimal code 32) and TABs (ASCII decimal code 9) must be explicitly and unambiguously encoded: this means that if encoded unescaped (i.e., left as they are) and if one of them is the last character of a line, then it must be followed by an equal symbol to avoid the possible stripping by intermediate processing of systems.
5.2.3. Percent Encoding
Percent encoding (also known as URL-encoding) is a technique employed to represent data using only the ASCII symbols allowed in a URI [6,66]. In [6], some characters are defined as reserved because they have special use and meaning in delimiting and thus representing parts of a URI; these characters are
- :/?#[]@!$&’()*+,;=
Printable ASCII characters that have no special use in [6] are called unreserved:
- ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789-._~
The percent character also has a special use and function, as will be clear in the following.
When a reserved character is being used in a URI, if it also appears without the reserved function, then, to avoid ambiguity, it must be encoded differently: in this case, it uses the percent encoding that is built with a percent sign % followed by two hexadecimal characters (case insensitive) representing the octet value associated with that character. For example, the reserved character “forward slash” is a reserved character; it has ASCII decimal value 47, which is , and when there is the possibility of ambiguity, if it does not have the reserved role, then it must be percent encoded as %2F. Also, it is obvious that the percent sign (ASCII decimal value 37) intended as such must be percent encoded as %25.
In case a reserved character is in a context where does not have a reserved role (i.e., there is no ambiguity), then it may or may not be percent encoded. Moreover, unreserved characters may be percent encoded. Care must be taken when comparing URIs where these modalities are used interchangeably because equality tests may have unexpected results.
Percent encoding may also be used to encode binary data: each octet is expressed with the percent sign and two hexadecimal characters coding the octet value. Moreover, if the octet represents an unreserved character, then the character itself may be used in place of the percent representation.
The RFC standard [6] mandates that URIs containing UCS characters should represent them by percent encoding their UTF-8 codes. For example, the character “B” should be represented as “B”, the euro sign “€” is represented with %E2%82%AC.
The communication of HTML data with GET and POST methods is based on percent encoding; in the case of POST, the data content type is set to application/x-www-form-urlencoded.
5.2.4. yEnc
We report yEnc in this survey for the sake of completeness, but we emphasize that it is not a true printable encoding for the reason that will be clear in the following.
yEnc is an encoding developed in the early 2000s (its latest release, v1.3, from Jürgen Helbing, is dated March 5th, 2002 [67]) for the transmission of binary files over Usenet. yEnc encodes a limited number of characters (from that it derives its name, sounding like Why encode?), namely Line Feed, Carriage Return, and Null, by escaping (i.e., preceding) them with the “=” (equal) character; also, the “=” character will be escaped, being itself the escape character. The reason for escaping (and shifting by 64) Line Feeds and Carriage Returns is that these characters are used by some RFCs to format messages, so they must not be present explicitly in message bodies.
The encoding algorithm is shown in Algorithm 2.
| Algorithm 2 Algorithm yEncode for an octet o. |
|
The input octet value is incremented (modulo 256) by 42 to avoid having to escape long strings of zero-valued octets (namely, null characters). Moreover, an escaped character has its value incremented (modulo 256) by 64.
yEncoded streams are preceded and terminated by the strings “=ybegin⌴” and “=yend”, respectively, where ⌴ represents a blank character.
5.2.5. Bech32
Bech32 is an address encoding format used by SegWit, a Bitcoin Improvement Proposal for the Bitcoin transaction format. Bech32 is based on the following 32 (case-insensitive) symbol alphabet:
- qpzry9x8gf2tvdw0s3jn54khce6mua7l
Starting from a binary public key, a cryptographic hash of the key is computed and appended to it, a header is prefixed, and a checksum (computed with a BCH code, named from Bose–Chaudhuri–Hocquenghem) is added at the end. The resulting bit string is divided into contiguous non-overlapping groups of 5 bits; finally, every group is mapped, according to its value, to the corresponding symbol of the alphabet, and the resulting string is prefixed by the characters bc1. The objective of computing these addresses and using this encoding is to have smaller addresses to save space and to implement a security mechanism that reduces the possibility of typing wrong addresses.
5.3. Computational Complexity
The computational complexity of binary-to-printable encoding schemes is generally linear in the length of the input chunk; that is true, e.g., for Base16 and Base64. In these methods, the conversion for each block of data involves a constant number of simple and fast operations like bit-shifting, masking, and use of lookup tables.
Schemes that involve conversion between bases suffer from worse performances if the source and target bases are not powers of a common integer value (typically 2), e.g., Base58: here, the input string is not processed in small, independent chunks but interpreted as a single and big integer N expressed in base 256 as a sequence of octets. The algorithm has to convert this large number to base 58, executing a loop calculating an integer division and the relative remainder. In this situation (see (A3) and Algorithm A1), the procedure has a non-linear complexity of , with k being the number of bits needed to represent N and expressing the complexity of the best implemented algorithm used for multiplication, since the division by a constant factor can be performed with multiplication [63].
6. Printable Encoding Applications
In this section, we report some widely used applications of printable encodings. The choice of a particular encoding in an application is often established by the nature of the data (predominantly textual or binary), the efficiency required, the human readability needs, and the specific constraints of the application.
Figure 4 provides a partition of those applications of printable encodings that are described in the following into three different categories. The “OS Commands” category includes all printable encoding applications that are somehow needed for the execution of a command related to some operating system procedure. The “Programming Languages” category contains, instead, functions and methods provided by different programming language libraries that implement some printable encoding technique. Finally, the “Software Applications” category groups format encodings used by certain software applications that allow the user to apply a printable encoding to their data inside the software itself.
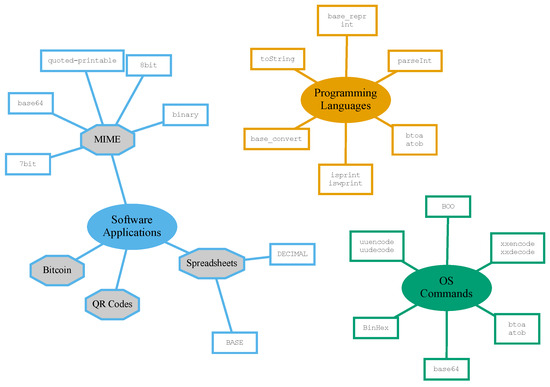
Figure 4.
Concept map of printable encoding applications, grouped by application field.
We emphasize the fact that printable encodings may be used in any context where binary data has to be carried over text-only channels. For example, even if not directly mentioned in the XML recommendation, a printable encoding may be used to embed binary data into an XML document. The same consideration can be applied to JSON fields.
6.1. btoa() and atob()
btoa() and atob() are generic names for functions available in different programming languages (e.g., JavaScript, available in all web browsers) or command shells (e.g., FreeBSD). Their names are acronyms for the conversion from binary-to-ASCII and ASCII-to-binary. Note that some operating systems have the command base64 for command-line conversions to and from printable format.
The implementations of btoa() and atob() use a Base64 or a Base85 encoding. The JavaScript version available as an API for most web browsers is based on a Base64 encoding [68,69]. The FreeBSD version [70] uses a Base85 encoding, as previously discussed: in addition to the encoding of four octets with five characters in the ASCII range from “!” to “u”, the case of four binary octets 0-valued returns the character “z” instead of the five Base85 symbols “!!!!!”, and also four octets valued (space) are encoded with the character “y”.
The btoa Javascript version is a method of the Window interface that accepts as input a binary string in UTF-16 format whose octets must be code points less than 256. The Window.atob companion function performs the inverse operation, returning the binary string encoded by the input Base64 string. On the other hand, the FreeBSD version of btoa (and atob) uses the more efficient Base85 encoding and produces files containing a header and, more importantly, a checksum for every row of the printable file. This fact increases the security of the file in case of non-intentional damages.
6.2. uuencode and uudecode
uuencode and its decoding companion uudecode are programs originally developed in the eighties for transmitting binary files between UNIX systems, eventually traversing systems that could operate modifications to binary data (e.g., not 8-bit clean) [71].
The original encoding represented three octets with four printable characters, splitting the original 24 bits into four groups of 6 bits each, adding 32 to each group value, and interpreting the result as an ASCII character ranging from “ ” (space) to “_” (underline). To avoid the presence of spaces in the encoded text, the character “ ” (space), used for a 0-valued octet, was substituted by “‘” (grave accent) by some implementations.
At the application level, the encoded file is prefixed by a row containing the word “begin” followed by the (UNIX) file access permissions and the file name and is followed by two rows, one containing a grave accent and the last with the word “end”. The lines encoding the file are of maximum length of 61 printable characters (encoding 45 octets): the first character specifies the number n of octets encoded by the line and is the ASCII symbol obtained by adding 32 to n, where the case of 0 length is expressed with the grave accent (ASCII code 96) instead of space.
A version of uuencode [72,73] (and uudecode) is based on the Base64 encoding using its alphabet and allowing lines of maximum length 76 characters, not requiring any length prefix in each line. Moreover, the header is “begin-base64” and the trailer is “====”: due to the Base64 encoding, it is always possible to know the exact octet length of the input, even if it is not a multiple of 3, and the trailer “====” cannot be present in the Base64 encoding of the data.
6.3. xxencode and xxdecode
xxencode and xxdecode are functions developed as an alternative to uuencode. The alphabet employed is composed, in order, of the plus and the minus signs, the ten decimal digits, the twenty-six uppercase letters of the Latin alphabet, and the twenty-six lowercase letters of the same alphabet. The objective is to avoid possible mis-translations between ASCII and EBCDIC by using a different alphabet from the one used by uuencode: in fact, all the punctuation and special characters are substituted by alphanumeric characters, retaining only plus and minus.
The other difference with (one version of) uuencode is the row format, which can encode a maximum of 45 octets, resulting in a maximum length of 60 characters plus the first character expressing the number of octets encoded in the row.
6.4. BinHex
The name BinHex refers to a set of encodings that evolved in time. The first version [74] used Base16, since the name recalls the encoding from binary to hexadecimal. The resulting files had lines of maximum length of 60 characters plus a checksum. A successive version encoded 6 bits per output character using a Base64 alphabet [75,76].
6.5. Multipurpose Internet Mail Extensions
After the introduction of the e-mail service, the necessity to send data using character sets different from ASCII and also the requirements to carry attachments of various data types led to the development of a set of recommendations, known as Multipurpose Internet Mail Extensions (MIME), to comply with for the transmission and communication of such information. These recommendations impacted not only the electronic mail systems but also the transmissions over HTTP.
MIME is specified in the Requests for Comments 2045, 2046, 2047, 2048, 2049, and successive modifications. Given that the objective of the present paper is to show the usage and applications of printable encodings, we direct the reader interested in MIME details to [31] as a starting point.
The purpose of MIME, as reported in [31], is to specify message formatting to allow the use of non-US-ASCII character sets in message headers and bodies and non-textual data in message bodies, along with the possibility to have messages composed of many parts, each one eventually encoded in different ways (as specified by the relevant RFCs).
RFC 2045 defines 7-bit data as composed of octets whose values are strictly greater than 0, strictly less than 128, and different from 10 (Line Feed) and 13 (Carriage Return); 8-bit data maintains the same constraints as 7-bit data with the exception of allowing values up to 255 included; binary data has no restrictions on the octet values.
When transferring binary data through systems that are not 8-bit clean (like SMTP servers not supporting the 8BITMIME extension), an encoding of this data into a printable format must be operated. This encoding is specified with a content-transfer-encoding header. The possible values for Content-transfer-encoding are “7bit”, “8bit”, “binary”, “quoted-printable”, “base64”, and possible extensions that are not pertinent to the present paper.
The content-transfer-encoding encodings “7bit”, “8bit”, “binary” specify that the data was left as-is and require systems able to cope with these formats.
Instead, “quoted-printable” means that octets were transformed as discussed in Section 5.2.2. To avoid possible problems with intermediate systems based on the EBCDIC code, it is suggested to escape with the equal sign also the octets representing
- !"#\$@[]^‘{|}~
The “base64” content-transfer-encoding encodes the data in lines not longer than 76 printable characters with the Base64 representation presented in Section 5.1.
RFC 2047 introduces the use of encoded words for message header fields to cope with possible problems with some systems when non-ASCII characters are used, or when the backslash character “\” is used to escape some symbols. RFC 2047 defines an encoded word with the following sentences: “certain sequences of “ordinary” printable ASCII characters (known as “encoded-words”) are reserved for use as encoded data”, and also “Generally, an “encoded-word” is a sequence of printable ASCII characters that begins with “=?”, ends with “?=”, and has two “?”s in between.” [77].
Thus, an encoded word has the following format:
with a maximum total length of 75 characters.
The sequences “=?”, “?=” and “?” have been chosen because it is highly unlikely that the resulting encoded word will appear as is in the header field.
The character set must indicate the character set used for the original string, for example ISO-8859-1.
The encoding mode may be “B”, “b” or “Q”, “q” and specifies the printable encoding used in the following field encoded text. The “B” (“b”) character means the use of the Base64 encoding [4] described in Section 5.1. The “Q” (“q”) character specifies the use of a Quoted printable (see Section 5.2.2) encoding with some changes: a character having decimal value 32 may be encoded with “_” (underscore), and the characters “=”, “?”, and “_” must always be represented with the encoding using the equal sign. The other ASCII characters that are printable may be left unaltered or escaped, but some restrictions may apply depending on the field using this encoding: refer to [77] for more details.
The Secure/Multipurpose Internet Mail Extensions (S/MIME) [78] is a protocol founded on MIME that allows the secure transmission of data, providing MIME with encryption, digital signatures, authentication, and integrity features. S/MIME inherits from MIME the usage of printable encodings.
6.6. BOO
The .boo format [79] is a printable encoding developed in the context of the Kermit project [80] to allow the transmission of binary data through systems that could perform translations on binary files (i.e., not having the property of 8-bit cleanness). (The string “boo” is the prefix of bootstrap, given that this encoding was also used to transmit files required to bootstrap a system.)
This printable encoding is similar to the Base64 encoding but uses an alphabet composed of the 64 ASCII characters from code to code . The maximum line length is 76 characters followed by a Carriage Return-Line Feed pair. Moreover, in case of a run of zero-valued octets, to compress the resulting file, a tilde (“~”) character was used to specify that the following symbol ASCII value encoded the number of zero octets plus 48, with a maximum of 78 octets represented in this manner: thus, for example, a tilde character followed by “w” (ASCII code 119) represented a sequence of zero-valued octets. It may be seen that for this run-length encoding a different alphabet was used with respect to the one used for the Base64 encoding.
The .boo format requires that the printable encoding of a file be preceded by a line containing the file name.
6.7. QR Codes
QR codes are images representing a binary sequence on a two-dimensional grid of squares. QR codes can store different kinds of information, like URLs, text, e-mail addresses, and vaccination certificates. Data may be stored with different modes, each one having its own character set. The numeric mode uses the ten digits and represents three decimal digits, from “000” to “999”, with ten bits (), whilst the alphanumeric mode uses the Base45 alphabet and encodes two Base45 characters with eleven bits ().
6.8. Library Functions
Some programming languages make available macros or functions that determine if a character is printable or not.
For example, the C language has the functions isprint() [81] and iswprint() [82]. Their prototypes (i.e., synopses) are (as specified in the C23 standard [83])
- int isprint(int ch);int iswprint(wint_t wch);
and are defined in the header files ctype.h and wctype.h, respectively.
The function isprint() requires its argument to be a signed integer but be valued as a non-negative value representing a character (i.e., less than ) or EOF : in this case the value returned is true () if ch is printable or false () if not printable. This function uses the C locale definition LC_CTYPE to establish if a character is printable or not and has an undefined behavior in case ch has a value outside the allowed range.
The function iswprint() receives an input value and returns true () if wch is printable or false () if not printable according to the C locale (the standard [84] defines the subset of printable Unicode characters for POSIX systems). The behavior of this function is undefined if the input parameter is not a wide character nor WEOF .
The equivalent C++ functions are std::isprint() [85] and std::iswprint() [86]. These function prototypes are
- int isprint(int ch);int iswprint(std::wint_t ch);
and are defined in the two header files cctype and cwctype.
In Javascript, the method toString() [33] of the type Number returns the representation in the base (radix) passed as an argument (the default is 10). Possible values of the base range from 2 to 36 (where the alphabet used starts from the ten decimal digits and continues with the capital letters of the Latin alphabet). The inverse operation is performed by the method parseInt() [34] that receives as input a string and possibly a base (radix) and converts into a number the numeral contained in the string expressed in the base.
In Python, the function with the prototype numpy.base_repr(num, b, pad) [35] converts num into the base b (having a range from 2 to 36, defaulting to 2); pad is optional and, if present, specifies the number of zeroes to prefix the result. Conversely, the function int(val, b) [36] converts into a number the string val interpreted in base b.
PHP has the function base_convert(string s, int fb, int tb): string [37] that converts the string s represented in the base fb into base tb and returns the resulting string. The two bases involved must be in the range from 2 to 36.
Also, spreadsheets have the function BASE() (see, for example, [56,58,60]) that converts a number into a base from 2 to 36 and the function DECIMAL() (e.g., [57,59,61]) that interprets a string in a base from 2 to 36, converting it into a number.
6.9. Printable and Alphanumeric Code
Printable (and even only alphanumeric) characters can be used to write programs. In general, this means that a wisely chosen sequence of printable (or alphanumeric) symbols represented with some character encoding (e.g., ASCII) can be interpreted as executable (or intermediate) code, that when run on a processor, can perform some actions. It is obvious that not all the machine instructions, nor immediate data or memory addresses, can be represented with a limited alphabet of printable characters, but it is possible to devise programs (eventually self-modifying, starting from a decoder coded with only printable characters) that have the desired behavior using only octets encoding printable or alphanumeric characters (see, for example, [87]). In fact, this method allows code to pass checks of Intrusion Detection Systems (IDS), appearing innocuous by being composed of characters used to write text. Given that the main objective of hiding the execution of a piece of code is to gain control over a machine, in general printable code is used to run a shell with administration privileges on the victim machine; thus, the name shellcode.
6.10. Data Hiding
By analyzing the various encodings, it may be noted that some of them use all the possible printable strings to represent the binary configurations: this is the case of Base64, which uses all the strings available to encode all the possible blocks of 24 bits, or Base16, which encodes an octet using all the possible hexadecimal strings.
At the same time, there are encodings, like Base41, Base45, and Base85, that have an inherent redundancy because not all the possible strings are required to encode the binary blocks. In this context, the work [88] proposes a framework to exploit the unused strings for embedding extra data into a printable encoded stream: briefly, each unused string is associated with a legal string, and when the latter should be used for encoding, then it is possible to embed a bit of information by choosing one among the pair of associated strings. Research papers [89,90] have proven the efficiency of this data hiding method, in particular when applied to the Base45 encoding; moreover, this framework is open to more research in finding more efficient methods to embed more data.
Ref. [91] proposed to employ the unused strings of a printable encoding to create a side channel in the stream to tag and/or convey extra data. In particular, some suggested embodiments consider the insertion of Cyclic Redundancy Checks, Message Authentication Codes or other security information that may be used to protect the integrity and/or authenticate the origin of data.
6.11. Security Considerations
It should be noted that printable encodings do not pose any security threat because they are a simple mapping between representations. On the other side, if an application is not implemented correctly, it may suffer from intentional attacks aimed at exploiting flaws in the use of the encoded data by the application itself. Also, some attacks may involve human users, and we will see how some encodings reduce the risks using the properties of the alphabet along with some security tools.
One kind of attack is based on encoding binary malicious code in printable form to avoid detection by security software (e.g., firewalls, Intrusion Detection Systems, antiviruses) and inducing an application to decode and execute it. Another possible attack is from printable code that does not need decoding, being composed only of instructions and data written with printable characters (see Section 6.9).
In the context of the Bitcoin system, addresses (or any other octet sequence requiring encoding) are converted into Base58. The first protection against human reading errors lies in the alphabet that avoids, as previously said, characters having similar glyphs. Moreover, Bitcoin uses Base58Check, an encoding that adds redundancy to the Base58 data representation: this protection is aimed at data integrity protection and also tries to limit malicious attacks that induce users to send money to similar but incorrect addresses. An improvement of Base58Check is Bech32: the latter produces shorter addresses and uses a more powerful error detection algorithm (a BCH code instead of the concatenation of two SHA-256 cryptographic hashes); moreover, Bech32 uses a smaller alphabet (that has only lowercase letters), reducing the probability of misinterpretation by humans.
Printable encodings are employed as a possible countermeasure to prompt injection attacks on Large Language Models (LLMs). A prompt injection attack is built by adding malicious commands in the data associated with the instructions for an LLM: a solution to contrast this threat is to clearly separate LLM directives from the data on which they operate, and in this context input data can be printably encoded. In [92], one of the considered possibilities is to Base64 encode the data on which the LLM must operate. [93] proposes a mixture of encodings and analyzes, among others, the encoding methods Base64, Base32, and Base58 for the input data: of these three encodings, Base64 allowed better performance of the used LLMs.
7. Perspectives and Conclusions
This paper has presented a survey on the printable encodings used in the past and those in use today. Care has been taken to present and discuss the algorithms involved in the encoding process. For completeness, due to the usage made by binary-to-text encodings, a part of the document has been devoted to character set encodings.
The paper also proposes a novel four-layered model that may be used to classify the printable encodings and to evaluate how they may fit into an encoding system, evidencing the parts needed to obtain a reversible encoding of binary data. Table 1 summarizes the presented printable encodings, recalling their characteristics, properties, peculiarities, and layers according to the presented classification model.
It should be noted that many printable encodings have widespread use today: to name a few, Base64 is widely used in the transfer of e-mails and web content, Base16 is used for immediate interpretation of octet strings content (like MAC addresses), Base45 is used in QR codes, and Base58 encodes Bitcoin addresses, Base85 is part of the Postscript Language Reference.
Moreover, many other printable encodings have been developed with efficiency or readability properties, like Base122 or Base41.
It should be pointed out that having knowledge of currently available printable encodings can improve interoperability between systems and data security (see, for example, printable and alphanumeric code).
The present survey aims also to inspire new research on printable encodings in the future.
Author Contributions
Conceptualization, M.B., D.C., A.D., M.L. and A.M.; methodology, M.B., D.C., A.D., M.L. and A.M.; investigation, M.B., D.C., A.D., M.L. and A.M.; resources, M.B., D.C., A.D., M.L. and A.M.; data curation, M.B., D.C., A.D., M.L. and A.M.; writing—original draft preparation, M.B., D.C., A.D., M.L. and A.M.; writing—review and editing, M.B., D.C., A.D., M.L. and A.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been supported by the Italian Ministero dell’Università e della Ricerca.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AIR | Asymptotic Inflation Ratio |
| API | Application Programming Interface |
| ASCII | American Standard Code for Information Interchange |
| BaseY | representation system that uses the base Y positional numeral system for encoding binary data, e.g., Base64 |
| BCDIC | Binary Coded Decimal Interchange Code |
| BCH | Bose–Chaudhuri–Hocquenghem code |
| BMP | Basic Multilingual Plane |
| BOM | byte order mark |
| CR | Carriage Return |
| DNS | Domain Name System |
| EBCDIC | Extended Binary Coded Decimal Interchange Code |
| HTML | HyperText Markup Language |
| HTTP | HyperText Transfer Protocol |
| IDN | Internationalized Domain Name |
| IDNA | Internationalizing Domain Names in Applications |
| IDS | Intrusion Detection System |
| LF | Line Feed |
| LLM | Large Language Model |
| LSO | Least Significant Octet |
| MAC | Media Access Control |
| MIME | Multipurpose Internet Mail Extensions |
| MSB | Most Significant Bit |
| MSO | Most Significant Octet |
| PEM | Privacy Enhanced Mail |
| QR code | Quick Response code |
| RFC | Request for Comments |
| S/MIME | Secure/Multipurpose Internet Mail Extensions |
| SHA-256 | Secure Hash Algorithm 256 |
| SMTP | Simple Mail Transfer Protocol |
| UCS | Universal Coded Character Set |
| URI | Uniform Resource Identifier |
| URL | Uniform Resource Locator |
| UTF | Unicode Transformation Format, or UCS Transformation Format |
| ZWNBSP | Zero Width No-break Space |
Appendix A. Support Material
This appendix reports some basic concepts, algorithms, and results related to the representation of numbers in different bases.
Appendix A.1. Converting a Number to Numeral in a Defined Base and Vice-Versa
Given a number n (for simplicity suppose ), it can be converted to a numeral Z in the base b positional system (having symbols in set ) obtained by repeated integer divisions by b, writing the remainders from right to left (see Algorithm A1).
| Algorithm A1 Algorithm for converting a number to base b with symbols . |
|
By the converse, the base b numeral
represents the number
according to the rule for the base b positional numeral system (see Algorithm A2).
| Algorithm A2 Algorithm for converting a base b numeral to the corresponding number n. |
|
Appendix A.2. Symbols in a Numeral Required to Represent a Number in a Base
Let us suppose we have a number n: how many symbols does the base b numeral representation of n require?
According to (A2), if , then k symbols (from to ) will be needed in writing the numeral expressing n in the base b. In general, the number of symbols required to write a number n in base b is
Appendix A.3. Asymptotic Inflation Ratio
As previously shown, when coding a number n in base b, the minimum number of characters is (A3). In particular, the number of binary digits is , and the number of octets is . Thus, for large n, the Asymptotic Inflation Ratio (AIR) that expresses the ratio of the number of characters required to represent a number in a base with respect to the number of octets necessary to represent that number is
but from
it follows that the AIR for base b is
References
- NAAPO—The North American Astrophysical Observatory. Big Ear Memorial Website. Available online: http://www.bigear.org/ (accessed on 5 June 2025).
- Ehman, J. Explanation of the Code “6EQUJ5” On the Wow! Computer Printout. Available online: http://www.bigear.org/6equj5.htm (accessed on 5 June 2025).
- Finney, H.; Donnerhacke, L.; Callas, J.; Thayer, R.L.; Shaw, D. OpenPGP Message Format. RFC 4880. 2007. Available online: https://www.rfc-editor.org/rfc/rfc4880.html (accessed on 5 August 2025). [CrossRef]
- Josefsson, S. The Base16, Base32, and Base64 Data Encodings. RFC 4648. 2006. Available online: https://www.rfc-editor.org/rfc/rfc4648.html (accessed on 5 August 2025). [CrossRef]
- Berners-Lee, T.; Masinter, L.M.; McCahill, M.P. Uniform Resource Locators (URL). RFC 1738. 1994. Available online: https://www.rfc-editor.org/rfc/rfc1738.html (accessed on 5 August 2025). [CrossRef]
- Berners-Lee, T.; Fielding, R.T.; Masinter, L.M. Uniform Resource Identifier (URI): Generic Syntax. RFC 3986. 2005. Available online: https://www.rfc-editor.org/rfc/rfc3986.html (accessed on 5 August 2025). [CrossRef]
- Cerf, V. ASCII Format for Network Interchange. RFC 20. 1969. Available online: https://www.rfc-editor.org/rfc/rfc20.html (accessed on 5 August 2025). [CrossRef]
- INCITS 4-1986[R2022]; Information Systems—Coded Character Sets—7-Bit Standard Code for Information Interchange (7-Bit ASCII). ANSI: Washington, DC, USA, 2022.
- Mackenzie, C.E. Coded Character Sets, History and Development; The Systems Programming Series; Addison-Wesley Publishing Company, Inc.: Indianapolis, IN, USA, 1980. [Google Scholar]
- ISO/IEC 646:1991; Information Technology—ISO 7-Bit Coded Character Set for Information Interchange. International Organization for Standardization: Geneva, Switzerland, 1991; p. 15.
- ISO/IEC JTC 1/SC 2 Working Group. Standards by ISO/IEC JTC 1/SC 2 Coded Character Sets. Available online: https://www.iso.org/committee/45050/x/catalogue/p/1/u/0/w/0/d/0 (accessed on 5 June 2025).
- The Unicode Consortium. UNICODE. Available online: https://home.unicode.org/ (accessed on 5 June 2025).
- Goldsmith, D.; Davis, M. UTF-7 A Mail-Safe Transformation Format of Unicode. RFC 2152. 1997. Available online: https://www.rfc-editor.org/rfc/rfc2152.html (accessed on 5 August 2025). [CrossRef][Green Version]
- Yergeau, F. UTF-8, a Transformation Format of ISO 10646. RFC 3629. 2003. Available online: https://www.rfc-editor.org/rfc/rfc3629.html (accessed on 5 August 2025). [CrossRef]
- Hoffman, P.E.; Yergeau, F. UTF-16, an Encoding of ISO 10646. RFC 2781. 2000. Available online: https://www.rfc-editor.org/rfc/rfc2781.html (accessed on 5 August 2025). [CrossRef]
- Davis, M. Unicode Standard Annex #19 UTF-32. Available online: https://www.unicode.org/reports/tr19/tr19-9.html (accessed on 5 June 2025).
- Umamaheswaran, V.S. UTF-EBCDIC, Unicode Technical Report #16; Technical Report; Unicode, Inc.: San Francisco, CA, USA, 2002. [Google Scholar]
- ISO/IEC JTC 1/SC2/WG2; UCS Transformation Format One (UTF-1). International Organization for Standardization: Geneva, Switzerland, 1993; ISO/IEC 10646, First edition 1993, Registration number 178.
- ISO/IEC JTC 1/SC2/WG2; UCS Transformation Format One (UTF-1). International Organization for Standardization: Geneva, Switzerland, 1995. Available online: https://web.archive.org/web/20150318032101/http://kikaku.itscj.ipsj.or.jp/ISO-IR/178.pdf (accessed on 5 June 2025).
- Seng, J.; Duerst, M.; Tan, T.W. UTF-5, a transformation format of Unicode and ISO 10646. Internet-Draft draft-jseng-utf5-01, Internet Engineering Task Force. 2000. Available online: https://datatracker.ietf.org/doc/html/draft-jseng-utf5-01.txt (accessed on 20 July 2025).
- Welter, M.; Spolarich, B. UTF-6—Yet Another ASCII-Compatible Encoding for IDN. Internet-Draft draft-ietf-idn-utf6-00, Internet Engineering Task Force. 2000. Available online: https://datatracker.ietf.org/doc/html/draft-ietf-idn-utf6-00.txt (accessed on 20 July 2025).
- Crispin, M. UTF-9 and UTF-18 Efficient Transformation Formats of Unicode. RFC 4042. 2005. Available online: https://www.rfc-editor.org/rfc/rfc4042.html (accessed on 5 August 2025). [CrossRef]
- Wikipedia. Comparison of Unicode Encodings. Available online: https://en.wikipedia.org/wiki/Comparison_of_Unicode_encodings (accessed on 5 June 2025).
- Allen, J.D.; Anderson, D.; Becker, J.; Cook, R.; Davis, M.; Edberg, P.; Everson, M.; Freytag, A.; Iancu, L.; Ishida, R.; et al. The Unicode Standard Version 7.0—Core Specification; Unicode, Inc.: San Francisco, CA, USA, 2014. [Google Scholar]
- ISO/IEC 2022:1994; Information Technology—Character Code Structure and Extension Techniques. International Organization for Standardization: Geneva, Switzerland, 1994. Available online: https://www.iso.org/standard/22747.html (accessed on 5 June 2025).
- CEN/TC 304 Project Team. Annex A, 8-Bit Character Sets. Available online: https://www.open-std.org/cen/tc304/guidecharactersets/guideannexa.html#_Toc443292242 (accessed on 5 June 2025).
- Murai, J.; Crispin, M.; van der Poel, E.M. Japanese Character Encoding for Internet Messages. RFC 1468. 1993. Available online: https://www.rfc-editor.org/rfc/rfc1468.html (accessed on 5 August 2025). [CrossRef][Green Version]
- Choi, U.; Chon, K.; Park, H. Korean Character Encoding for Internet Messages. RFC 1557. 1993. Available online: https://www.rfc-editor.org/rfc/rfc1557.html (accessed on 5 August 2025). [CrossRef][Green Version]
- Zhu, H.; Hu, D.; Wang, Z.; Kao, T.; Chang, W.; Crispin, M. Chinese Character Encoding for Internet Messages. RFC 1922. 1996. Available online: https://www.rfc-editor.org/rfc/rfc1922.html (accessed on 5 August 2025). [CrossRef]
- Wikipedia. Binary-to-Text Encoding. Available online: https://en.wikipedia.org/wiki/Binary-to-text_encoding (accessed on 5 June 2025).
- Freed, N.; Borenstein, D.N.S. Multipurpose Internet Mail Extensions (MIME) Part One: Format of Internet Message Bodies. RFC 2045. 1996. Available online: https://www.rfc-editor.org/rfc/rfc2045.html (accessed on 5 August 2025). [CrossRef]
- Linn, J. Privacy Enhancement for Internet Electronic Mail: Part I: Message Encryption and Authentication Procedures. RFC 1421. 1993. Available online: https://www.rfc-editor.org/rfc/rfc1421.html (accessed on 5 August 2025). [CrossRef]
- Mozilla Corporation. JavaScript Reference, Number Constructor, Number.prototype.toString() Method. Available online: https://developer.mozilla.org/en-US/docs/Web/JavaScript/Reference/Global_Objects/Number/toString (accessed on 5 June 2025).
- Mozilla Corporation. JavaScript Reference, Number Constructor, Number.parseInt() Method. Available online: https://developer.mozilla.org/en-US/docs/Web/JavaScript/Reference/Global_Objects/Number/parseInt (accessed on 5 June 2025).
- NumPy Developers. Python numpy.base_repr. Available online: https://numpy.org/doc/stable/reference/generated/numpy.base_repr.html (accessed on 5 June 2025).
- Python Software Foundation. Python Built-in Functions int(). Available online: https://docs.python.org/3/library/functions.html#int (accessed on 5 June 2025).
- The PHP Documentation Group. PHP Math Functions, base_convert() Function. Available online: https://www.php.net/manual/en/function.base-convert.php (accessed on 5 June 2025).
- Botta, M.; Cavagnino, D. Base41: A proposal for printable encoding of bit strings. Eng. Rep. 2023, 5, e12606. [Google Scholar] [CrossRef]
- Botta, M.; Cavagnino, D. Base41: A Method for Bit String Encoding in Printable Form. 2023. Available online: https://watermarking.di.unito.it/base41/index.html (accessed on 5 June 2025).
- Veljkovic, S. Base41. 2014. Available online: https://github.com/sveljko/base41 (accessed on 5 June 2025).
- Fältström, P.; Ljunggren, F.; van Gulik, D.W. The Base45 Data Encoding. RFC 9285. 2022. Available online: https://www.rfc-editor.org/rfc/rfc9285.html (accessed on 5 August 2025). [CrossRef]
- Kunzmann, N. base56. 2024. Available online: https://github.com/foss-fund/base56 (accessed on 5 June 2025).
- Nakamoto, S.; Sporny, M. The Base58 Encoding Scheme. Internet-Draft draft-msporny-base58-03, Internet Engineering Task Force. 2021. Available online: https://datatracker.ietf.org/doc/draft-msporny-base58/03/ (accessed on 20 July 2025).
- Antonopoulos, A.M. Mastering Bitcoin: Unlocking Digital Cryptocurrencies; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2014. [Google Scholar]
- Piasecki, P. Why Is Ripple’s base58 Alphabet So Weird? 2013. Available online: https://bitcoin.stackexchange.com/questions/14124/why-is-ripples-base58-alphabet-so-weird (accessed on 5 June 2025).
- Elliott-McCrea, K. Manufacturing flic.kr Style Photo URLs. 2009. Available online: https://www.flickr.com/groups/api/discuss/72157616713786392/ (accessed on 5 June 2025).
- He, K.; Xu, X.; Yue, Q. A Secure, Lossless, and Compressed Base62 Encoding. In Proceedings of the 2008 11th IEEE Singapore International Conference on Communication Systems, Guangzhou, China, 19–21 November 2008; pp. 761–765. [Google Scholar] [CrossRef]
- Wu, P.C. A base62 transformation format of ISO 10646 for multilingual identifiers. Softw. Pract. Exp. 2001, 31, 1125–1130. [Google Scholar] [CrossRef]
- Adobe Systems Incorporated. PostScript Language Reference, 3rd ed.; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1999. [Google Scholar]
- Elz, R. A Compact Representation of IPv6 Addresses. RFC 1924. 1996. Available online: https://www.rfc-editor.org/rfc/rfc1924.html (accessed on 5 August 2025). [CrossRef][Green Version]
- He, D.; Sun, Y.; Jia, Z.; Yu, X.; Guo, W.; He, W.; Qi, C.; Lu, X. A Proposal of Substitute for Base85/64–Base91. In Proceedings of the SUMMER 8th International Conference on Computing, Communications and Control Technologies, CCCT, Orlando, FL, USA, 29 June–2 July 2010. [Google Scholar][Green Version]
- Henke, J. basE91 Encoding. 2006. Available online: https://base91.sourceforge.net/ (accessed on 5 June 2025).[Green Version]
- vorakl. Convert Binary Data to a Text with the Lowest Overhead. 2020. Available online: https://vorakl.com/articles/base94/ (accessed on 5 June 2025).[Green Version]
- vorakl. The Zoo of Binary-to-Text Encoding Schemes. 2020. Available online: https://vorakl.com/articles/stream-encoding/ (accessed on 5 June 2025).[Green Version]
- Albertson, K. Base-122 Encoding. 2016. Available online: https://blog.kevinalbs.com/base122 (accessed on 5 June 2025).[Green Version]
- Microsoft Corporation. BASE Function. Available online: https://support.microsoft.com/en-us/office/base-function-2ef61411-aee9-4f29-a811-1c42456c6342 (accessed on 5 June 2025).[Green Version]
- Microsoft Corporation. DECIMAL Function. Available online: https://support.microsoft.com/en-us/office/decimal-function-ee554665-6176-46ef-82de-0a283658da2e (accessed on 5 June 2025).[Green Version]
- Apache OpenOffice Wiki. BASE Function. Available online: https://wiki.openoffice.org/wiki/Documentation/How_Tos/Calc:_BASE_function (accessed on 5 June 2025).[Green Version]
- Apache OpenOffice Wiki. DECIMAL Function. Available online: https://wiki.openoffice.org/wiki/Documentation/How_Tos/Calc:_DECIMAL_function (accessed on 5 June 2025).[Green Version]
- The Document Foundation. BASE Function. Available online: https://help.libreoffice.org/latest/lo/text/scalc/01/func_base.html (accessed on 5 June 2025).[Green Version]
- The Document Foundation. DECIMAL Function. Available online: https://help.libreoffice.org/latest/lo/text/scalc/01/func_decimal.html (accessed on 5 June 2025).[Green Version]
- Cavagnino, D.; Werbrouck, A.E. Efficient Algorithms for Integer Division by Constants Using Multiplication. Comput. J. 2008, 51, 470–480. [Google Scholar] [CrossRef]
- Warren, H.S. Hacker’s Delight, 2nd ed.; Addison-Wesley Professional: Boston, MA, USA, 2012. [Google Scholar][Green Version]
- Costello, A.M. Punycode: A Bootstring encoding of Unicode for Internationalized Domain Names in Applications (IDNA). RFC 3492. 2003. Available online: https://www.rfc-editor.org/rfc/rfc3492.html (accessed on 5 August 2025). [CrossRef]
- Fältström, P.; Hoffman, P.E. Internationalizing Domain Names in Applications (IDNA). RFC 3490. 2003. Available online: https://www.rfc-editor.org/rfc/rfc3490.html (accessed on 5 August 2025). [CrossRef]
- Dürst, M.J.; Suignard, M. Internationalized Resource Identifiers (IRIs). RFC 3987. 2005. Available online: https://www.rfc-editor.org/rfc/rfc3987.html (accessed on 5 August 2025). [CrossRef]
- Helbing, J. yEncode—A Quick and Dirty Encoding for Binaries. 2022. Available online: http://www.yenc.org/yenc-draft.1.3.txt Expired (accessed on 5 June 2025).
- MDN Web Docs. Function btoa. Available online: https://developer.mozilla.org/en-US/docs/Web/API/btoa (accessed on 2 July 2025).
- MDN Web Docs. Function atob. Available online: https://developer.mozilla.org/en-US/docs/Web/API/atob (accessed on 2 July 2025).
- The FreeBSD Project. FreeBSD Manual Pages, btoa. Available online: https://man.freebsd.org/cgi/man.cgi?query=btoa&apropos=0&sektion=0&manpath=FreeBSD+14.0-RELEASE+and+Ports (accessed on 2 July 2025).
- Horton, M. UUENCODE(1C) UNIX Programmer’s Manual. Available online: https://www.tuhs.org/cgi-bin/utree.pl?file=4BSD/usr/man/cat1/uuencode.1c (accessed on 5 June 2025).
- IEEE and The Open Group. UUENCODE and UUDECODE—The Open Group Base Specifications Issue 7. Available online: https://pubs.opengroup.org/onlinepubs/9699919799/utilities/uuencode.html and https://pubs.opengroup.org/onlinepubs/9699919799/utilities/uudecode.html (accessed on 5 June 2025).
- IEEE Std 1003.1-2017; IEEE Standard for Information Technology—Portable Operating System Interface (POSIX(TM)) Base Specifications, Issue 7; Revision of IEEE Std 1003.1-2008. IEEE Computer Society and The Open Group: Washington, DC, USA, 2018; pp. 1–3951. [CrossRef]
- Mann, T. Prehistory of BinHex. Available online: https://www.tim-mann.org/binhex.html (accessed on 5 June 2025).
- Lempereur, Y. Post on Prehistory of BinHex. Available online: https://www.tim-mann.org/trs80/yves.txt (accessed on 5 June 2025).
- Crocker, D.; Fair, E.E.; Fältström, P. MIME Content Type for BinHex Encoded Files. RFC 1741. 1994. Available online: https://www.rfc-editor.org/rfc/rfc1741.html (accessed on 5 August 2025). [CrossRef][Green Version]
- Moore, K. MIME (Multipurpose Internet Mail Extensions) Part Three: Message Header Extensions for Non-ASCII Text. RFC 2047. 1996. Available online: https://www.rfc-editor.org/rfc/rfc2047.html (accessed on 5 August 2025). [CrossRef]
- Schaad, J.; Ramsdell, B.C.; Turner, S. Secure/Multipurpose Internet Mail Extensions (S/MIME) Version 4.0 Message Specification. RFC 8551. 2019. Available online: https://www.rfc-editor.org/rfc/rfc8551.html (accessed on 5 August 2025). [CrossRef]
- Kermit Project Software Archive. BOO Files. Available online: https://www.kermitproject.org/archive.html#boofile (accessed on 5 June 2025).
- Columbia University Computer Center. The Kermit Project. 1981. Available online: https://web.archive.org/web/20231215030314/https://www.columbia.edu/kermit/ (accessed on 5 June 2025).
- cppreference.com. Function isprint(). Available online: https://en.cppreference.com/w/c/string/byte/isprint (accessed on 5 June 2025).
- cppreference.com. Function iswprint(). Available online: https://en.cppreference.com/w/c/string/wide/iswprint (accessed on 5 June 2025).
- ISO/IEC. ISO International Standard ISO/IEC 9899:2024(en): Information Technology—Programming Languages—C (Standard C23). 2024. Available online: https://www.iso.org/standard/82075.html (accessed on 5 August 2025).
- ISO/IEC. ISO International Standard ISO/IEC 30112:2020(en): Information Technology—Specification Methods for Cultural Conventions. 2020. Available online: https://www.iso.org/standard/71987.html (accessed on 5 August 2025).
- cppreference.com. Function std::isprint(). Available online: https://en.cppreference.com/w/cpp/string/byte/isprint (accessed on 5 June 2025).
- cppreference.com. Function std::iswprint(). Available online: https://en.cppreference.com/w/cpp/string/wide/iswprint (accessed on 5 June 2025).
- rix. Writing ia32 alphanumeric shellcodes. Phrack 2001, 57. Available online: https://phrack.org/issues/57/15.html#article (accessed on 5 August 2025).
- Botta, M.; Cavagnino, D. A Framework for Reversible Data Embedding into Base45 and Other Non-Base64 Encoded Strings. Appl. Sci. 2022, 12, 241. [Google Scholar] [CrossRef]
- Botta, M.; Cavagnino, D. Improving data embedding capacity into Base45 encoded strings. Eng. Rep. 2023, 5, e12622. [Google Scholar] [CrossRef]
- Botta, M.; Cavagnino, D.; Druetto, A. Hide45: A Method for Optimal Payload Data Hiding in Base45 Encoded Strings. Appl. Sci. 2023, 13, 9993. [Google Scholar] [CrossRef]
- Botta, M.; Cavagnino, D. Escaping Printable Encoded Streams to Embed Out-of-Band Data. Appl. Sci. 2023, 13, 6926. [Google Scholar] [CrossRef]
- Hines, K.; Lopez, G.; Hall, M.; Zarfati, F.; Zunger, Y.; Kiciman, E. Defending Against Indirect Prompt Injection Attacks with Spotlighting. arXiv 2024, arXiv:2403.14720. [Google Scholar]
- Zhang, R.; Sullivan, D.; Jackson, K.; Xie, P.; Chen, M. Defense against Prompt Injection Attacks via Mixture of Encodings. arXiv 2025, arXiv:2504.07467. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).