Abstract
Hyper-heuristics, or simply heuristics to choose heuristics, represent a powerful approach to tackling complex optimization problems. These methods decide which heuristic to apply throughout the solving process, aiming to improve the solving process. While they have demonstrated significant success across various domains, their suitability for all problem instances, even within a specific domain, is not guaranteed. The literature provides many examples of successful hyper-heuristic models for packing problems. Among those models, we can mention rule-based and fixed-sequence-based hyper-heuristics. These two models have proven useful in various scenarios. This paper investigates a genetic-based approach that produces hybrid hyper-heuristics. Such hybrid hyper-heuristics combine rule-based decisions while firing heuristic sequences. The rationale behind this hybrid approach is that we aimed to combine the strengths of both approaches. Although we expected to improve on the individual performance of the methods, we obtained contradictory results that suggest that, at least in this work, combining the strengths of different hyper-heuristic models may not be a suitable approach.
1. Introduction
Solving combinatorial optimization problems requires finding a subset of items that not only solves the problem but also maximizes or minimizes a quality criterion. Since many of these problems exhibit huge search spaces (which usually grow exponentially with the number of inputs), in most cases, it is unfeasible to conduct an exhaustive exploration of the search space. Consequently, we usually rely on approximate solving methods to deal with such problems. So, we only explore a fraction of the search space, which we consider likely to contain the best solutions. However, we cannot guarantee that the solution found is optimal when using approximated methods.
In this context, approximate methods such as heuristics and metaheuristics have provided interesting and straightforward ways to address these problems [1,2,3]. More recently, hyper-heuristics (heuristics that choose heuristics) have emerged as a valuable solving alternative [4,5]. Hyper-heuristics come in various forms, and many classifications have been proposed [6,7]. For example, based on the learning process, we can classify them as online, where hyper-heuristics learn “on the go” without previous training, and offline, where hyper-heuristics go through a training phase before properly using them. We can also classify hyper-heuristics based on the type of heuristics they choose. In this context, hyper-heuristics can be constructive, where the solving process starts from an empty solution and adds elements to the solution iteratively, or perturbatively, where the solving process starts with a complete and maybe unfeasiblesolution that improves through the solving process. Another way to classify hyper-heuristics concerns their internal representation, such as rule-based and fixed-sequence-based hyper-heuristics. With rule-based hyper-heuristics, a system of rules decides which heuristic to apply at a given search moment (defined by its current problem state), resulting in an adaptive sequence of heuristics that solves the instance [8,9]. The process is straightforward: the rule whose condition is closest to the problem state (using Euclidean distance) is the one that fires (it decides which heuristic to apply). For example, in packing problems, applying one heuristic leads to packing one item, which modifies the problem state. The hyper-heuristic repeats this process, selecting a suitable heuristic whenever it attempts to pack an item and stops when the problem is solved. Conversely, in fixed-sequence-based hyper-heuristics, the hyper-heuristic represents a fixed sequence of heuristics used to solve the instances [10,11,12]. So, the sequence itself determines which heuristics will be used in each decision. A distinctive characteristic of this approach is that it ignores the problem state since the sequence is fixed from the beginning of the search. Fixed-sequence-based hyper-heuristics also choose one heuristic whenever they attempt to pack an item. However, they ignore the problem state since the next heuristic to apply is already defined within the sequence.
Rule-based and fixed-sequence-based hyper-heuristics have proven reliable under different optimization scenarios, each exhibiting specific pros and cons. For example, rule-based hyper-heuristics adapt to different problem instances, which increases their versatility and applicability on large instance sets. However, they tend to be more complex since they require defining more elements (including a representative set of features that allow for the instance characterization), and their generation process usually requires more resources. On the other hand, fixed-sequence-based hyper-heuristics are easy to produce and interpret because of the few elements to define as part of their generation process. For example, they lack the need to define features that characterize the instances. However, they are limited to smaller instance sets since a fixed sequence of heuristics is unlikely to perform well on many instances without any further adjustment process.
The apparent success of hyper-heuristics in various domains and continual design improvements have led to the common assumption that more complex hyper-heuristic models invariably yield better solutions. This is exemplified by approaches like the squared hyper-heuristic model [13] and recursive hyper-heuristics [14]. However, this assumption may be a fallacy. Simply increasing complexity does not guarantee improved performance; there may be a point of diminishing returns or even a negative impact.
This work explores the feasibility of combining rule-based and fixed-sequence-based hyper-heuristic approaches into a unique and supposedly more powerful hyper-heuristic model. Our proposal defines a hybrid hyper-heuristic as a system of rules where each rule recommends a fixed sequence of heuristics to apply. With this, we aim to verify if such an approach can combine the benefits of both individual approaches. Unfortunately, as we will see later, combining the two models seems to be a step in the wrong direction of hyper-heuristic design.
We choose two widespread packing problems to test our proposal: the knapsack problem (KP) [15,16] and the bin packing problem (BPP) [17,18], but we could easily extend it to other problem domains. In both cases, we consider their most straightforward versions. Concerning the KP, the items can only be packed or unpacked, but we cannot split them. Regarding the BPP, we work with its one-dimensional online version. This means the bins and items only have one dimension: the length. Also, because we deal with its online version, we receive only one item at a time, and we cannot change the order in which we receive the items. Of course, the limitations exhibited by our hybrid model in this work should be taken with caution since they might not appear in other instances or problem domains.
We organize the remainder of this document as follows. Section 2 briefly reviews the most relevant works related to our research. Section 3 describes the solution model and its operation. Afterward, the experiments and results can be found in Section 4. Finally, Section 5 presents the conclusion and some ideas for future work derived from this investigation.
2. Background and Related Work
Hyper-heuristics represent a family of methods that either create or combine heuristics, attempting to improve the solution’s quality. They have become popular because of their many implementations and promising results in various problem domains.
Hyper-heuristics have proven a powerful paradigm for tackling complex optimization problems across several domains. Their ability to automate the design and selection of effective heuristics has led to significant advancements in problem-solving. Although a complete survey of hyper-heuristic successes is not feasible here, the following brief overview demonstrates the breadth of their applicability and explains their recent surge in popularity.
Among the various works related to hyper-heuristic generation, we must highlight those related to genetic programming (GP) and its contributions to various combinatorial optimization problems. For example, Burke et al. explored the idea of using hyper-heuristics to produce new heuristics that are currently unknown [19]. Later, Nguyen et al. proposed GPAM, which employs GP to evolve adaptive mechanisms that solve difficult optimization problems [20]. More recent studies have focused on extending the use of GP to produce hyper-heuristics. For example, Wang et al. used elitist mutation within GP to solve the integrated order batching and picker routing problem [21]. Later, Yang et al. improved the generalization capabilities of hyper-heuristics produced with GP to solve the dynamic workflow scheduling by using mini-batch sampling strategies [22].
Regardless of their importance, GP is not the only method used to produce hyper-heuristics. Aziz proposed ant colony hyper-heuristics to solve the traveling salesman problem (TSP), claiming that this approach produces reasonable quality solutions across different instances without extensive parameter tuning [23]. Ahmed et al. explored using hyper-heuristics to solve the urban transit route design problem (UTRP). Their approach consisted of a sequence-based selection method combined with the great deluge acceptance method [24]. Mahmud et al. explored self-adaptive hyper-heuristics to solve the integrated supply chain scheduling problem, where supplier, manufacturer, and batching decisions are simultaneously optimized in response to heterogeneous customer requirements with time window constraints [25]. Guo et al. proposed a general framework for automatically designing shop scheduling strategies based on hyper-heuristics. They summarized various state-of-the-art technical points in the development process [26].
Furthermore, there are interesting works that bridge machine learning into the realm of hyper-heuristics. Among those works, we can mention the work by Kletzander, where the authors combined reinforcement learning to produce hyper-heuristics on six distinct problem domains [27]. Ortiz et al. and Zárate and Ortiz used various machine learning algorithms to produce hyper-heuristics for solving constraint satisfaction problems [28] and the knapsack problem [29], respectively.
Among the many implementations available in the literature, this work focuses on two particular hyper-heuristic models: rule-based and fixed-sequence-based hyper-heuristics.
3. Solution Approach
As mentioned earlier, our solution approach combines rule-based and fixed-sequence-based hyper-heuristics. To do so, we generate rules that recommend sequences of heuristics. This way, we have merged the two hyper-heuristic models into a single unexplored hyper-heuristic model. Thus, our model produces hybrid hyper-heuristics, as depicted in Figure 1. As we can observe, a hybrid hyper-heuristic contains a set of rules. Such rules decide which heuristic sequence to use at a given search moment. Although the sequences within each rule will remain unchanged once a hyper-heuristic is generated, each instance is solved by the iterative application of distinct sequences of heuristics because the different rules fire on each instance. So, the order in which these fixed sequences of heuristics are applied to solve an instance changes from instance to instance according to its features, which determines the rules that are fired.

Figure 1.
A graphical representation of a hybrid hyper-heuristic combining the rule-based and fixed-sequence-based approaches.
For example, we depict three rules in Figure 1. Each of these rules has three features that characterize the problem state (the conditions), and for each rule, there is a corresponding three-heuristic sequence to apply (the rule’s action). Please note that the user determines the length of the heuristic sequences. So, if it drops to one, the model behaves as a traditional rule-based hyper-heuristic, where each rule fires a single heuristic as an action.
In our proposal, a genetic algorithm is responsible for producing the hyper-heuristics. The work of Ortiz et al. inspired this genetic algorithm [30], producing an initially random population of potential hyper-heuristics. These potential heuristics evolve using genetic operators such as selection, crossover, and mutation. After several generations, the genetic algorithm returns the best hyper-heuristic found so far, ready to be used on unseen instances. We provide a pseudo-code of how the genetic algorithm works in Algorithm 1.
| Algorithm 1 The genetic algorithm used to produce hybrid hyper-heuristics. |
| Input: n: population size, : crossover rate, : mutation rate. Output: A hybrid hyper-heuristic.
|
It is critical to mention that our genetic algorithm uses a binary representation (as depicted in Figure 1), so standard crossover and mutation operators can be used. However, the length of the chromosomes is variable since the genetic algorithm also finds the most suitable number of rules given the instances in the training set. Although the number of rules is variable and defined throughout the evolutionary process, the number of actions is the same for all the rules within the evolutionary process. In other words, the heuristic sequences within each rule’s action are the same length. Thus, the user defines the length of the fixed-sequence-based hyper-heuristics produced by the genetic algorithm.
Since the internal coding within the chromosome is binary, we used a conversion scheme to map such chromosomes into real numbers that we could use for the actual rules. For example, in Figure 1, we represent each feature using five bits, which results in 32 available values. Then, we divided the range into 32 discrete steps of each and multiplied by its corresponding feature value. Thus, () was multiplied by to obtain , the value of the first feature in the first rule. In the case of the heuristics, the conversion was straightforward: we just converted them from base 2 to base 10 to determine the index of the heuristic to use.
Whenever an instance needed to be solved, we characterized it (by calculating its current features). Then, we calculated the Euclidean distance between the vector of features that characterize the instance and each one of the conditions in the hyper-heuristic. The condition that minimizes the distance is the one that best matches the problem state. Then, we applied the heuristics coded in the action of the winning rule. The approach applied the heuristics in the exact order they appear in the rule. When we used such heuristics to solve the problem partially, the remaining instance exhibited features that differed from the previous ones, making it possible for a different rule to be selected the next time we invoked the hyper-heuristic.
Please note that, in traditional fixed-sequence approaches described for packing problems, the sequences are usually shorter than the number of items in the problem. Thus, the sequences rely on an “extension procedure” that extends the sequence to manage all the decisions to solve the instance. For example, if we use a sequence of three heuristics (, , and ) to solve an instance with nine items, some examples of extension procedures could be to repeat the sequence three times (, , , , , , , , and ) or to apply each heuristic in the sequence three times (, , , , , , , , and ), to mention a few examples. Each one of these strategies comes with pros and cons. However, we required no such procedure in our case because our model applied the rules as often as needed until it packed all the items or decided to stop packing.
3.1. Instance Characterization
For this work, we characterized the instances of the two problem domains using straightforward features. In the case of the KP, we used three features related to the weights and profits of unpacked items, described as follows:
- The average weight of all the unpacked items in the instance.
- The average profit of all the unpacked items in the instance.
- The correlation between the profits and weights of the unpacked items in the instance. To calculate the correlation, we relied on the Pearson correlation coefficient.
Concerning the BPP, we used five features related to the length of the items remaining to be packed. These features are described below:
- The average length of all the unpacked items in the instance.
- The scaled standard deviation of all the unpacked items in the instance (with respect to their length).
- The percentage of small-sized unpacked items (items with a length smaller than or equal to 15% of the bin’s capacity).
- The percentage of medium-sized unpacked items (items with a length between 15% (non-inclusive) and 30% (inclusive) of the bin’s capacity).
- The percentage of large-sized unpacked items (items with a length of over 30% of the bin’s capacity).
We calculated these features dynamically every time the solver decided which item to pack next. In both domains, the features were scaled to the range to facilitate mapping between features and heuristics. Additionally, we knew that other features might be considered to characterize the problem instances. However, we wanted to keep our analysis as simple as possible and compatible with recent studies that used these or similar sets of features on their corresponding problem domains [29,31].
3.2. Available Heuristics
Building upon previous research [29,32], we incorporated a set of well-established item-selection heuristics for the KP. These heuristics operate by selecting a single item for potential inclusion in the knapsack using the selection criteria outlined below.
- DEF packs the items in the order in which they appear in the instance (no additional ordering is conducted on them).
- MINW prefers the item with the smallest weight. MINW assumes that leaving the most space for the remaining decisions is likely to maximize the solution’s profit.
- MAXP packs the item with the largest profit first. MAXP follows a greedy approach to fill the knapsack since it assumes that maximizing the profit in each decision is likely to maximize the solution’s profit.
- MAXPW chooses the item that maximizes the profit-to-weight ratio. Although this heuristic also follows a greedy approach, it focuses on the ‘density’ associated with the profit of an item.
Note that the heuristics for the KP use information from zero (DEF), one (MINW and MAXP), and two (MAXPW) features, thus representing approaches with different levels of complexity.
Regarding the BPP, we selected four straightforward heuristics that consider information about open bins in the current problem state to decide where to pack the current item. These heuristics are described as follows:
- FF packs the item in the next available bin where the item fits.
- BF prefers the bin where the item fits the best, so it minimizes the waste. BF assumes that the less space we leave in the bin, the better it is for the overall solution.
- WF packs the item in the bin that maximizes the space once the item is packed. This heuristic attempts to leave the most space in the bin for future items.
- AWF propagates the idea from WF, allowing it to pack the item in the bin with the second-most waste derived from packing the item.
Whenever a tie occurs, the first item chosen is always preferred. For the KP, we estimated the quality of the solutions by calculating their profit, which is the sum of the profit obtained over all the instances solved. In this context, the larger the profit, the better the solution. For BPP, we used the bin usage, defined as follows: , where n is the number of items to pack, is the maximum bin capacity, and is the current bin capacity. When using bin usage as a metric, a value of 1 indicates that such a bin produces no waste. So, the best possible evaluation we can obtain when solving m instances is m.
3.3. Instances
For this work, we used synthetic instances generated using the method proposed by Plata et al. [33]. We created these instances through varied configurations to explore diverse scenarios for each problem domain. Before moving forward, we find it opportune to stress that, contrary to what occurs in machine learning applications, where the number of instances used for training is larger than the number of instances used for testing (usually a 70% to 30% distribution), in hyper-heuristic applications, it is usual to use fewer instances for training and more instances for testing [12,34].
For the KP, we generated 900 KP instances split into a training set of 100 instances and a test set of 800. Both sets were designed to be balanced, with each of the four available heuristics being the best performer on approximately 25% of the instances within each set. This balanced distribution ensured a representative evaluation. All 900 instances consisted of 100 items each, with weights and profits ranging from 1 to 64 units and a knapsack capacity of 128 weight units.
Regarding the BPP, we generated 1120 BPP instances. These instances were split into two sets: training, with 120 instances, and testing, with 1000 instances. As in the case of the KP, we also followed the idea of balancing the instances. So, each heuristic represented the best option in 25% of the instances in each set. All instances consisted of 100 items each, with weights ranging from 1 to 64 units and a bin capacity of 128 weight units.
These instances are freely accessible at https://drive.google.com/drive/folders/1BrDdTSpmheUmD8TZSoUcqHnFyvgL2yji?usp=sharing, accessed on 4 August 2025.
4. Experiments and Results
In this experiment, we analyzed the impact of heuristic sequence length on the performance of hybrid hyper-heuristics. We evaluated the hyper-heuristics on the training and test sets, systematically varying the length of the heuristic sequences triggered by the rules. Specifically, we generated ten hyper-heuristics designed to select a single heuristic, ten hyper-heuristics designed to select sequences of two heuristics, and up to ten hyper-heuristics designed to select sequences of ten heuristics. To generate each of these hyper-heuristics, we used the GA-based approach described in Section 3 using the following parameters: 200 individuals in the population, crossover and mutation rates of 0.9 and 0.1, respectively, and 5000 evaluations of the fitness function as a stopping criterion. Each run of the genetic algorithm produced one hybrid hyper-heuristic. As a result, we ran the genetic algorithm a total of 100 times per problem domain to produce 10 hybrid hyper-heuristics for 10 different sequence lengths for each problem domain.
4.1. Results for the Knapsack Problem
Figure 2 shows the performance of the hybrid hyper-heuristics on the test set for the KP. There is a fascinating, yet apparently contradictory performance. It seems that, as we increase the length of the sequences, the number of rules that can fire within the hybrid hyper-heuristics, as well as their performance, decreases. These results contradict those that we initially expected. Our idea was that using rules to fire sequences would be similar to providing the hybrid hyper-heuristics with the opportunity to use different heuristic sequences according to the problem state, thus increasing their adaptability. The results show that we were wrong to think that.
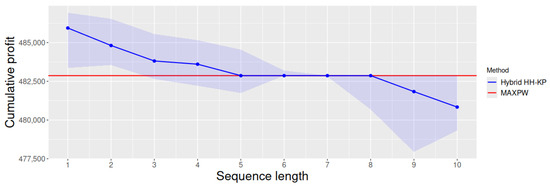
Figure 2.
Cumulative profit on the test set obtained by the hybrid hyper-heuristics produced with our approach. We present the median performer (among ten hybrid hyper-heuristics) per sequence length as a blue line. The shadowed blue region indicates the worst and best hybrid hyper-heuristic per sequence length (the wider this region, the more variance we found on the hyper-heuristic performance). The red line represents MAXPW, the best individual heuristic for this set, which we provide for comparison purposes.
To understand what occurs within the model, we studied the number of rules per hybrid-heuristic, based on the length of the heuristic sequences they can produce. We recalled that the genetic algorithm decides, through the evolutionary process, the number of rules per hyper-heuristic, but the length of the heuristic sequences is defined by the user. As we can observe from Figure 3, the number of rules decreased as we increased the length of the heuristic sequences that the rules could fire. This is an interesting finding since there is nothing coded within the genetic algorithm that explicitly describes this behavior. It is, to the best of our understanding, an emergent behavior resulting from the evolutionary process under these conditions.
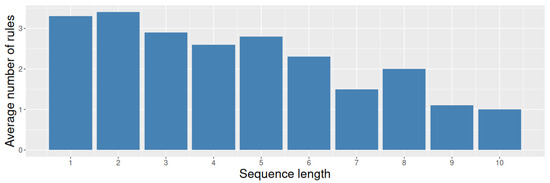
Figure 3.
Average number of rules per heuristic sequence length in 100 hybrid hyper-heuristics for the KP.
The number of rules per hyper-heuristic provides an interesting opportunity to analyze the sequences’ complexity once such hyper-heuristics solve the instances. When solving a KP instance, we had fewer decisions than items since the knapsack can run out of space before we analyze all the items. So, the number of decisions, , where n is the number of items in the instance. Assuming each rule can fire heuristic sequences of length l, a hybrid hyper-heuristic was invoked times when solving a KP instance (every decision packs l items). In this context, the number of rules, r, determines the potential recommendations of the hyper-heuristic every time it is called. In the best case, each rule within the hybrid hyper-heuristic fires a unique sequence of heuristics (assuming no repeated actions within the hyper-heuristic). Under these conditions, the number of different ways a hyper-heuristic can solve an instance is provided by . According to the data from Figure 3 and assuming a constant number of decisions (the average number of items in the solutions generated in this work), a hyper-heuristic that fires only one heuristic per action can generate around distinct ways to solve an instance (of course, this would be the behavior of a traditional rule-based hyper-heuristic). When we compared this result against the case of hyper-heuristics with rules that fire sequences of two heuristics, this number drastically decreased to around distinct ways to solve an instance (less than 0.7% the number of options of the previous case). It was clear that, for hyper-heuristics with rules that fire sequences of ten heuristics, the number was ridiculously small, reaching a value around , which meant that such hyper-heuristics attempted to solve all the instances using the same fixed sequence of ten heuristics. This analysis provides a potential answer to why the performance of the hybrid hyper-heuristics decreases as we increase the length of the heuristic sequences that the rules can fire.
Although we found that the number of rules decreased as we increased the number of heuristics within the action of such rules, we were also interested in finding the distribution of heuristics used within the rules. Figure 4 shows the proportions of how the hyper-heuristics use the heuristics as part of the sequences they produce. By a quick inspection, we observed that MAXPW was the most used heuristic within the rules. This behavior was consistent since this heuristic was the most successful when used in isolation. Although hyper-heuristics also consider other heuristics, their use is somewhat limited compared to MAXPW. It is worth noticing that these results suggest that what matters the most is the order in which these heuristics are applied, more than the frequency. For example, in Figure 4, the sequences of lengths 2 and 10 exhibit similar patterns regarding the frequency of use of MAXPW and MINW. However, their performance is entirely different (see Figure 2).
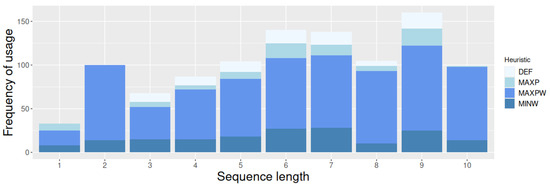
Figure 4.
Frequency of usage per heuristic sequence length in 100 hybrid hyper-heuristics for the KP.
4.2. Results for the Bin Packing Problem
Similar to what we observed in the KP, our experiments for the BPP show a trend where the larger the heuristic sequences the hybrid hyper-heuristics can fire, the worse their performance. Again, from Figure 5, we can conclude that combining rule-based hyper-heuristics and fixed-sequence-based ones did not work as expected. As in the KP, we expected this combination to provide the hyper-heuristics with additional adaptive capabilities. Instead, they seem to have had trouble as we increased the length of the heuristic sequences that the rules can fire.
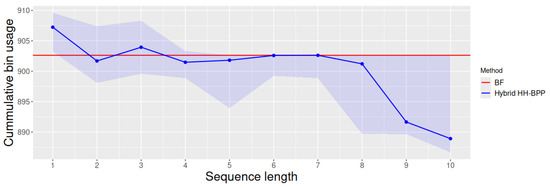
Figure 5.
Cumulative bin usage on the test set obtained by the hybrid hyper-heuristics produced with our approach. We present the median performer (among ten hybrid hyper-heuristics) per sequence length as a blue line. The shadowed blue region indicates the worst and best hybrid hyper-heuristic per sequence length (the wider this region, the more variance we found on the hyper-heuristic performance). The red line represents BF, the best individual heuristic for this set, which we provide for comparison purposes.
Just as we did when we previously analyzed the impact of the number of rules produced per sequence length for the KP, a similar analysis on the BPP shows comparable results. In the case of the BPP, the number of decisions per instance was equal to the number of items within the instance since all of them must be distributed among the bins (). Each rule fired heuristic sequences of length l, so we called a hyper-heuristic () times to solve the BPP instance. If we assumed no repeated actions in the rules of , the number of distinct ways can solve the instance was provided by , where r is the number of rules within hyper-heuristic . Based on the results in Figure 6, a traditional rule-based hyper-heuristic (one that recommends only one heuristic per rule) can generate up to distinct ways to solve an instance. However, when the number of heuristics in the sequence increases to two, the number of distinct ways the hyper-heuristic can solve an instance drastically decreases to . As we increased the length of the heuristic sequences within the rules, we observed how the number of ways to solve the instances rapidly decreased. For example, we had options for sequences of ten heuristics. Although this number is larger than what we observed for sequences of length 10 in the KP, it is still small and potentially explains the decrease in the performance of the hybrid hyper-heuristics when we increased the length of the sequences.
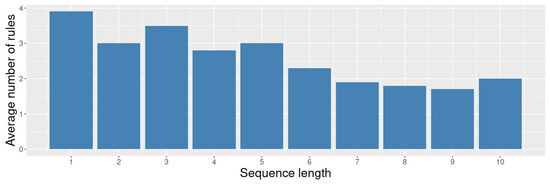
Figure 6.
Average number of rules per heuristic sequence length in 100 hybrid hyper-heuristics for the BPP.
Finally, as we did for the KP, we also analyzed the frequency of heuristics that the hyper-heuristics produced for the BPP could fire. Similarly to what we observed for the KP, Figure 7 shows that the most used heuristic in the BPP was BF, which showed the best performance when applied in isolation. Although the patterns for sequences with 6 to 10 heuristics were similar, their performance varied significantly. This result supports the idea that how we use the heuristics is more important than how many times we use them.
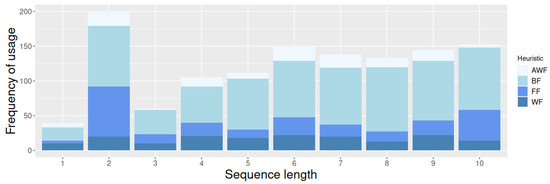
Figure 7.
Frequency of usage per heuristic sequence length in 100 hybrid hyper-heuristics for the BPP.
4.3. Discussion
The idea behind this work was to develop a new method that combines the strengths of existing hyper-heuristic models into a single, unified approach. Combining the power of rule-based and fixed-sequence-based hyper-heuristics through GAs initially seemed like a good idea. However, our experiments contradicted our initial expectations.
There are a few topics that we consider important to discuss concerning the results obtained. For example, it appears that combining the two hyper-heuristic approaches (rule-based and fixed-sequence-based) through a GA somehow restricts the individual capabilities of the model to solve the knapsack and bin packing problems. Different studies have demonstrated that the individual application of rule-based and fixed-sequence-based models yields competent hyper-heuristics on these domains. However, the proposed strategy to combine the two models into a single model underperformed, either because the individual strengths of the rule-based and fixed-sequence-based models interfere with each other or simply because our strategy for hybridizing hyper-heuristics was incorrect. Regardless of the reason, we failed to obtain the results we initially expected: hyper-heuristics that rival those produced by the models used as inspiration for our approach. However, we observed consistency among the results. For example, there is a clear trend of reducing the number of rules within the hyper-heuristics as the sequence length increases. Moreover, we observed a decrease in the performance of hyper-heuristics as we allow the rules to fire larger sequences of heuristics. We observed these trends in both problem domains (KP and BPP).
Although we cannot fully explain the results obtained, we have a few potential explanations for the unsatisfactory performance exhibited by our hybrid model. First, we consider it important to recall, as we briefly mentioned earlier, that other hyper-heuristics models from the literature utilize the idea of fixed sequences of heuristics to directly solve complete instances, rather than only fractions of them, as proposed in this manuscript. Those heuristic sequences are usually shorter than the number of variables within the problem. Therefore, the sequences rely on a mechanism that extends them so they can solve the complete instance. Different versions of this extension procedure are available in the literature. However, it is worth noting that some of them allow for a smoother transition between heuristics than the one presented in this work. For example, Sanchez et al. [11] relied on a procedure that generates sequences shorter than the number of items in the KP. Then, the solver extends the sequence by replicating heuristics as many times as needed to cover all the items. The procedure is straightforward: given a sequence of heuristics (, , , and ) and a KP with only 12 items, each heuristic will be replicated five times to produce a sequence that supports 12 decisions (one per item). This way, the sequence becomes , , , , , , , , , , , and . This extension procedure enables a smoother transition between heuristics, as the same heuristic is used multiple times before the solver is allowed to switch to a different one. In our model, we allowed changes in heuristics for every decision. Although we initially considered this an advantage because our approach used sequences to solve instances partially, and the process was repeated as many times as needed, we now view this as a potential drawback due to the numerous changes that may occur while solving an instance.
5. Conclusions and Future Work
As mentioned earlier, our solution approach combines rule-based and fixed-sequence-based hyper-heuristics. To do so, we generate rules that fire sequences of heuristics. This way, we merged the two hyper-heuristic models into a single unexplored hyper-heuristic model. Thus, our model produces hybrid hyper-heuristics, as depicted in Figure 1. As we can observe, a hybrid hyper-heuristic contains a set of rules. However, this model is unique because these rules decide which sequence of heuristics to use at a given search moment.
The literature has shown some encouraging results regarding various hyper-heuristic models. As described before, rule-based and sequence-based implementations have proven reliable in various scenarios. Our work went beyond the individual success of these two approaches. It explored the feasibility of combining these two approaches into a single one that generates hybrid hyper-heuristics that decide on the items to pack by using rules. However, the actions of such rules are heuristic sequences. So, when an action fires, various items may be chosen for packing. Although our results are still preliminary, we observed an unexpected result: using heuristic sequences as actions within the rules decreases the hyper-heuristic performance as the sequences’ length increases. This phenomenon was observed both in the KP and the BPP.
Although our results confirmed that some lengths allow for the improvement of the results obtained by MAXPW and BF (the best heuristics for the instances considered in this work for the KP and the BPP, respectively), we conclude that, at least for the cases studied in this work, it is not a good idea to allow the rules to fire heuristic sequences. Instead, the traditional rule-based model (in which each rule fires a single heuristic) obtained the best results in both the training and test sets for both domains.
How is this possible? We are going to be honest. When we started working on the hybrid hyper-heuristics concept described in this document, we expected to improve existing results. Since almost all ideas regarding hyper-heuristics we had implemented before had succeeded, we were also positive this time. However, despite our efforts, we could not improve our results further. We already explained how the number of rules coded within the hybrid hyper-heuristics might affect their performance when recommending sequences of heuristics. Unfortunately, we are unable to explain why the genetic algorithm tends to reduce the number of rules as the length of the sequences increases.
We do not consider our results a complete failure since we observed that, in the case of the KP, 56% of the hybrid hyper-heuristics improved on the average result of MAXPW, which was the best individual heuristic for such instances. In the BPP, we observed a similar result, where 44% of the hybrid hyper-heuristics improved the average result produced by BF. Moreover, we also confirmed an important lesson: combining solvers that work on an individual level might not always result in a better one. In other words, sometimes, it may be better not to combine.
We must mention that our model, as proposed in this document, exhibits a potential limitation that might be related to its incapacity to improve on the traditional rule-based model. This potential limitation is that the rules within the hybrid hyper-heuristics can only fire sequences of a fixed length. This means all the rules within the hyper-heuristic are forced to fire heuristic sequences of the same length.
However, we want to stress the preliminary nature of this work since it is the first attempt to explore combining these two hyper-heuristic approaches into one. For this reason, future research is rich in opportunities. First, we should explore a different process for optimizing hyper-heuristics. In this work, we delegated this task to the genetic algorithm. The genetic algorithm is responsible for evolving the rules’ conditions and their corresponding action. Although this seems sufficient when the sequences are short (less than five heuristics), the task becomes more challenging as the sequences’ length increases. Based on these observations, exploring two independent optimization fronts seems natural: one that focuses on finding the regions of the feature space to be affected (the conditions of the rules) and another that improves the sequences that fire for those regions. Another path worth exploring is to include other features and heuristics and extend our analysis to other relevant KP instances. More importantly, future work must validate our preliminary findings and confirm whether hybridization in hyper-heuristics harms the solving process.
Finally, how much is too much regarding hyper-heuristics? We do not really know yet. Although we cannot answer this to its full extent, we can answer that, at the very least, our proposed approach is already too much. The GA that powers our approach failed to produce rules that improved the results of the individual hyper-heuristic models. The hyper-heuristics produced by the GA tended to decrease the number of rules within the hyper-heuristics as we allowed for longer sequences of heuristics within the actions of the rules. This behavior was solely a consequence of the evolutionary process, as it was not predefined within the GA in any way. Furthermore, we identified some potential drawbacks in our proposal, as the fact that we used sequences of a predefined length and did not allow the hyper-heuristic process to decide on the best length, or that the changes between heuristics may be abrupt, harming the search process.
Overall, we learned an important lesson from this work: combining is not always the solution to our problems. We are used to consulting works that extend our knowledge in hyper-heuristics by presenting models that achieve promising results. This time, we presented a model that, contrary to our expectations, produced poor results when compared with the individual hyper-heuristic models that inspired our proposal. We are aware that the negative result may be due to the flawed design of the hybrid strategy, but we require further experimentation to confirm or refute this idea.
Author Contributions
Conceptualization, J.C.O.-B., A.V.M. and I.A.; Data curation, J.C.O.-B.; Formal analysis, J.C.O.-B., A.V.M. and I.A.; Funding acquisition, I.A.; Investigation, J.C.O.-B., A.V.M. and I.A.; Methodology, J.C.O.-B.; Project administration, J.C.O.-B.; Resources, I.A.; Software, J.C.O.-B.; Supervision, J.C.O.-B. and I.A.; Validation, J.C.O.-B., A.V.M. and I.A.; Visualization, J.C.O.-B.; Writing—original draft, J.C.O.-B.; Writing—review and editing, J.C.O.-B., A.V.M. and I.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The instances used in this work are freely accessible at https://drive.google.com/drive/folders/1BrDdTSpmheUmD8TZSoUcqHnFyvgL2yji?usp=sharing, accessed on 4 August 2025.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Blum, C.; Roli, A. Metaheuristics in combinatorial optimization: Overview and conceptual comparison. ACM Comput. Surv. 2003, 35, 268–308. [Google Scholar] [CrossRef]
- Desale, S.; Rasool, A.; Andhale, S.; Rane, P. Heuristic and Meta-Heuristic Algorithms and Their Relevance to the Real World: A Survey. Int. J. Comput. Eng. Res. Trends 2015, 2, 296–304. [Google Scholar]
- Salhi, S.; Thompson, J. An Overview of Heuristics and Metaheuristics. In The Palgrave Handbook of Operations Research; Salhi, S., Boylan, J., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 353–403. [Google Scholar] [CrossRef]
- Burke, E.K.; Gendreau, M.; Hyde, M.; Kendall, G.; Ochoa, G.; Özcan, E.; Qu, R. Hyper-heuristics: A survey of the state of the art. J. Oper. Res. Soc. 2013, 64, 1695–1724. [Google Scholar] [CrossRef]
- Sánchez, M.; Cruz-Duarte, J.M.; Ortiz-Bayliss, J.c.; Ceballos, H.; Terashima-Marin, H.; Amaya, I. A Systematic Review of Hyper-Heuristics on Combinatorial Optimization Problems. IEEE Access 2020, 8, 128068–128095. [Google Scholar] [CrossRef]
- Burke, E.K.; Hyde, M.R.; Kendall, G.; Ochoa, G.; Özcan, E.; Woodward, J.R. A Classification of Hyper-Heuristic Approaches: Revisited. In Handbook of Metaheuristics; Gendreau, M., Potvin, J.Y., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 453–477. [Google Scholar] [CrossRef]
- Dokeroglu, T.; Kucukyilmaz, T.; Talbi, E.G. Hyper-heuristics: A survey and taxonomy. Comput. Ind. Eng. 2024, 187, 109815. [Google Scholar] [CrossRef]
- Ortiz-Bayliss, J.C.; Juárez, J.; Falcón-Cardona, J.G. Using μ Genetic Algorithms for Hyper-heuristic Development: A Preliminary Study on Bin Packing Problems. In Proceedings of the 2023 10th International Conference on Soft Computing & Machine Intelligence (ISCMI), Mexico City, Mexico, 25–26 November 2023; pp. 54–58. [Google Scholar] [CrossRef]
- Silva-Gálvez, A.; Orozco-Sanchez, J.; Lara-Cárdenas, E.; Ortiz-Bayliss, J.C.; Amaya, I.; Cruz-Duarte, J.M.; Terashima-Marín, H. Discovering Action Regions for Solving the Bin Packing Problem through Hyper-heuristics. In Proceedings of the 2020 IEEE Symposium Series on Computational Intelligence (SSCI), Canberra, ACT, Australia, 1–4 December 2020; pp. 822–828. [Google Scholar] [CrossRef]
- Rodríguez, D.; Cruz-Duarte, J.M.; Ortiz-Bayliss, J.C.; Amaya, I. A Sequence-Based Hyper-Heuristic for Traveling Thieves. Appl. Sci. 2023, 13, 56. [Google Scholar] [CrossRef]
- Sánchez-Díaz, X.F.C.; Ortiz-Bayliss, J.C.; Amaya, I.; Cruz-Duarte, J.M.; Conant-Pablos, S.E.; Terashima-Marín, H. A Preliminary Study on Feature-independent Hyper-heuristics for the 0/1 Knapsack Problem. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Sánchez, M.; Cruz-Duarte, J.M.; Ortiz-Bayliss, J.C.; Amaya, I. Sequence-Based Selection Hyper-Heuristic Model via MAP-Elites. IEEE Access 2021, 9, 116500–116527. [Google Scholar] [CrossRef]
- Vela, A.; Cruz-Duarte, J.M.; Ortiz-Bayliss, J.C.; Amaya, I. Beyond Hyper-Heuristics: A Squared Hyper-Heuristic Model for Solving Job Shop Scheduling Problems. IEEE Access 2022, 10, 43981–44007. [Google Scholar] [CrossRef]
- Vela, A.; Cruz-Duarte, J.M.; Ortiz-Bayliss, J.C.; Amaya, I. Recursive Hyper-Heuristics for the Job Shop Scheduling Problem. In Proceedings of the 2023 IEEE Congress on Evolutionary Computation (CEC), Chicago, IL, USA, 1–5 July 2023; pp. 1–8. [Google Scholar] [CrossRef]
- Assi, M.; Haraty, R.A. A Survey of the Knapsack Problem. In Proceedings of the 2018 International Arab Conference on Information Technology (ACIT), Werdanye, Lebanon, 28–30 November 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Pisinger, D. Where are the hard knapsack problems? Comput. Oper. Res. 2005, 32, 2271–2284. [Google Scholar] [CrossRef]
- Munien, C.; Mahabeer, S.; Dzitiro, E.; Singh, S.; Zungu, S.; Ezugwu, A.E.S. Metaheuristic Approaches for One-Dimensional Bin Packing Problem: A Comparative Performance Study. IEEE Access 2020, 8, 227438–227465. [Google Scholar] [CrossRef]
- Seiden, S.S. On the online bin packing problem. J. ACM 2002, 49, 640–671. [Google Scholar] [CrossRef]
- Burke, E.K.; Hyde, M.R.; Kendall, G.; Ochoa, G.; Ozcan, E.; Woodward, J.R. Exploring Hyper-heuristic Methodologies with Genetic Programming. In Computational Intelligence: Collaboration, Fusion and Emergence; Mumford, C.L., Jain, L.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 177–201. [Google Scholar] [CrossRef]
- Nguyen, S.; Zhang, M.; Johnston, M. A genetic programming based hyper-heuristic approach for combinatorial optimisation. In Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation, New York, NY, USA, 12–16 July 2011; GECCO ’11. pp. 1299–1306. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, N.; Chen, N.; Ma, H.; Chen, G. Genetic Programming Hyper Heuristic with Elitist Mutation for Integrated Order Batching and Picker Routing Problem. IEEE Trans. Evol. Comput. 2025, 29, 346–359. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, G.; Ma, H.; Hartmann, S.; Zhang, M. Enhancing generalization in genetic programming hyper-heuristics through mini-batch sampling strategies for dynamic workflow scheduling. Inf. Sci. 2024, 678, 120975. [Google Scholar] [CrossRef]
- Aziz, Z.A. Ant Colony Hyper-heuristics for Travelling Salesman Problem. Procedia Comput. Sci. 2015, 76, 534–538. [Google Scholar] [CrossRef]
- Ahmed, L.; Mumford, C.; Kheiri, A. Solving urban transit route design problem using selection hyper-heuristics. Eur. J. Oper. Res. 2019, 274, 545–559. [Google Scholar] [CrossRef]
- Mahmud, S.; Abbasi, A.; Chakrabortty, R.K.; Ryan, M.J. A self-adaptive hyper-heuristic based multi-objective optimisation approach for integrated supply chain scheduling problems. Knowl.-Based Syst. 2022, 251, 109190. [Google Scholar] [CrossRef]
- Guo, H.; Liu, J.; Zhuang, C. Automatic design for shop scheduling strategies based on hyper-heuristics: A systematic review. Adv. Eng. Inform. 2022, 54, 101756. [Google Scholar] [CrossRef]
- Kletzander, L.; Musliu, N. Large-State Reinforcement Learning for Hyper-Heuristics. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 12444–12452. [Google Scholar] [CrossRef]
- Ortiz-Bayliss, J.C.; Amaya, I.; Cruz-Duarte, J.M.; Gutierrez-Rodriguez, A.E.; Conant-Pablos, S.E.; Terashima-Marín, H. A General Framework Based on Machine Learning for Algorithm Selection in Constraint Satisfaction Problems. Appl. Sci. 2021, 11, 2749. [Google Scholar] [CrossRef]
- Zárate-Aranda, J.E.; Ortiz-Bayliss, J.C. An Exploratory Study on Machine-Learning-Based Hyper-heuristics for the Knapsack Problem. In Proceedings of the Pattern Recognition; Mezura-Montes, E., Acosta-Mesa, H.G., Carrasco-Ochoa, J.A., Martínez-Trinidad, J.F., Olvera-López, J.A., Eds.; Springer Nature: Cham, Switzerland, 2024; pp. 119–128. [Google Scholar]
- Ortiz-Bayliss, J.C.; Terashima-Marín, H.; Conant-Pablos, S.E. Combine and conquer: An evolutionary hyper-heuristic approach for solving constraint satisfaction problems. Artif. Intell. Rev. 2016, 46, 327–349. [Google Scholar] [CrossRef]
- Ortiz-Bayliss, J.C.; Gárate-Escamilla, A.K.; Terashima-Marín, H. Missing Data and Their Effect on Algorithm Selection for the Bin Packing Problem. In Proceedings of the Pattern Recognition; Mezura-Montes, E., Acosta-Mesa, H.G., Carrasco-Ochoa, J.A., Martínez-Trinidad, J.F., Olvera-López, J.A., Eds.; Springer Nature: Cham, Switzerland, 2024; pp. 34–43. [Google Scholar]
- Zárate-Aranda, J.E.; Ortiz-Bayliss, J.C. Exploring Classificational Cellular Automaton Hyper-heuristics for Solving the Knapsack Problem. In Proceedings of the Advances in Soft Computing; Martínez-Villaseñor, L., Ochoa-Ruiz, G., Eds.; Springer Nature: Cham, Switzerland, 2025; pp. 57–69. [Google Scholar]
- Plata-González, L.F.; Amaya, I.; Ortiz-Bayliss, J.C.; Conant-Pablos, S.E.; Terashima-Marín, H.; Coello-Coello, C.A. Evolutionary-based tailoring of synthetic instances for the Knapsack problem. Soft Comput. 2019, 23, 12711–12728. [Google Scholar] [CrossRef]
- Olivas, F.; Amaya, I.; Ortiz-Bayliss, J.C.; Conant-Pablos, S.E.; Terashima-Marín, H. Enhancing Hyperheuristics for the Knapsack Problem through Fuzzy Logic. Comput. Intell. Neurosci. 2021, 2021, 8834324. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).