An Adaptive Overcurrent Protection Method for Distribution Networks Based on Dynamic Multi-Objective Optimization Algorithm

Abstract

With the large-scale integration of renewable energy into distribution networks, traditional fixed-setting overcurrent protection strategies struggle to adapt to rapid fluctuations in renewable energy (e.g., wind and photovoltaic) output. Optimizing current settings is crucial for enhancing the stability of modern distribution networks. This paper proposes an adaptive overcurrent protection method based on an improved NSGA-II algorithm. By dynamically detecting renewable power fluctuations and generating adaptive solutions, the method enables the online optimization of protection parameters, effectively reducing misoperation rates, shortening operation times, and significantly improving the reliability and resilience of distribution networks. Using the rate of renewable power variation as the core criterion, renewable power changes are categorized into abrupt and gradual scenarios. Depending on the scenario, either a random solution injection strategy (DNSGA-II-A) or a Gaussian mutation strategy (DNSGA-II-B) is dynamically applied to adjust overcurrent protection settings and time delays, ensuring real-time alignment with grid conditions. Hard constraints such as sensitivity, selectivity, and misoperation rate are embedded to guarantee compliance with relay protection standards. Additionally, the convergence of the Pareto front change rate serves as the termination condition, reducing computational redundancy and avoiding local optima. Simulation tests on a 10 kV distribution network integrated with a wind farm validate the effectiveness of the proposed method.

1. Introduction

Renewable energy generation is a critical component of energy strategies, supporting economic growth while promoting clean and low-carbon power sources [1]. Against this backdrop, the integration capacity of distributed generator (DG) continues to increase [2,3]. High-penetration DG integration reduces power losses and provides voltage support during faults [4]. However, as DG capacity grows, traditional current protection faces challenges such as misoperation, failure to operate, loss of selectivity, and reduced sensitivity, failing to meet setting principles. Adaptive three-stage current protection, widely used in 10 kV distribution networks due to its simplicity, low cost, and reliability, requires further improvement under DG integration. Scholars worldwide have conducted extensive research: Reference [5] conducted an evaluation of fault characteristic differences in differential protection for distribution networks containing distributed generators. It revealed that traditional current differential protection may lead to reduced transition resistance when applied to active distribution networks. In response to this conclusion, an adaptive current differential protection method was proposed by adjusting the phase angle constraints based on the proportional relationship of power frequency full current components at both ends of the line. Reference [6] addressed the fault current differences caused by boundary condition variations induced by Inverter-Interfaced Distributed Generator (IIDG) integration. By jointly calculating fault currents in distribution networks without IIDG and bus currents connected to IIDG, this study optimized setting value calculation time and improved computational accuracy. Reference [7] presented a composite sequence network current protection scheme for photovoltaic-integrated distribution networks, effectively expanding local protection coverage. However, its exclusive consideration of single DG integration makes it unsuitable for current multi-DG integration trends. Reference [8] proposed a DG access capacity calculation method considering distribution network current protection constraints, but imposed limitations on maximum DG integration capacity. Reference [9] introduced comprehensive protection improvement methods for multi-DG distribution networks, resolving the low DG permeability issue in traditional current protection. Nevertheless, this setting method fails to adapt to DG capacity variations. Reference [10] incorporated DG transient stability duration as temporal constraints in protection coordination, proposing a novel optimized coordination scheme for inverse-time overcurrent protection characteristics considering DG transient stability. Reference [11] implemented power flow calculation and fault analysis using system-wide synchronous state signals collected by the main station, then transmitted calculated current protection settings to individual protection devices via communication systems. This formed the basis for an adaptive current protection coordination scheme utilizing main station communication. Reference [12] addressed coordination challenges between upper/lower-level inverse-time overcurrent protections after DG integration by segmentally linearizing traditional inverse-time operating characteristics, thereby reducing protection operating time while enhancing selectivity. Reference [13] established multiple setting groups based on short-circuit types and DG capacity, optimizing operating time according to grid-connection status through real-time switching to improve protection sensitivity. Reference [14] improved overcurrent protection setting methods using the Grey Wolf Algorithm, optimizing premature convergence and low precision issues. Through constraints on protection operating time and setting values, inverse-time overcurrent protection was re-coordinated to meet protection requirements. Some teams investigated potential maloperations of distance relays in wind farm grid-connected substations under different operational conditions, proposing an adaptive protection scheme that calculates quadrilateral distance relay settings based on wind power penetration rates [15]. Reference [16] improves the traditional Multi-Objective Artificial Hummingbird Algorithm (MOAHA) by addressing its limitations in initial population diversity, convergence stability, and local optimization capabilities. This enhanced algorithm is applicable to multi-objective optimization in complex engineering fields; however, its effectiveness in scenarios involving new energy grid integration requires further investigation. Reference [17] proposes an improved algorithm, SACLMOGOA, to tackle issues such as poor initial population diversity and ergodicity, slow convergence speed, and susceptibility to local optima in the traditional Multi-Objective Grasshopper Optimization Algorithm (MOGOA). The algorithm demonstrated certain efficacy in the application of the hybrid energy storage system (HESS) for Changsha Metro Line 1. Nevertheless, the case study is limited to the specific HESS configuration of Changsha Metro Line 1, without considering topological variations in different urban rail transit networks, collaborative optimization of multiple energy storage types, or complex power grid scenarios with renewable energy integration. Reference [18] proposes to transform the multi-objective optimization problem into a single-objective one for optimization. By using the weighted sum method to balance the priorities of communication and sensing, it is found that when the target angle is close to the angle of the communication user, the sensing and communication channels share information, and the pilot design can optimize the performance of both simultaneously. This method solves multi-objective problems with a single-objective mindset, which effectively reduces the signal conduction error in communication. However, the sensing model of this method assumes that the angles of the target and clutter are known, and does not involve dynamic angle estimation of multiple targets, thus limiting its applicability in mobile target scenarios. Therefore, its universality warrants further validation. After the integration of new energy sources, power fluctuations will change the direction and magnitude of fault currents, which may cause the originally coordinated upper and lower-level protection devices to lose coordination (e.g., the upper-level protection operates before the lower-level one), thus undermining selectivity and expanding the fault impact range. Relay protection must meet such constraints as sensitivity, selectivity, and false operation rate. Power fluctuations of new energy sources may cause these indicators to deviate from the standard range. By dynamically adjusting the protection settings, it can be ensured that the regulatory requirements are still met under different fluctuation scenarios, avoiding the degradation of protection performance caused by parameter mismatch.

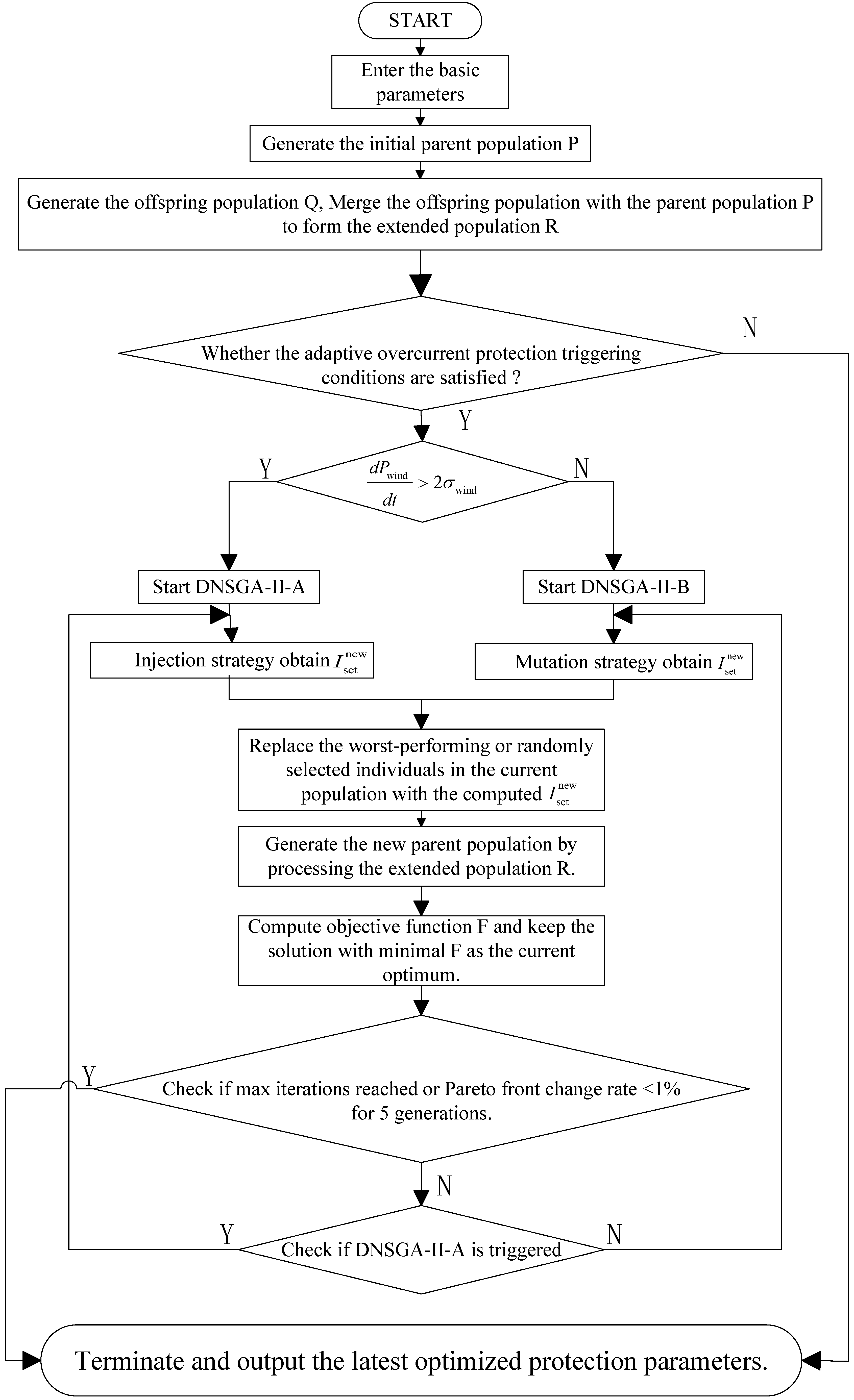
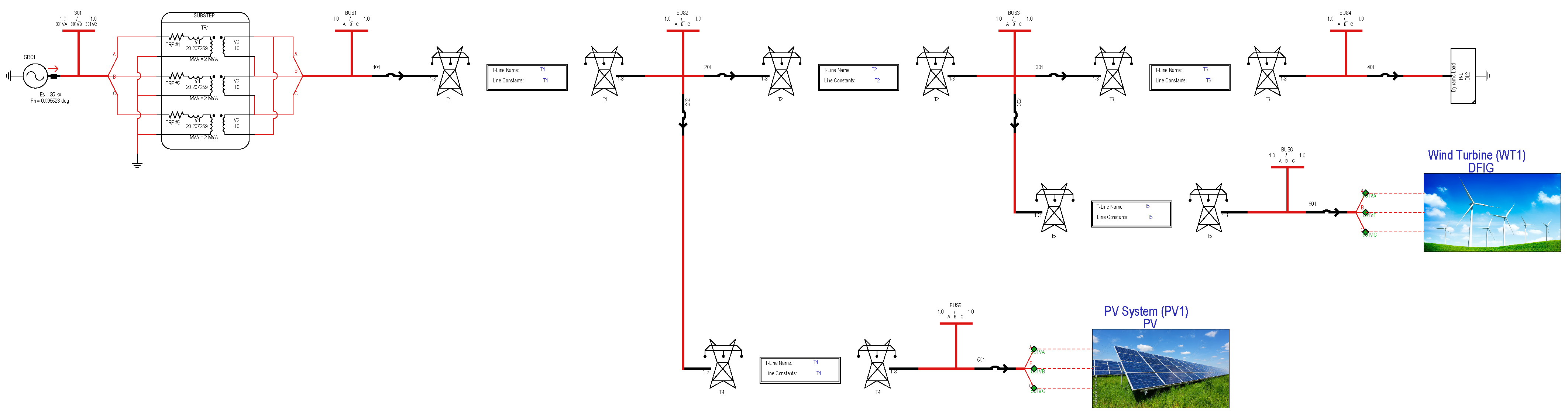
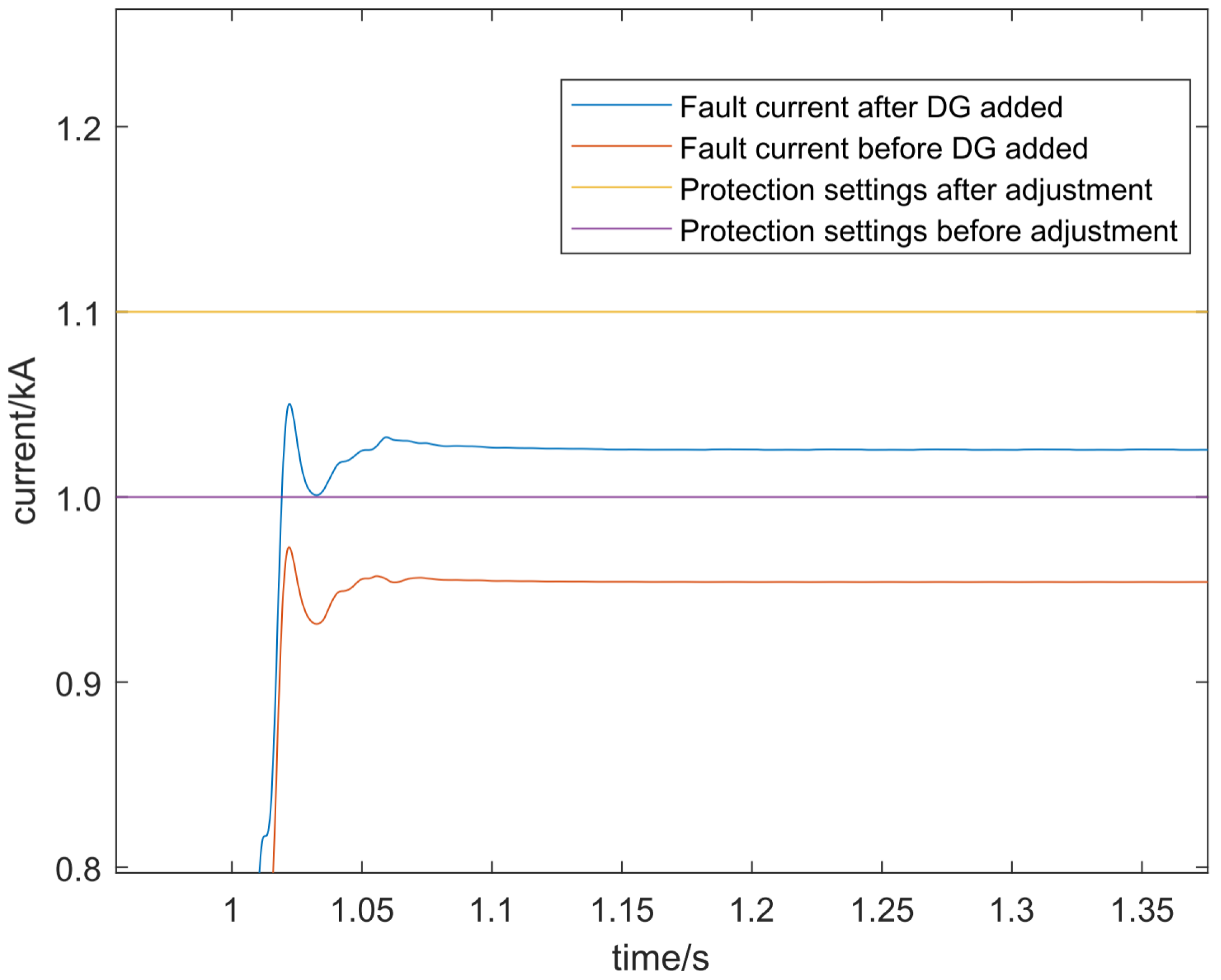
To address the aforementioned issues, this paper proposes a dynamic multi-objective optimization and adaptive overcurrent protection method for distributed networks with renewable energy integration based on an improved NSGA-II (Non-dominated Sorting Genetic Algorithm II) algorithm. This method dynamically detects renewable energy power fluctuations and generates adaptive solutions. Through deep integration of a dynamic triggering mechanism and multi-objective optimization algorithms, it achieves adaptive real-time adjustment of protection settings and online optimization of protection parameters, thereby significantly enhancing the reliability and disturbance resistance capability of the distribution network.

2. Materials and Methods

Practical search and optimization problems in real-world production and daily life often evolve over time, necessitating treatment as online optimization problems. These variations manifest in aspects such as objective functions, constraint functions, or variable boundaries. Ideally, solutions should be promptly derived upon problem variations, with temporal parameters corresponding to the iteration counter of optimization algorithms. The NSGA-II (Non-dominated Sorting Genetic Algorithm II), a representative multi-objective evolutionary algorithm (MOEA), is designed to efficiently solve complex multi-objective optimization problems and identify uniformly distributed Pareto optimal solution sets. The NSGA-II algorithm is developed from the NSGA-I (Non-dominated Sorting Genetic Algorithm I). Proposed by Srinivas and Deb in 1995, NSGA-I is the first generation of multi-objective evolutionary algorithms based on Pareto dominance. Its core idea is to solve multi-objective optimization problems through non-dominated sorting and sharing functions, aiming to generate a uniformly distributed Pareto optimal solution set. Under this algorithm, the population is stratified into multiple non-dominated fronts, where solutions in higher-level fronts obtain higher fitness. Meanwhile, the similarity between solutions is calculated using the sharing radius parameter, and finally, offspring are generated through roulette selection based on fitness. However, this algorithm has three non-negligible drawbacks: high computational complexity, parameter sensitivity, and the absence of an elitism preservation mechanism. To address these flaws of NSGA-I, Kalyanmoy Deb’s team proposed three groundbreaking improvements: fast non-dominated sorting, replacement of the sharing function with crowding distance, and the elitism preservation strategy. These improvements have made NSGA-II a milestone in the field of multi-objective optimization and laid the foundation for dynamic multi-objective optimization.

Table 1. Comparison table of NSGA-I and NSGA-II algorithms.

Characteristics	NSGA-I	NSGA-II	Significance of Improvements
Non-dominated Sorting	Ordinary stratification	Quick sorting	10–100× Faster Computational Efficiency
Diversity Preservation	Sharing function	Crowding distance	Eliminated Parameter Tuning Burden, 40–90% Enhanced Distribution Uniformity
Elitism Strategy	None	Parent-offspring merging and rank selection	Preserved Historical Optimal Solutions, 30%+ Accelerated Convergence Speed
Selection Mechanism	Roulette wheel	Binary tournament	Reduced Selection Bias, Balanced Exploration and Exploitation
Constraint Handling	None	Constraint dominance principle	Direct Support for Engineering Constraints
Computational Resource Requirement	High	Low	Capability to Handle Real-World Problems
Parameter Dependency	Strong	Weak	Strong Robustness, Reduced Debugging Costs

presents a comparison of the algorithm before and after improvement.

Building upon the traditional NSGA-II workflow, this study implements modifications and enhancements to address the dynamic optimization challenges of relay protection setting coordination in distribution networks following renewable energy integration. A testing mechanism is introduced prior to algorithm execution to detect variable changes in each generation, thereby selecting more appropriate execution strategies. In this research, real-time distribution network parameters—including renewable energy output, load power, line impedance, transformer tap ratios, and historical protection settings—are used as inputs to initialize the parent population. Each individual is encoded as a protection parameter vector. The structure is formulated as $[I_{\mathrm{set}1},I_{\mathrm{set}2},t_{\mathrm{delay}},∆t]$; here, $I_{\mathrm{set}1}$ is the Overcurrent Stage I setting, $I_{\mathrm{set}2}$ is the Overcurrent Stage II setting, $t_{\mathrm{delay}}$ is the time delay, and $∆t$ is the time coordination margin. During the testing and decision-making phase, a small number of solutions are randomly selected from the parent population and re-evaluated. If the differences between their objective functions, constraint values, or historical records exceed a threshold, it is determined that significant changes in renewable energy output have occurred. The threshold is defined as ${\theta }_{\mathrm{threshold}}=k·max\left({\sigma }_{\mathrm{wind}},{\sigma }_{\mathrm{pv}}\right)$, where k is adjustment coefficient, and ${\sigma }_{\mathrm{wind}}$ and ${\sigma }_{\mathrm{pv}}$ are the standard deviations of wind power and photovoltaic power outputs, respectively. If the testing mechanism determines that the solution injection strategy (DNSGA-II-A) should be executed, this strategy requires generating uniformly distributed random solutions according to Equation (1) for 20–$70\%$ of the population individuals. These solutions will replace either the worst-performing individuals or randomly selected individuals within the population.

$$I_{\mathrm{set}}^{\mathrm{new}}=I_{\mathrm{set}}^{\mathrm{current}}·U(1-\alpha ,1+\alpha )$$

(1)

where $\alpha =k·{\sigma }_{\mathrm{wind}}$, where U denotes the uniformly distributed random number generation function, and ${\sigma }_{\mathrm{wind}}$ represents the standard deviation of wind power output. If the testing mechanism determines that the Gaussian mutation strategy (DNSGA-II-B) should be executed, this strategy requires performing Gaussian mutation adjustments on the setting values according to Equation (2), which will replace either the individuals with the lowest crowding distance or redundant individuals in the population.

$$I_{\mathrm{set}}^{\mathrm{new}}=I_{\mathrm{set}}^{\mathrm{current}}·\mathcal{N}(1,{\sigma }_{\mathrm{mut}})$$

(2)

where ${\sigma }_{\mathrm{mut}}=\eta ·{\displaystyle \frac{{\sigma }_{\mathrm{pv}}}{\sqrt{n}}}$, $\eta$ is the scaling factor, ${\sigma }_{\mathrm{pv}}$ is the standard deviation of renewable energy output, n is the current iteration count, N denotes the normal-distributed random number generation functions. Subsequently, the merged extended population undergoes non-dominated sorting, crowding distance calculation, and elitist preservation based on the composite objective function F to generate a new parent population. The calculation of F is defined by Equation (3).

$$F=w_1·T_{\mathrm{action}}+w_2·(-S)+w_3·K_{\mathrm{sens}}+w_4·(-R)+w_5·E$$

(3)

where $w_1-w_5$ are the weight coefficients, $T_{\mathrm{action}}$ denotes the operation time, S represents selectivity, $\mathrm{K}\mathrm{sens}$ is the sensitivity coefficient, R signifies reliability, and E corresponds to the misoperation rate. The misoperation rate E is calculated as:

$$E={\displaystyle \frac{|I_{\mathrm{set}}-I_{\mathrm{opt}}|}{I_{\mathrm{opt}}}}$$

(4)

where $I_{\mathrm{opt}}$ denotes the theoretical optimal setting. When the maximum iteration count is reached or the convergence of the Pareto front change rate (defined as the rate of change in the Pareto front remaining below 1% for five consecutive generations) is achieved, the protection parameter set satisfying the constraint conditions is output to the protection devices. The constraints include: sensitivity $K_{\mathrm{sens}}>1.5$, selectivity $t_{\mathrm{upper}}>t_{\mathrm{lower}}+∆t$, misoperation rate $E<1\%$. In terms of computational complexity analysis, the proposed Dynamic Non-dominated Sorting Genetic Algorithm II (DNSGA-II) introduces a scenario-adaptive mechanism based on the conventional NSGA-II framework. The computational complexity of the traditional NSGA-II algorithm is given by:

$$\mathcal{O}(M{N}^2+N^3)$$

(5)

where M represents the number of objective functions (in this study, M = 5: operation time, selectivity, sensitivity coefficient, reliability, and maloperation rate); and N denotes the population size (typically ranging from 100 to 200). In the enhanced multi-objective optimization algorithm, the dynamic mechanism introduces additional computational complexity. Specifically, it requires re-evaluation of 10% of the population individuals per generation, contributing the following complexity term:

$$\mathcal{O}(0.1N·C_f)$$

(6)

where $C_f$ represents the cost of a single objective function calculation (power flow calculation for distribution networks takes approximately 0.1–1 ms per time). In addition, different execution schemes will increase different computational complexities. For the DNSGA-II-A scheme, replacing 50% of the individuals requires uniform distribution sampling, and the computational complexity is:

$$\mathcal{O}(0.5N·D)$$

(7)

where D represents the dimension of decision variables (D = 4 in this study: $I_{set1},I_{set2},t_{delay},∆t$). For the DNSGA-II-B scheme, which is a mutation operation based on the normal distribution, the computational complexity is:

$$\mathcal{O}(N·D·logD)$$

(8)

Synthesizingthe above steps, the complexity per generation in the worst-case scenario (frequent triggering of DNSGA-II-A) is:

$${\mathcal{O}}_{\mathrm{proposed}}=\mathcal{O}(M{N}^2+N^3+0.1N·C_f+0.5N·D)$$

(9)

Under typical parameters ($N=100,M=5,D=4,C_f\approx 100\mathrm{FLOPs}$), it is calculated that the computational complexity of the traditional NSGA-II algorithm is approximately $5\times {10}^4$ FLOPs per generation, while that of the improved algorithm in this paper is about $5.2\times {10}^4$ FLOPs per generation, with an increase of approximately 4% in computational complexity.

Based on the aforementioned improvements to the NSGA-II algorithm, the workflow of the adaptive overcurrent protection method proposed in this study is illustrated in Figure 1. (1) Initialize the population by inputting fundamental parameters from the distribution network, including: real-time renewable power outputs $P_{wind}\left(t\right)$, $P_{pv}\left(t\right)$, load power $P_{load}\left(t\right)$, renewable power fluctuation rates ${\sigma }_{\mathrm{wind}}$, line impedance $Z_{line}$, transformer tap ratio k, and historical protection settings (Overcurrent Stage I setting $I_{set1}$ and Stage II setting $I_{set2}$); (2) Generate the initial parent population P, where each individual is encoded as a protection parameter vector: $[I_{\mathrm{set}1},I_{\mathrm{set}2},t_{\mathrm{delay}},∆t]$, with $t_{\mathrm{delay}}$ denoting the time delay and $∆t$ the time coordination margin. Each encoded individual represents a candidate solution. Following the standard NSGA-II workflow (crossover, mutation), crossover operations are applied to selected parent individuals to produce the offspring population Q. Offspring individuals undergo perturbation, and the parent population P is merged with the offspring population Q to form the extended population R. (3) Determine whether the adaptive overcurrent protection setting optimization triggering conditions are satisfied by detecting if renewable energy power or load fluctuation amplitudes exceed predefined thresholds, which initiates the optimization process. Specifically, at the start of each generation iteration, $10\%$ of parent individuals are randomly selected for re-evaluation of their objective functions and constraint values. If any individual’s objective or constraint deviation from historical records exceeds the threshold, significant renewable energy output variation is confirmed: $max({\displaystyle \frac{d{P}_{\mathrm{wind}}}{dt}},{\displaystyle \frac{d{P}_{\mathrm{pv}}}{dt}},{\displaystyle \frac{d{P}_{\mathrm{load}}}{dt}})>{\theta }_{\mathrm{threshold}}$, where ${\theta }_{threshold}$ is the preset rate-of-change threshold correlated with renewable output standard deviations: ${\theta }_{\mathrm{threshold}}=k·max({\sigma }_{\mathrm{wind}},{\sigma }_{\mathrm{pv}})$; (4) Based on renewable energy output state variations, evaluate the applicability of two strategies within the proposed adaptive overcurrent protection method: DNSGA-II-A (random solution injection strategy) and DNSGA-II-B (mutated solution strategy). A rapid state transition is defined by ${\displaystyle \frac{d{P}_{\mathrm{wind}}}{dt}}>2{\sigma }_{\mathrm{wind}}$. If renewable power fluctuates drastically or grid topology changes rapidly, apply DNSGA-II-A; if renewable states evolve gradually, apply DNSGA-II-B.

(5) Perform non-dominated sorting, crowding distance calculation, and elitist preservation on the extended population R to generate the new parent population. A composite objective function F is proposed to quantify multiple conflicting optimization objectives into a comparable metric. The optimization objectives for this distribution network overcurrent protection are defined as follows: minimizing the operation time $T_{\mathrm{action}}$, maximizing selectivity S, minimizing the sensitivity coefficient $K_{\mathrm{sens}}$, and minimizing the misoperation rate E. Compute F and select the individual with the smallest F value as the current optimal solution. (6) Terminate iterations if the maximum iteration count (set to 100 generations) is reached or the Pareto front change rate remains below $1\%$ for 5 consecutive generations. Validate optimized protection parameters against constraints: sensitivity $K_{\mathrm{sens}}>1.5$, selectivity $t_{\mathrm{upper}}>t_{\mathrm{lower}}+∆t$, and misoperation rate $E<1\%$. Output qualified parameters (overcurrent protection thresholds $\mathrm{Iset}$, time delay $t_{\mathrm{delay}}$) to protection devices to ensure real-time adaptation to short-circuit current variations caused by renewable fluctuations, thereby enhancing protection reliability, selectivity, and speed.

3. Results

To validate the practical application effectiveness of the improved adaptive overcurrent protection method in real-world distribution networks, a 10 kV typical distribution network with a wind farm integration scenario (as shown in Figure 2) is constructed using RSCAD software for simulation-based verification of the proposed method.

In Figure 2, 101, 201, 202, 301, 302, 401, 501, and 601 denote the protection installation locations at the head of each line. By setting different wind power output variations, a simulation model as shown in Figure 3 was built in RSCAD software to verify the optimization of output parameters of DNSGA-II-A (random solution injection strategy) and DNSGA-II-B (mutation solution strategy) in response to sudden wind power changes.

3.1. Validation of DNSGA-II-A (Random Solution Injection Strategy)

The scenario is configured as a 10 kV distribution network integrated with a wind farm subjected to abrupt wind power surges, with initial parameters set as shown in

Table 2. Initial parameter setting in a sudden wind surge scenario.

Parameters	Value
Voltage level (kV)	10
Wind Power Change Rate (MW/s)	0.4
Volatility (standard deviation)	0.4
Initial protection setpoint 1 (kA)	1.0
Initial protection setpoint 2 (kA)	0.8
Adjustment coefficient	0.5
replacement ratio	50%

: a sudden wind speed increase causes wind power output $P_{\mathrm{wind}}$ to rise from 1 MW to 3 MW within 5 s, with a fluctuation rate ${\sigma }_{\mathrm{wind}}=0.4$ (standard deviation). An individual in the initial population is configured with $I_{set1}=1.0\mathrm{kA},·I_{set2}=0.8\mathrm{kA}$, adjustment coefficient k = 0.5, and a replacement ratio of $50\%$. (Here, Protection 1 refers to the protection device 202 in Figure 2, and Protection 2 refers to the protection device 302 in Figure 2).

According to the DNSGA-II-A (random solution injection strategy) algorithm process, generate random solutions by calculating the perturbation range $\alpha =k·{\sigma }_{\mathrm{wind}}=0.5\times 0.4=0.2$, defined as $U(1-0.2,1+0.2)=U(0.8,1.2)$. Generate new settings $I_{\mathrm{set}}^{\mathrm{new}}$ assuming a uniformly distributed random number $U(0.8,1.2)=1.1$, then $l_{\mathrm{set}1}^{\mathrm{new}}=1.0\mathrm{kA}\times 1.1=1.1\mathrm{kA}$, $I_{\mathrm{set}2}^{\mathrm{new}}=0.8\mathrm{kA}\times 1.1=0.88\mathrm{kA}$. Replace the worst individual (with the largest F value) in the current population with the new solution. The final optimized parameters are: $I_{\mathrm{set}1}=1.1\mathrm{kA},I_{\mathrm{set}2}=0.88\mathrm{kA},t_{\mathrm{delay}}=0.2\mathrm{s},∆t=0.25\mathrm{s}$. The comparison of parameters before and after optimization is shown in

Table 3. Algorithm optimization results in wind surge scenario.

Objective	Original Value	Optimized Values	Adjustment Ratio
Protection Setting $I_{\mathrm{set}1}$	1.0	1.1	+10%
Protection Setting $I_{\mathrm{set}2}$	0.8	0.88	+10%

.

To ensure the selectivity of the protection devices’ operation, it is necessary to verify the protection operation setting values of the optimized protection devices 202 and 302. If the upper and lower level protection devices cannot effectively coordinate with the optimized protection settings, it is also required to perform optimization calculations on the protection devices of the upper and lower level lines.

Table 4. Operating values of protection devices before and after optimization under sudden new energy power change scenarios.

Objective	Original Value	Optimized Values
$I_{\mathrm{set}101}$	1.3	1.3
$I_{\mathrm{set}202}$	1.0	1.1
$I_{\mathrm{set}201}$	1.2	1.2
$I_{\mathrm{set}302}$	0.8	0.88
$I_{\mathrm{set}301}$	0.9	0.9
$I_{\mathrm{set}401}$	0.6	0.6

presents a comparison of the protection settings of protection devices 101, 202, 201, 302, 301, and 401 before and after this optimization under the scenario of sudden changes in new energy power.

It can be concluded from Table 4 that after the optimization calculation of protection devices 202 and 302, the selective coordination relationship between the protection devices of the upper and lower level lines can still be satisfied, and there is no need to further perform optimization calculations on the protection devices of the upper and lower level lines.

The waveform data diagram of the fault current obtained through simulation is shown in Figure 4. The diagram respectively illustrates the magnitude of the fault current flowing through Protection 1 before and after the fault, as well as the setting values of Protection 1’s fixed values before and after adjustment. From the simulation waveform diagram, it can be obtained that due to the integration of photovoltaic power sources, the fault current flowing through Protection 1 rises above the original protection setting value. At this time, if the fault current value exceeds the protection setting value, Protection 1 will malfunction. In contrast to the original protection setting value, the optimized setting value is increased by 10%, which effectively avoids the malfunction caused by the sudden increase in wind power output leading to the short-circuit current exceeding the original setting value.

3.2. Validation of DNSGA-II-B (Mutated Solution Strategy)

The scenario is configured as a 10 kV distribution network integrated with a wind farm subjected to gradual wind power variations, with initial parameters set as shown in

Table 5. Initial parameter settings in a gradual changing wind scenario.

Parameters	Value
Voltage level (kV)	10
Wind Power Change Rate (MW/s)	0.1
Volatility (standard deviation)	0.1
Initial protection setpoint 1 (kA)	1.0
Initial protection setpoint 2 (kA)	0.8
Scaling factor	0.1
Iteration count	10

: wind power rate of change ${\displaystyle \frac{d{P}_{\mathrm{wind}}}{dt}}=0.1\mathrm{MW}/\mathrm{s}$, fluctuation rate ${\sigma }_{\mathrm{wind}}=0.1$, iteration count t = 10; an individual in the initial population is configured with $I_{set1}=1.0\mathrm{kA},·I_{set2}=0.8\mathrm{kA}$, and scaling factor $\eta =0.1$. (Here, Protection 1 refers to the protection device 202 in Figure 2, and Protection 2 refers to the protection device 302 in Figure 2).

Apply DNSGA-II-B (mutated solution strategy) to perform Gaussian mutation for addressing gradual wind power variations. Calculate the mutation strength ${\sigma }_{\mathrm{mut}}=\eta ·{\displaystyle \frac{{\sigma }_{\mathrm{pv}}}{\sqrt{t}}}=0.1\times {\displaystyle \frac{0.1}{\sqrt{10}}}\approx 0.0032$. Generate new settings $I_{set}^{\mathrm{new}}$; assuming a normally distributed random number $N(1,0.0032)=1.005$, then $I_{\mathrm{set}1}^{\mathrm{new}}=1.0\mathrm{kA}\times 1.005=1.005\mathrm{kA}$, $I_{\mathrm{set}2}^{\mathrm{new}}=0.8\mathrm{kA}\times 1.005=0.804\mathrm{kA}$. Replace the individual with the lowest crowding distance (indicating dense neighboring solutions and high redundancy) in the current population with the new solution. After optimization, the output parameters are $I_{\mathrm{set}1}=1.005\mathrm{kA},I_{\mathrm{set}2}=0.804\mathrm{kA},t_{\mathrm{delay}}=0.18\mathrm{s},∆t=0.22\mathrm{s}$. The comparison of parameters before and after optimization is shown in

Table 6. Algorithm optimization results in wind surge scenario.

Objective	Original Value	Optimized Values	Adjustment Ratio
Protection Setting $I_{\mathrm{set}1}$	1.0	1.005	+0.5%
Protection Setting $I_{\mathrm{set}2}$	0.8	0.804	+0.5%

.

To ensure the selectivity of the protection devices’ operation, it is necessary to verify the protection operation setting values of the optimized protection devices 202 and 302. If the upper and lower level protection devices cannot effectively coordinate with the optimized protection settings, it is also required to perform optimization calculations on the protection devices of the upper and lower level lines.

Table 7. Operating values of protection devices before and after optimization under gradual new energy power change scenarios.

Objective	Original Value	Optimized Values
$I_{\mathrm{set}101}$	1.3	1.3
$I_{\mathrm{set}202}$	1.0	1.005
$I_{\mathrm{set}201}$	1.2	1.2
$I_{\mathrm{set}302}$	0.8	0.804
$I_{\mathrm{set}301}$	0.9	0.9
$I_{\mathrm{set}401}$	0.6	0.6

presents a comparison of the protection settings of protection devices 101, 202, 201, 302, 301, and 401 before and after this optimization under the scenario of sudden changes in new energy power.

It can be concluded from Table 7 that after the optimization calculation of protection devices 202 and 302, the selective coordination relationship between the protection devices of the upper and lower level lines can still be satisfied, and there is no need to further perform optimization calculations on the protection devices of the upper and lower level lines.

The waveform data diagram of the fault current obtained through simulation is shown in Figure 5. The diagram depicts the magnitude of the fault current flowing through Protection 1 before and after the fault, as well as the setting values of Protection 1’s threshold before and after optimization and adjustment, respectively.

From the simulation waveform diagram, it can be observed that, similar to the abrupt change scenario, the integration of photovoltaic power sources causes the fault current flowing through Protection 1 to rise above the original protection threshold. When the fault current exceeds this threshold, Protection 1 will malfunction. In contrast to the original protection threshold, the optimized threshold is fine-tuned by 0.5.

The computational examples above demonstrate that DNSGA-II-A employs uniformly distributed random perturbations to broaden the search space and rapidly adapt to severe fluctuations, preventing misoperation, while DNSGA-II-B utilizes Gaussian mutation to refine settings precisely, balancing protection performance and stability. The synergistic interplay between these two strategies ensures that renewable-integrated distribution networks achieve dynamic optimization across varying fluctuation intensities, significantly enhancing the robustness of the protection system.

4. Discussion

In the sudden wind surge scenario, compared to the original protection settings, the optimized settings are increased by 10%, effectively preventing misoperation caused by short-circuit currents exceeding the original thresholds due to sudden wind power surges. In the gradual changing wind scenario, compared to the original protection settings, the optimized settings exhibit a 0.5% adjustment, tailored to gradual variation scenarios, thereby minimizing disruption to the original protection logic. The computational examples above demonstrate that DNSGA-II-A employs uniformly distributed random perturbations to broaden the search space and rapidly adapt to severe fluctuations, preventing misoperation, while DNSGA-II-B utilizes Gaussian mutation to refine settings precisely, balancing protection performance and stability. The synergistic interplay between these two strategies ensures that renewable-integrated distribution networks achieve dynamic optimization across varying fluctuation intensities, significantly enhancing the robustness of the protection system.

5. Conclusions

This paper proposes an adaptive overcurrent protection method for distribution networks based on a dynamic multi-objective optimization algorithm. By using real-time monitoring of wind power, photovoltaic power fluctuations, and load changes, the method dynamically triggers an improved NSGA-II optimization algorithm to perform online optimization of overcurrent protection settings and time parameters. A composite objective function is introduced to integrate multi-objective conflicts such as operation time, selectivity, sensitivity coefficient, and misoperation rate, combined with hard constraints on sensitivity and misoperation rate to ensure compliance with relay protection regulations. For scenarios with intense renewable energy fluctuations, DNSGA-II-A rapidly expands the search range through uniformly distributed random perturbations; for gradual variation scenarios, DNSGA-II-B employs adaptive Gaussian mutation for precise parameter tuning. The research results effectively address the issues of misoperation and failure-to-operate in traditional fixed-setting protection systems under dynamic renewable energy integration. The optimized protection system reduces misoperation rates, shortens operation times, and significantly enhances the reliability and disturbance resistance of distribution networks. Future work will explore optimization scenarios with higher-capacity renewable energy integration and conduct further research on more practical conditions. Currently, our researchers have only applied the optimization algorithm to radial power network topologies. The applicability of this algorithm to meshed (ring-shaped) distribution networks has not yet been investigated. As a next step, our team will conduct research on the adaptability of this algorithm in meshed distribution networks.