Engine Optimization Model for Accurate Prediction of Friction Model in Marine Dual-Fuel Engine
Abstract
1. Introduction
2. Engine Specifications
3. Engine Optimization Model
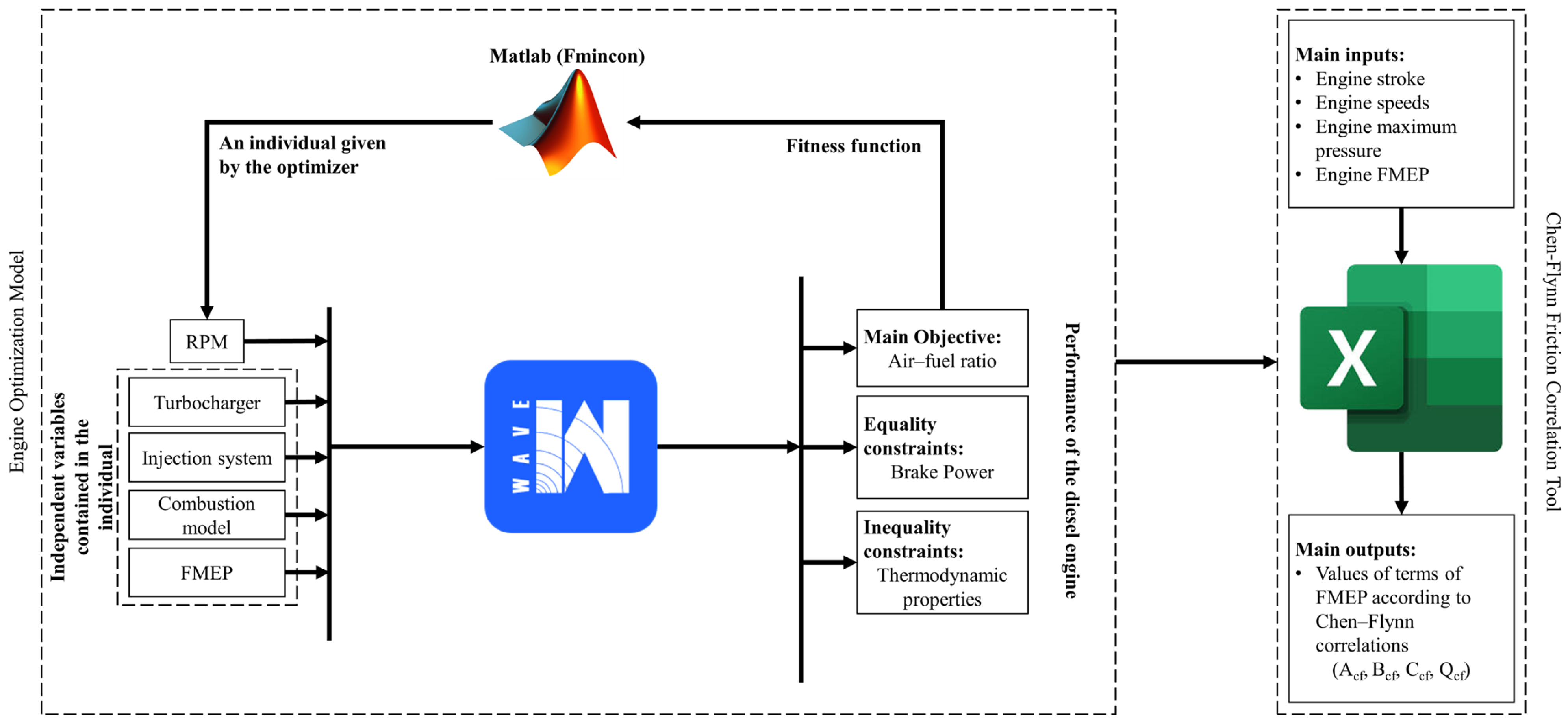
3.1. Overview of the Numerical Engine Model
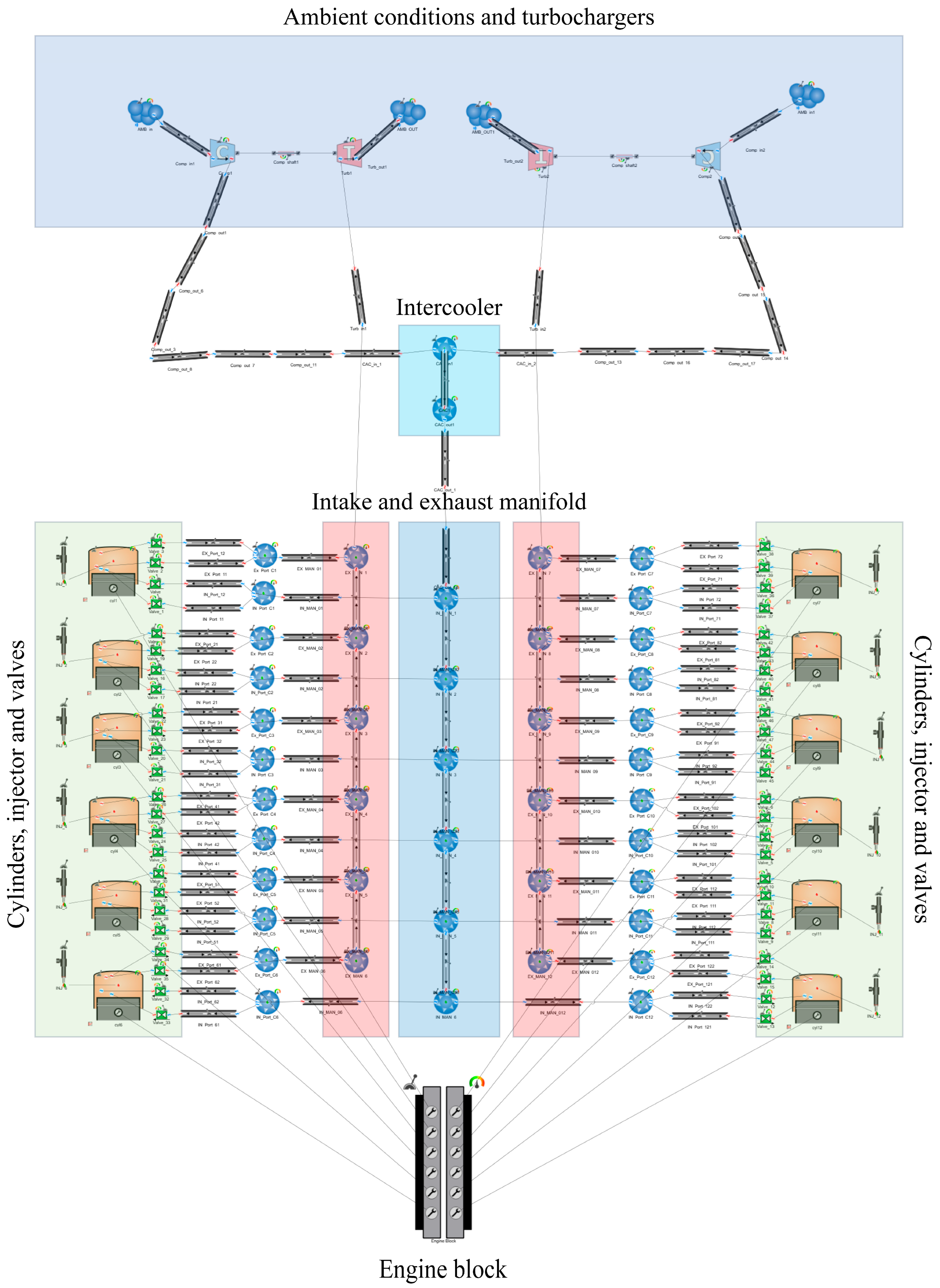
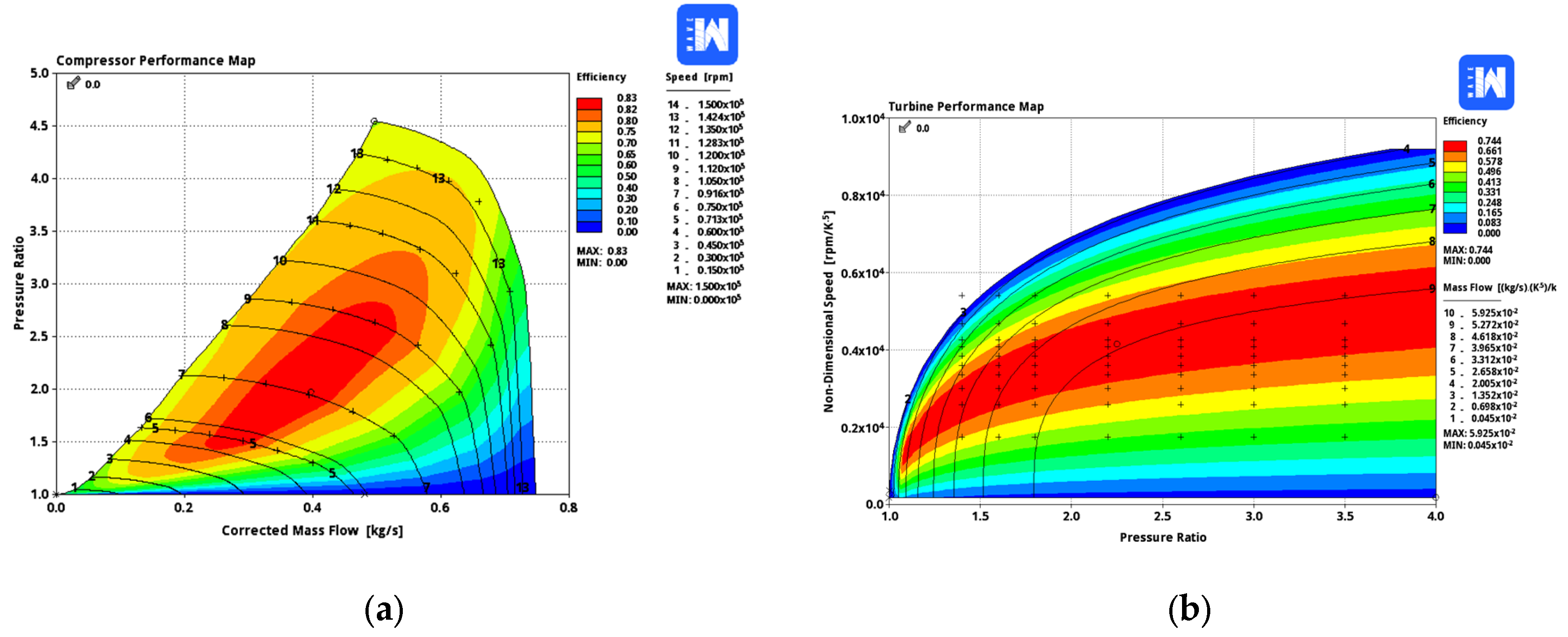
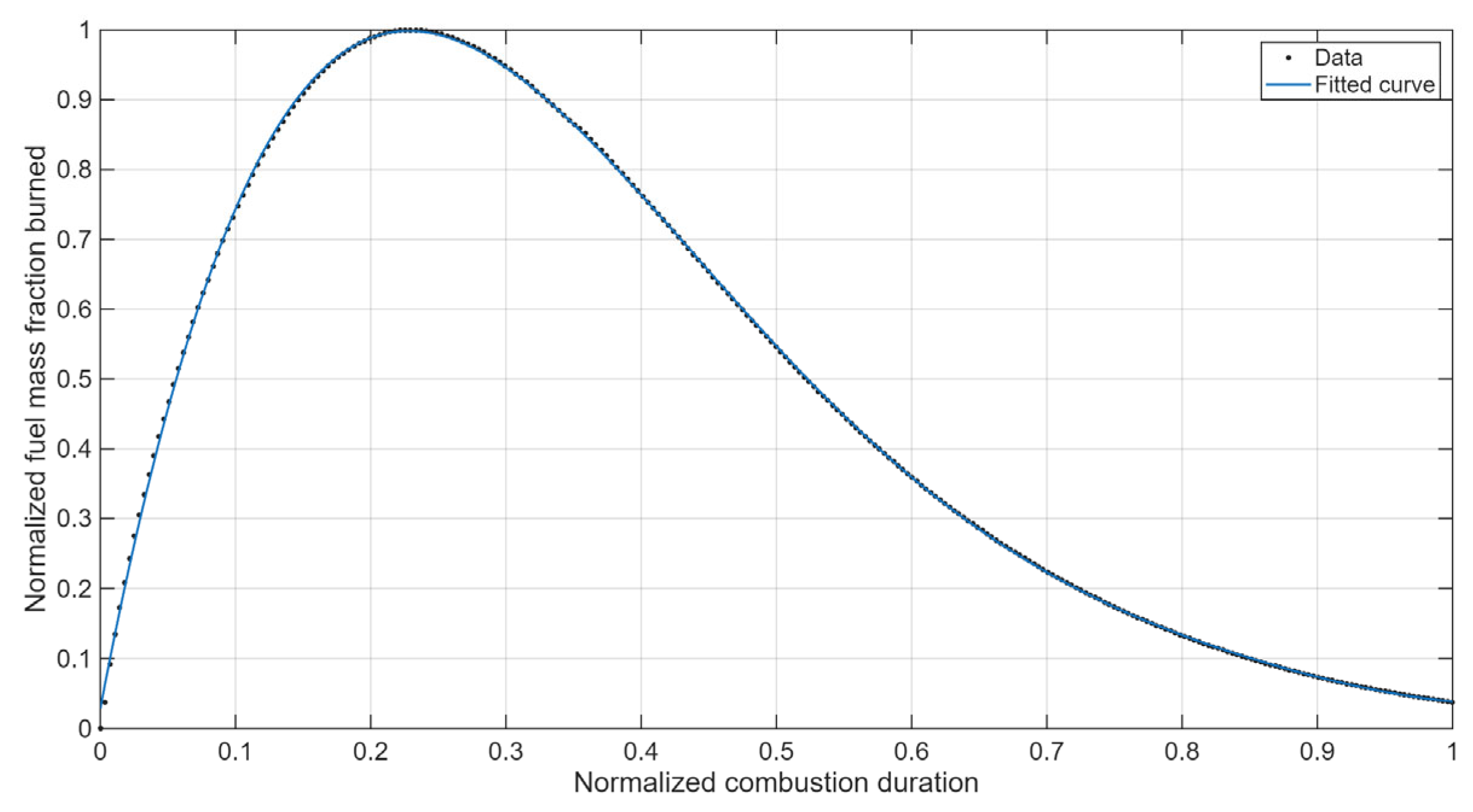
3.2. Description of WAVE Model
3.3. Nonlinear Optimizer
4. Results and Discussions
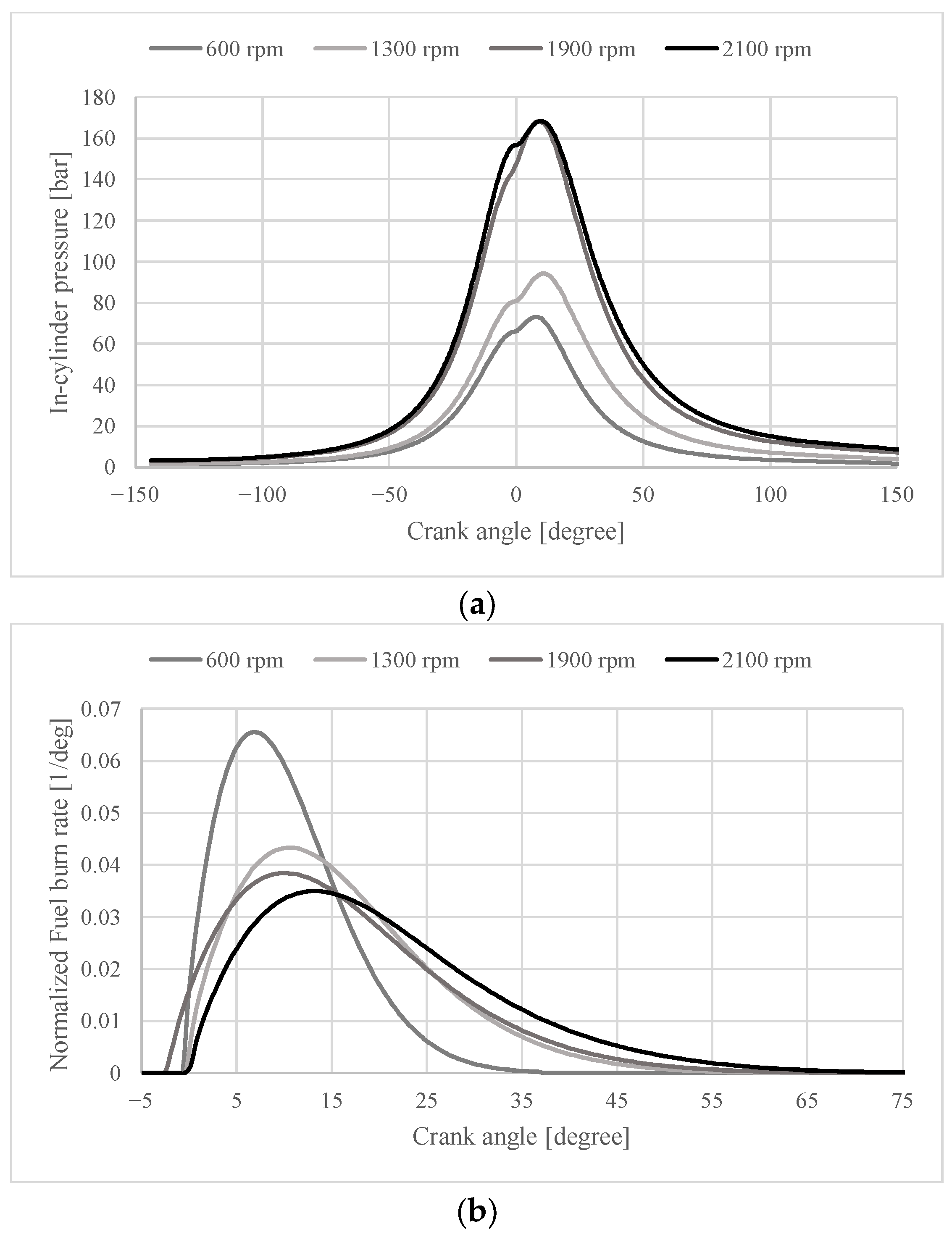
4.1. Simulation of Marine Diesel Engine
4.2. Computation of the Terms of the Friction Model
5. Conclusions and Further Research
- The engine model facilitates maximizing the AFR by optimizing the turbocharger performance, injection system parameters, combustion characteristics, and the FMEP. This results in values of up to 68.89 at low-load operation, while maintaining combustion stability (R2 ≥ 0.9998).
- The engine optimization model demonstrates excellent capability in meeting all predefined constraints, ensuring reliability and applicability under varying conditions.
- The numerical model is computationally efficient and compatible with standard computer systems, offering fast simulation times while maintaining high accuracy in calculated results. It helps to match real engine performance with an error of less than 0.05% in brake power and BSFC, confirming both accuracy and efficiency.
- The developed approach supports the precise determination of the Chen–Flynn correlation coefficients, enhancing the accuracy of engine performance predictions across the load diagram.
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| 0D | Zero-dimensional |
| 1D | One-dimensional |
| 3D | Three-dimensional |
| A, b | Linear inequality constraints |
| Acf, | Constant term |
| Aeq, beq | Linear equality constraints |
| AFR | Air–fuel ratio |
| API | Application Programming Interfaces |
| Aw | Area of cylinder walls |
| Bcf | Load-dependent term |
| BMEP | Brake mean effective pressure |
| BRPM | Reference speed |
| BSFC | Brake-specific fuel consumption |
| c | Inequality constraints |
| Ccf | Hydrodynamic friction term |
| cd3 | Burn duration coefficients for the diffusion burn curves |
| ceq | Equality constraints |
| CFD | Computational fluid dynamics |
| ct3 | Burn duration coefficients for the tail burn curves |
| CV | Calorific value |
| df | Mass fractions of the diffusion burn curves |
| dQ | Total heat added |
| dQw | Heat exchange |
| ECU | Engine control unit |
| EGR | Exhaust gas recirculation |
| EIVC | Early Intake Valve Closure |
| f(x) | Optimization model objective |
| FMEP | Friction mean effective pressure |
| FR | Fuel rate |
| g, h | Penalty functions |
| GA | Genetic algorithm |
| h | Heat transfer coefficient |
| H2 | Hydrogen |
| HFO | Heavy fuel oil |
| HRR | Heat release rate |
| IMEP | Indicated mean effective pressure |
| IMO | International Maritime Organization |
| INJDur | Injection duration |
| lb | Lower bounds |
| ṁa | Air mass flow rate |
| LCA | Life-cycle assessment |
| MARPOL | International Convention for the Prevention of Pollution from Ships |
| MDO | Marine diesel oil |
| mfuel | Amount of injected fuel |
| ncyl | Number of cylinders |
| NG | Natural gas |
| NN | Neural network |
| NO | Nitric oxide |
| NOx | Nitrogen oxides |
| NSGA II | Non-dominated Sorting Genetic Algorithm |
| PB | Brake power |
| Pf | Mass fractions of the premix burn curves |
| Pmax | Maximum cylinder pressure |
| Qcf | Windage loss term |
| Qcomb | Heat released from fuel combustion |
| R | Constant |
| R2 | Coefficient of determination |
| RPM | Engine speed |
| S | Mean piston speed |
| SOI | Start of injection |
| TA | Turbo-assisted |
| TAfterCylinder | Exhaust temperature after cylinder |
| TDC | Top dead center |
| tf | Mass fractions of the tail burn curves |
| Tg | Burn gas temperature |
| Tmax | Maximum average temperature inside the cylinder |
| TS | Turbocharger speed |
| Tw | Cylinder wall temperature |
| ub | Upper bounds |
| VGTs | Variable Geometry Turbines |
| x | Optimization variables |
| xb | Burned mass fraction |
| ηm | Mechanical efficiency |
| θ | Crank angle |
| θo | Start angle of combustion |
| τ | Burn duration |
| ω | Engine speed |
References
- Tadros, M.; Ventura, M.; Guedes Soares, C. Review of the IMO Initiatives for Ship Energy Efficiency and Their Implications. J. Mar. Sci. Appl. 2023, 22, 662–680. [Google Scholar] [CrossRef]
- Theotokatos, G.; Stoumpos, S.; Bolbot, V.; Boulougouris, E. Simulation-based investigation of a marine dual-fuel engine. J. Mar. Eng. Technol. 2020, 19, 5–16. [Google Scholar] [CrossRef]
- IMO. EEXI and CII-Ship Carbon Intensity and Rating System. Available online: https://www.imo.org/en/MediaCentre/HotTopics/Pages/EEXI-CII-FAQ.aspx (accessed on 10 November 2022).
- Karatuğ, Ç.; Ejder, E.; Tadros, M.; Arslanoğlu, Y. Environmental and Economic Evaluation of Dual-Fuel Engine Investment of a Container Ship. J. Mar. Sci. Appl. 2023, 22, 823–836. [Google Scholar] [CrossRef]
- Tauzia, X.; Maiboom, A.; Karaky, H.; Chesse, P. Experimental analysis of the influence of coolant and oil temperature on combustion and emissions in an automotive diesel engine. Int. J. Engine Res. 2019, 20, 247–260. [Google Scholar] [CrossRef]
- Jia, B.; Mikalsen, R.; Smallbone, A.; Roskilly, A.P. A study and comparison of frictional losses in free-piston engine and crankshaft engines. Appl. Therm. Eng. 2018, 140, 217–224. [Google Scholar] [CrossRef]
- Karatuğ, Ç.; Ceylan, B.O.; Arslanoğlu, Y. A hybrid predictive maintenance approach for ship machinery systems: A case of main engine bearings. J. Mar. Eng. Technol. 2025, 24, 12–21. [Google Scholar] [CrossRef]
- Heywood, J.B. Internal Combustion Engine Fundamentals; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Tadros, M.; Ventura, M.; Guedes Soares, C. Review of current regulations, available technologies, and future trends in the green shipping industry. Ocean. Eng. 2023, 280, 114670. [Google Scholar] [CrossRef]
- Huang, Y.; Surawski, N.C.; Zhuang, Y.; Zhou, J.L.; Hong, G. Dual injection: An effective and efficient technology to use renewable fuels in spark ignition engines. Renew. Sustain. Energy Rev. 2021, 143, 110921. [Google Scholar] [CrossRef]
- Sander, D.E.; Knauder, C.; Allmaier, H.; Damjanović-Le Baleur, S.; Mallet, P. Friction Reduction Tested for a Downsized Diesel Engine with Low-Viscosity Lubricants Including a Novel Polyalkylene Glycol. Lubricants 2017, 5, 9. [Google Scholar] [CrossRef]
- Feneley, A.J.; Pesiridis, A.; Andwari, A.M. Variable Geometry Turbocharger Technologies for Exhaust Energy Recovery and Boosting-A Review. Renew. Sustain. Energy Rev. 2017, 71, 959–975. [Google Scholar] [CrossRef]
- Cong, Y.; Gan, H.; Wang, H. Parameter investigation of the pilot fuel post-injection strategy on performance and emissions characteristics of a large marine two-stroke natural gas-diesel dual-fuel engine. Fuel 2022, 323, 124404. [Google Scholar] [CrossRef]
- Xiang, L.; Theotokatos, G.; Ding, Y. Parametric investigation on the performance-emissions trade-off and knocking occurrence of dual fuel engines using CFD. Fuel 2023, 340, 127535. [Google Scholar] [CrossRef]
- Bejger, A.; Chybowski, L.; Gawdzińska, K. Utilising elastic waves of acoustic emission to assess the condition of spray nozzles in a marine diesel engine. J. Mar. Eng. Technol. 2018, 17, 153–159. [Google Scholar] [CrossRef]
- Tadros, M.; Ventura, M.; Guedes Soares, C. Optimization procedure to minimize fuel consumption of a four-stroke marine turbocharged diesel engine. Energy 2019, 168, 897–908. [Google Scholar] [CrossRef]
- Wei, S.; Wu, C.; Yan, S.; Ding, T.; Chen, J. Miller Cycle with Early Intake Valve Closing in Marine Medium-Speed Diesel Engines. J. Mar. Sci. Appl. 2022, 21, 151–160. [Google Scholar] [CrossRef]
- Kim, J.; Vallinmaki, M.; Tuominen, T.; Mikulski, M. Variable valve actuation for efficient exhaust thermal management in an off-road diesel engine. Appl. Therm. Eng. 2024, 246, 122940. [Google Scholar] [CrossRef]
- Güler, M.; Özkan, M. Energy balance analysis of a DI diesel engine with multiple pilot injections strategy and optimization of brake thermal efficiency. Appl. Therm. Eng. 2022, 204, 117972. [Google Scholar] [CrossRef]
- Singh, D.; Gu, F.; Fieldhouse, J.D.; Singh, N.; Singal, S.K. Prediction and Analysis of Engine Friction Power of a Diesel Engine Influenced by Engine Speed, Load, and Lubricant Viscosity. Adv. Tribol. 2014, 2014, 928015. [Google Scholar] [CrossRef]
- Allmaier, H.; Knauder, C.; Salhofer, S.; Reich, F.; Schalk, E.; Ofner, H.; Wagner, A. An experimental study of the load and heat influence from combustion on engine friction. Int. J. Engine Res. 2016, 17, 347–353. [Google Scholar] [CrossRef]
- Spencer, A.; Avan, E.Y.; Almqvist, A.; Dwyer-Joyce, R.S.; Larsson, R. An experimental and numerical investigation of frictional losses and film thickness for four cylinder liner variants for a heavy duty diesel engine. Proc. Inst. Mech. Eng. Part J. 2013, 227, 1319–1333. [Google Scholar] [CrossRef]
- Li, R.; Wen, C.; Meng, X.; Xie, Y. Measurement of the friction force of sliding friction pairs in low-speed marine diesel engines and comparison with numerical simulation. Appl. Ocean. Res. 2022, 121, 103089. [Google Scholar] [CrossRef]
- Chybowski, L.; Kowalak, P.; Dąbrowski, P. Assessment of the Impact of Lubricating Oil Contamination by Biodiesel on Trunk Piston Engine Reliability. Energies 2023, 16, 5056. [Google Scholar] [CrossRef]
- Mujtaba, M.A.; Masjuki, H.H.; Kalam, M.A.; Noor, F.; Farooq, M.; Ong, H.C.; Gul, M.; Soudagar, M.E.M.; Bashir, S.; Rizwanul Fattah, I.M.; et al. Effect of Additivized Biodiesel Blends on Diesel Engine Performance, Emission, Tribological Characteristics, and Lubricant Tribology. Energies 2020, 13, 3375. [Google Scholar] [CrossRef]
- Mosarof, M.H.; Kalam, M.A.; Masjuki, H.H.; Alabdulkarem, A.; Habibullah, M.; Arslan, A.; Monirul, I.M. Assessment of friction and wear characteristics of Calophyllum inophyllum and palm biodiesel. Ind. Crops Prod. 2016, 83, 470–483. [Google Scholar] [CrossRef]
- Tiruvenkadam, N.; Thyla, P.R.; Senthilkumar, M.; Bharathiraja, M. Development of optimum friction new nano hybrid composite liner for biodiesel fuel engine. Transp. Res. Part D Transp. Environ. 2016, 47, 22–43. [Google Scholar] [CrossRef]
- Thangarasu, V.; Balaji, B.; Ramanathan, A. Experimental investigation of tribo-corrosion and engine characteristics of Aegle Marmelos Correa biodiesel and its diesel blends on direct injection diesel engine. Energy 2019, 171, 879–892. [Google Scholar] [CrossRef]
- Singh, P.; Goel, V.; Chauhan, S.R. Impact of dual biofuel approach on engine oil dilution in CI engines. Fuel 2017, 207, 680–689. [Google Scholar] [CrossRef]
- Mousavi, S.B.; Zeinali Heris, S.; Estellé, P. Viscosity, tribological and physicochemical features of ZnO and MoS2 diesel oil-based nanofluids: An experimental study. Fuel 2021, 293, 120481. [Google Scholar] [CrossRef]
- Dey, S.; Moni Reang, N.; Deb, M.; Kumar Das, P. Experimental investigation on combustion-performance-emission characteristics of nanoparticles added biodiesel blends and tribological behavior of contaminated lubricant in a diesel engine. Energy Convers. Manag. 2021, 244, 114508. [Google Scholar] [CrossRef]
- Kapłan, M.; Klimek, K.; Maj, G.; Zhuravel, D.; Bondar, A.; Lemeshchenko-Lagoda, V.; Boltianskyi, B.; Boltianska, L.; Syrotyuk, H.; Syrotyuk, S.; et al. Method of Evaluation of Materials Wear of Cylinder-Piston Group of Diesel Engines in the Biodiesel Fuel Environment. Energies 2022, 15, 3416. [Google Scholar] [CrossRef]
- Abril, S.O.; García, C.P.; León, J.P. Numerical and Experimental Analysis of the Potential Fuel Savings and Reduction in CO Emissions by Implementing Cylinder Bore Coating Materials Applied to Diesel Engines. Lubricants 2021, 9, 19. [Google Scholar] [CrossRef]
- Lyu, B.; Meng, X.; Wang, C.; Cui, Y.; Wang, C.e. Piston ring and cylinder liner scuffing analysis in dual-fuel low-speed engines considering liner deformation and tribofilm evolution. Int. J. Engine Res. 2024, 25, 1776–1798. [Google Scholar] [CrossRef]
- Albrecht, A.; Grondin, O.; Le Berr, F.; Le Solliec, G. Towards a Stronger Simulation Support for Engine Control Design: A Methodological Point of View. Oil Gas Sci. Technol. 2007, 62, 437–456. [Google Scholar] [CrossRef]
- Wei, S.; Zhao, X.; Liu, X.; Qu, X.; He, C.; Leng, X. Research on effects of early intake valve closure (EIVC) miller cycle on combustion and emissions of marine diesel engines at medium and low loads. Energy 2019, 173, 48–58. [Google Scholar] [CrossRef]
- AVL. AVL-Development, Testing & Simulation of Powertrain Systems. Available online: https://www.avl.com/ (accessed on 4 October 2017).
- Mocerino, L.; Guedes Soares, C.; Rizzuto, E.; Balsamo, F.; Quaranta, F. Validation of an Emission Model for a Marine Diesel Engine with Data from Sea Operations. J. Mar. Sci. Appl. 2021, 20, 534–545. [Google Scholar] [CrossRef]
- Ricardo Wave Software, WAVE 2019.1 Help System; Ricardo plc: Shoreham-by-Sea, UK, 2019.
- Shen, H.; Yang, F.; Jiang, D.; Lu, D.; Jia, B.; Liu, Q.; Zhang, X. Parametric Investigation on the Influence of Turbocharger Performance Decay on the Performance and Emission Characteristics of a Marine Large Two-Stroke Dual Fuel Engine. J. Mar. Sci. Eng. 2024, 12, 1298. [Google Scholar] [CrossRef]
- Gamma Technologies LLC. GT-POWER Engine Simulation Software. Available online: https://www.gtisoft.com/gt-suite-applications/propulsion-systems/gt-power-engine-simulation-software/ (accessed on 4 October 2017).
- Stoumpos, S.; Theotokatos, G.; Mavrelos, C.; Boulougouris, E. Towards Marine Dual Fuel Engines Digital Twins—Integrated Modelling of Thermodynamic Processes and Control System Functions. J. Mar. Sci. Eng. 2020, 8, 200. [Google Scholar] [CrossRef]
- Karatuğ, Ç.; Tadros, M.; Ventura, M.; Guedes Soares, C. Decision support system for ship energy efficiency management based on an optimization model. Energy 2024, 292, 130318. [Google Scholar] [CrossRef]
- Tadros, M.; Ventura, M.; Guedes Soares, C. A nonlinear optimization tool to simulate a marine propulsion system for ship conceptual design. Ocean. Eng. 2020, 210, 107417. [Google Scholar] [CrossRef]
- Tadros, M.; Ventura, M.; Guedes Soares, C. Surrogate models of the performance and exhaust emissions of marine diesel engines for ship conceptual design. In Maritime Transportation and Harvesting of Sea Resources; Guedes Soares, C., Teixeira, A.P., Eds.; Taylor & Francis Group: London, UK, 2018; pp. 105–112. [Google Scholar]
- Tadros, M.; Ventura, M.; Guedes Soares, C. Data Driven In-Cylinder Pressure Diagram Based Optimization Procedure. J. Mar. Sci. Eng. 2020, 8, 294. [Google Scholar] [CrossRef]
- Kolakoti, A.; Tadros, M.; Ambati, V.K.; Gudlavalleti, V.N.S. Optimization of biodiesel production, engine exhaust emissions, and vibration diagnosis using a combined approach of definitive screening design (DSD) and artificial neural network (ANN). Environ. Sci. Pollut. Res. 2023, 30, 87260–87273. [Google Scholar] [CrossRef]
- ASTM D6751-24; Standard Specification for Biodiesel Fuel Blendstock (B100) for Middle Distillate Fuels. ASTM: West Conshohocken, PA, USA, 2024.
- Chen, S.K.; Flynn, P.F. Development of Single Cylinder Compression Ignition Research Engine; SAE Technical Paper; SAE: Warrendale, PA, USA, 1965. [Google Scholar] [CrossRef]
- Tormos, B.; Martín, J.; Blanco-Cavero, D.; Jiménez-Reyes, A.J. One-Dimensional Modeling of Mechanical and Friction Losses Distribution in a Four-Stroke Internal Combustion Engine. J. Tribol. 2020, 142, 011703. [Google Scholar] [CrossRef]
- Chen, Y.; Deng, B.; Chen, M.; Hou, K. An approach to estimate CCV (cycle-to-cycle variation) of effective energy output of thermal engine: A case study on a high speed gasoline engine. Case Stud. Therm. Eng. 2021, 28, 101624. [Google Scholar] [CrossRef]
- Özgül, E.; Bedir, H. Fast NOx emission prediction methodology via one-dimensional engine performance tools in heavy-duty engines. Adv. Mech. Eng. 2019, 11, 1687814019845954. [Google Scholar] [CrossRef]
- Realis Simulation, WAVE 2024.1 Help System; Realis Simulation: Shoreham-by-Sea, UK, 2024.
- MAN Diesel & Turbo. Four-Stroke Project Guides. Available online: https://www.man-es.com/marine/products/planning-tools-and-downloads/project-guides/four-stroke (accessed on 22 July 2022).
- MAN Diesel & Turbo. Technical Data Sheet: Marine Diesel Engine D2862 LE428. Available online: https://www.man.eu/ntg_media/media/content_medien/doc/man_engines_1/produkte/marine_1/Marine_DualFuel_EN.pdf (accessed on 15 April 2023).
- OEM Off-Highway. MAN Updates Engine Portfolio for Stage IV and Tier 4 Final Construction Machinery. Available online: https://www.oemoffhighway.com/engines/press-release/12163906/man-updates-engine-portfolio-for-stage-iv-and-tier-4-final-construction-machinery (accessed on 15 April 2020).
- Watson, N.; Janota, M.S. Turbocharging the Internal Combustion Engine; Palgrave: London, UK, 1982. [Google Scholar]
- Bai, F.; Zhang, Z.; Du, Y.; Zhang, F.; Peng, Z. Effects of Injection Rate Profile on Combustion Process and Emissions in a Diesel Engine. J. Combust. 2017, 2017, 9702625. [Google Scholar] [CrossRef]
- Maroteaux, F.; Saad, C. Diesel engine combustion modeling for hardware in the loop applications: Effects of ignition delay time model. Energy 2013, 57, 641–652. [Google Scholar] [CrossRef]
- Maroteaux, F.; Saad, C.; Aubertin, F. Development and validation of double and single Wiebe function for multi-injection mode Diesel engine combustion modelling for hardware-in-the-loop applications. Energy Convers. Manag. 2015, 105, 630–641. [Google Scholar] [CrossRef]
- Woschni, G. A Universally Applicable Equation for the Instantaneous Heat Transfer Coefficient in the Internal Combustion Engine; SAE Technical Paper; SAE: Warrendale, PA, USA, 1967. [Google Scholar]
- Watson, N.; Pilley, A.D.; Marzouk, M. A Combustion Correlation for Diesel Engine Simulation; SAE: Warrendale, PA, USA, 1980; Volume SAE Paper 800029. [Google Scholar]
- Tadros, M.; Ventura, M.; Guedes Soares, C. Assessment of the performance and the exhaust emissions of a marine diesel engine for different start angles of combustion. In Maritime Technology and Engineering 3; Guedes Soares, C., Santos, T.A., Eds.; Taylor & Francis Group: London, UK, 2016; pp. 769–775. [Google Scholar]
- Tadros, M.; Ventura, M.; Guedes Soares, C. Simulation of the performance of marine Genset based on double-Wiebe function. In Sustainable Development and Innovations in Marine Technologies; Georgiev, P., Guedes Soares, C., Eds.; Taylor & Francis Group: London, UK, 2020; pp. 292–299. [Google Scholar]
- Byrd, R.H.; Mary, E.H.; Nocedal, J. An Interior Point Algorithm for Large-Scale Nonlinear Programming. SIAM J. Optim. 1999, 9, 877–900. [Google Scholar] [CrossRef]
- The MathWorks Inc. Fmincon. Available online: https://www.mathworks.com/help/optim/ug/fmincon.html (accessed on 2 June 2017).
- Zhu, Z.; Zhang, F.; Li, C.; Wu, T.; Han, K.; Lv, J.; Li, Y.; Xiao, X. Genetic algorithm optimization applied to the fuel supply parameters of diesel engines working at plateau. Appl. Energy 2015, 157, 789–797. [Google Scholar] [CrossRef]
- Zhao, J.; Xu, M. Fuel economy optimization of an Atkinson cycle engine using genetic algorithm. Appl. Energy 2013, 105, 335–348. [Google Scholar] [CrossRef]
- Challen, B.; Baranescu, R. Diesel Engine Reference Book, 2nd ed.; Challen, B., Baranescu, R., Eds.; Butterworth-Heinemann Ltd.: Oxford, UK, 1999. [Google Scholar]
- Woodyard, D. Pounder’s Marine Diesel Engines, 8th ed.; Butterworth-Heinemann: Oxford, UK, 2004. [Google Scholar]
- Tormos, B.; Martín, J.; Pla, B.; Jiménez-Reyes, A.J. A methodology to estimate mechanical losses and its distribution during a real driving cycle. Tribol. Int. 2020, 145, 106208. [Google Scholar] [CrossRef]
- Chen, R.; Zhao, B.; He, T.; Tu, L.; Xie, Z.; Zhong, N.; Zou, D. Study on coupling transient mixed lubrication and time-varying wear of main bearing in actual operation of low-speed diesel engine. Tribol. Int. 2024, 191, 109159. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| Bore (mm) | 128 |
| Stroke (mm) | 157 |
| No. of cylinders | 12 |
| Displacement (liter) | 24.24 |
| Number of valves per cylinder | 4 |
| Compression ratio | 19:1 |
| BMEP (bar) | 17.66 |
| Piston speed (m/s) | 10.99 |
| Engine speed (rpm) | 2100 |
| Brake-specific fuel consumption (g/kW.h) | 208 |
| Power-to-weight ratio (kW/Kg) | 0.329 |
| Parameter | Unit | Real Value | Simulated Value | Percentage of Error [%] | |
|---|---|---|---|---|---|
| Optimized variables | TS | [rpm] | - | 131,529 | - |
| SOI | [BTDC] | - | −1.406 | - | |
| INJDur | [degree] | - | 32.98 | - | |
| FMEP | [bar] | - | 2.54 | - | |
| BRPM | [rpm] | - | 2957 | - | |
| Constraints parameters | TAfterCylinder | [K] | - | 915 | - |
| Tmax | [K] | - | 1771 | - | |
| Pmax | [bar] | - | 168.4 | - | |
| AFR | [-] | - | 26.2 | - | |
| R2 | [-] | - | 0.9999 | - | |
| Validation parameters | PB | [kW] | 749 | 748.74 | 0.034 |
| BSFC | [g/kW.h] | 208 | 208 | 0 | |
| ṁa | [kg/h] | 4084 | 4082.56 | 0.035 | |
| Texh | [K] | 711 | 733 | 3.09 |
| Parameter | Unit | Case 1 | Case 2 | Case 3 | |
|---|---|---|---|---|---|
| Engine speed | [rpm] | 1900 | 1300 | 600 | |
| Loading ratio | [%] | 78.5 | 30.2 | 4.5 | |
| Optimized variables | TS | [rpm] | 120,659 | 67,592 | 35,956 |
| SOI | [BTDC] | −3.69 | −2.23 | −1.69 | |
| INJDur | [degree] | 25.68 | 23.99 | 17.31 | |
| FMEP | [bar] | 2.48 | 1.86 | 1.17 | |
| Constraints parameters | TAfterCylinder | [K] | 808 | 758 | 494 |
| Tmax | [K] | 1717 | 1706 | 1334 | |
| Pmax | [bar] | 168.5 | 94.2 | 73.0 | |
| AFR | [-] | 30.19 | 31.03 | 68.89 | |
| R2 | [-] | 0.9999 | 0.9998 | 0.9999 |
| Term | Standard Value | Optimized Value |
|---|---|---|
| Acf | 0.5 | 0.4309 |
| Bcf | 0.006 | 0.006 |
| Ccf | 600 | 655.3842 |
| Qcf | 0.2 | 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tadros, M. Engine Optimization Model for Accurate Prediction of Friction Model in Marine Dual-Fuel Engine. Algorithms 2025, 18, 415. https://doi.org/10.3390/a18070415
Tadros M. Engine Optimization Model for Accurate Prediction of Friction Model in Marine Dual-Fuel Engine. Algorithms. 2025; 18(7):415. https://doi.org/10.3390/a18070415
Chicago/Turabian StyleTadros, Mina. 2025. "Engine Optimization Model for Accurate Prediction of Friction Model in Marine Dual-Fuel Engine" Algorithms 18, no. 7: 415. https://doi.org/10.3390/a18070415
APA StyleTadros, M. (2025). Engine Optimization Model for Accurate Prediction of Friction Model in Marine Dual-Fuel Engine. Algorithms, 18(7), 415. https://doi.org/10.3390/a18070415










