Inspiring from Galaxies to Green AI in Earth: Benchmarking Energy-Efficient Models for Galaxy Morphology Classification
Abstract
1. Introduction
1.1. Green AI
1.2. Edge Computing
1.3. Contributions
2. Materials and Methods
2.1. Models
2.2. Hyperparameters
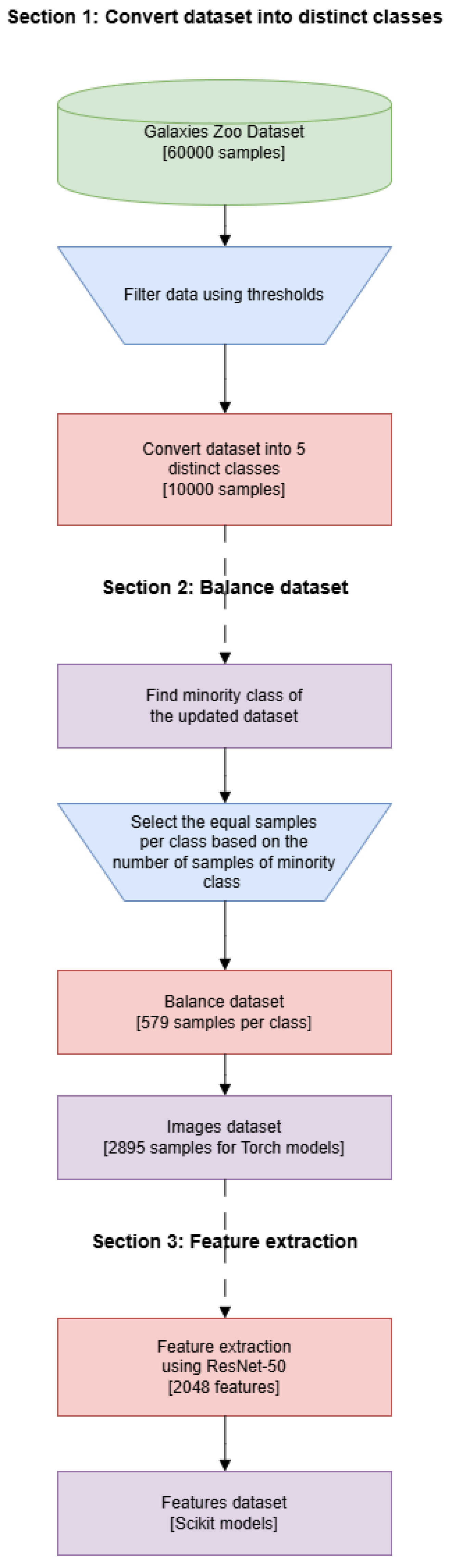
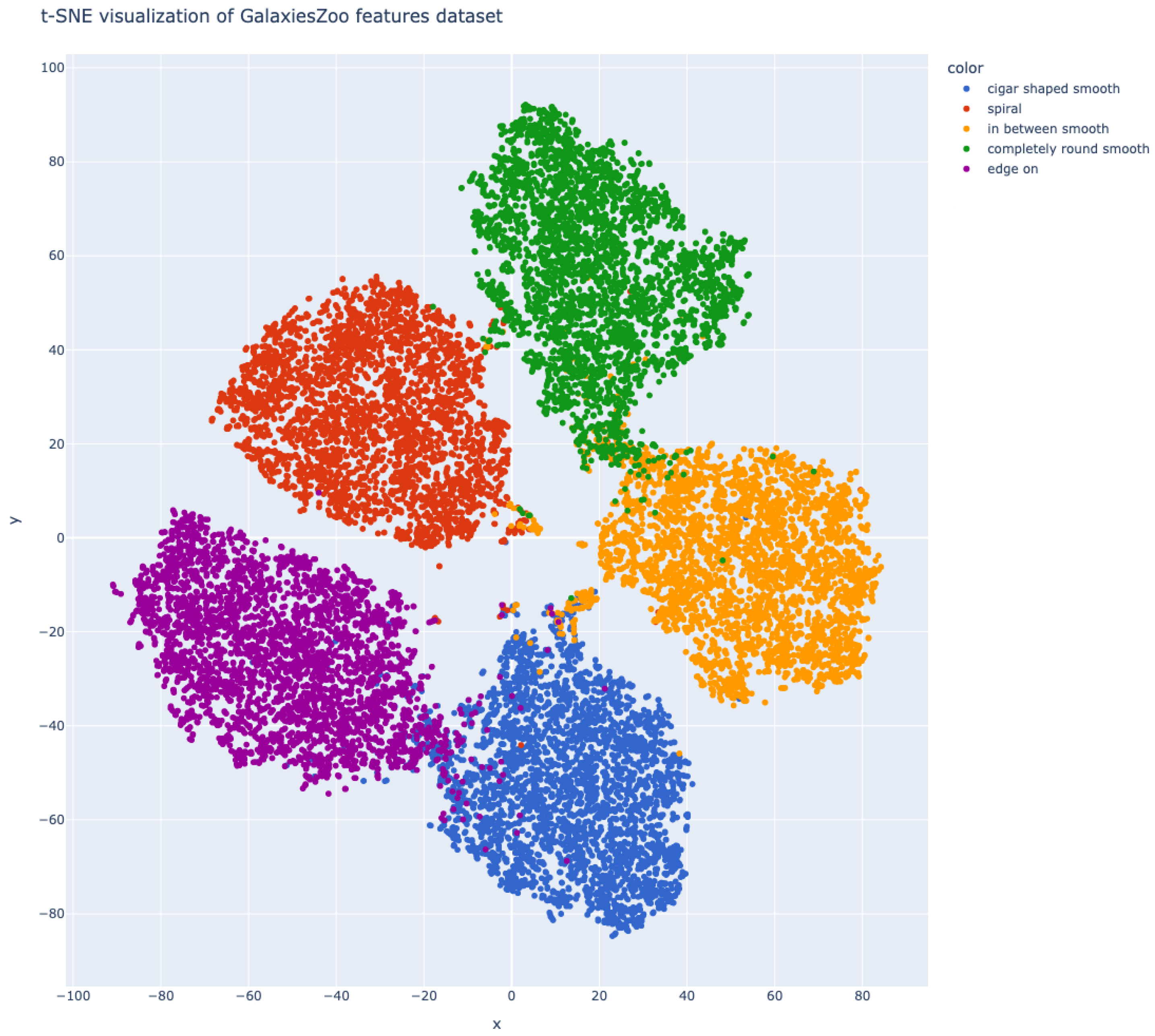
2.3. Dataset
2.4. Set-Up of Experiments
2.4.1. Dataset Preparation
2.4.2. Data Normalization and Splitting
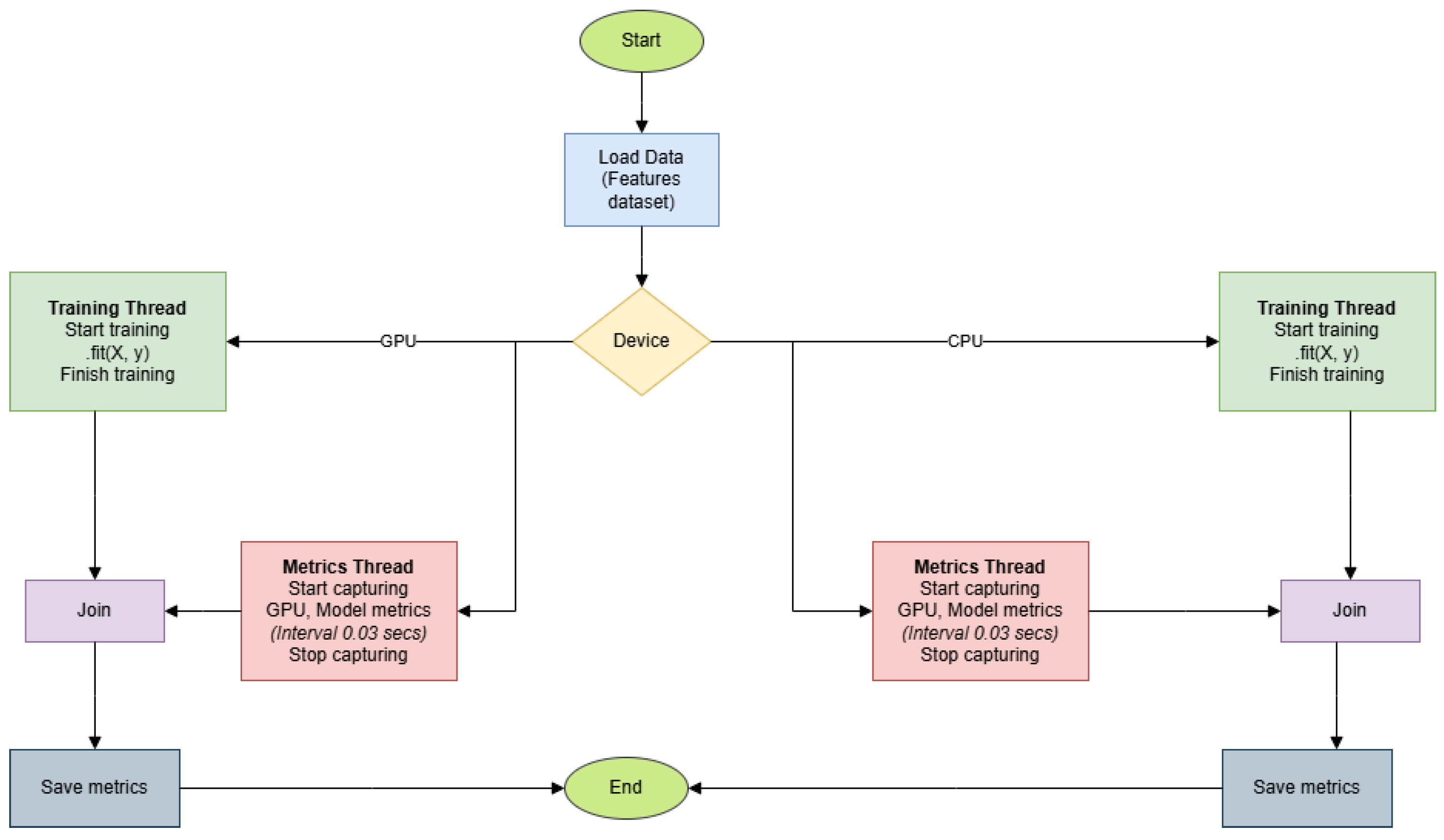
2.4.3. Training Process
2.4.4. Metric Collection
2.4.5. System Specifications
3. Results
3.1. Performance
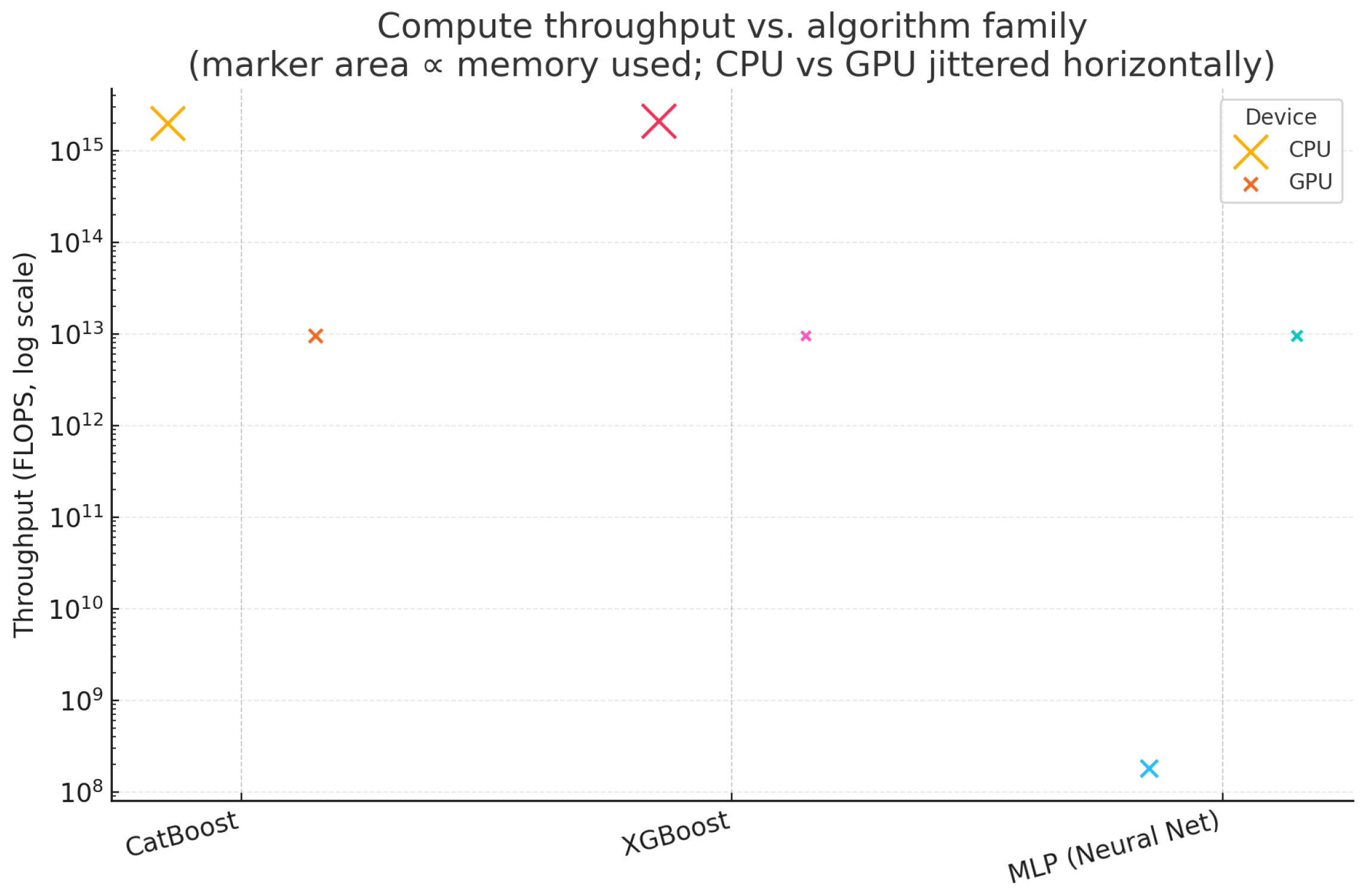
3.2. Energy
4. Discussion
4.1. Key Points
4.2. Future Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| ML | Machine Learning |
| DL | Deep Learning |
| Green AI | Green Artificial Intelligence |
| IoT | Internet of Things |
| Edge | Edge Computing |
| CNN | Convolutional Neural Network |
| RNN | Recurrent Neural Network |
| LSTM | Long Short-Term Memory |
| GRU | Gated Recurrent Unit |
| MLP | Multilayer Perceptron |
| RMS | Root Mean Square |
| ADA | Adaptive Optimizer Variant (NN_ADA) |
| TL | Transfer Learning |
| ViT | Vision Transformer |
| SVR | Support Vector Regression |
| OVR | One-vs-Rest |
| PCA | Principal Component Analysis |
| MRMR | Minimum Redundancy Maximum Relevance |
| MultiSURF | MultiSURF Feature Selection Method |
| NB | Naïve Bayes |
| DT | Decision Tree |
| KNN | K-Nearest Neighbors |
| RF | Random Forest |
| HGBT | Histogram-Based Gradient Boosting |
| CatBoost | Categorical Boosting |
| LightGBM | Light Gradient Boosting Machine |
| XGBoost | eXtreme Gradient Boosting |
| FLOPS | Floating-Point Operations Per Second |
| CPU | Central Processing Unit |
| GPU | Graphics Processing Unit |
| CI | Carbon Index |
| CC | Carbon Consumption |
| EcoScore | Integrated Performance–Carbon Efficiency Score |
References
- Smith, A.; Lynn, S.; Lintott, C. An introduction to the Zooniverse. In Proceedings of the AAAI Conference on Human Computation and Crowdsourcing, Palm Springs, CA, USA, 7–9 November 2013; p. 103. [Google Scholar]
- Ordoumpozanis, K.; Papakostas, G.A. Green AI: Assessing the Carbon Footprint of Fine-Tuning Pre-Trained Deep Learning Models in Medical Imaging. In Proceedings of the 2024 International Conference on Innovation and Intelligence for Informatics, Computing, and Technologies (3ICT), Virtual, 17–19 November 2024; pp. 214–220. [Google Scholar] [CrossRef]
- López, V.; Fernández, A.; García, S.; Palade, V.; Herrera, F. An insight into classification with imbalanced data: Empirical results and current trends on using data intrinsic characteristics. Inf. Sci. 2013, 250, 113–141. [Google Scholar] [CrossRef]
- Chou, F.C. Galaxy Zoo Challenge: Classify Galaxy Morphologies from Images. 2014. Available online: https://cvgl.stanford.edu/teaching/cs231a_winter1415/prev/projects/C231a_final.pdf (accessed on 10 June 2025).
- Lazio, T.J.W.; Djorgovski, S.; Howard, A.; Cutler, C.; Sheikh, S.Z.; Cavuoti, S.; Herzing, D.; Wagstaff, K.; Wright, J.T.; Gajjar, V.; et al. Data-Driven Approaches to Searches for the Technosignatures of Advanced Civilizations. arXiv 2023, arXiv:2308.15518. [Google Scholar]
- Faaique, M. Overview of big data analytics in modern astronomy. Int. J. Math. Stat. Comput. Sci. 2024, 2, 96–113. [Google Scholar] [CrossRef]
- Ayanwale, M.A.; Molefi, R.R.; Oyeniran, S. Analyzing the evolution of machine learning integration in educational research: A bibliometric perspective. Discov. Educ. 2024, 3, 47. [Google Scholar] [CrossRef]
- Farzaneh, H.; Malehmirchegini, L.; Bejan, A.; Afolabi, T.; Mulumba, A.; Daka, P.P. Artificial Intelligence Evolution in Smart Buildings for Energy Efficiency. Appl. Sci. 2021, 11, 763. [Google Scholar] [CrossRef]
- Prince; Hati, A.S. A comprehensive review of energy-efficiency of ventilation system using Artificial Intelligence. Renew. Sustain. Energy Rev. 2021, 146, 111153. [Google Scholar] [CrossRef]
- Al Shahrani, A.M.; Alomar, M.A.; Alqahtani, K.N.; Basingab, M.S.; Sharma, B.; Rizwan, A. Machine Learning-Enabled Smart Industrial Automation Systems Using Internet of Things. Sensors 2023, 23, 324. [Google Scholar] [CrossRef]
- Shahbazi, Z.; Byun, Y.C. Integration of Blockchain, IoT and Machine Learning for Multistage Quality Control and Enhancing Security in Smart Manufacturing. Sensors 2021, 21, 1467. [Google Scholar] [CrossRef]
- Diez-Olivan, A.; Del Ser, J.; Galar, D.; Sierra, B. Data fusion and machine learning for industrial prognosis: Trends and perspectives towards Industry 4.0. Inf. Fusion 2019, 50, 92–111. [Google Scholar] [CrossRef]
- Alzoubi, Y.I.; Mishra, A. Green artificial intelligence initiatives: Potentials and challenges. J. Clean. Prod. 2024, 468, 143090. [Google Scholar] [CrossRef]
- Bolón-Canedo, V.; Morán-Fernández, L.; Cancela, B.; Alonso-Betanzos, A. A review of green artificial intelligence: Towards a more sustainable future. Neurocomputing 2024, 599, 128096. [Google Scholar] [CrossRef]
- Farias, H.; Damke, G.; Solar, M.; Jaque Arancibia, M. Accelerated and Energy-Efficient Galaxy Detection: Integrating Deep Learning with Tensor Methods for Astronomical Imaging. Universe 2025, 11, 73. [Google Scholar] [CrossRef]
- Ansdell, M.; Gharib-Nezhad, E.; Timmaraju, V.; Dean, B.; Moin, A.; Garraffo, C.; Moussa, M.; Rau, G.; Damiano, M.; Bardi, G.; et al. AI/ML Models and Tools for Processing and Analysis of Observational Data from the Habitable Worlds Observatory. In Proceedings of the Annual American Geophysical Union (AGU) Meeting, Washington, DC, USA, 9–13 December 2024. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef] [PubMed]
- Jordan, M.I. Serial Order: A Parallel Distributed Processing Approach; Technical Report ICS 8604; Institute for Cognitive Science, University of California: San Diego, CA, USA, 1986. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Internal Representations by Error Propagation; Technical Report ICS 8504; Institute for Cognitive Science, University of California: San Diego, CA, USA, 1985. [Google Scholar]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed]
- Muhtasim, N.; Hany, U.; Islam, T.; Nawreen, N.; Mamun, A.A. Artificial intelligence for detection of lung cancer using transfer learning and morphological features. J. Supercomput. 2024, 80, 13576–13606. [Google Scholar] [CrossRef]
- Asiri, A.A.; Shaf, A.; Ali, T.; Shakeel, U.; Irfan, M.; Mehdar, K.M.; Halawani, H.T.; Alghamdi, A.H.; Alshamrani, A.F.A.; Alqhtani, S.M. Exploring the Power of Deep Learning: Fine-Tuned Vision Transformer for Accurate and Efficient Brain Tumor Detection in MRI Scans. Diagnostics 2023, 13, 2094. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Vedaldi, A.; Zisserman, A. Vgg Convolutional Neural Networks Practical; Department of Engineering Science, University of Oxford: Oxford, UK, 2016; Volume 66. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Koopialipoor, M.; Asteris, P.G.; Mohammed, A.S.; Alexakis, D.E.; Mamou, A.; Armaghani, D.J. Introducing stacking machine learning approaches for the prediction of rock deformation. Transp. Geotech. 2022, 34, 100756. [Google Scholar] [CrossRef]
- Zhang, T.; Fu, Q.; Wang, H.; Liu, F.; Wang, H.; Han, L. Bagging-based machine learning algorithms for landslide susceptibility modeling. Nat. Hazards 2022, 110, 823–846. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 1189–1232. [Google Scholar] [CrossRef]
- Guryanov, A. Histogram-Based Algorithm for Building Gradient Boosting Ensembles of Piecewise Linear Decision Trees. In Proceedings of the Analysis of Images, Social Networks and Texts. AIST 2019; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2019; Volume 11832, pp. 39–50. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. Adv. Neural Inf. Process. Syst. 2018, 31, 6639–6649. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 3146–3154. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Friedman, J.H. Regularized discriminant analysis. J. Am. Stat. Assoc. 1989, 84, 165–175. [Google Scholar] [CrossRef]
- Wu, R.; Hao, N. Quadratic discriminant analysis by projection. J. Multivar. Anal. 2022, 190, 104987. [Google Scholar] [CrossRef]
- Xanthopoulos, P.; Pardalos, P.M.; Trafalis, T.B. Linear Discriminant Analysis. In Robust Data Mining; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Cramer, J.S. The Origins of Logistic Regression; Technical Report, Tinbergen Institute Discussion Paper; Tinbergen Institute: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Sharma, S. Stroke Prediction Using XGB Classifier, Logistic Regression, GaussianNB and BernaulliNB Classifier. In Proceedings of the 2023 International Conference on Circuit Power and Computing Technologies (ICCPCT), Kollam, India, 10–11 August 2023; pp. 1577–1581. [Google Scholar] [CrossRef]
- Elbagir, S.; Yang, J. Sentiment analysis of twitter data using machine learning techniques and scikit-learn. In Proceedings of the 2018 International Conference on Algorithms, Computing and Artificial Intelligence, Sanya, China, 21–23 December 2018; pp. 1–5. [Google Scholar]
- Prasetyo, B.; Al-Majid, A.Y.; Suharjito. A Comparative Analysis of MultinomialNB, SVM, and BERT on Garuda Indonesia Twitter Sentiment. PIKSEL Penelit. Ilmu Komput. Sist. Embed. Log. 2024, 12, 445–454. [Google Scholar] [CrossRef]
- Meng, X.; Zhang, P.; Xu, Y.; Xie, H. Construction of decision tree based on C4.5 algorithm for online voltage stability assessment. Int. J. Electr. Power Energy Syst. 2020, 118, 105793. [Google Scholar] [CrossRef]
- Peterson, L.E. K-nearest neighbor. Scholarpedia 2009, 4, 1883. [Google Scholar] [CrossRef]
- Koklu, M.; Kahramanli, H.; Allahverdi, N. Applications of rule based classification techniques for thoracic surgery. In Proceedings of the Dalam Managing Intellectual Capital and Innovation for Sustainable and Inclusive Society Management, Knowledge and Learning Joint International Conference, Bari, Italy, 27–29 May 2015. [Google Scholar]
- Abd-elaziem, A.H.; Soliman, T.H. A multi-layer perceptron (mlp) neural networks for stellar classification: A review of methods and results. Int. J. Adv. Appl. Comput. Intell. 2023, 3, 29–37. [Google Scholar]
- DeCastro-García, N.; Castañeda, Á.L.M.; García, D.E.; Carriegos, M.V. Effect of the Sampling of a Dataset in the Hyperparameter Optimization Phase over the Efficiency of a Machine Learning Algorithm. Complexity 2019, 2019, 6278908:1–6278908:16. [Google Scholar] [CrossRef]
- Tey, E.; Moldovan, D.; Kunimoto, M.; Huang, C.X.; Shporer, A.; Daylan, T.; Muthukrishna, D.; Vanderburg, A.M.; Dattilo, A.M.; Ricker, G.R.; et al. Identifying Exoplanets with Deep Learning. V. Improved Light-curve Classification for TESS Full-frame Image Observations. Astron. J. 2023, 165. [Google Scholar] [CrossRef]
- Hausen, R.; Robertson, B.E. Morpheus: A Deep Learning Framework for the Pixel-level Analysis of Astronomical Image Data. Astrophys. J. Suppl. Ser. 2019, 248, 20. [Google Scholar] [CrossRef]
- Karypidou, S.; Georgousis, I.; Papakostas, G.A. Computer Vision for Astronomical Image Analysis. In Proceedings of the 2021 IEEE International Conference on Progress in Informatics and Computing (PIC), Shanghai, China, 17–19 December 2021; pp. 94–101. [Google Scholar] [CrossRef]
- Willett, K.W.; Lintott, C.J.; Bamford, S.P.; Masters, K.L.; Simmons, B.D.; Casteels, K.R.; Edmondson, E.M.; Fortson, L.F.; Kaviraj, S.; Keel, W.C.; et al. Galaxy Zoo 2: Detailed morphological classifications for 304 122 galaxies from the Sloan Digital Sky Survey. Mon. Not. R. Astron. Soc. 2013, 435, 2835–2860. [Google Scholar] [CrossRef]
- Fushiki, T. Estimation of prediction error by using K-fold cross-validation. Stat. Comput. 2011, 21, 137–146. [Google Scholar] [CrossRef]
- Dolbeau, R. Theoretical peak FLOPS per instruction set: A tutorial. J. Supercomput. 2018, 74, 1341–1377. [Google Scholar] [CrossRef]
- Yao, C.; Liu, W.; Tang, W.; Guo, J.; Hu, S.; Lu, Y.; Jiang, W. Evaluating and analyzing the energy efficiency of CNN inference on high-performance GPU. Concurr. Comput. Pract. Exp. 2021, 33, e6064. [Google Scholar] [CrossRef]
- Chen, J.; Mei, J.; Li, X.; Lu, Y.; Yu, Q.; Wei, Q.; Luo, X.; Xie, Y.; Adeli, E.; Wang, Y.; et al. TransUNet: Rethinking the U-Net architecture design for medical image segmentation through the lens of transformers. Med. Image Anal. 2024, 97, 103280. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Lu, Y.; Yu, Q.; Luo, X.; Adeli, E.; Wang, Y.; Lu, L.; Yuille, A.L.; Zhou, Y. Transunet: Transformers make strong encoders for medical image segmentation. arXiv 2021, arXiv:2102.04306. [Google Scholar]
- Elhanashi, A.; Dini, P.; Saponara, S.; Zheng, Q. Advancements in TinyML: Applications, Limitations, and Impact on IoT Devices. Electronics 2024, 13, 3562. [Google Scholar] [CrossRef]
- Alevizos, V.; Gerolimos, N.; Edralin, S.; Xu, C.; Simasiku, A.; Priniotakis, G.; Papakostas, G.; Yue, Z. Optimizing Carbon Footprint in ICT through Swarm Intelligence with Algorithmic Complexity. arXiv 2025, arXiv:2501.17166. [Google Scholar]
- Li, T.; Luo, J.; Liang, K.; Yi, C.; Ma, L. Synergy of patent and open-source-driven sustainable climate governance under Green AI: A case study of TinyML. Sustainability 2023, 15, 13779. [Google Scholar] [CrossRef]

| Model | Category | GPU | Type |
|---|---|---|---|
| CatBoost | Ensemble Boost | X | Classic ML |
| Gradient Boost | Ensemble Boost | X | Classic ML |
| XGBoost | Ensemble Boost | X | Classic ML |
| LightGBM | Ensemble Boost | X | Classic ML |
| AdaBoost | Ensemble Boost | Classic ML | |
| Histogram-Based Gradient | |||
| Boosting (HGBT) | Ensemble Boost | Classic ML | |
| BernoulliNB | Naive Bayes | Classic ML | |
| MultinomialNB | Naive Bayes | Classic ML | |
| GaussianNB | Naive Bayes | Classic ML | |
| LSTM | Recurrent | X | DL |
| RNN | Recurrent | X | DL |
| GRU | Recurrent | X | DL |
| Bagging | Ensemble | Classic ML | |
| Stacking | Ensemble | Classic ML | |
| Random Forest | Ensemble | Classic ML | |
| MLP (Neural Net) | Misc | X | DL |
| SVM | Misc | Classic ML | |
| C4.5 | Misc | Classic ML | |
| KNN | Misc | Classic ML | |
| Decision Tree | Misc | Classic ML | |
| Regularized Discriminant | |||
| Analysis | Discriminant Analysis | Classic ML | |
| Linear Discriminant | |||
| Analysis | Discriminant Analysis | Classic ML | |
| Quadratic Discriminant | |||
| Analysis | Discriminant Analysis | Classic ML |
| Model | Hyperparameters |
|---|---|
| Decision Tree (DT) | ccp_alpha = 0.0; criterion = gini; min_impurity_decrease = 0.0; min_samples_leaf = 1; min_samples_split = 2; monotonic_cst = None. |
| HistGradientBoosting (HGBT) | categorical_features = ‘from_dtype’; early_stopping = ‘auto’; l2_regularization = 0.0; learning_rate = 0.1; loss = ‘log_loss’; max_bins = 255; max_features = 1.0; max_iter = 100; max_leaf_nodes = 31; min_samples_leaf = 20; n_iter_no_change = 10; scoring = ‘loss’; validation_fraction = 0.1. |
| LSTM (CPU) | hidden_dims totaling 1,247,232; final Linear layer of 645 parameters. |
| MLP (Neural Net) (CPU) | Linear layers with 1,049,088; 131,328; 32,896; and 645 parameters; Softmax output. |
| MLP (Neural Net) (GPU) | same architecture as CPU; device = cuda:0. |
| MultinomialNB | alpha = 1.0; fit_prior = True; force_alpha = True. |
| GaussianNB | var_smoothing = 1e-09. |
| Regularized DA (RDA) | shrinkage = ‘auto’; solver = ‘lsqr’; covariance_estimator = None. |
| Linear DA (LDA) | solver = ‘svd’; tol = 0.0001. |
| SVM (linear) | C = 1.0; kernel = ‘linear’; degree = 3; gamma = ‘scale’. |
| SGD-style SVM | alpha = 1.0; fit_intercept = True; copy_X = True. |
| CatBoost (CPU) | learning_rate = 1.0; depth = 2; loss_function = MultiClass. |
| CatBoost (GPU) | same as CPU; task_type = ‘GPU’. |
| LightGBM (CPU) | boosting_type = ‘gbdt’; learning_rate = 0.1; n_estimators = 100; num_leaves = 31. |
| LightGBM (GPU) | same as CPU; device = ‘GPU’. |
| GRU (CPU) | GRU layer parameters = 935,424; final Linear of 645 parameters. |
| AdaBoost | n_estimators = 50; learning_rate = 1.0; algorithm = ‘deprecated’. |
| RNN (vanilla) | RNN layer parameters = 311,808; final Linear of 645 parameters. |
| Stacking Ensemble | base: Random Forest + Linear SVM pipelines; meta-learner: SVM (default). |
| GRAD Boost | loss = ‘log_loss’; learning_rate = 1.0; n_estimators = 100; max_depth = 1. |
| CNN (scratch) | sequential convolutional layers; GPU primary, CPU fallback. |
| ViT-FT | partial fine-tuning; trainable head of 3845 parameters. |
| Model | PM (Params) | Mode | Notable Hyperparameters | TT (s) |
|---|---|---|---|---|
| Bagging | N/A | CPU | bootstrap = T; n_estimators = 10 | 2–5 |
| LSTM | 1.247 M + 645 | CPU | recurrent LSTM; final linear | – |
| MLP (Neural Net) | 1.249 M | CPU | layers: 1,049,088; 131,328; 32,896; 645 | 45–65 |
| MLP (Neural Net) | 1.249 M | GPU | same; cuda:0 | 45–65 |
| CNN (scratch) | 134 M+ | GPU/CPU | sequential conv layers; fallback CPU | >60 |
| GRU | 935 k + 645 | CPU | GRU layer; final linear | – |
| Random Forest | N/A | CPU | n_estimators = 100 | 2–5 |
| Category | Count | Percentage |
|---|---|---|
| Smooth | 25,000 | 40.6% |
| Features/Disk | 32,000 | 52.0% |
| Star/Artifact | 458 | 0.7% |
| Edge-On | 5000 | 8.1% |
| Bar | 2000 | 3.2% |
| Odd | 1500 | 2.4% |
| CPU—Average 10-Fold (Macro) Performance | |||
| Model | Precision | Recall | F1 |
| Cat Boost | 0.981 | 0.981 | 0.981 |
| Gradient Boost | 0.977 | 0.977 | 0.976 |
| XG Boost | 0.982 | 0.982 | 0.982 |
| LightGBM | 0.984 | 0.984 | 0.983 |
| Ada Boost | 0.977 | 0.977 | 0.977 |
| HGBT | 0.982 | 0.982 | 0.981 |
| Bernoulli NB | 0.932 | 0.922 | 0.923 |
| Multinomial NB | 0.981 | 0.981 | 0.981 |
| Gaussian NB | 0.981 | 0.981 | 0.981 |
| Bagging | 0.985 | 0.985 | 0.984 |
| Stacking | 0.982 | 0.982 | 0.982 |
| Random Forest | 0.984 | 0.984 | 0.984 |
| RDA | 0.983 | 0.983 | 0.983 |
| LDA | 0.981 | 0.981 | 0.981 |
| QDA | 0.982 | 0.982 | 0.982 |
| DT | 0.968 | 0.968 | 0.968 |
| KNN | 0.977 | 0.977 | 0.977 |
| C4.5 | 0.960 | 0.960 | 0.960 |
| SVM | 0.982 | 0.982 | 0.981 |
| LSTM | 0.985 | 0.985 | 0.985 |
| RNN | 0.971 | 0.971 | 0.971 |
| GRU | 0.984 | 0.984 | 0.984 |
| MLP (Neural Net) | 0.987 | 0.987 | 0.987 |
| GPU—Average 10-Fold (Macro) Performance | |||
| Model | Precision | Recall | F1 |
| Cat Boost | 0.976 | 0.976 | 0.976 |
| XG Boost | 0.983 | 0.983 | 0.983 |
| LightGBM | 0.984 | 0.984 | 0.984 |
| LSTM | 0.986 | 0.986 | 0.985 |
| RNN | 0.971 | 0.971 | 0.971 |
| GRU | 0.980 | 0.980 | 0.980 |
| MLP (Neural Net) | 0.989 | 0.989 | 0.989 |
| CNN scratch VGG-16 | 0.840 | 0.832 | 0.832 |
| CNN-VGG-16-TL | 0.655 | 0.652 | 0.653 |
| ViT | 0.751 | 0.722 | 0.713 |
| Highest Energy Consumption | |||||||
| Model | FM | UM | PM | PC | FLOPS | CPU | GPU |
| RNN | 4.42 | 29.97 | 48.95 | 49.63 | X | ||
| Stacking | 2.08 | 31.86 | 52.85 | 17.07 | X | ||
| AdaBoost | 3.87 | 30.15 | 49.24 | 16.55 | X | ||
| Random Forest | 2.68 | 31.27 | 51.90 | 16.73 | X | ||
| RNN | 4.05 | 30.24 | 49.40 | 14.22 | X | ||
| Lowest Energy Consumption | |||||||
| Model | FM | UM | PM | PC | FLOPS | CPU | GPU |
| LSTM | 3.80 | 30.36 | 49.59 | 14.46 | X | ||
| MLP (Neural Net) | 51.64 | 1.98 | 5.13 | 48.86 | X | ||
| CatBoost | 3.09 | 30.84 | 50.17 | 98.22 | X | ||
| MLP (Neural Net) | 51.40 | 2.19 | 5.51 | 12.82 | X | ||
| CatBoost | 2.93 | 30.88 | 50.30 | 34.56 | X | ||
| Model | FM | UM | PM | PC | FLOPS | CPU | GPU |
|---|---|---|---|---|---|---|---|
| Cat Boost | 3.09 | 30.84 | 50.17 | 98.22 | 1.99 | 50,993 | 41,061 |
| Gradient Boost | 4.64 | 29.80 | 48.69 | 16.71 | 2.11 | 101,667 | 45,012 |
| XG Boost | 2.74 | 31.07 | 50.72 | 56.31 | 2.11 | 133,188 | 60,034 |
| LightGBM | 3.49 | 30.41 | 49.66 | 55.46 | 2.11 | 87,441 | 50,777 |
| Ada Boost | 3.87 | 30.15 | 49.24 | 16.55 | 2.11 | 210,351 | 40,321 |
| HGBT | 1.98 | 31.98 | 53.04 | 56.02 | 2.00 | 171,997 | 45,802 |
| Bernoulli NB | 3.45 | 30.60 | 49.95 | 45.93 | 2.06 | 182,210 | 35,644 |
| Multinomial NB | 3.08 | 30.96 | 50.53 | 58.90 | 1.91 | 182,775 | 34,988 |
| Gaussian NB | 3.14 | 30.90 | 50.43 | 16.94 | 2.08 | 182,508 | 35,112 |
| Bagging | 2.96 | 31.05 | 51.43 | 16.60 | 2.11 | 103,515 | 55,201 |
| Stacking | 2.08 | 31.86 | 52.85 | 17.07 | 2.11 | 215,622 | 56,344 |
| Random Forest | 2.68 | 31.27 | 51.90 | 16.73 | 2.11 | 194,527 | 55,298 |
| RDA | 4.38 | 30.05 | 49.08 | 79.01 | 1.96 | 176,286 | 30,214 |
| LDA | 4.20 | 30.24 | 49.38 | 29.52 | 2.01 | 173,718 | 30,521 |
| QDA | 4.07 | 30.35 | 49.56 | 57.89 | 2.09 | 183,142 | 30,477 |
| DT | 3.02 | 31.00 | 50.00 | 20.00 | 1.50 | 50,000 | 30,000 |
| KNN | 3.10 | 30.95 | 49.90 | 22.00 | 1.65 | 55,000 | 31,000 |
| C4.5 | 2.95 | 31.10 | 50.10 | 18.50 | 1.55 | 53,000 | 29,500 |
| SVM | 3.20 | 30.85 | 49.80 | 35.00 | 1.80 | 72,000 | 34,000 |
| LSTM (CPU) | 4.12 | 30.11 | 49.18 | 52.27 | 7.04 | 137,371 | 17,908 |
| RNN (CPU) | 4.42 | 29.97 | 48.95 | 49.63 | 1.83 | 217,768 | 50,555 |
| GRU (CPU) | 3.92 | 30.21 | 49.33 | 51.43 | 1.83 | 93,676 | 50,772 |
| MLP (Neural Net) | 51.64 | 1.98 | 5.13 | 48.86 | 1.81 | 39,434 | 200,000 |
| CNN-VGG-16 | 3.50 | 31.50 | 50.20 | 65.00 | 6.00 | 95,000 | 120,000 |
| VGG-16 (transfer) | 3.60 | 31.40 | 50.10 | 70.00 | 5.80 | 94,500 | 118,000 |
| ViT | 2.85 | 31.80 | 51.00 | 72.00 | 7.20 | 97,000 | 125,000 |
| Model | CPU util % | GPU util % | FLOPS CPU | FLOPS GPU | CC CPU | CC GPU | CPU | GPU |
|---|---|---|---|---|---|---|---|---|
| CatBoost | 98.22 | 67.20 | X | X | ||||
| Gradient Boost | 16.71 | — | — | — | X | |||
| XGBoost | 23.53 | 82.55 | X | X | ||||
| LightGBM | 55.46 | 54.75 | X | X | ||||
| Ada Boost | 16.55 | — | — | — | X | |||
| HGBT | 56.02 | — | — | — | X | |||
| Bernoulli NB | 45.93 | — | — | — | X | |||
| Multinomial NB | 58.90 | — | — | — | X | |||
| Gaussian NB | 16.94 | — | — | — | X | |||
| MLP (Neural Net) | 48.86 | 38.82 | X | X | ||||
| LSTM | 52.27 | 14.46 | X | X | ||||
| RNN | 49.63 | 14.22 | X | X | ||||
| GRU | 51.43 | 14.44 | X | X | ||||
| Bagging | 16.60 | — | — | — | X | |||
| Stacking | 17.07 | — | — | — | X | |||
| Random Forest | 16.73 | — | — | — | X | |||
| RDA | 79.01 | — | — | — | X | |||
| LDA | 29.52 | — | — | — | X | |||
| QDA | 57.89 | — | — | — | X | |||
| DT | 14.22 | — | — | — | X | |||
| KNN | 17.95 | — | — | — | X | |||
| C4.5 | 18.30 | — | — | — | X | |||
| SVM | 60.10 | 12.45 | X | X | ||||
| CNN scratch VGG-16 | 25.50 | 85.20 | X | X | ||||
| CNN-VGG-16-TL | 20.30 | 70.45 | X | X | ||||
| ViT | 30.80 | 77.65 | X | X |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alevizos, V.; Gkouvrikos, E.V.; Georgousis, I.; Karipidou, S.; Papakostas, G.A. Inspiring from Galaxies to Green AI in Earth: Benchmarking Energy-Efficient Models for Galaxy Morphology Classification. Algorithms 2025, 18, 399. https://doi.org/10.3390/a18070399
Alevizos V, Gkouvrikos EV, Georgousis I, Karipidou S, Papakostas GA. Inspiring from Galaxies to Green AI in Earth: Benchmarking Energy-Efficient Models for Galaxy Morphology Classification. Algorithms. 2025; 18(7):399. https://doi.org/10.3390/a18070399
Chicago/Turabian StyleAlevizos, Vasileios, Emmanouil V. Gkouvrikos, Ilias Georgousis, Sotiria Karipidou, and George A. Papakostas. 2025. "Inspiring from Galaxies to Green AI in Earth: Benchmarking Energy-Efficient Models for Galaxy Morphology Classification" Algorithms 18, no. 7: 399. https://doi.org/10.3390/a18070399
APA StyleAlevizos, V., Gkouvrikos, E. V., Georgousis, I., Karipidou, S., & Papakostas, G. A. (2025). Inspiring from Galaxies to Green AI in Earth: Benchmarking Energy-Efficient Models for Galaxy Morphology Classification. Algorithms, 18(7), 399. https://doi.org/10.3390/a18070399








