In this section, we apply tools from dynamical systems and chaos theory to guide the selection of parameter values in our fractional-order schemes. This approach facilitates the selection of suitable initial guesses, which can improve both the convergence rate and the accuracy in solving complex nonlinear problems.
3.1. Chaos-Based Parameter Optimization and Bifurcation Diagrams
Stability and bifurcation analysis in iterative schemes has emerged as a significant area of research in the development of numerical methods for solving nonlinear engineering models. These phenomena are often investigated through bifurcation diagrams, Lyapunov exponent plots [
22], and detailed visualizations of basins of attraction, which illustrate how small variations in initial guesses or iteration parameters can substantially influence convergence outcomes. Fractal basin boundaries and the high sensitivity to initial conditions show how chaotic dynamics in iterative methods can be highly complex and difficult to predict.
When these concepts are applied to fractional-order iterative methods for solving nonlinear equations, the presence of memory effects associated with fractional derivatives introduces additional challenges. In such schemes, each iteration depends not only on the current state but also on the full history of the process. This memory dependence alters the stability characteristics and the conditions under which chaotic behavior may emerge. Key factors influencing the dynamics of fractional iterative schemes include the fractional order parameter
, the choice of initial values, the memory kernel, the structure of the nonlinearity, and the specific definition of the fractional derivative employed (e.g., Caputo and Riemann–Liouville [
23]). Compared with classical integer-order methods, fractional-order schemes solve the same underlying problem by using derivatives that incorporate memory effects. These additional features can significantly influence the system’s behavior: they may shift the point at which bifurcations occur, delay or hasten the onset of chaotic dynamics, and lead to more complex and detailed patterns in the system’s evolution (see
Table 1).
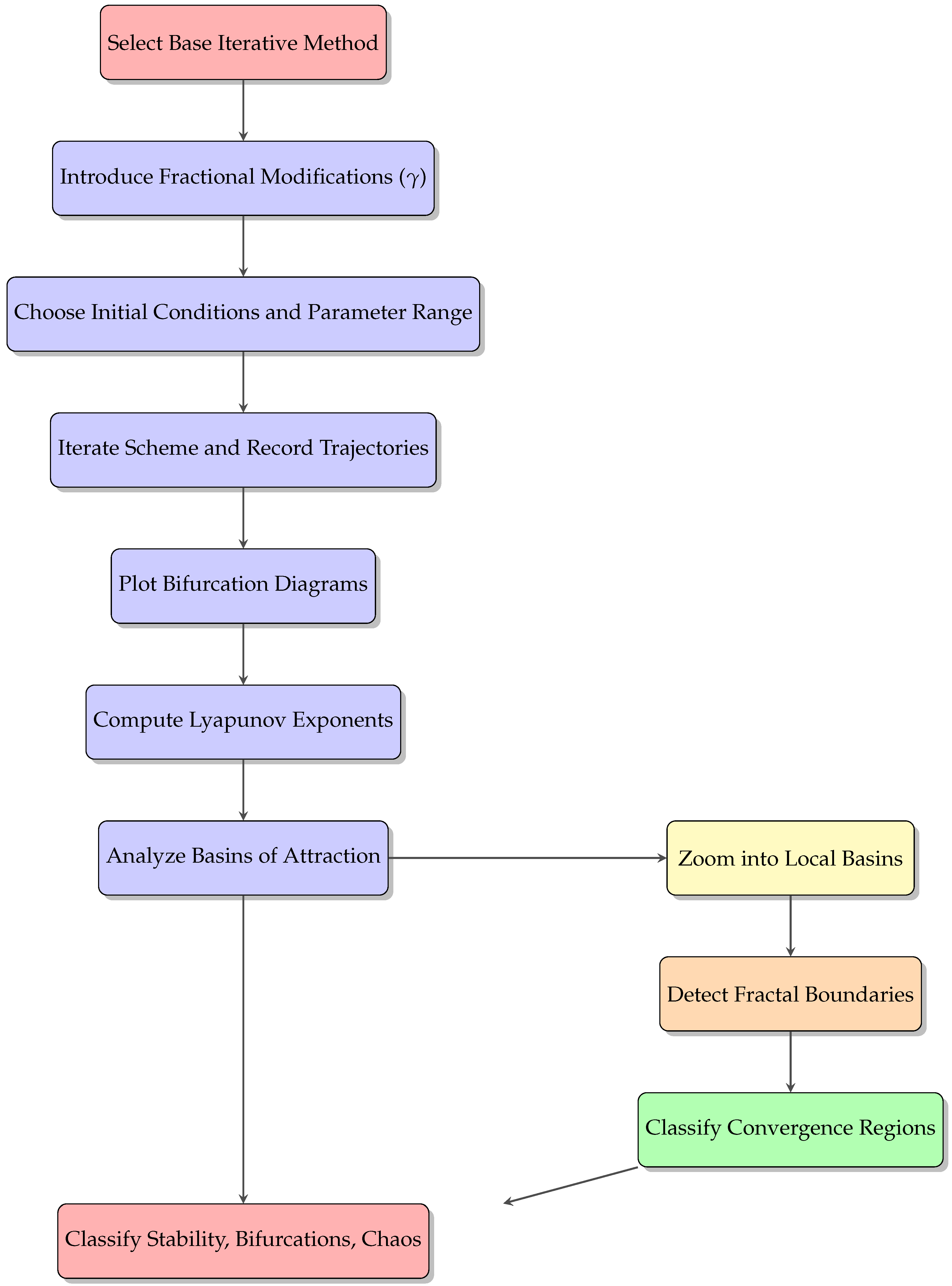
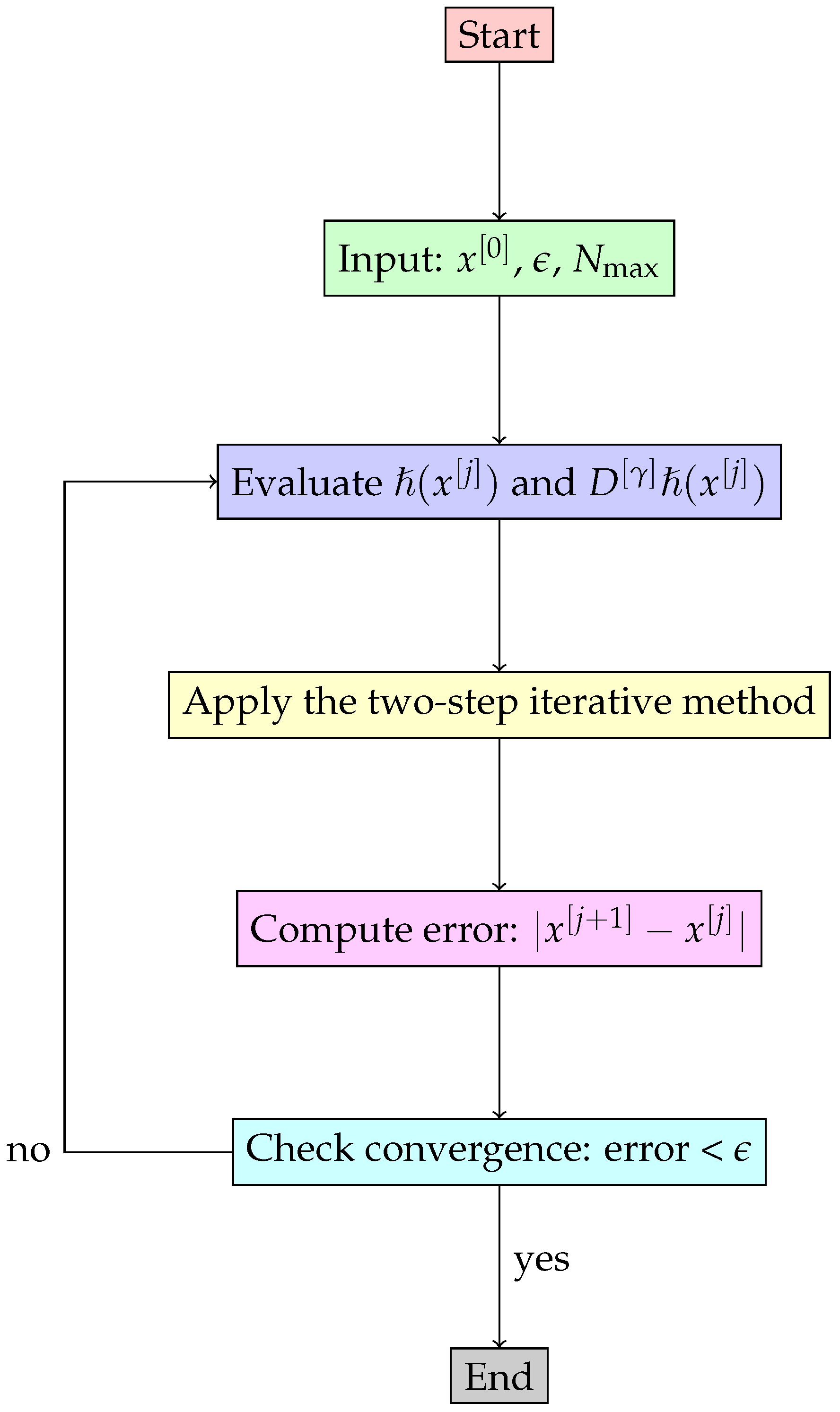
To investigate the emergence of chaos in fractional-order iterative models, we adopt a general computational framework (see the flowchart in
Figure 1). This approach involves selecting a base iterative method, introducing fractional-order modifications, systematically varying key parameters, computing the resulting Lyapunov spectra and bifurcation diagrams, and analyzing the associated stability regimes. To study bifurcation and chaos in the context of fractional-order schemes, we consider the nonlinear function
This function serves as a representative case for exploring the dynamical behavior of iterative processes, particularly under the influence of the damping parameter
, as discussed in [
24,
25]. When the parameter
is varied within the fractional iterative method, the system exhibits significant changes in behavior. As
crosses certain critical values, the system transitions through different dynamical regimes—namely, stability, bifurcation, and chaos. These transitions are summarized in
Table 1.
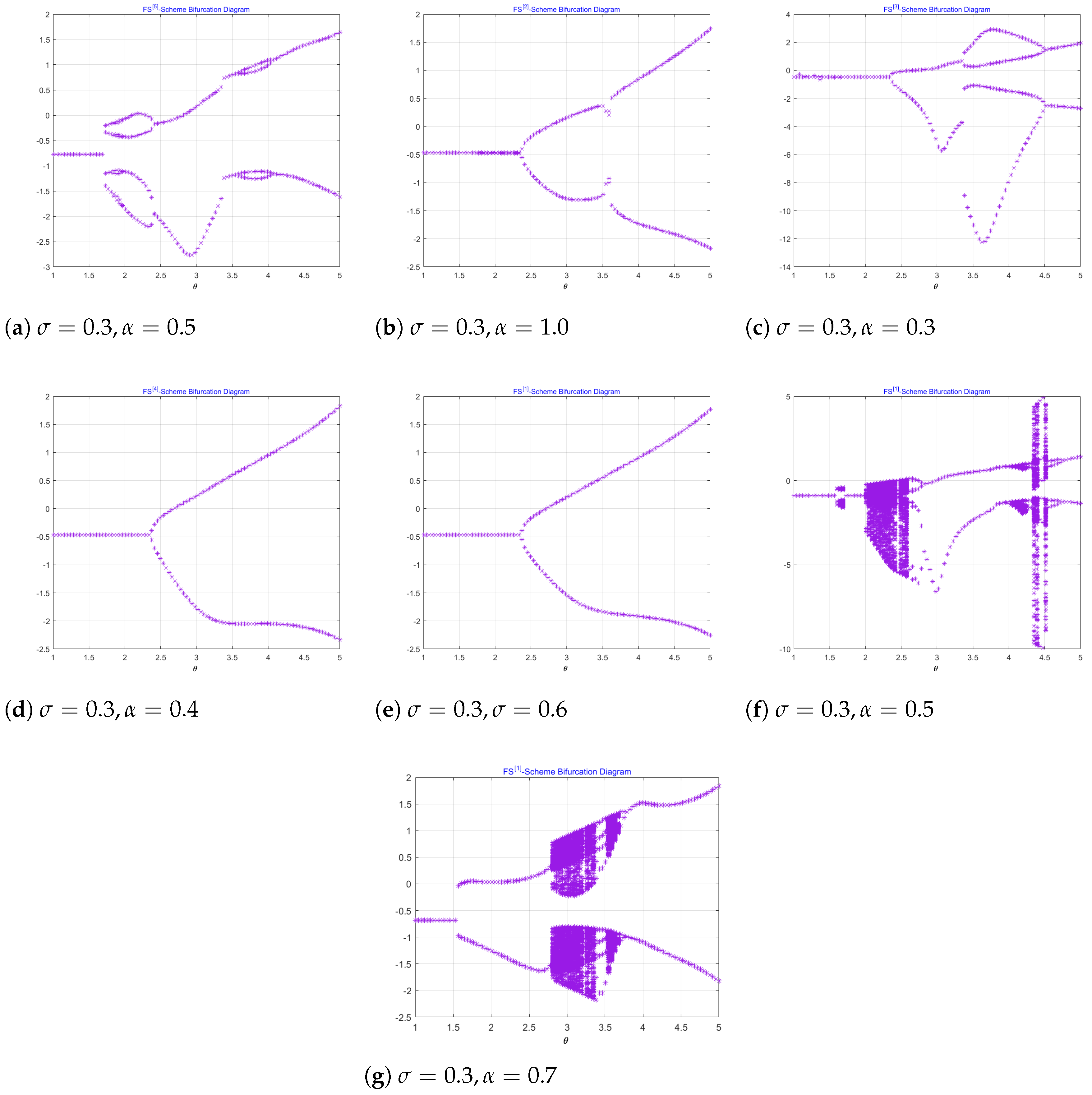
Figure 2a–g present the corresponding bifurcation diagrams, where the y-axis indicates the steady-state or long-term values of the system variable and the x-axis represents values of the parameters
and
. These diagrams illustrate how the nature of the solution—whether a fixed point, a periodic orbit, or a chaotic trajectory—evolves as the parameters change.
The iterative sequence remains stable for small to moderate values of
, leading to smooth and predictable convergence toward fixed points or periodic orbits (see
Figure 2a–e). As
increases, the system experiences period-doubling bifurcations (
Figure 2c–f), transitioning from simple periodic behavior (e.g., one-period cycles) to increasingly complex periodic patterns (e.g., two-period and four-period orbits). Further increases in
lead to chaotic behavior in the iterative scheme (
Figure 2f,g), characterized by a loss of periodicity and the emergence of irregular, scattered trajectories that exhibit high sensitivity to initial conditions.
This chaotic regime reflects the system’s strong nonlinearity and its tendency to diverge in certain parameter ranges. Deterministic chaos implies that small variations in or initial values can produce significantly different outcomes. However, the system also exhibits transitional zones where, through suitable adjustments of the parameters, the dynamics can return to stability. Within these zones, the system may resume convergence to stable fixed points or periodic orbits, indicating that chaotic behavior is both parameter-dependent and potentially reversible.
Table 1 presents an analysis of the bifurcation behavior of the iterative scheme, highlighting both stable and unstable dynamical regions. The notation is as follows:
denotes stability;
marks the onset of bifurcation;
indicates period doubling;
corresponds to higher-order periodic transitions (e.g., four-period and eight-period cycles); and
represents the chaotic regime, where the scheme becomes unstable for all values of
and
. All bifurcation diagrams are generated for
. These observations underscore the importance of carefully selecting and tuning damping parameters in iterative parallel methods, particularly in engineering applications where robustness and convergence stability are critical. The bifurcation analysis and visualizations presented in this study clearly illustrate how parameter variations influence the system’s dynamical structure and convergence behavior.
In practical applications, this approach enhances convergence stability by identifying parameter ranges that lead to chaotic dynamics and providing guidance for their adjustment. A deeper understanding of chaotic behavior in fractional iterative schemes supports the development of more reliable solvers for highly nonlinear engineering problems, including those with multiple roots, sensitive dependencies, or fractional-order characteristics.
The integration of chaos with fractional iterative schemes offers several advantages:
Chaotic sequences enhance the exploration of the solution space, reducing the likelihood of premature convergence.
Fractional memory effects contribute to smoother iteration behavior and mitigate abrupt changes in the solution trajectory.
This combined strategy enables the application of iterative methods to challenging classes of nonlinear problems, such as those exhibiting multistability, sensitivity to initial conditions, or ill-posed behavior.
3.2. Dynamical Analysis for Parameter Tuning via Bifurcation and Chaotic Behavior
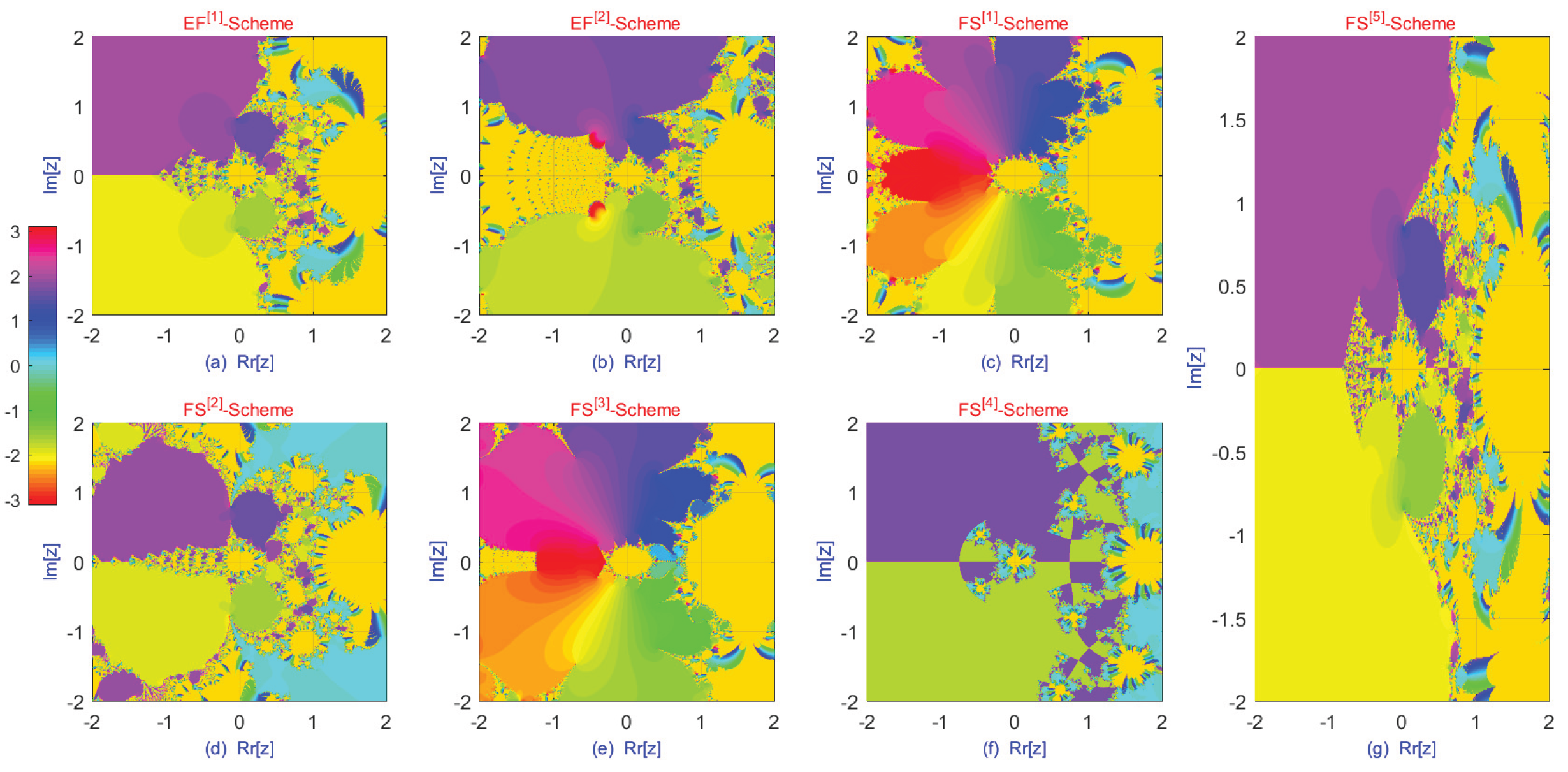
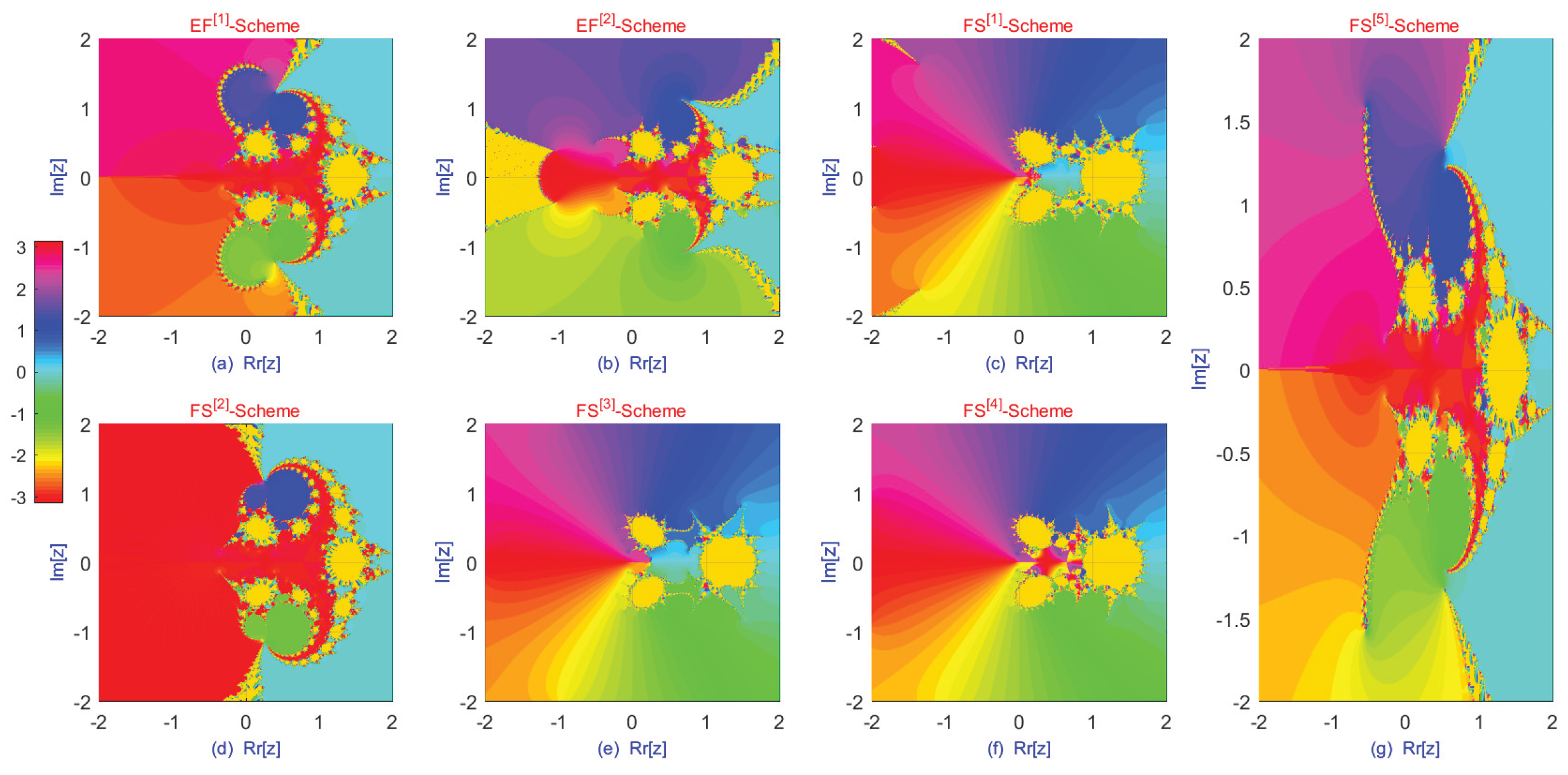
In addition to conventional analyses based on spectral radius or contraction mappings, the study of
dynamical planes offers further insights into the stability properties of fractional-order iteration schemes. A dynamical plane is a graphical representation in which each point in the complex (or real) plane corresponds to an initial guess, and its color indicates the behavior of the iteration—specifically, whether it converges to a root (or attractor) or diverges [
26,
27,
28]. In fractional-order schemes, the memory effect governed by the fractional order
, along with any introduced chaotic perturbations, significantly influences the structure of these planes. For stable schemes, the dynamical plane typically exhibits wide, smooth, and well-separated basins of attraction associated with different roots or solutions, reflecting robustness to initial guesses. The boundaries between these basins are often fractal, indicating sensitivity to initial conditions. Lowering the fractional order
tends to smooth these fractal boundaries, thereby reducing sensitivity and enlarging regions of stable convergence. Properly tuned chaotic components can help prevent the iteration from becoming trapped in non-optimal attractors; however, excessive chaos may distort the basin structure, leading to fragmented or discontinuous convergence regions and signaling instability.
Moreover, dynamical planes provide a more comprehensive view of global stability than local linearization techniques. As parameters such as and vary, bifurcation phenomena—abrupt transitions from connected, stable basins to highly fragmented and chaotic regions—can be visually identified. This visual framework enables researchers to distinguish between stable and unstable parameter regimes and assess the robustness of an iterative method in the presence of noise or imprecise initial guesses. In engineering contexts where initial conditions are uncertain or only approximately known, this global perspective is especially valuable. Consequently, dynamical plane analysis serves as a powerful complement to traditional mathematical stability proofs, particularly for fractional-order iterative methods incorporating chaotic dynamics.
The following rational map
is obtained by applying the fractional order to the polynomial
, yielding
where
By applying a Möbius transformation of the form
, the map
becomes conjugate to the function
, given by
for
, and this representation is independent of the parameters
a and
b [
29]. The rational maps corresponding to other fractional-order schemes are given as follows:
Interpretation of Dynamical Planes for Stability Analysis Using Chaos
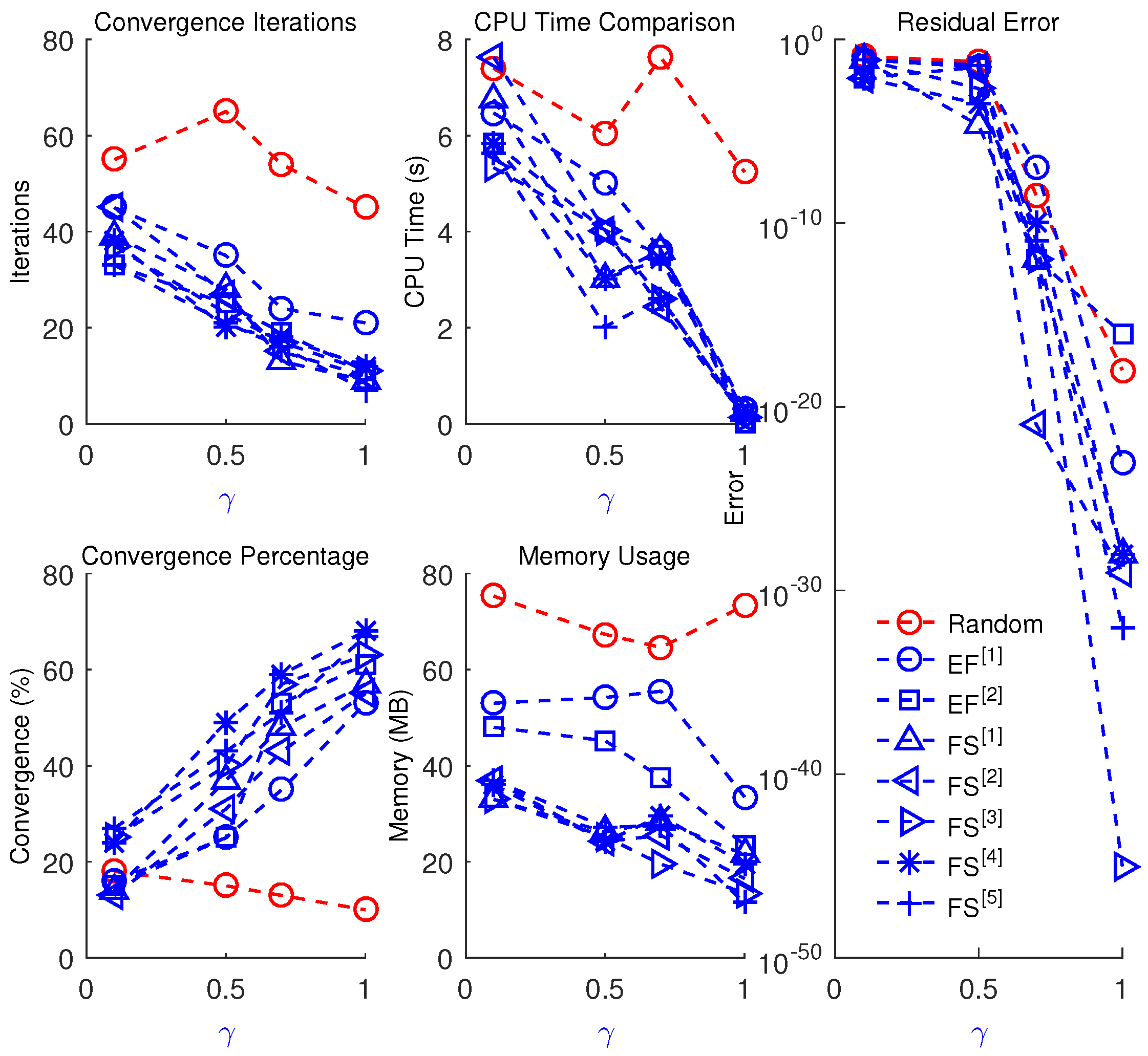
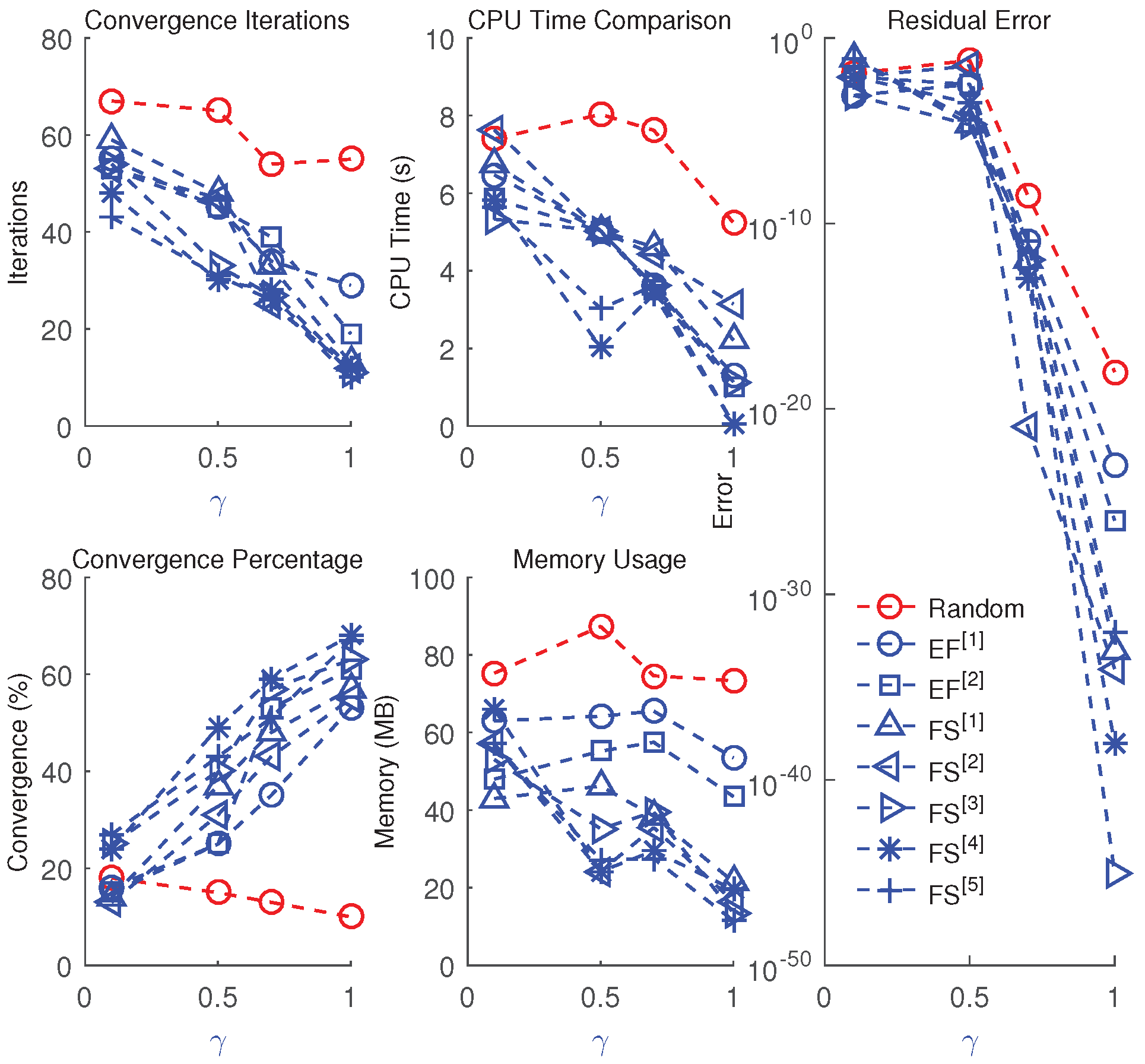
Based on the bifurcation and chaos analysis, the values of the fractional parameter significantly affect the system’s dynamics. These changes correspond to specific regions identified in the bifurcation diagram, as outlined below:
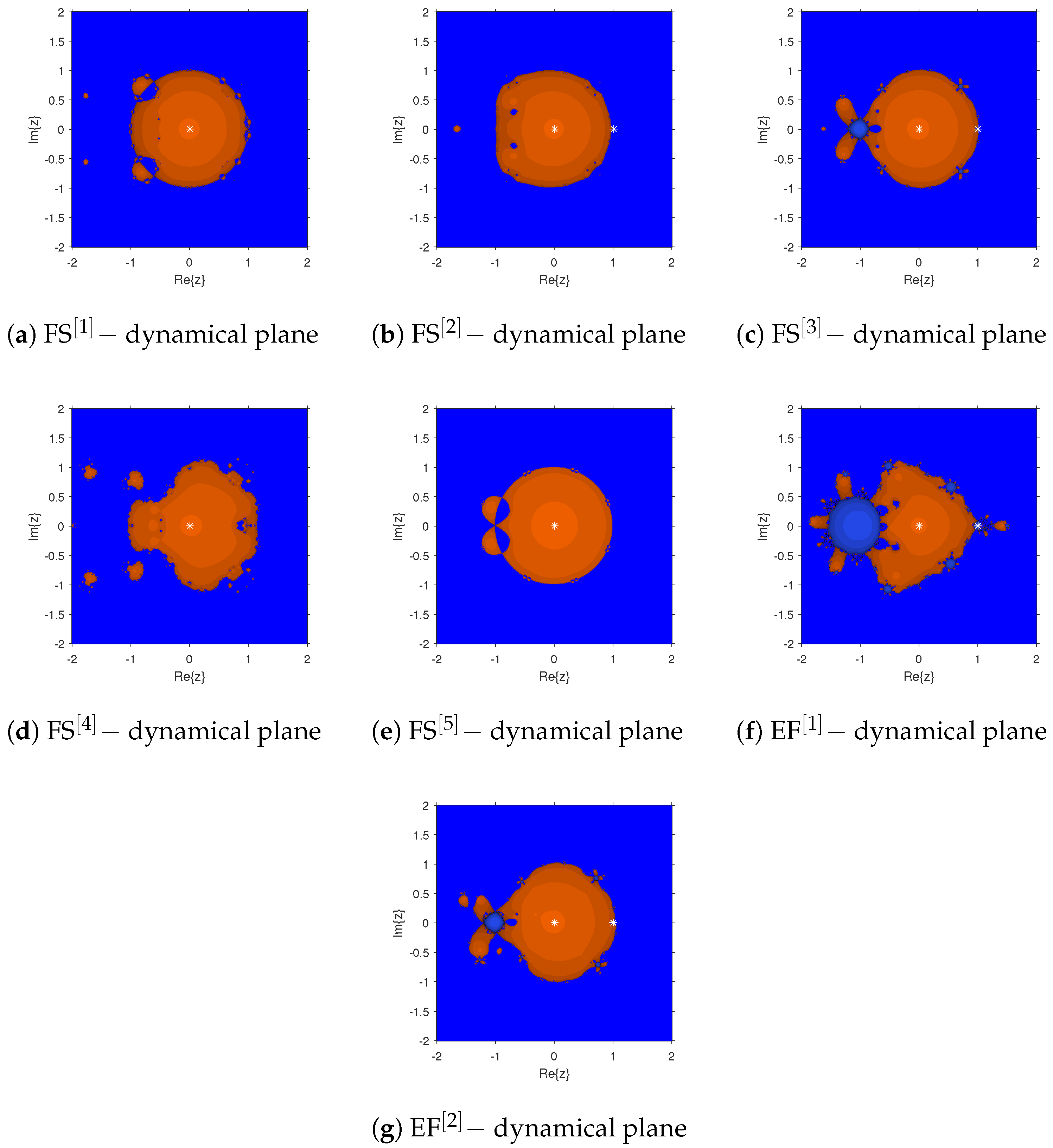
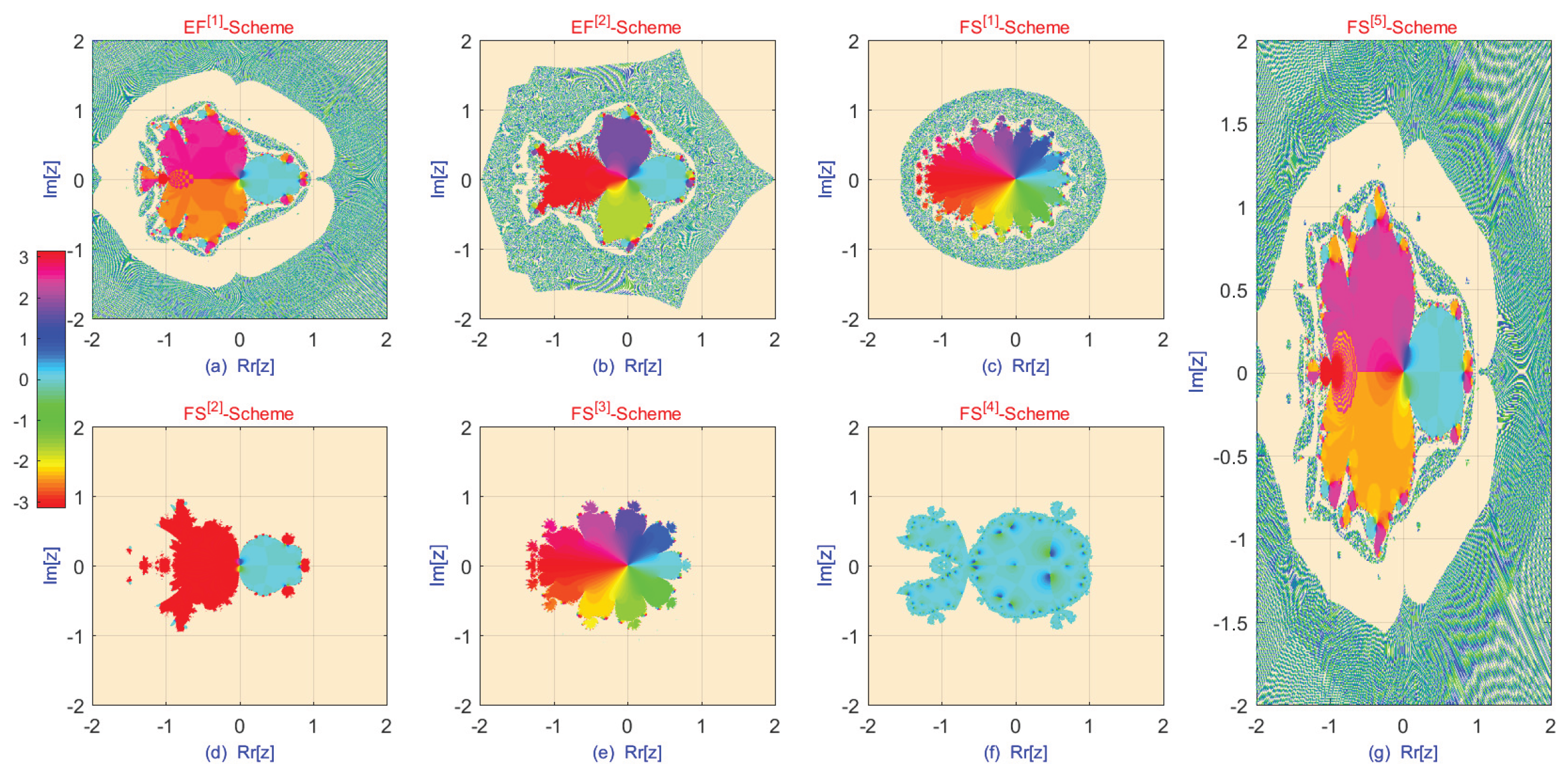
Smooth, Connected Basins: Selecting values of
and
from the stable region (
Table 1, Column 4;
Figure 2a–g), where no bifurcations are present, leads to stable dynamical behavior in the iterative schemes (
Figure 3a–e).
Robust Convergence near Bifurcations: When
is chosen near the first or second bifurcation thresholds (
Table 1, Columns 5 and 6), the dynamical plane (
Figure 3f) still exhibits stability. In these cases, large basins indicate robustness, and convergence can be achieved even from coarse initial guesses, albeit at a slower rate.
Higher-Period Bifurcation Regions: For parameter values corresponding to higher-order bifurcations (e.g., four- and eight-period cycles; see
Table 1, Column 7), the schemes continue to display stable behavior, as shown in
Figure 3g. However, convergence is typically slower and involves a higher computational cost.
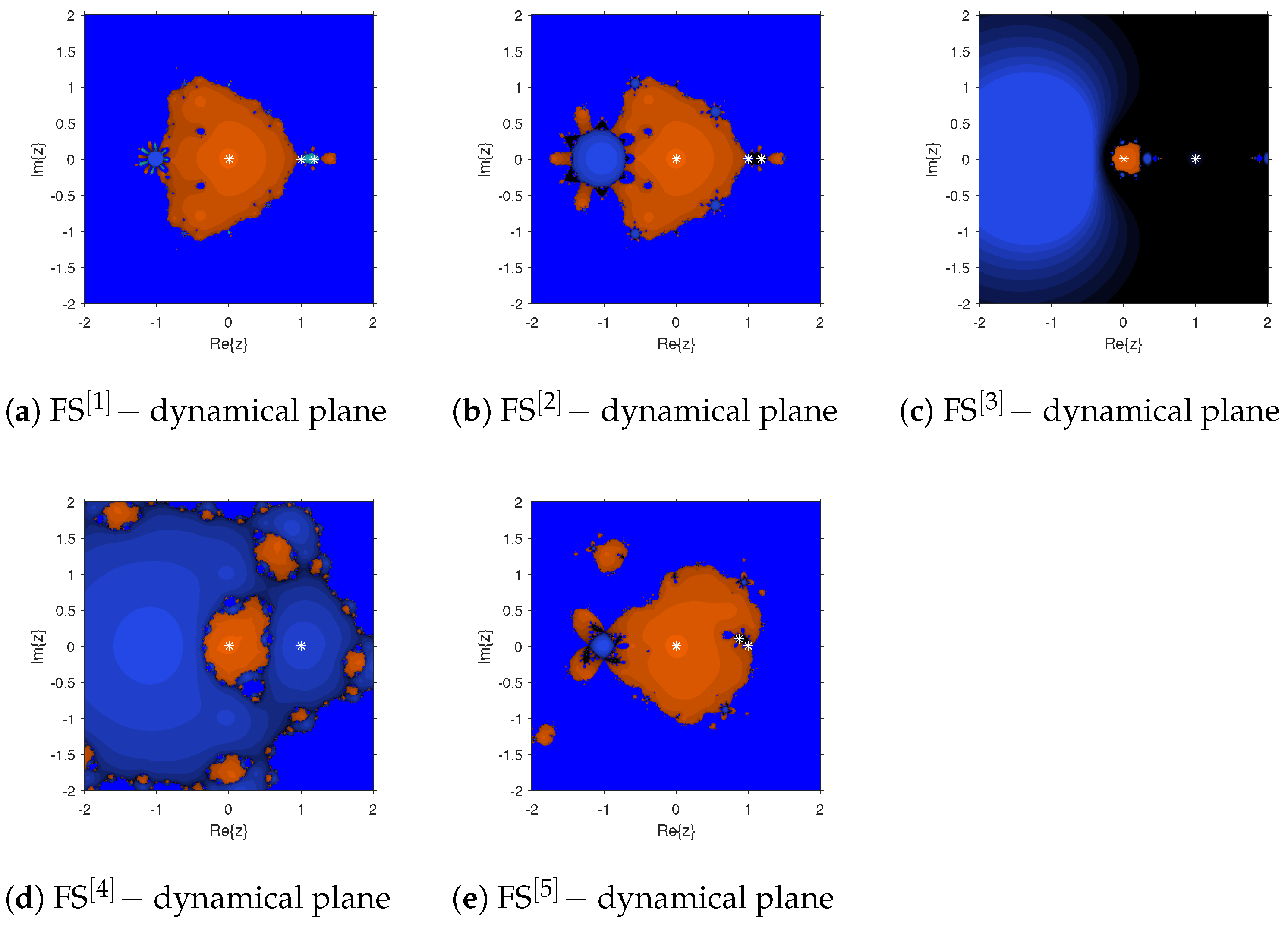
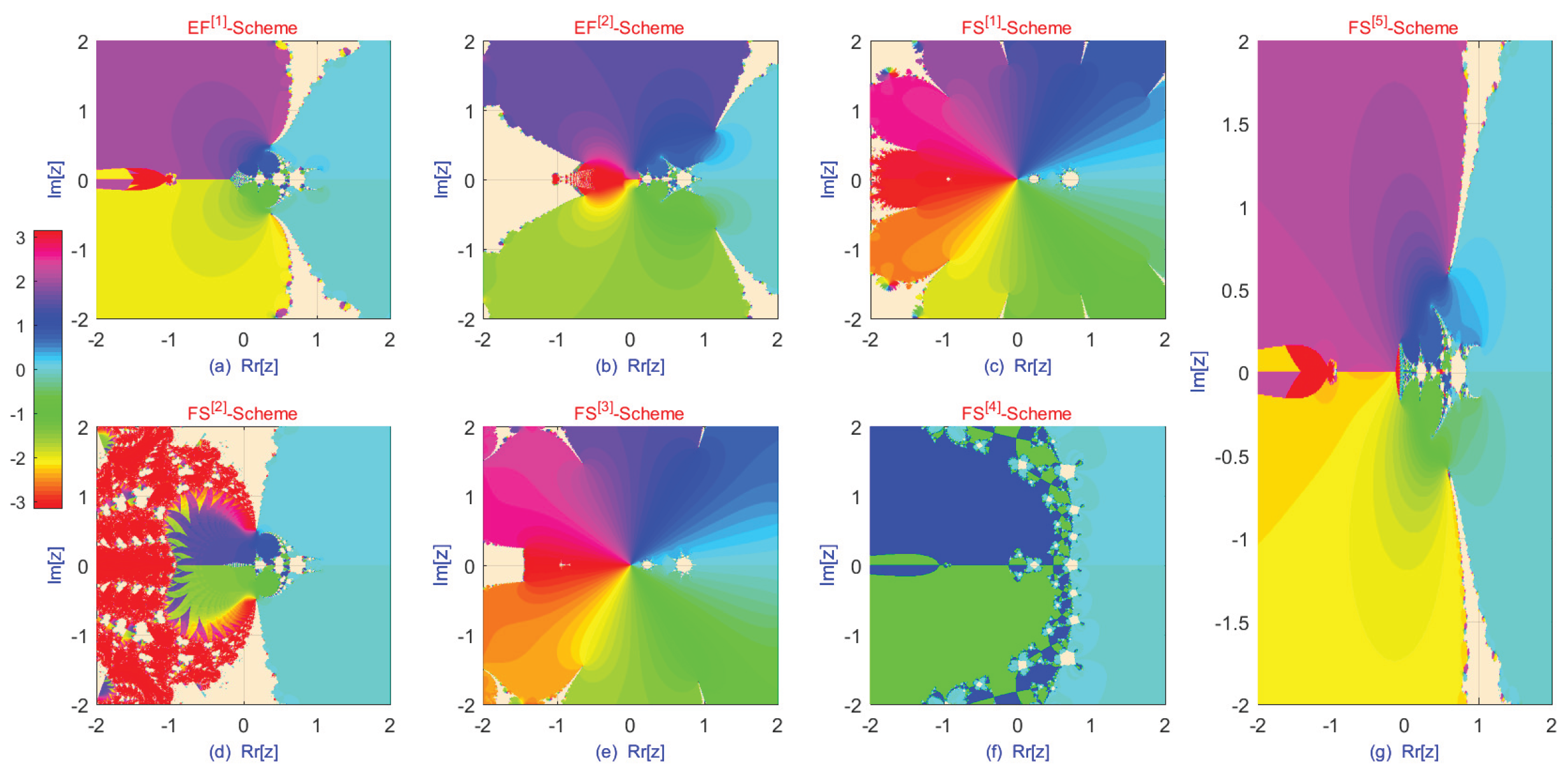
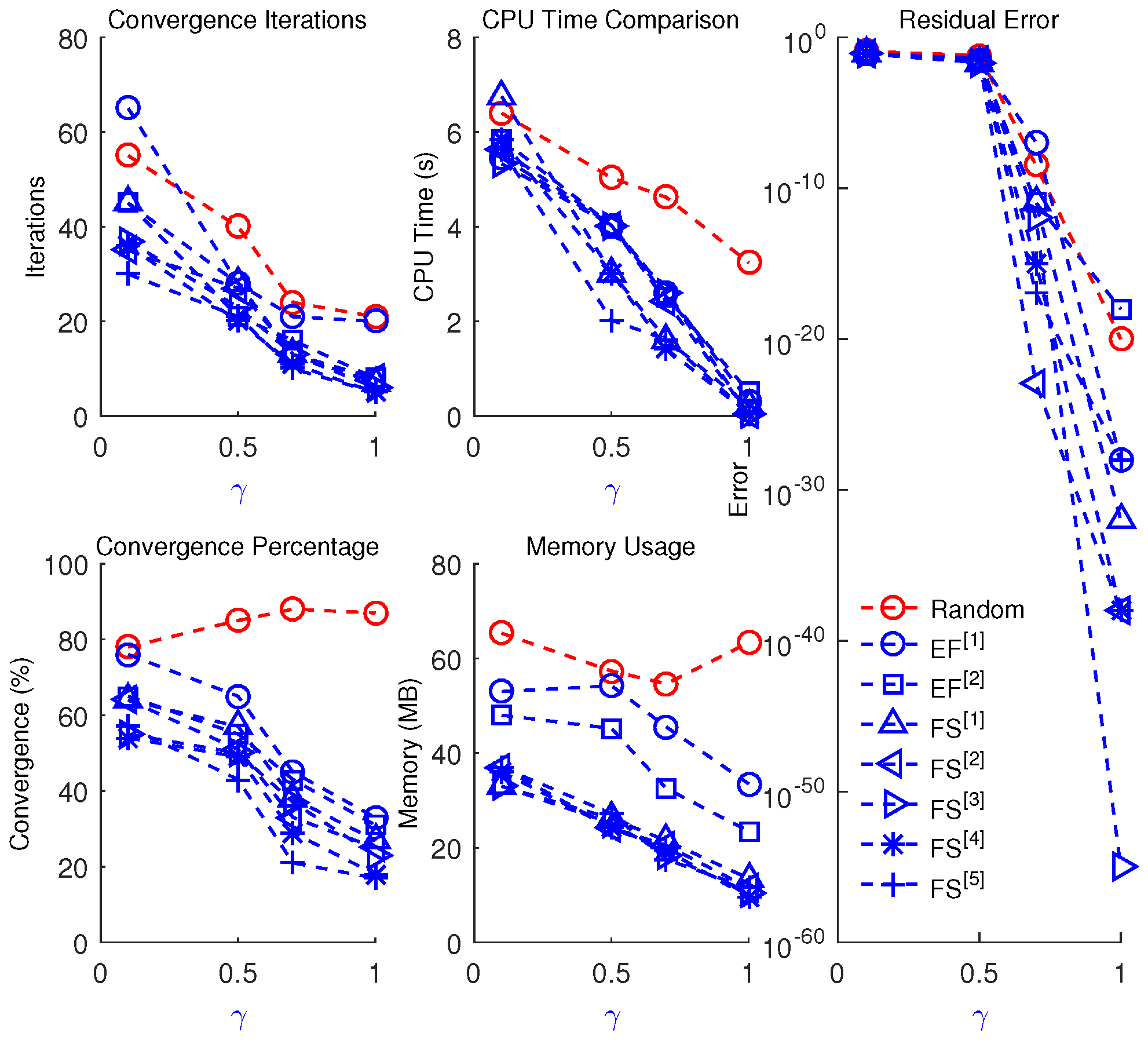
Disconnected or Scattered Basins: In regions associated with chaotic or unstable behavior (
Table 1, Column 8), the iteration may converge to unintended solutions or fail to converge altogether. These behaviors are illustrated in
Figure 4a–e, where the parameter
lies within the chaotic regime.