Abstract
This study introduces an Enhanced Error-Adaptive Extended-State Kalman Filter Model Predictive Control (EEA-ESKF-MPC) method to tackle strong coupling and inertia in supercritical power plants. By enhancing the ESKF-MPC framework with a mechanism that dynamically adjusts error weights based on real-time deviations and employs exponential smoothing, alongside a BP neural network for thermal unit simulation, the approach achieves superior performance. Simulations show reductions in the Integrated Absolute Error (IAE) for load and temperature by 3.05% and 2.46%, respectively, with a modest 0.43% pressure IAE increase compared to ESKF-MPC. Command disturbance tests and real condition tracking experiments, utilizing data from a 350 MW supercritical unit, reinforce the method’s effectiveness, highlighting its exceptional dynamic performance and precise tracking of operational parameter changes under multivariable coupling conditions, offering a scalable solution for modern power systems.
1. Introduction
Despite the increasing adoption of renewable energy in modern power grids, supercritical coal-fired power plants still play a key role in modern energy systems, offering higher thermal efficiency and lower emissions compared to traditional subcritical designs [1]. However, the complex boiler–turbine systems of these plants pose significant control challenges due to their strong multivariable coupling, large inertia, and obvious nonlinearity [2]. Traditional control strategies, such as proportional–integral–derivative (PID) controllers, have been widely employed [2,3]. While effective in simpler systems, PID controllers struggle to manage the intricacies of supercritical units, particularly under variable operating conditions. Time delays, parameter variations, and external disturbances often lead to suboptimal performance.
These limitations have prompted the exploration of more advanced solutions, with Model Predictive Control (MPC) emerging as a promising solution. MPC leverages a predictive framework to optimize control actions while respecting operational constraints, making it well suited to handling the multivariable interactions and nonlinearities inherent in power plants [4]. Researchers have developed various MPC variants to tackle specific challenges. Hui et al. [5] proposed an adaptive second-order non-singular terminal sliding mode control method, which effectively solved the lumped disturbance problem in nuclear power plant power control. López-Bautista et al. [6] suggested a robust Model Predictive Control solution for the control problem caused by solar radiation fluctuations in solar thermal power plants, which solved the uncertainty problem well. Yang et al. [7] proposed a dual-timescale nonlinear Model Predictive Control strategy (T-NMPC) to address the problems of dynamic response timescale mismatch, nonlinear control problems, and the difficulty of coordination between flexibility and stability in the coupled operation of coal-fired power plants and carbon capture systems. Frejo et al. [8] suggested a distributed Model Predictive Control algorithm based on logic to solve the problems of the high computational complexity of centralized Model Predictive Control (MPC) in parabolic trough thermal power field thermal power optimization, difficulties in the real-time control of large- and medium-sized power stations and the insufficient performance of local controllers.
However, MPC’s effectiveness hinges on the quality of its underlying dynamic model; traditional modeling methods such as transfer function [9] and state space [10,11,12] representation find it difficult to fully capture the nonlinear, time-varying dynamics of these systems, which complicates the development of precise control strategies. In order to enhance MPC’s performance, researchers have incorporated filtering techniques and neural network-based system identification. Standard methods like the Kalman Filter (KF) [13,14,15] offer optimal state estimation for linear systems, but the nonlinear nature of supercritical plants has driven the adoption of advanced variants, such as the Extended Kalman Filter (EKF) [16]. These approaches improve robustness by accounting for nonlinear dynamics and disturbances. Additionally, Guo et al. [17] proposed a Model Predictive Control (ESKF-MPC) strategy based on an extended-state Kalman Filter (ESKF) in view of the flexible peaking demand, energy-saving transformation problems, and control performance constrained by model uncertainty faced by coal-fired power plants with a high proportion of renewable energy that are under the grid. Kim et al. [18] proposed a steam generator pipeline degradation prediction method based on particle filter (PF), aiming to solve the problems existing in the aging management of nuclear power plant systems, such as the contradiction between the general aging model and the individual differences of the system, the insufficient accuracy of degradation prediction, and the uncertainty of measurement data affecting the reliability of evaluation. Meanwhile, machine learning have proven to be highly effective in modeling complex system behaviors [19,20], surpassing traditional methods like transfer functions and state-space models. By training on extensive operational data, neural networks accurately replicate the intricate dynamics of supercritical plants, providing a solid foundation for control improvements. There are also many studies on predictive control based on machine learning [21,22,23,24]. For example, Dong et al. [25] built a predictive model for nuclear superheated-steam supply systems (Su-NSSS) through multi-layer perceptron, and combined the model predictive control method to dynamically optimize the thermal power response of nuclear power plant Su-NSSS. Guo et al. [26] employed LSTM to accurately model the dynamic characteristics of supercritical power plants, and combined ESKF-EMPC to optimize the thermal power response. These combined advancements in filtering and identification have demonstrated tangible benefits in enhancing MPC’s adaptability and precision.
Despite these advancements, current MPC strategies, even when bolstered by advanced filtering techniques, encounter significant hurdles in meeting the dynamic control needs of supercritical coal plants. For instance, while the EKF and its extended-state variant enhance disturbance rejection, their static parameter configurations struggle to cope with rapid operational shifts, such as those driven by fluctuating grid demands or aging infrastructure. Existing MPC variants, including distributed and dual-timescale approaches, often face trade-offs between computational efficiency and responsiveness, particularly under wide-ranging load conditions or when confronted with strong multivariable coupling and large inertia. These shortcomings reveal a critical gap in achieving real-time adaptability without sacrificing control precision or stability. For rapid changes in the operating conditions of supercritical power plants, a single filtering or modeling technique may still not be sufficient to fully optimize the control performance.
Therefore, the complex, dynamic and variable operating conditions of supercritical power plants require the control strategy to have higher adaptability. Adaptive control provides an effective way to achieve accurate and stable multivariable control by dynamically adjusting parameters to deal with nonlinearity, disturbance and parameter drift. Baldassarre et al. [27] combined digital twins with augmented state-extended Kalman Filters to model industrial system energy consumption and predict power consumption more accurately by dynamically updating parameters. Plankenbühler et al. [28] analyzed the quality of biomass fuel through image processing and machine learning, adaptively adjusted furnace setpoints to more accurately adapt to fuel changes, and improved the adaptive control ability of industrial furnaces. Hui et al. [5] used adaptive second-order non-singular terminal sliding mode control to dynamically estimate nuclear power plant disturbances and adjust control inputs to stabilize power more accurately.
In this study, backpropagation neural networks were used to create high-fidelity simulations of supercritical power plants that accurately reflect their complex properties. Building on this foundation, the main contribution of this work is the development of an enhanced error-adaptive error state Kalman Filter Model Predictive Control (EEA-ESKF-MPC) framework, which integrates a transfer function-based predictive model with an innovative adaptive error correction mechanism, combined with ESKF’s robust interference estimation. The EA-ESKF-MPC’s adaptive mechanism goes beyond standard filtering by dynamically adjusting control priorities based on real-time deviations and using exponential smoothing to reduce overreaction to transient disturbances and ensure smooth and stable control actions. This adaptability significantly improves the tracking accuracy and system stability compared to fixed-parameter KF or ESKF methods, providing a tailored solution to the multivariable coupling and large inertia challenges inherent in supercritical power plants.
2. Methodology
2.1. Supercritical Power Generation System
Figure 1 shows the structure of a supercritical unit. The fuel burns in the furnace to release heat. After the feed water is pressurized, it is preheated by the economizer and re-entered into the water wall to absorb the heat of the high-temperature flue gas into the water vapor mixture, because the supercritical pressure has no obvious phase interface. The steam is extracted by the separator, passes through the superheater and reheater to become high-temperature and high-pressure supercritical steam, and drives the steam turbine to convert the heat energy into mechanical energy. The turbine drives the generator to generate electricity, and the electric energy is sent to the power grid through the transformer. The exhaust steam is recycled after condensation. This process efficiently converts the chemical energy of the fuel into electricity, and the supercritical unit improves efficiency and reduces coal consumption and emissions.
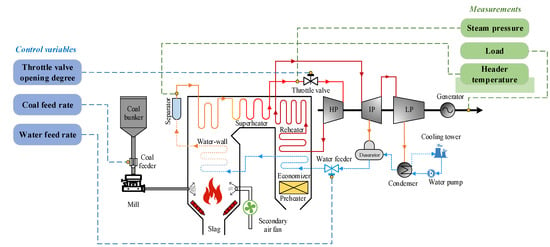
Figure 1.
Schematic diagram of a supercritical power generation system.
2.2. System Modeling and Identification
The transfer function method and the neural network method are used to identify the model of the generator set, respectively. The two identification models obtained in the end will be used as the prediction model inside the MPC controller and the controlled model of the simulation process.
The neural network model architecture is depicted in Figure 2. Drawing on prior research [29], we selected an appropriate neural network structure and training parameters to optimize performance. The dataset for parameter identification was split into a training set and a validation set at a ratio of 8:2, with preprocessing steps such as normalization applied to ensure data consistency. The Adam optimization algorithm was employed for training, with a learning rate set to 0.01. Additionally, an early stopping mechanism was implemented to halt training if the validation set error did not improve for 10 consecutive epochs, preventing overfitting and enhancing model generalization.
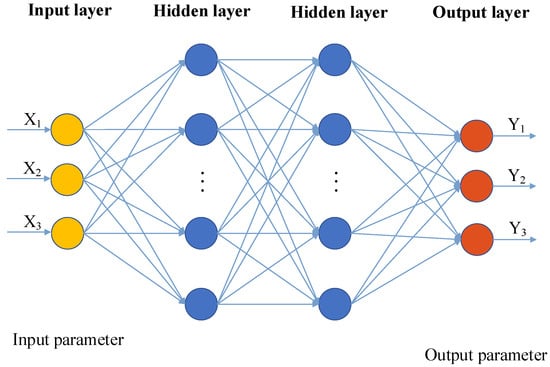
Figure 2.
Schematic diagram of the BP model.
For the transfer function identification method, the tools in the MATLAB R2024B identification toolbox are used, and the transfer function model is defined in the following form:
where G(s) is the transfer function, representing the relationship between the system’s output and input. num(s) is a molecular polynomial that represents the zero of the transfer function. den(s) is the denominator polynomial, representing the poles of the transfer function. s is the complex frequency, a variable in the Laplace transform.
where a1, a2, … an is the coefficient of the denominator polynomial. b1, b2, … bn is the coefficient of the molecular polynomial. n is the order of the denominator polynomial, representing the order of the system.
2.3. Design of the Enhanced Error-Adaptive ESKF-MPC
In order to use the transfer function model in a digital controller, it needs to be converted from a continuous time domain (S-domain) to a discrete time domain (Z-domain). In a real system, the input signal u(t) is usually kept sampled by zero-order, i.e., constant over each sampling period . Therefore, the discretization equation of the transfer function is as follows:
where denotes the inverse Laplace transform, denotes the Z-transform, and is the sampling period.
The discrete transfer function can be converted into a difference equation. Take single-input single-output as an example:
The corresponding difference equation is summarized as follows:
For a multiple-input multiple-output system, each output is a linear combination of all inputs :
where and are the coefficients of , and and are the orders of the corresponding transfer function.
For ESKF state estimation, the transfer function is converted into an observable canonical form:
where is the disturbed state, and is the disturbed rate of change noise.
The equation for prediction is as follows:
The equation for updating is as follows:
The prediction model of MPC predicts the future step output based on the difference equation:
The prediction vector is as follows:
The objective function is as follows:
The secondary form is as follows:
where and are, respectively, the output error weight matrix and control increment weight matrix. The constraint is set to the following:
In this paper, the core innovation of the adaptive mechanism lies in incorporating a dynamic weight into the optimization objective of MPC, which modulates the error weight Sq for each prediction step. By dynamically adjusting , the prediction steps exhibiting larger errors are assigned higher weights, enabling the controller to prioritize optimizing the tracking performance of those steps. This selective prioritization enhances the overall tracking accuracy and robustness, particularly in challenging scenarios like load variations in coal-fired power plants. The mathematical formulation of this adaptive weighting, as presented in the accompanying equation, forms the foundation of the EA-ESKF-MPC framework. This mechanism ensures that the controller adapts to real-time operational dynamics, improving performance over traditional MPC approaches. The basic EA-ESKF-MPC introduced here serves as the starting point for further refinements, as detailed in the subsequent sections.
To further enhance the adaptability of the dynamic weight , an amplification factor is introduced to make more responsive to prediction errors, particularly when errors are significant. This amplification ensures that the controller can swiftly address large deviations, improving tracking performance in critical operating conditions, such as rapid load changes in power plant control. However, overly rapid adjustments to driven by transient error spikes could lead to excessive control actions, potentially causing instability or oscillations in the system. To address this, an exponential smoothing filter is applied to , as shown in the corresponding equation. This filter smooths out abrupt changes in , ensuring that the controller remains stable and responsive without overreacting to short-term fluctuations. The combination of amplification and smoothing allows the EA-ESKF-MPC to achieve a balance between sensitivity to errors and steady control performance, making it well suited to industrial applications, where both precision and reliability are paramount.
To verify the stability of the EEA-ESKF-MPC, a Lyapunov-based stability analysis was performed. A Lyapunov candidate function is defined as follows:
where represents the tracking error vector for the MIMO system outputs (steam pressure, unit load, and header temperature), and P is a positive definite matrix ensuring . The control law, incorporating the adaptive weights and exponential smoothing filter, minimizes the error dynamics. Stability is assessed by evaluating the time difference , which must satisfy for asymptotic stability. The MPC optimization ensures that the control input reduces the predicted error , while the ESKF updates provide accurate state estimation under disturbances, as validated in the disturbance tests (Section 3.3). The exponential smoothing filter prevents abrupt changes in , avoiding oscillatory control actions that could destabilize the system. For bounded errors and disturbances, as observed in the load variation tests (70–320 MW, Section 3.2), the closed-loop system satisfies , confirming asymptotic stability across the operating conditions. This analysis demonstrates that the adaptive error mechanism and robust ESKF estimation enhance the tracking performance while maintaining system stability, supporting the controller’s reliability for supercritical power plant applications.
Through an iterative testing process, the amplification factor and smoothing factor of the basic EA-ESKF-MPC were carefully tuned, with the amplification factor selected from a range of 0 to 2 to balance sensitivity to prediction errors and system stability. After numerous adjustments, the values of 1.7 for the amplification factor and 0.8 for the smoothing factor were identified as an effective parameter combination, resulting in the enhanced EA-ESKF-MPC framework used in this paper. This configuration maintains strong adaptability to dynamic operating conditions, such as load variations in coal-fired power plants, while significantly improving the smoothness of the control actions, as evidenced by reduced oscillations in the control signal. Figure 3 is referenced as the control system schematic.
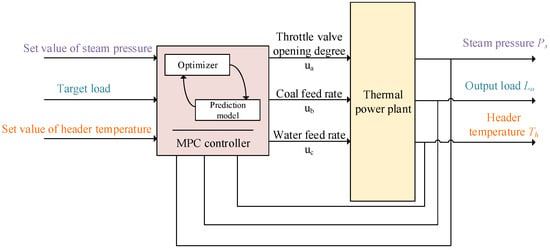
Figure 3.
Schematic of the control system.
The supercritical power plant is modeled as a multiple-input multiple-output (MIMO) system, with key control inputs including throttle valve opening, coal feed rate, and water feed rate, and corresponding outputs such as steam pressure, unit load, and header temperature. This MIMO structure inherently exhibits strong coupling and pronounced nonlinearity, thereby demanding a control strategy capable of effectively managing these interdependencies. Although the derivation of the filter parameters in this study adopts a single-input single-output (SISO) formulation for the sake of clarity and conciseness, the proposed EEA-ESKF-MPC framework is inherently designed to accommodate MIMO systems. The SISO formulation serves to elucidate the core mechanisms—adaptive error correction and exponential smoothing—in a more accessible manner. However, the actual controller implementation is based on a MIMO model, as reflected in both the architecture of the neural network and the multivariable optimization within the MPC scheme.
The methodology scales naturally across all input–output channels. It can tolerate weak coupling due to the robustness of the predictive model, while stronger coupling can be mitigated through existing decoupling strategies or appropriate tuning. This scalability enables the EEA-ESKF-MPC to coordinate all control inputs and outputs simultaneously, ensuring optimized performance across the complex dynamics of the supercritical unit.
2.4. Evaluation Index
In order to evaluate the effect of each model, the R2, RMSE and fit value were adopted as the evaluation indexes of the identification model, and the IAE and ME were selected as the performance evaluation indexes of the controller. The IAE takes into account the long-term operational performance of the control system, as well as the amplitude and duration of the error. It evaluates the control effect by calculating the cumulative sum of absolute errors. The smaller the IAE value, the closer the output of the control system is to the set value, and the better the control performance. The IAE takes into account the accumulation of errors throughout the control process, so that the performance of the control system can be evaluated more comprehensively. The ME is a comprehensive measure of the maximum difference between the actual output and the desired output. It is concerned with the maximum error that occurs during the control process. The smaller the ME value, the smaller the maximum deviation between the output of the control system and the set value, and the better the control performance. The ME emphasizes the extreme cases in the control process and can be used to evaluate the robustness and anti-interference ability of the control system. These indicators are defined in the following equation:
where y is the actual value, ŷ represents the predicted value, is the mean of the actual value, is the set value of the i-th control loop at the k-th sampling moment, and is the actual output value of the i-th control loop at the k-th sampling time. Δt is the sampling period.
3. Results and Discussion
3.1. Identification Model Validation
This study utilizes a 350 MW supercritical unit in China, with a dataset of 86,400 data points extracted over 24 h for the system identification process. These data encompass a wide range of operating conditions, including throttle valve opening (50–100%), coal feed rate (50–250 t/h), and water feed rate (180–1200 t/h) as inputs, and steam pressure (7.94–24.52 MPa), unit load (63.77–323.67 MW), and header temperature (303.22–409.01 °C) as outputs, ensuring robust training of the backpropagation neural network across steady-state and transient scenarios. To address the generalization ability of the neural network, particularly under unseen operating conditions, the training dataset was deliberately designed to cover the primary operating range of the unit, from around a 20% to 90% load. This range avoids low-load conditions below 20%, which risk boiler flameout, and high-load conditions above 90%, which may reduce the thermal efficiency and increase safety risks—scenarios rarely encountered in practice. While neural networks typically exhibit limited extrapolation performance outside the training data distribution, the selected data window sufficiently captures most real-world operating demands, ensuring model reliability within these bounds. The explicit testing of extrapolated scenarios (e.g., loads 10% above or below this range) was not conducted, but the comprehensive coverage of typical conditions supports the model’s practical applicability. To verify the accuracy of the identification model, an additional test dataset comprising 20,600 data points was used. The selected neural network architecture is a 3-9-18-9-3 structure, with input layer neurons corresponding to the throttle valve opening, coal feed rate, and water feed rate, and output layer neurons representing the predicted steam pressure, unit load, and header temperature. The transfer function model, in contrast, is a second-order system. The fit of both identification models against the test data was evaluated, with the results presented in Figure 4 and Table 1. Figure 4 demonstrates that both methods accurately capture trends in real field data. Table 1 highlights the neural network’s superior performance for steam pressure and header temperature, reducing the RMSE by 30.6% and 27.4%, respectively, and yielding higher coefficients of determination and fit values, indicative of better accuracy. However, for the unit load, the performance of both methods is comparable, with evaluation metrics on the same order of magnitude, likely due to the relatively smooth variation in load, which both models effectively capture. These findings underscore the neural network’s significant potential for unit parameter identification, offering enhanced capability to handle nonlinear systems and complex data compared to the traditional transfer function model, with a greater prediction accuracy and improved fit.
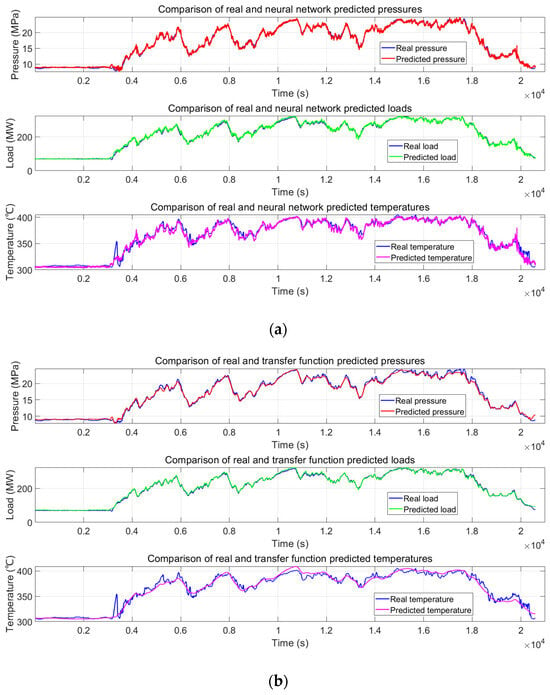
Figure 4.
Identification results of the identification model in the test set. (a) Neural network; (b) transfer function.

Table 1.
Prediction results of the two identification methods in the test set.
3.2. Load Variation Test
To evaluate the performance of the proposed Enhanced Error-Adaptive Extended-State Kalman Filter Model Predictive Control (EEA-ESKF-MPC) against baseline controllers, a load variation test was conducted across an extensive operating range from 70 MW to 320 MW. This range simulates the wide load fluctuations encountered in supercritical power plants, providing a rigorous evaluation of the controllers’ setpoint tracking capabilities under dynamic conditions. The simulation results, depicted in Figure 5 and summarized in Table 2, compare the EEA-ESKF-MPC against the standard ESKF-MPC, EA-ESKF-MPC, and traditional MPC through a Kalman Filter, focusing on the control of pressure, load, and intermediate point temperature.
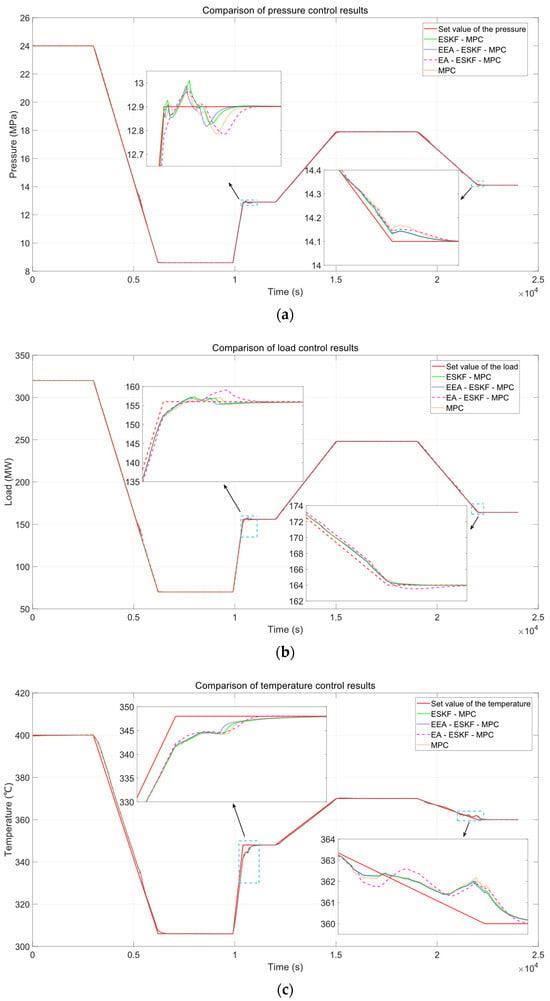
Figure 5.
Comparison of control results for controllers. (a) Pressure; (b) load; (c) temperature.

Table 2.
Comparison of control results of different controllers.
Figure 5 illustrates the dynamic responses of the process outputs under varying load conditions. In Figure 5a, the pressure response of the EEA-ESKF-MPC shows a slightly slower rise time compared to the ESKF-MPC, but it avoids the pronounced overshoot observed in the EA-ESKF-MPC, suggesting improved stability during transients. Figure 5b highlights the load tracking performance, where the EEA-ESKF-MPC closely follows the setpoint with minimal deviation, outperforming the EA-ESKF-MPC, which exhibits significant oscillations. Similarly, Figure 5c demonstrates that the EEA-ESKF-MPC maintains tighter temperature control compared to the baseline controllers, reducing fluctuations around the setpoint.
The quantitative metrics in Table 2 further elucidate these observations. For pressure control, the EEA-ESKF-MPC yields an IAE1 of 118.548, a marginal increase of 0.43% over the ESKF-MPC’s 118.045, and an ME1 of 0.285 MPa, slightly higher than the ESKF-MPC’s 0.283 MPa. This indicates a minor trade-off in pressure control precision, likely due to the prioritization of load and temperature tracking in the adaptive mechanism. In contrast, the load control performance is notably enhanced, with an IAE2 of 1651.894 (a 3.05% reduction from the ESKF-MPC’s 1703.785) and an ME2 of 4.754 MW (a 1.41% reduction over 4.809 MW), reflecting superior tracking accuracy and stability. For temperature control, the EEA-ESKF-MPC achieves an IAE3 of 3716.664, a 2.46% reduction from the ESKF-MPC’s 3810.075, and an ME3 of 6.099 °C, reduced by 2.23% from 6.242 °C, underscoring its effectiveness in minimizing temperature deviations.
Compared to the EA-ESKF-MPC and traditional MPC, the EEA-ESKF-MPC consistently outperforms across most metrics. The EA-ESKF-MPC, despite a lower IAE3 (3583.273), suffers from a significantly higher IAE1 (151.675) and IAE2 (3004.522), indicating poor handling of pressure and load under wide-ranging conditions. The traditional MPC, with IAE1, IAE2, and IAE3 values of 125.830, 1752.969, and 3859.232, respectively, lags behind in all aspects, highlighting the limitations of fixed-parameter approaches.
These results demonstrate that the EEA-ESKF-MPC, with its multiple dynamic error compensation and adaptive weighting (Equations (32) and (33)), effectively balances the trade-offs among pressure, load, and temperature control. The incorporation of an amplification factor and exponential smoothing enhances its responsiveness to large setpoint changes while maintaining smoothness, making it well suited for the multivariable coupling and large inertia of supercritical units. This tighter and more accurate control has the potential to reduce the use of coal and abatement water.
3.3. Instruction Disturbance Test
In order to further verify the effectiveness of the proposed EEA-ESKF-MPC strategy in actual power plant operation, this section tests its performance under command disturbance through simulation experiments. Three typical disturbance scenarios were designed in the experiment: throttle opening disturbance (3000 s), coal volume disturbance (6000 s), and water volume disturbance (9000 s), respectively, to simulate the interference of valve adjustment, fuel change, and water volume fluctuation in actual operation. Figure 6 shows the response of process outputs and control inputs, and Table 3 shows the IAE and ME metrics for different controllers.
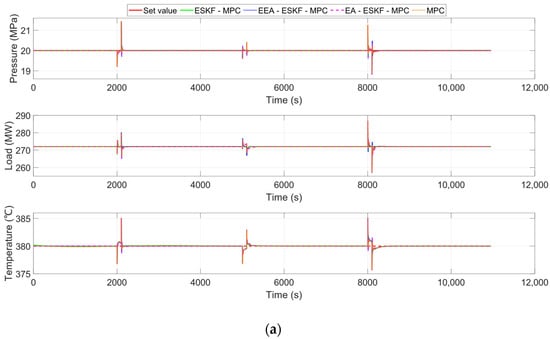
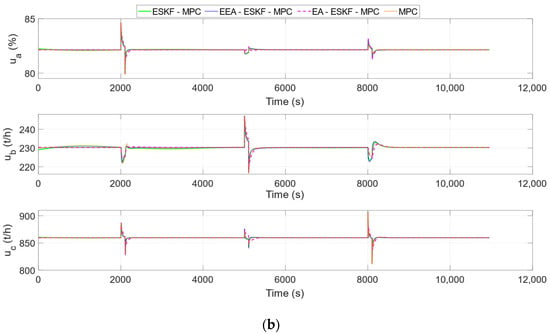
Figure 6.
Simulation comparison of control strategies in the uncertainty disturbances case. (a) Process outputs; (b) control inputs.

Table 3.
Control Performance of Different Controllers under Disturbance Cases.
Under the throttle opening disturbance (Case 1), the pressure IAE1 (7.473) of EEA-ESKF-MPC is lower than that of ESKF-MPC (7.837) and MPC (8.423), and the load IAE2 (47.529) and temperature IAE3 (37.314) are also significantly better than other controllers. In particular, it shows a strong error suppression ability in temperature control (IAE3 is about 41.7% lower than ESKF-MPC). This shows that the adaptive mechanism effectively improves the response ability to fast disturbances.
Under the coal feed disturbance (Case 2), the load IAE2 (37.170) of EEA-ESKF-MPC is lower than that of ESKF-MPC (38.490) and EA-ESKF-MPC (95.535), and the temperature IAE3 (44.765) is also better than that of other controllers. However, pressure IAE1 (3.058) was slightly higher than ESKF-MPC (2.973), possibly due to the insufficient adjustment of pressure errors by adaptive weights. The control input (Figure 6b) shows that the EEA-ESKF-MPC achieves good tracking performance while maintaining smoothness.
Under water feed disturbance (Case 3), EA-ESKF-MPC performs well in three indexes: the pressure IAE1 (9.540), load IAE2 (116.083), and temperature IAE3 (73.964) are all lower than ESKF-MPC and MPC, indicating its robustness to complex disturbances. The change in the ME index is small, indicating that the maximum deviation control ability is comparable to that of other controllers.
Overall, the EA-ESKF-MPC demonstrated excellent dynamic performance and robustness in the command perturbation experiments, especially in temperature and load control, which significantly reduced error accumulation. The adaptive weight mechanism enhances the adaptive ability of the system to the disturbance by dynamically adjusting the prediction error weight, and the exponential smoothing filter avoids the overreaction of the control input. These results further validate the potential application of EEA-ESKF-MPC in multivariable coupling control in supercritical power plants.
3.4. Real Condition Tracking
To validate the practical applicability of the proposed EEA-ESKF-MPC strategy, real condition tracking experiments were conducted using operational data from the Distributed Control System (DCS) of a 350 MW supercritical power plant. This test assesses the controller’s ability to track setpoints under realistic scenarios, including normal operation, load variations, and disturbance responses, thereby reflecting the complex dynamics of actual plant operations. The results, presented in Figure 7 and Table 4, compare the EEA-ESKF-MPC against the existing power plant controller (typically a PID-based strategy), focusing on pressure, load, and temperature tracking performance.
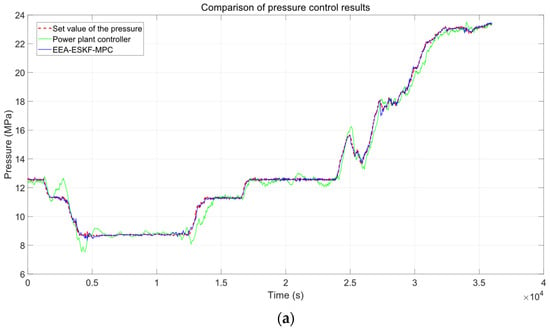
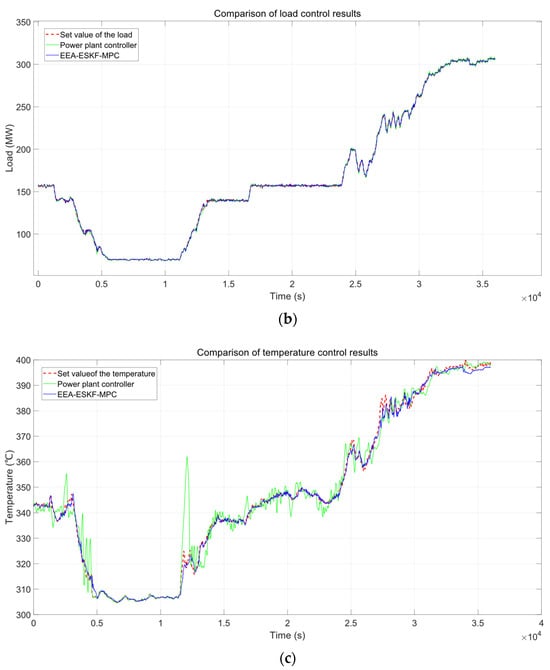
Figure 7.
Comparison between the real controller and the proposed controller. (a) Pressure; (b) load; (c) temperature.

Table 4.
Comparison of control results between power plant controller and EA-ESKF-MPC.
Figure 7 provides a visual comparison of the control effects. In Figure 7a, the pressure response of the EEA-ESKF-MPC closely tracks the setpoint with minimal deviation, contrasting with the power plant controller’s larger fluctuations. Figure 7b shows the load tracking, where the EEA-ESKF-MPC maintains a stable output despite rapid changes, while the power plant controller exhibits noticeable lag and overshoot. Figure 7c highlights the temperature control, with the EEA-ESKF-MPC achieving significantly tighter regulation compared to the power plant controller’s oscillatory behavior.
Table 4 quantifies these improvements. For pressure control, the EEA-ESKF-MPC reduces the IAE1 to 605.807, a 77.25% improvement over the power plant controller’s 2667.670, and the ME1 to 0.923 MPa, a 40.83% reduction from 1.560 MPa. In load control, the IAE2 drops to 4384.299 (a 27.05% decrease from 6010.110), and the ME2 improves to 6.498 MW (a 5.30% reduction from 6.860 MW), indicating enhanced tracking accuracy. The most pronounced improvement occurs in temperature control, where the IAE3 decreases to 8000.564 (a 65.25% reduction from 23025.860), and the ME3 falls to 10.411 °C (a 75.08% improvement from 41.780 °C), showcasing exceptional stability and precision.
These results underscore the superiority of the EEA-ESKF-MPC in real-world conditions. The adaptive error mechanism, coupled with the neural network-based prediction model (Section 2.2), enables the controller to dynamically adjust to operational variations, effectively mitigating the limitations of the power plant’s PID controller, which struggles with the system’s nonlinearity and coupling. The significant reductions in IAE and ME across all variables highlight the EEA-ESKF-MPC’s ability to minimize cumulative errors and peak deviations, enhancing both dynamic performance and robustness.
Compared to the simulation-based tests in Section 3.2 and Section 3.3, the real condition tracking experiment further validates the practical efficacy of the proposed method. The substantial improvements over the power plant controller suggest that the EEA-ESKF-MPC can meet the stringent demands of supercritical power plant operations, offering a viable upgrade to existing control systems.
4. Conclusions
This study proposes an Enhanced Error-Adaptive ESKF-MPC controller that significantly improves the control quality of supercritical power plants through hybrid modeling and dynamic error compensation. The main conclusions are as follows:
- The neural network-based identification method outperforms the traditional transfer function approach, achieving a higher accuracy with RMSE reductions of 30.6% for pressure and 27.4% for temperature. This highlights its potential for precise parameter identification in complex power systems.
- The EEA-ESKF-MPC demonstrates fast response, minimal overshoot, and high robustness in handling wide load variations and command disturbances. Compared to ESKF-MPC, it reduces the load and temperature IAE by 3.05% and 2.46%, and the ME by 1.14% and 2.31%, respectively, with a slight 0.43% increase in the pressure IAE. In disturbance scenarios, it demonstrated the ability to balance out the errors of each control, enhancing the tracking accuracy and system smoothness.
- Real condition tracking experiments using data from a 350 MW supercritical unit demonstrate substantial improvements over the plant’s PID controller, with reductions in the IAE by 77.25% (pressure), 27.05% (load), and 65.25% (temperature), and in the ME by 40.83%, 5.30%, and 75.08%, respectively. These results affirm the EEA-ESKF-MPC’s capability to enhance control quality under realistic operating conditions, offering practical benefits like enhanced efficiency and potential reductions in coal use.
The EEA-ESKF-MPC offers robust scalability, enabling its adaptation to diverse power generation systems beyond supercritical units, such as ultra-supercritical units and combined cycle plants, which feature distinct thermodynamic properties and operational constraints; however, applying the method to these systems requires re-identification of the system model to capture their unique nonlinear dynamics and multivariable coupling, along with the recalibration of parameters like the adaptive weights and exponential smoothing factors to optimize control performance for their specific response characteristics. Although the controller has demonstrated promising results in simulations and real-condition tracking using data from a 350 MW supercritical unit, its deployment in an operational power plant remains unrealized, facing significant challenges including integration with existing DCS, which demands standardized communication protocols and compatibility with legacy hardware to ensure seamless operation, as well as rigorous safety certifications to comply with industry standards for critical control loops and real-time computational optimization to meet stringent response time requirements essential for plant reliability. Addressing these practical barriers is crucial to transition the EEA-ESKF-MPC from simulation to real-world application, and future work will focus on adaptively tuning additional parameters and optimizing weight assignments within the MPC framework to enhance control precision, while incorporating online optimization techniques, reinforcement learning, and semi-physical simulations to further improve practical applicability and robustness in diverse operational scenarios.
Author Contributions
Conceptualization, G.C., S.H. and L.S.; methodology, G.C., C.F. and L.S.; software, C.F. and C.W.; validation, C.F. and S.W.; formal analysis, G.C.; investigation, G.C.; resources, S.H.; data curation, C.W.; writing—original draft preparation, G.C.; writing—review and editing, S.H.; visualization, C.F.; supervision, L.S.; project administration, G.C. and L.S.; funding acquisition, G.C. and L.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Grant of Guoneng Nanjing Electric Power Test & Research Limited, grant number DY2024Y02.
Data Availability Statement
The datasets used in this article are confidential.
Conflicts of Interest
Authors Gang Chen, Shan Hua, Changhao Fan, Chun Wang, and Shuchong Wang were employed by the company Guoneng Nanjing Electric Power Test & Research Limited, China. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Sun, L.; Li, D.; Lee, K.Y.; Xue, Y. Control-oriented modeling and analysis of direct energy balance in coal-fired boiler-turbine unit. Control Eng. Pract. 2016, 55, 38–55. [Google Scholar] [CrossRef]
- Yang, Q.; Chen, G.; Guo, M.; Chen, T.; Luo, L.; Sun, L. Model Predictive Hybrid PID Control and Energy-Saving Performance Analysis of Supercritical Unit. Energies 2024, 17, 6356. [Google Scholar] [CrossRef]
- Çetin, G.; Özkaraca, O.; Keçebaş, A. Development of PID based control strategy in maximum exergy efficiency of a geothermal power plant. Renew. Sustain. Energy Rev. 2021, 137, 110623. [Google Scholar] [CrossRef]
- Prasanth, S.; Narayanan, S.; Sivakumaran, N.; Pratheesh, H. The control of superheater steam temperature in power plants using model predictive controller. Comput. Electr. Eng. 2024, 115, 109109. [Google Scholar] [CrossRef]
- Hui, J.; Yuan, J. Adaptive second-order nonsingular terminal sliding mode power-level control for nuclear power plants. Nucl. Eng. Technol. 2022, 54, 1644–1651. [Google Scholar] [CrossRef]
- López-Bautista, A.O.; Flores-Tlacuahuac, A.; Gutiérrez-Limón, M.A. Robust model predictive control for a nanofluid based solar thermal power plant. J. Process Control 2020, 94, 97–109. [Google Scholar] [CrossRef]
- Yang, C.; Guo, W.; Shao, Y.; Lin, Y.; Pu, X.; Wang, Y.; Zheng, C.; Ding, Y.; Fan, H.; Zhu, Y.; et al. Two-timescale nonlinear model predictive control for flexible operation of coal-fired power plant with post combustion CO2 capture system. Appl. Therm. Eng. 2024, 256, 124139. [Google Scholar] [CrossRef]
- DFrejo, J.R.; Camacho, E.F. Centralized and distributed Model Predictive Control for the maximization of the thermal power of solar parabolic-trough plants. Sol. Energy 2020, 204, 190–199. [Google Scholar] [CrossRef]
- Huang, Y.; Yang, W.; Liao, Y.; Zhao, Z.; Ma, W.; Yang, J.; Yang, J. Improved transfer function method for flexible simulation of hydraulic-mechanical-electrical transient processes of hydro-power plants. Renew. Energy 2022, 196, 390–404. [Google Scholar] [CrossRef]
- Sánchez, A.J.; Gallego, A.J.; Escaño, J.M.; Camacho, E.F. Adaptive incremental state space MPC for collector defocusing of a parabolic trough plant. Sol. Energy 2019, 184, 105–114. [Google Scholar] [CrossRef]
- Americano Da Costa, M.V.; Narasimhan, A.; Guillen, D.; Joseph, B.; Goswami, D.Y. Generalized distributed state space model of a CSP plant for simulation and control applications: Single-phase flow validation. Renew. Energy 2020, 153, 36–48. [Google Scholar] [CrossRef]
- Matsuda, Y.; Suyama, D.; Sugi, T.; Goto, S.; Yasunaga, T.; Ikegami, Y. Construction of a State Space Model for an OTEC Plant Using Rankine Cycle with Heat Flow Rate Dynamics. IFAC-PapersOnLine 2020, 53, 13042–13047. [Google Scholar] [CrossRef]
- Lu, X.; Liang, Z. Application of Model Predictive Control Based on Kalman Filter in Solar Collector Field of Solar Thermal Power Generation. Energy Eng. 2021, 118, 1171–1183. [Google Scholar] [CrossRef]
- Li, H.; Liu, P.; Guo, S.; Cheng, L.; Huang, K.; Feng, M.; He, S.; Ming, B. Deriving adaptive long-term complementary operating rules for a large-scale hydro-photovoltaic hybrid power plant using ensemble Kalman filter. Appl. Energy 2021, 301, 117482. [Google Scholar] [CrossRef]
- Schaum, A. Autoencoder-Based Reduced Order Observer Design for a Class of Diffusion-Convection-Reaction Systems. Algorithms 2021, 14, 330. [Google Scholar] [CrossRef]
- Saini, V.; Bhattacharyya, D.; Purdy, D.; Parker, J.; Boohaker, C. Nonlinear state estimation of a power plant superheater by using the extended Kalman filter for differential algebraic equation systems. Appl. Therm. Eng. 2024, 251, 123471. [Google Scholar] [CrossRef]
- Guo, M.; Hao, Y.; Lee, K.Y.; Sun, L. Extended-state Kalman filter-based model predictive control and energy-saving performance analysis of a coal-fired power plant. Energy 2025, 314, 134169. [Google Scholar] [CrossRef]
- Kim, G.; Kim, H.; Zio, E.; Heo, G. Application of particle filtering for prognostics with measurement uncertainty in nuclear power plants. Nucl. Eng. Technol. 2018, 50, 1314–1323. [Google Scholar] [CrossRef]
- Chan, K.H.; Dozal-Mejorada, E.J.; Cheng, X.; Kephart, R.; Ydstie, B.E. Predictive control with adaptive model maintenance: Application to power plants. Comput. Chem. Eng. 2014, 70, 91–103. [Google Scholar] [CrossRef]
- Hou, G.; Fan, Y.; Wang, J. Intelligent fuzzy neural network modeling for flexible operation of combined heat and power plant with heat-power decoupling technology. Energy 2024, 309, 133099. [Google Scholar] [CrossRef]
- Wang, W.; Wang, Y.; Tian, Y.; Wu, Z. Explicit machine learning-based model predictive control of nonlinear processes via multi-parametric programming. Comput. Chem. Eng. 2024, 186, 108689. [Google Scholar] [CrossRef]
- Yang, S.; Wan, M.P.; Chen, W.; Ng, B.F.; Dubey, S. Model predictive control with adaptive machine-learning-based model for building energy efficiency and comfort optimization. Appl. Energy 2020, 271, 115147. [Google Scholar] [CrossRef]
- Zhao, A.; Toudeshki, A.; Ehsani, R.; Viers, J.H.; Sun, J.-Q. Evaluation of Neural Network Effectiveness on Sliding Mode Control of Delta Robot for Trajectory Tracking. Algorithms 2024, 17, 113. [Google Scholar] [CrossRef]
- Li, H.; Wang, C.; Yuan, S.; Zhu, H.; Li, B.; Liu, Y.; Sun, L. Energy Scheduling of Hydrogen Hybrid UAV Based on Model Predictive Control and Deep Deterministic Policy Gradient Algorithm. Algorithms 2025, 18, 80. [Google Scholar] [CrossRef]
- Dong, Z.; Zhang, Z.; Dong, Y.; Huang, X. Multi-layer perception based model predictive control for the thermal power of nuclear superheated-steam supply systems. Energy 2018, 151, 116–125. [Google Scholar] [CrossRef]
- Guo, M.; Hao, Y.; Lu, Y.; Sun, L. Long-short term memory modeling and performance analysis of extended-state Kalman filter-based energy-saving model predictive control for supercritical unit. Appl. Therm. Eng. 2025, 272, 126202. [Google Scholar] [CrossRef]
- Baldassarre, A.; Dion, J.-L.; Peyret, N.; Renaud, F. Digital twin with augmented state extended Kalman filters for forecasting electric power consumption of industrial production systems. Heliyon 2024, 10, e27343. [Google Scholar] [CrossRef] [PubMed]
- Plankenbühler, T.; Müller, D.; Karl, J. An adaptive and flexible biomass power plant control system based on on-line fuel image analysis. Therm. Sci. Eng. Prog. 2023, 40, 101765. [Google Scholar] [CrossRef]
- Li, Q.; Zhan, Q.; Yu, S.; Sun, J.; Cai, W. Study on thermal-hydraulic performance of printed circuit heat exchangers with supercritical methane based on machine learning methods. Energy 2023, 282, 128711. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).