Abstract
Landslides are hazardous events that occur mainly in mountainous areas and cause substantial losses of various kinds worldwide; therefore, it is important to investigate them. In this study, a specific Machine Learning (ML) method was further analyzed due to the good results obtained in the previous stage of this research. The algorithm implemented is Extreme Gradient Boosting (XGBoost), which was used to evaluate the susceptibility to landslides recorded in the city of Cuenca (Ecuador) and its surroundings, generating the respective Landslide Susceptibility Maps (LSM). For the model implementation, a landslide inventory updated to 2019 was used and several sets from 15 available conditioning factors were considered, applying two different methods of random point sampling. Additionally, a hyperparameter tuning process of XGBoost has been employed in order to optimize the predictive and computational performance of each model. The results obtained were validated using AUC-ROC, F-Score and the degree of landslide coincidence adjustment at high and very high susceptibility levels, showing a good predictive capacity in most cases. The best results were obtained with the set of the six best conditioning factors previously determined, as it produced good values in validation metrics (AUC = 0.83; F-Score = 0.73) and a degree of coincidence of landslides in the high and very high susceptibility levels above 90%. The Wilcoxon text led to establishing significant differences between methods. These results show the need to perform susceptibility analyses with different data sets to determine the most appropriate ones.
1. Introduction
Landslides are catastrophic events that occur mainly in mountainous areas and cause substantial losses of various kinds throughout the world [1,2,3]. These losses, evidenced in damage to infrastructure and human casualties, show the impact of these events. One way to counteract this impact is to generate resources that promote prevention and help mitigate their effects. To this end, the susceptibility to landslide occurrence should be analyzed through the generation of Landslide Susceptibility Maps (LSM). Susceptibility is the spatial probability of landslide occurrence, i.e., the possibility of a region being affected by this phenomenon based on certain characteristics (environmental, geological, geomorphological, among others) [4,5].
Susceptibility makes it possible to know the areas with the highest probability of landslides [4,6]; therefore, LSMs optimize landslide risk management and contribute to better territorial planning, since they show the probable distribution of landslides in a sector [7,8]. These mapping resources are useful in places crossed or close to mountain ranges such as the Andes, where tragic events have occurred. Some of them are of recent occurrence as in Colombia: the cases of Mocoa in March 2017 (García-Delgado et al. [9]) and Chocó in January 2024. While in Ecuador, Gulag-Marianza, near Cuenca in March 2022 (Bravo-López et al. [7]) and Alausí in March 2023 (Macías et al. [10]), among others, were recorded. Due to the losses caused by these phenomena, it is necessary that competent institutions make the appropriate decisions and accurately determine the areas susceptible to these phenomena [11].
Previous research [7,12] mentions the importance of Machine Learning (ML), which is based on quantitative methods widely used in Landslide Susceptibility Prediction (LSP) due to its higher predictive accuracy compared to other methods (heuristic, statistical, etc.) [13,14]. In addition, several ML methods have been applied in different study areas around the world, and due to their popularity, they have also been implemented in areas with no previous studies or little research. Specifically, in some regions of Ecuador and Colombia, recent LSP research has been developed with different ML methods such as: Artificial Neural Networks (ANN) [12,15], Random Forests (RF) [7,15], XGBoost [7] and Linear Discriminant Analysis (LDA) [15]. Furthermore, in Ecuador, there is research applying ML such as Guerrero-Rodriguez et al. [16], who improved landslide prediction with deep learning on the Alóag-Santo Domingo highway; or Di Napoli et al. [17], who analyzed landslide exposure in fast-growing cities such as Cuenca (Ecuador). Similarly, in Colombia, Vega et al. [18] generated landslide models in a tropical mountain basin (La Liboriana, Antioquia) using ML and Calderón-Guevara et al. [19] compared susceptibility models based on data (including ML) in the eastern cordillera of the Colombian Andes.
The association between past landslides and conditioning factors in each area should be considered [5], since the susceptibility is different in each sector, mainly due to their intrinsic characteristics and the types of data used [20]. It is still of interest to the scientific community to implement ML models with the appropriate combination of different conditioning factors and their spatial distribution [5,20,21]. Determining the optimal conditioning factors for LSP is still a challenge, as no rule defines which ones are the most important, nor how many are sufficient for a specific analysis [5]. However, several studies have been conducted in which the importance of conditioning factors in various areas has been determined using feature selection algorithms. In the study area proposed for this research, Bravo-López et al. [7] elaborated an analysis of conditioning factors using ML, obtaining six main factors for this area, which are described in that study. This research is pioneering both in the study area and in Ecuador.
Several investigations have combined conditioning factors according to a given criterion. Kavzoglu et al. [5] generated LSM using genetic algorithms in Macka (Turkey). Their 16 factors were classified according to the dependence on a Digital Elevation Model (DEM) or those obtained from satellite images. Al-Najjar et al. [20] implemented LSP combining 14 conditioning factors (morphometric and non-morphometric) in Sajadrood (Iran) applying ML. In the same area, Kalantar et al. [22] compared three sets of conditioning factors for LSP. Liao et al. [23] identified essential conditioning factors for LSM in Wushan and Wuxi (China), grouping 28 factors into geological, environmental, meteorological and human activities. Chang et al. [15] studied 15 conditioning factors for LSP generation in Chongyi (China), classifying them into topographical, geological, hydrological, anthropogenic and land occupation. Of all these studies, none applied XGBoost to obtain LSP.
Previously [7], XGBoost was determined to be the best performing ML algorithm in the study area. Therefore, it was further analyzed in this research. Although XGBoost performs optimally for different types of problems [24], it has recently been implemented in some LSM studies [25,26,27,28,29,30,31]. In all these cases, XGBoost has presented good performance, having as an advantage its ability to avoid overfitting with proper configuration of its regularization hyperparameters [32], although despite its versatility and good performance [33], it can be computationally demanding [24]. There are several approaches to optimize hyperparameters, with Bayesian Optimization (BO) being widely used [29]. BO has been implemented in studies applying XGBoost for LSM [29,34]. It is highlighted that XGBoost significantly reduces overfitting when the configuration of its hyperparameters is appropriate [35], therefore, it is necessary to implement models that consider this test to obtain computationally affordable performance with acceptable prediction results.
This research aligns with previously published studies [7,12] on LSM with ML. For further research, XGBoost was chosen for LSM since this method is not too widely employed and generates good results. First, an optimization of this algorithm was applied by testing its main hyperparameters with a trial-and-error method to verify its computational performance and predictive capability. Second, this study analyzed combinations of conditioning factors to obtain LSM with XGBoost. Out of 15 conditioning factors, the combinations were based on the dependent (ten factors) and non-dependent (five factors) factors of the DEM in a sector of Cuenca, Ecuador, which has no previous studies. Two different random sampling methods were also evaluated and applied to each combination of conditioning factors to verify variations in LSP. Finally, a statistical analysis was performed using the Wilcoxon test to verify the significance of the susceptibility levels determined by each model. The main contribution, besides testing the efficiency of XGBoost optimized for LSM, is to determine whether combinations of conditioning factors based on one criterion (dependence and not on a DEM) and with different types of sampling, improve the performance of LSP in the study area, compared to the results achieved when considering the six most relevant conditioning factors, obtained with the implementation of feature selection algorithms.
2. Materials and Methods
2.1. Study Area
The study area (Figure 1) is the same as previous studies [7,12] and corresponds to the urban area of the city of Cuenca (Ecuador) and a surrounding area in the province of Azuay, located in Southern Ecuador. A landslide inventory was conducted in this area in 2019 [12,36] and is currently being updated. It is important to mention that most of the landslides inventoried (approximately 75%) are rotational. The area is located on a branch of the Andean mountain range and, therefore, has mountainous characteristics, with an elevation that fluctuates between approximately 2300 and 3700 m above sea level (m.a.s.l.). In addition, it has annual rainy periods (between December and May) and dry periods (from June to November) with an average rainfall of 940 mm. The geological characteristics of the study area present heterogeneity of materials and are detailed in Bravo-López et al. [7].
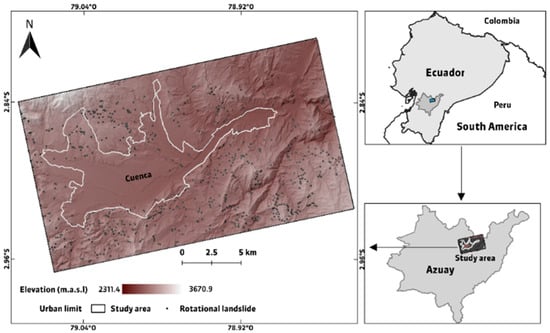
Figure 1.
Map of study area with landslide locations.
2.2. Materials
2.2.1. Landslides Inventory
The landslide inventory was elaborated in 2019, as a joint work between the Instituto de Estudios de Régimen Seccional del Ecuador (IERSE), of Universidad del Azuay (Cuenca, Ecuador) and Università degli Studi di Napoli Federico II (Naples, Italy), to characterize the landslides that have occurred in the area and to identify the areas susceptible to these events. The inventory covered an area of 380 km2 divided into 36 quadrants of 13.5 km2 to facilitate data collection. The methodology for the preparation of this inventory, in which 710 landslides were recorded (529 rotational landslides, about 75%), was based on field work for the collection of information using the Mobile Application for Regional Landslide Inventories (MARLI) [37]; photointerpretation with Planet satellite images, orthophotos of the area and differential interferometry processes (DInSAR) with COSMO-Skymed and Copernicus Sentinel-1 images to identify ground movements. In addition to rotational landslides, also falls and earthflows are described, with a landslide density per km2 of 45.8 and an average landslide size of 2.2 ha [37]. Most rotational landslides were located in well-weathered andesitic conglomerates with sandstone intercalations, while the highest landslide density value corresponded to shales and sandy clays [7]. The landslide inventory applied in this study is currently being updated to improve the quality of its information and thus improve the accuracy of the models. The technical details of the inventory are described in the studies by Miele et al. [36], Bravo-López et al. [12] and Bravo-López et al. [7].
2.2.2. Conditioning Factors
A fundamental aspect for an adequate generation of LSM, in addition to the landslide inventory, are the conditioning factors of the study area. In this sense, a first analysis was performed by applying ANN in this area using 10 of the 15 available factors [12]. In a second study, the six most important factors resulting from the application of feature selection algorithms were considered [7]. Details of all these factors can be found in Section 2.3.1 of this study and in previous research [7,12]. In this research, the factors were combined based on their dependence or lack of dependence on the DEM, to compare the results of these combinations with those obtained in the previous study mentioned above. Table 1 shows the combination elaborated for the present study. It is relevant to indicate that this combination can be effective to improve the predictive performance of the landslide susceptibility models, especially at a regional level [38].

Table 1.
Conditioning factors combination implemented in this study.
The information has been obtained from different official sources of the government of Ecuador. Topographic factors were derived from a three meter spatial resolution DEM obtained from Sistema Nacional de Información y Gestión de Tierras Rurales e Infraestructura Tecnológica (SIGTIERRAS) updated to 2010. The land cover map was also obtained from SIGTIERRAS, whose scale is 1:25,000 and is updated to 2018. The distance maps to rivers and roads (scale 1:25,000) were obtained from Instituto Geográfico Militar (IGM) and are updated to 2013. Lithological information was obtained from Sistema Nacional de Información (SNI), using a 1:100,000 scale geological map, updated to 2005. The land cover map was also obtained from SIGTIERRAS, whose scale is 1:25,000 and is updated to 2018. The distance maps to rivers and roads (scale 1:25,000) were obtained from IGM and are updated to 2013. Lithological information was obtained from SNI using a 1:100,000 scale geological map, updated to 2005.
2.3. Methods
Since this study is a continuation of the research carried out in the proposed area, the methodology was applied taking into account certain steps elaborated in those studies. From the landslide inventory data, only those of rotational type were selected. The stages followed in this research were (0) information gathering: landslide inventory and conditioning factors (described in Section 2.2); (1) analysis of conditioning factors for landslide susceptibility prediction (LSP); (2) sampling methods implementation; (3) training and testing data selection; (4) XGBoost model implementation; (5) XGBoost hyperparameter tuning and model performance evaluation; (6) results validation; (7) obtaining landslide susceptibility maps (LSM) and (8) statistical comparison between LSM obtained with Wilcoxon test (Figure 2).
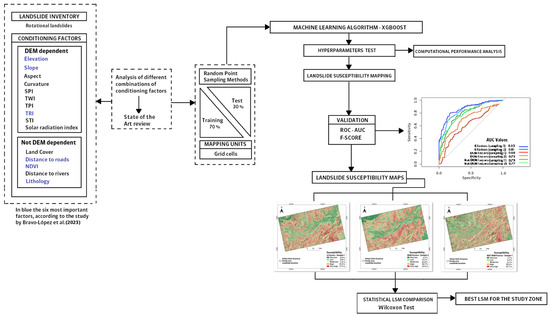
Figure 2.
Methodology implemented in this research.
2.3.1. Analysis of Conditioning Factors
In this research, 15 conditioning factors were applied [7,12]. Table 2 shows some details of these factors. In the first stage, the relationship between landslides and the factors was studied by determining their density in each of the classes of factors considered, which made it possible to determine the conditions in which landslides originate [12]; among them, the most important are lithology of shales and sandy clays, crop areas, altitudes between 2700 and 3000 m, slopes lower than 20°, high TWI values and proximity to rivers and roads. In a second stage, multicollinearity analysis was addressed by determining the Spearman correlation coefficient [7,12] or the variance inflation factor (VIF) [7], which led to discarding the factors of solar radiation, SPI and STI, all correlated with each other and with slope, which was retained as a very important and influential factor. Finally, feature selection algorithms were applied using various methods (Classification and Regression Tree (CART), Random Forests, Boruta and Recursive Feature Elimination (RFE)), that determined the most important conditioning factors for the study area [7]: elevation, slope, TRI, lithology, NDVI and distance to roads. In this study, based on previous research, a new approach is proposed. It consists of dividing the set of conditioning factors into DEM-dependent and non-DEM-dependent factors, which is explained below.

Table 2.
Conditioning factors utilized in this research.
Although the main characteristics of the factors used have been described in previous research [7,12], it is important to point out some specific aspects that reflect the relevance of these factors for this study.
Dependent DEM Factors
Elevation is a crucial factor in LSM, especially in mountainous regions. In low elevation ranges, it is associated with human activities and with the presence of loose materials that increase the possibility of landslide occurrence [29], however, high elevation ranges have a greater susceptibility to landslides [39]. The importance of this factor increases if combined with slope, orientation, curvature and lithology, among others [40]. Slope is important because it is related to vegetation growth due to the amount of sunlight it receives [29] and by the susceptibility to landslides themselves, depending on the degree of slope [41], it is also a critical factor in assessing and understanding landslide risk [42]. Orientation (aspect) is directly related to three characteristics that condition soil stability: (i) exposure to sunlight, (ii) moisture accumulation and (iii) vegetation growth [43]. Curvature is important because it is related to the direction of movement of the slides and also influences the speed of the slides [44], it also affects the intensity of soil erosion [29]. SPI is important because of its relationship to the strength of water flows and is an indicator of erosion potential [45]. TWI is an essential hydrological factor, especially in shallow landslides, as it indicates the tendency of water to accumulate and move down the slopes [46]. TPI is relevant because it characterizes the topographic position of a sector with its surroundings and because of its association with the physical processes of slopes [47]. TRI quantifies the roughness of the terrain, which makes it possible to obtain a better topographic characterization that influences the instability of slopes, as well as the runoff rate [48]. STI provides an understanding of the dynamics of sediment transport, which is crucial for understanding landslide hazards and their consequences at specific sites such as dams [49]. Finally, the solar radiation index is important because it influences aspects such as evapotranspiration, which has an impact on soil moisture levels and, therefore, on soil stability [50].
Not DEM Dependent Factors
These factors also play a crucial role in LSM. Land cover is related to the occurrence and distribution of landslides since land use transition processes, such as urbanization, increase the danger of their occurrence [51]. These changes have a significant influence on the susceptibility to landslides, with, for example, abandoned cultivated land being very susceptible to landslides [52]. Distance to roads is important because roads generate disturbances that cause landslides due to the cutting of slopes to build them, which also produces geological disturbances that increase the probability of failures and, therefore, landslides [53]. Distance to rivers and streams is essential because the proximity of these streams to slopes increases water infiltration and soil saturation, leading to changes in slope stability [54]. Furthermore, according to Caputa and Gorczyca [55], there is a higher density of landslides along rivers, which decreases as the distance to the rivers increases. Another critical factor is NDVI, as it provides information on vegetation growth and its spatial distribution. In addition, with the changes reflected by this index, it is possible to identify alterations in the vegetation cover since it indicates areas potentially prone to landslides [56]. Last but not least, lithology is widely used in landslide susceptibility analyses, as it is considered a critical factor in the mechanical and hydraulic properties of bedrock and soil cover [46].
Because the conditioning factors are the same as those previously applied [7,12], they have not been included in this study. The corresponding maps can be found in Section 2.3.1 (p. 8–11) [7] and Section 3.2 (p. 8–9) [12].
2.3.2. Sampling Methods Implementation
Sampling is fundamental in LSM generation, as it improves the accuracy and reliability of the models by incorporating both landslide and non-landslide samples [57,58]. Two random sampling methods were evaluated in the present study. The first is the same as the one applied in the previous stages of this research, i.e., the points were obtained randomly in areas without landslides (labeled with 0) and based on the centroid of the polygons corresponding to landslides (labeled with 1). The points in this sample were generated in a balanced manner (Figure 3a), with 529 points labeled 0 and 529 points labeled 1. The second method consisted of generating a sampling with a larger number of points (5000 samples) (Figure 3b) both in the polygons corresponding to landslides and 5000 points distributed in areas without landslides, similar to the method applied in Herrera-Coy et al. [15]. It is important to consider different sampling methods and strategies, some of them being oversampling and increasing the number of non-slides in areas that do not present this event. With this, the generated models have a greater effectiveness [59]. In both sampling methods, the numerical values of each conditioning factor were considered according to the location of the random points in the areas with and without landslides. As in the previous studies, the cartographic unit used was grid cells.
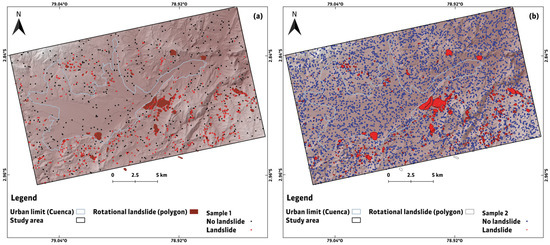
Figure 3.
Sampling points in the study area: (a) Sample 1, (b) Sample 2.
2.3.3. Training and Testing Data Selection
To evaluate the susceptibility models, the data set for training and testing was divided in a 70–30% ratio [7,12]. The importance of these data sets lies in the fact that they teach the model the classes to predict, check its degree of fit through training data and verify its predictive capability through testing data [60]. In addition, several papers emphasize the use of the 70–30% data ratio in the generation of landslide susceptibility maps, mainly because this approach allows training the models with most of the data in the set and reserving a subset to independently validate the model, which guarantees robustness in the models [40,61,62].
2.3.4. Machine Learning Model Implementation
In this study, LSMs were generated by applying XGBoost due to the good results obtained in the previous stage of this research. In this sense, the values obtained for the area under the ROC curve (AUC) with the test data show a greater predictive power of the XGBoost models, both using 15 and 6 factors (0.87 and 0.85), compared to those obtained with RF (0.79 and 0.80) and ANN (0.63 and 0.73). In this research and to analyze the accuracy of the model considering the different combinations of factors and sampling methods, hyperparameter tests were carried out to determine the most accurate models based on the characteristics described above, as well as on this computational aspect. Next, the main characteristics of XGBoost are described and then the hyperparameter configuration elaborated with the corresponding tuning process is detailed.
Extreme Gradient Boosting (XGBoost)
This algorithm belongs to Gradient Boosting Models (GBM). The main feature of GBMs is to build a set of shallow trees sequentially. Each tree built learns from the previous one and improves it [32]. Shallow trees are weak predictive models in themselves, however, they are boosted and adjusted appropriately, and it is this feature that provides much power to boosting-based algorithms. One of the main features of boosting is that each sequentially trained model is imparted with additional knowledge, which reduces bias and improves overall model performance [35], while gradient boosting implies that parameter tuning is performed iteratively to reduce the cost of the function [32]. XGBoost is one of the most powerful variants of gradient boosting and is itself a decision tree-based algorithm; it is fast, especially when implemented with parallel computing, efficient [33] and versatile since it is useful for classification and regression tasks. Its popularity has increased in recent years for LSM development, although it is used for several applications due to its superior performance compared to other supervised learning algorithms [24]. One of the main features of XGBoost is regularization. This method is useful in tree building process as it prevents the parameters of a model from becoming too large, it also prevents individual predictors from having a large impact on the overall prediction which helps to avoid overfitting (or reduces it), allows to control the complexity of the model [24,35] and improves its computational efficiency [29].
2.3.5. XGBoost Hyperparameter Tuning
XGBoost is a powerful algorithm; however, this power can be increased if its main hyperparameters are properly tuned to generate an optimized model. It is important to mention that XGBoost usually works well with the default hyperparameter settings, although this is not always true, as on occasion, random forests has outperformed XGBoost [35]. Hyperparameters are parameters that are set before the execution of the algorithm and in the case of XGBoost it is possible to configure the traditional ones based on boosting and trees, together with hyperparameters specific to the algorithm in question, whose function is mainly to reduce overfitting, thus achieving lower variability of predictions and therefore greater accuracy [32]. A simple way to tune XGBoost hyperparameters is with the trial-and-error method, used in the previous research stage [7] and chosen for its ease of implementation as a pilot test to verify the results that would be initially obtained with this test. However, in addition to this strategy whose limitation is being too general, it is also possible to implement hyperparameter optimization algorithms such as Bayesian Optimization (BO), Particle Swarm Optimization (PSO), Hyperband Optimization (HO) and Shapley Additive Explanations (SHAP), which are described in detail in Sun et al. [29] and could be implemented in future research in the proposed area. In this study, we continued with the trial-and-error method for tuning, considering additional hyperparameters to those implemented previously [7], in which the essential hyperparameters for the execution of the algorithm were considered, namely: nrounds, max_depth, colsample_bytree and subsample. Three hyperparameters were added in this study: eta, gamma and min_child_weight. The values set for tuning, together with their definitions, taken from Rhys [24], are described in Table 3.

Table 3.
Hyperparameter settings of XGBoost model to determine the best values.
The above values were determined based on those implemented in the previous stage of this research and on the acceptable ranges for each hyperparameter, as defined in the official documentation of the algorithm (DMLC XGBoost Documentation. Available online: https://xgboost.readthedocs.io/en/stable/parameter.html (accessed on 23 August 2024)). It is important to mention that in general, boosting algorithms have many parameters that are difficult to implement and the more they are considered, the more complex the algorithm will be. For this reason, only those considered to be the main ones were chosen [29].
The range of nrounds is [1, ∞]. This parameter does not have a default value; although it is recommended to be 100 or close to it, it depends on the computational characteristics available. The range of max_depth is [0, ∞]. Although it does not have a standard value, the higher its value, the more complex the model will be and the greater the probability of overfitting. The range of eta is [0, 1] and does not have a standard value; however, the lower this value is, the slower the computation process will be. The range of gamma is [0, ∞]. The higher its value, the more conservative the algorithm will be and, therefore, the higher the regularization will be. The range colsample_bytree is [0, 1] but a value around 0.5 is recommended. The range of min_child_weight is [0, ∞]. The higher its value, the more conservative the algorithm will be. The range of colsample_bytree and subsample is [0, 1]. A value close to 0.5 is recommended for both parameters.
Once the hyperparameter tuning is finished, it is possible to determine the ideal values for model generation (these values are described in Section 3); however, to analyze the runtime, an additional test was performed by varying some of them as alternative values. The values of the validation metric (ROC-AUC), according to each set of conditioning factors and considering only the first sampling method, are also detailed in Section 3 to verify the variation of the model accuracy.
An important aspect is that the algorithm, both in this and previous research stages and with its different configurations, was implemented in RStudio Server (version 2022.02.2 Build 485) and executed in a high-performance computer (HPC) of the Corporación Ecuatoriana para el Desarrollo de la Investigación y la Academia (CEDIA), whose performance is detailed in Table 4. The R package caret [63] was used to implement this model.

Table 4.
Main HPC features for algorithms execution.
2.3.6. Results Validation
Validation tools are used to evaluate the predictive performance of a model applied to analyze landslide susceptibility. In this research, as in the previous stages, the predictive ability of the models obtained with the applied algorithm was validated using the area under the receiver operating characteristic (ROC) curve (AUC) method, which, besides being a widely used and intuitive metric, allows an easy comparison of different modeling approaches [64]. As mentioned in previous steps, the “area under the curve” method quantitatively summarizes the ROC curve, describing the predictive ability of a model to predict landslide susceptibility [7,65]. The AUC value quantifies this capacity with values fluctuating between 0 and 1. The closer the AUC value is to 1, the greater the accuracy and reliability of the model; whereas, if the value is 0.5 or less, the prediction is a random guess. Generally, an AUC value of 0.75 or higher indicates that the model would have good predictive performance [64]. The ROC AUC was applied on test data (30%) and was performed with ROCR 1.0-11 [66], pROC 1.18.5 [67] and caret 6.0-94 [63] R software packages.
This study also used the F-Score as a validation metric. F-Score presents a balanced view of the classified data as it is the harmonic mean of the data. In the previous stages of this research, details of this metric have been explained [7,12], however, it is important to note that this metric works adequately with unbalanced data, considering not only the number of prediction errors but also the type of errors that are committed [68]. It should be noted that the higher the F-Score value, the fewer false positives and false negatives the prediction will have, which makes this metric very efficient for implementation in various ML applications [69].
Additionally, in this study, the percentage of landslides for each susceptibility level was analyzed as a validation metric. This method consists of applying spatial analysis techniques to count the number of points corresponding to landslides that fall within each susceptibility level. It is inferred that most of the points should coincide with the high and very high susceptibility levels.
2.3.7. Landslide Susceptibility Mapping (LSM)
Once the hyperparameter tests have been performed and determined their best values to achieve the most optimal model performance, the prediction results are obtained, which are the basis of the LSMs. These results should be organized into classes or levels of susceptibility for which, as in the previous stages of this research, the quantile method was used since it divides the data into classes of equal size, ensuring that each class contains the same amount of data, avoiding that certain classes have too few or too many values, generating a balanced representation of the susceptibility levels and avoiding the proliferation of some of them [70,71]. By convention and to continue with previously elaborated, the same five levels of susceptibility were defined in this study: very low, low, medium, high and very high, using an appropriate range of colors. LSM and spatial analysis procedures carried out in this research were developed entirely with free software (QGIS 3.28, GRASS 8.3.1 and SAGA 7.8.2).
2.3.8. Statistical Comparison Between LSM with Wilcoxon Test
As in the previous study [7], in this one the nonparametric Wilcoxon signed-rank test was implemented to evaluate the statistical significance of pairwise systematic differences between the landslide susceptibility models obtained, considering a significance level α = 0.05. This test is based on the null hypothesis that there is no significant difference between the models. The null hypothesis is rejected if the p-value is less than 0.05 and the z-value is outside the interval from −1.96 to +1.96. If both conditions are met, it is considered that there is a significant difference between the models compared [7,72,73,74,75,76].
3. Results
3.1. Hyperparameter Tuning
In this research, hyperparameter tuning was performed to verify the performance of the algorithm with different sets of conditioning factors and samples. Although boosting algorithms have several hyperparameters, only those implemented in the previous stage of this research and three additional ones whose use is common (see Section 2.3.5) have been chosen. A general analysis was performed using a trial-and-error method with a range of values detailed in Table 3. Table 5 describes the values that optimize the performance of the algorithm, which are similar and, in some cases, equal to the recommended default and alternative values. It is important to note that the alternative values used in the tuning are random and fluctuate between the optimal and default values for each hyperparameter considered. The objective of implementing tuning with alternative values is to verify the variation of both the validation metrics and the execution time of the algorithm since the latter is an important computational parameter when implementing an ML model; therefore, in this analysis, the execution times of both configurations were verified, obtaining significant differences.

Table 5.
Hyperparameter test values to find the most accurate model.
Algorithm execution with the best hyperparameters took a considerable time of approximately 11 h, while the alternative test was executed in a much shorter time of approximately 51 min. Additionally, all factor sets and the first sampling were used to determine the performance of the algorithm based on the area under the ROC curve. Table 6 shows the differences with each data set, showing that the best hyperparameter values produce a superior performance, although not so far away from those obtained with the alternative values.

Table 6.
AUC values resulting from the hyperparameter test with values established with data from sample 1.
3.2. Machine Learning Models Validation
The values obtained with the ROC AUC and F-Score validation metrics with the test data are shown in Table 7 and Figure 4. Most of the implemented models show acceptable performance (greater than 0.7) except the model implemented with the set of DEM-dependent factors applying the first sampling, whose AUC is 0.68 and its F-Score is 0.61, the lowest of all models for both validation metrics. In this context, the model with the best predictive capacity is the one that considers six conditioning factors with the first sampling (AUC = 0.83, F-Score = 0.73); followed nearly by the model with the same set of conditioning factors, but with the second sampling (AUC = 0.81, F-Score = 0.72). The model that considered the DEM-dependent conditioning factors and sampling 2 has an acceptable AUC value (0.73) and an F-Score of 0.63, although lower than those obtained with the set of non-DEM-dependent conditioning factors, whose values are AUC = 0.79 and F-Score = 0.71 with sampling 1, and AUC = 0.77 and F-Score = 0.70 with sampling 2.

Table 7.
ROC AUC and F-Score values for test datasets.
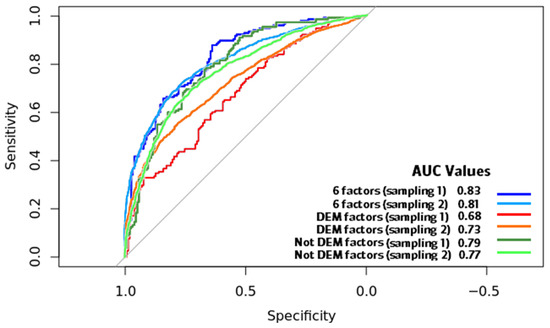
Figure 4.
ROC curves of ML LSM algorithms implemented.
3.3. Landslide Susceptibility Analysis
Once the optimal hyperparameter values were established for the algorithm execution with the established data sets and sampling, LSM of the study area were generated. As in previous studies, pixels that do not correspond to any susceptibility level (mainly belong to water bodies) were discarded. In addition, five susceptibility levels, described in Section 2.3.7 were defined. The six maps obtained have differences based on each data set and sampling applied (Figure 5). All the maps have uniformity in the number of pixels assigned to the susceptibility levels since all the models present values very close to 20% of pixels for each level, as corresponds to the use of the quantile method for classification.
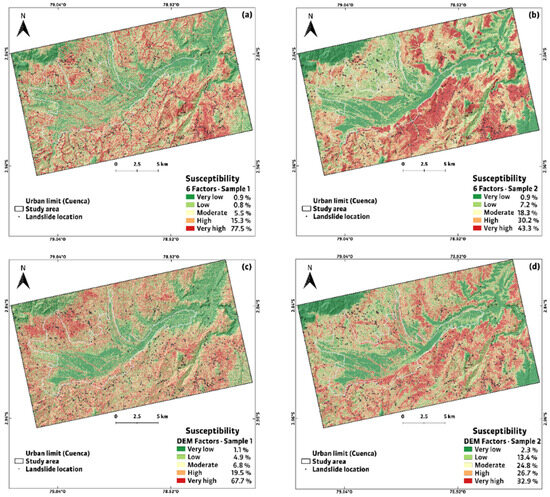

Figure 5.
Landslide Susceptibility Maps (LSM) obtained with XGBoost algorithm and factors selection: (a) 6 Factors (sample 1), (b) 6 Factors (sample 2), (c) DEM Factors (sample 1), (d) DEM Factors (sample 2), (e) Not DEM Factors (sample 1), (f) Not DEM Factors (sample 2).
Table 8 shows the number of landslides assigned to each susceptibility level. In all cases the highest number of landslides accumulated at the high and very high levels: 92.8% in the set of six factors (sampling 1) and 73.5% for the same set of factors but with sampling 2; 87.2% in the set of DEM-dependent factors (sampling 1) and 59.6% for the same set with sampling 2; finally, 86.2% in the set of non-DEM-dependent factors and 68.4% for the same set but with sampling 2. Another remarkable aspect is the minimal number of landslides (less than 5% in all cases) that fall in the very low susceptibility level: 0.9% in the set of six factors with the two samplings; 1.1% for the set of DEM-dependent factors (sampling 1) and 2.3 for the same set with sampling 2; 1.7% for the set of non-DEM-dependent factors (sampling 1) and 4.7% for the same set of factors with sampling 2. The distribution of susceptibility levels for each model generated is shown in Figure 6. It is important to point out that these levels not only provide ease of interpretation but also show in a specific way the areas with greater susceptibility, which affects a better planning strategy, especially when landslides fall in the levels that are apparently more susceptible [77].

Table 8.
Susceptibility classes per algorithm and percentage of landslides per class.
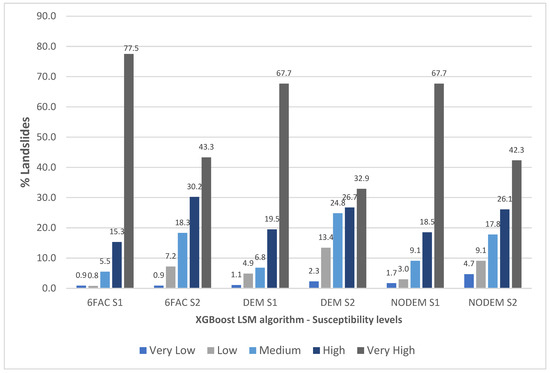
Figure 6.
Distribution of susceptibility levels per each LSM.
3.4. Models Statistical Significance Analysis
In addition to the metrics mentioned above, the nonparametric Wilcoxon signed-rank test was used to evaluate the statistical significance of the differences between pairs of landslide susceptibility models. Table 9 shows the results of the Wilcoxon test applied to the six susceptibility models resulting from this research.

Table 9.
Wilcoxon test results for susceptibility models.
The results obtained using the Wilcoxon test analysis reveal notable differences in the efficacy or characteristics of the variants of the XGBoost models analyzed. Specifically, there are significant differences between the 6 factors (sampling 1) and 6 factors (sampling 2) models, as well as between 6 factors (sampling 1), DEM (sampling 1 and 2) and NO DEM (sampling 2), with p-values close to 0.01 and lower. On the other hand, the results indicate that there are no significant differences between the models 6 factors (sampling 2) with DEM (sampling 1); between DEM (sampling 1) with DEM (sampling 2) and NO DEM (sampling 1 and 2) and between DEM (sampling 2) and NO DEM (sampling 2). All of them show values close to and above 0.75.
4. Discussion
4.1. Results Interpretation
The results obtained corroborate the efficiency and good performance of XGBoost; however, with the sets of factors proposed in this study, the performance obtained was lower than that obtained considering the 15 factors for which information is available [7], whose AUC = 0.87. When considering only the six best factors previously determined [7] and with the hyperparameter test implemented to optimize performance, an AUC of 0.83 was obtained with the first sampling, this being the best performance obtained with all the data sets applied. This verifies the veracity of the results obtained with the feature selection algorithms applied in the previous stage of this research; however, it is observed that the overall performance of the algorithm (based on its AUC) has not improved (even it has decreased slightly) when implementing the hyperparameter tuning, which makes it necessary to go deeper into these tunings to understand the causes of this behavior. With the same set of factors, but with the second sampling, the performance shows some decrease (AUC = 0.81), however, it is still a good predictive model according to the values of the implemented metrics. Additionally, with these two data sets, the F-Score value is the highest (0.73 and 0.72, respectively), which supports the good predictive capacity of the model with these data sets, although it is also lower than that obtained with the 15 factors (0.78). On the other hand, the coincidence of landslides in the high and very high susceptibility levels exceeds 90% when considering the first sampling, which is an additional indication of the predictive efficiency of the model. In this case, this percentage is higher than that obtained with the 15 factors, which was approximately 78%. With the second sampling, the coincidence in the aforementioned susceptibility levels decreases, although it is still acceptable since it presents a value of approximately 73%.
The results obtained with DEM-dependent factors set show a much lower performance, which allows inferring that these factors, although important, are not the only ones that should be considered to implement LSP in the study area. When applying this set of factors, the first sampling yielded an AUC of 0.68, a value that could not be considered acceptable; however, when considering the second sampling, the performance shows a certain improvement (AUC = 0.73) that would be considered acceptable. In the case of this data set, F-Score presents the lowest values of all the data sets applied. In this sense, the F-Score value with the first sample is 0.61, and with the second sample, it is 0.63. Although the metrics present low values, it is striking that the coincidence of landslides in the susceptibility levels is not low, since in the first case more than 87% of landslides fall in high and very high susceptibility zones; whereas, in the second case, this coincidence decreases, since approximately 60% of landslides coincide with such levels, being the lowest value of all the analyzed data sets. The values are lower than those obtained with all 15 factors, which indicates the need to use non-DEM dependent factors that introduce variables such as lithology, which are essential for the mechanical strength of materials [46], NDVI as an expression of the vegetation that plays an important role in the stability of the surface layer; or the distance to roads, as an anthropic factor that induces instability [53].
When considering the conditioning factors not dependent on the DEM, interesting and, above all, acceptable results were obtained, which corroborates what was previously said about the importance of these factors. In the case of the first sampling, the AUC is 0.79, and with the second sampling, an AUC of 0.77 was obtained. In both cases, the performance is higher than that obtained with the set of DEM-dependent factors but lower than that obtained with the 15 factors and even with 6 factors, which suggests the need to have a heterogeneous mix of conditioning factors, as this will improve the predictive level of the model. The F-Score values also reflect an acceptable predictive capacity of the model with values of 0.71 and 0.70, respectively, exceeding with some amplitude the results obtained with the DEM-dependent data set and being minimally lower than those obtained with the set of the six best factors. On the other hand, the levels of landslide coincidence in the high and very high susceptibility levels show differences. With the first sampling, the coincidence level of landslides falling into these susceptibility levels is 86%. Although this value is high, it is lower than those obtained with the data sets described above. With the second sampling, the level of coincidence could be cataloged as acceptable since approximately 68% of landslides fall into these susceptibility levels.
What is observed is a reduction in the percentage of movements in models obtained with the second sampling (random) to the first (centroids) in all the combinations of factors considered. This can be explained by the difference in the size of the movements, which is greater in the southern part of the study area than in the northern part, where the size is smaller. Thus, the models obtained with sampling 1 show a greater susceptibility in the northwest zone, where smaller movements are concentrated and therefore more sensitive to the centroid, and also in the south and southeast where movements are greater; in general, the fit of the models with the centroids is good in both zones, hence the high proportions of movements in zones of high and very high susceptibility. On the contrary, the models obtained with sampling 2 show greater susceptibility in the south and southeast, where the largest movements are concentrated and, therefore, a greater number of random points, and not so much in the northwest, where the movements have a smaller size. Hence, when crossed with the centroids, the fit of the centroids with the high and very high susceptibility zones is lower in these models; a crossover with the full landslide area would provide a better fit.
4.2. Comparison with Previous Studies
As mentioned in the introduction, few studies have analyzed combinations of factors to verify the variability of the predictive models, especially those in which XGBoost has been implemented. Most of these studies use the totality of available factors, without factor selection, presenting a very good performance, according to their AUC value. Thus, Badola et al. [25] applied XGBoost in a road corridor in Chamoli (India), obtaining an AUC = 0.91, higher than that achieved in this study. Can et al. [26] obtained an even higher performance (AUC = 0.96) by hyperparameter tuning. Wei et al. [30], despite not performing hyperparameter tuning, obtained a very good performance of the model they implemented with XGBoost (AUC = 0.94). Sahin in his two studies [27,28] where he implemented LSM with XGBoost obtained similar performances (AUC = 0.88 and AUC = 0.89, respectively, which are slightly higher than those obtained in the present study); however, in the second case he did perform a combination of conditioning factors as in our study. Finally, Sun et al. [29] and Zhang et al. [31] obtained an AUC = 0.86, a performance closer to that achieved in the present study; in the first case, no hyperparameter tuning or combination of factors was performed, and in the second, several hyperparameter tunings were performed. The above reflects the scarcity of research applying hyperparameter tests for XGBoost, so new studies should implement these tests with several algorithms to optimize the model performance and obtain better predictive capacity.
4.3. Additional Study Implications
Hyperparameter tuning is necessary and beneficial to optimize an algorithm. Although several ML algorithms have been tested so far in the research, only RF and XGBoost allow this optimization to be performed. XGBoost and boosting algorithms in general could be a scientific reference for landslide susceptibility research [29], however, finding its most accurate performance is a challenge because of the difficulty that this test presents due to the large number of parameters that XGBoost allows to configure. In this research, the tuning process was performed using the trial-and-error method, which determined the best values of the main hyperparameters considered; however, the performance of the algorithm did not improve when compared to the model applied in the previous research [7] in which the fifteen available conditioning factors and a selection of the six most relevant ones were considered. Given this, it would be necessary to implement optimization algorithms such as those implemented in the study by Sun et al. [29], which would help to improve the tuning and, therefore, increase the performance of the model. A particularity that was found in this evaluation consisted of the ostensible difference in runtimes with the optimal and alternative values. Due to this difference, it can be noted that nrounds has a direct impact on the runtime since its variation was significantly higher in obtaining optimal values (see Table 5). Other parameters such as eta, gamma and subsample obtained optimal values lower than the alternative ones, which allows us to deduce that the higher the value of nrounds, the longer the model will take to run; however, if the predictive capacity does not vary significantly, it is possible to choose a not so large value of nrounds to avoid an excessive model execution time.
Regarding the comparison between LSM with the test of Wilcoxon, the presence of significant differences in some pairs and the absence of significant differences in others invites reflection on the consistency and sensitivity of XGBoost. This highlights the importance of deeply understanding how each variable and model configuration affects overall performance, especially in environments where small differences can have significant practical impacts. The results of this analysis provide a solid basis for the continuous improvement and refinement of predictive models based on XGBoost, highlighting the importance of a meticulous evaluation of each model variant before its implementation in applied scenarios. The model with the greatest differences from the rest is the one that uses six factors and sampling 1 (by centroids), while the one with the greatest overall similarities is the one that uses the DEM factors and sampling 2 (random). In general, the models using six factors show more differences between them as a function of sampling (p-value = 0.0198) than the models with non-DEM dependent factors (p = 0.1212), and especially to DEM dependent models (p = 0.8338), which show greater similarities with different sampling. This is explained by the fact that the variables not dependent on DEM are discrete, with sharp breaks between the different units, as opposed to the more gradual nature of those dependent on DEM (continuous variables). Thus, in the first case, the estimation of susceptibility is very sensitive to the position of the centroids and, therefore, the models obtained with centroid sampling may be different from those obtained with random sampling; on the contrary, in the DEM dependent variables, the very gradualness and randomness of the variables means that the position of the centroids is not so decisive, and therefore, the maps obtained with the two types of sampling are more similar. On the other hand, it is observed that in general the models with centroid sampling show a greater difference between them than the models with random sampling; this confirms what was said above, in that the former are more sensitive to changes, in this case to the factors involved, than the latter, which are more stable, due to the greater number and representativeness of the sampling.
4.4. Study Limitations and Future Research
The methodology applied in this study contributes to the analysis of landslide susceptibility in the study area (although it could also be evaluated in other areas), since, from the early stages of the research, it has been sought to find the ML model with the best predictive results, as well as the best combination of conditioning factors that affect such predictive capacity; however, some limitations must still be considered, such as the scarcity of quality data, especially based on official information. In this context, the models run do not consider important parameters such as precipitation levels in the area, deep vegetation aspects or exhaustive land cover details, precisely because of the scarcity of reliable data. Precipitation and meteorological data could be resolved using freely available datasets, such as TRMM or CHIRPS (for precipitation), considering their characteristics to make them useful in the study. Vegetation or land cover data could be modeled using satellite image processing analysis to calculate vegetation or land cover indices. Moreover, although validation metrics reflect a good predictive capability of the model, uncertainty should always be taken into account as part of this type of analysis.
As for future research, the model could be implemented with XGBoost but considering additional hyperparameters, as well as emphasizing the application of hyperparameter optimization algorithms to obtain a new approach that improves the values obtained with the trial-and-error method and, therefore, increases the accuracy of the model. It is also essential to apply new models focused on deep learning, such as convolutional neural networks (CNNs), since deep learning increases the degree of automation and recognition of complex entities in large datasets [78] and, therefore, improves predictive ability. In addition, models could be improved by assessing model sensitivity and robustness by applying extended cross-validation to ensure generalizability of results; investigating interactions between demographic variables and other predictors; evaluating the practical effectiveness of models through case studies; or developing hybrid models by integrating additional ML techniques.
It is also important to consider the practical implications of the research conducted in the study area, especially in high and very high susceptibility zones, as they would be useful for generating preventive and emergency protocols, territorial planning and habitability regulation plans for these sectors. All this is with the objective of reducing the risk associated to landslides, generating a prevention vision and increasing the resilience of people, property and infrastructures.
5. Conclusions
This study analyzed the landslide susceptibility in the area surrounding the city of Cuenca (Ecuador) and used XGBoost for LSM generation because its results have been the best predictive capacity for the study area, according to the findings obtained previously. Several sets of factors were also used: the six best ones, obtained with feature selection in a previous stage: elevation, slope, TRI, distance to roads, lithology and NDVI; the DEM-dependent ones: aspect, curvature, elevation, slope, SPI, STI, TPI, TRI, TWI and solar radiation; and the non-DEM-dependent ones: land cover, distance to roads, distance to rivers, lithology and NDVI. In addition, two sampling methods were tested, the first based on the centroid of the landslides available in the applied inventory, and the second, by intensive point sampling, also based on the landslide polygons.
To optimize the LSP model, hyperparameter tuning was performed based on seven important parameters of XGBoost and applying the trial-and-error method to find the ideal values of these parameters as well as to verify the computational performance of the model. The different LSMs showed different results, as each set of conditioning factors presented specific results, considering the aforementioned sampling methods. In this sense, it was determined that the six best factors obtained through feature selection applying the first sampling present the highest accuracy for the study area, according to the validation parameters and the level of coincidence of landslides in the high and very high susceptibility zones. This finding also confirmed the adequacy of the results obtained in the previous study of this research. On the contrary, and under the same conditions, the poorest result was obtained when applying the set of DEM-dependent factors with the first sampling. Thus, in general terms, the best adjustments are produced with the six selected factors, which integrate both DEM dependent and non-DEM dependent factors, indicating the need to use both sets; and the worst adjustments occur when only the DEM is used, which reinforces the importance of the non-DEM dependent factors, which allow modeling variables that have to do with the resistance of materials, soil support with vegetation cover and the influence of human actions. Sampling also influences the final result, with the former (by centroids) showing slightly better results than the latter (random), except in models obtained with no DEM-dependent factors, where random sampling better captures the discrete spatial variability of these variables. Although these results, together with those obtained in the previously elaborated studies, contribute to the scientific and preventive knowledge of landslides and allow defining crucial aspects to improve the accuracy of LSMs in the area, it is still necessary to implement additional models in future studies and to consider more conditioning factors, as well as to analyze other hyperparameter optimization algorithms, to improve the predictive capacity of the models.
The research line generated with this study and its predecessors provides scientifically grounded inputs for the study of landslides in the proposed area, which has an evident lack of research applying the implemented methods and is prone to suffer the onslaught of these destructive events. These studies are expected to contribute to the management of natural risks in the area and generate a benefit for society in terms of prevention.
Author Contributions
Conceptualization, E.B.-L. and T.F.; data selection and preparation, E.B.-L. and C.S.; software implementation, E.B.-L.; methodology, E.B.-L., T.F. and C.S.; validation E.B.-L. and T.F.; investigation, E.B.-L.; writing—original draft preparation, E.B.-L.; writing—review and editing, E.B.-L., T.F., C.S. and J.D.-G.; supervision T.F. and J.D.-G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Universidad del Azuay (project No. 2023-0173) and by the project “Captura de Información Geográfica mediante sensores móviles redundantes de bajo coste. Aplicación a la gestión inteligente del territorio” (FEDER-UJA project No. 1265116); y SPS-LIDAR (National Research Agency of Spain; ref. RTI2018-099638-B-I00).
Data Availability Statement
The data presented in this study are available on request from the corresponding author due to technical reasons.
Acknowledgments
The authors are grateful to the Photogrammetric and Topometric Systems Research Group of Universidad de Jaén; IERSE and Vicerrectorado de Investigaciones of Universidad del Azuay for the support provided to develop this research. We also thank the reviewers for their suggestions for improving this research.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Geertsema, M.; Alcántara-Ayala, I. Mountain Landslides: An Overview of Common Types and Future Impacts. In Montology Palimpsest: A Primer of Mountain Geographies; Springer: Berlin/Heidelberg, Germany, 2022; pp. 187–209. [Google Scholar] [CrossRef]
- Petley, D. Global patterns of loss of life from landslides. Geology 2012, 40, 927–930. [Google Scholar] [CrossRef]
- UNDRR. Global Assessment Report on Disaster Risk Reduction. Geneva, Switzerland. United Nations Office for Disaster Risk Reduction (UNDRR). 2019. Available online: https://www.undrr.org/publication/global-assessment-report-disaster-risk-reduction-2019 (accessed on 23 August 2024).
- Brabb, E. Innovative Approaches to Landslide Hazard and Risk Mapping. In Proceedings of the 4th International Symposium on Landslides, Toronto, ON, Canada, 16–21 September 1984; pp. 307–323. [Google Scholar]
- Kavzoglu, T.; Kutlug Sahin, E.; Colkesen, I. Selecting optimal conditioning factors in shallow translational landslide susceptibility mapping using genetic algorithm. Eng. Geol. 2015, 192, 101–112. [Google Scholar] [CrossRef]
- Varnes, D.J. Landslide Hazard Zonation: A Review of Principles and Practice; United Nations: Paris, France, 1984; No. 3. [Google Scholar]
- Bravo-López, E.; Fernández Del Castillo, T.; Sellers, C.; Delgado-García, J. Analysis of Conditioning Factors in Cuenca, Ecuador, for Landslide Susceptibility Maps Generation Employing Machine Learning Methods. Land 2023, 12, 1135. [Google Scholar] [CrossRef]
- Meena, S.R.; Puliero, S.; Bhuyan, K.; Floris, M.; Catani, F. Assessing the importance of conditioning factor selection in landslide susceptibility for the province of Belluno (region of Veneto, northeastern Italy). Nat. Hazards Earth Syst. Sci. 2022, 22, 1395–1417. [Google Scholar] [CrossRef]
- Garcia-Delgado, H.; Petley, D.N.; Bermúdez, M.A.; Sepúlveda, S.A. Fatal landslides in Colombia (from historical times to 2020) and their socio-economic impacts. Landslides 2022, 19, 1689–1716. [Google Scholar] [CrossRef]
- Macías, L.; Quiñonez-Macías, M.; Toulkeridis, T.; Pastor, J.L. Characterization and geophysical evaluation of the recent 2023 Alausí landslide in the northern Andes of Ecuador. Landslides 2024, 21, 529–540. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Teke, A. Predictive Performances of Ensemble Machine Learning Algorithms in Landslide Susceptibility Mapping Using Random Forest, Extreme Gradient Boosting (XGBoost) and Natural Gradient Boosting (NGBoost). Arab. J. Sci. Eng. 2022, 47, 7367–7385. [Google Scholar] [CrossRef]
- Bravo-López, E.; Fernández Del Castillo, T.; Sellers, C.; Delgado-García, J. Landslide Susceptibility Mapping of Landslides with Artificial Neural Networks: Multi-Approach Analysis of Backpropagation Algorithm Applying the Neuralnet Package in Cuenca, Ecuador. Remote Sens. 2022, 14, 3495. [Google Scholar] [CrossRef]
- Chang, Z.; Catani, F.; Huang, F.; Liu, G.; Meena, S.R.; Huang, J.; Zhou, C. Landslide susceptibility prediction using slope unit-based machine learning models considering the heterogeneity of conditioning factors. J. Rock Mech. Geotech. Eng. 2023, 15, 1127–1143. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth-Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Herrera-Coy, M.C.; Calderón, L.P.; Herrera-Pérez, I.L.; Bravo-López, P.E.; Conoscenti, C.; Delgado, J.; Sánchez-Gómez, M.; Fernández, T. Landslide Susceptibility Analysis on the Vicinity of Bogotá-Villavicencio Road (Eastern Cordillera of the Colombian Andes). Remote Sens. 2023, 15, 3870. [Google Scholar] [CrossRef]
- Guerrero-Rodriguez, B.; Garcia-Rodriguez, J.; Salvador, J.; Mejia-Escobar, C.; Cadena, S.; Cepeda, J.; Benavent-Lledo, M.; Mulero-Perez, D. Improving landslide prediction by computer vision and deep learning. Integr. Comput. Aided Eng. 2023, 31, 77–94. [Google Scholar] [CrossRef]
- Di Napoli, M.; Miele, P.; Guerriero, L.; Annibali Corona, M.; Calcaterra, D.; Ramondini, M.; Sellers, C.; Di Martire, D. Multitemporal relative landslide exposure and risk analysis for the sustainable development of rapidly growing cities. Landslides 2023, 20, 1781–1795. [Google Scholar] [CrossRef]
- Vega, J.; Sepúlveda-Murillo, F.H.; Parra, M. Landslide Modeling in a Tropical Mountain Basin Using Machine Learning Algorithms and Shapley Additive Explanations. Air Soil Water Res. 2023, 16, 11786221231195824. [Google Scholar] [CrossRef]
- Calderón-Guevara, W.; Sánchez-Silva, M.; Nitescu, B.; Villarraga, D.F. Comparative review of data-driven landslide susceptibility models: Case study in the Eastern Andes mountain range of Colombia. Nat. Hazards 2022, 113, 1105–1132. [Google Scholar] [CrossRef]
- Al-Najjar, H.A.H.; Kalantar, B.; Pradhan, B.; Saeidi, V. Conditioning factor determination for mapping and prediction of landslide susceptibility using machine learning algorithms. In Proceedings of the Earth Resources and Environmental Remote Sensing/GIS Applications X, Strasbourg, France, 10–12 September 2019; SPIE: Bellingham, WA, USA, 2019; Volume 11156, pp. 97–107. [Google Scholar] [CrossRef]
- Sahin, E.K. Implementation of free and open-source semi-automatic feature engineering tool in landslide susceptibility mapping using the machine-learning algorithms RF, SVM, and XGBoost. Stoch. Environ. Res. Risk Assess. 2023, 37, 1067–1092. [Google Scholar] [CrossRef]
- Kalantar, B.; Ueda, N.; Al-Najjar, H.A.H.; Saeidi, V.; Gibril, M.B.A.; Halin, A.A. A comparison between three conditioning factors dataset for landslide prediction in the Sajadrood catchment of Iran. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 5, 625–632. [Google Scholar] [CrossRef]
- Liao, M.; Wen, H.; Yang, L. Identifying the essential conditioning factors of landslide susceptibility models under different grid resolutions using hybrid machine learning: A case of Wushan and Wuxi counties, China. Catena 2022, 217, 106428. [Google Scholar] [CrossRef]
- Rhys, H. Part 2 Classification. 8 Improving decision trees with random forests and boosting. 8.3 Building your first XGBoost model. In Machine Learning with R, the Tidyverse, and Mlr; Simon and Schuster: New York, NY, USA, 2020. [Google Scholar]
- Badola, S.; Mishra, V.N.; Parkash, S. Landslide susceptibility mapping using XGBoost machine learning method. In Proceedings of the 2023 International Conference on Machine Intelligence for GeoAnalytics and Remote Sensing (MIGARS), Hyderabad, India, 27–29 January 2023; IEEE: Piscataway, NJ, USA, 2023; Volume 1, pp. 1–4. [Google Scholar] [CrossRef]
- Can, R.; Kocaman, S.; Gokceoglu, C. A comprehensive assessment of XGBoost algorithm for landslide susceptibility mapping in the upper basin of Ataturk dam, Turkey. Appl. Sci. 2021, 11, 4993. [Google Scholar] [CrossRef]
- Sahin, E.K. Assessing the predictive capability of ensemble tree methods for landslide susceptibility mapping using XGBoost, gradient boosting machine, and random forest. SN Appl. Sci. 2020, 2, 1308. [Google Scholar] [CrossRef]
- Sahin, E.K. Comparative analysis of gradient boosting algorithms for landslide susceptibility mapping. Geocarto Int. 2022, 37, 2441–2465. [Google Scholar] [CrossRef]
- Sun, D.; Wang, J.; Wen, H.; Ding, Y.; Mi, C. Landslide susceptibility mapping (LSM) based on different boosting and hyperparameter optimization algorithms: A case of Wanzhou District, China. J. Rock Mech. Geotech. Eng. 2024, 16, 3221–3232. [Google Scholar] [CrossRef]
- Wei, A.; Yu, K.; Dai, F.; Gu, F.; Zhang, W.; Liu, Y. Application of Tree-Based Ensemble Models to Landslide Susceptibility Mapping: A Comparative Study. Sustainability 2022, 14, 6330. [Google Scholar] [CrossRef]
- Zhang, W.; He, Y.; Wang, L.; Liu, S.; Meng, X. Landslide Susceptibility mapping using random forest and extreme gradient boosting: A case study of Fengjie, Chongqing. Geol. J. 2023, 58, 2372–2387. [Google Scholar] [CrossRef]
- Boehmke, B.; Greenwell, B. 12 Gradient Boosting. 12.5 XGBoost. In Hands-on Machine Learning with R; Chapman and Hall/CRC: Boca Raton, FL, USA, 2019. [Google Scholar] [CrossRef]
- Ghatak, A. 5 Classification. 5.6 Other Variants. 5.6.3 XGBoost. In Machine Learning with R; Springer Nature: Singapore, 2017. [Google Scholar]
- Wang, S.; Zhuang, J.; Zheng, J.; Fan, H.; Kong, J.; Zhan, J. Application of Bayesian Hyperparameter Optimized Random Forest and XGBoost Model for Landslide Susceptibility Mapping. Front. Earth Sci. 2021, 9, 712240. [Google Scholar] [CrossRef]
- Ramasubramanian, K.; Moolayil, J. Classification. XGBoost. In Applied Supervised Learning with R: Use Machine Learning Libraries of R to Build Models That Solve Business Problems and Predict Future Trends; Packt Publishing Ltd.: Birmingham, UK, 2019. [Google Scholar]
- Miele, P.; Di Napoli, M.; Guerriero, L.; Ramondini, M.; Sellers, C.; Annibali Corona, M.; Di Martire, D. Landslide awareness system (Laws) to increase the resilience and safety of transport infrastructure: The case study of pan-American highway (Cuenca–Ecuador). Remote Sens. 2021, 13, 1564. [Google Scholar] [CrossRef]
- Sellers, C.A.; Buján, S.; Miranda, D. MARLI: A mobile application for regional landslide inventories in Ecuador. Landslides 2021, 18, 3963–3977. [Google Scholar] [CrossRef]
- Guo, Z.; Tian, B.; Li, G.; Huang, D.; Zeng, T.; He, J.; Song, D. Landslide susceptibility mapping in the Loess Plateau of northwest China using three data-driven techniques-a case study from middle Yellow River catchment. Front. Earth Sci. 2023, 10, 1033085. [Google Scholar] [CrossRef]
- Chowdhury, M.S.; Hafsa, B. Landslide Susceptibility Mapping Using Bivariate Statistical Models and GIS in Chattagram District, Bangladesh. Geotech. Geol. Eng. 2022, 40, 3687–3710. [Google Scholar] [CrossRef]
- Addis, A. GIS-Based Landslide Susceptibility Mapping Using Frequency Ratio and Shannon Entropy Models in Dejen District, Northwestern Ethiopia. J. Eng. 2023, 2023, 1062388. [Google Scholar] [CrossRef]
- El Hamdouni, I.; Brahim, L.A.; El Mahsani, A.; Abdelouafi, A. The Prevention of Landslides Using the Analytic Hierarchy Process (AHP) in a Geographic Information System (GIS) Environment in the Province of Larache, Morocco. Geomat. Environ. Eng. 2022, 16, 77–93. [Google Scholar] [CrossRef]
- Fobert, M.A.; Singhroy, V.; Spray, J.G. InSAR monitoring of landslide activity in Dominica. Remote Sens. 2021, 13, 815. [Google Scholar] [CrossRef]
- Wu, Y.; Wu, J.; Li, Y.; Jiang, J.; Zheng, S. Large scale landslide susceptibility assessment based on machine-learning methods. In Proceedings of the International Conference on Computer Graphics, Artificial Intelligence, and Data Processing (ICCAID 2023), Qingdao, China, 1–3 December 2023; Li, H., Wu, H., Eds.; SPIE: Bellingham, WA, USA, 2024; Volume 13105, pp. 310–320. [Google Scholar] [CrossRef]
- Selamat, S.N.; Majid, N.A.; Taha, M.R.; Osman, A. Landslide Susceptibility Model Using Artificial Neural Network (ANN) Approach in Langat River Basin, Selangor, Malaysia. Land 2022, 11, 833. [Google Scholar] [CrossRef]
- Vorpahl, P.; Elsenbeer, H.; Märker, M.; Schröder, B. How can statistical models help to determine driving factors of landslides? Ecol. Model. 2012, 239, 27–39. [Google Scholar] [CrossRef]
- Conforti, M.; Ietto, F. Modeling shallow landslide susceptibility and assessment of the relative importance of predisposing factors, through a GIS-based statistical analysis. Geosciences 2021, 11, 333. [Google Scholar] [CrossRef]
- Shu, H.; Guo, Z.; Qi, S.; Song, D.; Pourghasemi, H.R.; Ma, J. Integrating landslide typology with weighted frequency ratio model for landslide susceptibility mapping: A case study from Lanzhou city of northwestern China. Remote Sens. 2021, 13, 3623. [Google Scholar] [CrossRef]
- Mitra, R.; Das, J. A comparative assessment of flood susceptibility modelling of GIS-based TOPSIS, VIKOR, and EDAS techniques in the Sub-Himalayan foothills region of Eastern India. Environ. Sci. Pollut. Res. 2023, 30, 16036–16067. [Google Scholar] [CrossRef]
- Li, J.; Cao, Z.; Liu, Q. Waves and Sediment Transport Due to Granular Landslides Impacting Reservoirs. Water Resour. Res. 2019, 55, 495–518. [Google Scholar] [CrossRef]
- Nhu, V.H.; Shirzadi, A.; Shahabi, H.; Singh, S.K.; Al-Ansari, N.; Clague, J.J.; Jaafari, A.; Chen, W.; Miraki, S.; Dou, J.; et al. Shallow landslide susceptibility mapping: A comparison between logistic model tree, logistic regression, naïve bayes tree, artificial neural network, and support vector machine algorithms. Int. J. Environ. Res. Public Health 2020, 17, 2749. [Google Scholar] [CrossRef]
- Isola, F.; Lai, S.; Leone, F.; Zoppi, C. Land Take and Landslide Hazard: Spatial Assessment and Policy Implications from a Study Concerning Sardinia. Land 2023, 12, 359. [Google Scholar] [CrossRef]
- Dandridge, C.; Stanley, T.; Kirschbaum, D.; Amatya, P.; Lakshmi, V. The influence of land use and land cover change on landslide susceptibility in the Lower Mekong River Basin. Nat. Hazards 2023, 115, 1499–1523. [Google Scholar] [CrossRef]
- Makonyo, M.; Zahor, Z. GIS-based analysis of landslides susceptibility mapping: A case study of Lushoto district, north-eastern Tanzania. Nat. Hazards 2023, 118, 1085–1115. [Google Scholar] [CrossRef]
- Qi, T.; Zhao, Y.; Meng, X.; Chen, G.; Dijkstra, T. AI-based susceptibility analysis of shallow landslides induced by heavy rainfall in Tianshui, China. Remote Sens. 2021, 13, 1819. [Google Scholar] [CrossRef]
- Caputa, J.; Gorczyca, E. The role of landslides in the evolution of a small mountain river valley (Polish Carpathians). Epis. J. Int. Geosci. 2021, 44, 227–239. [Google Scholar] [CrossRef]
- Tubog, M.V.; Villahermosa, R.L.; Perong, J.G. Landslide Susceptibility Modeling Derived From Remote Sensing, Multi-Criteria Decision Analysis, and GIS Techniques: A Case Study in the Southeast Bohol Province, Philippines. Res. Sq. 2023; Preprint (Version 3). [Google Scholar] [CrossRef]
- Oh, H.J.; Lee, S.; Hong, S.M. Landslide Susceptibility Assessment Using Frequency Ratio Technique with Iterative Random Sampling. J. Sens. 2017, 2017, 3730913. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, X.; Chen, Z.; Ren, F.; Feng, L.; Du, Q. Optimizing the predictive ability of machine learning methods for landslide susceptibility mapping using smote for Lishui city in Zhejiang province, China. Int. J. Environ. Res. Public Health 2019, 16, 368. [Google Scholar] [CrossRef] [PubMed]
- Nam, K.; Wang, F. The performance of using an autoencoder for prediction and susceptibility assessment of landslides: A case study on landslides triggered by the 2018 Hokkaido Eastern Iburi earthquake in Japan. Geoenviron. Disasters 2019, 6, 19. [Google Scholar] [CrossRef]
- Deparday, V.; Gevaert, C.; Molinario, G.; Soden, R.; Balog-Way, S. Machine Learning for Disaster Risk Management; World Bank: Carroll, NH, USA, 2019. [Google Scholar]
- Dam, N.D.; Amiri, M.; Al-Ansari, N.; Prakash, I.; Le, H.V.; Nguyen, H.B.T.; Pham, B.T. Evaluation of Shannon Entropy and Weights of Evidence Models in Landslide Susceptibility Mapping for the Pithoragarh District of Uttarakhand State, India. Adv. Civ. Eng. 2022, 2022, 6645007. [Google Scholar] [CrossRef]
- Tran, T.H.; Dam, N.D.; Jalal, F.E.; Al-Ansari, N.; Ho, L.S.; Phong, T.V.; Iqbal, M.; Le, H.V.; Nguyen, H.B.T.; Prakash, I.; et al. GIS-Based Soft Computing Models for Landslide Susceptibility Mapping: A Case Study of Pithoragarh District, Uttarakhand State, India. Math. Probl. Eng. 2021, 2021, 9914650. [Google Scholar] [CrossRef]
- Kuhn, M.; Wing, J.; Weston, S.; Williams, A.; Keefer, C.; Engelhardt, A.; Cooper, T.; Mayer, Z.; Kenkel, B.; Benesty, M.; et al. caret: Classification and Regression Training. R Package Version 6.0-94. 2023. Available online: https://cran.r-project.org/web/packages/caret/index.html (accessed on 24 February 2024).
- Conoscenti, C.; Ciaccio, M.; Caraballo-Arias, N.A.; Gómez-Gutiérrez, Á.; Rotigliano, E.; Agnesi, V. Assessment of susceptibility to earth-flow landslide using logistic regression and multivariate adaptive regression splines: A case of the Belice River basin (western Sicily, Italy). Geomorphology 2015, 242, 49–64. [Google Scholar] [CrossRef]
- Conforti, M.; Pascale, S.; Robustelli, G.; Sdao, F. Evaluation of prediction capability of the artificial neural networks for mapping landslide susceptibility in the Turbolo River catchment (northern Calabria, Italy). Catena 2014, 113, 236–250. [Google Scholar] [CrossRef]
- Sing, T.; Sander, O.; Beerenwinkel, N.; Lengauer, T. ROCR: Visualizing classifier performance in R. Bioinformatics 2005, 21, 3940–3941. [Google Scholar] [CrossRef] [PubMed]
- Robin, X.; Turck, N.; Hainard, A.; Tiberti, N.; Lisacek, F.; Sanchez, J.C.; Müller, M. pROC: An open-source package for R and S+ to analyze and compare ROC curves. BMC Bioinform. 2011, 12, 77. [Google Scholar] [CrossRef] [PubMed]
- Shao, L.; Zhang, X.; Hu, T.; Chen, Y.; Zhang, C.; Dong, L.; Ling, S.; Dong, Z.; Zhou, W.D.; Zhang, R.H.; et al. Prediction of the Fundus Tessellation Severity With Machine Learning Methods. Front. Med. 2022, 9, 817114. [Google Scholar] [CrossRef]
- Lee, C.; Kim, H. Machine learning-based predictive modeling of depression in hypertensive populations. PLoS ONE 2022, 17, e0272330. [Google Scholar] [CrossRef]
- Milevski, I.; Dragićević, S. Landslide susceptibility zonation of the territory of North Macedonia using Analytical Hierarchy Process approach. Contrib. Sect. Nat. Math. Biotech. Sci. 2019, 40, 115–126. [Google Scholar] [CrossRef]
- Silalahi, F.E.S.; Yukni Arifianti, P.; Hidayat, F. Landslide susceptibility assessment using frequency ratio model in Bogor, West Java, Indonesia. Geosci. Lett. 2019, 6, 10. [Google Scholar] [CrossRef]
- Chung, C.J.F.; Fabbri, A.G. Validation of spatial prediction models for landslide hazard mapping. Nat. Hazards 2003, 30, 451–472. [Google Scholar] [CrossRef]
- Dou, J.; Yunus, A.P.; Tien Bui, D.; Merghadi, A.; Sahana, M.; Zhu, Z.; Chen, C.W.; Khosravi, K.; Yang, Y.; Pham, B.T. Assessment of advanced random forest and decision tree algorithms for modeling rainfall-induced landslide susceptibility in the Izu-Oshima Volcanic Island, Japan. Sci. Total Environ. 2019, 662, 332–346. [Google Scholar] [CrossRef]
- Merghadi, A.; Abderrahmane, B.; Tien Bui, D. Landslide susceptibility assessment at Mila basin (Algeria): A comparative assessment of prediction capability of advanced machine learning methods. ISPRS Int. J. Geo-Inf. 2018, 7, 268. [Google Scholar] [CrossRef]
- Tien Bui, D.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual Comparisons by Ranking Methods. In Breakthroughs in Statistics: Methodology and Distribution; Springer: New York, NY, USA, 1992; pp. 196–202. [Google Scholar] [CrossRef]
- Taalab, K.; Cheng, T.; Zhang, Y. Mapping landslide susceptibility and types using Random Forest. Big Earth Data 2018, 2, 159–178. [Google Scholar] [CrossRef]
- Li, B.; Han, L.; Li, L. A Spatiotemporal Fusion Network to multi source heterogeneous data for landslide recognition. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, 10, 77–84. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).