Situationally Sensitive Path Planning

Abstract

We examine how site-based path planning algorithms for enclosed spaces can be enhanced with situational detail. Addressing this question has led to value propositions in facility design, where there is often a call to match, map, and merge infrastructure considerations and configurations with potential implications for individual, group, and crowd flow through enclosed spaces. Responding to this question also invokes computational propositions, as facility design software is often computationally conservative with few resources devoted to simulation. We show that situational factors—the peculiarities and momentarily fleeting shifts in an individualized context that embody people in their movement through spaces—can be embedded into traditional, computationally lean path planning heuristics in ways that are actionable in widely used facility design software. We achieve this with algorithmic expansion of well-known planning algorithms using node-based architectures that permit the inclusion detail if, when, and where needed in a hyper-localized situational context that nests within site considerations. We demonstrate a proof of concept for use in the popular Unity 3D modeling platform, showing that situationally sensitive path planning can be achieved during the simulation run time of prototypical design scenarios for enclosed spaces with moving individuals, groups, and crowds.

1. Introduction

How people occupy built spaces is a critical consideration in the design and operation of built facilities [1]. Human movement involving pedestrians through enclosed spaces—corridors, tunnels, passageways, and other transition spaces—can be particularly sensitive to site factors, where space is limited and where pedestrian flow in low-density scenarios must be accommodated alongside design considerations for the extremes of crowding and occupancy. These include the available amount of open space, the distance between walls, the placement of necessary structures such as pillars and load-bearing supports, and their potential barriers to movement [2,3,4,5,6,7,8]. In some design scenarios, open-plan concepts are preferred to enhance free and unconstrained movement, and the corresponding design considerations for pedestrians can be driven unilaterally by that goal [9]. In other design applications, such as those for casinos [10] or supermarkets [11,12,13,14,15], the hyper-local geography of site factors must be carefully coordinated to deliberatively enclose, confine, and even confuse pedestrians in ways that produce desired patterns of individual and collective movement past displays and other touchpoints.

These considerations of human pedestrian movement must be taken into account in the design process when layouts are being conceived (Figure 1), which places emphasis on the provision of pedestrian modeling tools that can work with design software. Existing software tools for the design of enclosed spaces essentially mimic the traditional manual design process. A designer will construct a facility design in silico, in the cyberspace of the software, as an inert space. Considerations of how the design might influence pedestrian flow under given motion behaviors are proposed through the expertise and knowledge base of the designer and perhaps by building codes that dictate ingress and egress distances and occupancy-based density constraints, if available. Tools for quickly matching pedestrian flows to designs are relatively limited in popular computer-aided design and drafting (CAD) packages. Generally, designers rely on shortest path planning heuristics that can rapidly deliver moving pedestrians along heuristic journeys through designed spaces. These algorithms take a given design, convert it into a graph traversal space, and model the set of shortest paths that are available given a design scenario. This is generally achieved through greedy search [16]: a planning algorithm will traverse the graph from a pedestrian’s trip origin to a destination, returning graph nodes that are required for that trip and offloading those that are not, and then will assess the level of effort required to cover the remaining space through a combination of minimizing the total distance to the goal and the step-by-step traversal required (Figure 2). This search space can be swept by the heuristic for every possible source and sink, essentially providing a path map that pedestrians can draw from as they encounter each node sub-space in the graph, either online (during the run time of a simulation scenario) or offline (as a stored set of instructions to be loaded at the onset of a trip). Shortest path (and least-effort) pedestrian planning has a theoretical basis in anchor-based navigation and wayfinding [17], which posits that at a high level of cognition (that is, by rote memory, habit, routine, or with relatively little attention to the environment), people will move by the minimal distance between a source and a sink. Sources and sinks can be matched to design features such as entryways and exits, for example. Path planning algorithms [18] are graph-based, which means that they can straightforwardly accept designed features as path-avoidance obstacles embedded in the graph. Operationally, they are cheap, require limited resource usage for computing, and interface well as data structures with geometry objects from design software (e.g., as navigation meshes, or NavMesh structures). In practice, path planning heuristics also generate realistic-looking motion for agent characters in animation software, for example.

However, in the real world, pedestrians do not move solely by path planning [19] and it is generally preferrable for design problems that pedestrian models produce realistic-behaving pedestrians. In reality, pedestrians’ path planning decision is just one component of a very complex set of behaviors that they employ to move through space and time [20]. Path planning provides a guide for movement and a way for pedestrians to assess their progress in terms of time geography [21,22], a preliminary sketch of their so-called space–time path, or their perception of the spacing and timing available for them to complete an activity (at coarse scale of space–time) or action (at fine-scale). Along the way, using the path as a guide, pedestrians are dynamically influenced by their embodiment in a space [23] or a grounded and enlivened connection to the situational factors that associate them to spatial and geographical context. From this, pedestrians draw meaning from their surroundings, and this meaning informs their trajectory in space and time and the encounters that they perceive as relevant along the way. This embodiment generally takes on two forms: physical embodiment in the space [24] and social embodiment with other pedestrians [25]. Both embodiments require consideration of site (the configurational properties of a space) and situation (the uses that the spaces affords to an individual pedestrian or to a group of pedestrians). Importantly, pedestrians’ assessment of embodiment takes hold in very small bubbles of space and time, such that their space–time path can be considered a series of beads of encounter and experience [26].

In this paper, we consider how we might computationally string these beads as situational factors onto existing threads of heuristic paths provided by site factors. We reason that, algorithmically, the shortest path can provide a useful starting point, particularly paths that are instantiated as NavMesh data structures (graphs) in popularly used CAD and animation software. We reason that situational factors can be added to this graph structure in ways that preserve the computational economy of path planning but that add some of the localized “beads” of context that are necessary to enliven designs with realistic-behaving (and not just realistic-looking) pedestrians. Further, we do so with consideration of the computational burden of popularly used design platforms such as Unity 3D, which already load an array of packages and functions during run time and may often have limited available resources for dynamic models.

Specifically, we examine an interstitial solution that bridges the current state of practice in CAD design software, with advances from agent perception modeling. Our approach takes site-based models for path planning and expands them to incorporate situational context, doing so in a manner that is locally sensitive to the plan suggested by the global path. We introduce an initial proof of concept for (1) a virtual pedestrian crowd model built around (2) individually motivated agents who (3) consider hyper-local, situational conditions of their environment when conducting (4) macro-scale path planning through (5) constrained, enclosed spaces.

Methodologically, we represent this convergence between the situational environment and agents’ path planning behavior by introducing scalar representations of individual-based perception (safety, cleanliness), localized site factors, and emergent crowd phenomena (congestion) across a segmented traversable area, which we conceive as being actionable for design principles. Agents themselves maintain scalar representations of preferences towards situational factors and consider these preferences when determining optimal paths through local segments. Our approach here, which we term “situationally sensitive path planning”, allows for compatibility with traditional, heuristic graph-weighted planning schemes, and we show its implementation relative to Dijkstra’s shortest path heuristic [27] as a working example. The contribution of our approach to conceptual science is centered around movement studies [28] and behavioral geography. We aim to show that situationally sensitive path planning can be resolved algorithmically by leveraging known hierarchies of spatial behavior. Specifically, we focus on pedestrians’ cognitive mapping and navigation at the macro-scale during site-wide path planning, as well as their ability to revise their autonomic spatial behavior and wayfinding in response to local, micro-scale environmental and situational changes.

2. Related Work

Briefly, we discuss existing contributions to the literature in three categories. The first covers common shortest path algorithms. The second discusses physical approaches that address macro-scale phenomena of crowd formation, flow, and congestion patterning in enclosed spaces. The third reviews relativistic approaches from the geographical sciences (urban geography, human geography, social geography, and movement geography). Relativistic concerns—those rooted in context-specific, subjective experiences—form the backbone of social and behavioral traditions in urban science, which has relevance because of its strong tradition of urban design [29,30,31] and considerations of pedestrian interactions with built morphology [32,33].

2.1. Path Planning Heuristics

Path planning models for pedestrian movement generally take a heuristic approach to treating both space and pedestrians as users of that space. In planners, space is usually represented using a graph that is mapped to the metric space of a design by absolute means: nodes on the graph represent discrete locations in the counterpart real space (or designed space), while the edges of the graph correspond to real metric distances (or the effort required to traverse them), following conventions from algorithm design in computational geometry [34]. Heuristic approaches allow for a greedy search of the graph to find an optimal solution to a problem that is confined within the space. Generally, the problem is formulated as finding the shortest (or least-effort) metric-distance and graph-distance path from an origin to a destination [35]. Once this path is found, a model pedestrian is moved, node by node, along the graph edges of the resolved path, and the nodes may be weighted to produce different speeds of movement.

Dijkstra’s path planning algorithm is among the most popular schemes (we use it partially in our approach later in the text (Section 4.1.1.), and we provide a detailed explanation then). It will find the shortest path from an origin to every node in the graph space, and these paths then become available for guidance for model pedestrians as they move. The positions of existing pedestrians in the space can be embedded in the graph so that those locations are removed from consideration, and this can be achieved via an update cycle ahead of movement so that it resembles real-time collective movement patterns. The equally popular A* heuristic [35] adapts this approach primarily by allowing for the pruning of unlikely-to-be-visited paths from the search based on a reference to the currently estimated progress in advancing to the destination.

2.2. Adaptive Roadmaps

The adaptive roadmap technique represents a variant of path planning for NavMesh data structures [36,37]. Adaptive road mapping allows for localized collision avoidance on planned paths. This is necessary, for example, because at the fine resolution of locomotion, model pedestrians may end up pursuing similar paths through the environment. Dijkstra’s heuristic, after all, would have movers follow the shortest path, which could be identical for NavMesh with a coarse resolution and shared sources such as entryways. This runs the risk of collisions, which path planning cannot resolve beyond routing a pedestrian around counterpart model pedestrians. In an adaptive roadmap solution, path-planned pedestrians can engage in particle-type repulsion dynamics that will essentially “rubber-band” them free from collisions. In other solutions, a sub-space tessellation is performed (Voronoi tessellation is efficient in these cases) to project the semblance of a personal space buffer around model pedestrians [38,39,40,41].

2.3. Continuum Mechanics Models

2.3.1. Macroscopic Mechanics of Aggregate Crowd Flow

Macro-scale models drive collective (usually group and crowd) movements by approximating global continuum functions. Traditionally, these are physics-based due to the ease of transfer between considerations of physical particles and pedestrians as point masses with velocity and rotation: both are traditions that were carried into early models of pedestrian flow and traffic flow [42,43]. Significant success has been achieved in generating substantive patterns of crowd behavior from the mathematics of particle interactions [44,45], and a set of case studies have shown that particle models can reproduce the statistical patterns of crowd flow and outcomes that exhibit properties of complex adaptive systems [46,47,48,49]. We note, however, that most of the applications from physics are focused on phase shifts in crowd behavior, i.e., the emergent continuum or the tipping point at which a crowd begins to behave as excitable media [50]. Invariably, this draws the models into applications that focus on the extremes of crowd density. Consider, for example, how Hughes [51] (p. 171) outlaid the particle approach: “A crowd of pedestrians can generally be treated as a continuum, provided the characteristic distance scale between pedestrians is much less than the characteristic distance scale of the region in which the pedestrians move.” This brings to mind the dense packing of moving people at festivals [52] during large-volume crowd flow events such as parades and carnivals [53] and dense assemblies that are common during entertainment shows [54]. This dense-packing approach evokes crowd behavior, rather than the individual movement that one would expect through an enclosed space, i.e., continuum approaches address relatively uncommon events such as emergency egress [5], crowd panic [55], and crowd quakes [56] in which there are sudden shifts in crowd flow that block or injure participants [57]. Our interest is in more mundane and quotidian patterns of behavior. As such, the physics of excitable media are not appropriate representations. Nonetheless, a concise review is appropriate.

Traditionally, physics-based approaches to indoor pedestrian movement make an initial assumption that pedestrian particles can be treated as moving in a continuum; they use variants of the Navier–Stokes [58] equation or assumptions of Maxwell–Boltzmann [59] distributions to consider pedestrian movement and collective crowd flow as analogous to the flow of granular media, gas, or liquids [60,61,62]. Examples of applications to urban design are common in the literature, and scenarios include Henderson’s [60] work to model crowds as fluid phenomena in a gaseous phase. Indeed, Henderson tested his model with an application to a featureless model passageway, but performed validation for real designs (including the footpath outside the University of Sydney’s Fisher Library). Hughes’ [43,51] partial differential equation-based models are another canonical example of pedestrian particle models, alongside a stream of physics-inspired models by Hoogendoorn and Bovy and colleagues [63,64,65]. Popular extensions of continuum mechanics include variants to account for excitation [44,66], potential fields [67,68], velocity fields [69,70,71], and implementations as cellular automata and finite-state machines on Turing-like [72] lattices of discretized space models [73].

2.3.2. Microscopic Mechanics Between Pedestrians

The flow-forming particle-to-particle dynamics of the continuum approach can be extended to micro-scale considerations of the specific interactions that might form between people and objects during motion. In these instances, the general physics flow framework holds, but further specification of interactions underneath a coarser crowd flow are matched, conceptually, to physical effects of proximity and collision avoidance between pedestrians and between pedestrians and physical obstacles. This has some basis in reality, as people do try to avoid bumping into each other in some instances (although in cities, it may actually be acceptable to jostle and brush against other people), but the approach still misses out on the behavioral processes of steering that drive pedestrian perception and cognition against locomotion. So, again, we note that microscopic mechanics are mathematical approximation of human behavior, designed for convenience in simulation, but the resulting collective, emergent, up-scale dynamics have been shown to reveal valuable, actionable, and realistic (coarse-scale) signatures of complexity, mixing, and turbulence effects in crowds that are useful for design goals, especially for extremes of crowd volume, movement velocities, and the density of compaction in enclosed spaces [49,74,75,76,77].

Micro-scale models allow for high-fidelity control of pedestrian motion (just motion, not usually behavior), chiefly when inter-pedestrian collision avoidance is required to resolve intersecting path motion (essentially the cases of movement “ties” in planner updates that place pedestrians in unrealistic proximity). We consider that path planning is typically implemented in a “one and done” approach since online resolution is costly and usually defeats the utility of a global greedy heuristic in the first place. We mention again that there are prevalent issues in using path planning in small and enclosed spaces, where there is a high likelihood that many agents will start moving from around the same origins and have goals to move to the same destinations. A common side effect of this is the appearance of what looks like trains of pedestrians plodding along in an animation in unison. In reality, pedestrians will likely enforce some buffer of personal distance around them when moving alone [78,79,80,81,82] (there are even suggestions that this is a neural function of the brain [83]) or clump with other pedestrians for which they have a dyadic relationship for shared movement [84,85,86,87,88].

These localized effects can be added to path planning models, either using adaptive roadmap techniques or inter-particle collision dynamics, but there are complications with both. First, micro-scale models often need to be updated on an ongoing basis. This invokes computational cost that is always quite expensive; should each state machine require input from the states of all machines in a simulation, the required computational power and resources needed can grow non-linearly [71,89,90,91,92,93]. Second, both adaptive roadmap and particle-type solutions produce very sudden and unrealistic-appearing surge-type behaviors at a local scale (see [94] for empirical benchmarks of these approaches based on fractal sinuosity, with comparisons to real GPS-based motion trajectories). Particle-type models, such as the widely used social force models, have been shown to over-estimate the amount of displacement between pedestrians, as well as producing excessive amounts of sinuosity [20]. Further, social force models require modifications to handle low- or high-density scenarios [95,96].

To sidestep the challenge of both computational cost and the introduction of unrealistic movement artifacts, pedestrian models can rely on localized polling through automata input functions (neighborhoods, for example) to reduce the amount of state data a state machine must consider for state transition operations. In this regard, Reynolds’ [97,98,99] Boids algorithms for complex swarming and flocking have proven to be computationally efficient, and information polling also has conceptual foundations in offering a real-world understanding of pedestrian vision and motion responses to events that unfold in localized surroundings through perception [100,101,102,103,104,105,106].

Although particle-type schemes are mathematically tractable, it is well understood that pedestrians do not move as particles. Intentional vision and inter-personal egotistical motion [107] are the main missing behaviors from particle approaches. Here, we approximate them using the most commonly used velocity-based models. These include Velocity Obstacles (VOs) [108,109,110], Reciprocal Velocity Obstacles (RVOs) [111,112,113], Optimal Reciprocal Collision Avoidance (ORCA) [114], Hybrid RVO (HRVO) [115,116], and their various cousins [117] that prioritize velocity-based collision prediction schemes. Some variants of this approach invest in synthetic vision for pedestrians, and as such velocity-based models provide a solid basis for locally aware agents that react accordingly to neighboring agents’ anticipated movement. We use the approach in our pipeline, further incorporating aspects of vision-based models that mimic motor motion response maneuver behaviors as synthesized visual fields [40,118,119]. Vision-based models are a related subset of cognitive and socio-behavioral agent models that move away from physics as inspiration and toward behavioral parity with real-world agency [105,120].

Although tangential to our approach, which is focused on weak agency [121] (i.e., just enough artificial intelligence to produce design-relevant motion behavior as a response to embodied situation, and not as much investment in stronger agency that would directly recreate pedestrian cognition–movement–motion behavior), a range of pedestrian psychology models pickup essentially where particle and vision-based models leave off and weave in aspects of agents’ socio-psychological interactions. Notable in this tradition is the prevalence of personality, emotion, and reinforcement learning-based models from psychology that have been featured in agent computing for character movement in animation [122]. These include iterations of the personality and emotional hypothesis such as OCEAN (Openness, Conscientiousness, Extraversion, Agreeableness, and Neuroticism) [123,124]; PEN (Psychoticism, Extraversion, and Neuroticism) [125]; and the OCC (Ortony, Clore, and Collins) [126] methodology. Each concept pays considerable attention to the authenticity and diversity of individual agents/agency. When expressed as states and rules in simulation, these concepts allow for a focus on parameterizing the behavioral, temperamental, and mental characteristics of pedestrians as states in a finite-state machine approach [127] to driving pedestrian motion. For example, OCEAN and OCC have been used to generate distinct pedestrian and character movement models, and they have been successfully bridged together within aggregate multi-agent systems [128].

We also mention that data mining and machine learning-based models [129,130] can be used for situations in which trajectory samples of motion in enclosed spaces are available. For example, data mining and knowledge discovery have been built into agency to poll highly localized conditions from agent vision filters, e.g., data mining can accommodate very fast lookups of the type “I am this far from a wall, and in front of me is a barrier with this orientation; I am also surrounded by neighboring pedestrians, and I estimate that I will collide with them here, here, and there if I continue on my planned path”. These types of declarations can be expressed, collated, and quizzed in knowledge discovery architectures, which can be parameterized as k-d trees for storage and organization [131,132,133,134,135] and which can use the k nearest neighbor (k-NN) search algorithm [136] to efficiently recover results during the run time for quick consultation with a database. These databases can then be used by pedestrian simulations as libraries that will tell an agent what the next collision-free steps could be based on samples of trajectories that have similar parameters. Some machine learning-based models of indoor movement have been demonstrated to mimic realistic human behaviors [94,130] by relying heavily on training with trajectory sample data [137]. However, machine-based models typically prioritize navigational behaviors over personality and psychology.

2.4. Urban Science Models

Other approaches to modeling come from urban science, particularly from civic design and civil engineering approaches to pedestrian flow along streetscape segments [138,139,140] and at key transition sites in the pedestrian journey, such as crossing locations and curb areas [141,142]. Generally, design considerations for street segments usually begin in conceptual form [143] or from case studies of streetscape pedestrian behavior [144], and they are targeted at simulating pedestrian level of service. Rooted in empirical attributes of urban settings, localized (e.g., streetscape or street segment) urban design is largely occupied with consideration of distance, either egocentric from the pedestrian to things near them, and/or allocentric as vectors between objects and other objects [107,145,146]. Distance may be metric (and empirical) but can also be social and psychological [147], including considerations of safety relative to dangerous streetscape entities (moving vehicles) as well as (designed) built fixture elements such as road crossings [32,148,149]. Topics of how pedestrians move relative to landmarks on streetscapes [150,151,152,153] are also well covered in these schemes. Other site-based design considerations are also examined, including path complexity, the availability of citizen facilities, and pedestrian egress times [143]. Environmental factors include protection from the elements and attractiveness and aesthetics [154]. Modeling approaches in urban pedestrian simulation accommodate some of these factors in ways that are relevant to our approach for enclosed spaces. For example, path complexity is correlated with the presence of landmarks, the number of decision points along a path, and region connectivity across alternative paths [153,155,156,157,158,159,160], and these may feature as space–time anchors for design decisions [1,161]. The (mostly architectural) field of space syntax, for example, has developed design principles with a strong coupling to simulation [162]. Much of this science is theoretical, but facets have practical applications. For example, Paul and colleagues [163] suggested that subgroups within crowds may evaluate the pedestrian level of service (PLOS) of routes on different criteria depending on their current trip goals. The space syntax approach to depth mapping, as another example, adopts a graph-based approach that combines geometric and built morphology properties of streets (as well as indoor spaces) with motion considerations [9,162,164].

3. Implementation Considerations

Our aim is to develop an algorithm that is faithful to path planning heuristics but which allows for more detailed representations of hyper-localized movement around graph nodes and during traversal of graph edges. We aim for sensitivity to behavioral factors of embodiment and movement, but not full behavioral replication. Consider the example in Figure 2. It is obvious, even visually, that the shortest path movement instructions being delivered to a model pedestrian are much more straight and more robotic than one would expect of real human movement. This linear artifact of path planning will always persist, even across finer and finer resolutions of graph mesh. Particle-type motion, by contrast, is much more sinuous, but overly so. A compromise between the two would therefore be desirable in reflecting real-world patterns of movement. At the same time, the behaviors by which real pedestrians traverse enclosed spaces include distinct phases of planning, steering, and collision avoidance [165] that are substantively different in the decision-making that they invoke [159,166,167], in the patterns of motion that they produce [168], and in the information that pedestrians draw from their embodied surroundings to animate them in space and time [104,169,170,171,172,173,174,175]. Our aim of faithfulness to path planning heuristics also involves the preservation of computational economy, particularly as the cost of running companion motion algorithms in popularly used design software is always a feature that could be decreased in favor of other resources that are more mission-focused for design tasks.

Our objectives relative to these twin aims, then, are as follows. First, we wish to instantiate an extensible path planning scheme in popularly used design software. We will show that this can be achieved in Unity 3D through implementation of a base planner using Dijkstra’s formulation for greedy shortest paths. Second, we will flex this implementation to add hyper-localized deviations to the graph that account for situational factors of the enclosed space and situational awareness of model pedestrians. At the graph edge, we will adapt the planner to accommodate specifications of hyper-specific and movement-sensitive peculiarities of the environment, some of which are fixed over the term of movement and others that are dynamic. Then, at the graph node, we will instantiate a set of agent preferences that map to situation factors, as well as sub-models that run hyper-localized steering algorithms. The combined result will be (1) a typical site-based path planner that (2) accommodates CAD-compatible specifications of situational factors and (3) agent pedestrian models that are capable of generating site-aware and situationally sensitive movement behaviors, (4) running (efficiently) on popular commercial software (Unity 3D) (5) in run time.

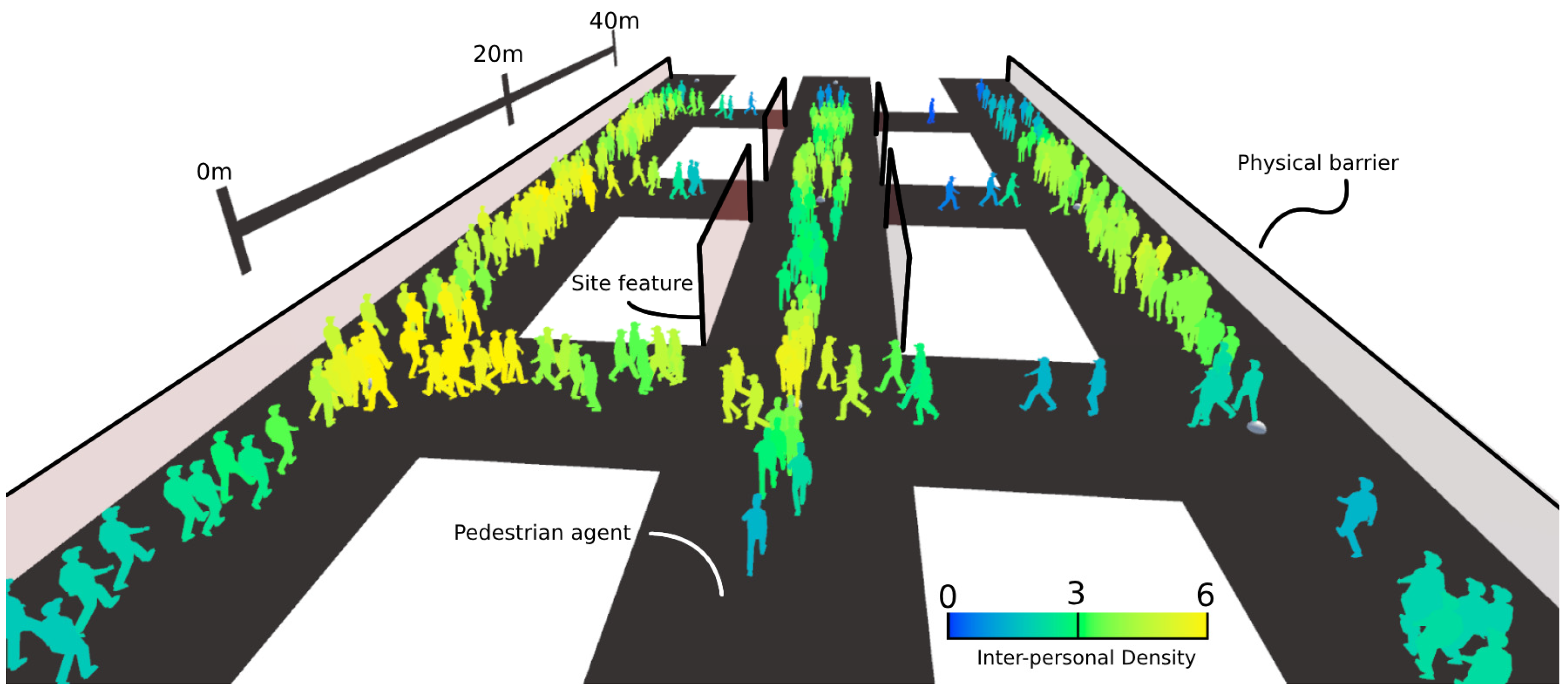
4. Methodology

In practice, our implementation is divided into two intertwined layers (Figure 3). First, a global manifold stores and updates the current physical (geometric and geographical) space of all traversable regions, as well as their properties/attributes. In essence, this functions as a Geographic Information System (GIS): a geometry interface to an underlying spatial database with lookup functions to convert (map) queries between the two. However, unlike traditional cartographic or geomatic user-facing GIS, our system is designed for model pedestrian lookup and geographic querying to the geometry layer. Further, we maintain a graph layer that is fully connected to the geometry, so that the GIS affords interoperability across a hyperspace (i.e., geographic slipstreaming [176]). In practical terms, the physical layer corresponds to the design space, with a layout of an enclosed space, interior features, and some fixed and movable objects. We refer to this as a “site”. These site factors are the central terms of adjustment and design manipulation in CAD software, representing walls, barriers, entrances and exits, assembly spaces, required egress distances, and so forth [177].

A second layer of the implementation is realized as the cognitive space of model pedestrians that will occupy the site and that will animate it with their individual and collective motion. We consider these as “situational”. Critically, agents should be responsive to both site factors, as well as being sensitive to situational factors. In our implementation, situational factors will be (1) at fine resolution, embedded within the site space, and (2) be of a higher degree of specificity than site factors relative to model agency. Motion through the enclosed space design, then, should be a converged product of site factors, as well as situational factors. Further, it should be driven by a GIS that allows for typical CAD-based design layouts, as well as agent-based pedestrians that can enliven those designs with space–time occupancy and emergent dynamics of movement that result from the design.

Our implementation of agency warrants a more detailed explanation. In our pipeline, we follow the concept of situated cognition [149] as the basis for designing and specifying agency, i.e., the notion that pedestrians will move through an environment with a comparatively low level of cognitive load up to the point of encountering situational properties of the (very localized) environment and/or socio-situational factors of ambient pedestrians. At the point of encounter, then, pedestrians context switch from a default of path-following (which is often routine and habitual, and which generally follows a shortest path or least-effort driver) to an alternative movement behavior of perception and response that is driven primarily by vision, and which is likely to be deliberative and bespoke to a given situation. Generally, this context switch takes place through inter-personal proxemics [178,179,180,181,182]. For example, one generally knows how to walk in a straight line and avoid walls, but it may take some careful choreography of steering and locomotion to avoid bumping into another person, particularly when that person is also counter-considering how to avoid a collision with you [183,184,185,186].

To fold situational agency into the system, we implement a second system, functioning on an agent-based state space composed of individualized automata neighborhoods (synthetic visual fields) that are projected as geography (geometry) downward (in resolution) to individual agents. This projection (a mapping) works interactively with the GIS, forming a third hyper-space in the slip-streamed architecture. Within this state space, agents operate as finite-state machines and poll state conditions within their unique individual situational lens. Our specification of this lens draws upon the conceptual literature from proxemics and spatial perception, which posits that pedestrians will view site-based obstacles and opportunities, as well as situational factors that embody them within their space–time path, and that they will do so in a visual field (frustum) that shifts fixture along with their intended motion velocity. We handle this lensing with malleable, interactive, and reciprocating geometries that can be provided by Velocity Obstacle formulations (and which, again, can be mapped to our GIS as a hyper-space) (Figure 3). Thus, we are simultaneously able to handle sites as geometry with regional properties (e.g., graph traversal) and to treat situations using partial space–time geometries as RVOs (while also retaining preferences toward regional properties). This has real-world practical foundation. As in mental map concepts, we assume that agents have access to a general rubric of traversal through the full regional scope of the enclosed space (i.e., they are not nudging into every nook and cranny of the space like insect motion) and that they may call upon that knowledge when calculating their actual (preferred) path through the environment. (The path planning heuristic ensures that agents, at any point in space and time, have only partial, although region-spanning, knowledge of the global space, rather than total awareness.)

Similarly, based on real-world movement in enclosed spaces, an interim space between path planning and steering and collision detection and avoidance is usually observed as wayfinding [187]. Generally, this interim space is used in cognition to first anchor pedestrians to destinations for their motion, second to guide them along a habitual or rote path, and (importantly, with relevance to our implementation) third to essentially break up that path into a series of check-ins along the way. In this manner, movement adheres to global (geographical) knowns of the pedestrian’s preferred motion, but can hot-glue to intervening (local, spatial) beacons along the way. Waypoints generally appear as fixed, reliable, and visible sub-sites along a path. Different people seek out different waypoints when walking, including landmarks, fixed attributes of spaces such as wall corners, or even approximated metrics of space and/or time [188]. As pedestrians near waypoints, for example, they may look up from their locomotion to essentially reorient and redraw their cognitive/mental map of the enclosed space. We accommodate this in our implementation using waypoints that are embedded as nodes in the graph structure. Again, this all runs in ways that are compatible with the GIS architecture of our implementation as a hyper-space.

Our model implements properties of site and situation as either dynamic or scalar float values:

• Segment Length: Geographic (Euclidean) length of route segment, calculated online from the endpoint node;
• Path Condition: Qualitative (physical) condition of a route segment, calculated via scene detection of streetscape design objects (user-placed objects in the design phase, e.g., trash cans);
• Pedestrian Level of Service (PLOS): The occupancy (i.e., crowd density and congestion) of a route segment, calculated as a ratio of agents per segment of traversable surface area;
• Risk: The level of risk associated with the route segment; this parameter is manually configurable by the user.

Although not discussed here for brevity, we can set path complexity, attractiveness, and landmarks using other parameterizations, including procedural modeling, style sheets, dynamic lookups to GIS, and generative AI. Also, in the approach in this paper, we parameterized agents with transition rule homogeneity for path preference, but this can be configured with classifications, individuality, or roles as a shifting consideration.

4.1. Global Environment Layer

The global layer (Figure 3) provides, to an agent (yellow bubble in Figure 3) upon request, a least-cost path—from one waypoint in the virtual geography of the enclosed space design to another waypoint along that path. One of these waypoints will be a terminal node, which forms the destination for the classic shortest path planner. This is consistent with origin–destination (source-to-sink) trip planning: people usually come from one location and have in mind their next, global destination, and the locations at each “end” of the trip are usually site-specific anchors (or the “anchor” in an anchor point hypothesis of spatial behavior [189]). The global path therefore represents the substantive “big picture” that a pedestrian will have of how they wish to move through the designed space (e.g., from here to there, with the shortest distance, with these waypoints along the way). The local trajectory to be followed as that path will then consider situational factors of the hyper-local details of the space, as well as the dyadic, group, and crowd patterns that emerge during motion [140,190,191].

Agents default to a simple traversal-by-wayfinding along the shortest path if moving alone in the space. This straightforwardly sets the serial node in the graph as the next destination goal for movement, which is articulated as a steer-by-seeking maneuver. Upon reaching a waypoint, the model pedestrian will then recompute their path. This implies that agents in our model commit to their current paths and only reconsider site factors upon reaching a pivotal point in their current path, such as intersections. This is consistent with the “looking up” type of behavior we discussed above. It is also consistent with case study evidence from behavioral geography that shows that pedestrian walkers will decompose their initial global path to subdivide their traversal space using waypoints. Similar observations have been made in case studies from civil engineering [177] and from the movement psychology literature [19]. Evidence from environmental psychology has also indicated that landmarks anchor one’s space–time paths to localized, situational factors.

In implementation, the global layer treats the traversable virtual environment as a weighted graph with nodes and edges serving as waypoints and pathways, respectively. When an agent reaches a waypoint and subsequently requests an updated optimal path to their target node, the global layer returns a least-cost path calculated from Dijkstra’s shortest path algorithm with edge costs computed using each edge’s property values and a unique set of preference weights provided by the requesting agent. Here, nodes represent the physical nature of the waypoints: their positions in the world and acceptable radii that an agent can use to consider themselves as having reached the node. The radii are considered conceptually to be touchpoints with that waypoint, and we leave this open in implementation: they could be artifacts of the space that are individualized, or environmental affordances that are specific to a set of agents, or they could be generalized atmospherics designed for touchpoint appeal to all agents. Meanwhile, the edges are also open as design levers and can be manually input or they may be designed procedurally, e.g., using different area-based traversal schema such as retail zoning in shops [192], education stations in schools [193], assembly sites in transit stations [194], or even layouts in buses and trains themselves [195]. Similarly, the edges could be auto-computed as parameter values used in travel cost determination: [196], for example, showed that this can be achieved using the principles of least effort for outdoor path planning.

4.1.1. Dijkstra’s Algorithm for Path Planning: A Review

We base our global layer on Dijkstra’s algorithm (Algorithm 1) (we refer to this as “Dijkstra” from here on out), which is one of the most well-known and widely used shortest path heuristics in computing. Dijkstra greedily calculates the minimal distances between a source node and all other nodes on a weighted graph. The term “greedy” here broadly describes a class of functions that makes optimal choices in graph space (with respect to the current state and knowledge of the system at each time step) without reconsidering previous steps. Dijkstra’s algorithm operates on a weighted graph with edges that each maintain a scalar distance value. At the start of its computing, Dijkstra sets the initial distances for all vertices: 0 for the source node, and infinity (or some large scalar value) for all other nodes. At each time step, the heuristic then carries out the following:

• Selects, among a subset of unvisited nodes, the node that has the smallest distance cost. In the first algorithm step, this would default to the source node, which has a distance of 0.
• For the selected node, considers all its unvisited neighbors and updates their distance values through the selected node. This is a form of knowledge updating whereby if a previous time step has already set a distance cost to an unvisited node but the new distance cost through the selected node is smaller, the smaller distance cost (through the selected node) overwrites the larger distance cost.
• Marks the selected node as “visited”, and loops back to Step 1, then continues looping until no more vertices remain in the unvisited set.

The original version of Dijkstra’s algorithm produces the path cost from the source node to all other vertices but does not provide the shortest path itself. The shortest path variant of Dijkstra can be straightforwardly implemented by storing not just the shortest distance cost to each node but also a reference to a previous node that produced the shortest distance. Provided with both a source and target node, Dijkstra can return the shortest path by moving backwards from the target node to the source node after all distance calculations. Furthermore, this variant of Dijkstra can terminate the distance calculation loop early if the target node is visited, as there is no need to continue updating distances if the system has managed to reach the target node.

4.1.2. Global Environment Graph Definition

To extend Dijkstra to situational preference-based path planning, let us define the weighted graph with respect to situation domain values. Consider the designed virtual environment as a weighted graph with environmental waypoints taking the place of the graph’s nodes. Let us define each waypoint pair connected by an edge as a region segment $s$. Each segment $s$ must terminate with a waypoint at each end and must connect to at least one other segment. Model pedestrians (supplied by the local model) will traverse between waypoints in the environment along these segments and will adjust their path determination at each waypoint. Conceptually, this translates to habitual motion along the path, with a context switch to situational factors at the waypoint.

Algorithm 1 Dijkstra’s Algorithm for Shortest Path

procedure Dijkstra(Graph G, node source, node, target)   $dist\leftarrow \left[\right], prev\leftarrow \left[\right], U\leftarrow \left[\right]$  $\mathbf{for} \mathrm{node} n\in G.Nodes \mathbf{do}$    $dist\left[n\right]\leftarrow \infty$   $prev\left[n\right]\leftarrow \mathrm{undefined}$    $U.push\left(n\right)$   $dist\left[source\right]\leftarrow 0$  $\mathbf{while} U \mathrm{is} \mathrm{not} \mathrm{empty} \mathbf{do}$   $c\leftarrow \underset{u\in U}{\mathit{min}} dist\left[u\right]$   $\mathrm{remove} c \mathrm{from} U$    $\mathbf{for} \left\{\left(c,u\right) | u\in U,\left(c,u\right)\in G.Edges\right\} \mathbf{do}$     $d\leftarrow dist\left[c\right]+G.Edges\left[\left(c,u\right)\right]$     $\mathbf{if} d<dist\left[u\right] \mathbf{do}$      $dist\left[u\right]\leftarrow d$      $prev\left[u\right]\leftarrow c$     $\mathbf{end} \mathbf{if}$    $\mathit{e}\mathit{n}\mathit{d} \mathit{f}\mathit{o}\mathit{r}$    $\mathbf{if} c==target \mathbf{break}$   $\mathbf{end} \mathbf{while}$   $S\leftarrow \left[\right]$   $n\leftarrow target$   $\mathbf{if} prev\left[n\right] \mathrm{is} \mathrm{defined} \mathbf{do}$    $\mathbf{while} n \mathrm{is} \mathrm{defined} \mathbf{do}$     $S.push\left(n\right)$     $n\leftarrow prev\left[n\right]$    $\mathbf{end} \mathbf{while}$   $\mathbf{end} \mathbf{if}$   $\mathbf{return} S$ $\mathbf{end} \mathbf{procedure}$

4.1.3. Site and Situation Factors

Recall that in our implementation we consider four broad classes of site and situation properties: segment length, footpath condition, PLOS, and risk. These are open to design levers, but as an example, here we represent these properties in terms of four factors: distance (segment length, dist), cleanliness/dirtiness (footpath quality, dirt), safety (the inverse of risk, safe), and crowd density (PLOS, density). In addition, we consider a static fifth base cost to each segment that allows the system designer to dictate a consistent cost to each segment of their choice (see the “base cost graph” illustration in Figure 3). Both segments and individual agents internally maintain scalar weight values that correspond to each factor and are considered during Dijkstra’s distance cost calculations.

Site and situation weight factors for segments and agents can either remain statically set or dynamically alter with respect to environmental changes. For example, if a segment accumulates an increasing number of agents over time, its density weight will naturally increase, resulting in an increased cost value for that segment. Similarly, agents can be modified to have dynamic personalized weight values that conceptually correspond to different emotional moods or cognitive states. More broadly, agents can be spawned with randomized combinations of different preferences to elicit dynamic perspectives among pedestrians.

In implementation, it is expected that each region segment s tracks the following:

• base cost set by the system designer ($s_{base});$
• Its Euclidean length between its end waypoints ($s_{dist});$
• Its spatial area with respect to the scale of the virtual environment ($s_{area});$
• The number of active agents moving along it ($s_{pop});$
• Any contextual virtual artifacts that thematically impact a segment’s quality, such as trash items, animals, etc. (s_dirt, s_Safe).

Each agent $a$ also maintains a similar set of personality weights (i.e., $a_{dist}$, $a_{density}$, $a_{dirt}$, $a_{safe}$) with an exception to the $base$ cost (which is a segment-specific property).

4.1.4. Situational Preference-Based Path Planning: Cost and Shortest Path Calculations

Let us consider the global environmental layer’s graph $G$ and an agent $a\in A$. When agent $a$ performs a path query, the global layer calculates the path by running Dijkstra’s algorithm on a modified instance of the original weighted graph (Algorithm 2). This modified instance contains personalized edge costs calculated from both environmental and agent personality factors. This instance calculation is performed prior to Dijkstra’s algorithm returning the shortest path (Algorithm 3).

$$\begin{array}{cc}\hfill C(s,a)& =s_{base}\hfill \\ \hfill & +\left(s_{dist}·a_{dist}\right)\hfill \\ \hfill & +\left({\displaystyle \frac{s_{pop}}{s_{area}}}·a_{density}\right)\hfill \\ \hfill & +\left(s_{dirt}·a_{dirt}\right)\hfill \\ \hfill & +\left(s_{safe}·a_{safe}\right)\hfill \end{array}$$

(1)

Algorithm 2 Calculating the Modified Graph

procedure$CalculateCosts\left(\mathit{Graph} G, \mathit{agent} a\right)$   $E\leftarrow \left[\right]$   $\mathbf{for} \left\{\left(u,v\right) | u\in G, v\in G, \left(u,v\right)\in G.Edges\right\} \mathbf{do}$    $c_{dist}\leftarrow s_{dist}·a_{dist}$    $c_{density}\leftarrow {\displaystyle \frac{s_{agents}}{s_{area}}}·a_{density}$    $c_{dirt}\leftarrow s_{dirt}·a_{dirt}$    $c_{safe}\leftarrow s_{safe}·a_{safe}$    $E\left[\left(u,v\right)\right]\leftarrow s_{base}+c_{dist}+c_{density}+c_{dirt}+c_{safe}$   $\mathbf{end} \mathbf{for}$   $G.Edges\leftarrow E$   $\mathbf{return} G$ $\mathbf{end} \mathbf{procedure}$

Algorithm 3 Situational Preference-Based Shortest Path

procedure$CalculatePath\left(\mathit{Graph} G, \mathit{agent} a, \mathit{current} \mathit{node} source, \mathit{target} \mathit{node} target\right)$   $G\prime \leftarrow CalculateCosts\left(G,a\right)$   $P\leftarrow Dijkstra\left(G^{\prime },source,target\right)$   $\mathbf{return} P$ $\mathbf{end} \mathbf{procedure}$

4.2. Local Agent Layer

The local agent layer consists of individual agent entities that conduct their autonomous, independent, and perspective-dependent motion via synthetic visual fields, RVO-based inter-agent collision avoidance, and internally held scalar values that represent preferences during path determination.

4.2.1. Synthetic Visual Fields

Briefly states, our model considers vision as an event-driven system rather than a global knowledge system: agents are visible to other agents if their mesh colliders intersect with the other agents’ view frustum colliders (see the collision inset illustration in Figure 3). Agents’ synthetic visual fields are represented as monocular view frustums that egocentrically follow agents’ forward orientation and position. These view frustums appear as sideways square pyramids, with a 160-degree total horizontal spread and a 130-degree total vertical spread. For simplicity, we assume that the agents’ field of view (FOV) is purely horizontal in nature. Rather than using Unity3D’s Camera component, we employ Unity3D’s PhysX collision logic and treat view frustums and agent meshes as convex colliders.

4.2.2. RVO-Based Local Collision Avoidance

We employ RVO for agent collision avoidance at very localized resolutions. The Reciprocal Velocity Obstacles method is one of several velocity-based local collision avoidance models derived from Fiorini and Shiller’s Velocity Obstacles [108,109,110]. RVO proceeds from one important assumption: in a paired scenario with two agents $A$ and $B$ heading into a collision course, both agents will actively adjust their velocities to avoid collisions (Figure 3). This is well understood in behavioral science, following significant observational work in proxemics and inter-personal social effects. RVO reflects situational proxemics, particularly by introducing the idea of “shared responsibility” between agents, rather than putting all the onus on one agent, as is in the VO paradigm. This sharing of the small bundle of space and time that can open up ahead of a potential collision has important corollaries in the conceptual literature, particularly in social psychology of shared gaze and the exchange of non-verbal communications as body language signals among mobile pedestrians in encounter-based dyads.

Consider two agents $A$ and $B$ with positions $p_A$, $p_B$ current velocities $v_A,v_B$, and preferred velocities $v_A^{\mathit{pref}},v_B^{\mathit{pref}}$. The generalized form of $RV{O}_B^A$ is defined as follows:

$$RV{O}_B^A\left(v_B,v_a,a_B^A\right)=\left\{v_A^{\prime }|{\displaystyle \frac{1}{a_B^A}}{v}_A^{\prime }+\left(1-{\displaystyle \frac{1}{a_B^A}}\right)v_A\in V{O}_B^A\left(v_B\right)\right\}$$

(2)

Observe the parameter ${\alpha }_B^A\in \left[0, 1\right]$, which incorporates agent $A$’s willingness to share responsibility with other agents. As this weight approaches 1, the RVO operation more closely resembles the original VO formulation. Conversely, as this weight approaches 0, the more likely it becomes that $A$will ignore collision avoidance. Designers can thus use this parameter to adjust the overall balance of the crowd flow, e.g., introducing self-centered agents who do not adjust their velocities, versus selfless agents who bear all the responsibility for reconciling the encounter.

In practice, multiple candidate velocities can be viable at the same time (e.g., moving backwards can be just as viable as making a hard right to an incoming agent on the left). In the RVO paradigm, a penalty value is assigned to each possible candidate velocity $v_A^{\prime }\in V_A^{\prime }$. A penalty minimization process (Algorithm 4 and Algorithm 5) is required to identify the candidate velocity with the smallest penalty cost $p^{min}$. In van der Berg’s RVO implementation [112,197], this penalty cost is the additive combination of two sub-heuristics: (1) time to collision (TTC) and (2) the Euclidean distance between a candidate velocity and the agent’s preferred velocity (Algorithm 6). We deploy a penalty function, with a “safety” weight ${\omega }_A$ adjusting the TTC penalty:

$$penalty\left(v_A^{\prime }\right)={\omega }_A{\displaystyle \frac{1}{TTC\left(v_A^{\prime }\right)}}+‖v_A^{pref}-v_A^{\prime }‖$$

(3)

Algorithm 4 Local Agent Layer: Penalty-Minimizing RVO

procedure$RVO\left(p_A, {\alpha }_A, v_A^{pref}, {\alpha }_B^A, {\omega }_A\right)$   $v^{opt}\leftarrow v_A^{pref}$   $p^{min}\leftarrow PENALTY\left(v_A^{pref},v_A^{pref},p_A,v_A, {\alpha }_B^A, {\omega }_A\right)$   $\mathit{f}\mathit{o}\mathit{r} v_A^{\prime }\in V_A^{\prime } \mathit{d}\mathit{o}$    $p\leftarrow PENALTY\left(v_A^{\prime },v_A^{pref},p_A,v_A, {\alpha }_B^A,{\omega }_A\right)$    $\mathit{i}\mathit{f} p<p^{min} \mathit{t}\mathit{h}\mathit{e}\mathit{n}$     $v^{opt}\leftarrow v_A^{\prime }$     $p^{min}\leftarrow p$    $\mathit{e}\mathit{n}\mathit{d} \mathit{i}\mathit{f}$   $\mathit{e}\mathit{n}\mathit{d} \mathit{f}\mathit{o}\mathit{r}$   $\mathit{r}\mathit{e}\mathit{t}\mathit{u}\mathit{r}\mathit{n} {\mathit{v}}^{\mathit{o}\mathit{p}\mathit{t}}$ $\mathit{e}\mathit{n}\mathit{d} \mathit{p}\mathit{r}\mathit{o}\mathit{c}\mathit{e}\mathit{d}\mathit{u}\mathit{r}\mathit{e}$

Algorithm 5 Local Agent Layer: Calculation

procedure  $PENALTY\left({v^{\prime }}_A,v_A^{pref},p_A, v_A, {\alpha }_B^A, {\omega }_A\right)$   $p^{time}\leftarrow \infty$   $\mathit{f}\mathit{o}\mathit{r} neighbor B\in N_A \mathit{d}\mathit{o}$    $v_B^A\leftarrow {\displaystyle \frac{1}{{\alpha }_B^A}}{v}_A^{\prime }+\left(1-{\displaystyle \frac{1}{{\alpha }_B^A}}\right)v_A-v_B$    $p\leftarrow TTC\left(p_A,p_B,v_B^A,r_A+r_B\right)$    $\mathit{i}\mathit{f}p<p^{time} \mathit{t}\mathit{h}\mathit{e}\mathit{n}$     $p^{time}\leftarrow p$    $\mathit{e}\mathit{n}\mathit{d} \mathit{i}\mathit{f}$   $\mathit{e}\mathit{n}\mathit{d} \mathit{f}\mathit{o}\mathit{r}$   $\mathit{r}\mathit{e}\mathit{t}\mathit{u}\mathit{r}\mathit{n} {\mathit{\omega }}_{\mathit{A}}{\displaystyle \frac{1}{p^{time}}}+‖v_A^{pref}-v_A^{\prime }‖$ $\mathit{e}\mathit{n}\mathit{d} \mathit{p}\mathit{r}\mathit{o}\mathit{c}\mathit{e}\mathit{d}\mathit{u}\mathit{r}\mathit{e}$

Algorithm 6 Local Agent Layer: Time to Collision

procedure  $TTC\left(p_A,p_B, v_B^A,r\right)$   $t\leftarrow \infty$   $p\leftarrow p_B-p_A$   $v\leftarrow v_B^A\circ v_B^A$   $d\leftarrow -{\left(v_B^A\times p\right)}^2+r^2·v$   $\mathit{i}\mathit{f} d>0 \mathit{t}\mathit{h}\mathit{e}\mathit{n}$    $t={\displaystyle \frac{v_B^A-\sqrt{d}}{v}}$    $\mathit{i}\mathit{f} t<0 \mathit{t}\mathit{h}\mathit{e}\mathit{n}$     $t=\infty$    $\mathit{e}\mathit{n}\mathit{d} \mathit{i}\mathit{f}$   $\mathit{e}\mathit{n}\mathit{d} \mathit{i}\mathit{f}$   $\mathit{r}\mathit{e}\mathit{t}\mathit{u}\mathit{r}\mathit{n} t$ $\mathit{e}\mathit{n}\mathit{d} \mathit{p}\mathit{r}\mathit{o}\mathit{c}\mathit{e}\mathit{d}\mathit{u}\mathit{r}\mathit{e}$

5. Experiments

As a prototypical test of our pipeline’s ability to support a design task, we ran a limited test on an indoor, enclosed space (Figure 4). Using the design, we then explored our model’s ability to embody situationally sensitive agency of virtual pedestrians with respect to both static and dynamic environmental factors in simulation. Virtual pedestrians were spawned at 0.1 s intervals into an entry space and tasked with finding their way to an exit space, with simple intervening barriers in the design of the site. The model pedestrians’ task, then, is to move to that destination by initially pursuing the shortest path. What constitutes the shortest path is updated dynamically to account for intervening obstacles that may appear. For local collisions, agents engage RVOs as we discussed above.

In addition, to approximate personality, five distinct personality preferences are used to predispose agents toward embodiment as they dynamically encounter situational context that they maintain (personal) sensitivity to along a given path, and these are activated individually on virtual pedestrians. This allows us to observe their influence on the emergent crowd flow and distribution across the virtual manifold.

We developed a set of seven scenarios to form a test-bed simulation for our approach. A control scenario (CONTROL) was used with A* path planning [35] alone as a comparison to Dijkstra. This was enabled through Unity3D’s in-built NavMesh plugin, which also features an RVO implementation for local agent collision avoidance that emphasizes run-time efficiency. Algorithmically, NavMesh RVO is similar to our model, which allowed us to isolate our observations and findings to the alterations that we made specifically to localize pathing behavior. Together, CONTROL approximates what would be available to a programmer using the available Unity functions.

Another simulation was run with a Dijkstra heuristic (DIJKSTRA) alone as a benchmark. A* and Dijkstra simulations yield path planning that considers site factors of collision with fixed obstacles of the built environment, distance to destination, and time to destination. Both graph distance and metric distance are factors.

A third static scenario was run with portions of the space coded as “risky” (S-RISK). Pedestrians with (personal) risk aversion in their profile will adjust their planning for locomotion away from these fixed sites.

We then introduced a set of dynamic scenarios. The first examined dynamic risk: a dog character was introduced to the space, on the loose and running through the enclosed space and crowd in the reverse direction of predominant flow (D-RISK). The dog is designed to introduce a sudden uncharacteristic event to the simulation, which should nudge pedestrians off their paths and require that they generate response motion. Agents with a predisposition to risk that encountered the dog in their view would adjust their planning for locomotion paths around the dog. Others without that personality trait (without that sensitivity) would ignore the dog. We also programmed some agents to drop litter (banana peels) on the space as they moved, seeding the space with a dynamic geography of cleanliness/dirtiness (DIRT). Agents with an aversion to littered space would move accordingly when encountering this dirt. Finally, we established a scenario to account for congestion (DENSITY), as polled by agents that are predisposed based on the number of counterpart agents that they encounter in their vision. The final scenario ran all of these factors simultaneously (ALL).

For our pipeline, the simulation environment, including the underlying run time scripts and animation blending, was developed in C# within the Unity3D game engine. Furthermore, all walking, standing, and body rotation animations were based upon Mixamo’s animation library. We used motion blending on mobility state and velocity to control the animation cycles during simulation run time. Humanoid meshes were generated with character creation tools available in the Unity Asset Store, while non-humanoid meshes such as trash and dog models were imported from poly.pizza. During software run time, agents were animated via Unity3D’s Mecanim Animation System, which provides in-built solutions to motion blending and inverse kinematics for animation skeleton matching.

6. Results

To evaluate the relative influence of each experimental factor on (1) collective movement and (2) individual movement through the urban space, we exported agents’ positions on NavMeshes to a space–time GIS to visualize both global (site, design) and local (situational) implications for the design space. Our analysis covers all seven available experimental conditions: the control group (CONTROL), distance aversion (DIJKSTRA), static risk aversion (S-RISK), dynamic risk aversion (D-RISK), dirtiness aversion (DIRT), density aversion (DENSITY), and a combination of all factors (ALL). We additionally ran spatial analysis on the results. Figure 5 shows the results for the ebb and flow of crowd flows, as both velocity streams and kernel density estimations (KDEs) of pedestrians’ positions, with respect to these preferences over time.

6.1. Preference for Detours

Observations of CONTROL and DIJKSTRA, both of which employ greedy shortest path preferences in pedestrians, appear to show that basic, global path planning prevents agents from diverting into the side corridors of the design space. This is unrealistic as these form large swaths of the enclosed space that real people would likely be apt to explore and move through. Figure 5 shows that under CONTROL and DIJKSTRA, rather than proceeding around the gaps in the layout, agents will instead hug the wall and congregate at corners until they are provided sufficient clearance to enter the central flow. This is in stark contrast to the nimble and adaptive crowd flows observed in S-RISK, D-RISK, and DIRT, which demonstrate agents opting to detour rather than wait at corners. Interestingly, alternative path choices are not strongly reflected in DENSITY, instead showing that participants will prefer to follow the crowd flow through the central corridor. This observation makes sense upon comparison with real-world observations of directional crowd flow, especially follow-the-leader behavior that pedestrians make use of to slipstream in synchrony with fellow pedestrians as pelotons that are (temporarily) moving in the same local direction and velocity as them. Following the crowd offers pedestrians fewer moments to dedicate their attention to collision avoidance and re-establishing shortest paths. These crowd flows echo observations in social science where pedestrians in naturally forming groups begin to reproduce the actions of dominant local motion behaviors within these groups: people go with the flow, if they believe it in their heads and if it is safe to play along. At the meso-scale, this can result in the formation of platoons, while at the macro-scale, long-lasting and resilient patterns of unidirectional crowd flow can emerge and persist, even as different individual agents join and exit the stream.

6.2. Dynamic Situations and Path Variation

Out of these preferences, the DIRT condition appears to have the most consistent effect of causing pedestrians to alternatively choose other paths, rather than follow a single alternative corridor as seen in S-RISK. In this situation, a small minority of pedestrians opt to “throw away” trash behind them as they walk. The subsequent build-up of trash articles in the scene appears to have caused agents to prefer alternative corridors without any trash. Though trash articles are scripted to disappear 40 s after they spawn, a space–time wave/lagging effect on path choice is nonetheless observed. In other words, subsequent pedestrians end up reacting to the perception of the situation that was encountered by pedestrians that came before them, much like in traffic jams.

To explain the cause of divergent path preferences, we look towards S-RISK and D-RISK, both of which feature agents only choosing the right-hand side corridor in Figure 4A. We consider this to be an artifact of our choice of Dijkstra as the base for the model, rather than an indicator of emergent behavior among agents. Specifically, under an assumed tie-break situation where the cost of traveling to either right-hand-side or left-hand-side corridor is equal (agents are in between and have no collisions or local situational sensitivity factors that are relevant to their choice), agents will pick the right-hand-side path as a default. (Colloquially, this mimics decades of literature showing that the peculiarity of pedestrians’ tendencies to move to the right when all else is equal, regardless of whether they are right-handed or whether people drive on the right-hand side of the road.) In the case of S-RISK, the dog remains stationary in the center of the map. Thus, with no other recourse and personality factors affecting path choice, agents will divert to the right-hand side. D-RISK sees similar behavior where agents will pick either the central or right corridors depending on the location of the dog. When trash is dynamically added to the scene, the pedestrians that divert to the right may begin to throw trash in the right corridor: this creates geographical inertia for that sensitivity factor. As the global environment manifold detects these instances, subsequent agents will begin to prefer the left corridor. In cyclical fashion, the end of the simulation sees agents beginning to prefer the right path once more after all agents begin to move to the left, leaving behind trash. This sequence of events, sourced in behavior, illustrates how macro-scale phenomena such as path dependence and lock-in can form from small and very local (a banana peel) sensitivities as agents’ reactions accumulate around them. Because the trash in our simulations has a temporary physical manifestation on the ground, it acts in ways that approach stigmergy in insect behavior, e.g., akin to pheromone trails.

We also note the prevalence of pedestrians still choosing to follow the central corridor in D-RISK and DENSITY situations. Alternatively, S-RISK and DIRT demonstrate sizeable populations of pedestrians opting for the side corridors. In fact, DIRT appears to have the most varied pedestrian distribution across all individual factors. While some variation is visibly noticeable in DENSITY, most agents prefer the central corridor. Again, this has basis in the theoretical literature, especially in urban design and the concept of space syntax, which advocates the primacy of preserving viewsheds in pedestrian movement along sidewalks in cities.

The ALL condition demonstrates the most non-uniform situation of crowd flow in contrast to individual preferences. This would make sense: as agents begin to embody multiple preferences, we begin to see agents demonstrating forms of congestion, shortest path preference along the central corridor, divergences into the left and right corridor, and an overall balanced distribution at the end of the simulation. The variability in the virtual manifold can be attributed to dynamic environmental conditions instigated by agents themselves in the form of dynamic crowd densities and trash items, as well as external events such as the presence of the dog. We observe time-lag effects where the behaviors of past pedestrians begin to affect subsequent pedestrians, requiring pedestrians to make choices regarding their path preferences. Again, this matches wave-type formations in traffic jamming behavior and gridlock in automotive flow with collision avoidance.

7. Discussion

Modeling methodologies that explore both the coarse-scale space of enclosed sites and the micro-conditions of hyper-local, agent–environment encounters, encompassing situations with fine and subtle contextual, localized details, could be very useful as experimental tools for planning support. Yet this approach remains an open problem in design software. Current efforts that explore the micro-scale potential for enlivening designs with considerations of embodying possible pedestrian encounters reflect notions from Non-Representational Theory: treating small, fleeting encounters as situational building blocks of streetscape phenomena.

Our approach to implementing software that can accommodate movement-relevant sensitivities in design modifies Dijkstra’s algorithm—common in traditional global path planning models—to consider situational contexts driven by the interplay between site properties and individual agent preferences. We propose that, starting with path planners, lean design software such as Unity could begin to consider economically deployable pedestrian models that provide sensitivity (to design factors) as agency. With few modifications to cost functions and parameters, we demonstrate that individual semantics and preferences can in fact be encoded into and alter the behavior of the macroscopic components of design simulations that are based on graph-oriented path planning heuristics. In doing so, we draw parallels with embodiment, emphasizing how enclosed spaces can be treated as “places”, i.e., as the sum of both site and the (often individual) meanings that connect people to its interleaved situation.

We tested the usefulness of our approach with some simple design problems. Our analysis of emergent crowd dynamics around localized sensitivity factors show how certain environmental factors and preferences, insofar as we have implemented them, appear to affect crowd trajectories with knock-on effects that are individual, but which may also easily become crowd-wide. Greedy shortest path preferences, embedded into Dijkstra’s algorithm and reflective of preferences for shortest paths among real-world pedestrians, clash with preferences against risks, cleanliness/dirtiness, and crowding and congestion. When combined, as demonstrated in our “ALL” scenario, we recorded large variation in crowd dynamics (through adaptation as well as emergence and path dependency) as agents switch back and forth between shortest paths and detours. These results show promise in how simulation designs can be modified to generate life-like dynamics while maintaining the algorithmic parsimony that makes these models so efficient and powerful to begin with. Furthermore, our results demonstrate the potential of how agents themselves can maintain and use scalar representations of personality and cognition to affect their movement patterns across time and space. Implemented in simple form here, we hope that the reader can envisage how more complex and complicated instantiations could be introduced.

7.1. Hardware Stress Testing

Our idea is founded on algorithmic modification. Therefore, we tested the simulation’s performance under two different scenarios. The first scenario featured a simulation variant that continuously increased the number of active pedestrians until the flow rate of the simulation environment reached a consistent equilibrium. In this scenario, two separate hardware setups were compared.

The first setup was a desktop PC with an NVIDIA GeForce RTX 4070 GPU, an AMD Ryzen 5 5600X 6-Core processor, and 16 Gb of RAM. The second setup was an MSI Gs75 Stealth gaming laptop with an NVIDIA GeForce RTX 2080 with Max-Q Design GPU, an Intel i7 6-Core processor, and 32 Gb of RAM. Broadly, the purpose of this scenario was to identify how the number of active agents and the choice of hardware would scale with simulation performance. This in turn may provide performance guidelines to simulation engineers regarding the appropriate crowd scale required to maintain optimal performance.

The second stressor was used to identify the maximum number of possible agents that could be active on the field while maintaining at least 30 frames per second (FPS). This scenario was tested only on the 4070 desktop PC. Though similar to the first scenario, this set of simulation runs specifically considers possible case situations where a lower bound of performance is expected. To ensure consistent metrics, twenty distinct two-minute sessions were conducted on each computer for each scenario. The simulation was set up to record, per every frame, the current number of active agents, the delta time difference between the previous frame and the current frame, the estimated raw framerate at that current frame, and an interpolated “smoothed” frame rate calculated from the mean FPS across the last three frames. The smoothed frame rate was purely to reduce noisy FPS measurements caused by occasional stutters in data output from Unity. The results are illustrated by timing and computational load in Figure 6.

For the first scenario, we used data from both hardware setups and compared the number of active agents to FPS performance (see Figure 6, at left). The 4070 and 2070 both adhere to a similar decreasing logarithmic curve whereby FPS decreases as the number of agents increases. Perhaps unsurprisingly, for any number of active agents, the 4070 is noted to always have a higher FPS. Interestingly, the disparity between the performance curves generated by the 4070 and 2070 seems to diminish as the number of agents increases. This indicates that further stressing the simulation may allow for more agents with relatively minor decreases in FPS. For the second scenario (see Figure 6, at right), we similarly compared the number of active agents and the FPS but solely with the 4070. When fitted with a logarithmic regression model, the curve predicts that 406.6 agents (approximately 406–407 agents) is the maximum number of active agents that the 4070 could theoretically handle while staying above 30 FPS.

7.2. Limitations

At present, one of the major limitations of the described enclosed space simulations is the performance cost for increased quantities and densities of pedestrian agents. For small designs of around 100 agents, there are no issues in resolving a full-stack design scenario and matching simulation, even running on an older laptop, and we show that this can be pushed to ~400 agents with a relatively modestly equipped commercial computer. This is likely sufficient for even a large design space, and a web of such models could straightforwardly be run on a cluster of CPUs, or via threading to expand this to encompass even larger spaces and bigger designs with more pedestrians. Because our approach is based on a GIS for data handling, geographic models such as the entropy-maximizing spatial interaction models can handle the edge cases between different designs, exchanging agent loads at the interface of different graphs in real time without a hit on run-time performance. Nonetheless, there are several practical computing resource considerations that require improvement, mainly due to the use of finite state machines that are difficult to scale even with any available shortcuts. Within our implementation, PhysX calculations between agent rigid bodies also introduce a bottleneck, as our system is run fully in Unity 3D. Other approaches could be used, including Unity’s lighter in-built physics functions or the Bullet Physics engine.

In preparing the environments for pedestrians to walk on, no automatic tool exists to help create or connect nodes on the path, and they must be created and connected manually. This limitation potentially reduces the practical use of the approach we showed in this paper as it requires some technical knowledge and time to operate. In future work, we aim to explore the use of bipartite matching algorithms from deep learning, particularly the Hungarian algorithm, which has successfully been used in paired motion estimation (via Kalman filtering) and data association to provide automation pathways. This would open up this parameterization step to generative AI, which is already being widely used in design tasks and could be of use in specifying nodes to respond to style sheets, or to 3D generative tools [198] being developed for related software such as Blender, for example.

Finally, our pedestrians lack behaviorally robust actions for managing local interactions in highly crowded situations, such as being blocked by pedestrians attempting to walk in another direction and being trapped in corners. In our simulations, crowding can lead to scenarios where intersections become jammed due to many pedestrians attempting to traverse different directions and being unable to successfully navigate around one another using RVOs due to the sheer density of pedestrians. Their current approach to resolve this is “wait and see”, which is polite, but in reality, several special evasion behaviors would likely take over. How pedestrians act, react, and interact in groups and crowds (groups that have adopted particular movement behavior) is qualitatively different than how we would expect them to react in dyads (pairs or chains of pairings), and this warrants further investigation.

8. Future Work

Future extensions of our base model will require efforts to (1) optimize agent movement operations to increase the number of available agents during simulation, (2) reduce the need for user annotation of either graph generation or agent parameterization, (3) expand path properties to consider more factors such as landmarks and atmospherics, and (4) add a larger variety of population and personality types driven by goals and subgoals. We have sketched proposed pathways to resolve each of these facets above, which we consider to be achievable within the situationally sensitive path planning framework that we have described.

To increase the number of active pedestrians during simulation, there are promising opportunities to utilize parallelization schemes compatible with either GPU-based HLSL computational/animation shaders or multi-threaded burst compilation, both of which are available within Unity3D’s architecture. Such parallelization schemes will be compatible with the RVO-based local collision avoidance system and general transformation operations in Unity3D. Furthermore, we are considering further optimizations to the synthesized visual fields (i.e., k-d tree-based vision search) and automated node graph generation techniques (i.e., customized NavMesh calculations, possibly including PageRank for link analysis directly on graphs or for different emergent streams of pedestrian crowds as they pass waypoits). We are currently exploring avenues for these optimizations within the available extensibility of Unity3D’s software design.

On a lower (behavioral and computational) level of resolution, agent behaviors may be improved in intricacy with more robust navigation techniques such as rerouting to follow crowds instead of attempting to resist the direction of motion and creating collisions at intersections. We are also considering an expansion of global path properties such as the presence of landmarks, overhangs, lighting, and proximity to dangerous zones such as sensitive machinery in enclosed spaces such as factories or prohibited areas near exhibits in museums. The introduction of these special cases would further improve the believability and usability of the simulation by offering a wider variety of ways in which pedestrians may treat enclosed spaces, including dedicated zoning of micro-places within a design, such that a user could specify intended space-use design scenarios at a very hyper-local level and examine them in real time as specified in CAD. Regarding agents themselves, we will consider the addition of demographic groups, implied through shared pathing parameters across groups of agents, to further drive collective actions among our virtual crowds.

9. Conclusions

This paper proposes an adjustment to popularly used high-level graph-based movement heuristics to accommodate more theoretically relevant and observationally realistic local pedestrian behavior that can “sit under” crowd simulation. Our approach considers both the environmental properties of footpaths through enclosed spaces (enclosed site factors) and preferences embedded into agents (situational factors, as mediated by individual embodiment in individualized encounters, chiefly in collision dyads). Our model follows design trends from both macroscopic and microscopic models and demonstrates visually convincing dynamism in crowd path dynamics in aggregate, with plausible knock-on crowd effects and physical reactions to (simple) design elements and sensitivities. It also aligns with conventional conceptual understanding in behavioral science and aspects of emergent phenomena from complexity theory.

Situationally sensitive path planning, we reason, extends well-known heuristics in ways that expand the utility of path-based modeling to an extended, deeper, and detailed consideration of encounter-based situations that are commonly being explored in design around the twin concepts of embodiment (particularly environmental embodiment) and Non-Representational Theory, i.e., the idea that geographical phenomena can be best understood through an examination of the intricacies of everyday lived experiences.

The experimental levers that we showed in this paper focus on basic small-space enclosed site design, although with situationally aware modifications we were able to add aspects of public safety (a dog on the loose), public works (littering), and foot traffic (density patterns and phenomena). Each has practical utility in design, planning, and management considerations for enclosed spaces with pedestrians moving through those spaces. With minimal configuration (really, as little as a weight file), it is hopefully straightforward for the reader to envisage that these design levers could be extended to include additional factors such as atmospherics, displays, diversion tactics for casinos and supermarkets, building code evaluations, assistive planning for pedestrians with non-typical mobility, and testing of location-based services for mobile crowds. Our implementation of the system in CAD (for site geometry) and animation (for embodied experience) also extends the modalities by which data might be introduced to the simulations and by which users might interact with them, for example urban design charettes or immersive human participant testing ahead of design approval.