The Behavior of Tree-Width and Path-Width Under Graph Operations and Graph Transformations

Abstract

Tree-width and path-width are well-known graph parameters. Many NP-hard graph problems admit polynomial-time solutions when restricted to graphs of bounded tree-width or bounded path-width. In this work, we study the behavior of tree-width and path-width under various unary and binary graph transformations. For considered transformations, we provide upper and lower bounds for the tree-width and path-width of the resulting graph in terms of those of the initial graphs or argue why such bounds are impossible to specify. Among the studied unary transformations are vertex addition, vertex deletion, edge addition, edge deletion, subgraphs, vertex identification, edge contraction, edge subdivision, minors, powers of graphs, line graphs, edge complements, local complements, Seidel switching, and Seidel complementation. Among the studied binary transformations, we consider the disjoint union, join, union, substitution, graph product, 1-sum, and corona of two graphs.

1. Introduction

A graph parameter is a function that associates every graph with a non-negative integer. One of the most famous graph parameters is tree-width, which was defined by Robertson and Seymour [1]. Graphs of bounded tree-width are interesting from an algorithmic point of view, as several NP-complete graph problems can be solved in polynomial time for graph classes of bounded tree-width. For example, tree-decompositions allow for many efficient algorithms in dynamic programming [2,3,4,5]. The same holds for the similar graph parameter path-width. This is because every path-decomposition can be interpreted as a special case of a tree-decomposition. Both parameters play a crucial role in the field of structural graph theory, especially in the graph minor theory of Robertson and Seymour [6].

Trees and forests have tree-width at most one. Series-parallel graphs have tree-width at most two [7]. Outerplanar graphs (and subclasses such as cactus graphs and maximal outerplanar graphs) have tree-width at most two, and k-outerplanar graphs have tree-width at most $3k-1$ [7]. Halin graphs have tree-width at most three [7]. For other classes of graphs with bounded tree-width, we refer the reader to the works of Bodlaender [7,8,9].

Determining whether the tree-width or path-width of a graph is at most a given value w is NP-complete [10]. However, for every fixed integer k, one can decide in linear time whether a given graph G has tree-width or path-width k (see Bodlaender [11]). For an in-depth overview of tree-width and path-width, we again refer the reader to the work by Bodlaender [7].

A graph transformation f is a function that creates a new graph $f(G_1,\dots ,G_n)$ from a number of $n\ge 1$ input graphs $G_1,\dots ,G_n$. Examples of graph transformations include taking an induced subgraph of a graph, adding an edge to a graph, or generating the join of two graphs. A graph operation is a graph transformation that is deterministic and invariant under isomorphism. Examples of graph operations include the edge complementation of a graph or generating the join of two graphs. Please note that by our definition, the two graph transformations that involve taking an induced subgraph of a graph and adding an edge to a graph are not graph operations. The graph theory books by Bondy and Murty [12] and Harary [13] provide a large number of graph transformations.

The impact of graph operations, which can be defined by monadic second-order formulas (so-called MS transductions), on graph parameters can often be shown in a very short way. Unfortunately, the resulting bounds are typically rather imprecise [14,15].

Transformations that reduce graphs can be used to characterize classes of graphs by forbidden subgraphs. For example, the property that a graph has tree-width at most k is preserved under the graph transformation “taking minors”. This fact is used to show that the set of graphs of tree-width at most k can be characterized by a finite set of forbidden minors [6].

The effect of graph transformations on graph parameters has been well studied, e.g., for bandwidth [16], for tree-width [7], for clique-width [17,18,19], and for rank-width [18].

In this paper, we study the behavior of tree-width and path-width under various graph transformations and graph operations. We consolidate known results from various works and prove novel results. In doing so, this work provides a comprehensive overview of the effects of unary and binary graph transformations on tree-width and path-width. This paper is organized as follows. In Section 2, we recall the definitions of tree-width and path-width. In Section 3, we consider the effects of the following unary graph transformations on tree-width and path-width: vertex deletion, vertex addition, edge deletion, edge addition, subgraphs, vertex identification, edge contraction, edge subdivision, minors, powers of graphs, line graphs, edge complements, local complements, Seidel switching, and Seidel complementation. If it is possible to bound the tree-width or path-width of the resulting graph $f\left(G\right)$, we show how to compute a corresponding decomposition in time linear in the size of the decomposition for G. In Section 4, we give an overview of the effects of the following binary graph operations on tree-width and path-width: disjoint union, join, union, substitution, graph products, 1-sum, and corona. If it is possible to bound the tree-width or path-width of the combined graph $f(G_1,G_2)$ in terms of the tree-width or path-width of the graphs $G_1$ and $G_2$, we show how to compute a corresponding decomposition in time linear in the size of the decompositions for $G_1$ and $G_2$. Finally, we summarize our results and provide some conclusions, as well as an outlook for future work, in Section 5.

2. Preliminaries

2.1. Graphs

We work with finite, undirected graphs G, where $V\left(G\right)$ is a finite set of vertices and $E\left(G\right)\subseteq \left\{\right\{u,v\}\mid u,v\in V(G),u\ne v\}$ is a finite set of edges without loops or multiple edges. For a vertex $v\in V\left(G\right)$, we denote by $N_G\left(v\right)$ the set of all vertices adjacent to v in G, i.e., $N_G\left(v\right)=\{w\in V\left(G\right)\mid \{v,w\}\in E\left(G\right)\}$. The vertex set $N_G\left(v\right)$ is called the set of all neighbors of v in G or the neighborhood of v in G. Note that v itself does not belong to $N_G\left(v\right)$. The degree of a vertex $v\in V\left(G\right)$, denoted by ${deg}_G\left(v\right)$, is the number of neighbors of v in G, i.e., ${deg}_G\left(v\right)=\left|N_G\left(v\right)\right|$, and the maximum degree of G, denoted by $\Delta \left(G\right)$, is the maximum of the vertices’ degrees, i.e., $\Delta \left(G\right)={\max }_{v\in V\left(G\right)}{deg}_G\left(v\right)$. In this work, we discuss graphs only up to isomorphism. This allows us to define the path with n vertices as $P_n=(\{v_1,\dots ,v_n\},\{\{v_1,v_2\},\dots ,\{v_{n-1},v_n\}\})$, which is useful in several examples. For definitions of further special graphs, we refer to the book by Brandstädt et al. [20].

2.2. Tree-Width

One of the most famous tree-structured graph classes is the class of graphs of bounded tree-width. The first notion equivalent to tree-width, the dimension of a graph, was introduced by Bertelè and Brioschi [21] in 1973. The following definition of tree-width was given by Robertson and Seymour [1] in 1986.

Definition 1 

(Tree-width). A tree-decomposition of a graph G is a pair $(\mathcal{X},T)$, where T is a tree and $\mathcal{X}=\{X_u\subseteq V\left(G\right)\mid u\in V\left(T\right)\}$ is a family of subsets of $V\left(G\right)$, called bags, such that the following three conditions hold:

(tw-1) 

${\bigcup }_{u\in V\left(T\right)}{X}_u=V\left(G\right)$.

(tw-2) 

For every edge $\{v_1,v_2\}\in E\left(G\right)$, there is a node $u\in V\left(T\right)$ with $v_1,v_2\in X_u$.

(tw-3) 

For every vertex $v\in V\left(G\right)$, the subgraph of T induced by the nodes $u\in V\left(T\right)$ with $v\in X_u$ is connected.

The width of a tree-decomposition $(\mathcal{X}=\{X_u\mid u\in V\left(T\right)\},T)$ is defined as

$$\begin{array}{c}\hfill \underset{u\in V\left(T\right)}{\max }\left|X_u\right|-1.\end{array}$$

Finally, the tree-width of a graph G, denoted by $\mathit{tw}\left(G\right)$, is the smallest integer k, such that there is a tree-decomposition $(\mathcal{X},T)$ for G of width k.

Please note that (tw-1) has no influence on the width of a tree-decomposition. It merely ensures that isolated vertices are covered by a tree-decomposition, which is useful for the design of algorithms along tree-decompositions.

Obviously, the tree-width of every graph G is bounded by $\left|V\right(G\left)\right|-1$, as one can always place all its vertices in a single bag. Conversely, determining whether the tree-width of a given graph is at most a given integer w is NP-complete, even for bipartite graphs and complements of bipartite graphs [10].

Example 1 

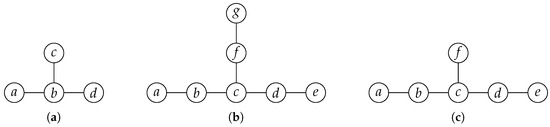
(Tree-decomposition). Figure 1 depicts a graph together with a corresponding tree-decomposition of width 1.

Figure 1. (a) A graph and (b) a corresponding tree-decomposition.

In addition to the previous definition of tree-width, tree-width can also be defined by bramble numbers [22] (also known as the size of screens [23]) or partial k-trees [24]. We refer the reader to the work by Bodlaender [7] for an overview of equivalent definitions.

Throughout the course of our work, we make use of the following lemma by Scheffler [25] several times.

Lemma 1. 

Every graph of tree-width at most k has a vertex of degree at most k.

Proof. 

Let G be a graph with $\mathrm{tw}\left(G\right)=k$ and $(\mathcal{X},T)$ be a tree-decomposition of width k for G, such that $\left|V\right(T\left)\right|$ is as small as possible. Let ℓ be a leaf of T and denote its parent in T as v. Since $\left|V\right(T\left)\right|$ is as small as possible, there must exist a vertex $u\in X_{\ell }$ with $u\notin X_v$. Otherwise, $X_{\ell }\subset X_v$ holds, and we can delete $X_{\ell }$, contradicting the minimality of $V\left(T\right)$. Thus, due to (tw-2) and (tw-3), all neighbors of u must be in $X_{\ell }$ and, as $X_{\ell }$ contains at most $k+1$ vertices, it follows that u has degree at most k. □

The following proposition was stated by Bodlaender [7], who credited it to Rose [24]. As Rose’s proof makes use of k-trees, we provide, for the sake of self-containment, a proof that relies only on Lemma 1 and tree-width.

Proposition 1. 

Let G be a graph. Then, it holds that

$$\begin{array}{c}\hfill \left|E\left(G\right)\right|\le \mathit{tw}\left(G\right)\left|V\left(G\right)\right|-{\displaystyle \frac{1}{2}}\mathit{tw}\left(G\right)(\mathit{tw}\left(G\right)+1).\end{array}$$

Proof. 

By Lemma 1, we know that there exists at least one vertex v in G of degree at most $\mathrm{tw}\left(G\right)$, such that v has at most $\mathrm{tw}\left(G\right)$ incident edges in G. Let us denote the graph we obtain by removing v from G as $G_1$. Then, we know that from G to $G_1$, we removed at most $\mathrm{tw}\left(G\right)$ edges from G. It is easy to see that removing v and all its incident edges from G can reduce the tree-width of G but not increase it. Hence, $\mathrm{tw}\left(G_1\right)\le \mathrm{tw}\left(G\right)$ holds, and we can repeat the previous argument for $G_1$, i.e., remove a vertex and at most $\mathrm{tw}\left(G\right)$ edges from $G_1$. Repeating this argument for all vertices of G results in $\left|E\right(G\left)\right|\le \mathrm{tw}\left(G\right)\left|V\right(G\left)\right|$. After several repetitions of the previous argument, i.e., removing a vertex with at most $\mathrm{tw}\left(G\right)$ incident edges from the remaining graph, there are at most $\mathrm{tw}\left(G\right)$ vertices left in the remaining graph. This remaining graph can have a tree-width of at most $\mathrm{tw}\left(G\right)-1$, such that by Lemma 1, it follows that in this graph, there is a vertex with degree at most $\mathrm{tw}\left(G\right)-1$. Removing this vertex from the remaining graph, we remove at most $\mathrm{tw}\left(G\right)-1$ edges. Repeating this argument for all of the $\mathrm{tw}\left(G\right)$ remaining vertices in sequence yields

$$\begin{array}{cc}\hfill \left|E\right(G\left)\right|& \le \mathrm{tw}\left(G\right)\left(\right|V\left(G\right)|-\mathrm{tw}\left(G\right))+\sum _{i=1}^{\mathrm{tw}\left(G\right)}(\mathrm{tw}\left(G\right)-i)\hfill \\ \hfill & =\mathrm{tw}\left(G\right)\left(\right|V\left(G\right)|-\mathrm{tw}\left(G\right))+\mathrm{tw}\left(G\right)\mathrm{tw}\left(G\right)-\sum _{i=1}^{\mathrm{tw}\left(G\right)}i\hfill \\ \hfill & =\mathrm{tw}\left(G\right)\left|V\left(G\right)\right|-{\displaystyle \frac{1}{2}}\mathrm{tw}\left(G\right)(\mathrm{tw}\left(G\right)+1).\hfill \end{array}$$

This completes the proof of the proposition. □

While the previous proposition provides an upper bound for the number of edges of a graph in terms of the number of its vertices and its tree-width, the following proposition by Kneis et al. [26] provides an upper bound for the tree-width of a graph in terms of the number of its edges and vertices.

Proposition 2. 

Let G be a graph. Then, it holds that

$$\begin{array}{c}\hfill \mathit{tw}\left(G\right)\le {\displaystyle \frac{\left|E\right(G\left)\right|}{5.769}}+\mathcal{O}(log(\left|V\left(G\right)\right|\left)\right).\end{array}$$

Recall that a graph is said to be k-connected if and only if every pair of its vertices is connected by at least k vertex-disjoint paths [27]. Using Lemma 1, we obtain the following lower bound for the tree-width of k-connected graphs.

Lemma 2. 

Every k-connected graph has tree-width at least k.

Proof. 

Let G be a k-connected graph. By definition, it holds that for all vertices $u,v\in V\left(G\right)$, there exist k vertex-disjoint paths from u to v in G. Consequently, ${deg}_G\left(u\right)\ge k$ and ${deg}_G\left(v\right)\ge k$ must be true. In other words, every vertex of G has degree at least k. By the contraposition of Lemma 1, we immediately obtain $\mathrm{tw}\left(G\right)\ge k$. □

To conclude the preliminary subsection on tree-width, we cite two lemmas by Bodlaender and Möhring [28] that we make use of in later sections.

Lemma 3 

(Clique containment). Let $(\mathcal{X},T)$ be a tree-decomposition for a graph G and $C\subseteq V\left(G\right)$ be a clique in G. Then, there exists some $u\in V\left(T\right)$ with $C\subseteq X_u$.

Lemma 4 

(Complete bipartite subgraph containment). Let $(\mathcal{X},T)$ be a tree-decomposition for a graph G and $A,B\subseteq V\left(G\right)$ with $A\cap B=\varnothing$ and $\left\{\right\{u,v\}\mid u\in A,v\in B\}\subseteq E\left(G\right)$. Then, there exists a vertex $u\in V\left(T\right)$ with $A\subseteq X_u$ or $B\subseteq X_u$.

2.3. Path-Width

In 1983, three years prior to their definition of tree-width, Robertson and Seymour introduced the notion of path-width [29].

Definition 2 

(Path-width). A path-decomposition of a graph G is a sequence $(X_1,\dots ,X_r)$ of subsets of $V\left(G\right)$, called bags, such that the following three conditions hold:

(pw-1) 

${\bigcup }_{1\le i\le r}{X}_i=V\left(G\right)$.

(pw-2) 

For every edge $\{u,v\}\in E\left(G\right)$, there is a set $X_i$, $1\le i\le r$, with $u,v\in X_i$.

(pw-3) 

For all $i,j,\ell$ with $1\le i<j<\ell \le r$, it holds that $X_i\cap X_{\ell }\subseteq X_j$.

The width of a path-decomposition $(X_1,\dots ,X_r)$ is defined as

$$\begin{array}{c}\hfill \underset{1\le i\le r}{\max }\left|X_i\right|-1.\end{array}$$

Finally, the path-width of a graph G, denoted by $\mathit{pw}\left(G\right)$, is the smallest integer k, such that there is a path-decomposition $(X_1,\dots ,X_r)$ for G of width k.

Please note that (pw-1) has no influence on the width of a path-decomposition.

Similar to the tree-width of a graph, the path-width of a graph G is limited by $\left|V\right(G\left)\right|-1$, as all vertices of G can be stored in a single bag. However, deciding whether the path-width of a graph is at most a given integer w is NP-complete [30]. Even for special graph classes, such as bipartite graphs, complements of bipartite graphs [10], chordal graphs [31], bipartite distance hereditary graphs [32], and planar graphs with maximum vertex degree 3 [33], it is NP-complete to decide whether the path-width is at most a given integer w. On the other hand, there are also special graph classes, such as permutation graphs [34], circular arc graphs [35], and co-graphs [28], for which one can decide in polynomial time whether the path-width is at most a given integer w.

Example 2 

(Path-decomposition). $\mathcal{X}=\left(\right\{a,b,c\},\{c,f,g\},\{c,d,e\left\}\right)$ is a path-decomposition of width 2 for the graph shown in Figure 1a.

Besides the definition of path-width by Robertson and Seymour, there are other definitions of path-width, for example, by the vertex separation number [36]. Again, we refer to the work by Bodlaender [7] for an overview of equivalent definitions.

With a small adaptation to the proof for Lemma 1, we obtain a similar result for path-width.

Lemma 5. 

Every graph of path-width at most k has a vertex of degree at most k.

Using this lemma, we obtain the following proposition for path-width with the same proof as that used for Proposition 1, adapted to path-width.

Proposition 3. 

Let G be a graph. Then, it holds that

$$\begin{array}{c}\hfill \left|E\left(G\right)\right|\le pw\left(G\right)\left|V\left(G\right)\right|-{\displaystyle \frac{1}{2}}\mathit{pw}\left(G\right)(\mathit{pw}\left(G\right)+1).\end{array}$$

The same work by Kneis et al. [26], which provides an upper bound for the tree-width of a graph in terms of its edges and vertices, also provides an upper bound for the path-width of a graph in terms of its edges and vertices.

Proposition 4. 

Let G be a graph. Then, it holds that

$$\begin{array}{c}\hfill \mathit{pw}\left(G\right)\le {\displaystyle \frac{\left|E\right(G\left)\right|}{5.769}}+\mathcal{O}(log(\left|V\left(G\right)\right|\left)\right).\end{array}$$

Following the same line of argument as in Lemma 1, we obtain the following result for the path-width of k-connected graphs.

Lemma 6. 

Every k-connected graph has path-width at least k.

As every path is a tree, every path-decomposition $\mathcal{X}=(X_1,\dots ,X_r)$ can be interpreted as a tree-decomposition, such that the results from Lemmas 3 and 4 also hold for path-decompositions. Subsequently, we provide reformulations of the results by Bodlaender and Möhring [28], adjusted for path-width.

Lemma 7 

(Clique containment). Let $\mathcal{X}=(X_1,\dots ,X_r)$ be a path-decomposition for a graph G and $C\subseteq V\left(G\right)$ a clique in G. Then, there exists some $1\le i\le r$ with $C\subseteq X_i$.

Lemma 8 

(Complete bipartite subgraph containment). Let $\mathcal{X}=(X_1,\dots ,X_r)$ be a path-decomposition for a graph G and $A,B\subseteq V\left(G\right)$ with $A\cap B=\varnothing$ and $\left\{\right\{u,v\}\mid u\in A,v\in B\}\subseteq E\left(G\right)$. Then, there exists some $1\le i\le r$ with $A\subseteq X_i$ or $B\subseteq X_i$.

2.4. Graph Parameters and Relations

In this subsection, we provide results relating the parameters tree-width and path-width to each other as well as to other well-known graph parameters, such as the following:

• The independence number $\alpha \left(G\right)$, specifying the size of the largest independent set in G;
• The clique number $\omega \left(G\right)$, specifying the size of the largest clique in G;
• The chromatic number $\chi \left(G\right)$, specifying the least number of distinct colors required to color all vertices of G, such that no two adjacent vertices obtain the same color.

Using the following theorem, we prove that the tree-width of a graph is always bounded by the path-width of the graph, whereas the path-width of a graph cannot be bounded only in the graph’s tree-width but in the tree-width and the number of vertices.

Theorem 1. 

For a graph G, it holds that

$$\begin{array}{c}\hfill \mathit{tw}\left(G\right)\le \mathit{pw}\left(G\right)\mathit{and}\mathit{pw}\left(G\right)\le (\mathit{tw}\left(G\right)+1)({log}_3\left(2\right|V\left(G\right)|+1)+1)-1.\end{array}$$

Proof. 

The first relation follows from the definitions of tree-width and path-width, as every path-decomposition can also be interpreted as a tree-decomposition.

The second relation, making use of the idea of Theorem 6 in the work by Korach and Solel [37], can be shown as follows. Let $(\mathcal{X},T)$ be a tree-decomposition for G and denote its bags by $X_u\in \mathcal{X}$ for $u\in V\left(T\right)$. According to the result (10.16) in the book by Kleinberg and Tardos [38], we can assume $(\mathcal{X},T)$ to be a non-redundant tree-decomposition for G, i.e., $\left|V\right(T\left)\right|\le \left|V\right(G\left)\right|$ holds. Following Scheffler [25], the path-width of any tree S can be limited from above by $\mathrm{pw}\left(S\right)\le {log}_3\left(2\right|V\left(S\right)|+1)$. Thus, since $(\mathcal{X},T)$ is a non-redundant tree-decomposition for G, it follows that there exists a path-decomposition $\mathcal{Y}$ for T of path-width $\mathrm{pw}\left(T\right)\le {log}_3\left(2\right|V\left(G\right)|+1)$. We denote the bags of $\mathcal{Y}$ by $Y_i\in \mathcal{Y}$ for $1\le i\le r$. Given this path-decomposition $\mathcal{Y}$ for T, we construct $\mathcal{Z}=(Z_1,\dots ,Z_r)$ with $Z_i={\bigcup }_{u\in Y_i}{X}_u$. By Theorem 6 in the work by Korach and Solel [37], it follows that $\mathcal{Z}$ is a path-decomposition for G. We know that $|X_u|\le \mathrm{tw}\left(G\right)+1$ holds for all $u\in V\left(T\right)$ and that $|Y_i|\le {log}_3\left(2\right|V\left(G\right)|+1)+1$ for $1\le i\le r$. Consequently, it follows that $|Z_i|\le (\mathrm{tw}\left(G\right)+1)({log}_3\left(2\right|V\left(G\right)|+1)+1)$ is true for $1\le i\le r$, such that we obtain $\mathrm{pw}\left(G\right)\le (\mathrm{tw}\left(G\right)+1)({log}_3\left(2\right|V\left(G\right)|+1)+1)-1$. □

By Lemmas 3 and 7, we know that for a complete graph with $n\in \mathbb{N}$ vertices, $K_n$, it holds that $\mathrm{tw}\left(K_n\right)=n-1=\mathrm{pw}\left(K_n\right)$. Consequently, the first inequality stated in Theorem 1 is tight.

For the second inequality, we recall that the path-width of perfect 2-ary trees of height h is $\lceil h/2\rceil$ (cf. [25]) and that for $k\ge 3$, the path-width of perfect k-ary trees of height h is exactly h from [39] (Corollary 3.1). Thus, trees have tree-width one while their path-width grows asymptotically in height, which is at least logarithmic in the number of vertices, implying that the second inequality is asymptotically optimal.

The same two lemmas imply that for a graph G, every clique of G is a subset of at least one bag of every tree-decomposition and path-decomposition for G. With this in mind, the following proposition follows immediately.

Proposition 5. 

For a graph G, it holds that

$$\begin{array}{c}\hfill \omega \left(G\right)-1\le \mathit{tw}\left(G\right)\mathit{and}\omega \left(G\right)-1\le \mathit{pw}\left(G\right).\end{array}$$

Chlebíková [40] proved the following proposition’s first bound, i.e., the one for tree-width. To do so, the author argued that by splitting a graph G’s vertices into an independent set I of size $\alpha \left(G\right)$ and $\left|V\right(G\left)\right|-\alpha \left(G\right)$ subsets $V_i\subseteq V\left(G\right)\setminus I$ of size one, it follows that G is a subgraph of a complete $\left(\right|V\left(G\right)|-\alpha (G)+1)$-partite graph. Then, it is easy to see that the bags $X_v=(V\left(G\right)\setminus I)\cup \left\{v\right\}$ for $v\in I$ allow a tree-decomposition of width $\left|V\right(G\left)\right|-\alpha \left(G\right)$ for the $\left(\right|V\left(G\right)|-\alpha (G)+1)$-partite graph. As the same bags $X_v$, $v\in I$, allow a path-decomposition as well, the same bound follows for path-width.

Proposition 6. 

For a graph G, it holds that

$$\begin{array}{c}\hfill \alpha \left(G\right)+\mathit{tw}\left(G\right)\le \left|V\right(G\left)\right|\mathit{and}\alpha \left(G\right)+\mathit{pw}\left(G\right)\le \left|V\right(G\left)\right|.\end{array}$$

Finally, Chlebíková [40] also proved the following proposition’s first bound. Making use of the first bound in Theorem 1, we extended this result to path-width, too.

Proposition 7. 

For a graph G, it holds that

$$\begin{array}{c}\hfill \chi \left(G\right)\le \mathit{tw}\left(G\right)+1\mathit{and}\chi \left(G\right)\le \mathit{pw}\left(G\right)+1.\end{array}$$

3. Unary Graph Operations and Graph Transformations

Let G be a non-empty graph and f be a unary graph transformation that creates a new graph $f\left(G\right)$ from G. In this section, we consider the tree-width and path-width of graph $f\left(G\right)$ with respect to the tree-width and path-width of G. In particular, we consider the following graph transformations: vertex deletion, vertex addition, edge deletion, edge addition, taking a subgraph, edge subdivision, vertex identification, edge contraction, taking a minor, powers of graphs, line graphs, edge complements, local complements, Seidel switching, and Seidel complementation.

3.1. Vertex Deletion and Vertex Addition

3.1.1. Vertex Deletion

Let G be a graph and $v\in V\left(G\right)$ a vertex of G. By $G-v$, we denote the graph we obtain from G when removing v and all its incident edges, i.e.,

$$\begin{array}{c}\hfill G-v=(V\left(G\right)\setminus \left\{v\right\},E\left(G\right)\setminus \{\{v,u\}\mid u\in N_G\left(v\right)\}).\end{array}$$

With the graph operation of vertex deletion defined, we now consider the tree-width and path-width of $G-v$.

Theorem 2. 

For a graph G and vertex $v\in V\left(G\right)$, it holds that

$$\begin{array}{cc}\hfill \mathit{tw}\left(G\right)-1& \le \mathit{tw}(G-v)\le \mathit{tw}\left(G\right)\mathit{and}\hfill \\ \hfill \mathit{pw}\left(G\right)-1& \le \mathit{pw}(G-v)\le \mathit{pw}\left(G\right).\hfill \end{array}$$

Proof. 

By removing v from every bag of a tree-decomposition (path-decomposition) for G and deleting all resulting empty bags, we obtain a tree-decomposition (path-decomposition) for $G-v$. Consequently, we obtain $\mathrm{tw}(G-v)\le \mathrm{tw}\left(G\right)$ and $\mathrm{pw}(G-v)\le \mathrm{pw}\left(G\right)$. Adding v and its incident edges to $G-v$ results in G, such that the lower bounds follow from the upper bounds of Theorem 3. □

3.1.2. Vertex Addition

Let G be a graph, $N\subseteq V\left(G\right)$ be a subset of vertices from G, and $v\notin V\left(G\right)$ be a newly introduced vertex. By $G{+}_{N}v$, we denote the graph we obtain from G when inserting v with neighborhood $N_G\left(v\right)=N$, i.e.,

$$\begin{array}{c}\hfill G{+}_{N}v=(V\left(G\right)\cup \left\{v\right\},E\left(G\right)\cup \{\{v,u\}\mid u\in N\}).\end{array}$$

In the special case when $N_G\left(v\right)=\left\{u\right\}$ holds for a vertex $u\in V\left(G\right)$, we call v a pendant vertex of G. If $N_G\left(v\right)=V\left(G\right)\setminus \left\{v\right\}$ is true, we call v a dominating vertex of G. With vertex addition defined, we consider the tree-width and path-width of graph $G{+}_{N}v$ in the following theorem.

Theorem 3. 

For a graph G, a subset of vertices $N\subseteq V\left(G\right)$, and a vertex $v\notin V\left(G\right)$, it holds that

$$\begin{array}{cc}\hfill \mathit{tw}\left(G\right)& \le \mathit{tw}\left(G{+}_{N}v\right)\le \mathit{tw}\left(G\right)+1\mathit{and}\hfill \\ \hfill \mathit{pw}\left(G\right)& \le \mathit{pw}\left(G{+}_{N}v\right)\le \mathit{pw}\left(G\right)+1.\hfill \end{array}$$

Proof. 

By introducing v to all bags of a tree-decomposition (path-decomposition) of G, we obtain a tree-decomposition (path-decomposition) of $G{+}_{N}v$. Thus, it follows that $\mathrm{tw}\left(G{+}_{N}v\right)\le \mathrm{tw}\left(G\right)+1$ and $\mathrm{pw}\left(G{+}_{N}v\right)\le \mathit{pw}\left(G\right)+1$ are true. By removing v from $G{+}_{N}v$, we obtain G. Consequently, the lower bounds follow from the upper bounds of Theorem 2. □

We can always add a pendant vertex to a graph without increasing the graph’s tree-width. To do so, we introduce a new bag that contains the new vertex and its sole neighbor. Then, the new bag is connected to any bag of a tree-decomposition for the graph that already contains the neighbor.

Corollary 1. 

For a graph G, a vertex $u\in V\left(G\right)$, and a newly introduced vertex $v\notin V\left(G\right)$, it holds that

$$\begin{array}{c}\hfill \mathit{tw}\left(G{+}_{\left\{u\right\}}v\right)=\max (\mathit{tw}\left(G\right),1).\end{array}$$

Conversely, the following example shows that the previous statement does not hold with respect to path-width. Introducing a pendant vertex to a graph can increase its path-width.

Example 3. 

The path-decomposition $\mathcal{X}=\left(\right\{a,b\},\{b,c\},\{c,f\},\{c,d\},\{d,e\left\}\right)$ shows that the path-width of graph C in Figure 2c is one. By introducing pendant vertex g to C, as depicted in the graph $I\left(K_{1,3}\right)$ in Figure 2b, the path-width increases to two: ${\mathcal{X}}^{\prime }=(\{a,b\},\{b,c\},\{c,f,g\},\{c,d\},\{d,e\})$.

Figure 2. Special graphs. (a) $K_{1,3}$; (b) $I\left(K_{1,3}\right)$; (c) C.

3.2. Edge Addition and Edge Deletion

3.2.1. Edge Deletion

Let G be a graph and $v,w\in V\left(G\right)$ be two vertices. For $\{v,w\}\in E\left(G\right)$, we define by $G-\{v,w\}$ the graph we obtain from G by deleting the edge $\{v,w\}$, i.e.,

$$\begin{array}{c}\hfill G-\{v,w\}=\left(V\right(G),E(G)\setminus \{\{v,w\}\left\}\right).\end{array}$$

With edge deletion defined, the following theorem shows that removing an edge from a graph decreases the width of the graph by at most one.

Theorem 4. 

For a graph G and two different vertices $v,w\in V\left(G\right)$, it holds that

$$\begin{array}{cc}\hfill \mathit{tw}\left(G\right)-1& \le \mathit{tw}(G-\{v,w\left\}\right)\le \mathit{tw}\left(G\right)\mathit{and}\hfill \\ \hfill \mathit{pw}\left(G\right)-1& \le \mathit{pw}(G-\{v,w\left\}\right)\le \mathit{pw}\left(G\right).\hfill \end{array}$$

Proof. 

The upper bound follows immediately because a tree-decomposition (path-decomposition) for G is also a tree-decomposition (path-decomposition) for $G-\{v,w\}$.

As G can be obtained from $G-\{v,w\}$ by adding edge $\{v,w\}$, the lower bound follows from the upper bound of Theorem 5. □

3.2.2. Edge Addition

Let G be a graph and $v,w\in V\left(G\right)$ be two vertices. For $\{v,w\}\notin E\left(G\right)$, we define by $G+\{v,w\}$ the graph we obtain from G when adding the edge $\{v,w\}$, i.e.,

$$\begin{array}{c}\hfill G+\{v,w\}=\left(V\right(G),E(G)\cup \{\{v,w\}\left\}\right).\end{array}$$

Having defined edge addition, our next theorem shows that inserting an edge into a graph increases the graph’s width by at most one.

Theorem 5. 

For a graph G and two different vertices $v,w\in V\left(G\right)$, it holds that

$$\begin{array}{cc}\hfill \mathit{tw}\left(G\right)& \le \mathit{tw}(G+\{v,w\left\}\right)\le \mathit{tw}\left(G\right)+1\mathit{and}\hfill \\ \hfill \mathit{pw}\left(G\right)& \le \mathit{pw}(G+\{v,w\left\}\right)\le \mathit{pw}\left(G\right)+1.\hfill \end{array}$$

Proof. 

Given a tree-decomposition (path-decomposition) for G, we obtain a tree-decomposition (path-decomposition) for $G+\{v,w\}$ by adding one of the two vertices, v or w, to all its bags. Consequently, $\mathrm{tw}(G+\{v,w\left\}\right)\le \mathrm{tw}\left(G\right)+1$ and $\mathrm{pw}(G+\{v,w\left\}\right)\le \mathrm{pw}\left(G\right)+1$ hold.

The lower bounds follow from the fact that a tree-decomposition (path-decomposition) for $G+\{v,w\}$ is also a tree-decomposition (path-decomposition) for G. □

3.3. Subgraph

So far, we have only studied unary graph operations in this work. However, in this subsection, we deviate from this path and study the unary graph transformation of taking a subgraph. This act of modifying a graph is not deterministic, since there are various subgraphs one can take from any given graph, and it is not explicitly defined which one should be taken. Consequently, taking a subgraph of a graph multiple times can result in different subgraphs, making the studied modification a graph transformation but not a graph operation.

Note that taking a subgraph of a graph can be interpreted as a sequence of vertex-deletion and edge-deletion operations. Hence, every subgraph of a graph can be obtained by deleting selected vertices and edges from the original graph, such that the corollary below follows immediately from Theorems 2 and 4.

Corollary 2. 

For a graph G and any subgraph H of G, it holds that $\mathit{tw}\left(H\right)\le \mathit{tw}\left(G\right)$ and $\mathit{pw}\left(H\right)\le \mathit{pw}\left(G\right)$.

3.4. Vertex Identification

For a graph G and two different vertices $v,w\in V\left(G\right)$, the identification of v and w in G, denoted by $\mathrm{Ident}(G,v,w)$, consists of a vertex set $\left(V\right(G)\setminus \{v,w\left\}\right)\cup \left\{u\right\}$ and an edge set

$$\begin{array}{cc}\hfill E\left(G\right)& \setminus \left\{\right\{x,y\}\mid x\in V(G),y\in \{v,w\left\}\right\}\hfill \\ \hfill & \cup \{\{x,u\}\mid x\in (N_G\left(v\right)\cup N_G\left(w\right))\setminus \{v,w\}\}.\hfill \end{array}$$

Given this definition of vertex identification, the following result summarizes the graph operation’s effect on the tree-width and path-width of the involved graph.

Theorem 6. 

For a graph G and two different vertices $v,w\in V\left(G\right)$, it holds that

$$\begin{array}{cc}\hfill \mathit{tw}\left(G\right)-1& \le \mathit{tw}\left(\mathit{Ident}\right(G,v,w\left)\right)\le \mathit{tw}\left(G\right)+1\mathit{and}\hfill \\ \hfill \mathit{pw}\left(G\right)-1& \le \mathit{pw}\left(\mathit{Ident}\right(G,v,w\left)\right)\le \mathit{pw}\left(G\right)+1.\hfill \end{array}$$

Proof. 

For the upper bounds, let $(\mathcal{X},T)$ be a tree-decomposition ($\mathcal{X}$ be a path-decomposition) for G of width $\mathrm{tw}\left(G\right)$ ($\mathrm{pw}\left(G\right)$). To obtain a tree-decomposition (path-decomposition) for $\mathrm{Ident}(G,v,w)$, we proceed as follows. In the first step, replace all occurrences of v and w in all bags of $\mathcal{X}$ with u and denote the result by ${\mathcal{X}}^{\prime }$. Since $\{v,w\}$ is not necessarily an edge of G, ${\mathcal{X}}^{\prime }$ could violate (tw-3) ((pw-3)), i.e., the bags of ${\mathcal{X}}^{\prime }$ containing u might not be connected. In this case, we add u to all bags between the disconnected components. With this, $({\mathcal{X}}^{\prime },T)$ is a valid tree-decomposition (${\mathcal{X}}^{\prime }$ is a valid path-decomposition) for $\mathrm{Ident}(G,v,w)$. To obtain ${\mathcal{X}}^{\prime }$ from $\mathcal{X}$, we increase the width by at most one, such that $\mathrm{tw}\left(\mathrm{Ident}\right(G,v,w\left)\right)\le \mathrm{tw}\left(G\right)+1$ ($\mathrm{pw}\left(\mathrm{Ident}\right(G,v,w\left)\right)\le \mathrm{pw}\left(G\right)+1$) follows.

For the lower bounds, we proceed as follows. First, rename vertex u of $\mathrm{Ident}(G,v,w)$ to v and denote the resulting graph by $G^{\prime }$. Next, add a new vertex w with neighborhood $N_G\left(w\right)$ to $G^{\prime }$. By Theorem 3, it follows that $\mathrm{tw}\left(G^{\prime }{+}_{N_G\left(w\right)}w\right)\le \mathrm{tw}\left(G^{\prime }\right)+1$ and $\mathrm{pw}\left(G^{\prime }{+}_{N_G\left(w\right)}w\right)\le \mathrm{pw}\left(G^{\prime }\right)+1$ are true. Since G is a subgraph of $G^{\prime }{+}_{N_G\left(w\right)}w$, with Corollary 2, we obtain that

$$\begin{array}{cc}\hfill \mathrm{tw}\left(G\right)& \le \mathrm{tw}\left(G^{\prime }{+}_{N_G\left(w\right)}w\right)\le \mathrm{tw}\left(\mathrm{Ident}(G,v,w)\right)+1\mathrm{and}\hfill \\ \hfill \mathrm{pw}\left(G\right)& \le \mathrm{pw}\left(G^{\prime }{+}_{N_G\left(w\right)}w\right)\le \mathrm{pw}\left(\mathrm{Ident}(G,v,w)\right)+1\hfill \end{array}$$

hold, which yields the lower bounds $\mathrm{tw}\left(G\right)-1\le \mathrm{tw}\left(\mathrm{Ident}\right(G,v,w\left)\right)$ and $\mathrm{pw}\left(G\right)-1\le \mathrm{pw}\left(\mathrm{Ident}\right(G,v,w\left)\right)$. □

Note that the upper bounds specified in the previous theorem are tight, since a vertex identification on the end vertices of a path results in a cycle with increased tree-width and path-width.

3.5. Edge Contraction

In the case that the two vertices $v,w\in V\left(G\right)$ of a vertex identification $\mathrm{Ident}(G,v,w)$ are adjacent, i.e., $\{v,w\}\in E\left(G\right)$, we call the operation an edge contraction.

Theorem 7. 

For a graph G and two different vertices $v,w\in V\left(G\right)$ with $\{v,w\}\in E\left(G\right)$, it holds that

$$\begin{array}{cc}\hfill \mathit{tw}\left(G\right)-1& \le \mathit{tw}\left(\mathit{Ident}\right(G,v,w\left)\right)\le \mathit{tw}\left(G\right)\mathit{and}\hfill \\ \hfill \mathit{pw}\left(G\right)-1& \le \mathit{pw}\left(\mathit{Ident}\right(G,v,w\left)\right)\le \mathit{pw}\left(G\right).\hfill \end{array}$$

Proof. 

Let $(\mathcal{X},T)$ be a tree-decomposition ($\mathcal{X}$ be a path-decomposition) for G of width $\mathrm{tw}\left(G\right)$ ($\mathrm{pw}\left(G\right)$). We replace all occurrences of v and w in all bags of $\mathcal{X}$ with u and denote the resulting decomposition by ${\mathcal{X}}^{\prime }$. Since v and w are adjacent in G, we know by (tw-2) ((pw-2)) that there is at least one bag in $\mathcal{X}$ that contains v and w. Consequently, (tw-3) ((pw-3)) must hold for ${\mathcal{X}}^{\prime }$, and it follows that $({\mathcal{X}}^{\prime },T)$ is a valid tree-decomposition (${\mathcal{X}}^{\prime }$ is a valid path-decomposition) for $\mathrm{Ident}(G,v,w)$ of width at most $\mathrm{tw}\left(G\right)$ ($\mathrm{pw}\left(G\right)$). Because $\{v,w\}\in E\left(G\right)$ is true, we can argue that (tw-3) ((pw-3)) holds for ${\mathcal{X}}^{\prime }$. This argument is not valid for an arbitrary vertex identification, as v and w are not guaranteed to be adjacent (see Theorem 6).

The lower bounds follow from the same argument as for the lower bounds in the proof of Theorem 6. □

Contracting any edge of a clique $K_n$ of size n results in a clique $K_{n-1}$ of size $n-1$. By Lemma 3 (Lemma 7), we know that $\mathrm{tw}\left(K_n\right)=n-1$ ($\mathrm{pw}\left(K_n\right)=n-1$) holds. Consequently, the lower bounds specified in the previous theorem are tight.

3.6. Edge Subdivision

Let G be a graph, $u\notin V\left(G\right)$ be a newly introduced vertex, and $\{v,w\}\in E\left(G\right)$ be an edge of G. The edge subdivision of $\{v,w\}$ in G, denoted by $\mathrm{Subdiv}(G,v,w)$, consists of a vertex set $V\left(G\right)\cup \left\{u\right\}$ and an edge set $\left(E\right(G)\setminus \{\{v,w\}\left\}\right)\cup \left\{\right\{v,u\},\{u,w\left\}\right\}$.

With this definition, the following theorem states the effect of an edge subdivision on the tree-width and path-width of a given graph.

Theorem 8. 

For a graph G and an edge $\{v,w\}\in E\left(G\right)$, it holds that

$$\begin{array}{cc}\hfill \mathit{tw}\left(\mathit{Subdiv}\right(G,v,w\left)\right)& =\mathit{tw}\left(G\right)\mathit{and}\hfill \\ \hfill \mathit{pw}\left(G\right)\le \mathit{pw}\left(\mathit{Subdiv}\right(G,v,w\left)\right)& \le \mathit{pw}\left(G\right)+1.\hfill \end{array}$$

Proof. 

G is isomorphic to $\mathrm{Ident}\left(\mathrm{Subdiv}\right(G,v,w),u,w)$, such that the upper bounds of Theorem 7 yield

$$\begin{array}{cc}\hfill \mathrm{tw}\left(G\right)& =\mathrm{tw}\left(\mathrm{Ident}\right(\mathrm{Subdiv}(G,v,w),u,w\left)\right)\le \mathrm{tw}\left(\mathrm{Subdiv}\right(G,v,w\left)\right)\mathrm{and}\hfill \\ \hfill \mathrm{pw}\left(G\right)& =\mathrm{pw}\left(\mathrm{Ident}\right(\mathrm{Subdiv}(G,v,w),u,w\left)\right)\le \mathrm{pw}\left(\mathrm{Subdiv}\right(G,v,w\left)\right),\hfill \end{array}$$

resulting in this theorem’s lower bounds.

For the upper bound of tree-width, let us distinguish the following two cases:

Case 1: 

$\mathrm{tw}\left(G\right)=1$. In this case, G is a forest. Since an edge subdivision does not alter this fact, $\mathrm{Subdiv}(G,v,w)$ is still a forest, and $\mathrm{tw}\left(\mathrm{Subdiv}\right(G,v,w\left)\right)=1$ must hold.

Case 2: 

$\mathrm{tw}\left(G\right)>1$. In this case, the biggest bag of every tree-decomposition of G contains at least three vertices. Furthermore, by (tw-2), it follows that in every tree-decomposition of G, there is at least one bag that contains v and w. Let us denote this bag by X. Adding a new bag $X^{\prime }$ with vertices $\{u,v,w\}$ and making it adjacent to X results in a tree-decomposition of $\mathrm{Subdiv}(G,v,w)$ with unaltered size, such that $\mathrm{tw}\left(\mathrm{Subdiv}\right(G,v,w\left)\right)\le \mathrm{tw}\left(G\right)$ follows.

For the upper bound of path-width, we proceed as follows. By (pw-2), we know that in every path-decomposition of G there exists a bag containing v and w. Adding u to this bag, we obtain a valid path-decomposition for $\mathrm{Subdiv}(G,v,w)$. Consequently, $\mathrm{pw}\left(\mathrm{Subdiv}\right(G,v,w\left)\right)\le \mathrm{pw}\left(G\right)+1$ follows. □

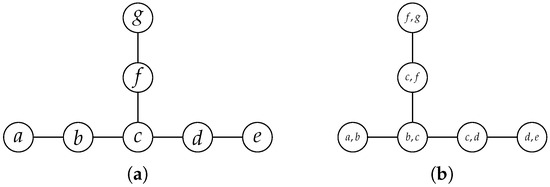
The upper bound for path-width given in the previous theorem is tight. The path-width of the caterpillar graph C in Figure 2c is equal to one. A caterpillar graph is a tree for which the removal of all pendant vertices results in a chordless path. Conversely, the path-width of the graph obtained by subdividing edge $\{c,f\}$ of C, depicted as $I\left(K_{1,3}\right)$ in Figure 2b, is two. Please note that $I\left(K_{1,3}\right)$ is one of the two forbidden minors of the set of all graphs of path-width one (see [41] and Section 3.7).

After subdividing all edges of a graph, the resulting graph must be bipartite. The resulting graph obtained after subdividing all edges of a graph G is called the incidence graph of G, denoted by $I\left(G\right)$. The following corollary provides bounds for a graph’s incidence graph and follows from Theorem 8.

Corollary 3. 

For a graph G, it holds that

$$\begin{array}{cc}\hfill \mathit{tw}\left(I\right(G\left)\right)& =\mathit{tw}\left(G\right)\mathit{and}\hfill \\ \hfill \mathit{pw}\left(G\right)\le \mathit{pw}\left(I\right(G\left)\right)& \le \mathit{pw}\left(G\right)+1.\hfill \end{array}$$

Proof. 

The result for tree-width follows directly from Theorem 8.

By contracting all subdivided edges of $I\left(G\right)$, we obtain G. By Theorem 7, we know that edge contractions do not increase the resulting graph’s path-width, such that $\mathrm{pw}\left(G\right)\le \mathrm{pw}\left(I\right(G\left)\right)$ follows.

Denote by $\mathcal{X}$ a path-decomposition for G of width $\mathrm{pw}\left(G\right)$, and let $\{v,w\}\in E\left(G\right)$ be an edge of G and $x_{\{v,w\}}$ be the node introduced to subdivide the edge. By (pw-2), we know that there is a bag X in $\mathcal{X}$ with $v,w\in X$. We introduce a new bag $X^{\prime }=X\cup \left\{x_{\{v,w\}}\right\}$ to $\mathcal{X}$ as a successor to X and denote the resulting decomposition by ${\mathcal{X}}^{\prime }$. Then, ${\mathcal{X}}^{\prime }$ is a path-decomposition for $\mathrm{Subdiv}(G,v,w)$ of width $\mathrm{pw}\left(G\right)+1$.

Vertex $x_{\{v,w\}}$ appears in exactly one modified bag, $X^{\prime }$, and $X^{\prime }$ is a superset of the original bag X. Therefore, for every edge of G, we can repeat the previous argument and add a separate, modified bag to the same path-decomposition without increasing its final width by more than one. If required, multiple modified copies of the same original bag can be lined up as successors to each other. By doing so, we obtain a path-decomposition for $I\left(G\right)$ of width $\mathrm{pw}\left(G\right)+1$, such that $\mathrm{pw}\left(I\right(G\left)\right)\le \mathrm{pw}\left(G\right)+1$ follows. □

3.7. Minor

Every graph H one may obtain from a given graph G, by applying a finite sequence of arbitrary edge-deletion and edge-contraction operations, is called a minor of G. Obviously, taking a minor is a graph transformation but not a graph operation, as the applied sequence of operations is not deterministic.

Given this definition, the theorem below follows immediately from Theorem 4 and Theorem 7.

Theorem 9. 

For a graph G and a minor H of G, it holds that $\mathit{tw}\left(H\right)\le \mathit{tw}\left(G\right)$ and $\mathit{pw}\left(H\right)\le \mathit{pw}\left(G\right)$.

In other words, the fact that a graph has tree-width (path-width) at most $k\in \mathbb{N}$ is preserved under the graph transformation of taking a minor.

Subsequently, we cite probably one of the most important theorems in graph theory, the minor theorem, shown by Robertson and Seymour [42].

Theorem 10 

(Minor theorem). In every infinite set of graphs, there are two graphs such that one of them is a minor of the other.

Before the minor theorem was proven by Robertson and Seymour, it was known as Wagner’s conjecture [43]. The following theorem is an important corollary of the minor theorem [42].

Theorem 11. 

Every set of graphs that is closed under minors can be defined by a finite set of forbidden minors.

For $k\in \mathbb{N}$, Theorem 9 implies that the set of graphs with tree-width (path-width) at most k is closed under minors. Consequently, Theorem 11 then implies that the set of graphs with tree-width (path-width) at most k can be characterized by a finite set of forbidden minors. For small values of k, these sets of forbidden minors are known. For example, Kinnersley and Langston [41] characterized the set of all graphs with path-width at most one by the forbidden minors $K_3$ and $I\left(K_{1,3}\right)$ (cf. Figure 2). Furthermore, they characterized the set of graphs with path-width at most two by 110 forbidden minors [41]. The set of all graphs with tree-width at most one is characterized by the forbidden minor $K_3$, and the set of all graphs with tree-width at most two is characterized by the forbidden minor $K_4$ (see the work by Bodlaender and van Antwerpen-de Fluiter [44]). For the four forbidden minors that characterize the set of all graphs with tree-width at most three, see the work by Arnborg, Proskurowski, and Corneil [45].

The main algorithmic consequence of the minor theorem is stated in the following theorem, the minor test, also shown by Robertson and Seymour [46].

Theorem 12 

(Minor test). For a fixed graph H and a given graph G, one can decide in time in $\mathcal{O}\left(\right|V\left(G\right){|}^3)$ whether H is a minor of G.

A more precise formulation of the runtime would be $\mathcal{O}\left(f\left(k\right)\right|V\left(G\right){|}^3)$ for some function f and $k\le \mathrm{size}\left(H\right)$.

From a parameterized point of view, the minor test is fixed-parameter tractable with respect to the parameter $\mathrm{size}\left(H\right)$. However, the constant behind the $\mathcal{O}$-notation in Theorem 12 depends on the parameter $\mathrm{size}\left(H\right)$ and is huge. Kawarabayashi, Kobayashi, and Reed [47] showed an improved version of the previous result, allowing one to decide the minor test in time in $\mathcal{O}\left(\right|V\left(G\right){|}^2)$.

The corollary below follows immediately from Theorem 11 and the application of Theorem 12 for every forbidden minor.

Corollary 4. 

For every set of graphs $\mathcal{G}$ that is closed under minors, and for every graph G, one can decide in time polynomial in the size of G whether $G\in \mathcal{G}$ holds.

Nevertheless, an implicit precondition of the corollary is that the set of all forbidden minors characterizing $\mathcal{G}$ is known.

Another result by Robertson and Seymour [48] is the so-called grind minor theorem, also known as the excluded grid theorem.

Theorem 13 

(Grid minor theorem). There is a function $f:\mathbb{N}\to \mathbb{N}$, such that every graph with tree-width at least $f\left(k\right)$ has a $k\times k$-grid graph as a minor.

Even if the grid minor theorem seems very technical at first, it has a direct effect on the tree-width of a graph, as shown by the following theorem from the same work by Robertson and Seymour [48].

Theorem 14. 

For every planar graph H, there is an integer $k\in \mathbb{N}$, such that every graph without H as a minor has tree-width at most k.

Prior to this result for tree-width, Robertson and Seymour [29] proved an analogue result with respect to path-width.

Theorem 15. 

For every forest H, there is an integer $k\in \mathbb{N}$, such that every graph without H as a minor has path-width at most k.

3.8. Power of a Graph

For $d\in \mathbb{N}$ and a graph G, we denote the d-th power of G by $G^d$. Thus, $G^d$ has the same set of vertices as G, i.e., $V\left(G^d\right)=V\left(G\right)$, and two vertices of $G^d$ are adjacent if and only if there exists a path of length at most d in G between these vertices.

To begin, the following lemma provides an upper bound on the number of neighbors each vertex might have in the d-th power of a graph G.

Lemma 9. 

Given $d\in \mathbb{N}$ and a graph G, for every vertex $v\in V\left(G\right)$, it holds that

$$\begin{array}{c}\hfill {deg}_{G^d}\left(v\right)\le \Delta \left(G\right)\sum _{i=0}^{d-1}{(\Delta \left(G\right)-1)}^i.\end{array}$$

Proof. 

Let $v\in V\left(G\right)$ be a vertex of G. To obtain an upper bound on the number of neighbors v might have in $G^d$, we derive an upper bound for the number of vertices reachable from v within a distance of at most d in G. By definition, we know that ${deg}_G\left(v\right)\le \Delta \left(G\right)$ holds, such that v has at most $\Delta \left(G\right)$ neighbors in G. By the same argument, every neighbor u of v in G has at most $\Delta \left(G\right)$ neighbors. However, one of those neighbors of u is v, such that u has at most $\Delta \left(G\right)-1$ not-yet-considered neighbors. Repeating the previous argument $d-1$ times, we obtain an upper bound on the number of vertices at an exact distance d to v,

$$\begin{array}{c}\hfill \Delta \left(G\right){(\Delta \left(G\right)-1)}^{d-1}.\end{array}$$

Since we are interested in an upper bound on the number of vertices with a distance of at most d to v, we need to sum up the upper bounds for all intermediate distances from one up to d. By doing so, we obtain

$$\begin{array}{c}\hfill \Delta \left(G\right)+\Delta \left(G\right)(\Delta \left(G\right)-1)+\dots +\Delta \left(G\right){(\Delta \left(G\right)-1)}^{d-1}=\Delta \left(G\right)\sum _{i=0}^{d-1}{(\Delta \left(G\right)-1)}^i.\end{array}$$

As every vertex that is reachable from v in G within a distance of at most d is adjacent to v in $G^d$, it follows that

$$\begin{array}{c}\hfill {deg}_{G^d}\left(v\right)\le \Delta \left(G\right)\sum _{i=0}^{d-1}{(\Delta \left(G\right)-1)}^i\end{array}$$

holds. □

Note that the previously stated upper bound is tight. To see this, consider a tree T with root $v\in V\left(T\right)$ and three binary subtrees of equal but arbitrary depth adjacent to v.

The following theorem makes use of this upper bound for a vertex’s number of neighbors in the d-th power of a graph to study the effect of raising a graph to the power of d with respect to tree-width and path-width.

Theorem 16. 

For $d\in \mathbb{N}$ and a graph G, it holds that

$$\begin{array}{cc}\hfill \mathit{tw}\left(G\right)& \le \mathit{tw}\left(G^d\right)\le (\mathit{tw}\left(G\right)+1)\left(1+\Delta \left(G\right)\sum _{i=0}^{d-1}{(\Delta \left(G\right)-1)}^i\right)-1\mathit{and}\hfill \\ \hfill \mathit{pw}\left(G\right)& \le \mathit{pw}\left(G^d\right)\le (\mathit{pw}\left(G\right)+1)\left(1+\Delta \left(G\right)\sum _{i=0}^{d-1}{(\Delta \left(G\right)-1)}^i\right)-1.\hfill \end{array}$$

Proof. 

The lower bounds follow from Corollary 2, as G is a subgraph of $G^d$.

For the upper bounds, denote by $(\mathcal{X},T)$ a tree-decomposition (by $\mathcal{X}$ a path-decomposition) of G. By constructing $G^d$, we know all neighbors of every vertex $v\in V\left(G\right)$ in $G^d$. To obtain a tree-decomposition (path-decomposition) for $G^d$, for every vertex $v\in V\left(G\right)$, we add all neighbors of v in $G^d$, i.e., $N_{G^d}\left(v\right)$, to every bag $X\in \mathcal{X}$ containing v. We denote the resulting bag by $X^{\prime }$ and the resulting set of bags by ${\mathcal{X}}^{\prime }$. Then, by Lemma 9, every bag of ${\mathcal{X}}^{\prime }$ contains at most

$$\begin{array}{c}\hfill (\mathrm{tw}\left(G\right)+1)\left(1+\Delta \left(G\right)\sum _{i=0}^{d-1}{(\Delta \left(G\right)-1)}^i\right)\\ \hfill \left((\mathrm{pw}\left(G\right)+1)\left(1+\Delta \left(G\right)\sum _{i=0}^{d-1}{(\Delta \left(G\right)-1)}^i\right)\right)\end{array}$$

vertices. Taking G to the power of d does not alter the set of vertices, i.e., $V\left(G\right)=V\left(G^d\right)$, such that $({\mathcal{X}}^{\prime },T)$ (${\mathcal{X}}^{\prime }$) still satisfies (tw-1) ((pw-1)). By adding, for every vertex $v\in V\left(G\right)$, all neighbors of v in $G^d$ to every bag containing v, all new edges introduced into $G^d$ are covered, such that $({\mathcal{X}}^{\prime },T)$ (${\mathcal{X}}^{\prime }$) satisfies (tw-2) ((pw-2)). To see that $({\mathcal{X}}^{\prime },T)$ (${\mathcal{X}}^{\prime }$) satisfies (tw-3) ((pw-3)), let $v\in V\left(G\right)$ be any vertex of G and denote by $X_s^{\prime },X_t^{\prime }\in {\mathcal{X}}^{\prime }$ two bags with $v\in X_s^{\prime },X_t^{\prime }$. We consider three cases:

• If it holds that $v\in X_s,X_t$ for $X_s,X_t\in \mathcal{X}$, it immediately follows that v is also in all bags connecting $X_s^{\prime }$ and $X_t^{\prime }$, since $(\mathcal{X},T)$ ($\mathcal{X}$) satisfies (tw-3) ((pw-3)).
• If it holds that $v\in X_s$ but $v\notin X_t$, there must be a vertex $u\in X_t$ with ${\mathrm{dist}}_G(u,v)\le d$, as otherwise, $v\in X_t^{\prime }$ would not hold. Since ${\mathrm{dist}}_G(u,v)\le d$, there is a path $p_G$ between u and v in G of length at most d. Consequently, with $(\mathcal{X},T)$ ($\mathcal{X}$) satisfying (tw-2) ((pw-2)) and (tw-3) ((pw-3)), there must also be a path $p_T$ between s and t, such that for every $t^{\prime }$ in $p_T$, there is a vertex $v^{\prime }$ in $p_G$ with $v^{\prime }\in X_{t^{\prime }}$. For every such vertex $v^{\prime }$, it holds that ${\mathrm{dist}}_G(v^{\prime },v)\le {\mathrm{dist}}_G(u,v)\le d$, so that by the construction of ${\mathcal{X}}^{\prime }$, it follows that $v\in X_{t^{\prime }}^{\prime }$ holds. Therefore, also in this case, all bags between $X_s^{\prime }$ and $X_t^{\prime }$ must contain v.
• Finally, if $v\notin X_s$ and $v\notin X_t$, there must be at least one bag $X_r\in \mathcal{X}$ with $v\in X_r$, and we can repeat the previous argument for $X_r^{\prime },X_s^{\prime }$ and $X_r^{\prime },X_t^{\prime }$.

Consequently, $({\mathcal{X}}^{\prime },T)$ (${\mathcal{X}}^{\prime })$ is a tree-decomposition (path-decomposition) for $G^d$ of width

$$\begin{array}{c}\hfill (\mathrm{tw}\left(G\right)+1)\left(1+\Delta \left(G\right)\sum _{i=0}^{d-1}{(\Delta \left(G\right)-1)}^i\right)-1\\ \hfill \left((\mathrm{pw}\left(G\right)+1)\left(1+\Delta \left(G\right)\sum _{i=0}^{d-1}{(\Delta \left(G\right)-1)}^i\right)-1\right)\end{array}$$

and the upper bound follows. □

3.9. Line Graph

In this subsection, we study the graph operation of creating a graph’s line graph, using the notation formulated by Harary and Norman [49].

For a graph G, its line graph, $L\left(G\right)$, is defined by

$$\begin{array}{cc}\hfill V\left(L\right(G\left)\right)& =\{x_{\{u,v\}}\mid \{u,v\}\in E\left(G\right)\}\mathrm{and}\hfill \\ \hfill E\left(L\right(G\left)\right)& =\{\{x_e,x_f\}\mid |e\cap f|=1\}.\hfill \end{array}$$

In other words, the line graph $L\left(G\right)$ of a graph G has a vertex for every edge of G, and two vertices of $L\left(G\right)$ are adjacent if the corresponding edges in G are adjacent. The concept of a line graph, although not explicitly called a line graph, was first used by Whitney [27] in 1932.

Furthermore, the underlying graph G of a given line graph $L\left(G\right)$ is called the root graph of $L\left(G\right)$.

Given a graph G, it is possible to bound the tree-width (path-width) of its line graph in terms of the tree-width (path-width) of G and G’s maximum vertex degree.

Theorem 17. 

For a graph G, it holds that

$$\begin{array}{cc}\hfill \mathit{tw}\left(G\right)-1& \le \mathit{tw}\left(L\right(G\left)\right)\le \left(\mathit{tw}\right(G)+1)\Delta \left(G\right)-1\mathit{and}\hfill \\ \hfill {\displaystyle \frac{1}{2}}(\mathit{pw}\left(G\right)+1)-1& \le \mathit{pw}\left(L\right(G\left)\right)\le \left(\mathit{pw}\right(G)+1)\Delta \left(G\right)-1.\hfill \end{array}$$

Proof. 

The stated lower bound for the tree-width of $L\left(G\right)$ was shown by Harvey and Wood [50] in Proposition 2.3.

A slightly weaker bound can be obtained as follows. Let $(\mathcal{X},T)$ be a tree-decomposition for $L\left(G\right)$ of width $\mathrm{tw}\left(L\right(G\left)\right)$. In every bag of $(\mathcal{X},T)$, replace each edge of G with both of its endpoints. Then, we can obtain a tree-decomposition for G of width at most $2\left(\mathrm{tw}\right(L\left(G\right))+1)-1$, such that ${\displaystyle \frac{1}{2}}(\mathrm{tw}\left(G\right)+1)-1\le \mathrm{tw}\left(L\left(G\right)\right)$ follows. A similar argument results in the stated lower bound for path-width.

The upper bounds are known from several works [51,52,53] and can be obtained as follows. Let $(\mathcal{X},T)$ be a tree-decomposition ($\mathcal{X}$ a path-decomposition) for G of width $\mathrm{tw}\left(G\right)$ ($\mathrm{pw}\left(G\right)$). If we replace every bag $X_u\in \mathcal{X}$ with the set of all edges incident to at least one vertex in $X_u$, we obtain a tree-decomposition (path-decomposition) for $L\left(G\right)$ of width at most $\left(\mathrm{tw}\right(G)+1)\Delta \left(G\right)-1$ ($\left(\mathrm{pw}\right(G)+1)\Delta \left(G\right)-1$). □

Stricter upper bounds than the ones shown in Theorem 17 can be found in Theorem 1.3 in the work by Harvey and Wood [50].

Furthermore, it is easy to confirm that for every graph G, the edges incident to a vertex of G with degree $\Delta \left(G\right)$ form a clique of size $\Delta \left(G\right)$ in $L\left(G\right)$. With Lemmas 3 and 7, the following corollary follows immediately.

Corollary 5. 

For a graph G, it holds that $\mathit{tw}\left(L\right(G\left)\right)\ge \Delta \left(G\right)-1$ and $\mathit{pw}\left(L\right(G\left)\right)\ge \Delta \left(G\right)-1$.

For special graphs, the inequality turns into an equality, as the following result shows.

Proposition 8. 

Let G be a graph. If $\mathit{tw}\left(G\right)=1$ is true, it holds that $\mathit{tw}\left(L\right(G\left)\right)=\Delta \left(G\right)-1$. If $\mathit{pw}\left(G\right)=1$ is true, it holds that $\mathit{pw}\left(L\right(G\left)\right)=\Delta \left(G\right)-1$.

The statement for tree-width was shown by Harvey and Wood [50]. The statement for path-width follows from two arguments. For the lower bound, we refer to Corollary 5. For the upper bound, we know from Section 3.7 that a graph G of path-width one can be identified as a disjoint union of caterpillar graphs, allowing one to construct a path-decomposition of width at most $\Delta \left(G\right)-1$ for $L\left(G\right)$.

In addition to providing a direct equation for how to obtain a line graph’s tree-width (path-width) from its root graph’s tree-width (path-width) if the root graph is a forest (caterpillar graph), the previous proposition shows that a line graph’s tree-width (path-width) cannot be bounded in terms of its root graph’s tree-width (path-width).

We conclude this subsection with a theorem by Harvey and Wood [54], showing how to derive a line graph’s tree-width (path-width) from its root graph if the root graph is a complete graph.

Theorem 18. 

For $n\ge 2$, it holds that

$$\begin{array}{c}\hfill \mathit{tw}\left(L\left(K_n\right)\right)=\mathit{pw}\left(L\left(K_n\right)\right)=\left\{\begin{array}{cc}\left({\displaystyle \frac{n-1}{2}}\right)\left({\displaystyle \frac{n-1}{2}}\right)+n-2,\hfill & \mathit{if}n\mathit{is}\mathit{odd},\hfill \\ \left({\displaystyle \frac{n-2}{2}}\right)\left({\displaystyle \frac{n}{2}}\right)+n-2,\hfill & \mathit{if}n\mathit{is}\mathit{even}.\hfill \end{array}\right.\end{array}$$

3.10. Edge Complement

In this subsection, we study the graph operation of creating a graph’s edge complement graph. The edge complement graph of a graph G, denoted by $\text{co-}G$, has the same vertex set as G, and two vertices are adjacent in $\text{co-}G$ if and only if they are not adjacent in G, i.e.,

$$\begin{array}{cc}\hfill V\left(\text{co-}G\right)& =V\left(G\right)\mathrm{and}\hfill \\ \hfill E\left(\text{co-}G\right)& =\left\{\right\{u,v\}\mid u,v\in V(G),u\ne v,\{u,v\}\notin E(G\left)\right\}.\hfill \end{array}$$

Let $K_{1,\ell }$ be a star graph with one dominating vertex v in the center and ℓ vertices $u_i$, $1\le i\le \ell$, as satellites, all only adjacent to v. Then, the edge complement graph of $K_{1,\ell }$, $\text{co-}{K}_{1,\ell }$, consists of an isolated vertex v and a clique of size ℓ formed by all satellites $u_i$, $1\le i\le \ell$. Since neither $K_3$ nor $I\left(K_{1,3}\right)$ is a minor of $K_{1,\ell }$, we know from Section 3.7 that $\mathrm{pw}\left(K_{1,\ell }\right)=\mathrm{tw}\left(K_{1,\ell }\right)=1$ holds. However, by Lemmas 3 and 7, it follows that $\mathrm{tw}\left(\text{co-}{K}_{1,\ell }\right)=\mathrm{pw}\left(\text{co-}{K}_{1,\ell }\right)=\ell -1$ is true. Therefore, it is generally impossible to bound the tree-width (path-width) of an edge complement graph $\text{co-}G$ in terms of the tree-width (path-width) of the original graph G.

Nevertheless, Joret and Wood [55] proved the following theorem, providing a lower bound for the tree-width of a graph’s edge complement graph. Note that formulating bounds of the form $f\left(G\right)+f\left(\text{co-}G\right)$ for a graph parameter f is known as the Nordhaus–Gaddum problem.

Theorem 19. 

For a graph G, it holds that

$$\begin{array}{c}\hfill \mathit{tw}\left(G\right)+\mathit{tw}\left(\mathit{co}\text{-}G\right)\ge \left|V\right(G\left)\right|-2.\end{array}$$

In their work, Joret and Wood also showed that the specified bound is tight. As $\mathrm{pw}\left(G\right)\ge \mathrm{tw}\left(G\right)$ is true for every graph G, the corollary below follows immediately.

Corollary 6. 

For a graph G, it holds that

$$\begin{array}{c}\hfill \mathit{pw}\left(G\right)+\mathit{pw}\left(\mathit{co}\text{-}G\right)\ge \left|V\right(G\left)\right|-2.\end{array}$$

For the path with four vertices, $P_4$, it holds that $\text{co-}{P}_4\cong P_4$ as well as $\mathrm{pw}\left(P_4\right)=1$. Consequently, we obtain

$$\begin{array}{c}\hfill \mathrm{pw}\left(P_4\right)+\mathrm{pw}\left(\text{co-}{P}_4\right)=\mathrm{pw}\left(P_4\right)+\mathrm{pw}\left(P_4\right)=2=\left|V\left(P_4\right)\right|-2,\end{array}$$

such that the bound specified in Corollary 6 is also tight.

3.11. Local Complementation

In his work, Bouchet [56] introduced the graph operation local complementation. Given a graph G and a vertex $v\in V\left(G\right)$, the local complementation of G, denoted by $LC(G,v)$, is defined by

$$\begin{array}{cc}\hfill V\left(LC\right(G,v\left)\right)=V\left(G\right)& \mathrm{and}\hfill \\ \hfill E\left(LC\right(G,v\left)\right)=E\left(G\right)& \setminus \{\{u,w\}\mid u,w\in N_G\left(v\right)\}\hfill \\ \hfill & \cup \{\{u,w\}\mid u,w\in N_G\left(v\right),u\ne w,\{u,w\}\notin E\left(G\right)\}.\hfill \end{array}$$

In other words, $LC(G,v)$ is obtained from a graph G by replacing the subgraph of G induced by $N_G\left(v\right)$ with its edge complement. Recall that $v\notin N_G\left(v\right)$ holds, such that the neighborhood of v in $LC(G,v)$ is the same as in G.

Denote by $K_{1,\ell }$ the star graph we already made use of in Section 3.10. By applying a local complementation to the dominating vertex v, it is easy to see that $LC(K_{1,\ell },v)$ equals a clique of size $\ell +1$. The star $K_{1,\ell }$ has tree-width and path-width one, while $LC(K_{1,\ell },v)$ has tree-width and path-width ℓ. Therefore, in general, the tree-width (path-width) of a graph G’s local complement $LC(G,v)$ cannot be bounded in terms of the tree-width (path-width) of G.

3.12. Seidel Switching

The Seidel switching operation was introduced by the Dutch mathematician J.J. Seidel in connection with regular structures, such as systems of equiangular lines, strongly regular graphs, or so-called two-graphs [57,58,59]. Several examples of applications of Seidel switching can be found in algorithms, e.g., in a polynomial-time algorithm for the $P_3$-structure recognition problem [60] or in an algorithm for the construction of bi-join decompositions of graphs [61].

For a graph G and a vertex $v\in V\left(G\right)$, the graph resulting from a Seidel switching operation, denoted by $S(G,v)$, is defined as follows. The vertex set of $S(G,v)$ is the same as the vertex set of G, i.e., $V\left(S\right(G,v\left)\right)=V\left(G\right)$, and the edge set of $S(G,v)$ is defined as

$$\begin{array}{cc}\hfill E\left(S\right(G,v\left)\right)=E\left(G\right)& \setminus \{\{v,w\}\mid w\in N_G\left(v\right)\}\hfill \\ \hfill & \cup \{\{v,w\}\mid w\in V\left(G\right)\setminus (N_G\left(v\right)\cup \left\{v\right\})\}.\hfill \end{array}$$

In other words, every neighbor of v in G is a non-neighbor of v in $S(G,v)$, and every non-neighbor of v in G is a neighbor of v in $S(G,v)$.

Given this definition of Seidel switching, by extending a result by Bodlaender and Hage [62], we show that a single Seidel switching operation increases or decreases a graph’s tree-width and path-width by at most one.

Theorem 20. 

For a graph G and a vertex $v\in V\left(G\right)$, it holds that

$$\begin{array}{cc}\hfill \mathit{tw}\left(G\right)-1& \le \mathit{tw}\left(S\right(G,v\left)\right)\le \mathit{tw}\left(G\right)+1\mathit{and}\hfill \\ \hfill \mathit{pw}\left(G\right)-1& \le \mathit{pw}\left(S\right(G,v\left)\right)\le \mathit{pw}\left(G\right)+1.\hfill \end{array}$$

Proof. 

For the upper bounds, let $(\mathcal{X},T)$ be a tree-decomposition ($\mathcal{X}$ a path-decomposition) for G of width $\mathrm{tw}\left(G\right)$ ($\mathrm{pw}\left(G\right)$). When we add v to all bags of $\mathcal{X}$, denoting the resulting set of bags by ${\mathcal{X}}^{\prime }$, we obtain a tree-decomposition $({\mathcal{X}}^{\prime },T)$ (a path-decomposition ${\mathcal{X}}^{\prime }$) for $S(G,v)$ of width at most $\mathrm{tw}\left(G\right)+1$ ($\mathrm{pw}\left(G\right)+1$). Consequently, $\mathrm{tw}\left(S\right(G,v\left)\right)\le \mathrm{tw}\left(G\right)+1$ ($\mathrm{pw}\left(S\right(G,v\left)\right)\le \mathrm{pw}\left(G\right)+1$) follows.

Since $S\left(S\right(G,v),v)=G$ holds, we can derive the lower bound from the upper bound via $\mathrm{tw}\left(G\right)=\mathrm{tw}\left(S\right(S(G,v),v)\le \mathrm{tw}(S(G,v))+1$ ($\mathrm{pw}\left(G\right)=\mathrm{pw}\left(S\right(S(G,v),v\left)\right)\le \mathrm{pw}\left(S\right(G,v\left)\right)+1$). □

Note that the bounds shown in Theorem 20 are tight. To convince oneself of this fact, consider the path with four vertices, $P_4$. Its tree-width and path-width are one. Denote by v one of the two vertices in $P_4$ with degree one. Then, $S(P_4,v)$ contains $K_3$ as a minor, such that a tree-width and path-width of at least two follow. Following the example in the opposite direction, i.e., applying the Seidel switching operation to $S(P_4,v)$ for the same vertex v provides an example that the lower bound is also tight.

In 1980, Colbourn and Corneil [63] studied the complexity of the decision problem of whether two graphs are switching equivalent. In their work, they proved that this decision problem is polynomial-time equivalent to the decision problem of graph isomorphism. Thus, two graphs G and $G^{\prime }$ with the same vertex set V are called switching equivalent if there exists a sequence of vertices $(v_1,\dots ,v_{\ell })$ in V, such that for $G^0=G$ and $G^i=S(G^{i-1},v_i)$, $1\le i\le \ell$, it holds that $G^{\ell }=G^{\prime }$. In 2012, Bodlaender and Hage [62] considered in their work the tree-width of switching classes. By the definition of switching equivalence and via Theorem 20, we can formulate the following corollary, contributing to the research on the tree-width of switching classes initiated by Bodlaender and Hage.

Corollary 7. 

Let G and $G^{\prime }$ be two switching equivalent graphs and denote by $(v_1,\dots ,v_{\ell })$ a sequence of vertices such that $G^{\ell }=G^{\prime }$ is true. Then, it holds that

$$\begin{array}{c}\hfill \mathit{tw}\left(G^{\prime }\right)\le \mathit{tw}\left(G\right)+\ell \mathit{and}\mathit{pw}\left(G^{\prime }\right)\le \mathit{pw}\left(G\right)+\ell .\end{array}$$

3.13. Seidel Complementation

Limouzy [64] defined the Seidel complementation operation in order to provide a characterization for permutation graphs. For a graph G and a vertex $v\in V\left(G\right)$, the graph resulting from the Seidel complementation operation, denoted by $SC(G,v)$, has the same vertices as G, i.e., $V\left(SC\right(G,v\left)\right)=V\left(G\right)$, and edge set

$$\begin{array}{c}\hfill E\left(SC\right(G,v\left)\right)=E\left(G\right)▵\left\{\right\{x,y\}\mid \{v,x\}\in E(G),\{v,y\}\notin E(G\left)\right\}.\end{array}$$

In other words, the edge set of $SC(G,v)$ equals the edge set of G, with edges and non-edges between the neighborhood and non-neighborhood of v complemented.

Let G be a graph that consists of two parts. The first part is a star with vertex v as the dominating vertex and $\ell \in \mathbb{N}$ satellites $u_1,\dots ,u_{\ell }$, adjacent to v. The second part is a set of ℓ isolated vertices, $w_1,\dots ,w_{\ell }$. Since G has neither a $K_3$ nor an $I\left(K_{1,3}\right)$ as a minor, we know that $\mathrm{tw}\left(G\right)=\mathrm{pw}\left(G\right)=1$ holds. By applying the Seidel complementation operation to vertex v, $SC(G,v)$ contains a complete bipartite subgraph formed by the vertices $u_1,\dots ,u_{\ell },w_1,\dots ,w_{\ell }$. By Lemma 4 (Lemma 8), it follows that $\mathrm{tw}\left(SC\right(G,v\left)\right)\ge \ell -1$ ($\mathrm{pw}\left(SC\right(G,v\left)\right)\ge \ell -1$) is true. Consequently, we conclude that, given a graph G and a vertex $v\in V\left(G\right)$, the tree-width (path-width) of $SC(G,v)$ cannot be bounded by the tree-width (path-width) of G.

4. Binary Graph Operations

Let $G_1$, $G_2$ be two non-empty graphs and f be a binary graph operation that creates a new graph $f(G_1,G_2)$ from $G_1$ and $G_2$. In this section, we consider the tree-width and path-width of $f(G_1,G_2)$ with respect to those of the initial graphs $G_1$ and $G_2$. In particular, we study the following binary graph operations disjoint union, join, union, substitution, various types of graph products, 1-sum, and corona.

4.1. Disjoint Union

The disjoint union of two vertex-disjoint graphs $G_1$ and $G_2$, denoted by $G_1\oplus G_2$, is defined as the graph with vertex set $V\left(G_1\right)\cup V\left(G_2\right)$ and edge set $E\left(G_1\right)\cup E\left(G_2\right)$.

Bodlaender and Möhring [28] proved the following theorem with respect to the tree-width and path-width of a graph that is the disjoint union of two vertex-disjoint graphs.

Theorem 21. 

Let $G_1$ and $G_2$ be two vertex-disjoint graphs. Then, it holds that

$$\begin{array}{c}\hfill \mathit{tw}(G_1\oplus G_2)=\max (\mathit{tw}\left(G_1\right),\mathit{tw}\left(G_2\right))\end{array}$$

and

$$\begin{array}{c}\hfill \mathit{pw}(G_1\oplus G_2)=\max (\mathit{pw}\left(G_1\right),\mathit{pw}\left(G_2\right)).\end{array}$$

These bounds imply that the tree-width and path-width of a graph can be derived from the tree-width and path-width of its connected components.

Corollary 8. 

Let G be a graph. It holds that the tree-width of G is equal to the maximum tree-width, and the path-width of G is equal to the maximum path-width of its connected components.

4.2. Join

The join of two vertex-disjoint graphs $G_1$ and $G_2$, denoted by $G_1\otimes G_2$, is defined as the graph with vertex set $V\left(G_1\right)\cup V\left(G_2\right)$ and edge set

$$\begin{array}{c}\hfill E\left(G_1\right)\cup E\left(G_2\right)\cup \{\{v_1,v_2\}\mid v_1\in V\left(G_1\right),v_2\in V\left(G_2\right)\}.\end{array}$$

As with the disjoint union of two graphs, Bodlaender and Möhring [28] proved the following theorem with respect to the tree-width and path-width of a graph that is the join of two vertex-disjoint graphs.

Theorem 22. 

Let $G_1$ and $G_2$ be two vertex-disjoint graphs. Then, for the join of $G_1$ and $G_2$, it holds that

$$\begin{array}{c}\hfill \mathit{tw}(G_1\otimes G_2)=min(\mathit{tw}\left(G_1\right)+|V\left(G_2\right)|,\mathit{tw}\left(G_2\right)+|V\left(G_1\right)\left|\right)\end{array}$$

and

$$\begin{array}{c}\hfill \mathit{pw}(G_1\otimes G_2)=min(\mathit{pw}\left(G_1\right)+|V\left(G_2\right)|,\mathit{pw}\left(G_2\right)+|V\left(G_1\right)\left|\right).\end{array}$$

Combining Theorems 21 and 22 implies that for every co-graph G, it holds that $\mathrm{tw}\left(G\right)=\mathrm{pw}\left(G\right)$, and both widths can be computed in linear time [28].

4.3. Union

The union of two graphs $G_1$ and $G_2$ with $V\left(G_1\right)=V\left(G_2\right)$, denoted by $G_1\cup G_2$, is defined as the graph with vertices $V\left(G_1\right)$ and edge set $E\left(G_1\right)\cup E\left(G_2\right)$. Thus, two vertices are adjacent in $G_1\cup G_2$ if and only if they are adjacent in $G_1$ or in $G_2$.

In general, it is not possible to bound the tree-width (path-width) of the union of two graphs in terms of the tree-widths (path-widths) of the individual graphs. To see why this is the case, consider the following example.

Example 4. 

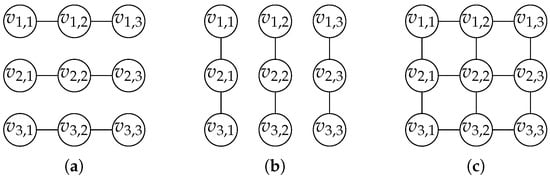
For $m,n\in \mathbb{N}$, define the set of vertices $V=\{v_{i,j}\mid 1\le i\le m,1\le j\le n\}$. Next, denote by $G_1$ the disjoint union of m paths with n vertices from V, $P_n^i=(\{v_{i,j}\mid 1\le j\le n\}$, $\{\{v_{i,j},v_{i,j+1}\}\mid 1\le j<n\})$, $1\le i\le m$, and by $G_2$ the disjoint union of n paths on m vertices from V, $P_m^j=(\{v_{i,j}\mid 1\le i\le m\},\{\{v_{i,j},v_{i+1,j}\}\mid 1\le i<m\})$, $1\le j\le n$. Since paths have a tree-width (path-width) of 1, it follows from Theorem 21 that $\mathit{tw}\left(G_1\right)=\mathit{tw}\left(G_2\right)=1$ ($\mathit{pw}\left(G_1\right)=\mathit{pw}\left(G_2\right)=1$) holds.

The union, $G_1\cup G_2$, of $G_1$ and $G_2$ is an $n\times m$-grid graph, and Bodlaender [7] proved that the tree-width (path-width) of an $n\times m$-grid graph equals $min(n,m)$. Consequently, it is not possible to bound the tree-width (path-width) of $G_1\cup G_2$ in the tree-widths (path-widths) of $G_1$ and $G_2$.

See Figure 3 for an explicit example of $G_1,G_2$ and the resulting union $G_1\cup G_2$.

Figure 3. (a) $G_1$, (b) $G_2$, and (c) $G_1\cup G_2$ for $m=n=3$ in Example 4.

4.4. Substitution

Let $G_1$ and $G_2$ be two vertex-disjoint graphs, and let $v\in V\left(G_1\right)$ be a vertex. The substitution of v by $G_2$ in $G_1$, denoted by $G_1[v/G_2]$, is defined as the graph with vertex set $(V\left(G_1\right)\setminus \left\{v\right\})\cup V\left(G_2\right)$ and edge set

$$\begin{array}{c}\hfill (E\left(G_1\right)\setminus \{\{v,w\}\mid w\in N_{G_1}\left(v\right)\})\cup \{\{u,w\}\mid u\in V\left(G_2\right),w\in N_{G_1}\left(v\right)\}\cup E\left(G_2\right).\end{array}$$

The vertex set $V\left(G_2\right)$ is called a module of the graph $G_1[v/G_2]$, since all vertices of $V\left(G_2\right)$ are adjacent to the same vertices of $V\left(G_1[v/G_2]\right)\setminus V\left(G_2\right)$ in $G_1[v/G_2]$.

Given this definition of substitution, the following theorem considers the tree-width (path-width) of $G_1[v/G_2]$ in terms of the tree-width (path-width) of $G_1$ and $G_2$.

Theorem 23. 

For two vertex-disjoint graphs $G_1$, $G_2$ and vertex $v\in V\left(G_1\right)$, it holds that

$$\begin{array}{c}\hfill \max (\mathit{tw}\left(G_1\right),\mathit{tw}\left(G_2\right))\le \mathit{tw}\left(G_1[v/G_2]\right)\le min(\mathit{tw}\left(G_1\right)+|V\left(G_2\right)|,\mathit{tw}\left(G_2\right)+|V\left(G_1\right)\left|\right)-1\end{array}$$

and

$$\begin{array}{c}\hfill \max (\mathit{pw}\left(G_1\right),\mathit{pw}\left(G_2\right))\le \mathit{pw}\left(G_1[v/G_2]\right)\le min(\mathit{pw}\left(G_1\right)+|V\left(G_2\right)|,\mathit{pw}\left(G_2\right)+|V\left(G_1\right)\left|\right)-1.\end{array}$$

Proof. 

The lower bounds follow from Corollary 2, as $G_1$ and $G_2$ are subgraphs of $G_1[v/G_2]$. For the upper bounds, this can be achieved in two ways:

• Replace v in every bag of a tree-decomposition (path-decomposition) of width $\mathrm{tw}\left(G_1\right)$ ($\mathrm{pw}\left(G_1\right)$) for $G_1$ with $V\left(G_2\right)$;
• Add to every bag of a tree-decomposition (path-decomposition) of width $\mathrm{tw}\left(G_2\right)$ ($\mathrm{pw}\left(G_2\right)$) for $G_2$ the set $V\left(G_1\right)\setminus \left\{v\right\}$.

As both alternatives result in a valid tree-decomposition (path-decomposition) for $G_1[v/G_2]$, the upper bound follows. □

Note that the upper bounds described in the previous theorem are tight, as for two cliques $K_n,K_m$ and a vertex $v\in V\left(K_n\right)$, we have $K_n[v/K_m]=K_{n+m-1}$ with

$$\begin{array}{c}\hfill \mathrm{tw}\left(K_{n+m-1}\right)=n+m-2=min(\mathrm{tw}\left(K_n\right)+m,\mathrm{tw}\left(K_m\right)+n)-1\mathrm{and}\\ \hfill \mathrm{pw}\left(K_{n+m-1}\right)=n+m-2=min(\mathrm{pw}\left(K_n\right)+m,\mathrm{pw}\left(K_m\right)+n)-1.\end{array}$$

Besides this general upper bound for tree-width, the following proposition can provide an even stricter upper bound in specific situations.

Proposition 9. 

Let $G_1$, $G_2$ be two vertex-disjoint graphs, and let $v\in V\left(G_1\right)$ be a non-isolated vertex. Then, it holds that

$$\begin{array}{c}\hfill \mathit{tw}\left(G_1[v/G_2]\right)\le \max (\mathit{tw}\left(G_1\right)-1,\mathit{tw}\left(G_2\right))+\left|N_{G_1}\left(v\right)\right|.\end{array}$$

Proof. 

Let $({\mathcal{X}}_1,T_1)$ be a tree-decomposition for $G_1$ of width $\mathrm{tw}\left(G_1\right)$, and let $({\mathcal{X}}_2,T_2)$ be a tree-decomposition for $G_2$ of width $\mathrm{tw}\left(G_2\right)$. Replace v with $N_{G_1}\left(v\right)$ in every bag of ${\mathcal{X}}_1$, and denote the modified set of bags by ${\mathcal{X}}_1^{\prime }$. Then, $({\mathcal{X}}_1^{\prime },T_1)$ is a tree-decomposition for $G_1\setminus \left\{v\right\}$ of width at most $\mathrm{tw}\left(G_1\right)-1+\left|N_{G_1}\left(v\right)\right|$. Subsequently, add $N_{G_1}\left(v\right)$ to all bags of ${\mathcal{X}}_2$, and denote the modified set of bags by ${\mathcal{X}}_2^{\prime }$. Let $v_1\in V\left(T_1\right)$ be a vertex of $T_1$ with $N_{G_1}\left(v\right)\subseteq X_{v_1}$ for $X_{v_1}\in {\mathcal{X}}_1^{\prime }$, and let $v_2$ be any vertex of $T_2$. Then, $(\mathcal{X},T)$ with $\mathcal{X}={\mathcal{X}}_1^{\prime }\cup {\mathcal{X}}_2^{\prime }$, $V\left(T\right)=V\left(T_1\right)\cup V\left(T_2\right)$, and $E\left(T\right)=E\left(T_1\right)\cup E\left(T_2\right)\cup \{v_1,v_2\}$ is a tree-decomposition for $G_1[v/G_2]$ of width at most $\max (\mathrm{tw}\left(G_1\right)-1,\mathrm{tw}\left(G_2\right))+\left|N_{G_1}\left(v\right)\right|$. □

4.5. Graph Product

The graph product of two vertex-disjoint graphs $G_1$ and $G_2$ is a new graph with vertex set $V\left(G_1\right)\times V\left(G_2\right)$ and an edge set derived from the adjacency, equality, or non-adjacency of vertices in the original graphs $G_1$ and $G_2$. In this work, we consider the Cartesian [65], categorical [66], co-normal [67], lexicographic [68], and normal [65] graph products, as well as the symmetric difference [67] and the rejection [67]. Weichsel introduced the categorical graph product as the “Kronecker product”, while Harary and Wilcox referred to it as the “conjunction”. The normal graph product was introduced by Sabidussi as the “strong product”. The co-normal graph product was introduced by Harary and Wilcox as the “disjunction”, and the lexicographic graph product was initially defined by Harary as the “composition”. All graph products, their respective notations, and the edge sets of the resulting graphs are listed in Table 1. For more exhaustive definitions and in-depth results on these graph products, we refer to the works by Imrich and Klavzar [69] and Jensen and Toft [70].

Table 1. Graph products.

Graph Product	Notation	Edge Set $\{\{({\mathit{u}}_1,{\mathit{u}}_2),({\mathit{v}}_1,{\mathit{v}}_2)\}\mid$
Cartesian	$G_1\times G_2$	$(u_1=v_1\wedge \{u_2,v_2\}\in E\left(G_2\right))$
		$\vee (u_2=v_2\wedge \{u_1,v_1\}\in E\left(G_1\right))\}$
Categorical	$G_1{\star }_{\mathrm{cat}}{G}_2$	$\{u_1,v_1\}\in E\left(G_1\right)\wedge \{u_2,v_2\}\in E\left(G_2\right)\}$
Co-Normal	$G_1\vee G_2$	$\{u_1,v_1\}\in E\left(G_1\right)\vee \{u_2,v_2\}\in E\left(G_2\right)\}$
Lexicographic	$G_1\left[G_2\right]$	$(\{u_1,v_1\}\in E\left(G_1\right))\vee (u_1=v_1\wedge \{u_2,v_2\}\in E\left(G_2\right))\}$
Normal (strong)	$G_1\star G_2$	$(u_1=v_1\wedge \{u_2,v_2\}\in E\left(G_2\right))$
		$\vee (\{u_1,v_1\}\in E\left(G_1\right)\wedge u_2=v_2)$
		$\vee (\{u_1,v_1\}\in E\left(G_1\right)\wedge \{u_2,v_2\}\in E\left(G_2\right))\}$
Symmetric difference	$G_1▵G_2$	$\{u_1,v_1\}\in E\left(G_1\right)⊻\{u_2,v_2\}\in E\left(G_2\right)\}$
Rejection	$G_1|G_2$	$\{u_1,v_1\}\notin E\left(G_1\right)\wedge \{u_2,v_2\}\notin E\left(G_2\right)\}$

Besides these graph products, Teh and Yap defined the $\gamma$-product of two graphs $G_1$ and $G_2$ as $\overline{\overline{G_1}\vee \overline{G_2}}$ [71]. By transforming the edge set of the $\gamma$-product of two graphs $G_1$ and $G_2$, it follows that $\overline{\overline{G_1}\vee \overline{G_2}}=G_1\star G_2$ holds. In other words, the $\gamma$-product is merely a different formulation for the normal product of two graphs. Furthermore, by transforming the edge set of $G_1|G_2$, we obtain $G_1|G_2=\overline{G_1}\star \overline{G_2}$, while transforming the edge set of $G_1▵G_2$ results in $G_1▵G_2=(G_1\times G_2)\cup \left(G_1{\star }_{\mathrm{cat}}\overline{G_2}\right)\cup \left(\overline{G_1}{\star }_{\mathrm{cat}}{G}_2\right)$.

For two paths $P_n$, $P_m$ with $n,m\in \mathbb{N}$, it holds that $P_n\times P_m$ is an $n\times m$-grid graph. Consequently, for two graphs $G_1$ and $G_2$, it is generally not possible to bound the tree-width (path-width) of $G_1\times G_2$ from above by the tree-widths (path-widths) of $G_1$ and $G_2$ (cf. Example 4). With $P_n\times P_m$ being a subgraph of $P_n\vee P_m$, $P_n\star P_m$, and $P_n▵P_m$, the same result follows from Corollary 2 for the co-normal and normal graph products, as well as the symmetric difference. Next, $P_n{\star }_{\mathrm{cat}}{P}_m$ has an $a\times a$-grid graph, with a proportional to $min(n,m)$ as a subgraph, so that by the same argument as before, the tree-width (path-width) of $G_1{\star }_{\mathrm{cat}}{G}_2$ can generally not be bound from above by the tree-widths (path-widths) of $G_1$ and $G_2$. For $n,m\in \mathbb{N}$, let $I_n$ and $I_m$ denote the graphs that contain n and m isolated vertices. From our earlier observation, we know that $I_n|I_m=K_n\star K_m$ holds. Consequently, the tree-width (path-width) of $I_n|I_m$ cannot be bound from above by the tree-widths (path-widths) of $I_n$ and $I_m$, as $\mathrm{tw}\left(I_n\right)=\mathrm{pw}\left(I_n\right)=1$ holds, while $K_n$ and $K_m$ are subgraphs of $I_n|I_m$, such that by Lemma 3 (Lemma 7), $\mathrm{tw}\left(I_n\right|I_m)\ge \max (n,m)-1$ ($\mathrm{pw}\left(I_n\right|I_m)\ge \max (n,m)-1$) follows. Therefore, for two graphs $G_1$ and $G_2$, the tree-width (path-width) of the rejection $G_1|G_2$ can generally not be bound from above by the tree-widths (path-widths) of $G_1$ and $G_2$. The following corollary summarizes these observations.

Corollary 9. 

Let $G_1$ and $G_2$ be two graphs. It is not possible to provide an upper bound for the tree-width (path-width) of the two graphs’ Cartesian, categorical, co-normal, and normal graph products, as well as their rejection or symmetric difference, in terms of the tree-widths (path-widths) of $G_1$ and $G_2$.

Lower bounds for the tree-width (using the notation of bramble number [22]) of the Cartesian and the normal product of two graphs are given in terms of the Hadwiger, PI, and bramble number in the work by Kozawa, Otachi, and Yamazaki [72].

Having discussed all previously defined graph products, except for the lexicographic graph product, we now provide bounds for this operation. First, for two graphs $G_1$ and $G_2$, it holds that $G_1$ and $G_2$ are subgraphs of $G_1\left[G_2\right]$. Consequently, from Corollary 2, it follows that the tree-width (path-width) of $G_1\left[G_2\right]$ is at least as large as the maximum over the tree-widths (path-widths) of $G_1$ and $G_2$. Second, to obtain a tree-decomposition (path-decomposition) for $G_1\left[G_2\right]$, we begin with a tree-decomposition (path-decomposition) for $G_1$ and replace every vertex $v_i\in V\left(G_1\right)$ in every bag with $(v_i,v_j)$ for all $v_j\in V\left(G_2\right)$. This results in a tree-decomposition (path-decomposition) for $G_1\left[G_2\right]$ of width $(\mathrm{tw}\left(G_1\right)+1)\left|V\left(G_2\right)\right|-1$ ($(\mathrm{pw}\left(G_1\right)+1)\left|V\left(G_2\right)\right|-1$).

Corollary 10. 

Let $G_1$ and $G_2$ be two vertex-disjoint graphs. It holds that

$$\begin{array}{cc}\hfill \max (\mathit{tw}\left(G_1\right),\mathit{tw}\left(G_2\right))& \le \mathit{tw}\left(G_1\left[G_2\right]\right)\le (\mathit{tw}\left(G_1\right)+1)\left|V\left(G_2\right)\right|-1\mathit{and},\hfill \\ \hfill \max (\mathit{pw}\left(G_1\right),\mathit{pw}\left(G_2\right))& \le \mathit{pw}\left(G_1\left[G_2\right]\right)\le (\mathit{pw}\left(G_1\right)+1)\left|V\left(G_2\right)\right|-1.\hfill \end{array}$$

Bodlaender et al. [73] showed that if $G_2$ is a clique, the upper bounds for $\mathrm{tw}\left(G_1\left[G_2\right]\right)$ and $\mathrm{pw}\left(G_1\left[G_2\right]\right)$, as stated above, are tight.

Theorem 24. 

Let G be a graph and $q\in \mathbb{N}$. It holds that $\mathit{tw}\left(G\left[K_q\right]\right)=(\mathit{tw}\left(G\right)+1)q-1$ and $\mathit{pw}\left(G\left[K_q\right]\right)=(\mathit{pw}\left(G\right)+1)q-1$.

4.6. 1-Sum

Let $G_1$ and $G_2$ be two vertex-disjoint graphs, and let $v\in V\left(G_1\right)$ and $w\in V\left(G_2\right)$ be two vertices. The 1-sum of $G_1$ and $G_2$, denoted by $G_1{\oplus }_{v,w}{G}_2$, consists of the disjoint union of $G_1$ and $G_2$, with vertices v and w identified. More specifically, graph $G_1{\oplus }_{v,w}{G}_2$ has vertex set $(V\left(G_1\right)\cup V\left(G_2\right)\cup \left\{z\right\})\setminus \{v,w\}$ for a newly introduced vertex z and edge set

$$\begin{array}{cc}\hfill E\left(G_1\right)\cup E\left(G_2\right)\setminus & \{\{v,v_1\}\mid v_1\in N_{G_1}\left(v\right)\}\hfill \\ \hfill \setminus & \{\{w,w_1\}\mid w_1\in N_{G_2}\left(w\right)\}\hfill \\ \hfill \cup & \{\{z,z_1\}\mid z_1\in (N_{G_1}\left(v\right)\cup N_{G_2}\left(w\right))\}.\hfill \end{array}$$

With the 1-sum of two graphs $G_1$ and $G_2$ formally defined, the following theorem considers the tree-width and path-width of $G_1{\oplus }_{v,w}{G}_2$.

Theorem 25. 

Let $G_1$ and $G_2$ be two vertex-disjoint graphs, and let $v\in V\left(G_1\right)$ and $w\in V\left(G_2\right)$ be two vertices. Then, it holds that

$$\begin{array}{cc}\hfill \mathit{tw}\left(G_1{\oplus }_{v,w}{G}_2\right)& =\max (\mathit{tw}\left(G_1\right),\mathit{tw}\left(G_2\right))\mathit{and}\hfill \\ \hfill \max (\mathit{pw}\left(G_1\right),\mathit{pw}\left(G_2\right))\le \mathit{pw}\left(G_1{\oplus }_{v,w}{G}_2\right)& \le \max (\mathit{pw}\left(G_1\right),\mathit{pw}\left(G_2\right))+1.\hfill \end{array}$$

Proof. 

The lower bounds follow from Corollary 2, as $G_1$ and $G_2$ are subgraphs of $G_1{\oplus }_{v,w}{G}_2$.

Let $({\mathcal{X}}_1,T_1)$ be a tree-decomposition for $G_1$ of width $\mathit{tw}\left(G_1\right)$, and let $({\mathcal{X}}_2,T_2)$ be a tree-decomposition for $G_2$ of width $\mathrm{tw}\left(G_2\right)$. To define a tree-decomposition $(\mathcal{X},T)$ for $G_1{\oplus }_{v,w}{G}_2$, we replace every occurrence of v in ${\mathcal{X}}_1$ and every occurrence of w in ${\mathcal{X}}_2$ with z. Then, we choose a vertex $u_1$ in $V\left(T_1\right)$ such that z belongs to $X_{u_1}\in {\mathcal{X}}_1$, and a vertex $u_2$ in $V\left(T_2\right)$ such that z belongs to $X_{u_2}\in {\mathcal{X}}_2$. We define T as the disjoint union of $T_1$ and $T_2$ with the additional edge $\{u_1,u_2\}$ and $\mathcal{X}$ as the union of ${\mathcal{X}}_1$ and ${\mathcal{X}}_2$. This results in a tree-decomposition $(\mathcal{X},T)$ for $G_1{\oplus }_{v,w}{G}_2$ of width $\max (\mathrm{tw}\left(G_1\right),\mathrm{tw}\left(G_2\right))$.

In order to define a path-decomposition for $G_1{\oplus }_{v,w}{G}_2$, let ${\mathcal{X}}_1$ be a path-decomposition for $G_1$ of width $\mathrm{pw}\left(G_1\right)$, and let ${\mathcal{X}}_2$ be a path-decomposition for $G_2$ of width $\mathrm{pw}\left(G_2\right)$. Then, we can either proceed as with tree-width, replacing v in all bags of ${\mathcal{X}}_1$ and w in all bags of ${\mathcal{X}}_2$ with z, and concatenate both sequences of bags into a new path $\mathcal{X}$, resulting in a path-decomposition for $G_1{\oplus }_{v,w}{G}_2$ of width $\max (\mathrm{pw}\left(G_1\right),\mathrm{pw}\left(G_2\right))$, or, if the resulting concatenation violates (pw-3), add z to all remaining bags of $\mathcal{X}$, resulting in a path-decomposition of width at most $\max (\mathrm{pw}\left(G_1\right),\mathrm{pw}\left(G_2\right))+1$. □

If $v\in V\left(G_1\right)$ and $w\in V\left(G_2\right)$ have degree at least one in $G_1$ and $G_2$, i.e., they are not isolated vertices, the new vertex z in $G_1{\oplus }_{v,w}{G}_2$ is called an articulation vertex of $G_1{\oplus }_{v,w}{G}_2$, since $\left(G_1{\oplus }_{v,w}{G}_2\right)-z$ has more connected components than $G_1{\oplus }_{v,w}{G}_2$. For a graph G, a maximal biconnected subgraph without any articulation vertex is called a block or a biconnected component of G. The bounds of Theorem 25 for tree-width imply that the tree-width of a graph equals the maximum tree-width of its biconnected components.

Corollary 11. 

Let G be a graph. It holds that the tree-width of G equals the maximum tree-width of its biconnected components.

Conversely, the following example shows that Corollary 11 does not hold for path-width.

Example 5. 

Denote the vertices of $P_3$ by $V\left(P_3\right)=\{v_1,v_2,v_3\}$ and the vertices of $P_5$ by $V\left(P_5\right)=\{u_1,u_2,u_3,u_4,u_5\}$. Then, the incidence graph $I\left(K_{1,3}\right)$ from Figure 2b can be created as $P_3{\oplus }_{v_3,u_3}{P}_5$. We know that $\mathit{pw}\left(P_3\right)=\mathit{pw}\left(P_5\right)=1$ holds, and we showed in Example 2 that $\mathit{pw}\left(I\left(K_{1,3}\right)\right)=2$ is true. As all biconnected components of $I\left(K_{1,3}\right)$ are subgraphs of $P_3$ or $P_5$, it follows that all biconnected components have a path-width of one. Consequently, the path-width of $I\left(K_{1,3}\right)$ cannot equal the maximum path-width of any of its biconnected components.

However, the bounds of Theorem 25 for path-width imply that the path-width of a graph can be bounded by its number of biconnected components and their maximum path-widths.

4.7. Corona

Frucht and Harary [74] introduced the corona of two graphs when they constructed a graph whose automorphism group is the wreath product of the two graphs’ automorphism groups. The corona of two vertex-disjoint graphs $G_1$ and $G_2$, denoted by $G_1\wedge G_2$, consists of the disjoint union of one copy of $G_1$ and $\left|V\right(G_1\left)\right|$ copies of $G_2$, where each vertex of the copy of $G_1$ is connected to all vertices of one copy of $G_2$. In other words, $|V\left(G_1\right)\left|\right|V\left(G_2\right)|$ edges are inserted into the disjoint union of the $\left|V\right(G_1\left)\right|+1$ graphs.

Alternatively, the corona of $G_1$ and $G_2$ can also be obtained by applying 1-sum and dominating vertex operations as follows. Let $V\left(G_1\right)=\{v_1,\dots ,v_n\}$ be the vertex set of $G_1$. For $i=1,\dots ,n$, we take a copy of $G_2$, insert a dominating vertex $w_i$ (cf. Section 3.1) into that copy, and obtain the resulting graph $G_{2,i}$. Then, the following sequence of 1-sums,

$$\begin{array}{c}\hfill \left(\dots \left(\left(G_1{\oplus }_{v_1,w_1}{G}_{2,1}\right){\oplus }_{v_2,w_2}{G}_{2,2}\right)\dots \right){\oplus }_{v_n,w_n}{G}_{2,n},\end{array}$$

(1)

results in the corona $G_1\wedge G_2$ of $G_1$ and $G_2$.

With this observation, we can bound the tree-width (path-width) of $G_1\wedge G_2$ in the tree-width (path-width) of its combined graphs as follows.

Theorem 26. 

Let $G_1$ and $G_2$ be two vertex-disjoint graphs. Then, it holds that

$$\begin{array}{cc}\hfill \max (\mathit{tw}\left(G_1\right),\mathit{tw}\left(G_2\right))& \le \mathit{tw}(G_1\wedge G_2)\le \max (\mathit{tw}\left(G_1\right),\mathit{tw}\left(G_2\right))+1\mathit{and}\hfill \\ \hfill \max (\mathit{pw}\left(G_1\right),\mathit{pw}\left(G_2\right))& \le \mathit{pw}(G_1\wedge G_2)\le \max (\mathit{pw}\left(G_1\right),\mathit{pw}\left(G_2\right))+\left|V\left(G_1\right)\right|.\hfill \end{array}$$

Proof. 

The lower bounds follow from Corollary 2 since $G_1$ and $G_2$ are subgraphs of $G_1\wedge G_2$.

For the upper bounds, we make use of our earlier observation that we can obtain the corona of $G_1$ and $G_2$ by applying 1-sum and dominating vertex operations as described in Equation (1). By Theorem 3, it follows that $\mathrm{tw}\left(G_{2,i}\right)\le \mathrm{tw}\left(G_2\right)+1$ and $\mathrm{pw}\left(G_{2,i}\right)\le \mathrm{pw}\left(G_2\right)+1$. By Theorem 25 and Equation (1), it follows that $\mathrm{tw}(G_1\wedge G_2)\le \max (\mathrm{tw}\left(G_1\right),\mathrm{tw}\left(G_2\right))+1$ and $\mathrm{pw}(G_1\wedge G_2)\le \max (\mathrm{pw}\left(G_1\right),\mathrm{pw}\left(G_2\right))+\left|V\left(G_1\right)\right|$. □

With the previous theorem proved, we ask ourselves whether there exists a constant integer $c\in \mathbb{N}$, such that for all graphs $G_1,G_2$, it holds that $\mathrm{pw}(G_1\wedge G_2)\le \max (\mathrm{pw}\left(G_1\right),\mathrm{pw}\left(G_2\right))+c$, similar to the upper bound for tree-width. The following proposition provides a negative answer to this question.

Proposition 10. 

For $n\ge 2$ and $m\ge 1$, it holds that

$$\begin{array}{c}\hfill \mathit{pw}(K_n\wedge K_m)=n+\max \left(0,m-⌊{\displaystyle \frac{n}{2}}⌋\right)-1.\end{array}$$

Proof. 

We write $K_n=(\{v_1,\dots ,v_n\},\{\{v_i,v_j\}\mid 1\le i<j\le n\})$ and $K_m=(\{u_1,\dots ,u_m\},\{\{u_i,u_j\}\mid 1\le i<j\le m\})$. For $1\le i\le n$, we denote the n copies of $K_m$ in $K_n\wedge K_m$ as $K_m^i$ with $V\left(K_m^i\right)=\{u_1^i,\dots ,u_m^i\}$. By construction of $K_n\wedge K_m$, every vertex $v_i$ of $K_n$ gets connected to all vertices of $K_m^i$, resulting in n cliques of size $m+1$, which we denote by $K_{m+1}^i$ with $V\left(K_{m+1}^i\right)=V\left(K_m^i\right)\cup \left\{v_i\right\}$ for $1\le i\le n$.

Since $K_{m+1}^i$, $1\le i\le n$, and $K_n$ are subgraphs of $K_n\wedge K_m$, it follows from Corollary 2 that $\max (n-1,m)\le \mathrm{pw}(K_n\wedge K_m)$ must hold.

Next, let us construct the following path-decomposition $\mathcal{X}=(X_1,\dots ,X_{n+1})$ for $K_n\wedge K_m$. We define the following:

• $X_i=V\left(K_m^i\right)\cup \{v_1,\dots ,v_i\}$ for $1\le i\le ⌊{\displaystyle \frac{n}{2}}⌋$;
• $X_{⌊{\displaystyle \frac{n}{2}}⌋+1}=V\left(K_n\right)$;
• $X_{i+1}=V\left(K_m^i\right)\cup \{v_i,\dots ,v_n\}$ for $⌊{\displaystyle \frac{n}{2}}⌋<i\le n$.

It is easy to check that $\mathcal{X}$ satisfies all three requirements of a path-decomposition for $K_n\wedge K_m$. Furthermore, we note that (a) ${\max }_{1\le i\le ⌊{\displaystyle \frac{n}{2}}⌋}\left|X_i\right|=m+⌊{\displaystyle \frac{n}{2}}⌋$, (b) $|X_{⌊{\displaystyle \frac{n}{2}}⌋+1}|=n$, and (c) ${\max }_{⌊{\displaystyle \frac{n}{2}}⌋<i\le n}\left|X_{i+1}\right|=m+n-⌊{\displaystyle \frac{n}{2}}⌋$ hold.

Next, let us differentiate two cases, $m\le ⌊{\displaystyle \frac{n}{2}}⌋$ and $m>⌊{\displaystyle \frac{n}{2}}⌋$:

Case 1: 

$m\le ⌊{\displaystyle \frac{n}{2}}⌋$

In this case, we have for (a) $m+⌊{\displaystyle \frac{n}{2}}⌋\le ⌊{\displaystyle \frac{n}{2}}⌋+⌊{\displaystyle \frac{n}{2}}⌋\le n$ and for (c) $m+(n-⌊{\displaystyle \frac{n}{2}}⌋)\le ⌊{\displaystyle \frac{n}{2}}⌋+n-⌊{\displaystyle \frac{n}{2}}⌋=n$, such that ${\max }_{1\le i\le n+1}\left|X_i\right|=n$ holds. Thus, we know that the path-decomposition $\mathcal{X}$ has a width of $n-1$, yielding

$$\begin{array}{c}\hfill \max (n-1,m)=n-1\le \mathrm{pw}(K_n\wedge K_m)\le n-1.\end{array}$$

Consequently, in this case, we obtain

$$\begin{array}{c}\hfill \mathrm{pw}(K_n\wedge K_m)=n-1=n+\max \left(0,m-⌊{\displaystyle \frac{n}{2}}⌋\right)-1.\end{array}$$

Case 2: 

$m>⌊{\displaystyle \frac{n}{2}}⌋$

In this case, we have for (a) $m+n-⌊{\displaystyle \frac{n}{2}}⌋=m+⌈{\displaystyle \frac{n}{2}}⌉\ge m+⌊{\displaystyle \frac{n}{2}}⌋$ and for (c) $m+n-⌊{\displaystyle \frac{n}{2}}⌋=m+⌈{\displaystyle \frac{n}{2}}⌉\ge ⌊{\displaystyle \frac{n}{2}}⌋+1+⌈{\displaystyle \frac{n}{2}}⌉=n+1\ge n$, such that ${\max }_{1\le i\le n+1}\left|X_i\right|=m+n-⌊{\displaystyle \frac{n}{2}}⌋$ holds. Thus, the width of path-decomposition $\mathcal{X}$ is $m+n-⌊{\displaystyle \frac{n}{2}}⌋-1=n+\max (0,m-⌊{\displaystyle \frac{n}{2}}⌋)-1$, and it follows that

$$\begin{array}{c}\hfill \mathrm{pw}(K_n\wedge K_m)\le n+\max (0,m-⌊{\displaystyle \frac{n}{2}}⌋)-1\end{array}$$

holds. Lastly, we show that there cannot exist any path-decomposition ${\mathcal{X}}^{\prime }$ for $K_n\wedge K_m$ of width smaller than $n+\max (0,m-⌊{\displaystyle \frac{n}{2}}⌋)-1$. To do so, let us assume that ${\mathcal{X}}^{\prime }$ is a minimum path-decomposition for $K_n\wedge K_m$ of the smallest possible width.

As $K_n$ is a subgraph of $K_n\wedge K_m$, we know by Lemma 7 that there must exist at least one bag X in ${\mathcal{X}}^{\prime }$ with $V\left(K_n\right)\subseteq X$. Furthermore, as $K_{m+1}^i$ is a subgraph of $K_n\wedge K_m$ for $1\le i\le n$, we know by the same argument that there must exist at least one bag $Y_i$ in ${\mathcal{X}}^{\prime }$ with $V\left(K_{m+1}^i\right)\subseteq Y_i$ for every $1\le i\le n$.

Assuming that X and $Y_i$, $1\le i\le n$, contain no more than the previously mentioned sets of vertices, $V(K_n\wedge K_m)=X\cup {\bigcup }_{i=1}^n{Y}_i$ is true, and for every edge $\{u,v\}\in E(K_n\wedge K_m)$, it holds that $u,v\in X$ if $u,v\in V\left(K_n\right)$ or $u,v\in Y_i$ if $u,v\in V\left(K_{m+1}^i\right)$. Consequently, the bags $X,Y_1,\dots ,Y_n$ satisfy (pw-1) and (pw-2). Furthermore, note that every $u_j^i\in V\left(K_m^i\right)$, $1\le j\le m$, $1\le i\le n$, satisfies $N_{K_n\wedge K_m}\left(u_j^i\right)\subseteq Y_i$, such that $u_j^i$ only needs to be part of bag $Y_i$ and would violate the assumption of ${\mathcal{X}}^{\prime }$ being minimal.

As every $v_i$, $1\le i\le n$, is part of X and exactly one other bag, namely $Y_i$, no ordering of the bags $X,Y_1,\dots ,Y_n$ can satisfy (pw-3). The minimal size-increasing modification of the bags, such that they satisfy (pw-3) is to add the set $\{v_1,\dots ,v_i\}$ to $Y_i$ for $1\le i\le ⌊{\displaystyle \frac{n}{2}}⌋$ and the set $\{v_j,\dots ,v_n\}$ to $Y_j$ for $⌊{\displaystyle \frac{n}{2}}⌋<j\le n$. In other words, allocate vertices $v_1,\dots ,v_{⌊{\displaystyle \frac{n}{2}}⌋}$ to the predecessor bags of X and vertices $v_{⌊{\displaystyle \frac{n}{2}}⌋+1},\dots ,v_n$ to the successor bags of X, resulting in

$$\begin{array}{c}\hfill Y_1\cup \left\{v_1\right\},\dots ,Y_{⌊{\displaystyle \frac{n}{2}}⌋}\cup \{v_1,\dots ,v_{⌊{\displaystyle \frac{n}{2}}⌋}\},X,Y_{⌊{\displaystyle \frac{n}{2}}⌋+1}\cup \{v_{⌊{\displaystyle \frac{n}{2}}⌋+1},\dots ,v_n\},\dots ,Y_n\cup \left\{v_n\right\}.\end{array}$$

Every other allocation of the vertices of X to its predecessor and successor bags satisfying (pw-3) would result in its direct predecessor or successor containing at least $⌈{\displaystyle \frac{n}{2}}⌉+1$ additional vertices, i.e., one more than in the current allocation, violating the assumption that ${\mathcal{X}}^{\prime }$ is minimal. But then, ${\mathcal{X}}^{\prime }$ is equal to $\mathcal{X}$, and $\mathcal{X}$ is already a minimal path-decomposition for $K_n\wedge K_m$, such that

$$\begin{array}{c}\hfill \mathrm{pw}(K_n\wedge K_m)=n+\max (0,m-⌊{\displaystyle \frac{n}{2}}⌋)-1\end{array}$$

follows.

This completes the proof of the proposition. □

Note that for $n=1$, one can verify that $\mathrm{pw}(K_1\wedge K_m)=\mathrm{pw}\left(K_{m+1}\right)=m$ holds.

5. Conclusions and Outlook

In Section 3, we showed how the tree-width or path-width of a given graph changes if we apply a certain, unary graph transformation f to this graph. In all cases in which it is possible to bound the tree-width or path-width of the resulting graph $f\left(G\right)$, we also showed how to compute the corresponding decomposition in time linear in the size of the decomposition for G. Table 2 summarizes the results. It is noteworthy that the behavior of tree-width and path-width under the considered transformations is almost identical.

Table 2. Let G be a graph of tree-width (path-width) k, and let f be the unary graph transformation in the first column. The second column lists the upper bound for the tree-width, and the third column lists the upper bound for the path-width of $f\left(G\right)$.

Transformation f	$\mathbf{tw}\left(\mathit{f}\right(\mathit{G}\left)\right)$	$\mathbf{pw}\left(\mathit{f}\right(\mathit{G}\left)\right)$
Vertex deletion	k	k
Vertex addition	$k+1$	$k+1$
Edge deletion	k	k
Edge addition	$k+1$	$k+1$
Subgraph	k	k
Vertex identification	$k+1$	$k+1$
Edge contraction	k	k
Edge subdivision	k	$k+1$
Minor	k	k
Switching	$k+1$	$k+1$

Furthermore, in Section 4, we considered various binary graph operations f, creating a new graph $f(G_1,G_2)$ out of two graphs $G_1$ and $G_2$. In all cases in which it is possible to bound the tree-width or path-width of the combined graph $f(G_1,G_2)$ in terms of the tree-width or path-width of $G_1$ and $G_2$, we showed how to compute the corresponding decomposition in time linear in the size of the decompositions for $G_1$ and $G_2$, such that our results are constructive. In Table 3, we summarize these results, which show that, with the exception of the corona of two graphs, the behavior of tree-width and path-width under the considered operations is nearly identical.

Table 3. Let $G_1$ and $G_2$ be two graphs of tree-width (path-width) $k_1$ and $k_2$, respectively, and let f be the binary graph operation from the first column. Let $n_1$ denote the number of vertices of $G_1$ and $n_2$ the number of vertices of $G_2$. The second column lists the upper bound for the tree-width, and the third column lists the upper bound for the path-width of the graph $f(G_1,G_2)$.

Operation f	$\mathbf{tw}\left(\mathit{f}({\mathit{G}}_1,{\mathit{G}}_2)\right)$	$\mathbf{pw}\left(\mathit{f}({\mathit{G}}_1,{\mathit{G}}_2)\right)$
Disjoint union	$\max (k_1,k_2)$	$\max (k_1,k_2)$
Join	$min(k_1+n_2,k_2+n_1)$	$min(k_1+n_2,k_2+n_1)$
Substitution	$min(k_1+n_2,k_2+n_1)-1$	$min(k_1+n_2,k_2+n_1)-1$
Lexicographic product	$(k_1+1)n_2-1$	$(k_1+1)n_2-1$
1-sum	$\max (k_1,k_2)$	$\max (k_1,k_2)+1$
Corona	$\max (k_1,k_2)+1$	$\max (k_1,k_2)+n_1$

The results in Section 3.2 and Section 3.3 allow for generalizing known results on the stability of trees and forests [75,76] to the stability of graph classes of bounded tree-width [77].

Most of our results provide tight upper and lower bounds for the tree-width and path-width of the resulting graph in terms of those of the initial graphs or argue why such bounds are impossible.

For the remaining case, it has yet to be shown whether our bounds are the best possible or whether stricter bounds can be provided. The bounds for the tree-width and path-width of the power of a graph, as shown in Section 3.8, are very rough, as all vertex degrees are approximated by the maximum degree of the graph. Furthermore, we did not provide lower bounds for the tree-width (path-width) of the categorical or co-normal graph product of two graphs, nor for the symmetric difference or rejection of two graphs.