Abstract
To assess the condition of cultural heritage assets for conservation, reality-based 3D models can be analyzed using FEA (finite element analysis) software, yielding valuable insights into their structural integrity. Three-dimensional point clouds obtained through photogrammetric and laser scanning techniques can be transformed into volumetric data suitable for FEA by utilizing voxels. When directly using the point cloud data in this process, it is crucial to employ the highest level of accuracy. The fidelity of r point clouds can be compromised by various factors, including uncooperative materials or surfaces, poor lighting conditions, reflections, intricate geometries, and limitations in the precision of the instruments. This data not only skews the inherent structure of the point cloud but also introduces extraneous information. Hence, the geometric accuracy of the resulting model may be diminished, ultimately impacting the reliability of any analyses conducted upon it. The removal of noise from point clouds, a crucial aspect of 3D data processing, known as point cloud denoising, is gaining significant attention due to its ability to reveal the true underlying point cloud structure. This paper focuses on evaluating the geometric precision of the voxelization process, which transforms denoised 3D point clouds into volumetric models suitable for structural analyses.
1. Introduction
To conduct diagnostic research geared toward assessing the cutting-edge stage of degradation and the ongoing charge of deterioration in particular cultural heritage (CH) sites, the implementation of remote non-destructive testing (NDTs) is essential. Identifying the best method for correct analysis is essential. FEA is a technique used to model the strain conduct of gadgets and structures, using 3D CAD (Computer Aided Design) models made from Non-Uniform Rational B-splines (NURBS) surfaces, which constitute an appropriate geometry of the item being simulated [1,2]. Within FEA software program (Ansys 19.2), mesh creation modules are utilized to convert a NURBS model, which consists entirely of its outside surfaces, into a volumetric model [3]. This volumetric version features nodes distributed all over the model, using tetrahedra or hexahedra. When applied to 3D analysis of cultural heritage, which changes over time, the use of geometric CAD models can lead to over-simplifications, resulting in misguided simulation effects. Presently, the 3D documentation of CH has drastically progressed due to the use of both active and passive sensors. The initial result of this process is a dense 3D point cloud, which is later converted into a triangular mesh. These models accurately represent the exterior surfaces of the surveyed items and have usually high resolution, meaning millions of triangular elements. However, this high density makes them unsuitable for direct use in FEA. It is necessary to convert meshes into a volumetric model and reduce their density, as the processing effort increases rapidly with the number of nodes representing the simulated object in the computational complexity of the analysis. The model developed aims to simulate stress behavior and predict potential damage, which enhances protection efforts, but several challenges have to be faced and addressed: (a) the process of generating volume suitable for finite element analysis from raw 3D data lacks clear guidelines, which can significantly affect the results; (b) the 3D acquisition process is often a mismatch between geometric resolution and reliability of simulation results compared to the 3D model obtained from the process. FEA is commonly employed in engineering as a standard technique for structural evaluation. In the context of ancient structures, to mitigate the risk of error propagation, one viable approach is to create a volumetric model directly from a 3D point cloud. The primary concern is ensuring that the model created for FEA closely resembles the original structure. The established methodology utilizes NURBS surfaces to define the form of the object intended for simulation. However, applying this method to 3D cultural heritage models may introduce significant approximations, potentially resulting in inaccurate simulation outcomes. A review of previous studies indicates various strategies have been adopted: (a) employing a CAD modeler to develop a new model from the surface mesh derived from the acquired 3D data; (b) directly utilizing the triangular mesh for volumetric models; (c) creating a volume from the point cloud; (d) transitioning from reality-based 3D models to BIM/HBIM (Building/Heritage Building Information Modeling) for FEA; (e) developing a new tool. The first approach was applied to simulate the behavior of various cultural heritage buildings [4,5,6,7], further refined by incorporating a few patches of reality-based surface meshes [8] and for both 2D façade models [9,10] as well as 2D and 3D modeling [11,12], which also involved a significant discretization of the model using both a 3D model and a 3D composite beam model [13]. The second approach employs multiple techniques: (i) the simplification of the triangular mesh prior to its conversion into a volumetric form, which may introduce significant discrepancies between the actual and simulated shapes [14]; (ii) a streamlined representation of shapes as discretized profiles that provide a low-resolution depiction of the structure as a whole, from which a volumetric model can be derived [15,16,17]; and the adaptation of the obtained 3D model into a parametric format suitable for volumetric transformation [18]. The third strategy disregards the mesh entirely, opting instead to generate a volumetric approximation of the 3D mesh from the point cloud [19], which the same authors later compare with alternative methods [2,20]. The fourth methodology utilizes a reality-based 3D model to create HBIM models intended for finite element analysis (FEA), involving two levels of approximation: (i) the initial phase pertains to the drafting of a BIM model; (ii) the subsequent phase involves generating volumes for FEA from these BIM models. In [21], the authors explored the application of BIM to aid in site observing and administration, extracting thematic information for structural analysis, although they did not conduct a finite element analysis of the structure. Another instance includes the development of HBIM from archival data and laser scanner surveys [22,23]. Several sequential steps are involved in the creation of volumetric models for structural analysis, each of which adds a degree of approximation. Approximations resulting from 3D surface reconstruction are used to convert an unstructured point cloud to a mesh. Retopology simplification improves surface smoothness while preserving high accuracy [24]. To approximate the shape of the object, NURBS is created by applying patches equal to the number of surface elements in the mesh. Considering all these steps, the process starts with accurate data (point cloud), leads to an inaccurate mesh, and, because the structural analysis using FEA adds another approximation, the results will be far from reality.
1.1. Denoising
Converting an unstructured 3D point cloud into a coherent surface reconstruction (3D mesh) poses significant challenges, particularly in scenarios involving the digitization of architectural sites, the development of virtual environments, reverse engineering for CAD model creation, and geospatial analysis. The progress of technologies, particularly in scanning techniques, has enabled the collection of dense 3D point clouds containing millions of points. A crucial aspect of preserving cultural heritage is understanding its geometric complexity. Since the objects being detected and analyzed have experienced modifications over the centuries, such as repairs, alterations, and reconstructions, this task is inherently complex. These modifications frequently result in the formation of cracks and damage that is typically challenging to identify and understand. Accurate diagnosis, which facilitates the identification and interpretation of crack patterns in cultural heritage objects and structures, is vital for comprehending the structural behavior of these artifacts and for guiding subsequent interventions. This identification process is primarily visual but may not always be practical. Consequently, it is imperative to establish an optimal workflow that produces results that are as true to reality as possible. Another important aspect to be addressed in the upcoming sections of this research is the segmentation of the 3D models, concentrating on the key components that define the object under investigation. Three-dimensional point clouds derived from photogrammetric and laser scanning surveys frequently present noise due to various influences, such as non-collaborative materials or surfaces, insufficient lighting, intricate geometries, and the limited accuracy of the tools used. This noise not only alters the unstructured geometry of the point clouds but also introduces irrelevant information, reducing the geometric precision of the resulting mesh model and subsequently impacting the results of any analyses performed on it. Therefore, it is crucial to clean the raw data. The process of eliminating noise from point clouds has become a key area in 3D geometric data processing, as it allows for the extraction of the true ground point cloud while refining the ideal surface. This research examines the effectiveness of a current algorithm for creating various cultural heritage models intended for structural analysis. Point clouds were post-processed and evaluated compared with the original data, profiles have been extrapolated from raw and denoised data, and compared, and the 3D meshes from the denoised data have been exported to assess the algorithm’s performance across different geometries and case studies. The objective was to investigate its capability to generate more accurate volumetric data from 3D meshes to support structural analysis. Bilateral filtering [25] is acknowledged as a nonlinear method for image smoothing, and its principles have been adapted for denoising point clouds [26]. Techniques employing bilateral filtering apply this method directly to point clouds, considering factors such as point position, point normal, and point color [27]. Guided filtering [28] acts as a specific image filter that can function as an edge-preserving smoothing operator [29]. Recently, numerous filter-based algorithms have utilized point normals as guiding data, iteratively refining and updating points to conform to the estimated normals. Furthermore, graph-based point cloud denoising techniques treat the input point cloud as a graph filter [30], implementing denoising through selected graph filters. Patch-based graph representations create a graph using surface patches derived from point clouds, with each patch represented as a node [31]. Optimization-driven denoising techniques aim to produce a denoised point cloud that closely resembles the original input cloud [32]. Additionally, deep learning methods have been utilized in point cloud processing, where denoising typically initiates with noisy inputs and seeks to establish a mapping that aligns with the ground truth data. Deep learning techniques can be divided into two categories: supervised denoising approaches, such as those utilizing PointNet [33], and unsupervised denoising methods [30]. The implementation of the denoising algorithm has demonstrated a significant enhancement in geometric precision and reconstruction accuracy [34]. The improved distribution of points within the cloud suggests that the generated mesh exhibited fewer topological inaccuracies. This enhancement is largely due to the denoising algorithm, which effectively reduced geometric errors and smoothed areas with high concentrations of noise. As a result, the final mesh showed lower noise levels while preventing intersecting elements or spikes that could compromise the model’s surface. Although such geometric modifications may not greatly affect outcomes in visualization or virtual applications, they can result in further approximations of outcomes or even failures in structural finite element analyses.
1.2. Retopology and NURBS
The application of reality-based 3D models in FEA offers significant benefits by removing the need for approximations. Nevertheless, to ensure these original models are compatible with FEA software (Ansys 19.2), they must undergo a process of simplification. The most effective method for achieving this while maintaining the fidelity of the original reality-based 3D model is through retopology. This technique involves a thorough simplification of the mesh and a reconfiguration of its topology, resulting in a newly established topology for the 3D model. Typically, this mesh is composed of quadrangular elements (quads), which enhance the organization of the polygonal surface elements, thereby improving their distribution across the surface. The transition from triangular to quadrangular elements greatly simplifies the mesh without compromising its intrinsic accuracy. Topology emphasizes the geometric characteristics and spatial relationships among polygons within a mesh, irrespective of continuous variations in their shapes and sizes. Any abrupt alteration in these relationships is classified as a topological error, such as the inversion of normals between two adjacent polygons. Triangular meshes consist of a series of triangles, with the centroid providing a linear representation of the surface. A mesh can be depicted as a collection of vertices
V = {v1,…, vV}
and a set of triangles connecting them
F = {f1,…,fF}, fi ∈ V × V × V
although it is more efficient to define the triangular mesh with the edges of the polygons
ε = {e1, …, eE}, ei ∈ V × V
and a set of triangles connecting them
F = {f1,…,fF}, fi ∈ V × V × V
although it is more efficient to define the triangular mesh with the edges of the polygons
ε = {e1, …, eE}, ei ∈ V × V
The process of reconstructing surfaces from an oriented point cloud poses considerable difficulties. The irregularity of point sampling, combined with noise in both positions and normals due to sampling errors and misalignment during scanning, complicates this task. Under these circumstances, the meshing aspect of surface reconstruction must rely on assumptions regarding the unknown surface topology, aiming to accurately fit the noisy data while effectively addressing any gaps. Various methodologies, such as Delaunay triangulations, alpha shapes, and Voronoi diagrams, are employed to interpolate the available points. However, the inherent noise in the data often necessitates additional processing steps, including roughening, smoothing, or re-fitting, to improve accuracy. Surface reconstruction techniques are typically divided into global and local approaches. Global fitting methods represent the implicit function as a sum of radial basis functions (RBFs) centered on the data points, while local fitting techniques analyze subsets of closely located points at any given time. A basic method involves estimating tangent planes and defining the implicit function as the signed distance from the tangent plane of the nearest point. Notably, Poisson reconstruction is recognized for its ability to generate smooth surfaces that closely approximate noisy datasets. Quad-based topology is characterized by a grid of rows and columns. This topology offers numerous benefits: it results in a cleaner mesh, facilitates the incorporation of edge loops, and enhances the model’s adaptability for animation. Quad-based models feature straightforward topology, allowing for manageable adjustments in edge flow and ease of subdivision. In contrast, triangle-based topology may introduce sharp corners that can adversely affect mesh design. Quads allow for smoother deformation through simpler manipulation of edge loops, ultimately leading to more refined models.
The quadrangulation technique samples the initial mesh at a lower spatial resolution while achieving greater precision compared to conventional triangle element sampling. This method effectively preserves the geometry of the original mesh by reconstructing its topological arrangement from the ground up. The retopology process is particularly beneficial when converting the mesh into NURBS, a transition that can be automated using software such as Rhinoceros 8. This conversion improves the coherence between quad elements and the quadrangular patches that make up NURBS, thereby reducing the number of patches required for accurate representation. This is especially relevant when working with reality-based 3D models of cultural heritage, which often exhibit complex geometries while demanding precision. The resulting NURBS can then be transformed into volumetric models, representing a critical advancement since NURBS surfaces allow for the generation of curves, facilitating the accurate depiction of conical shapes. They provide local control and enable the creation of intricate forms without necessitating a substantial increase in the polynomial degree. To highlight the distinction, consider that a mesh depicts 3D surfaces using discrete polygonal faces, where smoothness depends on the polygon count—analogous to how pixels constitute an image with colored points. Conversely, NURBS surfaces are mathematical entities defined by parametric cubic curves; their edges connect to create a continuous surface grid, proficient in modeling complex geometries. Typically, a NURBS-based 3D model comprises a defined number of NURBS patches (or surfaces) that are interconnected to maintain various types of continuity—positional (G0), tangential (G1), or curvature (G2). This continuity relates to how curves or surfaces merge seamlessly. The execution of this process involves several stages, which may introduce potential inaccuracies and approximations. Naturally, the degree of approximation is influenced by the extent of modifications made to the mesh and the complexity of the object under analysis. From point cloud to mesh:
- Post-processing of the mesh.
- Retopology (smoothing).
- Closing holes and checking the topology.
- NURBS.
1.3. Voxel
Voxelization is undoubtedly a quicker method than retopology for generating NURBS, but careful selection of parameters is essential, as excessive smoothing can often be applied to the model. Nevertheless, this approach appears to be the most advantageous in terms of both time efficiency and precision, as it circumvents the complications associated with the various stages involved in handling a 3D mesh and its conversion. Voxelization can be performed using specialized software such as Blender 4.1 and Meshmixer 3.5.474, which automatically generate a voxel model from the mesh, as well as the open-source library Open3D. Blender offers a straightforward process, allowing the operator to control only the number of approximated elements by specifying the resolution or detail level of the re-meshed model. This value determines the size of the voxel. The voxels are organized on the mesh to establish the new geometry; for instance, a value of 0.5 m will yield topological patches approximately 0.5 m in size. Smaller values retain finer details but result in a mesh with a significantly denser topology. Meshmixer, on the other hand, constructs a watertight solid by converting the object into a voxel representation. The process is user-friendly, with the operator able to adjust only the solid type—either fast or accurate—along with the volume accuracy using a sliding tool that provides a numerical value as the density. It is important to note that these parameters do not directly correlate to the final polygon count of the volume. Open3D offers core functionalities that include (i) 3D data structure, (ii) 3D data processing algorithms, (iii) scene reconstruction, (iv) surface alignment, and (v) 3D visualization. To date, no research has conducted a comparative analysis of volumetric models generated through various techniques and procedures to determine which method offers the highest precision and accuracy. Most related studies utilize voxelization for object detection [14,35,36,37,38,39], particularly in the contexts of autonomous driving and feature detection for 3D point cloud segmentation. Voxel-based modeling has extensive applications in the medical sector [40,41,42,43,44]. Some experiments have explored the application of voxels in FEA, such as assessing ballistic impacts on ceramic–polymer composite panels [45], where voxel-based micro-modeling facilitated the creation of a parametric model of the composite structure. Additionally, another investigation used voxel modeling to estimate roof collapses, successfully addressing challenges in reconstructing geometries and overcoming limitations associated with the software used [46]. To enhance the accuracy of FEA, it is noted that while voxel usage decreases mesh generation time, it may compromise precision when handling curved surfaces: reference [47] proposes a homogenization method for voxel elements to address this issue.
2. Material and Methods
The idea of this work is to analyze the usefulness of the denoising algorithm on 3D point clouds of cultural heritage used as a basis for the creation of models suitable for structural analysis. The process has been tested on point clouds of different objects differing in shape, size, geometric complexity, materials and position in the environment. In this way, the results are based on heterogeneous samples that can provide a more accurate analysis spectrum. The objects chosen for the analysis are visible in Figure 1a–d and the parameters of the Camera and lens for the survey are summarized in Table 1:


Figure 1.
Objects surveyed and used as test objects in this study: (a) statue of Moses, (b) medieval pillar, (c) copy of scorpionide, (d) Samnite tomb, (e) chair from the Royal Palace of Caserta.

Table 1.
Camera and point cloud specification for each object surveyed.
- The statue of Moses from the tomb of Pope Julius II in Rome. The problems were related to the position of the statue, so it was impossible to detect the back (Figure 1a). The problem was overcome by adding more photos of the back using illuminators to better highlight the part and using a wide lens (16 mm) that increased the field of view of the camera.
- A masonry pillar from a medieval cloister, Oppido (Italy). The problems were the presence of trees and weeds and the impossibility to detect the top of the structure (Figure 1b). This was addressed by adding images acquired with a drone. Since the cameras used were different, the point clouds were manually aligned with CloudCompare software (2.13.1).
- A wooden reproduction of a Roman throwing weapon (scorpionide), with complex and detailed geometry and small and thin parts (Figure 1c). In this case, the use of a macro lens (60 mm) helped in capturing the small details. The point clouds were aligned manually with CloudCompare.
- A Samnite tomb in the archaeological park of Santa Maria Capuavetere. The structure is located on one side of the park, completely covered with ivy (Figure 1d). The point cloud was intentionally left dirty to specifically analyze the impact of the denoising algorithm on very noisy data.
3. Results
3.1. Denoising
Each point cloud was created using Agisoft Metashape 2.2 and scaled with a metal ruler alongside several designated metric targets. The denoising algorithm utilized for the point cloud is one of the most important algorithms in modern research [47]. This approach includes a denoiser that assesses the point cloud’s score within a three-dimensional framework [16]. It employs deep learning methodologies to train the model and identify the most suitable fitting region for each point. A gradient ascent technique is used to align groups of outliers with the estimated evaluation function. Essentially, this method simulates an intelligent smoothing of the underlying surface based on majority selection or the density and size of points. The workflow comprises several stages: a score estimation network, an objective function for training it, and a score-based denoising algorithm. The first component is a custom network that evaluates the scoring function around each point. The training objective focuses on comparing the predicted scores from the network with the actual ground truth scores (denoised point cloud points). Ultimately, the score-based denoising algorithm modifies the position of each point through gradient rake. The methodology includes the following: (i) utilizing the Git repository of the original project; (ii) creating an Anaconda environment that fulfills all project requirements and installing the necessary packages; (iii) running a large model denoising algorithm (Large Point Cloud Denoising for over 50,000 Points) on the model, yielding an XYZ mesh output. The system integrates two libraries: pytorch3d for handling 3D components and pytorch for training deep learning models. The latter component functions as the system’s core, proficiently extracting features from the input data and relaying them to the evaluation network, which classifies these features utilizing a threshold-based clustering methodology. This process subsequently aligns the data points to meet the threshold criteria and removes outliers, thereby enhancing the model’s accuracy.
For the comparison of data, after the denoised point clouds have been saved, each original point cloud was juxtaposed with the respective one processed with CloudCompare 2.13 software. By employing a Gaussian distribution defined by its mean and standard deviation, in conjunction with a signed cloud-to-cloud (C2C) distance; only the closest points are identified for comparison. These parameters were chosen due to the denoising algorithm’s efficacy in displacing noise points away from the target surface, where most of the points are concentrated, and directing them towards the reference surface.
To achieve a more precise assessment of shape variations, profiles were extrapolated along the principal axes to highlight the displacements between the point clouds. The data was exported in *.dxf format and analyzed using Rhinoceros software (Version 8) to determine the maximum distance between the two lines, with the non-denoised point cloud indicated in red and the denoised one in blue. The overlap of these profiles illustrates the algorithm’s impact on the geometric arrangement of points, realigning noisy data to conform to the ideal surface. As far as the test objects are concerned (Table 2, Figure 2), the profiles derived from the Samnite tomb reveal significant discrepancies, with the red line markedly deviating from the actual geometry of the object. This deviation is ascribed to the tomb’s surface being covered by ivy and because of the limited survey space. Conversely, the profiles of the statue of Moses exhibit minimal differences, attributed to favorable survey conditions, including compatible material properties, sufficient survey space, and adequate lighting.

Table 2.
Mean and standard deviation of each point cloud analyzed after the denoising.

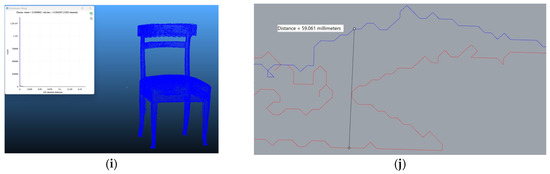
Figure 2.
The comparison of the two point clouds, raw and denoised, and of the profiles extrapolated for each object’s model: (a,b) Moses; (c,d) medieval pillar, (e,f) scorpionide, (g,h) Samnitic tomb, (i,j) chair from the Royal Palace of Caserta.
Table 2 gathers all the main data obtained from the comparisons: mean and standard deviation for each comparison, as shown in Figure 2a,c,e,g,i, and the difference in profiles, visible geometrically in Figure 2b,d,f,h,j. The images are fundamental to highlight the trend of the Gaussian distribution of the point in the comparison. In probability theory and statistics, Gaussian distribution (or a normal distribution) is a type of continuous probability distribution for a real-valued random variable. The Gaussian distribution represents a real-valued random variable with unknown distribution. Its importance is based on, among other things, the central limit theorem. This states that, under certain conditions, the average of many samples (observations) of a random variable with a finite mean and a finite variance is itself a random variable—its distribution converges to a normal distribution as the number of samples increases. Therefore, physical quantities that may be the sum of many independent processes (e.g., measurement errors) often have an almost normal distribution. The graph of the Gaussian distribution depends on two factors—the mean and the standard deviation. The mean of the distribution determines the location of the center of the graph, and the standard deviation determines the height and width of the graph. The height is determined by the scaling factor and the width is determined by the factor in the power of the exponential. When the standard deviation is large, the curve is short and wide; when the standard deviation is small, the curve is tall and narrow. All Gaussian distributions look like symmetric, bell-shaped curves. Even with a standard deviation of less than one centimeter, the profile arrangement uncovers inaccuracies where the geometric distribution of points appears disordered and erratic (Figure 2).
These inconsistencies contribute to errors in the geometric reconstruction of the 3D mesh. The algorithm exhibits interesting performance with point clouds derived from objects made of non-cooperative materials or those featuring intricate geometries. Nevertheless, the restricted acquisition baseline presents a challenge, as inaccuracies or insufficient overlap led to excessively dense noise, topological inaccuracies, and overlapping areas.
For the Moses statue, a 3D mesh was constructed utilizing the Poisson surface reconstruction method in Meshlab 2023.12. Initially, normals for each point were calculated using default parameters prior to executing the reconstruction without any post-processing, preserving all settings at their defaults. This approach enabled a direct evaluation of comparison outcomes based on the raw data. The original and denoised point cloud meshes were analyzed under consistent conditions, focusing primarily on the influence of denoising on the geometric approximation during the meshing process and whether improving the geometric precision of the point cloud enhances the overall workflow. The initial phase involved examining topological inaccuracies within the meshes using Meshmixer 3.5 software. The mesh generated from raw data exhibited numerous topological issues, whereas the denoised mesh presented none, signifying a notable enhancement in geometric accuracy attributable to denoising. Following the meshing process, the models were simplified through retopology using the free software InstantMeshes and subsequently transformed into NURBS utilizing the “MeshToNURBS” tools in Rhinoceros 6. An analysis of the results indicated that both mesh types displayed negligible topological inaccuracies, with the denoised mesh demonstrating superior performance. Additionally, when the retopologized meshes were transformed into NURBS for evaluating the precision of the volumetric model, the model based on raw data faced construction failures. This problem highlighted that excessive noise and density within the raw point cloud data made it inadequate for producing precise NURBS models (Figure 3).
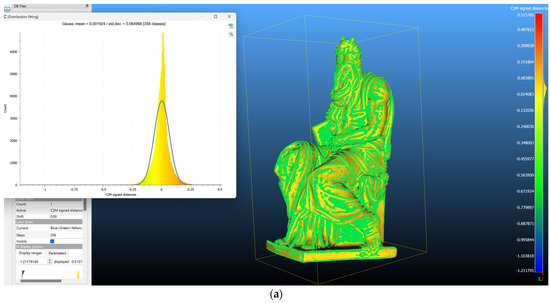

Figure 3.
The comparison of 3D meshes: (a) raw and denoised data, topological errors (red lines); (b) non-denoised mesh; (c) non-denoised, retopologized mesh; (d) denoised mesh; (e) denoised retopologized mesh.
3.2. Voxelization
Regarding voxelization, the challenge associated with intricate geometries, particularly those of cultural heritage artifacts, is that voxelization algorithms tend to oversimplify. A robust algorithm for voxel processing is referenced in [48]. The open-source Open3D library [49] was employed, utilizing the voxel_down_sample (self, voxel_size) function, which yields an output point cloud represented by single voxels, with normals and colors averaged when available. The methodology employed consists of the following steps:
- Applying a voxel size constraint for downsampling.
- Explanation of the voxel grid’s resolution.
- Generation of a voxel grid.
- Generation of a two-state occupancy grid.
- For each voxel, the corresponding index within a binary grid is triggered.
- Implementation of the Marching Cubes method for surface mesh extraction.
- The STL file is subsequently stored.
Only the point clouds of two objects have been voxelized, the scorpionide and the pillar, because of their geometric complexity and different dimensions (Figure 4). The process in the voxel algorithm follows different steps:


Figure 4.
The voxel models of the pillar, (a) scorpionide (b), and the chair from the Royal Palace of Caserta (c).
Voxelization is performed using Open3D’s VoxelGrid.create_from_point_cloud() function. Voxelization Parameters:
- voxel_size = 0.2: Defines the resolution of the voxel grid. A smaller value results in a higher resolution but increases processing time and memory usage. The value set for this project was 0.2 because, after several tries, it was the best compromise between the best result in terms of accuracy of data obtained from the process and the exploitation of memory. The process started with the value of 0.01 and increased it considering the use of resources in terms of memory and CPU of the computer. Of course, the decision was made considering the processing effort and the accuracy of results. After several tries, 0.2 was the best choice considering the models of the object tested. It is probable that it will be possible to decrease the value in the case of smaller objects, while with bigger, more complex objects, the value will need to be increased. The voxel grid is then saved for future use.
A binary occupancy grid is generated from the voxel grid. For each voxel, its corresponding index in the binary grid is activated. The Marching Cubes algorithm is then applied to extract the mesh surface. Marching Cubes Parameters:
- -
- Level = 0.5: Defines the isovalue for surface extraction. A value of 0.5 ensures that the generated mesh follows the midpoint of occupied and unoccupied voxels.
- -
- Spacing = (voxel_size, voxel_size, voxel_size): Ensures correct scaling of the output mesh relative to the original point cloud dimensions.
The extracted mesh is formatted into an STL-compatible structure using numpy-stl. The STL file is then saved. For validation, the trimesh library is used to visualize the result.
The parameters applied to the voxelization of the point clouds are the following:
voxel_size (float)–Voxel size to downsample to.
open3d.geometry.PointCloud
voxel_size = 0.2.
voxel_grid = o3d.geometry.VoxelGrid.create_from_point_cloud(pcd, voxel_size)
o3d.io.write_voxel_grid(“voxelized_output.bin”, voxel_grid)
grid_dim = (voxel_grid.get_max_bound() - voxel_grid.get_min_bound())/voxel_size
grid_dim = grid_dim.astype(int) + 1
binary_grid = np.zeros(grid_dim, dtype = bool)
for voxel in voxel_grid.get_voxels():
binary_grid[voxel.grid_index [0], voxel.grid_index [1], voxel.grid_index [2]] = True
verts, faces, normals, _ = measure.marching_cubes(binary_grid, level = 0.5, spacing = (voxel_size, voxel_size, voxel_size))
mesh_data = mesh.Mesh(np.zeros(faces.shape [0], dtype = mesh.Mesh.dtype))
for i, face in enumerate(faces):
for j in range(3):
mesh_data.vectors[i][j] = verts[face[j], :]
mesh_data.save(output_file)
stl_mesh = trimesh.load(output_file)
stl_mesh.show()
The complete workflow followed is summarized in Figure 5.
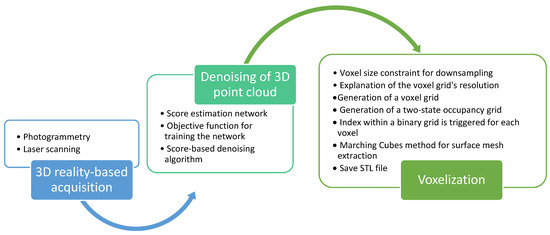
Figure 5.
Diagram of the workflow followed.
The resulting volumetric models present two different levels of accuracy. Visually, it is evident that the model of the pillar is missing many features, probably because the point cloud was too sparse. This may be due to aggressive application of the denoising algorithm or the photogrammetric processing, which resulted in an incomplete model. The volumetric model of the scorpionide, on the other hand, is more accurate and visually complete. Finally, the chair resulted in a more accurate voxel model, likely because of the geometry of the surveyed object and the fact that it was possible to capture it in 360°, both above and below. To highlight the differences, the voxelized models were compared to the meshes created from the denoised point clouds to see the differences and to analyze if the accuracy has been lost during all the passages (Figure 6).
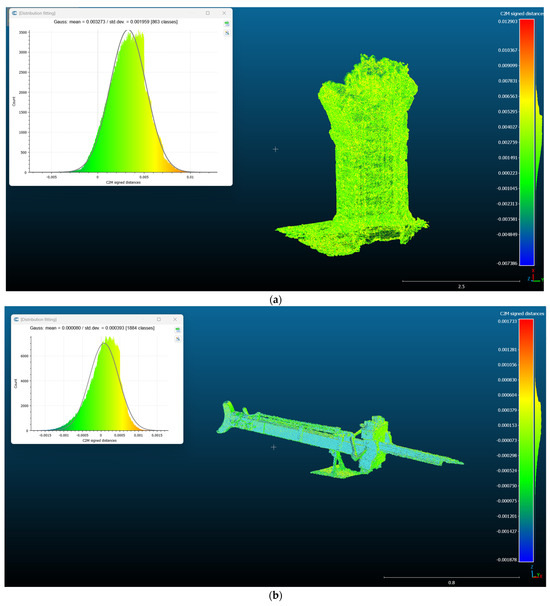

Figure 6.
The comparison of the voxel models of the pillar (a), the scorpionide (b) and the chair (c) with the 3D reference meshes.
The mean and standard deviation are summarized in Table 3, which shows how the two voxelized models show a huge difference in accuracy and precision. Figure 6 is fundamental for analyzing the Gaussian distribution of the compared models. In all the cases analyzed in this paper, the distribution of points compared follows a non-Gaussian distribution. This means that a class of probability distributions deviates from the symmetric and bell-shaped pattern of the Gaussian distribution (also known as the normal distribution). Unlike the normal distribution, non-Gaussian distributions exhibit various shapes. Standard deviation is still a measure of average distance from the mean; the difference is that in normal distributions the area under the curve can be determined easily because the standard deviations correspond to set cumulative areas, as normal distribution is a one-to-one function.

Table 3.
Mean and standard deviation of the voxelized models.
3.3. Test on FEA
The test of the voxelized model for FEA was performed using the chair as test-object. The decision was made because the voxel model was complete and because, like other similar models, it will be analyzed in FEA with thermographic analysis, combined with thermographic data acquired during periodic surveys in the Royal Palace in Caserta. The import in the software did not cause any problems, and the software recognized the model as volumetric, giving the possibility to mesh it with tetrahedrons or hexahedrons. When imposing the different parameters on the models, however, fundamental problems arose that hindered achieving an accurate result. First, it was impossible to mesh the model with hexahedrons, something that, even if not mandatory, could provide a better result. The parameters imposed on the meshing module were determined by the dimensions of the elements composing the model. Hence, the dimension of volumetric elements was equal to the voxel size. Secondly, it was not possible to impose boundary conditions or incorporate thermographic data, since the model is treated as a whole (Figure 7). This poses a serious problem because integrating thermographic data acquired on-site is fundamental for the analysis; therefore, it is mandatory to include these data on the model.

Figure 7.
The problems in FEA software (Ansys 19.2): (a) meshing of the voxel model, (b) difficulties in imposing the boundary conditions.
4. Discussion
Volumetric models employed in structural analysis software are created through a series of iterative processes, each introducing a level of approximation to the final output. This approximation begins with the transformation of an unorganized point cloud into a mesh through 3D surface reconstruction. Further simplification via retopology refines the surface, achieving a smoother appearance while still preserving a high degree of accuracy [44]. NURBS construction utilizes patches corresponding to the surface mesh elements, approximating the object’s form. Given this, beginning with less precise data (like a noisy point cloud) inevitably leads to a less accurate outcome. Furthermore, structural analysis via FEA may introduce different levels of approximation, and the cumulative effect of these steps results in a final product significantly deviating from reality. The denoising process demonstrated its effectiveness in enhancing geometrical truthfulness and reconstruction quality. The improved point distribution within the cloud indicated that the generated mesh had less topological errors, effectively mitigating geometric inaccuracies caused by clusters of noisy points. Consequently, it exhibited reduced noise, free from intersecting elements or spikes that could distort the model’s surface geometry. While this geometric modification might not significantly impact visualizations or virtual applications, it can potentially worsen the accuracy of structural finite element analyses, providing, at most, a rougher approximation, or even causing the analysis to fail. This study investigated the effectiveness of utilizing algorithms to produce volume for FEA directly from reality-based point clouds. The primary challenges encountered stem from the input data requirements. When dealing with closed 3D shapes, converting their mesh into a volume using automated tools introduces minimal approximation errors. However, if the input is merely a surface, generating a volume requires specifying a thickness for the model to ensure proper closure, a feature not always available in custom software. Based on the observed outcomes, it appears that automatic tools are ineffective for creating precise volumes when the initial mesh is incomplete or not a full 3D representation. Using point clouds directly can increase the accuracy of the resultant volume.
5. Conclusions
The Open3D library test provided the best results in creating voxel models from geometrically well-defined and correctly structured 3D point clouds, while oversimplifying point clouds with complex geometry or small details. On the other hand, the algorithm was able to voxelize models created from complete point clouds, but the details were poor due to the proximity of the meshes to particularly complex shapes. The same problem occurred when using the algorithm to create meshes from voxel grid. The reason lies in the Open3D voxelization function “voxel_down_sample”, which sometimes does not clearly display planes passing through the figure. The problem seems to be a known issue with the library and leads to poor performance of the algorithm output. This issue may be related to the calculated normals of the input point cloud. Further investigation will be conducted in the future.
The set-up of the parameters for the voxelization process can be expressed as follows:
- Voxel Size Tradeoff: A finer voxel size (voxel_size < 0.2) improves surface accuracy but increases memory consumption.
- Marching Cubes Complexity: The algorithm operates on a binary grid rather than the raw point cloud, reducing noise but potentially introducing geometric artifacts.
- Denoising Optimization: Adjusting std_ratio allows for controlling the tradeoff between data retention and outlier removal.
Future work will focus on analyzing and discussing possible reasons for the mediocre results of voxel modeling. The goal is to test different algorithms and use point clouds of various objects differing in shape, geometric complexity, and size to check if there is an algorithm or a tool that would allow starting directly from real 3D point clouds to perform the structural analysis using volumes in FEA, without adding the inherent approximations of the process. It is hoped that testing different algorithms will provide a better understanding of the improvements needed to write scripts that better adapt to the geometric complexity of the analyzed models. It seems that there is not a script, an algorithm, or software that can provide the accuracy required for the proposed pipeline. Another option would be to pre-segment the point cloud and then apply voxelization to create a model more suitable for FEA (subdivided in its specific characteristics of material properties). This process, on the other hand, can introduce other problems and inaccuracies due to the modeling of single parts instead of the complexity of the object as a unique body. Furthermore, as expected, this procedure works better on single objects such as statues because they can be modeled as a closed volume filling the inside with voxels. Buildings need a more careful and complex survey step to acquire both the outside and the inside; the cleaning of the point cloud is longer and must be performed carefully to have a proper, complete, and accurate 3D reproduction of the structure. Only from this kind of data will it be possible to start the voxelization process.
Author Contributions
Conceptualization, S.G.B. and E.N.; methodology, S.G.B. and E.N.; software, S.G.B. and E.N.; validation, S.G.B.; formal analysis, S.G.B. and E.N.; investigation, S.G.B.; resources, S.G.B. and E.N.; data curation, S.G.B. and E.N.; writing—original draft preparation, S.G.B.; writing—review and editing, S.G.B. and E.N.; visualization, S.G.B. and E.N.; supervision, S.G.B.; funding acquisition, S.G.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by PRIN PNRR RESEARCH PROJECTS OF RELEVANT NATIONAL INTEREST—2022 Call for proposals: “low coSt tools and machIne learniNg for prEdiction of heRitaGe wood’s mechanical decay—SINERGY”, grant number P20224YMW9, PI. Rosa De Finis, University of Salento, co-PI Sara Gonizzi Barsanti, University of Campania Luigi Vanvitelli.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
The authors want to thank the Director of the Reggia di Caserta, Tiziana Maffei and Anna Manzone, conservatory restorer officer responsible for the maintenance and restoration of works of art, museum deposits, and loan contact at Reggia di Caserta, for accepting the collaboration on this project and helping us with the survey procedures.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Höllig, K. Finite Element Methods with B-Splines; Society for Industrial and Applied Mathematic: Philadelphia, PA, USA, 2003. [Google Scholar]
- Shapiro, V.; Tsukanov, I.; Grishin, A. Geometric Issues in Computer Aided Design/Computer Aided Engineering Integration. J. Comput. Inf. Sci. Eng. 2011, 11, 21005. [Google Scholar] [CrossRef]
- Alfio, V.S.; Costantino, D.; Pepe, M.; Restuccia Garofalo, A. A Geomatics Approach in Scan to FEM Process Applied to Cultural Heritage Structure: The Case Study of the “Colossus of Barletta”. Remote Sens. 2022, 14, 664. [Google Scholar] [CrossRef]
- Brune, P.; Perucchio, R. Roman Concrete Vaulting in the Great Hall of Trajan’s Markets: A Structural Evaluation. J. Archit. Eng. 2012, 18, 332–340. [Google Scholar] [CrossRef]
- Castellazzi, G.; Altri, A.M.D.; Bitelli, G.; Selvaggi, I.; Lambertini, A. From Laser Scanning to Finite Element Analysis of Complex Buildings by Using a Semi-Automatic Procedure. Sensors 2015, 15, 18360–18380. [Google Scholar] [CrossRef]
- Erkal, A.; Ozhan, H.O. Value and vulnerability assessment of a historic tomb for conservation. Sci. World J. 2014, 2014, 357679. [Google Scholar] [CrossRef]
- Milani, G.; Casolo, S.; Naliato, A.; Tralli, A. Seismic assessment of a medieval masonry tower in northern Italy by limit, non-linear static and full dynamic analyses. Int. J. Archit. Herit. 2012, 6, 489–524. [Google Scholar] [CrossRef]
- Zvietcovich, F.; Castaneda, B.; Perucchio, R. 3D solid model updating of complex ancient monumental structures based on local geometrical meshes. Digit. Appl. Archaeol. Cult. Herit. 2014, 2, 12–27. [Google Scholar] [CrossRef]
- Kappos, A.J.; Penelis, G.G.; Drakopoulos, C.G. Evaluation of Simplified Models for Lateral Load Analysis of Unreinforced Masonry Buildings. ASCE J. Struct. Eng. 2002, 128, 890–897. [Google Scholar] [CrossRef]
- Nochebuena-Mora, E.; Mendes, N.; Lourenço, P.B.; Greco, F. Dynamic behavior of a masonry bell tower subjected to actions caused by bell swinging. Structures 2021, 34, 1798–1810. [Google Scholar] [CrossRef]
- Kyratsis, P.; Tzotzis, A.; Davim, J.P. A Comparative Study Between 2D and 3D Finite Element Methods in Machining. In 3D FEA Simulations in Machining; SpringerBriefs in Applied Sciences and Technology; Springer: Cham, Switzerland, 2023. [Google Scholar] [CrossRef]
- Pegon, P.; Pinto, A.V.; Géradin, M. Numerical modelling of stone-block monumental structures. Comput. Struct. 2001, 79, 2165–2181. [Google Scholar] [CrossRef]
- Peña, F.; Meza, M. Seismic Assessment of Bell Towers of Mexican Colonial Churches. Adv. Mater. Res. 2010, 133–134, 585–590. [Google Scholar] [CrossRef]
- Deng, J.; Shi, S.; Li, P.; Zhou, W.; Zhang, Y.; Li, H. Voxel r-cnn: Towards high performance voxel-based 3d object detection. In Proceedings of the AAAI Conference on Artificial Intelligence, Online, 11–15 October 2021; Volume 35, pp. 1201–1209. [Google Scholar]
- Bitelli, G.; Castellazzi, G.; D’Altri, A.M.; De Miranda, S.; Lambertini, A.; Selvaggi, I. Automated Voxel Model from Point Clouds for Structural Analysis of Cultural Heritage. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2016, 41, 191–197. [Google Scholar] [CrossRef]
- Doğan, S.; Güllü, H. Multiple methods for voxel modeling and finite element analysis for man-made caves in soft rock of Gaziantep. Bull. Eng. Geol Environ. 2022, 81, 23. [Google Scholar] [CrossRef]
- Karanikoloudis, G.; Lourenço, P.B.; Alejo, L.E.; Mendes, N. Lessons from Structural Analysis of a Great Gothic Cathedral: Canterbury Cathedral as a Case Study. Int. J. Archit. Herit. 2021, 15, 1765–1794. [Google Scholar] [CrossRef]
- Shapiro, V.; Tsukanov, I. Mesh free simulation of deforming domains. CAD Comput. Aided Des. 1999, 31, 459–471. [Google Scholar] [CrossRef]
- Bagnéris, M.; Cherblanc, F.; Bromblet, P.; Gattet, E.; Gügi, L.; Nony, N.; Mercurio, V.; Pamart, A. A complete methodology for the mechanical diagnosis of statue provided by innovative uses of 3D model. Application to the imperial marble statue of Alba-la-Romaine (France). J. Cult. Herit. 2017, 28, 109–116. [Google Scholar] [CrossRef]
- Freytag, M.; Shapiro, V.; Tsukanov, I. Finite element analysis in situ. Finite Elem. Anal. Des. 2011, 47, 957–972. [Google Scholar] [CrossRef]
- Oreni, D.; Brumana, R.; Cuca, B. Towards a methodology for 3D content models: The reconstruction of ancient vaults for maintenance and structural behaviour in the logic of BIM management. In Proceedings of the 18th International Conference on Virtual Systems and Multimedia, Milan, Italy, 2–5 September 2012; pp. 475–482. [Google Scholar] [CrossRef]
- Barazzetti, L.; Banfi, F.; Brumana, R.; Gusmeroli, G.; Previtali, M.; Schiantarelli, G. Cloud-to-BIM-to-FEM: Structural simulation with accurate historic BIM from laser scans. Simul. Model. Pract. Theory 2015, 57, 71–87. [Google Scholar] [CrossRef]
- Bommes, D.; Zimmer, H.; Kobbelt, L. Mixed-integer quadrangulation. ACM Trans. Graph. 2009, 28, 77:1–77:10. [Google Scholar] [CrossRef]
- Gonizzi Barsanti, S.; Guagliano, M.; Rossi, A. 3D Reality-Based Survey and Retopology for Structural Analysis of Cultural Heritage. Sensors 2022, 22, 9593. [Google Scholar] [CrossRef]
- Tomasi, C.; Manduchi, R. Bilateral filtering for gray and color images. In Proceedings of the Sixth International Conference on Computer Vision, Bombay, India, 4–7 January 1998; pp. 839–846. [Google Scholar]
- Chen, H.; Shen, J. Denoising of point cloud data for computer-aided design, engineering, and manufacturing. Eng. Comput. 2018, 34, 523–541. [Google Scholar] [CrossRef]
- Digne, J.; Franchis, C.D. The bilateral filter for point clouds. Image Process. Online 2017, 7, 278–287. [Google Scholar] [CrossRef]
- He, K.; Sun, J.; Tang, X. Guided image filtering. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1397–1409. [Google Scholar] [CrossRef] [PubMed]
- Han, X.; Jin, J.S.; Wang, M.; Jiang, W. Guided 3D point cloud filtering. Multimed. Tool Appl. 2018, 77, 17397–17411. [Google Scholar] [CrossRef]
- Irfan, M.A.; Magli, E. Exploiting color for graph-based 3d point cloud denoising. J. Vis. Commun. Image Represent. 2021, 75, 103027. [Google Scholar] [CrossRef]
- Dinesh, C.; Cheung, G.; Bajíc, I.V. Point cloud denoising via feature graph Laplacian regularization. IEEE Trans. Image Process. 2020, 29, 4143–4158. [Google Scholar] [CrossRef]
- Xu, Z.; Foi, A. Anisotropic denoising of 3D point clouds by aggregation of multiple surface-adaptive estimates. IEEE Trans. Vis. Comput. Graph. 2021, 276, 2851–2868. [Google Scholar] [CrossRef]
- Rakotosaona, M.J.; La Barbera, V.; Guerrero, P.; Mitra, N.J.; Ovsjanikov, M. Pointcleannet: Learning to denoise and remove outliers from dense point clouds. Comput. Graph. Forum 2021, 39, 185–203. [Google Scholar] [CrossRef]
- Shitong, L.; Hu, W. Score-based point cloud denoising. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 4563–4572. [Google Scholar]
- Sun, J.; Ji, Y.M.; Wu, F.; Zhang, C.; Sun, Y. Semantic-aware 3D-voxel CenterNet for point cloud object detection. Comput. Electr. Eng. 2022, 98, 107677. [Google Scholar] [CrossRef]
- He, C.; Li, R.; Li, S.; Zhang, L. Voxel set transformer: A set-to-set approach to 3d object detection from point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 8417–8427. [Google Scholar]
- Mahmoud, A.; Hu, J.S.; Waslander, S.L. Dense voxel fusion for 3D object detection. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–7 January 2023; pp. 663–672. [Google Scholar]
- Shrout, O.; Ben-Shabat, Y.; Tal, A. GraVoS: Voxel Selection for 3D Point-Cloud Detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 21684–21693. [Google Scholar]
- He, C.; Zeng, H.; Huang, J.; Hua, X.S.; Zhang, L. Structure Aware Single-Stage 3D Object Detection from Point Cloud. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 11870–11879. [Google Scholar]
- Lv, C.; Lin, W.; Zhao, B. Voxel Structure-Based Mesh Reconstruction From a 3D Point Cloud. IEEE Trans. Multimed. 2022, 24, 1815–1829. [Google Scholar] [CrossRef]
- Sas, A.; Ohs, N.; Tanck, E.; van Lenthe, G.H. Nonlinear voxel-based finite element model for strength assessment of healthy and metastatic proximal femurs. Bone Rep. 2020, 12, 100263. [Google Scholar] [CrossRef] [PubMed]
- Lee, T.Y.; Weng, T.L.; Lin, C.H.; Sun, Y.N. Interactive voxel surface rendering in medical applications. Comput. Med. Imaging Graph. 1999, 23, 193–200. [Google Scholar] [CrossRef] [PubMed]
- Han, G.; Li, J.; Wang, S.; Wang, L.; Zhou, Y.; Liu, Y. A comparison of voxel- and surface-based cone-beam computed tomography mandibular superimposition in adult orthodontic patients. J. Int. Med. Res. 2021, 49, 300060520982708. [Google Scholar] [CrossRef] [PubMed]
- Goto, M.; Abe, O.; Hagiwara, A.; Fujita, S.; Kamagata, K.; Hori, M.; Aoki, S.; Osada, T.; Konishi, S.; Masutani, Y.; et al. Advantages of Using Both Voxel- and Surface-based Morphometry in Cortical Morphology Analysis: A Review of Various Applications, Magnetic Resonance. Med. Sci. 2022, 21, 41–57. [Google Scholar] [CrossRef]
- Sapozhnikov, S.B.; Shchurova, E.I. Voxel and Finite Element Analysis Models for Ballistic Impact on Ceramic-polymer Composite Panels. Procedia Eng. 2017, 206, 182–187. [Google Scholar] [CrossRef]
- Cakir, F.; Kucuk, S. A case study on the restoration of a three-story historical structure based on field tests, laboratory tests and finite element analyses. Structures 2022, 44, 1356–1391. [Google Scholar] [CrossRef]
- Gonizzi Barsanti, S.; Marini, M.R.; Malatesta, S.G.; Rossi, A. A Study of Denoising Algorithm on Point Clouds: Geometrical Effectiveness in Cultural Heritage Analysis. In ICGG 2024, Proceedings of the 21st International Conference on Geometry and Graphics. ICGG 2024. Lecture Notes on Data Engineering and Communications Technologies; Takenouchi, K., Ed.; Springer: Cham, Switzerland, 2025; Volume 218. [Google Scholar] [CrossRef]
- Baert, J. Cuda Voxelizer: A Gpu-Accelerated Mesh Voxelizer. 2017. Available online: https://github.com/Forceflow/cuda_voxelizer (accessed on 6 February 2025).
- Zhou, Q.Y.; Park, J.; Koltun, V. Open3D: A modern library for 3D data processing. arXiv 2018, arXiv:1801.09847. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).