A Novel Model for Accurate Daily Urban Gas Load Prediction Using Genetic Algorithms
Abstract
1. Introduction
1.1. Background
1.2. Literature Review
1.3. Contributions
- (1)
- The establishment and integration of a multiple weather parameter (MWP) prediction framework that incorporates cumulative temperature, solar radiation, wind speed, and building foundation temperature breaks through the simplification limitations of traditional single variable models and captures the complex coupling relationship between environmental factors and gas demand. The results show that the maximum relative error of the model prediction was 8.2%, and the mean absolute percentage error (MAPE) was 2.68%, effectively depicting the load fluctuation characteristics driven by multiple factors.
- (2)
- Based on the MWP, the effects of cumulative temperature, solar radiation, wind power, and building foundation temperature on the daily gas load were considered, and the coefficients of cumulative temperature, solar radiation. and wind power were modified to change the STD value. This mechanism enhanced the model’s adaptability to temperature changes in different seasons and between day and night. In scenarios of extreme sudden drops in temperature, the maximum deviation between the predicted value and the actual value always remained at a relatively low level. It significantly improved the model’s response ability to sudden load changes.
- (3)
- Taking a city as the research object, the MWP-DLP model was established, and the genetic algorithm was used to predict and solve the daily gas load. The initial population size was 60, with 1100 iterations. GA optimization converged the model variance to 5379, and the prediction accuracy was significantly improved compared with traditional methods. Finally, the accuracy of the model was verified by the measured data.
1.4. Paper Organization
2. Influencing Factors of City Gas Daily Load
2.1. Air Temperature
2.2. Solar Radiation
2.3. Holidays
3. Mathematic Model
3.1. Establishment of MWP-DLP Model
3.2. Solving of the MWP-DLP Model
3.2.1. Basic Data
3.2.2. Solving Process
- (1)
- Population Initialization: Randomly generate an initial set of solutions (individuals) within the problem’s solution space. Each individual is encoded (commonly using binary or real-number encoding), and the collection of all individuals forms the population.
- (2)
- Fitness Evaluation: Define a fitness function to measure the quality of each individual. A higher fitness value indicates a better solution tailored to the problem.
- (3)
- Selection Operation: Based on fitness values, select individuals from the current population as parents for the next generation. Common selection methods include roulette wheel selection and tournament selection, prioritizing individuals with higher fitness.
- (4)
- Crossover Operation: Combine the selected parent individuals to generate offspring. This mimics biological recombination by exchanging genetic segments (e.g., binary bits or real-number parameters) between parents, creating new trait combinations in offspring.
- (5)
- Mutation Operation: Introduce small random changes to offspring individuals to maintain population diversity. Mutation simulates genetic mutations, altering specific bits or parameters in the encoding to explore new solutions.
- (6)
- Replacement Operation: Replace part of the current population with newly generated offspring, forming a new population for the next iteration.
- (7)
- Termination Check: Determine if the termination condition is met (e.g., maximum iterations, converged fitness value). If satisfied, the algorithm ends and outputs the optimal solution; otherwise, return to Step 2 for further iteration.
3.2.3. Solution Result
4. Case Analysis
4.1. Results Analysis
- (1)
- Comparative analysis of predicted value and actual value
- (2)
- Change trend analysis
4.2. Error Analysis
4.3. Case Verification
4.4. Comprehensive Evaluation of Prediction Performance
5. Conclusions
- (1)
- In the research of daily gas load prediction, the influence of the dynamic change of building foundation temperature on daily gas load should be fully considered, which becomes the key breakthrough point to improve the prediction accuracy. Through in-depth analysis of the internal relationship between temperature fluctuation and gas consumption, the coefficients of key environmental factors, such as cumulative temperature, solar radiation, and wind power, were carefully corrected, and the MWP-DLP model was successfully constructed.
- (2)
- In order to obtain the optimal solution of MWP-DLP model, the genetic algorithm was used for deep optimization. The genetic algorithm, with its powerful global search ability, is constantly iteratively optimized in complex solution space. The MWP-DLP model was successfully solved after 1100 carefully set iterations. In order to verify the reliability of the model, city data with typical climate characteristics and energy consumption patterns were selected as control samples. The city’s geographical environment, climatic conditions, and urban energy consumption characteristics made it an ideal case to test the performance of the model.
- (3)
- By analyzing the data of a city in detail, the daily gas load predicted by the MWP-DLP model was compared with the actual value. The results show that the variation trends of the two were basically consistent, which fully indicates that the strategy of considering variable building base temperature and modifying cumulative temperature, solar radiation, and wind coefficient can significantly improve the prediction accuracy of daily gas load. In the error analysis, the maximum error value of the model was 12 × 104 m3, the maximum relative error was −8.2%, and the mean absolute percentage error (MAPE) was 2.68%. Such a low error range strongly proves that the established MWP-DLP model not only has good feasibility and can run effectively in practical applications but also has high effectiveness and can provide a reliable decision-making basis for gas supply management.
- (4)
- The prediction model constructed in this study not only realizes the high-precision prediction of short-term gas load but also provides technical support for the adjustment of energy structure. The quantitative analysis of the dynamic relationship between meteorological factors and load can optimize the cooperative scheduling of natural gas and renewable energy and promote the cross-season storage and efficient utilization of intermittent energy, such as wind power and photovoltaic. In view of the increase in baseline load caused by urban population growth, the model can include slow-changing variables such as population and industry in the future to provide cross-time scale support for gas infrastructure planning and alleviate the contradiction between supply and demand of limited resources. In the long run, the model’s accurate capture of extreme weather load mutations also lays a foundation for the assessment of peak load balancing capacity of alternative energy sources, such as hydrogen energy, and promotes the transformation of the energy system to a diversified and sustainable one.
- (5)
- Although this study improves the prediction accuracy by combining weather variables and genetic algorithm, there are still limitations in the characterization of complex load models by linear models. In the future, nonlinear models such as gradient lift tree and long and short-term memory network can be explored to build a multi-modal fusion forecasting framework combining non-weather variables such as residents’ gas consumption habits, the industrial production index, and natural gas price fluctuations.
- (6)
- The current model is designed for single urban climate characteristics and building energy consumption characteristics, and its core parameters have strong regional dependence. Future studies can focus on the adaptability verification of cross-regional climate zones and combine the differences of building types and energy structures in different cities to build dynamic parameter calibration models based on spatial and temporal differentiation (Supplementary Materials).
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, F.; Zheng, H.; Li, X.; Yang, F. Day-ahead city natural gas load forecasting based on decomposition-fusion technique and diversified ensemble learning model. Appl. Energy 2021, 303, 117623. [Google Scholar] [CrossRef]
- Peng, J.; Zhou, J.; Liang, G.; Li, C.; Qin, C. Multi-period integrated scheduling optimization of complex natural gas pipeline network system with underground gas storage to ensure economic and environmental benefits. Energy 2024, 302, 131837. [Google Scholar] [CrossRef]
- Wen, K.; Qiao, D.; Nie, C.; Lu, Y.; Wen, F.; Zhang, J.; Miao, Q.; Gong, J.; Li, C.; Hong, B. Multi-period supply and demand balance of large-scale and complex natural gas pipeline network: Economy and environment. Energy 2023, 264, 126104. [Google Scholar] [CrossRef]
- China Natural Gas Development Report; Petroleum Industry Press: Beijing, China, 2020.
- Distributed Energy Research Report; China Energy Network Research Center: Beijing, China, 2020.
- China Natural Gas Development Report; National Energy Administration: Beijing, China, 2024.
- China City Gas Development Report; National Energy Administration: Beijing, China, 2024.
- Peng, S.; Chen, R.; Yu, B.; Xiang, M.; Lin, X.; Liu, E. Daily natural gas load forecasting based on the combination of long short term memory, local mean decomposition, and wavelet threshold denoising algorithm. J. Nat. Gas Sci. Eng. 2021, 95, 104175. [Google Scholar] [CrossRef]
- Ma, D.; Wu, R.; Li, Z.; Cen, K.; Gao, J.; Zhang, Z. A new method to forecast multi-time scale load of natural gas based on augmentation data-machine learning model. Chin. J. Chem. Eng. 2022, 48, 166–175. [Google Scholar] [CrossRef]
- Zhou, C. The Voltage and Reactive Power Load Forecasting Control Based on Cluster Analysis and Fuzzy RBF Neural Network. Master’s Thesis, School of Electrical Engineering and Automation, Tianjin University, Tianjin, China, 2007. [Google Scholar]
- Wei, N.; Li, C.; Duan, J.; Liu, J.; Zeng, F. Daily natural gas load forecasting based on a hybrid deep learning model. Energies 2019, 12, 218. [Google Scholar] [CrossRef]
- Peng, J.; Bu, H.; Chen, H.; Lang, X.; Ma, J.; Zheng, F. National climate trend outlook from summer 2016 to spring 2017. Proc. Chin. Acad. Sci. 2016, 31, 830–834. [Google Scholar]
- Guo, L. Research and Development of LSTM Urban Gas Load Forecasting Technology. Master’s Thesis, Xi’an Shiyou University, Xi’an, China, 2020. [Google Scholar]
- Qian, H.; Yu, H.; Fan, G. A gas consumption prediction method based on incremental random forest regression algorithm. J. East China Univ. Sci. Technol. 2019, 45, 133–139. [Google Scholar]
- Zeng, B.; Meng, W.; Tong, M. A self-adaptive intelligence greypredictive model with alterable structure and its application. Eng. Appl. Artif. Intell. 2016, 50, 236–244. [Google Scholar] [CrossRef]
- Akkurt, M.; Demirel, O.F.; Zaim, S. Forecasting Turkey’s natural gas consumption by using time series methods. Eur. J. Econ. Political Stud. 2010, 3, 1–21. [Google Scholar]
- Akpinar, M.; Yumusak, N. Year ahead demand forecast of city natural gas using seasonal time series methods. Energies 2016, 9, 727. [Google Scholar] [CrossRef]
- Herbert, J.H.; Sitzer, S.; Eades-Pryor, Y. A statistical evaluation of aggregate monthly industrial demand for natural gas in the USA. Energy 1987, 12, 1233–1238. [Google Scholar] [CrossRef]
- Erdogdu, E. Natural gas demand in Turkey. Apply. Energy 2010, 87, 211–219. [Google Scholar]
- Melikoglu, M. Vision 2023: Forecasting Turkey’s natural gas demand between 2013 and 2030. Renew. Sustain. Energy Rev. 2013, 22, 393–400. [Google Scholar] [CrossRef]
- Zeng, B.; Li, C. Forecasting the natural gas demand in china using a self-adapting intelligent grey model. Energy 2016, 112, 810–825. [Google Scholar] [CrossRef]
- Ma, X.; Xie, M.; Wu, W.Q.; Zeng, B.; Wang, Y.; Wu, X.X. The novel fractional discrete multivariate grey system model and its applications. Appl. Math. Model. 2019, 70, 402–424. [Google Scholar] [CrossRef]
- Jiao, W.; Zhan, C.; Lian, L.; Yan, M. Research on short-term load forecasting of city gas. Gas Heat 2001, 6, 483–487. [Google Scholar]
- Jiao, W.; Lian, L.; Cui, J.; Yan, M. A time series model for short-term cycle load forecasting of city gas. Nat. Gas Ind. 2002, 1, 92–94. [Google Scholar]
- Jiao, W.; Zhao, L.; Qim, Y. Research on periodicity of hourly gas load for city gas. Gas Heat 2003, 9, 515–518. [Google Scholar]
- Hong, T.; Wang, P. Fuzzy interaction regression for short term load forecasting. Fuzzy Optim. Decis. Mak. 2014, 13, 91–103. [Google Scholar] [CrossRef]
- Hasan, H.C.; Mehmet, C. Short-term load forecasting using fuzzy logic and ANFIS. Neural Comput. Appl. 2015, 26, 1355–1367. [Google Scholar]
- Aly, H.H.H. A proposed intelligent short-term load forecasting hybrid models of ANN, WNN and KF based on clustering techniques for smart grid. Electr. Power Syst. Res. 2020, 182, 106191. [Google Scholar] [CrossRef]
- Kumar, U.; Jain, V.K. Time series models (Grey-Markov, Grey Model with rolling mechanism and singular spectrum analysis) to forecast energy consumption in India. Energy 2010, 35, 1709–1716. [Google Scholar] [CrossRef]
- Zhu, L.; Li, M.S.; Wu, Q.H.; Jiang, L. Short-term natural gas demand prediction based on support vector regression with false neighbours filtered. Energy 2015, 80, 428–436. [Google Scholar] [CrossRef]
- Khan, G.M.; Zafari, F. Dynamic feedback neuro-evolutionary networks for forecasting the highly fluctuating electrical loads. Genet. Program. Evolvable Mach. 2016, 17, 391–408. [Google Scholar] [CrossRef]
- Lu, H.F.; Azimi, M.; Iseley, T. Short-term load forecasting of urban gas using a hybrid model based on improved fruit fly optimization algorithm and support vector machine. Energy Rep. 2019, 11, 666–667. [Google Scholar] [CrossRef]
- Lin, B.Q.; Wang, T. Forecasting natural gas supply in China: Production peak and import trends. Energy Policy 2012, 49, 225–233. [Google Scholar] [CrossRef]
- Peng, S. Methods of city gas load forecasting and their analysis. J.-Chongqing Jian Zhu Univ. 2005, 27, 137. [Google Scholar]
- Xu, P.; Song, Y.; Du, J.; Zhang, F. Town gas daily load forecasting based on machine learning combinatorial algorithms: A case study in North China. Chin. J. Chem. Eng. 2024, 75, 239–252. [Google Scholar] [CrossRef]
- Ni, X.; Yang, D.; Qin, J.; Wang, X. A multivariate natural gas load forecasting method based on residual recurrent neural network. Electron. Lett. 2023, 59, e12927. [Google Scholar] [CrossRef]
- Gu, T.; Luo, Y.; Zhang, Q.; Zhu, Z. Research on gas load forecasting of Hangzhou based on meteorological factors. J. Meteorol. Environ. 2017, 33, 107–112. [Google Scholar]
- He, C.; Duan, Y.; Wu, Z.; Yang, G. A short-term forecasting model of city gas daily load based on air temperature. Nat. Gas Ind. 2013, 33, 131–134. [Google Scholar]
- Farfar, K.E.; Khadir, M.T. A two-stage short-term load forecasting approach using temperature daily profiles estimation. Neural Comput. Appl. 2019, 31, 3909–3919. [Google Scholar] [CrossRef]
- Li, Q.; Wu, Y. Forecast on daily gas load based on accumulative effect of temperature in winter: A case study of Xi’an. Oil Gas Storage Transp. 2016, 35, 1014–1017. [Google Scholar]
- Hu, X. Urban Gas Long-Term Load Forecasting Based on Competitiveness Evaluation. Master’s Thesis, Beijing University of Architecture, Beijing, China, 2018. [Google Scholar]
- Wang, G. Consumption law and load forecast of city natural gas. Gas Heat 2004, 24, 391–394. [Google Scholar]
- Ramon, D.; Allacker, K.; De Troyer, F.; Wouters, H.; Lipzig, N. Future heating and cooling degree days for Belgium under a high-end climate change scenario. Energy Build. 2020, 216, 109935. [Google Scholar] [CrossRef]
- Harvey, L.D.D. Using modified multiple heating-degree-day (HDD) and cooling-degree-day (CDD) indices to estimate building heating and cooling loads. Energy Build. 2020, 229, 110475. [Google Scholar] [CrossRef]
- National Grid. Gas Demand Forecasting Methodology. 2012. Available online: https://www.nationalgas.com/sites/default/files/documents/Gas%20Demand%20Forecasting%20Methodology%202020_v1.pdf (accessed on 30 May 2025).
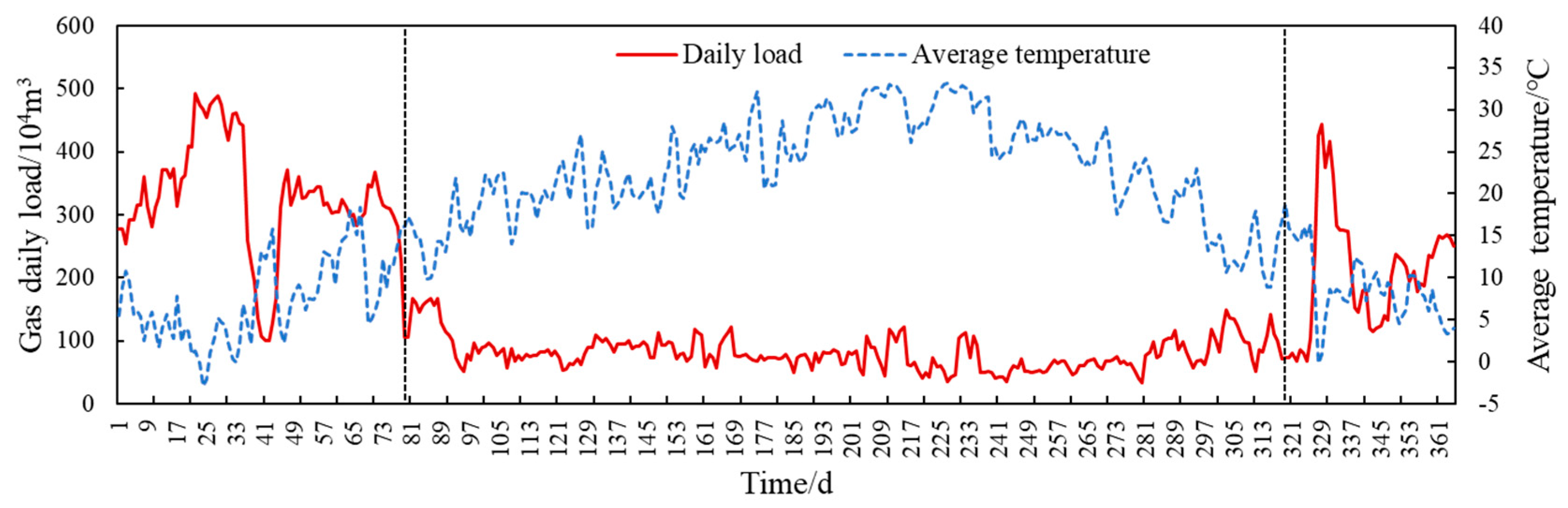

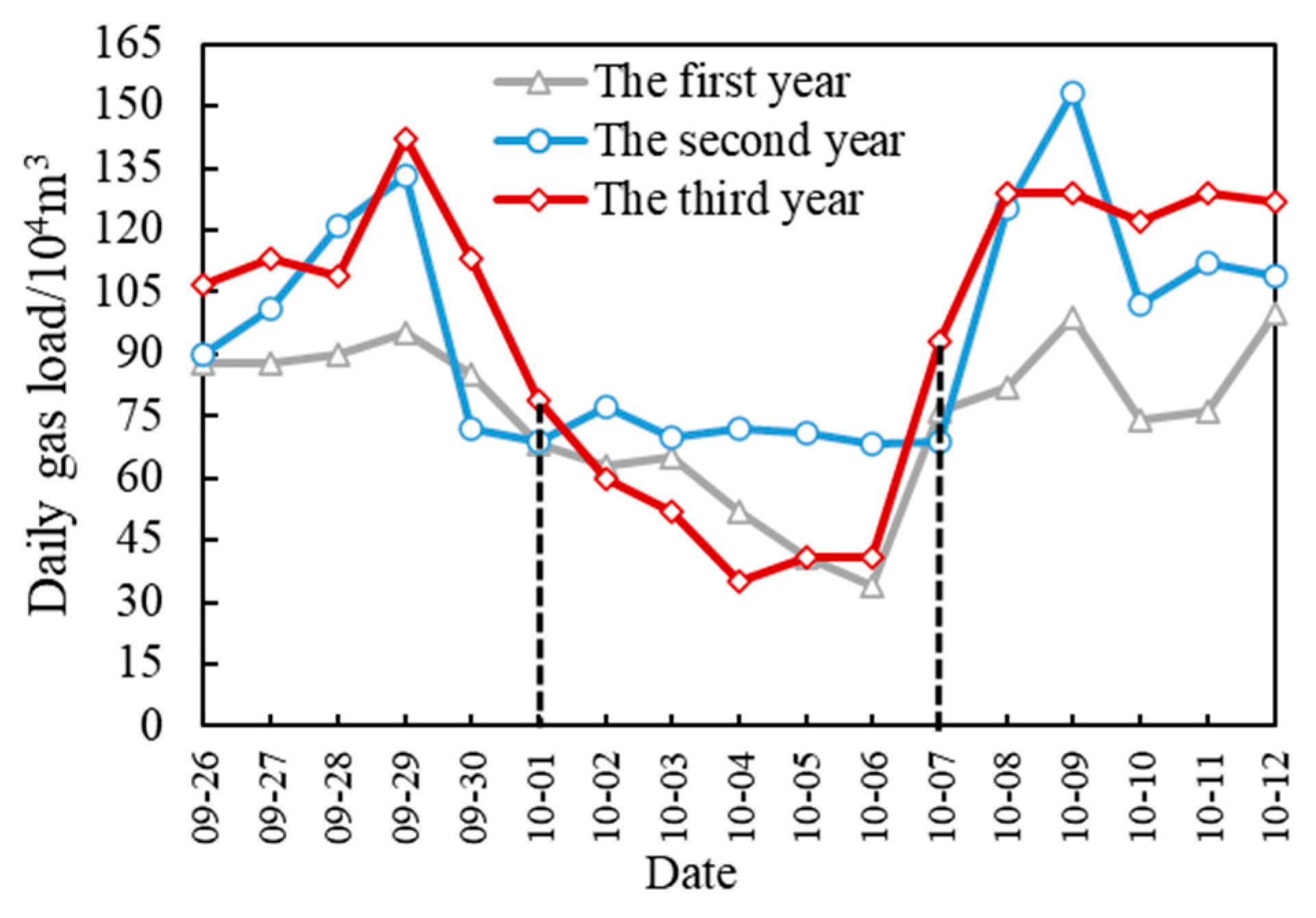







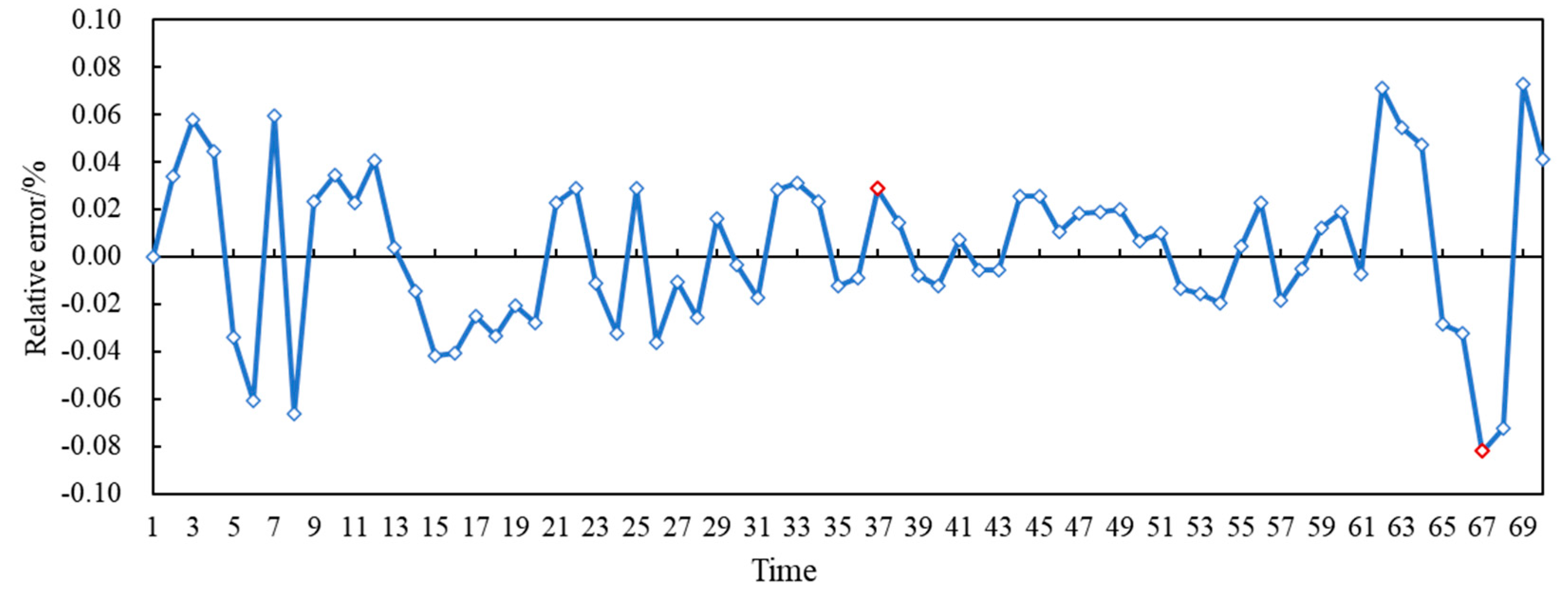
| Number | Date | Daily Load (104 m3) | Average Temperature (°C) | Average Temperature of the Previous Day (°C) | Cumulative Temperature (°C) | Wind (Section) | Solar Radiation (J/cm2) |
|---|---|---|---|---|---|---|---|
| 1 | First year-11-21 | 310 | 11.9 | 9.5 | 10.7 | 0.2 | 1664 |
| 2 | First year-11-22 | 245 | 3.8 | 15.8 | 9.8 | 13 | 869 |
| 3 | First year-11-23 | 425 | −0.6 | 3.8 | 1.6 | 13 | 308 |
| 4 | First year-11-24 | 443 | 1 | −0.6 | 0.2 | 4.9 | 309 |
| 5 | First year-11-25 | 374 | 5 | 1 | 3 | 0.2 | 581 |
| 6 | Second year-02-24 | 212 | 7.2 | 6.3 | 6.75 | 0.2 | 664 |
| 7 | Second year -02-27 | 65 | 10.8 | 9.6 | 10.2 | 0.2 | 1356 |
| 8 | Second year-02-28 | 64 | 11.1 | 10.8 | 11 | 4.9 | 1414 |
| 9 | Second year-03-01 | 74 | 12.2 | 11.1 | 11.7 | 18.3 | 1672 |
| Coefficient | Variance Sum | |||||||
|---|---|---|---|---|---|---|---|---|
| 100 | 69.1 | 19.2 | 0.100 | 0.095 | 0.3200 | 9.49 | 18.46 | 7167 |
| 500 | 94.9 | 22.6 | 0.010 | 0.010 | 0.1914 | 12.60 | 19.75 | 6168 |
| 700 | 99.6 | 23.3 | 0.041 | 0.002 | 0.1641 | 4.92 | 19.98 | 5632 |
| 1000 | 79.6 | 20.6 | 0.032 | 0.032 | 0.1914 | 12.83 | 18.99 | 5381 |
| 1100 | 79.6 | 20.6 | 0.032 | 0.032 | 0.1914 | 12.83 | 18.99 | 5381 |
| Number | Date | Actual Value (104 m3) | Predicted Value (104 m3) | Average Temperature (°C) | Solar Radiation (J/cm2) | Difference Value (104 m3) | Relative Error (%) |
|---|---|---|---|---|---|---|---|
| 5 | First year-11-21 | 310 | 300 | 11.9 | 1664 | 10 | 0.03 |
| 6 | First year-11-22 | 245 | 235 | 3.8 | 869 | 10 | 0.04 |
| 7 | First year-11-23 | 425 | 437 | −0.6 | 308 | 12 | −0.03 |
| 8 | First year-11-24 | 443 | 440 | 1 | 309 | 3 | 0.01 |
| 9 | First year-11-25 | 374 | 379 | 5 | 581 | −5 | −0.01 |
| 58 | Second year-02-24 | 212 | 220 | 7.2 | 664 | −8 | −0.04 |
| 59 | Second year -02-27 | 65 | 71 | 10.8 | 1356 | −6 | −0.09 |
| 60 | Second year -02-28 | 64 | 69 | 11.1 | 1414 | −5 | −0.08 |
| 61 | Second year -03-01 | 74 | 78 | 12.2 | 1672 | −4 | −0.05 |
| Number | Date | Daily Load (104 m3) | Average Temperature (°C) | Average Temperature of the Previous day (°C) | Cumulative Temperature (°C) | Wind (Section) | Solar Radiation (J/cm2) |
|---|---|---|---|---|---|---|---|
| 33 | Second year-12-29 | 290 | 8.4 | 8.7 | 8.55 | 0.2 | 680 |
| 34 | Third year-01-03 | 301 | 3.3 | 7.2 | 5.25 | 13 | 592 |
| 35 | Third year-01-04 | 321 | −0.1 | 3.3 | 1.6 | 0.2 | 265 |
| 36 | Third year-01-05 | 330 | −0.7 | −0.1 | −0.4 | 0.2 | 274 |
| 37 | Third year-01-08 | 421 | −0.4 | −0.7 | 0.2 | 13 | 264 |
| 65 | Third year-03-08 | 248 | 5.8 | 5.6 | 5.7 | 0.2 | 1299 |
| 66 | Third year-03-09 | 248 | 6.7 | 5.8 | 6.25 | 4.9 | 1415 |
| 67 | Third year-03-12 | 134 | 14.2 | 13.8 | 14 | 4.9 | 1858 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Wang, F.; Xu, L.; Xia, T.; Wang, M.; Chen, G.; Chen, L.; Zhou, J. A Novel Model for Accurate Daily Urban Gas Load Prediction Using Genetic Algorithms. Algorithms 2025, 18, 347. https://doi.org/10.3390/a18060347
Chen X, Wang F, Xu L, Xia T, Wang M, Chen G, Chen L, Zhou J. A Novel Model for Accurate Daily Urban Gas Load Prediction Using Genetic Algorithms. Algorithms. 2025; 18(6):347. https://doi.org/10.3390/a18060347
Chicago/Turabian StyleChen, Xi, Feng Wang, Li Xu, Taiwu Xia, Minhao Wang, Gangping Chen, Longyu Chen, and Jun Zhou. 2025. "A Novel Model for Accurate Daily Urban Gas Load Prediction Using Genetic Algorithms" Algorithms 18, no. 6: 347. https://doi.org/10.3390/a18060347
APA StyleChen, X., Wang, F., Xu, L., Xia, T., Wang, M., Chen, G., Chen, L., & Zhou, J. (2025). A Novel Model for Accurate Daily Urban Gas Load Prediction Using Genetic Algorithms. Algorithms, 18(6), 347. https://doi.org/10.3390/a18060347





