Abstract
Background: High in-domain accuracy in healthcare machine learning (ML) models does not guarantee reliable clinical performance, especially when training and validation protocols are insufficiently robust. This paper presents a standardized framework for training and validating ML models intended for classifying medical conditions, emphasizing the need for clinically relevant evaluation metrics and external validation. Methods: We apply this framework to a case study in knee osteoarthritis grading, demonstrating how overfitting, data leakage, and inadequate validation can lead to deceptively high accuracy that fails to translate into clinical reliability. In addition to conventional metrics, we introduce composite clinical measures that better capture real-world utility. Results: Our findings show that models with strong in-domain performance may underperform on external datasets, and that composite metrics provide a more nuanced assessment of clinical applicability. Conclusions: Standardized training and validation protocols, together with clinically oriented evaluation, are essential for developing ML models that are both statistically robust and clinically reliable across a range of medical classification tasks.
1. Introduction
Machine Learning (ML) models have been a topic of interest in medical diagnostics since the late 20th century, primarily due to their potential to assist clinicians in detecting diseases and predicting patient outcomes [1,2,3,4,5,6]. Over the decades, advancements in computational power and the advent of deep learning architectures, such as convolutional neural networks (CNNs) and transformers [7,8], have significantly accelerated research in this field [9]. These models promise to transform healthcare, with applications ranging from medical imaging analysis [10,11], like detecting tumors in X-rays and MRIs [12,13,14], to predicting patient outcomes based on electronic health records (EHR) [15,16,17,18,19]. Recent frameworks have enhanced this capability through temporal learning with dynamic range features and transfer learning techniques that leverage large observational EHR databases [20]. Many recent studies report exceptional accuracy and precision, boasting metrics that often surpass human-level performance in specific diagnostic tasks. For instance, CNN-based models trained on large datasets have demonstrated specificities and accuracies of over 90% in tasks such as breast cancer detection from mammograms [21], or diabetic retinopathy diagnosis from fundus images [22]. These numbers have garnered attention and optimism within the medical community and beyond. AI implementation in medical imaging is demonstrably linked to enhanced efficiency, with roughly two-thirds of studies reporting improvements [23], yet meta-analyses reveal that its benefits vary widely across different applications [24]. Moreover, while many studies note reduced processing times, a significant number also disclose conflicts of interest that could bias study design or outcome estimation [25]. Moreover, these impressive results can be misleading. In many cases, the reported accuracy and precision do not necessarily reflect a model’s clinical utility. A closer look often reveals significant methodological issues.
A critical issue in the development of ML models for medical diagnostics is overfitting to test sets. This occurs when a model becomes excessively tailored to the specific data it was trained and validated on, leading to inflated performance metrics that do not reflect its ability to generalize to new, unseen data. In many studies, models are evaluated on the same datasets used during development or on overly similar validation sets, which results in a performance boost that can create a false sense of accuracy and precision. This practice, known as data leakage, occurs when there is too much overlap between training and testing data, or when the data is not sufficiently diversified to represent real-world variability.
While high accuracy on the training and test datasets may seem promising, it does not guarantee that the model will perform equally well in clinical environments where the data may differ significantly from the training set. Testing the model on entirely unseen datasets, sourced from different hospitals, clinics, or imaging devices, is important for assessing the true generalizability of an ML model. Unfortunately, many studies neglect this critical step, limiting their findings to “in-domain” validation, which only tests the model on data from the same or very similar sources. As a result, performance metrics, such as accuracy and precision, may be misleading, failing to capture the true performance of the model in diverse real-world settings.
It is also understandable that obtaining relevant external data can be challenging or even impossible due to ethical, legal, or logistical constraints, as well as the inherent limitations in data availability across institutions. In many practical scenarios, researchers are compelled to work with limited external datasets, making comprehensive out-of-domain validation difficult. Nonetheless, as demonstrated in this article, the absence of adequate external data makes it even more pivotal to establish robust ML training protocols and to scrutinize the underlying learning dynamics. In particular, a close examination of learning curves, reflecting the model’s behavior during training and validation, can serve as an essential diagnostic tool. When learning curves behave as desired, with a close alignment between training and validation performance, there is greater assurance that the model has captured generalizable patterns; conversely, abnormal or “bad-behaving” learning curves can signal overfitting or data leakage, thus foreshadowing inferior performance on unseen external data. This emphasis on thorough training evaluation underscores the importance of reliable training practices and serves as an effective surrogate for external validation when such data is not readily available.
Recent literature has increasingly emphasized the importance of standardization and trust in the development and validation of AI models for healthcare. For example, Wierzbicki et al. provide a comprehensive review of approaches to standardizing medical descriptions for clinical entity recognition, highlighting the implications for AI implementation [26]. Arora et al. discuss the value of standardized health datasets in enabling robust AI-based applications [27], while Um et al. examine trust management from a standardization perspective [28]. These studies underscore the necessity of adopting standardized frameworks and data practices to ensure the reliability, generalizability, and clinical acceptance of ML models. Our work builds on these insights by proposing a validation methodology that not only aligns with these emerging standards but also addresses the specific challenges of clinical utility and external validation in real-world healthcare settings.
Aims, Contributions, and Organization
Recent advances in ML have led to a proliferation of studies reporting high accuracy in medical classification tasks; however, many of these models lack standardized validation and do not adequately reflect clinical utility when deployed beyond their development settings. This work addresses the specific challenge of bridging the gap between promising in-domain ML performance and the need for robust, clinically meaningful validation protocols that can ensure generalizability and regulatory alignment for real-world healthcare applications.
The primary goal of this article is to present a standardized validation framework for developing clinically actionable healthcare ML models, specifically demonstrated through the case study of knee osteoarthritis grading. Central to our approach is the integration of credibility assessment by analyzing training dynamics (e.g., learning curves and overfitting diagnostics) alongside traditional performance metrics, highlighting the necessity of protocols and evaluation methods that align model performance with true clinical utility and external validity. Our original contributions are threefold: (1) we synthesize and implement a practical, FDA-aligned validation framework applicable to real-world clinical ML workflows; (2) we propose and evaluate composite clinical utility metrics to capture clinically meaningful model performance; and (3) we demonstrate it with a case study on knee osteoarthritis grading, highlighting the importance of robust training assessment and clinically oriented evaluation for improving model generalizability and patient safety. The remainder of this article is organized as follows: Section 2 details the materials and methods, including the proposed validation framework and evaluation protocols; Section 3 presents experimental results, including in-domain and cross-domain validation; Section 4 discusses the clinical implications of our findings; and Section 5 summarizes the key insights and recommendations for future research and clinical practice.
2. Materials and Methods
2.1. Establishing Model Clinical Credibility Through Standardized Validation
Establishing clinical credibility in ML models requires following a validation framework that adheres to regulatory standards. The validation process encompasses five interconnected domains as illustrated in Figure 1: model description, data description, model training, model evaluation, and life-cycle maintenance. These components form a structured pathway for ensuring model reliability and clinical applicability in healthcare settings.
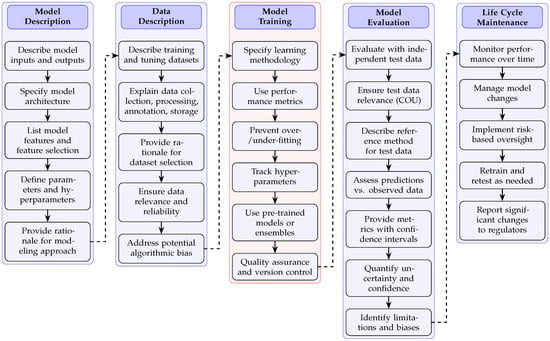
Figure 1.
Standardized validation framework for establishing and maintaining clinical credibility in healthcare machine learning models. The framework presents five interconnected domains (model description, data description, model training, model evaluation, and life-cycle maintenance) with sequential validation steps within each domain. Arrows indicate the logical progression within domains (solid lines) and dependencies between domains (dashed lines). This structured approach addresses critical FDA regulatory requirements for AI credibility assessment, ensuring comprehensive documentation of model development, rigorous evaluation with independent test data, and continuous performance monitoring throughout the model life cycle.
The model description phase establishes foundational elements by specifying model inputs, outputs, architecture, and parameter definitions. This transparency enables proper assessment of a model’s theoretical underpinnings and computational approach. The framework then progresses to data description, where training datasets undergo rigorous characterization to ensure relevance and reliability. Particular attention must be directed toward data collection methodologies, annotation processes, and potential sources of algorithmic bias that could compromise model performance across diverse patient populations.
Model training represents a critical validation component requiring detailed documentation of learning methodologies, performance metrics, and hyperparameter optimization. This documentation establishes computational reproducibility and enables independent verification of model development processes. As outlined in FDA guidance [29], training procedures should incorporate appropriate strategies to prevent overfitting while maintaining model generalizability across diverse clinical scenarios.
The model evaluation phase introduces stringent requirements for testing with independent datasets that were not utilized during development. This separation between training and testing data constitutes a fundamental validation principle that reveals a model’s true clinical utility. Models demonstrating high performance exclusively on development datasets yet failing with independent test data manifest what regulatory frameworks identify as deceptively high accuracy—signaling inadequate clinical validation. The evaluation process must include comprehensive metrics with confidence intervals, uncertainty quantification, and a systematic assessment of limitations and potential biases. Additionally, the careful consideration of sample size and statistical power is essential for meaningful clinical validation of ML models, as underscored by recent sample size analyses in the field [30].
Life-cycle maintenance completes the validation framework by establishing protocols for longitudinal performance monitoring, model updates, and risk-based oversight. This phase acknowledges the dynamic nature of clinical environments and ensures sustained model credibility through structured retraining procedures and regulatory reporting mechanisms. According to FDA guidance, models deployed in clinical settings require ongoing performance verification to maintain credibility as patient populations and clinical practices evolve.
In the context of Figure 1, the “Data Description” domain is pivotal for ensuring that the model is developed on datasets that are both representative and reliable for the intended clinical application. This step involves thorough documentation of the origin and characteristics of all datasets used in model development, including details about patient demographics, clinical diversity, acquisition protocols, and annotation standards. Specific attention is paid to data collection methodologies (e.g., multi-center versus single-center sourcing), data preprocessing and augmentation techniques, storage protocols, and the handling of missing or imbalanced data [31]. Annotation processes are described in terms of both the clinical expertise involved and the consistency of grading or labeling (for example, the use of standardized scales such as the Kellgren–Lawrence grading for osteoarthritis). Additionally, this domain requires a careful evaluation of potential sources of bias, such as class imbalance, sampling artifacts, or systematic differences between data sources, and mandates strategies for mitigating such biases to enhance fairness and generalizability. By systematically addressing these aspects, the “Data Description” domain provides the foundation for subsequent model training, evaluation, and regulatory credibility.
Thorough implementation of this standardized validation framework addresses key regulatory concerns regarding model credibility. By establishing the transparent documentation of model development, rigorous testing with independent data, and structured maintenance protocols, healthcare machine learning applications can progress from promising research tools to clinically validated decision support systems. The framework systematically mitigates risks associated with algorithmic bias, overfitting, and performance degradation while providing regulatory authorities with comprehensive evidence of model reliability for specific clinical contexts of use.
2.2. Beyond FDA Guidance
While our validation framework is explicitly aligned with recent FDA draft guidance on AI for drug and biological product regulation [29], its structure is intentionally designed for broad applicability across regulatory and best-practice contexts. The FDA’s approach, emphasizing transparency, rigorous evaluation, and continuous monitoring, reflects foundational principles also found in international standards. For example, the International Council for Harmonisation (ICH) Quality guidelines and the FDA’s Office of Pharmaceutical Quality both stress lif-ecycle management, risk-based oversight, and robust model and data control, highlighting the need for clear standards in areas like adaptive systems, data integrity, and cloud/edge computing [32,33].
These principles are echoed in the European Union’s Medical Device Regulation (EU MDR) [34], which mandates quality management, systematic risk assessment, clinical evaluation, and ongoing post-market surveillance for medical devices, including AI-based software. The EU MDR’s focus on traceability, transparency, and technical documentation closely aligns with our framework, supporting harmonization between US and EU regulatory expectations. The EU’s Artificial Intelligence Act [35] further strengthens this alignment by establishing a comprehensive, risk-based legal framework for high-risk AI systems, including those in healthcare. The Act requires strict risk management, data governance, technical documentation, transparency, human oversight, and continuous monitoring, directly mirroring our framework’s core domains. By embedding these requirements into law and complementing sectoral regulations like the EU MDR, the AI Act promotes regulatory convergence and cross-border trust.
Finally, the World Health Organization’s guidance on AI ethics and governance [36] reinforces the global relevance of these principles, calling for harmonized ethical, legal, and technical standards to ensure safety, equity, and public trust. Hence, our framework is consistent with both US and international regulatory expectations, supporting global adoption of best practices for trustworthy, clinically relevant AI validation in healthcare.
2.3. Comparison to Existing Validation Frameworks
Several validation frameworks for ML in healthcare have been proposed in recent years, including those recommended by regulatory bodies such as the FDA and detailed in the broader literature on clinical AI evaluation. These frameworks (such as the FDA’s Good Machine Learning Practice (GMLP) and the model reporting guidelines of MI-CLAIM and CONSORT-AI [37,38,39]) typically emphasize clear documentation of model development, data transparency, rigorous internal and external validation, and ongoing model monitoring. Our proposed framework builds upon these principles but addresses gaps by (i) providing a mathematically formalized approach for validation; (ii) integrating composite clinical utility metrics; and (iii) offering practical, stepwise guidance for model training, evaluation, and life-cycle maintenance tailored to real-world clinical needs. Unlike many prior frameworks, which may focus primarily on statistical metrics or narrative reporting, our approach prioritizes a clinically actionable assessment and robust mitigation with a deceptively high accuracy. As a result, our methodology offers a more comprehensive and practically implementable solution for healthcare ML model validation.
2.4. Standardized Validation Framework for Clinical Credibility
In order to address the issue of deceptively high accuracy in healthcare machine learning and to ensure reliable clinical applicability, a standardized model training framework (see Figure 1’s rectangle highlighted in red) is established following the recent FDA guidance [29]. The framework is designed to document and verify every aspect of model training and evaluation, thereby guaranteeing that performance metrics reflect true clinical utility rather than artifacts arising from specific data characteristics.
2.4.1. Specify Learning Methodology
The learning methodology is explicitly defined from preprocessing through model architecture. Let an input image be represented by
with , , and channels. The preprocessing function is defined as
where and are the channel-wise mean and standard deviation computed on the ImageNet dataset. This normalization ensures consistency when using the pre-trained VGG16 preprocessing function.
The VGG16 was selected for this study due to its well-established performance and interpretability in medical image analysis, as well as its availability as a robust, pre-trained backbone in most deep learning frameworks. While newer architectures such as ResNet and transformer-based models (e.g., Vision Transformers) often achieve higher performance on large-scale natural image benchmarks, VGG16 remains a strong baseline in medical imaging tasks, particularly when dataset size is limited and model transparency is a priority. Comparative studies in other biomedical domains have similarly shown that the choice of ML algorithm and architecture can substantially affect detection performance, highlighting the need for careful benchmarking and selection based on the specific clinical context [40].
Our primary goal was to establish a standardized validation framework and demonstrate the risks of deceptively high accuracy in a reproducible and interpretable setting, for which VGG16 is well suited. We applied ImageNet normalization to the input images to ensure compatibility with the pre-trained VGG16 weights. This approach is standard practice, as the initial convolutional layers of the network are sensitive to the input distribution; using the same normalization statistics as in pre-training allows optimal transfer learning and stable feature extraction from medical images, even though these images differ from natural images in content.
The primary model is implemented as a convolutional neural network (CNN) using the Keras framework. The network can be mathematically described as a function that approximates the mapping from the preprocessed input to a vector of logits . The first fully connected layer applies a linear transformation followed by a nonlinear activation:
where and , with d representing the flattened dimensionality of the feature maps. A dropout layer is applied subsequently:
where indicates dropout with probability 0.5. The next dense layer is defined as
with and . Finally, the output layer employs a softmax function to generate probabilistic predictions for each of the five clinical classes:
where with appropriate dimensions for and . The loss function is given by the sparse categorical cross-entropy,
where N is the number of samples and is the true label for sample n. Training is performed for 20 epochs using a batch size , and the full dataset is partitioned with an 80/20 stratified split to ensure balanced representation of classes.
2.4.2. Use Performance Metrics
A broad range of performance metrics is computed to provide a comprehensive evaluation of the model. The overall accuracy is defined as
where is the indicator function. For each class , the precision and recall are calculated as follows:
The F1 score for class k is the harmonic mean of precision and recall:
Moreover, Cohen’s Kappa is computed to adjust for chance agreement:
where is the observed agreement and is the expected agreement calculated from the marginal probabilities of the classes. Furthermore, the Matthews Correlation Coefficient (MCC) is used as a robust measure even in imbalanced data conditions:
where , , , and denote the total true positives, true negatives, false positives, and false negatives, respectively.
2.4.3. Prevent Overfitting and Underfitting
To prevent overfitting and underfitting, learning curves are generated by tracking the model’s performance on both training and validation sets. Let and denote the training and validation loss at epoch t. The convergence criterion for early stopping is defined by
for k consecutive epochs, where is a small constant (e.g., ). In parallel, a 5-fold cross-validation scheme is implemented by partitioning the dataset D into five subsets . For each fold i, the model is trained on and validated on , and the mean validation loss is computed as
which ensures that the final model is robust to variations within the data. The choice of resampling and cross-validation methods can significantly impact the generalizability of ML models, especially in settings where spatial or domain-specific data structures are present, as demonstrated in recent studies [41].
2.4.4. Track Hyperparameters
Reproducibility is maintained by precisely tracking all hyperparameters. The main hyperparameters include the learning rate , dropout rate , number of epochs , and batch size . These values are recorded continuously via TensorBoard. Moreover, a grid search is performed over the hyperparameter space:
with the performance averaged over the cross-validation folds. All changes are managed using a Git-based version control system, thereby providing an audit trail and facilitating systematic, iterative tuning.
2.4.5. Use Pre-Trained Models or Ensembles
Enhancements to the training protocol include the adoption of pre-trained models and ensemble strategies. A pre-trained VGG16 network, denoted as , is employed as a fixed feature extractor such that for a given image X, the deep feature representation is
The classifier is then trained on these high-level features. In addition, ensemble methods combine the outputs of multiple models to reduce variance and improve generalizability. The final ensemble prediction is computed by
Such ensemble techniques help in mitigating biases that may arise from relying on a single model architecture.
2.4.6. Quality Assurance and Version Control
Quality assurance is integrated into every phase of development through automated testing and continuous integration. Let be a performance metric before a code update and after; then the change is acceptable if
where is a predetermined tolerance threshold. Scheduled code reviews and systematic audits are performed in accordance with regulatory standards [29]. All modifications are managed via a Git version control system, ensuring comprehensive traceability and compliance with clinical validation protocols. Recent work has highlighted the value of dedicated tool support for improving software quality and reproducibility in ML programs, which can further enhance the reliability of clinical ML pipelines [42].
By integrating these six methodological components, explicit learning specification, performance metrics, measures to prevent overfitting and underfitting, hyperparameter tracking, strategic use of pre-trained and ensemble methods, and quality assurance, the framework provides a mathematically based approach to transforming in-domain accuracy into clinically reliable and generalizable models. This systematic methodology is important for translating promising ML prototypes into trusted tools for clinical application.
2.5. Datasets
Two distinct datasets were processed using an identical training protocol, employing the same architecture, hyperparameters, and training procedures, with the only difference being the input data. The base neural network architecture and dataset preparation are similar to those described in our prior work [43], but the current study expands upon that work by introducing new composite performance metrics and a standardized evaluation protocol aligned with recent FDA guidance. Specifically, the model was trained on Dataset A and also, separately, on Dataset B, and each model was subsequently cross-tested on the alternate dataset to evaluate their performance on external data. Dataset A was acquired from Kaggle [44] and contains knee X-ray images labeled with Kellgren–Lawrence (KL) grades from 0 (healthy) to 4 (severe osteoarthritis). This dataset provides data for both knee joint detection and KL grading. The images have a balanced distribution across grades and were preprocessed to standardize resolution and orientation. Dataset B was obtained from Mendeley Data [45] and similarly comprises knee X-ray images with KL annotations (grades 0–4) following the same definitions as Dataset A. Including Dataset B allowed us to perform external validation and assess our model’s generalizability across different sources.
The selection of Datasets A and B was guided by the need to assess both the in-domain performance and the generalizability of the proposed model for knee osteoarthritis grading. Dataset A (Kaggle) was chosen due to its widespread use in benchmarking ML models for musculoskeletal radiographs and its balanced distribution of KL grades, which enables robust model training. Dataset B (Mendeley Data) was selected as an independent source to enable external validation, as it provides KL-graded knee X-rays collected separately from Dataset A, thus differing in imaging conditions, patient demographics, and potential annotation variability. Including two distinct, publicly available datasets ensures that our evaluation reflects real-world variability and addresses the critical issue of domain shift, thereby supporting a more clinically relevant assessment of model robustness and transferability.
2.6. Clinically Oriented Evaluation Protocol
The clinically oriented evaluation protocol is designed to bridge the gap between high statistical performance and the nuanced requirements of patient-centered healthcare. In this protocol, two composite metrics are defined that integrate standard performance measures with clinical priorities. These metrics are central to the clinically oriented evaluation framework and are used to both select and validate models in a manner that aligns with clinical decision making.
The first composite metric is the overall model score, which is defined as
where:
- is the Area Under the Receiver Operating Characteristic (ROC) Curve, computed bywith the True-Positive Rate (TPR) defined asand the False-Positive Rate (FPR) given by
- , which is equivalent to the TPR, quantifies the model’s ability to correctly detect positive cases.
- is defined asand reflects the model’s capacity to correctly identify negative cases.
- The weighting coefficients , , and are selected based on clinical priorities; for instance, in many healthcare applications, a higher weight is assigned to sensitivity to minimize the risk of missing a critical diagnosis.
For example, in cancer screening tasks such as mammography for breast cancer detection, prioritizing sensitivity is important to ensure that cases of malignancy are not missed, as a false negative could result in delayed treatment and adverse outcomes [21]. Similarly, in diabetic retinopathy screening, high sensitivity is often emphasized to minimize the risk of overlooking patients who require urgent ophthalmologic intervention [22]. These examples underscore why, in many healthcare applications, the weighting of sensitivity over other metrics is not only justified but necessary for patient safety.
Equation (20) is important in ML for healthcare because it integrates global discriminative performance (via AUC) with more clinically meaningful sensitivities and specificities. This combination ensures that a high overall score is achieved only when the model both discriminates well across classes and meets the clinical requirements for minimizing false negatives and false positives.
The second metric, referred to as the clinical utility score, is defined as
where the components are defined as follows:
Here, TPR is as defined in Equation (22).
Equation (25) is pivotal in healthcare ML because it consolidates three key aspects of clinical performance. By integrating PPV, NPV, and the F1 score, the equation directly correlates the algorithm’s predictions with outcomes that are of clinical importance. This is particularly critical in scenarios where the consequences of misclassification are high, and there is a need to balance the trade-offs between over-diagnosis and under-diagnosis.
Together, Equations (20) and (25) form a dual-layered evaluation framework. The first layer (Equation (20)) assesses the inherent discriminative power of the model while accounting for statistical robustness. The second layer (Equation (25)) translates statistical performance into clinically actionable insights by emphasizing the predictive values and balanced accuracy. This structured approach ensures that models not only achieve high performance metrics computationally but also translate effectively into real-world clinical environments by addressing the specific risks and rewards associated with medical diagnoses.
In summary, the clinical evaluation protocol leverages these equations to create a quantifiable standard for model assessment relevant to healthcare. By incorporating both statistical and clinical considerations, the protocol mitigates the risk of deceptively high accuracy that lacks clinical relevance and emphasizes the development of models that deliver robust, patient-centered decision support.
2.7. Weighted Confusion Matrix Utility Metric
In healthcare applications such as grading knee osteoarthritis severity, where classes range from 0 (healthy) to 4 (severe osteoarthritis), it is pivotal to emphasize accurate prediction of the endpoints, namely the healthy state and the severely affected state. Misclassifications that confuse healthy knees with osteoarthritic states or vice versa may lead to adverse clinical decisions. To address this concern, a novel metric is introduced, termed the Weighted Endpoint Accuracy Score (WEAS), for evaluating the usefulness of confusion matrices in multi-class classification tasks.
Let denote the -th element of the confusion matrix, corresponding to the number of instances with true class i predicted as class j. The per-class accuracy is defined as
where n is the highest classification index (i.e., in this study’s knee osteoarthritis example).
To reflect clinical priorities, a heavier weight w is assigned to the endpoint classes (i.e., classes 0 and n) and a weight of 1 to all intermediate classes (). The overall metric is computed as:
For instance, in the case of grading knee osteoarthritis (with ), choosing (or another clinically-motivated value) ensures that high accuracy in classifying a healthy knee (class 0) and a severely affected knee (class 4) substantially influences the overall metric. This metric is designed to capture the clinical utility of the model by highlighting performance in the most critical classification regions.
Furthermore, the metric can be extended to incorporate a misclassification penalty based on the distance between true and predicted classes. Let a penalty function be defined as
which imposes larger penalties for misclassifications that deviate further from the true class. A composite utility function can then be formulated as
with balancing the trade-off between the weighted endpoint accuracy and the overall misclassification cost.
By adopting the WEAS and its extensions, the proposed metric enhances the evaluation of machine learning models in healthcare settings, ensuring that models which excel in distinguishing clinically essential endpoints are favored, thereby better aligning performance measures with clinical decision-making requirements.
Summary of Notation
For clarity, we summarize below the notation and symbols used in Equations (29)–(32) and throughout the manuscript:
- : Element in the i-th row and j-th column of the confusion matrix, indicating the number of samples with true class i predicted as class j.
- n: Highest class index (e.g., for five classes labeled 0 to 4).
- : Per-class accuracy for class i.
- w: Weight assigned to endpoint classes ( and ) to emphasize their clinical importance; all other classes have weight 1.
- : Weighted Endpoint Accuracy Score, as defined in Equation (30).
- : Penalty function, defined as the absolute difference between true and predicted class.
- U: Composite utility function, combining and the misclassification penalty, as defined in Equation (32).
- : Trade-off parameter that balances the emphasis between and the misclassification penalty.
- ∑: All summations are taken over the specified class indices as indicated in the equations.
3. Results
As a reminder, a concise description of the model and training protocol utilized in this study are as follows. The model is a CNN implemented in Keras, based on a VGG16 backbone pre-trained on ImageNet. Input images were resized to pixels and normalized using ImageNet statistics. The classification head consists of two dense layers (1024 and 512 units, respectively, each followed by ReLU activation and dropout at ), ending with a five-unit softmax output corresponding to the KL grades. Training was performed for 20 epochs with a batch size of 32 and learning rate of 0.001, using sparse categorical cross-entropy loss and Adam optimizer. Stratified 80/20 splits ensured class balance, and all key hyperparameters were tracked and are available upon request. The model’s performance was evaluated using accuracy, Cohen’s Kappa, Matthews Correlation Coefficient, precision, recall, F1 score, and clinically oriented composite metrics as described above.
The following subsection examines a case study in which an ML model was independently trained on two distinct datasets using the same methodology. Although both training processes yielded confusion matrices with similar overall patterns of class distribution, the learning curves exhibited markedly different behaviors. One training instance produced learning curves that deviated from the expected pattern, suggesting issues such as potential overfitting or ineffective regularization. In contrast, the other instance displayed learning curves that progressed in a more stable and predictable manner. This discrepancy ultimately manifested in the model’s external performance, where the training exhibiting unfavorable learning dynamics corresponded to inferior results when evaluated on an external dataset. The subsections that follow detail the performance metrics from the within-dataset evaluations, the outcomes of the cross-dataset external testing, and an analysis of the learning curves, thereby linking training behavior to generalizability outcomes.
3.1. ML Model Trained on Two Datasets
The performance of CNN based on the Keras framework when it is trained and evaluated on two separate datasets (Dataset A and Dataset B) is presented as follows. Figure 2 shows two confusion matrices that detail the classification outcomes for each dataset. In these matrices, the rows denote the true class labels while the columns represent the predicted labels for a 5-class problem. This visualization helps to pinpoint where misclassifications occur and highlights which classes are most often confused by the model.
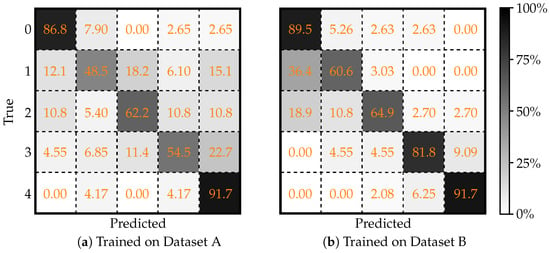
Figure 2.
Two confusion matrices, evaluated on (a) Dataset A, and (b) Dataset B, illustrating the performance of Keras framework in classifying knee X-ray images. Each matrix shows the true classifications (rows) versus the predicted classifications (columns). Adapted from [43].
Complementing the visual analysis, Table 1 summarizes a set of quantitative performance metrics including overall accuracy, Cohen’s Kappa, MCC, precision, recall, and F1 score. By comparing the metrics between Dataset A and Dataset B, one can observe that the model achieves improved performance on Dataset B, indicated by higher accuracy and better inter-class agreement, suggesting potential differences in data quality or inherent feature distinctiveness between the two datasets.

Table 1.
Performance metrics of the ML model trained and (in-domain) tested on Datasets A and B.
3.2. Cross-Dataset External Testing
To further evaluate the generalizability of this model, cross-dataset (i.e., external) testing was performed. In this scenario, the model trained on one dataset was tested on the other to expose its resilience against domain shifts. Figure 3 presents the confusion matrices obtained under these conditions. Figure 3a displays the confusion matrix when the model trained on Dataset A is tested on Dataset B, while Figure 3b shows the matrix for the case where the model trained on Dataset B is evaluated using data from Dataset A. These cross-dataset comparisons help to understand how variations in data distributions can affect model predictions.
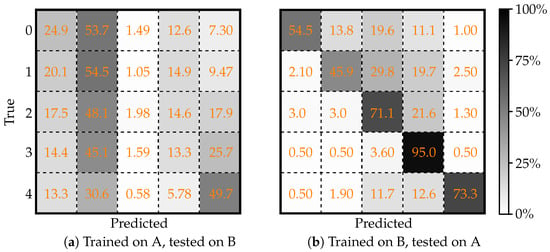
Figure 3.
Confusion matrices illustrating the cross-dataset evaluation of the deep learning model for a five-class classification problem using the Keras framework. (a) Model trained on Dataset A and tested on Dataset B; (b) model trained on Dataset B and tested on Dataset A. Adapted from [43].
Table 2 details the corresponding performance metrics for the cross-dataset experiments. The metrics demonstrate a notable performance drop compared to the within-dataset evaluations. Particularly, the model trained on Dataset A suffers a more significant decrease in accuracy when tested on Dataset B. In contrast, the model trained on Dataset B shows a comparatively better generalization on Dataset A. These results underscore the importance of rigorous external validation to ensure that models remain reliable when exposed to data from different sources.

Table 2.
Performance metrics for ML model trained on Datasets A and B and (externally) tested on Datasets B and A, respectively.
3.3. Learning Curves
The anomalous learning curves for the model trained on Dataset A (Figure 4a), where the validation accuracy is higher than the training accuracy, are an immediate red flag. The ideal scenario is to see a small gap between the training and validation curves with the validation accuracy slightly lower than the training accuracy (as seen in Figure 4b). This gap reflects that the model is learning useful patterns from the training data while still being somewhat regularized, ensuring it can generalize well. When the two curves are nearly overlapping or, worse, when the validation accuracy exceeds the training accuracy, it is a red flag. It often that the validation procedure is contaminated or that the model suffers from improper regularization or data leakage. In this case, the validation set from Dataset A may have been overly “friendly” or unrepresentative of the true complexity present in the training examples, leading the model to appear as if it were generalizing better than it really was.
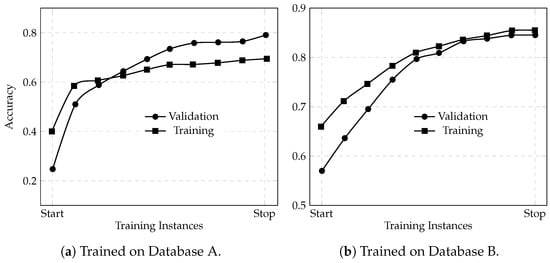
Figure 4.
Learning curves for accuracy returned by the deep learning model using the Keras framework trained on Dataset A (a) and Dataset B (b).
This deceptive behavior means that the model’s apparent in-domain performance (70% overall accuracy on Dataset A during training) is not a reliable indicator of its true generalization ability. When the model is later tested on an external dataset (Dataset B), the mismatch in data characteristics is exposed and the performance deteriorates significantly; dropping to 49.94% overall accuracy with similarly reduced Cohen’s Kappa and Matthews CC values. Essentially, the inflated validation accuracy masked underlying issues such as overfitting to Dataset A’s spurious patterns or artifacts. As a result, the model failed to adapt to the new data distribution in Dataset B.
In contrast, the model trained on Dataset B, which did not suffer from such deceptive learning curves, maintained higher performance even when tested on Dataset A (68.36% accuracy). This comparison underscores that a reliable validation strategy, reflected by proper learning curves where training accuracy at least matches or exceeds validation accuracy, is critical to developing models that generalize well across datasets. Thus, the “bad-behaving” learning curves for the model from Dataset A are directly linked to its poor cross-dataset performance: they reveal that the validation metrics were misleading, and that the model had not truly learned robust features but rather had adapted to quirks in its in-domain data.
3.4. Composite Clinical Score Analysis
To bridge the quantitative performance evaluation with clinical applicability, two composite metrics are computed as defined above: the overall model score (Equation (20)) and the clinical utility score (Equation (25)). These scores integrate standard statistical measures with clinically relevant priorities, providing a single performance index that reflects both the model’s discriminative power and its potential impact in a clinical setting.
As reported in Table 1, the macro-averaged sensitivity (i.e., recall), PPV, and F1 score for Dataset B are 0.7769, 0.7919, and 0.7770, respectively. The remaining metrics required for the composite scores were computed directly from the confusion matrix. Specifically, a macro-averaged specificity is of approximately 0.9478 and a macro-averaged negative predictive value (NPV) of about 0.9487.
Using these values, and an independently computed AUC of 0.87, the overall model score is calculated by equally weighting AUC, sensitivity, and specificity:
Similarly, the clinical utility score is computed by equally weighting the PPV, NPV, and F1 score:
These composite scores, an overall model score of approximately 86.5% and a clinical utility score of roughly 83.9%, demonstrate that the model not only achieves strong statistical performance but also meets key clinical requirements. In other words, the model’s high global discriminative ability is well aligned with its capability to provide clinically actionable insights, thereby supporting its potential as a reliable decision support tool.
In the context of knee osteoarthritis grading, concrete clinical requirements refer to criteria that ensure the model’s outputs are directly useful for patient care and decision making. These include (1) high sensitivity for detecting severe and healthy cases to minimize missed diagnoses and unnecessary interventions, (2) high specificity to avoid over-diagnosis, (3) strong positive and negative predictive values to support reliable clinical triage, and (4) robust performance in distinguishing clinically actionable endpoints (such as differentiating between grades that mandate intervention versus those that do not). The weighting schemes and composite scores used in this study are explicitly designed to align with these requirements, prioritizing the accurate identification of cases with significant clinical implications.
3.5. Evaluation of Weighted Endpoint Accuracy Score
The utility of the proposed WEAS is evaluated using the confusion matrix derived from the test set after the ML model was trained on Dataset B (see Figure 2b). It is important to note that the confusion matrix reflects the model’s performance on the independent test (or validation) data, not on the training data itself. Thus, the total number of instances reported in the confusion matrix corresponds to the size of the test set used for evaluation, rather than the dataset used for model training. This distinction is relevant, as the confusion matrix and associated metrics (such as WEAS) provide an assessment of how well the trained model generalizes to unseen data, rather than its performance on the data it was trained on.
For this 5-class problem (with class labels 0–4, where class 0 signifies healthy patients and class 4 represents severe pathology), the per-class accuracies, as reported in Figure 2b, are as follows:
Recognizing the higher clinical importance of correctly predicting the endpoints (classes 0 and 4), we assign them a weight , while the intermediate classes (1, 2, and 3) remain unweighted (i.e., weight = 1). The overall WEAS (Equation (30)) is defined as
Substituting the computed accuracies with , we obtain:
This metric indicates an overall utility of approximately 81.4%, underscoring the model’s strong performance on the clinically critical endpoints.
An extension to the WEAS incorporates a misclassification penalty that accounts for the severity of off-diagonal errors. With a distance penalty defined as , the cumulative penalty for misclassifications is given by
For the ML model trained on Dataset B, yielding the following confusion matrix
the penalty per row is computed as follows:
- Row 0 (): .
- Row 1 (): .
- Row 2 (): .
- Row 3 (): .
- Row 4 (): .
Summing these penalties yields a total penalty of . Dividing by the total number of instances (), we obtain
This penalty is then integrated into a composite utility function (Equation (32): ), where is a parameter that balances the importance of endpoint accuracy against the cost of misclassification. For example, with , the utility becomes
These findings indicate that, while the elevated WEAS (81.4%) demonstrates robust discrimination between healthy and severely ill patients, the composite utility metric U provides a more comprehensive evaluation by also accounting for the cost of misclassifications. Such an assessment aligns the model’s evaluation with clinical priorities, ensuring that both endpoint accuracy and the severity of errors are appropriately reflected.
4. Discussion
Ensuring robust and well-documented training of ML models in healthcare is pivotal for their clinical utility, as described in Figure 1 (especially the middle square highlighted in red). The model training phase, which encompasses proper learning methodologies, the prevention of overfitting or underfitting, and uthe se of appropriate performance metrics, is foundational to achieving clinically actionable outcomes. Without rigorous training protocols, high accuracy metrics may be deceptive, creating a false sense of reliability in a model’s clinical applicability.
A model trained inadequately or with methodological flaws, such as overfitting to training data or insufficient validation, can yield inflated accuracy metrics that fail to generalize to real-world scenarios [46]. For instance, as demonstrated in the case study, a model achieving 70% accuracy on its training dataset catastrophically failed during cross-dataset evaluation, with accuracy plummeting to under 2% for a critical grade 2 osteoarthritis classification. This highlights a systemic issue where models validated solely on in-domain data appear promising but ultimately lack the robustness necessary for diverse clinical environments. Robust training ensures that the model learns meaningful patterns from data rather than memorizing noise or artifacts. Overfitting, characterized by exceptional performance on training data but poor generalization to unseen data, can render a model clinically useless. Similarly, underfitting, where a model fails to capture the underlying data structure, results in subpar performance across all datasets. Both scenarios undermine the validity of reported performance metrics, making them clinically irrelevant.
Properly trained models are better equipped to handle variability in patient data, imaging protocols, and disease presentations, ensuring they are reliable tools for clinical decision-making. Incorporating standardized training methodologies, as outlined in regulatory frameworks like the FDA’s guidance on AI credibility, bridges the gap between research prototypes and bedside applications. By adhering to these practices, healthcare ML models can transition from deceptively high accuracy metrics to robust, actionable tools that prioritize patient safety and ethical deployment.
4.1. Clinical Implications of Learning-Curve Behaviors in ML Models
In ML model training, learning curves, i.e., plots of training and validation performance over time or epochs, serve as critical diagnostic tools for assessing the health of the training process. A well-trained ML model typically exhibits learning curves where the training and validation curves converge and plateau together, with the training curve slightly above the validation curve (see Figure 4b). This behavior indicates that the model has learned meaningful patterns from the data without overfitting or underfitting. However, deviations from this ideal behavior can signal significant issues in the training process, which, if unaddressed, can lead to clinically unreliable models. Table 3 summarizes various problematic learning-curve behaviors, their potential causes, and their clinical implications.

Table 3.
Problematic learning (accuracy) curve behaviors, their potential causes, and clinical implications.
4.1.1. Analysis of Problematic Learning-Curve Behaviors
The analysis of problematic learning-curve behaviors reveals several key patterns that can indicate issues in ML model training, each with distinct causes and clinical implications (summarized in Table 3). When the validation curve is higher than the training curve, it often points to data leakage, where information from the validation set inadvertently influences the training process. This can also occur if the training data is overly simplistic or lacks diversity. Clinically, such a model may appear to perform well during validation but fail catastrophically when exposed to real-world data, leading to misdiagnoses or inappropriate treatment recommendations.
Non-converging curves, where the training and validation curves fail to converge, indicate underfitting. This issue arises from insufficient model complexity, poor feature engineering, or inadequate training data. Clinically, an underfitted model is incapable of capturing the underlying patterns in the data, resulting in low diagnostic accuracy and unreliable predictions. On the other hand, non-plateauing curves, where the curves converge but fail to plateau, suggest overfitting to noise or artifacts in the data. This behavior implies that the model is learning spurious patterns rather than clinically relevant features, which could lead to unreliable predictions, particularly in edge cases or less common conditions.
A large gap between the training and validation curves is a hallmark of overfitting. This occurs when the model is too complex relative to the amount of training data, allowing it to memorize the training data rather than generalize. Clinically, this results in a model that performs well on training data but poorly on unseen data, undermining its utility in real-world settings. Oscillating curves, characterized by significant fluctuations in performance, often indicate an unstable optimization process, potentially due to a high learning rate or poor initialization. Clinically, this instability translates to unpredictable model behavior, making it unsuitable for deployment in critical healthcare applications.
Another problematic behavior is validation-curve deterioration, where the validation curve initially improves but later deteriorates. This is a clear sign of overfitting, typically occurring when training continues beyond the point of optimal generalization. Clinically, this could lead to a model that performs well during initial testing but fails to maintain accuracy over time, especially as patient populations or data distributions evolve.
The clinical implications of these poor learning-curve behaviors are significant. Overfitting can lead to false positives, resulting in unnecessary treatments or interventions, while underfitting can result in missed diagnoses, delaying critical care for patients. Data leakage can create a false sense of confidence in the model’s performance, leading to its premature deployment in clinical settings. To mitigate these risks, it is essential to monitor learning curves during training and address any anomalies promptly. Techniques such as cross-validation, early stopping, regularization, and robust data preprocessing can help ensure that the model learns meaningful patterns and generalizes well to unseen data. By understanding and addressing problematic learning-curve behaviors, researchers and clinicians can develop ML models that are not only statistically robust but also clinically reliable. This ensures that the models are capable of improving patient outcomes and advancing the field of healthcare AI.
4.1.2. Assessing Learning Dynamics Beyond Learning Curves
While this study demonstrates the value of analyzing learning curves to diagnose overfitting, data leakage, and generalization issues, it is important to recognize that other forms of training dynamics analysis can further strengthen model validation. In particular, recent work in AI-based glaucoma detection [47] has highlighted the importance of reporting and interpreting model performance metrics (such as accuracy, precision, recall, and F1-score) across each data subset: training, validation, test, and external (cross-dataset) evaluation. As shown in that study, a properly trained and generalizable ML model should exhibit a slight and continuous decrease in performance metrics as evaluation moves from the training set to the validation set, to the test set, and finally to external data. This expected trend reflects the model’s ability to generalize, with only modest declines in performance as the data becomes less similar to the training distribution. In contrast, large drops or erratic changes in these metrics across subsets are indicative of overfitting, data leakage, or poor generalization.
Although this current work focuses on learning curve analysis as a primary tool for diagnosing training issues, incorporating subset-wise performance metric analysis (following the approach demonstrated in [47]) would provide an additional layer of insight into the model’s learning dynamics and generalizability. It is recommended that future studies routinely include such analyses to complement learning-curve evaluation, thereby ensuring a more comprehensive assessment of model robustness and clinical applicability.
4.2. Clinical Implications of the Composite Utility Metric
In order to bridge the gap between traditional performance metrics and the nuanced requirements of clinical decision making, a series of composite measures have been proposed to evaluate ML models in healthcare. Table 4 summarizes four key metrics—the overall model score (Equation (20)), clinical utility score (Equation (25)), Weighted Endpoint Accuracy Score (WEAS; Equation (30)), and the composite utility metric (Equation (32)). These metrics not only capture a model’s global discriminative capacity (via AUC, sensitivity, and specificity) but also incorporate predictive values and a misclassification penalty, thereby aligning model evaluation with clinical priorities. Such an integrated approach is essential to ensure that the models are both statistically robust and clinically actionable.

Table 4.
Suggested clinical evaluation metrics for ML in healthcare.
The resulting composite utility U is of significant clinical relevance as it combines the model’s performance on critical endpoints with an explicit penalty for misclassification errors. While the WEAS of approximately 81.4% demonstrates that the model reliably distinguishes between the healthy (class 0) and severely pathological cases (class 4), the composite metric U further addresses the impact of misclassifications across all classes.
Specifically, the penalty component in U quantifies the cost of errors based on their distance from the true class, reflecting the clinical intuition that misclassifying a healthy patient as severely ill (or vice versa) is more consequential than errors involving intermediate classes. For example, with a balancing parameter , the computed utility indicates that, despite robust performance at the endpoints, the model incurs a non-negligible cost when it strays from accurate classification in a clinically meaningful way.
This approach aligns with clinical decision protocols where endpoint accuracy remains paramount but intermediate class errors still require mitigation. The integration of macro-averaged sensitivity (77.69%) and specificity (94.78%) in the composite model score provides critical insights into real-world functionality. These metrics reveal how well models balance the detection of positive cases (minimizing false negatives) against the ability to correctly identify negative cases (minimizing false positives); both fundamental requirements for clinical adoption. Similarly, the clinical utility score (83.9%) emphasizes predictive values that directly correlate with patient management outcomes, as clinicians prioritize minimizing diagnostic ambiguity through high positive and negative predictive values.
In a healthcare setting, such as grading knee osteoarthritis severity [43,48], this composite measure provides a more holistic evaluation of the model’s clinical usefulness. It ensures that models selected for clinical use not only exhibit high accuracy in discriminating between the most critical cases but also maintain an acceptable level of performance across intermediate stages. Consequently, U serves as a relevant tool for clinicians and stakeholders by aligning the performance evaluation with clinical priorities, thus supporting safer and more effective patient management decisions.
The clinical prioritization of endpoint accuracy through weighting ( for classes 0 and 4 vs. intermediate classes) mirrors established medical protocols where clear differentiation between normal and severely affected states drives treatment pathways. However, the additional penalty mechanism acknowledges that even smaller misclassifications between adjacent grades (e.g., class 2 mislabeled as class 3) accumulate operational costs through unnecessary referrals, repeated imaging, or delayed interventions. This dual focus, prioritizing critical distinctions while disincentivizing all errors proportionally, creates performance benchmarks that better reflect clinical workflows compared to conventional accuracy metrics.
Ultimately, composite scoring methodologies address a fundamental disconnect between ML evaluation and medical practice. By translating statistical performance into risk-adjusted utility measures, they provide frameworks for model assessment that account for both diagnostic priorities and the asymmetric consequences of different error types. This alignment is essential for validating AI systems in healthcare, where computational metrics must be subordinated to patient safety considerations and clinical decision-making realities. A critical consideration in the clinical deployment of ML models is the selection and justification of weighting coefficients for composite evaluation metrics. The optimal balance between sensitivity and specificity is not universal, but rather context-dependent and should be tailored to the intended clinical application. For example, in population-level screening programs (e.g., national mammography campaigns or infectious disease surveillance) the primary objective is to identify as many true-positive cases as possible, even at the expense of increased false positives. In these scenarios, maximizing sensitivity is paramount to ensure that no cases are missed, as the public health consequences of undetected disease can be severe. Conversely, when managing the care of an individual patient, the clinical focus often shifts toward specificity. Here, the goal is to minimize false positives to avoid unnecessary anxiety, invasive follow-up procedures, or unwarranted treatments. For instance, a highly specific confirmatory test is essential before initiating a potentially harmful therapy. Thus, the weighting coefficients in composite metrics must be carefully chosen to reflect whether the model is intended for broad screening or for guiding individual patient management, ensuring that the evaluation framework aligns with real-world clinical priorities.
4.3. Limitations and Future Research Directions
While our work has addressed core issues in the standardized validation of ML models for medical classification, several avenues for future research remain. First, the development and evaluation of advanced model architectures that further mitigate overfitting and improve domain generalization should be explored, particularly in more heterogeneous and multi-center clinical datasets. Second, the real-world deployment of such validated models (integrating them into clinical workflows and assessing their ongoing impact on patient outcomes and care efficiency) warrants thorough investigation. Third, the creation of standardized benchmarks and open challenges for external validation in diverse clinical settings would further advance the field. Finally, additional work is needed to align composite utility metrics with evolving clinical guidelines and regulatory standards, ensuring models remain relevant and actionable as healthcare practices progress.
Additionally, while the composite evaluation metrics and their associated formulas (including weighting schemes, penalty functions, and aggregation strategies) were designed to be consistent with established clinical reasoning and to reflect priorities commonly recognized in medical decision making, we acknowledge that these formulas were not formally validated through direct physician input or structured expert consensus in this study. Future work could incorporate expert clinician feedback or employ a formal Delphi consensus process [49] to systematically refine and validate these formulas and weighting strategies, thereby ensuring that all aspects of the evaluation framework are optimally aligned with real-world clinical priorities and expert judgment.
Furthermore, benchmarking composite clinical scores against baseline models (such as random or majority-class classifiers) and, when available, against human expert performance would provide valuable context and further strengthen the clinical relevance of these findings. Incorporating such comparisons represents an important direction for future work and would help to more clearly position the utility of the evaluation framework within real-world clinical practice.
5. Conclusions
While a robust assessment of an ML model’s training process is an important precursor to interpreting its reported performance, we emphasize that learning dynamics (such as the analysis of learning curves and detection of overfitting or data leakage) should be considered as a valuable complement to, rather than a replacement for, established performance metrics. Insights into training dynamics can help identify potential pitfalls that may not be immediately evident from final accuracy or F1 scores alone, particularly in situations where external validation data is limited. However, it is important to recognize that no single evaluation approach is universally sufficient; both the trajectory of model learning and the ultimate performance metrics provide distinct, meaningful information about model reliability and generalizability. Accordingly, we recommend integrating the assessment of learning dynamics alongside comprehensive performance evaluation, in order to build a more holistic and reliable understanding of model readiness for clinical deployment.
Our results demonstrate that even models with strong in-domain performance, such as the 79% accuracy and 0.78 F1 score obtained on Dataset B, may exhibit substantial drops in external validity (e.g., to 68% accuracy when cross-tested) if robust training and validation protocols are not rigorously enforced. The observed discrepancies between in-domain and out-of-domain performance, as well as the analysis of learning-curve behaviors, directly highlight the risks of overfitting and data leakage. Importantly, the application of composite clinical utility metrics provided a more nuanced assessment of the model’s clinical relevance than conventional accuracy alone. For instance, a WEAS of 81.4% for Dataset B emphasizes the model’s strength in predicting clinically critical endpoints, while the composite utility metric additionally penalizes misclassifications in a manner reflective of clinical risk. These findings underscore that standardized protocols and clinically oriented evaluation are essential for ensuring that ML models for medical classification deliver reliable, generalizable, and patient-centered results in real-world settings.
Author Contributions
All authors (D.N. (Daniel Nasef), D.N. (Demarcus Nasef), M.S. and M.T.) contributed to all aspects of this work. This includes but is not limited to conceptualization, methodology, software management, validation, formal analysis, investigation, resources management, data curation, writing—original draft preparation, writing—review and editing, and visualization. The supervision, and project administration were handled by M.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data is contained within the article; the original contributions presented in this study are included in the article material.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ML | Machine Learning |
| AI | Artificial Intelligence |
| EHR | Electronic Health Records |
| FDA | Food and Drug Administration |
| CNN | Convolutional Neural Network |
| VGG16 | Visual Geometry Group 16 |
| MVGG16 | Modified VGG16 |
| ReLU | Rectified Linear Unit |
| COU | Context of Use |
| TPR | True-Positive Rate |
| FPR | False-Positive Rate |
| PPV | Positive Predictive Value |
| NPV | Negative Predictive Value |
| MCC | Matthews Correlation Coefficient |
| AUC | Area Under the Curve |
| ROC | Receiver Operating Characteristic |
| WEAS | Weighted Endpoint Accuracy Score |
| KL | Kellgren–Lawrence |
| TP | True Positive |
| FP | False Positive |
| TN | True Negative |
| FN | False Negative |
| F1 | F1 Score |
| Cohen’s Kappa | |
| CT | Computed Tomography |
| MRI | Magnetic Resonance Imaging |
References
- Wolberg, W.H.; Street, W.N.; Mangasarian, O.L. Image analysis and machine learning applied to breast cancer diagnosis and prognosis. Anal. Quant. Cytol. Histol. 1995, 17, 77–87. [Google Scholar] [PubMed]
- Agar, J.W.; Webb, G.I. Application of machine learning to a renal biopsy database. Nephrol. Dial. Transplant. 1992, 7, 472–478. [Google Scholar] [PubMed]
- Liu, W.; White, A.; Hallissey, M.; Fielding, J. Machine learning techniques in early screening for gastric and oesophageal cancer. Artif. Intell. Med. 1996, 8, 327–341. [Google Scholar] [CrossRef]
- Kukar, M.; Kononenko, I.; Silvester, T. Machine learning in prognosis of the femoral neck fracture recovery. Artif. Intell. Med. 1996, 8, 431–451. [Google Scholar] [CrossRef]
- Laurikkala, J.; Juhola, M. A genetic-based machine learning system to discover the diagnostic rules for female urinary incontinence. Comput. Methods Programs Biomed. 1998, 55, 217–228. [Google Scholar] [CrossRef] [PubMed]
- Shankle, W.R.; Mania, S.; Dick, M.B.; Pazzani, M.J. Simple models for estimating dementia severity using machine learning. Stud. Health Technol. Inform. 1998, 52, 472–476. [Google Scholar]
- Kuang, H.; Wang, Y.; Tan, X.; Yang, J.; Sun, J.; Liu, J.; Qiu, W.; Zhang, J.; Zhang, J.; Yang, C.; et al. LW-CTrans: A lightweight hybrid network of CNN and Transformer for 3D medical image segmentation. Med. Image Anal. 2025, 102, 103545. [Google Scholar] [CrossRef]
- Zhang, L.; Guo, X.; Sun, H.; Wang, W.; Yao, L. Alternate encoder and dual decoder CNN-Transformer networks for medical image segmentation. Sci. Rep. 2025, 15, 8883. [Google Scholar] [CrossRef]
- Dayarathna, S.; Islam, K.T.; Uribe, S.; Yang, G.; Hayat, M.; Chen, Z. Deep learning based synthesis of MRI, CT and PET: Review and analysis. Med. Image Anal. 2024, 92, 103046. [Google Scholar] [CrossRef]
- Chen, X.; Wang, X.; Zhang, K.; Fung, K.M.; Thai, T.C.; Moore, K.; Mannel, R.S.; Liu, H.; Zheng, B.; Qiu, Y. Recent advances and clinical applications of deep learning in medical image analysis. Med. Image Anal. 2022, 79, 102444. [Google Scholar] [CrossRef]
- de Bruijne, M. Machine learning approaches in medical image analysis: From detection to diagnosis. Med. Image Anal. 2016, 33, 94–97. [Google Scholar] [CrossRef] [PubMed]
- Bajaj, A.S.; Chouhan, U. A Review of Various Machine Learning Techniques for Brain Tumor Detection from MRI Images. Curr. Med. Imaging 2020, 16, 937–945. [Google Scholar] [CrossRef] [PubMed]
- Fauzi, A.; Yueniwati, Y.; Naba, A.; Rahayu, R.F. Performance of deep learning in classifying malignant primary and metastatic brain tumors using different MRI sequences: A medical analysis study. J. -Ray Sci. Technol. 2023, 31, 893–914. [Google Scholar] [CrossRef] [PubMed]
- Song, L.; Li, C.; Tan, L.; Wang, M.; Chen, X.; Ye, Q.; Li, S.; Zhang, R.; Zeng, Q.; Xie, Z.; et al. A deep learning model to enhance the classification of primary bone tumors based on incomplete multimodal images in X-ray, CT, and MRI. Cancer Imaging 2024, 24, 135. [Google Scholar] [CrossRef]
- Heo, J.; Yoon, J.G.; Park, H.; Kim, Y.D.; Nam, H.S.; Heo, J.H. Machine Learning–Based Model for Prediction of Outcomes in Acute Stroke. Stroke 2019, 50, 1263–1265. [Google Scholar] [CrossRef]
- Dong, J.; Feng, T.; Thapa-Chhetry, B.; Cho, B.G.; Shum, T.; Inwald, D.P.; Newth, C.J.L.; Vaidya, V.U. Machine learning model for early prediction of acute kidney injury (AKI) in pediatric critical care. Crit. Care 2021, 25, 288. [Google Scholar] [CrossRef]
- Lynch, C.M.; Abdollahi, B.; Fuqua, J.D.; de Carlo, A.R.; Bartholomai, J.A.; Balgemann, R.N.; van Berkel, V.H.; Frieboes, H.B. Prediction of lung cancer patient survival via supervised machine learning classification techniques. Int. J. Med. Inform. 2017, 108, 1–8. [Google Scholar] [CrossRef]
- Hassan, A.M.; Biaggi-Ondina, A.; Rajesh, A.; Asaad, M.; Nelson, J.A.; Coert, J.H.; Mehrara, B.J.; Butler, C.E. Predicting Patient-Reported Outcomes Following Surgery Using Machine Learning. Am. Surg. 2022, 89, 31–35. [Google Scholar] [CrossRef]
- Zhang, T.; Nikouline, A.; Lightfoot, D.; Nolan, B. Machine Learning in the Prediction of Trauma Outcomes: A Systematic Review. Ann. Emerg. Med. 2022, 80, 440–455. [Google Scholar] [CrossRef]
- Mataraso, S.J.; Espinosa, C.A.; Seong, D.; Reincke, S.M.; Berson, E.; Reiss, J.D.; Kim, Y.; Ghanem, M.; Shu, C.H.; James, T.; et al. A machine learning approach to leveraging electronic health records for enhanced omics analysis. Nat. Mach. Intell. 2025, 7, 293–306. [Google Scholar] [CrossRef]
- Lotter, W.; Diab, A.R.; Haslam, B.; Kim, J.G.; Grisot, G.; Wu, E.; Wu, K.; Onieva, J.O.; Boyer, Y.; Boxerman, J.L.; et al. Robust breast cancer detection in mammography and digital breast tomosynthesis using an annotation-efficient deep learning approach. Nat. Med. 2021, 27, 244–249. [Google Scholar] [CrossRef] [PubMed]
- Tsiknakis, N.; Theodoropoulos, D.; Manikis, G.; Ktistakis, E.; Boutsora, O.; Berto, A.; Scarpa, F.; Scarpa, A.; Fotiadis, D.I.; Marias, K. Deep learning for diabetic retinopathy detection and classification based on fundus images: A review. Comput. Biol. Med. 2021, 135, 104599. [Google Scholar] [CrossRef]
- Wenderott, K.; Krups, J.; Zaruchas, F.; Weigl, M. Effects of artificial intelligence implementation on efficiency in medical imaging—A systematic literature review and meta-analysis. Npj Digit. Med. 2024, 7, 265. [Google Scholar] [CrossRef] [PubMed]
- Preti, L.M.; Ardito, V.; Compagni, A.; Petracca, F.; Cappellaro, G. Implementation of Machine Learning Applications in Health Care Organizations: Systematic Review of Empirical Studies. J. Med. Internet Res. 2024, 26, e55897. [Google Scholar] [CrossRef]
- Boutron, I.; Page, M.J.; Higgins, J.P.; Altman, D.G.; Lundh, A.; Hrobjartsson, A. Considering bias and conflicts of interest among the included studies. In Cochrane Handbook for Systematic Reviews of Interventions; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2019. [Google Scholar] [CrossRef]
- Wierzbicki, M.P.; Jantos, B.A.; Tomaszewski, M. A Review of Approaches to Standardizing Medical Descriptions for Clinical Entity Recognition: Implications for Artificial Intelligence Implementation. Appl. Sci. 2024, 14, 9903. [Google Scholar] [CrossRef]
- Arora, A.; Alderman, J.E.; Palmer, J.; Ganapathi, S.; Laws, E.; McCradden, M.D.; Oakden-Rayner, L.; Pfohl, S.R.; Ghassemi, M.; McKay, F.; et al. The value of standards for health datasets in artificial intelligence-based applications. Nat. Med. 2023, 29, 2929–2938. [Google Scholar] [CrossRef]
- Um, T.W.; Kim, J.; Lim, S.; Lee, G.M. Trust Management for Artificial Intelligence: A Standardization Perspective. Appl. Sci. 2022, 12, 6022. [Google Scholar] [CrossRef]
- U.S. Food and Drug Administration (FDA). Considerations for the Use of Artificial Intelligence to Support Regulatory Decision-Making for Drug and Biological Products. Technical Report, U.S. Department of Health and Human Services, Food and Drug Administration, 2025. Available online: https://www.fda.gov/media/184830/download (accessed on 22 May 2025).
- Goldenholz, D.M.; Sun, H.; Ganglberger, W.; Westover, M.B. Sample Size Analysis for Machine Learning Clinical Validation Studies. Biomedicines 2023, 11, 685. [Google Scholar] [CrossRef]
- Husain, G.; Nasef, D.; Jose, R.; Mayer, J.; Bekbolatova, M.; Devine, T.; Toma, M. SMOTE vs. SMOTEENN: A Study on the Performance of Resampling Algorithms for Addressing Class Imbalance in Regression Models. Algorithms 2025, 18, 37. [Google Scholar] [CrossRef]
- International Council for Harmonisation of Technical Requirements for Pharmaceuticals for Human Use (ICH). Q13 Continuous Manufacturing of Drug Substances and Drug Products: Guidance for Industry. Technical Report, U.S. Department of Health and Human Services, Food and Drug Administration, Center for Drug Evaluation and Research (CDER), Center for Biologics Evaluation and Research (CBER), 2023. Available online: https://www.fda.gov/media/165775/download (accessed on 22 May 2025).
- U.S. Food and Drug Administration (FDA), Center for Drug Evaluation and Research (CDER). Artificial Intelligence in Drug Manufacturing: Discussion Paper. Technical Report, U.S. Department of Health and Human Services, Food and Drug Administration, Center for Drug Evaluation and Research, 2023. Available online: https://www.fda.gov/media/165743/download (accessed on 22 May 2025).
- European Parliament and Council of the European Union. Regulation (EU) 2017/745 of the European Parliament and of the Council of 5 April 2017 on Medical Devices, Amending Directive 2001/83/EC, Regulation (EC) No 178/2002 and Regulation (EC) No 1223/2009 and Repealing Council Directives 90/385/EEC and 93/42/EEC (Text with EEA Relevance). Technical Report, European Union, 2017. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:32017R0745 (accessed on 22 May 2025).
- European Parliament and Council of the European Union. Regulation (EU) 2024/1689 of the European Parliament and of the Council of 13 June 2024 Laying Down Harmonised Rules on Artificial Intelligence and Amending Regulations (EC) No 300/2008, (EU) No 167/2013, (EU) No 168/2013, (EU) 2018/858, (EU) 2018/1139 and (EU) 2019/2144 and Directives 2014/90/EU, (EU) 2016/797 and (EU) 2020/1828 (Artificial Intelligence Act). Technical Report, European Union, 2024. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=OJ:L_202401689 (accessed on 22 May 2025).
- World Health Organization (WHO). Ethics and Governance of Artificial Intelligence for Health: WHO Guidance. Technical Report, World Health Organization, 2021. Available online: https://apps.who.int/iris/handle/10665/341996 (accessed on 22 May 2025).
- U.S. Food and Drug Administration (FDA); Health Canada; Medicines and Healthcare Products Regulatory Agency (MHRA). Good Machine Learning Practice for Medical Device Development: Guiding Principles. Technical Report, U.S. Food and Drug Administration (FDA), Health Canada, and MHRA, 2021. Available online: https://www.fda.gov/medical-devices/software-medical-device-samd/good-machine-learning-practice-medical-device-development-guiding-principles (accessed on 22 May 2025).
- Norgeot, B.; Quer, G.; Beaulieu-Jones, B.K.; Torkamani, A.; Dias, R.; Gianfrancesco, M.; Arnaout, R.; Kohane, I.S.; Saria, S.; Topol, E.; et al. Minimum information about clinical artificial intelligence modeling: The MI-CLAIM checklist. Nat. Med. 2020, 26, 1320–1324. [Google Scholar] [CrossRef]
- Liu, X.; Cruz Rivera, S.; Moher, D.; Calvert, M.J.; Denniston, A.K.; Chan, A.W.; Darzi, A.; Holmes, C.; Yau, C.; Ashrafian, H.; et al. Reporting guidelines for clinical trial reports for interventions involving artificial intelligence: The CONSORT-AI extension. Nat. Med. 2020, 26, 1364–1374. [Google Scholar] [CrossRef] [PubMed]
- Hoang, M.L.; Matrella, G.; Ciampolini, P. Comparison of Machine Learning Algorithms for Heartbeat Detection Based on Accelerometric Signals Produced by a Smart Bed. Sensors 2024, 24, 1900. [Google Scholar] [CrossRef] [PubMed]
- Tziachris, P.; Nikou, M.; Aschonitis, V.; Kallioras, A.; Sachsamanoglou, K.; Fidelibus, M.D.; Tziritis, E. Spatial or Random Cross-Validation? The Effect of Resampling Methods in Predicting Groundwater Salinity with Machine Learning in Mediterranean Region. Water 2023, 15, 2278. [Google Scholar] [CrossRef]
- Cheng, K.S.; Huang, P.C.; Ahn, T.H.; Song, M. Tool Support for Improving Software Quality in Machine Learning Programs. Information 2023, 14, 53. [Google Scholar] [CrossRef]
- Nasef, D.; Nasef, D.; Sawiris, V.; Girgis, P.; Toma, M. Deep Learning for Automated Kellgren–Lawrence Grading in Knee Osteoarthritis Severity Assessment. Surgeries 2024, 6, 3. [Google Scholar] [CrossRef]
- Ahmad, H.N. Annotated Dataset for Knee Arthritis Detection, 2023. Available online: https://www.kaggle.com/datasets/hafiznouman786/annotated-dataset-for-knee-arthritis-detection/ (accessed on 22 May 2025).
- Chen, P. Knee Osteoarthritis Severity Grading Dataset, 2018. Available online: https://data.mendeley.com/datasets/56rmx5bjcr/1 (accessed on 22 May 2025).
- Chong, L.; Husain, G.; Nasef, D.; Vathappallil, P.; Matalia, M.; Toma, M. Machine Learning Strategies for Improved Cardiovascular Disease Detection. Med. Res. Arch. 2025, 13, 1–13. [Google Scholar] [CrossRef]
- Remyes, D.; Nasef, D.; Remyes, S.; Tawfellos, J.; Sher, M.; Nasef, D.; Toma, M. Clinical Applicability and Cross-Dataset Validation of Machine Learning Models for Binary Glaucoma Detection. Information 2025, 16, 432. [Google Scholar] [CrossRef]
- Jose, R.; Lewis, N.; Satti, Z.; Steinberg, R.; Toufexis, A.; Nasef, D.; Toma, M. Machine-learning-based diagnosis and progression analysis of knee osteoarthritis. Discov. Data 2025, 3, 6. [Google Scholar] [CrossRef]
- Xing, X.; Wang, Y.; Zhu, J.; Shen, Z.; Cicuttini, F.; Jones, G.; Aitken, D.; Cai, G. Predictive validity of consensus-based MRI definition of osteoarthritis plus radiographic osteoarthritis for the progression of knee osteoarthritis: A longitudinal cohort study. Osteoarthr. Cartil. Open 2025, 7, 100582. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).