Abstract
This paper presents a narrative review on the Resource-Constrained Multi-Project Scheduling Problem (RCMPSP) under uncertainty and resource flexibility. Traditional project scheduling assumes complete information and a deterministic environment where a pre-computed baseline schedule is executed. However, real-world projects frequently face uncertainty, such as variable task durations and fluctuating resource availability. Analyzing studies from 2013 to 2024, this review examines optimization models addressing multiple objectives, including minimizing project duration, cost, and resource leveling. It categorizes solution approaches, from exact algorithms to heuristic and metaheuristic methods, while reviewing the primary instance sets and benchmarks used in the field. Additionally, it highlights the value of flexible resource management approaches that enable adaptive responses to real-time project demands, thereby enhancing scheduling robustness. By systematically addressing RCMPSP under uncertainty, this paper provides a valuable framework for researchers and practitioners seeking to develop resilient, adaptive scheduling solutions for complex, dynamic project environments.
1. Introduction
In realistic scheduling situations, companies typically manage multiple projects concurrently rather than a single one [1]. This transition from single-project to multi-project management introduces a significant layer of complexity to the scheduling process. The scheduling process becomes more challenging in this multi-project case, as some resources might need to be shared across multiple projects (e.g., facilities, machines, human resources). This resource dispute gives rise to intricate scheduling challenges, as decisions made for one project can have cascading effects on the timelines and budgets of others. The study of these complexities and the development of effective methodologies to navigate them is known as the Resource-Constrained Multi-Project Scheduling Problem (RCMPSP) [2].
The RCMPSP aims to optimize allocation of resources across multiple projects while adhering to project-specific constraints, such as activity precedence relationships and deadlines. However, the inherent assumption of deterministic conditions—where activity durations, resource availability, and project parameters are known with certainty—underlies many traditional RCMPSP models. This assumption is a significant oversimplification of real-world project environments, which are characterized by a high degree of uncertainty.
During project execution, random events such as activities taking different durations than expected, introducing new projects, and resources being unavailable cause production instability and significant delays. Therefore, these uncertainties must be considered in project scheduling.
To increase flexibility, workloads corresponding to each activity can be defined, and resource requirements can be adjusted flexibly. This approach, rooted in the concept of the Flexible Resource Constrained Project Scheduling Problem (FRCPSP) [3], has led to the development of several models/methods aimed at optimizing resource allocation under uncertainty [4], with further exploration into resource flexibility [5,6,7,8]. This paper looks closely at both uncertainty and flexibility with RCMPSP. Therefore, the two main contributions of this paper are (i) a comprehensive review of the literature analyzing and discussing the characteristics and objective functions proposed so far for the RCMPSP, as well as solution methods and existing benchmark datasets; and (ii) an examination of the main trends over the last 12 years, along with insights into how the RCMPSP is applied in real-world environments, helping to point out future research directions. The structure of this paper is organized as described below.
The findings of this research will offer valuable guidance for both researchers and practitioners in multi-project scheduling. By synthesizing the existing body of knowledge and highlighting key research gaps, it seeks to advance the development of more effective, resilient, and practical scheduling methodologies for multi-project environments.
Section 2 provides the background. In Section 3, the methodology used to carry out this research is described. In Section 4, a review of resource characteristics and the variants used to address the RCMPSP is explored. Discussion and findings are presented in Section 5, and finally, the conclusion appears in Section 6.
2. Background
2.1. Resource-Constrained Multi-Project Scheduling Problem (RCMPSP)
In practical scheduling scenarios, companies typically manage multiple projects simultaneously. This multi-project case increases the complexity of the scheduling process due to the possible existence of resources that need to be shared across multiple projects. This challenge is studied under the term Resource-Constrained Multi-Project Scheduling Problem (RCMPSP) [9].
RCMPSP is an expanded version of the Resource-Constrained Project Scheduling Problem (RCPSP), which involves scheduling multiple projects concurrently while sharing common resources. This extension also incorporates consideration of each project’s arrival time; that is, the time at which the activities can start. It is a practical problem that aims at minimizing project duration under resource constraints by determining start dates for each activity within a portfolio of projects. Since the RCMPSP, which is based on the RCPSP, is NP-hard [2,10], it becomes computationally challenging for large-scale instances. Consequently, researchers have developed heuristics and meta-heuristics to solve the related problems [11,12,13,14].
2.2. Uncertainty
Project execution in a real environment involves considerable uncertainty. Several factors contribute to uncertainty in multi-project scheduling. These uncertainties can be broadly divided into two main categories. The first kind is the uncertainty caused by the external environment; for example, adding more activities due to temporary increased orders, information uncertainty, and weather conditions. The second type of uncertainty relates to production factors, known as resource uncertainty. The most common uncertainties in project scheduling are a temporary shortage of resources and equipment failure [15].
During project execution, uncertainty is a significant factor that frequently affects the baseline scheduling plan, leading to delayed start times and resource supply interruptions. For instance, project duration may fluctuate because of a temporary change in activity duration, a new activity introduced during project execution, or cancellation of the original activity. Consequently, the entire project scheduling process becomes difficult to control [15]. According to Fox and Ringer’s survey, about 5% of scheduling time is spent developing new schedules, while 95% is dedicated to revising and maintaining schedules in response to daily progress and changes in assumptions [16].
Uncertainty factors may impact multi-project scheduling schemes in more complex ways at any point during project execution. A multi-project scheduling plan cannot accurately predict the completion times of each activity, thereby weakening its performance. Furthermore, the impact of these uncertain factors on multi-project scheduling leads to frequent modifications of scheduling plans, which significantly diminishes scheduling robustness and greatly increase the risk of delays [15].
2.3. Resource Flexibility
By introducing flexibility in resource allocation, the problem extends the RCPSP, leading to an optimal makespan that is at least as efficient as the makespan of the RCPSP. In this new scenario, the usage of resources and the duration of each activity are not predetermined. Instead, they are determined when scheduling the activities based on their starting times. This problem is known as the RCPSP with Flexible Resource Profiles (FRCPSP) [7].
This problem is initially introduced by Kolisch et al. [17] in the context of pharmaceutical research. Despite its significant potential, the problem has not been as extensively explored as the RCPSP. However, in recent years, the FRCPSP has attracted wider attention from researchers, resulting in the development of various model formulations and heuristic methods.
While the RCPSP assumes that the resources are allocated in constant amounts over the entire duration of each activity, Kolisch et al. [17] proposed a model in which resource allocation must be determined. In Ranjbar and Kianfar’s [18] proposal, RCPSP-FWP (RCPSP with Flexible Work Profiles) is used with the same meaning as FRCPCP. The RCPS-FWP is a different version of the well-known RCPSP, which consists of interrelated activities with a zero-time lag that are interconnected via finish-start-type precedence relations, where a single renewable resource is available, and activity duration and resource usage to a single renewable resource are known constants. The total work content of each activity is given, instead of the duration and resources required for each activity, which essentially indicates how much work needs to be done. In other words, activities’ durations and resource usage at any time are unknown. FRCPSP assumes that activity duration is not set, being part of the problem to be solved [18].
Naber and Kolisch [7] presented the FRCPSP. They used a Mixed Integer Programming (MIP) approach to address this problem. In addition to the MIP formulation, a priority rule (PR) heuristic is proposed, along with a scheme for creating both serial and parallel schedules. In their schedule generation scheme (SGS), activities are scheduled as early as possible, and the greatest number of resources is allocated per iteration.
This means that, in each iteration of the scheduling process, resources are assigned to activities based on their availability and the requirements of the activities being scheduled at that point [8].
This new approach to RCPSP, renamed Resource Constraint Project Scheduling Problem with Flexible Resource Management (RCPSP-FRM), takes into account the flexibility of limited resources [5].
3. Research Methodology
The following section outlines the methodology applied to collect and analyze relevant works to address key research questions within the research field of this study and derive new insights from publications. Specifically, the research seeks to answer the following questions:
- RQ1.
- What are the objectives in multi-project scheduling problems?
- RQ2.
- What are the different types of solving methods in multi-project scheduling problems?
- RQ3.
- What types of instance sets are used in multi-project scheduling problems?
- RQ4.
- What are the potential future research directions in multi-project scheduling problems?
To find the answers to the above questions, Aghileh et al. [19] was used as a reference paper. An extensive Systematic Literature Review (SLR) was conducted, sourcing relevant publications from academic databases such as Scopus, Web of Science, and Google Scholar. The SLR spanned studies published between 2013 and 2023 and applied specific keywords—such as “multi-project scheduling problem”, “uncertainty”, and “flexibility”—to capture a comprehensive view of developments in this field. After the initial identification of 826 records, a screening process yielded a refined selection of 108 studies that fit the established criteria. These included both qualitative studies lacking formalized models and calculations and quantitative studies that presented specific models and statistical analyses.
The primary distinction between qualitative and quantitative research lies in data collection and analysis. Quantitative research focuses on numerical data and employs statistical analysis, whereas qualitative research provides descriptive insights, exploring concepts and experiences in depth.
Given this study’s emphasis on evaluating optimization models, the final selection prioritized quantitative studies. A total of 53 quantitative papers were chosen, since this research is based on a previous study and aims to evaluate optimization models, supplemented by 23 additional papers containing relevant insights published in 2024 for further review. This process resulted in a comprehensive pool of 76 studies (as shown in Figure 1).
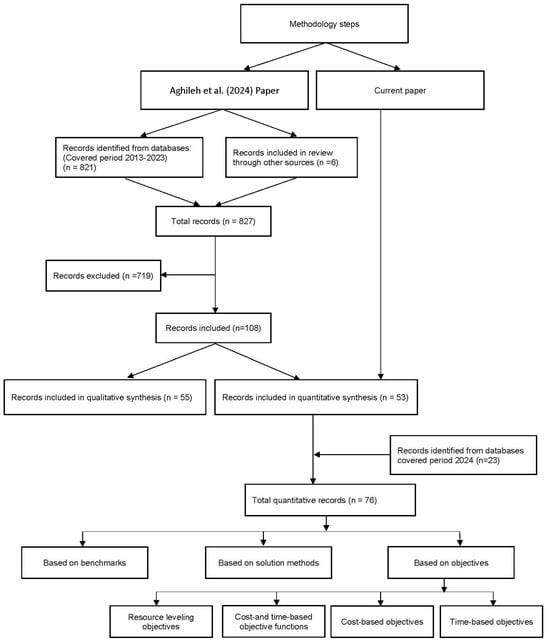
Figure 1.
Methodology, Aghileh et al. [19].
The design of this study is oriented toward analysis of the RCMPSP and related variants through the detailed study of each included paper in terms of problem characteristics, solution approaches, proposed benchmarks, and analysis through various statistics.
This methodology thus enabled a robust foundation for responding to each research question. While RQ2 was only partially addressed in Aghileh et al. [19], this study significantly expanded upon it, providing a thorough and detailed investigation into the diverse solution methods used within multi-project scheduling.
4. A Review of Variants in Project Scheduling Problem
This section presents a brief overview of the project scheduling problem variants studied in the literature and enables precise responses to each question within the study’s broader inquiry. Given the nature of the problem and collected papers, variants are analyzed in terms of objectives in multi-project scheduling problems to address the RQ1, different types of solving methods to provide insights for the RQ2, types of instance sets to address the RQ3, and potential directions for future research to address the RQ4.
4.1. Based on Objectives
4.1.1. Time-Based Objectives
The following classification groups those objective functions that evaluate completion time or the delays that may occur during projects.
- Delays: Project delays occur when completion exceeds the due date. A project delay is formally defined as the difference between the finishing date of a project and its desired due date if, and only if, the first exceeds the latter; otherwise, the delay is zero. There are several objective functions associated with the delays. Commonly used delay-based metrics include minimizing the average project delay (APD). Other metrics, including those related to delays and the efficiency of the schedules generated, were analyzed in terms of the average percentage of project delay, efficiency, and robustness. In this review, measures related to efficiency, either average or total values, are classified as minimization of the average percent project delay (APPD) if the activity duration is deterministic; and maximization of robustness in the cases of the research presented by Zhu et al. [20], Chen et al. [21], and Wang et al. [22]. On the other hand, delays are also influenced by project weights, leading to the weighted project delay minimization (WPD) objective.
- Completion: The completion time of a project, or makespan, is defined as the time when all activities related to the project are fully completed. Meanwhile, weights are used to minimize the weighted makespan (WM), where the makespan value is multiplied by the corresponding weight, so the higher the weight, the greater the impact it has on the objective function. Table 1 shows the existing research in the reviewed literature that addresses time-based objective functions.
 Table 1. Research works that address time-based objective functions.
Table 1. Research works that address time-based objective functions.
4.1.2. Cost-Based Objectives
The goal of minimizing project costs in an RCMPSP is to optimize allocation of resources across multiple projects, thereby reducing the total expenses associated with project execution. Maximizing total profit while minimizing project costs can involve various factors, such as minimizing the expenses associated with the allocation and utilization of resources, including labor, equipment, and materials. This ensures that resources are not idle and are used effectively across multiple projects. In addition, projects must be completed on or before deadlines to avoid penalties. This also allows for quicker project finishes, increasing the capacity for taking on new projects. This dual focus on cost minimization and profit maximization ensures that projects are both cost-effective and financially rewarding. Table 2 shows the existing research addressing cost-based objective functions.

Table 2.
Research works that address cost.
4.1.3. Cost- and Time-Based Objective Functions
Project completion time and resource use are two of the most extensively studied factors in the literature. In the previous sections, the related objective functions were defined individually. Table 3 now shows the existing research that addresses both resource and time objectives together.

Table 3.
Research works that address cost-and-time-based objectives.
4.1.4. Resource Leveling Objectives
Resources should be managed in such a way that all activities get completed without encountering shortages. Resource management enables a project to be accomplished on time, at or below cost, and without compromising quality. Nevertheless, resource scarcity and common activity requirements will lead to conflicts in schedules. These conflicts worsen when dealing with a limited number of resources assigned to multiple simultaneous projects. Hence, there should be an efficient approach to consuming available resources [82]. Resource leveling addresses this issue by trying to make resource consumption as efficient as possible without extending the project completion time [87].
In Maenhout and Vanhoucke’s [63] approach, an attempt was made to level staffing requirements over the planning horizon, which reduced the need for costly temporal resources and overtime significantly.
Table 4 shows the existing research that addresses the resource leveling objective.

Table 4.
Research works that address the resource leveling objective.
4.1.5. Research on Objective Functions: Summary and Analysis
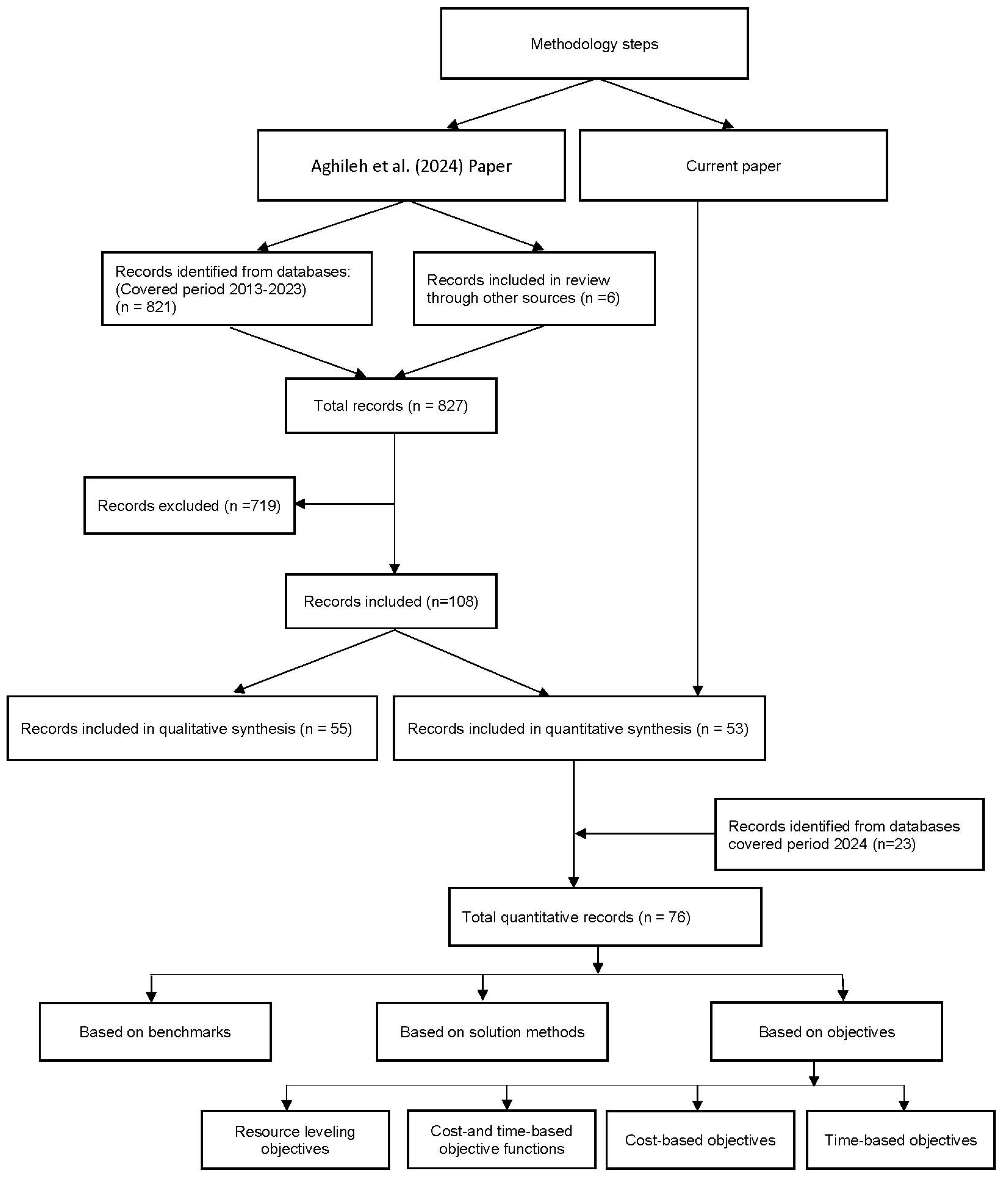
Figure 2 classifies the works’ percentages according to the different classifications proposed. The most frequently considered objective functions are makespan minimization (38.75%), total project cost minimization (18.75%), and cost-time (12.50%). Weighted project delay (7.50%) and resource leveling (6.25%) are the next most pursued objectives corresponding to completion and delay sub-classifications.
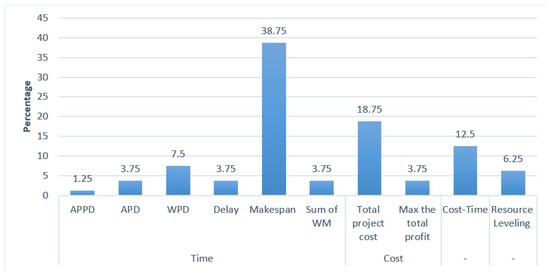
Figure 2.
Percentage of research by classification of the different objective functions studied.
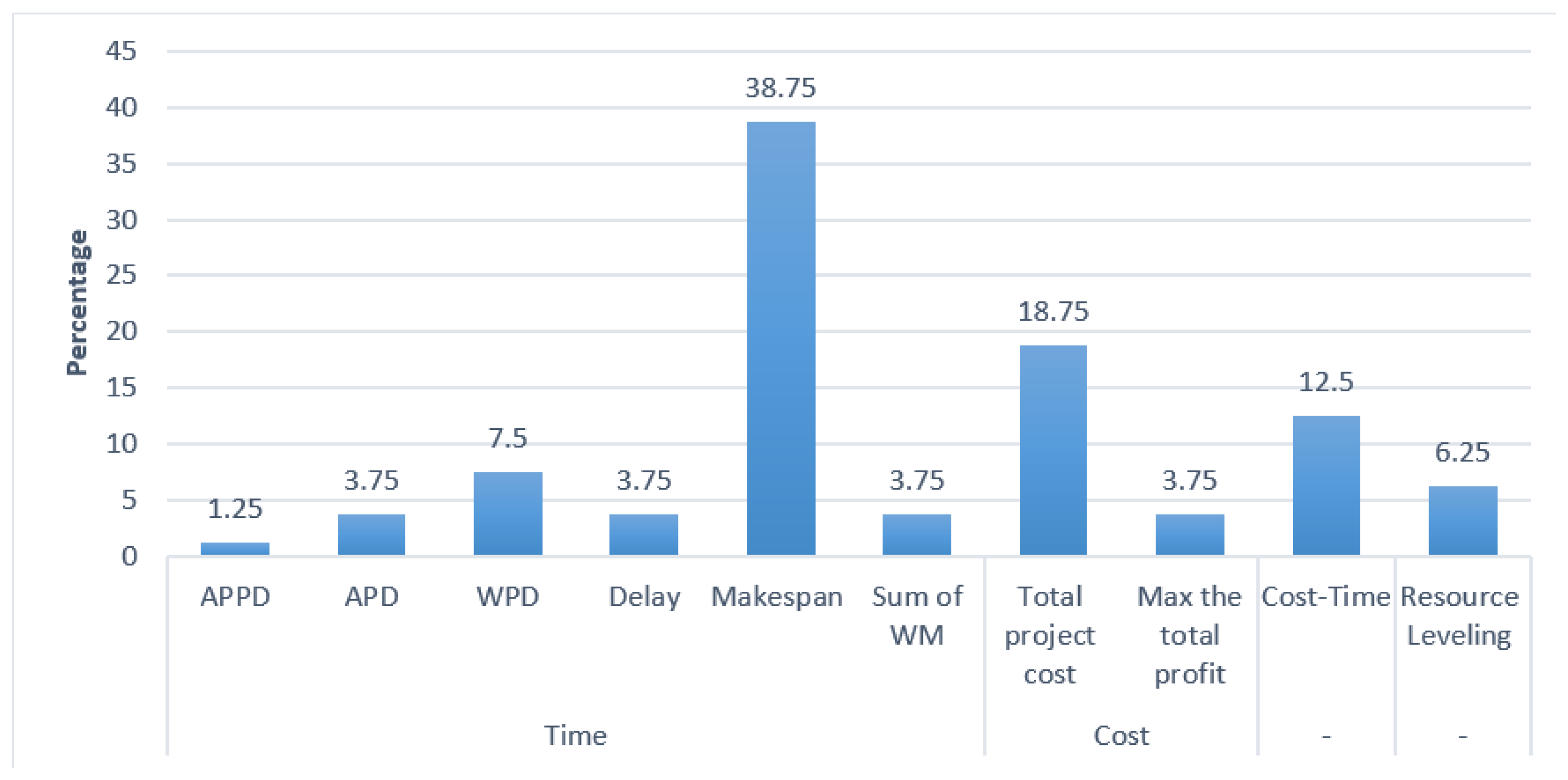
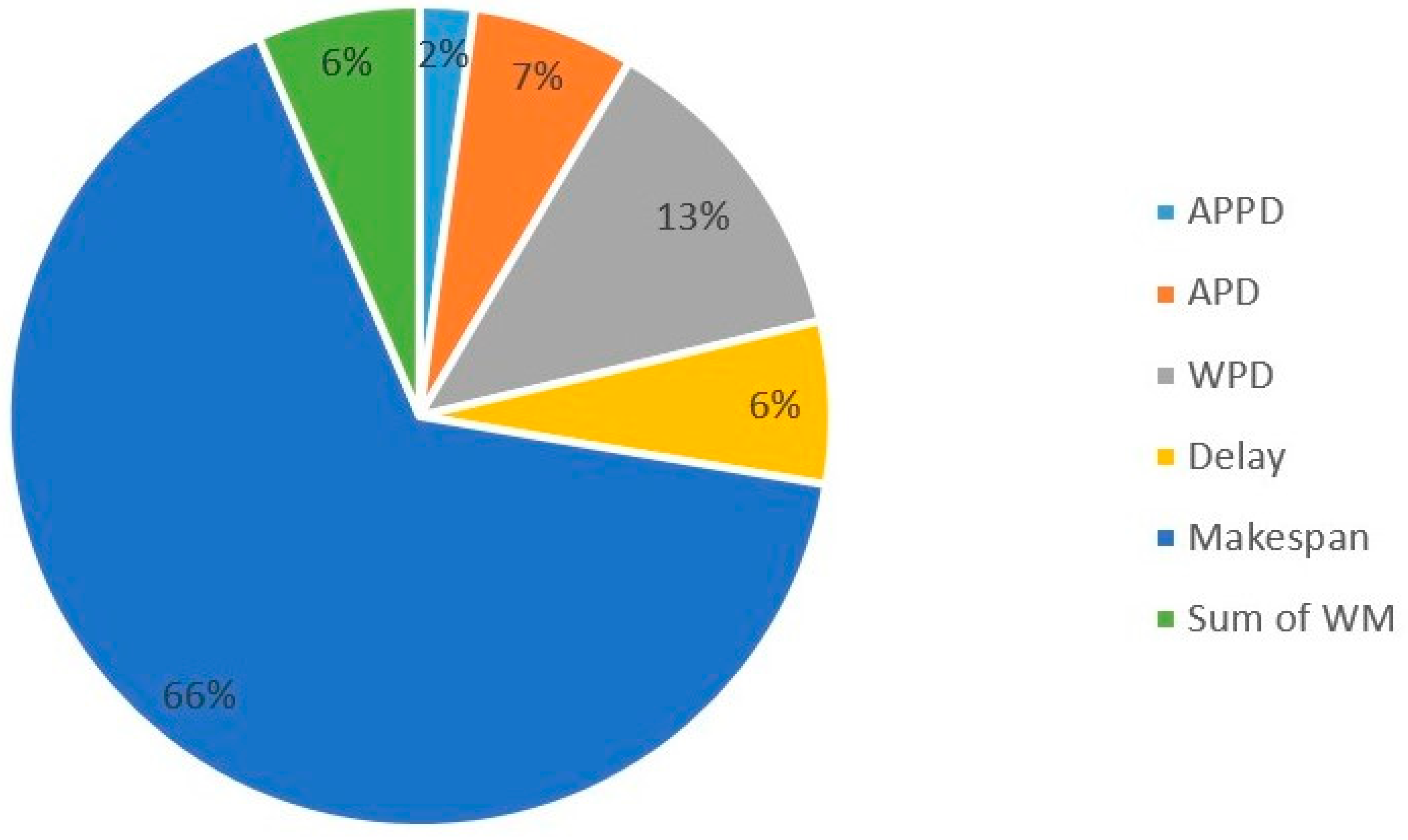
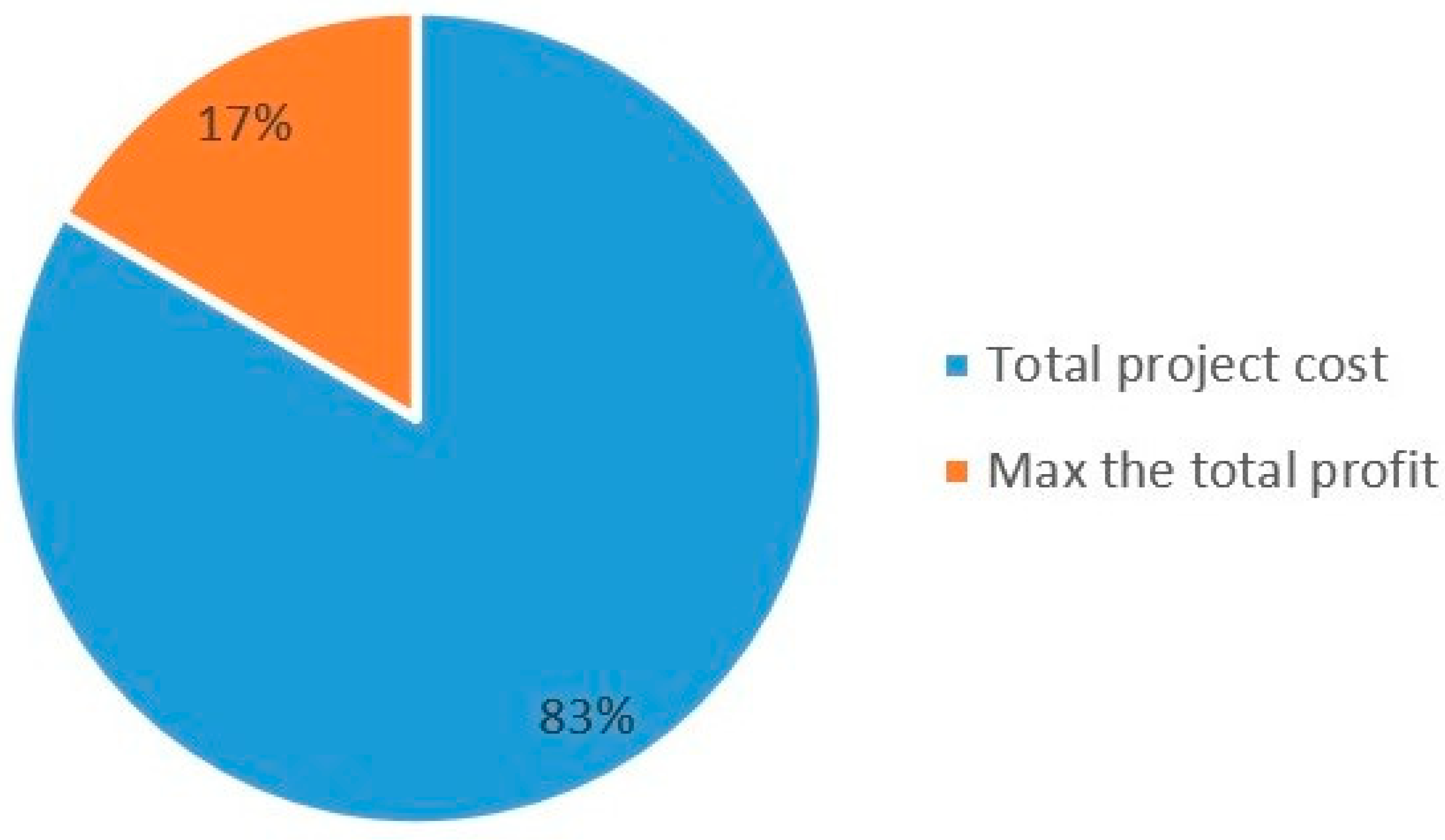
For a more in-depth review, Figure 3 and Figure 4 show the percentage of works that consider time-based and cost-based objective functions, respectively. As can be observed in Figure 3 and Figure 4, makespan (66%) and total project cost (83%) are the most studied.
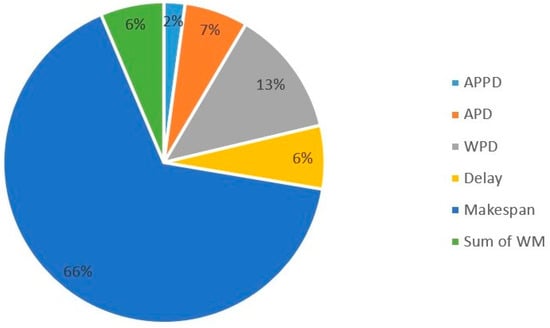
Figure 3.
Percentage of research by classification of time-based objective function studied.
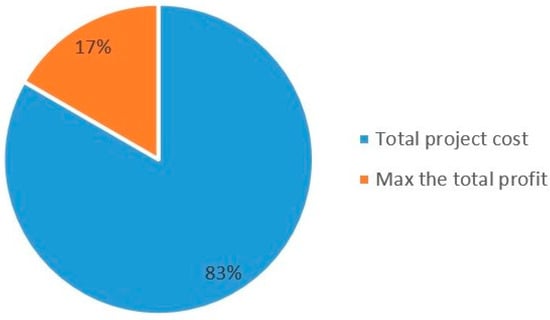
Figure 4.
Percentage of research by classification of cost-based objective function studied.
4.2. Based on Solution Methods
In real life, project constraints present only one of the challenges in project planning. Over the past two decades, various techniques of planning project scheduling under resource constraints were proposed, implemented, and controlled, which can broadly be categorized into exact and approximate methods. In fact, it is known that the Resource-Constrained Project-Scheduling Problem has a history longer than 40 years. There are two approaches, exact and approximate, for solving the problem. Each of these approaches has disadvantages and advantages. Exact approaches for solving the RCPSP were first proposed by Talbot [88], followed by Sprecher and Drexl [89]. Exact methods provide optimal results. Exact methods include Dynamic Programming, Constraint Programming, and Mixed Integer Programming, including Lagrangian Relaxation, Zero-One Programming, and Branch and Bound (B&B). These algorithms only solve small problems and cannot find optimal solutions in reasonable computation times. Thus, these algorithms cannot work for large and complex projects. Many research papers have employed exact methods to deal with RCPSP [90,91].
To overcome the computational burden of exact methods, at the expense of optimality, approximate methods are an alternative. These methods, instead of searching the entire problem space, search only a part of it, so the results may not be optimal. They aim, instead, to achieve an approximate solution, but they can solve huge problems quickly.
The approaches are categorized into two different groups: (1) approaches based on heuristic methods such as PR-based approaches, Forward and Backward Improvement (FBI), and Network analysis; and (2) approaches based on meta-heuristic methods such as genetic algorithm (GA), Tabu Search (TS), Simulated Annealing (SA), and Ant Colony Optimization (ACO) [14,16,30,47,67,92,93]. Recent years have witnessed a rise in hybrid optimization approaches for solving complex variants, like the Multi-Mode Resource-Constrained Project Scheduling Problem (MRCPSP). For instance, Toffolo et al. [40] proposed an integer programming-based approach for multi-mode scheduling, while Zarei et al. [77] explored a bi-objective hybrid model combining MILP with GAs. Other hybrid algorithms merge TS with decomposition methods [94] or integrate local searching within evolutionary algorithms to improve convergence speed and solution diversity.
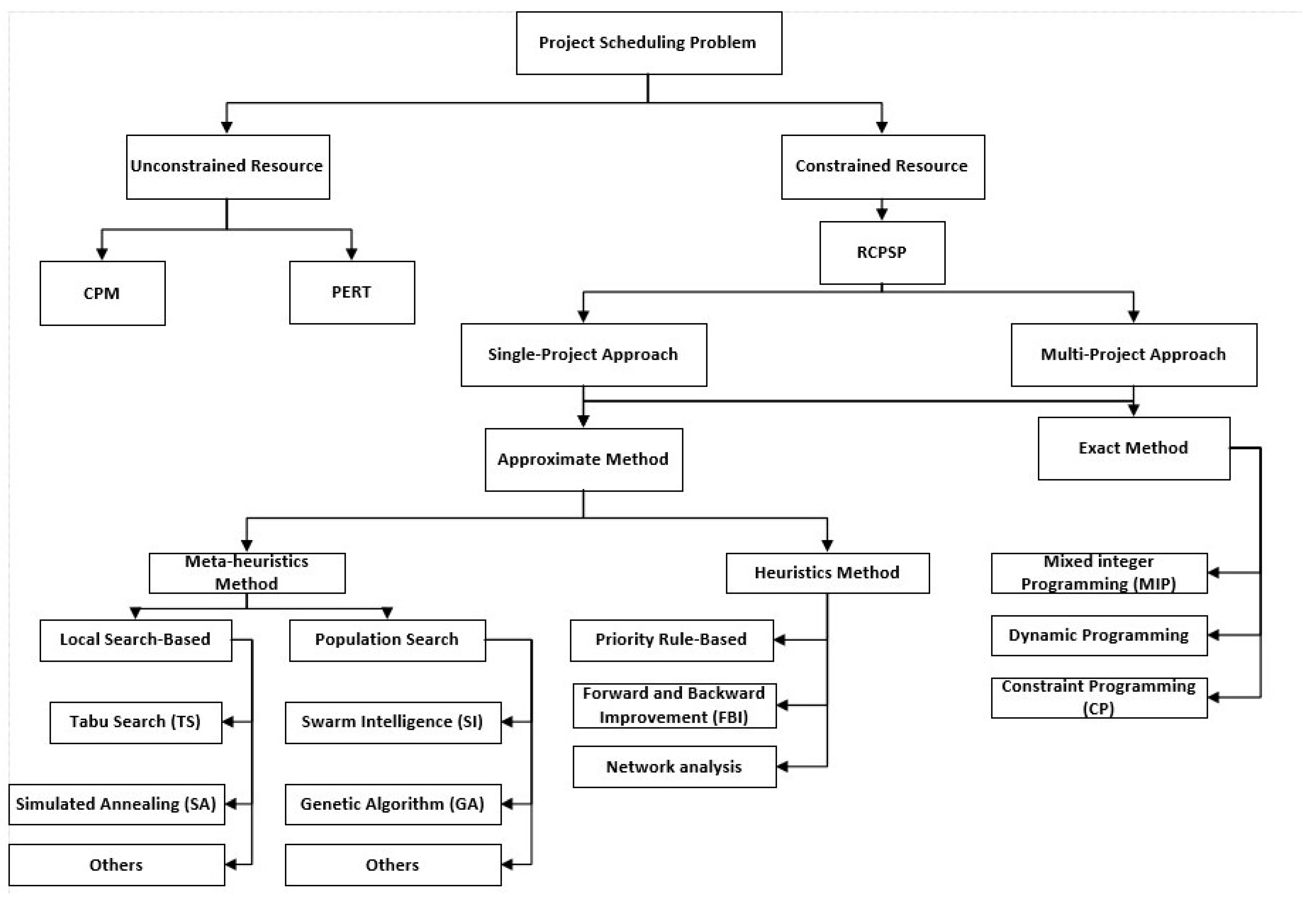
In addition, Artificial Intelligence (AI) and machine learning techniques are increasingly applied in project scheduling. Chen et al. [54] proposed a genetic programming framework for stochastic RCMPSP under project insertions. Neural networks have also been explored for predictive modeling of activity durations and decision support in dynamic environments (e.g., Hematian et al. [80] and Yuan et al. [95]). These AI-based approaches enhance adaptability and robustness in uncertain and multi-mode settings. An overview of the project scheduling problem can be seen in Figure 5.
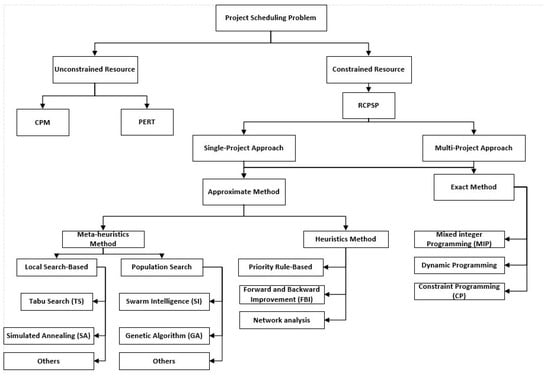
Figure 5.
An overview of project-scheduling problems and solving methods.
Table 5 and Table 6 show the works that used each exact or approximate algorithm, respectively, to solve the problem.

Table 5.
Reports of exact solution methods for RCMPSP variants.

Table 6.
Reports of approximate solution methods for RCMPSP variants.
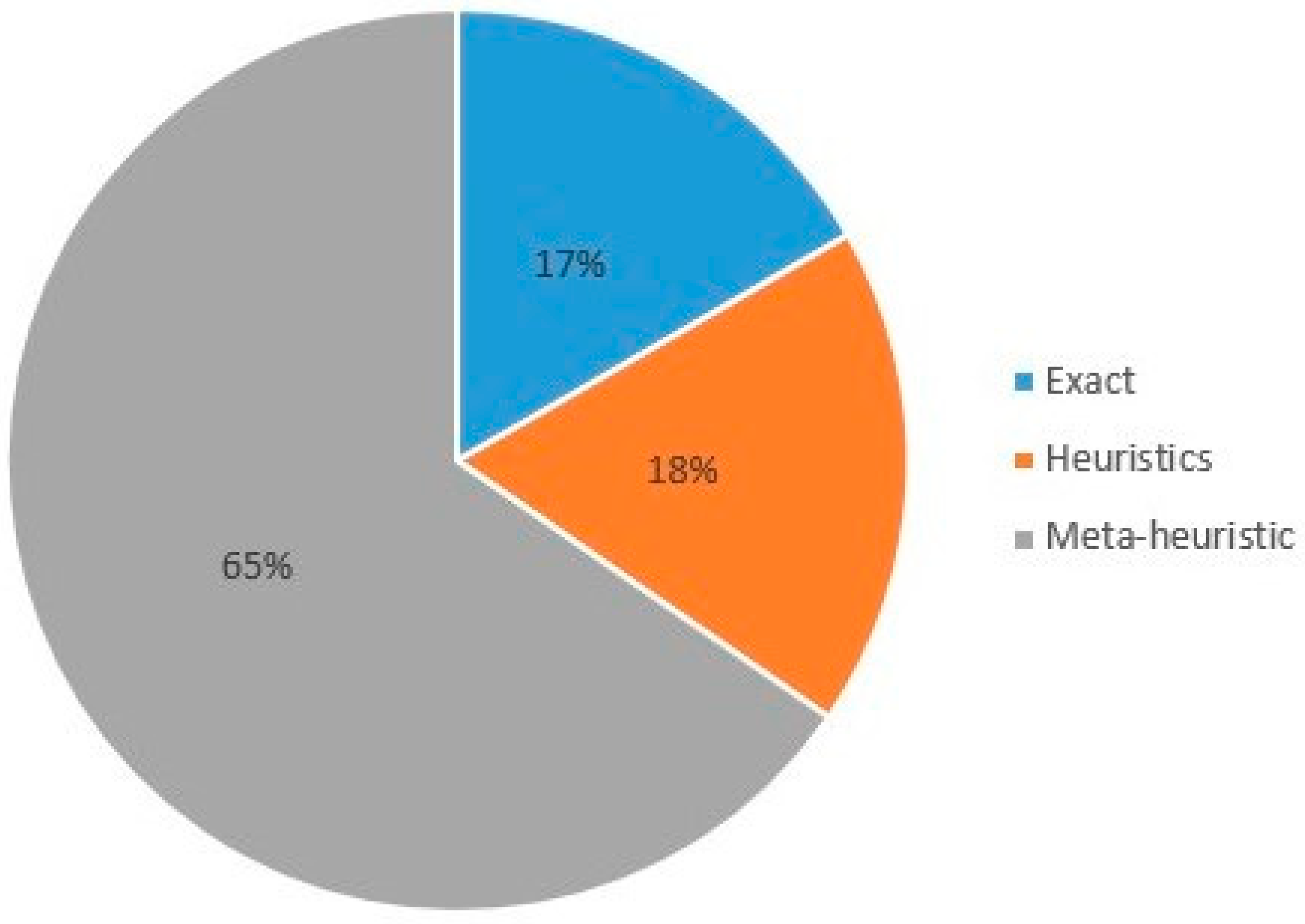
Initially, RCMPSP variants were solved mainly using mathematical models and PR-based heuristics. With increasing complexity and the emergence of new solution techniques, a broader array of proposed solution methodologies was expanded. Figure 6 shows the percentages of use of approximate and exact algorithms. It is clear that meta-heuristics are the most widely used (65%).
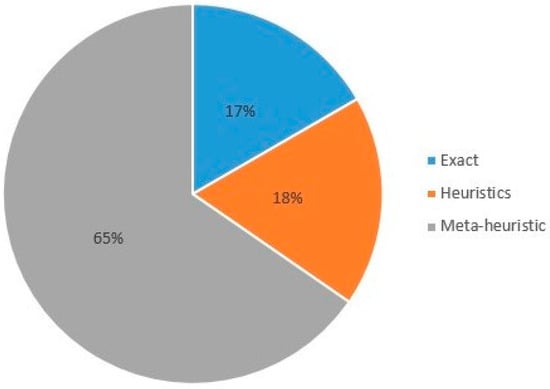
Figure 6.
Percentages of different solution methods applied to the RCMPSP.
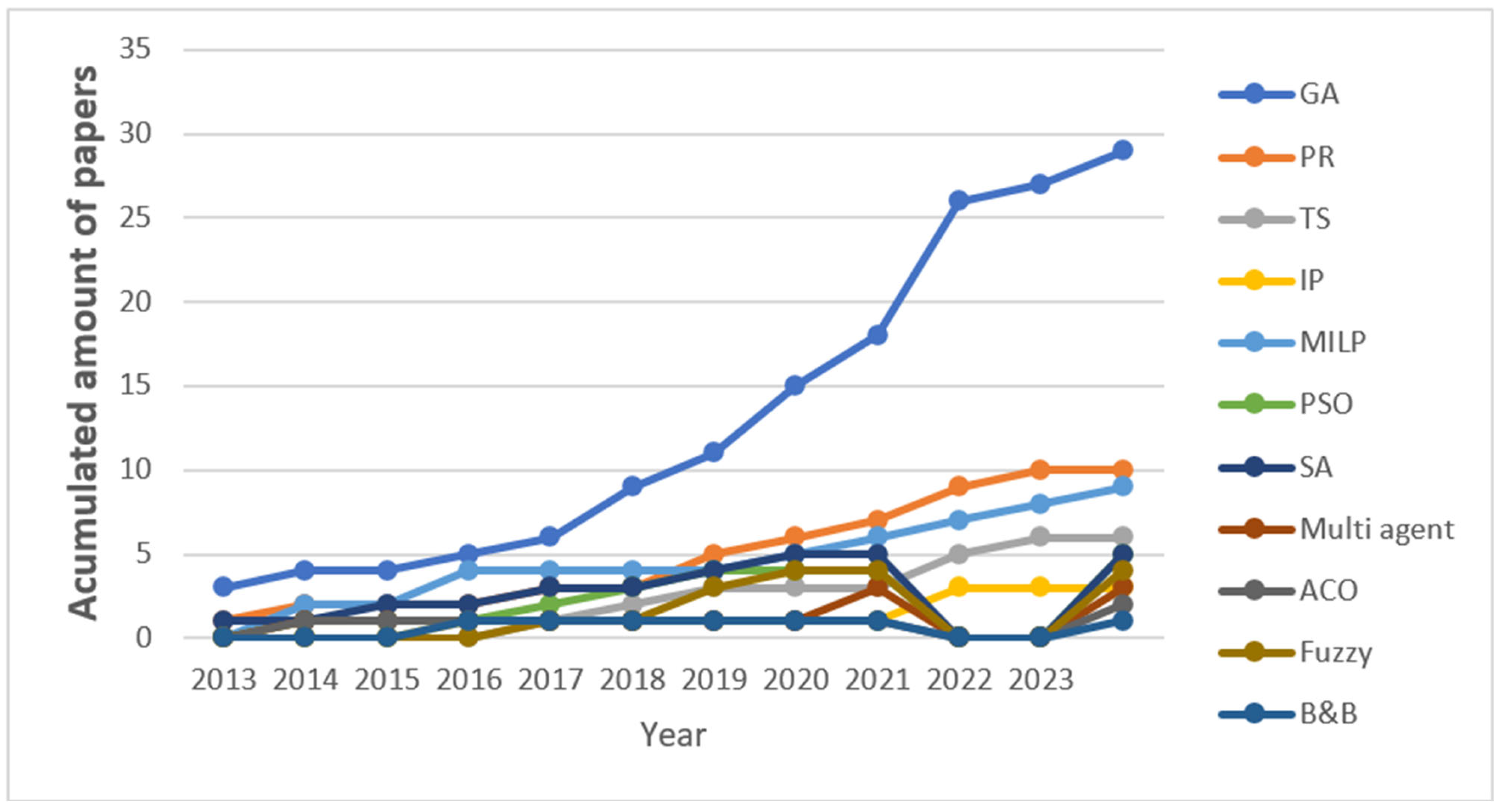
To identify the primary solution methods employed for addressing the problem in recent years, Figure 7 illustrates the research conducted since 2013, focusing on methods that have been examined in a minimum of 12 studies.
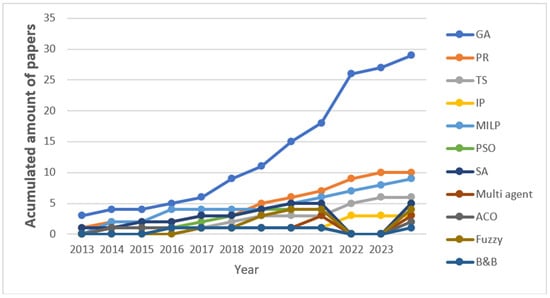
Figure 7.
Contribution of different algorithms applied to scheduling problems since 2013.
To the best of our knowledge, PR-based heuristic and genetic algorithms are the most used algorithms for solving the problem since the beginning, presenting a stable growth since 2013, with 37% and 14% of studies, respectively. Algorithms based on Tabu search (8%), Particle Swarm Optimization (PSO), and simulated annealing appear in up to 6% of the works. Furthermore, algorithms based on multi-agent systems and integer programming are used in 4% of the works. Finally, algorithms based on linear programming showed important growth in the last three years.
4.3. Based on Benchmarks
When research on the RCMPSP first began, there were no established instance sets available to assess the performance of the proposed algorithms, so most studies relied on problem examples for validation. This approach is still common in recent studies, primarily because of the numerous features introduced and the absence of instance sets for each specific problem variant. Furthermore, many studies evaluate their models and algorithms using instances they generate themselves for the particular RCMPSP variant they are examining. Kolisch and Sprecher [97] proposed a project scheduling problem library (PSPLIB) for study of the RCPSP. Subsequently, numerous studies on the RCMPSP utilized that benchmark in their numerical experiments by merging two or more single-project instances, incorporating the necessary elements to address the relevant features, and creating specific multi-project instances. Additionally, various studies were conducted using real-world instances, highlighting the significance of this problem in the industrial sector. The initial and most well-known set of instances is the multi-project scheduling problem library (MPSPLIB), presented by Homberger [98], which focuses on RCMPSP with local resources. MPSPLIB contains 80 generated instances from the combination of 2, 5, 10, or 20 projects from the PSPLIB, each consisting of 30, 90, or 120 activities. Each project is assigned an arrival time, and resources can be utilized both globally and locally. Later, this library was expanded by Homberger [99], adding 60 more instances that vary in terms of access to local resources. MPSPLIB supports the online evaluation of solutions and offers a range of objective functions. Another notable variant with a specific set of instances is the multi-mode RCMPSP. This set was developed for the MISTA-2013 challenge and is composed of project groups taken from the PSPLIB by adding multiple execution modes. Table 7 shows the research in the reviewed literature that uses each instance set.

Table 7.
Research works that address benchmarks.
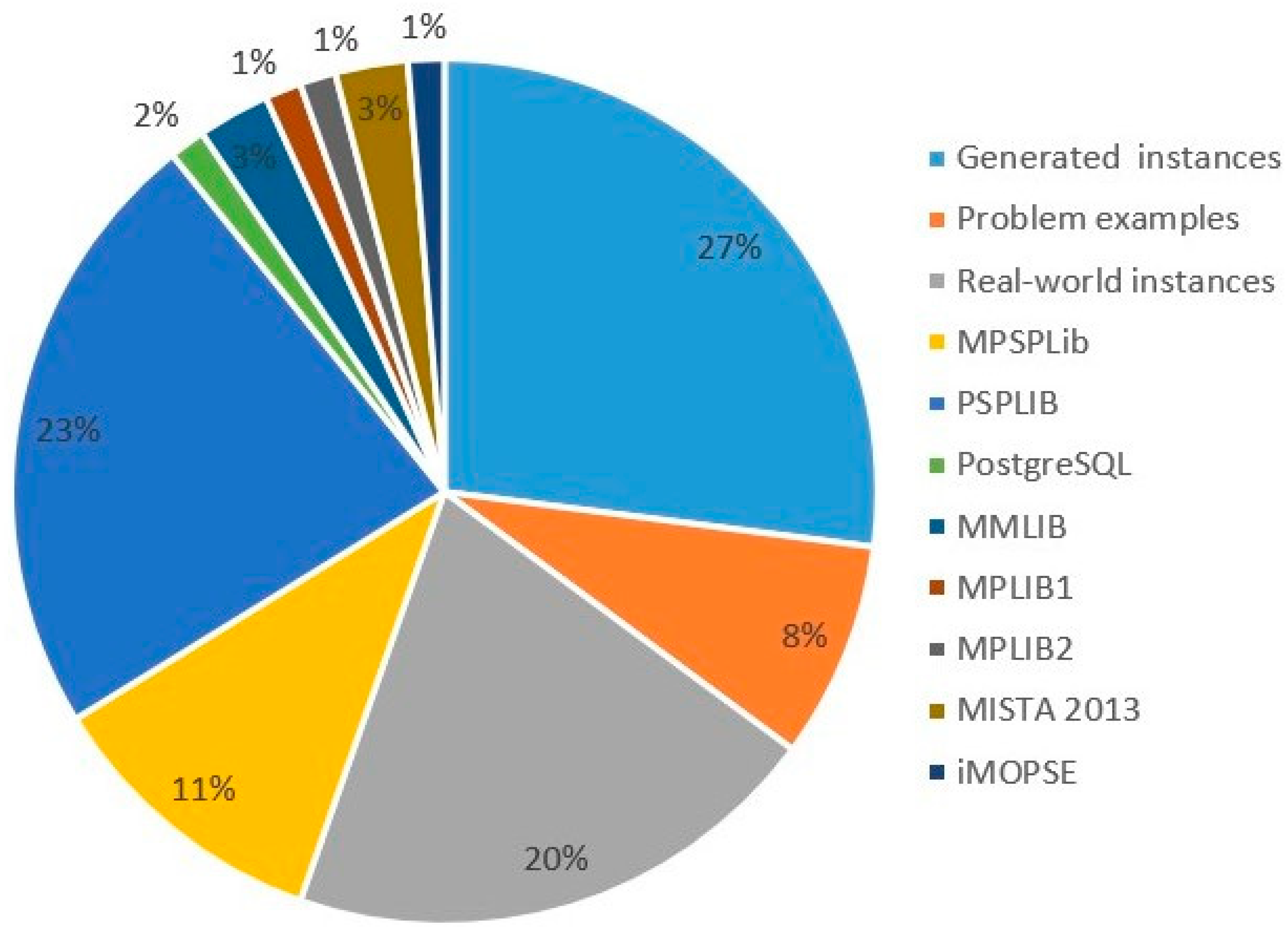
Figure 8 shows the percentages of works using the different instance sets described above. The generated sets represent the highest percentage of the most used benchmark (27%). Then, the second highest percentage is represented by the PSPLIB in the different works, at 23%. It is important to note that 20% of the research was conducted using real-world-based instances.
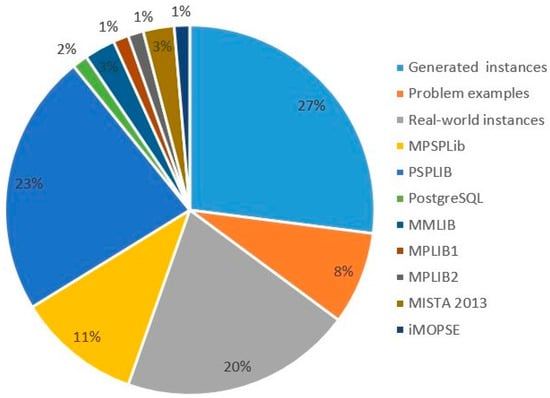
Figure 8.
Percentage of research on a different set of instances.
5. Discussion and Findings
The main goal of this section is to provide an insightful analysis of advancements in multi-project scheduling under conditions of uncertainty and resource flexibility. A brief description of them was presented in Section 2, and in the following section achievements will be reported for each of them.
Key findings are organized around the major objectives in this domain, such as minimization of project makespan, minimization of project cost, or resource leveling. Overall, while minimization of project delay or project makespan is not always considered an objective in papers about RCMPSP, some papers take it into account and propose novel algorithms or models to optimize it, along with other objectives such as minimization of project cost. This is because delay, which refers to the amount of time by which a project is postponed or extended beyond its original due date, is often seen as a result.
This section provides a detailed analysis of the studies reviewed in earlier sections, focusing exclusively on those addressing real-world-based case studies, to survey the gap between theoretical approaches and practical applications concerning the RCMPSP and related variants. Table 8 presents research developed in real environments, highlighting the significance of this problem within the industrial sector. Column 2 shows the application domain. Columns 3–5 show the dimensions of the scenarios handled by each case in terms of the maximum number of projects, the maximum number of activities, and the maximum number of different resources considered. Following the categorization provided in Section 4, columns 6–10 report the objective functions.

Table 8.
Research works applied to real environments.
Additionally, to analyze the different objective functions applied in real environments, this table shows the applications in the manufacturing field that are the most representative ones, while 15 real-world-based cases are examined. The most used objectives are related to time-based objective functions. Based on the reported works, it can be observed that makespan minimization is the most used one, followed by minimization of total project cost.
To provide a broader perspective, a separate table (Table 9) was compiled in which the key contributions, strengths, weaknesses, and future suggestions of some related studies were randomly reviewed. Through this comparative analysis, existing research gaps are identified, and the novelty and relevance of the proposed approach are clarified. In this way, a more comprehensive understanding of the current state of the field is facilitated, and the positioning of the present work within the broader academic discourse is strengthened.

Table 9.
Comparison of the papers.
6. Conclusions
This paper shows a comprehensive review of multi-project scheduling approaches, with a focus on uncertainty and resource flexibility methodologies. This is a topic of growing interest for academics and users. From the SLR [19], the authors initially selected a limited number of studies (52 papers) from a pool of 108 papers. Additional relevant works and newly published papers from 2024 were subsequently incorporated, resulting in a final set of 76 papers being curated for review.
The paper presented a review of RCMPSP evolution by analyzing related variants in terms of the objective functions, proposed solution methods, benchmarks, and connection to practice. The following text will report the achievements in light of the research questions.
- RQ1.
- What are the objectives in multi-project scheduling problems?
The objective functions in multi-project scheduling typically include time-based, cost-based, cost-and-time-based, and resource leveling objectives. Among these, time-based and cost-based objectives are the most extensively studied. Specifically, minimization of the makespan, weighted project delay, and total project cost are the predominant goals within these categories.
- RQ2.
- What are the different types of solving methods in multi-project scheduling problems?
There are two primary approaches for solving multi-project scheduling problems: exact and approximate methods. Among these, approximate algorithms are the most frequently used for addressing RCMPSP. Notably, genetic algorithms and PR-based algorithms are particularly prominent in the resolution of these issues.
- RQ3.
- What types of instance sets are used in multi-project scheduling problems?
Regarding benchmarks, various instance sets are utilized, including generated instances, problem examples, real-world instances, MPSPLIB, PSPLIB, PostgreSQL, MMLIB, MPLIB1, MPLIB2, MISTA 2013, and iMOPSE. Among these, generated sets and the PSPLIB are the most frequently used, representing the two highest percentages of instance sets employed in research and practical applications.
- RQ4.
- What are the potential future research directions in multi-project scheduling problems?
It is hoped that this work will encourage future research to explore this area further, fostering the development of more effective strategies and methodologies. A summary of the identified problems, objectives, and proposed future research directions is presented in Table 10.

Table 10.
Problem, objective, and future work.
This research brings the user a researcher database for existing methodologies to improve investigation in the future to solve the problem using the available information on these topics and approaches. For example, consider the following:
- Integrating concepts such as activity flexibility and activity priority into project scheduling.
- Different types of uncertain factors should be considered, for example, dynamic project arrival, stochastic resource availability, etc., and their impact on the resource usage deviation levels of the projects should be measured.
- Deviation in customer demand.
- Different scenarios for project duration (pessimistic, most probable, and optimistic).
- Design different PRs for the stochastic environment and compare them to the performance of the previous PRs.
- Use the exact method along with a heuristic or meta-heuristic method to compare the results.
- Analyze whether the company accepts delays and late penalty fees or outsourcing.
Funding
This work was supported by Fundação para a Ciência e Tecnologia, IP (FCT) under grant [UI/BD/151165/2021] and within the R&D Units Project Scope: UID/00319/Centro ALGORITMI (ALGORITMI/UM). Furthermore, we would like to thank the Research Centre in Digital Services (CISeD) and the Instituto Politécnico de Viseu for their support. I.P. was funded by National Funds through the Foundation for Science and Technology (FCT) within the scope of project UIDB/05583/2020 and DOI identifier https://doi.org/10.54499/UIDB/05583/2020.
Data Availability Statement
No new data were created or analyzed in this study.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| Abbreviation | Description |
| ACO | Ant Colony Optimization Algorithm |
| AI | Artificial Intelligence |
| APD | Average Project Delay |
| APPD | Average Percent Project Delay |
| B&B | Branch and Bound |
| CPM | Critical Path Method |
| FBI | Forward and Backward Improvement |
| FRCPSP | Flexible Resource-Constrained Project Scheduling Problem |
| GA | Genetic Algorithm |
| IP | Integer Programming |
| MIP | Mixed Integer Programming |
| MILP | Mixed Integer Linear Programming |
| MPSPLIB | Multi-Project Scheduling Problem Library |
| MRCPSP | Multi-Mode Resource-Constrained Project Scheduling Problem |
| NP-hard | Nondeterministic Polynomial-Time Hard |
| PERT | Program Evaluation and Review Technique |
| PSO | Particle Swarm Optimization |
| PR | Priority Rule |
| PSPLIB | Project Scheduling Problem Library |
| RCPSP | Resource-Constrained Project Scheduling Problem |
| RCMPSP | Resource-Constrained Multi-Project Scheduling Problem |
| RCPSP-FRM | RCPSP with Flexible Resource Management |
| RCPSP-FWP | RCPSP with Flexible Work Profiles |
| RQ | Research Question |
| SA | Simulated Annealing |
| SGS | Schedule Generation Scheme |
| SLR | Systematic Literature Review |
| TS | Tabu Search |
| WPD | Weighted Project Delay |
| WM | Weighted Makespan |
References
- Villafañez, F.; Lopez-Paredes, A.; Pajares, J.; de la Fuente, D. From the RCPSP to the DRCMPSP: Methodological foundations. In Proceedings of the International Conference on Artificial Intelligence (ICAI), Sousse, Tunis, 18–20 January 2014; The Steering Committee of the World Congress in Computer Science, Computer Engineering and Applied Computing (WorldComp). Kluwer Academic: Athens, Greece, 2014; pp. 1–6. [Google Scholar]
- Villafáñez, F.; Poza, D.; López-Paredes, A.; Pajares, J.; Olmo, R.D. A generic heuristic for multi-project scheduling problems with global and local resource constraints (RCMPSP). Soft Comput. 2019, 23, 3465–3479. [Google Scholar] [CrossRef]
- Rokou, E.; Dermitzakis, M.; Kirytopoulos, K. Multi-project flexible resource profiles project scheduling with Ant Colony Optimization. In Proceedings of the 2014 IEEE International Conference on Industrial Engineering and Engineering Management, Selangor, Malaysia, 9–12 December 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 642–646. Available online: http://ieeexplore.ieee.org/document/7058717/ (accessed on 12 March 2015).
- Davari, M.; Demeulemeester, E. The proactive and reactive resource-constrained project scheduling problem. J. Sched. 2019, 22, 211–237. [Google Scholar] [CrossRef]
- Faria, J.; Araújo, M.; Demeulemeester, E.; Tereso, A. Project management under uncertainty: Using flexible resource management to exploit schedule flexibility. Eur. J. Ind. Eng. 2020, 14, 599. [Google Scholar] [CrossRef]
- Lima, R.; Tereso, A.; Faria, J. Project management under uncertainty: Resource flexibility visualization in the schedule. Procedia Comput. Sci. 2019, 164, 381–388. [Google Scholar] [CrossRef]
- Naber, A.; Kolisch, R. MIP models for resource-constrained project scheduling with flexible resource profiles. Eur. J. Oper. Res. 2014, 239, 335–348. [Google Scholar] [CrossRef]
- Tritschler, M.; Naber, A.; Kolisch, R. A hybrid metaheuristic for resource-constrained project scheduling with flexible resource profiles. Eur. J. Oper. Res. 2017, 262, 262–273. [Google Scholar] [CrossRef]
- Pritsker, A.A.B.; Waiters, L.; Wolfe, P. Multiproject Scheduling with Limited Resources: A Zero-One Programming Approach. Manag. Sci. 1969, 16, 1–148. [Google Scholar] [CrossRef]
- Marimuthu, K.; Raphael, B.; Ananthanarayanan, K.; Palaneeswaran, E.; Bodaghi, B. An overview of multi-project scheduling problems in India with resource constrained and unconstrained settings. In Proceedings of the 22nd International Conference on Advancement of Construction Management and Real Estate, Melbourne, Australia, 20–23 November 2017; CRIOCM 2017 Organising Committee: Melbourne, Australia, 2017; pp. 988–995. [Google Scholar]
- ElFiky, H.; Owida, A.; Galal, N.M. Resource Constrained Multi-Project Scheduling Using Priority Rules: Application in the Deep-Water Construction Industry. In Proceedings of the International Conference on Industrial Engineering and Operations Management, Dubai, United Arab Emirates, 10–12 March 2020; pp. 353–363. [Google Scholar]
- Yan, R.; Li, W.; Jiang, P.; Zhou, Y.; Wu, G. A Modified Differential Evolution Algorithm for Resource Constrained Multi-project Scheduling Problem. J. Comput. 2014, 9, 1922–1927. [Google Scholar] [CrossRef]
- Sonmez, R.; Uysal, F. Backward-Forward Hybrid Genetic Algorithm for Resource-Constrained Multiproject Scheduling Problem. J. Comput. Civ. Eng. 2015, 29, 04014072. [Google Scholar] [CrossRef]
- Shu, X.; Su, Q.; Wang, Q.; Wang, Q. Optimization of Resource-Constrained Multi-Project Scheduling Problem Based on the Genetic Algorithm. In Proceedings of the 2018 15th International Conference on Service Systems and Service Management (ICSSSM), Hangzhou, China, 21–22 July 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. Available online: https://ieeexplore.ieee.org/document/8465086/ (accessed on 16 September 2018).
- Weixin, W.; Xianlong, G.; Lvcheng, L.; Jiafu, S. Proactive and Reactive Multi-Project Scheduling in Uncertain Environment. IEEE Access 2019, 7, 88986–88997. [Google Scholar] [CrossRef]
- Zheng, Z.; Shumin, L.; Ze, G.; Yueni, Z. Resource-constraint Multi-project Scheduling with Priorities and Uncertain Activity Durations. Int. J. Comput. Intell. Syst. 2013, 6, 530. [Google Scholar] [CrossRef]
- Kolisch, R.; Meyer, K.; Mohr, R.; Schwindt, C.; Urmann, M. Ablaufplanung für die Leitstrukturoptimierung in der Pharmaforschung (Scheduling of lead structure optimization in pharmaceutical research). Z. Für Betr. Swirtschaft 2003, 73, 825–848. [Google Scholar]
- Ranjbar, M.; Kianfar, F. Resource-Constrained Project Scheduling Problem with Flexible Work Profiles: A Genetic Algorithm Approach. Sci. Iran. 2010, 17, 25–35. [Google Scholar]
- Aghileh, M.; Tereso, A.; Alvelos, F.; Monteiro Lopes, M.O. Multi-project scheduling under uncertainty and resource flexibility: A systematic literature review. Prod. Manuf. Res. 2024, 12, 2319574. [Google Scholar] [CrossRef]
- Zhu, H.; Lu, Z.; Lu, C.; Ren, Y. Modeling and algorithm for resource-constrained multi-project scheduling problem based on detection and rework. Assem. Autom. 2021, 41, 174–186. [Google Scholar] [CrossRef]
- Chen, H.; Ding, G.; Zhang, J.; Qin, S. Research on priority rules for the stochastic resource constrained multi-project scheduling problem with new project arrival. Comput. Ind. Eng. 2019, 137, 106060. [Google Scholar] [CrossRef]
- Wang, Y.; He, Z.; Kerkhove, L.-P.; Vanhoucke, M. On the performance of priority rules for the stochastic resource constrained multi-project scheduling problem. Comput. Ind. Eng. 2017, 114, 223–234. [Google Scholar] [CrossRef]
- Van Eynde, R.; Vanhoucke, M. New summary measures and datasets for the multi-project scheduling problem. Eur. J. Oper. Res. 2022, 299, 853–868. [Google Scholar] [CrossRef]
- Kühn, M.; Völker, M.; Schmidt, T. An Algorithm for Efficient Generation of Customized Priority Rules for Production Control in Project Manufacturing with Stochastic Job Processing Times. Algorithms 2020, 13, 337. [Google Scholar] [CrossRef]
- Bredael, D.; Vanhoucke, M. Multi-project scheduling: A benchmark analysis of metaheuristic algorithms on various optimisation criteria and due dates. Eur. J. Oper. Res. 2023, 308, 54–75. [Google Scholar] [CrossRef]
- Okada, I.; Weng, W.; Yang, W.; Fujimura, S. A genetic algorithm with local search using activity list characteristics for solving resource-constrained multiproject scheduling problem. IEEJ Trans. Electr. Electron. Eng. 2016, 11, S34–S43. [Google Scholar] [CrossRef]
- Besikci, U.; Ulusoy, G.; Bilge, U. A Combination of Different Resource Management Policies in a Multi-Project Environment. In Proceedings of the International Conference on Industrial Engineering and Systems Management, Rabat, Morocco, 8–30 October 2013. [Google Scholar]
- Ranjbar, M.; Hosseinabadi, S.; Abasian, F. Minimizing total weighted late work in the resource-constrained project scheduling problem. Appl. Math. Model. 2013, 37, 9776–9785. [Google Scholar] [CrossRef]
- Nabipoor Afruzi, E.; Aghaie, A.; Najafi, A. Robust Optimization for the Resource Constrained Multi-Project Scheduling Problem with Uncertain Activity Durations. Sci. Iran. 2018, 17, 361–376. [Google Scholar] [CrossRef]
- Cheng, C.; Lo, C.; Chu, C. Solving Multi-Mode Resource-Constrained Multi-Project Scheduling Problem with Combinatorial Auction Mechanisms. Int. J. Inf. Manag. Sci. 2019, 30, 143–167. [Google Scholar]
- Melchiors, P.; Kolisch, R.; Kanet, J.J. The performance of priority rules for the dynamic stochastic resource-constrained multi-project scheduling problem: An experimental investigation. Ann. Oper. Res. 2024, 338, 569–595. [Google Scholar] [CrossRef]
- Zhao, Y.; Hu, X.; Wang, J.; Cui, N. A robust multi-project scheduling problem under a resource dedication-transfer policy. Ann. Oper. Res. 2024, 337, 425–457. [Google Scholar] [CrossRef]
- Pinha, D.C.; Ahluwalia, R.S.; Senna, P. The Combinatorial Multi-Mode Resource Constrained Multi-Project Scheduling Problem. Int. J. Supply Oper. Manag. 2016, 3, 1391–1412. [Google Scholar]
- Korotkov, V.; Matveev, M. Individual Scheduling for the Multi-Mode Resource_Constrained Multi-Project Scheduling Problem. In Proceedings of the CEUR Workshop Proceedings, Aachen, Germany, 1–3 July 2024. [Google Scholar]
- He, N.; Zhang, D.Z.; Yuce, B. Integrated multi-project planning and scheduling—A multiagent approach. Eur. J. Oper. Res. 2022, 302, 688–699. [Google Scholar] [CrossRef]
- Besikci, U.; Bilge, Ü.; Ulusoy, G. Resource dedication problem in a multi-project environment. Flex. Serv. Manuf. J. 2013, 25, 206–229. [Google Scholar] [CrossRef]
- Nie, H.; Liu, B. Combining MILP with Memetic Algorithm for Scheduling and Staffing Construction Project with a Multi-skilled Workforce. In Proceedings of the 2013 International Conference on Computational and Information Sciences, Shiyang, China, 21–23 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1150–1153. [Google Scholar]
- Chen, J.; Zhu, J.; Zhang, D. Multi-project scheduling problem with human resources based on dynamic programming and staff time coefficient. In Proceedings of the 2014 International Conference on Management Science & Engineering 21st Annual Conference, Helsinki, Finland, 17–19 August 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1012–1018. [Google Scholar]
- Can, A.; Ulusoy, G. Multi-project scheduling with two-stage decomposition. Ann. Oper. Res. 2014, 217, 95–116. [Google Scholar] [CrossRef]
- Toffolo, T.A.M.; Santos, H.G.; Carvalho, M.A.M.; Soares, J.A. An integer programming approach to the multimode resource-constrained multiproject scheduling problem. J. Sched. 2016, 19, 295–307. [Google Scholar] [CrossRef]
- González, G.; Calderón, C.; González, D.; Trujillo, J. Priority Rules Performance Analysis as a GA Initial Population for RCMPSP. In Proceedings of the International Conference on Industrial Engineering and Operations, Management, Bogota, Colombia, 25–26 October 2017. [Google Scholar]
- Taheri Amiri, M.J.; Haghighi, F.R.; Eshtehardian, E.; Abessib, O. Optimization of Time, Cost and Quality in Critical Chain Method Using Simulated Annealing. Int. J. Eng. 2017, 30, 627–635. [Google Scholar]
- Li, S.; Dong, X.; Han, S. Research on a Multi-project Scheduling Optimization Algorithm with Resource Time-Windows. In Proceedings of the 2nd International Conference on Computational Modeling, Simulation and Applied Mathematics, Beijing, China, 22–23 October 2017. [Google Scholar]
- Tian, J.; Han, X.; Dong, S. Optimizing for a Resource-constrained Multi-project Scheduling Problem with Planned Resource Unavailability. In Proceedings of the 3rd International Conference on Modelling, Simulation and Applied Mathematics, Shanghai, China, 22–23 July 2018. [Google Scholar]
- Yuan, P.; Han, W.; Su, X.; Liu, J.; Song, J. A Dynamic Scheduling Method for Carrier Aircraft Support Operation under Uncertain Conditions Based on Rolling Horizon Strategy. Appl. Sci. 2018, 8, 1546. [Google Scholar] [CrossRef]
- Maher, G.; Abd-El-Roaf, O.; El-Hefnawy, N.; Kfafy, A. A Novel Approach for Multi-Resource Planning in Construction Engineering. In Proceedings of the 2019 Ninth International Conference on Intelligent Computing and Information Systems (ICICIS), Cairo, Egypt, 8–10 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 278–284. [Google Scholar]
- Jiang, C.; Hu, X.; Xi, J. A hybrid algorithm of product-service framework for the multi-project scheduling in ETO assembly process. Procedia CIRP 2019, 83, 298–303. [Google Scholar] [CrossRef]
- Yang, D.; Zhou, X.; Yang, Z.; Jiang, Q.; Feng, W. Multi-objective optimization Model for Flexible Job Shop Scheduling Problem Considering Transportation Constraints: A Comparative Study. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–8. Available online: https://ieeexplore.ieee.org/document/9185653/ (accessed on 3 September 2020).
- Hauder, V.A.; Beham, A.; Raggl, S.; Parragh, S.N.; Affenzeller, M. Resource-constrained multi-project scheduling with activity and time flexibility. Comput. Ind. Eng. 2020, 150, 106857. [Google Scholar] [CrossRef]
- Somy, S.; Shafaei, R.; Ramezanian, R. Resilience-based mathematical model to restore disrupted road-bridge transportation networks. Struct. Infrastruct. Eng. 2021, 18, 1334–1349. [Google Scholar] [CrossRef]
- Liu, D.; Xu, Z.; Li, F. A three-stage decomposition algorithm for decentralized multi-project scheduling under uncertainty. Comput. Ind. Eng. 2021, 160, 107553. [Google Scholar] [CrossRef]
- Cui, L.; Liu, X.; Lu, S.; Jia, Z. A variable neighborhood search approach for the resource-constrained multi-project collaborative scheduling problem. Appl. Soft Comput. 2021, 107, 107480. [Google Scholar] [CrossRef]
- Winklehnera, P.; Hauder, V.A. Flexible job-shop scheduling with release dates, deadlines and sequence dependent setup times: A real-world case. In Proceedings of the 3rd International Conference on Industry 4.0 and Smart Manufacturing, Linz, Austria, 2–4 November 2022; pp. 1654–1663. [Google Scholar]
- Chen, J.C.; Lee, H.-Y.; Hsieh, W.-H.; Chen, T.-L. Applying hybrid genetic algorithm to multi-mode resource constrained multi-project scheduling problems. J. Chin. Inst. Eng. 2022, 45, 42–53. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, J.; Li, R.; Ding, G.; Qin, S. A two-stage genetic programming framework for Stochastic Resource Constrained Multi-Project Scheduling Problem under New Project Insertions. Appl. Soft Comput. 2022, 124, 109087. [Google Scholar] [CrossRef]
- Chen, H.; Ding, G.; Zhang, J.; Li, R.; Jiang, L.; Qin, S. A filtering genetic programming framework for stochastic resource constrained multi-project scheduling problem under new project insertions. Expert Syst. Appl. 2022, 198, 116911. [Google Scholar] [CrossRef]
- Zohrehvandi, S. A Project-Scheduling and Resource Management Heuristic Algorithm in the Construction of Combined Cycle Power Plant Projects. Computers 2022, 11, 23. [Google Scholar] [CrossRef]
- Sadeghloo, M.; Emami, S.; Divsalar, A. A Benders decomposition algorithm for the multi-mode resource-constrained multi-project scheduling problem with uncertainty. Ann. Oper. Res. 2023, 339, 1637–1677. [Google Scholar] [CrossRef]
- Kopanos, G.M.; Kyriakidis, T.S.; Georgiadis, M.C. New continuous-time and discrete-time mathematical formulations for resource-constrained project scheduling problems. Comput. Chem. Eng. 2014, 68, 96–106. [Google Scholar] [CrossRef]
- Wu, Y.N.; Ding, Y. Research on the resource-constrained government investment multi-project scheduling problems. In Proceedings of the International Conference on Material Science and Environmental Engineering, Wuhan, China, 5–6 June 2015. [Google Scholar]
- Liu, M.; Shan, M.; Wu, J. Multiple R&D Projects Scheduling Optimization with Improved Particle Swarm Algorithm. Sci. World J. 2014, 2014, 1–7. [Google Scholar] [CrossRef]
- Farizal, F.; Rachman, A.; Tandean, T.; Sudarto, S.; Takahashi, K. Multi-Project Scheduling Cost Optimization in a Machine Manufacturer Engineer-to-Order. Makara J. Technol. 2016, 20, 13. [Google Scholar] [CrossRef]
- Maenhout, B.; Vanhoucke, M. An exact algorithm for an integrated project staffing problem with a homogeneous workforce. J. Sched. 2016, 19, 107–133. [Google Scholar] [CrossRef]
- Cheng, C.; Lo, C. Multi-Project Scheduling by Fuzzy Combinatorial Auction. In Proceedings of the 2017 3rd IEEE International Conference on Cybernetics (CYBCONF), Exeter, UK, 21–23 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. Available online: http://ieeexplore.ieee.org/document/7985794/ (accessed on 20 July 2017).
- Fu, X.; Qi, L.; Wang, F. Hybrid constrained flexible city resource scheduling scheme based on particle swarm optimization. J. Acta Tech. 2017, 62, 1447–1458. [Google Scholar]
- Li, F.; Xu, Z. A multi-agent system for distributed multi-project scheduling with two-stage decomposition. PLoS ONE 2018, 13, e0205445. [Google Scholar] [CrossRef]
- Rostami, M.; Bagherpour, M. A lagrangian relaxation algorithm for facility location of resource-constrained decentralized multi-project scheduling problems. Oper. Res. 2020, 20, 857–897. [Google Scholar] [CrossRef]
- Abdzadeh, B.; Noori, S.; Ghannadpour, S.F. Simultaneous scheduling of multiple construction projects considering supplier selection and material transportation routing. Autom. Constr. 2022, 140, 104336. [Google Scholar] [CrossRef]
- Chen, J.C.; Chen, Y.-Y.; Chen, T.-L.; Lin, Y.-H. Multi-project scheduling with multi-skilled workforce assignment considering uncertainty and learning effect for large-scale equipment manufacturer. Comput. Ind. Eng. 2022, 169, 108240. [Google Scholar] [CrossRef]
- Yu, Y.; Xu, Z.; Liu, D.; Zhao, S. A two-stage approach with softmax scoring mechanism for a multi-project scheduling problem sharing multi-skilled staff. Expert Syst. Appl. 2022, 203, 117385. [Google Scholar] [CrossRef]
- Javanmard, S.; Afshar-Nadjafi, B.; Akhavan Niaki, S. A bi-objective model for scheduling of multiple projects under multi-skilled workforce for distributed load energy usage. Oper. Res. 2022, 22, 2245–2280. [Google Scholar] [CrossRef]
- Ryu, J.; Park, S. A branch-and-price algorithm for the robust single-source capacitated facility location problem under demand uncertainty. EURO J. Transp. Logist. 2022, 11, 100069. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, X.; Cao, X.; Wu, C. An efficient hybrid integer and categorical particle swarm optimization algorithm for the multi-mode multi-project inverse scheduling problem in turbine assembly workshop. Comput. Ind. Eng. 2022, 169, 108148. [Google Scholar] [CrossRef]
- Shou, Y.; Xiang, W.; Li, Y.; Yao, W. A Multiagent Evolutionary Algorithm for the Resource-Constrained Project Portfolio Selection and Scheduling Problem. Math. Probl. Eng. 2014, 2014, 1–9. [Google Scholar] [CrossRef]
- Nieto, A.; Serra, M.; Juan, A.A.; Bayliss, C. A GA-simheuristic for the stochastic and multi-period portfolio optimisation problem with liabilities. J. Simul. 2022, 17, 632–645. [Google Scholar] [CrossRef]
- Ghoroqi, M.; Ghoddousi, P.; Makui, A.; Shirzadi Javid, A.A.; Talebi, S. An Integrated Model for Multi-Mode Resource-Constrained Multi-Project Scheduling Problems Considering Supply Management with Sustainable Approach in the Construction Industry under Uncertainty Using Evidence Theory and Optimization Algorithms. Buildings 2023, 13, 2023. [Google Scholar] [CrossRef]
- Zarei, F.; Arashpour, M.; Mirnezami, S.-A.; Shahabi-Shahamiri, R.; Ghasemi, M. Multi-skill resource-constrained project scheduling problem considering overlapping: Fuzzy multi-objective programming approach to a case study. Int. J. Constr. Manag. 2024, 24, 820–833. [Google Scholar] [CrossRef]
- Weixin, W.; XU, W.; Xianlong, G.; Lin, Y.; Yang, C.; Jia, G. Research of multi-attribute trade-off optimization on critical Chain Multi-project scheduling. J. Theor. Appl. Inf. Technol. 2013, 48, 2. [Google Scholar]
- Luo, X.; Guo, S.; Du, B.; Luo, X.; Guo, J. Multi-Objective Multi-Skill Resource-Constrained Project Scheduling Considering Flexible Resource Profiles. Appl. Sci. 2024, 14, 1921. [Google Scholar] [CrossRef]
- Hematian, M.; Seyyed Esfahani, M.M.; Mahdavi, I.; Mahdavi-Amiri, N.; Rezaeian, J. A multiobjective integrated multiproject scheduling and multiskilled workforce assignment model considering learning effect under uncertainty. Comput. Intell. 2020, 36, 276–296. [Google Scholar] [CrossRef]
- Chen, R.; Liang, C.; Gu, D.; Leung, J.Y.-T. A multi-objective model for multi-project scheduling and multi-skilled staff assignment for IT product development considering competency evolution. Int. J. Prod. Res. 2017, 55, 6207–6234. [Google Scholar] [CrossRef]
- Sayyadi, A.; Esmaeeli, H.; Hosseinian, A.H. A community detection approach for the resource leveling problem in a multi-project scheduling environment. Comput. Ind. Eng. 2022, 169, 108202. [Google Scholar] [CrossRef]
- Peng, W.; Lin, J.; Zhang, J.; Chen, L. A bi-objective hierarchical program scheduling problem and its solution based on NSGA-III. Ann. Oper. Res. 2022, 308, 389–414. [Google Scholar] [CrossRef]
- Uysal, F.; Sonmez, R.; Isleyen, S.K. A graphical processing unit-based parallel hybrid genetic algorithm for resource-constrained multi-project scheduling problem. Concurr. Comput. Pract. Exp. 2021, 33, e6266. [Google Scholar] [CrossRef]
- Weixin, W.; Xianlong, G.; Jiafu, S. Multi-Project Scheduling with Multi-Factor Disruptions Under Uncertain Environments. In Proceedings of the 2019 8th International Conference on Industrial Technology and Management (ICITM), Cambridge, UK, 2–4 March 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 295–300. Available online: https://ieeexplore.ieee.org/document/8710663/ (accessed on 13 May 2019).
- Li, F.; Xu, Z.; Li, H. A multi-agent based cooperative approach to decentralized multi-project scheduling and resource allocation. Comput. Ind. Eng. 2021, 151, 106961. [Google Scholar] [CrossRef]
- Brinkmann, K.; Neumann, K. Heuristic procedures for resource—Constrained project scheduling with minimal and maximal time lags: The resource—Levelling and minimum project—Duration problems. J. Decis. Syst. 1996, 5, 129–155. [Google Scholar] [CrossRef]
- Talbot, F.B. Resource-Constrained Project Scheduling with Time-Resource Tradeoffs: The Nonpreemptive Case. Manag. Sci. 1982, 28, 1197–1210. [Google Scholar] [CrossRef]
- Sprecher, A.; Drexl, A. Solving multi-mode resource-constrained project scheduling problems by a simple general and powerful sequencing algorithm. Part I: Theory. In Manuskripte aus den Instituten fur Betriebs Wirtschaftslehre 385; University of Kiel: Kiel, Germany, 1996. [Google Scholar]
- Hartmann, S.; Sprecher, A. A note on “Hierarchical models for multi-project planning and scheduling”. Eur. J. Oper. Res. 94 1996, 94, 377–383. [Google Scholar] [CrossRef]
- Zhu, G.; Bard, J.; Yu, G. A Branch-and-Cut Procedure for the Multimode Resource-Constrained Project-Scheduling Problem. Inf. J. Comput. 2006, 18, 283–406. [Google Scholar] [CrossRef]
- Abdolshah, M. A Review of Resource-Constrained Project Scheduling Problems (RCPSP) Approaches and Solutions. Int. Trans. J. Eng. 2014, 5, 253–286. [Google Scholar]
- Fu, F.; Zhou, H. A combined multi-agent system for distributed multi-project scheduling problems. Appl. Soft Comput. 2021, 107, 107402. [Google Scholar] [CrossRef]
- Ma, Y.; He, Z.; Wang, N.; Demeulemeester, E. Tabu search for proactive project scheduling problem with flexible resources. Comput. Oper. Res. 2023, 153, 106185. [Google Scholar] [CrossRef]
- Yuan, P.; Xiao, W.; Li, Z.; Liang, H.; Zhao, Z. A Robust Optimization Scheduling for Carrier Aircraft Support Operation Based on Critical Chain Method. IOP Conf. Ser. Mater. Sci. Eng. 2019, 627, 012007. [Google Scholar] [CrossRef]
- Ben Issa, S.; Patterson, R.A.; Tu, Y. Solving resource-constrained multi-project environment under different activity assumptions. Int. J. Prod. Econ. 2021, 232, 107936. [Google Scholar] [CrossRef]
- Kolisch, R.; Sprecher, A. PSPLIB—A project scheduling problem library. Eur. J. Oper. Res. 1997, 96, 205–216. [Google Scholar] [CrossRef]
- Homberger, J. A multi-agent system for the decentralized resource-constrained multi-project scheduling problem. Int. Trans. Oper. Res. 2007, 14, 565–589. [Google Scholar] [CrossRef]
- Homberger, J. A (μ, λ)-coordination mechanism for agent-based multi-project scheduling. OR Spectr. 2012, 34, 107–132. [Google Scholar] [CrossRef]
- Herroelen, W.; Leus, R. Project scheduling under uncertainty: Survey and research potentials. Eur. J. Oper. Res. 2005, 165, 289–306. [Google Scholar] [CrossRef]
- Ben Issa, S.; Tu, Y. A survey in the resource-constrained project and multi-project scheduling problems. J. Proj. Manag. 2020, 5, 117–138. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).