1. Introduction
In recent years, the rapid development of distributed machine learning has increased the attention paid to Federated Learning (FL), which is a collaborative learning framework for privacy protection. Unlike traditional centralized learning models, federated learning allows for multiple participants to train the model locally and update the global model parameters without sharing the raw data. However, in practice, synchronous federated learning often faces problems such as differences in computing power, network latency, and device availability, which require all participants to participate in each iteration simultaneously. To meet these challenges, Asynchronous Federated Learning (AFL) has gradually become a research focus.
Aynchronous federated learning allows for different clients to update the global model parameters at different frequencies at different times, thus improving the flexibility and efficiency of the system. Compared with synchronization methods, asynchronous methods can better adapt to computational power and network conditions of different devices, while reducing the impact of clients with a longer waiting time on the overall training schedule. In recent years, the research has mainly focused on the following aspects:
(1) Optimization of the algorithm design using an adaptive aggregation strategy: We proposed a variety of adaptive aggregation methods, such as FedAvg based on a weighted average [
1], and its improved version, to improve the speed and robustness of model convergence by dynamically adjusting the weight of the client’s contribution. Asynchronous gradient descent methods and asynchronous optimization algorithms based on SGD (stochastic gradient descent), such as Async-SGD [
2] and its variants, have been widely studied. These algorithms significantly improve the training efficiency by parallelizing the training tasks of the client and the parameter-updating process of the server.
(2) Privacy protection mechanism: In AFL, communication latency can lead to data from some clients being used multiple times, increasing the risk of privacy leakages. For this problem, the researchers proposed a method based on differential privacy [
3] and homomorphism encryption [
4] to ensure the privacy of client data. In response to model theft attacks and intermediate results leakage, some work combines federated learning and federated enhanced learning [
5] to further improve security in an asynchronous environment.
(3) Model heterogeneity treatment: Clients in AFL often have different computational powers and data distribution rates, leading to inconsistencies in model updates. To this end, the researchers proposed [
6], a method based on federated meta-learning, to balance the contributions of different clients by introducing a meta-optimizer to the server side. In addition, for the data heterogeneity problem, some work uses task-decomposition-based methods, such as FedMD [
7] and Task-Aware FL [
8], to decompose global tasks into multiple subtasks and assign them to different clients.
(4) Scalability and fault tolerance: To improve the scalability of AFL, researchers proposed the hierarchical federated learning framework [
9], which effectively reduces communication latency and reduces bandwidth consumption by adding intermediate server nodes. In terms of fault tolerance, some work explores how to handle client drops or long unresponsive cases, such as the retransmission mechanism based on timeout detection [
10] and the redundant backup policy [
11].
(5) Practical application and exploration: AFL has been widely used in multiple fields, such as Medical Data Collaboration [
12], recommended system [
13], and edge computing [
14]. The heterogeneity of the devices and the complexity of the network environment in these application scenarios further promote research on and the development of asynchronous methods. In recent years, federated learning has emerged as a revolutionary approach, addressing challenges related to data privacy, security, and distributed data silos across various domains. In the realm of traffic control, the advent of intelligent transportation systems has brought about a new era of traffic management [
15]. Traffic signal control (TSC) is a crucial aspect of this, aiming to mitigate congestion, reduce travel time, and cut down on emissions and energy consumption. Reinforcement learning (RL) has been a primary technique for TSC. However, traditional centralized learning models face significant communication and computing bottlenecks, while distributed learning struggles to adapt across different intersections. As proposed by Bao et al. [
16], federated learning provides a novel solution. It integrates the knowledge of local agents into a global model, overcoming the variations among intersections through a unified agent state structure. The model aggregates a segment of the RL neural network to the cloud, and the remaining layers undergo fine-tuning during the convergence of the training process. Experiments have demonstrated a reduction in queuing and waiting times globally, and the model’s scalability has been validated on a real-world traffic network in Monaco. In the field of image processing, federated learning has also shown great potential. With the increasing generation of image data from diverse sources, such as surveillance cameras, medical imaging devices, and mobile applications, data privacy becomes a major concern. Federated learning allows for edge devices or local servers to train models on their local data without sharing the raw data, thus safeguarding privacy. As elaborated in the review paper “A review on federated learning towards image processing” by Khokhar et al. [
17], federated learning in image processing can be applied to various tasks like image recognition, segmentation, and classification. For example, in medical image segmentation across multiple healthcare centers, each center can train a model on its local patient data, and then the model parameters are aggregated to build a global model that can be beneficial for all participating centers while protecting patient privacy [
18]. The applications of federated learning in traffic control and image processing are still in the process of continuous exploration and development. As technology advances, more innovative applications and optimized algorithms are expected to emerge, further enhancing the efficiency and effectiveness of these two important fields.
Although asynchronous federal learning has made remarkable progress in recent years, there are still some challenges, as follows [
19,
20,
21]:
(1) Communication efficiency: The asynchronous method can lead to conflicts between parameter updates on the server side. Recent studies such as [
22] have explored dynamic communication scheduling to mitigate such conflicts. However, how to effectively and orderly coordinate communication between the client and the server in heterogeneous environments remains an open problem that must urgently be solved.
(2) Convergence guarantee: Most existing studies are based on experimental verification and lack rigorous theoretical analysis and proof of convergence.
(3) Robustness: Malicious attacks in the asynchronous environment (such as model poisoning) may have a serious impact on the global model. Recent work [
23] proposed the use of gradient anomaly detection frameworks to filter poison updates, but the integration of such methods into AFL requires further investigation. How to effectively improve the anti-attack ability of the system remains an important direction of future research.
In general, AFL, a flexible and efficient distributed learning method, shows great potential in the protection of privacy and in scenarios with limited computing resources. With the development of theoretical research and technical practice, its performance in practical applications will improve. In the massive data-driven machine learning method, the data pollution problem inevitably affects the robustness of the model, leading to learning shock and an insufficient prediction ability. However, through establishing a complete data cleaning process, adopting an anomaly detection algorithm, and establishing a data-quality evaluation system, the model can improve its tolerance of data pollution faults, thus improving its robustness. Under the federated learning framework, there are two main sources of data pollution:
(1) Incontamination of raw data: This kind of pollution is relatively common. For classification and regression models, the cause of data pollution may be the change in sample distribution or disordered sample labeling. When the original data are contaminated, the detection and filtering of contaminated samples become the focus of research. Whether abnormal samples can be detected quickly and effectively is crucial to the training of machine learning models.
(2) Contamination generated during data transmission: In the federal learning framework, there is frequent data transfer between global trainers and the local trainers, which can easily produce pollution in the process of data transmission. When the trainer uploads gradient pollution, the upload gradient security aggregation from the global trainer to the local trainers is prone to improper aggregation and algorithm training shock, and may even fail to converge. In this case, the parameters are broadcast to the local trainers, leading to the pollution of the model parameters under the federal framework.
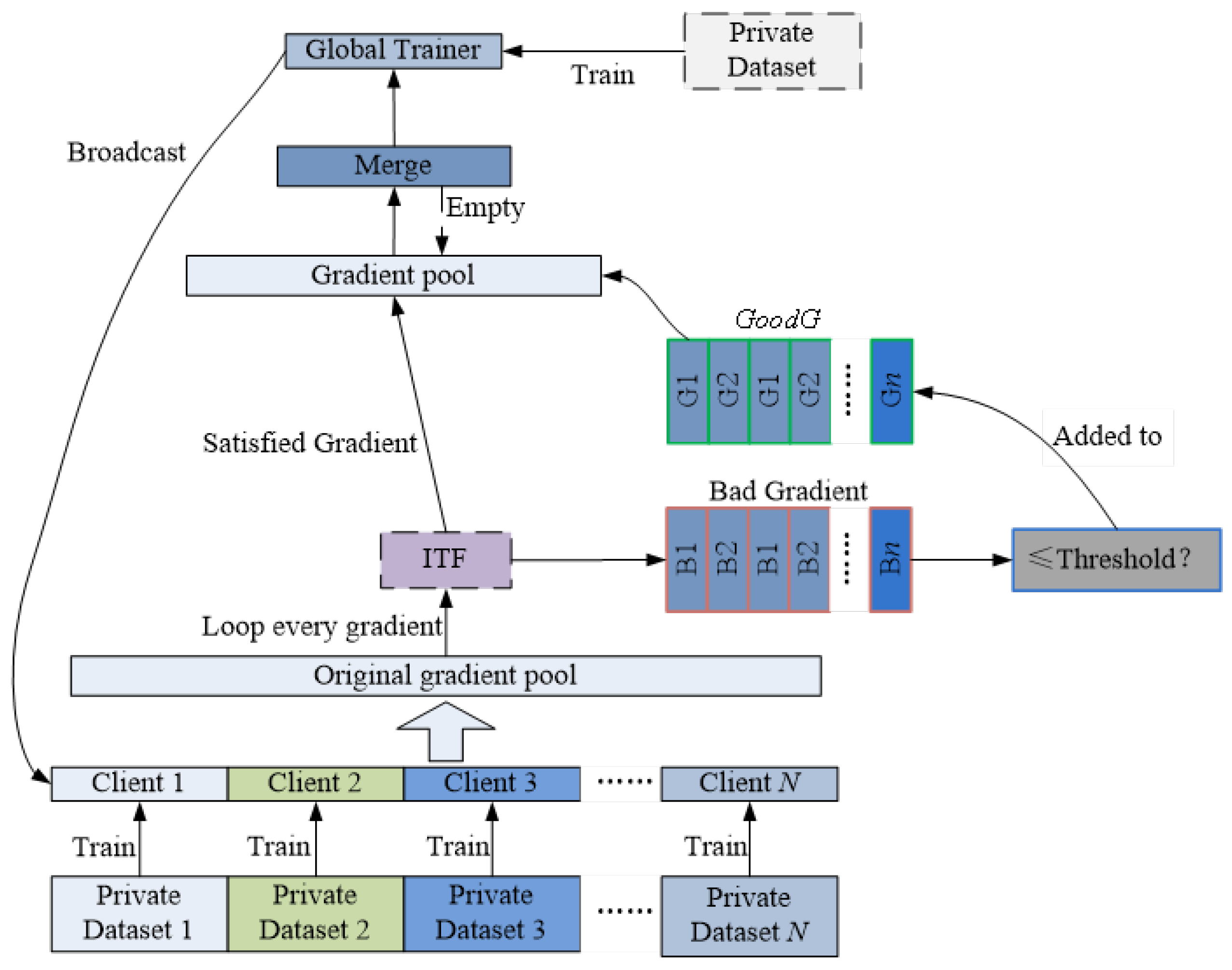
In conclusion, this article studies an important AFL issue:how to detect gradient anomalies in a data pollution environment—and proposes an improved algorithm named Asynchronous Federated Learning Improving (AFLI), which focuses on the impact of data injection contamination on gradient information.
The main work and contributions of this article are as follows:
(1) When the original data are contaminated, it is difficult for the local trainer to accurately identify and filter the data, which transfers the parameter gradient of the abnormal data to the global trainer and then causes the systematic parameter pollution problem. In this article, we preprocess existing datasets to improve the ability of the algorithm to identify noise data.
(2) An anomaly detection algorithm is used during the gradient transmission process. There is frequent transmission of parameters between the local trainer and the global trainer. When the local trainer transfers its own gradient to the global trainer, severe gradient contamination will cause the global trainer to effectively update the parameters. In order to solve this problem, this article mainly adopts two methods: first, the gradient is uploaded by each local trainer through the experience pool technology; second, the ITF (Isolation Forest) algorithm is used to detect and eliminate the abnormal gradient, and only the normal gradients are used to update the parameters of the global trainer to effectively alleviate the influence of the abnormal gradient on the parameter update.
(3) Based on previous work, this article achieved relatively high accuracy in two data sets, including two CLS and ZXSFL. Various experiments demonstrate that the algorithm can effectively detect contaminated data sets and achieve high accuracy.