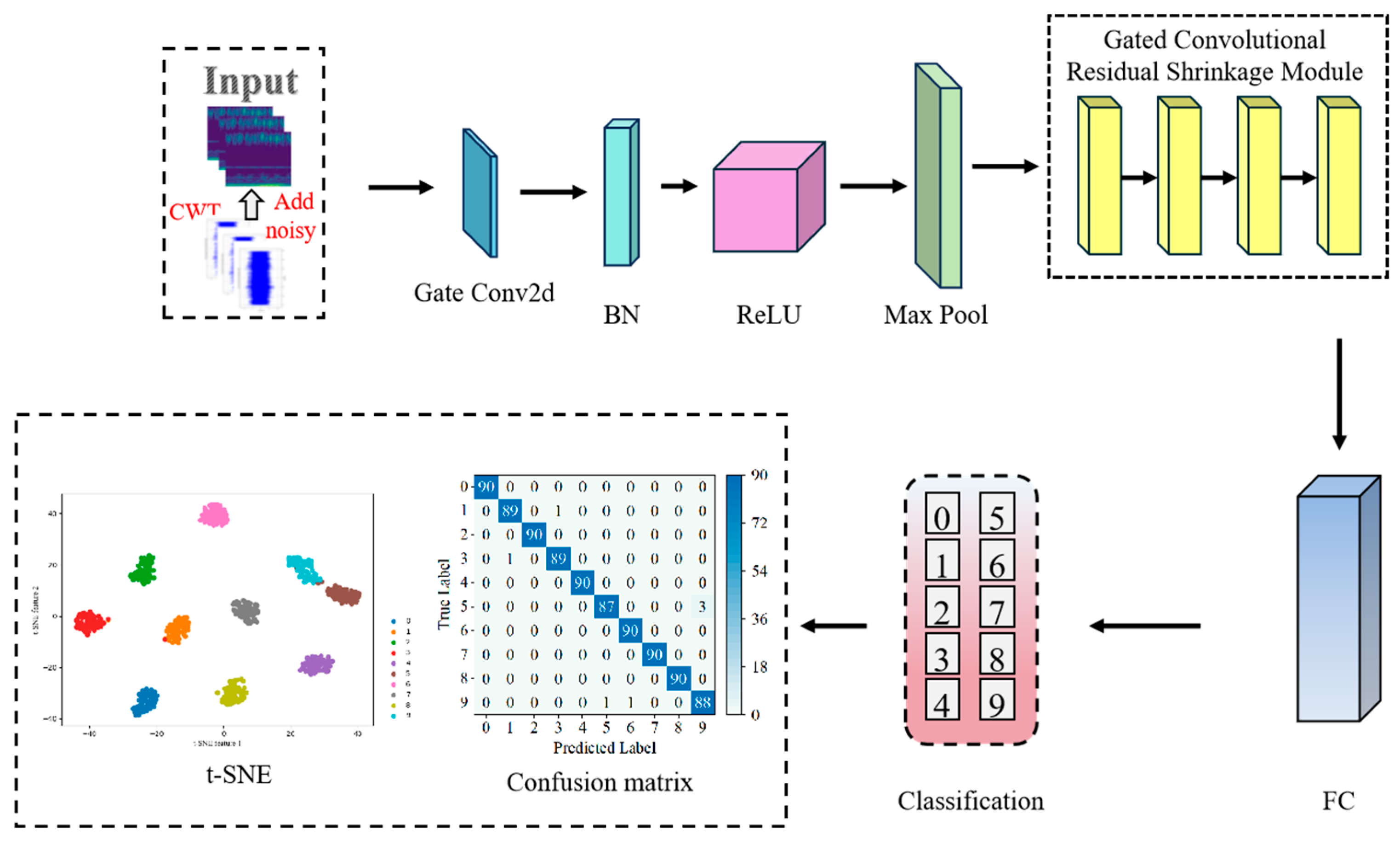
4.2. Introduction to the Experimental Dataset
In this paper, a generally recognized public bearing dataset is used for experimental analysis, which makes the proposed model instructive for fault diagnosis of rolling bearings under actual working conditions.
The Case Western Reserve University (CWRU) experimental setup is shown in
Figure 3. The experimental rig consists of a 2hp motor, dynamometer, and torque transducer. The dataset was collected using SKF6205-2RSJEM bearings at sampling frequencies of 12 kHz and 48 kHz, and a single point of failure was set up by EDM. For signal acquisition, the experimental platform was fitted with piezoelectric accelerometers (mainly PCB Piezotronics type 352C33 accelerometers), which were mounted on the drive end bearing cover (DE, Drive End) and the fan end (FE, Fan End) of the motor, and held in place by means of magnetic bases. The acquired signals were captured by a National Instruments (NI) data acquisition card and transferred to a computer for processing. The types of bearing failures include three types: rolling element failures, inner ring failures, and outer ring failures. Each failure type contains three different levels of damage diameters, and we divided the data into ten categories: one category represents normal operating conditions, and the remaining nine categories cover failure conditions. Rolling body failures with failure diameters of 0.1778 mm, 0.3556 mm, 0.5334 mm (labeled BA_I, BA_II, and BA_III, respectively), inner ring failures with failure diameters of 0.1778 mm, 0.3556 mm, 0.5334 mm (labeled IR_I, IR_II, and IR_III, respectively), and outer ring failure diameters of 0.1778 mm, 0.3556 mm, 0.5334 mm (labeled OR_I, OR_II, and OR_III, respectively) were investigated. In this study, we constructed the dataset using vibration signals from the drive-end (DE) bearings with noise artificially added to the vibration signals to simulate noise-containing signals in real industrial environments, sampled at 12 kHz with a rotational speed of 1730 rpm. Each bearing condition includes 300 samples, totaling 3000 samples, and each sample contains 2048 data points. Dividing the training set and validation set according to the ratio of 7:3, 2100 training samples and 900 validation samples can be obtained. The dataset details are shown in
Table 2.
To simulate the vibrations that contain noise, we added different noise types to the vibration signals to simulate this noise. In the next experiments, we added noise to simulate the noise-containing vibration signal. Based on other research in the field of bearing diagnostics in noisy environments, we also added other non-Gauss noises to the vibration signals to make them more consistent with real industrial scenarios. For example, Lapace noise is a more complex and randomized non-Gauss noise in the real industrial scene. Salt-and-Pepper noise is also a common non-ideal noise simulation in the field of rolling bearing fault diagnosis. There is also Poisson noise, a typical non-Gauss noise. We set different signal-to-noise ratio (SNR) levels for each noise type to simulate various noise intensities, as shown in
Table 3. The noise-laden vibration signals are then subjected to a continuous wavelet transform to generate a two-dimensional colored wavelet time-frequency plot, as shown in
Figure 4.
The wavelet plots of time and frequency are shown in
Figure 4, for different bearings states, with a signal-to-noise ratio (SNR) of −5. In
Figure 4, there is a lot of noise that has a random distribution. The noises cause confusion, blurring, and masking of local images. They also make it hard to recognize fault modes.
4.3. Ablation Experiment
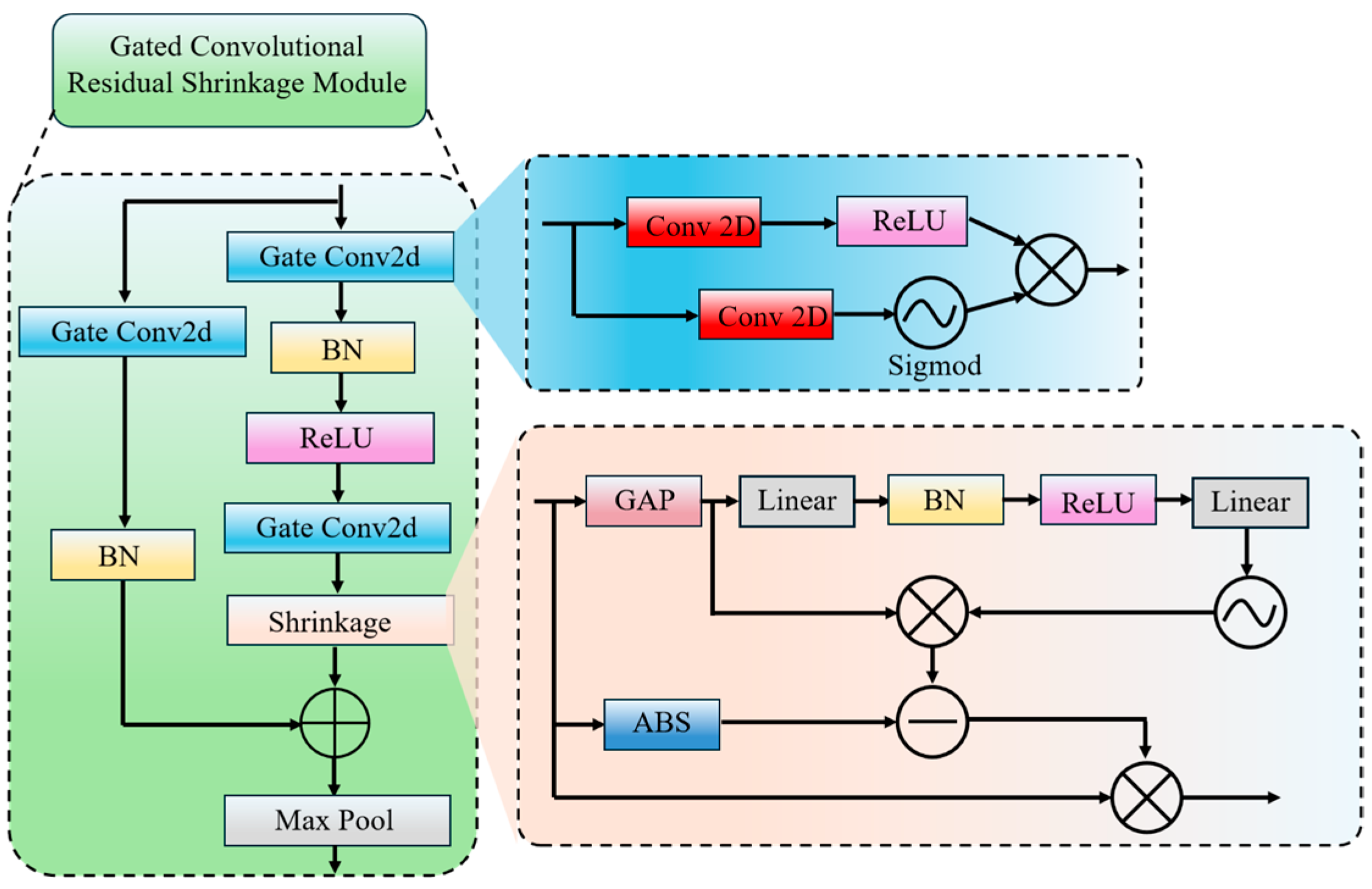
Ablation experiments on the model are conducted to determine the efficacy of the Gated Convolutional Residual Shrinkage Module. The rolling bearing vibratory signal has a high level of intrinsic noise that is similar to Gauss. Therefore, it is chosen as an input because the signal contains the highest frequency Gauss. Method 1 used a layer of gated convolutional residual contraction module, method 2 spliced two layers, and so on incrementally, setting up six different cases through the experiment to determine the number of layers of this module spliced.
As can be seen from
Table 4, Method 4 (i.e., four modules were selected for splicing) has the highest accuracy, while Methods 1, 2, and 3 have lower accuracy, and as the number of modules spliced increases (Methods 5 and 6), the accuracy decreases instead. Ablation experiments demonstrate that the design of four Convolutional Residual Gated Modules for this model is reasonable. They also show that using four module splicing balances both the complexity and ability to extract features of the model. It will not lead to low accuracy because the number of layers is too small to extract features effectively, nor will it lead to overfitting because the number of layers is too large, which affects the accuracy instead.
4.4. Comparison Test
For fault classification identification in the case of rolling bearing vibration signals affected by noise, in addition to Gauss noise, there are Laplace noise, Salt-and-Pepper noise, Poisson noise, and so on. In order to simulate the actual industrial environment, this paper introduces these noises as interferences, which are used to evaluate the robustness of the diagnostic model under various types of noise interferences.
In order to verify the effectiveness of the model in this paper, we compared it with other deep learning models (1D-CNN, CNN-Transformer, Swin Transformer, 1D-DRSN, 1DRSN–GCE). Both Gauss noise and Laplace noise (non-Gauss noise) were added to the vibration signal to obtain the mean and standard deviation of the diagnostic accuracy, precision, recall, F1 score of each batch of models with different signal-to-noise ratios.
Table 5,
Table 6 and
Table 7 show the results. In
Table 5, we can see that this model’s diagnostic accuracy is best at signal-to-noise ratios between −5 dB and 3 dB. In
Table 5, we can see that this model’s diagnostic accuracy reaches 99.22% with a signal-to-noise ratio of −5. According to
Table 5, the accuracy of other models is 78.81, 90.89%, 95.11%, 96.89%, and 95.44%. This paper’s diagnostic accuracy is 4.11% greater than the 1D-DRSN model, while at the same it is 3.78% more accurate than the 1DRSN–GCE model without CWT. CWT also makes it possible to better diagnose and classify the signals by converting a one-dimensional signal of time into a two-dimensional image. In
Table 6, the paper’s accuracy is the best in low-frequency conditions. This shows that the model has the ability to cope with noise frequency variations. In
Table 7, the performance of this model is superior to other models, in terms such as precision, recall, and F1 score.
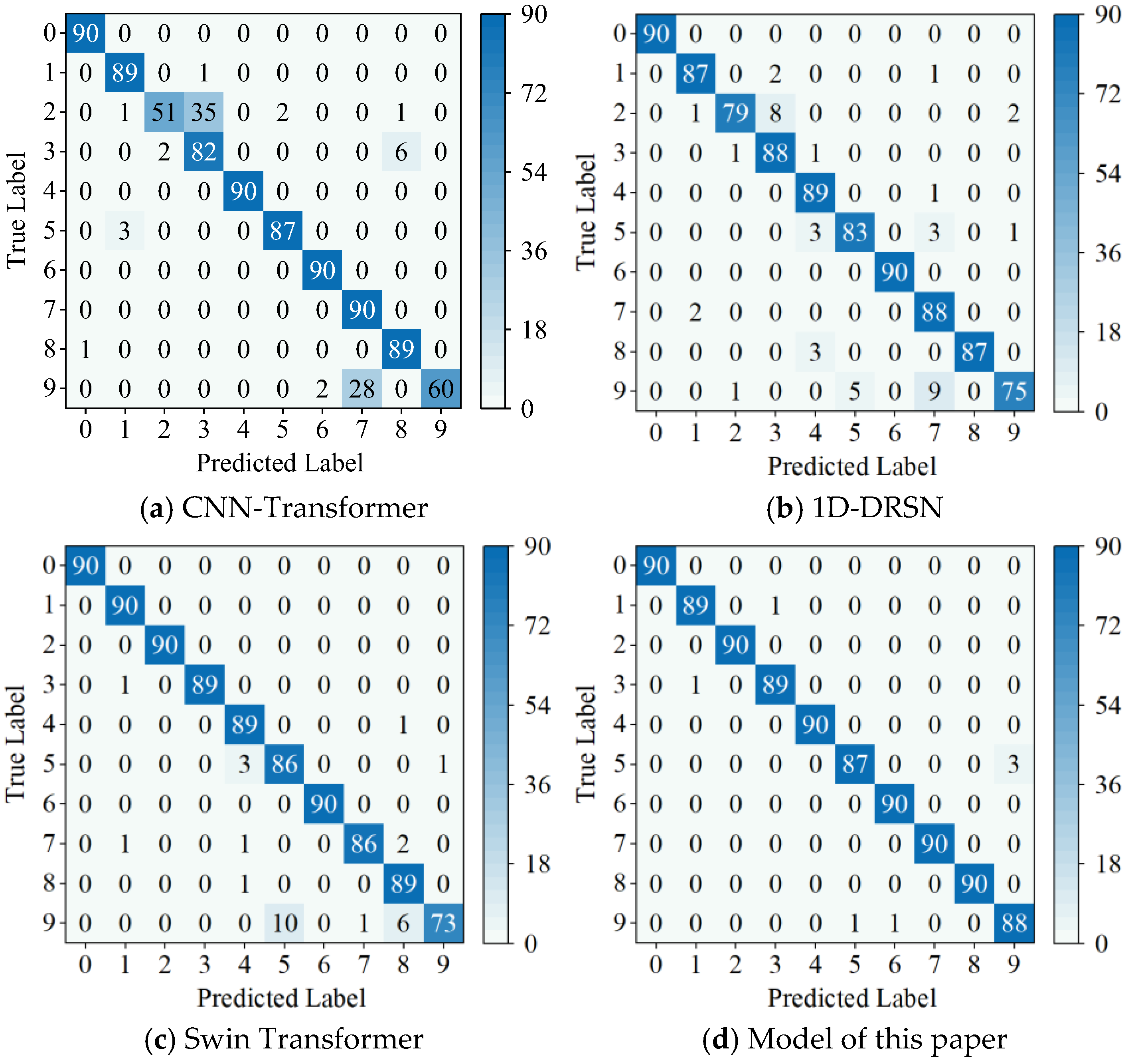
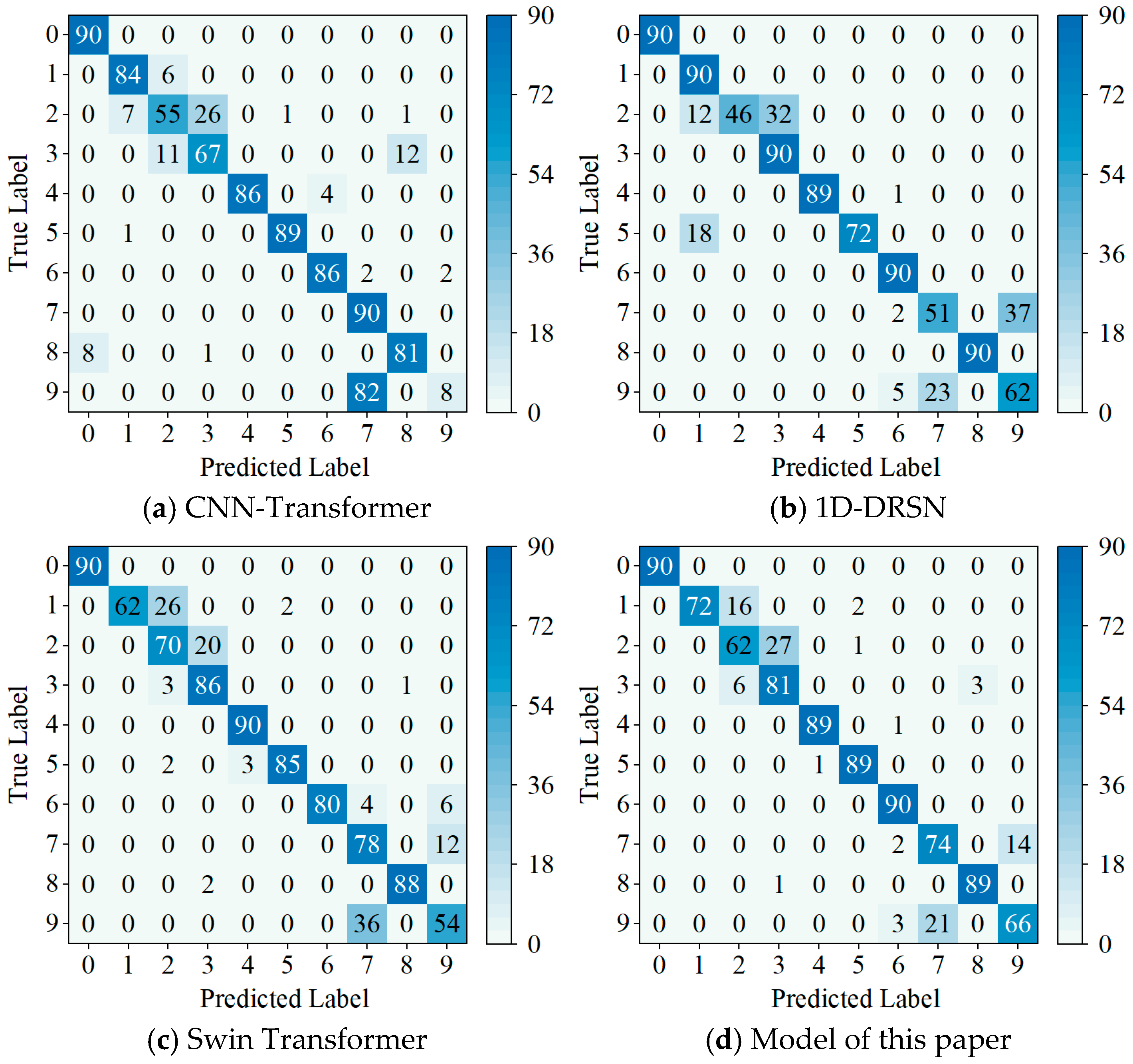
A confusion matrix was introduced to better reflect clustering of fault data and the misclassification. The confusion matrix is shown in
Figure 5, which shows the results of bearing fault diagnosis using different models for high-frequency noise and a signal-to-noise ratio of −5 dB. Plot (b) of
Figure 5 shows that the 1D-DRSN is able to predict faults with labels 0 and 6 perfectly, and 90 out of 100 samples have been predicted correctly. The other diagnoses, however, are incorrect to various degrees. This is especially true for marker 9 (Outer Ring Failure OR_III), as it has been misclassified by 15 of the 90 samples. The graph (d), in
Figure 5, shows that the method proposed by this paper is relatively accurate at identifying these 10 types of faults. It can be observed that this method is relatively accurate in identifying these faults. At most, only three samples are incorrectly classified (Marker 5), which is the least misidentification rate. This paper shows how the method can achieve high-precision diagnosis with robustness in a noisy environment.
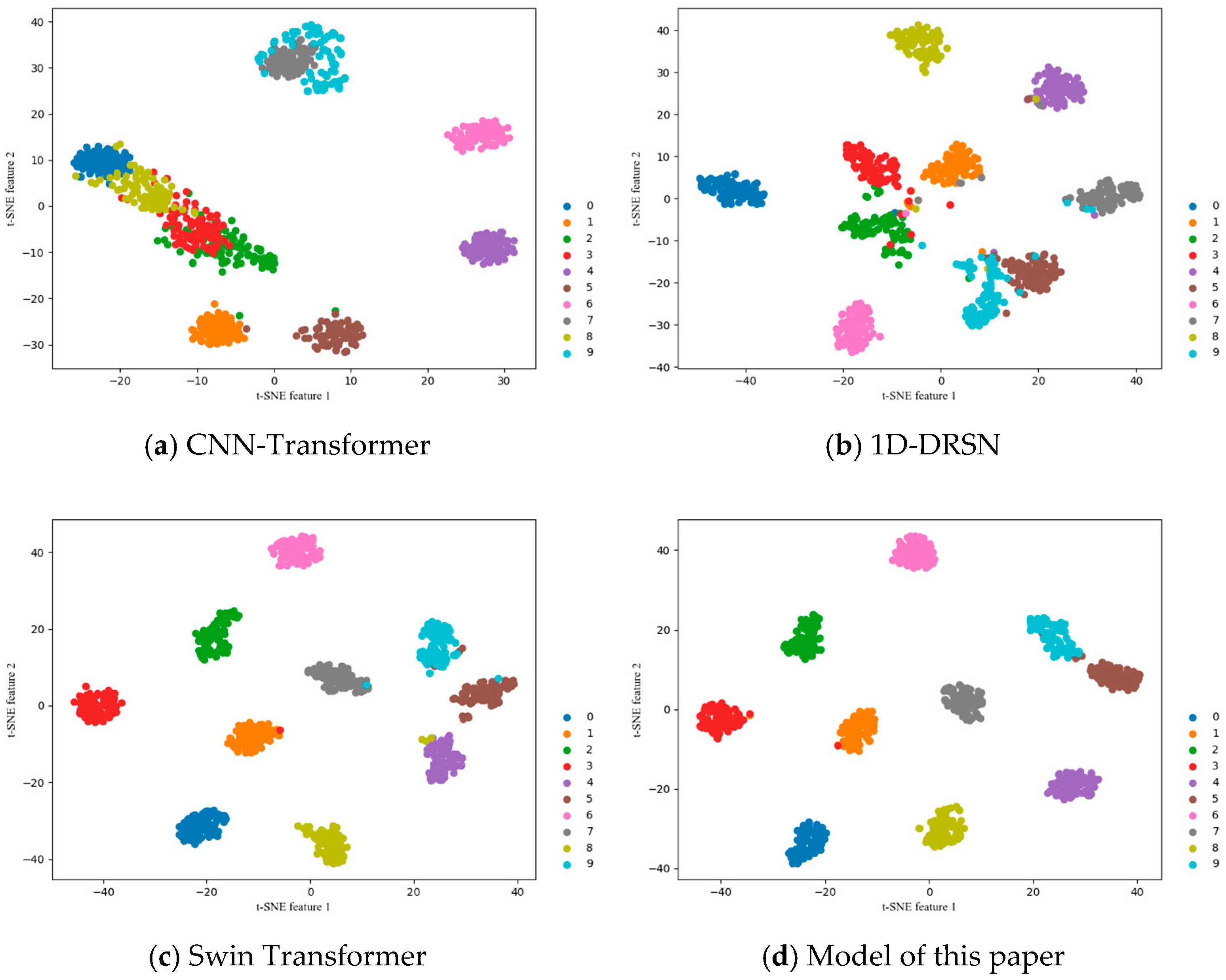
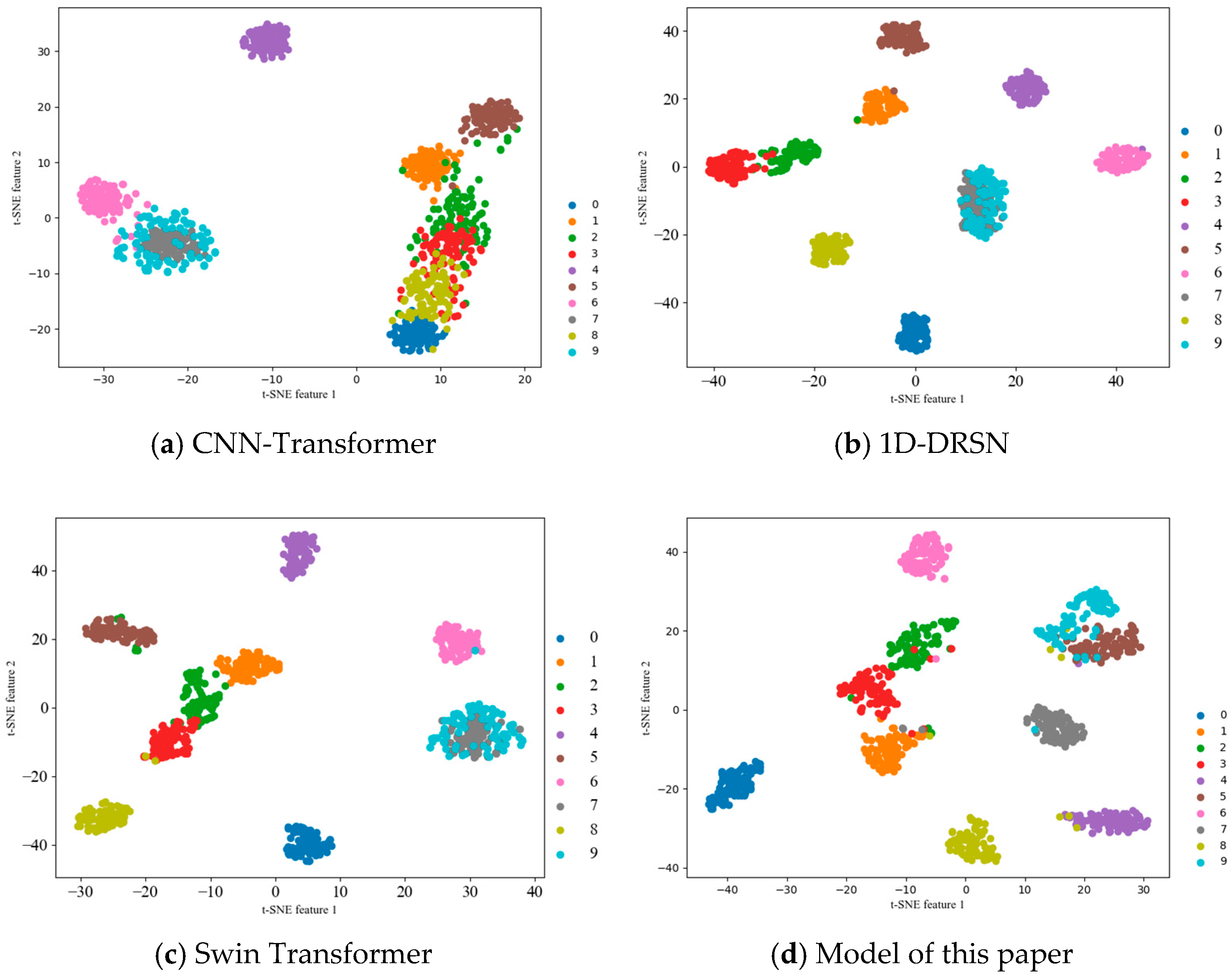
The t-SNE graph was introduced to help show fault classification more clearly. The t-SNE plots in
Figure 6 show the outputs from each model with a signal-to-noise ratio of −5 dB. It is clear that this model is better than others for clustering fault features and classification of bearings.
In order to verify the effectiveness of the model in this paper, Gauss noise and non-Gauss noise (Salt-and-Pepper noise and Poisson noise) are added to the vibration signals at the same time to simulate a bearing diagnosis more consistent with a noisy environment, and again to compare the other deep learning models (1D-CNN, CNN-Transformer, Swin Transformer, 1D-DRSN, 1DRSN–GCE) to evaluate the noise immunity of other models under different noise conditions, as shown in
Table 8,
Table 9 and
Table 10. From
Table 8, it can be seen that the diagnostic accuracies of the models in this paper are the highest at signal-to-noise ratios ranging from −5 dB to 3 dB. From
Table 8, it can be seen that the diagnostic accuracy of this paper’s model reaches 89.11% at a signal-to-noise ratio of −5. The other models are 76.33%, 82.01%, 85.55%, 87.00%, and 86.11% in order of accuracy from top to bottom according to
Table 8. The diagnostic accuracy of this paper’s model is 3.56% higher than that of 1D-DRSN, and 3% higher than that of the 1DRSN–GCE model without CWT, which indicates that this paper’s model has good stability and noise immunity. From
Table 9, it can be seen that in the low-frequency noise conditions, the accuracy of this paper’s model is also the highest in all cases, indicating that the model can cope with the frequency variation of noise. From
Table 10, it can be seen that the model of this paper compared with other models in terms of precision, recall, F1 score, and so on has a more excellent performance.
The confusion matrix in
Figure 7 is a comparison of the different bearing fault diagnostic models with signal-to-noise ratios of −5 dB. The confusion matrix plot of the model in this paper has the highest accuracy, and lowest misidentification rates. This paper shows how the methods can be used to achieve high-precision diagnosis with robustness in noisy environments.
The outputs of each model are visualized using t-SNE at a signal-to-noise ratio of −5 dB. The graph (d), in
Figure 8, shows that this model is superior to other deep learning models in clustering fault features and identifying bearings of different health states. It also provides a more accurate classification.
4.5. Single Noise Experiment
In the above noise experiments, we used Gauss and Laplace noise as input noises, but also added Gauss, Poisson, and Salt-and Pepper noises to the signal. These two experiments showed that adding Salt-and-Pepper noise and Poisson to the vibration signals reduced the accuracy of the models. The following experiments will be based on this model, and we will add Salt-and-Pepper noise and Poisson to the vibration signals as one input signal to investigate the impact of the two noise types on bearing fault diagnosis.
The experiment yielded
Table 11, which showed that a single Salt-and-Pepper noise caused more localized damage, making it harder for the model to extract effective features. This led to relatively poor diagnostic accuracy. The model is still able to perform well despite a Salt-and-Pepper noise. Its accuracy remains over 85%. We usually believe that noise in vibration signal processing will reduce the recognition of certain features. This, in turn, affects the accuracy. However, experimental results show that the simultaneous addition of Gauss noise, Salt-and-Pepper noise, and Poisson noise to the signal, on the contrary, achieves a higher recognition accuracy than when pretzel noise is added alone. From the perspective of noise type, Salt-and-Pepper noise is a sparse discrete noise, which is mainly manifested by the abrupt change of individual points in the signal, and it is very easy to destroy the continuity and local characteristics of the signal, whereas Gauss noise is a kind of additive continuous and widely distributed random noise [
31]. When these two types of noise act together on the vibration signal, a “complementary effect” is formed to some extent [
32], and the Gauss noise smooths out some of the extreme pretzel points to make the signal trend more coherent, which helps the model to extract effective features. From the perspective of signal preprocessing and feature extraction, the main components of the signal after multi-noise perturbation are still preserved when it is processed by filtering (e.g., continuous wavelet transform) or feature extraction, while the Salt-and-Pepper noise may be diluted in the frequency domain, which has less impact on the fault features. As a result, the model can focus more on stable, global information rather than being misled by local noise. The introduction of multiple noises not only effectively counteracts the local destructive effect of a single noise type on model training, but also enhances the model’s ability to adapt to complex disturbed environments. This “noise against noise” strategy [
33], to a certain extent, improves the accuracy of bearing fault diagnosis in the noise environment. The accuracy of this model is almost 100% in the Poisson environment. This indicates that it can deal well with vibration signals containing Poisson sound.