A Novel Algorithm for Personalized Federated Learning: Knowledge Distillation with Weighted Combination Loss

Abstract

Federated learning (FL) offers a privacy-preserving framework for distributed machine learning, enabling collaborative model training across diverse clients without centralizing sensitive data. However, statistical heterogeneity, characterized by non-independent and identically distributed (non-IID) client data, poses significant challenges, leading to model drift and poor generalization. This paper proposes a novel algorithm, pFedKD-WCL (Personalized Federated Knowledge Distillation with Weighted Combination Loss), which integrates knowledge distillation with bi-level optimization to address non-IID challenges. pFedKD-WCL leverages the current global model as a teacher to guide local models, optimizing both global convergence and local personalization efficiently. We evaluate pFedKD-WCL on the MNIST dataset and a synthetic dataset with non-IID partitioning, using multinomial logistic regression (MLR) and multilayer perceptron models (MLP). Experimental results demonstrate that pFedKD-WCL outperforms state-of-the-art algorithms, including FedAvg, FedProx, PerFedAvg, pFedMe, and FedGKD in terms of accuracy and convergence speed. For example, on MNIST data with an extreme non-IID setting, pFedKD-WCL achieves accuracy improvements of $3.1\%$, $3.2\%$, $3.9\%$, $3.3\%$, and $0.3\%$ for an MLP model with 50 clients compared to FedAvg, FedProx, PerFedAvg, pFedMe, and FedGKD, respectively, while gains reach $24.1\%$, $22.6\%$, $2.8\%$, $3.4\%$, and $25.3\%$ for an MLR model with 50 clients.

1. Introduction

Federated learning (FL) has emerged as a transformative approach in distributed machine learning, enabling a diverse set of clients, such as mobile devices, edge nodes, or institutions, to collaboratively train a shared model while preserving data privacy by keeping local datasets on the device [1]. This privacy-preserving algorithm framework is particularly valuable in domains such as healthcare, finance, and IoT systems, where sensitive data cannot be centralized [2,3]. However, a significant challenge in FL algorithms is the statistical heterogeneity among clients, often termed non-independent and identically distributed (non-IID) data, where local data distributions differ due to varying user behaviors or contexts [4,5]. This diversity causes local models to drift from the global objective, slowing convergence and limiting the global model’s ability to generalize across clients [6,7].

Traditional FL methods, such as FedAvg [1], rely on a central server to aggregate local model updates into a global model through parameter averaging. While effective when data is similarly distributed, FedAvg struggles with non-IID data, as local optima diverge from the global target, leading to poor performance on individual clients [8]. Conversely, relying solely on individual learning without FL collaboration leads to poor generalization as well, as clients lack sufficient data to train robust models independently [9]. To overcome this, personalized FL has gained attention, aiming to tailor models to each client’s unique data while still benefiting from collaborative learning [10]. Personalized FL seeks to strike a balance between global knowledge sharing and local adaptation, a task complicated by the need to maintain privacy and efficiency in heterogeneous settings [11].

Numerous strategies have been developed to enable personalization in FL. For example, local customization techniques, such as FedProx [4], modify FedAvg by introducing regularization to align local updates with the global model. FedPer [12] splits neural networks into shared base layers trained server-side and personalized layers fine-tuned by clients. Bi-level optimization offers another avenue, exemplified by pFedMe [13], which separates global model aggregation from local personalization, using the global model as a reference point to guide client-specific solutions, an approach that proves effective, but less so with limited data. Meta-learning strategies, like PerFedAvg [14], draw from Model-Agnostic Meta-Learning to craft an initial shared model that clients can quickly adapt, though computational challenges arise from Hessian approximations [15]. Multi-task learning contributes frameworks like MOCHA [16], which tackles both statistical and system-level diversity by treating clients as distinct tasks. Meanwhile, methods like APFL [17] blend local and global models adaptively, balancing personalization with collaboration. Clustering-based approaches, such as those proposed by Ghosh et al. [18], group clients with similar data distributions to improve personalization efficiency. Despite these advances, many PFL approaches grapple with overfitting when client datasets are small, underscoring the need for robust solutions tailored to data scarcity [19].

Knowledge Distillation (KD), introduced by Hinton et al. [20], provides another powerful tool to enhance FL under heterogeneity. KD transfers knowledge from a complex teacher model to a simpler student model using a weighted combination of loss terms, enabling the student to learn both from ground-truth labels and the teacher’s broader predictive patterns. In FL, KD has been adapted to distill global knowledge into local models, improving convergence and robustness to non-IID data. FedMD [21], for instance, leverages a shared public dataset where clients compute and exchange logits, allowing the server to aggregate these into a consensus that guides local training through KD. Similarly, FedDF [22] employs a server-side proxy dataset to refine a global model by distilling predictions from client models, enhancing robustness across varied architectures. Yet, the reliance on such proxy datasets poses a limitation, as curating a suitable dataset may not be feasible in all scenarios, particularly in resource-constrained or privacy-sensitive applications where server-side data availability is restricted. These advancements underscore the potential of KD in FL while highlighting the need for methods that can operate effectively without depending on external datasets. Recent works have sidestepped the need for curated external data. For instance, Jeong and Kountouris [23] proposed KD-PDFL. Unlike FedMD or FedDF, KD-PDFL operates without any proxy dataset; instead, each client leverages its local private dataset to compute intermediate outputs, using these to measure model similarity via KD in a peer-to-peer fashion. Seo et al. [24] introduced Federated Distillation (FD), which reduces communication costs by sharing model outputs instead of parameters, though it sacrifices accuracy in highly non-IID scenarios [25]. Zhu et al. [25] introduced a data-free KD method for FL: the server employs a lightweight generator to synthesize ensemble knowledge from client models, which is then broadcast to guide local training via KD. FedMKD, proposed by Zheng et al. [26], leverages Mutual Knowledge Distillation (MKD) alongside Elastic Weight Consolidation (EWC) to mitigate catastrophic forgetting in global models, achieving superior performance in non-IID scenarios and reducing communication overhead through uniform and exponential quantization techniques. PFedSKD, introduced by Zheng et al. [27], employs self-knowledge distillation to retain personalized knowledge, addressing unreliable teacher models by stratifying neural network layers and incorporating auxiliary classifiers. Yao et al. [28] presented FedGKD, which regularizes local training with an ensemble of historical global models via KD, achieving strong performance but relying on increased communication. These studies underscore the synergy of KD and FL in tackling data heterogeneity, enhancing model robustness, and optimizing resource-constrained environments like edge computing, paving the way for more scalable and privacy-preserving machine learning frameworks.

We propose a novel FL algorithm that integrates KD with a weighted combination loss to tackle non-IID challenges in a centralized setting. Our approach draws from the insight of bi-level optimization, separating global and local optimization and using the global model as a teacher to guide local models via KD, while optimizing both levels concurrently. Compared to methods such as FedDF or FedMD, which depend on proxy or public datasets, our algorithm operates solely on clients’ private datasets, ensuring privacy preservation without external data dependencies. Unlike FD, which prioritizes communication efficiency, or KD-PDFL, which emphasizes personalization, our method balances global convergence and local regularization. Compared to FedGKD, we streamline the process by focusing on the current global model rather than historical ensembles, enhancing efficiency and robustness. We evaluate our algorithm on the MNIST dataset and a synthetic dataset under non-IID conditions, demonstrating improved accuracy and convergence speed over other state-of-the-art (SOTA) algorithms.

The remainder of this manuscript is organized as follows: Section 2 details the problem formulation and our proposed algorithm; Section 3 presents experimental results; and Section 4 concludes with future research directions.

2. Materials and Methods

In this section, we outline the problem formulation and introduce our proposed FL algorithm that integrates KD with a weighted combination loss to address data heterogeneity. We begin by describing the conventional FL model, followed by an overview of KD as a foundational technique, and conclude with the details of our proposed method.

2.1. Conventional FL Model

In conventional FL, a system comprises a central server and N clients, each holding a local dataset ${\mathcal{D}}_i$ drawn from a potentially distinct distribution $P_i$, reflecting the non-IID nature of real-world scenarios. The objective is to collaboratively train a global model parameterized by $w\in {\mathbb{R}}^d$ without sharing raw data. This is typically formulated as an optimization problem:

$$\underset{w\in {\mathbb{R}}^d}{min}\left\{f(w):={\displaystyle \frac{1}{N}}\sum _{i=1}^N{f}_i(w)\right\},$$

(1)

where $f_i(w)={\mathbb{E}}_{{\mathcal{D}}_i\sim P_i}\left[{\tilde{f}}_i(w;{\mathcal{D}}_i)\right]$ represents the expected loss over client i’s data distribution, and ${\tilde{f}}_i(w;{\mathcal{D}}_i)$ is the loss for a specific data sample ${\mathcal{D}}_i$. A widely adopted approach to solve this is FedAvg [1], where at each round t: (1) The server broadcasts the global model $w_t$ to a subset of clients; (2) Each selected client i performs local updates (e.g., via stochastic gradient descent) on $w_t$ using ${\mathcal{D}}_i$ to obtain a local model $w_{i,t+1}$; and (3) The server aggregates these updates as $w_{t+1}={\sum }_{i\in {\mathcal{S}}_t}{\displaystyle \frac{|{\mathcal{D}}_i|}{{\sum }_{j\in {\mathcal{S}}_t}\left|{\mathcal{D}}_j\right|}}{w}_{i,t+1}$, where ${\mathcal{S}}_t$ is the sampled client subset. While effective under IID conditions, FedAvg struggles with non-IID data, as local objectives diverge, leading to client drift and poor generalization [8].

2.2. Knowledge Distillation

Knowledge Distillation (KD), introduced by Hinton et al. [20], is a technique to transfer knowledge from a pre-trained teacher model to a student model. In its original form, the student is trained to minimize a weighted combination of two loss terms: the cross-entropy (CE) loss with hard labels and the Kullback–Leibler (KL) divergence between the teacher’s and student’s softened predictions (logits). For a student model with parameters $\theta$ and a teacher model with parameters w, the KD loss is:

$${\mathcal{L}}_{\mathrm{KD}}(\theta )=(1-\gamma )·{\mathcal{L}}_{\mathrm{CE}}(\theta ,y)+\gamma ·T^2·\mathrm{KL}\left({\displaystyle \frac{p_w}{T}},{\displaystyle \frac{p_{\theta }}{T}}\right),$$

(2)

where ${\mathcal{L}}_{\mathrm{CE}}$ is the CE loss with true labels y, $p_w$ and $p_{\theta }$ are the teacher’s and student’s output probabilities, T is a temperature parameter softening the logits, and $\gamma \in [0,1]$ balances the two terms. The factor $T^2$ adjusts the KL divergence magnitude due to temperature scaling. KD enables the student to inherit the teacher’s generalization capabilities, making it a promising tool for regularizing local models in FL under heterogeneity.

2.3. Proposed Method

We propose a novel FL algorithm, termed pFedKD-WCL (Personalized Federated Knowledge Distillation with Weighted Combination Loss), to balance global convergence and local personalization in non-IID settings. Our method decouples global and local optimization, using the global model as a teacher to guide local updates via KD, while refining the global model with insights from local data.

2.3.1. Problem Formulation

We formulate pFedKD-WCL as a bi-level optimization problem. At the client level, each client i optimizes a personalized model ${\theta }_i\in {\mathbb{R}}^d$ using a KD-based loss with the global model w as the teacher:

$$\underset{{\theta }_i\in {\mathbb{R}}^d}{min}\left\{F_i({\theta }_i,w):=(1-\gamma )·f_i({\theta }_i)+\gamma ·\mathrm{KL}(p_w,p_{{\theta }_i})\right\},$$

(3)

where $f_i({\theta }_i)={\mathbb{E}}_{{\mathcal{D}}_i\sim P_i}\left[{\tilde{f}}_i({\theta }_i;{\mathcal{D}}_i)\right]$ is the local CE loss, and $\mathrm{KL}(p_w,p_{{\theta }_i})$ measures the divergence between the global model’s predictions $p_w$ and the local model’s predictions $p_{{\theta }_i}$ on ${\mathcal{D}}_i$, with standard softmax outputs ($T=1$). The parameter $\gamma \in [0,1]$ balances the two loss terms, with a low $\gamma$ allowing each client’s model to stick with its unique data patterns, while a high $\gamma$ prioritizes alignment with the global teacher’s predictions via KL divergence, enabling flexible personalization in non-IID settings.

At the server level, the global model w is optimized to minimize the average divergence from local models:

$$\underset{w\in {\mathbb{R}}^d}{min}\left\{F(w):={\displaystyle \frac{1}{N}}\sum _{i=1}^N\mathrm{KL}(p_w,p_{{\widehat{\theta }}_i(w)})\right\},$$

(4)

where ${\widehat{\theta }}_i(w)=arg{min}_{{\theta }_i}{F}_i({\theta }_i,w)$ is the optimal local model for client i given w. This formulation encourages the global model to align with local predictions, enhancing robustness to heterogeneity. KL divergence is preferred over MSE in knowledge distillation loss because it aligns probability distributions, effectively capturing the teacher’s class relationships. Unlike MSE, which compares raw logits and may over-penalize differences irrelevant to probabilities, KL preserves the distributional structure, ensuring the student mimics the teacher’s predictive behavior. In federated learning, KL’s focus on distributions enhances robustness to non-IID data, reducing client drift.

2.3.2. Algorithm Description

Our algorithm operates in rounds, as outlined in Algorithm 1. We assume client datasets are non-independent and identically distributed (non-IID), local datasets ${\mathcal{D}}_i$ are drawn from a distinct distribution $P_i$, and that clients do not share raw data to preserve privacy. A central server coordinates the federated learning process, broadcasting the global model and aggregating updates from a subset of clients in each round. Clients perform local training on private datasets and communicate model parameters or gradients with the server. We additionally assume that the client can communicate with the global server with minimal lag, so that global updates may be computed efficiently. The client-level time complexity is $\mathcal{O}(R·m_c)$, where $m_c$ is the computation cost of the local loss function. At the global server level, the complexity is $\mathcal{O}(T·m_g)$, where $m_g$ is the computational cost of the server weight optimization. Therefore, our algorithm is linear in the number of global and local iteration steps. Unlike traditional knowledge distillation, where the teacher model is pre-trained on a dedicated dataset, our approach requires no server-side training data. Instead, the global model w, which serves as the teacher, is optimized solely through aggregated gradients of the KL divergence computed on clients’ local datasets ${\mathcal{D}}_i$. This design aligns with conventional federated learning principles, such as FedAvg, ensuring privacy by keeping all training data decentralized while leveraging KD to enhance personalization in non-IID settings. The parameter $\gamma$ controls the trade-off between local fit and global alignment, with $\gamma =0$ reducing to standalone local training and $\gamma =1$ prioritizing global consistency. Compared to pFedMe, which uses an ${\ell }_2$-norm penalty, our KD-based approach captures richer predictive relationships, potentially improving generalization on non-IID data.

Algorithm 1 pFedKD-WCL Algorithm

1: Input: T (rounds), R (local steps), S (clients per round), $\eta$ (learning rate), $\gamma$ (KD weight), $w_0$ (initial global model)   2: for $t=0$ to $T-1$ do   3:     Server samples subset ${\mathcal{S}}_t$ of S clients   4:     Server broadcasts $w_t$ to all clients in ${\mathcal{S}}_t$   5:     for each client in ${\mathcal{S}}_t$ in parallel do   6:        for $r=0$ to $R-1$ do   7:             Sample mini-batch ${\mathcal{D}}_{i,r}^t$ from ${\mathcal{D}}_i$   8:             Compute loss $F_i({\theta }_{i,r}^t,w_t)$ using Equation (3)   9:             Update ${\theta }_{i,r+1}^t={\theta }_{i,r}^t-\eta {\nabla }_{{\theta }_i}{F}_i({\theta }_{i,r}^t,w_t)$ 10:        end for 11:        Set ${\widehat{\theta }}_i^t={\theta }_{i,R}^t$ 12:   end for 13:   Clients in ${\mathcal{S}}_t$ send ${\widehat{\theta }}_i^t$ to server 14:   Server updates $w_{t+1}=w_t-\eta {\displaystyle \frac{1}{S}}{\sum }_{i\in {\mathcal{S}}_t}{\nabla }_w\mathrm{KL}(p_{w_t},p_{{\widehat{\theta }}_i^t})$ with Equation (4) 15: end for 16: Output: Global model $w_T$, personalized models $\left\{{\widehat{\theta }}_i^T\right\}$

3. Experiments and Results

To evaluate the performance of our proposed method, we conducted a series of experiments comparing it against four established federated learning algorithms: FedAvg [1], FedProx [4], PerFedAvg [14], pFedMe [13] and FedGKD [28]. These experiments were performed on two datasets—MNIST and a synthetic dataset—both configured with non-IID data distributions to simulate realistic federated learning scenarios with heterogeneous client data. For instance, our general settings are adaptable to scenarios like smart mobile devices, where user-specific app data varies; edge nodes, such as IoT devices with diverse sensor inputs; or data silos, like hospitals with distinct patient distributions, all exhibiting non-IID characteristics. In the following subsections, we describe the experimental settings, including the datasets, their non-IID partitioning, and the model architectures used, followed by a detailed discussion of the hyperparameter configurations for all methods.

3.1. Experimental Setting

The experiments utilize two datasets: MNIST and a synthetic dataset. The MNIST dataset, introduced by LeCun et al. [29], comprises 70,000 grayscale images of handwritten digits (0–9), each $28\times 28$ pixels, with 60,000 training and 10,000 testing samples. Following the approach suggested by Hsu et al. [30], we generate non-IID settings across clients using a Dirichlet distribution with parameter $\alpha$, where a smaller $\alpha$ increases data heterogeneity. We evaluate two non-IID settings, each with 20 and 50 clients. The first setting employs a Dirichlet distribution with $\alpha =0.05$. The second setting uses $\alpha =0.5$ and selects the top two classes with the highest proportions, ensuring each client holds data for exactly two digits. Each client is randomly assigned a sample size ranging from 1665 to 3834. The synthetic dataset is generated to test generalization under controlled heterogeneity, following the methodology of Li et al. [4]. It consists of 100 clients, for each client i, we create data ${\mathcal{D}}_i=(X_i,Y_i)$ using the model $y=argmax(\mathrm{softmax}(Wx+b))$, with features $x\in {\mathbb{R}}^{60}$, weights $W\in {\mathbb{R}}^{10\times 60}$, and biases $b\in {\mathbb{R}}^{10}$. We draw $W_i$ and $b_i$ from $\mathcal{N}(u_i,1)$, where $u_i\sim \mathcal{N}(0,\alpha )$, and generate features $x_i\sim \mathcal{N}(v_i,\mathsf{\Sigma })$, with a diagonal covariance matrix $\mathsf{\Sigma }$ satisfying ${\mathsf{\Sigma }}_{j,j}=j^{-1.2}$. The mean vector $v_i$ has elements sampled from $\mathcal{N}(B_i,1)$, with $B_i\sim \mathcal{N}(0,\beta )$. Thus, $\alpha$ regulates the variation among local models, while $\beta$ governs the diversity of data distributions across clients. Here we set $\alpha =\beta =0.5$. The dataset of each client is partitioned into training and test sets, with 75% of the samples allocated to training and 25% to testing, using random permutation to ensure an unbiased split, and the data are converted to PyTorch tensors for compatibility with deep learning frameworks.

Two models are employed to assess performance across varying complexities. The multinomial logistic regression (MLR) model is a simple linear classifier with an input layer of 784 units (for MNIST or 60 units for synthetic input) and an output layer of 10 classes, followed by a log-softmax activation to produce log-probabilities. The multilayer perceptron (MLP) is a neural network with an input layer of 784 units (for MNIST or 60 units for synthetic input), a hidden layer of 128 units with ReLU activation, and an output layer of 10 units with log-softmax activation. The MLP’s additional capacity allows it to capture more complex patterns, while the MLR provides a lightweight baseline. Both models are trained to minimize the negative log-likelihood (NLL) loss, consistent with their log-softmax outputs and standard classification objectives in federated learning.

We perform all experiments in this paper using a server node with four NVIDIA V100 GPUs with 16GB memory, four Intel(R) Xeon(R) CPUs with 12 cores @ 2.40GHz), and 360 GB memory. All experiments are performed with Python 3.12.7 and PyTorch 2.6.0 with CUDA 12.6.

3.2. Experimental Hyperparameter Settings

To ensure a fair and comprehensive comparison, we carefully configure hyperparameters for each method while maintaining a consistent experimental framework. All methods share a baseline setting: 20 or 50 clients participate in the training (100 in synthetic data), $25\%$ of which are selected per round ($10\%$ in synthetic data), balancing communication efficiency and model updates. Local training uses a batch size of 20 and runs for 20 local epochs per round, with a learning rate of 0.01 applied via stochastic gradient descent (SGD) without momentum. For FedAvg, these common hyperparameters suffice, as it relies solely on local SGD and global averaging without additional tuning parameters. FedProx introduces a proximal term weight ($\mu$) set to 0.01, which controls the regularization strength towards the global model. PerFedAvg incorporates a beta parameter ($\beta$) set to 0.002. For pFedMe, the regularization parameter $\lambda$ is configured as follows: $\lambda =5$ for MLR model and $\lambda =15$ for MLP model on MNIST data, whereas $\lambda =30$ is utilized for synthetic data. For FedGKD, we set the temperature in knowledge distillation to 1, the penalty weight on Kullback-Leibler divergence to 0.001, and the buffer length for historical models to 5. Our pFedKD method uses a knowledge distillation weight $\gamma =0.1$ in Equation (3), weighting the KL-divergence loss between local and global model predictions. All models are initialized randomly, and client data is pre-partitioned to ensure identical non-IID distributions across methods. Evaluation metrics differ by algorithm design: FedAvg and FedProx report global model accuracy, while PerFedAvg, pFedMe, FedGKD and pFedKD-WCL provide personalized metrics after local adaptation, reflecting their focus on client-specific performance.

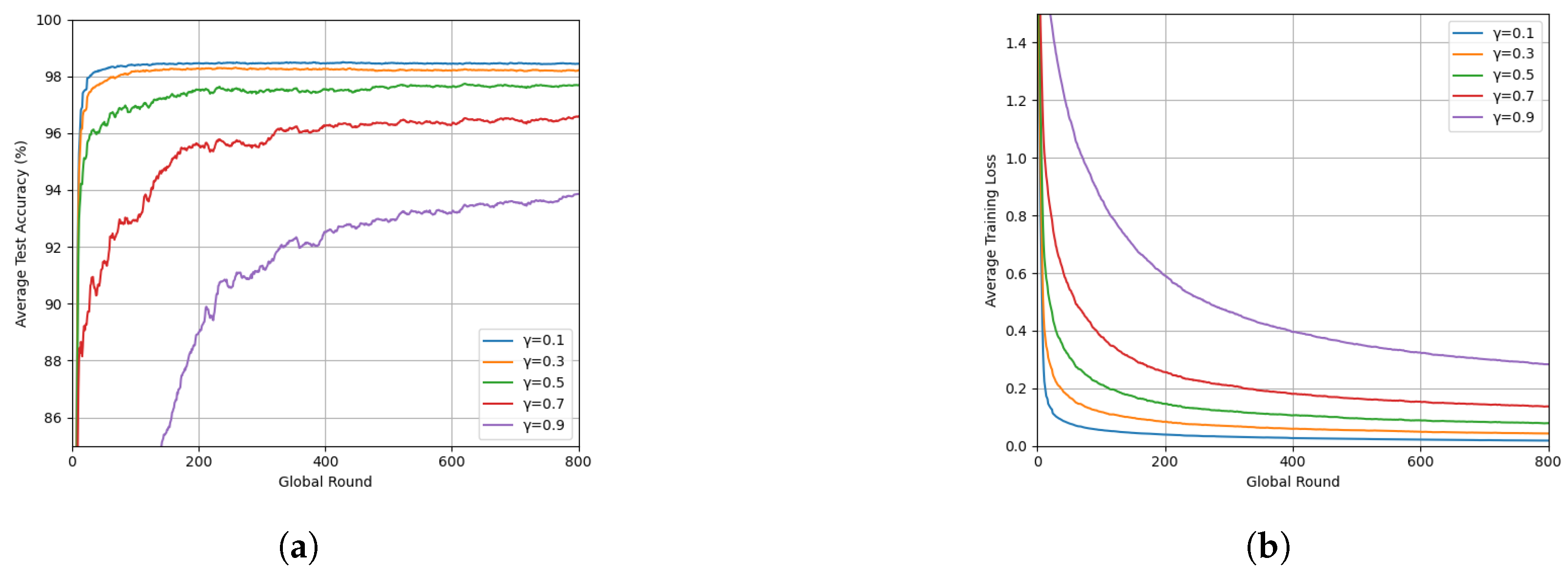
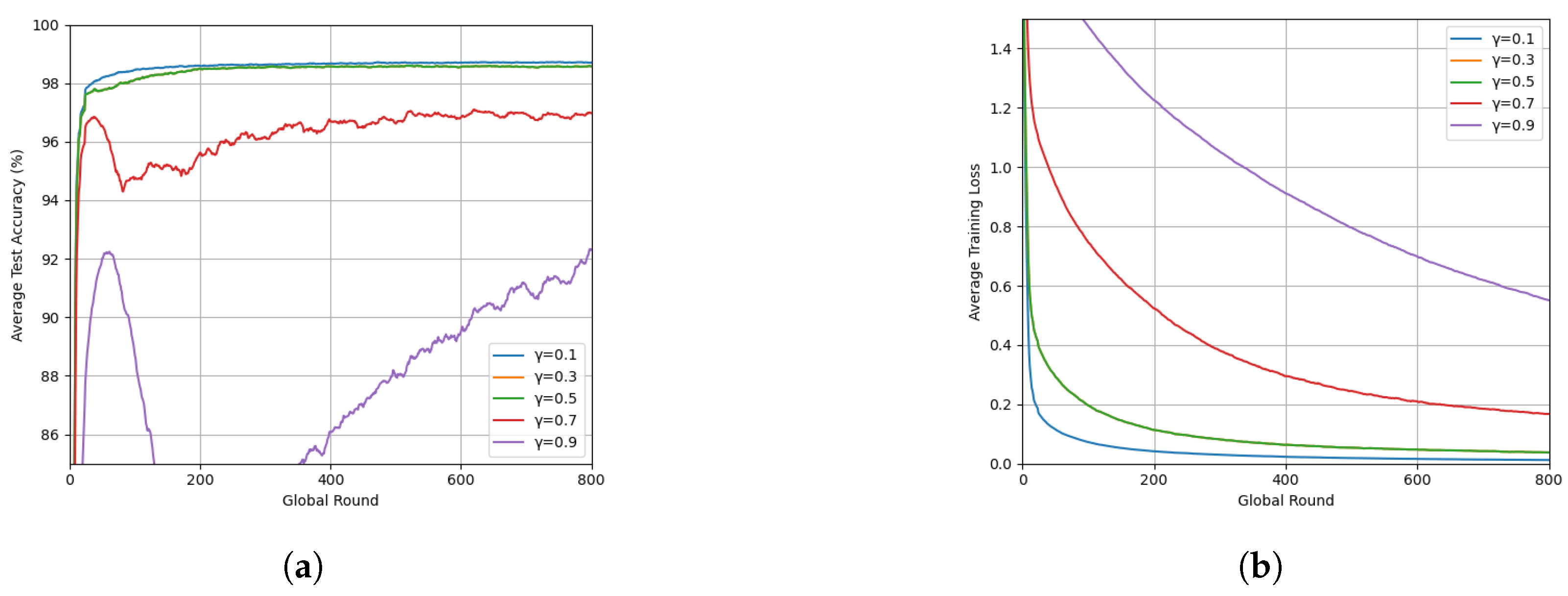
3.3. Effect of the Hyperparameter

To evaluate the effect of the KD weight parameter $\gamma$ in our algorithm, we conducted experiments on the MNIST data with top two classes per client for two models: a MLR model and a MLP model with $\gamma =0.1,0.3,0.5,0.7,0.9$. For the MLR model, Figure 1a shows that average test accuracy stabilizes above 98% within 200 rounds, with $\gamma =0.1$ and $\gamma =0.3$, while $\gamma =0.9$ fluctuates and plateaus around 94%. The corresponding training loss (Figure 1b) indicates that $\gamma =0.1$ and $\gamma =0.3$ converge to below 0.1 after 200 rounds, whereas $\gamma =0.9$ retains a higher loss of approximately 0.28. In contrast, the MLP model exhibits more pronounced variability (Figure 2): accuracy initially surges but drops sharply for $\gamma =0.9$ (below 90% after 100 rounds) before gradually recovering to around 92% by 800 rounds, while $\gamma =0.1$ and $\gamma =0.3$ maintain around 98% with slight fluctuations. The MLP’s training loss decreases steadily for all $\gamma$ values, but $\gamma =0.9$ remains elevated (above 0.5), compared to lower losses (below 0.2) for $\gamma =0.1$ and $\gamma =0.3$. This behavior indicates that with high $\gamma$, the MLP may over-adjust its weights to mimic the global model, ignoring local data patterns, which exacerbates the accuracy drop compared to the simpler MLR model. The MLP’s deeper architecture makes it more sensitive to the choice of $\gamma$, highlighting the need for careful tuning in non-IID settings. The results suggest that for deeper models like MLPs in non-IID settings, a lower $\gamma$ (e.g., 0.1 or 0.3) strikes a better balance between local adaptation and global regularization, avoiding the instability seen with high $\gamma$. These findings underscore the importance of model-specific tuning to mitigate instability in complex architectures under heterogeneous data distributions. Specifically, $\gamma$’s role in weighting the KL divergence ensures local models benefit from global knowledge without overfitting to the teacher, as evidenced by stable 98% accuracy for $\gamma =0.1$.

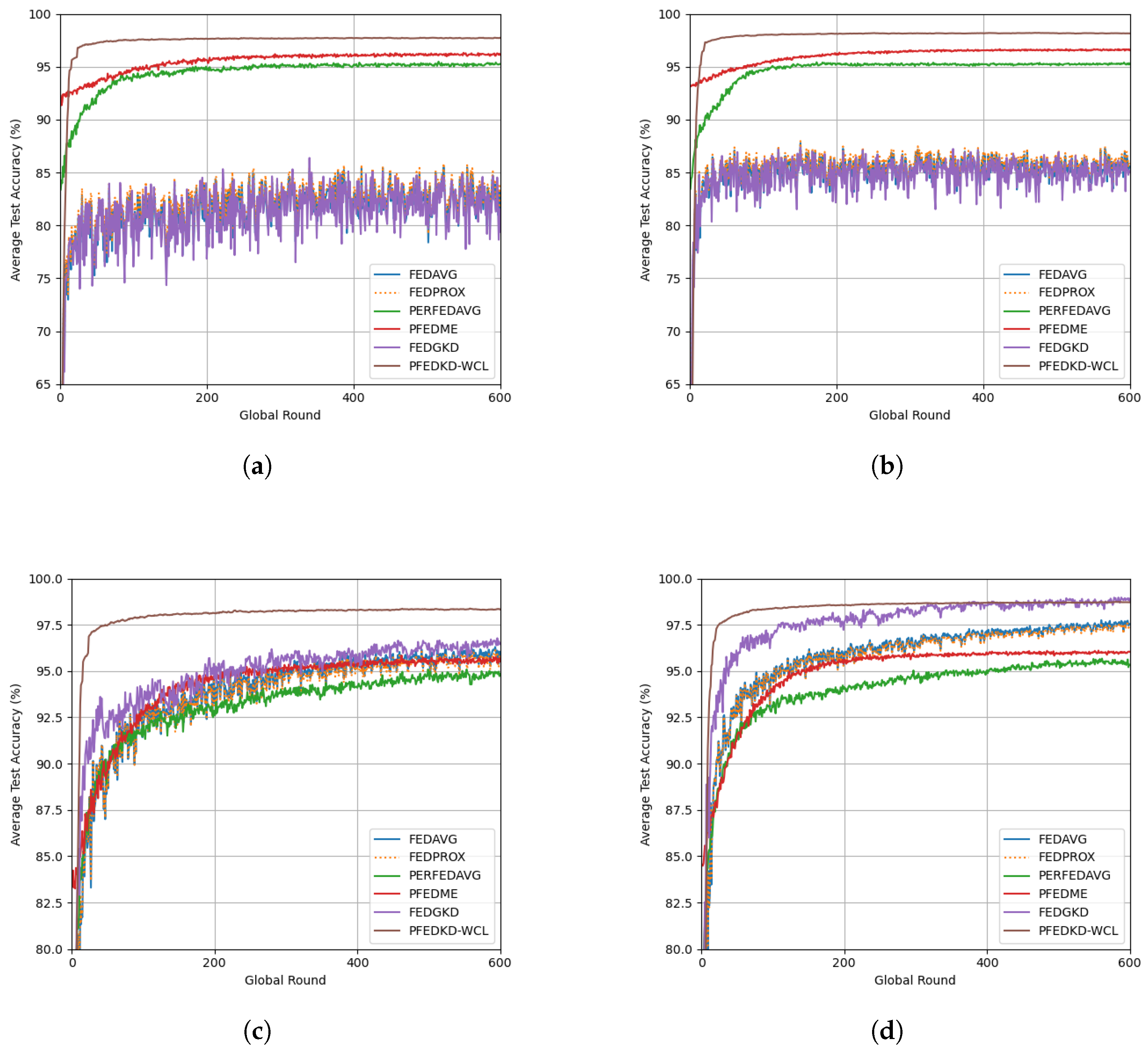
3.4. Performance Comparison Results

Figure 3 illustrate the performance comparison of SOTA FL algorithms on the MNIST dataset, generated using a Dirichlet distribution with $\alpha =0.05$, for MLR and MLP models with 20 and 50 clients.

Table 1. Performance comparisons of the average test accuracy on MNIST with different levels of heterogeneity and numbers of clients.

Algorithm	Model	$\mathit{\alpha }=0.5$ with Top-2 Classes		$\mathit{\alpha }=0.05$
		N = 20	N = 50	N = 20	N = 50
FedAvg	MLR	$89.45\pm 0.10$	$78.94\pm 0.40$	$81.05\pm 0.30$	$85.51\pm 0.06$
FedProx	MLR	$89.57\pm 0.10$	$79.94\pm 0.40$	$81.60\pm 0.30$	$85.90\pm 0.07$
PerFedAvg	MLR	$96.62\pm 0.01$	$95.30\pm 0.01$	$95.25\pm 0.02$	$95.23\pm 0.01$
pFedMe	MLR	$96.25\pm 0.01$	$94.72\pm 0.01$	$96.13\pm 0.01$	$96.56\pm 0.01$
FedGKD	MLR	$83.85\pm 0.30$	$78.21\pm 0.40$	$79.39\pm 0.30$	$85.06\pm 0.07$
pFedKD-WCL	MLR	$\mathbf{98.45}\pm \mathbf{0.01}$	$\mathbf{97.97}\pm \mathbf{0.01}$	$\mathbf{97.72}\pm \mathbf{0.01}$	$\mathbf{98.14}\pm \mathbf{0.01}$
FedAvg	MLP	$91.11\pm 0.20$	$95.57\pm 0.06$	$95.70\pm 0.04$	$97.54\pm 0.02$
FedProx	MLP	$89.82\pm 0.20$	$95.44\pm 0.06$	$95.46\pm 0.05$	$97.41\pm 0.02$
PerFedAvg	MLP	$96.94\pm 0.01$	$94.85\pm 0.02$	$94.84\pm 0.02$	$95.34\pm 0.01$
pFedMe	MLP	$96.75\pm 0.01$	$95.37\pm 0.01$	$95.52\pm 0.02$	$96.04\pm 0.01$
FedGKD	MLP	$97.40\pm 0.05$	$98.24\pm 0.04$	$96.46\pm 0.05$	$\mathbf{98.79}\pm \mathbf{0.01}$
pFedKD-WCL	MLP	$\mathbf{98.70}\pm \mathbf{0.01}$	$\mathbf{98.50}\pm \mathbf{0.01}$	$\mathbf{98.33}\pm \mathbf{0.01}$	$98.71\pm 0.01$

summarizes the average test accuracy after 600 training rounds across two non-IID settings of the MNIST dataset with fine-tuned hyperparameters. In terms of prediction accuracy in MNIST dataset for the MLR model, under high heterogeneity ($\alpha =0.05$), pFedKD-WCL outperforms all methods. For $N=20$, it improves upon FedAvg, FedProx, PerFedAvg, pFedMe, and FedGKD by $20.6\%$, $19.8\%$, $2.6\%$, $1.7\%$, and $23.1\%$, respectively. For $N=50$, the gains remain substantial: $14.8\%$, $14.3\%$, $3.1\%$, $1.6\%$, and $15.4\%$. Under more extreme heterogeneity ($\alpha =0.5$ with top two classes), pFedKD-WCL yields improvements of $10.1\%$, $9.9\%$, $1.9\%$, $2.3\%$ and $17.4\%$ over FedAvg, FedProx, PerFedAvg, pFedMe, and FedGKD, respectively, when $N=20$. In the most challenging setting $N=50$, the gains are even more pronounced: $24.1\%$, $22.6\%$, $2.8\%$, $3.4\%$, and $25.3\%$ over the same baselines, indicating that pFedKD-WCL scales well with larger numbers of clients. For the MLP model, with $\alpha =0.05$ and $N=20$, pFedKD-WCL maintains performance gains of $2.8\%$, $3.0\%$, $3.7\%$, $2.9\%$, and $1.9\%$. Under $\alpha =0.05$ and $N=50$, pFedKD-WCL outperforms FedAvg, FedProx, PerFedAvg, and pFedMe by $1.2\%$, $1.3\%$, $3.5\%$, and $2.8\%$, but is slightly outperformed by FedGKD by $0.1\%$. Under $\alpha =0.5$ and $N=20$, pFedKD-WCL achieves improvements of $8.3\%$, $9.9\%$, $1.8\%$, $2.0\%$, and $1.3\%$ over the five baselines. With $N=50$, the margins narrow but remain positive: $3.1\%$, $3.2\%$, $3.9\%$, $3.3\%$, and $0.3\%$.

Table 2. Performance comparisons of the average test accuracy on synthetic data.

Algorithm	Model	Accuracy
FedAvg	MLR	$67.76\pm 0.09$
FedProx	MLR	$69.11\pm 0.02$
PerFedAvg	MLR	$81.86\pm 0.03$
pFedMe	MLR	$83.84\pm 0.02$
FedGKD	MLR	$30.14\pm 0.30$
pFedKD-WCL	MLR	$\mathbf{89.48}\pm \mathbf{0.01}$
FedAvg	MLP	$72.22\pm 0.09$
FedProx	MLP	$73.22\pm 0.09$
PerFedAvg	MLP	$76.51\pm 0.10$
pFedMe	MLP	$79.71\pm 0.10$
FedGKD	MLP	$22.78\pm 0.01$
pFedKD-WCL	MLP	$\mathbf{89.12}\pm \mathbf{0.02}$

depicts the performance of algorithms on the synthetic dataset using MLR and MLP models, respectively. With the MLR model, pFedKD-WCL outperforms FedAvg, FedProx, PerFedAvg, and pFedMe by 32.0%, 30.0%, 7.6%, and 6.7%, respectively. Similarly, with the MLP model, the improvements are 23.4%, 21.7%, 12.6%, and 11.6% compared to the same baseline methods. However, FedGKD did not perform well with the synthetic data. The two-class per client setting exacerbates client drift, and FedGKD’s historical ensemble fails to provide effective guidance.

4. Conclusions

This study has demonstrated the effectiveness of our proposed FedKD-WCL algorithm in addressing the challenges posed by statistical heterogeneity in FL, particularly in non-IID data settings. Experimental results show faster convergence and higher accuracy compared to state-of-the-art methods, particularly in high-heterogeneity settings. By integrating knowledge distillation with a bi-level optimization framework, FedKD-WCL successfully balances global model convergence and local personalization, outperforming established baseline methods across diverse datasets. The experimental results underscore the advantage of using the global model as a teacher to guide local training, with deeper models like multilayer perceptrons showing sensitivity to the KD weight parameter, highlighting the importance of model-specific tuning in non-IID environments. The algorithm performs well with both simple (MLR) and complex (MLP) models, demonstrating adaptability to varying model capacities. In addition, unlike methods like FedMD or FedDF, which rely on proxy or public datasets, pFedKD-WCL operates solely on clients’ datasets, enhancing privacy and applicability in resource-constrained or privacy-sensitive scenarios. While these findings affirm the robustness of FedKD-WCL, its reliance on centralized coordination and potential computational demands present areas for improvement, especially in large-scale deployments. Although pFedKD-WCL performs well across MLR and MLP models, deeper architectures (e.g., MLPs) are more sensitive to $\gamma$, exhibiting sharper accuracy drops with suboptimal settings. Future research could explore adaptive tuning strategies for the KD weight, thereby enhancing the algorithm’s applicability to real-world FL scenarios.